Liquid drop impact on granular beds: the influence of drop inertia and grain size

Abstract

This paper explores crater formation resulting from the impact of a liquid drop on a densely packed granular bed composed of lightweight polystyrene beads. Several regimes based on the drop impact velocity v and diameter D, and the grain diameter d_g are identified. These regimes are discussed in terms of several dimensionless numbers, including a Froude number Fr, which compares the droplet's kinetic energy to its potential energy at impact, the Weber number We, which compares the inertial to capillary forces, and the size ratio d_g/D. At low We, Fr, and d_g/D, the dimensionless crater diameter D_max/D follows a power-law scaling as We^1/4, consistent with previous studies on droplet impacts on granular surfaces, where the crater size reflects the maximum droplet spreading observed on a solid surface. This situation is thus analysed using a so-called signature approach. In this situation, the crater size is also shown to quantitatively depend on d_g/D. When We exceeds a critical value We_c(d_g/D), the scaling deviates from We^1/4 and the crater size depends mainly on d_g/D. This transition is discussed in connection with the onset of droplet splashing. For larger d_g/D, a different power-law scaling emerges with an exponent smaller than 1/4, regardless of the value of Fr or We, and the splash transition no longer occurs under these conditions. This is consistent with other studies, highlighting the significant amount of energy transfer in crater formation, therefore referred to as the energetic approach. Overall, the final crater size is found to depend strongly on d_g/D among the droplet impact characteristics. To unify part of these observations, the role of local dissipation due to grain contact friction during crater formation is incorporated. This leads to the definition of a new dimensionless number [scr F, script letter F], which combines the effects of grain-to-drop size ratio d_g/D and droplet inertia (via Fr). This parameter enables the collapse of D_max/D data onto a single curve for the range of parameters investigated in this study.

---

1. Introduction

The formation of craters on the surface of a substrate due to the impact of a falling object has been extensively studied in the literature as a fundamental process relevant to various applications, from erosion caused by rainfall to meteorite impacts. Depending on the situation, the nature of both the falling object and the substrate can vary greatly, ranging from liquids to non-deformable solids. In the present study, we focus on the case of a liquid drop impacting a granular bed, which can be seen as a canonical configuration to mimic erosion caused by rainfall. This configuration has also been used in the literature to mimic fundamental processes in meteorite impacts, as the impactor can be subjected to melting and strong deformations upon impact.¹

The impact of a droplet on a solid surface has been extensively studied for over a century,² and the well-documented characterization of its spreading phase on the substrate makes it a valuable reference case for analyzing and understanding the fundamental aspects of crater formation—particularly in light of the analogies observed in experiments and discussed later in this work. Its dynamics strongly depend on the inertia prior to impact as well as on the surface properties (e.g., roughness, wettability, elasticity).^3,4 Accordingly, different regimes of drop impact can be observed and are divided into two main regimes for the purpose of the present study. In the first, mostly associated with low impact velocity, and referred to as the elastic regime, the volume of the initial drop remains conserved during the entire dynamics. In the second regime, mostly associated with high impact velocity, and known as the splash, atomization of the initial drop occurs, leading to highly irreversible dynamics.

In the elastic regime, the temporal evolution of a water droplet impacting a solid surface can be divided in several phases: including spreading phases, followed by a relaxation and an equilibrium phase.⁵ During a short initial kinematic phase, the dynamics is dominated by the inertia of the drop and is mostly independent of the surface and fluid properties.^6–8 This phase is followed by a second phase during which the droplet keeps spreading along the surface until reaching its maximum extension. In this phase, the dynamics is controlled by a balance between inertia, gravity, capillarity and viscosity. To characterize this balance, the dimensionless Reynolds, Froude and Weber numbers are usually introduced as

where ρ_f, η and σ are the density, the dynamic viscosity and the surface tension of the liquid droplet, respectively, D is its diameter, v is its final vertical velocity prior impact and g is the gravitational acceleration. Different laws of drop extension have been proposed in the literature depending on the relative values of these dimensionless numbers, specifically Re and We. For the case of water droplet impact, considered in the present study, Re is usually high. At high Re, the dynamics is governed by capillary forces if We is small enough. Even though several scaling laws linking the maximum droplet extension D^l_max with We can be found in these limits, the relationship D^l_max/D ∝ We^1/4 has often been observed.^9–11 Moreover, the latter scaling can be simply obtained as a force balance between inertia and capillary forces.⁹ As We increases, inertia becomes dominant, leading to marked differences in behavior.

In the splash regime, the impacting droplet breaks apart into several secondary droplets. This regime is usually observed at higher inertia, when a crown emerges at the front of the spreading droplet and the spreading drop no longer wets the substrate. Secondary droplets then form due to the tearing of the fluid film at the crown fingers, which result from the Rayleigh–Taylor instability between the air and the fluid.¹² A splash criterion has been discussed in the literature to quantify the transition from the elastic regime to the splash regime.¹³ This criterion is usually expressed in the form We_s = K_s²Re^α, with We_s a critical Weber number above which splash is observed. Unfortunately, even if α = −1/2 is often used in the literature, this splash criterion appears to be still controversial in the literature.^14,15 Rationalization of these different results remains difficult, and probably strongly depends on the substrate properties.^6,16,17 Moreover, in the limit of small We^1/2/Re, often observed for water drop impact, it is suggested that the splash criterion becomes independent of Re. In the latter case, values of We_s would mostly depend on the substrate properties, similarly to K_s in a more general frame. Values reported in the literature are around We_s ≈ 100–1000,¹⁶ with We_s decreasing with increasing substrate roughness lengthscale.

When the droplet impacts a granular substrate, it generates a crater in the medium. Two distinct processes are then involved: (i) the dynamics of the drop impacting and spreading on, or mixing with, the substrate, and (ii) the deformation of the substrate resulting in the formation of a crater. Regarding (i), a strong analogy with the impact dynamics of a drop on a solid surface, discussed previously, can be done as long as the drop is mostly spread on the granular bed.^18,19 The latter is often observed for a compact granular bed and low impact velocity. In particular, the maximal drop extension can highlight strong correlations with the final crater dimension.²⁰ On the other hand, for loose packing or high impact velocity, this analogy does not seem to hold anymore.^1,21 Moreover, the processes involved in (ii) also depends on the drop dynamics and can be expected, in some situations, to share similarities with the case of a solid object impacting a granular medium.²²

Two different approaches have been developed according to these observations. For a compact granular medium, the crater morphology can be considered as the signature of the droplet spreading. This assumes that the granular bed deformation remains localized at the surface, preventing deep cratering and maintaining horizontal spreading. In this context, referred to here as the signature approach, the maximum spreading drop D^l_max is assumed to be correlated to the final crater diameter D_max.²⁰ D_max is then usually linked to We.^19,23 Another approach, referred to here as the energetic approach, considers the drop's kinetic energy, which is partially transmitted to the granular medium, resulting in its deformation. The final crater diameter D_max is then linked to the kinetic energy E_k. The latter approach is more often used to characterise crater formation for an initially loose granular bed and/or high inertial drop impact. However, distinction or overlap between both approaches remains unclear.

For the signature approach, Katsuragi,¹⁸ Delon et al.,¹⁹ Nefzaoui and Skurtys,²⁰ and Katsuragi²³ have shown the reliability of this analogy, highlighting a scaling law D_max/D ∼ We^1/4, for low enough We, typically We < 600. Note that smaller law dependence, 1/5 instead of 1/4, have also been reported in experimental studies.^20,24,25 Otherwise, for We values exceeding 600, Katsuragi¹⁸ observed a departure from the previous We^1/4 trend, and a saturation of the crater size D^c_max, which remains constant with We. It should be mentioned that for We > 600, the drop is probably no longer in its elastic regime considering the range of transition We_s reported in the case of impact over a solid surface. Then other processes are expected to control the dynamics at this stage. The latter regime suggests that the crater is not necessarily a simple signature of the droplet spreading, but that more complex inertial effect and momentum or energy transfer must be accounted for.

For the energetic approach, several studies focused on the role of kinetic energy E_k independently of capillary forces to provide a scaling for the crater size.^1,26,27 In particular, Zhao et al.¹ found a law of the form D_max ∝ E_k^1/6 to unify their experimental results. Moreover, by analogy with craters generated by the impact of a solid intruder or a hydrogel drop, de Jong et al.,²⁷ and Ye and Van Der Meer²⁸ showed that D_max/D scales with E_k/E_g, E_g ∝ ρ_gϕgD⁴ being the potential energy of a cavity in the sand of typical size D and ϕ the volume fraction of the granular bed. These studies suggest that D_max/D ∝ (E_k/E_g)^γ with γ ∈ [1/6, 1/4], even though a correction to E_k/E_g is also required to account for significant variation of the initial volume fraction ϕ.^21,26 Although the approach is different from Delon et al.¹⁹ and Katsuragi,¹⁸ the obtained scaling laws show some similarities. In particular, the link between D_max and v, which is one of the main parameters varied in experiments, can be written from the different scalings as: D_max ∝ v^1/2,²³ D_max ∝ v^1/3 (ref. 1) or D_max ∝ v^2γ,^21,26 i.e. with the power law exponent between 1/3 and 1/2. Yet, these differences between the scaling laws are clear, suggesting different mechanisms from case to case.

To summarize, it remains challenging to rationalize the results of craters induced by a liquid droplet impact using a single dimensionless number and to unify them with a given scaling law. Moreover, the link between the splash transition and crater extension remains poorly understood. Furthermore, the dependence of crater size on the grain diameter d_g has not been thoroughly investigated in the literature. The aim of the present paper is thus to explore both the role of drop inertia and grain size in the case of a densely packed granular substrate, in order to characterize the elastic-to-splash transition and to discuss their influence on the crater regime—whether interpreted through the signature approach or the energetic approach, or more likely through the scaling laws obtained for the final crater size. In order to avoid confusion with the above mentioned approaches, we first consider the Froude Fr as the relevant dimensionless number to define the dimensionless impact velocity.

2. Experimental methodology

2.1. Setup

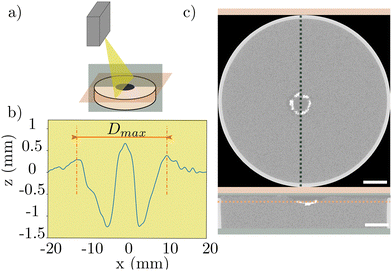
A sketch of the experimental setup used along the study is shown in Fig. 1. The water droplet generation system consists of a needle-syringe connected to a volume controlled syringe pump, allowing reproducible droplets. The droplet is characterised by its diameter D only, as its properties remain constant for all experiments which have been carried out at fixed temperature T = 19 ± 1 °C (density ρ_f = 1000 kg m⁻³, surface tension σ = 72 × 10⁻³ N m⁻¹ and viscosity η_f = 10⁻³ Pa s). In the present study, the needle diameter and the input volume of water are kept constant, resulting in droplets of uniform diameter for each experimental campaign. In the first campaign, D = 4.3 ± 0.2 mm, and in the second campaign, D = 4.9 ± 0.2 mm, corresponding respectively to the laser acquisition and the camera acquisition campaigns (see Section 2.2).

Fig. 1 Descriptive schema of the experiment. The graph shows the evolution of velocity as a function of drop height: in green are the measurement points, in blue a free-fall model and in orange a constant-drag model with C_d = 0.6.

Once the droplet is generated, it falls under gravity from a height h before impacting a densely packed granular bed composed of a monodisperse granular material, contained in a Petri dish of 2.5 cm depth. h is measured between the end of the needle and the top of the granular bed (see the sketch in Fig. 1). To vary the impact velocity v of the droplet, h is varied in the range 5–200 cm. Note that, under identical initial conditions, droplet detachment from the needle may lead to an oscillation of its shape. However, the oscillation amplitude is observed to decrease with distance from the needle, and does not significantly influence the results. Yet, this oscillatory effect may influence the impact velocity of the droplet. Accordingly, the evolution of v with h in the experiments is first characterised and fitted from a simple model based on Newton's law. Green dots in the inset of Fig. 1 correspond to the measured velocity. It is found to follow a simple solution accounting for droplet inertia (acceleration term), weight and a quasi-steady inertial drag model of constant drag coefficient. Data are fitted with this model using the drag coefficient as the adjusting coefficient (see the orange line in the insert of Fig. 1). The obtained drag coefficient is relatively high, C_d = 0.6. This could be due to both the drag model approximation for such an unsteady configuration and the influence of droplet oscillation on the total dissipation. Based on these observations, the model-fitted impact velocity v(h) is preferred over h as the control parameter in the rest of the study.

The granular bed substrate is made of polystyrene beads @Silibeads (ρ_g = 1050 kg m⁻³), characterised by their diameter d_g. In the present study, the range of diameter investigated is d_g = 40, 80, 140, 230, 580 μm. Although referred to as a monodisperse granular material, the beads exhibit a small polydispersity ranging between 2% and 10% depending on grain size, which prevents crystal-like patterns in the bulk. In each experiment, the Petri dish is filled up with the granular material, which is subjected to a compaction protocol to obtain a densely packed bed. This protocol allows a reproducible initial solid volume fraction between samples ϕ = 0.62, measured from X-ray tomography imaging described in the following section and analysis discussed in Section 3.1. Note that the effect of grain wettability may depend on both the grain material and diameter.²⁹ A measurement of the contact angle between a water droplet and various substrates composed of different granular materials is presented in Appendix A.1.

The varied control parameters of the experimental system are mainly (v, d_g) and slightly D. In the following, this will be discussed in terms of associated dimensionless parameters (Fr or We, d_g/D), with Fr and We being defined in (1). Accordingly, these dimensionless parameters are varied in the range Fr ∈ [2. 30],^2,30 We ∈ [30, 3000] and d_g/D = {8, 9, 16, 18, 29, 31, 47, 53, 118 × 10⁻³}. It is important to note that in the present experiments the value of Re as defined in (1) is 10 to 100 times larger than We. Accordingly, the dynamics is expected to be mostly controlled by inertia and capillarity, i.e. We, and not by viscous dissipation, as discussed in Section 1. Moreover, an extra dimensionless parameter will also be used and adapted to the present study in Section 5. This dimensionless parameter is based on a balance between the initial kinetic energy E_k, following previous studies as reported in Section 1, and a frictional based dissipation of the moving grains.

2.2. Metrology and typical observations

Data acquisition consists of a laser profilometer @Micro-epsilon scan-control 2900-100v46 and a high-speed camera @Phantom-V2012. X-ray tomography, operating @RX-Solutions EasyTom XL, is also used to provide quantitative and qualitative information on the initial and final states.

The 1D laser profilometer allows us to measure the vertical granular bed height along a diameter of the Petri dish, prior and after impact (Fig. 2). The vertical accuracy of the profilometer is of few μm below the smallest grain diameter d_g = 40 μm. The crater depth profile after impact is then obtained by subtracting the after-impact profile and the prior-impact one (Fig. 2(a)). The crater diameter D_max is defined as the peak-to-peak distance of the positive levees surrounding the trough.

Fig. 2 (a) Schematic of the planar-laser and orientations of the tomographic slices relative to the sample. (b) Description of analysis with a plane laser and 2D cross-sectional view of the crater from using a Gaussian filter with schematisation of a peak-to-peak diameter. (c) Characteristic tomographic slices extracted from 3D reconstruction after droplet impact, scale bar = 10 mm.

X-ray micro-computed tomography (μCT) is a non-destructive imaging technique that uses 2D radiographies taken at different angles to reconstruct 3D images of the inside features of the sample.^30,31 It allows extracting 3D information of these initial and final states. Scans were conducted using a laboratory tomograph at 150 kV and 280 μA with an isotropic voxel size of 42 μm. Reconstruction was performed using @RX-Solutions software. The results on μCT data presented in this paper come from a 3D reconstructed volume of 12 mm height and 42 mm width equivalent to around 310 tomographic horizontal slices (Fig. 2(c), top) and 1000 vertical slices (Fig. 2(c), bottom).

Finally, cameras allow us to extract 2D dynamics of the crater formation as a function of time t, with t = 0 corresponding to the drop hitting the granular bed. A typical time scale of a bouncing drop impacting a solid surface is known to be very short, of the order of 10 ms.⁹ The acquisition frame rate of the high-speed camera is thus set to 10 kHz in order to capture a sufficient number of images during an event. Two different field of views have been considered. First, the dynamics in the vertical plane is recorded using a horizontally mounted camera whose optical axis is aligned with the initial undisturbed granular surface (see Fig. 3(b)). The light source consists of a LED panel, installed behind the Petri Dish resulting in shadowgraphy images. This shadowgraphy approach allows us to extract contours of the dynamics in the vertical (r, z) plane with r the radial coordinate and z the vertical coordinate both originating from the impact point of the drop. An example for (v, d_g) = (4.6 m s⁻¹,140 μm) is shown in Fig. 3(b). This highlights a crown of grain-water mixture emanating from an intersecting point X_r with the horizontal granular surface (see the insert of figure Fig. 3(b)). The spreading dynamics close to the granular bed is then captured by extracting the horizontal pixel line just above the undisturbed granular surface (red dash-dot horizontal line in Fig. 3(b)), leading to the spatio-temporal evolution in the (r, t) plane. This allows extracting the temporal evolution X_r(t) (red dashed line in Fig. 3(b)). Second, images of the horizontal spreading are captured. This is done by combining a horizontally mounted camera with a 45° inclined mirror (see Fig. 3(a)). The light source is an annular polarized LED device positioned on top of the Petri dish. An example of image sequence for the case (v, d_g) = (4.6 m s⁻¹, 140 μm) is shown in Fig. 3(a). As observed here, grey levels of these images, corresponding to the intensity of reflected light, give a qualitative representation of height levels (levees towards the lighter grey scale and trough in dark). This allows us to follow the radial expansion of the levees in time, eventually leading to D_max at a long time, comparably to the 1D laser profilometer (see Appendix A.2 for a comparison). During the experiments, no significant grain movement or droplet deformation was observed on the images prior to impact, suggesting that the air film between the droplet and the granular bed may not play a significant role in this setup.

Fig. 3 Schematic representation of the experimental setup using a high-frequency camera in vertical (a) and horizontal (b) point of view. (a) Images recorded during the impact for (v, d_g) = (4.6 m s⁻¹, 140 μm) are shown below the schema. (b) Image of the impact recorded from the horizontal point of view for (v, d_g) = (3.3 m s⁻¹, 140 μm), the horizontal orange segment is the line used for the space-time picture represented on the right. This space-time picture permits building a space-time-plot of Section IV with the red curve.

3. Description of the final granular state

3.1. Inside the granular bed: X-ray

X-ray micro-computed tomography (μCT) is regularly used to provide 3D structural information of a sample without disrupting it.^32–34 In the present study, it was employed to probe the compaction of the sample and its modification with the drop impact. In this section, only results with polystyrene beads of size d_g = 580 μm are presented. It should be noted that the tomographic device used here does not allow us to obtain resolved enough images for smaller grains, given the sample size. Yet, it is assumed that the same conclusions for the compaction states can be drawn for other samples.

Data are first binarized in order to separate the three phases: air in black, the grains in grey and the water (supplemented with potassium iodide to increase the contrast) in white, as shown in Fig. 4(a). These vertical tomographic slices before and after impact allow us to highlight the initial and final states of the sample. In particular, it is shown that the drop entraps grains within it during spreading phase (Fig. 4(2a)). This suggests an almost nonexistent relaxation phase compared to that observed with a solid substrate. One can also observe the formation of the granular levees surrounding the crater and containing the grains initially at the position of the crater.

Fig. 4 (1) and (2) Prior to and after droplet impact for d_g = 580 μm and v = 2.3 m s⁻¹. (a) Segmented vertical tomographic slice of the granular bed, (b) vertical map of ϕ, and (c) 3D average compaction with depth of the sample. The black dashed line is the mean considering all z positions. The red dashed line is the mean considering only the z position below the red dashed line on (a).

A quantitative description of the granular bed can be obtained from the local volume fraction ϕ. Then to map the density in the sample, a 3D cartography of the compaction ϕ is generated. Fig. 4(b) shows vertical slices located in a plane of symmetry of the crater. First, the initial state is found to be homogeneous with ϕ ≈ 0.62 in the bed (Fig. 4(1b); below the red dashed line corresponding to the bed upper surface). A vertical profile ϕ(z) is extracted using 3D regions of interest (ROI) with a length and width equal to the sample size and a height of 2.1 mm. The ROI are 90% overlapping in the vertical direction. Results are presented in Fig. 4(c). Fig. 4 confirm that the granular substrate is densely packed in our set of experiment, with a typical volume fraction of ϕ ≈ 0.62 in the bed. Moreover, Fig. 4(2) suggests that after impact, the substrate evolution remains localized near the drop, while the ϕ(z) profile underneath remains mostly unchanged with ϕ ≈ 0.62. Thus, the transfer of momentum and mass would be mostly horizontal from the crater position towards the levees surrounding the crater, leaving the rest of the substrate unaffected.

To support this observation, one defines the volume fraction ratio as r_ϕ = ϕ_after/ϕ_before to highlight changes from the initial state (before) and the final one (after). Two cases are reported in Fig. 5(1) and (2) for v = 2.3 m s⁻¹ and v = 3.3 m s⁻¹ respectively. The blue-green color represents r_ϕ = 1 which means that there is no difference in compaction, at the tomographic scale, before and after the drop impact. Vertical profiles r_ϕ in Fig. 5(a) suggest a small variation of the volume fraction under the crater (below the solid lines in Fig. 5). Moreover, it indicates that increasing v leads to a deeper influence of the drop impact on the sample volume fraction. Nevertheless, these variations remain marginal for both v, confirming the very local behaviour of the impact. Note that the constant value of r_ϕ = 1.02 through the sample depth in Fig. 5(2a) is associated with the measurement uncertainties more than an actual variation in the volume fraction. A mass transfer from the trough to the levees of the crater can be assumed to be the main process, during which most of the dissipation in the sample takes place through frictional contacts.

Fig. 5 (1) and (2) are for v = 2.3 m s⁻¹ and v = 3.3 m s⁻¹ for d_g = 580 μm respectively. (a) 3D average volume fraction ratio (r_ϕ) with depth of the sample evaluated from the center of remaining droplet (dotted line). (b) Vertical map of the ϕ ratio after and before drop impact. The solid line indicates the bottom of the crater, just below the droplet.

3.2. Crater size: dependence on (Fr, d_g/D)

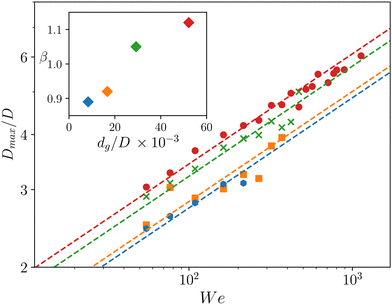
Based on the experimental campaign, it appears that the final crater size D_max varies with the impact velocity v and d_g. In dimensionless form, this is equivalent to a final crater size D_max/D function of the Froude number Fr and d_g/D as shown in Fig. 6.

Fig. 6 Evolution of the scaled crater diameter D_max/D with Fr of the water drop for an impact into polystyrene grains for d_g/D = 9 × 10⁻³ (a), d_g/D = 18 × 10⁻³ (b), d_g/D = 32 × 10⁻³ (c) and d_g/D = 53 × 10⁻³ (d). The intersection between the dashed Fr^1/2 line and solid horizontal line indicates Fr_c. Measurements were performed using the laser profilometer.

As observed in Fig. 6 (see also Fig. 14), two regimes can be identified depending on Fr at least for d_g/D ≤ 53 × 10⁻³. Therefore, only data for d_g/D ≤ 53 × 10⁻³ are presented in the following, while the entire set of data will be discussed in Section 5. In particular, for Fr lower than a critical value Fr_c, D_max/D increases with Fr, while it seems to remain constant for Fr > Fr_c. Even if these two regimes are identified for all grain sizes, the specific critical Froude Fr_c varies with d_g/D, i.e. Fr_c(d_g/D).

For Fr < Fr_c, the crater size is found to follow a power law dependence on the impact velocity, as D_max/D ∝ Fr^1/2 (see the dashed lines in Fig. 6). As D does not vary significantly, this scaling law corresponds to D_max/D ∝ v^1/2. This observation is consistent with previous studies^18,19 which found D_max/D ∝ We^1/4 since . This v^1/2 evolution is obtained for all d_g/D. Note that this scaling law D_max/D ∝ We^1/4 is also obtained when considering the maximal extension of a liquid drop impacting a solid surface.^9–11 This is attributed to the balance between surface tension and inertia during drop spreading in the elastic regime (see Section 1). Based on this observation, this suggests that for Fr < Fr_c the final crater is the signature of the elastic-regime spreading of the impacting drop. This regime will therefore be referred to as the elastic regime. Although the mechanism seems to be the same as for a solid surface, one obtains here different crater size with the grain diameter.

For Fr > Fr_c, another regime emerges where the final crater size no longer evolves as Fr^1/2. In the first approach, one can assume that the crater diameter reaches a constant value whatever Fr, as suggested by the solid lines in Fig. 6. Such plateau-regime was also observed in previous studies, although not specifically discussed.^10,18 Katsuragi¹⁸ briefly suggested a link between this plateau and the appearance of the drop splash, i.e. atomization of the grain-water crown into smaller droplets (see Section 2.2). This regime will therefore be referred to as the Splash regime, yet the link with the droplet splash still requires further investigations as discussed later in the paper. As for Fr_c, a critical We_c can be associated with the transition since surface tension is unchanged in these experiments. We_c obtained here corresponds to the same range as the transition towards the splash regime for impacts on a liquid film, We_s = 400.³⁵ Note that when splash occurs, volume conservation of the initial droplet is no longer satisfied—a condition required to recover the We^1/4 dependence observed in the elastic regime (see Section 1). This is consistent with a crater signature that differs from the elastic regime beyond We_c or equivalently Fr_c here. However, the specific crater size evolution, plateau or not, for Fr > Fr_c, the link with the splash emergence at Fr ≈ Fr_c and the influence of the grain diameter d_g/D remain elusive.

Finally, these results support the use of a signature approach to characterize the final crater size for d_g/D ≤ 53 × 10⁻³ in the case of an initially dense packing, as developed by Katsuragi¹⁸ and Delon et al.¹⁹ In the following section, a detailed description of both Elastic and Splash regimes will be provided for these conditions. Accordingly, the discussion will be conducted with respect to We.

4. Regimes and dynamics

4.1. Elastic regime We < We_c

Here, we recall that the final crater diameter D_max increases with the impact velocity v, following a power law in dimensionless form as D_max/D ∝ We^1/4 for d_g/D ≤ 53 × 10⁻³ (see Fig. 7). Yet, one finds a dependence on the grain size d_g/D. As observed here, d_g/D mostly modifies the scaling factor of the power law, and to a lesser extent the exponent value 1/4. Then, the influence of d_g/D can be included in the law as D_max/D = β(d_g/D)We^1/4. The inset of Fig. 7 shows that β increases with d_g/D. This indicates that the larger the grain, the larger the final crater diameter. Note that such result may seem counterintuitive, as larger grains are heavier and could be expected to be more difficult to displace by a similar impacting droplet.

Fig. 7 Scaled diameter of crater D_max/D as a function of We of the water drop for an impact into polystyrene dimensionless diameter of grain d_g/D = 9 × 10⁻³ (blue hexagons), d_g = 18 × 10⁻³ (orange squares), d_g = 32 × 10⁻³ (green crosses) and d_g = 53 × 10⁻³ (red circles). The insert-graph shows β, the prefactor of the We^1/4 dashed color lines as a function of d_g/D (units × 10⁻³). Measurement were performed using the laser profilometer.

We now investigate the dynamics of the contact point X_r(t), characterizing the temporal evolution of the contact point between the fluid crown, i.e. drop expansion, and the granular layer, obtained from the side view (see Section 2.2 for details). The evolution of its dimensionless form r = 2X_r/D is shown in Fig. 8 as a function of t̃ = tv/D for different values of We < We_c and d_g/D. The origin of time t = 0 corresponds to the impact of the drop with the granular surface. Note that from Fig. 8, the spreading dynamics of the crater starts at (t̃, r) ≈ (1, 1), suggesting that the observable edge of the crater spreading from the side is initiated at time D/v and radial position D/2. It is also worth mentioning that this evolution gives insight into the crater formation but does not allow us to capture the final size of the crater. This is thus considered as an estimate of the precursor of the crater formation.

Fig. 8 Early time evolution of r = 2X_r/D as a function of t̃ = tv/D for different sizes of polystyrene grains at the same We = 67; and for different We at the same grain size d_g/D = 29 × 10⁻³.

Fig. 8 shows a similar trend with an initial acceleration of the contact point r which then reaches a nearly constant spreading velocity dr/dt after t̃ ≈ 2. Moreover, this constant velocity seems to remain nearly independent of both grain size d_g/D and We [Fig. 8]. This means that dX_r/dt ∝ v, i.e. the initial crater spreading scales with the impact drop velocity in this regime.

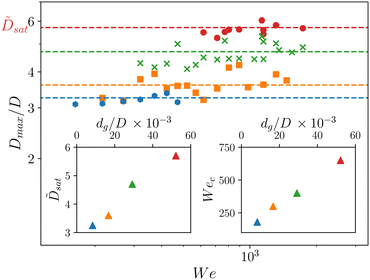
4.2. Splash regime We > We_c

In the second regime, i.e. We > We_c and d_g/D ≤ 53 × 10⁻³, the evolution of crater size with We deviates significantly from the trends observed in the previous regime. In a first approach, the dimensionless crater diameter D_max/D is considered as constant, i.e. becomes independent of We. This manifests as a plateau into the (We, D_max/D) diagram of Fig. 6 (see also Fig. 9 for details and Fig. 14). Yet, the transition between the two regimes as well as the specific value of this plateau remain d_g/D dependent.

Fig. 9 Scaled crater diameter D_max/D evolution with We for polystyrene granular material of diameter d_g/D = 9 × 10⁻³ (blue hexagons), d_g/D = 18 × 10⁻³ (orange squares), d_g/D = 32 × 10⁻³ (green crosses) and d_g = 53 × 10⁻³ (red circles). Inserts show D̃_sat, the estimated constant value of D_max/D for We > We_c, as a function of d_g/D. Measurement were performed using the laser profilometer.

The characteristics of the Splash regime are shown in Fig. 9. The transition We_c is plotted as a function of d_g/D in the insert. The mean crater diameter in this regime defined as D_sat/D ≡ 〈D_max〉/D for We > We_c, then only depends on d_g/D (insert of Fig. 9). One observes that both increase with d_g/D.

As for the first regime, we now investigate the dynamics of the contact point X_r(t), extracted from the side view (see Section 2.2 for detail). The dimensionless position r is plotted as a function of t̃ in Fig. 10 (dark green lines) for d_g/D = 32 × 10⁻⁴. For the record the evolution r(t) in the first regime, We < We_c, is also shown here (light green lines). At early times, as predicted theoretically,³⁶ numerically³⁷ and experimentally³⁸ for impact on liquid film, r ∼ t̃^1/2, independently of experimental parameters, but beyond t̃ ≈ 3, differences between the two regimes are emerging. In the splash regime, the precursor dynamics of the crater edge is found to be strongly different from the elastic regime. In particular, the velocity of the contact point dr/dt is no longer constant but strongly decreases with time. It also remains mostly independent of We. Then, in this case, dX_r/dt < v. The notable difference in dX_r/dt confirms the distinction between two regimes, as well as a connection between crater size and the fluid-grain crown dynamics. Yet the full link leading to a prediction of the final crater size remains elusive. For instance, when We < We_c, r increases linearly with t̃ before stopping abruptly, while for We > We_c, the crater somewhat continuously expands toward the constant plateau (see Fig. 10).

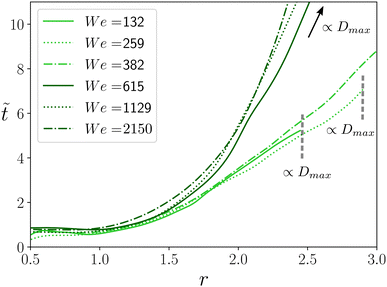Fig. 10 r = 2X_r/D as a function t̃ = tv/D for d_g/D = 29 × 10⁻³ at different We: We < We_c (light green) and We > We_c (dark green).

4.3. A qualitative description of transition We_c

From video recordings, a link seems to emerge between We_c and the splash transition of the spreading drop We_s. However, the measurement uncertainties make it challenging to definitely conclude on this statement, and specifically to extract a quantitative correlation between these two processes. Nevertheless, to discuss the reliability of this possible link, one focuses on experiments performed for similar initial conditions (We, d_g/D) close to We = We_c. It is important to note that up to now, the values reported for (We_c, D̃_sat) are found to be an average estimation from the set of experiments performed. Actually, given the variability in the repeatability of experiments, probably associated with the local structure of the granular soil and the initial drop generation, (We_c, D̃_sat) are not strictly unique, but slightly depend on other non-controlled parameters. Then, experiments discussed here, i.e. close to the reported We_c can lead to spreading dynamics with or without splash, i.e. belonging to the Splash regime or Elastic regime respectively, and slightly different associated value of D̃_sat. Note that the latter is supported by the obtained dispersion of dataset around the mean plateau value at high We reported in Fig. 9.

Fig. 11 shows five distinct experiments for (We; d_g/D) = (332; 29 × 10⁻³) highlighting the influence of variability discussed previously. The different lines correspond to the scaled diameter of the crater with a corresponding image of the final state, showing the shape of the marble-type drop.³⁹ From the green to the orange line, the final crater size slightly increases. However, the complexity of the shape of the final droplet becomes more pronounced as the crater size decreases. Moreover, the complexity of the final drop shape is clearly the signature of dynamics of the spreading drop, eventually leading to its atomization induced by the splash (see the small isolated droplet for smaller crater cases, green lines, in Fig. 11). It is then interesting to note that if one associates the splash of the drop with the number of small droplets generated after impact, then it allows to distinguish crater sizes, with in particular the stronger the splash, the smaller the crater size. Then, the splash transition prevents the drop from spreading, consequently freezing the crater size at the radial extension of this transition. According to a previous study,²⁹ the splash threshold should follow v ∼ d_g^2/5 or d_g^1/5, depending on whether inertial or capillary pressure dominates. Given that We and Re are not clearly distinguishable in the present study, it is found that We_c ∼ (d_g/D)^0.7 (see the insert of Fig. 9) corresponding to v ∼ d_g^0.35, consistent with laws reported in the literature.

Fig. 11 Comparison of scaled crater diameters D_max/D as a function of the nature of the crown for (We; d_g/D) = (332; 29 × 10⁻³). Photos are taken at t = 17 ms after impact.

Altogether, the splash modifies crater evolution when systematically occurring above a critical value We_c. Moreover, the constant value of D_max/D for We > We_c at constant d_g/D then suggests that splashing always occur at the same radial position whatever We. Note that this argument does not involve crater formation, which would suggest similar observations on a solid surface. To the best of our knowledge, such results have not yet been reported in the literature.

5. Accounting for size effect

If the existence of two regimes in crater size evolution with the inertia of the spreading drop is clear, its sharp transition from D_max/D ∝ We^1/4 for We < We_c to D_max/D ∝ C_ste for We > We_c when d_g/D ≤ 53 × 10⁻³ is less obvious. In particular, the decrease in crater size with decreasing d_g/D is not necessarily intuitive. The spreading drop onto the rigid rough surface suggests that increasing roughness size would lead to smaller We_s,^40,41 and consequently smaller We_c in our configuration. Moreover, the dependence of the scaling laws with the grain diameter d_g/D remains unclear, as specifically highlighted in Fig. 14(d) for larger grains d_g/D = 118 × 10⁻³. A typical power law D_max/D ∝ We^1/6 seems to emerge when increasing particle size. As observed in Fig. 14 the transition between a 1/4 power law with a plateau threshold above We_c towards a 1/6 power law without a plateau is not sharp when increasing d_g/D, but tends to appear around d_g/D = 53 × 10⁻³ (c) and is clearly evident at d_g/D = 118 × 10⁻³ (d). Finally, and altogether, disregarding the specific laws, crater size tends to increase with increasing grain diameter, which is not necessarily intuitive, as increasing grain size both increases roughness thus dissipation, and reduces grain mobility. We aim to resolve part of these paradoxes by applying a basic mechanical concept that considers the resistance of the granular soil determined by the number of grain contacts at the local level, i.e. the typical size of the forcing object, D here. The objective of this model is not to provide a clear physical explanation of mechanisms highlighted in the present experiments leading to the richness of behaviours, but to provide an analysis allowing us to globally merge data in a single and dominant trend describing a dissipation process involved during crater formation through d_g/D which is not accounted for in We or Fr.

The dimensionless grain size d_g/D is directly linked to a number of grains on the length scale of the droplet n_c ∼ D/d_g. In order to include this parameter in a dissipating mechanism due to friction between grains, one assumes the dynamics of a single grain set in motion at velocity v by the impact drop and subjected to n_c friction contact when traveling on the granular substrate. The variation in momentum of this grain traveling over a typical distance D from velocity v to rest is

The same grain would experience a resistance to motion induced by the solid friction with the bed at each contact. Assuming that the contact friction force F^c_μ is of Coulomb type based on the own weight of the grain, one writes

On the typical travel distance D, the grain encounters n_c grains, generating as many shocks which participate to its variation in momentum. At first order, a simplistic approach consists in considering these dissipation forces proportional to the number of contacts and to the force F^c_μ, leading to the total friction force F_f

F_f = n_cF^c_μ (4)

Following this approach, one therefore defines a new dimensionless parameter [scr F, script letter F] as the ratio between F_i and F_f as

with the Froude number of the droplet.

The dimensionless crater size is reported as a function of [scr F, script letter F] in Fig. 12. This representation demonstrates that [scr F, script letter F] successfully collapses the various data from the present experiments onto a single curve, excluding the splash regime data discussed earlier. Moreover, experimental data shown here also include results from polystyrene beads of diameter d_g/D = 118 × 10⁻³ and silica sand with grains size d_g/D = 25 × 10⁻³ and density ρ_g = 2.5 kg m⁻¹. Therefore, the dimensionless number [scr F, script letter F] is shown to include the relevant physical processes to account for different granular material. Note that this model only considers inertial effect and contact dissipation neglecting other forces such as electrostatic forces that may play a role during the crater formation. However, results suggest that they do not vary significantly with grain size and are thus subsumed under contact dissipation, allowing for data collapse using the [scr F, script letter F] number. Finally, data mostly collapse on a typical trend as:

corresponding to a v^1/3, i.e. Fr^1/3 or equivalently We^1/6 for our set of experiments, aligning with prior experimental findings.^1,26

Fig. 12 Evolution of the scaled crater diameter D_max/D with (a) Fr and We and (b) [scr F, script letter F]. Grains used are polystyrene except for black squares corresponding to sand. The black dashed line represents a 1/6 slope for We and [scr F, script letter F] (1/3 slope for Fr) and the grey dotted line a 1/4 slope (1/2 for Fr). Data corresponding to the splash regime where We > We_c(d_g/D) are not represented. Measurement performed using both the high speed camera and the laser profilometer.

Then, even though a 1/4 power law and a plateau transition is still observed here, when considering independently trends for each d_g/D, the 1/6 power law indicates a slightly different global trend. Note that, interestingly, largest grain, d_g/D = 118 × 10⁻³, strictly follows this 1/6 trend over the entire range of [scr F, script letter F] (see Appendix A.2 for details). Within the current parameter range, this suggests a notable impact of the grain size d_g/D on a possible transition from a signature approach regime towards an energetic approach regime for increasing crater size. However, further investigation is needed to clarify this aspect, which remains unresolved in the literature.

Conclusion

This paper presents an experimental study of the impact of a water drop on a granular substrate. Only dense packing of the granular substrate is considered, using the same initial compaction protocol. The initial volume fraction is found to be around ϕ = 0.62 in the bulk for all grain sizes d_g. Moreover, the droplet impact has been shown to have a local effect on the granular substrate, whose signature remains localised at the bed surface, while the material below the crater trough is mostly unaffected. This allows assuming dissipation in the granular material to be localised in the transfer of mass from the trough to the levees.

The influence of impact velocity and grain size on the crater diameter has then been investigated. Both are shown to have a significant influence according to their associated dimensionless numbers (We or Fr, d_g/D). The experimental observations confirm that, for a given grain size d_g/D, if d_g/D ≤ 53 × 10⁻³, the crater size D_max/D increases with drop inertia up to a critical We_c above which its diameter remains constant. It is also exhibited that, for a given Weber number, D_max/D increases with the grain diameter. Moreover, for d_g/D > 53 × 10⁻³, the scaling law of crater size with impact velocity, either We or Fr, evolves towards a different power law with a smaller exponent, while We_c is no longer obtained in the range of impact velocity considered here.

For d_g/D ≤ 53 × 10⁻³, the link between splash transition on the granular substrate and We_c has been discussed and seems to be relevant. Yet, this suggests that decreasing d_g/D promotes splashing. This is opposite to the trend reported on a solid surface in the literature, suggesting that increasing roughness length scale promotes splashing We_s. However, discriminating vertical and horizontal length scales of the roughness leads to contradictory results on We_s trend.¹⁷ In any case, it appears that granular deformation and droplet spreading dynamics indeed affects the We^1/4 scaling at high impact velocities and/or large grain diameter, leading to alternative relationships.

In order to rationalize results in the range of (v, d_g, and D) considered here, a dimensionless number [scr F, script letter F] is introduced. It reflects the ratio between the initial inertia transmitted to the grains and the local discrete frictional forces acting on the moving grains at the surface of the granular substrate, evaluated over a characteristic length scale associated with the droplet size. This new parameter allows unifying the different data to a single law of the form D_max/D ∝ [scr F, script letter F]^1/6. Note that the entire dissipation effect highlighted here, seen in the influence of d_g/D on the crater size, has been attributed to friction mechanisms. However, it remains unclear how other material properties can also affect dynamics and crater size, as for instance wettability highlights a dependency on grain diameter d_g (see Appendix A.1).

Conflicts of interest

There are no conflicts to declare.

Data availability

Experimental data are available at https://doi.org/10.5281/zenodo.13135577.

Appendix A

A.1 Wettability of the substrate

In order to quantify the wettability of the substrate, several experiments have been performed including the measurement of the contact angle of a droplet at rest on a given granular material. Following the experimental procedure of Klein et al.,⁴² the equivalent granular bed is made using a polyvinyl chloride plate covered with double-sided adhesive tape and a homogeneous one-grain layer of particles. This glued-particle device immobilizes the grains during measurement, enabling the extraction of the effects of roughness and material wettability on the contact angle. Examples of such measurement are presented in Fig. 13(a) and (b) for a droplet at rest on polystyrene beads of d_g = 80 μm and d_g = 230 μm respectively. A summary of all the measurement is presented in Fig. 13(c). Our results show that increasing the grain diameter of polystyrene and glass beads leads to a more hydrophobic substrate, as indicated by a higher contact angle. In contrast, for silica sand, larger grain sizes result in a more hydrophilic behavior. This may be explained by the difference in the chemical properties, rugosity or sphericity of the different material. Note however that, for small d_g, all materials have similar contact angles, likely controlled by the substrate roughness through d_g rather than by its material properties.

Fig. 13 Experimental measurement of the contact angle between the droplet and the different substrates. Pictures (a) and (b) show examples of a hydrophilic (polystyrene d_g = 80 μm) and hydrophobic (polystyrene d_g = 230 μm) substrate respectively. (c) Evolution of the contact angle with the grain diameter for different materials.

A.2 Exploration of v^1/2 vs. v^1/3 scalings and the influence of measurement methods

The evolution of the scaled crater size with the Webber number is presented in Fig. 14. Both power law We^1/4 and We^1/6 are also reported. From this representation, it remains difficult to discriminate one scaling from the other, specifically for larger d_g. However, it seems that small inertia is better described by the 1/4 power law while the 1/6 looks like a compromise between the different regime over the entire range of inertia covered. Moreover, both laser and camera measurements are shown in Fig. 14 for d_g = 230 μm. Although a small shift is observed between both methods the general trend and scaling remain the same.

Fig. 14 Evolution of the scaled crater diameter D_max/D with We of the water drop for an impact on polystyrene grains (a, b, c and d) with different grain diameter (respectively 40, 140, 230 and 580 μm). Both We^1/4 (dashed-line) and We^1/6 (solid line) trends are represented.

Acknowledgements

This study has been partially supported through the grant EUR TESS N°ANR-18-EURE-0018 in the framework of the Programme des Investissements d'Avenir.

References

1. R. Zhao, Q. Zhang, H. Tjugito and X. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 342–347.
2. A. M. Worthington, Proc. R. Soc. London, 1877, 25, 261–272.
3. M. Pasandideh-Fard, Y. Qiao, S. Chandra and J. Mostaghimi, Phys. Fluids, 1996, 8, 650–659.
4. D. Richard and D. Quéré, Europhys. Lett., 2000, 50, 769.
5. R. Rioboo, M. Marengo and C. Tropea, Exp. Fluids, 2002, 33, 112–124.
6. R. Rioboo, C. Tropea and M. Marengo, Atomization Sprays, 2001, 11, 155–165.
7. A.-L. Biance, C. Clanet and D. Quéré, Phys. Rev. E, 2004, 69, 016301.
8. J. Philippi, P.-Y. Lagrée and A. Antkowiak, J. Fluid Mech., 2016, 795, 96–135.
9. C. Clanet, C. Béguin, D. Richard and D. Quéré, J. Fluid Mech., 2004, 517, 199–208.
10. P. Tsai, M. H. Hendrix, R. R. Dijkstra, L. Shui and D. Lohse, Soft Matter, 2011, 7, 11325–11333.
11. N. Laan, K. G. de Bruin, D. Bartolo, C. Josserand and D. Bonn, Phys. Rev. Appl., 2014, 2, 044018.
12. R. F. Allen, J. Colloid Interface Sci., 1975, 51, 350–351.
13. C. Mundo, M. Sommerfeld and C. Tropea, Int. J. Multiphase Flow, 1995, 21, 151–173.
14. J. Palacios, J. Hernández, P. Gómez, C. Zanzi and J. López, Exp. Therm. Fluid Sci., 2013, 44, 571–582.
15. M. Rein and J.-P. Delplanque, Acta Mech., 2008, 201, 105–118.
16. K. Range and F. Feuillebois, J. Colloid Interface Sci., 1998, 203, 16–30.
17. C. D. Stow and M. G. Hadfield, Proc. R. Soc. London, Ser. A, 1981, 373, 419–441.
18. H. Katsuragi, Phys. Rev. Lett., 2010, 104, 218001.
19. G. Delon, D. Terwagne, S. Dorbolo, N. Vandewalle and H. Caps, Phys. Rev. E, 2011, 84, 046320.
20. E. Nefzaoui and O. Skurtys, Exp. Therm. Fluid Sci., 2012, 41, 43–50.
21. S.-C. Zhao, R. de Jong and D. van der Meer, Soft Matter, 2015, 11, 6562–6568.
22. D. Van Der Meer, Annu. Rev. Fluid Mech., 2017, 49, 463–484.
23. H. Katsuragi, J. Fluid Mech., 2011, 675, 552–573.
24. Q. Zhang, M. Gao, R. Zhao and X. Cheng, Phys. Rev. E, 2015, 92, 042205.
25. J. Marston, S. T. Thoroddsen, W. Ng and R. Tan, Powder Technol., 2010, 203, 223–236.
26. R. de Jong, S.-C. Zhao and D. van der Meer, Phys. Rev. E, 2017, 95, 042901.
27. R. de Jong, S.-C. Zhao, D. Garcia-Gonzalez, G. Verduijn and D. van der Meer, Soft Matter, 2021, 17, 120–125.
28. X. Ye and D. Van Der Meer, J. Fluid Mech., 2021, 929, A24.
29. S.-C. Zhao, R. de Jong and D. van der Meer, et al., Phys. Rev. Lett., 2017, 118, 054502.
30. P. J. Withers, C. Bouman, S. Carmignato, V. Cnudde, D. Grimaldi, C. K. Hagen, E. Maire, M. Manley, A. Du Plessis and S. R. Stock, Nat. Rev. Methods Primers, 2021, 1, 18.
31. A. Sibellas, J. Drummond, D. M. Martinez and A. B. Phillion, Tomogr. Mater. Struct., 2024, 5, 100026.
32. E. Maire, J. Y. Buffière, L. Salvo, J. J. Blandin, W. Ludwig and J. M. Létang, Adv. Eng. Mater., 2001, 3, 539.
33. S.-C. Zhao, R. De Jong and D. Van Der Meer, J. Fluid Mech., 2019, 880, 59–72.
34. S. Nadimi, J. Mendes, A. López, L. Schröer, S. Manoorkar, S. Ellman, V. Cnudde and A. W. Bruno, Sci. Data, 2024, 11, 78.
35. R. L. Vander Wal, G. M. Berger and S. D. Mozes, Exp. Fluids, 2006, 40, 33–52.
36. A. L. Yarin and D. A. Weiss, J. Fluid Mech., 1995, 283, 141–173.
37. M. Rieber and A. Frohn, Int. J. Heat Fluid Flow, 1999, 20, 455–461.
38. G. Cossali, M. Marengo, A. Coghe and S. Zhdanov, Exp. Fluids, 2004, 36, 888–900.
39. P. Aussillous and D. Quéré, Nature, 2001, 411, 924–927.
40. M. Lan, X. Wang, P. Chen and X. Zhao, Case Stud. Therm. Eng., 2016, 8, 218–225.
41. I. V. Roisman, A. Lembach and C. Tropea, Adv. Colloid Interface Sci., 2015, 222, 615–621.
42. N. S. Klein, J. Bachmann, A. Aguado and B. Toralles-Carbonari, Cem. Concr. Res., 2012, 42, 1611–1620.

---