 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modeling the structure and relaxation in glycerol-silica nanocomposites†
Koksal
Karakus
 ab,
Valeriy V.
Ginzburg
ab,
Valeriy V.
Ginzburg
 c,
Keith
Promislow
d and
Leela
Rakesh
c,
Keith
Promislow
d and
Leela
Rakesh
 *ab
*ab
aDepartment of Mathematics, Center for Applied Mathematics and Polymer Fluid Dynamics, Central Michigan University, Mt. Pleasant, Michigan 48859, USA. E-mail: lrakesh@seas.upenn.edu
bDoctoral Program in Mathematical Sciences, Central Michigan University, Mt. Pleasant, Michigan 48859, USA
cChemical Engineering and Materials Science Department, Michigan State University, East Lansing, Michigan 48824, USA
dDepartment of Mathematics, Michigan State University, East Lansing, Michigan 48824, USA
First published on 25th November 2024
Abstract
The relationship between the dynamics and structure of amorphous thin films and nanocomposites near their glass transition is an important problem in soft-matter physics. Here, we develop a simple theoretical approach to describe the density profile and the α-relaxation time of a glycerol-silica nanocomposite (S. Cheng et al., J. Chem. Phys., 2015, 143, 194704). We begin by applying the Derjaguin approximation, where we replace the curved surface of the particle with the planar one; thus, modeling the nanocomposite is reduced to that of a confined thin film. Subsequently, by employing the molecular dynamics (MD) simulation data of Cheng et al., we approximate the density profile of a supported liquid thin film as a stationary solution of a fourth-order partial differential equation (PDE). We then construct an appropriate density functional, from which the density profile emerges through the minimization of free energy. Our final assumption is that of a consistent, temperature-independent scaled density profile, ensuring that the free volume throughout the entire nanocomposite increases with temperature in a smooth, monotonic fashion. Considering the established relationship between glycerol relaxation time and temperature, we can employ Doolittle-type analysis (“naïve” free-volume model), to calculate the relaxation time based on temperature and film thickness. We then convert the film thickness into the interparticle distance and subsequently the filler volume fraction for the nanocomposites and compare our model predictions with experimental data, resulting in a good agreement. The proposed approach can be easily extended to other nanocomposite and film systems.
1. Introduction
Glasses (metallic, ceramic, low-molecular-weight organic, and polymer) play an important role in the modern world.1–4 Glassy materials are usually, though not always, obtained by a rapid cooling from melt state so that the system does not have enough time to crystallize. The transition from melt to glass is called “glass transition”. It is an intriguing and still poorly understood phenomenon, characterized by many features (rapid change in viscosity, nearly-singular jumps in the coefficient of thermal expansion and the heat capacity, etc.)5 The temperature range around which glass transition occurs is quite narrow and allows the definition of a Tg (glass transition temperature) as the temperature at which the viscosity reaches a certain value, or at which the relaxation time becomes longer than a certain timescale (generally 100 s).4–10Of particular interest is the glass transition in thin films, as thin films have important applications (coatings, electronics, etc.) Due to the thickness of the film, the thermodynamic and dynamic properties of the material are often different from those in the bulk, and consequently understanding these changes becomes important.10–19 In particular, the glass transition temperature depends strongly on the film thickness and the film type. In free standing films, Tg of an amorphous material is depressed with respect to the bulk value as the film thickness decreases.20,21 In supported films, however, the dependence of Tg on film thickness is determined by a variety of factors, but generally a weak depression of Tg is observed as the film gets thinner.11,22 In some exceptional cases where the interaction between the glass-former and the substrate is very strong, the dependence can be reversed and Tg can increase in thin films relative to the bulk.22
The inhomogeneous glassy dynamics typical of supported thin films are also present in nanocomposites.23–32 In these systems, the nanofiller volume fraction can be related to the average distance between nanofiller particles. This allows for comparing a nanocomposite to a supported thin film with a thickness equal to the interparticle distance. By varying the filler volume fraction, one effectively varies the “equivalent film thickness”. As the filler volume fraction is increased, this equivalent film thickness decreases, leading to a slight increase in the glass transition temperature (ΔTg ∼ 0–10 K,33–44 although significantly larger shifts were reported by Wang et al. for PS-in-SiO2 films45). The underlying reasons for this relatively small magnitude of the Tg shift in nanocomposites – as compared to thin films – still remain unclear.33
To better understand the experimental data on the glassy dynamics of thin films and nanocomposites, multiple computer simulations have been performed12,34,46–52 and several theoretical approaches have been proposed.48,53–59 Many of those approaches start from a “bulk” theory of the glass transition and then introduce additional gradient terms capturing the distribution of relaxation times in an inhomogeneous system like nanocomposite or thin film. Thus, Lipson, White, and co-workers utilize their combined “LCM-CFV” (“lattice cluster model” and “cooperative free volume” theory),22,57,58,60,61 grounded in the “free volume” concept originally proposed by Doolittle.62 Schweizer and co-workers use the elastic collective nonlinear Langevin equation (ECNLE) theory,29,48,53–55,63 in which the glassy dynamics are the result of collective elastic modes. Ginzburg59 modeled the dynamics of free-standing thin films using the “TS2” (“two-state, two (time)scales”) approach, in which the sharp increase in the relaxation time near Tg is ascribed to the rapid increase in the fraction of “solid” elements in the material.64–67 In all these studies, the main emphasis is on the details of the relaxation time gradients near the surfaces, emphasizing the role of the “interphase”. Other approaches consider the system as a whole, aiming to elucidate the relationships between the Tg-shift, nanofiller loading, filler–matrix interaction, and filler size.34,49–52 These relationships often agree well with experimental trends, such as smaller nanoparticles having a stronger influence on system dynamics than larger ones due to their higher surface area-to-volume ratio, greater interfacial effects, more uniform distribution, enhanced nanoconfinement effects, and stronger interactions with the matrix. However, molecular simulations are limited to short times (tens to hundreds of nanoseconds), relying on extrapolations for the glass transition predictions. Thus, simple theories are still needed to bridge the gaps between simulations and experiments.
Here, we attempt to formulate a new simple theoretical approach based on the classical (“naïve”) free-volume analysis. (The “naïve” or Doolittle free volume model breaks down at temperatures below the glass transition but can be a reasonable approximation in a narrow temperature range close to and slightly above Tg). Our starting point is the glycerol-silica nanocomposite density and α-relaxation time data from a 2015 study by Cheng et al.29 (Other groups have modeled nanoconfined glycerol in cylindrical silica pores68 and in the vicinity of rutile TiO2 and graphene nanofillers,69 with qualitatively similar results.) This specific model system is chosen because it represents a unique case where a stable nanocomposite can be prepared using a low-molecular-weight liquid matrix. (While several authors70–72 have suggested that glycerol should be regarded as an exceptional material because of the prevalence of hydrogen bonding over van der Waals interactions, recent studies suggest that its dynamics are not as anomalous and can be effectively described using advanced free-volume-type theories.67,73–78) Thus, we can expect the density profile to be described by a relatively simple model. Generalization to polymer-based nanocomposites would require a detailed knowledge of the polymer conformations at the filler–matrix interface and would be the subject of future work.79
We start by analyzing the molecular dynamics (MD) simulated density profile of glycerol near a silica surface and reconstructing a free energy density functional minimized by this density profile. Next, we compute the locally-averaged free volume and use the “naïve” free-volume theory to calculate the relaxation time as a function of temperature and film thickness. After converting from the “effective” film thickness back to the nanofiller volume fraction, we compare our model prediction to the experimental data. Finally, we discuss the advantages and limitations of the proposed approach, and its possible extensions and generalizations to other systems.
2. The model
2.1. The equilibrium density profile and the free energy density functional
The density profiles of liquids and polymers near hard surfaces are typically complex and non-monotonic, with several minima and maxima corresponding to “atomic” or “molecular” layers. This non-monotonic behavior persists for several nanometers away from the filler surface; eventually, the density reaches its equilibrium, “bulk” limit. In general, the density profiles depend on the filler–matrix (in this case, silica-glycerol) interactions, as well as the filler radius. For sufficiently “large” nanofillers (R > 10 nm), one can simplify the problem by invoking the Derjaguin80 approximation and representing the particles as planar surfaces. (For more details on the Derjaguin approximation, see the ESI†). The interparticle distance, H, can be related to the particle volume fraction, f, as will be discussed below. As shown in Fig. 1, the density profile in the space between two nearby spherical particles can be modeled as a “decaying exponential” function,ρ(x) = ρb[1 + a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−bx)cos(cx − d)] exp(−bx)cos(cx − d)] | (1) |
Eqn (1) is used for 0 < x ≤ H/2; for H/2 < x ≤ H, we replace x with (H − x). The coefficients in eqn (1) are determined so that the model density profile (orange line) closely matches the results from molecular dynamics (MD) simulations (blue line). The details of the parameterization will be discussed below in Section 3.1.
The density profile described by eqn (1) can be thought of as a solution of a fourth-order linear ordinary differential equation (ODE),
 | (2) |
We now stipulate that eqn (2) is the result of the free energy minimization with respect to the density and attempt to reconstruct the free energy functional, F(u). Assuming that the free energy solely depends on u and its spatial derivatives, we can express it as follows,
 | (3) |
 , where T is temperature, R is the gas constant, and ξ is the correlation length (see below). For our current analysis, the exact value of U0 plays no role, unlike in the case of free-standing films. The dimensionless functional
, where T is temperature, R is the gas constant, and ξ is the correlation length (see below). For our current analysis, the exact value of U0 plays no role, unlike in the case of free-standing films. The dimensionless functional  is the free energy density.
is the free energy density.
The free energy minimization condition is,
 | (4) |
The boundary conditions are specified as follows. At the silica surface, x = 0, the density and the density gradients are prescribed, u(0) = us, and ux(0) = vs. At the mid-point, x = H/2, the density equals the bulk density, u(H/2) = 1, and the density profile is symmetric, i.e., ux(H/2) = 0.
The local energy term, g(u), is given by,
 | (5) |
The above analysis assumes that the density variations are small and thus, linear treatment is sufficient. We note that this is not the case for, say, free-standing films where the density transitions from the “bulk liquid” value to the near-zero “vapor” value over the course of 1–2 nm interface.59 Thus, the function g(u) must be thought of as a local expansion of the “true” function around the potential energy minimum u = 1. The true function should include two minima corresponding to both liquid and vapor phases and a maximum corresponding to a barrier between them. One such function could be a cosine potential,  ; in that case, the density profile across a film/air surface would be described by a sine-Gordon kink. We will address this topic and explore the integration of free energy expressions for supported and free surfaces in future publications.
; in that case, the density profile across a film/air surface would be described by a sine-Gordon kink. We will address this topic and explore the integration of free energy expressions for supported and free surfaces in future publications.
2.2. The spatial averaging of the density profile
To understand the dynamics of the nanocomposite material near the matrix Tg, we need to consider the effects of cooperativity. It is well-known that molecular motions are correlated with the correlation length, ξ, usually on the order of 1–4 molecular (or monomer) size; the volume Vcorr = ξ3 is known as the cooperatively rearranging region (CRR). Thus, as one prepares to calculate the relaxation time distribution within the nanocomposite, it is necessary to first coarse-grain the density profiles to smooth the variations within the CRRs.Here, we make the simplest possible assumption – one CRR consists of two neighboring layers, as shown in Fig. 2. (For a brief analysis of how the results would differ when considering alternative models, where one CRR consisted of three or four layers, see the ESI†). Thus, the first layer (density maximum) and the second layer (density minimum) are averaged to form the first CRR; likewise, the third and fourth layer combine into the second CRR (the middle panel of Fig. 2). The new, coarse-grained density profile becomes smooth and monotonically decreases as a function of the distance from the filler surface (the right panel of Fig. 2). This coarse-grained density profile is then used to calculate the relaxation times, as discussed in the next section.
2.3. The calculation of the relaxation times
We proceed to model the relaxation time distribution in the material. This analysis is restricted to temperatures above the glass transition of the matrix (glycerol), where the material is in equilibrium. The coarse-grained density profile describes the distribution of the free volume and thus can be related to the local relaxation time based on the Doolittle62 model (the “naïve” free volume theory). To begin with, we use the Vogel–Fulcher–Tammann–Hesse (VFTH)85–87 parameterization for the α-relaxation time of pure glycerol, | (6) |
 | (7a) |
 | (7b) |
Here, fv is the fractional free volume (FFV) at temperature T, fv,g is the fractional free volume (FFV) at T = Tg, and τg is the α-relaxation time at T = Tg (set to be equal to 100 s). (The relationship between τg and τ∞ is simple,  ). Eqn (7a) and (7b) are identical if, and only if,
). Eqn (7a) and (7b) are identical if, and only if,
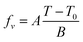 | (8) |
Eqn (8) holds within a limited temperature range where fv ≪ 1, yet this range is broad enough for practical purposes, given the smallness of the A/B ratio, as will be illustrated below.
Within the “naïve” free volume approach, one can evaluate the parameter A by assuming that the slope of the temperature dependence of the FFV is equal to the coefficient of thermal expansion (CTE) of the material in the liquid state (i.e., above the glass transition temperature), αL. (Note that more elaborate free volume theories sometimes question whether all or part of the change in the specific volume can be ascribed to the change in the free volume,60,67 but here we use the simplest possible approach; for justification of this assumption, see the ESI†). In that case,
| fv = αL[T − T0] | (9a) |
| A = αLB | (9b) |
Typically, αL ∼ (4–6) × 10−4 K−1,88 so the restriction fv ≪ 1 is satisfied for T − T0 < 200 K, or T − Tg < 150 K.
We now need to express free volume in terms of density, rather than temperature. This is fairly straightforward, given that the density is the inverse of the specific volume which (above Tg) is given by,60,89
| V = V0[1 + αLT] | (10) |
Substituting eqn (10) into eqn (9a), eliminating T, and replacing V = 1/ρ, we obtain,
 | (11) |
Obviously, eqn (11) is applicable only for T > T0. Since we are concerned with T > Tg, and Tg is significantly larger than T0 (usually, Tg − T0 is roughly 40–50 K),90 this requirement is satisfied automatically.
Next, we need to calculate the relaxation time profiles and the averaged relaxation time. The former is done by substituting the coarse-grained density, ρ(x), into eqn (11), and then substituting the calculated fv(x) into eqn (7), with A given by eqn (9b), and the VFTH parameters B and τ∞ determined from the dielectric measurements performed on the pure glycerol (no fillers). The averaged relaxation time is then calculated as,
 | (12a) |
 | (12b) |
In writing eqn (12a), we re-defined x from a continuous to a discrete variable with the increment equal to the CRR dimension ξ.
Finally, to compute the temperature dependence of τavgα, we need to prescribe how ρ(x) depends on T. We make an assumption that the dimensionless density profile, u(x) = ρ(x)/ρb, does not depend on the temperature, at least in the relatively narrow temperature range considered here. Obviously, the bulk density depends on the temperature as described in eqn (10), ρb(T) = (V0[1 + αLT])−1. Consequently, we can express the temperature dependence of eqn (12b) explicitly as follows,
 | (13) |
| u(x) = 1 + a〈exp(−bx)cos(cx − d)〉 | (14) |
Here, 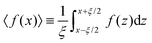 , and x is restricted to locations at the centers of CRRs, i.e., x/ξ = 0.5, 1.5, 2.5 etc. Note that
, and x is restricted to locations at the centers of CRRs, i.e., x/ξ = 0.5, 1.5, 2.5 etc. Note that  . It can be shown that u(x) = 1 + A
. It can be shown that u(x) = 1 + A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−bx), where
exp(−bx), where  . In practical applications, A is small and positive. The exponential decay of the density as a function of the distance from the surface will be utilized later in deriving the expressions for the relaxation time and Tg-shift.
. In practical applications, A is small and positive. The exponential decay of the density as a function of the distance from the surface will be utilized later in deriving the expressions for the relaxation time and Tg-shift.
Before proceeding to compare the model predictions with experimental data, we again recap two main assumptions and limitations of our model. First, the model is only applicable at temperatures close to and slightly above Tg (approximately Tg to Tg + 50 K) where the density of the nanocomposite is close to equilibrium and the fractional free volume changes are expected to be linear in temperature and thus proportional to the overall specific volume changes. Second, the model is limited to low-to-medium nanofiller loadings where the “interphases” around different particles do not overlap and there exists a “bulk” region with the properties of the pure glycerol. These conditions were satisfied in the experiments discussed below.
3. Results and discussion
3.1. Glycerol-silica nanocomposite density profiles
The glycerol density profile was simulated by Cheng et al.29 Glycerol liquid in contact with an amorphous silica (SiO2) surface was modeled using atomistic molecular dynamics (MD) with generalized amber force field (GAFF) for temperature T = 293 K. Their simulation results, depicted by the blue curve in Fig. 3, are spaced at intervals of 0.025 nm (0.25 Å). | ||
| Fig. 3 Molecular dynamics (MD) simulation (blue) and model fit (orange) glycerol density profiles for T = 293 K. The MD simulation data are from Cheng et al.29 | ||
The orange line corresponds to the best fit using eqn (1), with the fit parameters and their uncertainties summarized in Table 1. In the fitting analysis, the coefficient c was obtained from the average period between the first and last visible peaks (in this case, the fourth), while the coefficient b was derived from the amplitude ratio, indicating the decay rate. Following this, the parameters d and a were calculated. Additionally, the coefficients α and β in eqn (2) and (3) and the boundary conditions us and vs were determined, assuming their constancy within the temperature range 200 K < T < 260 K. (Given that the parameters α, β, us and vs are uniquely determined by the parameters a, b, c, and d, we do not provide their uncertainties in the table).
| Parameter | Value | Units |
|---|---|---|
| a | 0.28 (±0.02) | |
| b | 1.4 (±0.4) | nm−1 |
| c | 13.8 (±0.5) | nm−1 |
| d | 0.9 (±0.2) | |
| α | 2.57 × 10−5 | nm−4 |
| β | 1.0 × 10−2 | nm−2 |
| u s | 1.13 | |
| v s | 3.35 | nm−1 |
The density of glycerol as a function of temperature was computed based on the literature data77,88,91 parameterized according to eqn (10), with aL = 4.0 × 10−4 K−1, and V0 = 0.678 cm3 g−1.
Spatially averaged density profiles smooth out the short-range oscillations, resulting in a monotonic decrease in density as a function of the distance from the substrate. The spatially averaged profile for T = 224 K (about 35 K above the glass transition) is shown in Fig. 4. The symbols denote successive “bilayer-CRRs”, where the density of the first CRR is 1.309 g cm−3, the second 1.3065 g cm−3, the third 1.305 g cm−3, and so forth. Overall, the density difference between the first CRR and the bulk is about 0.5%. The approximate expression for this function is an exponential,  , with q = 0.066 and ξ = 0.88 nm. We can now determine how this difference influences the relaxation time behavior.
, with q = 0.066 and ξ = 0.88 nm. We can now determine how this difference influences the relaxation time behavior.
3.2. Glycerol-silica nanocomposite relaxation times
We begin by fitting the dielectric relaxation time of glycerol as measured by Cheng et al.29 to the VFTH functional form (eqn (6)), thereby obtaining parameters shown in Table 2. The fitting was performed in Excel using the generalized reduced gradient (GRG) solver. The minimization (with respect to B and T0) was repeated for multiple values of log(τ∞,s) in the range between −12.5 and −15, and the averages and uncertainties were then computed for both B and T0.| Parameter | Value | Units |
|---|---|---|
| log(τ∞,s) | −13.275 (±1.3) | |
| B | 759 (±213) | K |
| T 0 | 141.5 (±11) | K |
Once the VFTH parameters are known, we can calculate the Doolittle parameter A (eqn (9b)) and then compute the relaxation time profiles for each individual temperature. In Fig. 5a, the relaxation time profile is shown for T = 224 K. The relaxation time corresponding to the first CRR is approximately 1–1.5 orders of magnitude (10–30 times) larger than the bulk value, indicating a significant slowing down of all molecular mobility near the substrate, as compared to the bulk. The relaxation time decay as a function of position is consistent with a “double-exponential” form, log[τα(x)/τα,bulk] = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−x/ξ), with k = 1.84 and ξ = 0.88 nm. This behavior is consistent with other models, such as the ECNLE theory developed by Schweizer and co-workers.92
exp(−x/ξ), with k = 1.84 and ξ = 0.88 nm. This behavior is consistent with other models, such as the ECNLE theory developed by Schweizer and co-workers.92
 | ||
| Fig. 5 (a) Coarse-grained relaxation time profile for T = 224 K. (b) Normalized relaxation time profiles for T = 222 K – the current FV theory (grey), MD simulations (blue circles), and ECNLE theory (orange). MD and ECNLE results are from Cheng et al.29 | ||
To compare our results with the ECNLE theory in greater detail, in Fig. 5b we plot the normalized relaxation time as a function of position at T = 222 K (grey line). This is compared with the MD simulations (blue circles) and the ECNLE calculations (orange line), with both MD and ECNLE data taken from Fig. 7b of ref. 29. The agreement between the two theories and the simulations is quite reasonable. The free-volume approach seems to over-estimate the apparent correlation length compared to the ECNLE theory. Both theories estimate the relaxation time increase near the surface to be about 20–30, which is slightly higher than the values suggested by MD simulations.
We can now use eqn (12a) to compute the average relaxation times of silica-glycerol nanocomposites and compare them with experimental data from Cheng et al.29 Using their calculated interparticle distances, we modeled the glycerol-silica nanocomposites with silica volume fractions of 8.8% and 23.6%, corresponding to distances of 20.3 nm and 7.61 nm, respectively. The relaxation time dependence on temperature for these nanocomposites and pure glycerol are illustrated in Fig. 6. The model predictions (lines) match well with the experimental data (symbols). As expected, the largest discrepancy between model and experiment is seen at low temperatures for the highest filler loading (the smallest effective film thickness), as the two separate “interphases” of neighboring particles can no longer be treated as fully independent.
 | ||
| Fig. 6 Temperature dependence of the nanocomposite relaxation times. Lines are model predictions; symbols are the dielectric spectroscopy data from Cheng et al.29 “Hyp. model” refers to a hypothetical nanocomposite with very high filler loading. | ||
We can quantify our model predictions further by computing the dependence of the glass transition temperature on the nanocomposite composition. Let us define Tg as the temperature for which log(τα) = 2.0 (i.e., relaxation time is equal to 100 s). The dependences of Tg on H and on the silica volume fraction, f, are shown in Fig. 7a and b. As anticipated, decreasing H or increasing f leads to an increase in Tg, although the extent of change is fairly small as compared to, for instance, free-standing thin films. The dependence of ΔTg on f is weakly nonlinear and can be modeled by a second-order (quadratic) polynomial (Fig. 7b).
3.3. Model generalization and master curves
Let us generalize the model in the following way. Based on the functional form of the density profile in eqn (1), we can stipulate that the coarse-grained dimensionless density, u(x) can be approximated as a double-exponential function, | (15) |
This is based on the approximate equality ez ≈ 1 + z in the limit of small z. Thus, fractional free volume as a function of location is given by,
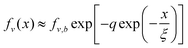 | (16) |
In eqn (15) and (16), the subscript “b” refers to the bulk value of the density or fractional free volume in the bulk at the temperature of interest. Substituting eqn (16) into eqn (7b), we can compute the dependence of the relaxation time on the distance from the surface, x,
 | (17) |
For the relaxation time vs. temperature, we can analytically integrate eqn (17) to obtain,
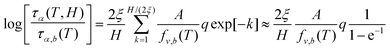 | (18) |
Since  , we can re-write eqn (18) as,
, we can re-write eqn (18) as,
log[τα(T,H)] = (1 + x)log[τα,b(T)] − x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[τ∞] log[τ∞] | (19a) |
 | (19b) |
The bulk relaxation time,  , is given by the VFTH expression (eqn (6)). The dimensionless parameter x combines two factors – the ratio of the correlation length, ξ, to the equivalent thickness, H, and the density enhancement factor, q. Thus, stronger bonding between the filler and the matrix leads to a larger q and larger relaxation time increase if everything else is kept constant. Hydrogen-bonding glass-formers, such as glycerol, typically exhibit lower ξ values (1–2 nm), while many other glass formers—such as van der Waals liquids, covalent and ionic glasses, rigid molecules, and polymers—can reach significantly higher ξ values (3–5 nm).94,95 Again, these results are qualitatively consistent with the predictions of the ECNLE theory, but are based on slightly different frameworks.
, is given by the VFTH expression (eqn (6)). The dimensionless parameter x combines two factors – the ratio of the correlation length, ξ, to the equivalent thickness, H, and the density enhancement factor, q. Thus, stronger bonding between the filler and the matrix leads to a larger q and larger relaxation time increase if everything else is kept constant. Hydrogen-bonding glass-formers, such as glycerol, typically exhibit lower ξ values (1–2 nm), while many other glass formers—such as van der Waals liquids, covalent and ionic glasses, rigid molecules, and polymers—can reach significantly higher ξ values (3–5 nm).94,95 Again, these results are qualitatively consistent with the predictions of the ECNLE theory, but are based on slightly different frameworks.
Before discussing the model predictions, we re-cast the VFTH equation in the form proposed by Rössler et al.94,95
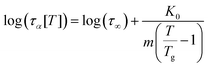 | (20) |
 is the dynamic fragility, and K0 = 2 − log(τ∞). Using this form will enable us to describe the shifts in relaxation time and glass transition in terms of reduced temperature, T/Tg.
is the dynamic fragility, and K0 = 2 − log(τ∞). Using this form will enable us to describe the shifts in relaxation time and glass transition in terms of reduced temperature, T/Tg.
Fig. 8a shows relaxation time versus reduced temperature for a glycerol-like material (fragility m = 58.9) with fairly strong filler surface attraction (q = 0.15), varying the “equivalent reduced thickness, 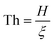 , from 1000 (bulk-like) to 6 (the smallest separation), where the two “interphases” can still be treated as independent. The curves shift upwards as Th decreases. By recording the intersections of the curves with the horizontal line log(τα[T]) = 2, we determine the glass transition temperature of the shifts. Those shifts are plotted in Fig. 8b for three different values of q: 0.15 (strong matrix–filler attraction), 0.1 (intermediate attraction), and 0.05 (relatively weak attraction). In all cases, the Tg shift linearly depends on the inverse effective thickness.
, from 1000 (bulk-like) to 6 (the smallest separation), where the two “interphases” can still be treated as independent. The curves shift upwards as Th decreases. By recording the intersections of the curves with the horizontal line log(τα[T]) = 2, we determine the glass transition temperature of the shifts. Those shifts are plotted in Fig. 8b for three different values of q: 0.15 (strong matrix–filler attraction), 0.1 (intermediate attraction), and 0.05 (relatively weak attraction). In all cases, the Tg shift linearly depends on the inverse effective thickness.
The results in Fig. 8b can be simplified by examining the normalized Tg – change, 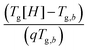 (see Fig. 9a). Assuming that log(τ∞) is constant, the normalized Tg – change depends solely on dynamic fragility and form a straight line with zero intercept. The slope, K, is an inverse function of the fragility (Fig. 9b),
(see Fig. 9a). Assuming that log(τ∞) is constant, the normalized Tg – change depends solely on dynamic fragility and form a straight line with zero intercept. The slope, K, is an inverse function of the fragility (Fig. 9b),
 | (21) |
 | (22a) |
 | (22b) |
 | ||
| Fig. 9 (a) Normalized Tg-change as a function of normalized inverse thickness. All parameters are the same as in Fig. 8. (b) Dependence of the slope K on the dynamic fragility, m. | ||
The above analysis is based on the assumption that the density profile, manifested here via q and ξ, does not depend on the temperature, at least in the narrow temperature range between Tg and about 1.2Tg, where the dynamics shift from VFTH to Arrhenius.97 In general, the density profile might be temperature-sensitive, in which case multiple simulations are needed to incorporate this dependence in the model.
While this model has been applied to nanocomposites, it could also be relevant for other types of confinement, such as liquids in nanopores. For confined liquids, both polymeric and non-polymeric, the glass transition temperature can either increase or decrease depending on the interaction between the walls and the liquid. For example, we consider the recent study of N,N′-bis(3-methylphenyl)-N,N′-bis(phenyl)benzidine (TPD) confined within the polymer-nanoparticle systems (capillary-rise infiltration [CaRI]).98 In this study, Wang et al. used refraction index measurements to observe very large increases in Tg (∼10–30 K) as compared to the bulk glass transition temperature. They hypothesized that the unique CaRI geometry leads to substantial changes in molecular conformations near the surface, making the Tg increase mainly due to entropic factors rather than strong surface interactions with the TPD.
Without going into the molecular details, we can ask whether the experimentally observed Tg-shift obeys eqn (22b) and, if yes, what can be hypothesized on that basis. Fig. 10 shows the normalized Tg-shift for CaRI-confined TPD plotted against the inverse of the average pore radius. The linear dependence is fairly good, given the model's approximations.
 | ||
| Fig. 10 The normalized Tg-shift for CaRI-confined TPD – data (circles) and the linear fit. The data are from Fig. 1b of Wang et al.;98 the point corresponding to the smallest pore (R ≈ 1.5 nm) is not included in this analysis. | ||
The slope of the line in Fig. 10,  , depends on the correlation length, ξ, fragility, m, and density enhancement, q. While the fragility of TPD is known, m ≈ 98,99 estimating the other two parameters is more difficult. Assuming that ξ is fully determined by m and scales as ∼m2 (see Torkelson et al.96), we obtain ξ ∼ 3–4 nm. Thus, we can estimate the density enhancement, q, from
, depends on the correlation length, ξ, fragility, m, and density enhancement, q. While the fragility of TPD is known, m ≈ 98,99 estimating the other two parameters is more difficult. Assuming that ξ is fully determined by m and scales as ∼m2 (see Torkelson et al.96), we obtain ξ ∼ 3–4 nm. Thus, we can estimate the density enhancement, q, from  ; substituting P = 0.28 nm, m = 98, Λ = 48, we have q between 0.19 (for ξ = 3 nm) and 0.14 (for ξ = 4 nm). These estimates indicate that the reduction in free volume of TPD near the particle surfaces is substantial. Further analysis for these and other systems is ongoing.
; substituting P = 0.28 nm, m = 98, Λ = 48, we have q between 0.19 (for ξ = 3 nm) and 0.14 (for ξ = 4 nm). These estimates indicate that the reduction in free volume of TPD near the particle surfaces is substantial. Further analysis for these and other systems is ongoing.
3.4. Discussion
We have demonstrated that a simple approach combining a “naïve” free-volume theory with the assumption that one cooperatively rearranging region (CRR) corresponds to two molecular layers can successfully capture the dynamics of simple nanocomposites. Note that predicting the relaxation time does not require any new adjustable parameters. Once the equilibrium density profile of the matrix near the filler surface is known (e.g., from MD simulations) and the relaxation time of the matrix as a function of temperature is also known, our model can quickly predict the nanocomposite relaxation time. Although this initial success is promising, several questions remain to be addressed, as discussed below.First – how much do the results depend on the selected model for the local relaxation time? The use of the “naïve” free volume theory implies that the relaxation time depends only on the free volume and not, say, on both free volume and temperature. While this question becomes important at temperatures close to Tg, at temperatures above Tg, a material is in its equilibrium state. Thus, for a homogeneous material, either temperature or free volume can serve as an independent variable, with one being a unique function of the other (see the ESI† for more details).
The second question – directly related to the first one – is the free volume change with temperature accurately captured by the experimentally measured coefficient of thermal expansion (CTE)? In other words – should all the volume added as the temperature is increased count as a “free volume”? For example, within the TS2 framework of Ginzburg et al.,59,64,65,67 the specific volume change is due to two contributions, the “true” free volume, (1 − ν), and the volume change resulting from the transition between a low-density “liquid” and a higher-density “solid” component. However, we expect that within a limited temperature span ranging between Tg and, say, Tg + 60 K, the relationship between the variously defined fractional free volumes is linear, and therefore, the main results from the current analysis will remain valid following the adjustment of certain constants, such as A in eqn (7b). Additional details are provided in the ESI.†
The third question is – how does the current description compare to alternative models of the glassy dynamics in thin films and nanocomposites, e.g., the ECNLE theory of Schweizer et al.,48,53–55,63,100 the cooperative free volume (CFV) theory of Lipson et al.,56–58 or the generalized entropy theory (GET) of Douglas and co-workers.101–105 One important output of any theory is the spatial profile of the relaxation time near the matrix–filler interface. The logarithm of the relaxation time decays as an exponential function of the distance to the surface in GET-type models, as a double-exponential function in ECNLE-type models, and as a more complex and parameter-dependent function in CFV-type models. Schweizer and Simmons93 presented a broad justification of the double-exponential form based on general physical principles. Our result is consistent with this finding, although more analysis is needed. A recent article by Cheng et al.106 described a novel approach (“continuous Havriliak–Negami analysis”) to directly calculate the relaxation time profiles from the dielectric measurement data.
The final question is – how universal are the findings of this analysis and whether they could also be used for polymer–inorganic nanocomposites. This question itself can be split in two – the importance of the hydrogen-bonding vs. van-der-Waals interactions (highly vs. moderately polar vs. non-polar liquids) and the differences between low-molecular-weight and polymeric matrices. Based on the arguments of Ferrer et al.,72 Merabia and Long70,71,107 suggested that strongly hydrogen-bonding fluids (such as glycerol) cannot be described by free-volume-type theories. Casalini, Roland, and co-workers examined the relative influences of pressure and temperature on the segmental relaxation in both hydrogen-bonding and non-hydrogen-bonding glass-formers;74–77,108–114 they concluded that strong hydrogen bonding can disrupt the dynamic “τTV” scaling and make the temperature and pressure dependence of the relaxation time more complicated; they also indicated that for systems where the scaling is observed (including most polymers and many low-molecular glass-formers), one can use both free-volume-type and free-energy type theoretical models. Win and Menon115 demonstrated that glycerol exhibits a reasonable “τTV” scaling with γ ∼ 1.4, indicating that relaxation depends on both temperature and volume (with temperature dependence more pronounced). Subsequently, Ginzburg, Zaccone, and Casalini67 used their lattice free-volume-type SL-TS2 theory to describe relaxation and the equation of state for glycerol in the same way as several other non-polymeric and polymeric glass-formers. Recent analysis of the glycerol viscosity data by Ferreira et al.78 suggested that the data could be interpreted within a free-volume framework, as well as on the basis of an alternative “bond strength-coordination number fluctuation” model of Anaya et al.116,117 Our current approach is based on the SL-TS2 ideas that can be reduced to the “naïve” free volume form in the limit of equilibrium behavior at temperatures above T = Tg. The question of polymeric vs. low-molecular-weight matrices is equally complicated. Due to low viscosities of most low-molecular-weight glass-forming fluids (glycerol being an exception), it is difficult to use them as matrices for stable nanocomposites. Yet, the magnitude of the Tg-change in glycerol-silica nanocomposites is comparable to those observed for polymer-based nanocomposites.31,33,118,119 We hypothesized that the magnitude of the Tg-change depends on the fragility, correlation length, and the matrix–filler interaction strength; it appears that the combined effect of all those factors generally results in sub-10 K Tg-shifts, with few notable exceptions. Obviously, the impact of factors such as the presence of grafted chains (if any) and the molecular weight and dispersity of matrix chains requires further exploration. This research is ongoing.79
4. Conclusions
We proposed a simple model describing the relaxation time as a function of temperature for nanocomposite materials with strong filler–matrix interaction. The model starts with the equilibrium density profile which is coarse-grained with the “bin” size corresponding to the cooperatively rearranging region (CRR) size (or the dynamic correlation length). The density profile is then converted into the fractional free volume profile, followed by the application of Doolittle's “naïve” free volume approach to compute the relaxation time as a function of spatial coordinate and temperature. The results are compared with the experimental data of Cheng et al.,29 and a good qualitative and semi-quantitative agreement is found.The proposed approach could be readily extended to other nanocomposite systems, given the availability of both dielectric relaxation and density profiles are known (either measured or simulated). In addition, it can be generalized to free-standing thin films, supported thin films, and filled thin films. These areas could be explored further in future research.
Author contributions
K. K.: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, analysis, visualization, writing – original draft, review & editing. V. V. G.: conceptualization, data curation, formal analysis, investigation, methodology, validation, writing – review & editing. K. P.: conceptualization, methodology, writing – review & editing. L. R.: conceptualization, methodology, investigation, writing – review & editing, supervision, professional development, collaboration, teaching concepts, funding acquisition, academic support, project administration/management, resources, correspondence. All authors reviewed and approved the final manuscript.Data availability
All data supporting the findings of this study are publicly available through the references cited in this paper. No new data were generated or analyzed in this study. The ESI† (attached), including detailed datasets and methodologies, can be found in the referenced publications and their associated websites.Conflicts of interest
All authors declare no conflicts of interest.Acknowledgements
K. K. extends gratitude to Central Michigan University's Department of Mathematics and Office of Graduate Studies for their pivotal support via Research Assistantship and American Physical Society (March) meeting registration assistance, essential for this research phase. We also appreciate Central Michigan University for enabling L. R.'s sabbatical at the University of Pennsylvania, which significantly influenced this research article. K. P. acknowledges NSF support through grant DMS 2205553. Special thanks to Prof. Shiwang Cheng (MSU) for providing invaluable experimental and simulation data, as well as for insightful discussions. Finally, we thank the anonymous reviewers for their many helpful suggestions.References
- C. Suryanarayana and A. Inoue, Bulk metallic glasses, CRC Press, 2017 Search PubMed.
- A. Gujral, L. Yu and M. D. Ediger, Curr. Opin. Solid State Mater. Sci., 2018, 22, 49–57 CrossRef CAS.
- D. Möncke, B. Topper and A. G. Clare, Rev. Mineral. Geochem., 2022, 87, 1039–1088 CrossRef.
- C. B. Roth, Polymer glasses, CRC Press, 2016 Search PubMed.
- G. B. McKenna and S. L. Simon, Macromolecules, 2017, 50, 6333–6361 CrossRef CAS.
- D. Cangialosi, J. Phys.: Condens. Matter, 2014, 26, 153101 CrossRef CAS PubMed.
- D. Cangialosi, A. Alegria and J. Colmenero, Prog. Polym. Sci., 2016, 54, 128–147 CrossRef.
- M. D. Ediger and P. Harrowell, J. Chem. Phys., 2012, 137, 080901 CrossRef CAS.
- L. Berthier and M. D. Ediger, Phys. Today, 2016, 69, 40–46 CrossRef CAS.
- M. D. Ediger and J. A. Forrest, Macromolecules, 2014, 47, 471–478 CrossRef CAS.
- W. Zhang, J. F. Douglas and F. W. Starr, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5641–5646 CrossRef CAS.
- Y. Zhang, E. C. Glor, M. Li, T. Liu, K. Wahid, W. Zhang, R. A. Riggleman and Z. Fakhraai, J. Chem. Phys., 2016, 145, 114502 CrossRef.
- J. A. Forrest and K. Dalnoki-Veress, Adv. Colloid Interface Sci., 2001, 94, 167–195 CrossRef CAS.
- D. B. Hall, J. C. Hooker and J. M. Torkelson, Macromolecules, 1997, 30, 667–669 CrossRef CAS.
- H. Zha, Q. Wang, X. Wang, D. Cangialosi and B. Zuo, Macromolecules, 2021, 54, 2022–2028 CrossRef CAS.
- S. Napolitano, E. Glynos and N. B. Tito, Rep. Prog. Phys., 2017, 80, 036602 CrossRef.
- A. Debot, R. P. White, J. E. G. Lipson and S. Napolitano, ACS Macro Lett., 2018, 8, 41–45 CrossRef PubMed.
- M. Wübbenhorst and S. Napolitano, Dynamics in geometrical confinement, Springer, 2014, pp. 247–277 Search PubMed.
- S. Capponi, S. Napolitano, N.-R. Behrnd, G. Couderc, J. Hulliger and M. Wubbenhorst, J. Phys. Chem. C, 2010, 114, 16696–16699 CrossRef CAS.
- C. B. Roth and J. R. Dutcher, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 103–107 CrossRef.
- C. B. Roth and J. R. Dutcher, J. Electroanal. Chem., 2005, 584, 13–22 CrossRef CAS.
- R. P. White, C. C. Price and J. E. G. Lipson, Macromolecules, 2015, 48, 4132–4141 CrossRef CAS.
- K. I. Winey and R. A. Vaia, MRS Bull., 2007, 32, 314–322 CrossRef CAS.
- D. R. Paul and L. M. Robeson, Polymer, 2008, 49, 3187–3204 CrossRef CAS.
- R. Tao and S. L. Simon, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 1131–1138 CrossRef CAS.
- D. Cangialosi, V. M. Boucher, A. Alegría and J. Colmenero, Soft Matter, 2013, 9, 8619–8630 RSC.
- V. V. Ginzburg and L. M. Hall, Theory and Modeling of Polymer Nanocomposites, Springer, 2021 Search PubMed.
- S. Cheng, Broadband dielectric spectroscopy: a modern analytical technique, ACS Publications, 2021, pp. 157–183 Search PubMed.
- S. Cheng, S. Mirigian, J.-M. Y. Carrillo, V. Bocharova, B. G. Sumpter, K. S. Schweizer and A. P. Sokolov, J. Chem. Phys., 2015, 143, 194704 CrossRef PubMed.
- S. Cheng, B. Carroll, W. Lu, F. Fan, J.-M. Y. Carrillo, H. Martin, A. P. Holt, N.-G. Kang, V. Bocharova and J. W. Mays, Macromolecules, 2017, 50, 2397–2406 CrossRef CAS.
- S. Cheng, S.-J. Xie, J.-M. Y. Carrillo, B. Carroll, H. Martin, P.-F. Cao, M. D. Dadmun, B. G. Sumpter, V. N. Novikov and K. S. Schweizer, ACS Nano, 2017, 11, 752–759 CrossRef CAS PubMed.
- S. Cheng, B. Carroll, V. Bocharova, J.-M. Carrillo, B. G. Sumpter and A. P. Sokolov, J. Chem. Phys., 2017, 146, 203201 CrossRef PubMed.
- J. Moll and S. K. Kumar, Macromolecules, 2012, 45, 1131–1135 CrossRef CAS.
- B. Natarajan, Y. Li, H. Deng, L. C. Brinson and L. S. Schadler, Macromolecules, 2013, 46, 2833–2841 CrossRef CAS.
- H. Montes, F. Lequeux and J. Berriot, Macromolecules, 2003, 36, 8107–8118 CrossRef CAS.
- A. Papon, H. Montes, F. Lequeux and L. Guy, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 2490–2496 CrossRef CAS.
- J. Berriot, F. Lequeux, H. Montes and H. Pernot, Polymer, 2002, 43, 6131–6138 CrossRef CAS.
- J. Berriot, H. Montes, F. Lequeux, D. Long and P. Sotta, Macromolecules, 2002, 35, 9756–9762 CrossRef CAS.
- J. Berriot, H. Montes, F. Lequeux, D. Long and P. Sotta, Europhys. Lett., 2003, 64, 50 CrossRef CAS.
- A. Papon, H. Montes, M. Hanafi, F. Lequeux, L. Guy and K. Saalwächter, Phys. Rev. Lett., 2012, 108, 65702 CrossRef.
- A. Papon, K. Saalwächter, K. Schäler, L. Guy, F. Lequeux and H. Montes, Macromolecules, 2011, 44, 913–922 CrossRef CAS.
- D. Long and F. Lequeux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 371–387 CrossRef CAS.
- P. Rittigstein and J. M. Torkelson, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2935–2943 CrossRef CAS.
- P. Rittigstein, R. D. Priestley, L. J. Broadbelt and J. M. Torkelson, Nat. Mater., 2007, 6, 278–282 CrossRef CAS.
- H. Wang, J. L. Hor, Y. Zhang, T. Liu, D. Lee and Z. Fakhraai, ACS Nano, 2018, 12, 5580–5587 CrossRef CAS PubMed.
- D. V. Guseva, P. V. Komarov and A. V. Lyulin, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 473–485 CrossRef CAS.
- R. J. Lang and D. S. Simmons, Macromolecules, 2013, 46, 9818–9825 CrossRef CAS.
- A. Ghanekarade, A. D. Phan, K. S. Schweizer and D. S. Simmons, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 2104398118 CrossRef.
- H. Zhang, D.-D. Sun, Y. Peng, J.-H. Huang and M.-B. Luo, Phys. Chem. Chem. Phys., 2019, 21, 23209–23216 RSC.
- E. Sharifzadeh and K. Cheraghi, Mech. Mater., 2021, 160, 103990 CrossRef.
- R. A. A. Khan, H.-K. Qi, J.-H. Huang and M.-B. Luo, Soft Matter, 2021, 17, 8095–8104 RSC.
- K. J. Lee, D. K. Lee, Y. W. Kim, W.-S. Choe and J. H. Kim, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 2232–2238 CrossRef CAS.
- A. D. Phan and K. S. Schweizer, Macromolecules, 2018, 51, 6063–6075 CrossRef CAS.
- A. D. Phan and K. S. Schweizer, J. Chem. Phys., 2019, 150, 44508 CrossRef PubMed.
- A. D. Phan and K. S. Schweizer, J. Phys. Chem. B, 2018, 122, 8451–8461 CrossRef CAS PubMed.
- J. DeFelice and J. E. G. Lipson, Soft Matter, 2019, 15, 1651–1657 RSC.
- R. P. White and J. E. G. Lipson, Soft Matter, 2021, 17, 9755–9764 RSC.
- R. P. White and J. E. G. Lipson, Phys. Rev. Lett., 2020, 125, 58002 CrossRef CAS PubMed.
- V. Ginzburg, Macromolecules, 2022, 55, 873–882 CrossRef CAS.
- R. P. White and J. E. G. Lipson, Macromolecules, 2016, 49, 3987–4007 CrossRef CAS.
- R. P. White and J. E. G. Lipson, ACS Macro Lett., 2017, 6, 529–534 CrossRef CAS PubMed.
- A. K. Doolittle, J. Appl. Phys., 1951, 22, 1471–1475 CrossRef CAS.
- S. Mirigian and K. S. Schweizer, J. Chem. Phys., 2014, 140, 194506 CrossRef PubMed.
- V. Ginzburg, Soft Matter, 2020, 16, 810–825 RSC.
- V. Ginzburg, Soft Matter, 2021, 17, 9094–9106 RSC.
- V. Ginzburg, Macromolecules, 2021, 54, 2774–2782 CrossRef CAS.
- V. V. Ginzburg, A. Zaccone and R. Casalini, Soft Matter, 2022, 18, 8456–8466 RSC.
- R. Busselez, R. Lefort, Q. Ji, F. Affouard and D. Morineau, Phys. Chem. Chem. Phys., 2009, 11, 11127–11133 RSC.
- W. Zhu, C. Zhang, Y. Zhu, R. An, X. Lu, Y. Shi and S. Jiang, J. Mol. Liq., 2019, 291, 111238 CrossRef CAS.
- S. Merabia and D. Long, Macromolecules, 2008, 41, 3284–3296 CrossRef CAS.
- S. Merabia, P. Sotta and D. Long, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 15, 189–210 CrossRef CAS PubMed.
- M. L. Ferrer, C. Lawrence, B. G. Demirjian, D. Kivelson, C. Alba-Simionesco and G. Tarjus, J. Chem. Phys., 1998, 109, 8010–8015 CrossRef CAS.
- R. Casalini and C. M. Roland, Phys. Rev. Lett., 2014, 113, 85701 CrossRef CAS.
- R. Casalini, U. Mohanty and C. M. Roland, J. Chem. Phys., 2006, 125, 14505 CrossRef CAS.
- C. M. Roland, S. Bair and R. Casalini, J. Chem. Phys., 2006, 125, 124508 CrossRef CAS PubMed.
- C. M. Roland, R. Casalini, R. Bergman and J. Mattsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 12201 CrossRef.
- M. Paluch, R. Casalini, S. Hensel-Bielowka and C. M. Roland, J. Chem. Phys., 2002, 116, 9839–9844 CrossRef CAS.
- A. G. M. Ferreira, A. P. V. Egas, I. M. A. Fonseca, A. C. Costa, D. C. Abreu and L. Q. Lobo, J. Chem. Thermodyn., 2017, 113, 162–182 CrossRef CAS.
- V. V. Ginzburg, arXiv, 2024, preprint, arXiv:2409.01471 DOI:10.48550/arXiv.2409.01471.
- B. Derjaguin, Kolloid-Z., 1934, 69, 155–164 CrossRef.
- W. A. Curtin, Phys. Rev. Lett., 1987, 59, 1228 CrossRef CAS PubMed.
- J. Wu, AIChE J., 2006, 52, 1169–1193 CrossRef CAS.
- J. Wu and Z. Li, Annu. Rev. Phys. Chem., 2007, 58, 85–112 CrossRef CAS PubMed.
- L. D. Landau, L. P. Pitaevskii, A. M. Kosevich and E. M. Lifshitz, Theory of Elasticity, Elsevier Science, 2012, vol. 7 Search PubMed.
- H. Vogel, Phys. Z., 1921, 22, 645–646 CAS.
- G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339–355 CrossRef CAS.
- G. Tammann and W. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245–257 CrossRef CAS.
- W. Kauzmann, Chem. Rev., 1948, 43, 219 CrossRef CAS.
- R. P. White and J. E. G. Lipson, J. Chem. Phys., 2017, 147, 184503 CrossRef PubMed.
- M. L. Williams, R. F. Landel and J. D. Ferry, J. Am. Chem. Soc., 1955, 77, 3701–3707 CrossRef CAS.
- G. P. Johari and E. Whalley, Faraday Symp. Chem. Soc., 1972, 6, 23–41 RSC.
- A. D. Phan and K. S. Schweizer, ACS Macro Lett., 2020, 9, 448–453 CrossRef CAS PubMed.
- K. S. Schweizer and D. S. Simmons, J. Chem. Phys., 2019, 151, 240901 CrossRef PubMed.
- T. Blochowicz, C. Gainaru, P. Medick, C. Tschirwitz and E. A. Rössler, J. Chem. Phys., 2006, 124, 134503 CrossRef CAS PubMed.
- B. Schmidtke, N. Petzold, R. Kahlau and E. A. Rössler, J. Chem. Phys., 2013, 139, 84504 CrossRef CAS PubMed.
- C. M. Evans, H. Deng, W. F. Jager and J. M. Torkelson, Macromolecules, 2013, 46, 6091–6103 CrossRef CAS.
- J. Bicerano, Prediction of polymer properties, CRC Press, Boca Raton, FL, 3rd edn, 2002 Search PubMed.
- H. Wang, K. L. Kearns, A. Zhang, A. Arabi Shamsabadi, Y. Jin, A. Bond, S. M. Hurney, C. Morillo and Z. Fakhraai, Nano Lett., 2021, 21, 1778–1784 CrossRef CAS.
- D. M. Walters, R. Richert and M. D. Ediger, J. Chem. Phys., 2015, 142, 134504 CrossRef PubMed.
- S. Mirigian and K. S. Schweizer, J. Chem. Phys., 2014, 140, 194507 CrossRef.
- W. Zhang, F. W. Starr and J. F. Douglas, J. Chem. Phys., 2021, 155, 174901 CrossRef CAS.
- P. Z. Hanakata, J. F. Douglas and F. W. Starr, J. Chem. Phys., 2012, 137, 244901 CrossRef PubMed.
- B. A. Pazmiño Betancourt, J. F. Douglas and F. W. Starr, Soft Matter, 2013, 9, 241–254 RSC.
- W.-S. Xu, J. F. Douglas, W. Xia and X. Xu, Macromolecules, 2020, 53, 7239–7252 CrossRef CAS.
- D. S. Simmons, M. T. Cicerone, Q. Zhong, M. Tyagi and J. F. Douglas, Soft Matter, 2012, 8, 11455–11461 RSC.
- S. Cheng, D. Kogut, J. Zheng, S. Patil, F. Yang and W. Lu, J. Chem. Phys., 2024, 160, 114904 CrossRef CAS PubMed.
- S. Merabia and D. Long, J. Chem. Phys., 2006, 125, 234901 CrossRef PubMed.
- R. Casalini and C. M. Roland, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 14210 CrossRef.
- C. M. Roland and R. Casalini, J. Chem. Phys., 2005, 122, 134505 CrossRef CAS PubMed.
- C. M. Roland and R. Casalini, Macromolecules, 2005, 38, 8729–8733 CrossRef CAS.
- C. M. Roland and R. Casalini, Macromolecules, 2003, 36, 1361–1367 CrossRef CAS.
- R. Casalini and C. M. Roland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 62501 CrossRef CAS PubMed.
- M. Paluch, C. M. Roland, R. Casalini, G. Meier and A. Patkowski, J. Chem. Phys., 2003, 118, 4578–4582 CrossRef CAS.
- K. L. Ngai, R. Casalini, S. Capaccioli, M. Paluch and C. M. Roland, J. Phys. Chem. B, 2005, 109, 17356–17360 CrossRef CAS PubMed.
- K. Z. Win and N. Menon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 40501 CrossRef PubMed.
- M. Ikeda and M. Aniya, Materials, 2010, 3, 5246–5262 CrossRef CAS PubMed.
- M. Ikeda and M. Aniya, Glass Phys. Chem., 2021, 47, 427–430 CrossRef CAS.
- I. Popov, B. Carroll, V. Bocharova, A.-C. Genix, S. Cheng, A. Khamzin, A. Kisliuk and A. P. Sokolov, Macromolecules, 2020, 53, 4126–4135 CrossRef CAS.
- J. Yang, M. Melton, R. Sun, W. Yang and S. Cheng, Macromolecules, 2019, 53, 302–311 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00846d |
| This journal is © The Royal Society of Chemistry 2025 |





