 Open Access Article
Open Access ArticleA unified active learning framework for photosensitizer design
Yizhe
Chen†
a,
Shomik
Verma†
b,
Kevin P.
Greenman†
 cde,
Haoyu
Yin
a,
Zhihao
Wang
cde,
Haoyu
Yin
a,
Zhihao
Wang
 a,
Lanjing
Wang
f,
Jiali
Li
*g,
Rafael
Gómez-Bombarelli
a,
Lanjing
Wang
f,
Jiali
Li
*g,
Rafael
Gómez-Bombarelli
 *h,
Aron
Walsh
*h,
Aron
Walsh
 *i and
Xiaonan
Wang
*i and
Xiaonan
Wang
 *a
*a
aDepartment of Chemical Engineering, State Key Laboratory of Chemical Engineering and Low-carbon Technology, Tsinghua University, Beijing 100084, China. E-mail: wangxiaonan@tsinghua.edu.cn
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: skverma@mit.edu
cDepartment of Chemical Engineering, Catholic Institute of Technology, Cambridge, Massachusetts, USA. E-mail: kgreenman@catholic.tech
dDepartment of Chemistry, Catholic Institute of Technology, Cambridge, Massachusetts, USA
eDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA
fInstitute of Flexible Electronics (IFE) & Frontiers Science Center for Flexible Electronics, Northwestern Polytechnical University, Xi'an, Shaanxi 710072, China. E-mail: wanglanjing@mail.nwpu.edu.cn
gResearch Center for Eco-Environmental Sciences, Chinese Academy of Sciences, Beijing 100085, China. E-mail: jlli@rcees.ac.cn
hDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: rafagb@mit.edu
iDepartment of Materials, Imperial College London, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
First published on 10th November 2025
Abstract
The design of high-performance photosensitizers for next-generation photovoltaic and clean energy applications remains a formidable challenge due to the vast chemical space, competing photophysical trade-offs, and computational limitations of traditional quantum chemistry methods. While machine learning offers potential solutions, existing approaches suffer from data scarcity and inefficient exploration of molecular configurations. This work introduces a unified active learning framework that systematically integrates semi-empirical quantum calculations with adaptive molecular screening strategies to accelerate photosensitizer discovery. Our methodology combines three principal components: (1) A hybrid quantum mechanics/machine learning pipeline generating a chemically diverse molecular dataset while maintaining quantum chemical accuracy at significantly reduced computational costs; (2) a graph neural network architecture and uncertainty quantification; (3) Novel acquisition strategies that dynamically balance broad chemical space exploration with targeted optimization of photophysical objectives. The framework demonstrates superior performance in predicting critical energy levels (T1/S1) compared to conventional screening approaches, while effectively prioritizing synthetically feasible candidates. By open-sourcing both the curated molecular dataset and implementation tools, this work establishes an extensible platform for data-driven discovery of optoelectronic materials, with immediate applications in solar energy conversion and beyond.
1 Introduction
Photosensitizers (PSs) have emerged as critical functional materials in modern energy and biomedical technologies, driving innovations from solar energy harvesting to photodynamic therapy.1–4 Their expanding applications in wearable devices, sterilization systems, and optical sensors demand precise control over photophysical properties such as triplet yields and excited-state lifetimes.5,6 However, the rational design of high-performance PSs faces three fundamental challenges that hinder rapid progress.First, previous work has shown that combinatorial D–A assembly yields libraries containing more than one million PS candidates, far exceeding the capacity of conventional trial-and-error approaches.7–9 For example, subtle structural variations in porphyrin derivatives—such as peripheral substituent patterns—can shift absorption maxima by over 50 nm while altering quantum yields by orders of magnitude.7,10,11 Second, the intricate balance between competing photophysical properties creates a complex optimization landscape. A PS optimized for strong visible light absorption may suffer from rapid triplet–triplet annihilation, while molecules with ideal S1/T1 energy ratios often exhibit poor solubility or photostability.12,13 Third, computational screening methods such as time-dependent density-functional theory (TD-DFT), though theoretically rigorous, become prohibitively expensive for geometry optimization and large-scale exploration, requiring days of computation for a single medium-sized molecule (50+ atoms).14,15
Recent advances in machine learning (ML) offer promising solutions to these bottlenecks.16,17 By establishing quantitative structure–property relationships (QSPRs), ML models can predict key PS characteristics like singlet-triplet energy gaps (ΔEST) with millisecond inference times.10 Nevertheless, existing ML approaches face two critical limitations:1 Public datasets contain less than 0.1% of the required photophysical data for PS design, creating severe data scarcity issues;2 conventional ML workflows prioritize passive learning from static datasets, inefficiently allocating computational resources to chemically redundant regions.12–14
Active learning (AL) is a machine learning approach where the model selects the most informative data points for labeling, aiming to improve performance with fewer labeled examples.18 It addresses these limitations through iterative cycles of prediction and targeted data acquisition.15,19–21 Unlike traditional methods that treat all molecules equally, AL algorithms dynamically identify the most informative candidates for quantum chemical calculations—those with high prediction uncertainty or high potential to improve model performance.22–24 Recent demonstrations in catalyst discovery achieved 32× acceleration over random screening by prioritizing metal alloys with optimal d-band centers15,25 For PS design specifically, AL's ability to navigate high-dimensional chemical spaces while respecting synthetic constraints could revolutionize molecular discovery pipelines.26–30
Despite these promising developments, existing AL applications in molecular and materials discovery remain limited in generality and methodological scope. Yoo et al. developed an iterative inverse-design workflow combining density-functional tight binding (DFTB) for property labeling, a graph convolutional neural network (GCNN) surrogate, and a masked-language-model (MLM) generator to optimize the HOMO–LUMO gap (HLG) of molecules.31 Their selection strategy primarily relies on property-value thresholds and periodic surrogate retraining, rather than a formal uncertainty-based acquisition loop. In addition, the target property (HLG) is not directly related to photosensitizer photophysics, and the implementation is available only upon request, which constrains reproducibility and extension.
By contrast, Dodds et al. integrated active learning with reinforcement learning (RL–AL) to enhance sample efficiency under multi-objective optimization oracles such as docking and ROCS, and released their implementation openly.32 While this framework effectively explores exploration–exploitation trade-offs, it is tailored to generic molecular design tasks and lacks photophysical objectives or physics-informed acquisition strategies specific to photosensitizer discovery.
Building upon these directions, our study establishes a unified active-learning (AL) framework that extends beyond task-specific implementations and explicitly targets photosensitizer discovery. The framework integrates three tightly coupled components: (i) a large-scale ML–xTB-calibrated dataset of 655![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 photosensitizer candidates labeled for T1/S1, achieving sub-0.08 eV mean absolute error (MAE) and reducing computational cost by 99% compared with TD-DFT;33 (ii) a hybrid acquisition strategy that combines ensemble-based uncertainty estimation with a physics-informed objective function and an early-cycle diversity schedule, enabling balanced exploration and exploitation during iterative sampling; and (iii) a fully open-source, reproducible implementation that facilitates transparent benchmarking and community reuse.
197 photosensitizer candidates labeled for T1/S1, achieving sub-0.08 eV mean absolute error (MAE) and reducing computational cost by 99% compared with TD-DFT;33 (ii) a hybrid acquisition strategy that combines ensemble-based uncertainty estimation with a physics-informed objective function and an early-cycle diversity schedule, enabling balanced exploration and exploitation during iterative sampling; and (iii) a fully open-source, reproducible implementation that facilitates transparent benchmarking and community reuse.
Experimental benchmarks demonstrate that the proposed sequential AL strategy, which first explores chemical diversity before focusing on target regions, consistently outperforms static baselines by 15–20% in test-set MAE. By integrating data calibration, uncertainty-driven acquisition, and open implementation in a single workflow, this framework overcomes the methodological limitations of previous AL systems and provides a generalizable, data-efficient paradigm for photosensitizer discovery, offering immediate applications in solar fuels, photocatalysis, and optoelectronic materials design.
2 The unified active learning framework
2.1 Overview of the active learning workflow
Our active-learning platform for photosensitizer discovery consists of four main stages: (i) preparation of the molecular dataset and chemical space definition, (ii) training of graph neural network surrogates to predict key photophysical properties, (iii) molecule selection through complementary acquisition strategies, and (iv) validation via quantum-chemical calculations or experiments. This workflow enables iterative improvement of the surrogate model and efficient exploration of the vast molecular design space (Fig. 1). The following subsections describe the construction of the chemical space and the details of the active-learning protocol.2.2 Design space generation
The construction of a chemically relevant and computationally tractable design space forms the foundation of our active learning framework. Traditional approaches relying solely on expert intuition or brute-force enumeration fail to address the dual challenges of chemical diversity and computational feasibility.34,35We combined Simplified Molecular-Input Line-Entry System (SMILES) data from numerous public molecular datasets to construct a unified library of 655![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 candidate photosensitizer molecules. Each source dataset was chosen because it contributes molecules with relevant excited-state or optical properties, thereby ensuring that our merged collection covers a broad range of photophysical characteristics. Starting from an initial seed set of 50
197 candidate photosensitizer molecules. Each source dataset was chosen because it contributes molecules with relevant excited-state or optical properties, thereby ensuring that our merged collection covers a broad range of photophysical characteristics. Starting from an initial seed set of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules, we expanded the library by integrating many diverse data sources (computational, experimental, and even patent-derived). We then predicted the lowest singlet and triplet energies (S1 and T1) for all candidates using our ML-xTB workflow, achieving DFT-level accuracy at 1% of the typical cost. We performed the analysis of the dataset in Fig. 3. (Full details of the datasets, including their names, references, and selection criteria, are provided in the SI (Text S5).)
000 molecules, we expanded the library by integrating many diverse data sources (computational, experimental, and even patent-derived). We then predicted the lowest singlet and triplet energies (S1 and T1) for all candidates using our ML-xTB workflow, achieving DFT-level accuracy at 1% of the typical cost. We performed the analysis of the dataset in Fig. 3. (Full details of the datasets, including their names, references, and selection criteria, are provided in the SI (Text S5).)
1. Initial seed generation: A diverse set of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules was curated from public databases (PubChemQC,36 QMspin37) and expert-designed scaffolds (porphyrins, phthalocyanines). SMILES strings were standardized using RDKit, with stereochemistry and tautomer states normalized via Morgan fingerprint clustering (radius = 2, 1024 bits).
000 molecules was curated from public databases (PubChemQC,36 QMspin37) and expert-designed scaffolds (porphyrins, phthalocyanines). SMILES strings were standardized using RDKit, with stereochemistry and tautomer states normalized via Morgan fingerprint clustering (radius = 2, 1024 bits).
2. xTB-sTDA high-throughput calculations: Each molecule underwent geometry optimization and excited-state calculation using the geometry, frequency, noncovalent–tight binding (GFN2-xTB)38 method combined with the simplified Tamm–Dancoff approximation (sTDA)39 implemented in xtb (GFN2-xTB/xtb-sTDA):
| S1 = Esinglet − Eground | (1) |
| T1 = Etriplet − Eground | (2) |
| ΔEST = S1 − T1 | (3) |
For the initial seed set (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules), additional TD-DFT calculations (B3LYP/6-31+G(d), Gaussian 16) were performed on the xTB-optimized geometries to provide accurate reference values (details provided in SI).
000 molecules), additional TD-DFT calculations (B3LYP/6-31+G(d), Gaussian 16) were performed on the xTB-optimized geometries to provide accurate reference values (details provided in SI).
3. Machine learning calibration: A 10-model ensemble of Chemprop Message Passing Neural Networks (Chemprop-MPNN) was trained to correct systematic errors between the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 xTB-sTDA and TD-DFT calculations for the S1 and T1 excitations separately. Each network dynamically generated molecular representations from SMILES strings without static fingerprints, predicting state-specific errors:
000 xTB-sTDA and TD-DFT calculations for the S1 and T1 excitations separately. Each network dynamically generated molecular representations from SMILES strings without static fingerprints, predicting state-specific errors:
 | (4) |
 | (5) |
The multitask loss function minimized during training was:
 | (6) |
The calibrated energies were then computed as:
 | (7) |
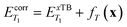 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 molecules). We performed only xTB-sTDA calculations for the remaining molecules beyond the seed set and then applied the ML correction model. This calibration approach reduced the mean absolute error (MAE) from 0.23 eV (raw xTB) to 0.08 eV (ML-corrected) with respect to TD-DFT for the 50
197 molecules). We performed only xTB-sTDA calculations for the remaining molecules beyond the seed set and then applied the ML correction model. This calibration approach reduced the mean absolute error (MAE) from 0.23 eV (raw xTB) to 0.08 eV (ML-corrected) with respect to TD-DFT for the 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules in the calibration set.
000 molecules in the calibration set.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 additional molecules were sampled from the remaining pool, with a total of 8 rounds conducted for each acquisition strategy. This protocol enables model development and tuning on one portion of the data, while reserving a representative set of promising candidates for unbiased final evaluation (Fig. 4).
000 additional molecules were sampled from the remaining pool, with a total of 8 rounds conducted for each acquisition strategy. This protocol enables model development and tuning on one portion of the data, while reserving a representative set of promising candidates for unbiased final evaluation (Fig. 4).
2.3 Surrogate model: Chemprop-MPNN
This choice was driven by two key advantages: (1) Its explicit modeling of bond directionality (e.g., single, double, conjugated) reduces noise from undirected representations, which is critical for capturing electronic transitions in photoactive molecules; and (2) its native ensemble support enables simultaneous quantification of model and data uncertainties, making it highly suitable for active learning strategies.
 | (9) |
 | (10) |
During the active learning process, as we incrementally increased the training set size from 5k to 165k samples, we conducted independent Bayesian hyperparameter optimizations at each data scale to determine the optimal model architectures. The hyperparameter search employed Root Mean Square Error (RMSE), the default evaluation metric in Chemprop, as the criterion for selecting the best configuration.
Our analysis showed that the optimal architecture did not converge to a single universal configuration; instead, the best-performing hyperparameters varied distinctly with the dataset size, including model depths (ranging from 3 to 6), hidden layer widths (hidden_size ranging from 1600 to 1900), and dropout rates (0.05–0.25). In medium-to-large data regimes (65–165k), shallow architectures (depth = 3), wider hidden layers (hidden_size = 1900), and lower dropout rates (0.05) consistently outperformed other configurations. Adopting these individually optimized hyperparameters at each training set size reduced the test RMSE by approximately 8–15% compared to an untuned baseline model (e.g., depth = 3, hidden_size = 1200, dropout = 0.10). This stage-specific optimization strategy ensured optimal architecture selection at each phase of the active learning cycle, thereby eliminating potential bias from a fixed architecture and enabling fair comparisons across different acquisition strategies.
2.4 Acquisition strategies
Four strategies were systematically benchmarked to balance exploration and exploitation (Fig. 5):42,43:| Ascore(x) = σS12(x)+σT12(x), | (11) |
 | (12) |
 discards a candidate if its radius-2, 2048 bit Morgan fingerprint yields a Tanimoto similarity greater than 0.6 to any member of B, thereby guaranteeing sufficient structural diversity while still prioritizing high-uncertainty points.
discards a candidate if its radius-2, 2048 bit Morgan fingerprint yields a Tanimoto similarity greater than 0.6 to any member of B, thereby guaranteeing sufficient structural diversity while still prioritizing high-uncertainty points.
The Tanimoto similarity between two molecules x and x′, based on their binary fingerprint vectors f(x) and f(x′), is defined as:
 | (13) |
 are the numbers of ‘on’ bits in each fingerprint, and
are the numbers of ‘on’ bits in each fingerprint, and  is the number of bits shared by both fingerprints. Here, f(x) denotes the Morgan fingerprint of molecule x; the Tanimoto similarity measures the overlap between the binary features of two molecules.
is the number of bits shared by both fingerprints. Here, f(x) denotes the Morgan fingerprint of molecule x; the Tanimoto similarity measures the overlap between the binary features of two molecules.
is close to either of two design targets: emitter and sensitizer.33 The overall score is a weighted sum of the two targets, with tunable weights we, ws ≥ 0 satisfying we + ws = 1 (default we = ws = 0.5).
v1 — Probability-within-band kernel
 | (14) |
v2 — Exponential alignment kernel
 | (15) |
v3 — Expected-improvement kernel. An EI-style variant that accounts for correlation between T1 and S1 is derived in Text S3; its numerical results are reported in Fig. S3 and therefore omitted here for brevity.
Detailed derivations, hyperparameter sweeps, and a head-to-head comparison of v1–v3 are provided in SI (Text S1–S3).
• µ(x), σ2(x) — mean and variance of the ensemble prediction for m(x);
• τe = 0.5, τs = 1.0 — emitter-like and sensitizer-like targets;44,45
• we, ws — weights for the two targets (0.5, 0.5);
• ɛ — half-width of the tolerance band (0.05);
• η — selectivity parameter in v2 (5).
2.7 × 105 emitter, sensitizer and analogue structures were subjected to AiZynthFinder. A molecule was labeled synthesized (y = 1) if the planner discovered at least one complete route to commercially available precursors within a user-defined search limit (maximum nstep retrosynthetic steps or tmax seconds). Molecules for which no route was found under these restrictions were labeled non-synthesizable (y = 0). The resulting binary data set was used to train a Chemprop message-passing neural network that outputs a continuous probability Psynth(x) ∈ [0, 1]. We refer to this domain-adapted score as the PhotoSynthScore.
During each AL iteration, we down-weight candidates that are unlikely to be synthesizable:
 | (16) |
 is the indicator function. Only molecules with Psynth ≥ 0.6 pass the filter, focusing computational effort on candidates that are both high-performing and practically attainable. Empirically, incorporating the PhotoSynthScore improves search efficiency and maintains chemical realism throughout the discovery campaign.
is the indicator function. Only molecules with Psynth ≥ 0.6 pass the filter, focusing computational effort on candidates that are both high-performing and practically attainable. Empirically, incorporating the PhotoSynthScore improves search efficiency and maintains chemical realism throughout the discovery campaign.
3 Results and discussion
3.1 Sampling strategy benchmarking
Random sampling (baseline): To establish a fair reference, five independent random-sampling baselines were conducted under identical model architectures, hyperparameters, and labeling budgets. At each acquisition round, molecules were uniformly drawn from the unlabeled pool with the same batch size as in the active learning cycles. Averaged over five random seeds, the random baseline yielded a final external-test MAE of 0.083 eV. This result confirms that the observed performance improvement originates from the acquisition strategy besides data volume, demonstrating that the active learning framework effectively prioritizes more informative molecules for labeling.Uncertainty sampling: Reduced MAE from 0.091 eV to 0.077 eV within 4 rounds, with performance plateauing at Round 8. Deepening hidden layers further improved accuracy across all test sets, particularly for large molecules (>20 non-H atoms).
Diversity-enhanced sampling: Introducing Tanimoto similarity thresholds (<0.6) increased heterocyclic system coverage by 25%, but aggressive thresholds (<0.4) raised RMSE by 15% due to oversampling of chemically irrelevant regions.
Target-property optimization: Focused screening of T1/S1 ratios (1 for sensitizers, 0.5 for emitters) reduced emitter MAE from 0.065 eV → 0.061 eV versus uncertainty sampling.
Synthetic feasibility integration: Threshold filtering (Psynth ≤ 0.6) eliminated over 20% of all candidates, as these were judged to be impractical for synthesis.
3.2 Model performance and dataset size
As the size of the training dataset increases, the overall prediction accuracy of our model improves significantly, reflected by decreasing mean absolute error (MAE) and root mean square error (RMSE). However, this improvement demonstrates diminishing returns, indicating that once the dataset is sufficiently large, further additions yield limited performance gains. This trend is clearly depicted by the error curves across active learning rounds (Fig. 6), where initial rounds substantially reduce prediction errors, followed by a gradual plateau indicating saturation of the model's capacity to extract useful information.Most predictions achieve high accuracy within acceptable chemical precision thresholds. However, a small fraction of compounds exhibit notably larger errors, likely arising from unique or rare structural motifs not adequately represented in the training set. This highlights areas for future model refinement, particularly addressing the “long-tail” of challenging cases.
3.3 Impact of sampling strategies on data distribution and model generalization
We investigated how various active learning sampling strategies, uncertainty sampling, diversity sampling, target property optimization, and synthesizability-guided sampling, impact data set composition and model generalization.Uncertainty sampling prioritizes molecules that the model finds the most ambiguous, thus rapidly improving the model precision by identifying informative samples. Diversity sampling aims to maximize coverage of chemical space, ensuring structural heterogeneity and preventing redundancy. Target-property optimization selects molecules with extreme property values, facilitating efficient exploration of high-performance regions, but potentially neglecting broader chemical diversity. Lastly, synthesizability-guided sampling incorporates synthetic feasibility, prioritizing practical compounds that are experimentally accessible.
These differences directly affect model training dynamics and generalization performance. Uncertainty sampling yields rapid initial reductions in prediction errors, demonstrating superior efficiency. Diversity sampling ensures broader chemical generalization but shows moderate accuracy improvements. Target-property sampling initially contributes less to global error reductions but significantly enhances predictions for extreme property cases. Synthesizability-guided strategies moderately slow accuracy gains due to conservative selections but ensure higher practical relevance.
We further summarized efficiency and error metrics for each strategy in Table 1, providing comprehensive comparisons on test MAE, and chemical space coverage. This analysis facilitates the selection of strategies that align with research priorities, balancing prediction accuracy, scope of the study, and practical applicability.
| Strategy | Initial MAE (eV) | Final MAE (eV) | Rounds to convergence | Chemical space coverage |
|---|---|---|---|---|
| Pure random (baseline) | 0.149 | 0.083 ± 0.001 | — | — |
| Pure uncertainty | 0.149 | 0.077 | 8 | Moderate |
| Uncertainty + batch diversity | 0.149 | 0.078 | 9 | High |
| Target property + batch diversity | 0.149 | 0.062 | 9 | Moderate (target-focused) |
| Portfolio strategy | 0.149 | 0.059 | 9 | High (balanced) |
| Portfolio + synthesizability | 0.149 | 0.074 | 9 | High (practically feasible) |
3.4 Portfolio strategies: multi-phase active learning and synthesizability constraints
Given the trade-offs above, an effective approach is to combine exploration and exploitation in a staged or simultaneous fashion—what we term a portfolio strategy. The idea is to first use uncertainty sampling to broadly train the model (exploration), and then gradually or abruptly shift toward selecting for the target property as the model becomes more reliable (exploitation). This latter approach dynamically balances exploration vs. exploitation within each iteration, rather than in separate phases.Specifically, the filtered portfolio strategy shows a slight uptick or oscillation in MAE during the final rounds. After the switch to target-driven selection, the model begins choosing molecules that it predicts have extreme target values—some of these are likely unusual, highly complex structures that the model is less familiar with (and which might be chemically difficult to synthesize in reality). Incorporating such exotic compounds can momentarily worsen the model's overall performance: the newly added data might lie outside the domain where the model has predictive strength, leading to higher prediction errors for those points (and possibly disrupting the model's previously learned correlations). In other words, without the synthesizability filter, the model sometimes ventures into out-of-distribution regions in pursuit of high target property, and as a result the global MAE stops decreasing and even increases slightly in that phase. This phenomenon can be interpreted as a form of model extrapolation or overfitting issue—the model is essentially overextending into chemical space where its predictions are not reliable, analogous to how an overly aggressive exploitative strategy can mislead the model.
One notable advantage of the hybrid strategy is that it avoids an abrupt transition that might destabilize the model. In the sequential strategies, we sometimes see a kink or change in the MAE trend at the point of switching from uncertainty to target mode—if the switch happens too early, the model could struggle (as discussed, a slight MAE rise can occur if the model isn't ready to accurately handle the exploitation picks). The continuous strategy softens this by always maintaining a mix; effectively, it performs a dynamic rebalancing: as the model's confidence grows, more of the selected batch inherently contributes to exploitation (since fewer points will be at high uncertainty, the focus naturally shifts to high predicted property, without ever entirely ignoring uncertainty). This dynamic adjustability is a strong point of the hybrid method. The only slight drawback observed is that the hybrid strategy can be a bit slower to find the very top-performing molecules compared to a full-on exploitation in later rounds. Since it's never selecting only target-optimal candidates, it might miss a few opportunities to immediately test the absolute top predicted molecule in favor of an uncertain one. However, in practice this seems to be a minor penalty—the hybrid still discovers high-performing molecules throughout, just interspersed with exploratory picks. In exchange, it maintains the lowest MAE curve among the methods, indicating it never compromises the model's learning too much in pursuit of the objective.
4 Conclusions
In this work, we present a unified computational framework to tackle the main challenges in photosensitizer discovery by introducing three key innovations:• We developed a hybrid pipeline that combines fast semi-empirical quantum calculations with machine learning correction, enabling us to generate a large dataset of 655![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 diverse candidate molecules. This approach keeps the speed of computation high while ensuring the accuracy of quantum chemistry.
197 diverse candidate molecules. This approach keeps the speed of computation high while ensuring the accuracy of quantum chemistry.
• We designed a sequential active learning strategy that separates the exploration and exploitation phases. First, the model explores chemical space broadly using uncertainty-driven sampling to find new promising areas, and then focuses on finding molecules with the desired T1/S1 energy ratios (1 for sensitizers, 0.5 for emitters).
Our open dataset and modular workflow offer a useful resource for the research community to speed up the development of new energy materials. Through detailed analysis, we show that an active learning approach which combines uncertainty sampling, target-driven optimization, diversity filters, and synthesizability constraints is most effective. This balanced strategy helps us find high-performing molecules faster, while also making sure the predictive model works well on different types of molecules. Adding diversity filters prevents the model from overfitting to very similar compounds, and considering synthesizability ensures the candidates found are likely to be made in real experiments.
While our model works well for small and moderate-sized molecules,48 it is less accurate for larger molecules with highly delocalized electronic structures or strong long-range interactions. This is mainly because the current graph neural networks are better at capturing local structure, and we only use 2D information rather than 3D shapes. For molecules whose properties depend on their 3D arrangement, this can limit our model's performance.
To overcome these issues, future work could explore hybrid architectures that insert multi-head transformer self-attention directly into the message-passing layers of a GNN, going beyond the readout functions currently used in Chemprop, thus capturing both local chemical environments and long-range interatomic dependencies. Adding 3D geometric features, such as distances and angles between atoms, will also help the model better predict properties that depend on molecular shape.49
We also see value in combining multiple types of molecular information, such as electron density and orbital properties, and predicting a range of photophysical properties at once. This multi-task and multimodal approach can make the model stronger and easier to interpret.
Additionally, looking forward, computational methods for molecular discovery have evolved significantly, moving from simple virtual screenings to fully automated experimental platforms. Initially, high-throughput virtual screening (HTVS) allowed researchers to computationally evaluate thousands of candidate molecules from static libraries to quickly identify promising leads.9 Next, active learning methods greatly improved efficiency by selectively and iteratively choosing the most informative candidates, thereby reducing computational cost and speeding up discovery. More recently, a new generation of closed-loop discovery systems has emerged, combining active learning with fully automated laboratories that autonomously synthesize, test, and validate molecular candidates in continuous cycles.50 By incorporating these successive advancements into photosensitizer discovery, future workflows could efficiently and automatically discover effective molecules for practical applications in energy and medicine.
In parallel, a promising direction for future work is to extend our framework from selecting candidates in fixed libraries to generating new molecular structures from scratch. This can be achieved by combining the trained surrogate model with generative techniques such as variational autoencoders, graph-based molecular generators, language-model-driven design, or fragment-based human-in-the-loop strategies. These methods would allow the model to propose novel compounds tailored to target singlet–triplet energy ratios and other design constraints, while exploring chemical space beyond the initial dataset.
For active learning, specifically, adaptive strategies, those that dynamically adjust sampling rules throughout different learning stages, can further improve efficiency and generalization. By smoothly moving between uncertainty, diversity, and target-based sampling, the model can learn more with fewer experiments.
In summary, by applying smart active learning, we were able to further increase the accuracy and usefulness of our method. These steps helped bridge the gap between fast ML predictions and high-accuracy quantum methods, making our framework a reliable tool for discovering new photoactive molecules. Our work highlights the importance of balancing exploration and exploitation, including chemical diversity and synthesizability, and adjusting learning strategies as the model grows, laying a practical foundation for future AI-driven molecular discovery.
Author contributions
Yizhe Chen conceptualized the study, developed the overall framework, implemented the active learning algorithms, and drafted the manuscript. Shomik Verma provided the datasets, performed the implementation of the computational method. Kevin P. Greenman contributed to the algorithm design within Chemprop and provided critical analysis and suggestions regarding the active learning methodologies and reviewed and edited the manuscript. Haoyu Yin, Zhihao Wang, and Lanjing Wang assisted with data visualization, figure preparation, and content curation. Jiali Li, Rafael Gómez-Bombarelli, Aron Walsh, and Xiaonan Wang supervised the project, reviewed and edited the manuscript, and provided oversight throughout the study.Conflicts of interest
The authors declare no competing interests.Data availability
The curated dataset of 655![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 197 photosensitizer candidates and the complete active-learning code are available at https://github.com/jiali1025/A_General_Active_learning_framework_for_MoleDesign. The dataset is released under a CC-BY-4.0 licence and the code under an MIT licence. No further restrictions apply.
197 photosensitizer candidates and the complete active-learning code are available at https://github.com/jiali1025/A_General_Active_learning_framework_for_MoleDesign. The dataset is released under a CC-BY-4.0 licence and the code under an MIT licence. No further restrictions apply.
Supplementary information (SI): additional methodological details, acquisition-function formulations, computational protocols, and a description of the unified dataset supporting this work. See DOI: https://doi.org/10.1039/d5sc05749c.
Acknowledgements
This work is supported by the National Key R&D Program of China (No. 2022ZD0117501), the Scientific Research Innovation Capability Support Project for Young Faculty (ZYGXQNJSKYCXNLZCXM-E7) and Tsinghua University Initiative Scientific Research Program. K. P. G. was supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1745302 and the DARPA Accelerated Molecular Discovery (AMD) program under contract HR00111920025. The authors acknowledge additional support from collaborating institutions and funding agencies.Notes and references
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- Y. Cai, T. Chai, W. Nguyen, J. Liu, E. Xiao, X. Ran, Y. Ran, D. Du, W. Chen and X. Chen, Signal Transduction Targeted Ther., 2025, 10, 115 CrossRef.
- T. Froitzheim, S. Grimme and J.-M. Mewes, J. Chem. Theory Comput., 2022, 18, 7702–7713 CrossRef CAS.
- H. Kim, Y. R. Lee, H. Jeong, J. Lee, X. Wu, H. Li and J. Yoon, Smart Mol., 2023, 1, e20220010 CrossRef.
- F. Hu, S. Xu and B. Liu, Adv. Mater., 2018, 30, 1801350 CrossRef PubMed.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, ACS Cent. Sci., 2020, 6, 513–524 CrossRef CAS PubMed.
- S. Xu, J. Li, P. Cai, X. Liu, B. Liu and X. Wang, J. Am. Chem. Soc., 2021, 143, 19769–19777 CrossRef CAS.
- K. Chen, X. Zhang, J. Wang, D. Li, T. Hou, W. Yang and Y. Kang, Chem. Sci., 2025, 16, 14698–14709 RSC.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, et al. , Nat. Mater., 2016, 15, 1120–1127 CrossRef.
- P. Xu, X. Ji, M. Li and W. Lu, npj Comput. Mater., 2023, 9, 42 CrossRef.
- X. Kang, Z. Du, S. Yang, M. Liang, Q. Liu and J. Qi, Smart Mol., 2024, 2, e20240033 CrossRef CAS PubMed.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Nat. Commun., 2021, 12, 2312 CrossRef CAS.
- M. Sumita, X. Yang, S. Ishihara, R. Tamura and K. Tsuda, ACS Cent. Sci., 2018, 4, 1126–1133 CrossRef CAS PubMed.
- X. Li, P. M. Maffettone, Y. Che, T. Liu, L. Chen and A. I. Cooper, Chem. Sci., 2021, 12, 10742–10754 RSC.
- J. Moon, W. Beker, M. Siek, J. Kim, H. S. Lee, T. Hyeon and B. A. Grzybowski, Nat. Mater., 2024, 23, 108–115 CrossRef CAS.
- Y. Zhao, Q. Liu, J. Du, Q. Meng and L. Zhang, Smart Mol., 2023, 1, e20230012 CrossRef PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- B. Settles, Active Learning Literature Survey) publisher (University of Wisconsin–Madison, Computer Sciences Technical Report 1648, 2009 Search PubMed.
- H. Chun, J. R. Lunger, J. K. Kang, R. Gómez-Bombarelli and B. Han, npj Comput. Mater., 2024, 10, 246 CrossRef CAS.
- C. Duan, A. Nandy, G. G. Terrones, D. W. Kastner and H. J. Kulik, JACS Au, 2022, 3, 391–401 CrossRef.
- R. Ding, J. Liu, K. Hua, X. Wang, X. Zhang, M. Shao, Y. Chen and J. Chen, Sci. Adv., 2025, 11, eadr9038 CrossRef CAS.
- M. Kim, Y. Kim, M. Y. Ha, E. Shin, S. J. Kwak, M. Park, I.-D. Kim, W.-B. Jung, W. B. Lee and Y. Kim, et al. , Adv. Mater., 2023, 35, 2211497 CrossRef CAS.
- L. Wang, Z. Zhou, X. Yang, S. Shi, X. Zeng and D. Cao, Drug Discovery Today, 2024, 103985 CrossRef CAS PubMed.
- T. Yin, G. Panapitiya, E. D. Coda and E. G. Saldanha, J. Cheminf., 2023, 15, 105 Search PubMed.
- H. H. Loeffler, S. Wan, M. Klahn, A. P. Bhati and P. V. Coveney, J. Chem. Theory Comput., 2024, 20, 8308–8328 CAS.
- B. Cree, M. K. Bieniek, S. Amin, A. Kawamura and D. J. Cole, Digital Discovery, 2025, 4, 438–450 RSC.
- P. Shetty, A. Adeboye, S. Gupta, C. Zhang and R. Ramprasad, Chem. Mater., 2024, 36, 7676–7689 CAS.
- S. Thaler, F. Mayr, S. Thomas, A. Gagliardi and J. Zavadlav, npj Comput. Mater., 2024, 10, 86 CrossRef.
- L. Kavalsky, V. I. Hegde, B. Meredig and V. Viswanathan, Digital Discovery, 2024, 3, 999–1010 RSC.
- D. Buterez, J. P. Janet, S. J. Kiddle, D. Oglic and P. Lió, Nat. Commun., 2024, 15, 1517 CrossRef CAS.
- P. Yoo, D. Bhowmik and K. Mehta, et al. , Sci. Rep., 2023, 13, 20031 CrossRef CAS PubMed.
- M. Dodds, J. Guo, T. Löhr, A. Tibo, O. Engkvist and J. P. Janet, Chem. Sci., 2024, 15, 4146–4160 RSC.
- S. Verma, M. Rivera, D. O. Scanlon and A. Walsh, J. Chem. Phys., 2022, 156(13), 134116 CrossRef CAS.
- G. Schneider and U. Fechner, Nat. Rev. Drug Discovery, 2005, 4, 649–663 CrossRef CAS.
- L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- M. Nakata, T. Shimazaki and H. Nakai, J. Chem. Inf. Model., 2017, 57, 1300–1308 CrossRef CAS.
- M. Schwilk, D. N. Tahchieva and O. A. von Lilienfeld, The QMspin data set: Several thousand carbene singlet and triplet state structures and vertical spin gaps computed at MRCISD+Q-F12/cc-pVDZ-F12 level of theory, Materials Cloud Archive, 2020 DOI:10.24435/materialscloud:2020.0051/v1.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- S. Grimme and C. Bannwarth, J. Chem. Phys., 2016, 145(5), 054143 CrossRef.
- E. Heid, K. P. Greenman, Y. Chung, S.-C. Li, D. E. Graff, F. H. Vermeire, H. Wu, W. H. Green and C. J. McGill, J. Chem. Inf. Model., 2024, 64, 9–17 CrossRef CAS.
- J. Westermayr and P. Marquetand, Chem. Rev., 2020, 121, 9873–9926 CrossRef.
- M. Martyka, L. Zhang, F. Ge, Y.-F. Hou, J. Jankowska, M. Barbatti and P. O. Dral, npj Comput. Mater., 2025, 11, 1–12 CrossRef.
- A. Nigam, R. Pollice, G. Tom, K. Jorner, J. Willes, L. Thiede, A. Kundaje and A. Aspuru-Guzik, Adv Neural Inf Process Syst, 2023, 36, 3263–3306 Search PubMed.
- L. Naimovičius, P. Bharmoria and K. Moth-Poulsen, Mater. Chem. Front., 2023, 7, 2297–2315 RSC.
- J. L. Weber, E. M. Churchill, S. Jockusch, E. J. Arthur, A. B. Pun, S. Zhang, R. A. Friesner, L. M. Campos, D. R. Reichman and J. Shee, Chem. Sci., 2021, 12, 1068–1079 RSC.
- A. Thakkar, V. Chadimová, E. J. Bjerrum, O. Engkvist and J.-L. Reymond, Chem. Sci., 2021, 12, 3339–3349 RSC.
- S. Genheden, A. Thakkar, V. Chadimová, J.-L. Reymond, O. Engkvist and E. Bjerrum, J. Cheminf., 2020, 12, 70 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef.
- X. Fang, L. Liu, J. Lei, D. He, S. Zhang, J. Zhou, F. Wang, H. Wu and H. Wang, Nat. Mach. Intell., 2022, 4, 127–134 CrossRef.
- T. Wu, S. Kheiri, R. J. Hickman, H. Tao, T. C. Wu, Z.-B. Yang, X. Ge, W. Zhang, M. Abolhasani and K. Liu, et al. , Nat. Commun., 2025, 16, 1473 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |







