Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Orbital-based bonding analysis in solids
Peter C.
Müller
 ,
Linda S.
Reitz
,
Linda S.
Reitz
 ,
David
Hemker
,
David
Hemker
 and
Richard
Dronskowski
and
Richard
Dronskowski
 *
*
Chair of Solid-State and Quantum Chemistry, Institute of Inorganic Chemistry, RWTH Aachen University, D-52056 Aachen, Germany. E-mail: drons@HAL9000.ac.rwth-aachen.de; Fax: +49-241 80 92642; Tel: +49-241 80 93642
First published on 9th June 2025
Abstract
As of today, there is certainly no doubt about the quantum character of the atomistic world, most straightforwardly calculated by using wave mechanics and Schrödinger's fundamental equation from 1926. Even though one century has passed, the paramount importance of the wave function, which determines everything down to the last detail, remains unchanged, and the wave function is most conveniently approximated by a combination of orbitals, one-electron wave functions for atoms, molecules, and also solids. And it is precisely this “orbital basis” that serves as a gateway to understanding the very interactions that cause atoms to condense into solids, just like for molecules. The analysis of quantum-chemical interactions and the nature of the chemical bonding between atoms in solids by use of orbitals will be our topic in this perspective, starting with the glorious past, going over to the current practice and, of course, the magnificent prospects for the future. As electronic structures for periodic solids are most often calculated using plane waves (instead of orbitals), for simple reasons of translational symmetry and Bloch's fundamental theorem, a unitary transformation to atomic or molecular orbitals is needed for final inspection, technically solved by the LOBSTER quantum-chemistry package. LOBSTER allows for the calculation of wave function-based atomic charges, various population analyses and periodic bonding indicators, first-principles bond orders, two- and multi-centre bonding analysis, fragment-molecular analysis, and a lot more. All those techniques are illustrated from three solid-state systems deriving from carbonate chemistry.
1 Introduction
The concept of the “chemical bond” is probably the most important ingredient in the intellectual toolbox of any chemist. While the term itself was first coined by the English chemist Frankland in 1866 already,1 its current notion was essentially shaped by Lewis in 1916,2 even before the advent of Heisenberg's quantum mechanics in 1925,3 this being the reason why Lewis had difficulties understanding how two negatively charged electrons would approach each other in a “single” bond represented by a simple dash symbol, e.g., H–H. Already then, however, Lewis recognised the importance of distinguishing ionic and covalent bonding in chemical systems, and chemists quickly picked up on the idea and developed the model into the incredibly successful concept it is today. The discovery of quantum mechanics in the form of wave mechanics, that is, in the formulation of Schrödinger's famous equation from 1926 (ref. 4 and 5) quickly led chemistry-affine physicists, such as Heitler and London, to search for the origins of the chemical bond in the emerging quantum theory. While working as postdocs with Schrödinger, Heitler and London discovered the chemical bond's nature in the first quantum-chemical solution to the H2 wave function, namely by the so-called valence-bond (VB) approach assuming both electrons being strictly “correlated”, that is, without ionic terms.6 This topic is large enough to be discussed on its own, so we refer the interested reader to a recent review.7 In particular, Heitler and London recognised the importance of interfering wave functions, at that time dubbed “Schwebungsphänomen” in the German original. (Atomic) wave functions interfere, that is what covalent bonding between atoms is all about, no matter how it is actually calculated.This first bonding analysis on quantum-chemical footing is the fundament of a rich set of theories, tools, and algorithms that would be developed in the following century, until today.8 We will shortly review the historic developments of chemical bonding analyses within this section, followed by a brief overview on LOBSTER,9–11 a software suite implementing every major development in the field of wave function-based bonding analysis within a periodic solid-state context. This is followed by several sections detailing the mathematical backgrounds, results, and interpretational strength of the bonding analyses discussed in this article.
Fig. 1 summarises the history of what we think are key developments in the context of quantum chemistry-based tools targeted at bonding analyses or at least alluding to chemical bonding. Shortly after the proof of concept was delivered by Heitler and London, Condon as well as Mulliken and Hund found yet another and quite different solution to the same problem, the molecular-orbital theory (MO theory),12–16 namely by assuming the electrons being “uncorrelated”, totally independent from each other, thereby also allowing for “ionic” terms, in contrast to VB theory. By doing so, they offered an efficient ansatz to approach electronic wave functions of complex molecular systems based on a superposition of overlapping atomic orbitals—an approach that inspired and nowadays goes under the name linear combination of atomic orbitals (LCAO). The rather delocalised nature of the solutions to the MO wave functions led to hesitation within the chemical community at first since models based on valence-bond theory, in particular those invented by Pauling17 looked a little more intuitive or “chemical”, but success stories using Hückel MO theory on aromatic molecules,18 the Woodward–Hoffmann19 rules based on the shapes of molecular orbitals and also Fukui functions20 targeting molecular reactivities quickly led to a broad acceptance of MO theory among chemists.
Still pursuing a detailed understanding of chemical bonding, chemists started developing tools to divide and conquer the delocalised molecular wave function into quantities that are suitable for analyzing the chemical bond between two (or even more) atomic centres. First was Mulliken who suggested an electronic population analysis, yielding overlap populations and atomic charges, allowing to investigate covalent and ionic bonding between two atoms in an MO-like wave function.21–24 An alternative to Mulliken's population analysis can be achieved when using an orthonormal basis set, e.g., by orthogonalising the atomic-orbital basis first using Löwdin's symmetric orthogonalization.25 Foster and Boys,26 Edmiston and Ruedenberg,27 and Pipek and Mezey28 came up with protocols to generate so-called localised molecular orbitals, the first developments starting in 1960. Using the fact that, within MO theory approaches, the overall wave function is invariant regarding unitary transformations among the molecular orbitals, one may generate a set of maximally localised molecular orbitals that perfectly reflect early ideas of single, double or triple bonds as formulated by Lewis, even including “hybridised” (that is, mixed) atomic orbitals. The localisation idea was later introduced to the solid state by our physicist friends via so-called maximally localised Wannier functions (MLWF),29 albeit the protocols to generate these MLWFs are more involved.
This rather qualitative analysis of quantum-mechanical bond orders was later supplemented by Wiberg's quantitative bond index,30 which analyses the density matrix (incorporating the eigenvectors), obtained from the molecular orbital LCAO coefficients, to determine bond orders. The idea was further generalised by Mayer31–33 to non-orthogonal orbital bases. The year 1973 saw yet another profoundly chemical idea, namely an approach to investigate bonding between fragments (each comprised of several atoms), rather than between atoms, in order to further cater the chemist's view of matter, where molecular entities would show distinct properties, different from the individual atoms they are composed of. Hoffmann and coworkers developed the fragment molecular orbital (FMO) method to obtain molecular orbitals strictly localised on a fragment within a larger chemical compound, highly useful when trying to investigate interactions between different fragments (think about functional groups) that together form a whatever complex compound.34 In 1983, Hughbanks and Hoffmann generalised the Mulliken overlap population to periodic wave functions by means of the Crystal Orbital Overlap Population (COOP), offering a quantum-chemical bonding analysis for solid-state chemists for the first time.35
 | (1) |
Without doubt, COOP completely changed the way solid-state chemists thought about solids because up to 1983 essentially every periodic solid was oversimplified as being ionic, whether truly ionic (such as NaCl) or not. Even far more covalent materials such as GaP were often written (and “understood”) as Ga3+P3− before the advent of COOP.
In the 1960s, when density-functional theory (DFT) originating from metal physics36–39 slowly gained attraction in the solid-state field and, much later, also in the molecular community,40 a second stream of developments emerged, density-based analyses. The interest in these techniques were a result of three main factors: first, density-functional theory originally rests on the density of the system, not its wave function, although—an information often suppressed—the density must be reconstructed using one-electron wave functions, and these usually go under the name Kohn–Sham orbitals. Second, the real-space density is an observable quantity as given by, e.g., electron microscopy and X-ray diffraction, thereby suggesting a more direct footing of any analysis, let alone bonding analysis. Third, the superior efficiency of plane-wave DFT codes for periodic electronic structures did not allow for an atomic decomposition of MO-like wave functions, as all available analyses require LCAO-type molecular orbitals. Hence, traditional bonding analyses from MO theory were inapplicable to the solid state. It is rather unfortunate for any density-based analysis, however, that the density lacks the phase of the wave function which determines bonding or antibonding behavior (the constructive or destructive interference phenomenon recognised by Heitler and London), so the most vital information for any bonding analysis is also lacking. An early example is provided by the so-called Hirshfeld method, dividing the total electron density based on a comparison to the promolecular density, a superposition of atomic densities.41 Densities superimpose, only wave functions interfere, as we know since 1927.
The most popular density-based analysis is the so-called quantum theory of atoms in molecules (QTAIM), invented by Bader in 1985.42 QTAIM operates via the analysis of the topology of the electron density, the latter being chopped into atomic regions by evaluating so-called “zero-flux surfaces” resting on the second derivative of the density. It was soon followed by the so-called electron localisation function (ELF)43 defined by an inverse relationship with the like-spins pair probability which decorates (i.e., colours) the density as regards “localised” electron pairs. The course of aesthetically pleasing ELF plots and 3D shapes was quickly shown to be a function of the underlying atomic-orbital topology.44 Combinations of ELF and QTAIM have been applied to a wide range of materials to augment chemical bonding analysis45 even though ELF, just like the density, does not contain the phases, so it cannot distinguish between bonding, nonbonding and antibonding interactions, easily visible for the 5s4d metal series where neither ELF nor density detect the changing bonding strength upon filling electrons into the bands.46 Likewise, increased bonding by unpairing spins as in the 3O2vs.1O2 scenario is hard to imagine using ELF. Eventually, there is the single exponential decay detector (SEDD)47 allowing for identification of bonding and non-bonding electrons based on the electron density alone, while antibonding electrons remain elusive to these analyses. These density-based approaches, including ELF, present a topic worth discussion on its own, as other authors already did.45,48
On the wave-function front, the ideas of COOP were adjusted to the new Kohn–Sham wave function yielding the Crystal Orbital Hamilton Population (COHP) approach, a COOP successor using DFT.49
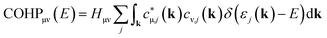 | (2) |
The COHP method, state of the art for investigating chemical bonding in periodic electronic structures for at least two decades, was only made possible since an orbital-based theory for band-structure calculations (Linear Muffin-Tin Orbital, LMTO)50 was available at that time, also using short-ranged basis sets (TB-LMTO-ASA).51 Both COOP and COHP can be pictorially derived as an overlap/Hamilton weighted DOS. Fig. 2 shows the general calculus starting from a band structure (Fig. 2a), diamond in this case. For both plane-wave and tight-binding basis, the band structure can be integrated over the Brillouin zone, resulting in the DOS (Fig. 2b). In case a tight-binding basis is employed, the DOS can be split into individual orbital contributions (see Fig. 2c) and—by multiplication with the overlap integral Sμν or Hamilton integral Hμν—result in the COOP or COHP, respectively (Fig. 2d). Conventionally, COOP and COHP are plotted such that bonding interactions point to the right-hand side, antibonding points to the left. Hence, we plot positive COOP and negative COHP (a simple graphical convention) because positive overlap and negative energy refer to stabilising (=bonding) interactions.
Quite recently, the Crystal Orbital Bond Index52 (COBI) came as a natural extension to COOP and COHP, and COBI is the generalization of the Wiberg and Mayer bond indices for periodic matter and, as such, provides a chemically intuitive quantification of covalent bonds. In addition, COBI allows to look at multi-centre bonds, not only two-centre interactions.
2 Lobster
As alluded to before, solid-state chemists need to resort to periodic electronic-structure codes which may come in three different variants for the likewise periodic wave function. To arrive at the latter,53 one either starts with numerical partial waves on the individual atoms augmented by plane waves (cellular methods, most accurate), or uses fixed atomic basis functions (tight binding, resembling LCAO), or employs nodeless plane waves (pseudopotential approach).54,55 The third approach has turned out so numerically effective that the vast majority of today's DFT simulations is carried out with it. Hence, the plane-wave pseudopotential approach has grown to be a community standard, evident from the large number of citations on codes like VASP56–59 or Quantum ESPRESSO.60–62 Local chemical-bonding analysis, however, was practically impossible to perform using delocalised plane waves for many years, but this limitation was lifted in 2011 (ref. 9) when the foundations of the LOBSTER code, eventually published in 2013,10 were introduced, allowing to seamlessly switch between plane-wave and atomic-orbital bases as well as between reciprocal and real-space representation of electronic structures via analytical projection techniques.63,64In LOBSTER, everything is achieved by first reading the plane-wave wave function information from widely used codes such as VASP, Quantum ESPRESSO, or ABINIT (and, since LOBSTER 5.0, also from any electronic-structure code). Afterwards, the overlap integrals between the plane-wave wave functions and predefined contracted all-electron Slater-type orbitals are evaluated in order to generate a transfer matrix, T, capable of transferring the information of the periodic electronic wave function, encoded by a plane-wave coefficient matrix CPW(k) to a chemically intuitive atomic-orbital basis without loss of electrons.
| CAO(k) = T(k) CPW(k) | (3) |
The coefficient matrix in the AO basis, CAO(k), can now be used in whatever chemical-bonding analyses discussed in the preceding section. Methods like COHP additionally need the Hamilton matrix in the same basis, which can be reconstructed from the band eigenvalues by a simple unitary transformation:
| HAO(k) = CAO(k) EPW(k) CAO†(k), | (4) |
The resulting mathematical objects are now suitable for all orbital-based tools mentioned in the preceding section, as schematically shown in Fig. 3. In fact, LOBSTER naturally implements DOS, COOP, COHP, and also COBI, as these solid-state bonding analyses are the bread and butter of its users. Mulliken and Löwdin population analyses have been implemented in 2019,65 and Wiberg and Mayer bond indices are available through the COBI implementation.52 Localised MOs (LMOs) have been made accessible to the solid-state community for the first time in LOBSTER in 2023,66 and fragment molecular orbitals (FMO) have been applied to periodic DFT calculations in 2024 via the Linear Combination of Fragment Orbitals (LCFO)67 technique, made available to the scientific community with LOBSTER 5.1. Thus, every major development in wave function-based bonding analysis of the past century is now accessible through LOBSTER and can be used by our scientific colleagues around the world, free of charge. In the course of this perspective we will guide the reader through the different orbital-based descriptors currently implemented into LOBSTER.
To do so, it would be natural to showcase the LOBSTER capabilities by a collection of differently bonded solid-state materials, say, metals, semiconductors, oxides, and so forth,52,68 or by grouping them into different bonding categories.46 On purpose, we here chose a different strategy in which everything will rest on just three compounds, carefully selected. There is the recently identified crystal structure of carbonic acid,69 representing a “molecular” crystal containing H bonds. Next, we look at the crystal structure of sodium hydrogen carbonate,70 a system comprising both ionic but also H bonding. Finally, sodium carbonate71 will serve as another study case, an ionic crystal still containing the complex carbonate anion in which there are covalent bonds. And let us now aim at demonstrating how much can be learned about a compound in just a single LOBSTER calculation.
3 Charge analysis
We start the analysis of our study cases with orbital populations, local DOS and charges that do not necessarily allude to (covalent) interatomic bonding but, instead, mirror the consequences of the bonding in terms of “atomic” properties, hence we regard them as “one-centre” bonding indicators. The local density of states (DOS) is calculated using eqn (5) and the total DOS consists of the sum over all local DOS. | (5) |
 | (6) |
The resulting DOS plots are presented in Fig. 4, showing the total DOS in light grey and the most significant orbital contributions highlighted in other colors.
 | ||
| Fig. 4 Total density of states as well as the most significant atomic contributions for (a) H2CO3, (b) NaHCO3 and (c) Na2CO3. | ||
The occupied valence bands below the Fermi level εF can be described best by viewing them as consisting of two parts in which the lower one approximately ranges from −23 to −18 eV. In the case of H2CO3 this part is mainly composed of oxygen 2s orbitals shown in red mixing with the C 2p (dark grey) and H 1s (light grey) orbitals, contributing to the covalent (σ) backbone of the molecule. The contributions from the O atom, however, clearly predominate here. In the cases of NaHCO3 and Na2CO3 the Na 2p contributions shown in blue are the largest in this energy region, reflecting filled and sharp semi-core levels, not engaged in chemical bonding. The virtual, unoccupied Na 3s levels, on the other hand, are way above the Fermi level, not given in the figure. Right below the Fermi level, the O 2p orbitals form the valence band maximum in all three systems by mixing with the C 2p (also generating π bonding) and H 1s orbitals. Within the unoccupied conduction band, the 2p orbitals of C predominate.
The analysis of the density of states can be further complemented by the orbital gross populations which are calculated using the approaches introduced by Mulliken21–24 and Löwdin.25 Following Mulliken's technique, the gross population (GPμ) is determined via the density-matrix formalism given in eqn (7). Alternatively, one may formulate the gross population as an integral of the corresponding local DOS to the Fermi level.
 | (7) |
P μν(k) and Sμν(k) are the k-dependent density and overlap matrix elements for the orbitals μ and ν. The density matrix element is computed from the LCAO coefficients cμ,j(k) in reciprocal space as demonstrated in eqn (8) whereas Sμν(k) depends on the basis functions χμ(k).
 | (8) |
| Sμν(k) = 〈χμ(k)|χν(k)〉 | (9) |
Upon applying Löwdin's symmetrical orthonormalization (LSO), a new density matrix P′ = S−½PS−½ is obtained, and this then leads to the Löwdin gross population having the following form
 | (10) |
The numerical results of both Mulliken and Löwdin population analyses for H2CO3, NaHCO3 and Na2CO3 are presented in Tables 1 and 2.
| Atom | Orbital | H2CO3 | NaHCO3 | Na2CO3 |
|---|---|---|---|---|
| C | 2s | 0.71 | 0.74 | 0.79 |
| 2p | 0.80 | 0.81 | 0.83 | |
| O | 2 s | 1.72 | 1.73 | 1.74 |
| 2p | 1.61 | 1.65 | 1.69 | |
| H | 1s | 0.55 | 0.59 | — |
| Na | 2p | — | 2.00 | 2.00 |
| 3s | — | 0.12 | 0.16 |
| Atom | Orbital | H2CO3 | NaHCO3 | Na2CO3 |
|---|---|---|---|---|
| C | 2s | 0.76 | 0.77 | 0.79 |
| 2p | 0.76 | 0.86 | 0.87 | |
| O | 2s | 1.56 | 1.60 | 1.62 |
| 2p | 1.62 | 1.65 | 170 | |
| H | 1s | 0.65 | 0.67 | — |
| Na | 2p | — | 2.00 | 2.00 |
| 3s | — | 0.27 | 0.26 |
A short analysis of these population data yields that similar trends can be deduced from both, not too surprisingly. On carbon and oxygen, respectively, the 2s and 2p orbitals are almost equally populated which, in an organic chemist's terminology, can easily be explained by significant orbital mixing (or hybridization), mirroring the special role of the first long period46 (also going under the term primogenic repulsion).72 It is also worth mentioning that upon increasing Na content the population of all orbitals (except for Na 3s in the Löwdin approach) is increased since more electron density is dumped on the complex anion by the least electronegative atom, Na.
From the gross orbital populations it is only a short path to the calculation of wave function-charges. The Mulliken or Löwdin charges qA for an atom A are formulated as the difference of the valence electrons N and the sum of the gross orbital populations of all orbitals μ on atom A.
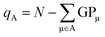 | (11) |
The charges computed according to eqn (11) for H2CO3, NaHCO3, and Na2CO3 are depicted in Fig. 5a and b. In addition, so-called Bader charges are included in (c) for comparison with a density-based approach. As alluded to already, Bader's calculus42,73–75 partitions the electron density into atomic regions using a topology criterion. These so-called basins are determined via the zero-flux condition given in eqn (12) where ρ(r) is the electron density at any point r on the surface with the normal vector n(r). Once the atomic basins have been determined, Bader charges can be calculated analogous to Mulliken and Löwdin populations, not from the (unavailable) wave function but from the density.
| ∇ρ(r)·n(r) = 0 | (12) |
One glance at Fig. 5 immediately reveals that the charges obtained using orbital-based approaches (a and b) differ rather significantly from those obtained using Bader's density-based technique (c). Nonetheless, with increasing Na content the charge transfer is increased, especially between O and Na, a consequence of their very different electronegativities.
This increasing ionicity is not only reflected from the charges but also from the Madelung energies since, in a crystalline solid, ionicity straightforwardly leads to the so-called Madelung field and an (electrostatically defined) lattice energy.76 The purely electrostatic part of the lattice energy, i.e., the Madelung energy, is automatically calculated in LOBSTER based on Mulliken or Löwdin charges. The results for all three study cases are given in Table 3. All of them arrive at large values, even for a molecular crystal like carbonic acid, on the order of rock salt. Nonetheless, these—rather fictitious—Madelung energies become more negative with increasing sodium content which clearly indicates the increasing ionicity of those systems.
| System | ε M Mulliken (kJ·mol−1 ) | ε M Löwdin (kJ·mol−1 ) |
|---|---|---|
| H2CO3 | −1807 | −1042 |
| NaHCO3 | −2108 | −1401 |
| Na2CO3 | −2356 | −1763 |
Coming back to the comparison between orbital- and density-based charges, the trend seen for the three compounds is mirrored by the atomic charges obtained with all three approaches, although the Bader charges arrive at much larger values (more than twice) compared to Mulliken and Löwdin charges. Such stronger emphasis on electron transfer is rather typical for the Bader approach, a consequence of chopping the density.
Bader's larger absolute values of the net charges77 therefore paint a more ionic picture of the structures under investigation which is closer to what is expected from the classical oxidation state, mirroring the semi-classical methodology lacking the wave function. As mentioned earlier, Bader cuts the electron density based on topology into non-overlapping domains, as if there were no overlap (as in ionic compounds). In compounds like those treated in this perspective, however, it is obvious that covalency is at play and raises concerns whether the treatment as non-overlapping domains is at all suitable. We recall that the covalent bond is an interference phenomenon of overlapping wave functions, exactly that. For carbonic acid, the covalent character of the bonds has already been identified in an earlier work by some of the authors.69 In the following analyses, we will further discuss and evaluate the ionic picture painted by the Bader charges for the strongly covalent systems under investigation.
4 Bond orders
While the “ionicity notion” has prevailed in solid-state chemistry for many decades (even for GaP, see above), the reason being that quantum-chemical approaches were simply unavailable, hence Madelung arguments are found in virtually every solid-state chemistry textbook, and we did the same in the preceding section on purpose. The situation in molecular chemistry, in particular organic chemistry is very different. Here, covalent bonding is the norm almost playfully. Formation and cleavage of, e.g., C–C bonds is regularly used to understand and predict experimental phenomena such as reactivity and stability. These relations of chemical bonding are backed even more so by quantum mechanics and orbital theory, and the Woodward–Hoffmann rules serve as a fitting example,19 mirroring the fact that the covalent bond originates from interfering wave functions. Even though an ionic notion then seems totally counterintuitive for a molecule, the strength of a covalent bond may be quantified by considering the atomic valence, borrowing structural ideas from Pauling.17 The method going under the name bond length-bond strength is fairly mature, and in this context let us highlight a modern descendent, the empirical bond valence sum78 (BVS) recipe which correlates the bond order with the interatomic distance, given that a plethora of experimental data is available. While this kind of analysis serves well as semi-quantitative measure, it is essentially non-quantum-chemical and does not reflect the underlying orbital overlap or symmetry. The latter consideration requires a wave function based on, say, atomic orbitals,24,79 plane Bloch-waves,80,81 or maximally localised Wannier functions.29One method to calculate orbital-based bond orders was published 2021 by the authors in the framework of the LOBSTER package. In the spirit of Hughbanks' and Hoffmann's COOP approach involving the overlap and density matrices, the original molecular bond index by Wiberg30 and Mayer31,32 was generalised to the solid state and dubbed crystal orbital bond index (COBI) as shown in eqn (13).52
 | (13) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, N
O, N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, etc. Coming from a density-centred analysis, such as QTAIM, a covalent bonding analysis is not directly possible but requires an auxiliary wave function (which then delivers phases). Based on the latter, so-called delocalisation indices (DI) are calculated from the overlap Si,j between the auxiliary wave functions ϕi and ϕj integrated over the QTAIM basins ΩA,82 so the density-based approach is no longer exclusively focusing on the density.
N, etc. Coming from a density-centred analysis, such as QTAIM, a covalent bonding analysis is not directly possible but requires an auxiliary wave function (which then delivers phases). Based on the latter, so-called delocalisation indices (DI) are calculated from the overlap Si,j between the auxiliary wave functions ϕi and ϕj integrated over the QTAIM basins ΩA,82 so the density-based approach is no longer exclusively focusing on the density. | (14) |
Fig. 6a–c shows the bond orders of various bonds in H2CO3, NaHCO3, and Na2CO3, either calculated quantum-chemically with ICOBI, empirically (or classically) by the BVS approach, and also density-based including auxiliary orbitals using QTAIM-DI. A quick inspection of the values for the C–O (red curves in Fig. 6) as well as the O–H bonds (dark blue curves) reveals a striking similarity between quantum-chemical ICOBI and empirical BVS in that all C–O bond orders lie between 1.23 and 1.42 with only minor differences between both fundamentally different methods. This correlation comes to no surprise as C–O bonds have been widely studied in organic chemistry, hence forming an extraordinarily large and also reliable reference database for the empirical BVS parameters. The QTAIM-DI values, on the other hand, are lower than the single bond order in all cases which requires explanation. While both ICOBI and QTAIM-DI rely on a wave function, the latter only indirectly, the partitioning is quite different in both methods. QTAIM cuts the electron density based on topology, resulting in non-overlapping domains by definition. Such a treatment may raise concern in strongly covalent materials because—again—the covalent bond is an interference phenomenon of overlapping wave functions. In contrast, a likewise simplifying approximation does not apply when atomic orbitals are employed for the calculation of ICOBI, so the resulting bond orders are more in line with the empirical expectations. The Na–O bonds show a different trend, however: in this case, the bond orders from ICOBI and QTAIM-DI are extremely small for both NaHCO3 and Na2CO3, and the empirical BVS arrives at about 0.3 in both compounds, a number that must be considered even qualitatively incorrect. The underlying reason is easily found in the bonding mechanism of these contacts, namely ionicity, mirroring the large EN difference between oxygen and sodium. Both compounds feature Na+ cations that do not form any covalent bonds due to their closed-shell nature, so the amount of covalency can only be very minor, in harmony with both QTAIM-decomposition as well as ICOBI (projection to atomic orbitals) which arrive at similar results. The empirical BVS overestimates the covalent strength since a change in bonding mechanism (covalency vs. ionicity) is not built in, the simple parametrization does not reflect it, and even grossly different oxidation states, i.e., Na+, Na0, and Na−, would be treated equally despite different valence-electron numbers, different atomic sizes, etc.
One key difference between (I)COBI and BVS or QTAIM-DI discussed before is its energy-as well as orbital-resolved analysis, similar to preceding methods such as COOP and COHP because they rely on an energy-resolved density-of-states matrix including entries from all atomic orbitals. Hence, Fig. 6d–f shows the energy-resolved COBI plots for all previously discussed bonds in H2CO3, NaHCO3, and Na2CO3. A glance at these evidences that the bonding in all three compounds occurs mainly within energy levels around −5, −10, and −20 eV. Second, the levels close to the valence-band maximum, directly below the Fermi level, appear as essentially nonbonding. Not too surprisingly, the levels generating the unoccupied conduction bands reflect antibonding interactions throughout, as expected from basic MO-theory.79
The bonding analysis thus far focused on intra-molecular bonds, the by far strongest interactions, but the cohesion of a molecular crystal, however, arises from interactions between molecules, in inter-molecular bonds. In the present examples, hydrogen-bonding can clearly be identified as the driving force for the condensation of H2CO3 and NaHCO3, the latter compound also including ionic interactions stemming from the Na+ cations, see above. Fig. 7a and b visualise the intra- and inter-molecular O–H-bonds for both compounds and their bond orders as determined with COBI. The shorter (intra-molecular) O–H bonds possess larger bond orders of 0.62 and 0.54, indicating significant covalency in these contacts. The longer bonds would typically be described as H-bonds or H-bridges but clearly mirror a certain covalency with ICOBI of 0.22 and even 0.29 for NaHCO3, in harmony with hydrogen-bond covalency quantified before.83 Interestingly, the sum of both bonds, inter- and intra-molecular, is about 0.83 for both cases, meaning that the overall bonding capacity is comparable and only shifted differently to the individual bonds, suggesting some form of cooperativity, that is, questioning whether this sort of bonding can be described as two distinctive bonds or if a collective picture is more appropriate. An answer can easily be found using a multi-centre bonding analysis84–86 that is accessible with COBI(3)—the superscript symbol indicating three-centre interactions—as given in eqn (15).
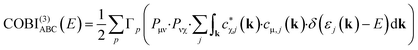 | (15) |
Multi-centre interactions are well known from metals, of course, defining how covalency turns into metallicity if too few electrons must be distributed over a plethora of atoms, namely by occupying a wave function that encompasses more than two atoms, possibly even an infinite numbers atoms. In the present molecular case, the situation is not that extreme, as exemplified by the COBI(3) plots of the O–H–O three-centre bonds shown in Fig. 7c and d. Clearly, three-centre interactions are found in both compounds, and they span the entire occupied region, as seen from the red curves. Another important detail relates to the negative sign of the energy-resolved COBI(3) as well as the energy-integrated ICOBI(3). Negative numbers typically occur for electron-rich three-centre bonding and have been interpreted as such46 but we note that similarly negative values have also been found for H-bonding.87 Interestingly, the effect of multi-centre bonding is stronger in the more symmetric bond of NaHCO3 by about 20%.
On a more technical level, every multi-centre bond index can—in principle—be generalised to any number of centres involved, and the case of metallicity proves the point. In practice, however, one will reach real-world limits due to finite computational power and also error propagation. Additionally, the numerical analysis of higher-order bonding is far from being trivial (except the metallicity extreme) so we will restrict ourselves to two- and three-centre bonding here. Let us recap, however, that such multi-centre-bonding analysis is a consequence of collective orbital interactions beyond classical pairwise bonding, thereby mirroring the quantum character of covalency as a wave function is not bound to two atoms. If such a multi-centre bond index adopts non-zero values, a truly delocalised bond (at least to some degree) is indicated, for example in the electron-rich XeF2 or the electron-deficient B2H6 molecules.46,52
5 Fragmentation
The previous sections have focused on interactions based on charges and covalent pairwise as well as multi-centre bonding between individual atoms. Yet, chemistry is more than that since molecules or molecular (complex) ions can also be understood as being composed of groups of atoms. Hence, molecular chemists very often divide a large molecule into multiple functional groups that help categorise and generalise the reactivity of the entire molecule. Similarly, crystal chemistry features molecular ions and complex polyhedra that can be described, at least approximately, as almost isolated entities. For example, one may of course understand crystalline Na2CO3 as being composed of two Na, one C, and three O atoms but a more chemical notion of two Na+ cations and one CO2−3 carbonate anion is far more fitting, alluding to the fragments showing up in aqueous solution chemistry.Such a fragmentation analysis is also part of the quantum-mechanical toolkit provided by the LOBSTER package. In order to extract a localised fragment from a delocalised reciprocal-space Bloch wave function, the wave function needs to be transformed into real space. Using a so-called embedding approach,88,89 the total density ρtot is split into an active part ρact and an environmental part ρenv. Therein, the active density is calculated explicitly whereas the environmental density acts as an external potential onto the active one. For the exact details we refer the interested reader to the literature.88,89
| ρtot(r) = ρact(r) + ρenv(r) | (16) |
Once the environment density has been generated, it is then used to calculate the wave function of the active system in real space which finally can be analysed in an analogous manner to isolated molecules. For this, we implemented a Pipek–Mezey28 algorithm into LOBSTER that generates Localised Molecular Orbitals66 (LMO) by maximising the Mulliken gross population P of the molecular orbitals ϕi:
 | (17) |
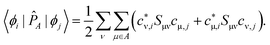 | (18) |
 | ||
| Fig. 8 Localised molecular orbitals of (a–c) H2CO3, and (d–f) NaHCO3, indicating σ bonds (top), π bonds (middle), and H bonds (bottom). | ||
An alternative theory was introduced in the same LOBSTER framework. Based on the fragment molecular orbital method34,90 as developed with extended Hückel theory decades ago, the Linear Combination of Fragment Orbitals (LCFO)67 follows essentially the same idea, this time based on a first-principles approach and involving periodic boundary conditions. Similar to the LMO technique discussed before, LCFO uses a Fourier transform of the delocalised wave function to real space according to eqn (19).
 | (19) |
This real-space Hamiltonian is then diagonalised following eqn (20), yielding the unitary transformation matrix U including the LCAO coefficients of the local atomic orbitals forming the local molecular or fragment orbitals.
| HAO = UHMOU† | (20) |
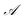 and
and 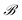 . This total matrix is a block diagonal matrix containing the individual matrices
. This total matrix is a block diagonal matrix containing the individual matrices 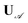 and
and  on its diagonal whereas all other elements are zero.
on its diagonal whereas all other elements are zero. | (21) |
This total transformation matrix is then used to transform the atomic-orbital basis in reciprocal space into a fragment-orbital basis. Eqn (22)–(24) cover the transformation of coefficient, Hamilton and density matrices. For technical reasons, the overlap matrix is not available for analysis, on purpose, as the LOBSTER fragmentation is performed for an orthonormal basis.
| cMOtotal(k) = U†totalcAOtotal(k) | (22) |
| HMOtotal(k) = U†totalHAOtotal(k) Utotal | (23) |
| PMOtotal(k) = U†totalPAOtotal(k) Utotal | (24) |
With this new fragment-orbital basis, we can now use LOBSTER's complete toolkit that is available for the atomic-orbital basis, i.e., DOS, COHP, and COBI.
 | (25) |
 | (26) |
 | (27) |
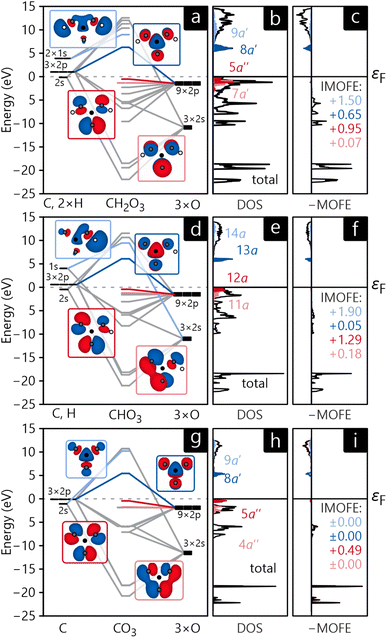
The MO diagrams and DOS in the MO basis of crystalline H2CO3, NaHCO3, and Na2CO3 are shown in Fig. 9a, b, d, e, g and h. Unsurprisingly, the molecular orbitals of all three crystals are very similar in shape and have the same energetic trends, corroborating the chemical concept of viewing all three compounds as H/Na-bonded variants of an carbonate anionic core. The HOMO of all compounds (shown in dark red in Fig. 9) has the shape of the carbonate anion and essentially consists of p-orbitals of oxygen while a quick visual inspection identifies them as non-bonding. The LUMO (marked in dark blue in Fig. 9) is formed by an antibonding combination of p-orbitals, however, residing on carbon and oxygen perpendicular to the anion's plane. The DOS curves reveal that HOMO and LUMO form valence and conduction bands, respectively, for all three compounds. These findings are in perfect agreement with the atomic orbital-based DOS shown in section 3, not too surprising as both are calculated from exactly the same electronic structure.
As an additional tool, let us introduce the molecular orbital formation energy (MOFE) which quantifies the band-energy contribution of an atomic orbital μ towards the formation of a molecular orbital α. Depending on the exact question to be answered, MOFE either measures the total contribution of an atomic or molecular orbital to the overall molecule or—if a more detailed analysis is required—it can be broken down into individual μ–α contributions.
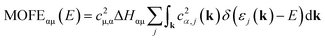 | (28) |
For illustration, the MOFE plots in Fig. 9c, f, and i allow a very detailed analysis of the molecular orbitals. Interestingly, the IMOFE of all orbitals explicitly shown in this analysis has a positive sign, meaning that these orbitals destabilise the molecule to a certain extent as they increase the total energy. Naturally, this destabilisation is more than counteracted by bonding interactions at lower energies not shown explicitly. As the absolute values of all IMOFE are rather small, however, it is safe to designate these molecular orbitals as essentially nonbonding (as said before), so phrasing them as “lone pairs” looks reasonable. For reference, a C–C single bond in diamond has a stabilising effect of about −9.66 eV to the one-particle band-structure (Kohn–Sham) energy, not to be confused with an experimental C–C single-bond dissociation enthalpy of about 348 kJ mol−1.91
As already alluded to before, the LCFO method can also be used to calculate interactions between molecules. For this consideration, we chose to exclude Na2CO3 as inter-molecular bonding is primarily ionic in this compound. Hence, Fig. 10 only depicts the COBI diagrams for a H2CO3–H2CO3 bond as well as a HCO−3–HCO−3 bond. From an atomic-orbital perspective, these bonds have already been identified as hydrogen-bonds, now confirmed by the molecular-orbital-based COBI. Interestingly, the total bond order is larger for H2CO3 (0.64) than for NaHCO3 (0.43), even though the ICOBI of the individual H-bonds indicate the opposite trend but this tentative disagreement is easily explainable by the multiplicity of these bonds in the respective compounds: H2CO3 adopts a dimeric structure and is involved in two H-bonds per molecule pair whereas NaHCO3 only has one such bond, resulting in a lower total bond order. When comparing the ICOBI of the MO basis and the AO basis, we find that the H-bonding accounts for about 68% of the total bond strength, and other more long-ranged effects such as ionicity contribute to the rest.
6 Conclusion and outlook
In the course of this perspective we have summarised major developments in chemical bonding analysis ranging from the beginnings in 1916 until the present day, with a special focus on wave function-based approaches. To correctly analyse solid-state (periodic) materials in terms of chemical bonding, the LOBSTER suite makes orbital-based descriptors, known from molecular chemistry, easily available for crystalline matter, too, namely through an accurate analytical (unitary) transformation from the plane-wave into an atomic-orbital picture. Three carbonate study cases known to all readers with a chemistry background have been presented, including currently implemented bonding descriptors which relate to wave function-based atomic charges and pairwise covalent as well as multi-centre bonding. Complementing the atomic-orbital basis, further analyses have been carried out, highlighting local molecular as well as fragment orbitals that allow for a deeper understanding of solids based on concepts from molecular chemistry.As density-based analytic techniques alluding to chemical bonding have been popular (thanks to their simplicity of calculation) in the solid-state context, the LOBSTER orbital-based results have been compared with descriptors stemming from Bader's QTAIM method. It is clear from the outset that the quasi-molecular solid-state systems investigated here are driven by covalency but charges calculated from Bader's QTAIM approach paint a far more ionic picture than Mulliken or Löwdin charges obtained via wave functions (LOBSTER). Likewise, while wave function-based ICOBI values corroborate the expected covalency in the investigated systems, density-based QTAIM-DI yields much lower bond orders. This is unsurprising since QTAIM cuts the electron density into non-overlapping domains, a somewhat unfitting description for covalently bonded systems. Despite such problem, we do not intend to categorically withhold the value of density-based approaches. Alternative partitioning schemes such as Hirshfeld's method41 and derived approaches92–97 allow the atomic basins to overlap, drawing a picture closer related to wave-function theory. Such an implementation may benefit from the local-orbital framework as provided by LOBSTER's tool set, so a modified Hirshfeld-based population and charge analysis seems promising in this context.
Additionally, one may already now envision other wave function-based extensions to the orbital toolkit, for the betterment of solid-state chemical-bonding analysis. For example, orbital-based descriptors may also include atom/element-specific information, unavailable for any density-based approach, as orbital extent by contraction parameters as a function of effective nuclear charge, for example, are only available in the former. In contrast, orbital-based techniques, typically depicting bonding criteria in an energy-resolved way, may adopt the style known from density-based approaches which drop the (unavailable) energy dependency in favor of a real-space representation, that is, a density map known from, say, X-ray crystallography. In principle, this can also be accomplished using orbital-based methods, so it is under development right now. Taken together, we trust that all those techniques will create further bridges between theoretical and synthetic chemists.
7 Computational details
Electronic-structure calculations involving structural optimizations were carried out using the Vienna ab initio simulation package (VASP) 5.4 (ref. 56–59) with PAW-based98 pseudopotential-like electronic wave functions. As H2CO3 is a high-pressure phase and comparison with the two other compounds had to be performed, an external pressure of 2 GPa was applied to all three structures during optimization. The simulations were considered converged for energetic differences of 10−8 eV for electronic and 10−6 eV for ionic optimizations. The kinetic energy cutoff was set to a large 700 eV. Electronic exchange and correlation were described using the PBEsol functional.99 To also include van-der-Waals interactions, D3 correction with Becke–Johnson damping100,101 was applied. The k-point meshes were generated using the Monkhorst–Pack scheme102 which yielded a 9 × 11 × 9 mesh for H2CO3, 17 × 7 × 7 for NaHCO3 and 7 × 11 × 9 for Na2CO3. Brillouin-zone integrations were performed using Blöchl's tetrahedron method.103 The Local Orbital Basis Suite Towards Electronic-Structure Reconstruction (LOBSTER) 5.1.19–11,49,52,104 package was then used to project the PAW wave function onto the local, all-electron, contracted multiple-ζ Slater-type orbital basis set pbeVASPfit201511 to gain the chemical information provided in this article. The basis set itself rests on prior many-body work105 known for supreme accuracy in terms of energy (μHartrees) and density (0.002% average error).106 Local orbitals were selected to correspond to the minimal basis of the respective pseudopotentials, a fundamental choice allowing for self-consistency in the end. The calculation of Bader charges was performed with the program Critic2 1.274,75 using Henkelman integration.107–109 For technical reasons, the Bader-DI were calculated using Critic2 interfaced with Quantum ESPRESSO60–62 as this method is not supported for VASP. All other output was ensured to be consistent with both DFT programs.Data availability
The original data supporting this perspective article have been generated (and may be reproduced) from the LOBSTER code which can be downloaded freely at http://www.cohp.de, based on the crystallographic data for carbonic acid, sodium hydrogen carbonate, and sodium carbonate published in ref. 69–71.Author contributions
Peter C. Müller: conceptualization, investigation, writing – original draft, writing – review & editing, project administration. Linda S. Reitz: conceptualization, investigation, writing – original draft, writing – review & editing. David Hemker: conceptualization, writing – original draft. Richard Dronskowski: resources, writing – review & editing, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank all contributors to the LOBSTER code over its existence in the past 12 years, full-time programmers and students equally.References
- E. Frankland, J. Chem. Soc., 1866, 18, 372–395 RSC.
- G. N. Lewis, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
- W. Heisenberg, Z. Phys., 1925, 33, 879–893 CrossRef CAS.
- E. Schrödinger, Ann. Phys., 1926, 385, 437–490 CrossRef.
- E. Schrödinger, Ann. Phys., 1926, 386, 109–139 CrossRef.
- W. Heitler and F. London, Z. Angew. Phys., 1927, 44, 455–472 CAS.
- S. Shaik, D. Danovich and P. C. Hiberty, Molecules, 2021, 26, 1624 CrossRef CAS PubMed.
- K. Gavroglu and A. Simões, Neither Physics nor Chemistry. A History of Quantum Chemistry, The MIT Press, Cambridge, Massachussets, London, England, 2012 Search PubMed.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- E. U. Condon, Proc. Nat. Acad. Sci., 1927, 13, 462–466 CrossRef CAS PubMed.
- R. S. Mulliken, Phys. Rev., 1928, 32, 761–772 CrossRef CAS.
- R. S. Mulliken, Phys. Rev., 1928, 32, 186–222 CrossRef CAS.
- F. Hund, Z. Angew. Phys., 1928, 51, 759–795 CAS.
- F. Hund, Z. Angew. Phys., 1932, 73, 1–30 CAS.
- L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 1960 Search PubMed.
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef.
- R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 82, 395–397 CrossRef.
- K. Fukui, T. Yonezawa, C. Nagata and H. Shingu, J. Chem. Phys., 1954, 22, 1433–1442 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1841–1846 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 2338–2342 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 2343–2346 CrossRef CAS.
- P. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- J. M. Foster and S. F. Boys, Rev. Mod. Phys., 1960, 32, 300–302 CrossRef CAS.
- C. Edmiston and K. Ruedenberg, Rev. Mod. Phys., 1963, 35, 457–464 CrossRef CAS.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS.
- A. Otero-de-la Roza, A. Martín Pendás and E. R. Johnson, J. Chem. Theory Comput., 2018, 14, 4699–4710 CrossRef CAS.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274 CrossRef CAS.
- I. Mayer, J. Comput. Chem., 2007, 28, 204–221 CrossRef CAS PubMed.
- I. Mayer, Bond Orders and Energy Components, CRC Press, Boca Raton, London, New York, 2017 Search PubMed.
- R. Hoffmann, H. Fujimoto, J. R. Swenson and C.-C. Wan, J. Am. Chem. Soc., 1973, 95, 7644–7650 CrossRef CAS.
- T. Hughbanks and R. Hoffmann, J. Am. Chem. Soc., 1983, 105, 3528–3537 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Clarendon Press, New York, 1st edn, 1989 Search PubMed.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- O. Gunnarsson, J. Harris and R. O. Jones, J. Chem. Phys., 1977, 67, 3970–3979 CrossRef CAS.
- F. Hirshfeld and T. Chim, Acta, 1977, 44, 129–138 CAS.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- J. K. Burdett and T. A. McCormick, J. Phys. Chem. A, 1998, 102, 6366–6372 CrossRef CAS.
- Y. Grin, A. Savin and B. Silvi, in The ELF Perspective of Chemical Bonding, John Wiley & Sons, Ltd, 2014, vol. 10, pp. 345–382 Search PubMed.
- R. Dronskowski, Chemical Bonding from Plane Waves via Atomic Orbitals, De Gruyter, Berlin, Boston, 2023 Search PubMed.
- P. de Silva, J. Korchowiec and T. A. Wesolowski, ChemPhysChem, 2012, 13, 3462–3465 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew Chem. Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 12, 3060–3083 CrossRef CAS.
- O. K. Andersen and O. Jepsen, Phys. Rev. Lett., 1984, 53, 2571–2574 CrossRef CAS.
- P. C. Müller, C. Ertural, J. Hempelmann and R. Dronskowski, J. Phys. Chem. C, 2021, 125, 7959–7970 CrossRef.
- R. Dronskowski, Computational Chemistry of Solid State Materials, Wiley, Weinheim, New York, 2005 Search PubMed.
- H. Hellmann, J. Chem. Phys., 1935, 3, 61 CrossRef.
- H. Hellmann, Einführung in die Quantenchemie, Franz Deuticke, Leipzig, Wien, 1937 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O.-d. la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105 CrossRef CAS PubMed.
- D. J. Chadi, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 3572 CrossRef CAS.
- D. Sánchez-Portal, E. Artacho and J. M. Soler, Solid State Commun., 1995, 95, 685–690 CrossRef.
- C. Ertural, S. Steinberg and R. Dronskowski, RSC Adv., 2019, 9, 29821–29830 RSC.
- M. Pauls, D. Schnieders and R. Dronskowski, J. Phys. Chem. A, 2023, 127, 6541–6551 CrossRef CAS PubMed.
- P. C. Müller, N. Schmit, L. Sann, S. Steinberg and R. Dronskowski, Inorg. Chem., 2024, 63, 20161–20172 CrossRef PubMed.
- P. C. Müller, D. Schnieders and R. Dronskowski, Chemical Concepts in Solids, in Exploring Chemical Concepts through Theory and Computation, ed. S. Liu, Wiley, Weinheim, New York, 2023 Search PubMed.
- S. Benz, D. Chen, A. Möller, M. Hofmann, D. Schnieders and R. Dronskowski, Inorganics, 2022, 10, 132 CrossRef CAS.
- B. D. Sharma, Acta Cryst., 1965, 18, 818–819 CrossRef CAS.
- W. van Aalst, J. den Holander, W. J. A. M. Peterse and P. M. de Wolff, Acta Crystallogr., Sect. B, 1976, 32, 47–58 CrossRef.
- M. Kaupp, J. Comput. Chem., 2007, 28, 320–325 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- A. Otero-de-la Roza, M. Blanco, A. Martín Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166 CrossRef CAS.
- A. Otero-de-la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018 CrossRef CAS.
- N. N. Greenwood, Ionic Crystals, Lattice Defects and Nonstoichiometry, Butterworth & Co., London, 1968 Search PubMed.
- C. Lepetit, P. Fau, K. Fajerwerg, M. L. Kahn and B. Silvi, Coord. Chem. Rev., 2017, 345, 150–181 CrossRef CAS.
- N. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B, 1991, 47, 192–197 CrossRef.
- R. Hoffmann, Solids and Surfaces, VCH Verlagsgesellschaft mbH, Weinheim, 1988 Search PubMed.
- A. I. Baranov and M. Kohout, J. Comput. Chem., 2011, 32, 2064–2076 CrossRef CAS PubMed.
- P. Golub and A. I. Baranov, J. Chem. Phys., 2016, 145, 154107 CrossRef PubMed.
- F. Cortés-Guzmán and R. F. Bader, Coord. Chem. Rev., 2005, 249, 633–662 CrossRef.
- V. L. Deringer, U. Englert and R. Dronskowski, Chem. Commun., 2014, 50, 11547–11549 RSC.
- M. Giambiagi, M. S. de Giambiagi and K. C. Mundim, Struct. Chem., 1990, 1, 423–427 CrossRef CAS.
- A. Sannigrahi and T. Kar, Chem. Phys. Lett., 1990, 173, 569–572 CrossRef CAS.
- R. Ponec and F. Uhlik, Croat. Chem. Acta, 1996, 69, 941–954 CAS.
- R. Ponec and I. Mayer, J. Phys. Chem. A, 1997, 101, 1738–1741 CrossRef CAS.
- C. R. Jacob and J. Neugebauer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 325–362 CAS.
- C. R. Jacob and J. Neugebauer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2024, 14, e1700 CAS.
- T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, John Wiley & Sons, Hoboken, New Jersey, 2nd edn, 2013 Search PubMed.
- J. Emsley, The Elements, Oxford University Press, Oxford, UK, 3rd edn, 1998 Search PubMed.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- T. C. Lillestolen and R. J. Wheatley, Chem. Commun., 2008, 5909–5911 RSC.
- T. C. Lillestolen and R. J. Wheatley, J. Chem. Phys., 2009, 131, 144101 CrossRef PubMed.
- T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468 CrossRef CAS.
- D. E. P. Vanpoucke, P. Bultinck and I. Van Driessche, J. Comput. Chem., 2013, 34, 405–417 CrossRef CAS PubMed.
- C. M. Zicovich-Wilson, M. Hô, A. M. Navarrete-López and S. Casassa, Theor. Chem. Acc., 2016, 135, 188 Search PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940 CrossRef CAS PubMed.
- C. Bunge, J. Barrientos and A. Bunge, At. Data Nucl. Data Tables, 1993, 53, 113–162 CrossRef CAS.
- T. Koga, K. Kanayama, S. Watanabe and A. J. Thakkar, Int. J. Quantum Chem., 1999, 71, 491–497 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |