Unlocking inverted singlet–triplet gap in alternant hydrocarbons with heteroatoms

Abstract

Fifth-generation organic light-emitting diodes exhibit delayed fluorescence enabled by exothermic reverse intersystem crossing due to a negative singlet–triplet gap, where the first excited singlet lies below the triplet. This phenomenon, termed delayed fluorescence from inverted singlet and triplet states (DFIST), has been experimentally confirmed only in two triangular molecules with a central nitrogen atom. Here, we report a high-throughput virtual screening of 30 797 BN-substituted polycyclic aromatic hydrocarbons (BNPAH) derived from 77 parent scaffolds with 2–6 rings. Using a multi-level workflow that combines structural stability criteria with accurate excited-state calculations, we identify the top 46 DFIST-BNPAH candidates with singlet–triplet gaps less than −0.015 eV. Notably, this set includes BN-helicenes, where inversion arises from through-space charge-transfer states. Our findings reveal new design motifs for DFIST that extend beyond known frameworks, thereby expanding the chemical space for next-generation emitters based on heteroatom-embedded aromatic systems.

---

1 Introduction

Thermally activated delayed fluorescence (TADF) enables 100% exciton harvesting in organic light-emitting diodes (OLEDs), circumventing the dependence on heavy elements to promote phosphorescence.¹ TADF operates via reverse intersystem crossing (RISC), where the population of the ‘dark’ first excited triplet state (T₁) is transferred to the ‘emissive’ higher-energy singlet state (S₁), if the singlet–triplet gap (STG) is ≲0.1 eV.² The RISC rate constant, k_RISC, decreases with temperature (T), following an Arrhenius-type relation, which in the logarithmic form is expressed as ln k_RISC = ln A − STG/k_BT, where k_B is the Boltzmann constant. The intercept, ln A, represents the effective pre-exponential factor within the measured range of T, while the slope corresponds to the STG divided by k_B.^1,3 In TADF molecules, the total photoluminescence quantum efficiency increases with T due to the delayed fluorescence component that is driven by RISC, which is a T₁ → S₁ upconversion process.^1,4–8 As stated by Aizawa et al.,⁹ for a thermodynamically favorable downconversion process, S₁ should energetically lie below T₁, violating the Hund's spin-multiplicity rule.

In ref. 9, Aizawa et al. computationally screened approximately 35 000 molecules and identified a derivative of heptazine or hepta-azaphenalene (7AP) as a promising candidate with a negative STG. Experimental measurements revealed a slight positive slope in the ln k_RISC vs. 1/T plot, indicating a negative STG giving rise to delayed fluorescence from inverted singlet and triplet states (DFIST). Molecules exhibiting such behavior are often referred to as inverted singlet–triplet energy gap (INVEST) light-emitters and represent a new frontier in the design of purely organic TADF materials.¹⁰ Direct spectroscopic evidence of a negative STG (−0.047 ± 0.007 eV) was later obtained for pentaazaphenalene (5AP) using anion photoelectron spectroscopy and fluorescence measurements,¹¹ consistent with transient photoluminescence data for dialkylamine-substituted 5AP.¹² Graphitic carbon nitride (g-CN), which is a polymeric form of 7AP, was studied by combining time-resolved electron paramagnetic resonance and steady-state optical spectroscopic techniques to show that the S₁ and T₁ exciton energies of this system are inverted by ≈0.2 eV.¹³ To date, 5AP and derivatives of 7AP remain the only molecular prototypes with experimentally confirmed negative STGs, while g-CN is the material counterpart with a negative STG at the excitonic level.

Theoretical studies^14,15 have predicted an inverted STG in cyclazine or azaphenalene (1AP) and 7AP, both featuring a central nitrogen (N) atom in a triangular framework. Notably, the structure of 1AP can be considered as an N-atom embedded in an anti-aromatic 12-annulene periphery.¹⁶ The possibility of a vanishing STG in 1AP was rationalized in ref. 16 as follows. Let S₁ and T₁ denote singly excited configurations, ¹χ_a→r and ³χ_a→r, where a and r are the occupied and virtual molecular orbitals (MOs) involved in the excitation determined self-consistently, by minimizing the energy of the ground state configuration, ¹χ₀. Then, the excitation energies are E (¹χ_a→r) − E (¹χ₀) = ε_r − ε_a − J_ar + 2K_ar and E (³χ_a→r) − E (¹χ₀) = ε_r − ε_a − J_ar, where ε_a and ε_r denote energies of the corresponding MOs, while J_ar and K_ar denote Coulomb and exchange integrals. Hence, the STG is defined as twice the exchange integral: E (¹χ_a→r) − E (³χ_a→r) = 2K_ar. As the frontier MOs (a and r) of 1AP are localized on different atoms, their spatial overlap decreases, resulting in a reduction of K_ar, and near-degenerate S₁ and T₁ levels.

However, a vanishing exchange interaction is a necessary condition for vanishing exchange interaction; it is insufficient to explain the negative STGs of 1AP and 7AP noted in ref. 14 and 15. A past study rationalized negative STGs in twisted aminoborane using the dynamic spin polarization effect.¹⁷ Accordingly, along with vanishing K_ar, mixing of the ¹χ_a→r configuration with that of the doubly-excited configuration, ¹χ_aa→rr has been shown to selectively stabilize the S₁ state compared to T₁, amounting to a negative STG. The mixing of low-lying configurations of charge-transfer (CT) and localized-excitation types was also proposed as the mechanism to promote negative STGs in ref. 14. This effect explains why qualitatively correct predictions of the STGs of 1AP and 7AP require the use of excited-state wavefunction methods or the time-dependent density functional theory (TD-DFT) formalism based on double-hybrid DFT (dh-DFT) approximations. In the dh-DFT formalism, TD-DFT excitation energies are corrected by incorporating double-excitation character through second-order perturbation theory (PT2). Hence, while popular hybrid-DFT approximations (without PT2 correction) have delivered accurate results for predicting the positive STGs of conventional organic molecules,¹⁸ they fail to predict negative STGs^19–22 as they lack the implicit incorporation of double-excitations.

Computational studies have suggested that azaphenalenes with other substitution patterns, as well as the boron (B) analog of 1AP, boraphenalene (1BP), also exhibit negative STGs.^{19,21,23–27} A comprehensive search in the structurally diverse small molecules chemical space, bigQM7ω, comprising about 13 000 molecules,²⁸ revealed no exceptions to Hund's rule. This indicates that achieving the electronic structure criteria for STG < 0 requires non-trivial molecular frameworks that are inaccessible to molecules with fewer atoms.²⁹ Non-alternant hydrocarbons and their derivatives have been shown to have the potential to exhibit negative STGs.^30–34 Notably, substituted analogs of the non-fused bicyclic hydrocarbon have demonstrated negative STGs that are attributed to through-bond CT states.³⁵ The geometric stability—i.e., whether a molecule corresponds to a minimum on the potential energy surface (PES)—of novel structural prototypes warrants careful selection of computational protocols, as antiaromatic frameworks combined with topological charge destabilizing substitutions effects are particularly susceptible to Jahn–Teller-type distortions, affecting the predicted STG.³⁶

Heteroatom-substituted polycyclic aromatic hydrocarbons (PAHs), particularly those incorporating B and N (BNPAH), constitute a vast chemical space³⁷ with significant potential for developing versatile organic semiconductors.^38–40 An emerging strategy is to enhance the efficiency of TADF-based OLEDs with multiresonant (MR) fluorophores, as exemplified by DABNA, a BNPAH molecule featuring a triphenyl boron core and two N atoms.⁷ BNPAH molecules with separated B and N centers present the possibility of through-bond CT states, which can result in a negative STG as noted in the hydrocarbon, calicene.³⁵ For instance, derivatives of tetracene⁴¹ and Clar's goblet diradical⁴² exhibit small positive STGs highlighting their potential for TADF applications. However, so far, DFIST candidates with STG < 0 have not been identified in the BNPAH chemical space, as the key challenge lies not only in selecting an appropriate PAH scaffold but also in finding a suitable substitution pattern. To identify such rare candidates, high-throughput ab initio virtual screening offers a solution. The approach enables a comprehensive exploration of the expansive BNPAH chemical space to uncover combinations of scaffold motifs and heteroatom substitution patterns that meet the stringent electronic structure requirements for achieving inverted STGs.

In this study, we comprehensively explore DFIST candidates with STG < 0 within a chemical space of 30 797 BNPAH molecules³⁷ of stoichiometry C_xB₁N₁. These molecules were combinatorially derived from 77 benzenoid Kekuléan PAHs containing 2–6 rings,⁴³ including coronene. The structures of these PAHs are shown in Fig. 1. By applying stringent criteria, we removed systems prone to de-excitations and structural distortions to identify 46 stable systems with negative STGs. Notably, the most prevalent candidates were non-planar helicene-type structures, as well as azaphenalene- and boraphenalene-based systems. A detailed analysis of these structures revealed key features contributing to their negative STGs, offering new directions for designing organic emitters with efficient DFIST properties.

Fig. 1 Set of 77 smallest polycyclic aromatic hydrocarbons (PAHs) comprising up to six benzene rings, adapted from ref. 37. These serve as parent scaffolds for the BNPAH chemical space explored in this work. Molecules include linear, angular, and helical topologies. Names and SMILES are collected in Table S1 of the ESI.†

2 Computational details

The geometries of 30 797 BNPAH molecules derived from 77 PAHs were determined using the TPSSh-DFT method and the def2-SVP basis set, as reported in ref. 37. We note that for helical PAHs that are chiral, only one enantiomeric form is considered in ref. 37. Screening for DFIST candidates within this dataset is carried out using the computational workflow illustrated in Fig. 2, which consists of four levels.

Fig. 2 Data distribution and high-throughput virtual screening workflow: (A) distribution of 30 797 BNPAH molecules categorized by PAH size in terms of the number of rings. (B) Correlation between STGs of 644 BNPAH molecules predicted by TDA/SCS-PBE-QIDH and L-CC2 methods. Out of the 2032 molecules with negative STGs at the DFT level, 644 molecules with S₁ energies >1 eV at the L-CC2 level are retained for further analysis. TP (true positives) and FP (false positives) indicate the classification accuracy of TDA/SCS-PBE-QIDH in predicting negative STGs, with L-CC2 serving as the reference. (C) High-throughput workflow for identifying DFIST-BNPAH candidates with reliable minimum-energy geometries and accurate excited-state characteristics.

At level-1, the initial screening of DFIST candidates is performed using linear-response time-dependent DFT (LR-TD-DFT) calculations within the Tamm–Dancoff approximation (TDA) using the SCS-PBE-QIDH dh-DFT method²² combined with the correlation-consistent polarized valence double-zeta (cc-pVDZ) basis set. Molecules with STG < 0 at this stage progress to the next level of the workflow for further evaluation. We selected this level of theory as it has been shown to be suitable for modeling negative STGs in three separate studies, as discussed below. For a benchmark set of azaphenalenes, SCS-PBE-QIDH was identified as one of the dh-DFT methods delivering consistent results in agreement with spin-component-scaled (SCS) CC2.¹⁹ For similar systems, when compared with theoretical best estimates of STGs, this dh-DFT method delivered the best performance.²⁶ Further, among twelve DFT methods, SCS-PBE-QIDH showed the best agreement with ADC(2)-predicted STGs of small magnitudes in a chemical space dataset comprising 12 880 small organic molecules.²⁹

Loos et al.²⁶ provided theoretical best estimates of STGs for ten triangular systems (and two additional entries in their ESI†) using a composite approach and benchmarked various theoretical methods; see also ref. 27. They concluded that the second-order algebraic diagrammatic construction method (ADC(2)) and second-order approximate coupled cluster singles and doubles model (CC2) are suitable methods for modeling STGs.^26,27 For modeling negative STGs, ADC(2) and CC2 agree with the predictions of high-level theories such as CASSCF/CASPT2.²¹

The large size of the BNPAH molecules considered in this study limits the feasibility of applying canonical ADC(2) or CC2 methods at level-2 of the workflow. In contrast, the Laplace-transformed, density-fitted local methods, L-ADC(2)⁴⁴ and L-CC2,^45,46 offer significant computational speed-ups without compromising accuracy. These local methods offer computational efficiency, enabling excited-state calculations of large organic molecules comprising over 100 atoms.^45,46 It is worth noting that a study¹⁰ on negative STG systems noted that the local variants of ADC(2) and CC2 hold potential for studying larger molecules. Accuracies of L-ADC(2) and L-CC2 were probed using the theoretical best estimates for twelve values of STGs from ref. 26 as the reference (see Table S2 of the ESI† for more details). For these systems, the canonical CC2 and ADC(2) with the aug-cc-pVTZ basis set resulted in mean absolute deviations (MADs): 0.013 and 0.019 eV, respectively, and standard deviations of the errors (SDEs): 0.011 and 0.016 eV. For the same set of molecules and with the same basis set, the local correlated methods—L-CC2 and L-ADC(2)—yielded MADs of 0.015 and 0.022 eV, respectively, and SDEs of 0.010 and 0.013 eV.

Overall, all four methods, ADC(2), CC(2), and their local variants, exhibit MADs and SDEs very close to those of CC3/aug-cc-pVDZ, as shown in Table S2.† While the mean signed error (MSE) of CC3 is centered around zero, as the reference is based on the results of CC3 with a large basis set, ADC(2) and CC(2) (as well as their local variants) show small negative MSEs, suggesting their tendency to mildly increase the number of false-positive predictions. However, this error is smaller than the magnitudes of STGs of several DFIST candidates reported in this study. Further, the final set of DFIST-BNPAH molecules is suggested using a threshold of STG ≤ −0.015 eV to minimize such false positive predictions. On the other hand, equation-of-motion coupled-cluster with singles and doubles (EOM-CCSD) exhibits an MSE of +0.090 eV. As this value is comparable to the magnitude of the most negative STG reported in this study, one can expect EOM-CCSD to suggest several false-negative predictions of DFIST-BNPAH candidates. The computational efficiency and low error of L-CC2 make it a cost-effective alternative to high-level methods for large-scale applications, yielding prediction errors that are slightly lower than those of L-ADC(2). Therefore, in the present study, we employ L-CC2 at levels 2 and 4 of our workflow, using the cc-pVDZ and aug-cc-pVDZ basis sets, along with the corresponding JKFIT and MP2FIT auxiliary basis sets.

Molecules with STG < 0 as predicted by L-CC2/cc-pVDZ in level-2 proceed to level-3 of the workflow, where the geometries of the candidate molecules are refined using the DFT method ωB97X-D3 with the def2-TZVP basis set. Vibrational analysis at the same level is performed to assess their geometric stability to determine whether they correspond to minimum-energy structures on the PES.

At level-4, excited-state calculations are performed using L-CC2 with the larger aug-cc-pVDZ basis set, utilizing the refined geometries obtained with ωB97X-D3/def2-TZVP. For the same set of molecules, we also report L-ADC2/aug-cc-pVDZ results (see Data availability). Of the molecules that pass this final stage, those with STG < −0.015 at the L-CC2/aug-cc-pVDZ level are identified as DFIST-BNPAH candidates with a higher degree of confidence. Furthermore, for four representative molecules, we performed ADC(2)/cc-pVDZ calculations to compare with L-ADC(2) and L-CC2 results (see Table S3 in the ESI†).

Multiwfn⁴⁷ was used for obtaining Λ-indices⁴⁸ for which excited states were calculated with TDA/SCS-PBE-QIDH/cc-pVDZ. The Λ-index (with 0 ≤ Λ ≤ 1) quantifies the degree of overlap between hole and electron in S₀ → S₁ and S₀ → T₁ excitations through the overlap integral ∫dr|Φ_a(r)‖Φ_r(r)| of the corresponding occupied and virtual MOs, Φ_a(r) and Φ_r(r), participating in the excitation. If the excitation couples multiple configurations, the overlap is weighted by the solution (i.e., elements of the eigenvector) of the TD-DFT equations, as defined in ref. 48.

Note that in the TDA/SCS-PBE-QIDH calculations, the ground state is modeled at the PBE-QIDH level while the SCS correction influences only the excited state energies. Furthermore, the PT2 treatment in PBE-QIDH affects only the ground and excited state total energies, while the MOs are treated at the baseline hybrid-DFT level using 31% PBE-level exchange and 69% exact exchange, along with 67% PBE-level correlation. Therefore, to be consistent with the TDA calculations, our MO analysis is based on this hybrid-DFT level, where we have used an isovalue of 0.01 a.u. for plotting. The MOs calculated with this hybrid-DFT level for four DFIST-BNPAH candidates shown in Fig. 8 are very similar to those calculated with CAM-B3LYP, as shown in Fig. S2,† indicating that the qualitative shapes of the MOs are less influenced by particular parameterization of hybrid-DFT methods. All L-CC2 and L-ADC(2) calculations were carried out using Molpro (version 2015.1),⁴⁹ all DFT calculations were performed using Orca (version 6.0.0),^50,51 and ADC(2) calculations using the cc-pVDZ basis set were performed with the resolution-of-the-identity (RI) approximation^52,53 as implemented in QChem (version 6.0.2).⁵⁴ In all excited state calculations, we calculated the lowest six singlet and triplet excited states.

3 Results and discussions

We present the results of this study in three parts. (i) The first part discusses the salient aspects, including the organization of the high-throughput screening workflow and the methods employed at each level of the workflow. (ii) In the second part, we present the structure–property correlation between L-CC2/cc-pVDZ-level STGs and the molecular structural features for a rational understanding of the origin of the property. We analyze 644 molecules (with S₁ energies >1 eV) out of 2032 that pass level-1 (Fig. 2) of the workflow, which includes both positive and negative STGs. (iii) Finally, we discuss the excited state characteristics of DFIST candidates that pass all levels of the workflow, with L-CC2/aug-cc-pVDZ-level modeling and geometries refined with ωB97X-D3/def2-TZVP.

3.1 Assessment of data quality

We begin with the geometries of 30 797 BNPAH molecules, calculated using the TPSSh-DFT method with the def2-SVP basis set, as reported in ref. 37. The computational workflow employed in the present study (see Fig. 2) systematically identifies DFIST candidates by progressively increasing theoretical rigor at each stage. The primary objective of the workflow is to ensure that the final set of identified candidates consists only of true positives, meaning they meet the required property criteria. While some true positives may be missed due to the sequential filtering steps, the workflow prioritizes minimizing false positives, ensuring high confidence in the candidates that successfully pass all levels of screening.

An ideal first step in the workflow would involve refining the geometries of BNPAH molecules using a more accurate DFT method, especially for geometry optimization, such as ωB97X-D3, with a larger def2-TZVP basis set. However, the computational cost of geometry refinement and vibrational frequency analysis for a dataset of this scale using a triple-zeta basis set exceeds the cost of excited-state calculations. Therefore, geometry refinement is deferred to the third stage of the workflow and applied only to candidate molecules that successfully pass the first two screening levels.

Level-1 of the computational workflow performs initial screening of 30 797 BNPAH molecules derived from the smallest 77 PAHs (see Fig. 1) using excited-state energies calculated at the TDA/SCS-PBE-QIDH/cc-pVDZ level. In particular, ref. 26 and 29 showed that TDA/SCS-PBE-QIDH systematically underestimates STG compared to more accurate reference values. Thus, the probability of false-negative predictions of inverted STGs with this method is very low. Consequently, molecules identified with positive STGs at this level are highly unlikely to exhibit negative STGs when evaluated with higher-level theories. From the initial set of 30 797 BNPAH molecules, we filtered out those exhibiting de-excitations with negative transition energies for S₁ or T₁. Such negative transition energies indicate wavefunction-instability, or a preference for open-shell singlet or triplet electronic ground states rather than a closed-shell singlet. We verified for some molecules that the ground state energy calculated by solving spin-unrestricted Kohn–Sham equations was lower than the energy obtained with a spin-restricted calculation. In the remaining 30 319 molecules, we selected those with STG < 0.0 eV, identifying 2032 candidate molecules for subsequent assessment.

At level-2 of the workflow, excited-state energies are computed for 2032 molecules using the L-CC2 method with the cc-pVDZ basis set. L-CC2 has demonstrated high accuracy in modeling excited states of BODIPY derivatives.^55,56 As discussed in Section 2, for twelve benchmark values of STGs, L-CC2 with the aug-cc-pVTZ basis set achieves very low errors similar to those of CC2/aug-cc-pVTZ. These results indicate that the local approximation in L-CC2 does not degrade predictive accuracy. Furthermore, as shown in Table S2 of the ESI,† L-CC2's accuracy with the aug-cc-pVDZ basis set closely matches that of the aug-cc-pVTZ basis set. In this study, we screen 2032 molecules using L-CC2 with the smaller cc-pVDZ basis set. For the benchmark set of twelve STGs, L-CC2/cc-pVDZ achieves MAD and SDE values of 0.039 and 0.020 eV, respectively, compared to the theoretical best estimates (see Table S2 of the ESI†).

Based on L-CC2/cc-pVDZ results for the 2032 molecules, we excluded 1388 molecules, of which 10 exhibit de-excitations and the remaining show E_S1 < 1 eV as they are prone to pseudo-Jahn–Teller distortions. This resulted in a final set of 644 molecules. The 1 eV transition energy threshold was chosen based on previous findings on azaphenalenes, which showed an increasing tendency for pseudo-Jahn–Teller distortions with decreasing S₀ → S₁ transition energies.³⁶ However, it is worth noting that the likelihood of structural distortions also depends on the strength of the vibronic coupling between the corresponding states. We analyzed the full set of 644 molecules, even though some exhibit STG > 0, as their STG magnitudes remain small due to prior screening at level-1. This broader structural analysis facilitates the identification of trends, such as the dependence of STGs on the choice of PAH scaffold and other main structural features.

Of the 644 molecules entering level-2, we focus on 119 with STG < 0 for further analysis in level-3, where their geometries are refined using the DFT method ωB97X-D3 with the def2-TZVP basis set. Vibrational analysis confirmed that 72 molecules are stable, meaning they correspond to the minimum-energy structures on the PES. This set includes six molecules with a soft mode, where the corresponding imaginary frequency magnitude is below 1 terahertz (1 THz = 33.356 cm⁻¹).

The choice of ωB97X-D3 for geometry refinement is motivated by its demonstrated reliability in large computed datasets, such as the QM9 chemical space,⁵⁷ where ωB97X-D3 has been shown to outperform B3LYP in predicting minimum-energy structures for molecules with unusual covalent bond connectivities, many of which have yet to be experimentally identified.⁵⁸ Furthermore, for azaphenalenes, ωB97X-D3 accurately predicts vibronic coupling-driven pseudo-Jahn–Teller symmetry-lowering in agreement with the coupled-cluster CCSD(T) method.³⁶ In contrast, the CCSD method results in excessive symmetry breaking, whereas commonly used geometry optimization methods, such as B3LYP hybrid-DFT and second-order perturbation theory (MP2), fail to adequately capture vibronic coupling effects, incorrectly predicting symmetric structures as minima that are actually saddle points at the CCSD(T) level.³⁶

Finally, at level-4, excited-state calculations for 72 stable DFIST-BNPAH candidates were performed using L-CC2 with the aug-cc-pVDZ basis set, utilizing the refined geometries obtained with ωB97X-D3/def2-TZVP. To verify the overall agreement of L-CC2 with another wavefunction-based method, we performed L-ADC(2)/aug-cc-pVDZ calculations for the 72 candidate molecules. A parity plot between STGs predicted by L-CC2 and L-ADC(2) is provided in Fig. S1 of the ESI,† showing overall good agreement. Importantly, among the 61 molecules showing negative STG with L-CC2, except for one molecule with STG ≈ 0, the remaining 60 exhibit negative values when using L-ADC2, with slight variations in the ranking.

3.2 Dependence of singlet–triplet gap on structural factors

The analysis in this subsection is based on the 644 molecules identified at level-2 of the workflow. As noted earlier, these molecules have E_S1 > 1 eV at the L-CC2/cc-pVDZ level (using TPSSh/def-SVP minimum energy geometries retrieved from the BNPAH dataset reported in ref. 37) and include 525 molecules with positive STGs and 119 molecules with negative STGs.

3.2.1 Variation of STG with B–N separation. Fig. 3 illustrates the variation of L-CC2 predicted STG with B–N distance (R_BN) for 644 BNPAH molecules. Notably, BNPAH molecules with directly bonded B and N atoms are absent from this plot, as they exhibited positive STGs at the SCS-PBE-QIDH level (did not pass level-1 of the workflow Fig. 2) and were therefore excluded from subsequent modeling with L-CC2. This is because only when a minimum distance of one bond separates the heteroatoms, charge-separation is possible due to decreasing spatial overlap between HOMO and LUMO, which is a prerequisite for reducing the STG. However, it is worth noting that molecules with different scaffolds, such as triangular boron carbon nitrides with directly bonded B and N atoms, have been computationally shown to exhibit negative STGs.⁵⁹ Additionally, molecules with B and N separated by two bonds, similar to meta-positions in benzene (indicated as 1,3 in Fig. 3), consistently show STG > 0 eV, suggesting that such configurations cannot support negative STGs. This is likely due to the shorter B–N distances increasing the spatial overlap of frontier MOs involved in the excitations, which in turn enhances exchange interaction that stabilizes T₁ relative to S₁. Similarly, negative STGs are not observed in systems where B and N are separated by two bonds, as seen in para-positions in benzene or the 1,4 positions of cis-butadiene (denoted as 1,4-cis in Fig. 3). However, for the 1,4-trans configuration, several molecules exhibit negative STGs, suggesting that an increase in R_BN plays a crucial role in minimizing exchange interactions, thereby facilitating negative STGs. In the cis configuration, R_BN is smaller than in the trans-configuration. Hence, in the former, the spatial overlap between frontier MOs is substantial, resulting in positive STGs. No particular selectivity for negative STG is noted in Fig. 3 for systems with R_BN > 4 Å based on the BNPAHs explored in this study.

Fig. 3 Dependence of L-CC2 STGs on the distance between B and N atoms in 644 BNPAH molecules. Typical distances for 2-bond separations (1,3) are shaded in magenta, while 3-bond separations are distinguished as 1,4-cis and 1,4-trans (analogous to cis/trans butadiene) and shaded in orange and blue, respectively. Distances beyond 3-bond separations are shaded in red.

3.2.2 BN-pyrene molecules with 1AP or 1BP core. To gain a more refined understanding of the qualitative trends, we selected all BN-pyrene molecules containing either a 1AP or a 1BP core, as illustrated in Fig. 4, from a total of 63 possible BN-pyrenes.³⁷ Each case consists of nine molecules, among which seven feature either directly bonded B & N pairs, a 2-bond-separated 1,3 configuration, or a 3-bond-separated 1,4-cis configuration. None of the seven molecules favors negative STGs as seen from the trends in Fig. 3. The remaining two systems in each set have larger B–N distances (R_BN): one exhibits a 3-bond-separated 1,4-trans configuration, while the other has a 4-bond separation. In both classes (with 1AP core or 1BP core) of BN-pyrenes shown in Fig. 4, for the left and right-most entries with a two-fold symmetry and short B–N distances, the frontier MOs resemble that of the aromatic species 14-annulene with no contribution from the heteroatoms. The frontier MOs of the 1,4-trans systems closely resemble those of 1AP and 1BP discussed in ref. 26. For the 4-bond-separated system with an 1AP core, the LUMO is similar to that of 1AP, but the HOMO exhibits different nodal structures. In contrast, for the 4-bond-separated system with a 1BP core, the HOMO resembles that of 1BP, whereas the LUMO does not. Additionally, while both systems show reduced STGs, the 1,4-trans systems (highlighted in boxes) exhibit slightly lower Λ_T1 compared to Λ_S1, suggesting diminished exchange energy in the triplet state, which favors a lower-energy singlet state. Overall, these results suggest that in B,N-substituted pyrenes, negative STG does not solely stem from the 1AP or 1BP core but also requires B and N to be connected in a 1,4-trans butadiene-like fashion with a sufficient spatial separation of the heteroatoms.

Fig. 4 B,N-substituted pyrenes with azaphenalene (1AP, panel A) and boraphenalene (1BP, panel B) cores: variation in transition energies of the S₁ and T₁ states, and the corresponding STGs predicted with L-CC2/cc-pVDZ. All energies are in eV. Also provided are the Λ-indices for S₁ and T₁ transitions, along with the corresponding frontier MOs, calculated at the dh-DFT level.

3.2.3 BN-benzo[a]pyrene molecules. From the 644-set, we selected 10 BNPAH molecules derived from PAH 21, benzo[a]pyrene (see Fig. 1). Their structures, along with L-CC2/cc-pVDZ excited-state energies, are shown in Fig. 5. All 10 BN-benzo[a]pyrene molecules feature either a 1AP or 1BP core. Note that the full set of BN-benzo[a]pyrene derivatives comprises 380 unique molecules,³⁷ many of which were filtered out at level-1 of the workflow.

Fig. 5 Structures and L-CC2/cc-pVDZ-level excited-state properties of 10 BN-benzo[a]pyrene molecules derived from PAH 21 (see Fig. 1 for the list of PAHs). White|green|black|blue atoms denote H|B|C|N.

Among them, eight molecules exhibit negative STGs (excluding I and J) and are related by permutational symmetry. Of these, four (A, B, D, and H) contain a 1BP core, while the other four (C, E, F, and G) are obtained by swapping the positions of B and N. Furthermore, within these eight systems with STG < 0, four (A, C, G, and H) have B and N connected via a 1,4-trans configuration. In A and C, the peripheral B and N atoms are bonded to hydrogen atoms, whereas in G and H, they occupy bridgehead positions. Overall, 1,4-trans connectivity promotes negative STG as stated above. However, if the heteroatom is in a bridgehead position, the individual transition energies (E_S1 and E_T1) increase. The shift is larger for S₁, making the STG less negative. This can be seen by comparing molecule A (STG = −0.11 eV) in Fig. 5 with H (STG = −0.05 eV). In both molecules, B and N are connected via a 1,4-trans configuration, but in H, the N atom is in a bridgehead position. A similar trend can be observed between C (STG = −0.10 eV) and G (STG = −0.06 eV).

The remaining four molecules (B, D, E, and F) feature a 1,6-hexatriene connectivity. Due to the extended conjugation length, their S₁ transition energies range from 1.2–1.3 eV, which is slightly higher than in 1,4-connected systems. While B and E are permutationally related with 1,6-trans-hexatriene connectivity, D and F exhibit 1,6-cis-hexatriene connectivity. Unlike in 1,4-systems, the cis/trans effect is not very pronounced in 1,6-connected molecules.

Interestingly, both I and J, with 1,5-cis and 1,5-trans pentadiene connectivity, exhibit STG ≥ 0. Since the B–N separation (R_BN) in 1,5-connected systems lies between that of 1,4- and 1,6-systems, this suggests that the R_BN does not solely dictate STG. The influence of substitution patterns on the spatial overlap of frontier MOs will also impact STGs. For example, structures A, I, and D in Fig. 5 show 1,4-, 1,5-, and 1,6-connectivity patterns. While the STGs of A and D are negative (−0.11 and −0.08 eV), the STG of I is zero. We calculated the Λ-indices of these molecules to find that molecule A has Λ_S1 = 0.51 and Λ_T1 = 0.51, while molecule D has Λ_S1 = 0.43 and Λ_T1 = 0.47. The drop in the value of these indices is because in D with 1,6 connectivity, opposite charges are separated by a larger R_BN than in A. However, for I, we found Λ_S1 = 0.52 and Λ_T1 = 0.61, suggesting that the T₁ state of I is preferentially stabilized, resulting in a positive value for the STG.

3.2.4 BN-helicene molecules. There is growing interest in utilizing intramolecular through-space CT states to enhance the TADF efficiency of OLEDs.^60–65 In particular, B-containing helicenes have been shown to exhibit appreciable photoluminescence quantum yields, opening up the new class of OLEDs that emit circularly-polarized light.⁶⁶ As helical heteroaromatics are still relatively underexplored molecules, BN-helicene molecules with negative STGs warrant further exploration for their potential applications in DFIST.

In helicenes where B and N atoms are positioned at opposite ends, the nature of the frontier MOs shifts from fully delocalized to localized, CT-type. In the latter case, the HOMO and LUMO densities become spatially localized in different regions of the molecule, a defining feature of S₁ and T₁ states with intramolecular CT character. The donor end of the molecule, where HOMO is localized lies around the B atom, while the acceptor end associated with LUMO is localized is around the N atom, implying an effective CT from B-to-N. A similar analysis had been done for the derivatives of calicene, where through-bond CT was shown between donor and acceptor parts of the molecules without alternating HOMO/LUMO orbitals.³⁵

Fig. 6 presents BNPAH molecules derived from PAHs—25, 53, 68, 67, and 45—exhibiting a gradual increase in helicity. We observe that as helicity increases, the STG decreases, with BN-helicene molecules based on PAHs 67 and 45 exhibiting negative STG. The frontier MO plots of these molecules (Fig. 6) indicate that while excitations in PAH 25 are fully delocalized, they gradually evolve into CT-type in helicenes. Since the localized HOMO and LUMO regions are not directly bonded through the PAH network, this suggests that a through-space CT interaction is responsible for the negative STG.

Fig. 6 Variation of the STG in selected 6-ring BNPAHs with increasing helicity. For each PAH scaffold, the molecule with the smallest STG at the L-CC2/cc-pVDZ level is shown. L-CC2/cc-pVDZ transition energies and STG values are provided in eV, along with Λ-indices and frontier MOs. White|green|black|blue atoms denote H|B|C|N.

Furthermore, as shown in Fig. 6, BN-helicenes maintain a sufficiently large B–N separation, preventing the formation of shorter B–N contacts upon relaxation and thereby preserving the CT-type nature of the frontier MOs. If B and N were too close, their interaction would lead to bond formation, suppressing CT-type behavior and preventing the emergence of negative STG. Hence, other substitutional isomers of the right-most structure in Fig. 6, where both heteroatoms are still at the opposite ends of the helicene, may not show negative STGs if the heteroatoms are not sufficiently separated, as illustrated in Fig. 7.

Fig. 7 Two BNPAH isomers based on PAH-45 showing the dependence of STG on the spatial separation between the heteroatoms. White|green|black|blue atoms denote H|B|C|N.

3.3 DFIST-BNPAH candidates

For the 119 molecules that passed level-2 of the workflow with STG < 0 at the L-CC2/cc-pVDZ level, we carried out refined geometry optimizations and vibrational frequency analyses using the ωB97X-D3/def2-TZVP method. Based on the criteria defined in Section 2, 72 systems were confirmed to be geometrically stable, indicating that they correspond to local minima on the PES. The remaining 47 systems were found to be geometrically unstable, as their initial TPSSh/def2-SVP geometries reported in ref. 37 deviated significantly from the minima characterized by ωB97X-D3/def2-TZVP. Hence, we exclude these 47 molecules from further analysis.

For the 72 stable molecules, we computed S₁ and T₁ excitation energies, STGs, and oscillator strengths (f) at the L-CC2/aug-cc-pVDZ level. These results are presented in Table 1. The corresponding molecular structures, frontier MO isosurfaces, and HOMA values are provided in Table S4 of the ESI.† These 72 molecules span 30 unique PAH scaffolds, with the most frequent contributors being: PAH 46 (10 molecules), PAH 21 (8 molecules), PAH 76 (6 molecules), PAH 49 (4 molecules), and PAH 55 (4 molecules).

Table 1 Excited-state properties of DFIST candidates calculated at the L-CC2/aug-cc-pVDZ level. The S₁ and T₁ excitation energies, along with singlet–triplet gaps (STG), are reported in eV. S₀ → S₁ oscillator strengths (f) are given in atomic units. No. refers to the index of the DFIST-BNPAH candidate sorted in increasing order of STG, with the class of compound as defined in Fig. 8 given in parentheses. PAH corresponds to the index of the parent PAH shown in Fig. 1. Structures, HOMA plots, and isosurfaces of frontier MOs of all 72 systems are collected in Table S4 of the ESI

No. (class)	PAH	S1	f	T1	STG	No. (class)	PAH	S1	f	T1	STG
1 (1)	46	1.276	0.007	1.374	−0.098	37 (4)	32	1.081	0.010	1.101	−0.020
2 (1)	21	1.383	0.002	1.468	−0.085	38 (4)	54	1.345	0.032	1.365	−0.020
3 (1)	46	1.835	0.012	1.911	−0.076	39 (1)	31	1.978	0.003	1.997	−0.019
4 (1)	46	1.748	0.013	1.821	−0.073	40 (1)	31	2.043	0.012	2.062	−0.019
5 (1)	76	1.061	0.001	1.134	−0.073	41 (3)	49	1.222	0.013	1.240	−0.018
6 (1)	6	1.914	0.012	1.983	−0.069	42 (4)	55	1.267	0.002	1.285	−0.018
7 (1)	21	1.384	0.004	1.452	−0.068	43 (4)	57	1.832	0.028	1.850	−0.018
8 (1)	21	1.685	0.011	1.753	−0.068	44 (3)	71	1.816	0.030	1.834	−0.018
9 (1)	6	1.844	0.005	1.912	−0.068	45 (1)	49	2.188	0.005	2.205	−0.017
10 (1)	21	1.601	0.004	1.668	−0.067	46 (4)	52	1.155	0.005	1.172	−0.017
11 (1)	46	1.306	0.009	1.373	−0.067	47	37	1.158	0.003	1.170	−0.012
12 (1)	46	1.683	0.005	1.749	−0.066	48	15	1.040	0.005	1.051	−0.011
13 (4)	67	1.178	0.001	1.240	−0.062	49	64	1.102	0.001	1.113	−0.011
14 (1)	46	1.810	0.013	1.869	−0.059	50	67	1.273	0.000	1.284	−0.011
15 (1)	21	1.301	0.002	1.357	−0.056	51	26	1.381	0.017	1.391	−0.010
16 (1)	21	1.919	0.008	1.973	−0.054	52	17	1.363	0.017	1.372	−0.009
17 (1)	76	1.084	0.002	1.138	−0.054	53	26	1.367	0.020	1.376	−0.009
18 (1)	21	1.890	0.010	1.942	−0.052	54	32	1.002	0.002	1.010	−0.008
19 (1)	76	1.317	0.000	1.366	−0.049	55	36	1.368	0.037	1.376	−0.008
20 (1)	21	1.270	0.000	1.316	−0.046	56	37	1.378	0.047	1.386	−0.008
21 (1)	76	1.477	0.004	1.522	−0.045	57	69	1.433	0.048	1.441	−0.008
22 (1)	76	1.370	0.006	1.414	−0.044	58	63	1.147	0.047	1.154	−0.007
23 (1)	76	1.563	0.013	1.607	−0.044	59	61	1.455	0.027	1.461	−0.006
24 (1)	46	1.330	0.000	1.373	−0.043	60	40	1.505	0.035	1.506	−0.001
25 (4)	45	1.166	0.003	1.205	−0.039	61	49	1.279	0.010	1.280	−0.001
26 (1)	46	1.028	0.006	1.064	−0.036	62	19	1.815	0.011	1.815	0.000
27 (4)	45	1.500	0.003	1.533	−0.033	63	46	1.093	0.010	1.092	0.001
28 (4)	55	1.069	0.005	1.096	−0.027	64	54	1.462	0.052	1.460	0.002
29 (3)	75	1.606	0.040	1.633	−0.027	65	61	1.339	0.007	1.336	0.003
30 (1)	46	1.324	0.000	1.349	−0.025	66	55	1.398	0.004	1.393	0.005
31 (2)	48	1.809	0.005	1.834	−0.025	67	15	1.560	0.007	1.554	0.006
32 (2)	48	1.823	0.007	1.846	−0.023	68	71	1.776	0.007	1.768	0.008
33 (4)	55	1.054	0.011	1.077	−0.023	69	49	1.478	0.015	1.467	0.011
34 (3)	38	1.216	0.011	1.238	−0.022	70	30	1.791	0.046	1.764	0.027
35 (4)	48	1.376	0.025	1.398	−0.022	71	34	1.317	0.068	1.275	0.042
36 (3)	17	1.419	0.016	1.440	−0.021	72	34	1.319	0.075	1.242	0.077

---

Among the 72 candidates, 61 molecules exhibit negative STGs, ranging from −0.098 eV to −0.001 eV, confirming their DFIST potential. The most pronounced inversion is observed in molecule 1 (PAH 46) with STG = −0.098 eV, followed by several derivatives of the same scaffold. Only 11 molecules show STG ≥ 0, all of which are close to zero, with the largest value being +0.077 eV. Out of 72 candidate molecules presented in Table 1, 36 show STGs < −0.02 eV, of which only two molecules have an oscillator strength >0.02. In the remaining 36 with STG ≥ −0.02 eV, several molecules feature oscillator strength >0.02. This indicates an overall trade-off between the STG and oscillator strength due to their contrasting HOMO–LUMO overlap requirements as shown in the case of azaphenalenes in ref. 10.

As stated in 3.1 L-CC2/aug-cc-pVDZ has a mean error similar to that of L-CC2/aug-cc-pVTZ (≈0.015 eV), when benchmarked against 12 reference STGs. Accordingly, STG values less than −0.015 eV can be considered robust, true-positive predictions within the method's uncertainty. Based on this threshold, the first 46 of the 72 molecules in Table 1 can be confidently classified as DFIST candidates. The remaining 26 molecules, although exhibiting STGs within the method's error margin, are still highly promising as TADF candidates, particularly given their small STGs.

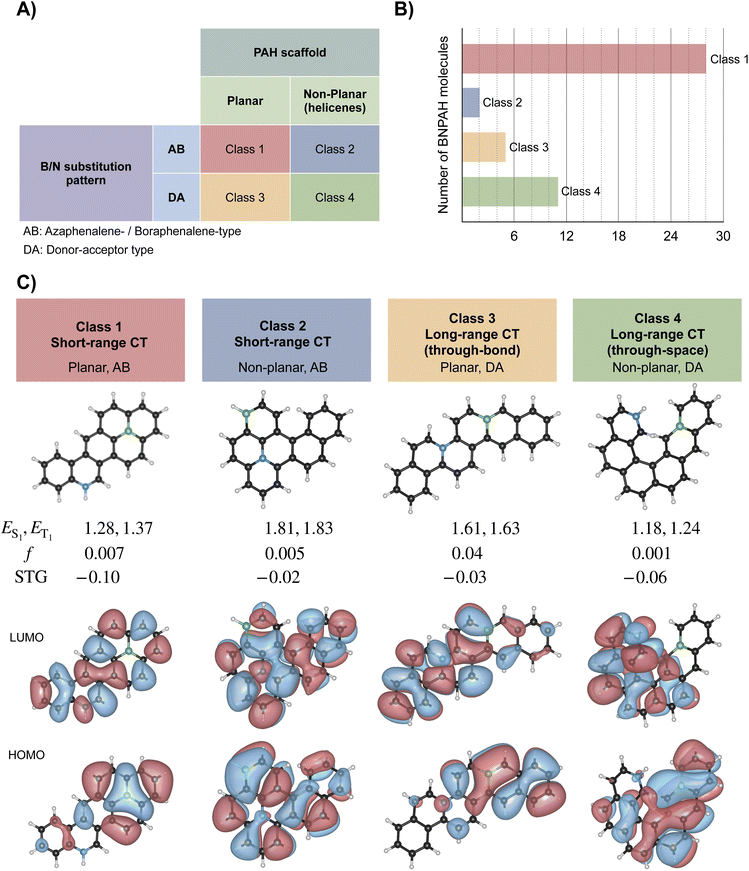
The shortlisted 46 DFIST BNPAH candidates with STG < −0.015 eV can be broadly categorized along two structural axes: (i) the geometry of the PAH scaffold, which is either planar or non-planar (helicene-type), and (ii) the B/N substitution pattern can be an AB-type motif (with embedded 1AP or 1BP cores, AB stands for azaphenalene or boraphenalene) or a DA-type motif (donor–acceptor with separated B and N) without an embedded 1AP or 1BP. AB-type structure also includes larger systems where both 1AP and 1BP cores are present. This classification results in four distinct classes of DFIST candidates, as illustrated in Fig. 8: planar, AB (class 1), non-planar, AB (class 2), planar, DA (class 3), and non-planar, DA (class 4). Both substitution patterns give rise to charge-transfer (CT) character; however, AB-type systems typically exhibit short-range CT localized within a triangular subunit, while DA-type systems feature long-range CT. The nature of this CT further depends on the molecular geometry: planar PAHs support through-bond CT, whereas non-planar PAHs, such as helicenes, enable through-space CT between spatially separated B and N atoms.

Fig. 8 Classification of top 46 DFIST candidates in the BNPAH chemical space with STG < −0.015 eV according to L-CC2/aug-cc-pVDZ: (A) classification of the top candidates based on PAH scaffold characteristics and B/N substitution patterns. (B) Bar plot showing the number of DFIST candidates in the four structural classes. (C) The representative molecule with the most negative STG from each class is shown along with its excited-state properties. White|green|black|blue atoms denote H|B|C|N. All energies are in eV, and f is in a.u.

To verify that the negative STGs predicted with L-CC2 are less susceptible to the theoretical level, we compare the L-CC2/cc-pVDZ-level STGs (based on ωB97X-D3/def2-TZVP geometries) of four representative molecules shown in Fig. 8 with values predicted with L-ADC(2) and ADC(2) in Table S3.† For the twelve benchmark values of STGs, ADC(2) delivers low prediction errors of less than 0.02 eV (see Table S2†). Hence, we used this method as a reference to compare the STGs of representative molecules predicted by L-CC2. Another popular method, EOM-CCSD, has been known to predict less negative STGs compared to high-level methods in a systematic manner, offering lower bounds for negative STGs. However, the mean error of 0.09 eV, noted for the benchmark systems (see Table S2†), is comparable to the least negative STGs encountered in the BNPAH molecules. Further, ref. 26 has shown that for some negative STG systems, while ADC(2) and CC2 are in good agreement with reference data, EOM-CCSD predicts positive STGs. Hence, we have not explored EOM-CCSD in this study. Overall, we find that both local methods deviate from the canonical ADC(2) method by ≈0.009 eV (calculated using values in Table S3 in the ESI†), indicating that the top-46 DFIST-BNPAH candidates will retain their qualitative nature (i.e., STG < 0) also when modeled with ADC(2). As ADC(2) calculations with a larger basis set were intractable, we performed L-ADC(2)/aug-cc-pVDZ calculations for all 72 molecules listed in Table 1. A comparison of STGs predicted by L-CC2 and L-ADC(2), with aug-cc-pVDZ, is shown in Fig. S1,† indicating an overall good agreement between these methods. Importantly, the signs of the STGs are in agreement between both theories, except for systems with nearly vanishing STGs.

To gain further understanding of the electronic structure of the DFIST-BNPAH candidate molecules, we performed the harmonic oscillator model of aromaticity (HOMA) analysis⁶⁷ of the 72 systems listed in Table 1 (see further details and Table S4 in the ESI†). The HOMA plots illustrate the disruption of aromaticity in the PAH systems resulting from the introduction of heteroatoms, where rings with a B atom show more diminished HOMA values than those with an N atom. Thus, HOMA provides complementary structural evidence for the spatial separation of frontier MOs, which is a critical electronic structure prerequisite for negative STGs.

Notably, the AB-type BNPAHs, although derived from triangular PAH motifs, deviate from perfect threefold symmetry, leading to partial HOMO–LUMO overlap and thus non-vanishing oscillator strengths. While these values are lower than those seen in high-efficiency TADF emitters such as DABNA, they are nonetheless significant given the orbital separation required to achieve a negative STG. It is well known that the key electronic feature enabling inverted singlet–triplet gaps—namely, minimal spatial overlap between frontier molecular orbitals—also inherently suppresses oscillator strength.⁹

Despite this tradeoff, the DFIST-BNPAH candidates reported here are novel examples based on alternant PAH cores offering non-planar (helical) structural prototypes. The most widely studied^{9,11,15,26,68} negative-STG systems are based on triangular molecular scaffolds, such as 1AP, 5AP, or 7AP, which are not derived from a benzenoid Kekulé alternant hydrocarbon. The larger triangular boron carbon nitrides exhibiting negative STGs also belong to the same class.⁵⁹ For example, in 1AP, if the central heteroatom is replaced by C, the resulting phenalenyl radical is a non-Kekulé benzenoid hydrocarbon. Another well-known class of negative-STG molecules explored in previous studies comprises non-alternant hydrocarbon frameworks with fused five and/or seven-membered rings (e.g., pentalene, isopyrene, etc.).^30–34 Further, studies^68,69 have also explored small aza-ring systems that are amenable to more detailed analysis.

The AB-type BNPAHs thus occupy a unique position in the landscape of DFIST emitters: their oscillator strengths are not negligible, and their emission profiles benefit from the multiresonant (MR) character^70,71 typical of rigid aromatic systems. These features position them as a new subclass of emitters that combine MR-like orbital separation with inverted singlet–triplet gaps. Accordingly, we refer to these as MR-DFIST emitters—molecules that unite the favorable oscillator strength and spectral sharpness of MR fluorophores with the inverted STG required for DFIST behavior.

Focusing on the top 18 DFIST candidates (those with STG < −0.05 eV), we find that most are derived from planar PAH scaffolds capable of supporting 1AP or 1BP moieties. However, molecule 13 derived from a helical PAH, also appears in this group. This represents the first example of a non-planar scaffold identified with negative STG, emphasizing the role of spatial orbital separation in enabling STG inversion.

4 Conclusions

The DFIST landscape remains sparsely populated in terms of experimental verification. To date, 5AP and the derivatives of 7AP are the only molecules with spectroscopically confirmed negative STGs. In this work, we present a multi-level high-throughput virtual screening framework as a complementary approach to rational molecular design, enabling the discovery of new molecular scaffolds that exhibit negative STGs. Our workflow, which incorporates stringent structural stability criteria and high-level excited-state calculations, provides a robust platform for minimizing false-positive predictions of negative STG systems.

By systematically exploring the BNPAH chemical space, we uncover a diverse array of DFIST candidates that extend beyond the well-known triangular frameworks or non-alternant hydrocarbons. Starting from a dataset of 30 797 BNPAH molecules derived from exhaustive combinatorial B,N substitutions in 77 benzenoid PAHs, we identify 61 molecules with negative STG and 46 with STG < −0.015 eV at the L-CC2/aug-cc-pVDZ level. These low-symmetry systems exhibit non-vanishing oscillator strengths for the S₀ → S₁ transition, making them promising candidates to observe DFIST. Additionally, our dataset includes several hundred BNPAH molecules with near-zero STGs, which could enable TADF through the RISC mechanism.

Our analysis reveals that the top-46 DFIST candidates can be categorized into four distinct structural classes, based on a combination of PAH topology (planar vs. non-planar) and heteroatom substitution pattern (AB: azaphenalene/boraphenalene-type vs. DA: donor–acceptor-type). This classification highlights how molecular geometry and substitution pattern jointly influence the STG, offering new handles for design and optimization. Importantly, we observe that some of the low-STG prototypes are structurally stable only in their fused PAH form, despite the instability of their isolated subunits.

For example, the symmetric structure of 1BP, while exhibiting a negative STG is geometrically unstable,²⁶ while our results show that when 1BP is embedded in a larger PAH scaffold such as pyrene or benzo[a]pyrene, the overall geometry is stabilized due to extended conjugation and the system retains negative STG. This finding highlights that unstable small molecular cores can be embedded in larger PAHs while retaining their desired electronic properties. We also identify non-planar BN-helicenes as promising DFIST candidates. These systems exhibit through-space charge transfer character, with spatially separated HOMO and LUMO that facilitate STG inversion. However, their non-planar geometry leads to limited stacking interactions, which may reduce exciton diffusion and energy transfer efficiency in solid-state applications.

Although we limit our exploration to BNPAHs containing only one B and one N atom, the complete BNPAH chemical space based on 77 PAHs with up to six benzene rings and the same number of B and N atoms comprises over 7.4 trillion unique molecules (7.4 × 10¹²).³⁷ Exploring such a vast space will require the integration of evolutionary algorithms, generative models, and other machine-learning-driven strategies. Finally, while ring-closing synthetic techniques can be used to incorporate B,N units into aromatic frameworks,^72–76 synthetic access to specific substitution patterns remains challenging.^77,78 The top-46 DFIST-BNPAH candidates identified here provide concrete molecular targets for synthesis and should be subjected to further refinement using high-level theoretical methods and experimental validation.

Data availability

The data that support the findings of this study are within the article and its ESI.† Data obtained at various levels of the workflow are provided in the GitHub repository: https://github.com/moldis-group/DFIST-BNPAH.

Author contributions

AM: conceptualization (lead); analysis (lead); data collection (lead); writing – original draft (lead); writing – review and editing (equal). SD: analysis (supporting); data collection (supporting); writing – original draft (supporting); writing – review and editing (equal). RR: conceptualization (lead); analysis (lead); data collection (supporting); funding acquisition; project administration; supervision; resources; writing – original draft (lead); writing – review and editing (equal).

Conflicts of interest

The authors have no conflicts of interest to disclose.

Acknowledgements

We acknowledge the support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI 4007. All calculations have been performed using the Helios computer cluster, which is an integral part of the MolDis Big Data facility, TIFR Hyderabad (http://moldis.tifrh.res.in).

References

1. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492(7428), 234–238,  DOI:10.1038/nature11687.
2. X.-K. Chen, D. Kim and J.-L. Brédas, Thermally activated delayed fluorescence (TADF) path toward efficient electroluminescence in purely organic materials: molecular level insight, Acc. Chem. Res., 2018, 51(9), 2215–2224,  DOI:10.1021/acs.accounts.8b00174.
3. K. Goushi, K. Yoshida, K. Sato and C. Adachi, Organic light-emitting diodes employing efficient reverse intersystem crossing for triplet-to-singlet state conversion, Nat. Photonics, 2012, 6(4), 253–258,  DOI:10.1038/nphoton.2012.31.
4. F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Triplet harvesting with 100% efficiency by way of thermally activated delayed fluorescence in charge transfer OLED emitters, Adv. Mater., 2013, 25(27), 3707–3714,  DOI:10.1002/adma.201300753.
5. T. Ye, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Thermally activated delayed fluorescence materials towards the breakthrough of organoelectronics, Adv. Mater., 2014, 26(47), 7931–7958,  DOI:10.1002/adma.201402532.
6. R. S. Nobuyasu, Z. Ren, G. C. Griffiths, A. S. Batsanov, P. Data, S. Yan, A. P. Monkman, M. R. Bryce and F. B. Dias, Rational design of TADF polymers using a donor–acceptor monomer with enhanced TADF efficiency induced by the energy alignment of charge transfer and local triplet excited states, Adv. Opt. Mater., 2016, 4(4), 597–607,  DOI:10.1002/adom.201500689.
7. T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Ultrapure Blue Thermally Activated Delayed Fluorescence Molecules: Efficient HOMO-LUMO Separation by the Multiple Resonance Effect, Adv. Mater. (Weinheim, Ger.), 2016, 28(14), 2777–2781,  DOI:10.1002/adma.201505491.
8. M. Y. Wong and E. Zysman-Colman, Purely organic thermally activated delayed fluorescence materials for organic light-emitting diodes, Adv. Mater., 2017, 29(22), 1605444,  DOI:10.1002/adma.201605444.
9. N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-i. Nakayama and S. Maeda, et al., Delayed fluorescence from inverted singlet and triplet excited states, Nature, 2022, 609(7927), 502–506,  DOI:10.1038/s41586-022-05132-y.
10. R. Pollice, P. Friederich, C. Lavigne, G. d. P. Gomes and A. Aspuru-Guzik, Organic molecules with inverted gaps between first excited singlet and triplet states and appreciable fluorescence rates, Matter, 2021, 4(5), 1654–1682,  DOI:10.1016/j.matt.2021.02.017.
11. K. D. Wilson, W. H. Styers, S. A. Wood, R. C. Woods, R. J. McMahon, Z. Liu, Y. Yang and E. Garand, Spectroscopic Quantification of the Inverted Singlet–Triplet Gap in Pentaazaphenalene, J. Am. Chem. Soc., 2024, 146(23), 15688–15692,  DOI:10.1021/jacs.4c05043.
12. Y. Kusakabe, K. Shizu, H. Tanaka, K. Tanaka and H. Kaji, An inverted singlet-triplet excited state in a pentaazaphenalene derivative (5AP-N (C12) 2), Appl. Phys. Express, 2024, 17(6), 061001,  DOI:10.35848/1882-0786/ad4e96.
13. A. Actis, M. Melchionna, G. Filippini, P. Fornasiero, M. Prato, M. Chiesa and E. Salvadori, Singlet-Triplet Energy Inversion in Carbon Nitride Photocatalysts, Angew. Chem., Int. Ed., 2023, 62(48), e202313540,  DOI:10.1002/anie.202313540.
14. P. de Silva, Inverted singlet–triplet gaps and their relevance to thermally activated delayed fluorescence, J. Phys. Chem. Lett., 2019, 10(18), 5674–5679,  DOI:10.1021/acs.jpclett.9b02333.
15. J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, Singlet–triplet inversion in heptazine and in polymeric carbon nitrides, J. Phys. Chem. A, 2019, 123(38), 8099–8108,  DOI:10.1021/acs.jpca.9b06215.
16. L. Werner and J. Wirz, Low-lying electronically excited states of cycl [3.3. 3] azine, a bridged 12. pi.-perimeter, J. Am. Chem. Soc., 1980, 102(19), 6068–6075,  DOI:10.1021/ja00539a016.
17. V. Bonacic-Koutecky and J. Michl, Charge-transfer-biradical excited states: relation to anomalous fluorescence.” Negative” S1-T1 splitting in twisted aminoborane, J. Am. Chem. Soc., 1985, 107(6), 1765–1766,  DOI:10.1021/ja00292a055.
18. D. Jacquemin, E. A. Perpète, I. Ciofini and C. Adamo, Assessment of functionals for TD-DFT calculations of singlet- triplet transitions, J. Chem. Theory Comput., 2010, 6(5), 1532–1537,  DOI:10.1021/ct100005d.
19. J. Carlos Sancho-Garcia, E. Bremond, G. Ricci, A. J. Pérez-Jiménez, Y. Olivier and C. Adamo, Violation of Hund's rule in molecules: Predicting the excited-state energy inversion by TD-DFT with double-hybrid methods, J. Chem. Phys., 2022, 156(3), 034105,  DOI:10.1063/5.0076545.
20. S. Ghosh and K. Bhattacharyya, Origin of the failure of density functional theories in predicting inverted singlet–triplet gaps, J. Phys. Chem. A, 2022, 126(8), 1378–1385,  DOI:10.1021/acs.jpca.1c10492.
21. L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, On the origin of the inverted singlet–triplet gap of the 5th generation light-emitting molecules, Phys. Chem. Chem. Phys., 2022, 24(31), 18713–18721,  10.1039/D2CP02364D.
22. M. Casanova Paez and L. Goerigk, Time-Dependent Long-Range-Corrected Double-Hybrid Density Functionals with Spin-Component and Spin-Opposite Scaling: A Comprehensive Analysis of Singlet-Singlet and Singlet-Triplet Excitation Energies, J. Chem. Theory Comput., 2021, 17(8), 5165–5186,  DOI:10.1021/acs.jctc.1c00535.
23. T. Won, K.-i. Nakayama and N. Aizawa, Inverted singlet–triplet emitters for organic light-emitting diodes, Chem. Phys. Rev., 2023, 4(2), 021310,  DOI:10.1063/5.0152834.
24. J. Li, Z. Li, H. Liu, H. Gong, J. Zhang, Y. Yao and Q. Guo, Organic molecules with inverted singlet-triplet gaps, Front. Chem., 2022, 10, 999856,  DOI:10.3389/fchem.2022.999856.
25. G. Ricci, E. San-Fabián, Y. Olivier and J.-C. Sancho-García, Singlet-triplet excited-state inversion in heptazine and related molecules: assessment of TD-DFT and ab initio methods, ChemPhysChem, 2021, 22(6), 553–560,  DOI:10.1002/cphc.202000926.
26. P.-F. Loos, F. Lipparini and D. Jacquemin, Heptazine, Cyclazine, and Related Compounds: Chemically-Accurate Estimates of the Inverted Singlet–Triplet Gap, J. Phys. Chem. Lett., 2023, 14(49), 11069–11075,  DOI:10.1021/acs.jpclett.3c03042.
27. P.-F. Loos, F. Lipparini and D. Jacquemin, Correction to “Heptazine, Cyclazine, and Related Compounds: Chemically-Accurate Estimates of the Inverted Singlet–Triplet Gap”, J. Phys. Chem. Lett., 2025, 16(10), 2570,  DOI:10.1021/acs.jpclett.5c00462.
28. P. Kayastha, S. Chakraborty and R. Ramakrishnan, The resolution-vs.-accuracy dilemma in machine learning modeling of electronic excitation spectra, Digital Discovery, 2022, 1(5), 689–702,  10.1039/D1DD00031D.
29. A. Majumdar and R. Ramakrishnan, Resilience of Hund's rule in the chemical space of small organic molecules, Phys. Chem. Chem. Phys., 2024, 26(20), 14505–14513,  10.1039/D4CP00886C.
30. M. H. Garner, J. T. Blaskovits and C. Corminboeuf, Double-bond delocalization in non-alternant hydrocarbons induces inverted singlet–triplet gaps, Chem. Sci., 2023, 14(38), 10458–10466,  10.1039/D3SC03409G.
31. J. Terence Blaskovits, M. H. Garner and C. Corminboeuf, Symmetry-Induced Singlet-Triplet Inversions in Non-Alternant Hydrocarbons, Angew. Chem., Int. Ed., 2023, 62(15), e202218156,  DOI:10.1002/anie.202218156.
32. M. H. Garner, J. Terence Blaskovits and C. Corminboeuf, Enhanced inverted singlet–triplet gaps in azaphenalenes and non-alternant hydrocarbons, Chem. Commun., 2024, 60(15), 2070–2073,  10.1039/D3CC05747J.
33. J. Terence Blaskovits, C. Corminboeuf and M. H. Garner, Excited-State Hund's Rule Violations in Bridged [10]-and [14] Annulene Perimeters, J. Phys. Chem. A, 2024, 128(48), 10404–10412,  DOI:10.1021/acs.jpca.4c06726.
34. A. K. Nigam, R. Pollice, P. Friederich and A. Aspuru-Guzik, Artificial design of organic emitters via a genetic algorithm enhanced by a deep neural network, Chem. Sci., 2024, 15(7), 2618–2639,  10.1039/D3SC05306G.
35. J. Terence Blaskovits, C. Corminboeuf and M. H. Garner, Singlet–Triplet Inversions in Through-Bond Charge-Transfer States, J. Phys. Chem. Lett., 2024, 15(40), 10062–10067,  DOI:10.1021/acs.jpclett.4c02317.
36. A. Majumdar, K. Jindal, S. Das and R. Ramakrishnan, Influence of pseudo-Jahn–Teller activity on the singlet–triplet gap of azaphenalenes, Phys. Chem. Chem. Phys., 2024, 26(42), 26723–26733,  10.1039/D4CP02761B.
37. S. Chakraborty, P. Kayastha and R. Ramakrishnan, The chemical space of B, N-substituted polycyclic aromatic hydrocarbons: Combinatorial enumeration and high-throughput first-principles modeling, J. Chem. Phys., 2019, 150(11), 114106,  DOI:10.1063/1.5088083.
38. K. Matsui, S. Oda, K. Yoshiura, K. Nakajima, N. Yasuda and T. Hatakeyama, One-shot multiple borylation toward BN-doped nanographenes, J. Am. Chem. Soc., 2018, 140(4), 1195–1198,  DOI:10.1021/jacs.7b10578.
39. A. Borissov, Y. Kumar Maurya, L. Moshniaha, W.-S. Wong, M. Zżła-Karwowska and M. Stepień, Recent advances in heterocyclic nanographenes and other polycyclic heteroaromatic compounds, Chem. Rev., 2021, 122(1), 565–788,  DOI:10.1021/acs.chemrev.1c00449.
40. C. Chen, Y. Zhang, X.-Y. Wang, J.-Y. Wang and J. Pei, Boron-and nitrogen-embedded polycyclic arenes as an emerging class of organic semiconductors, Chem. Mater., 2023, 35(24), 10277–10294,  DOI:10.1021/acs.chemmater.3c02106.
41. J. V. M. Pimentel, J. C. V. Chagas, M. Pinheiro Jr, A. J. A. Aquino, H. Lischka and F. B. C. Machado, Thermally Activated Delayed Fluorescence in B, N-Substituted Tetracene Derivatives: A Theoretical Pathway to Enhanced OLED Materials, J. Phys. Chem. A, 2025, 129(2), 470–480,  DOI:10.1021/acs.jpca.4c06481.
42. A. Derradji, M. Eugenia Sandoval-Salinas and G. Ricci, Ángel José Pérez-Jiménez, Emilio San-Fabián, Yoann Olivier, and Juan Carlos Sancho-García. Functionalization of Clar's Goblet Diradical with Heteroatoms: Tuning the Excited-State Energies to Promote Triplet-to-Singlet Conversion, J. Phys. Chem. A, 2025, 129(7), 1779–1791,  DOI:10.1021/acs.jpca.4c03820.
43. G. Brinkmann, C. Grothaus and I. Gutman, Fusenes and benzenoids with perfect matchings, J. Math. Chem., 2007, 42(4), 909–924,  DOI:10.1007/s10910-006-9148-z.
44. M. Schütz, Oscillator strengths, first-order properties, and nuclear gradients for local ADC (2), J. Chem. Phys., 2015, 142(21), 214103,  DOI:10.1063/1.4921839.
45. D. Kats, T. Korona and M. Schütz, Local CC2 electronic excitation energies for large molecules with density fitting, J. Chem. Phys., 2006, 125(10), 104106,  DOI:10.1063/1.2339021.
46. K. Freundorfer, D. Kats, T. Korona and M. Schütz, Local CC2 response method for triplet states based on Laplace transform: Excitation energies and first-order properties, J. Chem. Phys., 2010, 133(24), 244110,  DOI:10.1063/1.3506684.
47. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592,  DOI:10.1002/jcc.22885.
48. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation energies in density functional theory: An evaluation and a diagnostic test, J. Chem. Phys., 2008, 128(4), 044118,  DOI:10.1063/1.2831900.
49. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, et al., A package of ab initio programs, MOLPRO, Version 2015.1, 2015, https://www.molpro.net/.
50. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 . URL https://onlinelibrary.wiley.com/doi/full/10.1002/wcms.81.
51. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327 . URL https://onlinelibrary.wiley.com/doi/abs/10.1002/wcms.1327.
52. O. Vahtras, J. Almlöf and M. W. Feyereisen, Integral approximations for LCAO-SCF calculations, Chem. Phys. Lett., 1993, 213(5–6), 514–518,  DOI:10.1016/0009-2614(93)89151-7.
53. R. A. Kendall and H. A. Früchtl, The impact of the resolution of the identity approximate integral method on modern ab initio algorithm development, Theor. Chim. Acta, 1997, 97(1), 158–163 . URL https://link.springer.com/article/10.1007/s002140050249.
54. I. K. Anna and P. M. W. Gill, Q-Chem: an engine for innovation, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3(3), 317–326,  DOI:10.1002/wcms.1122.
55. M. Feldt and A. Brown, Assessment of local coupled cluster methods for excited states of BODIPY/Aza-BODIPY families, J. Comput. Chem., 2021, 42(3), 144–155,  DOI:10.1002/jcc.26442.
56. M. R. Momeni and A. Brown, A local CC2 and TDA-DFT double hybrid study on BODIPY/aza-BODIPY dimers as heavy atom free triplet photosensitizers for photodynamic therapy applications, J. Phys. Chem. A, 2016, 120(16), 2550–2560,  DOI:10.1021/acs.jpca.6b02883.
57. R. Ramakrishnan, P. O. Dral, M. Rupp and O. Anatole Von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1(1), 1–7,  DOI:10.1038/sdata.2014.22.
58. S. Senthil, S. Chakraborty and R. Ramakrishnan, Troubleshooting unstable molecules in chemical space, Chem. Sci., 2021, 12(15), 5566–5573,  10.1039/D0SC05591C.
59. S. Pios, X. Huang, A. L. Sobolewski and W. Domcke, Triangular boron carbon nitrides: An unexplored family of chromophores with unique properties for photocatalysis and optoelectronics, Phys. Chem. Chem. Phys., 2021, 23(23), 12968–12975,  10.1039/D1CP02026A.
60. C. Schäfer, R. Ringström, J. Hanrieder, M. Rahm, B. Albinsson and K. Börjesson, Lowering of the singlet-triplet energy gap via intramolecular exciton-exciton coupling, Nat. Commun., 2024, 15(1), 8705,  DOI:10.1038/s41467-024-53122-7.
61. T. Yang, N. Qiu, X. Lan, X. Dong, Z. T. Ben and Z. Zhao, Efficient Folded Molecules with Intramolecular Through-Space Charge Transfer for Near-Ultraviolet Organic Light-Emitting Diodes, J. Phys. Chem. C, 2024, 128(38), 16085–16092,  DOI:10.1021/acs.jpcc.4c02935.
62. H. Miranda-Salinas, Y.-T. Hung, Y.-S. Chen, D. Luo, H.-C. Kao, C.-H. Chang, K.-T. Wong and A. Monkman, Controlling through-space and through-bond intramolecular charge transfer in bridged D–D’–A TADF emitters, J. Mater. Chem. C, 2021, 9(28), 8819–8833,  10.1039/D1TC02316K.
63. K.-L. Woon, C.-L. Yi, K.-C. Pan, M. K. Etherington, C.-C. Wu, K.-T. Wong and A. P. Monkman, Intramolecular dimerization quenching of delayed emission in asymmetric D–D’–A TADF emitters, J. Phys. Chem. C, 2019, 123(19), 12400–12410 . URL https://pubs.acs.org/doi/10.1021/acs.jpcc.9b01900.
64. K. M. Rao, R. Rajavaram, D. Kolli, S. V. P. Vattikuti and M. Godumala, et al., Recent Breakthroughs in Through-Space Charge Transfer in π-Stacked Molecules as Thermally Activated Delayed Fluorescent Emitters for OLED Applications, J. Mater. Chem. C, 2025, 13(7), 3091–3122,  10.1039/D4TC05181E.
65. A. Landi and D. Padula, Optimising conformational effects on thermally activated delayed fluorescence, J. Mater. Chem. C, 2022, 10(29), 10699–10707,  10.1039/d2tc01722a.
66. A. Nowak-Król, P. T. Geppert and K. R. Naveen, Boron-containing helicenes as new generation of chiral materials: opportunities and challenges of leaving the flatland, Chem. Sci., 2024, 15(20), 7408–7440,  10.1039/D4SC01083C.
67. J. Kruszewski and T. M. Krygowski, Definition of aromaticity basing on the harmonic oscillator model, Tetrahedron Lett., 1972, 13(36), 3839–3842,  DOI:10.1016/S0040-4039(01)94175-9.
68. R. Pollice, B. Ding and A. Aspuru-Guzik, Rational design of organic molecules with inverted gaps between the first excited singlet and triplet, Matter, 2024, 7(3), 1161–1186,  DOI:10.1016/j.matt.2024.01.002.
69. M. Bedogni, D. Giavazzi, F. Di Maiolo and A. Painelli, Shining light on inverted singlet–triplet emitters, J. Chem. Theory Comput., 2023, 20(2), 902–913,  DOI:10.1021/acs.jctc.3c01112.
70. S. M. Suresh, D. Hall, D. Beljonne, Y. Olivier and E. Zysman-Colman, Multiresonant thermally activated delayed fluorescence emitters based on heteroatom-doped nanographenes: recent advances and prospects for organic light-emitting diodes, Adv. Funct. Mater., 2020, 30(33), 1908677,  DOI:10.1002/adfm.201908677.
71. L. Kunze, T. Froitzheim, A. Hansen, S. Grimme and J.-M. Mewes, ΔDFT predicts inverted singlet–triplet gaps with chemical accuracy at a fraction of the cost of wave function-based approaches, J. Phys. Chem. Lett., 2024, 15(31), 8065–8077,  DOI:10.1021/acs.jpclett.4c01649.
72. X.-Y. Wang, J.-Y. Wang and J. Pei, BN heterosuperbenzenes: synthesis and properties, Chem.–Eur. J., 2015, 21(9), 3528–3539,  DOI:10.1002/chem.201405627.
73. X. Chen, D. Tan and D.-T. Yang, Multiple-boron–nitrogen (multi-BN) doped π-conjugated systems for optoelectronics, J. Mater. Chem. C, 2022, 10(37), 13499–13532,  10.1039/D2TC01106A.
74. H. Gotoh, S. Nakatsuka, H. Tanaka, N. Yasuda, Y. Haketa, H. Maeda and T. Hatakeyama, Syntheses and Physical Properties of Cationic BN-Embedded Polycyclic Aromatic Hydrocarbons, Angew Chem. Int. Ed. Engl., 2021, 133(23), 12945–12950,  DOI:10.1002/ange.202103488.
75. Y. Appiarius, T. Stauch, E. Lork, P. Rusch, N. C. Bigall and A. Staubitz, From a 1, 2-azaborinine to large BN-PAHs via electrophilic cyclization: synthesis, characterization and promising optical properties, Org. Chem. Front., 2021, 8(1), 10–17,  10.1039/D0QO00723D.
76. J. A. Jaye, B. S. Gelinas, G. M. McCormick and E. H. Fort, Implications of the final ring closure to 10b-aza-10c-borapyrene for aryl–alkyne ring-closing mechanisms, Can. J. Chem., 2017, 95(4), 357–362,  DOI:10.1139/cjc-2016-0477.
77. S. Xu, L. N. Zakharov and S.-Y. Liu, A 1, 3-Dihydro-1, 3-azaborine Debuts, J. Am. Chem. Soc., 2011, 133(50), 20152–20155,  DOI:10.1021/ja2097089.
78. Z. X. Giustra and S.-Y. Liu, The state of the art in azaborine chemistry: new synthetic methods and applications, J. Am. Chem. Soc., 2018, 140(4), 1184–1194,  DOI:10.1021/jacs.7b09446.

---

Footnote

† Electronic supplementary information (ESI) available: (i) Details of HOMA analysis; (ii) comparison of L-CC2 and L-ADC(2) STGs (figure); (iii) CAM-B3LYP-level MO plots for representative molecules (figure); (iv) names and SMILES representations of the 77 parent PAHs used to construct the BNPAH chemical space (table); (v) benchmark error metrics for STGs predicted by various methods (table) (vi) L-CC2/cc-pVDZ, L-ADC(2)/cc-pVDZ, and ADC(2)/cc-pVDZ excited state energies for four DFIST-BNPAH molecules (table); (vii) structures, plots of frontier MOs, and HOMA indices for 72 DFIST-BNPAH candidates (table). See DOI: https://doi.org/10.1039/d5sc02309b

---