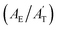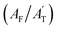Probing the freezing chemistry of singly levitated aqueous trifluoroacetic acid droplets in a cryogenically cooled simulation chamber relevant to Earth's upper troposphere

Abstract

Trifluoroacetic acid (CF₃COOH, TFA), the primary upper terrestrial atmospheric degradation product of several fluorinated hydrocarbons primarily used as refrigerants, poses a significant environmental challenge due to its growing atmospheric accumulation and extremely low reactivity. This combined experimental and theoretical study of TFA-doped water droplets, conducted inside a cryogenically cooled ultrasonic levitator simulation chamber utilizing time-dependent Raman spectroscopy and optical visualization techniques, addresses the dynamic chemical changes during the freezing event for the first time. The low-temperature experimental approach mimics TFA's interactions within water droplets in the upper troposphere and Arctic regions, particularly at subzero temperatures. Key findings reveal structural transformation towards the formation of undissociated neutral TFA in hexagonal ice environments compared to the anionic form, providing fundamental insight into the role of TFA in ice nucleation. Furthermore, state-of-the-art electronic structure calculations provide insights into the stability of this undissociated TFA within the hexagonal ice-encapsulated environment, wherein structural distortions of the regular hexagonal ice crystal and secondary F–H interactions mostly between anionic TFA forms and the ice lattice are evidenced at the molecular level. This research untangles the chemical insight into the TFA's role in ice nucleation leading to cloud glaciation, hence providing a plausible reason behind its unexpected presence in remote Arctic regions through long-range transport.

---

Introduction

Trifluoroacetic acid (CF₃COOH, TFA) represents one of the simplest fluorinated carboxylic acids in the terrestrial atmosphere^1–3 and also the most abundant per- and polyfluoroalkyl substance (PFAS). It is ubiquitously detected from the tropical zones to the most remote polar regions of Earth (Scheme 1a).^1,4–6 TFA primarily enters the atmosphere through the oxidation of polyfluoroalkyl refrigerants and particularly hydrofluorocarbons (HFCs) such as 1,1,1,2-tetrafluoroethane (CF₃CH₂F) and hydrofluoroolefins (HFOs) such as 2,3,3,3-tetrafluoropropene (CH₂=CFCF₃) and 3,3,3-trifluoropropene (CH₂=CHCF₃) (Scheme 1a).^7,8 Global monitoring data recorded by the National Oceanic and Atmospheric Administration (NOAA) have revealed an increase in 1,1,1,2-tetrafluoroethane (CF₃CH₂F) by more than one order of magnitude from 8.7 ppt to 121 ppt between 1998 and 2021.⁹ As a consequence, the concentration of TFA in the form of the trifluoroacetate anion (CF₃COO⁻) increased by a factor of six reaching a median concentration of 180 ng per litre in the hydrosphere.¹⁰ Although the most widely used hydrofluorocarbon refrigerants are phased out in favour of hydrofluoroolefin refrigerants due to their lower global warming potential, recent studies indicate that these next-generation hydrofluoroolefin refrigerants could contribute even more significantly to TFA formation compared to their hydrofluorocarbon predecessors.^1,2,4,11,12 The rise in TFA concentration poses a significant threat to the environment by bioaccumulating in aquatic organisms and terrestrial plants, as well as causing mammalian toxicity, which includes reproductive and liver damage.^2,13,14 Hence, physical chemists, computational scientists, and atmospheric chemists are beginning to engage in deciphering key pathways for TFA production and removal from the terrestrial atmosphere.¹⁵

Scheme 1 (a) Schematic representation of the formation of trifluoroacetic acid (TFA) via the oxidation of hydrofluorocarbons (HFCs) and hydrofluoro olefins (HFOs). TFA has lifetime of 10–15 days in the atmosphere, and it is 30,000 times more acidic than acetic acid. (b) Diagram of the cryogenic levitation setup combined with spectroscopic (Raman and FTIR) and optical (high-speed camera) diagnostic tools.

From a chemistry viewpoint, TFA is remarkably unreactive to atmospheric removal processes such as photolysis and reactions with abundant hydroxyl radicals (OH) and atomic oxygen (O); thus, it is often termed a ‘forever chemical’.^16,17 Instead, the primary removal pathway of TFA has been suggested to involve wet deposition, i.e. solvation and dissociation via deprotonation in aqueous media such as droplets; this process forms the highly stable trifluoroacetate anion (CF₃COO⁻). Neutral TFA (CF₃COOH) readily de-protonates in liquid solution due to the polarizability of the acetate functional group, as well as the ability of neutral TFA to adduct onto the surface of solvated TFA anions. The atmospheric lifetime of TFA through this deposition process lies in the range of 10 to 15 days.^1,4,16,18

The accumulation of TFA and its anion in water raises concerns about its long-term environmental impact, considering the resistance of TFA to natural degradation channels such as photolysis, reactions with reactive species such as hydroxyl (OH) and also to biodegradation, leading to an irreversible accumulation of TFA in aqueous bodies over time. Such accumulation poses a growing threat to the ecosystems, particularly in regions where TFA deposition rates are high, such as urban industrial areas.^1,2,4 In this context, it is crucial to note that Henry's law constant (K_H), which determines the solubility of vapor in water, is significantly higher for TFA at 298 K—ten times greater (9 × 10³ mol kg⁻¹ atm⁻¹) than that of analogous parent acetic acid (CH₃COOH, 0.9 × 10³ mol kg⁻¹ atm⁻¹).^18,19

Furthermore, as the temperature decreases to 240 K, the adsorption probability of TFA onto the ice surface increases to more than 50 times that of acetic acid, as indicated by their respective partition coefficients (K_linC); K_linC for TFA is 2100 cm, compared to 36 cm for acetic acid.²⁰

From a physical viewpoint, the transportation of tropospheric TFA leads to its incorporation into water droplets, involving the rapid hydrolysis of TFA vapor in water droplets, followed by ionization to its acetate form (Scheme 1a). The freezing of water droplets at subzero temperatures may provide a crucial link to the significant increase in TFA observed on ice surfaces in polar regions. This enhanced TFA deposition in the Arctic environment could have strong implications for ice melting. Therefore, the exploration of the freezing dynamics of TFA-doped aqueous droplets at subzero temperatures is vital not only to understand the composition of TFA-doped aqueous ices but also to decipher the missing link between ice melting and global warming potential. However, while several spectroscopic studies have explored TFA solutions at temperatures below 200 K on metal surfaces such as platinum, the freezing behaviour of TFA-doped water droplets at upper tropospheric sub-zero temperatures and temperature of Arctic regions of 262 K along with the temperature-dependent equilibrium between TFA and its anion has remained largely unexplored.^21,22 These fundamental data are critical to establish the environmental impact of TFA.

In this combined experimental and computational study, the freezing chemistry and dynamics of ultrasonically levitated single TFA-doped water droplets at subzero temperatures on the Celsius scale using a newly developed levitation setup are explored at the molecular level²³ (Scheme 1b). This setup merges ultrasonic levitation at cryogenic temperature with ultra-sensitive time-dependent Raman spectroscopy and high-speed imaging, thus enabling the exploration of low-temperature atmospheric chemistries and freezing processes in meticulously simulated terrestrial environments.^24–31 Stoke-shifted (red-shifted from intense Rayleigh scattering) vibrational features in the Raman spectrum bear the signature of the solvated molecules within the levitated droplet. Time-dependent Raman spectroscopy tracks changes in the spectral features of the water droplets and the dynamic changes of the molecular structure in the contactless freezing process, i.e. without interferences from any surfaces. These experimentally processed TFA-doped ice structures are simulated computationally at the molecular level to decipher elusive phase changes along with the molecular vs. ionic forms of TFA and the intriguing dynamic structural changes of ice-encapsulated TFA molecules in the upper troposphere and Arctic regions.

Results and discussion

Raman spectra of aqueous TFA droplets

To ascertain the Raman spectroscopic features of TFA in its aqueous form, 10% weight ratio to water (w/w) TFA-doped water droplets are levitated in a nitrogen atmosphere at 298 K; these droplets contain over 60 water molecules per TFA molecule (Table S1†). Since TFA exists in two forms in an aqueous solution (eqn (1)), Raman spectra of a 10% w/w TFA-doped water droplet (TFA : water = 1 : 62) (Fig. 1b, Tables 1 and S2a†) at room temperature are compared with those of a concentrated 80% w/w TFA-doped (TFA : water = 2 : 1) droplet as a reference (Fig. 1a, Tables 1 and S2a†). The Raman spectrum of 80% w/w can be described essentially as TFA in its undissociated form; hence, these spectra can be exploited to identify the spectral features originating from the undissociated form of TFA and to identify the corresponding features in diluted TFA-doped water droplets (10% w/w).

Fig. 1 Deconvoluted Raman spectra of TFA solutions: (a) 80% w/w TFA solution at room temperature at a molar ratio of TFA : water = 2 : 1. The spectral frequencies are represented with ν^t, where t denotes mostly undissociated TFA. (b) 10% w/w TFA solution at room temperature at a molar ratio of TFA : water = 1 : 62. The spectral frequencies are represented in this spectrum as ν₁ to ν₁₅. (c) 10% w/w TFA in ice at a freezing temperature of 262 K. Vibrational modes are represented with the symbol ν^I, where I signifies ice.

Table 1 Raman frequencies of the bands for a 10% TFA droplet at both room temperature and freezing temperature, along with Raman frequencies of an 80% TFA solution at room temperature

10% TFA solution at room temperature, 298 K (TFA : water = 1 : 62)		10% TFA solution at freezing temperature, 262 K (TFA : water = 1 : 62)		80% TFA solution at room temperature (TFA : water = 2 : 1)
Band	Wavenumber (cm^−1)	Band	Wavenumber (cm^−1)	Band	Wavenumber (cm^−1)
ν1	3405 (water)	ν^I1	3351 (water)	ν^I1	3466 (TFA-neutral)
ν2	3224 (water)	ν^I2	3144 (water)	ν^I2	2959 (TFA-neutral)
ν3	3035 (water)	ν^I3	3134 (water)	ν^I3	1771 (TFA-neutral)
ν4	1768 (TFA-ion)	ν^I4	1622 (water)	ν^I4	1461 (TFA-neutral)
ν5	1624 (water)	ν^I5	1444 (TFA-ion)	ν^I5	1213 (TFA-neutral)
ν6	1444 (TFA-ion)	ν^I6	1200 (TFA-mixed)	ν^I6	1170 (TFA-neutral)
ν7	1201 (TFA-ion)	ν^I7	1153 (TFA-mixed)	ν^I7	814 (TFA-neutral)
ν8	1154 (TFA-ion)	ν^I8	1034 (TFA-mixed)	ν^I8	713 (TFA-neutral)
ν9	846 (TFA-ion)	ν^I9	844 (TFA-ion)	ν^I9	599 (TFA-neutral)
ν10	818 (TFA-neutral)	ν^I10	820 (TFA-neutral)	ν^I10	520 (TFA-neutral)
ν11	724 (TFA-ion)	ν^I11	725 (TFA-mixed)	ν^I11	434 (TFA-neutral)
ν12	599 (TFA-ion)	ν^I12	601 (TFA-mixed)	ν^I12	406 (TFA-neutral)
ν13	521 (TFA-ion)	ν^I13	521 (TFA-mixed)	ν^I13	262 (TFA-neutral)
ν14	431 (TFA-ion)	ν^I14	435 (TFA-mixed)
ν15	409 (TFA-ion)	ν^I15	412 (TFA-mixed)
		ν^I16	287 (water)
		ν^I17	265 (TFA-neutral)

---

For the 80% case, a detailed analysis of the Raman spectra reveals that the most intense band corresponds to the C–C stretching mode of TFA (ν^t₇; 814 cm⁻¹), which is characteristic of its undissociated neutral form.³² In the diluted, 10% TFA solution, the most intense Raman bands (ν₁ to ν₃) emerge in the broad range between 2930 cm⁻¹ to 3660 cm⁻¹; these features correspond to a combination of O–H donor–acceptor (ν₁: 3405 cm⁻¹ O–H double donor single acceptor; ν₂: 3224 cm⁻¹ O–H double donor double acceptor of tetrahedral water environment) bands as those in liquid water.^33–35 The second most intense Raman feature appears at 1444 cm⁻¹ (ν₆) and corresponds to the C–O stretching of the trifluoroacetate anion (CF₃COO⁻).³⁶ The most intriguing aspect of the aqueous solution of trifluoroacetic acid (TFA) is observable in the spectral region between 770 cm⁻¹ and 880 cm⁻¹. This broad feature comprises two distinct bands at 846 cm⁻¹ and 818 cm⁻¹ corresponding to the C–C stretching vibration of TFA in the dissociated anionic and also in the undissociated neutral forms, respectively. In this context, it is important to mention that the frequency of C–C mode of the dissociated anionic TFA is higher as compared to the undissociated one, as the anionic form possesses partial double-bond characteristics. The Raman spectra of these diluted aqueous TFA droplets indicate the coexistence of both TFA and its anion, thus highlighting a dynamic equilibrium between the two forms of TFA, with a predominance of the anionic TFA form in diluted aqueous droplets at room temperature. Note that Raman spectra of even more diluted TFA-doped water droplets at 7.5%, 5%, 2.5%, and 1% also reveal analogous spectral characteristics at room temperature to those of 10% TFA-doped water droplets (Fig. S2a–S5a†).

CF₃COOH (aq) (neutral TFA) → CF₃COO⁻ (aq) (anionic TFA) + H⁺ (aq) (1)

Raman spectra of 10% TFA-doped aqueous ice

The Raman spectrum of the ice for the 10% aqueous solution at ∼262 K (freezing point) is presented in Fig. 1c (Tables 1 and S2b†). First, the Raman spectrum in the O–H stretching frequency region (ν_OH: 3800–2930 cm⁻¹) of the TFA-doped aqueous droplet at 262 K is dominated by the features of pure water ice, consisting of a sharp and prominent band formation at 3144 cm⁻¹, red-shifted from the 3224 cm⁻¹ band compared to pure water at room temperature indicating a phase change. This enhanced Raman intensity at 3144 cm⁻¹ corresponds to the double donor–double acceptor (DDAA) configuration of the pentameric unit in the hexagonal ice (I_h) crystal (ν_OH–DDAA) whereas, at room temperature, the tetrahedrally hydrogen-bonded water molecule shows a vibrational band at 3224 cm⁻¹.^33–35 The observation is similar to our previous report on the freezing of singly levitated pure water droplet.²³ Upon doping with TFA, apart from the significant spectral change in the O–H region indicating ice formation, remarkable differences in the C–C (800 cm⁻¹ to 850 cm⁻¹) and C–O (1444 cm⁻¹) stretching regions emerged compared to the spectra of TFA-doped liquid water droplets at 298 K. Upon ice formation, the C–O stretching mode of the trifluoroacetate anion (CF₃COO⁻) exhibits significant decrease in intensity, whereas the Raman intensity at 818 cm⁻¹ linked to the C–C stretching of undissociated, neutral TFA dominates over the C–C stretching of anionic TFA (846 cm⁻¹) in the 800–850 cm⁻¹ region.³⁷ The Raman spectra of even more diluted TFA-doped ice crystals exhibit similar spectral characteristics to those of 10% TFA-doped ice, as compiled in Fig. S2–S5.† It is important to highlight that the incorporation of TFA in the water droplet induces a significant depression in the freezing point as compared to pure water droplets. To investigate the impact of TFA concentrations on the freezing point of water droplets, we compared the freezing points of TFA-doped water droplets with those of pure water droplets. By analyzing the experimentally observed decrease in freezing temperature relative to pure water at various TFA concentrations, we constructed a freezing point depression profile (Fig. S6†), which reveals that for 10% TFA aqueous solution, the lowering is 10 ± 1 K.

Temporal profile of spectral changes during freezing

The spectroscopic and optical changes of the TFA-doped water droplets are tracked during the freezing process (Fig. 2), as demonstrated for the 10% aqueous solution. A significant alteration upon ice formation in the OH vibrational region (2900 cm⁻¹ to 3600 cm⁻¹) indicates the onset of ice formation.²³ Over varying freezing times, Fig. 2a illustrates the sequential changes in the Raman spectrum of the 10% TFA solution, corresponding to the initiation of ice formation just 30 seconds after the levitation of the aqueous TFA droplet in a nitrogen atmosphere transitioning into ice, as evidenced by a sharp spectral change in the O–H stretching region of water. The visible transformation from liquid to ice of a TFA-doped water droplet of 4 μL (Fig. 2b and S7†) volume is also captured using a high-speed optical camera alongside the corresponding spectral trace at specific time intervals. The temperature of the droplet is captured using a high-speed infrared camera, and a change in temperature due to ice formation is observed (Fig. S8†).

Fig. 2 (a) Temporal changes in the Raman spectra of 10% w/w TFA versus the progress of freezing at 262 K in the region of 4000 cm⁻¹ to 200 cm⁻¹. (b) Corresponding snapshots of the TFA droplet captured using a high-speed camera. (c) Magnified portion of the spectra in the region of 2000 cm⁻¹ to 200 cm⁻¹.

Although the band intensities representing the characteristics of the neutral and anionic forms of TFA in the aqueous solution are smaller compared to the O–H stretching frequencies of water by more than ten times, the spectral features in the 200 cm⁻¹ to 2000 cm⁻¹ region reveals intriguing dynamics between the two forms of TFA with the progress of freezing. Fig. 2c presents a magnified view of the Raman spectra, clearly indicating a decrease in intensity of the 1444 cm⁻¹ band, corresponding to the C–O stretching of the trifluoroacetate anion as freezing progresses. This change in intensity, represented as ν₆ in the room temperature liquid and ν^I₅ in the ice at 262 K, signifies a reduction in TFA ion concentration within the droplet as freezing advances.

To further explore the dynamic changes in the different TFA forms relative to ice formation, we compared the Raman spectra at three distinct freezing times (0 s, 90 s, and 135 s) in Fig. 3a. In addition to the changes in the O–H stretching region, the zoomed-in section in the 200 cm⁻¹ to 2000 cm⁻¹ (10 times) range exhibits a decrease in the ν₆ peak intensity corresponding to the CO stretching of the trifluoroacetate anion, alongside an increase in the ν₁₀ peak intensity associated with the C–C stretching of the neutral TFA form. The simultaneous reduction in the TFA ion band intensity and increase in the TFA band intensity (in neutral form) clearly illustrate the conversion of TFA ions to TFA as freezing progresses.

Fig. 3 (a) Spectral changes associated with ice formation in the O–H stretching region (3400 cm⁻¹ to 2900 cm⁻¹) of bands A₁ and A₂ belonging to water and the TFA region (2000 cm⁻¹ to 200 cm⁻¹), respectively. The TFA region is magnified by a factor of 10. (b) Deconvoluted spectra in the ranges 500 cm⁻¹ to 400 cm⁻¹ and 900 cm⁻¹ to 800 cm⁻¹. (c) Analysis extended to the deconvoluted spectra from 1300 cm⁻¹ to 900 cm⁻¹. (d) The upper trace illustrates the variation in the intensity ratio of band B (I_B) to band C (I_C) (TFA), while the lower trace denotes the change in the ratio of the area A₂ and A₁ (transition of liquid water to ice) in the O–H stretching region as freezing progresses in terms of first-order decay and growth, respectively. k_TFA and k_W are the rate constants for freezing TFA and water in TFA solution, respectively. (e) Upper trace: change in the deconvoluted band areas of bands C (A_C) and D (A_D) relative to the total area (A_T) in the range of 900 cm⁻¹ to 800 cm⁻¹. The contributions of bands C and D are represented as (A_C/A_T) and (A_D/A_T), respectively. The lower trace similarly depicts the change in the deconvoluted band areas of bands E (A_E) and F (A_F) concerning their overall area in the 500 cm⁻¹ to 400 cm⁻¹ range, denoted as and , respectively. (f) The analysis includes the change in the ratio of band area H, influenced by secondary H bonding interactions, in relation to band area G, which encompasses two C–F stretching vibrational modes (in phase and out of phase).

To quantify this dynamic change concerning ice formation, the ratio of the band intensities of ν₆ (B) and ν₁₀ (C) is plotted against the progress of freezing (Fig. 3d). The changes in the O–H stretching region define the extent of freezing and are quantified in terms of the ratio of area A₂ to A₁. Both plots of ice formation and interconversion between the neutral and anionic TFA forms demonstrate a significant change in the ratio A₂/A₁ or B/C during the same time interval between 30 s and 45 s. However, the rate constant of the ice formation (k_w = 0.025 ± 0.001 s⁻¹) is slightly higher compared to the rate constant of interconversion of the TFA droplet with the extent of freezing (k_TFA = 0.020 ± 0.005 s⁻¹); this finding indicates once again the interconversion between the neutral and ionic TFA forms after initiation of ice formation.

In addition, the deconvoluted spectra depict not only distinct forms of TFA but also reveal weak interactions that enhance upon ice formation. The deconvoluted peaks corresponding to TFA in its anionic form are shown in green, while the undissociated neutral forms are color-coded in purple. In the 800 cm⁻¹ to 900 cm⁻¹ region, two spectral features of both ionic and neutral TFA corresponding to the C–C stretching modes remain (ν₉ and ν₁₀ stretching according to Fig. 1b). The deconvoluted spectral bands connected with the C–C stretching of the TFA ion, with an intensity maximum at 846 cm⁻¹, is labelled as peak D, while an analogous vibrational mode for TFA in its neutral form, with intensity maxima at 818 cm⁻¹, is denoted as C (Fig. 3b). It is evident that the deconvoluted peak area corresponding to band C (A_C) increases, while that of band D (A_D) decreases with the progress of freezing. This change in the areal contribution of C (A_C/A_T) and D (A_D/A_T) to the total area in the 800 cm⁻¹ to 900 cm⁻¹ region (A_T) is plotted over time in Fig. 3e, indicating that the contribution of TFA in its undissociated neutral form increases over time, while its contribution in the ionic form decreases. A similar pattern is observed in the 400 cm⁻¹ to 500 cm⁻¹ region between the two deconvoluted peaks E and F, reflecting the same dynamic conversion between the two forms of TFA. The contributions of peak E and F 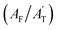, corresponding to the CF₃ rocking vibrational mode of TFA, are more likely associated with the intensity of TFA in the neutral form with the advancement of ice formation rather than the distribution observed in aqueous solution.

Fig. 3c highlights an intriguing feature indicating a secondary interaction between the C–F bond in TFA and the hydrogen-bonded framework of ice. The peak area representing hydrogen-bonded interactions (H) increases with the progression of ice formation, while the combined area of C–F in phase and out of phase (G) decreases over time. This is illustrated in Fig. 3f, where the ratio of H/G increases from 0.6 to 1. Notably, the existence of this hydrogen-bonded interaction emerges after the interconversion between the two forms of TFA. This interaction is important from the perspective of understanding the ice crystal structure in the Arctic region and, furthermore, its relevance to ice melting.

The interconversion between the neutral and anionic TFA forms (eqn (1)) is fundamental to the acid–base chemistry operating at subzero temperatures. It is also noteworthy to mention that Raman spectra of levitated TFA-doped water droplets at 298 K (Fig. 1b) and under super cooled conditions such as 262 K (Fig. 2a at 10 s) hardly show any change in the relative intensity distribution of the Raman features in the TFA region (200 cm⁻¹ to 2000 cm⁻¹). The drastic changes in the Raman spectra are observed solely with the progress of ice formation commencing at 262 K. However, it is also important to mention that although the amount of neutral undissociated TFA increases with the progress of ice formation, both the anionic TFA and neutral TFA exist under ice-encapsulated conditions; thus, the experimental Raman spectra show characteristic features of both forms. Since TFA is a strong carboxylic acid, its ionic form in the ice (although its contribution is less as compared to the solution) induces randomness as compared to pure ice by altering the internal motion as reported for hydrochloric acid (HCl), but in a lesser magnitude.³⁸

Theoretical calculation

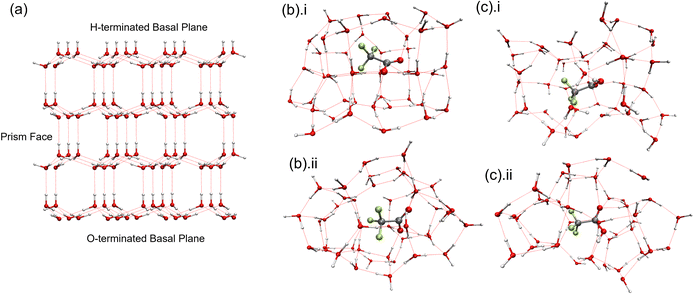
To elucidate the dynamic changes in TFA-doped water during freezing, quantum chemistry calculations using B3LYP-D3 density functional theory with the 6-31+G* basis set in NWChem were conducted.^39,40 The B3LYP functional—a hybrid exchange-correlation functional combining Hartree–Fock exchange with Becke's three-parameter exchange and the Lee–Yang–Parr correlation—is widely used for accurate predictions of molecular geometries, bond energies, and stereoelectronic effects. However, standard B3LYP lacks an explicit treatment of long-range dispersion interactions such as van der Waals forces, which are critical for systems dominated by noncovalent interactions. To address this, Grimme's D3 empirical dispersion correction was applied to account for dispersion forces in the hydrogen-bonded TFA–water network, thereby improving structural and energetic accuracy in the simulated ice-encapsulated molecular clusters.⁴¹ Hexagonal ice (I_h) is formed under our experimental conditions upon freezing. Hence, I_h encapsulating two distinct forms of TFA (anionic and neutral) was simulated computationally to interpret the spectral features of TFA-doped water droplets at the freezing point. A standard I_h crystal structure is illustrated in Fig. 4a; the optimized structures of the TFA-doped ice clusters (anionic and neutral) contain 42 water molecules and are depicted in Fig. 4b and c.

Fig. 4 (a) Typical hexagonal structure of the ice lattice. (b) Optimized structure of ice-encapsulated dissociated anionic TFA ((i) side view; (ii) top view). (c) Optimized structure of ice-encapsulated undissociated neutral TFA ((i) side view; (ii) top view).

The optimized structure of the two TFA-doped ice clusters reveals a significant distortion from the classical hexagonal ice crystal (Fig. 4b and c). The coordinates and the Mulliken charges on the individual atoms of the optimized structure are provided in the ESI (Table S4 and Fig. S9).† A scaling factor varying from 0.97 to 1.01 was applied to the computed frequency.⁴² This scaling factor accounts for both anharmonic corrections and calibrations between independent experimentally observed gas-phase TFA frequencies with those calculated with gas-phase TFA.⁴² The reported frequencies (Table 2) for the major vibrational modes under ice-encapsulated conditions not only clarify the Raman spectroscopic features of the two ice-encapsulated TFA forms (anionic versus neutral), but also provide compelling evidence for the experimentally observed secondary hydrogen bonding interactions. Here, among the key frequencies, the stretching frequencies of C–O and C–C corresponding to two distinct ice-encapsulated TFA forms (Table 2) support the experimentally observed Raman shifts. The computed C–O frequency for the anionic ice-encapsulated TFA is 1442 cm⁻¹, closely aligning with the experimentally observed absorption at 1444 cm⁻¹. In contrast, for the case of similar ice-encapsulated undissociated neutral TFA, the calculated C–O frequency is 1464 cm⁻¹ compared to the experimental value of 1461 cm⁻¹. Notably, the relative experimental intensity of the C–O frequency for neutral TFA is lower and is largely overshadowed by the band intensity of the anionic TFA form in the range of 1400 cm⁻¹ to 1500 cm⁻¹. In the region of 800 cm⁻¹ to 850 cm⁻¹, the computed C–C stretching frequency of undissociated neutral TFA is 815 cm⁻¹, while the experimentally observed frequency lies at 818 cm⁻¹. A similar calculated vibration of anionic ice-encapsulated TFA occurs at 841 cm⁻¹, compared to the experimental value of 844 cm⁻¹. Overall, scaled computed and experimental frequencies agree exceptionally well.

Table 2 Comparison of simulated frequencies with experimentally observed frequencies

Vibrational mode	Frequency of TFA in undissociated neutral form (cm^−1)		Frequency of TFA in dissociated ionic form (cm^−1)
	Experimental	Theory	Experimental	Theory
C–O stretch	1461	1464	1444	1442
C–C stretch	818	815	844	841
C–F–H stretch through OH	985–1070 broad	1100
C–F–H stretch (direct)			985–1070 broad	1080

---

In addition to the fundamental vibrations, a particularly intriguing aspect of the experimentally observed secondary hydrogen bond interactions can be elucidated through the ice-encapsulated anionic and neutral forms (Table 2). The anionic TFA interacts with the ice lattice via fluorine, whereas its neutral form engages with the ice lattice through long-range interactions involving the O–H terminal, indirectly influencing the C–F vibration mode. In both scenarios, the C–F frequencies are significantly impacted, as evidenced by a relative decrease in the Raman intensity associated with the C–F bond. Importantly, the optimized cluster of the ice-encapsulated TFA anion (C_2V) exhibits greater symmetry compared to that of the ice-encapsulated neutral TFA (C_s). This results in a higher number of degenerate vibrational modes, e.g. three such modes for the C=O vibration, being simulated for the TFA anion than for the neutral form (one mode), which may account for the enhanced Raman intensity observed for the former relative to its neutral counterpart. The formation of a stable ice-encapsulated TFA form in TFA-doped aqueous ice induces secondary interactions that lead to significant distortions in the regular hexagonal ice structure. Additionally, the same structural forms of TFA are optimized in an amorphous water environment (Fig. S10(i) & (ii)†), and the calculations reveal that neutral undissociated TFA shows a tendency to proton transfer, unlike the hexagonal ice-encapsulated environment beyond 8 water molecules, which is not supported by experimental Raman spectroscopic observations.

Atmospheric implications

Our findings provide direct experimental evidence for the significant transformation of TFA from its dissociated anionic form into its undissociated neutral form with the progress of freezing, thereby decreasing the acidity of the TFA-doped ice. TFA is the simplest and most abundant perfluorinated acid (PFA) distributed globally, which is known as a “forever chemical”, and plays a significant role in new particle formation (NPF) and ice-nucleating particle (INP) formation.^41–44 All these particles play a crucial role in heterogeneous upper tropospheric droplet freezing with implications for precipitation and cloud glaciation.^44–46 Our molecular level structural change of TFA in ice encapsulated environment aligns with the more facile ice nucleation of undissociated longer chain PFAs over their dissociated forms as proposed by Schwidetzky et al., wherein undissociated perfluorooctanoic acid (PFOA) initiate ice nucleation at 257 K as compared to the same event occurring at much lower temperature (247 K) for its dissociated form.⁴⁶ In addition to this, our experimental evidence also justifies the more prominent ice nucleation at lower acidity for certain mixed organic acids.⁴⁷ From the perspective of the role of NPF on cloud condensation, neutral nucleation is favoured more than ten times over the ion-induced nucleation, which once again supports the predominant existence of undissociated TFA in an ice-encapsulated environment. Active participation of TFA in cloud glaciation is probably the reason for its abundance in remote Arctic regions through long-range transportation through the clouds. Our experimental investigation also provides clear evidence of molecular-level interactions of both the TFA forms with ice crystals through F–H interactions. As evidenced theoretically, the anionic form of TFA mostly undergoes direct predominant F–H interactions; this secondary interaction plays a pivotal role in determining droplet-cloud interactions and hexagonal ice crystal distortion.

Moreover, the extracted kinetic data of the structural transformation could be incorporated into cloud glaciation and long-range transport models for accurately simulating the concentration of such forever chemicals in all regions of the atmosphere. Lastly, the observed freezing point depression and the anionic secondary interactions can plausibly induce ice melting.

Conclusion and outlook

This study presents a thorough experimental and theoretical exploration of TFA-doped water droplets under cryogenically cooled, contactless levitated conditions. By employing time-dependent Raman spectroscopy and optical techniques, this work carefully monitors the dynamic changes in TFA-doped water droplets, particularly at subzero temperatures pertinent to TFA's interactions with water droplets in the upper troposphere and Arctic regions. Key findings from Raman spectroscopy data reveal a dynamic structural transformation that leads to the formation of neutral TFA as hexagonal ice develops. This transition occurs from the more stable dissociated anionic TFA, which predominates in aqueous TFA-doped water droplets at room temperature. The theoretically optimized structures of ice-encapsulated undissociated neutral TFA demonstrate significant stability in the hexagonal environment compared to the amorphous environment, thus supporting the experimentally observed preference towards neutral TFA formation from the dissociated TFA anions as ice formation progresses. The observed rate constants for ice formation (k_w = 0.025 ± 0.001 s⁻¹) and TFA conversion (k_TFA = 0.020 ± 0.005 s⁻¹) further indicate TFA's concurrent structural changes alongside ice formation. However, the slightly higher value of k_w compared to k_TFA suggests that hexagonal ice formation is a critical step to trigger the neutral TFA formation within the ice lattice.

Molecular level understanding of the freezing process from a TFA-doped aqueous droplet to a highly ordered hexagonal ice induces changes in some elementary physical properties such as solvation and ion mobility of the TFA anion. Random arrangement of water molecules in an aqueous droplet to a highly ordered hexagonal lattice restricts ion mobility. Moreover, the electron affinity of fluorine in TFA (exothermic process), which plays a pivotal role in the determination of solvation of TFA anion, decreases with the progress of freezing. Thus, the cumulative effect of these elementary physical properties lowers the extent of solvation for the TFA anion, explaining the structural transformation of most simple perfluorinated acid TFA.

Additionally, the study highlights secondary F–H interactions between various TFA forms and ice crystals, as evidenced by changes in the relative Raman intensity of C–F stretching frequencies. The theoretically optimized structures of ice-encapsulated TFA reveal significant distortions in the regular hexagonal ice lattice. The calculated structures indicate distinct types of secondary F–H interactions with the ice crystal: anionic forms exhibit direct F–H interactions, while the undissociated neutral form displays long-range interactions.

These experimental observations, combined with theoretical calculations, provide compelling evidence for the role of neutral TFA in ice nucleation through ice-nucleating particle (INP) formation and new particle formation (NPF). The secondary F–H interactions in ice-encapsulated TFA provide further molecular-level insight into the ice crystal distortion. Furthermore, the kinetic data could be incorporated into cloud glaciation and long-range transport models for accurately simulating the concentration of TFA in all regions of the atmosphere. This is the first systematic molecular-level experimental investigation of droplet freezing chemistry exploiting the simplest perfluorinated acid (PFA). Further experimental investigations are earnestly required for a better understanding of the atmospheric implications of “forever chemicals” globally.

Data availability

All the data are included in the manuscript and/or the ESI.†

Author contributions

K. M., S. B., and R. I. K. designed the research; K. M. and S. B. performed the experimental work; N. M. performed the theoretical analysis; K. M. analyzed the experimental and theoretical data and wrote the manuscript; S. B., R. S., and R. I. K. edited the draft. R. I. K. supervised the research and edited the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This study was funded through the NSF award, 2330175, Center: NSF Engineering Research Center for Environmentally Applied Refrigerant Technology Hub.

References

1. M. D. L. A. Garavagno, R. Holland, M. A. H. Khan, A. J. Orr-Ewing and D. E. Shallcross, Sustainable, 2024, 16, 2382.
2. H. P. H. Arp, A. Gredelj, J. Glüge, M. Scheringer and I. T. Cousins, Environ. Sci. Technol., 2024, 58, 19925–19935.
3. J. Janda, K. Nödler, H. J. Brauch, C. Zwiener and F. T. Lange, Environ. Sci. Pollut. Res., 2019, 26, 7326–7336.
4. Y. Zhou, C. Wang, H. Dong and X. Wang, Sci. Bull., 2024, 69, 2483–2486.
5. W. F. Hartz, M. K. Björnsdotter, L. W. Y. Yeung, A. Hodson, E. R. Thomas, J. D. Humby, C. Day, I. E. Jogsten, A. Kärrman and R. Kallenborn, Sci. Total Environ., 2023, 871, 161830.
6. M. K. Björnsdotter, W. F. Hartz, R. Kallenborn, I. Ericson Jogsten, J. D. Humby, A. Kärrman and L. W. Y. Yeung, Environ. Sci. Technol., 2021, 55, 15853–15861.
7. V. R. Kotamarthi, J. M. Rodriguez, M. K. W. Ko, T. K. Tromp, N. D. Sze and M. J. Prather, J. Geophys. Res., 1998, 103, 5747–5758.
8. J. B. Burkholder, R. A. Cox and A. R. Ravishankara, Chem. Rev., 2015, 115, 3704–3759.
9. NOAA/ESRL Halocarbons and other Trace Species, available online: https://www.esrl.noaa.gov/gmd/dv/data.html, accessed 2022-01-15.
10. T. M. Cahill, Environ. Sci. Technol., 2022, 56, 9428–9434.
11. R. Holland, M. A. H. Khan, I. Driscoll, R. Chhantyal-Pun, R. G. Derwent, C. A. Taatjes, A. J. Orr-Ewing, C. J. Percival and D. E. Shallcross, ACS Earth Space Chem., 2021, 5, 849–857.
12. G. Salierno, ChemSusChem, 2024, 17, e202400280.
13. D. A. Blake, J. Q. Barry and H. F. Cascorbi, Naunyn-Schmiedeberg's Arch. Pharmacol., 1970, 265, 474–475.
14. A. G. Berends, J. C. Boutonnet, C. G. De Rooij and R. S. Thompson, Environ. Toxicol. Chem., 1999, 18, 1053–1059.
15. C. Austin, A. L. Purohit, C. Thomsen, B. R. Pinkard, T. J. Strathmann and I. V. Novosselov, Environ. Sci. Technol., 2024, 58, 8076–8085.
16. T. E. Mnrgelberg, O. J. Nielsen, J. Sehested, T. J. Wallington and M. Hurley, Chem. Phys. Lett., 1994, 226, 171–177.
17. Sierra Club, available online: https://www.sierraclub.org/sierra/environment-explained/tfa-pfas-forever-chemical-you-wish-wasn-t-everywhere.
18. D. J. Bowden, S. L. Clegg and P. Brimblecombe, Chemosphere, 1996, 32, 405–420.
19. B. J. Johnson, E. A. Betterton and D. Craig, J. Atmos. Chem., 1996, 24, 113–119.
20. A. Symington, R. A. Cox and M. A. Fernandez, Z. Phys. Chem., 2010, 224, 1219–1245.
21. S. Shin, Y. Park, Y. Kim and H. Kang, J. Phys. Chem. C, 2017, 121, 12842–12848.
22. Y. Park, S. Shin and H. Kang, J. Phys. Chem. Lett., 2018, 9, 4282–4286.
23. S. Biswas, D. Paul, K. Mondal and R. I. Kaiser, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2425543122.
24. S. Biswas, I. Antonov, K. Fujioka, G. L. Rizzo, S. D. Chambreau, S. Schneider, R. Sun and R. I. Kaiser, Phys. Chem. Chem. Phys., 2023, 25, 6602–6625.
25. D. Paul, S. Biswas, H. Yeom, K. Na, M. L. Pantoya and R. I. Kaiser, ACS Appl. Mater. Interfaces, 2024, 16, 53938–53949.
26. G. L. Rizzo, S. Biswas, I. Antonov, K. K. Miller, M. L. Pantoya and R. I. Kaiser, J. Phys. Chem. Lett., 2023, 14, 2722–2730.
27. G. L. Rizzo, S. Biswas, M. L. Pantoya and R. I. Kaiser, Chem. Phys. Lett., 2024, 842, 141212.
28. S. Biswas, K. Fujioka, I. Antonov, G. L. Rizzo, S. D. Chambreau, S. Schneider, R. Sun and R. I. Kaiser, Chem. Sci., 2023, 15, 1480–1487.
29. S. Biswas, K. Fujioka, D. Paul, M. Mcanally, G. L. Rizzo, S. D. Chambreau, S. Schneider, R. Sun and R. I. Kaiser, J. Phys. Chem. Lett., 2025, 16, 1831–1839.
30. G. L. Rizzo, S. Biswas, D. Ka, X. Zheng and R. I. Kaiser, J. Phys. Chem. A, 2025, 129, 288–300.
31. S. J. Brotton and R. I. Kaiser, Rev. Sci. Instrum., 2013, 84, 055114.
32. N. Fuson, M. L. Josien, E. A. Jones and J. R. Lawson, J. Chem. Phys., 1952, 20, 1627–1634.
33. Q. Sun and H. Zheng, Prog. Nat. Sci., 2009, 19, 1651–1654.
34. L. Shi, S. M. Gruenbaum and J. L. Skinner, J. Phys. Chem. B, 2012, 116, 13821–13830.
35. W. J. Smit, et al., J. Phys. Chem. Lett., 2017, 8, 3656–3660.
36. R. E. Robinson and R. C. Taylor, Spectrochim. Acta, 1962, 18, 1093–1097.
37. C. V. Berney, J. Am. Chem. Soc., 1973, 95, 708–716.
38. K. Köster, V. Fuentes-Landete and A. Raidt, et al., Nat. Commun., 2015, 6, 7349.
39. E. Aprà, et al., J. Chem. Phys., 2020, 152, 184102.
40. G. W. Spitznagel, T. Clark, J. Chandrasekhar and P. V. R. Schleyer, J. Comput. Chem., 1982, 3, 363–371.
41. G. A. DiLabio, E. R. Johnson and A. Otero-de-la-Roza, Phys. Chem. Chem. Phys., 2013, 15, 12821–12828.
42. Computational Chemistry Comparison and Benchmark DataBase Release 22 (May 2022) Standard Reference Database 101 National Institute of Standards and Technology, available online: https://cccbdb.nist.gov/vibscalejustx.asp.
43. Y. Zhou, X. Wang, C. Wang, Z. Ji, X. Niu and H. Dong, Earth-Sci. Rev., 2024, 259, 104973.
44. L. Liu, F. Yu, K. Tu, Z. Yang and X. Zhang, Atmos. Chem. Phys., 2021, 21, 6221–6230.
45. F. Bianchi, et al., Science, 2016, 352, 1109–1112.
46. R. Schwidetzky, Y. Sun, J. F. Nowoisky, A. T. Kunert, M. Bonn and K. Meister, J. Phys. Chem. Lett., 2021, 12, 3431–3435.
47. Z. Lei, B. Chen and S. D. Brooks, ACS Earth Space Chem., 2023, 7, 2562–2573.

---

Footnote

† Electronic supplementary information (ESI) available: Molarity and molar ratio of different types of TFA solutions (Table S1); detailed assignment of 10% and 80% TFA at room temperature (Table S2a); detailed assignment of 10% TFA at room and freezing temperatures (Table S2b); gas phase FTIR spectrum of TFA and its analysis (Fig. S1 and Table S3); Raman spectrum of diluted TFA solutions both in liquid & ice phases (Fig. S2–S5); depression in freezing point (Fig. S6); typical size and volume of a levitated droplet (Fig. S7); change in temperature during ice freezing recorded using an IR camera (Fig. S8); charge distribution of the optimized ice encapsulated different TFA forms (Fig. S9); optimized structure of ice encapsulated different TFA forms (Tables S4a & b); structure of amorphous TFA containing ice (Fig. S10i & ii). See DOI: https://doi.org/10.1039/d5sc01698c

---