Disentangling chemical pressure and superexchange effects in lanthanide–organic valence tautomerism

Abstract

Valence tautomerism in molecule-based f-block materials remains virtually elusive. As a result, the effects driving and controlling the valence conversion phenomenon are poorly understood. Herein, we unravel these fundamental factors by systematic chemical modification of a bona fide lanthanide coordination solid, SmI₂(pyrazine)₂(tetrahydrofuran), in which a complete, temperature-driven conversion between Sm(II) and Sm(III) occurs abruptly around 200 K. Solid solutions incorporating either divalent, diamagnetic metal ions or Sm(III) ions feature disparate behavior. Substitution with redox-inactive, divalent metal ions invariably leads to lower conversion temperatures and reduced cooperativity. In contrast, incorporation of redox-inactive Sm(III) ions leads to trapped pyrazine anion radicals in the ligand scaffold, shifting the valence tautomeric conversion phenomenon towards higher temperature with virtually no loss of cooperativity. These materials are rare examples of lanthanide–organic materials hosting mixed valency in both the lanthanide and organic scaffold, affording switchable conductivity associated with the valence tautomeric conversion.

---

Introduction

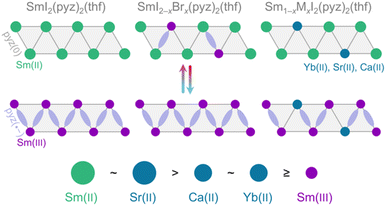
Materials with intrinsic switchability of physical properties are receiving increasing attention due to their potential applications in future electronics,¹ catalysis,² and sensing.^3–5 A given material can convert between states through a range of different mechanisms. One mechanism for switching is stimulated electron transfer between a metal ion and an organic ligand, leading to two (or more) valence tautomers existing in equilibrium.^6,7 The conversion between the valence tautomers may be actuated by temperature alterations through the competition of changes in enthalpy (ΔH) and entropy (ΔS). In transition metal chemistry, the thermodynamics of valence tautomeric (VT) conversions have been studied extensively since their discovery in 1980,⁸ and design principles for these materials have been developed.^9–11 In contrast, for the f-block elements, this level of understanding has not been achieved. Temperature-driven valence changes in lanthanide compounds date back more than a hundred years with their observation in elemental Ce, wherein the electron transfer is instead a promotion of a localized 4f electron to the s–d conduction band.^12–14 This behavior was later found to be paralleled in several inorganic solids, such as SmS and Sm_2.75C₆₀, which, however, seldom attain the limiting di- or trivalent states but reside in intermediate oxidation states at ambient pressure.^15,16 As such, molecular materials remain conceptually different from these purely inorganic f-block compounds. We recently reported a unique example of a lanthanide-based coordination solid, SmI₂(pyz)₃ (pyz = pyrazine), exhibiting a quantitative VT transition between integer oxidation states.¹⁷ At high temperature, Sm(II) is present, but below ∼190 K, Sm(II) reversibly and cooperatively transfers a single electron to a bridging pyz ligand yielding a Sm(III)-pyz(·−) tautomer (Fig. 1). This abrupt VT conversion is accompanied by both a structural change in the first coordination sphere and a significant change in the magnetic moment. Additionally, the VT event can be pushed to lower temperature by substituting Yb(II) into the material, which are trapped in the Yb(II)-pyz(0) state at all temperatures. The Yb(II) impurities compromise the cooperativity and exert chemical pressure which destabilizes the low temperature phase and thus decreases the VT conversion temperature. Herein, we provide new synthetic guidelines for these unique materials by uncovering the size dependence of divalent impurities and demonstrating how persistent Sm(III)-pyz(·−) impurities shift the VT transition towards room temperature while fully conserving cooperativity.

Fig. 1 Schematic overview of the VT conversion between the high temperature Sm(II)-pyz(0) and low temperature Sm(III)-pyz(·−) isomers in SmI₂(pyz)₂(thf) along pseudo-1D chains. In hetero-halide alloys (center), trapped Sm(III)-pyz(·−) units do not undergo conversion; in hetero-metal alloys (right), M(II) nodes are trapped. The relative sizes of the Sm and M(II) ions are indicated below, as inferred from Sm–N and M–N bond lengths.

Results and discussion

Synthesis and structural characterisation

The occurrence of the VT event is fundamentally related to the reduction potential of the metal ion node. This, in turn, can be modified by the ancillary ligands, as illustrated by SmI₂ (E_1/2 = −0.89 V vs. SCE) and SmBr₂ (E_1/2 = −1.6 V) in tetrahydrofuran (thf).¹⁸

We attempted to synthesize SmBr₂(pyz)₃ analogously to SmI₂(pyz)₃ by addition of SmBr₂(thf)₂ in acetonitrile to molten pyrazine, which was unsuccessful due to the poor solubility of the starting material. By performing the reaction in thf or thf/dimethoxyethane, both SmBr₂(pyz)₂(thf) and SmI₂(pyz)₂(thf) could be obtained. For SmI₂(pyz)₂(thf) (0%, Fig. 2a), single crystal X-ray diffraction (SCXRD) reveals the compound to be structurally analogous to the parent SmI₂(pyz)₃.¹⁷ Upon cooling from 230 K to 170 K, the average Sm–I and Sm–N bond lengths shrink significantly by 3% and 6%, respectively, accompanied by an 8% deviation of the ∠I–Sm–I bond angle from linearity (Table S1†). These structural changes suggest a Sm(II)-to-Sm(III) valence change, akin to that observed in SmI₂(pyz)₃. Furthermore, inspection of the pyz bond lengths suggests the presence of zig-zag chains of pyz(·−) radicals (Fig. 1).^19,20 Single crystals of SmBr₂(pyz)₂(thf) (100%) suitable for SCXRD were not obtained, and the structure was determined by Rietveld refinement of room temperature powder X-ray diffraction (PXRD) data (Fig. 3). 100% is isomorphous to the low temperature (LT) phase of 0% (Fig. 2bc and S1†). The average Sm–N (2.52 Å) bond length in 100% is similar to that found in LT-0% (2.55 Å), suggesting the presence of the Sm(III)-pyz(·−) tautomer at room temperature in 100%.

Fig. 2 (a) Coordination sphere of 0% determined by SCXRD at 230 K and at 170 K (in transparent violet). Selected bond lengths (Å) at 230 K (170 K): Sm–I 3.1950(5) (3.0940(7), 3.0810(7)); Sm–N 2.747(4) (2.620(7)), 2.758(4) (2.490(6)). Bond lengths (Å) in pyz (i) at 230 K (170 K): C–N 1.326(10) (1.335(11)), 1.329(10) (1.326(11)); C–C 1.385(18) (1.374(17)), 1.401(16) (1.381(17)). Bond lengths (Å) in pyz (ii) at 230 K (170 K): C–N 1.337(10) (1.359(10)), 1.336(10) (1.360(10)); C–C 1.378(12) (1.328(12)). (b) Coordination sphere of 100% based on Rietveld refinement. (c) Polymeric chain of 100% viewed along a Sm–Br bond. Color code: Sm, cyan; I, purple; Br, gold; N, light blue; O, red; C, gray. Hydrogen atoms have been omitted for clarity.

Fig. 3 Room-temperature powder X-ray diffractograms of pristine 0%, 100% and the 10% and 20% alloys. The black traces indicate the Rietveld refinement pattern for each of the compounds. The 0%, 10% and 20% were refined against the high temperature crystal structure of 0% while 100% was refined against the single crystal structure of LT-0%. The simulated peaks and difference plots for 100% are shown in purple and pink, respectively. The inset shows the unit cell volume as a function of Br-percentage as found by Rietveld refinement at room temperature; the cross shows the volume for 0% determined by SCXRD. The grey line shows the extrapolated volume decrease with increasing Br content if no valence change occurred.

Characterisation of the valence conversion

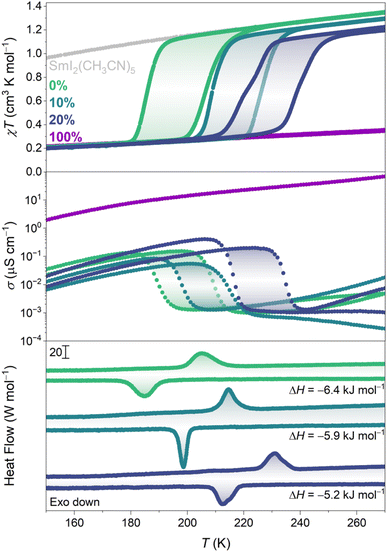
The temperature dependence of the magnetic susceptibility–temperature product (χT) of 0% and 100% is presented in Fig. 4. 0% has a χT value of 1.35 cm³ K mol⁻¹ at room temperature, as expected for Sm(II).²¹ Around , χT rapidly decreases before it plateaus, reaching a value of ∼0.05 cm³ K mol⁻¹ at 3 K (Fig. S15†). Ignoring the finite magnetic moment of Sm(III) at room temperature,²² the χT product of LT-0% can be modelled as an infinite chain of antiferromagnetically coupled pyz(·−), yielding J ≈ −75 cm⁻¹ (Fig. S14†), as a lower bound of the actual pyz(·−)⋯pyz(·−) superexchange coupling constant.^17,23 On heating, the reverse conversion occurs at , behaving almost identically to SmI₂(pyz)₃ (Fig. S13†). This observation is substantiated by the fact that the VT conversion does not involve significant change to the Sm–N bond of the exo-chain pyrazine in SmI₂(pyz)₃. This contrasts with the sensitivity of the other reported molecular lanthanide compounds, where minute changes in the local coordination sphere are detrimental to the VT event.^24,25 In contrast, 100% shows no signs of conversion up to the decomposition temperature (∼420 K, Fig. S20†), with a magnetic profile up to 400 K corresponding to the Sm(III)-pyz(·−) tautomer.

Fig. 4 Magnetic susceptibility–temperature product (top; sweep rate = 0.5 K min⁻¹), electrical conductivity (middle; sweep rate = 1 K min⁻¹) and differential scanning calorimetry (bottom; sweep rate = 2 K min⁻¹) of 0%, 10%, 20% and 100%.

Kahn's notion of molecular alloying elucidated that a solid solution of two spin crossover (SCO) complexes assumes a SCO conversion temperature in between those of the pristine phases.^26–28 As no VT conversion is observed in 100% below the decomposition temperature, we adopt Kahn's approach and hypothesize that alloying 0% with 100% shifts the VT conversion towards room temperature. The addition of a solution containing both SmI₂ and SmBr₂(thf)₂ to molten pyrazine leads to a single polycrystalline phase (Fig. 3, S4–S7†) for molar percentages of SmBr₂(thf)₂ up to 20% (SmI_1.8Br_0.2(pyz)₂(thf), 10% and SmI_1.6Br_0.4(pyz)₂(thf), 20%). Analysis of the powder X-ray diffractograms reveals that 10% and 20% are isomorphous to HT-0% at room temperature. Attempts to incorporate more than 20% Br invariably led to isolation of a mixture of two crystallographic phases (isomorphous to 0% and 100%), as observed by PXRD (Fig. S8†).

For 0%, 10%, and 20%, the unit cell volume contracts with increasing Br content (Table S4†). Br and I elemental analysis of 10% and 20% confirms the composition of each alloy (cf. Experimental section, ESI†). The temperature dependence of the χT product of 10% reveals an upward shift in by 21 K and a slightly smaller hysteresis width (18 K, Fig. 4, S15 and S18†). This shift is accompanied by a reduction in the χT product of the HT phase compared to 0% (vide infra). In 20%, T* is shifted an additional 13 K with conserved hysteresis width (19 K, Fig. S16 and S19†). Additionally, the VT conversion shows a slight step at approximately 50% conversion (Fig. S17†) and a further reduction in the magnetic moment of the HT phase.

The progressive drop in the magnetic moment of the HT phases casts ambiguity on the Sm oxidation state at these temperatures. The room temperature and 50 K Sm L₂-edge X-ray absorption near edge structure (XANES) spectra (Fig. 5 and S21†) of 100% are identical, corroborating the conclusion that only Sm(III) is present at all temperatures. Conversely, in HT-0%, at room temperature, the dipole-allowed 2s → 5d, 6s ‘white line’ is red-shifted by 7.6 eV from that of 100%, consistent with a Sm(II) oxidation state (Fig. 5 and S24†). At 50 K, the spectrum becomes virtually identical to that of 100%, with no indication of residual Sm(II). In stark contrast, 10% and 20% show a primary feature at the Sm(II) white line photon energy, with an additional minor feature at the energy corresponding to Sm(III). The progressive increase in intensity of the Sm(III) peak with increasing Br content is paralleled by a decrease in the intensity of the Sm(II) peak. At 50 K, however, the spectra overlap with 100%, demonstrating complete conversion to Sm(III). Upon reheating, the room temperature spectra are recovered, suggesting full reversibility. Notably, the room temperature spectra can be reproduced by a linear combination of the room temperature spectra of 0% and 100% with relative weights corresponding to the Br content (Fig. S22 and S23†).

Fig. 5 Sm L₂-edge XANES spectra of 0%, 10%, 20%, and 100% measured at room temperature (top) and ∼50 K (bottom). The dashed lines at 7311.3 eV and 7318.9 eV indicate the Sm(II) and Sm(III) white lines, respectively. The simulations of the room temperature spectra are described in the main text.

While the thermodynamics of both the transition metal spin crossover and VT phenomena have been studied in detail, there are no experimental reports on the enthalpy and entropy changes associated with VT conversions in molecule-based lanthanide compounds. The differential scanning calorimetry (DSC) data of 0%, 10%, and 20% are shown in Fig. 4 (Fig. S26†). The phase transitions observed by DSC correspond to the conversions observed by magnetometry. For 0%, the enthalpy change was determined to be −6.4 kJ mol⁻¹, which is comparable to spin crossover complexes.^29,30 The values of ΔH for VT conversions in transition metal compounds are similar.³¹ ΔH for 10% and 20% decreases to 5.9 kJ mol⁻¹ and 5.2 kJ mol⁻¹, respectively, which constitutes reductions by 8% and 19%, consistent with the decrease in I content (Table S6†).

Local coordination environments

The analyses of the XANES spectra and the DSC data independently point towards ∼10% and ∼20% of the Sm centers in 10% and 20%, respectively, not undergoing a VT conversion. The alloyed phases could contain {SmI₂}, {SmBr₂}, or {SmIBr} nodes. To ascertain the actual composition of the alloys, we consider a fully random statistical mixture. In the case of 20%, this gives a distribution of 64% {SmI₂}, 4% {SmBr₂}, and 32% {SmIBr}. We assume, based on the experimental findings in 0% and 100%, that {SmI₂} and {SmBr₂} exist solely as Sm(II) and Sm(III) at room temperature. If mixed {SmIBr} nodes contain Sm(II), the ratio of Sm(II) to Sm(III) is 96 : 4. Conversely, if they contain Sm(III) the ratio is 64 : 36. Both of these ratios are incompatible with the relative Sm(II) and Sm(III) peak intensities of 20% found by XANES spectroscopy. The fully analogous situation is observed in 10%. The experimental data, therefore, point towards conserved {SmI₂} and {SmBr₂} nodes, with no evidence of {SmIBr}. Further evidence for this conclusion is provided by the analysis of the aforementioned reductions in the χT product of 10% and 20% relative to 0% at 270 K, which reveal approximately 14% Sm(III) in 20% and 6% in 10%.

Electrical conductivity

Not only do 0%, 10%, 20% and 100% show mixed valency in the ligand scaffold, but 10% and 20% are also rare examples of compounds featuring lanthanide ions present in different oxidation states.^32–34 Mixed valency in ligand^35–37 and/or metal ion scaffolds^38–40 has been shown to be at the origin of high electrical conductivity in transition metal-based coordination solids. The 270 K-conductivity of 100% amounts to ∼0.15 mS cm⁻¹ (Fig. 4 and S25†) and decreases to reach ∼20 μS cm⁻¹ at 67 K, comparable to many conductive transition metal coordination polymers.^41,42 In contrast, 0% exhibits conductivity three to four orders of magnitude lower at room temperature (∼1 nS cm⁻¹), which increases sharply at and assumes a temperature dependence similar to that of 100%. A similar abrupt change in conductivity linked to the VT conversion is observed for 10% and 20% at the corresponding T*s. The behavior of the Sm(III)-pyz(·−) phases is comparable to that of some recent lanthanide-based metal–organic frameworks, which show conductivity in the range of ∼90 μS cm⁻¹ to 50 mS cm⁻¹.^43,44

M(II) alloys

The substitution of {SmI₂} nodes with {SmBr₂} nodes containing a trapped Sm(III) oxidation state has the opposite effect to that of substituting {YbI₂} nodes into SmI₂(pyz)₃, where the VT conversion decreases in temperature and loses cooperativity. The effective size, reflected by the average metal–N distance, of Sm(III) in a {SmBr₂} node (2.52(1) Å) is 4% smaller than that of Yb(II) in a {YbI₂} node (2.63(2) Å;¹⁷ Table S3†). In contrast to Yb(II), which has an intermediate size to that of Sm(II) (2.75(1) Å in HT-0%) and Sm(III) (2.55(1) Å in LT-0%) in a {SmI₂} node, the Sm(III) ion in a {SmBr₂} node is smaller than both. To further elucidate the apparent strong size-dependence of the dopant ion on T*, the analogous SrI₂(pyz)₂(thf) (Sr-100%) and CaI₂(pyz)₂(thf) (Ca-100%) were synthesized from SrI₂ and CaI₂ (Fig. S2 and S3†). The effective sizes of Sr(II) and Ca(II) are again inferred by the metal–N bond lengths of 2.77(1) Å and 2.66(1) Å, respectively. Ca(II) is virtually identical in size to Yb(II), while Sr(II) is identical in size to Sm(II). The isomorphism of Sr-100% and Ca-100% to 0% allows the substitution of Sm(II) in 0% by Sr(II) and Ca(II), in phases entitled Ca-10%, Ca-20%, Sr-7.5%, and Sr-15% (Tables S2, S5, S6, Fig. S9–S12†).

The temperature dependences of the χT products for the Sr(II) and Ca(II) alloyed phases are shown in Fig. 6. All M(II) alloys display a shift of T* towards lower temperatures. While the Ca(II) impurity concentration dependence of T* mirrors that of Yb(II), as expected for the similar effective volume, the Sr(II) substitution has a more pronounced concentration dependence on T*. In Sr-7.5% and Sr-15%, the larger Sr(II) ions stabilize the HT Sm(II) phase and push T* towards lower temperatures. Ca(II) and Yb(II), having effective sizes between those of Sm(II) and Sm(III) also stabilize the HT Sm(II) phase. The increasing substitution percentage of Sr(II) and Ca(II) is accompanied by a gradual loss of cooperativity, as reflected in the loss of abruptness of the VT conversion and a narrowing of the thermal hysteresis, due to the increased concentration of non-participating impurities (Fig. 1). In contrast, the substitution of Sm(II) with Sm(III) obtained upon introduction of {SmBr₂} nodes is fundamentally different. The effective size of Sm(III) in {SmBr₂} is identical to that of Sm(III) found in the {SmI₂} nodes in the LT-0% phase. Thus, following the same argument as above, the presence of valence trapped Sm(III) substituents will destabilize the HT phase and push T* towards higher temperatures. More remarkably, the alloying with Sm(III) nodes is accompanied by only a minute loss in cooperativity, even at a 20% substitution level, diametrically opposed to the alloys featuring divalent substituents, where the hysteresis is fully closed at such impurity concentrations.

Fig. 6 Magnetic susceptibility–temperature product of 0%, Ca-10%, and Ca-20% (top) and of 0%, Sr-7.5%, and Sr-15% (bottom).

Effects of superexchange

Despite the conceptual resemblance of the observed behavior of the {SmI₂}/{SmBr₂} alloys to SCO materials, it is rare for metal ion substitution in SCO materials to maintain the cooperativity of the parent compound.^45,46 However, the VT phenomenon in a polymeric network presents an important difference. The introduction of Sm(III) is unavoidably accompanied by the introduction of valence trapped pyz(·−) along the chain direction. Therefore, the charge distribution around an Sm(II) situated next to a valence-trapped Sm(III) resembles that of an Sm(II) in the pristine phase facing the domain wall of a cooperative VT conversion. Additionally, given the strong pyz(·−)⋯pyz(·−) superexchange coupling, previously predicted by DFT calculations (J = −750 cm⁻¹), the associated energy of ∼|2JS²| = 4.5 kJ mol⁻¹ is similar to that of the VT conversion, ΔH = −6.4 kJ mol⁻¹. The formation of pyz(·−)⋯pyz(·−) superexchange pathways may, therefore, be hypothesized to drive the VT conversion. The majority of coordination networks displaying a cooperative VT conversion feature only weak magnetic exchange coupling, so at this moment, further confirmation of this hypothesis is precluded. There is some evidence from computational studies of Fe(II) SCO coordination polymers that magnetic exchange coupling in the high-spin phase could be an important factor for the observed cooperativity, in addition to the elastic interactions.⁴⁷ In the case of the strong superexchange interactions presented here, we believe the effect cannot be neglected. This is consistent with the observation of reduced cooperativity when diamagnetic M(II) impurities are incorporated into the LT phases, whereas alloying with {SmBr₂} nodes does not affect the antiferromagnetically coupled radical chains in the LT phases, leading to conservation of the cooperativity and hysteresis width.

Conclusions

We find the novel phenomenon of valence tautomerism in molecule-based lanthanide materials to be robust and tunable in terms of conversion temperature and cooperativity. The enthalpy of the VT conversion is found to be comparable to that of transition metal analogues and SCO materials, although the underlying mechanism remains fundamentally different. The reversible charge injection into the organic scaffold results in increased electrical conductivity and the opening of strong superexchange channels, whose energy is comparable to that of the VT conversion enthalpy and thereby conserves the cooperativity in the alloyed phases. Such chemical tailoring of the local charge distribution to control the VT event is unprecedented despite theoretical predictions of strong sensitivity to applied electric fields in transition metal-based VT materials.⁴⁸

Data availability

The data supporting this article have been included as part of the ESI.† Deposition numbers 2420160–2420164 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via the joint Cambridge Crystallographic Data Centre (CCDC) and Fachinformationszentrum Karlsruhe Access Structures service. X-ray spectroscopy was performed at the European Synchrotron Radiation Facility at beamline ID12 and data are available at DOI: https://doi.org/10.15151/ESRF-ES-1435808919.

Author contributions

K. S. P., M. A. D. and A. V. conceived and planned the research project. A. V. and M. A. D. developed and performed the synthesis and the crystallographic analysis. M. A. D., K. S. P. and A. V. performed the characterization of the magnetic properties. N. J. Y., F. W. and A. R. acquired and analysed the X-ray spectroscopic data. M. A. D., A. C., F. T., N. P., and A. V. acquired and analyzed the resistivity data. D. P. acquired and analysed the differential scanning calorimetry data. The manuscript was written by K. S. P., M. A. D. and A. V. with input from all coauthors. All authors have given their consent to the publication of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Anna S. Manvell for helpful discussions. The X-ray spectroscopy experiments were performed at the ID12 beamline of the European Synchrotron Radiation Facility (Grenoble, France). We thank the Danish Agency for Science, Technology, and Innovation for funding the instrument center Danscatt. K. S. P. thanks the VILLUM Foundation for a VILLUM Young Investigator+ (42094) grant, the Independent Research Fund Denmark for a DFF-Sapere Aude Starting grant (no. 0165-00073B), and the Carlsberg Foundation for a research infrastructure grant (no. CF17-0637). A. C. and F. T. acknowledge support by research grant 37338 (SANSIT) from the VILLUM Foundation. D. P. acknowledges the financial support of the National Science Centre Poland within the Opus project 2020/37/B/ST5/02735.

Notes and references

1. B. Lowe, B. Field, J. Hellerstedt, J. Ceddia, H. L. Nourse, B. J. Powell, N. V. Medhekar and A. Schiffrin, Nat. Commun., 2024, 15, 3559.
2. N. Das and C. Maity, Commun. Chem., 2022, 5, 115.
3. W. Lee, D. Kim, S. Lee, J. Park, S. Oh, G. Kim, J. Lim and J. Kim, Nano Today, 2018, 23, 97–123.
4. O. Sato, Nat. Chem., 2016, 8, 644–656.
5. O. Sato, J. Tao and Y.-Z. Zhang, Angew. Chem., Int. Ed., 2007, 46, 2152–2187.
6. T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 23–40.
7. M. A. Dunstan and K. S. Pedersen, Chem. Commun., 2025, 61, 627–638.
8. R. M. Buchanan and C. G. Pierpont, J. Am. Chem. Soc., 1980, 102, 4951–4957.
9. E. Evangelio and D. Ruiz-Molina, Eur. J. Inorg. Chem., 2005, 15, 2957–2971.
10. G. K. Gransbury, M. E. Boulon, S. Petrie, R. W. Gable, R. J. Mulder, L. Sorace, R. Stranger and C. Boskovic, Inorg. Chem., 2019, 58, 4230–4243.
11. G. K. Gransbury, B. N. Livesay, J. T. Janetzki, M. A. Hay, R. W. Gable, M. P. Shores, A. Starikova and C. Boskovic, J. Am. Chem. Soc., 2020, 142, 10692–10704.
12. M. Owen, Ann. Phys., 1912, 37, 657.
13. J. M. Robinson, Phys. Rep., 1979, 51, 1–62.
14. J. M. Lawrence and R. D. Parks, J. Phys. Colloq., 1976, 37, 249–253.
15. M. Loewenhaupt and K. H. Fischer, in Handbook on the Physics and Chemistry of Rare earths, ed. K. A. Gschneider Jr and L. Eyring, Elsevier, Amsterdam, 1993, ch. 1, vol. 16, pp. 1–105.
16. J. Arvanitidis, K. Papagelis, S. Margadonna, K. Prassides and A. N. Fitch, Nature, 2003, 425, 599–602.
17. M. A. Dunstan, A. S. Manvell, N. J. Yutronkie, F. Aribot, J. Bendix, A. Rogalev and K. S. Pedersen, Nat. Chem., 2024, 16, 735–740.
18. M. Szostak, M. Spain and D. J. Procter, J. Org. Chem., 2014, 79, 2522–2537.
19. W. Kaim, Angew. Chem., Int. Ed., 1983, 22, 171–190.
20. N. Bajaj, N. Mavragani, A. A. Kitos, D. Chartrand, T. Maris, A. Mansikkamäki and M. Murugesu, Chem, 2024, 10, 2484–2499.
21. M. Kubus, L. Voigt and K. S. Pedersen, Inorg. Chem. Commun., 2020, 114, 107819.
22. L. Sorace and D. Gatteschi, in Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim Germany, 2015, ch. 1, pp. 1–26.
23. J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, A640.
24. I. L. Fedushkin, O. V. Maslova, A. G. Morozov, S. Dechert, S. Demeshko and F. Meyer, Angew. Chem., Int. Ed., 2012, 51, 10584–10587.
25. D. A. Lukina, A. A. Skatova, R. V. Rumyantcev, S. V. Demeshko, F. Meyer and I. L. Fedushkin, Dalton Trans., 2024, 53, 8850–8856.
26. O. Kahn and J. Kröber, Adv. Mater., 1992, 4, 718–728.
27. J. Kröber, E. Codjovi, O. Kahn, F. Grolière and C. Jay, J. Am. Chem. Soc., 1993, 115, 9810–9811.
28. Y.-Y. Wu, Z.-Y. Li, S. Peng, Z.-Y. Zhang, H.-M. Cheng, H. Su, W.-Q. Hou, F.-L. Yang, S.-Q. Wu, O. Sato, J.-W. Dai, W. Li and X.-H. Bu, J. Am. Chem. Soc., 2024, 146, 8206–8215.
29. K. P. Kepp, Inorg. Chem., 2016, 55(6), 2717–2727.
30. S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2020, 22, 4938–4945.
31. D. A. Schultz, in Magnetism: Molecules to materials II: Models and Experiments, ed. J. S. Miller and M. Drillon, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim Germany, 2001, ch. 8, pp. 281–306.
32. C. A. Gould, K. R. McClain, D. Reta, J. G. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
33. M. D. Roy, T. P. Gompa, S. M. Greer, N. Jiang, L. S. Nassar, A. Steiner, J. Basca, B. W. Stein and H. S. La Pierre, J. Am. Chem. Soc., 2024, 146, 5560–5568.
34. T. J. Obey, M. K. Singh, A. B. Canaj, G. S. Nichol, E. K. Brechin and J. B. Love, J. Am. Chem. Soc., 2024, 146, 28658–28662.
35. K. S. Pedersen, P. Perlepe, M. L. Aubrey, D. N. Woodruff, S. E. Reyes-Lillo, A. Reinholdt, L. Voigt, Z. Li, K. Borup, M. Rouzières, D. Samohvalov, F. Wilhelm, A. Rogalev, J. B. Noeaton, J. R. Long and R. Clérac, Nat. Chem., 2018, 10, 1056–1061.
36. P. Perlepe, I. Oyarzabal, A. Mailman, M. Yquel, M. Platunov, I. Dovgaliuk, M. Rouzières, P. Négrier, D. Mondieig, E. A. Suturina, M.-A. Dourges, S. Bonhommeau, R. A. Musgrave, K. S. Pedersen, D. Chernyshov, F. Wilhelm, A. Rogalev, C. Mathonière and R. Clérac, Science, 2020, 370, 587–592.
37. F. Aribot, L. Voigt, M. A. Dunstan, W. Wan, J. N. McPherson, M. Kubus, N. J. Yutronkie, C. J. McMonagle, M. Coletta, A. S. Manvell, A. Viborg, S. Wong, K. A. Stampe, V. Baran, A. Senyshyn, M. D. Le, H. C. Walker, A. Chanda, F. Trier, N. Pryds, F. Wilhelm, M. R. Probert, N. B. Christensen, E. K. Brechin, A. Rogalev and K. S. Pedersen, ChemRxiv, 2024 DOI:10.26434/chemrxiv-2024-rlsf8.
38. L. E. Darago, M. L. Aubrey, C. J. Yu, M. I. Gonzalez and J. R. Long, J. Am. Chem. Soc., 2015, 137, 15703–15711.
39. J. A. DeGayner, I. R. Jeon, L. Sun, M. Dincă and T. D. Harris, J. Am. Chem. Soc., 2017, 139, 4175–4184.
40. R. Murase, C. F. Leong and D. M. D'Alessandro, Inorg. Chem., 2017, 56, 14373–14382.
41. M. Wang, Z.-Y. Li, R. Ishikawa and M. Yamashita, Coord. Chem. Rev., 2021, 435, 213819.
42. G. Givaja, P. Amo-Ochoa, C. J. Gómez-García and F. Zamora, Chem. Soc. Rev., 2012, 41, 115–147.
43. G. Skorupskii, B. A. Trump, T. W. Kasel, C. M. Brown, C. H. Hendon and M. Dincă, Nat. Chem., 2020, 12, 131–136.
44. F. Manna, M. Oggianu, P. Auban-Senzier, G. Novitchi, E. Canadell, M. L. Mercuri and N. Avarvari, Chem. Sci., 2024, 15, 19247–19263.
45. A. Moneo-Corcuera, D. Nieto-Castro, J. Cirera, V. Gómez, J. Sanjosé-Orduna, C. Casadevall, G. Molnár, A. Bousseksou, T. Parella, J. M. Martínez-Agudo, J. Lloret-Fillol, M. H. Pérez-Temprano, E. Ruiz and J. R. Galán-Mascarós, Chem, 2023, 9, 377–393.
46. M. A. Halcrow, Dalton Trans., 2024, 53, 13694.
47. H. Banerjee, M. Kumar and T. Saha-Dasgupta, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 174433.
48. A. Droghetti and S. Sanvito, Phys. Rev. Lett., 2011, 107, 047201.

---

Footnote

† Electronic supplementary information (ESI) available: Materials and methods, experimental procedures, single crystal X-ray diffraction data, magnetic susceptibility and magnetization, PXRD and Rietveld refinement, electrical conductivity and differential scanning calorimetry. CCDC 2420160–2420164. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5sc01246e

---