Quinonoid radial π-conjugation

Abstract

Radially π-conjugated macrocycles with mixed aromatic and quinonoid units are considered. As a function of including an increasing number of aromatic units into a ring-like nanohoop with quinonoid units, a transition occurs where the HOMO and LUMO levels cross, leading to a topological transition described for the first time. Such transitions have been seen before in ethynylene-linked oligoacene polymers as a function of the acene size on gold surfaces and in various π-conjugated polymers as a function of external strain, but not in small molecular nanohoops or any other zero-dimensional system. Near the level crossing, the HOMO–LUMO gap becomes very small, offering novel photophysical properties while maintaining extensive delocalization. The open shell character of the rings changes continuously as the composition is gradually changed, switching from a singlet ground state to a triplet, providing a zero-dimensional analogy to topological transitions between a non-trivial to a trivial phase as observed in linear one-dimensional conjugated polymers. The spins of the triplet are localized near the two aromatic-quinonoid connections.

---

1. Introduction

In radial π-conjugation, the local π-orbitals point in the radial direction in a macrocycle, directing the 2p-orbitals into and out of the macrocycle core as illustrated in Fig. 1(c). The hypothesis of the presented work is that by mixing aromatic and quinonoid units in a π-conjugated macrocycle, a HOMO–LUMO crossing can occur which profoundly effects the properties and can lead to a switch between singlet and triplet ground states. We arrived at this hypothesis by making a connection to the recently discovered crossover of “trivial” and “non-trivial” topological phases of conjugated polymers.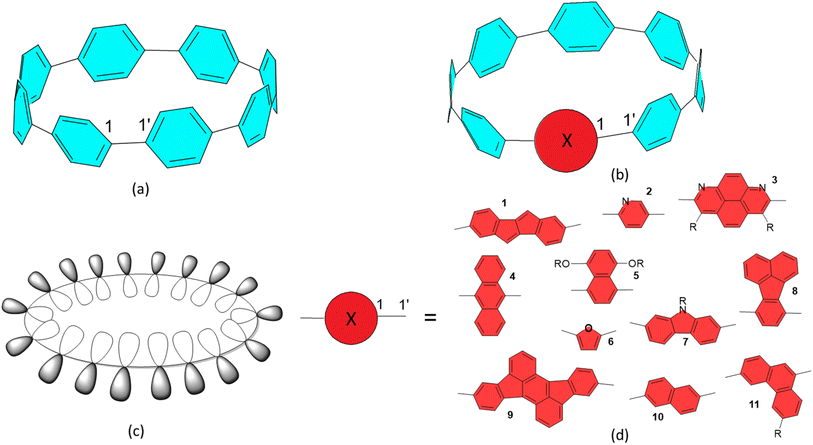

Fig. 1 (a) Illustration of [8]CPP, interring bond specified as 1–1′. (b) Generic π-conjugated unit (red circle, X) inserted into [8]CPP, denoted here as [8]C(X)₁(PP)₇. (c) Illustration of radial conjugation. (d) Typical π-conjugated units are inserted into various CPPs selected from the literature: 1,⁷ 2,^8,9 3,¹⁰ 4,¹¹ 5,¹² 6,¹³ 7,¹⁴ 8,¹⁵ 9,⁶ 10,¹⁶ 11.¹⁷

Typical radially π-conjugated molecules are [n]cyclo-p-phenylenes ([n]CPPs, consisting of n para-linked phenyls), which belong to the aromatic (A) category¹ as illustrated in Fig. 1(a) and offer a number of potential applications.^2,3 Recent synthetic developments expanded the available conjugated molecular elements that can be included in π-conjugated macrocycles^4–25 some of which are relevant for this work and are illustrated in Fig. 1(b) and (d). Note that a wide variety of conjugated molecular units constituting the nanohoops have been synthesized; this list is only a selection. The types of groups that were put into CPP nanohoops so far have included various aromatic and antiaromatic units and fluorophores, of which representative types are listed in Fig. 1(d), noting that in many cases, more than one group is inserted. In several cases, due to steric crowding (for example, 3 and 9), π-conjugation is interrupted, but other such inclusions maintain the π-conjugation. This article focuses on how unique inserted groups within radial π-conjugated networks may be designed such that they fundamentally change the character and electronic structure of these nanohoops. The key idea is to use quinonoid (Q) units, which promote π-conjugation, rather than restrict it through Hückel localization as aromatic units do. It turns out that integrating these quinonoid units within the aromatic (benzenoid) CPP macrocycles leads to dramatic changes in their properties due to the integration of two drastically different types of π-electron conjugation within one macrocycle.

Such quinonoid units have been designed and are in use²⁶ in the field of conducting polymers – specifically to realize low band-gap polymers – although most π-conjugated polymers are constructed from aromatic units.^27–29 Generally, polymers with Q structures display small HOMO–LUMO gaps compared to those built from A structures, and small gaps go hand in hand with fundamentally different electronic structures with a high degree of electron delocalization along the π-conjugated chain.³⁰ A few typical examples of conjugated polymer repeat units are illustrated in Fig. 2, where a shorter 1–1′ bond length is associated with the Q state, while a longer 1–1′ bond is associated with the A structure. These are the two fundamental types of linear π-conjugation found in conducting polymeric materials. Formally, a high-energy quinonoid valence bond structure can be drawn, for example, for (Th)_n. Likewise, a high-energy aromatic valence bond structure can be drawn, for example, for (TPz)_n. The preference for one ground state vs. the other is determined by the electronic structures, depending on the complex interplay of the connectivity of the π-electron network and heteroatoms. Previous work has determined these structural preferences for dozens of π-conjugated polymers.^30–32

Fig. 2 π-Conjugated polymer repeat units with two types of ground states. Two aromatic (A) and four quinonoid (Q) ones are shown. The aromatic ground state systems are polymers of thiophene (Th) and p-phenylene (PP). The quinonoid ones are thieno-3,4-[b]pyrazine (TPz), isothianaphthene (ITN), thieno[3,4-c]thiophene-1,4-dione (TTD), and pyrrolo[3,4-c]pyrrole-1,4-dione (PPD). Two chemical units are shown for each, and the inter-unit CC bonds are indicated as 1–1′. The 1–1′ bond distances (in Å) are provided in parentheses.^{32 a}For consistency, 1–1′ distance in (PP)_n is provided with the same method as in ref. 32.

Fig. 3 illustrates a case where TPz, a quinonoid-promoting unit, is inserted in place of one of the phenyl components of [8]CPP, designated as [8]C(TPz)₁(PP)₇. As this illustration shows, there is a potential mismatch between the connecting bond of the aromatic PP and the quinonoid TPz units at the 1–1′ carbon–carbon bond. This mismatch and its connection to the topological phase transition between the “trivial” and “non-trivial” phases are the subject of this work. The latter point is particularly interesting, given the possibility of perturbing the intrinsic A structure and moving it in the direction of the Q structure along the topological phase transition,^33–35 resulting in a fundamental modification of the electronic structure.

Fig. 3 A quinonoid unit, TPz (in blue), is inserted in place of one of the aromatic phenyls (in turquoise) of [8]CPP, designated as [8]C(TPz)₁(PP)₇.

As recently outlined, a convenient signature of a Q structure in a π-conjugated polymer is the in-phase (bonding) combination of the atomic orbitals in the HOMO at the linking C–C bond³² indicated as 1–1′ above. The LUMO displays out-of-phase (antibonding) character at this location. For the A structure, the roles are reversed, where the HOMO is antibonding and the LUMO is bonding at this location. Both of these features are related to the concept of quantum topological insulators³³ where the A structure corresponds to the “trivial phase” and the Q structure to the “non-trivial phase”.^32,34,35 A signature of the non-trivial phase is a high diradicaloid (open-shell) character represented by two unpaired spins at the two ends of the polymer, which are absent in the trivial phase.^33–35 A transition from the trivial to the non-trivial phase has been experimentally observed and analyzed for a series of π-conjugated ethynylene bridged [n]acene polymers fabricated on Au(111) surfaces concluding that these display a topological phase transition as a function of the linked acene size (n) between anthracene (n = 3) and pentacene (n = 5) from the trivial to the non-trivial phase.^34,35 We discuss to what extent the molecular macrocyclic (“0-dimensional”) case discussed here is analogous to the topological transition seen in conjugated polymers.

2. Results and discussion

In order to investigate the proposition of fundamentally modifying the electronic structure of a molecule by mixing A and Q units, we computationally modelled various radial π-conjugated nanohoops; one series of this selection is illustrated in Fig. 4. The trend from longer (A) to shorter (Q) 1–1′ bonds is clear. Table S1† lists further details for the 1–1′ bond distances around the [8]C(TPz)_8−x(PP)_x and the [8]C(ITN)_8−x(PP)_x series.

Fig. 4 Optimized geometries (B3LYP-D3/6-311G(d)) of selected π-conjugated macrocycles for the [8]C(TPz)_8−x(PP)_x series. Only isomers where the TPz and PP units are completely segregated from each other are shown. For x = 8 the system is a pure [8]CPP. Color code: grey: C, white: H, blue: N, yellow: S. Key bond distances are provided in Å.

The choice of the TPz units as the Q units is based on earlier work³² that shows their strong tendency for a quinonoid structure as indicated by the energetic preference of the Q vs. A structures in π-conjugated linear homopolymers. One typical aromatic and two typical quinonoid linear systems are illustrated in Fig. S1–S3† together with their respective HOMOs and LUMOs. In the presented novel hybrid macrocycles, the Q units are interspersed with para-phenylene (PP) units, the latter representing a typical A-type unit. This allows further questions to be posed: does the hybrid system maintain a high degree of π-electron delocalization and does the intermixing of the two types of A and Q units allow the realization of getting near the topological phase transition, where the HOMO–LUMO levels cross, potentially leading to a very small gap? n values of 6, 8, and 10 appear most relevant because smaller values would pose unsurmountable synthetic challenges due to ring strain from the small size of the nanohoop,^36–38 and larger values of n are expected to be approaching environments corresponding to polymer chains.

We first discuss the homogeneous macrocycles and establish their aromatic vs. quinonoid characters with n = 6, 8, and 10. Then we turn to the mixed macrocycles with n = 8 and a varying number of PP units mixed in with x = 1 through 7. The mixed systems have remarkably unique properties.

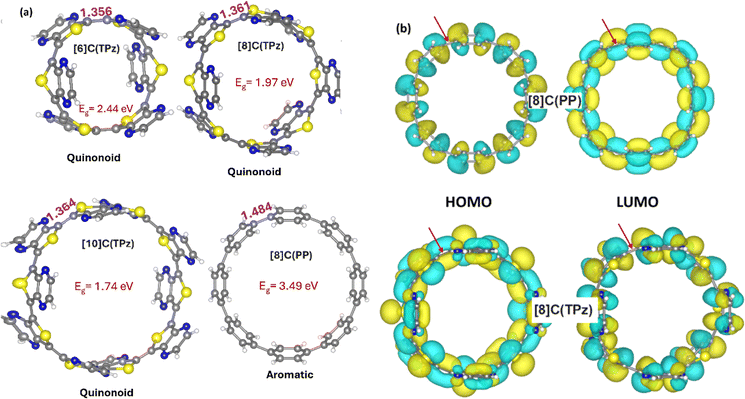
Fig. 5(a) shows the optimized geometries of n = 6, 8, and 10 for [n]C(TPz) and for [8]C(PP) homo-macrocycles, the together with the HOMOs and LUMOs of the n = 8 cases. The 1–1′ bonds indicate quinonoid ground states, and their variation with respect to n is typical and approaches the limiting linear polymer value of 1.370 Å. The HOMO–LUMO gaps are quite small and with increasing n approach the limiting value of 1.51 eV. The respective HOMO and LUMO display bonding combinations for HOMO and antibonding combinations for LUMO at the 1–1′ links as expected for quinonoid structures. For [n]CPPs, the reverse situation occurs, as expected for the aromatic structures. These orbitals are illustrated in Fig. 5(b). The n = 6 and 10 cases for [n]C(TPz) are shown in Fig. S4 and S5.† Note, that in agreement with their general reputation in the conducting polymer field, the quinonoid macrocycles turn out to have significantly smaller gaps than their respective aromatic congeners. Since the cyclic [n]C(ITN) molecules display similar properties as [n]C(TPz), the respective geometries, gaps, and orbitals are shown in the ESI† section only.

Fig. 5 (a) Cyclic [6,8,10]C(TPz) π-conjugated macrocycles, in their optimized geometries. The inter-unit 1–1′ carbon–carbon bond distances (in Å) indicate quinonoid structures. Their respective HOMO–LUMO gaps are also shown. For comparison, [8]CPP is shown as a typical π-conjugated macrocycle with a significantly longer, aromatic-type 1–1′ CC bond length (one of eight equivalent values are shown). (b) HOMO and LUMO orbitals of the quinonoid [8]C(TPz) and aromatic [8]CPP. The 1–1′ interactions are bonding for the HOMO of [8]C(TPz) and also bonding for the LUMO of [8]CPP. The 1–1′ interactions are antibonding for the LUMO of [8]C(TPz) and also antibonding for the HOMO of [8]CPP. Red arrows highlight one of these eight 1–1′ bonds.

We start now to describe the behavior of the hybrid macrocycles consisting of two different units, the putatively quinonoid one (purely quinonoid in the polymer or cyclic forms) and p-phenylene, the prototypical aromatic unit. The rest of the investigation is based on n = 8, a reasonably large system, with TPz as the Q unit. The ITN-based systems behave very similarly. In order to obtain directly comparable results, we look at the trends in the comparable unique series where the two types of units (A and Q) are fully segregated, as shown in Fig. 4. From an experimental perspective, synthesizing the most segregated isomer should be the easiest and most promising to make.³⁹ According to the Jasti method of CPP synthesis,¹ a curved clip of 5 or more rings (as a mix of phenylenes and non-aromatic cyclohexadienes) is used to form a CPP macrocycle precursor after being covalently joined with a bridging unit. We anticipate that small blocks of previously reported Q units (dimers/trimers) should be suitable bridging partners for this macrocyclization, thus leading to the segregated nanohoops.

The segregated hybrid macrocycles display the dependence of the HOMO–LUMO levels as a function of x for the prototypical case of [8]C(TPz)_8−x(PP)_x as shown in Fig. 6(a). Detailed geometric information on the members of the series are given in Fig. S6–S17.†

Fig. 6 (a) HOMO–LUMO energy gap as a function of x in the [8]C(TPz)_8−x(PP)_x series of π-conjugated macrocycles obtained by three different DFAs. (b) Orbital level crossing when the number of PP unit in the [8]C(TPz)_8−x(PP)_x nanohoop series changes between x = 4 to x = 5 with B3LYP-D3. The same orbital crossings with the other two DFAs are nearly identical (Fig. S22†).

The reduction and then increase of the gap as a function of x is dramatic. The implication is a level crossing and indeed, this is confirmed by the inspection of the nature of the HOMO and LUMO, which are shown in Fig. 6(b). The associated quinonoid to aromatic change (for convenience, one can perhaps call it a “transition”) in Fig. 6 is the key insight of this work.

The same effect is seen for the [6]C(TPz)_6−x(PP)_x series (Fig. S18†) and the [8]C(ITN)_8−x(PP)_x series (Fig. S19†). Fig. S20† shows the same type of level crossing diagram as Fig. 6 for both these series: [6]C(TPz)_6−x(PP)_x and [8]C(ITN)_8−x(PP)_x, indicating that this is a general phenomenon (orbital details are shown in Fig. S21–S23†). These molecules provide a possible route for designing very low-gap π-conjugated macrocycles. Note that, as a practical matter, the [6]C(TPz)_6−x(PP)_x series is the most promising where the transition occurs after two replacements of aromatic units by quinonoid ones. The reason for this earlier transition is likely due to the strain in the nanohoops that is larger for smaller sizes and favors quinonoid structures.³⁶

What makes this transition possible is that for x = 0, the cyclic systems maintain essentially the same quinonoid ground state as found in the polymer. Starting with this structure and mixing in one and then more aromatic PP units, the 1–1′ bonds gradually experience a mismatch, pushing the structure in the aromatic direction, eventually causing a level crossing between x = 4 and 5. The same effect can be viewed in the reverse direction, starting with the aromatic [8]CPP nanohoop and adding gradually quinonoid units, starting with one as shown in Fig. 3. As noted before, it is essential that aromatic and quinonoid units be mixed in the right proportions for the level crossing and the accompanying gap reduction to occur. The gap reduction is accompanied by a significant red shift in the predicted UV-vis spectra shown in Fig. S24–S31† indicating characteristic bimodality extending into the near-infrared for the mixed A–Q nanohoops.

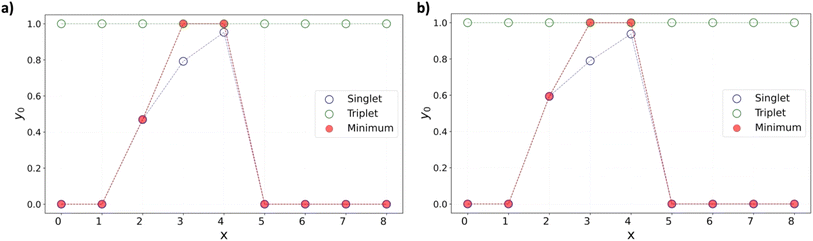
Near the level crossing, there is a possibility of the triplet state being lower in energy than the singlet. In fact, that is the case for both x = 3, and 4, at various DFT levels as shown in Fig. 7 for the [8]C(TPz)_8−x(PP)_x series where ΔE_ST is plotted as a function of the composition index, x.

ΔE_ST = |E_S − E_T| (1)

Fig. 7 Singlet triplet energy difference, ΔE_ST, relative to the lower of the two energies, in the (a) [8]C(TPz)_8−x(PP)_x series of nanohoops using three different DFAs and (b) [8]C(ITN)_8−x(PP)_x series of nanohoops. Both series show a more stable triplet for x = 3 and 4. For x = 2, the difference between the singlet and triplet is very small.

While the x = 2 composition is borderline, the x = 4 composition shows a clear case of a triplet ground state. The emergence of the triplet ground state near the aromatic–quinonoid transition is unexpected and an essential finding.

A similar singlet-triplet-singlet transition is observed in the [8]C(ITN)_8−x(PP)_x series at the B3LYP-D3 level, with a triplet ground state for x = 3 and 4 and a borderline case at x = 2 (Fig. 7b). Analogous behavior is also noted in the [6]C(TPz)_6−x(PP)_x series, where the triplet state is more stable for x = 3 and 4 (Fig. S32†). These findings suggest that the emergence of triplet ground states in mixed A–Q nanohoops may be a general phenomenon.

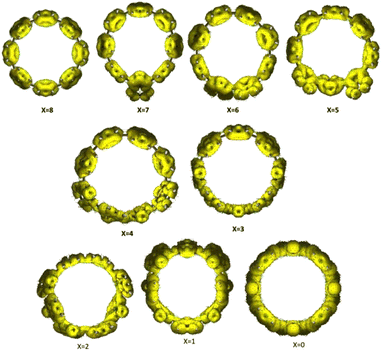
To quantify the extent of conjugation and delocalization within the macrocycle, anisotropy of the induced current density (ACID)⁴⁰ plots were generated for the [8]C(TPz)_8−x(PP)_x series and shown in Fig. 8. The variation in ACID isosurfaces across different x-values provides insight into the evolution of aromaticity and electronic delocalization with composition. For lower values of x (x = 0–2), where the system contains more TPz units, the ACID plots exhibit strong and continuous diatropic ring currents, suggesting significant macrocyclic conjugation. The uniform current density clearly indicates efficient electronic delocalization patterns across the macrocycle, and TPz units promote conjugation. As x increases (x = 3–5), the induced current density begins to fragment, indicating a disruption in conjugation. The current pathways appear less continuous, with localized distortions forming around certain regions of the macrocycle. This suggests that the benzene and TPz units do not interact as effectively in maintaining global delocalization, leading to a breakdown of the extended conjugation. The growing presence of benzene likely introduces electronic mismatches that limit the seamless flow of π-electrons. At higher values of x (x = 6–8), where the system is predominantly composed of benzene rings, the ACID plots show further localization of the induced current density. The ring currents become confined to individual benzene rings rather than forming a continuous macrocyclic flow. By x = 8, where the system consists entirely of benzene units, the plot suggests that the structure behaves more like a collection of isolated benzene rings rather than a fully conjugated macrocyclic system.

Fig. 8 Anisotropy of the induced current density (ACID) plots for cyclic [8]CPP derivatives containing varying numbers of benzene (x) and TPz (8−x) units. The yellow isosurfaces (iso = 0.025) represent induced current density under an external magnetic field applied perpendicular to the macrocycle. As x increases, the global aromatic ring current becomes more fragmented, indicating a transition from extended conjugation (in quinonoid TPz-rich systems) to localized aromaticity in benzene-rich systems.

To further support these observations, bond order and harmonic oscillator model of aromaticity (HOMA)⁴¹ analyses were performed and the results are plotted in Fig. S33.† Bond order data (black dashed lines in Fig. S33†) exhibit a decreasing trend with increasing x, reflecting a progressive disruption of conjugation. The bond order values corresponding to average of the 1–1′ bonds (red-filled circles correspond to the singlet or triplet, whichever is more stable) show a significant decline, aligning with the observed fragmentation of delocalization in the macrocycle seen in the ACID plots in Fig. 8. The HOMA index (blue-filled circles) provides additional confirmation; the index increases with x and plateaus near HOMA=1, indicating stronger localized aromaticity in benzene-rich systems.

Further computational analysis reveals a surprising connection to the topological phase transition. This connection arises from the degree of open-shell character in the wave function near the level crossing, which reflects variations in radicaloid character. To quantify this, we utilize Yamaguchi's y₀ index, obtained from the unrestricted Hartree–Fock (UHF) method. However, since UHF may be inadequate for systems with significant multireference character, it is crucial to assess the extent of multireference effects in these systems.

To this end, we performed DLPNO-CCSD(T) calculations⁴² on (U)B3LYP-D3 optimized structures to obtain the T1 diagnostic—a parameter used to estimate the extent of multireference character. A low T1 diagnostic value (typically <0.02, as suggested by Lee and Taylor⁴³) indicates that a multireference approach may not be necessary. As shown in Table S4,† the T1 diagnostic values for all [8]C(TPz)_8−x(PP)_x (x = 0 to 8) structures are below 0.02, suggesting that these systems are well-described by single-reference methods such as UHF.

Fig. 9 shows the evolution of the y₀ index,⁴⁴ which is often used to characterize the radicaloid nature of the state, as a function of x. The results are clear and show the dramatic change of the nature of the ground state at and near the transition with essentially closed shell electronic structures near x = 0 (dominantly quinonoid) and x = 8 (dominantly aromatic), while a clear diradical character emerges near the transition.

Fig. 9 y₀ diradical index as a function of x (a) for the [8]C(TPz)_8−x(PP)_x and (b) for the [8]C(ITN)_8−x(PP)_x, series of π-conjugated macrocycles. Values for both the triplet and singlet states are given. The more stable state is represented by filled symbols, the less stable by empty ones. These UHF y₀ values are based on (U)B3LYP-D3 optimized structures.

While any index of radical and open shell character has limitations, including y₀, by their nature of not being quantum mechanical observables, y₀ certainly serves well as a tool to compare the changes in these series of macrocycles.^45,46

For a 0-dimensional system, especially in a cyclic system as discussed here, there is an opportunity for a pair of localized spins to emerge, which would represent a diradical state. Such a pair of localized spin states are the analogs of a “non-trivial” topological phase as described for polymers.^33,34 The localization is not as extreme as indicated by the VB diagram in Fig. 10(c), but it is clearly present at the location where the aromatic and quinonoid units meet each other and is a consequence of the mismatch of the two structures at their linkage points. These localized spins come in pairs due to the topology of the nanohoop. The respective orbital energies are not exactly degenerate, but are very close, typically within less than 0.2 eV, as illustrated in Fig. S34.† This is one of the similarities with the topological non-trivial phases of linear conjugated polymers.

Fig. 10 (a and b) Spin density (iso-value = 0.01) distribution for the two nanohoops of the TPz series near the transition, where the triplet states are more stable than the singlet at the UB3LYP-D3/6-311G(d) level. The bottom portion are the TPz units, the top are the PP units. These are separated by a CC bond indicated by the black arrows. Red arrows indicate the largest localization of the spin density that occurs at the carbon site on the quinonoid side where the A and Q units meet. (c) The localization of spin in a hybrid nanohoop of segregated A and Q units is anticipated by the VB diagram where a symbolically aromatic unit (in turquoise) is adjacent to a quinonoid one (in blue).

A surprising but essential aspect is the robustness of the orbital delocalization of the HOMOs and LUMOs near the minimum gaps as shown in Fig. 6(b), and S22–S23.† As it turns out, based on our computations, we do not see significant charge transfer between the different units in any of these hybrid macrocycles. A typical charge transfer value in these systems is very small, of the order of 0.02e, with the largest value of 0.06e obtained for PP in [8]C(TPz)₇(PP)₁. This is another indication of a robust delocalization of both the HOMO and the LUMO among the A- and Q-type units in these systems. A number of examples of this wide-ranging orbital delocalization are listed in the ESI (Fig. S4–S12).† This property has important implications for the photophysics of new derivatives, given the possibility of functionalization of these A–Q hybrids into extended polymeric materials.⁴⁷ The incorporation of quinonoid units into CPPs offers new ways to realize a very high degree of radial-linear conjugation that is essential for their functioning as novel electronic materials.^4,47 These findings on the [8]C(TPz)_8−x(PP)_x series have been replicated for the [8]C(ITN)_8−x(PP)_x and the [6]C(TPz)_6−x(PP)_x series very closely and therefore the details are shown only in the ESI† section.

According to our further computational results, a similar gap reduction does not occur for [8]C(TTD) and [8]C(PPD). The orbitals and 1–1′ bond distances are illustrated in Fig. S35 and S36.† The polymer of TTD has a borderline quinonoid structure, while the polymer of PPD has a quinonoid ground state.³¹ However, the HOMO–LUMO gaps of these two nanohoops are still small near 1 eV with a singlet state lower than the nearby triplet separated by only 10 kcal mol⁻¹ and 8 kcal mol⁻¹ for [8]C(TTD) and [8]C(PPD), respectively. Their respective T1 values, shown in Table S4,† are also below 0.02.

3. Conclusions

Computational modeling of hybrid macrocycles with radial π-conjugation consisting of both aromatic and quinonoid units shows remarkably unique structural and electronic properties.

1. Ring-strain of the nanohoop does not suppress the quinonoid nature of the coupling between the repeat units in four purely quinonoid nanohoops in the investigated cases of [8]C(ITN) and [n]C(TPz) with n = 6, 8, and 10.

2. In the structures of the hybrid fully segregated macrocycles where a block of (n − x) quinonoid (Q) units are incorporated within a hybrid macrocycle with x other aromatic (A) units, the structure can be gradually moved from Q to A as x is increased.

3. A significant gap reduction can be achieved by exploiting the Q to A transition along the series due to a frontier orbital level crossing as a function of x.

4. Near the level crossing triplet states emerge as the ground state. In these triplet states the two radical sites are spatially separated, creating a diradicaloid state with the radical electrons being localized in the regions where the aromatic and quinonoid units join. This feature represents an analogy to the non-trivial topological state observed for diradical states of linear polymers, where the unpaired spins are localized that the chain ends.

5. Full delocalization of the frontier orbitals is maintained in many cases strongly affecting their photophysics.

6. We propose to think about these mixed macrocycles less as donor/acceptor systems but rather as aromatic/quinonoid ones. This approach helps to understand and to manipulate the dramatic gap reduction, the emergence of the diradicaloid triplet ground state as a function of composition, and the associated changes in physical properties.

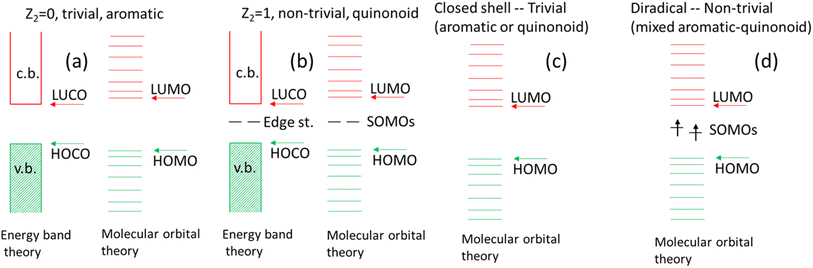
In addition to obtaining a tool to engineer the gaps and spin states of these mixed radially conjugated macrocycles, a connection to the related topological phase transition is observed. This analogy is limited, as no real phase transition can occur for a 0-dimensional insulator. Still, in designing new radially conjugated systems, it appears as useful to think about them as being on the scale between a trivial phase (quinonoid or aromatic) vs. the intermediate structure where the HOMO–LUMO nearly cross and a triplet state develops. This is a completely different situation compared to the 1D topological transition and is illustrated in Fig. 11 showing key similarities and differences between the linear topological polymer energy levels [in (a) and (b)] contrasting them with those in the radial π-conjugated macrocycles discussed in this work [in (c) and (d)]. Note that in the polymer case, two different theories describe the same effect. Due to their limited size, energy band theory is not applicable for the macrocycles. Note the triplet state in (d).

Fig. 11 (a) Polymer of aromatic units with matching termination (trivial topological state). (b) Polymer of quinonoid units with non-matching termination (non-trivial topological state). (c) Macrocycle of aromatic or quinonoid units (trivial topological state). (d) Macrocycle of mixed aromatic and quinonoid units (non-trivial topological state).

The variation of the properties of the presented macrocycles can be correlated with the varying degree of their quinonoid vs. aromatic characters, as their physical properties (gaps and open shell character) are controlled across a series. This research opens up the possibility to obtain topological transitions in zero dimensional molecular systems.

4. Methods

The traditional B3LYP-D3 hybrid density functional theory^48,49 with the 6-311G(d) basis set was used in combination with full geometry optimization in all cases except where explicitly mentioned otherwise. Gaussian 16 (ref. 50) default optimization criteria were used. Computed charges refer to natural population analysis, NPA, charges. The choice of this particular density functional approximation, DFA, is based on extensive validation on a variety of homo- and hetero-conjugated polymers and oligomers. It is particularly important in this regard, that the exact exchange component, A_x, in the hybrid should be around 20% for obtaining accurate HOMO–LUMO gaps.³⁰ The correlation between the bandgap and A_x is well known. B3LYP uses this compromise value, and it is therefore particularly well suited for the types of π-conjugated systems discussed here. We note that the D3 dispersion correction⁵¹ has a very small effect on the geometry, see Table S2.† To ensure the robustness of our results, the PBE0-D3 (ref. 52) and M06 (ref. 53) functionals were also employed for the [8]C(TPz)_8−x(PP)_x series. These functionals, which include A_x of 25% and 27%, respectively, further confirmed that the results are not dependent on the choice of functional. Functionals with A_x ∼20–30% reliably reproduced experimental λ_max values, whereas those with either higher or lower A_x values failed to provide accurate predictions (see Fig. S25†). Unless otherwise specified, the 6-311G(d) basis set was used. All orbitals were depicted using an isosurface value of 0.015 a.u.

There is no significant charge separation in the mixed nanohoops as tested for [8]C(TPz)₇(PP)₁, [8]C(TPz)₄(PP)₄-III, and [8]C(TPz)₁(PP)₇. Calculations using UB3LYP coupled with the computational “guess = mix” keyword in Gaussian 16(ref. 50) did not show any open-shell symmetry-breaking solutions for the cases where this issue was tested: [8]C(TPz), [8]C(TPz)₄(PP)₄, and [8]C(ITN); where in all cases we find that <S² ≥ 0.0. Furthermore, the stability of the ground-state wavefunctions has been confirmed using the “stable = opt” option in Gaussian 16 at both (U)B3LYP and (U)HF levels.

DLPNO-CCSD(T) (domain-based local pair natural orbital coupled cluster with singles, doubles, and perturbative triples)⁴² calculations were performed on the B3LYP-D3-optimized geometries of both the singlet and triplet ground states to estimate the multireference character using the T1 diagnostics.⁴³ DLPNO-CCSD(T) calculations were carried out using double-ζ quality basis set, def2-SVP.⁵⁴ The def2/j auxiliary basis set was used for the Coulomb integrals within the resolution-of-identity (RI) approximation, while the def2-SVP/C auxiliary basis set was utilized for the correlation treatment. To enhance computational efficiency, the RIJCOSX⁵⁵ approximation was applied for the evaluation of exchange integrals. All DLPNO-CCSD(T) calculations were performed with ORCA 5.0.4.⁵⁶

The diradical y₀ index is based on the natural orbital analysis and calculated using the following formula:⁴⁴

where η_HONO, and η_LINO refers to the natural orbital occupation numbers of the highest occupied natural orbital and lowest unoccupied natural orbital, respectively.

For completeness, TD-DFT (30 singlets and 30 triplets) computations were performed for selected macrocycles summarized in the ESI section (Fig. S24–S31†) showing significant red shifts for the segregated hybrid nanohoops compared to the homogeneous ones. Information on isomers of nanohoops are provided in Fig. S37–S39 and Table S3.†

Data availability

ESI† section: Tables of HOMO–LUMO gaps, structural parameters, images of HOMOs and LUMOs, information on isomers, predicted UV-vis spectra, xyz coordinates of optimized geometries, singlet-triplet gaps and energy levels, bond orders, HOMA indices.

Author contributions

R. B. carried out all the calculations. R. B., J. D. T., and M. K. conceptualized the work. M. K. supervised this project.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This material is based on work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under award number DE-SC-0019017 (MK and JDT). We thank Dr Adam Matej, Dr Sabyasachi Roy Chowdhury, and Professor Gen Yin for useful discussions.

References

1. E. R. Darzi and R. Jasti, Chem. Soc. Rev., 2015, 44, 6401–6410.
2. E. J. Leonhardt and R. Jasti, Nat. Rev. Chem., 2019, 3, 672–686.
3. S. E. Lewis, Chem. Soc. Rev., 2015, 44, 2221–2304.
4. M. Hermann, D. Wassy and B. Esser, Angew. Chem., Int. Ed., 2021, 60, 15743–15766.
5. C. Huang, Y. Huang, N. G. Akhmedov, B. V. Popp, J. L. Petersen and K. K. Wang, Org. Lett., 2014, 16, 2672–2675.
6. S. Hitosugi, S. Sato, T. Matsuno, T. Koretsune, R. Arita and H. Isobe, Angew. Chem., Int. Ed., 2017, 56, 9106–9110.
7. M. Hermann, D. Wassy, J. Kohn, P. Seitz, M. U. Betschart, S. Grimme and B. Esser, Angew. Chem., Int. Ed., 2021, 60, 10680–10689.
8. K. Matsui, Y. Segawa and K. Itami, Org. Lett., 2012, 14, 1888–1891.
9. J. M. Van Raden, S. Louie, L. N. Zakharov and R. Jasti, J. Am. Chem. Soc., 2017, 139, 2936–2939.
10. K. Ikemoto, M. Fujita, P. C. Too, Y. L. Tnay, S. Sato, S. Chiba and H. Isobe, Chem. Lett., 2016, 45, 658–660.
11. P. Della Sala, A. Capobianco, T. Caruso, C. Talotta, M. De Rosa, P. Neri, A. Peluso and C. Gaeta, J. Org. Chem., 2018, 83, 220–227.
12. H. Thakellapalli, B. Farajidizaji, T. W. Butcher, N. G. Akhmedov, B. V. Popp, J. L. Petersen and K. K. Wang, Org. Lett., 2015, 17, 3470–3473.
13. B. Farajidizaji, H. Thakellapalli, S. Li, C. Huang, N. N. Baughman, N. G. Akhmedov, B. V. Popp, J. L. Petersen and K. K. Wang, Chem.–Eur. J., 2016, 22, 16420–16424.
14. F. Lucas, L. Sicard, O. Jeannin, J. Rault-Berthelot, E. Jacques, C. Quinton and C. Poriel, Chem.–Eur. J., 2019, 25, 7740–7748.
15. Q. Huang, Y. Wu, Y. Zhou, H. Liu, J. Wang, S. Wang and P. Du, Synthesis, 2020, 52, 2535–2540.
16. H. Omachi, Y. Segawa and K. Itami, Org. Lett., 2011, 13, 2480–2483.
17. P. Sarkar, Z. Sun, T. Tokuhira, M. Kotani, S. Sato and H. Isobe, ACS Cent. Sci., 2016, 2, 740–747.
18. T. C. Lovell, Z. R. Garrison and R. Jasti, Angew. Chem., Int. Ed., 2020, 59, 14363–14367.
19. H. Chen, M. Shao, H. Li, H. Liu, W.-M. Wei, R.-H. Zheng, M. Song, R. Liu and D. Lu, New J. Chem., 2022, 46, 16670–16674.
20. G. George, O. A. Stasyuk, M. Solà and A. J. Stasyuk, Nanoscale, 2023, 15, 17373–17385.
21. K. Kovida, J. Malinčík, C. M. Cruz, A. G. Campaña and T. Šolomek, Chem. Sci., 2025, 16, 1405–1410.
22. P. Seitz, M. Bhosale, L. Rzesny, A. Uhlmann, J. S. Wössner, R. Wessling and B. Esser, Angew. Chem., Int. Ed., 2023, 62, e202306184.
23. R. Roy, C. Brouillac, E. Jacques, C. Quinton and C. Poriel, Angew. Chem., Int. Ed., 2024, 63, e202402608.
24. C. Brouillac, E. Dureau, O. Jeannin, J. Rault-Berthelot, C. Poriel and C. Quinton, J. Am. Chem. Soc., 2025, 147, 11267–11276.
25. X. Li, L. Liu, L. Jia, Z. Lian, J. He, S. Guo, Y. Wang, X. Chen and H. Jiang, Nat. Commun., 2025, 16, 467.
26. J. Brédas, A. Heeger and F. Wudl, J. Chem. Phys., 1986, 85, 4673–4678.
27. J. Roncali, Macromol. Rapid Commun., 2007, 28, 1761–1775.
28. P. M. Beaujuge and J. M. Fréchet, J. Am. Chem. Soc., 2011, 133, 20009–20029.
29. A. Leventis, J. Royakkers, A. G. Rapidis, N. Goodeal, M. K. Corpinot, J. M. Frost, D.-K. i. Bučar, M. O. Blunt, F. Cacialli and H. Bronstein, J. Am. Chem. Soc., 2018, 140, 1622–1626.
30. M. Kertesz, C. H. Choi and S. Yang, Chem. Rev., 2005, 105, 3448–3481.
31. G. Grover, G. M. Peters, J. D. Tovar and M. Kertesz, Phys. Chem. Chem. Phys., 2020, 22, 11431–11439.
32. R. Bhattacharjee and M. Kertesz, J. Am. Chem. Soc., 2024, 146, 26497–26504.
33. A. M. Pendás, J. Contreras-García, F. Pinilla, J. D. Mella, C. Cardenas and F. Muñoz, Chem. Commun., 2019, 55, 12281–12287.
34. B. Cirera, A. Sánchez-Grande, B. De la Torre, J. Santos, S. Edalatmanesh, E. Rodríguez-Sánchez, K. Lauwaet, B. Mallada, R. Zbořil and R. Miranda, Nat. Nanotechnol., 2020, 15, 437–443.
35. H. González-Herrero, J. I. Mendieta-Moreno, S. Edalatmanesh, J. Santos, N. Martín, D. Écija, B. de la Torre and P. Jelinek, Adv. Mater., 2021, 33, 2104495.
36. M. Peña-Alvarez, L. Qiu, M. Taravillo, V. G. Baonza, M. C. R. Delgado, S. Yamago, R. Jasti, J. T. L. Navarrete, J. Casado and M. Kertesz, Phys. Chem. Chem. Phys., 2016, 18, 11683–11692.
37. S. M. Bachrach and D. Stück, J. Org. Chem., 2010, 75, 6595–6604.
38. T. Iwamoto, Y. Watanabe, Y. Sakamoto, T. Suzuki and S. Yamago, J. Am. Chem. Soc., 2011, 133, 8354–8361.
39. Y. Shimizu, Z. Shen, S. Ito, H. Uno, J. Daub and N. Ono, Tetrahedron Lett., 2002, 43, 8485–8488.
40. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772.
41. T. M. Krygowski, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78.
42. C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109.
43. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207.
44. K. Yamaguchi, Chem. Phys. Lett., 1975, 33, 330–335.
45. T. Stuyver, B. Chen, T. Zeng, P. Geerlings, F. De Proft and R. Hoffmann, Chem. Rev., 2019, 119, 11291–11351.
46. S. Moles Quintero, M. M. Haley, M. Kertesz and J. Casado, Angew. Chem., Int. Ed., 2022, 61, e202209138.
47. G. M. Peters, G. Grover, R. L. Maust, C. E. Colwell, H. Bates, W. A. Edgell, R. Jasti, M. Kertesz and J. D. Tovar, J. Am. Chem. Soc., 2020, 142, 2293–2300.
48. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
49. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
50. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, et al., GaussView 5.0, Gaussian, Inc., Wallingford CT, 2016.
51. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
53. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
54. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
55. F. Neese, J. Comput. Chem., 2003, 24, 1740–1747.
56. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.

---

Footnote

† Electronic supplementary information (ESI) available: Tables of HOMO–LUMO gaps, structural parameters, images of HOMOs and LUMOs for the macrocycles discussed, information on isomers, predicted UV-vis spectra, xyz coordinates of optimized geometries, TD-DFT predicted UV-vis spectra, singlet-triplet gaps and energy levels, bond orders, HOMA indices. See DOI: https://doi.org/10.1039/d5sc00639b

---