Oxidation-induced double aromaticity in periodo-polycyclic hydrocarbons

Abstract

The doubly oxidized hexaiodobenzene [C₆I₆]²⁺ is a well-known example of a double aromatic molecule, exhibiting both π- and σ-aromaticity. In this study, a series of periodo-monocyclic molecules and their doubly oxidized forms were systematically investigated to explore the origin of their double aromaticity. These molecules were employed to provide insights into how the size and aromaticity of the central carbon atom ring influence the aromaticity of the resulting doubly oxidized structures. The knowledge gained in this study was subsequently applied to model periodo-derivatives of polycyclic (anti)aromatic hydrocarbons in which oxidation can induce additional σ-electron cyclic delocalization along the macrocyclic iodine ring, thus also achieving their double aromaticity.

---

Introduction

Aromaticity has historically been associated with the cyclic delocalization of π-electrons. However, it later became clear that σ-electrons can also participate in a similar type of cyclic delocalization, giving rise to the concept of σ-aromaticity.^1–3 In 1979, Schleyer introduced the idea of double aromaticity, of both π and σ natures.⁴ According to this author, the doubly aromatic molecule features two orthogonal cyclically delocalized electronic systems. The initial model proposed for the concept was the cationic C₆H₃⁺,⁴ which has been later experimentally characterized.⁵ A significant advancement in the understanding of double aromaticity was made by Sagl and Martin who synthesized the C₆I₆²⁺ dication.⁶ Their comprehensive study demonstrated that C₆I₆²⁺ is a stable system with a singlet ground state. Furthermore, they found that the geometric and magnetic properties of this molecule indicate the presence of both π- and σ-aromaticity. In more recent work, Saito et al. successfully synthesized and characterized hexakis(phenylselenyl)benzene dication.⁷ This molecule features a π-aromatic benzene unit, together with σ-aromatic ring formed by selenium atoms.

Double aromaticity has been extensively studied, with C₆I₆²⁺ often serving as a prototypical example of this phenomena.^8–10 This double aromaticity was substantiated by the calculation of ring current, NICS, aromatic stabilization energy, and electronic indices.^8–13 However, double aromaticity has also been identified in numerous molecules that do not necessarily contain a benzene core structure. Recent research by Escayola et al. examined double aromaticity in perhalogen-tropylium cation in both singlet and triplet states.¹¹ Among the systems studied, only triplet C₇Br₇⁺³ with an internal Hückel aromatic tropylium ring (6 π-electrons) and an external incipient Baird aromatic Br₇⁺² ring (12 σ-electrons) showed double π- and σ-aromaticity. Fowler and Havenith explored periodo-cyclooctatetraene derivatives, C₈I₈^q with charges q = 0, +1, ±2, and +4.¹⁴ However, the large I–I steric repulsion in these periodo-cyclooctatetraene species led to highly puckered structures with lack of both σ- and π-aromaticity. Additionally, double aromaticity has proven to be a valuable concept for explaining and rationalizing the structure and stability of various pure and doped boron clusters.^15–17 It has also been thoroughly investigated in C_n monocyclic clusters possessing π_in and π_out orthogonal (anti)aromaticities.^18–27 Moreover, double 3D-aromaticity has been analyzed in the B₁₂I₁₂ cluster,^12,13 but the authors found that, despite many favorable evidences, the potential double 3D-aromaticity of the I₁₂ shell did not contribute to any stabilization of the system and, consequently, it was concluded that this cluster does not display double aromaticity.

As demonstrated experimentally by Sagl and Martin,⁶ and confirmed in numerous computational studies,^8–10 oxidation of the neutral C₆I₆, which is π-aromatic, induces σ-aromaticity, resulting in the formation of the doubly aromatic dication C₆I₆²⁺. This oxidation process removes two electrons from the HOMO, which is a σ-orbital, and consequently, this leads to the existence of two Hückel aromatic cyclic systems: π-system with 6 and σ-system with 10 electrons. In nearly all previous studies on the double aromaticity of periodo-derivatives, the core carbon structure exhibits a monocyclic structure. In this contribution, we aim to address the following questions: can σ-aromaticity be induced by oxidizing a periodo-system that has a polycyclic core structure, where the iodine atoms form a macrocycle? We will start our investigation with a series of monocyclic periodo-derivatives (Fig. 1). These systems will help us understand how the size and aromatic character of the central ring influence the aromaticity of the resulting doubly oxidized system. In the second part of this study, we will examine a series of periodo-polycyclic hydrocarbons and their doubly oxidized forms (Fig. 1). To assess the extent of aromaticity in the studied molecules, we utilize two electronic indices (multicentre index (I_ring)²⁸ and electron density of delocalized bonds (EDDB)^29,30), along with a magnetic indicator, the magnetically induced current density (MICD)^31–33 and an energetic measure, namely the aromatic stabilization energy.^34,35

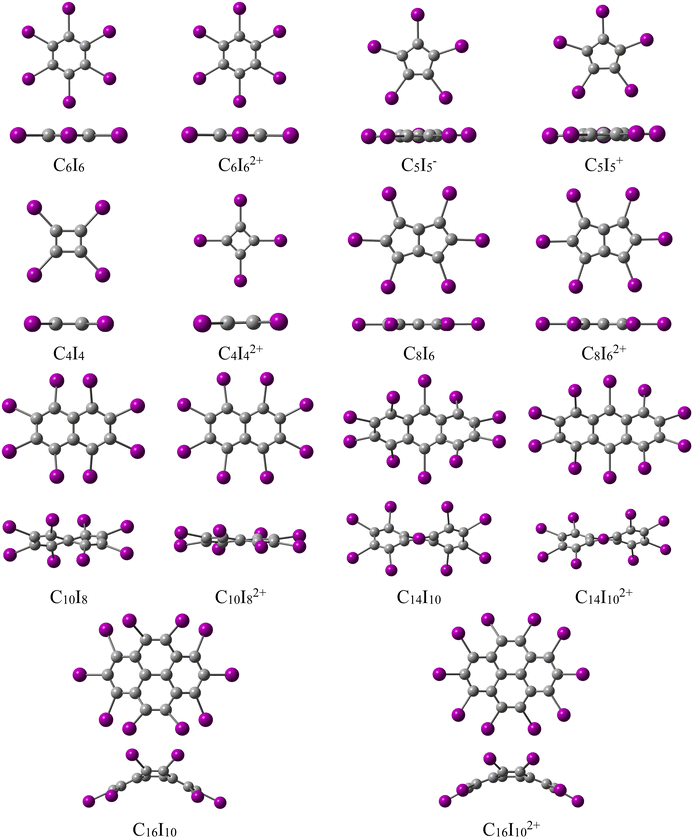Fig. 1 Top and side views of optimized structures for the studied periodated molecules and their oxidized forms.

Results and discussion

Periodo-monocyclic (anti)aromatic hydrocarbons

The double aromaticity of periodo-benzene dication has been demonstrated in numerous studies using various aromaticity descriptors.^8–11 The MICD map for periodo-benzene reveals its π-aromatic character, showing intensive diatropic circulations along the benzene ring and only local circulations around the iodine atoms (Fig. 2). On the other hand, the current density map of C₆I₆²⁺ displays two distinct diatropic circulations: one along the benzene ring and another along the iodine atom ring. The current density in these molecules can be dissected into contributions of π- and σ-electrons (Fig. 3). In what follows, π-MOs are considered as those having the main contributions from p_z-atomic orbitals on carbon atoms (assuming that the carbon atoms lie in the xy-plane), while σ-MOs are those having the dominant contributions from the in-plane 5p atomic orbitals of iodine atoms (Fig. S1†). As shown in Fig. 3, the π-electrons induce diatropic currents in both C₆I₆ and C₆I₆²⁺. Furthermore, in C₆I₆²⁺, the σ-electrons induce diatropic currents, whereas in C₆I₆ there are only local circulations around the iodine atoms. The observed magnetic aromaticity can be understood within the framework of Hückel's 4n + 2 rule.³⁶ In C₆I₆, there are 6 and 12 electrons in the π- and σ-electron molecular subgroup, respectively (Fig. S1†). Since the σ-MO subgroup is fully occupied, it does not show any significant magnetic response. Upon oxidation, the number of σ-electrons is reduced to 10, while the number of π-electrons remains unchanged.

Fig. 2 Total current density maps plotted 1 Bohr above molecular plane for C₆I₆, C₆I₆²⁺, C₅I₅⁻, C₅I₅⁺, C₄I₄, and C₄I₄²⁺.

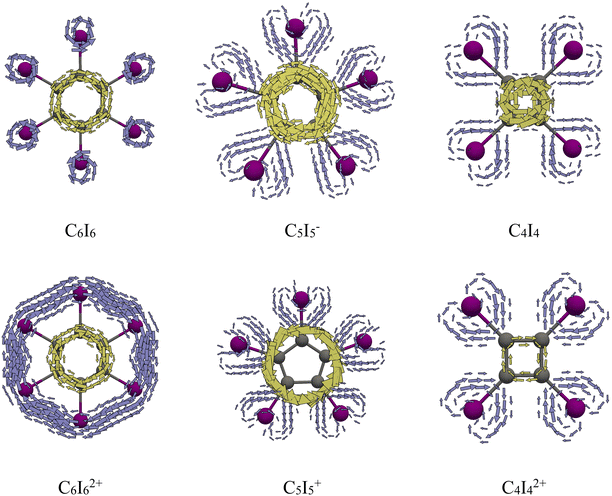Fig. 3 π (yellow) and σ (purple) current density maps plotted 1 Bohr above molecular plane for C₆I₆, C₆I₆²⁺, C₅I₅⁻, C₅I₅⁺, C₄I₄, and C₄I₄²⁺.

The double aromaticity of periodo-derivatives of cyclopentadienyl anion and cyclobutadiene, as well as their doubly oxidized forms, is examined below. In C₅I₅⁻, diatropic currents are observed within the five-membered ring, similar to those in cyclopentadienyl anion itself, while no global circulations occur along the perimeter formed by the iodine atoms (Fig. 2). However, in C₅I₅⁺ pronounced paratropic circulations are induced in the cyclopentadienyl unit, but no global circulations are found in I₅ unit. Similarly, in C₄I₄ strong paratropic currents circulate along the four-membered ring, while in C₄I₄²⁺ relatively weak diatropic currents can be seen, except in the center of the ring that remain paratropic (Fig. 2). The π- and σ-electron current density maps of C₅I₅⁻ and C₄I₄, and their oxidized forms provide a more detailed description of the magnetic aromaticity of these species (Fig. 3). The magnetic response of periodo-derivatives of cyclopentadienyl anion and cyclobutadiene, and their doubly oxidized products, can be understood using simple electron counting and Hückel's rule. In C₅I₅⁻, 6 π-electrons and in C₄I₄, 4 π-electrons give rise to magnetic aromaticity and antiaromaticity, respectively. In both C₅I₅⁻ and C₄I₄ the σ-electron molecular orbitals (MOs) are fully occupied with 10 and 8 electrons, respectively, and these electronic subsystems do not contribute to the global circulations (Fig. 3). A key difference between C₆I₆ on one hand, and C₄I₄ and C₅I₅⁻ on the other, is that latter molecules feature a π-type HOMO level, while the former one has a σ-type HOMO (Fig. S1 and Table S1†). For this reason, upon oxidation to C₅I₅⁺ and C₄I₄²⁺ the number of π-electrons decreases by 2 compared to their non-oxidized forms, which explains the drastic change in π-aromaticity. Contrary, the number of σ-electrons stays unchanged in both species.

The oxidation effects on aromaticity in the studied molecules are found to be independent of the aromatic character of the parent, non-oxidized molecules (Fig. 2 and 3). The primary factor influencing magnetic properties is found to be the structural characteristic of the starting compounds. The examined molecules in their ground singlet state show various geometries: C₆I₆ and C₆I₆²⁺ adopt planar D_6h geometries, C₅I₅⁻ adopts planar D_5h geometry, C₅I₅⁺ adopts planar C_2v geometry, while C₄I₄ adopts D_2h geometry, and C₄I₄²⁺ shows planar D_4h geometry in their ground singlet state (Fig. 1). Table 1 collects the iodine–iodine and carbon–carbon distances, along with the overlap integral values between the Pre-orthogonal Natural Bond Orbitals (PNBOs)³⁷ which depict the in-plane lone-pairs on I-atoms (Table 1 and Fig. S2†). As can be seen, the key structural feature influencing magnetic behavior upon oxidation is the size of carbon-atom ring. This factor ultimately determines the I–I distance, and consequently the overlap between the in-plane lone pair orbitals, which correspond to the 5p atomic orbitals on the iodine atoms (Fig. S3†). In C₆I₆ the I–I distance is 3.524 Å, while in the dication C₆I₆²⁺ this distance decreases to 3.475 Å. This reduction of the I–I distances upon oxidation is followed by a decrease in the C–C bond lengths. As a result, the overlap of the in-plane lone pair orbitals on adjacent iodine atoms in C₆I₆²⁺ is only slightly larger than that in C₆I₆. This suggests that significant overlap between the iodine in-plane lone pair orbitals is necessary for inducing σ-electron delocalization, but it is not the sole condition, as the number of σ-electrons also plays a crucial role. In the C₅I₅⁻ anion, oxidation results in a substantial change in the C–C distances due to a complete reversal of aromaticity in the five-membered carbon ring. On the other hand, there is no significant change in the I–I distances, as well as in the overlap between the in-plane lone pair orbitals of iodine atoms. For C₄I₄ and its dication C₄I₄²⁺, both C–C and I–I distances are reduced. However, the change in the I–I distance does not lead to any notable change in the overlap of specific orbitals in the iodine subunit, since the I–I distance remains above 4 Å, which prevents significant overlap of the iodine 5p orbitals.

Table 1 Bond lengths (in Å) for symmetry-unique C–C and I–I bonds and the absolute values of the overlap integral (S^PNBO) of in-plane lone pair PNBOs for C₆I₆, C₆I₆²⁺, C₅I₅⁻, C₅I₅⁺, C₄I₄, and C₄I₄²⁺

	C–C distance	I–I distance	S^PNBO
C6I6	1.405	3.524	0.124
C6I6^2+	1.389	3.475	0.129
C4I4	1.582	4.377	0.030
	1.329	4.333	0.032
C4I4^2+	1.450	4.269	0.026
C5I5^−	1.407	3.868	0.082
C5I5^+	1.448	3.812	0.070
	1.363	3.859	0.067
	1.534	3.837	0.066

---

The presented results show that the energy effect of mixing the in-plane lone pair orbitals on the iodine atoms, as indicated by the difference between the energies of the lowest and highest occupied σ-MOs (Table S1†), depends on the extent of the lone pair orbital overlap. Only when the overlap of the iodine 5p orbitals is sufficiently large does the energy of the highest occupied σ-MO, which has I–I antibonding character, become high enough to make this orbital the HOMO of the system from which electrons are removed in the oxidation process.

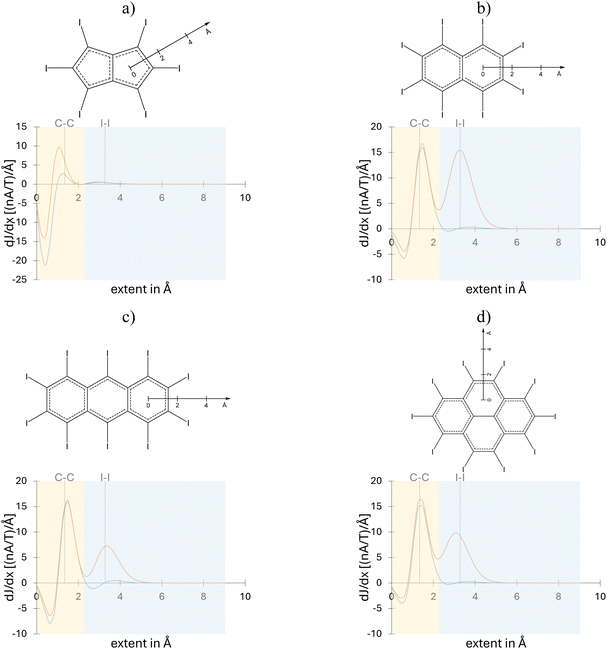
To provide more quantitative information on the induced current densities, an analysis based on the integrated current strengths was employed. For systems with a polycyclic structure, such as the studied molecules, the bond current strength profiles proved to be particularly insightful.¹⁰ The advantage of the bond strength profiles is illustrated for C₆I₆ and its doubly oxidized cation (Fig. 4). The total bond current strength profiles of neutral C₆I₆ (blue line in Fig. 4a) reveal that inside the benzene ring (r < 1 Å) there are relatively weak paratropic currents, while outside the benzene ring, much stronger diatropic currents are observed, primarily arising from π-electron contributions. However, this contribution practically vanishes at approximately 2 Å from the ring center, where the effect of the σ-MOs of the I₆-system becomes dominant, although these MOs induce only weak paratropic circulations. On the other hand, for C₆I₆²⁺ (orange line in Fig. 4a) two intensive peaks are found, corresponding to diatropic circulations around the carbon and around the iodine atom rings. The bond current strengths profiles dissected into π- and σ-electron contributions reveal that the oxidation of C₆I₆ causes a significant change in the magnetic response of the σ-electron system, while the π-electrons preserve their magnetic aromatic behavior. Bond current strengths profiles for C₅I₅⁻ and C₄I₄, as well as for their oxidized forms are provided in the ESI (Fig. S4 and S5†).

Fig. 4 Profiles of total (a), π (b), and σ (c) bond current strengths for C₆I₆ (blue line) and C₆I₆²⁺ (orange line). The yellow and blue surfaces describe the integration areas used to separate the total current strength. Positive and negative current strengths correspond to diatropic and paratropic ring currents, respectively.

As illustrated for C₆I₆²⁺ (Fig. 4a), the profile curve can be used to define an integration surface that allows for the division of the total currents into contributions from two circulations: one around the benzene ring and the other around the iodine atom ring. Using this approach, the total current strengths for all studied molecules were dissected into contribution from the carbon atom ring and the outer iodine atom ring. For the bond current strengths of both π- and σ-electrons, the integration surface was not separated, but rather used to the entire integration area. The bond current strengths calculated in this way for periodo-monocyclic molecules are collected in Table 2, along with the corresponding EDDB and I_ring values. The EDDB values were further decomposed into their π- and σ-electron contributions.

Table 2 Calculated bond current strengths (J, in nA T⁻¹), EDDB (in a.u.), and I_ring (in a.u.) values for the studied monocyclic molecules. The numbers in parentheses represent the total number of electrons

		J [nA T^−1]	EDDBF	Iring	J^π [nA T^−1]	EDDBπ	J^σ[nA T^−1]	EDDBσ
C6I6	C6	9.4	5.074	0.627	6.4	5.737 (6)	−2.0	0.623 (12)
	I6	−1.0	0.227	0.066
C6I6^2+	C6	8.6	5.038	0.624	6.6	5.733 (6)	17.6	5.812 (10)
	I6	18.7	5.333	0.310
C5I5^−	C5	9.4	5.470	0.617	8.3	5.569 (6)	−0.2	0.416 (10)
	I5	0.2	0.108	−0.042
C5I5^+	C5	−92.8	1.236	0.478	−83	2.164 (4)	−0.2	0.695 (10)
	I5	−0.7	0.529	−0.092
C4I4	C4	−12.3	0.211	0.216	−8.6	0.719 (4)	0.5	0.558 (8)
	I4	0.5	0.073	0.075
C4I4^2+	C4	−1.9	1.225	0.459	1.8	1.451 (2)	0.5	0.698 (8)
	I4	0.6	0.064	0.055

---

Before proceeding, it should be noted that the aromaticity indices for C₆I₆²⁺ were also obtained using different density functionals and basis sets (Table S2†). The comparison shows that the choice of functional and the size of the basis set have only a minor impact on the numerical values of the aromaticity indices, in agreement with a previous study.¹⁰ The largest difference is observed in the bond current strength for the I₆ unit, which is partly due to the practical challenge of accurately separating the currents circulating along the C₆ and I₆ rings.

As can be observed from the bond current strengths, the induced currents along the I₆ ring in the dication C₆I₆²⁺ are significantly stronger than those along the benzene ring. For C₆I₆, both EDDB and I_ring values indicate a significant increase in electron delocalization within the I₆ ring upon oxidation. Additionally, these indices confirm that in all parent (non-oxidized) molecules no cyclic delocalization occurs within the iodine atom units. Furthermore, the electronic indices show that the oxidation of C₅I₅⁻ and C₄I₄ does not affect the (non)aromatic character of the iodine atom rings. Contrary to predictions based on the bond current strengths, EDDB and I_ring values suggest that the cyclic delocalization in the I₆ unit of C₆I₆²⁺ is significantly weaker than that in the benzene fragment (Table 2). In particular, the I_ring values predict that the aromaticity of the I₆ ring is approximately half of that in the benzene ring. Similarly, in C₆I₆²⁺ the EDDB_π value is 5.737 (out of 6 electrons), while the EDDB_σ, which describes electron delocalization within the I₆ ring, is 5.812 (out of 10 electrons). As can be seen from the EDDB surfaces presented in Fig. 5, π-electrons are delocalized in C₆I₆, C₆I₆²⁺, C₅I₅⁻, and C₄I₄²⁺, while σ-electrons are delocalized only in C₆I₆²⁺.

Fig. 5 Isosurface of the EDDB_H function calculated for π-electrons (isovalue of 0.01 a.u.) and for σ-electrons (isovalue 0.001 a.u.).

To further investigate the significance of σ-aromaticity and to isolate its effects from those of π-electron aromaticity, we also examined periodo-borazine (Fig. S6†). It is worth noting that the aromaticity of borazine has been the subject of considerable debate.^38–40 Magnetic and energetic criteria have generally characterized borazine as weakly π-aromatic.⁴¹ Similarly, the bond current strengths suggest that B₃N₃I₆ is π-nonaromatic, while electronic indices predict relatively weak π-aromatic character (Fig. S7 and Table S3†). Both magnetic and electronic descriptors indicate that the oxidized species, B₃N₃I₆²⁺, exhibits pronounced σ-electron aromaticity, in agreement with a recent study.⁴² The oxidation of neutral B₃N₃I₆ to B₃N₃I₆²⁺ induces σ-aromaticity, which is clearly reflected in its structural properties: a reduction in I–I distances and planarization of the molecule (Fig. S6†). Notably, σ-electron aromaticity in B₃N₃I₆²⁺ completely annuls the distortive effect of the I-substituents. It is important to emphasize that the observed structural features are characteristic signatures of aromaticity and, more importantly, are readily accessible through experimental observation.

Periodo-polycyclic (anti)aromatic hydrocarbons

The study of periodo-derivatives of monocyclic conjugated hydrocarbons, as outlined above, clearly demonstrated that the main factor influencing the occurrence of oxidation induced σ-aromaticity is the size of the carbon atom rings. This structural factor determines the distance between iodine atoms, and consequently the overlap of their in-plane lone pair orbitals. Additionally, the number of σ-electrons is another factor that plays a crucial role in determining the σ-electron aromatic properties. This accumulated knowledge provides a solid foundation for exploring potential double aromaticity in periodo-derivatives of polycyclic (anti)aromatic hydrocarbons and their oxidized species. To begin, periodo-derivatives of bicyclic hydrocarbons such as pentalene and naphthalene are explored, before expanding the series to include periodo-derivatives of anthracene and perylene.

Periodo-pentalene (C₈I₆) adopts planar C_2h, while periodo-pentalene dication (C₈I₆²⁺) adopts D_2h geometry in their ground singlet state (Fig. 1). On the other hand, all other polycyclic periodo-derivatives exhibit nonplanar geometries with reduced symmetries. For this reason, in what follows aromaticity indices were not dissected into σ/π contributions. The critical atom distances and the overlap of the in-plane lone pair orbitals on neighboring iodine atoms are presented in Fig. 6. The structural features of the five-membered rings within the pentalene unit have a significant impact on the distances between iodine atoms. In C₈I₆ the I–I distance ranges from 3.818 to 4.038 Å, while in C₈I₆²⁺ this distance is only slightly reduced to 3.780–4.021 Å. These distances, and consequently the overlap of the iodine 5p atomic orbitals, are similar to those observed in C₅I₅⁻ and C₅I₅⁺. The small change in the I–I distance upon oxidation does not lead to any substantial alternation in the overlap of the iodine 5p atomic orbitals. Thus, it is not likely to expect any significant cyclic electron delocalization in the I₆ unit of C₈I₆²⁺. Indeed, the current density maps (Fig. 7) and profiles of the integrated current density (Fig. 8) for C₈I₆ show pronounced paratropic currents within the pentalene unit, while for C₈I₆²⁺, these currents become weak and diatropic. In both molecules, only local currents are induced around the iodine atoms. As shown for C₆I₆ (Fig. 4), the current strength profiles of C₈I₆ and C₈I₆²⁺ were used to extract the information on the strength of the current density circulations around the carbon and iodine atom rings (Table 3). The current strength profiles for periodo-pentalene resemble those of periodo-cyclobutadiene. The current density profile for neutral C₈I₆ is dominated by a negative peak, corresponding to paratropic currents along the pentalene unit (Fig. 8). In C₈I₆²⁺, these paratropic currents are significantly reduced, indicating an overall diatropic character, while there is no evidence of σ-electron currents around the I₆ macrocycle (Fig. 8). These results can be explained in a similar manner to C₄I₄: upon oxidation, the number of π-electrons changes from 8 to 6 (the HOMO of pentalene is relatively high in energy as expected from an antiaromatic molecule), while the number of σ-electrons remains constant. Because, in general, the HOMO of antiaromatic species is of π-character, we expect that such systems will not show double (anti)aromaticity after oxidation. The EDDB and I_ring values agree with the current density analysis regarding the aromaticity of the I₆ unit in both C₈I₆ and its oxidized form (Table 3). However, the EDDB does not predict such a significant change in the aromaticity of the pentalene unit when going from C₈I₆ to C₈I₆²⁺. On the other hand, the I_ring predicts an unreasonably high delocalization within the pentalene unit in both C₈I₆ and C₈I₆²⁺. Overall, the electronic aromaticity indices are inadequate for accurate differentiation between antiaromatic and nonaromatic species in periodo-pentalene.

Fig. 6 The absolute values of the overlap integral values of in-plane lone pair PNBOs (bold numbers), along with the C–C and I–I distances (in Å) for symmetry-unique bonds in C₈I₆, C₈I₆²⁺, C₁₀I₈, C₁₀I₈²⁺, C₁₄I₁₀, C₁₄I₁₀²⁺, C₁₆I₁₀, and C₁₆I₁₀²⁺.

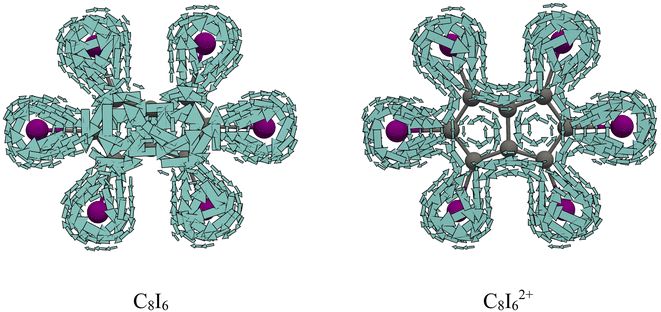Fig. 7 Total current density maps plotted 1 Bohr above the molecular plane for C₈I₆ and C₈I₆²⁺ (a) and (b).

Fig. 8 Total bond current strengths profiles of C₈I₆ (blue line) and C₈I₆²⁺ (orange line) (a); C₁₀I₈ (blue line) and C₁₀I₈²⁺ (orange line) (b); C₁₄I₁₀ (blue line) and C₁₄I₁₀²⁺ (orange line) (c); C₁₆I₁₀ (blue line) and C₁₆I₁₀²⁺ (orange line) (d).

Table 3 Calculated BFPI values, bond current strengths (J, in nA T⁻¹), EDDB (in a.u.), and I_ring (in a.u.) values for periodo-derivatives of polycyclic (anti)aromatic hydrocarbons

	BFPI [Å]		J [nA T^−1]	EDDB	Iring
C8I6	0.000	C8	−14.8	2.511	0.517
		I6	0.5	0.214	0.040
C8I6^2+	0.000	C8	3.1	4.481	0.546
		I6	1.0	0.530	−0.052
C10I8	6.779	C10	8.6	5.918	0.575
		I8	0.3	0.252	0.080
C10I8^2+	2.772	C10	10.5	7.085	0.592
		I8	21.4	5.825	0.204
C14I10	9.466	C14	6.4	8.130	0.557
		I10	−0.2	0.301	0.068
C14I10^2+	7.554	C14	8.3	8.916	0.571
		I10	9.6	6.089	0.141
C16I10	9.079	C16	10.2	7.233	0.545
		I10	0.1	0.266	0.087
C16I10^2+	7.318	C16	13.7	7.656	0.562
		I10	12.9	6.146	0.155

---

The periodo-naphthalene (C₁₀I₈) and periodo-naphthalene dication (C₁₀I₈²⁺) have nonplanar D₂ geometry. The extent of their nonplanarity was evaluated using the BFPI (brute-force planarity index)⁴³ (Table 3). In C₁₀I₈, the distance between iodine atoms ranges from 3.576 to 3.636 Å, whereas in C₁₀I₈²⁺ these distances are significantly shortened. This reduction is especially pronounced for the distance between the two I atoms in the α-positions on the adjacent hexagons, which decreases from 3.636 Å to 3.240 Å. Consequently, upon oxidation, the overlap of the corresponding iodine 5p atomic orbitals drastically increases from 0.026 to 0.168 (Fig. 6). The contraction in I–I distance is much more pronounced than that found during the oxidation of C₆I₆ (Table 1). The BFPI nonplanarity index further shows that oxidation of C₁₀I₈ enhances planarity of the corresponding product. This feature is already evident in the side-view geometries of these two species (Fig. 1). Current density maps and profiles of current density strengths of the C₁₀I₈²⁺ dication (Fig. 8 and 9) reveal its double aromatic nature. In C₁₀I₈²⁺, diatropic currents are induced along the perimeter formed by the iodine atoms, while there are no such currents in neutral C₁₀I₈. In both C₁₀I₈ and C₁₀I₈²⁺ the current density distribution in the naphthalene unit resembles that in naphthalene itself. The integrated current strengths for circulations along the carbon and iodine atom rings are 10.5 and 21.5 nA T⁻¹, respectively. According to the magnetically induced current density, both the naphthalene and macrocycle I₈ units of the C₁₀I₈²⁺ dication display significant aromatic character despite distortions in planarity. These findings are generally supported by the EDDB and I_ring values. Based on the magnetic and electronic indices, oxidation of C₁₀I₈ induces σ-aromaticity, while the resulting C₁₀I₈²⁺ dication gains additional planarity and enhanced aromaticity in the naphthalene unit in comparison to the neutral molecule. The C₁₀I₈²⁺ dication is a double Hückel 4n + 2 system, with 10 π-electrons and 14 σ-electrons. To further evaluate the effect of halogen lone-pair orbital overlap on oxidation induced σ-aromaticity, C₁₀Br₈ and C₁₀Br₈²⁺ were also included in this study (Fig. S8†). Oxidation of C₁₀Br₈ to C₁₀Br₈²⁺ results in shorter Br–Br distances and enhanced overlap of Br lone pair orbitals. Due to the smaller van der Waals radius of bromine compared to iodine, C₁₀Br₈²⁺ adopts a fully planar geometry, allowing more significant overlap of the corresponding in-plane lone pair orbitals on the two Br atoms in the α-positions on the adjacent hexagons. Both magnetic and electronic indices predict considerable σ-electron delocalization in C₁₀Br₈²⁺, although slightly less intense than in C₁₀I₈²⁺ (Fig. S9 and Table S4†). However, a more detailed investigation into how the nature of halogen substituents influences oxidation-induced σ-aromaticity in polycyclic molecules remains a task for future studies.

Fig. 9 Total current density maps plotted 1 Bohr above the molecular plane for C₁₀I₈ and C₁₀I₈²⁺.

The periodo-anthracene (C₁₄I₁₀) exhibits C₁ symmetry, periodo-anthracene dication (C₁₄I₁₀²⁺) adopts nonplanar D₂ geometry, while the periodo-perylene (C₁₆I₁₀) and periodo-perylene dication (C₁₆I₁₀²⁺) have nonplanar C_2v geometry (Fig. 1). In C₁₄I₁₀, the distance between iodine atoms ranges from 3.582 to 3.642 Å, while in C₁₄I₁₀²⁺ this distance decreases notably to 3.336–3.491 Å (Fig. 6). The I–I distance shortening is accompanied by a substantial increase of the overlap of the iodine lone pair orbitals (Fig. 6). Similarly, the oxidation of C₁₆I₁₀ to C₁₆I₁₀²⁺ leads to a reduction of I–I distances and to an enhanced overlap of the 5p iodine orbitals. Both C₁₄I₁₀²⁺ and C₁₆I₁₀²⁺ adopt more planar structure compared to their non-oxidized forms (Table 3 and Fig. 1). Based on these observations, one can anticipate that the double oxidation of C₁₄I₁₀ and C₁₆I₁₀ will induce σ-electron delocalization within the I₁₀ units of the corresponding oxidation products (Fig. 8, 10, and 11).

Fig. 10 Total current density maps plotted 1 Bohr above the molecular plane for C₁₄I₁₀ and C₁₄I₁₀²⁺.

Fig. 11 Total current density maps plotted 1 Bohr above the molecular plane for C₁₆I₁₀ and C₁₆I₁₀²⁺.

Current density maps and integrated current density profiles for neutral C₁₄I₁₀ and C₁₆I₁₀ reveal the aromatic characteristics of the anthracene and perylene units, despite notable geometric distortions in these molecules (Table 3 and Fig. 1), and additionally, no evidence of any global σ-electron current density circulations. Similar to the periodo-naphthalene dication, the magnetically induced currents support the presence of double aromaticity in the C₁₄I₁₀²⁺ and C₁₆I₁₀²⁺ molecules. The integrated bond current strengths suggest that the σ-electron currents within the I₁₀ macrocyclic are more intensive in C₁₆I₁₀²⁺ than in C₁₄I₁₀²⁺ (Fig. 8 and Table 3). This goes in line with the obtained EDDB and I_ring values (Table 3). Even though periodo-anthracene and periodo-perylene dications are highly nonplanar, significant overlap between the lone pair orbitals on the iodine atoms facilitates cyclic σ-electron delocalization, which is evident from both the magnetic and electronic aromaticity indices. EDDB surfaces presented in Fig. 12 further confirm double aromatic character in C₁₀I₈²⁺, C₁₄I₁₀²⁺, and C₁₆I₁₀²⁺.

Fig. 12 Isosurfaces of the EDDB_F function calculated for the C-atom units (isovalue of 0.01 a.u.) and for the I-atom units (isovalue of 0.001 a.u.) in the considered molecules.

As discussed above, both magnetic and electronic aromaticity indices consistently indicate that double oxidation of periodo-derivatives of naphthalene, anthracene, and perylene induces σ-electron delocalization within the I-containing macrocycles of the corresponding oxidation products. Furthermore, the presence of σ-aromaticity in the oxidized species should be readily observable experimentally, as these molecules exhibit shorter I–I distances and increased planarity compared to their non-oxidized forms (Fig. 1 and 6). A generally good correlation is observed between the shortening of I–I distances, enhanced overlap of iodine 5p atomic orbitals, and the increase in aromaticity indices upon oxidation in studied molecules (Fig. S10†).

Finally, we investigated the energetic aspect of oxidation induced σ-electron aromaticity using carefully designed homodesmotic reactions (Table 4). It is important to note that the selected reactions differ somewhat from those employed in recent work by some of the present authors.^12,13 This adjustment was made to provide a more balanced treatment of planarity distortions between reactants and products. Further details regarding these reactions are provided in Fig. S11.† As shown in Table 4, the stabilization effects of σ-electron aromaticity decrease rapidly with increasing size of the I-macrocycle, in agreement with previous studies.^44,45 Additionally, the relatively modest stabilization effects can be partly attributed to significant deviations from planarity within the σ-electron system.

Table 4 Zero-point (Δ_rZPE) and Gibbs (Δ_rG) reaction energies (kcal mol⁻¹) for selected homodesmotic reactions

	ΔrZPE	ΔrG
C6I^2+6 + C6I5H → C6I5H^2+ + C6I6	23.2	22.6
C10I^2+8 + C10I7H → C10I7H^2+ + C10I8	6.0	6.2
C14I^2+10 + C14I9H → C14I9H^2+ + C14I10	2.9	2.9
C16I^2+10 + C16I9H → C16I9H^2+ + C16I10	5.0	5.3

---

Conclusions

In this study, the aromatic character of a series of periodo-derivatives of monocyclic and polycyclic (anti)aromatic hydrocarbons, along with their doubly oxidized forms, was investigated using electronic (I_ring and EDDB), magnetic (MICD) and energetic (aromatic stabilization energy) indicators. The analysis of periodo-derivatives of monocyclic conjugated hydrocarbons clearly demonstrated that the primary factor influencing the appearance of oxidation-induced σ-aromaticity is the size of the carbon atom rings. This structural feature was found to govern the distance between iodine atoms, which, in turn, determinates the overlap of their in-plane lone pair orbitals. Only when the overlap of the iodine 5p orbitals becomes sufficiently large, the highest occupied σ-molecular orbital, can become the HOMO, from which electrons are removed during the oxidation process. Furthermore, it was found that the number of σ-electrons is another factor that plays a crucial role in determining the σ-electron aromaticity of the corresponding oxidized structures.

Based on this knowledge, potential double aromaticity in periodo-derivatives of polycyclic (anti)aromatic hydrocarbons was further explored. It was found that the oxidation of periodo-pentalene does not induce σ-electron delocalization in the iodine macrocyclic ring, as only the number of π-electrons is altered during this process. On the other hand, for periodo-derivatives of naphthalene, anthracene, and perylene, the oxidation was found to enhance planarity of the corresponding products, along with a significant increase in the overlap of the iodine 5p atomic orbitals. Both magnetic and electronic aromaticity indices revealed the presence of σ-aromaticity in the iodine macrocyclic rings and, more importantly, the double aromatic character of the oxidized forms of these molecules.

Computational methods

Geometry optimizations and vibrational frequency calculations for all studied molecules were performed at the B3LYP/def2-TZVP^46–49 level of theory using Gaussian 09 program package.⁵⁰ The magnetically induced current density (MICD) was calculated at the same level of theory, using the diamagnetic zero (DZ) version of the CTOCD method.^51–54 The MICD was calculated by applying the external magnetic field oriented perpendicular to the molecular planes. In the MICD maps, clockwise circulations denote diatropic currents, while counterclockwise circulations indicate paratropic currents. The maps were generated using the ParaView software.⁵⁵ The current strengths (J, in nA T⁻¹)⁵⁶ were obtained by numerical integration of the current densities passing through a rectangle which perpendicularly bisects the considered bond. The integration rectangle extends 5 Bohr above and 5 Bohr below the molecular plane, and it starts from the ring center and extends 15 Bohr outside the C-atom ring, to take into account all currents induced along the I-atom subunits. Diatropic (paratropic) currents give positive (negative) contributions to the current strength.

The multicenter index I_ring was calculated using the natural atomic orbital (NAO) density matrices obtained from NBO analysis.³⁷ The I_ring values were normalized based on the ring's size.⁵⁷

To assess the reliability of the B3LYP/def2-TZVP results, a set of test calculations for C₆I₆ and C₆I₆²⁺ was performed with three different density functionals (CAM-B3LYP,⁵⁸ BP86,^59,60 ωB97XD⁶¹) and two additional basis sets (def2-SVP and def2-TZVPPD).

The aromatic stabilization energy^34,35 was calculated through a set of properly designed homodesmotic reactions.

The extent of the deviation from planarity for the examined molecules was quantified by means of the brute-force planarity index (BFPI).⁴³ The BFPI presents the average distance of all atoms from the optimal plane, obtained by minimizing that distance in the given molecule.

MICD, I_ring, and BFPI were calculated using in-house FORTRAN codes, while the EDDB values were calculated using the RunEDDB code.⁶²

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. R. and S. Đ. would like to dedicate this paper to students and teachers who stood against corruption and the collapse of the educational system in Serbia during the 2024–2025 academic year. S. Đ. and S. R. thank the Serbian Ministry of Science, Technological Development, and Innovation (Agreement No. 451-03-137/2025-03/200122). J. P. and M. S. thank the Spanish Ministerio de Ciencia, Innovación y Universidades (MCIN/AEI/10.13039/501100011033, projects: PID2023-147424NB-I00, PID2022-138861NB-I00, and CEX2021-001202-M) and the Generalitat de Catalunya (projects: 2021SGR442 and 2021SGR623 and ICREA Academia 2024 Prize to M. S.).

References

1. M. J. S. Dewar, Bull. Soc. Chim. Belg., 1979, 88, 957–967.
2. D. Cremer, Tetrahedron, 1988, 44, 7427–7454.
3. R. W. A. Havenith, F. De Proft, P. W. Fowler and P. Geerlings, Chem. Phys. Lett., 2005, 407, 391–396.
4. J. Chandrasekhar, E. D. Jemmis and P. von R. Schleyer, Tetrahedron Lett., 1979, 20, 3707–3710.
5. E. D. Nelson and H. I. Kenttämaa, J. Am. Soc. Mass Spectrom., 2001, 12, 258–267.
6. D. J. Sagl and J. C. Martin, J. Am. Chem. Soc., 1988, 110, 5827–5833.
7. S. Furukawa, M. Fujita, Y. Kanatomi, M. Minoura, M. Hatanaka, K. Morokuma, K. Ishimura and M. Saito, Commun. Chem., 2018, 1, 60.
8. I. Ciofini, P. P. Lainé and C. Adamo, Chem. Phys. Lett., 2007, 435, 171–175.
9. R. W. A. Havenith, P. W. Fowler, S. Fias and P. Bultinck, Tetrahedron Lett., 2008, 49, 1421–1424.
10. M. Rauhalahti, S. Taubert, D. Sundholm and V. Liégeois, Phys. Chem. Chem. Phys., 2017, 19, 7124–7131.
11. S. Escayola, N. Proos Vedin, A. Poater, H. Ottosson and M. Solà, J. Phys. Org. Chem., 2023, 36, e4447.
12. J. Poater, S. Escayola, A. Poater, F. Teixidor, H. Ottosson, C. Viñas and M. Solà, J. Am. Chem. Soc., 2023, 145, 22527–22538.
13. J. Poater, S. Escayola, A. Poater, F. Teixidor, H. Ottosson, C. Viñas and M. Solà, J. Am. Chem. Soc., 2025, 147, 2914.
14. P. W. Fowler and R. W. A. Havenith, J. Phys. Chem. A, 2021, 125, 6374–6383.
15. J. Barroso, S. Pan and G. Merino, Chem. Soc. Rev., 2022, 51, 1098–1123.
16. S. Đorđević and S. Radenković, Phys. Chem. Chem. Phys., 2022, 24, 5833–5841.
17. S. Đorđević and S. Radenković, ChemPhysChem, 2022, 23, e202200070.
18. P. W. Fowler, N. Mizoguchi, D. E. Bean and R. W. A. Havenith, Chem.–Eur. J., 2009, 15, 6964–6972.
19. D. E. Bean, P. W. Fowler and A. Soncini, Chem. Phys. Lett., 2009, 483, 193–197.
20. A. J. Stasyuk, O. A. Stasyuk, M. Solà and A. A. Voityuk, Chem. Commun., 2020, 56, 352–355.
21. G. V Baryshnikov, R. R. Valiev, A. V Kuklin, D. Sundholm and H. Ågren, J. Phys. Chem. Lett., 2019, 10, 6701–6705.
22. G. V Baryshnikov, R. R. Valiev, R. T. Nasibullin, D. Sundholm, T. Kurten and H. Ågren, J. Phys. Chem. A, 2020, 124, 10849–10855.
23. G. V Baryshnikov, R. R. Valiev, L. I. Valiulina, A. E. Kurtsevich, T. Kurtén, D. Sundholm, M. Pittelkow, J. Zhang and H. Ågren, J. Phys. Chem. A, 2022, 126, 2445–2452.
24. K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299–1301.
25. H. Li, R. Parida, S. Mukamel and J. Y. Lee, Phys. Chem. Chem. Phys., 2024, 26, 10284–10288.
26. I. Rončević, F. J. Leslie, M. Rossmannek, I. Tavernelli, L. Gross and H. L. Anderson, J. Am. Chem. Soc., 2023, 145, 26962–26972.
27. Y. Lyu, Y. Cui, H. Xu, C. Zhang and Q. Meng, J. Org. Chem., 2024, 89, 18244–18254.
28. M. Giambiagi, M. S. de Giambiagi, C. D. dos Santos Silva and A. P. de Figueiredo, Phys. Chem. Chem. Phys., 2000, 2, 3381–3392.
29. D. W. Szczepanik, Comput. Theor. Chem., 2016, 1080, 33–37.
30. D. W. Szczepanik, M. Andrzejak, J. Dominikowska, B. Pawełek, T. M. Krygowski, H. Szatylowicz and M. Solà, Phys. Chem. Chem. Phys., 2017, 19, 28970–28981.
31. P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223.
32. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
33. D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378.
34. S. W. Slayden and J. F. Liebman, Chem. Rev., 2001, 101, 1541–1566.
35. M. K. Cyrański, Chem. Rev., 2005, 105, 3773–3811.
36. M. Solà, Nat. Chem., 2022, 14, 585–590.
37. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
38. D. Benker, T. M. Klapötke, G. Kuhn, J. Li and C. Miller, Heteroat. Chem., 2005, 16, 311–315.
39. J. J. Engelberts, R. W. A. Havenith, J. H. van Lenthe, L. W. Jenneskens and P. W. Fowler, Inorg. Chem., 2005, 44, 5266–5272.
40. R. Islas, E. Chamorro, J. Robles, T. Heine, J. C. Santos and G. Merino, Struct. Chem., 2007, 18, 833–839.
41. R. Báez-Grez and R. Pino-Rios, RSC Adv., 2022, 12, 7906–7910.
42. R. Pino-Rios, A. Vásquez-Espinal, O. Yañez and W. Tiznado, RSC Adv., 2020, 10, 29705–29711.
43. M. Antić, B. Furtula and S. Radenković, J. Phys. Chem. A, 2017, 121, 3616–3626.
44. M. Jirásek, M. Rickhaus, L. Tejerina and H. L. Anderson, J. Am. Chem. Soc., 2021, 143, 2403–2412.
45. L. Van Nyvel, M. Alonso and M. Solà, Chem. Sci., 2025, 16, 5613–5622.
46. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
47. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
48. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
49. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian Inc., Wallingford CT, 2009.
51. T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1993, 210, 223–231.
52. T. A. Keith and R. F. W. Bader, J. Chem. Phys., 1993, 99, 3669–3682.
53. P. Lazzeretti, M. Malagoli and R. Zanasi, Chem. Phys. Lett., 1994, 220, 299–304.
54. E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562.
55. U. Ayachit, The ParaView Guide: A Parallel Visualization Application, Kitware, 2015.
56. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
57. J. Cioslowski, E. Matito and M. Solà, J. Phys. Chem. A, 2007, 111, 6521–6525.
58. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
59. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
60. J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
61. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
62. D. W. Szczepanik, RunEDDB (version 11-Feb-2024), http://aromaticity.eu, accessed March 15, 2025.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc08696a

---