Rigorous treatment of polytopal rearrangements reveal surprising complexity of stereoisomerism configuration landscapes

Abstract

Previously we posited that a systematic and general description of stereoisomerism could be based upon the principles of the polytopal rearrangement model. The most daunting challenge to this end is to comprehensively describe all possible geometries for arbitrary n-coordinate centres, AB_n, and for this we have developed a physically-inspired rigorous approach. Here we demonstrate the detailed application of this approach to the AB₄ system focussing on e-symmetric distortions of tetrahedral geometry to generate an angular configuration space (the AB₄T-4 E-mode space). Analytic expressions for the A–Bⁱ unit vector configurations are presented and the resulting spherical (2D) configuration space is shown to exhibit the symmetries of a disdyakis dodecahedron. Detailed inspection and analysis of the angular configuration space reveals that, in addition to the expected (T-4-R) ⇌ (T-4-S) pseudorotation, it features numerous “orientation permutations” that are also pseudorotations. Through the worked examples of SiF₄, XeF₄, and a chiral silane, we generate the corresponding potential energy surfaces and examine the wider implications. We also outline experimental opportunities for investigating the unexpected configuration space complexity that this work has revealed. This rigorous and mathematically comprehensive approach and framework is part of the Polytope Formalism of isomerism and molecular structure.

---

Introduction

The shape of molecules, and the dynamical processes that interchange them, are key drivers of chemical properties. Central to this long-standing picture is stereoisomerism: the relationships between stereoisomers – chemical entities with the same atoms and connectivity but different spatial arrangements. Now, stereoisomerism is understood to be comprised of many facets as the subject matter has grown over almost 200 years in an ad hoc way in response to the independent treatment of each new discovery.

In 2018, we reported our discovery of a new fundamental form of stereoisomerism that we named akamptisomerism.^1,2 At that time, stereoisomerism was regarded as complete with no new forms left to be discovered – it being over 50 years since the last fundamental discovery. This led us to ponder if there are yet further forms to be discovered and where akamptisomerism fits within the larger picture?

Because of its ad hoc development, the present paradigm for describing stereoisomerism lacks a unifying framework. We conclude that it is only through the lens of a systematic mathematically complete framework, that the relationships between the different facets of stereoisomerism can be determined. Further, such a framework provides the means of determining the completeness of stereoisomerism. We are developing such a unifying systematic framework³ and here we detail its implementation to one aspect of stereoisomerism: the geometries of coordination centres AB_n, here demonstrated through a simple worked example relating to AB₄ that shows the principles and approach.

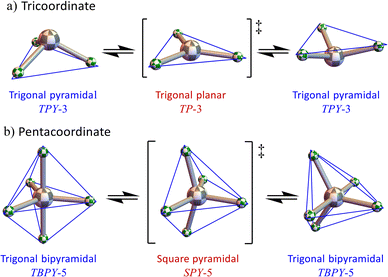
In the 1960s and 1970s, Muetterties et al.^4–18 and Mislow¹⁹ developed a general approach called the polytopal rearrangement model for analysing this type of stereoisomerism. In this context, a “polytope” is the coordination polyhedron and a “polytopal rearrangement” describes any shape changing “ligand permutating” process that interconverts between different coordination geometries. Familiar examples of polytopal rearrangements are the “inversion” (more accurately called a geometric reflection) of trigonal bipyramidal tricoordinate (TPY-3) NH₃ and simple amines,^20,21 and the Berry pseudorotation mechanism²¹ as occurs in trigonal bipyramidal pentacoordinate (TBPY-5) PF₅ (Fig. 1).

Fig. 1 Two polytopal rearrangement examples. The blue lines define the edges of the polytopes. (a) A geometric reflection of a TPY-3 geometry via a trigonal planar (TP-3) intermediate. (b) The Berry pseudorotation process whereby TBPY-5 geometries interconvert through a square pyramidal (SPY-5) intermediate.

Despite Muetterties' model making several simplifying approximations, such as using idealised geometries,¹⁶ it proved successful in addressing questions of interest at that time such as explaining the thermally facile stereoisomerisation phenomena referred to as fluxionality.^21–25 A key feature of the model is that, in addition to systematically describing the target coordination geometries, it mathematically encodes the relationships between them and provides insight into possible unimolecular stereoisomerisation mechanisms.^3,19

Notwithstanding these successes, the Muetterties model is not comprehensive and only approximately describes a very small subset of the full scope of possibilities within each complete AB_n “configuration space”. Later developments have mapped out larger regions of the configuration spaces but these, too, are not comprehensive.^26,27 Herein we demonstrate the generation of a full angular configuration space and how it is analysed.

As noted by earlier researchers studying polytopal rearrangements, vibrational atomic motions correspond to the beginning of rearrangement reaction coordinates.^21,28,29 For example, the geometric reflection (“inversion”) of trigonal pyramidal TPY-3 NH₃ involves the umbrella vibrational mode of a₁ symmetry,³⁰ and the Berry pseudorotation mechanism in trigonal bipyramidal TBPY-5 PF₅ is affected by a vibrational mode of e′ symmetry.³¹

In this work, a mathematically-rigorous method³ that we developed for describing AB_n configuration spaces and based upon the above principle, is applied to the AB₄ tetrahedral (T-4) system, focusing on angular atom displacements that have “e generic symmetry” (the E-mode).

Analytic expressions encoding the AB₄T-4 E-mode are presented, and the angular configuration space is described in detail. In addition to the expected pseudorotation T-4-R ⇌ T-4-S, the configuration space also features numerous and unexpected “orientation permutations” that are also pseudorotations in that they arise through polytopal rearrangement mechanisms.

We focus on the AB₄T-4 E-mode space as it provides the simplest example of a configuration space where discrete orientation permutations are “stereoisomerically connected” (there are feasible polytopal rearrangements connecting the orientation permutations). The AB₄T-4 E-mode space is a subspace of the full AB₄T-4 (E × T₂)-mode space – a far more complex 5-dimensional space.³²

Three chemical systems – SiF₄, XeF₄, and a chiral silane – are used to demonstrate the practical application of this rigorous approach and the corresponding potential energy surfaces (PESs) are presented. These reveal that, while configuration spaces are well-defined topological manifolds (continuous, smooth, and differentiable), the corresponding PES for a specific embodiment (specific atoms are assigned to AB₄) will contain discontinuities idiosyncratic of the system.

Consideration of the findings suggest how the surprising features of the configuration space may be experimentally probed and exploited. Finally, the approach outlined here is cast such that the higher-level, general features of the framework are seen to be transferrable for describing other types of isomerism and molecular structure more broadly. This general conceptual and mathematical framework we name the Polytope Formalism.

Approach

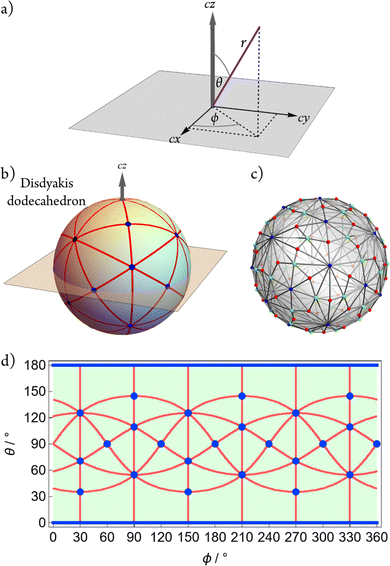
The AB₄T-4 E-mode angular configuration space was generated following method of Canfield, et al.,³² using the T-4-R “seed” polytope species, and its associated orthonormal e-symmetric angular-displacement basis, as shown in Fig. 2, in brief, the two components of the tetrahedral T-4 e-symmetric vibrational normal mode (E-mode) are used as an angular displacement basis and combined in a manner akin to that used to describe geometries in systems experiencing Jahn–Teller distortions. Two angular parameters are utilised within this approach with the angle ϕ determining the mixing of the two E-mode components and θ giving the magnitude of the angular displacement.

Fig. 2 The T-4-R seed polytope, orientation to the real space Cartesian axes, and two convenient orthonormal components of the E-mode: ε¹ digonal twist involving motions in parallel planes, and ε² “flex” orthogonal planes, both orthogonal to the “flex” motions planes. Colours differentiate B-atoms and do not denote specific chemical elements.

Requisite taxonomic-hierarchy terminology (class–family–genus–species) as presented in our recent Perspective³ and further elaborated in the mathematics paper³² is used throughout.

Density-functional theory calculations and generation of potential-energy surfaces (PESs) were carried out for the three chemical embodiments using the Gaussian16 (ref. 33) package.

Results – the configuration space

The compactified configuration space coordinates are defined using a spherical coordinate system (r, θ, ϕ) (see Fig. 3a) with r = 1, θ ∈ [0, 180°], and ϕ ∈ [0, 360°]. For convenience and pictorial depiction as a equirectangular map, we reverse the order of the angular components and plot ϕ (“longitude”) versus θ (“latitude”), and report the coordinates as (ϕ, θ). The full analytic expressions for the A–Bⁱ unit vector configurations resulting from the approach³² are provided in the ESI† along with interactive tools for exploring the angular configuration space.

Fig. 3 Symmetry relationships of the AB₄T-4 E-mode configuration space. (a) Configuration space coordinate system. (b) Configuration space coloured by dimension of polytope contiguous generic symmetry (point, line segment, area). (c) The undirected graph representation of the configuration space with colour-code corresponding to (b) mapped onto a sphere. (d) The equirectangular 2D projection of (b).

The configuration space exhibits the symmetry properties of a disdyakis dodecahedron as shown in Fig. 3b, namely, O_h symmetry, 26 “vertices”, 72 spherical “edges” comprising 9 great circles, and 48 spherical “faces”. The simple undirected graph (see later description) is shown in Fig. 3c and the equirectangular projection of the space is given in Fig. 3d.

The seven polytope genera comprising this space are listed in Table 1 along with some of their properties including the vibrational generic symmetries that act within the space. All polytope species (configurations) exhibit at least the D₂ generic symmetry point group.

Table 1 AB₄T-4 E-mode configuration space component polytope genera and properties

Polytope genus	Point group	Number species	Orient. perm.	Total	Config. space region	Vibration generic symmetries
a Symmetric “fusion”. b Gyfu planar. c Tetragonally compressed tetrahedral. d Tetragonally elongated tetrahedral. e Twisted tetrahedral. See polytope configuration symbols section for details.
T-4	T d	2	4	8	Points	e
SP-4	D 4h	3	4	12	Points	b 2u, b2g
SL-4^a	D ∞h	3	2	6	Points	?
GYP-4^b	D 2h	6	4	24	Line segments	a u , ag
TCT-4^c	D 2d	6	4	24	Line segments	b 1, a1
TET-4^d	D 2d	6	4	24	Line segments	b 1, a1
TT-4^e	D 2	2	24	48	Areas	a

---

Polytope configuration symbols

When naming chemical entities, polyhedral symbols need only approximately describe coordination geometries. In contrast, our usage is stricter and is based upon the precise symmetry of the AB_n unit where all A–B bonds are identical.

We name AB₄ polytope genera^3,32 (the “general shape” without indices) using existing IUPAC nomenclatural “polyhedral symbols” as outlined in the “Red Book”³⁴ section IR-9.3.2.1, augmenting where necessary with additional forms devised in an analogous way.³⁵ Here, we introduce the TCT-4 “tetragonally compressed tetrahedral” and TET-4 “tetragonally elongated tetrahedral” polytope genera – each formed by compressing or elongating a T-4 polytope, respectively, along an S₄ axis. Both TCT-4 and TET-4 exhibit D_2d symmetry. The GYP-4 “gyfu planar” polytope genus (named for the Anglo-Saxon rune) has a rectangular X-shaped planar geometry of D_2h symmetry. The TT-4 “twisted tetrahedral” polytope genus exhibits D₂ symmetry and results from a digonal twist along an S₄ axis of the T-4, TCT-4, TET-4, SP-4, and GYP-4 genera. The SL-4 “symmetric fusion” genus in the AB₄T-4 E-mode configuration space has the two pairs of coincident B-atom unit vectors forming a symmetric linear arrangement and exhibits D_∞h symmetry. All are shown in Fig. 4. Note that there are numerous other possible 4-vertex polytope genera in the full 5-dimensional³² AB₄ configuration space, but these require a non-zero t₂-symmetric contribution and do not exhibit at least D₂ symmetry.

Fig. 4 Polytope genera of the AB₄T-4 E-mode configuration space.

To name polytope species (the shape with distinct indices assigned to all B-atoms), we similarly adapt the IUPAC nomenclatural “polyhedral configuration” and “polyhedral absolute configuration” symbols as outlined in the “Red Book”³⁴ sections IR.9.3.3 and IR.9.3.4, respectively.

For the AB₄T-4 E-mode configuration space, we name the seven distinct polytope species using the following conventions based upon assigning distinct indices 1 to 4 to the four B-atoms and using these as priorities following Cahn–Ingold–Prelog priority rules:

T-4-X	with X = R or S as given in the IUPAC “Red Book”^34 section IR-9.3.4.2
SP-4-i	where vertex B^i is trans to B^1 (“Red Book”^34 section IR-9.3.3.3); i ∈ {2, 3, 4}
TCT-4-i-X	where bond angle B^1–A–B^i is bisected by the S4 axis (the short C2 axis), and X = R or S as for T-4 species; i ∈ {2, 3, 4}
TET-4-i-X	where bond angle B^1–A–B^i is bisected by the S4 axis (the long C2 axis), and X = R or S as for T-4 species; i ∈ {2, 3, 4}
GYP-4-i-j	where B^i is trans to B^1, B^j is closest adjacent vertex to B^1; i and j ∈ {2, 3, 4}
TT-4-X	where X = R or S as for T-4 species
SL-4-i	where B^1 and B^i are “co-spatial” as are the remaining two B-atoms with an overall linear geometry; i ∈ {2, 3, 4}

Examples of the implementation of these nomenclatural rules are given in the ESI.† We reiterate: these additional polytope configuration symbols are currently not intended for chemical nomenclature.

Composition of the configuration space

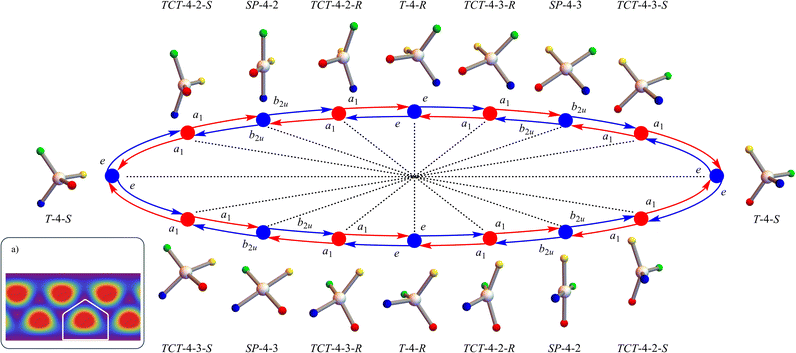
A notable, and indeed surprising, feature of the configuration space are the multiple orientation permutations of the component polytopes (see Table 1). Fig. 5 shows four orientation permutations of each of the two tetrahedral T-4 species, four orientation permutations of each of the three square planar SP-4 species, and the two orientation permutations of each of the three symmetric linear SL-4 “fusion” species, along with their (ϕ, θ) configuration space coordinates. A key consequence is that, within this frame of reference, not only does any E-mode symmetric stereotropic process involve permutation stereoisomer pseudorotations (e.g., T-4-R ⇌ T-4-S), but also orientation permutations (e.g., the four different relative orientations of T-4-R). Such orientation permutations may be experimentally observable, especially if the B-atoms are distinguishable though this is not strictly required.

Fig. 5 Locations (ϕ, θ) and orientation permutations of (a) tetrahedral T-4, (b) square planar SP-4, and (c) symmetric linear SL-4 “fusion” species in the AB₄T-4 E-mode configuration space. Locations are shown on the equirectangular projection of the configuration space (upper panels). For the depictions of the species, offset axes are shown for orientation purposes only. Colours differentiate B-atoms and do not denote specific elements.

An analogous situation exists for each of the other polytopes comprising the configuration space. The TT-4 “twisted tetrahedral” case is particularly striking. As with tetrahedral T-4, the twisted tetrahedral TT-4 genus has only two polytope species (TT-4-R and TT-4-S) but there are 24 different orientation permutations of each.

There are 9 great circles of high generic symmetry in the AB₄T-4 E-mode configuration space (red lines in Fig. 3) which can be divided into two sets: 6 that pass-through tetrahedral T-4 configurations and 3 that do not. The remaining 3 high-symmetry great circles only include planar and linear configurations (square planar SP-4, gyfu planar GYP-4, and symmetric linear SL-4) and are characterised as featuring two orientation permutations of two different symmetric linear SL-4 species along with four orientation permutations of SP-4 and gyfu planar GYP-4 configurations. Details are given in the ESI, Fig. S2 and S3,† and in the later Discussion.

Configuration space discretisation – generating finite graph representation a continuum space

The discretisation method³² we introduced is implemented to partition the configuration space into regions of contiguous generic symmetry. A worked example using a triangular segment of the configuration space from Fig. 3b is shown in Fig. 6a. This 2-dimensional curved configuration space is composed of the central 2-dimensional region (green-coloured) corresponding to polytopes of D₂ generic symmetry, bounded by the 1-dimensional line segment regions (red coloured) of D_2h and D_2d generic symmetries as indicated. These line segments are in turn bounded by the zero-dimensional points (blue coloured) of T_d, D_4h, and D_∞h generic symmetries as indicated. These zero-dimensional points also complete the full boundary of the 2D triangular region at its vertices (corners).

Fig. 6 Discretisation method for transforming the symmetry-structured continuum of configurations into finite graphs based upon distinct contiguous generic symmetries. (a) A triangular segment of the T-4 E-mode configuration space, from Fig. 3b, bounded by regions of different contiguous symmetry. (b) Detail of the finite directed graph representation of the configuration space region in (a) with specific configuration labels. Directed graph edges have generic symmetry labels. While the graph is an abstract mathematical object, to represent it in a neat pictorial form as shown here, the centroids of each region are used as the locations of each graph vertex. (c) Undirected simple graph version of (b). Graph vertices labelled by polytope genus.

It is worth noting that, in the configuration space, the configurations at these zero-dimensional regions (points) exhibit the highest generic symmetry group orders (T_d: group order 24; D_4h: group order 12, D_∞h: group order ∞), configurations at the 1-dimensional regions (line segments) exhibit lower generic symmetry group orders (D_2h: group order 8; D_2d: group order 8), and configurations in the 2-dimensional region still lower generic symmetry group order (the lowest for the configuration space D₂: group order 4).

In Fig. 6b is the directed graph representation corresponding to Fig. 6a. Graph vertices are conveniently placed at the centroids of their contiguous generic symmetry region to give a neatly laid out depiction of what is an abstract mathematical object. Directed graph out-edges are colour coded by their origin polytopes to emphasise the details. The directed graph edges are labelled by the generic symmetries of the polytope's transforming vibrations (see Table 1).

As the symmetric linear SL-4 “fusion” species are valid B-atom unit vector configurations, the topological manifold that is the configuration space is continuous and differentiable at these points. Consequently, the graph of the configuration space explicitly includes the symmetric linear SL-4 species. A corollary of this is that in terms of group theory, the character table of the D_∞h generic symmetry symmetric linear SL-4 “fusion” polytopes should include “exotic modes” with symmetries corresponding to “fission” processes. The mathematics of this awaits development.

For the AB₄T-4 E-mode configuration space, the discretisation method shown in Fig. 6 is applied to all 48 disdyakis dodecahedral “faces”. Utilising the approach in Fig. 6c, the corresponding undirected simple graph (undirected graph edges only, no multiple edges, no self-loops) is shown in Fig. 3c using the same colour code and at an oblique angle. Fig. S1 in the ESI† shows this representation of this graph oriented to illustrate the graph symmetries. Tables 2 and 3 gives a summary of the undirected graph properties.

Table 2 Discretised AB₄T-4 E-mode configuration space undirected simple graph global properties

Property	Value
Graph diameter	8
Graph radius	8
Vertex count	146
Edge count	432
Automorphism group order	48
Planar	Yes
Eulerian	Yes

---

Table 3 Discretised AB₄T-4 E-mode configuration space undirected simple graph vertex properties

Polytope genus	Region dimension	Vertex degree^a
a Total undirected graph edges at a graph vertex.
SL-4	0	16
T-4	0	12
SP-4	0	8
TCT-4	1	4
TET-4	1	4
GYP-4	1	4
TT-4	2	6

---

Example applications to chemical systems

Using our method for generating the configurations, qualitative PESs were generated for three chemical systems: the two simple tetrafluorides 1 and 2, and the chiral silane 3a-R. The tetrafluorides represent the two paradigmatic geometries of the AB₄T-4 E-mode configuration space: tetrahedral (1) and square planar (2), and the chiral silane illustrates the many details that emerge with more general chemical implementations of the analysis.

SiF₄ and XeF₄

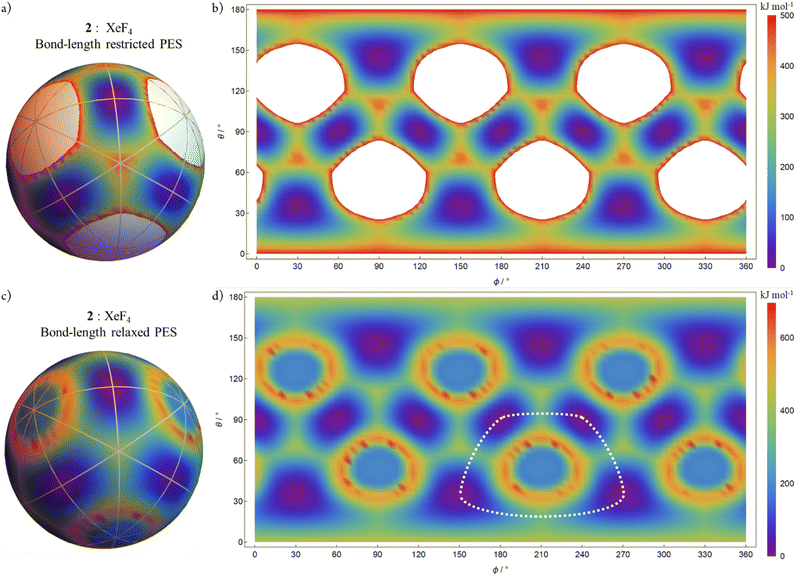
Fig. 7 shows the AB₄T-4 E-mode bond-length restricted and bond-length relaxed PESs for SiF₄, 1. The two-dimensional equirectangular projection of the bond-length relaxed PES, shown in Fig. 7d, is annotated with the locations of the tetrahedral T-4, square planar SP-4, and symmetric linear SL-4 polytope species. There are eight tetrahedral T-4 local minima structures corresponding to the eight potential-energy wells (purple), each one representing a pseudorotation (both permutation isomers and orientation permutations) of the others. Note that in Fig. 7d, there are relatively low energy pathways connecting all tetrahedral T-4 species. For example, encircling a symmetric linear SL-4-2 configuration there is the cyclic stereotropic sequence: (T-4-R ⇌ SP-4-4 ⇌ T-4-S ⇌ SP-4-3 ⇌ T-4-R ⇌ SP-4-4 ⇌ T-4-S ⇌ SP-4-3 ⇌ …).

Fig. 7 AB₄T-4 E-mode qualitative potential energy surfaces (PESs) for SiF₄. (a) Bond-length restricted PES (Si–F fixed at the local-minimum geometry length) corresponding to the spherical configuration space with an energy cutoff of 500 kJ mol⁻¹. (b) An “equirectangular projection” of the spherical PES from (a). (c) Bond-length relaxed PES for SiF₄ corresponding to the spherical configuration space. (d) An “equirectangular projection” of the spherical PES from (c). The map is annotated with the positions of the eight tetrahedral T-4, twelve square planar SP-4, and six symmetric linear SL-4 species. These eight tetrahedral T-4 configurations correspond to the local minimum wells (purple). The white dashed lines indicate a cycle of polytopal rearrangement trajectories through the configuration space that avoid the high energy regions centred on a symmetric linear SL-4-4 species (the portion of the line at θ = 0° is a singular configuration). The 9 great circles of the disdyakis dodecahedron are shown for (a) and (c).

Allowing for bond-length relaxation, trajectories approaching to the six “fusion” configurations results in the system dissociating to give “F₂ + Si + F₂” with a linear arrangement at infinite separations and with the F₂ fragments at right angles to the dissociation trajectory (see Discussion). The relative orientations between the two F₂ fragments is dependent upon which direction in the adjacent configuration space the symmetric linear SL-4 configuration is approached. Consequently, the SL-4 configurations are not uniquely defined for chemical embodiments. The PES is monotonically increasing for all direct approaches towards these symmetric linear SL-4 configurations.

Fig. 8 shows the AB₄T-4 E-mode bond-length restricted and bond-length relaxed PESs for XeF₄, 2. For each, there are 12 square planar SP-4 local minima structures corresponding to the 12 potential energy wells (purple), each one representing a pseudorotation permutation isomers and orientation permutations of the others.

Fig. 8 AB₄T-4 E-mode qualitative potential energy surfaces (PESs) for XeF₄. (a) Bond-length restricted PES (Xe–F fixed at the local-minimum geometry length) corresponding to the spherical configuration space with an energy cutoff of 500 kJ mol⁻¹. (b) An “equirectangular projection” of the spherical PES from (a). (c) Bond-length relaxed PES for XeF₄ corresponding to the spherical configuration space. (d) An “equirectangular projection” of the spherical PES from (c). There are 12 local minimum wells (purple) corresponding to square planar SP-4 geometries. The white dashed lines indicate polytopal rearrangement trajectories through the configuration space that avoid the high energy regions centred on the symmetric linear SL-4 species. For (a) and (c), the 9 great circles of the disdyakis dodecahedron are shown.

For the bond-length relaxed PES, at the six “fusion” configurations, the system dissociates as “F₂ + Xe + F₂” in an analogous manner to SiF₄. All direct approaches to the “fusion” configurations display a more complex behaviour than is the case for SiF₄ with symmetrical rings of maximal energies present at approximately 20° distant from the symmetric linear SL-4 configurations. This behaviour reflects the redox nature of the Xe–F₂ system.

For these two tetrafluorides, 1 and 2, the equivalence of the B-atoms results in the symmetry properties of the PESs recapitulating the symmetries of the configurations space. This is, however, not a general property of analogous PESs constructed from arbitrary combinations of vibrational normal modes. It occurs here as all chemical entities with configurations comprising this AB₄T-4 E-mode configuration space exhibit at least global molecular D₂ symmetry (i.e., all possible B-atom pairs and bond lengths are symmetric).

A chiral silane

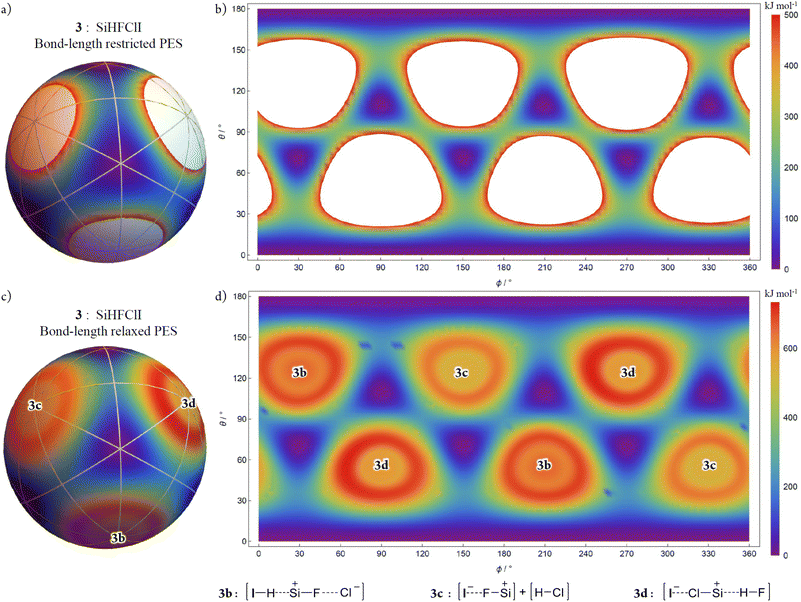
As a more general representative example, the chiral compound chloro(fluoro)iodosilane was examined using 3a-R (having an orientation as shown and corresponding to that in Fig. 9a) at a precisely tetrahedral T-4 configuration as the seed polytope. This system allows us to explore consequences of “non-idealised” geometries, distinct B-atoms, distinct A–Bⁱ bond lengths, and general issues concerning the molecular geometries near or at the “fusion” species.

Fig. 9 AB₄T-4 E-mode qualitative potential energy surfaces (PESs) for the chiral silane 3. (a) Bond-length restricted PES (all A–Bⁱ fixed at the local-minimum geometry lengths) corresponding to the spherical configuration space. (b) An “equirectangular projection” of the spherical PES from (a). (c) Bond-length relaxed PES of the chiral silane 3 corresponding to the spherical configuration space. (d) An “equirectangular projection” of the spherical PES from (c). Each map (c) and (d) is annotated by the location of the species 3b, 3c, and 3d. The 9 great circles of the disdyakis dodecahedron are shown for (a) and (c).

Fig. 9 shows the AB₄T-4 E-mode bond-length restricted, and bond-length relaxed, PESs for chloro(fluoro)iodosilane. Like the SiF₄ PESs, there are eight tetrahedral T-4 local minima structures corresponding to the eight potential energy wells (purple), each one representing a pseudorotation (permutation isomers and orientation permutations) of the others. With four distinct real B-atoms (H, F, Cl, and I), the pseudorotations of chloro(fluoro)iodosilane are more apparent. The potential energy local-minimum structures for chloro(fluoro)iodosilane are no longer of a precisely tetrahedral configuration (i.e., none of the six Bⁱ–A–B^j angles are precisely radians ≈ 109.47°) and their locations on the PES are displaced from these “idealised geometries”. Despite this and unsurprisingly, the PES still closely resembles that for 1, this being in keeping with early empirical findings and discussions concerning the applicability of idealised polytopal forms for real chemical systems.^16,35–39

The differing sizes of these real B-atoms (H, F, Cl, and I) of chloro(fluoro)iodosilane, in addition to the electronic effects they impose, lead to differing curvatures of the PESs' regions where close Bⁱ–B^j steric interactions begin to dominate. In Fig. 9a and b, the omitted regions from the PES with energy values over 500 kJ mol⁻¹ form three pairs with distinct extents which contrasts to those in Fig. 7a and b where all six regions are of identical extent.

For the bond-length relaxed PES (Fig. 9c and d), the complement of dissociation processes that occur as configurations approach the symmetric linear SL-4 “fusion” points is idiosyncratic for this chemical system. Approaching the two symmetric linear SL-4-4 configurations, and at this level of calculation, the chloro(fluoro)iodosilane system evolves to 3b comprised of a single collinear [I–H⋯Si⁺–F⋯Cl⁻] unit. An analogous scenario occurs approaching symmetric linear SL-4-2 species where the system evolves to 3d comprising a single collinear [I⁻⋯Cl–Si⁺⋯H–F] unit. A different scenario occurs approaching the symmetric linear SL-4-3 species where the system evolves to 3c comprised of two collinear fragments [I⁻⋯F–Si⁺] + [H–Cl] at infinite distance.

Discussion

Polytopal rearrangement trajectories through the configuration space reveal orientation permutations

Traditional analyses of polytopal rearrangements have tended to focus on very small regions of their configuration spaces and ignored the orientations of the species involved despite the term pseudorotation suggesting a species' orientation in real space being important. Analyses like the one given in this work, equip us with a full map of the corresponding configuration space from which we can see all possible configurations. Consequently, it becomes both possible and instructive to take the results of the earlier analyses and extrapolate their trajectories through the full configuration space.

A relevant example to the work presented here is polytopal rearrangements arising from a pair of antisymmetric orthogonal bond-angle flexions of a tetrahedral T-4 configuration such as the ε² “flex” depicted in Fig. 2. A traditional analysis based upon this motion would typically only look at the interconverting T-4-S and T-4-R species, and the intermediate square planar SP-4 species. The extrapolation of this trajectory is given in Fig. 10 along with its annotated directed graph representation. In this particular case, the trajectory forms a great circle (largest circle on a sphere) in the configuration space. Depending upon which B-atom pairs that corresponds to, for example, a longitudinal slice through the ϕ = 90° (and equivalently ϕ = 270°) spherical configuration space. This trajectory includes two different orientations of symmetric linear SL-4-2 polytopes. Examination reveals that these symmetric linear SL-4-2 polytopes divide the cycle into two sets of polytopal rearrangements that are equivalent except for their orientations in real space. Given the high energies and bond dissociation associated with symmetric linear SL-4 polytopes, it is understandable that none of the earlier analyses explicitly considered processes that transformed the configurations towards and “through” these. Consequently, the cyclicity of the geometric transformations were not explicitly examined and hence the importance of the orientation permutations within a configuration space not appreciated.

Fig. 10 A discretised great circle polytopal rearrangement trajectory through the configuration space highlighting orientation permutation pseudorotations. Trajectory shown as white path in spherical space (inset a) and equirectangular projection (inset b). Polytopal rearrangements arise from a pair of antisymmetric orthogonal bond-angle flexions of T-4 configurations (Fig. 2; ε², “flex”). This cyclic trajectory is composed of pairs (grouped within dotted grey enclosures) of each polytope species, each an orientation permutation of the other. Directed graph vertex colours are the same as for Fig. 6. B-atoms are distinctly coloured for tracking purposes.

A Mathematica⁴⁰ app for exploring great circle trajectories of arbitrary orientation in the S² AB₄T-4 E-mode configuration space is provided in the ESI.†

The question arises: are these orientation permutations chemically meaningful? Looking at the PESs for the three examples of chemical implementations of the AB₄T-4 E-mode configuration space, it is clear that each shows a network of local minima separated by saddle points of modest energies. Despite the high energies and bond-breaking behaviour at and near the symmetric linear SL-4 polytopes, depending upon the chemical elements involved, orientation permutations between the low-energy configurations are feasible and hence chemically relevant.

In Fig. 7d and in Fig. 8d, the white dotted lines indicate a cyclic trajectory through the configuration space (not a great circle) connecting local minima but avoiding the symmetric linear SL-4-4 species.

Looking in detail at that shown in Fig. 7d, the associated structures of this polytopal rearrangement sequence are given in Fig. 11 along with their annotated directed graph representation. There are some superficial similarities to the cycle shown in Fig. 10. Both feature two orientation permutations each of T-4-R and T-4-S, and both feature square planar SP-4 polytopes. The latter, however, does not include the tetragonally elongated tetrahedral TET-4 or symmetric linear SL-4 polytope species associated with the higher energies. Additionally, the positional relationships of the orientation permutations within the cyclic sequences shown in Fig. 10 and 11 are different.

Fig. 11 Discretised polytopal rearrangement trajectory through the configuration space corresponding to white dotted path in Fig. 7d and again in inset (a). Directed graph vertex colours are the same as for Fig. 6. Dotted lines join orientation permutations. B-atoms are distinctly coloured for tracking purposes.

Fig. 12 shows the polytopal rearrangement sequence for the trajectory depicted in Fig. 8d. As with the cyclic trajectory given in Fig. 11, this cyclic sequence is also centred on the symmetric linear SL-4-4 species. It does not include any tetrahedral T-4 species but does include four orientation permutations of two lower symmetry twisted tetrahedral TT-4 species. The positional relationships of the orientation permutations within the cyclic sequence are the same as for Fig. 11 (all pairs diametrically opposite).

Fig. 12 Discretised polytopal rearrangement trajectory through the configuration space corresponding to white dotted path in Fig. 8d and again in inset (a). Directed graph vertex colours are the same as for Fig. 6. Dotted lines join orientation permutations. B-atoms are distinctly coloured for tracking purposes.

General scope of chemical manifestation of SL-4 “fusion” polytopes

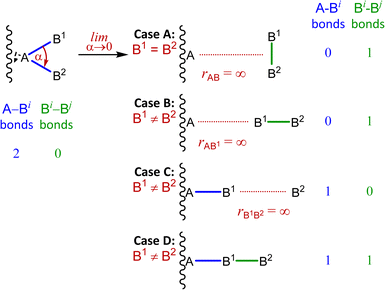
Despite their “stereoisomerically problematic” nature, the symmetric linear SL-4 “fusion” polytopes warrant a physical interpretation. In broadest terms, there are two extreme possibilities: either the real B-atoms literally fuse, or elongation of one or more A–Bⁱ bonds lead to a change in atom connectivity. In either case, these represent a departure from a stereotropic process – nuclear fusion in the former case, or formation of a different constitutional isomer in the latter.

Our worked example of the chiral silane demonstrated that changes in atom connectivity are idiosyncratic for the atoms involved. In general, there are four possible cases with these shown in Fig. 13. If both “fusing” B-atoms are chemically identical, a B₂ unit will dissociate orthogonally at infinite distance (Fig. 13, case A). When the “fusing” B-atoms are distinct, a B₂ unit can either dissociate collinearly at infinite distance (Fig. 13, case B), one B-atom may remain bonded to the A-atom while the other dissociates to infinite distance (Fig. 13, case C), or one B-atom may remain bonded to the A-atom while a B–B bond forms and a sequentially bonded linear A–B–B geometry results (Fig. 13, case D).

Fig. 13 Chemical manifestations of SL-4 polytopes. As bond angle α tends to zero, A–Bⁱ bond lengths increase leading to changes in atom connectivity (constitutional changes). Case A has B¹ = B² and a B₂ unit dissociating orthogonally at infinite distance. With B¹ ≠ B², a B₂ unit can dissociate collinearly to infinite distance (case B), one of the B-atoms remains bound while the other dissociates to infinite distance (case C) or form a bound collinear grouping (case D).

Some experimental opportunities revealed

Is the additional complexity inherent in these configuration spaces physically meaningful or, indeed, observable? An initial consideration towards answering this concerns energy scales. For the chemical examples given here, the potential energies associated with much of the configuration space are extraordinarily high. As such, these regions are essentially inaccessible for compounds at thermal equilibrium. What remains, however, is a connected network of potential energy wells separated by more modest barriers. This is expected to be a general feature of most polytopal rearrangement configuration spaces for AB_n systems. While for AB₄ the barriers are somewhat high for most combinations of elements, for AB₅ the closely analogous configuration space (the 4-dimensional AB₅TBPY-5 (E′×E′)-mode³²) contains pathways corresponding to the Berry pseudorotation mechanism (Fig. 1b) that is renowned for exhibiting extraordinarily low barriers between the potential energy wells.³ Consequently, consideration of comprehensively generated configuration spaces must be examined and the limited focus on energetically isolated subregions only employed when specific chemical implementations or a narrow focus warrant it.

There are other instances where the energy considerations become more nuanced. For example, if the chemical system has a vibrational mode selectively excited then the assumption of a thermal equilibrium no longer holds. Spectroscopists have looked for evidence of Berry pseudorotation manifesting in the rovibrational spectrum of compounds like PF₅.⁴¹ The Berry pseudorotation process leads to a significant change in the molecular moments of inertia, consequently and dependent upon the population of interconverting species, there could be a splitting of the rovibrational absorption bands, but evidence was not seen even in a system like PF₅ where the barrier is low (∼15 kJ mol⁻¹).⁴¹ Given the femtosecond time scale of the spectroscopic measurement, we suggest that the experiments performed while selectively exciting the Berry pseudorotation vibrational mode (e.g., under laser irradiation) would reveal the effect.

From a statistical thermodynamics perspective, we can also posit that, where barriers to polytopal rearrangements are low, the additional species comprising the configuration spaces suggests that, in principle, at high temperatures these would manifest in a system's entropy.

Another broad scenario where the full extent of pseudorotations could become apparent concerns molecular confinement. Molecular confinement describes an extremely diverse set of situations as wide ranging as the industrially important zeolite catalysts to the reaction sites of enzymes. A common feature in all cases is that the orientation of a guest molecule within the host has a frame of reference where molecular rotation is suppressed either partially or completely. Consequently, an orientation permutation via a polytopal rearrangement (pseudorotation) may manifest chemically. An analogous volume-conserving, concerted stereoisomerisation phenomenon precedent exists and is well studied, that of the torsion-based Hula-twist mechanism.⁴²

On the theme of a “frame of reference”, a strong external electric field can also provide this. For the low coordination numbers, molecules featuring the two-coordinate bent (A-2) and three-coordinate trigonal pyramidal (TPY-3) polytope configurations will, in general, have an electric dipole associated with them. Such molecular dipoles will respond to a strong external electric field. The maser – the forerunner to the now ubiquitous laser – was first realised in 1955 with the ammonia maser⁴³ and exploited a polytopal rearrangement within an external electric field polarised molecular beam.⁴³ Our transoid B(F)OB(F)-porphyrin systems also exhibited a significant dipole reversal upon thermally driven akamptisomerisation.¹ Additionally, experimental evidence of bond-angle reflection has been presented⁴⁴ for thermal effects on dipole moments and associated optical–configuration parameters in poly(dimethyl-siloxane).

More exotic scenarios are also possible. For example, a molecular system lacking an electric dipole but having a significant electric quadrupole will respond to a large electric field gradient. Intense electric field gradients are commonly encountered with highly focused or ultrashort pulsed lasers.

Looking at our analysis from a more theoretical standpoint we can make some general comments. For a particular chemical embodiment of a coordination centre AB_n, every configuration will have an energy associated with it. Consequently, for a given chemical embodiment there is a one-to-one relationship between a configuration space and its PES. Since our method³² completely defines AB_n configuration spaces and subspaces, and compactly encodes these as finite graphs, it can form the basis for compactly representing the corresponding PES.

General features of the Polytope Formalism: complete and rigorous framing of isomerisms

In this paper, the description of the AB₄T-4 E-mode configuration space provided a worked example of the Polytope Formalism: a higher-level conceptual and organisational framework for systematically describing isomerism and molecular structure in general.

The key parts of the Polytope Formalism are presented in Fig. 14 along with specific details for two aspects of stereoisomerism. In general form, the features of the Polytope Formalism are:

Fig. 14 Main features of the Polytope Formalism with specific details relating to two aspects of stereoisomerism: geometries of coordination centres AB_n and proper bond torsions.

• Generation of complete sets of isomeric configurations.

• Includes the relationships between the configurations.

• In combination, these are the “configuration spaces”.

• The configuration spaces are highly structured, and a taxonomic system has been developed for their description.

• In the cases of continuum configuration spaces, they can be discretised allowing for a discrete (finite) representation.

• Discrete configuration spaces can be represented as graphs which encode all their relevant properties.

• Nomenclatural systems for individual configurations double as elements of systematic chemical nomenclature.

• Precise terminology is useful for unambiguous and concise descriptions.

The Polytope Formalism provides four highly significant benefits:

• The formalism provides a common and hence unifying framework for the many disparate aspects of isomerism.

• The systematic and comprehensive nature of the outputs mathematically guarantee that nothing is missing.

• The structure of the configuration spaces map onto PESs (they are isomorphic) and hence describe the corresponding elementary mechanisms.

• The configuration spaces are “maps of”, or “guides to” the different aspects of chemical space; the outputs of the formalism both define and describe chemical space in a rigorous and meaningful way.

The approach presented here can generate the complete angular configuration space for arbitrary AB_n. For AB₄, the remaining angular displacements correspond to the triply degenerate T-4 T₂-mode. These give the 3-dimensional “AB₄T-4 T₂-mode” configuration space. The mathematically complete polytopal rearrangement configuration space for AB₄ is thus the Cartesian product of these spaces, i.e., the AB₄T-4 (E×T₂)-mode space – a 5-dimensional topological manifold.

The mathematical completeness of this approach guarantees all AB_n stereoisomeric variations are definable. But what about other aspects of isomerism?

An approach for the description of proper bond torsions can be constructed upon similar principles with this challenge being significantly simpler. Proper bond torsions, defined by a single angle, span the 1-sphere (a circle or S¹) and can be discretised as appropriate to a regular n-polygon. For a molecular entity featuring m proper bond torsions, the torsional configuration space is the product space (S¹)^m. Classical conformational analyses search such product spaces. This work will be elaborated elsewhere.

The treatment for these two aspects of stereoisomerism – AB_n geometries and proper bond torsions – are shown side-by-side in Fig. 14, emphasising their commonalities. This common framework for the description of different aspects of stereoisomerism we call the Polytope Formalism.

We have also applied the mathematical and conceptual framework of the Polytope Formalism to the problem of constitutional isomerism which we show in the companion paper.⁴⁵ In that treatment, the polytopes are abstract and the configuration spaces are discrete.

Conclusions

In this work we implemented a mathematically rigorous and general method for describing polytopal rearrangements to generate the complete AB₄T-4 E-mode configuration space. A discretisation theorem based on contiguous generic symmetry was also implemented to transform the continuum space into discrete form and representation as a finite graph.

The AB₄T-4 E-mode configuration space was shown to be spherical (the S² topological manifold) and exhibit the symmetry properties of a disdyakis dodecahedron. Examination of the configuration space revealed that each polytope species (configuration) appears multiple times but with different orientations (orientation permutations). These orientation permutations are identified as pseudorotations that stand in addition to the “permutation isomer” pseudorotations described by traditional analyses. Further, this AB₄T-4 E-mode example demonstrates that pathways connect all pseudorotated species without necessarily passing through, or near, the stereotropically-problematic (or in the extreme case, unphysical) “fusion” polytopes.

Chemical embodiments (SiF₄, XeF₄, and a chiral silane) of the configuration spaces were examined and the corresponding PESs generated. The chiral silane demonstrated general features for the configuration space.

We anticipate that the framework of the Polytope Formalism can be successfully applied to all aspects of isomerism including nuclear and electronic spin isomerisms. Such a common approach will lead to a unified picture of isomerism and a comprehensive “mapping” of chemical space.

Data availability

The data supporting this article have been included as part of the ESI:† two interactive Mathematica files and a document giving the analytic expressions, named polytope species, great circle trajectories, and the Gaussian16 script.

Author contributions

Both authors made substantive contributions to the work reported herein and to preparation of the manuscript. All computing and the development of the interactive software and numerous resource files was carried out by PJC.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by a Research Training Program Stipend (SC1999) to PJC, and the Australian Research Council grants DP0666378 and DP0773847 to MJC. Many thanks to R. and V. Canfield for ongoing support. Computational resources from the National Computational Infrastructure Australia (NCMAS d63) is acknowledged.

Notes and references

1. P. J. Canfield, I. M. Blake, Z.-L. Cai, I. J. Luck, E. Krausz, R. Kobayashi, J. R. Reimers and M. J. Crossley, Nat. Chem., 2018, 10, 615–624.
2. P. J. Canfield, PhD thesis, The University of Sydney, 2022.
3. P. J. Canfield, J. R. Reimers and M. J. Crossley, ACS Org. Inorg. Au, 2024, 4, 356–372.
4. E. L. Muetterties, J. Am. Chem. Soc., 1969, 91, 4115–4122.
5. E. L. Muetterties, J. Am. Chem. Soc., 1969, 91, 1636–1643.
6. E. L. Muetterties and A. T. Storr, J. Am. Chem. Soc., 1969, 91, 3098–3099.
7. P. Meakin, L. J. Guggenberger, J. P. Jesson, D. H. Gerlach, F. N. Tebbe, W. G. Peet and E. L. Muetterties, J. Am. Chem. Soc., 1970, 92, 3482–3484.
8. E. L. Muetterties, Acc. Chem. Res., 1970, 3, 266–273.
9. F. N. Tebbe, P. Meakin, J. P. Jesson and E. L. Muetterties, J. Am. Chem. Soc., 1970, 92, 1068–1070.
10. J. P. Jesson, P. Meakin, E. L. Muetterties and F. N. Tebbe, J. Am. Chem. Soc., 1971, 93, 4701–4709.
11. D. H. Gerlach, W. G. Peet and E. L. Muetterties, J. Am. Chem. Soc., 1972, 94, 4545–4549.
12. P. Meakin, E. L. Muetterties and J. P. Jesson, J. Am. Chem. Soc., 1972, 94, 5271–5285.
13. P. Meakin, E. L. Muetterties and J. P. Jesson, J. Am. Chem. Soc., 1973, 95, 75–88.
14. E. L. Muetterties, R. J. Wiersema and M. F. Hawthorne, J. Am. Chem. Soc., 1973, 95, 7520–7522.
15. E. L. Muetterties, Tetrahedron, 1974, 30, 1595–1604.
16. E. L. Muetterties and L. J. Guggenberger, J. Am. Chem. Soc., 1974, 96, 1748–1756.
17. L. J. Guggenberger and E. L. Muetterties, J. Am. Chem. Soc., 1976, 98, 7221–7225.
18. R. Hoffmann, B. F. Beier, E. L. Muetterties and A. R. Rossi, Inorg. Chem., 1977, 16, 511–522.
19. K. Mislow, Acc. Chem. Res., 1970, 3, 321–331.
20. J. A. le Bel, C. R. Hebd. Seances Acad. Sci., 1890, 110, 144–147.
21. R. S. Berry, J. Chem. Phys., 1960, 32, 933–938.
22. H. S. Gutowsky, D. W. McCall and C. P. Slichter, J. Chem. Phys., 1953, 21, 279–292.
23. F. A. Cotton, A. Danti, J. S. Waugh and R. W. Fessenden, J. Chem. Phys., 1958, 29, 1427–1428.
24. E. L. Muetterties and W. D. Phillips, J. Am. Chem. Soc., 1957, 79, 322–326.
25. E. L. Muetterties and W. D. Phillips, J. Am. Chem. Soc., 1959, 81, 1084–1088.
26. E. P. A. Couzijn, J. C. Slootweg, A. W. Ehlers and K. Lammertsma, J. Am. Chem. Soc., 2010, 132, 18127–18140.
27. W. Zou, Y. Tao and E. Kraka, J. Chem. Theory Comput., 2020, 16, 3162–3193.
28. L. C. Hoskins and R. C. Lord, J. Chem. Phys., 1967, 46, 2402–2412.
29. R. R. Holmes and S. R. M. Deiters, J. Am. Chem. Soc., 1968, 90, 5021–5023.
30. F. Bouakline, Phys. Chem. Chem. Phys., 2021, 23, 20509–20523.
31. A. Caligiana, V. Aquilanti, R. Burcl, N. C. Handy and D. P. Tew, Chem. Phys. Lett., 2003, 369, 335–344.
32. P. J. Canfield, M. J. Crossley, J. Spreer and S. Tillmann, ChemRxiv, 2025 DOI:10.26434/chemrxiv-2025-gc7s6.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
34. N. G. Connelly, T. Damhus, R. Hartshorn and A. T. Hutton, IUPAC Red Book, RSC Publishing, London, 2005.
35. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708.
36. S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, New J. Chem., 2002, 26, 996–1009.
37. D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763.
38. J. Cirera, P. Alemany and S. Alvarez, Chem.–Eur. J., 2004, 10, 190–207.
39. R. Asatryan, E. Ruckenstein and J. Hachmann, Chem. Sci., 2017, 8, 5512–5525.
40. I. Wolfram Research, Mathematica v14.1.0.0, Wolfram Research, Inc., Champaign, Illinois, 2024.
41. C. Styger and A. Bauder, J. Mol. Spectrosc., 1991, 148, 479–493.
42. R. S. H. Liu and G. S. Hammond, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 11153–11158.
43. J. P. Gordon, H. J. Zeiger and C. H. Townes, Phys. Rev., 1955, 99, 1264–1274.
44. L. C. Debolt and J. E. Mark, J. Polym. Sci., Part B: Polym. Phys., 1988, 26, 989–995.
45. P. J. Canfield and M. J. Crossley, ChemRxiv, 2025 DOI:10.26434/chemrxiv-2025-bts3z.

---

Footnote

† Electronic supplementary information (ESI) available: Further details (analytic expressions for AB_n configurations, polytope configuration symbol details, additional great circle trajectories, and the Gaussian¹⁶ script), interactive Mathematica tools for exploring the configuration space. See DOI: https://doi.org/10.1039/d4sc08628g

---