 Open Access Article
Open Access ArticleTRAP: a contrastive learning-enhanced framework for robust TCR–pMHC binding prediction with improved generalizability†
Jingxuan
Ge
 ab,
Jike
Wang
ab,
Qing
Ye
a,
Liqiang
Pan
a,
Yu
Kang
ab,
Jike
Wang
ab,
Qing
Ye
a,
Liqiang
Pan
a,
Yu
Kang
 a,
Chao
Shen
a,
Chao
Shen
 a,
Yafeng
Deng
b,
Chang-Yu
Hsieh
a,
Yafeng
Deng
b,
Chang-Yu
Hsieh
 *a and
Tingjun
Hou
*a and
Tingjun
Hou
 *a
*a
aCollege of Pharmaceutical Sciences, Zhejiang University, Hangzhou 310058, Zhejiang, China. E-mail: kimhsieh@zju.edu.cn; tingjunhou@zju.edu.cn
bCarbonSilicon AI Technology Company, Ltd, Hangzhou 310018, Zhejiang, China
First published on 29th April 2025
Abstract
The binding of T cell receptors (TCRs) to peptide-MHC I (pMHC) complexes is critical for triggering adaptive immune responses to potential health threats. Developing highly accurate machine learning (ML) models to predict TCR–pMHC binding could significantly accelerate immunotherapy advancements. However, existing ML models for TCR–pMHC binding prediction often underperform with unseen epitopes, severely limiting their applicability. We introduce TRAP, which leverages contrastive learning to enhance model performance by aligning structural and sequence features of pMHC with TCR sequences. TRAP outperforms previous state-of-the-art models in both random and unseen epitope scenarios, achieving an AUPR of 0.84 (a 22% improvement over the second-best model) and an AUC of 0.92 in the random scenario, and an AUC of 0.75 (almost 11% higher than the second-best model) in the unseen epitope scenario. Furthermore, TRAP demonstrates a noteworthy capability to diagnose potential issues of cross-reactivity between TCRs and similar epitopes. This highly robust performance makes it a suitable tool for large-scale predictions in real-world settings. A specific case study confirmed that TRAP can discover hit TCRs with binding free energies comparable to referenced experimental results. These findings highlight TRAP's potential for practical applications and its role as a powerful tool in developing TCR-based immunotherapies.
Introduction
T cells play a pivotal role in the adaptive immune system, particularly in combating viral infections and other internal threats, such as endogenous antigens.1,2 In this process, infected cells break down these antigens into peptide fragments, which are subsequently presented on the cell surface by major histocompatibility complex class I (MHC-I) molecules. The epitope, the distinctive peptide segment within the peptide-MHC (pMHC) complex, may trigger an immune response when it binds to T cell receptors (TCRs) located on the surface of CD8+ T cells, forming a TCR–pMHC complex, also known as the immune synapse. Inspired by the immunological responses triggered by TCR–pMHC, many immunotherapies have been developed in recent decades, aiming at engineering TCRs for enhanced tumor targeting.3 For instance, Kimmtrak4 was proposed as a TCR therapy by modifying TCRs to target tumor-specific antigens (TAAs). Hence, a comprehensive understanding of TCR–pMHC interaction is essential for further optimizing these immunotherapies.The specific interaction between TCRs and pMHC allows T cells to discriminate among a vast array of potential epitopes arising from pathogens or endogenous antigens. This specificity is attributed to the extensive diversity of TCRs, which is estimated to comprise a repertoire of 1015 unique specificities.5 However, the comprehensive exploration of the vast TCR sequence space is often impeded by reagent costs and labor requirements in experimental approaches. Recently, the advent of artificial intelligence (AI) in drug design has precipitated a surge of interest in immunotherapy, leading to the development of many models aimed at accelerating the exploration of the TCR space.
Accurate computational prediction of TCR binding to pMHC relies crucially on effectively capturing the features of the complementarity-determining regions (CDRs) within the TCR's αβ chains. Each chain contains three CDRs (i.e., CDR1, CDR2, and CDR3) that directly interact with the pMHC complex, with CDR3 playing a crucial role in epitope recognition.2,6,7 Until recently, most prediction models relied solely on the sequence information of the epitope and CDR3β, such as PanPep,8 TEIM-seq,9 and NetTCR-1.0,10 to infer TCR–pMHC binding. However, recent studies have highlighted the value of incorporating additional information beyond CDR3β to enhance model reliability. Indeed, newer models, such as pMTnet,11 TCRAI,12 NetTCR-2.0,13 epiTCR,14 and DeepAIR,15 have all attested to the importance of incorporating α chain, MHC I or gene information into the model inputs. Nevertheless, as models incorporate more specific TCR and pMHC information, the availability of relevant data proportionately decreases. For example, only about 4% of the TCR–pMHC binding data in existing databases explicitly specify both αβ chains.16 Therefore, balancing available data and information for input becomes a crucial consideration. While current models exhibit commendable performance, they are still plagued by significant limitations. First, most models are limited to exploiting sequence-level information. However, different MHC-Is presenting the same antigen-peptide may lead to different conformations, thereby influencing TCR–pMHC binding.17 Distinguishing subtle variations in binding strength attributed to epitope conformation solely based on sequence data remains challenging. While some studies have attempted to extract structural features from CDR3 loops using pre-trained AlphaFold 2 (AF2),18 prior research has revealed that AF2's predictive accuracy for CDR loop structures is hindered by the absence of evolutionary constraints on CDR sequence variability, potentially introducing noise into the predictions.19,20 Moreover, many models adopt a simple negative sampling strategy by uniformly sampling negative TCRs for each epitope, leading to dataset imbalances where the number of positive TCRs outweighs that of negative TCRs for certain epitopes and vice versa.21 Such imbalances predispose the model to learn shortcuts, basing its judgments on the distribution of TCRs for a given epitope rather than the actual TCR–pMHC binding. Although existing models perform well on certain evaluation metrics, they still fall short in addressing many critical challenges in real-world settings. For example, the performance of existing models often suffers a notable decline when epitopes are absent from the training set,8 which poses challenges in handling newly discovered epitopes in experiments. Furthermore, TCR cross-reactivity, where a single TCR may bind to multiple pMHCs, poses a risk of severe side effects.16 However, during the algorithmic development, scant attention has been paid to this crucial phenomenon. Given the importance of TCR-associated immunotherapies, such as T cell engagers, it is imperative to devise a screening pipeline tailored for the rational design of TAA arms. However, these critical aspects, relevant to how these models should be used in the development of novel immunotherapy, are underrepresented in the literature.
In this study, we proposed TRAP, a deep learning (DL)-based model for predicting TCR–pMHC binding. TRAP utilizes CDR3β and epitope sequence information, which is driven by data availability.8 Moreover, to overcome the limitations of existing models, TRAP incorporates several innovations. Firstly, TRAP enhances its feature space by incorporating structural information beyond sequences, focusing primarily on the pMHC structure due to the challenges in CDR structure predictions. Our main focus is on conformational changes near the epitope and their effect on binding. TRAP selectively utilizes pMHC fragments within a specified distance from the epitope to avoid excessive structural data. Secondly, TRAP uniquely employs contrastive learning, aiming to maximize the cosine similarity between the representations of CDR3β and pMHC for positive binding pairs, while minimizing it for unpaired instances. This approach aligns the features of pMHC and TCR (CDR3β), thereby enhancing TRAP's generalization capability when dealing with new epitopes. Thirdly, TRAP implements a negative sampling strategy to maintain a balance between positive and negative TCRs corresponding to the epitope. This strategy ensures that the model learns TCR–pMHC binding rather than the distribution of positive and negative TCRs, preventing inflated scores. Validation using a healthy human TCR repertoire corroborates the effectiveness of this approach in mitigating the risk of learning shortcuts.
Our results reveal that incorporating structural information and utilizing contrastive learning significantly enhance TRAP's performance. In the random-split scenario, TRAP demonstrated an AUPR of 0.84, exceeding the second-best model by 22.4%, and an AUC of 0.92. Notably, in the epitope-unseen scenario, TRAP achieved an AUPR of 0.35 and an AUC of 0.75, outperforming the second-best model by 10.8%. Validation using TCRs from healthy individuals shows that the implemented negative sampling strategy effectively reduces the false positive rate in model prediction. For instance, for the epitope YVLDHLIVV, TRAP's false positive rate drops from 43.2% to 13.2% when using the proposed method. Furthermore, our analysis revealed TRAP's ability to detect cross-reactive TCRs. The features extracted by TRAP provide valuable insights beyond sequence-level analysis, suggesting its potential as a powerful tool to mitigate side effects arising from cross-reactivity. Finally, our case studies demonstrate that TRAP can effectively screen hit TCRs with binding modes similar to those of crystal structures, highlighting its potential in TCR-related therapy development.
Results
Overview of TRAP
In this work, we proposed TRAP, a contrastive learning-enhanced DL framework for learning TCR–pMHC binding patterns with robust generalizability to unseen epitopes. The recognition of TCR and pMHC involves intricate residue interactions across multiple sites. TRAP utilized a sequence embedding module to process sequence-level features, as shown in Fig. 1A. In detail, the sequences of CDR3β and the epitope were fed into ESM2,22 a large language model pre-trained on extensive protein sequence data, to generate sequence-level embedding. In addition to sequence information, TRAP incorporated crucial structural information reflecting epitope conformations due to various MHCs. Initially, we predicted the 3D structures of the pMHC complexes with AlphaFold Multimer18,23,24 and then extracted relevant structural information to feed into the structural embedding module of TRAP (see the Methods). Particularly, we focused on the structural information within a specific cutoff distance from each epitope residue, rather than the entire pMHC structure, as shown in Fig. 1A. This approach minimizes the potential for extraneous noise from the entire MHC structure. Finally, the embeddings of CDR3βs and epitopes were passed to the encoder for feature encoding (Fig. 1B). For the encoder architecture, we employed a transformer-based multi-head self-attention layer to capture correlations between sequence contexts. Two separate encoders were trained for epitopes and CDR3β, sharing the same network architecture but differing in input feature dimensions.Another innovative aspect of TRAP lies in its utilization of contrastive learning among positive samples. Previous studies typically trained TCR–pMHC binding prediction models by creating negative samples through mismatched positive pairs.21 However, this approach completely overlooks cross-reactivity, which can be significant given the high similarity between many TCRs or epitopes in the dataset. To address this, TRAP employed contrastive learning among positive samples to maximize the utilization of positive data. As shown in the contrastive learning module in Fig. 1C, TRAP separates positive binding pairs into CDR3β and epitopes and then computes the cosine similarity between each CDR3β and epitope using the representations generated by the encoder to construct a similarity matrix. Classification training is applied to each row and column of the matrix, aiming to maximize the cosine similarity of positive sample pairs and align the representations of CDR3β with epitopes. Then, TRAP switched to binary training, adding negative binding pairs generated through a unified negative sample strategy,21 which mismatches binding pairs based on the frequency of pMHCs to generate negative samples (the details about the negative sample strategy can be seen in the Methods, and negative samples constructed this way give a more robust model as outlined in the section of Effective negative samples to circumvent learning shortcuts). In each training epoch, TRAP alternates between these two training modes.
Highly accurate and generalizable predictive power
In order to comprehensively evaluate TRAP's effectiveness, we set up two simulated application scenarios in which TRAP could offer valuable help in biological experiments: in scenario 1, we randomly divided the positive and negative samples into the training set and the test set in a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. It was supposed to simulate a common situation in which we predict the interactions of TCR–pMHC that are present in a database. In scenario 2, the training set comprised the pairs with epitopes that have more than 5 recorded positive binding CDR3βs in the dataset, and the test set included the remaining pairs with epitopes that have not been present in the training set, which means that there was no epitope appearing in both the training set and the test set. We analyzed the highest similarity between antigen peptides in the test and training sets. Most values ranged between 0 and 0.6, with an average of 0.341 (ESI Fig. 1†), indicating substantial differences between antigen peptides in the training and test sets. This zero-shot setting was designed to evaluate the generalization ability of various models. In this case, we compared TRAP with NetTCR-2.0,13 epiTCR14 (with epitope or pMHC information), and TEIM-seq.9 NetTCR-2.0 employs the BLOSUM50 matrix for the encoding of amino acids and utilizes a one-dimensional convolutional neural network (CNN) to produce satisfactory outcomes. epiTCR incorporates MHC-I information, and it exhibits robust performance in scenarios involving unseen epitopes. TEIM-seq effectively captures features at the sequence level, thereby contributing to the prediction of the residue interaction matrix at the structure level.
1 ratio. It was supposed to simulate a common situation in which we predict the interactions of TCR–pMHC that are present in a database. In scenario 2, the training set comprised the pairs with epitopes that have more than 5 recorded positive binding CDR3βs in the dataset, and the test set included the remaining pairs with epitopes that have not been present in the training set, which means that there was no epitope appearing in both the training set and the test set. We analyzed the highest similarity between antigen peptides in the test and training sets. Most values ranged between 0 and 0.6, with an average of 0.341 (ESI Fig. 1†), indicating substantial differences between antigen peptides in the training and test sets. This zero-shot setting was designed to evaluate the generalization ability of various models. In this case, we compared TRAP with NetTCR-2.0,13 epiTCR14 (with epitope or pMHC information), and TEIM-seq.9 NetTCR-2.0 employs the BLOSUM50 matrix for the encoding of amino acids and utilizes a one-dimensional convolutional neural network (CNN) to produce satisfactory outcomes. epiTCR incorporates MHC-I information, and it exhibits robust performance in scenarios involving unseen epitopes. TEIM-seq effectively captures features at the sequence level, thereby contributing to the prediction of the residue interaction matrix at the structure level.
Fig. 2 illustrates the metrics commonly used in binary classification models, AUC (area under the curve) and AUPR (area under the precision–recall curve), and TRAP outperformed in both scenarios among models. Specifically, TRAP achieved an AUC of 0.92 and an AUPR of 0.84 in scenario 1, outperforming the second-ranked model (epiTCR14 with pMHC information) by 22.4% in AUPR. In scenario 2, for the prediction of unseen epitope pairs, TRAP also achieved an AUC of 0.75 and an AUPR of 0.35, demonstrating commendable generalization capabilities and outperformed epiTCR by 10.8% and 18.1% in AUC with pMHC and epitope information, respectively. Detailed information about AUC and AUPR results can be found in ESI Tables 1 and 2.†
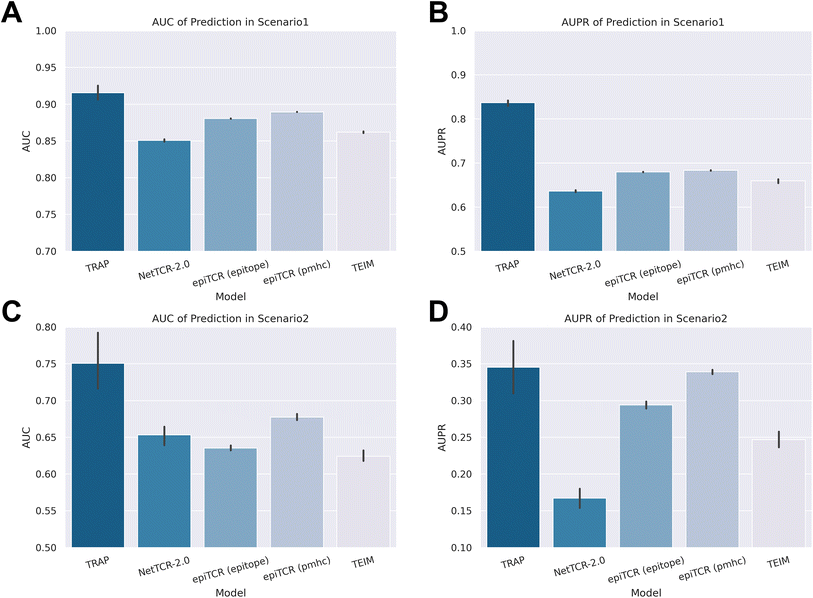 | ||
| Fig. 2 Results of classification task metrics from different models. (A) AUC and (B) AUPR in scenario 1, and (C) AUC and (D) AUPR in scenario 2. | ||
If the epitope had been identified and the prediction of the corresponding candidate CDR3βs had been considered, this scenario could be viewed as a recommender system problem for epitopes.21 To evaluate the TRAP's performance in this context, we applied the standard evaluation metrics used in recommender systems: precision@k and recall@k, which represent the ratio of correctly predicted related results (i.e., positive CDR3βs) among the top k results and the ratio of correctly predicted relevant results to all relevant results, respectively. Given that many epitopes in the dataset have a limited number of positive CDR3βs, we set k to 1 and 3 in scenario 1 and k to 1 in scenario 2. As shown in Tables 1 and 2, TRAP consistently outperforms all other models in terms of the recommendation system metrics. It is worth noting that the small value of k chosen here naturally results in a lower absolute value for recall@k.
| Model | Precision@1 | Recall@1 | Precision@3 | Recall@3 |
|---|---|---|---|---|
| TRAP | 0.7468 ± 0.4348 | 0.3290 ± 0.3982 | 0.5476 ± 0.3371 | 0.5214 ± 0.4031 |
| NetTCR-2.0 | 0.4031 ± 0.4905 | 0.1928 ± 0.3535 | 0.3337 ± 0.3006 | 0.3815 ± 0.4295 |
| epiTCR (epitope) | 0.6879 ± 0.4633 | 0.2920 ± 0.3855 | 0.4974 ± 0.3481 | 0.4854 ± 0.4149 |
| epiTCR (pMHC) | 0.6874 ± 0.4635 | 0.3035 ± 0.3925 | 0.5045 ± 0.3496 | 0.4890 ± 0.4133 |
| TEIM | 0.6441 ± 0.4788 | 0.2672 ± 0.3754 | 0.4640 ± 0.3438 | 0.4603 ± 0.4153 |
| Model | Precision@1 | Recall@1 |
|---|---|---|
| TRAP | 0.4716 ± 0.4992 | 0.3925 ± 0.4583 |
| NetTCR-2.0 | 0.2215 ± 0.4152 | 0.1807 ± 0.3665 |
| epiTCR (epitope) | 0.3443 ± 0.4751 | 0.2757 ± 0.4198 |
| epiTCR (pMHC) | 0.3928 ± 0.4884 | 0.3198 ± 0.4381 |
| TEIM | 0.3217 ± 0.4671 | 0.2555 ± 0.4087 |
The substantial variability observed in the recommender system's metrics highlighted the inconsistency in the model's performance across diverse epitopes. To investigate the model's sensitivity to different epitopes, we calculated the AUC and AUPR specifically at the epitope level (that is, we calculated the epitope–CDR3β pairs for each individual epitope). The results at the epitope level are shown in Fig. 3A–D, with detailed data available in ESI Tables 3 and 4.† In the epitope-level benchmarks, TRAP consistently emerged as the top-performing model, achieving an average AUC of 0.80 and an average AUPR of 0.64 in scenario 1. In scenario 2, where the predictive performance of most models significantly declined, TRAP still maintained an average AUC of 0.75 and an average AUPR of 0.48, outperforming the second-best model, epiTCR (pMHC information), by a margin of 24.1% in AUPR.
We were curious about the possibility of the existence of ‘hard epitopes’ within the dataset, which could potentially reduce all the models' ability to predict their corresponding pairs. To investigate this, we chose to compare the second-best model epiTCR (pMHC), with TRAP, to assess any disparities in their prediction performance across individual epitopes. Fig. 3E and F present the distributions of the AUC scores for both models in scenarios 1 and 2, respectively. Each red dot in the scatter plots represents an epitope, with the x-axis indicating TRAP's AUC score and the y-axis showing epiTCR's AUC score. It was evident from the figures that a significant proportion of epitopes were located in regions where the AUC of TRAP exceeded 0.5, while the AUC of epiTCR fell below 0.5 (the threshold for random guessing). Specifically, in scenarios 1 and 2, 10.22% and 23.00% of epitopes, respectively, were occupied in this region. Conversely, the regions with TRAP scores less than 0.5 and epiTCR scores higher than 0.5 accounted for only 3.64% and 3.62% in scenarios 1 and 2, respectively. The distribution patterns revealed that the number of epitopes with AUC scores less than 0.5 for both models is minimal. However, there are clear differences in the prediction performance of the two models for the same epitope. Notably, TRAP exhibited a higher success rate on a larger number of epitopes that epiTCR failed to predict accurately.
Comprehensively considering the results of all predictions as a unit or epitope-level AUC and AUPR scores, as well as the evaluation results based on the metrics of the recommender system, TRAP had demonstrated robust and remarkable prediction capabilities. Notably, in scenario 2, where the performance of other models significantly declined, TRAP maintained its strong performance, particularly in situations where epitopes were unseen. This suggested that TRAP holds great potential for application in the prediction of novel epitopes discovered in biological experiments or epitopes with limited binding CDR3β information.
Structure and sequence jointly informed decision making: better predictive power on cross-reactivity
Similar to small-molecule drugs, a TCR can bind to multiple pMHCs, a phenomenon known as cross-reactivity. In TCR-based immunotherapy, cross-reactivity may lead to reduced drug specificity, potentially posing safety concerns.16 Our dataset presented numerous instances of cross-reactivity, as depicted in Fig. 4A, where three types of pMHC (HLA-A*03:01 KLGGALQAK, HLA-A*11:01 AVFDRKSDAK and HLA-A*11:01 IVTDFSVIK) constituted the majority of cross-reactivity pairs. Next, we used these three pMHCs as representative examples to confirm TRAP's successful learning of cross-reactivity.Firstly, we compared the distributions of these three pMHCs across all pMHCs using different feature representations (BLOSUM62, input and output features of TRAP). In Fig. 4B and C, we employed Principal Component Analysis (PCA) to reduce the dimensionality of the feature spaces. It was observed that under the representation space of BLOSUM62 and the input of TRAP, the pMHCs appeared clustered together, making them indistinct. Fig. 4D illustrates the PCA result of the output of TRAP, demonstrating that different types of pMHCs were dispersed within the feature space, thereby reducing the difficulty in distinguishing them. Moreover, the three types of pMHCs that had cross-reactivity remained relatively close to each other. In Fig. 4E, we presented the reduced dimensionality using UMAP and clustering with the K-means algorithm, where the three kinds of pMHCs were located in similar regions, while dispersing into distinct clusters in the other two feature spaces (see ESI Fig. 2†). This suggested that TRAP did effectively capture the similarities among the three pMHCs across all the pMHCs. Furthermore, while certain pMHCs may be challenging to distinguish at the sequence level, they can be well discriminated through the features extracted by TRAP.
Next, we analyzed the binding pairs associated with HLA-A*11:01 AVFDRKSDAK (AVF) and HLA-A*11:01 IVTDFSVIK (IVT), as they were close in the pMHC feature space. To achieve this, we combined the representations of positive pMHCs and CDR3βs and scrutinized their distribution in the feature space. Fig. 4F–H depict binding pairs in different colors, where yellow represents pMHC–CDR3β pairs for cross-reactivity, while blue and pink represent AVF-exclusive and IVT-exclusive binding pairs, respectively. We found that in the feature space composed of BLOSUM62 and input of TRAP, the binding pairs appeared clustered in a manner that was challenging to differentiate. In the feature space of the output of TRAP, the binding pairs were dispersed and distinguishable, forming two different clusters based on pMHCs, while the pairs with cross-reactivity were away from the cluster centers, tending towards the other cluster. This highlights TRAP's ability to clearly distinguish binding pairs and capture the essence of cross-reactivity at the pair level.
Effective negative samples to circumvent learning shortcuts
TCR–pMHC binding data follow a long-tail distribution pattern,13,21 with approximately 70% of the TCR–pMHC pairs composed of only about 100 antigens.16 In this distribution, if the negative sample data are generated by randomly mismatching epitopes and their corresponding positive CDR3βs, the number of negative CDR3βs assigned to each epitope would be roughly equal. However, for epitopes with a high frequency of positive CDR3βs, the number of positive CDR3βs would significantly exceed the negatives. Conversely, for epitopes with a low frequency of positive CDR3βs, the negatives would greatly exceed the positives. This imbalance can lead the model to easily learn a shortcut, predicting positive results for high-frequency epitopes and vice versa for low-frequency epitopes. To avoid this imbalance, we adopted the unified negative sample strategy proposed by Jiang et al.,21 considering the frequency of pMHC in positive samples when mismatching negative samples, which ensures a similar positive-to-negative ratio for each individual pMHC.To assess the effectiveness of our negative sample strategy, we established a true negative dataset comprising CDR3βs sourced from the TCR pool of healthy donors, presuming that these CDR3βs lack binding capacity with any epitopes. We selected the top three pMHCs (i.e., HLA-A*03:01 KLGGALQAK, HLA-A*02:01 YVLDHLIVV, and HLA-A*02:01 GLCTLVAML) with the highest number of occurrences in binding pairs and paired them with CDR3βs in our true negative dataset. Ideally, all of these pairs should be predicted as negative bindings, enabling us to benchmark the success of our negative sample strategy based on the false positives obtained. To this end, we utilized TRAP and epiTCR, both trained on the scenario 1 training set, to test our true negative dataset. As shown in Fig. 5A and B, the models trained with random sampling data exhibited significantly higher false positive rates than those trained with unified sampling, with TRAP predicting a 43.2% false positive rate for HLA-A*02:01 YVLDHLIVV pairs, in contrast to a mere 13.2% with unified sampling (the detailed false positive rates are available in ESI Table 5†). This revealed the superiority of the unified strategy in addressing the TCR–pMHC binding problem. Moreover, TRAP demonstrated superior accuracy in predicting negative samples compared to epiTCR across all three pMHCs, further validating the outstanding performance of TRAP.
Ablation study
Next, we conducted an ablation study to assess the individual contributions of different modules to the prediction ability of TRAP. We set four tasks: removing structural information (no structure), excluding both structural information and sequence features generated by ESM2 (no structure & esm), removing the contrastive learning module (no contrastive), and removing the binary learning module (no binary). As demonstrated in Fig. 6, the performance of TRAP significantly declined in both the no structure & esm and no binary tasks. In the zero-shot setting of scenario 2, the AUPR of the no contrastive task also decreased markedly, highlighting the importance of these modules to TRAP's performance. Although the results of the no structure task indicated a limited contribution from structural information to predictions, further analysis revealed its continued importance.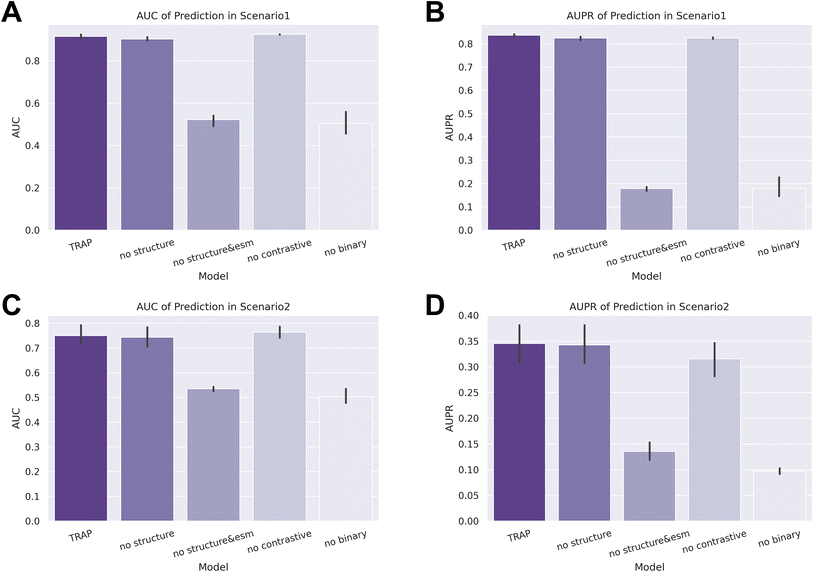 | ||
| Fig. 6 Results of classification task metrics from the ablation study. (A) and (B) AUC and AUPR in scenario 1, respectively, and (C) and (D) AUC and AUPR in scenario 2, respectively. | ||
Considering that the AUC and AUPR evaluate the prediction results of all samples collectively, while recommendation system metrics evaluate the unit of each epitope, the inclusion of more indicators will result in a more comprehensive assessment. We also applied recommendation system metrics to the evaluation of the ablation study, and as shown in Tables 3 and 4, the performance of no structure and no contrastive also showed significant performance degradation. Taking the results of two types of indicators into account, the addition of each module in TRAP improves the performance, especially when we aim for satisfactory results across multiple epitopes.
| Model | Precision@1 | Recall@1 | Precision@3 | Recall@3 |
|---|---|---|---|---|
| TRAP | 0.7468 ± 0.4348 | 0.3290 ± 0.3982 | 0.5476 ± 0.3371 | 0.5214 ± 0.4031 |
| Without structure | 0.7009 ± 0.4579 | 0.3088 ± 0.3944 | 0.5135 ± 0.3383 | 0.4929 ± 0.4055 |
| Without structure & esm | 0.2093 ± 0.4068 | 0.1241 ± 0.3094 | 0.1895 ± 0.2295 | 0.2926 ± 0.4140 |
| Without contrastive learning | 0.6303 ± 0.4827 | 0.2942 ± 0.3956 | 0.4882 ± 0.3157 | 0.5120 ± 0.4143 |
| Without binary learning | 0.1690 ± 0.3748 | 0.1173 ± 0.3044 | 0.1521 ± 0.1971 | 0.2720 ± 0.4165 |
| Model | Precision@1 | Recall@1 |
|---|---|---|
| TRAP | 0.4716 ± 0.4992 | 0.3925 ± 0.4583 |
| Without structure | 0.4689 ± 0.4990 | 0.3811 ± 0.4533 |
| Without structure & esm | 0.1847 ± 0.3881 | 0.1726 ± 0.3732 |
| Without contrastive learning | 0.4128 ± 0.4923 | 0.3400 ± 0.4463 |
| Without binary learning | 0.0883 ± 0.2837 | 0.0769 ± 0.2586 |
Case study of TRAP-based screening
We were looking forward to the application of our model to real-world biological experimental scenarios, and then we designed a workflow for screening case studies. Employing OLGA,25 we randomly generated 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CDR3β sequences, ensuring uniqueness by eliminating duplicates from the TRAP training dataset. CDR3βs were then designated as hit CDR3βs when their TRAP prediction scores exceeded 0.9. By leveraging molecular dynamics (MD) simulations and generalized Born and surface area solvation (MM/GBSA) calculations, we validated the utility of this workflow as a reliable reference for in silico screening.
000 CDR3β sequences, ensuring uniqueness by eliminating duplicates from the TRAP training dataset. CDR3βs were then designated as hit CDR3βs when their TRAP prediction scores exceeded 0.9. By leveraging molecular dynamics (MD) simulations and generalized Born and surface area solvation (MM/GBSA) calculations, we validated the utility of this workflow as a reliable reference for in silico screening.
We chose HLA-A*02:01 GLCTLVAML as the case, which has a TCR–pMHC complex crystal structure (PDB ID: 3O4L26). Notably, the TCR–pMHC interface in the crystal structure 3O4L exhibits only 20 contacts, a significantly lower count compared to other TCR–pMHC complexes.26 As shown in Fig. 7B, our analysis revealed an interaction area of 318.007 Å2 between CDR3β and the epitope in 3O4L. After TRAP screening, we narrowed down our selection to two hit CDR3βs (AITRGTQETQY and AIRQGGSYEQY) of equal length to the original CDR3β for further validation. The complex of AITRGTQETQY (AITR) has an interaction area of 319.323 Å2, which is similar to the 3O4L structure, while AIRQGGSYEQY (AIRQ) showed a larger area of 372.949 Å2, potentially enhancing the interaction. However, we avoided selecting a hit with a larger interaction area out of concern that steric hindrance might impede TCR–pMHC interactions.
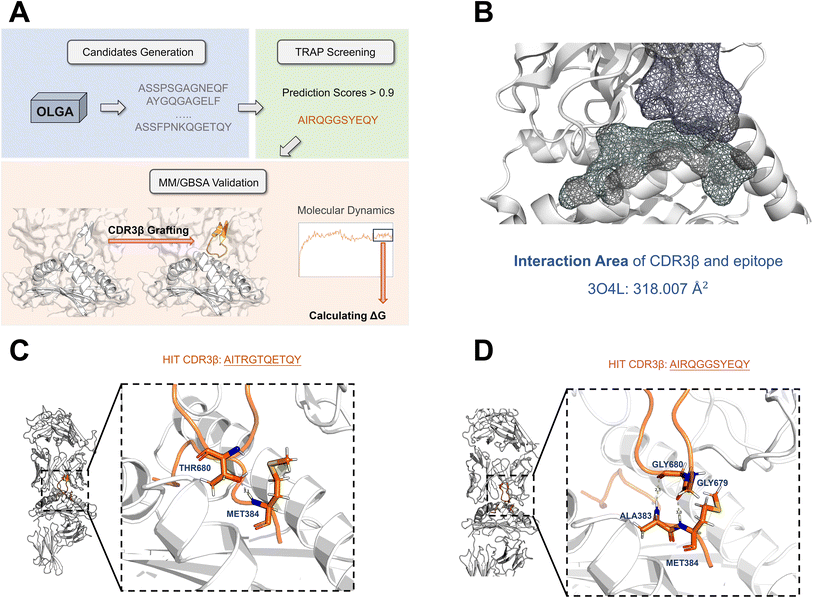 | ||
| Fig. 7 (A) The workflow of the screening case study utilizing TRAP. (B) The interaction area of CDR3β and the epitope in 3O4L is 318.007 Å2. (C) and (D) The interaction residues between the antigen peptide and CDR3β in the TCR–pMHC complex structure of two hit CDR3βs. | ||
Specifically, we used RCD27 to generate the initial conformation of the hit CDR3βs, subsequently grafting them onto the corresponding position of the crystal structure as the initial conformation for MD simulations. After around 100 ns, the root-mean-square deviation (RMSD) of TCR had reached a convergence state, and we chose 40 frames from the 98–100 ns conformation to calculate ΔG utilizing the MM/GBSA algorithm (outlined in the Methods). As a control, the crystal structure of 3O4L was also calculated using the same process.
The closeness or lower binding free energy relative to the crystal structure implied a potentially more stable binding for the grafted structures of the two hit CDR3βs (ESI Table 6†). Moreover, we analyzed the residue interaction between the epitope and the CDR3β for two hits based on the last frame of the MD. As shown in Fig. 7C and D, interactions were indeed formed between the CDR3β and the epitope. For AITR, the hydroxyl oxygen atom on the THR680 side chain forms a hydrogen bond with the hydrogen on the MET384 peptide bond, and for AIRQ, the oxygen atoms on the GLY680 and GLY679 peptide bonds formed polar interactions with the hydrogen atoms on the ALA383 and MET384 peptide bonds.
The low binding free energy and exact interactions suggest that TRAP has great application potential. However, for drug screening scenarios, our method requires further validation through biological experiments. This is a direction we intend to continue exploring in our future research.
Discussion
TRAP leverages contrastive learning to align the representation spaces of TCR and pMHC, and structural features further assist in distinguishing complex variations, enabling it to capture critical differences in scenarios with unknown epitopes, which enables TRAP to achieve a breakthrough with an AUC that surpasses the previous SOTA model by nearly 11%. Furthermore, TRAP achieves an AUC of 0.92 and an AUPR of 0.84 in the random-split scenario, surpassing the second-best model by 22%. The validation on a TCR pool from healthy individuals demonstrates that our negative sampling strategy effectively prevents the model from learning shortcuts that could inflate scores falsely. Moreover, by incorporating structural data and a contrastive learning framework, TRAP is able to distinguish various pMHCs and capture both cross-reactivity and specificity among TCRs. Our case study demonstrates TRAP's effectiveness in screening for TCR hits with binding patterns similar to those in the crystal structures, highlighting its potential in TCR-related therapeutic development.Although TRAP has achieved impressive performance, we may further improve the model in future work from the following perspectives. Firstly, we plan to optimize the processing of structural information to capture more intricate details. Secondly, we tend to fine-tune the protein language model used for sequence characterization in the context of antigen–antibody interactions to obtain more targeted sequence features. In addition, we will explore extending the application of the model, such as the design and optimization of antibody- and TCR-related drugs, thereby further demonstrating the strengths of TRAP.
Methods
Dataset
We retrieved TCR–pMHC binding pairs from VDJdb,28 McPAS-TCR,29 and IEDB,30 and saved the CDR3β sequences, HLA alleles, and epitope sequences for each pair. We narrowed down our selection to the binding pairs for MHC class I. For the VDJdb dataset, we excluded any binding pairs that have a confidence score of zero. Then, we confined the sequence length of CDR3β to a range of 10–20 amino acids. Specifically, for the binding pairs sourced from IEDB, the length of CDR3β is further limited to 8–18 amino acids after removing residues at anchor positions. To ensure data consistency, we also removed the residues at anchor positions from the CDR3β sequences in the other two database sources. Furthermore, we constrained the length of the epitopes to 8–12 amino acids. We also compiled the HLA alleles at protein-level resolution, for instance, recording HLA-A*01:01:73 as HLA-A*01:01. After eliminating duplicates, we compiled a comprehensive dataset of 38491 TCR–pMHC positive binding pairs for 531 pMHC types and 507 epitopes.Then, we generated negative samples by mismatching pMHC–CDR3β pairs. Specifically, for each CDR3β, we paired a non-binding pMHC based on its pMHC distribution frequency, ensuring a balanced representation of the positive and negative data for each pMHC.
True negative dataset
To ascertain the presence of false positives in the model prediction, we adopted the curation approach proposed by Liu et al.8 for negative TCRs and sourced TCRs from the peripheral blood of healthy donors31 as a pool of negative TCRs. Then we paired the top 3 most frequent pMHCs with CDR3βs from the negative TCR pool, as the true negative dataset.pMHC structure generation
We used AlphaFold Multimer/2.3.2 (ref. 18 and 23) to generate the structures of pMHC. The input sequences were retrieved from the IPD-IMGT/HLA32 database, specific to the respective HLA alleles. Regarding the parameters, we set the num_multimer_predictions_per_model to 1, while leaving the remaining settings at their default values. However, during the generation of HLA-A*02:01 (RLLQCTQQAV), an error occurred. Consequently, we utilized ColabFold33 to generate its structure instead.Model architecture
When engineering features for TRAP, we set sequence and structural embeddings separately. For sequence embedding, we fed the sequences of epitopes and CDR3βs into ESM2 (esm2_t33_650M_UR50D version)22 and extracted 1280-dimensional representation information as the sequence-level embedding. As for structural embedding, for each pMHC structure, we calculated several features, including the radius of gyration, BLOSUM62 representation, and the local environment within a certain distance of every residue in the epitope. The radius of gyration was calculated using calcGyradius of ProDy,34 yielding a 1-dimensional feature. For the BLOSUM62 representation, we obtained a 20-dimensional feature from the BLOSUM62 matrix. For the local environment within a certain distance of residue, we employed the Atom-centered Symmetry Functions of Dscribe35 to detect the structural features of each atom. We then calculated the average features of atoms from residues within 5 Å, 8 Å and 15 Å of the epitope residue, to capture environmental features at different scales, resulting in a 189-dimensional feature. Next, we concatenated the structural and sequence embeddings for pMHC, resulting in a 1470-dimensional feature for a single residue. For CDR3βs, we directly used the ESM2 embedding. To handle variable lengths of epitopes and CDR3βs, we padded the features to the maximum length. Specifically, we aligned CDR3βs to the IMGT numbering form using ANARCI36 and padded the gap using the tensor of the same shape composed of zeros. For epitopes of pMHCs, we padded only after the sequence.To encode the embeddings, we utilized a multi-head encoder layer with self-attention similar to the transformer model. Here, the feature vectors of each residue were transformed into query, key, and value vectors through learnable parameter mapping. Then, we added a contrastive learning module like CLIP.37 In TRAP, we applied a linear projection on both pMHC and CDR3β feature vectors to ensure consistency in their dimensionalities, followed by normalization.
For each batch in TRAP contrastive training, there were N positive pMHC–CDR3β binding pairs. We denoted the output of pMHCs in this batch as
| P = [P1,P2,…,PN] | (1) |
| B = [B1,B2,…,BN] | (2) |
 | (3) |
Specifically, we employed cross-entropy loss to achieve the contrastive training objective, which can be represented as
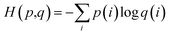 | (4) |
Therefore, we calculated CDR3β loss and pMHC loss as
| CDR3β loss = H(pB,qB) | (5) |
| pMHC loss = H(pP,qP) | (6) |
The contrastive loss can be represented as
 | (7) |
This approach was equivalent to conducting multi-class training for pairs corresponding to each column and row within the similarity matrix. Ultimately, the representation of CDR3βs would align closely with that of pMHCs.
Subsequently, we incorporated the negative pairs from the training set into binary training. In this process, we concatenated Bi and Pi together and fed them into the fully connected layers.
| V = FC(Bi‖Pi) | (8) |
After applying the sigmoid activation function, we obtained the binding prediction results:
| Binding probability = sigmoid (V) | (9) |
Focal loss (pT) = −α(1 − pT)γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pT pT | (10) |
 | (11) |
| γ = 2 | (12) |
 in TRAP training. γ is set to modulate the loss weights for easily classified pairs, increasing them for difficult ones, with a value of 2 in binary learning.
in TRAP training. γ is set to modulate the loss weights for easily classified pairs, increasing them for difficult ones, with a value of 2 in binary learning.
Benchmark with baseline models
We selected TEIM-Seq,9 NetTCR-2.0,13 and epiTCR14 (incorporating pMHC or epitope information) as our baseline models. For TEIM-Seq, we used the original default settings, including the pretrained epitope autoencoder model and hyperparameters. For NetTCR-2.0, we expanded the maximum input length of the epitope from 9 to 12 to suit our dataset, while maintaining the default values for the other parameters. epiTCR can be trained with either pMHC or epitope information, and for the pMHC version, we transferred MHC alleles into a 34-dimensional pseudo-sequence using netMHCpan-4.138 and also expanded the maximum input length of the epitope from 11 to 12. The remaining parameters were set to their default values. To minimize errors, we all trained and tested five times for the baseline models and TRAP.Applying TRAP to a case study
To generate CDR3β candidates, we used the command “olga-generate_sequences --humanTRB -n 1e5” in OLGA/1.2.4.25 After removing the CDR3β duplicates from the dataset, we used the TRAP model trained in scenario 1 to predict the binding scores for the CDR3β candidates. Subsequently, we filtered out the CDR3βs with scores exceeding 0.9 as hits and validated them using the MM/GBSA approach.To obtain the initial structures required for the MM/GBSA calculation, we used RCD/1.40,27 a protein loop closure program, to sample the conformation of the hit CDR3βs and then grafted these conformations on the corresponding positions of the TCR–pMHC complex crystal structure. Due to the limitations of the RCD algorithm, we only chose those hit CDR3βs that matched the length of the original CDR3β present in the crystal structure.
Then, we removed water molecules and other HETATM atoms from the structures using PYMOL/2.5. Prior to the MM/GBSA calculations, we employed molecular mechanics (MM) minimization and conventional MD simulation for TCR–pMHC complexes. The ff14SB force field was applied to parameterize TCR and pMHC components. A 5 Å-extended-cubic TIP3P water box was added for each TCR–pMHC structure. To balance the redundant charges, counterions of Na+ and Cl− were added using the Leap program of AMBER/20.39
Before conducting MD simulations, it is necessary to perform MM minimization to alleviate unfavorable interactions within the TCR–pMHC complexes. In this process, the real-space cutoff for van der Waals and short-range electrostatic interactions was set to 10 Å. Subsequently, we employed a four-step MM minimization procedure for each system using the pmemd program in AMBER/20. In these steps, we gradually removed the constraint on atoms for MM minimization. Specifically, in the first step, all non-hydrogen atoms were restrained; in the second step, the restraints on heavy atoms in solvents (i.e., Na+, Cl−, and oxygen atoms in water) were removed; in the third step, the restraints on the side chain atoms in TCR and pMHC were removed; in the fourth step, all atoms were minimized without any restraint. In steps 1 to 3, we applied a 5 kcal mol−1 Å−2 restraint to the systems for 1000 cycles of minimization, including 500 cycles of steepest descent and 500 cycles of conjugate gradient minimization. In step 4, the systems underwent 1000 cycles of steepest descent and 2000 cycles of conjugate gradient minimization.
Regarding the MD simulation, we employed a three-step simulation strategy for each system, while using the SHAKE algorithm to constrain all bonds that contain hydrogen atoms in the whole process of MD. In step 1, the simulation was conducted for a 50 ps heating simulation process from 0 to 300 K in the NVT ensemble, with a 2.0 kcal mol−1 Å−2 restraint on the heavy atoms of TCR and pMHC backbone atoms. In step 2, we applied the same restraint as in step 1 and performed a 50 ps equilibrium simulation in the NPT ensemble (T = 300 K and P = 1.0 atm). In the last step, we conducted a 100 ns MD simulation in the NPT ensemble without any restraint. The time step was set to 2 fs, and the coordinates were recorded at intervals of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. In all, we obtained 2000 frames from the third step of the MD simulations for each TCR–pMHC system. Then, the MM/GBSA method was used to calculate the binding free energy for TCR–pMHC using the MMPBSA.py module in AMBER/20 based on the last 2 ns of the MD frames.
000 steps. In all, we obtained 2000 frames from the third step of the MD simulations for each TCR–pMHC system. Then, the MM/GBSA method was used to calculate the binding free energy for TCR–pMHC using the MMPBSA.py module in AMBER/20 based on the last 2 ns of the MD frames.
Code availability
The source codes of TRAP are available on the GitHub repository at https://github.com/gejingxuan/TRAP.Data availability
The conda environment zip package used by TRAP and the pMHC structure data have been uploaded to https://zenodo.org/records/15062393 for easy reproduction.Author contributions
T. J. H., C. Y. S. and J. X. G. designed the research study. J. X. G. developed the method and wrote the code. J. X. G., J. K. W., Q. Y., L. Q. P., Y. K., C. S. and Y. F. D. performed the analysis. J. X. G., C. Y. S. and T. J. H. wrote the paper. All authors read and approved the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This study was supported by the National Key Research and Development Program of China (2024YFA1307501), the National Natural Science Foundation of China (82204279 and 82373791), and the Fundamental Research Funds for the Central Universities (226-2022-00220).References
- C. Szeto, C. A. Lobos, A. T. Nguyen and S. Gras, Int. J. Mol. Sci., 2020, 22, 68 CrossRef PubMed.
- J. Hennecke and D. C. Wiley, Cell, 2001, 104, 1–4 CrossRef CAS PubMed.
- M.-E. Goebeler and R. C. Bargou, Nat. Rev. Clin. Oncol., 2020, 17, 418–434 CrossRef PubMed.
- S. Dhillon, Drugs, 2022, 82, 703–710 CrossRef CAS PubMed.
- C. Soto, R. G. Bombardi, M. Kozhevnikov, R. S. Sinkovits, E. C. Chen, A. Branchizio, N. Kose, S. B. Day, M. Pilkinton, M. Gujral, S. Mallal and J. E. Crowe, Cell Rep., 2020, 32, 107882 CrossRef CAS PubMed.
- N. L. La Gruta, S. Gras, S. R. Daley, P. G. Thomas and J. Rossjohn, Nat. Rev. Immunol., 2018, 18, 467–478 CrossRef CAS PubMed.
- J. Rossjohn, S. Gras, J. J. Miles, S. J. Turner, D. I. Godfrey and J. McCluskey, Annu. Rev. Immunol., 2015, 33, 169–200 CrossRef CAS PubMed.
- Y. Gao, Y. Gao, Y. Fan, C. Zhu, Z. Wei, C. Zhou, G. Chuai, Q. Chen, H. Zhang and Q. Liu, Nat. Mach. Intell., 2023, 5, 236–249 CrossRef.
- X. Peng, Y. Lei, P. Feng, L. Jia, J. Ma, D. Zhao and J. Zeng, Nat. Mach. Intell., 2023, 5, 395–407 CrossRef.
- V. I. Jurtz, L. E. Jessen, A. K. Bentzen, M. C. Jespersen, S. Mahajan, R. Vita, K. K. Jensen, P. Marcatili, S. R. Hadrup, B. Peters and M. Nielsen, bioRxiv, 2018, preprint, DOI:10.1101/433706.
- T. Lu, Z. Zhang, J. Zhu, Y. Wang, P. Jiang, X. Xiao, C. Bernatchez, J. V. Heymach, D. L. Gibbons, J. Wang, L. Xu, A. Reuben and T. Wang, Nat. Mach. Intell., 2021, 3, 864–875 CrossRef PubMed.
- W. Zhang, P. G. Hawkins, J. He, N. T. Gupta, J. Liu, G. Choonoo, S. W. Jeong, C. R. Chen, A. Dhanik, M. Dillon, R. Deering, L. E. Macdonald, G. Thurston and G. S. Atwal, Sci. Adv., 2021, 7, eabf5835 CrossRef CAS PubMed.
- A. Montemurro, V. Schuster, H. R. Povlsen, A. K. Bentzen, V. Jurtz, W. D. Chronister, A. Crinklaw, S. R. Hadrup, O. Winther, B. Peters, L. E. Jessen and M. Nielsen, Commun. Biol., 2021, 4, 1–13 CrossRef PubMed.
- M.-D. N. Pham, T.-N. Nguyen, L. S. Tran, Q.-T. B. Nguyen, T.-P. H. Nguyen, T. M. Q. Pham, H.-N. Nguyen, H. Giang, M.-D. Phan and V. Nguyen, Bioinformatics, 2023, 39, btad284 CrossRef CAS PubMed.
- Y. Zhao, B. He, F. Xu, C. Li, Z. Xu, X. Su, H. He, Y. Huang, J. Rossjohn, J. Song and J. Yao, Sci. Adv., 2023, 9, eabo5128 CrossRef CAS PubMed.
- D. Hudson, R. A. Fernandes, M. Basham, G. Ogg and H. Koohy, Nat. Rev. Immunol., 2023, 23, 511–521 CrossRef CAS PubMed.
- J. A. L. Choo, J. Liu, X. Toh, G. M. Grotenbreg and E. C. Ren, J. Virol., 2014, 88, 10613–10623 CrossRef PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- R. Yin, B. Y. Feng, A. Varshney and B. G. Pierce, Protein Sci., 2022, 31, e4379 CrossRef CAS PubMed.
- T. Wang, L. Wang, X. Zhang, C. Shen, O. Zhang, J. Wang, J. Wu, R. Jin, D. Zhou, S. Chen, L. Liu, X. Wang, C.-Y. Hsieh, G. Chen, P. Pan, Y. Kang and T. Hou, Brief. Bioinform., 2024, 25, bbad486 CrossRef PubMed.
- Y. Jiang, M. Huo and S. Cheng Li, Brief. Bioinform., 2023, 24, bbad086 CrossRef PubMed.
- Z. Lin, H. Akin, R. Rao, B. Hie, Z. Zhu, W. Lu, A. D. S. Costa, M. Fazel-Zarandi, T. Sercu, S. Candido and A. Rives, bioRxiv, 2022, preprint, DOI:10.1101/2022.07.20.500902.
- R. Evans, M. O'Neill, A. Pritzel, N. Antropova, A. Senior, T. Green, A. Žídek, R. Bates, S. Blackwell, J. Yim, O. Ronneberger, S. Bodenstein, M. Zielinski, A. Bridgland, A. Potapenko, A. Cowie, K. Tunyasuvunakool, R. Jain, E. Clancy, P. Kohli, J. Jumper and D. Hassabis, bioRxiv, 2022, preprint, DOI:10.1101/2021.10.04.463034.
- J. Ge, D. Jiang, H. Sun, Y. Kang, P. Pan, Y. Deng, C.-Y. Hsieh and T. Hou, Cell Rep. Phys. Sci., 2024, 5, 101980 CrossRef CAS.
- Z. Sethna, Y. Elhanati, C. G. Callan, A. M. Walczak and T. Mora, Bioinformatics, 2019, 35, 2974–2981 CrossRef CAS PubMed.
- J. J. Miles, A. M. Bulek, D. K. Cole, E. Gostick, A. J. A. Schauenburg, G. Dolton, V. Venturi, M. P. Davenport, M. P. Tan, S. R. Burrows, L. Wooldridge, D. A. Price, P. J. Rizkallah and A. K. Sewell, PLoS Pathog., 2010, 6, e1001198 CrossRef PubMed.
- P. Chys and P. Chacón, J. Chem. Theory Comput., 2013, 9, 1821–1829 CrossRef CAS PubMed.
- M. Goncharov, D. Bagaev, D. Shcherbinin, I. Zvyagin, D. Bolotin, P. G. Thomas, A. A. Minervina, M. V. Pogorelyy, K. Ladell, J. E. McLaren, D. A. Price, T. H. O. Nguyen, L. C. Rowntree, E. B. Clemens, K. Kedzierska, G. Dolton, C. R. Rius, A. Sewell, J. Samir, F. Luciani, K. V. Zornikova, A. A. Khmelevskaya, S. A. Sheetikov, G. A. Efimov, D. Chudakov and M. Shugay, Nat. Methods, 2022, 19, 1017–1019 CrossRef CAS PubMed.
- N. Tickotsky, T. Sagiv, J. Prilusky, E. Shifrut and N. Friedman, Bioinformatics, 2017, 33, 2924–2929 CrossRef CAS PubMed.
- R. Vita, S. Mahajan, J. A. Overton, S. K. Dhanda, S. Martini, J. R. Cantrell, D. K. Wheeler, A. Sette and B. Peters, Nucleic Acids Res., 2019, 47, D339–D343 CrossRef CAS PubMed.
- J. Dean, R. O. Emerson, M. Vignali, A. M. Sherwood, M. J. Rieder, C. S. Carlson and H. S. Robins, Genome Med., 2015, 7, 123 CrossRef PubMed.
- D. J. Barker, G. Maccari, X. Georgiou, M. A. Cooper, P. Flicek, J. Robinson and S. G. E. Marsh, Nucleic Acids Res., 2023, 51, D1053–D1060 CrossRef CAS PubMed.
- M. Mirdita, K. Schütze, Y. Moriwaki, L. Heo, S. Ovchinnikov and M. Steinegger, Nat. Methods, 2022, 19, 679–682 CrossRef CAS PubMed.
- A. Bakan, A. Dutta, W. Mao, Y. Liu, C. Chennubhotla, T. R. Lezon and I. Bahar, Bioinformatics, 2014, 30, 2681–2683 CrossRef CAS PubMed.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- J. Dunbar and C. M. Deane, Bioinformatics, 2016, 32, 298–300 CrossRef CAS PubMed.
- A. Radford, J. W. Kim, C. Hallacy, A. Ramesh, G. Goh, S. Agarwal, G. Sastry, A. Askell, P. Mishkin, J. Clark, G. Krueger and I. Sutskever, arXiv, 2021, preprint, arXiv:2103.00020, DOI:10.48550/arXiv.2103.00020.
- B. Reynisson, B. Alvarez, S. Paul, B. Peters and M. Nielsen, Nucleic Acids Res., 2020, 48, W449–W454 CrossRef CAS PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc08141b |
| This journal is © The Royal Society of Chemistry 2025 |




