Improving the teaching of entropy and the second law of thermodynamics: a systematic review with meta-analysis

Abstract

Entropy and the second law of thermodynamics have long been identified as difficult concepts to teach in the physical chemistry curriculum. Their highly abstract nature, mathematical complexity and emergent nature underscore the necessity to better link classical thermodynamics and statistical thermodynamics. The objectives of this systematic review are thus to scope the solutions suggested by the literature to improve entropy teaching. ERIC and SCOPUS databases were searched for articles aiming primarily at this objective, generating N = 315 results. N = 91 articles were selected, among which N = 9 reported quantitative experimental data and underwent a meta-analysis, following PRISMA guidelines. Risk of bias was assessed by the standards criteria of What Works Clearinghouse. Results from the qualitative selection show diverse solutions to solve the entropy teaching hurdles, such as connection to everyday life, visualization, mathematics management by demonstrations, games and simulations, criticism and replacement of the disorder metaphor and curriculum assessment. The synthetic meta-analysis results show high but uncertain effect sizes. Implications for teachers and researchers are discussed.

---

Introduction

Physical chemistry is often despised by students (Donnelly and Hernández, 2018). At university, students and educators report many difficulties in its teaching and learning, including the lack of interest of students, the subject's abstract nature, its mathematical intricacies (Tsaparlis, 2016) or perceived lack of relevance to everyday life (Sözbilir, 2004). In physical chemistry education, thermodynamics is often described as hard to teach because it presents the same kind of hurdles: lack of positive attitude towards it and self-doubt among students, numerous alternative conceptions, hard-to-learn ability to transfer mathematical calculus to abstract notions such as work or heat, deep links to other known counter-intuitive notions, such as the particulate nature of matter (Partanen, 2016). However, the indispensability of thermodynamics, notably entropy, cannot be overstated, especially concerning contemporary challenges. It forms the bedrock for addressing pressing issues like providing an adequate conceptual basis for, e.g., understanding the climate crisis’ energy problems, the greenhouse effect, societal energy sources, and fossil fuel consumption (Grassian et al., 2007).

Energy and entropy are the two central concepts of thermodynamics (Leff, 2020). Entropy is itself hard to teach; the literature does not lack articles that list conceptual difficulties (e.g.Sreenivasulu and Subramaniam, 2013) or document mistakes to written conceptual tests (Bennett and Sözbilir, 2007). Atarés et al. (2021) recently listed these prominent learning difficulties: (i) a tendency towards strategic learning over deep conceptual comprehension, supported by findings in Sözbilir (2004), (ii) the abstract nature of entropy, (iii) inconsistency in the use of the disorder metaphor (see the second to last paragraph of this introduction), (iv) the prevalence of numerous alternative conceptions, and (v) the high mathematical proficiency required for inducing conceptual change.

Dreyfus et al.'s (2015) resource letter could qualify as a systematic review as it meticulously reports articles addressing the teaching of entropy and the second law of thermodynamics, though with minimal commentary. This article highlights the development of tutorials aimed at improving teaching of a specific subject, with a focus on language use. Regarding thermodynamics, disciplines have different aims and often operate in isolation: while chemistry education research targets the understanding of chemical equilibrium, physics education delves into the entropy's relationship to other concepts such as reversibility, and too little research has been performed in biology didactics to highlight a major trend.

To solve these numerous problems, the latest comprehensive review of teaching strategies pertaining to entropy and the second law of thermodynamics, to the best of our knowledge, is detailed in Bain et al.'s seminal work (2014). In this review about the improvement of thermodynamics teaching, and in particular entropy, the authors identified four main lines of research: elucidating the factors that impact the understanding of physical chemistry, refining mathematical instruction for thermodynamics, investigating students’ understanding of the particulate nature of matter, and probing students’ alternative conceptions. For entropy specifically, the authors advise researchers to (a) investigate the teaching of emergent processes – how the physical rules of the microscopic world sum up to produce the phenomena of the macroscopic world, referred to as “emergence” henceforth –, and (b) foster interdisciplinary approaches, recognizing thermodynamics as a cross-domain subject where discipline-centred research yields teaching prescriptions that are often too narrow to be coherent with other disciplines’ teaching paradigms. Concerning Bain et al.'s recommendation (a), thermodynamics might in general be improved by better connecting the three points of view of the chemistry triplet (microscopic, macroscopic, symbolic) (Johnstone, 1991), for example by simulations (Schwedler and Kaldewey, 2020), or by research-based teaching sequences (e.g.Partanen, 2016). Cognitive conflict provided by the disparities in the microscopic and the macroscopic approaches of thermodynamics might be the key to a deeper conceptual comprehension of entropy (Leinonen et al., 2015). Instead of the historical Johnstone chemistry triplet, we rather use Taber's (2013) version, reprinted in Fig. 1. The two main differences with Johnstone's triangle are the addition of the “experiential” level (on the left vertex) and the placement of the “symbolic” point of view on the side of the triangle between “micro” and “macro” representations. We believe these two changes to the triangle are useful in understanding hurdles to the teaching of entropy. Given the crucial emergent nature of entropy, the symbolic representations used to translate between the macroscopic and microscopic conceptualizations of the triangle are essential tools. In this new form, the triplet describes the symbolic aspect of teaching as the methods and the tools of expressing, representing, the “micro” or “macro” points of views. Symbolic representations can be microscopic (e.g. Boltzmann energy distributions, chemical equations), macroscopic (e.g. piston-and-cylinder systems, laboratory apparatuses), or a combination of both in the same representation (e.g. the superposition of the drawing of a beaker containing water and salt to illustrate the dissolution of the salt, with a “zoom-in” to “show” dissolution at the microscopic level). We find Taber's argument that “symbolic” cannot be considered a vertex on its own (which would mean it is a level of conceptualization on its own) convincing, since it cannot be isolated from the macroscopic and microscopic points of view. As Taber himself (2013) puts it: “the symbolic knowledge domain cannot be readily separated from the macroscopic and submicroscopic domains as a discrete level of chemical knowledge, as this domain is concerned with representing and communicating the concepts and models developed at those two ‘levels’. The symbolic is inherent in how we think about chemistry; and the processes of learning, teaching and applying chemistry commonly involve re-descriptions into and between components of the specialised symbolic ‘language’ used to describe chemical ideas at the two levels.” (p. 165)

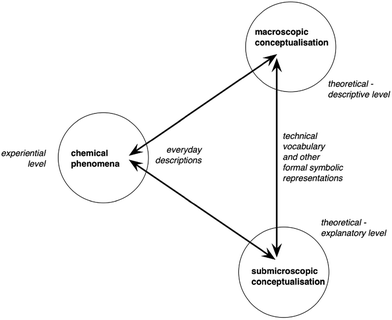Fig. 1 Taber's (2013) version of the chemistry triplet. Reprinted with permission from Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Taber K. S., (2013), Chem. Educ. Res. Practice, 14(156), 165.

More recently, Atarés et al. (2021) presented a comprehensive review of the solutions explored by the literature to teach entropy more qualitatively: (i) highlight paradoxical cases from everyday life, (ii) focus on the increase of entropy of the universe criterion for spontaneity, (iii) explain the history of the development of the entropy concept, (iv) present entropy as “paying the price” for the heat engine efficiency (e.g. in Tro, 2019), (v) give a molecular-microscopic explanation to entropy. A large part of the literature argues for more active involvement of students in activities to enhance the teaching of physical chemistry, be that with context-based approaches, teaching with technology or cooperative learning (Tsaparlis, 2007), with ongoing effort up to this day to produce innovative laboratories or student-centred activities in thermodynamics (e.g.Makahinda and Mawuntu, 2023).

To further Atarés et al.'s (2021) solutions (iii) and (v), the disorder metaphor has been heavily criticized as an inadequate connection between the macroscopic and microscopic points of view of the chemistry triplet (e.g.Laird, 1999; Styer, 2000; Kozliak and Lambert, 2005). As many other chemical parameters, entropy emerges from the behaviour of particles at the microscopic level and a clear link with macroscopically measured quantities (such as temperature or pressure) needs to be established to understand properly the statistical nature of entropy. In this perspective, disorder has been deemed too vague a concept to be considered as an appropriate descriptor of entropy (Styer, 2000) whereas other descriptors display more relevant properties, such as Shannon's measure of entropy (Ben-Naim, 2011) or energy spreading (Leff, 1996; Lambert, 2002, 2011; Phillips, 2016). In some instances, entropy can even be completely decorrelated from apparent order or disorder creation (Ben-Naim, 2012).

However, both Bain et al.'s (2014), and Dreyfus et al.'s (2015) articles are almost a decade old and need some updating, while Atarés et al.'s (2021) work does not offer a systematic review or meta-analysis. Entropy and the second law of thermodynamics, because of their well-known difficult teaching nature, need a systematic review of their own.

To improve the quality of this review, we used the PRISMA method (Page et al., 2021). Originally thought of for medical reviews, it was later extended to other kinds of reviews, including education science reviews. It focuses on transparency of the review process, reporting choices made by the authors, eligibility criteria, methods for computing gathered data and risk of biases.

Objectives and research questions

To better address the multifaceted challenges posed by entropy, we subdivided the first research question (RQ1) into two, aimed at tackling two primary hurdles: (a) abstraction and mathematical complexity, and (b) the lack of connection between the microscopic and macroscopic aspects of the chemistry triplet (Talanquer, 2011).

Among the existing ways to address abstraction and mathematical complexity in science education, we chose to focus on hands-on methods. It has long been shown that hands-on, practical approaches can effectively bridge the gap between abstract concepts and concrete understanding in STEM education (e.g.Pirker et al., 2015), which has also been supported by recent discoveries in neuroscience (Hayes and Kraemer, 2017). Among hands-on approaches, games, demonstrations and laboratories can provide explicit conceptual links for students between abstract concepts (e.g. dynamic equilibrium) and concrete, visualizable phenomena (e.g. a game where students move from one area to another at different rates, illustrating the “paradoxical” movement of particles while concentrations remained unaffected i.e. dynamic equilibrium). Moreover, simulations can alleviate mathematical burden by automatically calculating thermodynamical parameters (e.g. the variation of entropy in a gas cylinder-piston system) so students do not have to dig deep into the equations, letting them focus on well-chosen cases that illustrate key conceptual facts (e.g. entropy variations in adiabatic or isothermal processes). Thus, one of the assumptions of this work is that hands-on, practical solutions provide tools of a particular interest to address abstraction and mathematical complexity.

RQ1a: “What does the literature offer as hands-on, practical solutions for addressing the abstraction and mathematical complexity of the teaching of entropy and the second law of thermodynamics?”

Secondly, we wanted to address the challenge posed by the emergent nature of entropy (Volfson et al., 2019) and the criticisms that have been brought forth towards the disorder metaphor, which currently stands as the mainstream solution to this didactic problem. This second question takes a comprehensive look at existing macroscopic-oriented and microscopic-oriented teaching methodologies, examining their individual merits and exploring how they intersect with one another in the context of entropy education.

RQ1b: “What does the literature offer as microscopic and macroscopic solutions for the teaching of entropy and the second law of thermodynamics?”

In recent years, to improve the quality of reviews in educational sciences, it has become increasingly important to identify studies which measure their effectiveness (e.g.Hattie, 2008; Dachet, 2024), since these tests provide more tangible support to their pedagogical claims than pure proposals. Therefore, among the RQ1 selected articles, we performed a meta-analysis focusing on studies that conducted any quantitative evaluation of their methods, answering the following research question no. 2 (RQ2).

RQ2: “Among the RQ1 selection of articles, what is the measured effectiveness of the proposed teaching solutions?”

Positionality statement

The two authors of this study have obtained high-level diplomas (VN: master, BL: doctorate) in chemistry that have necessarily influenced their perspectives on science education and their preferred methods of research, which can be critically analysed in the choices of the research questions (RQ1a, RQ1b and RQ2). For example, the three questions are content-oriented, and only give a small place to students’ affective dimension towards the subject. VN is a young PhD student who graduated in chemistry, and teaches thermodynamics at university as a teaching assistant, whilst developing competence as a researcher in chemistry education. His opinions and choices of methods are thus probably influenced by natural science method, as opposed, for example, to methods used in the social science (e.g. interviews). BL is professor of physical chemistry and chemistry education. He is an experienced thermodynamics teacher, who developed research in molecular reaction dynamics and later on in chemistry education. His focus in chemical education is therefore more content-oriented. VN and BL both work at University of Liège in Belgium. There were no involvement from both researchers in any of the reviewed studies, so there were not any kind of authority relationship over any students.

Methods

Article selection

The selected articles came from 3 sources: (i) 3 online searches in two databases, ERIC and SCOPUS (see Table 1 for search strings), (ii) the references cited in these articles and (iii) the first author's own database of the literature, which are transparently reported in Appendix A in the ESI.†

Table 1 Search strings and dates of research in ERIC and SCOPUS databases. The update column completes the first search. In the ERIC search string, “pubyearmin: 2022” was added and any new article was added to the selection flowchart of articles, in the SCOPUS search string, “PUBYEAR AFT 2022” was added to do the same

Database	Search string	First consulted	Updated
ERIC	“entropy” AND “teaching”	June 2022	April 2024
ERIC	“second law of thermodynamics” AND “teaching”	June 2022	April 2024
Scopus	“second law of thermodynamics” AND “teaching” AND “science education” AND (“physics” OR “biology” OR “chemistry” OR “engineering”) AND (LIMIT-TO (PUBSTAGE, “final”)) AND (LIMIT-TO (DOCTYPE, “ar”) OR LIMIT-TO (DOCTYPE, “re”)) AND (EXCLUDE (SUBJAREA, “COMP”)) AND (LIMIT-TO (LANGUAGE, “English”) OR LIMIT-TO(LANGUAGE, “French”))	July 2022	April 2024

---

Following the database search, records were screened based on inclusion criteria and exclusion criteria listed in Table 2. The only person deciding if an article was included or not was the first author of this article, and no automation tools were used in the process.

Table 2 Inclusion and exclusion criteria for the selection of articles to answer the RQ1

Inclusion criteria for the RQ1

1. The article answers the RQ1.

2. The focus of the article is to improve teaching of entropy and the second law of thermodynamics.

3. The article was published in a scientific journal with peer-reviewing and not in a conference proceeding.

4. The article is in English or in French.

5. The target teaching audience of the article is primary, high school, college, undergraduate or graduate students.

6. The teaching discipline is biology, chemistry, physics, engineering, or interdisciplinary across these disciplines.

7. The article provides a teaching solution for introductory-level thermodynamics.

Exclusion criteria for the RQ1

1. If the article is focused on the teaching of advanced thermodynamics, it was excluded from the selection.

2. If the article is focused on the teaching of electrochemistry, it was excluded from the selection.

3. If the article is focused on a computer software (e.g. running on iMac G3) or programming language (e.g. Algol) that is not commonly in use today, it was excluded from the selection.

---

RQ1 data retrieval

In the articles retrieved, both authors sought for the following information.

• What is the main goal of the article?

• What is the theoretical framework of the article? To help with this item, we used Rodriguez et al.'s (2023) list of frameworks used in chemistry.

• What are the specificity and originality of the entropy teaching solution?

• Does the article provide a hands-on approach (i.e. a laboratory, a game, a computer simulation, or a demonstration), or a theoretical, concept-based approach (i.e. full teaching sequences, proposals of a new descriptor for entropy, commentary on the language teacher should use, the order in which thermodynamics concepts should be taught)?

• Does the article employ a microscopic-oriented point of view, or a macroscopic-oriented point of view, or a combination of both, by detecting keywords and typical concepts from both methods, such as, for example, for the microscopic method, the Boltzmann definition of entropy, the Boltzmann distribution, energy levels diagrams, degrees of freedom, phase space, and, for the macroscopic method, the Clausius definition of entropy, pressure–volume diagram, piston-and-cylinder problems, computations of state function variations, etc.?

• What is the teaching discipline? If no explicit mention of the discipline was found, the discipline was assumed based on the scope of the journal, or the concepts presented in the articles (if they were typical of e.g. physics, chemistry, or engineering textbooks).

• What is the teaching level (primary, secondary, tertiary)? If no mention of the level was found, the level was assumed based on the scope of the journal, or the concepts presented in the articles (if they were typical of textbooks of primary, secondary or tertiary science education).

• Does the article propose a generalist approach, i.e. a broad approach to teach entropy, or a specific approach, i.e. suggesting a way to teach a narrow, unique aspect of entropy or the second law?

• Has any quantitative measurement of the efficiency of the proposed solution been done? If so, the article was selected for the RQ2 meta-analysis.

The data retrieved from these questions were formally coded as follows:

• Theoretical framework: present or absent? If a theoretical frame is present, to what category from Rodriguez et al. (2023) does it correspond: constructivist, hermeneutic, critical theory or organization of chemistry knowledge?

• Point of view: microscopic, macroscopic, or both

• Aim: theoretical or hands-on

• Discipline: chemistry, biology, physics, interdisciplinary or non-scientific

• Age group: undergraduate or graduate, high school and undergraduate, high school, preservice teachers, primary school, or no specified level

• Approach: general or specific

All articles were split coded independently by the two authors of this review. Three measurements of interrater reliability were calculated:

1. Percentage agreement (%_a)

with N_agree the number of articles where the same code was chosen by the two raters, and N the total number of articles.

2. Cohen's Kappa

with κ_Cohen the value of Cohen's Kappa, p₀ the probability of agreement between raters, and p_r the probability of agreement by chance. This equation can be explicitly calculated as follows.where K is the matrix of code combination between the two raters, Q is the number of categories, i and j are the individual coding codes of, respectively, raters A and B (i and j can thus take values between 1 and Q), and N is the total number of articles. For example, K_2,5 is the number of articles where rater A attributed code “2” and rater B attributed code “5”.

Following Landis and Koch's (1977) recommendations, values of Kappa will be interpreted as <0, “poor”, 0–0.2, “slight”, 0.21–0.4, “fair”, 0.41–0.6, “moderate”, 0.61–0.8, “substantial”, 0.81–1, “almost perfect”.

3. Gwet's (2002) AC1

As Gwet (2002) have pointed out, Kappa values can be substantially lowered (for the same agreement percentage) if one category is overrepresented. As a solution, they have proposed the alternative metric AC1, which will be calculated as follows.

with

andwhere Q is the number of categories, N is the number of articles, r is the number of raters (here, r = 2) and r_iq is the number of qth code given to the ith article. For example, if for article no. 17, both raters gave code 5, then r_iq = r_17,5 = 2. Interpretation of AC1 values is analogous to Cohen's Kappa values.

RQ2 meta-analysis statistics

We define an intervention as any new teaching activity that was implemented to improve the teaching of entropy to students. If a selected article mentioned any efficiency measurement of its proposed solution to teach entropy and the second law of thermodynamics, it was included in the meta-analysis subgroup. In these articles, we found two types of measurements: student motivation (as measured by reported satisfaction and attitude towards the topic) and student performance, which we analysed differently.

a. Satisfaction with the teaching solution or positive attitude towards the teaching solution, was considered as a descriptive measurement and simply reported in the results.

b. Assessment of the performance of students was further analysed. We searched for the success rate, means and standard deviations at an evaluation that aimed at quantifying the efficiency of the teaching solution. When these measurements were reported for individual questions of, e.g., a multiple-choice questionnaire (MCQ), we only sought for aggregated, global values. In this article, the mean is noted M, standard deviation SD, and success rate F.

Other sought variables included the number of participants, the type and global aim of the intervention, the evaluation methodology, the country of intervention, and if the researchers used interviews to help interpret data.

Risk of bias analysis is quite uncommon in science education reviews, although it is a pivotal assessment in the PRISMA methodology. Thus, we opted for use of the standards of What Works Clearinghouse (Procedures and Standards Handbook, Version 5.0, 2022), which is a reviewing method developed by the US Department of Education that aims at producing high-quality reviews of the education literature. Their procedure handbook listed quality criteria that we adapted for this review.

1. Outcome measures

a. Face validity, i.e. true measurement of what the study aims at measuring.

b. Reliability between different measurements for a group.

c. No overalignment, i.e. the measurement test is not overly biased towards the concepts taught in the test groups (e.g. of overalignment: the intervention teaches the students how to use a new formula, the control group not, and the measurement only consists of using that new formula).

d. Consistency of assessment method between the test group and the control group.

2. Confounding factors

a. No group containing a “single study unit – such as a teacher, classroom, school, or district – and that unit is not present in the other condition” (p. 14)

b. Systematic difference between the control and the test group (e.g. age).

c. Time alignment (e.g. comparing the 2020 cohort to the 2021 cohort).

3. Type of randomization assignment to the test group or the control group, randomized control trials being the gold standard.

4. Compositional change during the study, i.e. students quitting or joining the study between the pre-test and post-test.

5. Baseline equivalence of the test group and the control group at the pre-test.

To allow comparison of educational efficiency, we computed effect sizes. Depending on the type of data gathered and the choice of report of metrics in the articles, the effect size was computed differently.

1. For reported success rates, (F) we computed the effect size ϕ for a chi-square test of independence of a 2 × 2 contingency table. Effect sizes are categorized as ϕ = 0.1 small, ϕ = 0.3 medium and ϕ = 0.5 large.

In eqn (7), χ² is the chi-square statistic of the chi-square test, and N is the combined number of students in both instances of the test (e.g. pre-test and post-test).

2. For reported means (M) and standard deviations (SD), we computed either d_Cohen or d_ppc2, depending on the measurements context.

– If the study employed only a post-test, we computed a d_Cohen as follows.

The subscripts “pre” and “post” indicate the pre-test and the post-test. The subscripts “T” and “C” indicate the test group, and the control group.

– If the study employed a pre-test and a post-test, we computed d_ppc2 for comparing two cohorts (test and control) post-test results effect sizes. The d_ppc2 metric, developed by Morris (2008), is comparable to d_Cohen for its interpretation but more accurate when considering populations from a pre-test-post-test-control design, since d_Cohen divides the means difference by the pooled standard deviation. The d_ppc2 effect size thus considers differences in student numbers between the control group and the test group (Morris, 2008).

where n indicates the number of students.

According to Cohen (1988), a d value between 0.2 and 0.4 can be considered as a small effect size, 0.5 to 0.7 intermediate and above 0.8, large. According to Hattie (Hattie, 2008), a d value comprised between 0 and 0.2 corresponds to developmental effects (what a student can achieve without schooling), between 0.2 and 0.4 to teacher effects, and superior to 0.4, to a desired, intervention-linked effect, though these values can be nuanced in tertiary education and will be commented on in the results.

Given the small number of studies reporting quantitative results from quasi-experimental research designs (N = 5, see results), and that no randomized control trials were selected, we did not perform any risk of bias due to reporting bias (item 14 in PRISMA checklist). For the same reason, we did not perform any heterogeneity (item 20c) or sensitivity (item 20d) analyses (Prisma 2020 Checklist, 2020). Moreover, we do not report item 13 because we did not produce any syntheses of a quantitative outcome. Finally, certainty in the body of evidence was assessed based on the magnitude of the effect size, and the risk of bias analysis of individual studies.

Results

Selection of articles

In the database-identified articles, we screened the records for inclusion, based on title and abstract, then full read. The first author's own database of the literature included 15 articles not found by the online searches but that met the inclusion criteria. Though this was not systematic, it was deemed reasonable to add some key articles to complete the panorama given by this review, and the articles are listed in Appendix A in the ESI.† 91 articles were eventually selected for the RQ1 and 9 of them were eligible for the RQ2 meta-analysis (Fig. 2).

Fig. 2 Flowchart of article selection. R for research in either ERIC or SCOPUS databases. N₁ indicates the June 2022 search, and N₂ the April 2024 update, while N_total = N₁ + N₂. The meta-review selection criterion was the presence of quantitative data testing the pedagogical proposition. Inclusion and exclusion criteria are listed in Table 2.

Articles that were excluded for a reason that could appear as ambiguous or arbitrary are listed in Appendix B in the ESI,† with the reason for which they were excluded.

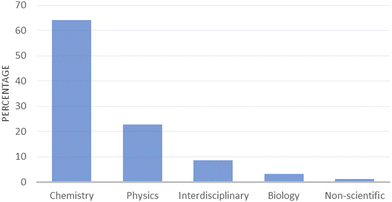
RQ1 results

The 91 articles spanned across multiple domains (Fig. 3): chemistry (64%), physics (23%), interdisciplinary (9%), biology (3%), and non-scientific (1%) (%_a: 80%, κ_cohen = 0.65, substantial, AC1 = 0.73, substantial). 74% of articles offered solutions for undergraduate (70%) or graduate students (4%), 12% did not specify what level they addressed and this information could not be deduced from journal scope, 10% for high school, 2% for preservice teachers and 1% for undergraduates and high schoolers (%_a: 85%, κ_cohen = 0.63, substantial, AC1 = 0.83, almost perfect). 73% of articles displayed a theoretical approach, often presenting the way a specialist or a researcher thinks that the theoretical concepts associated with entropy should be taught, or as Kincanon (2013) puts it in his article title: “How I teach the second law of thermodynamics”. Such articles offer perspectives on original approaches to improve the understanding of complex theoretical concepts, while 27% of articles (25 articles) presented hands-on, practical approaches: 5 demonstrations, 5 games, 8 laboratories and 7 computer simulations (%_a: 98%, κ_cohen = 0.95, almost perfect, AC1 = 0.97, almost perfect). A brief description of each hands-on article, hopefully helpful for the researcher and the teacher, is available in Table 3.

Fig. 3 Disciplines of the N = 91 articles from the RQ1 selection.

Table 3 Characteristics and short summary of hands-on approaches from the RQ1

Type	Ref.	Approach	Discipline	Level	Aim	Summary
Demonstration	(Plumb, 1964)	Micro	Chemistry	Undergraduate	General	Akin to Ellis's device, a mechanically controlled flow of air impulses a light bead to float between two sheets of Plexiglass. The device is separated into a high-energy state and a low-energy state, the width of each representing entropy, and the height, energy (Fig. 6).
	(Haber-Schaim, 1983)	Macro	Physical chemistry	High School	General	The article suggests two demonstrations: (a) a Daniell battery, to illustrate the need for a fuel (in this case, zinc) when a spontaneous reaction occurs, and that no “free” energy is completely available to humans to be used to do work because some has to be lost as heat and (b) a vibrating air table with discs to exemplify the spontaneous expansion of gases, showing its probabilistic nature.
	(Brady, 1989)	Both	Chemistry	Undergraduate	Specific	The author shares a demonstration that illustrates entropy of mixing by detecting the respective diffusions of air from inside a porous beaker to an external volume, and the opposite and quicker diffusion of hydrogen gas from the outside volume to inside the porous beaker, and showing that ΔG = −TΔS, with ΔS = nR ln(Vf/Vi) for each gas.
	(Ellis and Ellis, 2008)	Micro	Chemistry	No specified level	Specific	In this setup, beads are giggled around by a constant motor-induced vibration in a container that accounts for enthalpy by its height, and entropy by its width (see Fig. 5), while temperature is accounted for by the amplitude of the vibration movement, and activation energy by a barrier between reactants and products. The demonstration allows to see the spontaneity of counterintuitive entropically driven reactions. Author Mayorga (Fig. 7) proposes a spreadsheet version of the demonstration.
	(Jadrich and Bruxvoort, 2010)	Both	Physics	No specified level	Specific	Carbon dioxide-filled balloons are used to illustrate entropy-driven diffusion processes, and the central role of partial pressures, because CO2, contrary to air or helium, can rapidly absorb into the latex structure and migrate through it, leading to visible pressure equilibration within the timescale of a classic lecture.
Game	(Black et al., 1971)	Micro	Physics	Undergraduate	Specific	The article presents a serious game to elucidate the distribution of energy in an Einstein solid, by using random events (dice), to displace energy among positions in the crystal, and then extends the game with computer calculations; resembles the proposition of Phillips (2016).
	(Zinman, 1973)	Micro	Chemistry	No specified level	General	A deck of cards can simulate what Shannon's entropy is: the easier it is to transmit to another student the order of cards in a deck, the lower the entropy. Different cases are developed: completely ordered (low entropy) or shuffled (high entropy), a rubber band used to attach cards mimicking chemical bonds, and a comparison of states of matter.
	(Lechner, 1999)	Micro	Chemistry	Undergraduate	General	The article suggests two simple experiments to explain entropy: one qualitative, where beakers containing different coloured solutions are stacked on top of one another inside a closed cylinder before the latter is turned upside down to allow mixing, and one quantitative, where students are asked to glue back together (fake) shredded bills, to show the probabilistic nature of entropy.
	(Michalek and Hanson, 2006)	Micro	Chemistry	High school and undergraduate	General	The author proposes a game to explain the distribution of energy, by making students exchange fake money randomly between two facing circles, showing the predictability of the Boltzmann distribution. The game is then used to explain the role of different parameters, such as energy-level separation (by distributing twice less 2$ instead of 1$ bills, keeping the total amount of money constant), or temperature (by giving more money to start with), then using the results from the game to reflect about chemical reactions, or kinetics.
	(Phillips, 2016)	Micro	Physics	Undergraduate	Specific	Energy distribution in a solid can be modelled by random displacement of buttons between boxes on a sheet, which represent two Einstein solids in contact, and let the energy quanta move by rolling dice. Whatever the initial conditions, the systems evolve towards an equilibrium, thus showing the spontaneous spreading of energy. The approach resembles that of Black et al. (1971).
Laboratory	(Bindel, 1995)	Macro	Chemistry	Undergraduate	Specific	The author argues to show the power of predicting entropy by making students compute values of ΔSuniverse and ΔGsystem (showing their equivalence) for reactions they will later perform in the lab, to see if they are going to be spontaneous or not. Then, the computations extend to K, the equilibrium constant, to show its link with ΔSuniverse.
	(Bindel, 2007)	Macro	Chemistry	High school	Specific	Entropy analysis is a method developed by the author to better account for ΔSsystem and ΔSenvironment. In this follow-up article to his own 2004 article, the author extends entropy analysis to simultaneous equilibria in a laboratory, by studying the impact of adding different bases to a NH4^+/Cu^2+ aqueous solution.
	(Read and Kable, 2007)	Macro	Chemistry	Undergraduate	General	Multiple experiments to stimulate interest of students to entropy are proposed. The workshops are then briefly connected with entropy and entropy changes. The workshops include the rubber band experiment, iodine sublimation, nicotine/water miscibility, phenol/water miscibility, the drinking duck, study of the NO2/N2O4 equilibrium, dissolution of NH4NO3 and Ba(OH)2, and heat packs.
	(Castellón, 2014)	Macro	Chemistry for engineers	Undergraduate	Specific	Heat engines are explained with the help of three toys: the drinking bird, the radiometer, and the Stirling engine. Illustration by toys is used to promote explicitly student motivation around entropy and thermodynamics in general.
	(Eisen et al., 2014)	Both	Chemistry	Undergraduate	Specific	A laboratory that offers to complement the traditional teaching of insolubility of cations and anions in aqueous solutions, by investigating the entropy-driven mechanisms of dissolution when combining selected salts in droplets of water, and observing precipitates.
	(Samuelsson et al., 2019)	Macro	Chemistry	Primary	Specific	The authors use infrared cameras to experiment with a simple life example: putting a piece of paper on a glass of water. First, they introduced the subject with saunas and “getting out of the shower”, then used the camera to see the temperature differences in the paper and in the air. The author argues for using more real-life experiments, whilst using an IR camera.
	(Rogers and Zhang, 2020)	Both	Chemistry	Undergraduate	Specific	The authors investigate the Hofmeister series, which describes how anions influence the thermodynamic properties of solutions. More precisely, caffeine partitioning in aqueous solutions is monitored by spectroscopy to reveal the importance of entropy in solvation phenomena.
	(Munakata et al., 2022)	Macro	Interdisciplinary	Undergraduate	General	A climate change-based experiment where students measure CO2 produced by biking at different speeds in a sealed room. Entropy production is metaphorically equated to CO2 production, to show that different amounts of entropy are generated by different processes (different biking speeds), while getting students interested in anthropogenic CO2, one of the key concepts to explain climate change.
Simulation	(Brosnan, 1989)	Macro	Physical chemistry	Undergraduate	Specific	The author uses excel spreadsheets to observe entropy changes in reactions. The spreadsheet computes ΔSsystem, ΔSenvironment and ΔSuniverse in order to visualize entropy changes at different temperatures, with the final goal of computing equilibrium partial pressures.
	(Moore and Schroeder, 1997)	Micro	Physics	Undergraduate	Specific	Excel spreadsheets illustrate Einstein solids entropy, as a simplified model for the exchange of energy between systems in contact, and as an introductory course to statistical thermodynamics.
	(Ashbaugh, 2010)	Micro	Chemistry	Undergraduate	General	The article proposes a simulation for Ehrenfest's lottery, a game about moving numbered balls from one urn to another, randomly, which illustrates the probabilistic nature of entropy.
	(Salagaram and Chetty, 2011)	Micro	Physics	Undergraduate	General	The simulation represents the canonical ensemble of a system with a few energy states, and focuses on the quality of the computing algorithm used, as well as the influence of different thermodynamic parameters on the energy distribution.
	(Mayorga et al., 2012)	Micro	Biochemistry	Undergraduate	Specific	The author provides an excel spreadsheet for simulating boxes (Fig. 7) that illustrate biochemical reactions. In these boxes, enthalpy is represented as the depth of a well, and entropy as the width of the well, making the changes very visual. A teaching sequence is proposed together with the spreadsheets. See author Ellis and Ellis (2008) in this table for an experimental demonstration version of this simulation.
	(Jameson and Brüschweiler, 2020)	Micro	Physical chemistry	Undergraduate	Specific	The article offers a Matlab/Python program to compute energy values for systems of particles, to give an intuitive sense of the Boltzmann distribution, without referring to complex mathematical procedures like the Lagrange multiplier method.
	(Zhang, 2020)	Micro	Chemistry	Undergraduate	General	A lattice model is proposed, similar to Moore and Schroeder (1997) with an interesting simulation application (page D) to reactions linking two macrostates, one for the reactants and one for the products.

---

As explained in the introduction, the microscopic view of entropy, and the connection between microscopic and macroscopic aspects of entropy are known to be key to the teaching of entropy. In our selection, 36% of articles were more macroscopic-oriented, 35% were more microscopic-oriented, and 29% offered some kind of connection between the two approaches (Fig. 4) (%_a: 78%, κ_cohen = 0.66, substantial, AC1 = 0.67, substantial).

Fig. 4 Types of point of view of the N = 91 articles from the RQ1 selection.

62 articles (68%) adopted a generalist perspective, meaning that they proposed a method to teach entropy across diverse chemical contexts, while the remaining 29 articles (32%) had a more specific perspective, focusing on teaching entropy within a defined context (%_a: 98%, κ_cohen = 0.90, almost perfect, AC1 = 0.98, almost perfect). Despite their specificity, these articles occasionally advocated for the generalizability of their methodologies beyond their initial context of application. Among these 29 articles, specific subjects included: coupled or simultaneous reactions (Aledo, 2007; Bindel, 2007), entropy of mixing and demixing (Brady, 1989; Gary, 2004; Ben-Naim, 2011; Kozliak, 2014), the explicit link between ΔS_universe and K_eq (Bindel, 1995, 2010), gas phase reactions (Brosnan, 1989), heat engines (Castellón, 2014), salt (in)solubility (Eisen et al., 2014; Rogers and Zhang, 2020), concentration gradient (Jadrich and Bruxvoort, 2010), Boltzmann distribution (Kozliak, 2004; Jameson and Brüschweiler, 2020), piston-and-cylinder systems (Kang et al., 2015), heat transfer (Kiatgamolchai, 2015), configurational entropy (Kozliak, 2009), crystallization (Laird, 1999), entropy of solids (Lambert and Leff, 2009), thermal reservoir entropy (Langbeheim et al., 2014), Einstein solids (Black et al., 1971; Moore and Schroeder, 1997; Phillips, 2016), evaporation and condensation (Samuelsson et al., 2019), the disorder metaphor (Styer, 2019), and entropy-temperature diagrams (Wood, 1975).

85% of articles did not use any educational theoretical framework (%_a: 96%, κ_cohen = 0.82, almost perfect, AC1 = 0.94, almost perfect). For most of these, the focus is purely didactical: explaining a new way to teach entropy, with new visual tools, with a new laboratory, with pedagogical arguments, etc. The remaining 15% (10 articles), were all (in Rodriguez et al.'s (2023) nomenclature) constructivist, except for one article referring mainly to a hermeneutics theoretical framework (Chinaka, 2021), and one article referring more to an “organization of chemical knowledge” theoretical framework (Read and Kable, 2007). Among the 8 constructivist articles, 5 used the conceptual change theoretical framework (Teichert and Stacy, 2002; Haglund and Jeppsson, 2014; Samuelsson et al., 2019; Volfson et al., 2019; Velasco et al., 2022).

RQ1a: hands-on activities. In Table 3, four types of hands-on activities were identified: demonstrations, games, laboratories, and simulations. Among the five demonstrations, three consisted of visual experiments elucidating the spontaneous diffusion of gases (diffusion through a ceramic beaker, through a latex balloon, or the movement of gas particles in a box). Notably, two other demonstrations (Plumb, 1964; Ellis and Ellis, 2008) offer unique insights.

Ellis and Ellis' (2008) demonstration (Fig. 5) diverges from conventional gas diffusion experiments by focusing on a visual representation of the microscopic aspect of the entropy variation between reactants and products. This innovative approach shows why entropy is essential for explaining the spontaneity of endothermic reactions on a microscopic level. Such pedagogical narratives are frequently employed in thermodynamics courses to underscore the significance of the second law before its formal introduction (e.g. why the endothermic dissolution of NH₄NO_3(s) is spontaneous). Ellis' device effectively visualizes the enthalpy–entropy distinction, crucial for dispelling common misconceptions regarding these concepts (Carson and Watson, 2002). Plumb's (1964) demonstration (Fig. 6) complements Ellis' approach by spotlighting the energy and entropy dynamics of a single particle suspended by a stream of air. This setup allows students to observe the particle's random fluctuations between low and high-energy states, with the task of quantifying the duration spent in each state. Plumb's device offers an insightful illustration of entropy modulation by varying the “width” of the states, akin to Ellis' demonstration but applied to a two-state single particle system.

Fig. 5 Ellis and Ellis’ (2008) device that makes light beads jump by a constant up-and-down movement propelled by a power tool. Entropy is represented by the width of the box, and enthalpy by the depth of the box, with A and B indicating reactants and products. Reprinted with permission from Ellis F. B. and Ellis D. C., (2008), An Experimental Approach to Teaching and Learning Elementary Statistical Mechanics, J. Chem. Educ., 85(1), 78–82. Copyright 2008 American Chemical Society.

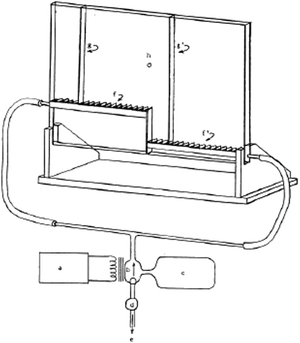Fig. 6 Plumb's (1964) device propels light beads up and down with an upwards flow of air, showing the random fluctuation of energy between two states. Reprinted with permission from Plumb R. C., (1964), Teaching the entropy concept, J. Chem. Educ., 41(5), 254–256. Copyright 1964 American Chemical Society.

The five games identified in this review highlight the microscopic statistical nature of entropy. By making students play with energy quanta, these games reveal the predictability of the Boltzmann distribution, in contradiction with the disorder metaphor, which completely hides this phenomenon. Michalek and Hanson's game (2006), for example, shows that, whatever the original distribution of (fake) money among the students, if they randomly interact (give each other one dollar whenever they lose a rock-paper-scissors game), then they always produce a Boltzmann distribution of energy (money) across all energy states (students).

Among the eight laboratories, two trends can be observed. One proposal is to increase the quality of the connection between reality and theory, either by a macroscopic, entropy-calculation approach (Bindel, 2004), or by a microscopic-oriented approach of solubility (Eisen et al., 2014; Rogers and Zhang, 2020). Each research team insists on a different, undertaught property of entropy. Bindel (2004) makes students compute ΔS_environment for multiple reactions, before performing the experiments in the lab. This approach underscores the importance of taking into consideration the increase or decrease of the entropy of the environment, which is usually obscured in chemistry teaching by the more often used ΔG_system = ΔH_system − TΔS_system < 0 spontaneity criterion at constant (T,P). Eisen et al. (2014) and Rogers and Zhang (2020) both reveal the underlying entropic phenomenon for salts (in)solubilities, by showing the water molecules clathrate-cage entropy changes that must be considered for understanding the solubility of aqueous ions. The other laboratory trend is the use of specific tools: toys (Read and Kable, 2007; Castellón, 2014) or infrared cameras (Samuelsson et al., 2019). For these authors, the two goals that toys can help with are motivating students in an often-despised subject, and giving a concrete, tangible, macroscopic view to entropy-driven phenomena. Samuelsson et al. (2019) agree with the later objective as they propose to use infrared cameras to visualize temperature and temperature changes for phase transitions accompanied by an entropy decrease of the system, such as condensation, whose enthalpy variation is notably counter-intuitive, because new bonds are created when water goes from the vapor to the liquid phase, and the exothermicity of chemical bond formation is a major difficulty in chemistry. Indeed, ΔS_system < 0 and ΔH_system < 0 for condensation, while T_{phase change} is constant.

The seven simulations exhibit a common trend reminiscent of one of the laboratories category: using simulation tools to provide intuitive insights into some phenomena without delving into extensive mathematical calculations. By introducing simulations, the researchers aimed to facilitate conceptual understanding while enhancing student motivation through interactive digital experiences. All the simulations included some elements of statistical thermodynamics, either by computing the Boltzmann distribution or the partition function, or enumerating micro- and macro-states in Excel, Python or MatLab. Among these simulations, the work by Mayorga et al. (2012) stands out for its unique focus on biochemical reactions—a rarity in the reviewed literature (4%). Biochemical reactions pose an apparent fundamental paradox with the disorder metaphor: how can such complex, intricate biochemical pathways, be spontaneous? To this question, Mayorga et al.'s (2012) boxes (Fig. 7) answer in a way similar to Ellis and Ellis’ device (2008), using excel spreadsheets to reproduce the demonstration apparatus, which uses wells to represent reactants or products’ energy and energy distribution, the depth of the well representing enthalpy and the width, entropy. We also highlight Brosnan's work (1989), because it focuses on entropy and entropy changes of individual reactants and products at different temperatures, which often lack in traditional thermodynamic teaching.

Fig. 7 Mayorga et al.'s (2012) simulation of boxes. Entropy is represented by the width of the box, and enthalpy by the depth of the box. Blue dots represent particles, and I and II indicate reactants and products. Reprinted with permission from Mayorga L. S., López M. J. and Becker W. M., (2012), Molecular Thermodynamics for Cell Biology as Taught with Boxes, CBE—Life Sci. Educ., 11(1), 31–38.

All simulation and game articles, except Brosnan (1989) used a microscopic approach, trying, in some way or another, to show the statistical nature of entropy. On the other hand, demonstrations and laboratories use either a macroscopic or a microscopic approach, or both. The two micro demonstrations (Plumb, 1964; Ellis and Ellis, 2008) joined objectives with games and simulations, providing machines to show the probabilistic evolution of entropy in chemical reactions, while the three others intend to show macroscopic phenomena, such as gas expansion (Haber-Schaim, 1983; Brady, 1989; Jadrich and Bruxvoort, 2010). Laboratories mainly have macroscopic-oriented objectives, like measuring heat exchange or temperature, or making students play with heat engines, with the notable exceptions of Eisen et al. (2014) and Rogers and Zhang (2020) who also have microscopic-oriented objectives, like explaining the statistical partitioning of molecules in different solvents, and other solvation phenomena.

RQ1b: microscopic vs. macroscopic approaches. The 66 theoretical, concept-based articles were further classified in their microscopic, macroscopic, or mixed teaching propositions, respectively 21 articles (32%), 30 articles (45%) and 15 articles (23%), to answer the RQ1b.

In the 21 microscopic-oriented articles, three trends were observed, even though some overlap occurred, since, for example, many articles criticize the disorder metaphor. We identified these trends considering the main goal of each article. A cluster of propositions (6 articles) centred on a microscopic-oriented sequence of lessons, which integrated some general introductory aspects of statistical thermodynamics, such as the Boltzmann distribution, micro- and macro-states, or the canonical partition function (Lambert, 2002; Novak, 2003; Kozliak, 2004; Jungermann, 2006), or went even further and provided a full teaching sequence (Schoepf, 2002; Cartier, 2009). Secondly, a group of authors (8 articles) argued that the disorder metaphor is too flawed to be used (Lambert, 1999; Styer, 2000), e.g. in the case of packing rigid spheres, where entropy and spatial disorder do not correlate (Laird, 1999), and/or offered a better descriptor for entropy, along with the corresponding interpretation of the second law of thermodynamics: quantum volume (Yu, 2020), Shannon's measure of entropy (Ben-Naim, 2011), energy spreading (Leff, 2007; Lambert, 2011). As a counterpoint, a single article (Jeppsson et al., 2013) argued for the use of the disorder metaphor, setting more explicit limits and offering suggestions for an improved metaphor use. Finally, 7 contributions suggested a microscopic-oriented entropy explanation focused on a specific topic: condensed phases (Kozliak, 2009), particle distinguishability (Kozliak, 2014), the proportionality of enthalpy and entropy in solids (Lambert and Leff, 2009), thermal reservoir entropy (Langbeheim et al., 2014), a connection between entropy and conceptual change (Volfson et al., 2019), and a three-chamber thought experiment (Zimmerman, 2010), using the thermal spreading of energy rather than the spatial spreading of particles (Lambert, 2007).

In the 30 macroscopic-oriented articles, two analogous trends were noticed, that is, full sequences or specific cases, as well as a 6-article group concerned with the ΔS_universe/ΔG_system articulation. 5 articles could not be categorized, showing a greater diversity of solutions. Firstly, 9 articles reported full sequences that relied on different improvements for teaching entropy: classical, reference textbook-like sequences (Williams and Glasser, 1991; Geller et al., 2014), a sequence with focus on heat engines (Cochran and Heron, 2006), a sequence with a focus on the common entropy conservation misconception (Christensen et al., 2009), a sequence proposal on energy degradation and environment (Ben-Zvi, 1999) or energy degradation in an interdisciplinary perspective (Poggi et al., 2017), the use of energy and entropy of atomization instead of standard entropy of formation (Spencer et al., 1996), as well as two articles emphasizing the need to change the traditional order of presentation of key concepts, introducing instead entropy before temperature and heat (Ross, 1988; De Abreu and Guerra, 2012).

Secondly, 6 articles centred on the transformation of the ΔS_universe > 0 spontaneity criterion into other criteria, putting forth the usefulness of the ΔS_universe > 0 criterion and the care and subtleness required to transform it into criteria based on ΔG_system or ΔA_system (Strong and Halliwell, 1970; Craig, 1988; Canagaratna, 2008; Gislason and Craig, 2013). Complementarily, Bindel (2004) argued for the use of the ΔS_universe > 0 criterion, because it puts into light the role of the environment, and a following article (Bindel, 2010) extended this “entropy analysis” method to equilibrium constants.

Thirdly, 10 specific cases were identified: a proof of Clausius’ equation without prior reference to the second law and using accessible mathematical background (integrating factor and arbitrary reversible cycle) (Hazelhurst, 1931), the friction generation in a piston-and-cylinder system (Kang et al., 2015), the positive entropy change of heat transfer between hot and cold objects (Kiatgamolchai, 2015), a visualization of the entropy of mixing (Gary, 2004), showing the interdependence of the first and the second laws (Kaufman and Leff, 2022), coupled reactions (Aledo, 2007), entropy-temperature diagrams (Wood, 1975), open systems (Kattmann, 2018), providing a macroscopic-oriented explanation of Lambert and Leff's spreading metaphor (Moore, 2022), and the non-zero work for non-spontaneous transformations (Keifer, 2019).

Finally, several contributions which could not be unambiguously classified in the previous categories deserve being mentioned, too. Teichert and Stacy (2002) proposed self-reflective exercises on the second law. Fuchs (1987) offered some advice on the use of specific words in thermodynamics. Velasco et al. (2022) integrated the teaching of entropy in class coordination theory (CCT), a conceptual change-based theory integrating sociocultural views where the limits of applications of laws and inferences are more clearly defined. Muller (2012) and Strnad (1984) suggested to connect entropy with the history of thermodynamics to better understand the origin of the concept and thus improve its teaching.

15 articles did not belong to any clear-cut microscopic or macroscopic category, either because the authors explicitly intended to connect both points of view or because it was not one of the major aspects of the article. For the former case, 4 articles tackled this connection: Akbulut and Altun (2020) by transposing the chemistry triplet into a three-tiered explanation based on, first, a macroscopic introduction of the connection between energy and entropy, then a probabilistic explanation based on the dispersal of energy and the unavailability of the energy to do useful work, and Baierlein (1994), Kincanon (2013) and Bhattacharyya and Dawlaty (2019) connecting the Clausius and Boltzmann definitions of entropy. For the latter case, a subgroup of 5 articles focused on the use of metaphors and analogies. Haglund and Jeppsson propose to use self-generated metaphors (Haglund and Jeppsson, 2012, 2014) or to use the disorder metaphor (Haglund, 2017) but in an improved way, while Wu and Wu (2020, 2021) developed an electricity/entropy analogy, defining terms like thermal charge (corresponding to electric charge) or momentum current (corresponding to electric current), at the risk of introducing a substantialist obstacle (Bachelard, 1938). Five articles that proposed mixed points of view were developed by the authors in full teaching sequences, giving recommendations on how to teach entropy from A to Z, but with different focuses: a thorough discussion of multiple points of view of the chemistry triplet (Leff, 1996, 2012), the use of semantic waves, a linguistic approach that proposes to go back and forth between concrete and abstract concepts (Chinaka, 2021), the help from computer visualizations and concrete examples (Langbeheim et al., 2020) or the use of pressure–volume diagrams (Iyengar and deSouza, 2014). Finally, Atarés et al. (2021) suggested a range of solutions as a small review in the fourth part of the article, along which the connection of microscopic and macroscopic methods.

RQ2: Measured effectiveness of the teaching proposals

To answer this research question, a subset of 9 articles from the N = 91 RQ1 selection qualified for the meta-analysis, because they reported a quantitative evaluation of their method. Thus, less than 10% of all methods proposed in our literature selection underwent a basic testing of their effectiveness, even less a quantitative replication procedure. The main article characteristics are summarized in Table 4. Among the 9 articles, 3 had been coded as hands-on activities (Read and Kable, 2007; Castellón, 2014; Munakata et al., 2022) (cf.Table 3) and the 6 others as theoretical articles.

Table 4 Main characteristics of the articles selected for the meta-review. MCQ for multiple-choices question, N for the number of students, M for mean, SD for standard deviation. Subscript C for control group, T for test group. If N has no subscript, the article did not use a control/test design. Columns 1 through 9 report data from the articles. Effect size column values are all calculated by our research team. The values of the “quantitative results” column were sometimes reported, sometimes calculated from the data of the articles; in that column, the reported pages are the pages used for calculations or report of values; if the values were calculated, they are signalled with an asterisk (*) and are explained in the “method of calculation if applicable” column. All cells that display at least one value calculated in the present work are shaded in grey

---

Almost all articles followed different teaching objectives and strategies. Poggi et al. (2017) aimed at improving teaching of energy transformation through a 6-week interdisciplinary sequence. Cochran and Heron (2006) developed two innovative tutorials to enhance the connection between heat engines and entropy. Ben-Zvi (1999) implemented a long module to improve non-science students' conceptions of energy, entropy, and science in general. The originality of the approach compared to the other reviewed articles is that it focuses on attitude towards science, not on performance. It is essentially non-mathematical. Teichert and Stacy (2002) used discussions of alternative conceptions to improve understanding of entropy. Christensen et al. (2009) created a “two-block” tutorial targeting the “entropy is conserved” alternative conception. Castellón (2014) and Read and Kable (2007) centred their laboratories on understanding simple yet striking phenomena or toys. Munakata et al. (2022) focused on interdisciplinary teaching of entropy through climate change illustration. Chinaka (2021) used a teaching sequence based on the semantic waves theory, which involves moving back and forth between abstractness and concreteness in lectures.

Accordingly, we observe that methodologies of reporting are diverse. For example, 4 out of the 9 articles used interviews to help interpret written answers from students. 4 articles assessed the achievement means (M) of entropy understanding (Ben-Zvi, 1999; Teichert and Stacy, 2002; Poggi et al., 2017; Munakata et al., 2022). In addition, the three latter articles provided standard deviations (SD) on assessment (Ben-Zvi, 1999; Teichert and Stacy, 2002; Poggi et al., 2017). 2 articles reported success rates in proportions of students that chose the correct answer (F) (Cochran and Heron, 2006; Christensen et al., 2009), while 3 articles did not assess achievement, only self-reported appreciation, motivation and understanding towards the innovative teaching (Read and Kable, 2007; Castellón, 2014; Chinaka, 2021). For the 5 articles that reported M, SD or F for student performance or attitude (and not satisfaction), we computed effect sizes (see methodology) that showed for all of them some level of significance in teaching entropy better and/or improving students’ image of science (see Table 4). These values should be considered with caution, given the small number of articles, the sometimes-small number of participants and the diversity of methods and objectives. For example, Ben-Zvi (1999) and Teichert and Stacy (2002) use a pre-post, control-test design that allows for a d_ppc2 computation, but have widely different objectives: respectively, improving the attitude of non-science students towards science (d_ppc2 = 4.4), and discussing alternative conceptions with students to improve their performance on conceptual tests (d_ppc2 = 0.64).

Effect size d values were very large for Poggi et al. (2017), d_Cohen = 2.1 and Ben-Zvi (1999), d_{ppc2,attitude} = 4.4 and d_ppc2,image = 3.0, and medium-large for Teichert and Stacy (2002), d_ppc2 = 0.64. ϕ values were large for Christensen et al. (2009), ϕ_Q1 = 0.48, ϕ_Q2 = 0.47 and moderate-large for Cochran and Heron (2006), ϕ_Carnot = 0.32 and ϕ_entropy = 0.38. These five studies were assessed for risk of bias (Table 5).

Table 5 Assessment of the risk of bias (RoB) of the meta-analysis articles. OA for overalignment, SP for single parameter, SD for systematic difference, TA for time alignment, SAT for Scholastic Aptitude Test, RoB for Risk of Bias. The authors of the reference (Cochran and Heron, 2006) were contacted for a clarification of comprehension of their article, but no ESI was added from that exchange. Details on the RoB criteria are provided in the Method section

Ref.	Outcome measure				Confounding factors			Assignment	Compositional change	Baseline equivalence	RoB evaluation
	Face validity	Reliability	No OA	Consistency	SP	SD	TA
(Poggi et al., 2017)	Energy degradation and entropy were effectively measured via 5 MCQ each in a 30 MCQ test on energy.	The results were consistent between the different parts of the test.	The same concepts were taught in the control group, and the number of teaching lessons and experiments were the same.	The same questionnaire was used for both groups.	Unclear. All the students came from the same school, the NC = 49 coming from three classes, but the number of classes of the NT = 39 students was not reported	No difference	No difference	Quasi-experimental design.	Not applicable since no pre-test	Not measured since no pre-test	Intermediate, because of the absence of baseline equivalence
								No reported reason for the choice of assignement of one class to control or test group
(Ben-Zvi, 1999)	Attitude towards science and image of science consisted of Likert scales appreciations pertaining to these subjects.	The results were consistent across different categories tested (e.g. importance, easiness for attitude towards science).	Unclear. It seemed to be the usual teaching method for the control group, but no further details	The same questionnaire was used for both groups.	In the same school, 7 classes for the test group and multiple classes (number not disclosed) for the control group	The test group consisted of non-science oriented students, and the control group of science-oriented students.	Not reported	Not reported	Not reported	Performance statistically the same at a junior high school 25-items questionnaire but attitude toward science and image of science significantly worse for the test group at pre-test	Unclear, because the authors did not address explicitly the pre-test difference of image of science and attitude towards science, and because the teaching conditions of the control group were unclear.
(Teichert and Stacy, 2002)	Performance about the spontaneity concept was measured via multiple appropriate variables: midterm scores, standardized tests (Scholastic Aptitude Test, SAT) and interviews.	The results were consistent between the three measurements for qualitative questions on spontaneity, not for quantitative questions on spontaneity.	No unfair advantage: the intervention group had the same discussion time on spontaneity concepts, only the method (control: lecture and test: discussion on misconceptions) was different. All other didactic aspects were the same (e.g. lecture and lab attendance).	The same questions were administered to both groups.	There was only one class for control, and one class for test.	No difference	No difference	Quasi-experimental design.	Not reported	SAT math, verbal and total, as well as a concept test were used for comparison. No statistically significant difference	Low
								Out of 9 simultaneous discussion classes, one was chosen as control, the other as test. No reported reason for the choice.
(Cochran and Heron, 2006)	Second law understanding was measured via three questions about heat engines and refrigerators requiring multi-step reasoning, but only one of the three question was completed by all groups.	The post-test results were consistent across the three control groups, and the three “entropy” test groups for the “heat engine” question.	Unclear. The authors state that the “Carnot” and “entropy” tutorials were supplemental, provided homework and non-mandatory, but there are no reports of length or clear difference with the control group.	The same question was administered to every group, and two groups (one control, one test), were given the three questions.	N = 3 different groups from two universities for the control group, N = 3 different groups from two different universities for the “entropy” test group, but N = 1 course from one university for the “Carnot” test group. Only one group from one university (UC) was compared between control and test.	It is unclear whether the UC test group and control group were from the same year, or from different years. UW and SPU groups were from different universities than the UC groups.	Unclear	Quasi-experimental design. Each group was an undefined section of a course at a different university.	Not applicable since no pre-test	Not measured (no pre-test)	Intermediate, because of the absence of baseline equivalence
(Christensen et al., 2009)	Second law understanding was measured by two questions, one in a general context, the other in a concrete context, by asking to predict the values of ΔSsystem, and ΔSenvironment.	The pre-test results were consistent across four groups of students.	No unfair advantage. The control group and the test group had the same kind of exercise-based tutorial, with the same topic covered, only in a formally different way.	The same questions were administered to all groups.	N = 4 groups in the pre-test (various groups from various universities), but N = 1 matched student group for the test group, in one university.	No difference	The control group was the 2005 cohort for the course, the test group was the 2006 cohort for the course.	Quasi-experimental design. The 2005 cohort was assigned to control, the 2006 cohort to test group.	Not reported	Answers to the questionnaire between the 2005 cohort and the 2006 cohort not statistically different, and not different from three other samples of students from different universities	Low

---

To answer the RQ2, we showed that even though articles that offer a solution to teach entropy and the second law of thermodynamics are numerous, they lack the assessment of their proposed method. Furthermore, the 9 articles that reported testing methods either focused on satisfaction or performance, or lead to very large effect sizes which seem unrealistic when compared with literature-reported usual ones. For example, Hill et al. (2008) showed that the mean effect size for math tests decreases from 1.14 in grade K-1 to 0.01 in grade 11–12, and advised caution when using Cohen's criterion to interpret effect sizes, suggesting to nuance the value when the students get older. Risk of bias among the five studies were evaluated as low for Teichert and Stacy (2002) and Christensen et al. (2009), unclear for Ben-Zvi (1999) and moderate for Poggi et al. (2017) and Cochran and Heron (2006). For the latter, the absence of measured baseline equivalence (no pre-test measurement) undermined any clear analysis of the intervention effect. For Ben-Zvi (1999), absence of discussion of the pre-test differences and of details of the teaching conditions of the control group rendered the evaluation of risk of bias difficult. For Teichert and Stacy (2002) and Christensen et al. (2009), minor concerns were raised in Table 5, but we estimated their risk of bias as low.

Given this risk of bias evaluation, and that the objectives, measurements, and methods of all the RQ2 articles were very diverse, we estimate the overall body of evidence as quite uncertain. This result calls for an improvement of quantitative methodology and a standardization of reported measurements of quasi-experimental studies in thermodynamics education, to improve review quality.

Discussion

The RQ1 examined how the literature offered to tackle abstraction, mathematical complexity, the emergent nature of entropy, and incidentally, perceived motivation towards learning thermodynamics. To address abstractness, our results showed that some laboratories offered connections between reality and theory, either using the macroscopic approach of thermodynamics, or the microscopic approach. Other laboratories proposed visualisation approaches, such as infrared cameras (Samuelsson et al., 2019), to help bridge microscopic properties of matter with macroscopic phenomena; so did some demonstrations, such as Ellis and Ellis (2008). Many authors also proposed to directly introduce the microscopic method, which can seem less abstract. However, as Tsaparlis (2016) states, undergraduate students find statistical thermodynamics more mathematically difficult. Though it is possible that students’ feelings do not necessarily reflect what fosters at best their conceptual understanding, the games and simulations presented in the results might lay the ground for a deeper understanding of concepts such as the Boltzmann distribution or micro-states, before entering the associated mathematical details later in the physical chemistry curriculum. Alleviating mathematical complexity was dealt in two ways. First, by using qualitative approaches that illustrate essential concepts with images, figures, or games. For example, a more intuitive perception of the key concept of Boltzmann distribution can be gained with the Michalek and Hanson (2006) Boltzmann game, where students just have to play at rock-paper scissors, before introducing the mathematical tool of factorials. Second, we identified seven simulations that computed quantitative parameters without the (sometimes heavy) burden of by-hand calculations. These simulations did not aim at replacing student computations, but rather accompany them, or illustrate core concepts of thermodynamics before considering mathematical aspects. With simple simulations, we can help students with what Brosnan (1989, p. 39) elegantly pointed out more than 30 years ago: “The entropy concept is a uniquely powerful unifying concept in chemistry, yet it can also quickly become so mathematical that its essentially simple and powerful ideas are lost in a welter of calculations.”

The review by Bain et al. (2014) underscored the key aspect of the back and forth between the microscopic and macroscopic points of view. Taber (2013, p. 166) pointed out in its redesign of the chemistry triplet that, going from Johnstone's symbolic, macroscopic and microscopic points of view towards a triangle made up of everyday experience, macroscopic conceptualization and microscopic conceptualization (the symbols establishing a link between macro and micro): “[…] ventures into the triangle should be about relating previously taught material, and should be modelled carefully by the teacher before students are asked to lead expeditions there; and such explorations should initially be undertaken with carefully structured support.” In the answers to RQ1b, we showed that several authors underscore the lack of careful explanation on the fundamental micro–macro connection between the Boltzmann and Clausius definitions of entropy, and proposed methods to address it. The disorder metaphor is described as a “cracked crutch” (Lambert 2002) that might make the ventures in the chemistry triplet, and the combination of the macroscopic and microscopic methods difficult. The literature does not lack ideas to replace the metaphor by other ones. As Souza et al. (2023, p. 51) put it: “Analogies and metaphors need not to be banned from chemistry teaching. However, they must be used appropriately, acknowledging their limitations and avoiding reinforcement of common-sense ideas and errors”. On the contrary, the disorder metaphor, as, for example Atarés et al. (2021) or Sreenivasulu and Subramaniam (2013) have pointed out, may generate several alternative conceptions about entropy and the second law of thermodynamics.

In the review, we gathered microscopic, macroscopic, or combined/hybrid symbolic representations of entropy that seemed particularly useful to address the emergent nature of entropy, which is a pivotal transition from the microscopic to the macroscopic conceptualization in the chemistry triplet, especially in the “both” coding categorization of articles of the RQ1b. Let us review three examples. First, Gary (2004) proposes a microscopic-oriented illustration of the entropy of mixing, which is notoriously difficult for students, for its conceptual connection with Gibbs free energy. It employs both a simple molecular visualization of molecules as spheres, and a visual analogy of “forces” (linked to ΔH, ΔS_nonmix and ΔS_mix) that “push” the system towards a certain position of equilibrium (Fig. 8). Second, Yu (2020) suggests a combination of microscopic and macroscopic symbols: a conceptualization of a piston-and-cylinder system (macro) combined with the concept of quantum volume (micro) of gas atoms, applied to an expansion–compression cycle (Fig. 9). Finally, Bhattacharyya and Dawlaty (2019) describe an adiabatic reversible compression from a classical statistical mechanics phase space perspective that includes both the compression of particles in real space and the expansion of their corresponding momentum space. Emergence is made apparent: the first volume (in red) is a macroscopic representation of the physical volume of the system, while the second volume (in blue) is a symbolic representation of the accessible momenta of the particles, so more microscopic-oriented (Fig. 10).

Fig. 8 Microscopic-oriented representation of mixing entropy, Reprinted with permission from Gary R. K., (2004), The Concentration Dependence of the ΔS Term in the Gibbs Free Energy Function: Application to Reversible Reactions in Biochemistry, J. Chem. Educ., 81(11), 1599–1604. https://doi.org/10.1021/ed081p1599.

Fig. 9 Combination of a microscopic (quantum volume) and macroscopic (piston-and-cylinder system) representations for an irreversible expansion and compression of an ideal gas. Reprinted with permission from Yu T. H., (2020), Teaching Thermodynamics with the Quantum Volume, J. Chem. Educ., 97(3), 736–740. https://doi.org/10.1021/acs.jchemed.9b00742.

Fig. 10 Combination of a microscopic (abstract momentum space) and macroscopic (real space) representations for an adiabatic reversible compression of an ideal gas. Reprinted with permission from Bhattacharyya D. and Dawlaty J. M., (2019), Teaching Entropy from Phase Space Perspective: Connecting the Statistical and Thermodynamic Views Using a Simple One-Dimensional Model, J. Chem. Educ., 96(10), 2208–2216. https://doi.org/10.1021/acs.jchemed.9b00134.

The literature targets the attitude towards thermodynamics, and entropy, in two ways. Theoretical concept-based proposals assume frustration comes from a misunderstanding of a specific concept, or from a general didactic problem in the thermodynamics teaching sequence and try to solve these problems. Articles reporting hands-on approaches assume gamification and laboratory practice will induce motivation, approximated by the measure of students’ reported satisfaction with an activity, or attitude towards thermodynamics. In the RQ2 results, Read and Kable (2007) and Castellón (2014) reported laboratories greatly appreciated by students. Finally, Ben-Zvi (1999) conducted the most robust experiment on student attitude towards science, though its risk of bias is unclear. The author found that, for non-science-oriented students, providing explicit links between everyday life and theory, as well as showing the usefulness of thermodynamics, could significantly increase students’ attitude towards science and image of science in the context of thermodynamics, though intrinsic motivation is difficult to measure and has, in the concerned articles, been accessed only through student self-reported data.

Some concept-based articles discuss purely didactical aspects of entropy, such as the choice of presenting either the ΔS_universe or the ΔG_system spontaneity criterion to students, the former one clearly emphasizing the contribution of ΔS_environment, which the latter evades with the advantage of easier applications to real cases. Moreover, some authors suggest to revisit the order in which information is presented and several articles offer innovative alternatives to the disorder metaphor, that have much more relevant properties, and clearer limits.

Chemistry and physics are represented in this review, but less so biology and biochemistry. Unfortunately, as Bain et al. (2014), and Dreyfus et al. (2015) already pointed out ten years ago, there are almost no interdisciplinary articles in the literature. The main hurdle to interdisciplinarity ought to be the division of thermodynamics into different, compartmented subjects, even though many shared learning points can be thought of: coupled reactions and equilibria in biochemistry, converging perspectives in statistical thermodynamics in physical chemistry, abstract concepts shared by physics and engineering, and so on. Different learning objectives (e.g. learn the rules of the universe in physics or make turbines in engineering) should not discourage teachers and researchers from pursuing a common base curriculum for thermodynamics, that encompasses and tackles all the problems highlighted in this review.

The meta-analysis of 9 articles underscored the fact that there are only a minority (about 10%) of articles containing quantitative data to be analysed. Reported methods were difficult to compare, and thus the computed effect sizes were also difficult to compare. We agree with Bain et al. (2014) on this point: testing methods, instead of creating new ones, should be the priority for research.

Limitations

The main limitation of this review is that the first author was the only person to screen all 300 initial articles of the database. However, both authors contributed to the retrieval of qualitative and quantitative data from the selection of 91 articles used to answer the research questions. Risks of bias, especially in the definition of categories, such as “microscopic-oriented” or “macroscopic-oriented”, “generalist perspective” or “specific perspective” might remain though the authors tried to attenuate this limitation by using as explicitly as possible the PRISMA method and interrater reliability was estimated. In addition, the restraint to two databases (ERIC and SCOPUS), which were chosen to cap the number of articles, could have induced some reporting bias in the results. Other databases, such as Web of Science or specific journal databases, should be included in further research. Finally, the What Works Clearinghouse criteria have not been used often in science education literature, and their use in the PRISMA method is not yet standard, though the authors hope having shown their interest to improve review quality.

Implications for teachers

Our synthesis of the literature points towards the replacement or the better use of the disorder metaphor when teaching entropy. Good practice could include any of the proposals mentioned in the results (section RQ1b) such as providing very explicit limits of the metaphor, replacing it by another word or concept, such as Shannon's measure of information, the space volume, the quantum volume, energy degradation, spreading, freedom, or others. Good practice could also include paradoxical cases, which the literature does not lack, such as the apparent contradiction between disorder and the predictability of the Boltzmann distribution, or between disorder and the spontaneous complexity of living organisms, or between disorder and spontaneous demixing cases. Multiple articles suggest ways to connect entropy to everyday life, and to its more intuitive statistical nature. In Table 3, as a possible way to tackle two of the key issues of entropy teaching (RQ1a, abstraction and mathematical complexity), we synthesized the characteristics of hands-on approaches to teach entropy, which we hope will be useful to the thermodynamics teachers. Finally, considering which teaching methods have the strongest support from experimental data, our meta-analysis shows that Christensen et al.'s, (2009) and Teichert and Stacy's (2002) methods, aimed at undergraduate students, have the lowest risk of bias in our selection.

Implications for researchers

We support Bain et al.'s (2014) call for more interdisciplinary testing of methods to teach entropy, especially with physics and engineering education research, which have different curriculum objectives, but the same didactical hurdles.

Methodologically, we observe that less than 10% of the selected articles provide quasi-experimental data to support their pedagogical claims. We thus advise future researchers to shift from theoretical suggestions to the testing of proposed method and hope this review will be of use to them. Moreover, our risk of bias assessment, based on the standard criteria of What Works Clearinghouse, show that methodological standards of randomized control trials, or quasi-experimental investigations, can be greatly improved, especially concerning the management of the students joining in the study, or leaving the study, the “single parameter” confounding factor, and the justification of randomization or assignment of each group to the test or control conditions. Accordingly, the use of validated thermodynamics tools such as THEDI (Sreenivasulu and Subramaniam, 2013) or TCRI (Firetto et al., 2021) should help research teams to produce easy-to-get and reproducible results.

Conclusion

Entropy and the second law of thermodynamics are hard to teach and to learn, but many solutions are offered in the literature: games, simulations, experimental demonstrations, and laboratories, to offer more links with everyday life, manage mathematical burden and make the entropy concept less abstract, while aiming at improving students’ motivation by making it more relevant and, possibly, more fun. Microscopic-oriented methods of teaching, that rely on an introductory, essentially non-mathematical, approach to statistical thermodynamics, help students grasp the predictable, probability-based nature of entropy, while evading the shortcomings of the disorder metaphor. The disorder metaphor is heavily criticized because of the didactical hurdles it poses to teach the emergent and statistical nature of entropy, but many authors suggest ways to replace or modify it. Our meta-analysis shows some promising yet uncertain effect sizes for tested methods, but more research work and homogenization of research practices, as well as risk of bias reduction, are needed.

Author contributions

VN retrieved the articles from the online databases, coded the articles, performed the systematic analysis and the meta-review. BL coded the articles. VN and BL both wrote the article.

Data availability

Since this is a systematic review with meta-analysis, no primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors would like to thank Dr Dylan Dachet for his help on how to use the PRISMA methodology in a science education review.

References

1. Akbulut F. and Altun Y., (2020). A Holistic Approach to Entropy in Science Education, Int. Online J. Sci. Educ., 7(4), 1913–1932.
2. Aledo J. C., (2007), Coupled reactions versus connected reactions: coupling concepts with terms, Biochem. Mol. Biol. Educ., 35(2), 85–88 DOI:10.1002/bmb.5.
3. Ashbaugh H. S., (2010), Ehrenfest's Lottery—Time and Entropy Maximization, Chem. Eng. Educ., 44(3), 229–235.
4. Atarés L., Canet M. J., Trujillo M., Benlloch-Dualde J. V., Paricio Royo J. and Fernandez-March A., (2021), Helping Pregraduate Students Reach Deep Understanding of the Second Law of Thermodynamics, Educ. Sci., 11(9), 539 DOI:10.3390/educsci11090539.
5. Bachelard G., (1938), La formation de l'esprit scientifique [The formation of the scientific mind], Vrin.
6. Baierlein R., (1994), Entropy and the second law: a pedagogical alternative, Am. J. Phys., 62(1), 15–26 DOI:10.1119/1.17732.
7. Bain K., Moon A., Mack M. R. and Towns M. H., (2014), A review of research on the teaching and learning of thermodynamics at the university level, Chem. Educ. Res. Pract., 15(3), 320–335 10.1039/C4RP00011K.
8. Ben-Naim A., (2011), Entropy: Order or Information, J. Chem. Educ., 88(5), 594–596 DOI:10.1021/ed100922x.
9. Ben-Naim A., (2012), Entropy and the Second Law: Interpretation and Misss-Interpretationsss, World Scientific Publishing.
10. Bennett J. M. and Sözbilir M., (2007), A Study of Turkish Chemistry Undergraduates’ Understanding of Entropy, J. Chem. Educ., 84(7), 1204–1208 DOI:10.1021/ed084p1204.
11. Ben-Zvi R., (1999), Non-science oriented students and the second law of thermodynamics, Int. J. Sci. Educ., 21(12), 1251–1267 DOI:10.1080/095006999290057.
12. Bhattacharyya D. and Dawlaty J. M., (2019a), Teaching Entropy from Phase Space Perspective: Connecting the Statistical and Thermodynamic Views Using a Simple One-Dimensional Model, J. Chem. Educ., 96(10), 2208–2216 DOI:10.1021/acs.jchemed.9b00134.
13. Bhattacharyya D. and Dawlaty J. M., (2019b), Teaching Entropy from Phase Space Perspective: Connecting the Statistical and Thermodynamic Views Using a Simple One-Dimensional Model, J. Chem. Educ., 96(10), 2208–2216 DOI:10.1021/acs.jchemed.9b00134.
14. Bindel T. H., (1995), Solution-Phase Thermodynamics: A “Spontaneity” Activity, J. Chem. Educ., 72(1), 34–35 DOI:10.1021/ed072p34.
15. Bindel T. H., (2004), Teaching Entropy Analysis in the First-Year High School Course and Beyond, J. Chem. Educ., 81(11), 1585–1594 DOI:10.1021/ed081p1585.
16. Bindel T. H., (2007), Discovering the Thermodynamics of Simultaneous Equilibria. An Entropy Analysis Activity Involving Consecutive Equilibria, J. Chem. Educ., 84(3), 449–452 DOI:10.1021/ed084p449.
17. Bindel T. H., (2010), Understanding Chemical Equilibrium Using Entropy Analysis: The Relationship Between ΔS_tot (sys°) and the Equilibrium Constant, J. Chem. Educ., 87(7), 694–699 DOI:10.1021/ed100192q.
18. Black P. J., Davies P. and Ogborn J. M., (1971), A Quantum Shuffling Game for Teaching Statistical Mechanics, Am. J. Phys., 39(10), 1154–1159 DOI:10.1119/1.1976594.
19. Brady K. T., (1989), Shine some light on entropy of mixing, J. Chem. Educ., 66(4), 339–341 DOI:10.1021/ed066p339.
20. Brosnan T., (1989), Teaching chemistry using spreadsheets—I: Equilibrium Thermodynamics, School Sci. Rev., 70(252), 39–47.
21. Canagaratna S. G., (2008), Zeroth Law, Entropy, Equilibrium, and All That, J. Chem. Educ., 85(5), 732–736 DOI:10.1021/ed085p732.
22. Carson E. M. and Watson J. R., (2002), Undergraduate Students’ Understandings of Entropy and Gibbs Free Energy, Univ. Chem. Educ., 6, 4–12.
23. Cartier S. F., (2009), An Integrated, Statistical Molecular Approach to the Physical Chemistry Curriculum, J. Chem. Educ., 86(12), 1397–1402 DOI:10.1021/ed086p1397.
24. Castellón E., (2014), Application of the Second Law of Thermodynamics To Explain the Working of Toys, J. Chem. Educ., 91(5), 687–691 DOI:10.1021/ed400085z.
25. Chinaka T. W., (2021), Introducing the second law of thermodynamics using Legitimation Code Theory among first year chemistry students, Cypriot J. Educ. Sci., 16(3), 981–994 DOI:10.18844/cjes.v16i3.5772.
26. Christensen W. M., Meltzer D. E. and Ogilvie C. A., (2009), Student ideas regarding entropy and the second law of thermodynamics in an introductory physics course, Am. J. Phys., 77(10), 907–917 DOI:10.1119/1.3167357.
27. Cochran M. J. and Heron P. R. L., (2006), Development and assessment of research-based tutorials on heat engines and the second law of thermodynamics, Am. J. Phys., 74(8), 734–741 DOI:10.1119/1.2198889.
28. Cohen J., (1988), Statistical Power Analysis for the Behavioral Sciences, Lawrence Erlbaum Associates.
29. Craig N. C., (1988), Entropy analyses of four familiar processes, J. Chem. Educ., 65(9), 760–764 DOI:10.1021/ed065p760.
30. Dachet D., (2024), Umbrella Review: De sa méthodologie aux considérations méthodologiques relatives à son application dans le champ des sciences de l’Éducation [Umbrella Review: From its methodology to methodological considerations relating to its application in the field of educational sciences] [Doctoral dissertation, University of Liège (Belgium)].
31. De Abreu R. and Guerra V., (2012), Introducing thermodynamics through energy and entropy, Am. J. Phys., 80(7), 627–637 DOI:10.1119/1.3698160.
32. Donnelly J. and Hernández F. E., (2018), Fusing a reversed and informal learning scheme and space: student perceptions of active learning in physical chemistry, Chem. Educ. Res. Practice, 19(2), 520–532 10.1039/C7RP00186J.
33. Dreyfus B. W., Geller B. D., Meltzer D. E. and Sawtelle V., (2015), Resource Letter TTSM-1: Teaching Thermodynamics and Statistical Mechanics in Introductory Physics, Chemistry, and Biology, Am. J. Phys., 83(1), 5–21 DOI:10.1119/1.4891673.
34. Eisen L., Marano N. and Glazier S., (2014), Activity-Based Approach For Teaching Aqueous Solubility, Energy, and Entropy, J. Chem. Educ., 91(4), 484–491 DOI:10.1021/ed4005563.
35. Ellis F. B. and Ellis D. C., (2008), An Experimental Approach to Teaching and Learning Elementary Statistical Mechanics, J. Chem. Educ., 85(1), 78–82 DOI:10.1021/ed085p78.
36. Firetto C. M., Van Meter P. N., Kottmeyer A. M., Turns S. R. and Litzinger T. A., (2021), An extension of the Thermodynamics Conceptual Reasoning Inventory (TCRI): measuring undergraduate students’ understanding of introductory thermodynamics concepts, Int. J. Sci. Educ., 43(15), 2555–2576 DOI:10.1080/09500693.2021.1975847.
37. Fuchs H. U., (1987), Entropy in the teaching of introductory thermodynamics, Am. J. Phys., 55(3), 215–219 DOI:10.1119/1.15216.
38. Gary R. K., (2004), The Concentration Dependence of the ΔS Term in the Gibbs Free Energy Function: Application to Reversible Reactions in Biochemistry, J. Chem. Educ., 81(11), 1599–1604 DOI:10.1021/ed081p1599.
39. Geller B. D., Dreyfus B. W., Gouvea J., Sawtelle V., Turpen C. and Redish E. F., (2014), Entropy and spontaneity in an introductory physics course for life science students, Am. J. Phys., 82(5), 394–402 DOI:10.1119/1.4870389.
40. Gislason E. A. and Craig N. C., (2013), Criteria for Spontaneous Processes Derived from the Global Point of View, J. Chem. Educ., 90(5), 584–590 DOI:10.1021/ed300570u.
41. Grassian V. H., Meyer G., Abruña H., Coates G. W., Achenie L. E., Allison T., Brunschwig B., Ferry J. and Garcia-Garibay M., (2007), Viewpoint: Chemistry for a Sustainable Future, Environ. Sci. Technol., 41(14), 4840–4846 DOI:10.1021/es0725798.
42. Gwet K., (2002), Kappa Statistic is not Satisfactory for Assessing the Extent of Agreement Between Raters, https://api.semanticscholar.org/CorpusID:140400911.
43. Haber-Schaim U., (1983), The role of the second law of thermodynamics in energy education, Phys. Teacher, 21(17), 17–20 DOI:10.1119/1.2341180.
44. Haglund J., (2017), Good Use of a ‘Bad’ Metaphor: Entropy as Disorder, Sci. Educ., 26(3–4), 205–214 DOI:10.1007/s11191-017-9892-4.
45. Haglund J. and Jeppsson F., (2012), Using self-generated analogies in teaching of thermodynamics, J. Res. Sci. Teach., 49(7), 898–921 DOI:10.1002/tea.21025.
46. Haglund J. and Jeppsson F., (2014), Confronting Conceptual Challenges in Thermodynamics by Use of Self-Generated Analogies, Sci. Educ., 23(7), 1505–1529 DOI:10.1007/s11191-013-9630-5.
47. Hattie J., (2008), Visible Learning. A Synthesis of Over 800 Meta-Analyses Relating to Achievement, Routledge.
48. Hayes J. C. and Kraemer D. J. M., (2017), Grounded understanding of abstract concepts: the case of STEM learning, Cogn. Res.: Princ. Implic., 2(1), 7 DOI:10.1186/s41235-016-0046-z.
49. Hazelhurst T. A., (1931), Exorcising a Spectre: Entropy. J. Chem. Educ., 8(3), 498–503.
50. Hill C. J., Bloom H. S., Black A. R. and Lipsey M. W., (2008), Empirical Benchmarks for Interpreting Effect Sizes in Research, Child Dev. Perspectives, 2(3), 172–177 DOI:10.1111/j.1750-8606.2008.00061.x.
51. Iyengar S. S. and deSouza R. T., (2014), Teaching Thermodynamics and Kinetics to Advanced General Chemistry Students and to Upper-Level Undergraduate Students Using PV Diagrams, J. Chem. Educ., 91(1), 74–83 DOI:10.1021/ed400480t.
52. Jadrich J. and Bruxvoort C., (2010), Investigating Diffusion and Entropy with Carbon Dioxide-Filled Balloons, Phys. Teacher, 48(6), 388–390 DOI:10.1119/1.3479716.
53. Jameson G. and Brüschweiler R., (2020), Active Learning Approach for an Intuitive Understanding of the Boltzmann Distribution by Basic Computer Simulations, J. Chem. Educ., 97(10), 3910–3913 DOI:10.1021/acs.jchemed.0c00559.
54. Jeppsson, F., Haglund, J., Amin, T. G. and Strömdahl, H., (2013), Exploring the Use of Conceptual Metaphors in Solving Problems on Entropy, J. Learn. Sci., 22(1), 70–120 DOI:10.1080/10508406.2012.691926.
55. Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assisted Learn., 7(2), 75–83 DOI:10.1111/j.1365-2729.1991.tb00230.x.
56. Jungermann A. H., (2006), Entropy and the Shelf Model: A Quantum Physical Approach to a Physical Property, J. Chem. Educ., 83(11), 1686 DOI:10.1021/ed083p1686.
57. Kang D.-Y., Liou K.-H. and Chang W.-L., (2015), Investigating Friction as a Main Source of Entropy Generation in the Expansion of Confined Gas in a Piston-and-Cylinder Device, J. Chem. Educ., 92(10), 1667–1671 DOI:10.1021/acs.jchemed.5b00361.
58. Kattmann U., (2018), A biologist's musing on teaching about entropy and energy: towards a better understanding of life processes, School Sci. Rev., 99(368), 61–68.
59. Kaufman R. and Leff H., (2022), Interdependence of the First and Second Laws of Thermodynamics, Phys. Teacher, 60(6), 501–503 DOI:10.1119/5.0074493.
60. Keifer D., (2019), Enthalpy and the Second Law of Thermodynamics, J. Chem. Educ., 96(7), 1407–1411 DOI:10.1021/acs.jchemed.9b00326.
61. Kiatgamolchai S., (2015), A Graphical Proof of the Positive Entropy Change in Heat Transfer Between Two Objects, Phys. Teacher, 53(2), 95–96 DOI:10.1119/1.4905807.
62. Kincanon E., (2013), How I teach the second law of thermodynamics, Phys. Educ., 48(4), 491–496 DOI:10.1088/0031-9120/48/4/491.
63. Kozliak E. I., (2004), Introduction of Entropy via the Boltzmann Distribution in Undergraduate Physical Chemistry: A Molecular Approach, J. Chem. Educ., 81(11), 1595–1598 DOI:10.1021/ed081p1595.
64. Kozliak E. I., (2009), Overcoming Misconceptions about Configurational Entropy in Condensed Phases, J. Chem. Educ., 86(9), 1063–1068 DOI:10.1021/ed086p1063.
65. Kozliak E. I., (2014), Entropy of Mixing of Distinguishable Particles, J. Chem. Educ., 91(6), 834–838 DOI:10.1021/ed4007666.
66. Kozliak E. I. and Lambert F. L., (2005), “Order-to-Disorder” for Entropy Change? Consider the Numbers! Chem. Educ., 10, 24–25 DOI:10.1333/s00897050864a.
67. Laird B. B., (1999), Entropy, Disorder, and Freezing, J. Chem. Educ., 76(10), 1388–1390 DOI:10.1021/ed076p1388.
68. Lambert F. L., (1999), Shuffled Cards, Messy Desks, and Disorderly Dorm Rooms – Examples of Entropy Increase? Nonsense! J. Chem. Educ., 76(10), 1385–1387 DOI:10.1021/ed076p1385.
69. Lambert F. L., (2002), Entropy Is Simple, Qualitatively, J. Chem. Educ., 79(10), 1241–1246 DOI:10.1021/ed079p1241.
70. Lambert F. L., (2007), Configurational Entropy Revisited, J. Chem. Educ., 84(9), 1548–1550 DOI:10.1021/ed084p1548.
71. Lambert F. L., (2011), The Conceptual Meaning of Thermodynamic Entropy in the 21st Century, Int. Res. J. Pure Appl. Chem., 1(3), 65–68 DOI:10.9734/IRJPAC/2011/679.
72. Lambert F. L. and Leff H. S., (2009), The Correlation of Standard Entropy with Enthalpy Supplied from 0 to 298.15 K, J. Chem. Educ., 86(1), 94–98 DOI:10.1021/ed086p94.
73. Landis J. R. and Koch G. G., (1977), The Measurement of Observer Agreement for Categorical Data, Biometrics, 33(1), 159–174 DOI:10.2307/2529310.
74. Langbeheim E., Abrashkin A., Steiner A., Edri H., Safran S. and Yerushalmi E., (2020), Shifting the learning gears: redesigning a project-based course on soft matter through the perspective of constructionism, Phys. Rev. Phys. Educ. Res., 16(2), 020147 DOI:10.1103/PhysRevPhysEducRes.16.020147.
75. Langbeheim E., Safran S. A. and Yerushalmi E., (2014), Visualizing the Entropy Change of a Thermal Reservoir, J. Chem. Educ., 91(3), 380–385 DOI:10.1021/ed400180w.
76. Lechner J. H., (1999), Visualizing Entropy, J. Chem. Educ., 76(10), 1382–1385 DOI:10.1021/ed076p1382.
77. Leff H. S., (1996), Thermodynamic entropy: The spreading and sharing of energy, Am. J. Phys., 64, 1261–1271 DOI:10.1119/1.18389.
78. Leff H. S., (2007), Entropy, Its Language, and Interpretation, Found. Phys., 37(12), 1744–1766 DOI:10.1007/s10701-007-9163-3.
79. Leff H. S., (2012), Removing the Mystery of Entropy and Thermodynamics—Part I, Phys. Teacher, 50(1), 28–31 DOI:10.1119/1.3670080.
80. Leff H. S., (2020), Energy and Entropy: A Dynamic Duo, CRC Press.
81. Leinonen R., Asikainen M. A. and Hirvonen P. E., (2015), Grasping the second law of thermodynamics at university: the consistency of macroscopic and microscopic explanations, Phys. Rev. Spec. Top.–Phys. Educ. Res., 11(2), 020122 DOI:10.1103/PhysRevSTPER.11.020122.
82. Makahinda T. and Mawuntu V. J., (2023), Development of Thermodynamics Learning With Empirical Approach and Portfolio Assessment Techniques, Studies Learn. Teach., 4(2), 285–295 DOI:10.46627/silet.v4i2.263.
83. Mayorga L. S., López M. J. and Becker W. M., (2012), Molecular Thermodynamics for Cell Biology as Taught with Boxes, CBE—Life Sci. Educ., 11(1), 31–38 DOI:10.1187/cbe.11-07-0053.
84. Michalek B. and Hanson R. M., (2006), Give Them Money: The Boltzmann Game, a Classroom or Laboratory Activity Modeling Entropy Changes and the Distribution of Energy in Chemical Systems, J. Chem. Educ., 83(4), 581–588 DOI:10.1021/ed083p581.
85. Moore T., (2022), Connecting Energy Dispersal and the Classical Definition of Entropy, Chem. Eng. Educ., 56(3), 175–180.
86. Moore T. A. and Schroeder D. V., (1997), A different approach to introducing statistical mechanics, Am. J. Phys., 65(1), 26–36 DOI:10.1119/1.18490.
87. Morris, S. B., (2008), Estimating Effect Sizes From Pretest-Posttest-Control Group Designs, Org. Res. Methods, 11(2), 364–386 DOI:10.1177/1094428106291059.
88. Muller E. A., (2012), What Carnot's Father Taught His Son About Thermodynamics, Chem. Eng. Educ., 46(3), 165–170.
89. Munakata M., Vaidya A. and Vanderklein D., (2022), Interdisciplinary Lessons on Energy and Entropy, J. College Sci. Teach., 51(5), 10–15 DOI:10.1080/0047231X.2022.12290576.
90. Novak I., (2003), The Microscopic Statement of the Second Law of Thermodynamics, J. Chem. Educ., 80(12), 1428–1431 DOI:10.1021/ed080p1428.
91. Page M. J., McKenzie J. E., Bossuyt P. M., Boutron I., Hoffmann T. C., Mulrow C. D., Shamseer L., Tetzlaff J. M., Akl E. A., Brennan S. E., Chou R., Glanville J., Grimshaw J. M., Hróbjartsson A., Lalu M. M., Li T., Loder E. W., Mayo-Wilson E., McDonald S., McGuinness L. A., Stewart L. A., Thomas J., Tricco A. C., Welch V. A., Whiting P. and Moher D., (2021), The PRISMA 2020 statement: an updated guideline for reporting systematic reviews, BMJ, 372(71) DOI:10.1136/bmj.n71.
92. Partanen L., (2016), Student oriented approaches in the teaching of thermodynamics at universities – developing an effective course structure, Chem. Educ. Res. Practice, 17(4), 766–787 10.1039/C6RP00049E.
93. Phillips J. A., (2016), The Macro and Micro of it Is that Entropy Is the Spread of Energy, Phys. Teacher, 54(6), 344–347 DOI:10.1119/1.4961175.
94. Pirker J., Gutl C. and Astatke Y., (2015), Enhancing online and mobile experimentations using gamification strategies, 2015 3rd Experiment International Conference (Exp.at’15), 224–229 DOI:10.1109/EXPAT.2015.7463270.
95. Plumb R. C., (1964), Teaching the entropy concept, J. Chem. Educ., 41(5), 254–256 DOI:10.1021/ed041p254.
96. Poggi V., Miceli C. and Testa I., (2017), Teaching energy using an integrated science approach, Phys. Educ., 52(1), 015018 DOI:10.1088/1361-6552/52/1/015018.
97. Read J. R. and Kable S. H., (2007), Educational analysis of the first year chemistry experiment ‘Thermodynamics Think-In’: An ACELL experiment, Chem. Educ. Res. Pract., 8(2), 255–273 10.1039/B6RP90034H.
98. Rodriguez J.-M. G., Nardo J. E., Finkenstaedt-Quinn S. A. and Watts F. M., (2023), The use of frameworks in chemistry education research, Chem. Educ. Res. Practice, 24(4), 1109–1126 10.1039/D3RP00149K.
99. Rogers B. A. and Zhang Y., (2020), Project-Based Experiment in a Physical Chemistry Teaching Laboratory: Ion Effects on Caffeine Partitioning Thermodynamics, J. Chem. Educ., 97(11), 4173–4178 DOI:10.1021/acs.jchemed.0c00961.
100. Ross K., (1988), Matter scatter and energy anarchy. The Second Law of Thermodynamics is simply common experience, Sch. Sci. Rev., 69(248), 438–445.
101. Salagaram T. and Chetty N., (2011), Enhancing the understanding of entropy through computation, Am. J. Phys., 79(11), 1127–1132 DOI:10.1119/1.3623416.
102. Samuelsson C. R., Elmgren M., Xie C. and Haglund J., (2019), Going through a phase: infrared cameras in a teaching sequence on evaporation and condensation, Am. J. Phys., 87(7), 577–582 DOI:10.1119/1.5110665.
103. Schoepf D. C., (2002), A statistical development of entropy for the introductory physics course, Am. J. Phys., 70(2), 128–136 DOI:10.1119/1.1419097.
104. Schwedler S. and Kaldewey M., (2020), Linking the submicroscopic and symbolic level in physical chemistry: how voluntary simulation-based learning activities foster first-year university students’ conceptual understanding, Chem. Educ. Res. Practice, 21(4), 1132–1147 10.1039/C9RP00211A.
105. Souza J. D., Passos C. G. and Netz P. A., (2023), Exploring Bachelard's Epistemological Obstacles in Physical Chemistry Textbooks: The Case of Thermodynamics Concepts, Acta Sci., 25(5), 30–58 DOI:10.17648/acta.scientiae.7781.
106. Sözbilir M., (2004), What Makes Physical Chemistry Difficult? Perceptions of Turkish Chemistry Undergraduates and Lecturers, J. Chem. Educ., 81(4), 573–578 DOI:10.1021/ed081p573.
107. Spencer J., Moog R. and Gillespie R., (1996), Demystifying Introductory Chemistry. Part 4. An Approach to Reaction Thermodynamics through Enthalpies, Entropies, and Free Energies of Atomization, J. Chem. Educ., 73(7), 631–636 DOI:10.1021/ed073p631.
108. Sreenivasulu B. and Subramaniam R., (2013), University Students’ Understanding of Chemical Thermodynamics, Int. J. Sci. Educ., 35(4), 601–635 DOI:10.1080/09500693.2012.683460.
109. Strnad J., (1984), The second law of thermodynamics in a historical setting, Phys. Educ., 19, 94–100 DOI:10.1088/0031-9120/19/2/317.
110. Strong L. E. and Halliwell H. F., (1970), An alternative to free energy for undergraduate instruction, J. Chem. Educ., 47(5), 347–352 DOI:10.1021/ed047p347.
111. Styer D., (2019), Entropy as Disorder: History of a Misconception, Phys. Teacher, 57(7), 454–458 DOI:10.1119/1.5126822.
112. Styer D. F., (2000), Insight into entropy, Am. J. Phys., 68(12), 1090–1096 DOI:10.1119/1.1287353.
113. Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Practice, 14(2), 156–168 10.1039/C3RP00012E.
114. Talanquer V., (2011), Macro, Submicro, and Symbolic: the many faces of the chemistry “triplet”, Int. J. Sci. Educ., 33(2), 179–195 DOI:10.1080/09500690903386435.
115. Teichert M. A. and Stacy A. M., (2002), Promoting understanding of chemical bonding and spontaneity through student explanation and integration of ideas, J. Res. Sci. Teach., 39(6), 464–496 DOI:10.1002/tea.10033.
116. Tro N., (2019), Chemistry: A Molecular Approach, Financial Times Prentice Hall.
117. Tsaparlis G., (2007), Teaching and Learning Physical Chemistry: A Review of Educational Research, Advances in Teaching Physical Chemistry, American Chemical Society, vol. 973, pp. 75–112.
118. Tsaparlis G., (2016), The logical and psychological structure of physical chemistry and its relevance to graduate students’ opinions about the difficulties of the major areas of the subject, Chem. Educ. Res. Practice, 17(2), 320–336 10.1039/C5RP00203F.
119. Velasco J., Buteler L., Briozzo C. and Coleoni E., (2022), Learning entropy among peers through the lens of coordination class theory, Phys. Rev. Phys. Educ. Res., 18(1), 010127 DOI:10.1103/PhysRevPhysEducRes.18.010127.
120. Volfson A., Eshach H. and Ben-Abu Y., (2019), Introducing the idea of entropy to the ontological category shift theory for conceptual change: the case of heat and sound, Phys. Rev. Phys. Educ. Res., 15(1), 010143 DOI:10.1103/PhysRevPhysEducRes.15.010143.
121. software What Works Clearinghouse Procedures and Standards Handbook, Version 5.0., (2022), U.S. Department of Education.
122. Williams D. and Glasser D., (1991), An Introduction to Equilibrium Thermodynamics. A Rational Approach to Its Teaching. Part 2: Internal Energy, Entropy, and Temperature, Chem. Eng. Educ., 25(2), 164–172.
123. Wood A., (1975), Graphical Representation of Thermodynamic Functions, J. Coll. Sci. Teach., 5(2), 102–104.
124. Wu G. and Wu A. Y., (2020), A new perspective of how to understand entropy in thermodynamics, Phys. Educ., 55(1), 015005 DOI:10.1088/1361-6552/ab4de6.
125. Wu G. and Wu A. Y., (2021), Analogies between momentum current, electric current and entropy current, Phys. Educ., 56(3), 035019 DOI:10.1088/1361-6552/abe83f.
126. Yu T. H., (2020), Teaching Thermodynamics with the Quantum Volume, J. Chem. Educ., 97(3), 736–740 DOI:10.1021/acs.jchemed.9b00742.
127. Zhang K., (2020), Illustrating the Concepts of Entropy, Free Energy, and Thermodynamic Equilibrium with a Lattice Model, J. Chem. Educ., 97(7), 1903–1907 DOI:10.1021/acs.jchemed.0c00225.
128. Zimmerman S., (2010), An instructive model of entropy, Int. J. Math. Educ. Sci. Technol., 41(6), 805–818 DOI:10.1080/0020739X.2010.486447.
129. Zinman W. G., (1973), Demonstration of Entropy and of the Second Law of Thermodynamics, Am. J. Phys., 41(11), 1284–1285 DOI:10.1119/1.1987545.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4rp00158c

---