How the addition of a polar aprotic solvent alters aldol-addition kinetics: exploring the role of solvent molecules and their dynamics

Abstract

This paper investigates how solvent composition, and dynamics influence the aldol-addition reaction, which is an important reaction in acid-catalyzed biomass transformations. The reaction between 5-hydroxymethylfurfural (5-HMF) and 5,6-enol is used as a case-study since this is also a key step in the formation of humins (undesired carbonaceous polymers) in the condensed phase biomass transformation. Using first principles based molecular simulations performed at experimental conditions, with finite temperature effects, reaction dynamics and quantum mechanically treated explicit solvent molecules, we show that polar, aprotic cosolvents like DMSO can alter reaction pathways, conformations of reacting species, and energetics of the aldol addition reaction. Open-chain conformations of 5,6-enol are stable in water due to hydrogen bonding, while the presence of DMSO promotes quasi-cyclic structures. In both pure water and water–DMSO mixtures, the aldol addition reaction can proceed via both, concerted and stepwise pathways. Analysis of the reaction free energy landscape reveals that the aldol addition reaction is kinetically more favorable in water compared to water–DMSO mixtures, for both the concerted and stepwise pathways. Dynamic solvent reorganization during the reaction has a higher free energy penalty in DMSO than in pure water, highlighting the role of DMSO in increasing the activation free energy for aldol-addition. This investigation advances our understanding of explicit and dynamic solvent effects in condensed phase biomass transformation and particularly on the key aldol-addition reaction.

---

1. Introduction

The use of lignocellulosic biomass as a renewable feedstock to produce value-added chemicals, such as biofuels, bioplastics, and specialty chemicals, has become a key focus in sustainable and green chemistry.^1,2 Lignocellulose derived molecules are attracting significant interest for their applications in bio-based solvents, biopolymers, adhesives, packaging and sustainable materials development. Notably, 5-HMF is a key intermediate for synthesizing polymers and biofuels.^3,4 However, the acid-catalyzed dehydration of biomass derived carbohydrates to 5-HMF is accompanied by undesired side reactions, leading to the formation of humins which are carbonaceous oligomeric by-products. Their formation also contributes to substantial carbon loss and catalyst deactivation.^5–9 Compositional characterization studies have provided conclusive insights into the reaction mechanisms and showed that humins formation during acid-catalyzed biomass reactions occurs via aldol-addition mechanism.^10–14 Quantum mechanical calculations have also revealed that, during the initial stages of humins formation, the aldol addition step is the rate-determining step, exhibiting the highest energy barrier compared to other reaction steps such as keto–enol tautomerization and condensation.¹⁵ Thus, aldol addition is crucial for humins formation as it enables the oligomerization of 5-HMF and its derivatives, thereby reducing yields of valuable platform chemicals. Moreover, on the positive side, aldol addition and subsequent condensation reactions are gaining prominence in sustainable chemistry, as they enable the utilization of biomass-derived molecules as viable alternatives to conventional feedstocks to produce polymers and fuels. Aldol condensation is also key for converting biomass into liquid alkenes.¹⁶ First, aqueous-phase reforming of carbohydrates generates hydrogen,¹⁷ while pentoses and hexoses from cellulose and hemicellulose are dehydrated into carbonyl compounds like 5-HMF or furfural.^18,19 Retro-aldol condensation breaks carbohydrates into smaller carbonyl molecules, such as glyceraldehyde, or fermented to form acetone which can react with 5-HMF via aldol addition and condensation.^20,21 This process generates larger, energy-dense molecules that are refined into aviation-grade hydrocarbons. The expanding sustainable aviation fuel (SAF) market relies on biomass to mitigate aviation industry's carbon footprint, addressing the sector's unique technical challenges and the limitations of electrification. Furthermore, the aldol addition reaction is gaining interest in sustainable chemistry, enabling the use of biomass-derived molecules as substitutes for traditional feedstocks in polymer production. Dumesic et al.²² synthesized polyurethanes by the aldol addition of 5-HMF and acetone, forming the monomer HMF-acetone-HMF to be hydrogenated and then make it react with other monomers, such as maleimide, giving rise to polymeric products. The polymer properties can be tuned based on the degree of hydrogenation, where fully hydrogenated monomers produce flexible materials suitable for energy-dissipating rubbers, while partially hydrogenated monomers produce stiffer materials ideal for packaging applications.

The conversion of biomass into biofuels, sustainable chemicals, or polymeric materials is highly dependent on the composition of the condensed phase in which the transformation occurs. It is well established that the addition of organic, protic and aprotic solvents can significantly alter both the reactivity and selectivity toward desired products.^23–28 For instance, the production of targeted alkanes in the jet fuel range (C7 to C14) via aldol condensation of aldehydes and ketones using Ni-based catalysts was found to be more efficient in an aqueous system compared to tetrahydrofuran (THF) as the organic solvent.²⁹ Additionally, Vlachos et al.⁹ demonstrated that the formation of acid-catalyzed humins derived from 5-HMF through aldol addition is significantly reduced by the inclusion of dimethyl sulfoxide (DMSO), a polar, aprotic solvent. Fourier-transform infrared (FTIR) spectroscopy of humins suggested that the nucleophilic attack on 5-HMF is suppressed in the presence of DMSO. This finding was corroborated by Mushrif et al.,³⁰ who used molecular dynamics simulations to show that DMSO preferentially coordinates around 5-HMF, creating a shielding effect that protects it from further degradation. In acid-catalyzed systems, computational studies revealed that DMSO reduces the stability of hydronium ions (acid catalysts) near 5-HMF, confining them to the bulk of the solvent in water–DMSO mixtures. This solvation shielding effect provided by organic aprotic solvents protects biomass-derived carbonyl compounds from acid attack.³¹ Neurock et al.,³² using ab initio molecular dynamics (AIMD) simulations, observed that the aldol addition reaction between 5-HMF and acetone is significantly suppressed at high acetone concentrations compared to aqueous solvent systems. Their findings suggest that, in the presence of acetone, 5-HMF preferentially resides within the hydrophobic domain, surrounded by acetone molecules, while acid protons remain confined to the hydrophilic domain.

Furthermore, the kinetics of the aldol addition reaction are also influenced by the molecular conformations of the reactants. Duarte et al.³³ investigated the aldol addition between proline and a series of hydroxylated cyclohexanone stereoisomers using density functional theory (DFT) calculations. Their findings demonstrated variations in transition state (TS) stabilities among the stereoisomers, driven by differences in intramolecular interactions that influence the overall stability of each stereoisomer. Specifically, the lengths of hydrogen bonds between the carboxyl hydrogen atoms and the forming alkoxide groups played a key role in determining the reaction's stereoselectivity. Furthermore, simulating the reaction in an implicit solvent environment of dichloromethane predicted lower activation energies compared to the gas phase but did not affect the product distribution. In contrast, introducing explicit water molecules in the simulation to create a water-rich environment around the TS disrupted the initial molecular configuration, and ultimately altering the stereoselectivity of the reaction. Also, solvents have shown to alter the molecular configurations of biomass-derived species. For instance, Plazinski et al.³⁴ studied the conformational changes of hexoses in different solvents, revealing that DMSO induced a shift in the preferred forms of D-galactose and D-talose from extended, almost linear chains to twisted, quasi-cyclic structures, increasing intramolecular hydrogen bonding. In contrast, water favors stronger interactions with hydroxyl groups, reducing intramolecular bonds, leading to extended, linear molecular configurations. Additionally, Lin et al.³⁵ showed that solvent selection in xylose conversion to furfural affects the anomeric equilibrium of xylose. With polar solvents like water, the equilibrium favors the β-anomer due to better stabilization and in contrast, less polar solvents shift the equilibrium toward the α-anomer disfavoring the dehydration reaction via steric hindrances. This suggests that solvent interactions can alter molecular configurations, thereby influencing the energetics and product distribution during the aldol addition reaction.

Hence, in this work, we investigate how solvent environment affects the aldol addition reaction between 5-HMF⁺, and 5,6-enol (see Scheme 1). The molecule 5,6-enol is chosen for the following reasons: (i) it is well established that this molecule is formed from the rehydration of 5-HMF during its acid-catalyzed conversion and (ii) that it undergoes aldol-addition reaction with 5-HMF in condensed phase transformations of 5-HMF.^13–15 Also, the chosen reaction provides key insights into solvent effects on aldol addition, relevant to biofuel and polymer applications. This reaction serves as a model for understanding reaction energetics and solvent effects in biomass conversion. AIMD coupled with the biasing method metadynamics is used to capture explicit and polarizable solvent molecules and finite temperature effects, as well as their dynamics under experimental reaction conditions. The aldol reaction is simulated in explicit water and water–DMSO solvent environments via stepwise and concerted pathways.

Scheme 1 Reaction mechanism of the aldol-addition between 5-HMF⁺ and 5,6-enol.

2. Methodology

2.1 Molecular mechanics based molecular dynamics (MD)

Classical molecular dynamics (MD) was implemented prior to AIMD to pre-equilibrate the system at experimental condensed phase density. MD simulations are conducted at 433 K using GROMACS 2020.4.³⁶ Force field parameters for all species involved in this study are detailed in Table S1 in the (ESI†). The reacting systems used in this paper are pure water and a water–DMSO mixture at a mass ratio of 1 : 3. The number of solvent molecules and the simulation cell dimensions for each system are detailed in Table S2 in the ESI.† The TIP3P model is employed for water, while the OPLS-AA force field is used to model DMSO, 5-HMF and 5,6 enol molecules.³⁷ The OPLS-AA force field has been extensively validated for liquid-phase simulations and has successfully predicted the strong hydrogen bonding between the hydroxyl groups of carbohydrates and the sulfonyl group of DMSO.^30,38 The temperature of the simulation system is kept constant using a Nosé–Hoover chain thermostat, with a coupling time constant of 1 ps.^39,40 To bring the systems to equilibrium, first energy minimization was performed using the steepest descent algorithm to bring the energy gradient below 25 kJ mol⁻¹ nm⁻¹, followed by a 0.4 ns of NVE equilibration. Next, isobaric isothermal (NPT) runs for 0.4 ns were conducted to ensure the system reaches the correct density (see Fig. S1†). Finally, simulations in the NVT ensemble were performed for 4 ns for both solvent compositions. All the simulations were performed using periodic boundary conditions in all directions. The cut-off of 0.7 nm is used with particle-mesh Ewald (PME) electrostatics. MD trajectories were analyzed using the visual molecular dynamics (VMD), version 1.9.3.⁴¹ The pre-equilibrated water and water–DMSO systems were further subjected to AIMD, as described in section 2.2.

2.2 Ab initio molecular dynamics (CPMD scheme)

The AIMD simulations were performed using version 4.3 of the CPMD code starting with the pre-equilibrated systems from classical MD. AIMD computations were performed using the plane-wave-pseudopotential framework of Kohn–Sham density functional theory (DFT), employing the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional within the generalized gradient approximation (GGA).⁴² Integration over the Brillouin zone in the reciprocal space was done with a single gamma point. An energy cutoff of 70 Rydberg was found to be optimal for achieving convergence in energy calculations. Within CPMD, the fictitious electron mass parameter of 400 atomic units (au) was set. Prior to the molecular dynamics run, geometry optimization of the system was performed. During the AIMD simulations, energies, including fictitious electronic kinetic energy, were continuously monitored to ensure adherence to the Born–Oppenheimer surface. Initially, this step was performed without a thermostat to verify the accuracy of the fictitious mass parameters and to ensure that the electronic kinetic energy does not deviate. Subsequently, a Nosé–Hoover chain thermostat was employed to regulate both ionic and electronic temperatures. The ionic thermostat frequency was set to 3000 cm⁻¹, aligning with typical C–H and O–H bond vibrations. Meanwhile, the electronic thermostat frequency was set to 10 000 cm⁻¹ to prevent coupling between ionic and electronic dynamics across all systems. The molecular dynamics time step utilized in the simulation was 0.0967 fs.

2.3 Metadynamics implementation

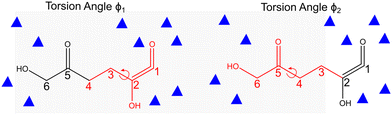
To be able to access reaction timescales in AIMD and to compute the free energy surface (FES) in the reaction coordinate space, we integrated metadynamics with CPMD. This combined approach accelerates dynamics along the selected reaction coordinates and also computes the free energy surface as a function of those reaction coordinates. Metadynamics technique is based on the addition of Gaussian potentials at specific time intervals, filling up the FES, a concept developed by Laio and Gervasio.^43,44 The potentials added during the simulations are tracked, enabling the construction of FES as a function of predefined collective variables (CVs) or reaction coordinates. The subsequent subsections explain the specification of CVs pertinent to conformational analysis and to aldol addition reactions.⁴⁵ The height of the Gaussian hill potential was maintained at 2.6 kJ mol⁻¹. The minimum and maximum number of steps for intermediate metadynamics iterations were 25 and 50 respectively, ensuring the system progresses steadily through the metadynamics simulation. The dynamics of the collective variables were decoupled from the ionic and fictitious electronic motions by selecting an appropriate fictitious mass for the collective variables. The temperature of the collective variables was set to 433 K and controlled within a window of ±200 K using velocity rescaling. To explore the effect of the solvent composition on the conformation of the 5,6-enol, FES in CPMD–metadynamics was computed as a function of torsion angles to identify the most stable conformation of the molecule in pure water and in the presence of DMSO. The combination of collective variables CV₁ and CV₂ are two torsion angles ϕ₁ and ϕ₂ (see Fig. 1), specifying two sets of carbon atoms of 5,6-enol, ϕ₁ (1–4) and ϕ₂ (3–6). The two torsion angles (ϕ₁ and ϕ₂) enable the efficient sampling of both the linear chain and quasi-cyclic conformations of the 5,6-enol. These angles capture the key conformational changes, facilitating the exploration of the molecule's free energy landscape.

Fig. 1 Collective variables (CV₁ = ∅₁; CV₂ = ∅₂) for the conformational sampling of 5,6-enol molecule in solvent, using CPMD–metadynamics. Structure highlighted in red denotes the atoms involved in the dihedral angle which is defined as the CV. Blue triangles represent solvent molecules, simulating a condensed phase environment.

To perform the aldol addition reaction, the system was first equilibrated, performing unbiased CPMD simulation, using the most stable 5,6 enol configuration from the conformational analysis for each solvent composition by keeping the torsion angles constant. After that, the aldol addition reaction was performed by implementing metadynamics, releasing the constraint on the torsion angles of the 5,6-enol molecule. Two collective variables (CVs) were chosen considering the carbon–carbon bond formation and deprotonation of the adjacent hydroxyl group of carbon 5 from 5,6-enol. CV₁ represents the coordination number between the carbon atoms of 5-HMF⁺ and the 5,6-enol (carbons 5 and 7), leading to dimer formation (refer to Fig. 2). CV₂ was defined as the difference in coordination number between the oxygen atom of the 5,6 enol and the oxygen atom (O_w) of a neighboring water molecule specified in CV₂. For the reactant state, the set of collective variables displays values of [0,1]. CV₁ equals 0 means there is no bond between carbon atoms 6 and 7, while CV₂ = 1 indicates that it is bonded with the oxygen atoms bonded to carbon 5. Meanwhile, [1,1] corresponds to the product, indicating the bond between the carbon atoms 6 and 7 and the deprotonation of the oxygen of carbon 5.

Fig. 2 Collective variables CVs for the aldol addition reaction using CPMD–metadynamics. Blue triangles represent solvent molecules, simulating a condensed phase environment.

2.4 DFT calculations in gas phase

To examine the impact of molecular conformational changes on the energy profiles of the aldol addition reaction without the influence of solvents (to decouple solvent effect from conformational effect on activation free energy), the most stable 5,6-enol conformations associated with pure water and a water–DMSO mixture (1,3 wt) were selected. The torsion angles corresponding to these conformations were fixed during quantum mechanical DFT gas-phase calculations to isolate and analyze the effect of molecular conformation on reaction energetics.³³ The hybrid functional B3LYP combined with 6-311++G (2d,p) basis set is used using Gaussian 09 code.⁴⁶ Before the TS calculations were performed using the Berny algorithm, the dihedral angles were kept constant, corresponding to the most stable configurations for the 5,6 enol in pure water and in water–DMSO mixture. Intrinsic reaction coordinate (IRC) analysis and frequency calculations were performed to confirm that the TS corresponds to both the reactant and product along the reaction coordinate.^47,48 Subsequently, the geometries of the reactant and product conformers were reoptimized to calculate the reaction-free energies at 433 K, the same temperature as for the CPMD simulations.¹⁴ The convergence criterion for the self-consistent field (SCF) was set to an energy change threshold of 1.00D-06. The Zundel cation, a simplified representation of the solvated proton H₅O₂⁺, was selected as the acid catalyst for this study. A conformational analysis was conducted to identify the ground state of the initial system formed by the interaction between the 5,6-enol and the Zundel structure. All energy values are reported in kJ mol⁻¹.

3. Results

3.1 Solvent influence on 5,6-enol molecular conformation

The kinetics of the aldol addition reaction can be influenced by the relative stability of the reactants, which, in turn, gets altered due to molecular conformations that reduce steric hindrances.³³ These conformational changes are strongly affected by solvent–reactant interactions.^34,35 It is well established that the addition of polar organic solvents, such as DMSO, can significantly modify the conformations of molecules containing polar functional groups, such as those derived from biomass.^35,49–51 The torsional flexibility of the open chain molecule, and the presence of functional groups such as hydroxyl and carbonyl, makes it sensitive to its surrounding solvent environment. Fig. 3 presents the FESs for the molecular conformational analysis of 5,6-enol, computed using CPMD–metadynamics, as detailed in section 2.3, for two different solvent systems: pure water and a water–DMSO mixture (1,3 mass ratio). The convergence criteria are presented in section 2 of the ESI.† It is observed in Fig. 3a for pure water system that the most stable conformation of 5,6-enol occurs at torsion angles (ϕ₁ = 196° and ϕ₂ = 206°), corresponding to the open-chain form which is almost linear. This conformation is approximately 135 kJ mol⁻¹ more stable than another local minimum at (ϕ₁ = 234° and ϕ₂ = 80°), which resembles a quasi-cyclic conformer. The enhanced stability of the linear configuration arises from hydrogen bonding between water molecules and the hydroxyl groups at carbons 2, 5, and 6, as well as the carbonyl group at carbon 1. This observation aligns with previous experimental and computational studies, which suggest that the polar groups of carbohydrates are stabilized by interactions with water molecules.^31,35 The enol polar groups' interactions with solvent molecules create water-rich domains that can influence and alter the molecule's configuration. In contrast, as shown in Fig. 3b, in the presence of DMSO, the torsion angles of the 5,6-enol undergo significant changes, causing the carbonyl oxygen at carbon 1 to interact with the anomeric carbon at position 6. This interaction leads to the formation of a quasi-cyclic conformer. To explain the change in molecular conformation, we computed the total number of hydrogen bonds between the polar groups of 5,6-enol (hydroxyl groups at carbons 6, 5 and 2, and carbonyl group at carbon 1) and the solvent molecules for both solvent composition throughout the simulation (see Fig. S7 in ESI†). The analysis revealed that the H-bond count of the 5,6-enol polar groups in the pure water system was three to five times higher than that in the water–DMSO system throughout the simulation (see Fig. S7†). This reduction can be attributed to DMSO's disruptive effect, where its polar sulfoxide group strongly interacts with water molecules, limiting their availability for hydrogen bonding.⁵² As a result, fewer water molecules can form hydrogen bonds with the polar groups, weakening the overall hydrogen bond network. Consequently, the decreased hydrogen bonding in the water–DMSO system reduces the stability of the 5,6-enol, suggesting that molecular conformational changes are driven by intramolecular interactions rather than hydrogen bonding with the solvent, as seen in pure water. These findings are aligned with those of Plazinski et al.,³⁴ who observed similar solvent-dependent shifts from extended to quasi-cyclic structures for D-galactose and D-talose when transitioning from water to DMSO as the solvent.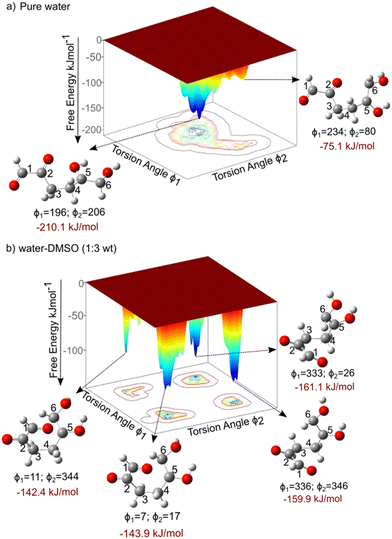

Fig. 3 Free energy landscape of the conformational analysis of 5,6-enol, computed using CPMD–metadynamics simulations. The free energy is computed as a function of dihedral angles in degrees, with explicit solvent molecules treated quantum mechanically. a) Pure water and b) water–DMSO mixture (1,3 mass ratio). Refer to Fig. 1 for the definitions of the collective variables CV₁ and CV₂. Free energies (ΔG_R) are reported in kJ mol⁻¹.

3.2 Solvent effect on reaction mechanisms and energetics of aldol addition

5,6-Enol can undergo aldol addition with 5-HMF⁺ due to the high nucleophilicity of its α-carbon.^13,14 This nucleophilicity allows it to attack the electrophilic carbonyl carbon of 5-HMF⁺, forming a new carbon–carbon bond and yielding a β-hydroxy carbonyl compound as the product.¹⁵ To investigate the aldol addition reaction between 5,6-enol and 5-HMF⁺, we employed CPMD–metadynamics as described in section 2.3. This approach accounts for solvent dynamics and polarizability by treating the explicit solvent molecules quantum mechanically and taking finite temperature dynamics into account. Here, we do not predetermine whether the aldol addition follows a concerted or stepwise reaction mechanism. This approach, shown in Fig. 2, allows for the determination of the kinetically preferred minimum energy pathway under different solvent compositions. Details regarding the convergence criteria for the aldol addition simulations can be found in section S3 of the ESI.† The aldol addition reaction consists of two steps: (i) the formation of the bond between carbons 6 and 7, and (ii) the transfer of the H_δ proton from the 5,6-enol to water, which acts as a proton acceptor—resulting in the conversion of the hydroxyl group at carbon 5 into a carbonyl group. These reaction steps are not biased to occur in a specific order.

Fig. 4 illustrates the FESs for both solvent compositions as a function of the two collective variables. In both systems, three distinct wells are observed on the 3D map, corresponding to the reactant state (identical for both systems), the intermediate state (which differs between the pure water system and the water–DMSO mixture), and the final product state (also identical for both systems). In the pure water system, the intermediate in the stepwise aldol addition corresponds to the formation of bond between carbon 6 and 7 (denoted as intermediate β in Fig. 4a). This is followed by the formation of the carbonyl group at carbon 5 because of proton transfer (H_δ) from the enol to water molecules in the system. In contrast, in the presence of DMSO, the intermediate reactions in the stepwise pathway occur in a different sequence. Initially, the 5,6-enol loses the hydroxyl hydrogen (H_δ) at carbon 5, forming intermediate γ. This is followed by the addition reaction between carbons 6 and 7, leading to product formation. In the concerted mechanism, the bond formation between carbons 6 and 7, and the transfer of the H_δ proton from 5,6-enol to water occur in a single step for both solvent compositions. These observations highlight two key points: (i) the solvent composition influences the reaction mechanism, and (ii) the aldol addition reaction can proceed either via a two-step mechanism or through a concerted pathway in both solvent environments. Both concerted and stepwise pathways were explored and evaluated in both solvent compositions. To find the minimum energy pathway from reactants to products, first, we identified the key minima (reactant, intermediate, and product) on the FES. Further, the minimum-energy path (valleys) was identified, connecting these minima via different saddle points.

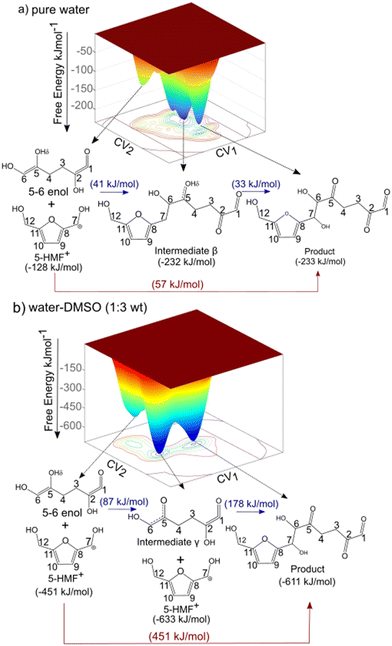Fig. 4 CPMD–metadynamics calculated free energy landscape for the aldol addition reaction in the presence of explicit, quantum mechanically treated solvent molecules. The free energy barrier is depicted in blue for the two-step mechanism and in red for the concerted mechanism. Free energy values are shown in parentheses. For definitions of collective variables CV₁ and CV₂, see Fig. 2. a) Pure water system b) water–DMSO 1 : 3 wt. Activation free energies (AE) and reaction free energies (ΔG_R) are reported in kJ mol⁻¹.

Fig. 5 shows the different pathways extracted from the FES in Fig. 4 and corresponding reaction energetics in a 2D representation. Activation barriers and free energy changes (ΔG_R) for the two-step and concerted mechanisms for aldol-addition in pure water and the water–DMSO (1,3 mass ratio) systems are shown. In contrast to our previous study using DFT calculations with implicit solvent models for water and DMSO, which found no differences in reaction mechanisms and only identified concerted pathways for both solvents,¹⁵ the current results reveal distinct variations in the reaction pathways by incorporating solvent dynamics and polarizability effects through the use of explicit solvent molecules. In the pure water solvent, the stepwise pathway presents free energy barriers of 41 kJ mol⁻¹ (from reactant to intermediate β) and 33 kJ mol⁻¹ (from intermediate β to product). The energy barrier for the concerted mechanism is 57 kJ mol⁻¹ (from reactant directly to product). Since the stepwise pathway has a slightly lower energy barrier (41 kJ mol⁻¹) compared to the concerted pathway (57 kJ mol⁻¹), the concerted stepwise pathway becomes kinetically preferred. On the other hand, in the presence of DMSO, the intermediate steps during the stepwise mechanism have free energy barriers of 87 kJ mol⁻¹ (from reactant to intermediate γ) 178 kJ mol⁻¹ (addition reaction between carbons 5 and 6). For the water–DMSO mixed solvent system, a comparison of the energetics between the stepwise mechanism and the concerted mechanism, (with the latter having an energy barrier of 451 kJ mol⁻¹) reveals that the aldol addition reaction would follows the stepwise mechanism in the presence of DMSO.

Fig. 5 Energetics of the aldol addition reaction between 5,6-enol and 5-HMF, as extracted from CPMD–metadynamics computed free energy surface, shown in Fig. 4. a) Concerted mechanism b) two-step mechanism. Activation free energies (AE) and reaction free energies (ΔG_R) are reported in kJ mol⁻¹.

It is further determined that the stepwise pathway is kinetically favored over the concerted pathway in both pure water and the water–DMSO mixture. However, the aldol addition reaction has lower free energy barriers for both mechanisms in pure water compared to the water–DMSO system. These results align with experimental findings showing that aldol addition reactions occur at higher rates in water than in DMSO, indicating that the addition of DMSO inhibits the formation of oligomeric by-products via aldol addition in acid-catalyzed biomass reactions.^{24,30,53–56}

To analyze the interaction of solvent molecules with the reacting species during the aldol addition reaction, we calculated the radial distribution function of the oxygen atom at carbon 5, where H_δ transfer occurs, with oxygen atoms of water and DMSO molecules (see Fig. S16†). Additionally, by tracking the distances between nearby water molecules and the H_δ proton, we determined that in pure water, the proton is stabilized by a nearby water molecule. This enables the addition reaction between carbons 6 and 7 without the need for complete proton migration to the bulk. This stabilization creates charge resonance effects between carbons 5 and 6, along with the bonded oxygen, resulting in a partial electrophilic site at carbon 6 (see Fig. S11†), which enables the addition reaction to occur without the full migration of the H_δ proton to the bulk. In contrast, in the water–DMSO mixture, the lack of nearby water molecules prevents the stabilization of H_δ until it migrates to the bulk of the solution (intermediate γ), thereby allowing the addition reaction to proceed (see Fig. S15†).

3.3 Effect of 5,6 enol molecular conformation on energetics of aldol-addition

As previously discussed, the configuration of the 5,6-enol—whether in its linear or quasi-cyclic form—can alter its stability and promote intramolecular self-stabilization, thereby influencing the reaction kinetics.^33,34 To validate this, we examined the effects of molecular conformation changes in 5,6-enol during its aldol addition reaction with 5-HMF⁺ using DFT calculations in gas phase, excluding, both implicit and explicit solvent effects. The most stable 5,6-enol configurations—corresponding to pure water and in water–DMSO (1 : 3 mass ratio) were selected. Torsion angles were fixed and held constant throughout the aldol addition reaction, as described in section 2.4.^33,57 The results demonstrated that the aldol addition between 5-HMF⁺ and the 5,6-enol proceeds in a concerted manner in gas phase, as shown in Fig. 6a. This finding aligns with our previous work, where the aldol addition reaction between 5-HMF⁺ and various enols derived from 5-HMF was studied under implicit solvent conditions.¹⁵ The energy profiles for the aldol addition reaction for the linear and quasi-cyclic conformations of 5,6-enol are shown in Fig. 6b. The activation free energy for the quasi-cyclic conformation of the 5,6-enol (corresponding to the water–DMSO 1 : 3 mass ratio) is 66.4 kJ mol⁻¹ whereas the enol's linear configuration has an activation free energy barrier of 61.5 kJ mol⁻¹. For the quasi-cyclic conformer, the anomeric electrophilic carbon 6 interacts with the carbonyl group at carbon 1, leading to intramolecular stabilization (see Fig. S17†). In contrast, the linear form of the 5,6-enol lacks intramolecular interactions, with its polar groups stabilized by water molecules from the Zundel structure. The linear conformation exhibits slightly higher (5 kJ mol⁻¹) free energy barrier compared to the quasi-cyclic conformer, attributed solely to differences in molecular configuration. However, this energy difference alone does not fully explain the observed changes in energetics in the presence of solvent. Therefore, further investigation into the influence of explicit, polarizable solvent environments is necessary.

Fig. 6 a) DFT computed reaction mechanism (without explicit solvent) of the aldol-addition reaction of 5,6-enol with 5-HMF⁺. Transition states of the reactions are depicted using square brackets and atoms not taking part in the reaction are faded. b) Free energy profile for the aldol addition reaction between 5,6-enol and 5-HMF. DFT computed free energy values for open-chain configuration (pure water) and cyclic form configuration (water–DMSO) are shown in blue and red, respectively. Activation free energies (AE) and reaction free energies (ΔG_R) are reported in kJ mol⁻¹.

3.4 Solvent reorganization energies during aldol addition reaction

Solvent reorganization energy is the energy required to reorient solvent molecules around a reacting species during an electron/charge transfer process.⁵⁸ The redistribution of charge within the reacting species during a chemical reaction induces solvent polarization, thereby modifying the neighboring solvent environment. This polarization can lead to solvent molecules' reorientation around the reactant. The energy penalty associated with the redistribution of solvent is known as the solvent reorganization energy (λ).⁵⁹ The free energy barrier of the reaction performed in the condensed phase includes λ, which represents the energy needed to shift the solvent from its equilibrium configuration around the reactant to the new equilibrium configuration of the products. During the aldol addition of 5-HMF⁺ and 5,6-enol, the hydroxyl at carbon 5 oxidizes to a carbonyl functional group, with H_δ transferring to a neighboring water molecule, while the C–C bond forms between carbons 6 and 7, leading to intramolecular charge redistribution within the reacting species. This would result in neighboring solvent molecules having to reorganize themselves. To assess the extent of solvent reorganization in response to the charge redistribution, we calculated the solvent reorganization energy (λ). The concerted aldol addition mechanism was chosen as the case study because it proceeds identically in both water and water–DMSO (1 : 3 wt) systems and the difference in activation free energies in water and water–DMSO environment is significant. In contrast, the stepwise mechanisms occur in a different sequence in pure water compared to that in the presence of DMSO. Additionally, since the charge redistribution in the reacting species is occurring in multiple steps, the effect on solvent molecules would be less pronounced as compared to the concerted mechanism and this is evident from the observation that the free energy barrier difference between water and water–DMSO system is much smaller for the stepwise mechanism. For both solvent compositions, the minimum energy pathways for the concerted aldol addition reaction were mapped to generate 2D free energy profiles. To determine λ, the reactant well was projected to the product well (post-aldol addition) using polynomial numerical fitting, as illustrated in Fig. 7. It is observed that the solvent reorganization energy (λ) is 157 kJ mol⁻¹ in pure water and 451 kJ mol⁻¹ in the water–DMSO (1 : 3 wt) mixture. The lower λ value in pure water indicates that the solvent environment needs lesser reorganization with the change in reactant species' charge distribution. This reduced λ in water leads to a lower activation energy barrier. In contrast, the higher λ in the water–DMSO (1 : 3 wt) mixture suggests that solvent molecules in presence of DMSO require more energy to reorient along the reaction coordinates, leading to an increased activation energy barrier. These findings align with previous work, where we determined that adding DMSO as a cosolvent in an aqueous system increased λ during the deprotonation reaction of 5-HMF in an acidic environment.⁶⁰ In that study, we demonstrated that water molecules undergo a more extensive molecular rearrangement due to the steric hindrance imposed by DMSO molecules. In contrast, in pure water, less reorientation is required to efficiently facilitate the charge transfer step, resulting in a lower associated energy penalty. Water's higher dielectric constant compared to DMSO enhances its ability to stabilize charge separation, reducing the energy required for solvent reorganization during the aldol addition reaction. DMSO (8.28 ų) exhibits higher molecular polarizability than water (1.34 ų),⁶¹ meaning its electron cloud is more readily distorted by electric charge redistribution from the reacting species. In contrast, the lower polarizability of water results in smaller perturbations to the solvent's electron cloud, leading to a reduced reorganization energy.⁶² These results are also in agreement with previous work studying the aldol addition reaction of 5-HMF⁺ with other enol molecules; the addition of acetone as a polar aprotic solvent into the aqueous system results in a higher energy barrier compared to pure water solvent.⁶³ Based on the results of this work, a similar conclusion can be drawn regarding the higher energy free energy barrier observed in the aldol addition reaction compared to the pure water solvent. Since acetone (6.27 ų) has higher polarizability than water, acetone may undergo more molecular reorganization in response to the redistribution of charge in the reacting species.⁶⁴ This increased reorganization leads to a higher solvation energy and consequently a higher free energy barrier for the reaction. These findings provide valuable insights into how the addition of aprotic solvents alters the kinetics of aldol addition through solvent dynamics and reorganization. In particular, the use of aprotic solvents, such as DMSO, has been widely employed to tune the properties of biopolymers and enhance the selectivity of specialty chemicals or biofuels produced via aldol addition.

Fig. 7 Free energy surface data projection in 2-D for the protonation for the aldol addition reaction between 5,6-enol and 5-HMF considering the minimum energy pathway for the concerted mechanism in a) pure water and b) water–DMSO. All free energy values are in kJ mol⁻¹.

4. Conclusions

This study investigates how solvent environment, and its characteristics affect the kinetics of the aldol addition reaction between 5-HMF⁺ and 5,6-enol, using ab initio molecular dynamics (AIMD) simulations that account for solvent polarizability, temperature effects, and dynamics. Solvent composition significantly impacted the reaction mechanisms. In pure water, the stepwise mechanism involved C–C bond formation followed by proton transfer, while in water–DMSO (1 : 3 mass ratio), proton loss preceded C–C bond formation. In both environments, the concerted mechanism had higher free energy barriers. In pure water, the stepwise pathway showed barriers of 41 and 33 kJ mol⁻¹, compared to 57 kJ mol⁻¹ for the concerted path. In water–DMSO, the concerted mechanism had a much higher barrier (451 kJ mol⁻¹), while the stepwise pathway had 87 kJ mol⁻¹ for deprotonation and 178 kJ mol⁻¹ for addition reaction. Conformational changes in 5,6-enol showed that it adopts an open structure in pure water, stabilized by hydrogen bonding, while DMSO favors a quasi-cyclic form. The difference in free energy barriers cannot be fully explained by these conformational changes, as the quasi-cyclic form is only ∼5 kJ mol⁻¹ higher in energy. Solvent reorganization energy during aldol addition is ∼157 kJ mol⁻¹ in pure water and ∼451 kJ mol⁻¹ in water–DMSO, highlighting the significant energy required for solvent reorientation in the presence of DMSO. This is due to water's higher dielectric constant and DMSO's higher polarizability. In conclusion, this study provides insights into how solvent environments alter reactant configurations and aldol addition kinetics, emphasizing the importance of accounting for solvent dynamics and polarizability in biomass conversion processes for fuels, biopolymers, and chemicals.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by funding from the Canada First Research Excellence Fund as part of the University of Alberta's Future Energy Systems Research Initiative, the Natural Sciences and Engineering Research Council of Canada (NSERC) via their Discovery Grants program, University of Alberta and the MITACS Graduate Fellowship Award. The Digital Research Alliance of Canada provided computational resources.

References

1. P. Gallezot, Catalytic Conversion of Biomass : Challenges and Issues, ChemSusChem, 2008, 1, 734–737.
2. C. H. Zhou, X. Xia, C. X. Lin, D. S. Tong and J. Beltramini, Chem. Soc. Rev., 2011, 40(11), 5588–5617.
3. J. N. Chheda and J. A. Dumesic, Catal. Today, 2007, 123(1–4), 59–70.
4. J. N. Chheda, G. W. Huber and J. A. Dumesic, Angew. Chem., Int. Ed., 2007, 46(38), 7164–7183.
5. P. Carniti, A. Gervasini and M. Marzo, Catal. Commun., 2011, 12(12), 1122–1126.
6. I. Van Zandvoort, E. J. Koers, M. Weingarth, P. C. A. Bruijnincx, M. Baldus and B. M. Weckhuysen, Green Chem., 2015, 17(8), 4383–4392.
7. S. Agarwal, D. van Es and H. J. Heeres, J. Anal. Appl. Pyrolysis, 2017, 123, 134–143.
8. A. Mija, J. C. van der Waal, J. M. Pin, N. Guigo and E. de Jong, Constr. Build. Mater., 2017, 139, 594–601.
9. G. Tsilomelekis, M. J. Orella, Z. Lin, Z. Cheng, W. Zheng, V. Nikolakis and D. G. Vlachos, Green Chem., 2016, 18(7), 1983–1993.
10. I. V. Sumerskii, S. M. Krutov and M. Y. Zarubin, Russ. J. Appl. Chem., 2010, 83(2), 320–327.
11. I. Van Zandvoort, Y. Wang, C. B. Rasrendra, E. R. H. Van Eck, P. C. A. Bruijnincx, H. J. Heeres and B. M. Weckhuysen, ChemSusChem, 2013, 6(9), 1745–1758.
12. S. J. Dee and A. T. Bell, ChemSusChem, 2011, 4(8), 1166–1173.
13. S. K. R. Patil and C. R. F. Lund, Energy Fuels, 2011, 25(10), 4745–4755.
14. S. K. R. Patil, J. Heltzel and C. R. F. Lund, Energy Fuels, 2012, 26(8), 5281–5293.
15. J. C. Velasco Calderón, J. S. Arora and S. H. Mushrif, ACS Omega, 2022, 7, 44786–44795.
16. G. W. Huber and J. A. Dumesic, Catal. Today, 2006, 111(1–2), 119–132.
17. R. D. Cortright, R. R. Davda and J. A. Dumesic, Nature, 2002, 418(6901), 964–967.
18. G. W. Huber, R. D. Cortright and J. A. Dumesic, Angew. Chem., Int. Ed., 2004, 43(12), 1549–1551.
19. G. W. Huber, J. N. Chheda, C. J. Barrett and J. A. Dumesic, Science, 2005, 308(5727), 1446–1450.
20. C. J. Barrett, J. N. Chheda, G. W. Huber and J. A. Dumesic, Appl. Catal., B, 2006, 66(1–2), 111–118.
21. L. Faba, E. Díaz and S. Ordõñez, ChemSusChem, 2014, 7(10), 2816–2820.
22. H. Chang, E. B. Gilcher, G. W. Huber and J. A. Dumesic, Green Chem., 2021, 23(12), 4355–4364.
23. J. N. Chheda, Y. Román-Leshkov and J. A. Dumesic, Green Chem., 2007, 9(4), 342–350.
24. R. Weingarten, A. Rodriguez-Beuerman, F. Cao, J. S. Luterbacher, D. M. Alonso, J. A. Dumesic, G. W. Huber, M. Alonso, J. A. Dumesic and G. W. Huber, ChemCatChem, 2014, 6(8), 2229–2234.
25. Y. Román-Leshkov and J. A. Dumesic, Top. Catal., 2009, 52(3), 297–303.
26. T. W. Walker, A. K. Chew, H. Li, B. Demir, Z. C. Zhang, G. W. Huber, R. C. Van Lehn and J. A. Dumesic, Energy Environ. Sci., 2018, 11(3), 617–628.
27. M. A. Mellmer, C. Sanpitakseree, B. Demir, P. Bai, K. Ma, M. Neurock and J. A. Dumesic, Nat. Catal., 2018, 1(3), 199–207.
28. A. K. Chew, T. W. Walker, Z. Shen, B. Demir, L. Witteman, J. Euclide, G. W. Huber, J. A. Dumesic and R. C. Van Lehn, ACS Catal., 2020, 10(3), 1679–1691.
29. S. Shao, Z. Ye, X. Hu, J. Sun, X. Li and H. Zhang, Fuel, 2023, 333(P1), 126238.
30. S. H. Mushrif, S. Caratzoulas and D. G. Vlachos, Phys. Chem. Chem. Phys., 2012, 14(8), 2637–2644.
31. J. C. Velasco Calderón, S. Jiang and S. H. Mushrif, ChemPhysChem, 2021, 22(21), 2222–2230.
32. C. Sanpitakseree, A. H. Motagamwala, J. A. Dumesic and M. Neurock, ACS Sustainable Chem. Eng., 2022, 10(26), 8275–8288.
33. F. J. S. Duarte, E. J. Cabrita, G. Frenking and A. G. Santos, Eur. J. Org. Chem., 2008, 19, 3397–3402.
34. W. Plazinski, A. Plazinska and M. Drach, Phys. Chem. Chem. Phys., 2016, 18(14), 9626–9635.
35. Q. Lin, Green Chem., 2020, 532–539.
36. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. Van Der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29(7), 845–854.
37. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118(45), 11225–11236.
38. V. Vasudevan and S. H. Mushrif, RSC Adv., 2015, 5(27), 20756–20763.
39. S. Nosé, J. Chem. Phys., 1984, 81(1), 511–519.
40. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1695–1697.
41. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
42. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(7), 3641–3662.
43. A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71(12), 126601.
44. G. Bussi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2006, 96(9), 10–13.
45. G. M. Pavan, A. Barducci, L. Albertazzi and M. Parrinello, Soft Matter, 2013, 9(9), 2593–2597.
46. Æ. Frisch, R. E. Plata and D. A. Singleton, Gaussian 09W Reference, J. Am. Chem. Soc., 2009, 137, 3811–3826.
47. J. S. Arora, J. W. Chew and S. H. Mushrif, J. Phys. Chem. A, 2018, 122(38), 7646–7658.
48. H. B. Mayes and L. J. Broadbelt, J. Phys. Chem. A, 2012, 116(26), 7098–7106.
49. R. Li, Q. Lin, Y. Liu, X. Wang, C. Liu, F. Peng and J. Ren, J. Catal., 2023, 424, 162–172.
50. J. V. Vermaas, M. F. Crowley and G. T. Beckham, ACS Sustainable Chem. Eng., 2020, 8(48), 17839–17850.
51. M. Mebrouki, T. Ouahrani and Y. Ö. Çiftci, Int. J. Thermophys., 2016, 37(7), 1–13.
52. V. Koverga, Á. Juhász, D. Dudariev, M. Lebedev, A. Idrissi and P. Jedlovszky, J. Phys. Chem. B, 2022, 126(36), 6964–6978.
53. J. He, M. Liu, K. Huang, T. W. Walker, C. T. Maravelias, J. A. Dumesic and G. W. Huber, Green Chem., 2017, 19(15), 3642–3653.
54. M. H. Tucker, R. Alamillo, A. J. Crisci, G. M. Gonzalez, S. L. Scott and J. A. Dumesic, ACS Sustainable Chem. Eng., 2013, 1(5), 554–560.
55. A. H. Motagamwala, K. Huang, C. T. Maravelias and J. A. Dumesic, Energy Environ. Sci., 2019, 12(7), 2212–2222.
56. X. Qi, M. Watanabe, T. M. Aida and R. L. Smith Jr., Green Chem., 2008, 10(7), 799–805.
57. S. H. Mushrif, J. J. Varghese and C. B. Krishnamurthy, Phys. Chem. Chem. Phys., 2015, 17(7), 4961–4969.
58. T. Kubař and M. Elstner, J. Phys. Chem. B, 2009, 113(16), 5653–5656.
59. L. Yang, G. Tsilomelekis, S. Caratzoulas, D. G. Vlachos, H. Guo, A. Duereh, Y. Su, E. J. M. Hensen, X. Qi, R. L. Smith, G. Yang, E. A. Pidko, E. J. M. Hensen, L. Yang, G. Tsilomelekis, S. Caratzoulas, D. G. Vlachos, Y. Kim, A. Mittal, D. J. Robichaud, H. M. Pilath, B. D. Etz, P. C. St. John, D. K. Johnson and S. Kim, ChemSusChem, 2015, 8(8), 1334–1341.
60. J. C. Velasco Calderón and S. H. Mushrif, React. Chem. Eng., 2023, 9(2), 273–286.
61. P. Pacak, J. Solution Chem., 1987, 16(1), 71–77.
62. H. L. Tavernier, A. V. Barzykin, M. Tachiya and M. D. Fayer, J. Phys. Chem. B, 1998, 102(31), 6078–6088.
63. M. A. Mellmer, C. Sanpitakseree, B. Demir, K. Ma, W. A. Elliott, P. Bai, R. L. Johnson, T. W. Walker, B. H. Shanks, R. M. Rioux, M. Neurock and J. A. Dumesic, Nat. Commun., 2019, 10(1), 1–10.
64. M. Gussoni, M. Rui and G. Zerbi, J. Mol. Struct., 1998, 447(3), 163–215.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5re00054h

---