Kinetic analysis of kraft lignin conversion via the Fenton process: process optimization and stochastic modelling

Abstract

Lignin is a macromolecule with a highly branched and complex structure, making it difficult to degrade. It is a by-product of the pulp and paper industry and extensive treatment is required to mitigate environmental issues associated with effluent discharge. As an alternative, lignin can be treated through advanced oxidative processes (AOPs) using the Fenton reaction, which involves hydrogen peroxide (H₂O₂) and iron ions. In this context, a rotational central composite design (RCCD) was conducted to optimize lignin degradation using different molar ratios of H₂O₂/Fe²⁺ and H₂O₂/Fe³⁺ to assess the synergistic catalytic action of ions. The reactions were conducted in a batch reactor (2 L capacity), and a kinetic study of lignin degradation was performed using a stochastic model to characterize the oxidative process. Optimized conditions for the Fenton reaction were predicted, adopting a molar ratio of H₂O₂/Fe²⁺ of 9.0 and H₂O₂/Fe³⁺ of 6.0. The optimal conditions resulted in a 47.3% reduction in total organic carbon (TOC), reaching a conversion of over 80% in the depolymerization process. A quadratic model performed for the response variable TOC reduction showed a correlation coefficient (R²) of 0.926, indicating the model's quality and its ability to predict the variable with the greatest influence on the lignin depolymerization process. Further, Pseudomonas putida exhibited growth on low-molecular-weight aromatic molecules after depolymerization of kraft lignin.

---

Introduction

Lignin is a complex aromatic structure that has become a subject of extensive study among researchers due to its potential in bioproduct production. However, currently, this macromolecule is a by-product of the pulp and paper industry that exhibits high resistance to biodegradation. Lignin presents a highly branched and complex macrostructure to degrade, thus requiring treatment of this by-product to reduce environmental problems related to effluents from these processes. Lignin from the pulp and paper industry is currently used for energy generation due to its high calorific value; however, its conversion into high commercial value products is necessary for advancing the circular bioeconomy and safe environment.^1,2

Industrial effluent treatment is extremely important not only from an environmental regulatory standpoint but also represents a significant opportunity for reusing resources present in the effluent to produce high commercial value products and promote socio-environmental responsibility.² Effluents containing the macromolecule lignin consist of aromatic compounds that require treatment prior to their discharge into water bodies. Among the potential applications of treated effluent, the use of depolymerized lignin as a carbon source for microorganisms stands as a sustainable and biotechnologically relevant alternative to produce bioproducts.

Among the main monomers derived from depolymerized lignin, phenolic monomers such as ferulic acid, coumaric acid, and p-coumaric acid stand out. It is crucial to ensure efficient lignin depolymerization. This way, oligomers will be cleaved into monomers and assimilated by lignin-degrading microorganisms. The presence of trimers, dimers, and smaller oligomers is toxic to these microorganisms.^3,4

The major challenge to developing the sustainable processes in pulp and paper industries is to utilize kraft lignin with maximum efficiency. The valorization of lignin presents an excellent opportunity for developing clean processes and expanding the biomass-utilizing supply chain.^3,4

Among the numerous ways to depolymerize lignin, the Fenton process is an effectively advanced oxidation process (AOP) technology for degradation of hazardous and organic pollutants in wastewater due to its relatively good efficiency, low toxicity, process simplicity and low cost.⁵ This approach, based on the utilization of hydrogen peroxide (H₂O₂) and iron ions (Fe²⁺ and Fe³⁺), has been the subject of extensive research due to its effectiveness in eliminating persistent organic pollutants such as phenols, dyes, pharmaceuticals, and other toxic compounds.

Fenton reactions use iron ions (Fe²⁺ and Fe³⁺) as catalysts for the activation of H₂O₂ and, consequently, the production of highly reactive species. The characteristic mechanisms of Fenton reactions are primarily based on the following equations:

OH· + H₂O₂ → HO₂· + H₂O (1)

Fe²⁺ + H₂O₂ → Fe³⁺ + OH· + OH⁻ (2)

Fe³⁺ + H₂O₂ → Fe²⁺ + HO₂· + H⁺ (3)

OH· + Fe²⁺ → Fe³⁺ + OH⁻ (4)

Fe³⁺ + HO₂· → Fe²⁺ + O₂H⁺ (5)

Fe²⁺ + HO₂· + H⁺ → Fe³⁺ + H₂O₂ (6)

2HO₂· → H₂O₂ + O₂ (7)

Several studies have explored the removal efficiency of the lignin stream by applying Fenton processes from pulp and paper mills.^6–9 The focus of most studies has been on the oxidative process; there has been less interest in the application of treated effluent streams and the mathematical modeling of reaction kinetics. In this context, mathematical tools can help predict conditions without the need for exhaustive experimentation.^10–12 By simulating reaction conditions based on the constructed mathematical model, valuable insights can be gained.

Therefore, the development of mathematical models, in this case utilizing stochastic modelling, facilitates process optimization and understanding of operational parameters throughout the entire reaction process. The literature contains similar studies that use stochastic modelling in the degradation of leachate.^10–12 However, using this stochastic model for the depolymerization of lignin is a novel approach.

This work employed an advanced oxidative process to depolymerize a kraft lignin solution derived from the pulp and paper industry. Statistical tools were utilized to study the oxidative process to elucidate the most influential variables affecting lignin degradation. Reactions were carried out in single-batch mode to study the kinetic degradation of this macromolecule. A rotational central composite design (RCCD) experiment was conducted to study the variables influencing the process of lignin oxidation and their interactions. Through response surface methodology, the conditions for kraft lignin degradation were optimized in diluted solutions. Furthermore, stochastic modelling was employed to determine the important parameters in the reaction kinetics and the depolymerized lignin was used as a carbon source for the growth of the Pseudomonas putida ATCC 12633 microorganism, which assimilates aromatic compounds derived from lignin.

Materials and methods

Reagents

Alkali lignin (kraft lignin) with 96% (w/w) purity and 4% (w/w) sulfur was received from Suzano Papel e Celulose (Jacareí, SP, Brazil). Hydrogen peroxide (H₂O₂) (29% (w/w)) and hydrochloric acid (HCl) were provided by Synth (Diadema, SP, Brazil). High-purity iron powder, iron(II) sulfate heptahydrate (FeSO₄·7H₂O), and iron(III) chloride hexahydrate (FeCl₃·6H₂O) were provided by Êxodo Scientific (Sumaré, SP, Brazil). All solutions were prepared by dissolving in distilled water containing <0.001 mg L⁻¹ iron.

Experimental procedures

Lignin solution (120 mg L⁻¹) was prepared by diluting alkali lignin with distilled water and adjusted to pH 3.0, and then the solution was added into a reactor (2 L) (Fig. 1). The synergistic catalytic action was employed by the addition of Fe²⁺ and Fe³⁺ into the lignin solution, with the concentration levels as shown in Table 1. After 5 min, H₂O₂ was immediately added to initiate the catalytic reactions. Samples were taken over time to obtain the kinetic profile of lignin degradation. The reactions were stopped instantaneously by the addition of NaOH to elevate the pH level to 12.0 (ref. 13 and 14) prior to the filtration process using membrane filter (0.45 μm) to remove the chemical precipitate before analysis. A portion of the final sample (depolymerized lignin) was set aside to supplement the culture medium by replacing glucose with aromatic rings derived from lignin.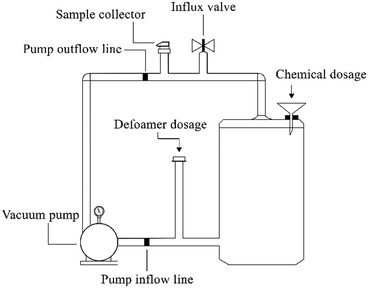

Fig. 1 Schematic drawing of the reactor used in the lignin depolymerization process employing advanced oxidative process (AOP).

Table 1 Rotational central composite design (RCCD) for lignin degradation by the Fenton reaction with the synergistic catalytic action and conversion rate (%) after 6-hour processes

Run	H2O2/Fe^2+	H2O2/Fe^3+	TOC reduction (%)	Lignin concentration (mg L^−1)
1	3.00	3.00	53.34	57.95
2	3.00	9.00	31.39	20.25
3	9.00	3.00	60.15	25.20
4	9.00	9.00	36.44	23.55
5	1.75	6.00	27.54	68.40
6	10.24	6.00	52.11	27.95
7	6.00	1.75	79.95	50.00
8	6.00	10.24	48.03	31.90
9	6.00	6.00	46.37	27.95
10	6.00	6.00	46.55	24.85

---

Analytical methods

Concentration levels of lignin and aromatic compounds were determined by measuring sample absorbance (Evolution 201 UV-visible spectrophotometer, Thermo Scientific, USA) at 280 nm.¹⁵ Total organic carbon (TOC) was determined using a Shimadzu TOC analyser (TOC-V CPN, Shimadzu, Japan). To avoid the interference of hydrogen peroxide with the lignin concentration and organic carbons, H₂O₂ was removed from the samples before analyses by adding 1 M NaOH and 0.9 mM NaHSO₃. The bacterial growth was measured using a spectrophotometer by reading absorbances at 620 nm (OD₆₂₀). The sugar content was measured using high-performance liquid chromatography (HPLC). All measurements were performed in triplicates.

Experimental design

A rotational central composite design (RCCD) was employed to estimate the coefficients of the mathematical model, predicting the response (Z-lignin concentration) and verifying the applicability of the model for the ratios H₂O₂/Fe²⁺ (X) and H₂O₂/Fe³⁺ (Y) (Table 1), as previously described by Tantiwa et al. (2013).¹⁶ Using the numerical optimization tool Design Expert (Version 8.0.7, Stat-Ease Inc), the response surface was constructed and applied to find the optimum levels, with the criterion being the maximum depolymerization of lignin. The TIBCO Statistica 14.0.0.15 software (Santa Clara, CA, USA) was used for the design of experiments and data analysis. The significance of the model equations and the model terms was evaluated in terms of p-value with a 95% confidence level.

Mathematical modelling of lignin degradation based on a stochastic equation

The stochastic differential equation used in this study is presented below in eqn (8).^10,11 The first part of the equation refers to the variation in lignin removal with long reaction times, and the second part represents the stochastic nature of the dispersion.where a, b, c, k, and p are model parameters that depend on experimental conditions and X_t is the lignin conversion at time t (min). Parameter a represents the reaction plateau slope (observed after the initial rapid lignin conversion), parameter b is the average baseline conversion value at which the plateau begins, parameter c is the dispersion of experimental data, parameter p is related to the correlation of experimental data, and parameter k is related to the time taken to reach the reaction plateau (eqn (9)). A geometric explanation of these parameters is given by eqn (14).¹¹

In eqn (8), for each t >0 in which X_t has a normal distribution, mean and variance values are given by eqn (10) and (11), respectively:

E(X_t) = at + b(1 − e^−kt) = μ_t (10)

Fig. 2 was plotted to better understand how model parameters influence the reaction. Parameter a defines the slope of the plateau that the reaction attains after the initial rapid conversion phase. Parameter b marks the baseline mean value of conversion at which the effects begin. Parameters c and p relate to the dispersion and correlation of experimental data. Parameter k is related to the reaction time required to reach the plateau. From eqn (9), it can be observed that when k is large, the curve shows a fast-exponential growth, stabilizing at a plateau with an initial value of b. After reaching the plateau, the expected value acquires a linear behaviour, modelled by the term a·t. By using eqn (9) and assuming a large k, it is possible to estimate the time taken by the reaction to reach the plateau.

Fig. 2 Geometric representation of the parameters of eqn (10) related to the average behaviour of degradation. Initially, a rapid (exponential) phase in the degradation is observed, followed by a slower (linear) phase.

Chemical characterization of lignin

The molar mass distribution of depolymerized lignin samples was estimated by high-performance size exclusion chromatography (HPSEC) using an ENrich SEC 70, 10 mm × 300 mm column (Bio-Rad, USA) eluted at 0.6 mL min⁻¹ with 10 mM NaOH containing 200 mM NaCl. Detection at 280 nm was achieved in an AKTA Purifier GE-900 chromatographic system (GE, Boston, MA, USA). Lignosulfonate standards (Sigma-Aldrich, Germany) calibrated the column system in the range of 77–4.3 kDa. Vanillic acid (0.168 kDa) also integrated the calibration standard set. Commercial lignosulfonate from softwoods (#471011, Sigma, USA) was also analyzed in the same chromatographic system.

Bacterial cultivation using lignin as a carbon source

The study employed bacterial strain P. putida ATCC 12633, procured from the Fundação Tropical de Pesquisas e Tecnologia André Tosello (Campinas/SP-Brazil). The stock culture vials were stored in glycerol at −20 °C.

The liquid culture medium experiments were conducted in 25 mL shake flasks, which contained 10 mL of M9 minimal medium, at 30 °C and 180 rpm. The M9 medium contained (per L) 6 g Na₂HPO₄, 3 g KH₂PO₄, 1 g NH₄Cl, 0.5 g NaCl, 2 mM MgSO₄, 100 μM CaCl₂, and 10 mL of 10× trace elements. The pH was adjusted to 7, and all medium components were sterilized by autoclaving or sterile filtering. The depolymerized lignin (DL) was tested as a carbon source replacing glucose.

Culture medium preparation was done by adding 50% (v/v) DL and 50% (v/v) M9 to 25 mL shaker flasks using 10 mL of total volume. Control tests were also conducted with glucose to evaluate the direct effect of DL on bacterial growth. The ‘seed culture’ inoculum was prepared in nutrient broth (NB) medium, and subsequently, 10% of the volume was inoculated into the two different media.

Results and discussion

Stochastic modelling for the kinetic profile of lignin depolymerization by means of the Fenton process

Based on the experimental plan shown in Table 1, the results of adjusting the stochastic model under different experimental conditions are shown in eqn (8). Fig. 3 and 4 show a good quality of fit (R² between 0.94 and 0.98, except for condition 7) of the model under different experimental conditions. In the study of all experimental conditions, except condition 7, a rapid increase in initial conversion was observed, followed by a slower phase in the lignin degradation process.

Fig. 3 Stochastic model for lignin degradation experiments by the Fenton process: (a) run 1, (b) run 2, (c) run 3, (d) run 4, (e) run 5, (f) run 6. Circles: experimental data points. Uniform centerline: average behavior of the model. External lines: 95% confidence intervals.

Fig. 4 Stochastic model for Fenton lignin degradation experiments: (g) run 7, (h) run 8, (i) run 9, (j) run 10, (k) run 11. Circles: experimental data points. Uniform centerline: average behavior of the model. External lines: 95% confidence intervals.

The parameters obtained from the stochastic model under different experimental conditions are presented in Table 2.

Table 2 Parameters obtained from the stochastic model and their influence on kraft lignin oxidation

Run	F2	F3	a	b	c	k	p	R ^2
1	3	3	6.83 × 10^−4	0.31	0.0091	0.06	0.31	0.97
2	3	9	9.74 × 10^−4	5.43 × 10^−1	0.0357	0.30	0.54	0.94
3	9	3	2.45 × 10^−4	6.95 × 10^−1	0.0252	0.09	0.38	0.96
4	9	9	7.35 × 10^−4	0.56	0.0224	0.09	0.49	0.98
5	1.75	6	2.61 × 10^−4	0.34	0.0097	0.04	0.40	0.97
6	10.24	6	1.28 × 10^−4	0.76	0.0276	0.06	0.43	0.94
7	6	1.75	3.19 × 10^−4	0.58	0.0066	0.02	0.13	0.84
8	6	10.24	9.02 × 10^−4	0.43	0.0235	0.13	0.53	0.94
9	6	6	4.93 × 10^−4	0.58	0.0197	0.05	0.45	0.96
10	6	6	5.25 × 10^−4	0.63	0.0287	0.11	0.57	0.98

---

Furthermore, stochastic modelling was developed in eqn (10) as an empirical model, where the average behaviour and variance of the model provide a good fit for the conversion and dispersion of experimental data related to the degradation of industrial effluents treated by AOPs. In eqn (11), it is shown that the average behaviour of the stochastic model exhibits a rapid initial phase followed by a slower phase of effluent degradation. The rapid phase can be approximated by two pseudo-first-order kinetic equations with apparent kinetic constants k₁ and k₂, where k₁ > k₂, and the slow phase can be approximated by a zero-order reaction. A notable point in eqn (10) is the geometric interpretation of the parameters of the stochastic model in relation to the rapid and slow phases of degradation.

Eqn (12)–(14) show the variations of the parameters of the stochastic model as a function of the operational conditions of AOPs, suggesting the most likely kinetic equations acting in the rapid and slow phases of the degradation profile.

Based on the data from Table 2, it was possible to build auxiliary regression models to explain how the parameters a, b and k, related to average conversion, are influenced by the process variables studied, that is, H₂O₂/Fe²⁺ (F2 variable) and H₂O₂/Fe³⁺ (F3 variable). These equations are presented below:

a = 0.000415 − 0.000003 × (F2)² + 0.000006 × (F3)² (12)

b = 0.2961 + 0.0413 × F2 (13)

k = 0.01594 × F3 (14)

The analysis of variance (ANOVA) of the equation parameters is presented in Tables 3–5.

Table 3 Regression coefficient of parameter a

Coefficient a
Term	Coef	EP coef	Value-T	p-Value
Constant	0.000415	0.000124	3.36	0.012
(F2)^2	−3 × 10^−6	0.000002	−1.94	0.094
(F3)^2	0.000006	0.000002	3.39	0.012

---

Table 4 Regression coefficient of parameter b

Coefficient b
Term	Coef	EP coef	Value-T	p-Value
Constant	0.2961	0.0698	4.25	0.003
F2	0.0413	0.0106	3.89	0.005

---

Table 5 Regression coefficient of parameter k

Coefficient k
Term	Coef	EP coef	Value-T	p-Value	VIF
F3	0.01594	0.00309	5.16	0.001	1

---

At the significance level of 10%, these equations show the influence of the operational variables F2 and F3 in both the fast and the slow phases on the lignin depolymerization profile. These equations suggest, together with the typical AOP reactions presented in the Introduction, that the reactions that probably most influence each phase (fast and slow) are:

Rapid initial phase

An increase in H2O2 concentration improved the fast phase	Fe^2+ + ·OH → Fe^3+
An increase in Fe^2+ worsened degradation
Fe^2+ interference in H2O2
An increase in Fe^3+ concentration made the initial phase longer

Slow phase

An increase in Fe^2+ concentration improved parameter a	Fe^2+ + H2O2 → ·OH + HO^−
A decrease in Fe^3+ concentration improved parameter a	Fe^3+ + H2O ↔ FeOH^2+ + H^+
	FeOH^2+ + H2O2 ↔ Fe(OH)(HO2)^+ + H^+

Kinetic profile of the lignin depolymerization by the Fenton process

Initially, the reaction was conducted using only one of the catalysts (i.e., it was conducted with H₂O₂ and Fe²⁺ ions), with the concentration of ferrous ion at 8 mM and peroxide at 16 mM, resulting in a molar ratio of 2. As shown in Fig. 5, a conversion of 41.6% was achieved, resulting in a concentration of 70.1 mg L⁻¹.

Fig. 5 Kinetic profile of lignin depolymerization using only hydrogen peroxide (16 mM) and iron(II) ion (8 mM) as catalysts.

Following these results, the strategy of using ferric ions (Fe³⁺) to help regenerate ferrous ions (Fe²⁺) through the adopted reaction was employed. This shift in ion equilibrium favored lignin degradation by AOPs. Under the same conditions, but adding 3 mM ferric ion Fe³⁺, the reaction conversion was 51.6%, corresponding to 58 mg L⁻¹ lignin. Comparatively, when the Fe³⁺ ion was used, there was a 13% reduction in the lignin concentration, and the process conversion increased by 10%. The experiments were conducted using catalysts on a mM (millimolar) scale; however, when considering a real process, these numbers will greatly impact both the efficiency and the cost of the process. The Fe³⁺ ion can provide advantages, but it can also hinder the catalysis of the reaction; the proportion of this ion in the reaction medium will indicate the efficiency of the catalytic process.

When present in excess, the Fe³⁺ ion will consume hydroxyl radicals, as detailed in eqn (1)–(7). This phenomenon is commonly referred to as ‘scavenging’ and was also mentioned by Stanbury (2022),¹⁷ elucidating all mechanisms involved in the Fenton process. Based on these preliminary results, it was decided to conduct the experimental design (RCCD) to determine the optimal concentration of iron ions in the reaction medium. The numerical optimization tool showed the most effective molar ratio of peroxide to iron ions, as presented in Table 1 of the experimental methodology.

Experiments were conducted following the rotational central composite design (RCCD), while other relevant factors for effective degradation, such as initial pH, temperature, and circulation flow rate, were maintained constant. There are few studies in the literature on the kinetics of lignin depolymerization; most of these studies focus on the kinetics of thermal degradation and lignin solvolysis. It is important to note that the synergy between iron ions will impact the cleavage of lignin bonds. Lignin depolymerization necessitates the cleavage of aryl–O ether bonds and decarbonylation reactions. In the proposed work, lignin concentration was experimentally monitored as a function of reaction time using the Fenton process.^14,17

The conducted experiments exhibited promising results and consistent lignin degradation profiles (Fig. 6). It is noteworthy that the concentration of soluble lignin in the medium decreased significantly over time, and the interactions caused by the synergistic effect of iron ions in the reaction medium enhanced the efficiency of total lignin degradation. The kinetic profile exhibits a trend, even though during the depolymerization of the macromolecule some groups may undergo repolymerization, causing the profile to oscillate slightly.^14,17 This phenomenon varies according to the amount of catalyst used. For example, Dhar et al. (2020) studied the sono-photocatalytic degradation kinetics of lignin using TiO₂ as a catalyst.¹⁸ These authors achieved 93% degradation of phenolic groups in lignin after 3 hours of the process; however, they used the strategy of combining ultrasonic frequency with the chemical catalyst. The kinetic profiles obtained fluctuated significantly depending on the combination of the catalyst with the ultrasonic frequency, emphasizing the importance of synergy in catalyzing the reaction.

Fig. 6 Kinetic profile of all conditions performed in lignin depolymerization (from the initial concentration of total lignin of 120 mg L⁻¹) by the Fenton process conducted in a reactor using iron ions Fe²⁺ and Fe³⁺.

Numerous studies in the literature examining Fenton reaction mechanisms emphasize that the Fe³⁺ ion aids in the cycling of iron and the continuous production of hydroxyl radicals, ensuring the occurrence of the oxidative process.^19,20 Wang et al. (2023) reported that the presence of two metals or two different ions enhances the oxidative process compared to a single metal, as the synergy between the ions regenerates the hydroxyl radical.²⁰ Seesuriyachan et al. (2015) studied the synergism among iron ions (Fe⁰, Fe²⁺, and Fe³⁺) in lignin degradation.¹⁴ These authors concluded that the synergistic effect of the three ions enhance the efficiency of lignin degradation through the Fenton process and also yields statistically significant differences. They found the best degradation using 7.61 mg L⁻¹ Fe⁰, 9.89 mg L⁻¹ Fe²⁺, 14.27 mg L⁻¹ Fe³⁺, and 376.88 mg L⁻¹ H₂O₂ for lignin removal.

Total organic carbon (TOC) in the depolymerized lignin samples

TOC is an important parameter to be monitored during wastewater treatment. In the experiments conducted, the initial TOC was 182.2 ± 5.3 mg L⁻¹. Based on total organic carbon (mg L⁻¹), the percentage of removal was calculated by considering the final and initial concentrations. The degradation of final TOC in the samples ranged from 27% to 80%, and this variable is dependent on the concentration of catalysts used and the synergism between iron ions. A higher TOC removal was found in the experimental conditions where a higher catalyst concentration was used. For example, experiment 5 used the lowest H₂O₂/Fe²⁺ ratio and showed lower degradation of TOC. Literature reports suggest that low hydrogen peroxide concentration does not favor catalysis due to the excessive formation of hydroxyl radicals (HO₂·). Conversely, experiment 7, which utilized an intermediate H₂O₂/Fe²⁺ ratio and a very low H₂O₂/Fe³⁺ ratio, exhibited the highest removal of TOC.

Naguib et al. (2023) studied the influence of ferrous ion concentration and hydrogen peroxide concentration on the degradation of organic compounds.¹⁹ These authors concluded that hydroxyl radicals (OH·) are highly reactive, attacking and eliminating organic compounds by causing dissociation of oxidants, but it is necessary to determine the optimal concentration of each of these reagents. Excess peroxide does not increase the degradation of organic compounds, as hydroxyl radicals react to form HO₂·; at low peroxide concentrations, degradation is also not efficient due to the low reaction rate. These authors also studied the concentration of ferrous ion (from 0.05 to 0.3 g L⁻¹) on removal of TOC and observed a concomitant increase in the reduction of organic compounds with an increase in ferrous ion concentration. The initial concentration of the organic compound also influences the amount of catalyst to be used (Fig. 7).

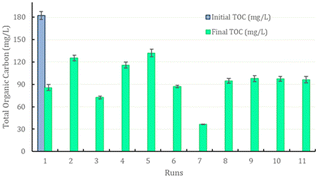Fig. 7 Initial and final total organic carbon (TOC) concentration profile in all experimental conditions of the depolymerization process as per the experimental design.

Catalkaya et al. (2007) studied the removal of pollutants from the pulp and paper industry using Fenton processes.⁶ These authors examined different concentrations of catalysts (Fe²⁺ from 1 mM to 10 mM and H₂O₂ from 5 mM to 100 mM) with the removal of 110 mg L⁻¹ TOC present in the effluent. They achieved 79% removal of TOC using 50 mM hydrogen peroxide and 2.5 mM Fe²⁺ ion at pH 5. The authors concluded that hydrogen peroxide concentrations above 50 mM caused a decrease in the TOC removal percentage, attributed to an excess of hydroxyl radicals forming (HO₂·). In another experiment, the hydrogen peroxide concentration was kept fixed (50 mM), and the Fe²⁺ ion concentration was varied. This led to an increased removal of TOC up to a concentration of 2.5 mM iron ions; above this value, there was a decrease in the TOC removal percentage. The excess of iron reduced the efficiency of the process, likely due to the formation of iron hydroxide. These results are consistent with the results of our present study.

Gel permeation chromatography (GPC) of depolymerized lignin

The molecular weight distribution of the kraft lignin samples depolymerized by Fenton reactions was measured using an AKTA Purifier GE-900 chromatography system with an ENrich SEC 70, 10 mm × 300 mm column and UV detection at 280 nm. Size exclusion chromatograms recorded for lignin samples after depolymerization, resulting from each processing step, exhibited a wide distribution of signals eluting from 13 to 18 mL after area normalization. Chromatograms were obtained as shown in Fig. 8. According to the column calibration with polystyrene sulfonate standards (shown in Fig. S1†), molecules eluting from 13 to 18 mL presented molar masses from 5 to 0.5 kDa.²¹

Fig. 8 High-performance size exclusion chromatograms from depolymerized lignin samples and native lignin sample.

Absolute molar mass determination in lignin and lignosulfonates by size exclusion chromatography is closely dependent on unavailable lignin or lignosulfonate calibration standards to date.²² Chromatographic column calibration with commercial polystyrene sulfonates is a common approach, as reported by Heinz (2022);²¹ however, this approach tends to underestimate the actual molar mass of lignin. This observation was also reported by Heinz et al. (2022),²¹ by analysing the molar mass distribution of commercial lignosulfonates prepared from softwoods with an average molar weight of approximately 33 kDa, according to the universal calibration and optimized multi-angle light scattering (MALS) shown in Fig. S1.†^21,22

The sugarcane bagasse lignin released during pretreatment provided a signal distribution slightly shifted to higher elution volumes (lower molar masses) compared to the commercial lignosulfonate analyzed under the same chromatographic conditions. In the analyses conducted with lignin, it is notable that there is likely a small amount of lignin adsorption occurring in the column used. This results in an underestimation of the lignin molecular size. It can also be observed from the line drawn on the graph that there is a slight shift to the right. This confirms a minor interaction of the analyzed lignin with the column, resulting in an underestimated molar mass. The literature reports that the average size of lignin ranges from 100 to 10 000 kDa, as shown in Fig. 8. The obtained size after the normalization area is ranged from 80 to 2000 kDa.

Kent et al. (2018)²³ conducted an analysis of the average molecular size of lignin and lignin transformed into water-soluble polymer. These authors used tetrahydrofuran (THF) as eluent, using an Agilent 1100 series with two Millipore Waters Styragel HR 4E columns. The authors found a lignin size ranging from 100 to 10 000 kDa for the original lignin and a size of 60 to 10 000 kDa for the water-soluble polymer derived from lignin. Despite using different systems for separation, the results of depolymerized lignin after area normalization are plausible and confirmed by the literature.^22,23

The particle size distribution is essential for monitoring the efficiency of the depolymerization process. Although there are different equipment, analytical methods, and separation columns, the technique proves effective in confirming the depolymerization of lignin, including alkaline depolymerization and consolidated bioprocessing depolymerization, among other types.^21,23

Design of experiments for lignin degradation through AOP

A total of 10 runs (as shown in Table 1) for optimizing the two variables in the current RCCD were performed, with reaction kinetics being assessed in all experiments. The final lignin concentration ranged from 20.3 to 68.4 mg L⁻¹, corresponding to a removal of 83% to 43% lignin. The average rates of removal of lignin were 3.38–11.33 mg L⁻¹ h⁻¹.

Statistical analysis was conducted on the results obtained from the experimental design, and the adjusted model was utilized to generate a fitted surface (Fig. 9). The fitted surface aided in selecting the catalyst concentration, with the criterion of achieving a high reduction in lignin concentration being adopted. In addition, an experiment was carried out to confirm the model. The model was experimentally verified, and the predicted lignin concentration was 23.24 mg L⁻¹ (with a molar ratio of 9 for H₂O₂/Fe²⁺ and 6 for the H₂O₂/Fe³⁺ ratio). This condition utilizes a small amount of catalyst to yield a significant quantity of depolymerized lignin. The experimental value obtained was 21.61 ± 1.5 mg L⁻¹. These findings suggest a good fit for the model (R², 0.821), the equation generated by the model, eqn (15), where (Z) represents the lignin concentration, (X) represents the molar ratio of H₂O₂/Fe²⁺, and (Y) represents the molar ratio of H₂O₂/Fe³⁺. The quality of the model can be confirmed by the close correspondence between the predicted values and the observed values.

Fig. 9 Fitted surface to lignin concentration calculated from quadratic models relating the effects of H₂O₂/Fe²⁺ and H₂O₂/Fe³⁺ molar ratios in the process of lignin depolymerization.

Additionally, a Pareto chart was generated, revealing the linear and quadratic influence of the studied variables. It is worth noting that for the response variable of final lignin concentration, the variable H₂O₂/Fe²⁺ exhibits a linear and negative effect of 2.88 with 95% confidence. The Pareto chart is shown in Fig. S2,† depicting the linear and quadratic effects of the variables H₂O₂/Fe²⁺ and H₂O₂/Fe³⁺ molar ratios on the lignin concentration.

Z = 147.3345693991 − 19.865139173718 × X + 0.85418775260826 × X² − 14.142641250995 × Y + 0.45253823757865 × Y² + 1.0013888888889 × X × Y (15)

Similar results have been found in the literature. For example, Torrades et al. (2011), studied the degradation of lignin solution starting from an initial solution (pH = 3, T = 298 K) with 1.978 absorbance units at λ_uv = 280 nm, corresponding to 100 mg L⁻¹ lignin.⁹ These authors used experimental design to optimize the lignin degradation process and achieved an 85% reduction in lignin concentration under optimized conditions (44.1 mM H₂O₂ and 4.65 mM Fe²⁺, corresponding to a molar ratio of approximately 9.5). The experimental conditions and results obtained are similar to that of the proposed work; however, the use of Fe³⁺ ions allowed for achieving the same results using a smaller amount of catalyst.

Ninomiya et al. (2013) carried out lignin depolymerization via the Fenton process (H₂O₂/Fe²⁺) assisted by sonication starting from an initial solution of 500 mg L⁻¹ at pH 4.0.²⁴ The catalyst concentration used was 3400 mg L⁻¹ peroxide and 280 mg of Fe²⁺ (molar ratio 12). These authors achieved a 50% removal in two hours of oxidation process. The same authors conducted the Fenton process without sonication and achieved a lignin degradation of 1.8%. These results emphasized the gain in efficiency when using combined processes or even the combination of catalysts.

Statistical analysis of the results obtained from the experimental design was conducted, with the percentage of TOC reduction considered as the response variable. Table 1 shows that the TOC reduction percentage ranged from 27% to 80%.

Additionally, it can be observed that the experiment using the lowest dosage of the H₂O₂/Fe²⁺ catalyst exhibited the least TOC degradation. The influence of the variables was statistically evaluated using a Pareto chart (Fig. S3†), where the bars represent the standardized effects related to the response variables. It is noted that the H₂O₂/Fe³⁺ variable demonstrates a significant negative linear effect, with 95% confidence, on the response variable. The remaining variables do not exhibit significant effects on the response variable (i.e., percentage of TOC reduction) with 95% confidence. Eqn (16) was generated by the model, where (Z) represents the reduction of TOC in percentage (%), (X) is the independent variable H₂O₂/Fe²⁺, and (Y) is the independent variable H₂O₂/Fe³⁺. For this response variable, the model achieved a higher coefficient of correlation (R²), and a graph of predicted values versus observed values (Fig. S4†) was generated (Fig. 10).

Fig. 10 Fitted surface showing the influence of the variables H₂O₂/Fe²⁺ and H₂O₂/Fe³⁺ molar ratios on total organic carbon (TOC).

For the response variable of total organic carbon (TOC) reduction (%), the data from the experimental design were statistically analyzed; test analysis of variance (ANOVA) was performed to confirm model approach, as shown in Table 6. The quality of the model was expressed in terms of the R² value. For instance, an R² value of 0.926 indicates that 92.6% of the response variability is explained by the model. A good correlation was obtained, indicating a good fit by the model, for which the criterion of R² of at least 0.80 is suggested.^25,26

Table 6 Analysis of variance (ANOVA) results for TOC reduction (%)

Factor	Sum of squares	Degrees of freedom	Mean square	F	p-Value
(X)	270.704	1	270.704	7.15028	0.055574
(X)^2	112.336	1	112.336	2.96720	0.160071
(Y)	1028.705	1	1028.705	27.17182	0.006460
(Y)^2	231.153	1	231.153	6.10559	0.068877
(X) × (Y)	0.774	1	0.774	0.02045	0.893190
Error	151.437	4	37.859
Total SS	2046.381	9
R ^2 = 0.926

---

Statistically, the H₂O₂/Fe³⁺ molar ratio is the only significant factor, as it has a p-value of 0.006460, below the significance level of 0.05. The other factors and the interaction between the variables do not seem to have a significant influence on the response variable.

Z = 64.353374200922 + 8.836625317927 × X − 0.55040078546977 × X² − 12.95989389884 × Y + 0.78953129477714 × Y² − 0.048888888888888 × X × Y (16)

Biological conversion of depolymerized lignin

The batch fermentation experiment allowed a preliminary understanding of the assimilation of depolymerized lignin (DL) as a source of carbon and energy for P. putida ATCC 12633. The study was conducted by growing P. putida ATCC 12633 in two different culture media (a medium containing M9 salts and glucose, 1.8 g L⁻¹, and another containing M9 salts and depolymerized lignin supplemented in M9 50%, v/v) for 72 h. Fig. 11 reveals the microbial cell growth, showing the relation between optical density (λ, 620 nm) and substrate consumption (g L⁻¹).

Fig. 11 Kinetic profile of substrate consumption (y-axis on the right side) measured in g L⁻¹ and optical density (y-axis on the left side) of cell growth of the microorganism P. putida measured at 620 nm, with fermentation time in hours on the x-axis.

It can be observed that there was higher cell growth in the medium containing M9 and glucose. However, despite growing at a slower rate, the microorganism also grew in a medium where the only carbon source is depolymerized lignin. Despite the growth of microorganisms, other factors related to their metabolism need to be elucidated. Furthermore, identifying monomers is crucial for investigating the growth kinetics of P. putida, as the presence of oligomers is toxic to these lignin-degrading microorganisms.^27,28

This approach has also been reported by other authors, demonstrating the capacity of microorganisms to assimilate low-molecular-weight aromatic compounds derived from various lignin streams.

Salvachúa et al. (2015) studied the ability of 14 different bacteria to produce ligninolytic enzymes and their capacity to catabolize aromatics derived from depolymerized lignin, based on the consolidated bioprocess (CBP) for polysaccharides (enzyme production, saccharification, and fermentation).²⁷ These authors conducted a simultaneous CBP process for a biological system (enzyme production, enzymatic catalysis, and bioproduct formation). Among the 14 species screened, P. putida bacteria showed good results in consuming funneling lignin-derived aromatics. In another study, Kamimura et al. (2017) investigated, in a review article, the metabolic pathways of aromatic-degrading bacteria derived from low-molecular-weight lignin.²⁸ These authors elucidated the pathways involved in the catabolism, the enzymes responsible for cleaving the bonds, and the genes responsible for the synthesis of these oxidative enzymes.

Conclusions

The Fenton process was proven to be an effective process for kraft lignin degradation, with high percentage reductions of lignin, especially in the first 90 minutes of the oxidation process. The optimized conditions obtained high levels of lignin degradation, and the kinetic study was successfully applied to the design of an accurate kinetic model. Both the quadratic model developed for the reduction in lignin concentration as a response variable and the model constructed for TOC reduction are suitable and representative for explaining the dosage of the catalyst factor within the studied range. The variable H₂O₂/Fe²⁺ exerts a significant influence, with 95% confidence, demonstrating a negative linear effect of 2.88 on the lignin concentration reduction as a response variable. Similarly, the variable H₂O₂/Fe³⁺ also exerts a significant influence, with a negative linear effect of 5.21 on the TOC response variable, at a 95% confidence level. Statistically, the H₂O₂/Fe³⁺ molar ratio is the only significant factor, as it has a p-value of 0.006460, below the significance level of 0.05. The other factors and the interaction between the variables do not seem to have a significant influence on the response variable of TOC. The stochastic model satisfactorily fit the kinetic data and separated the reaction kinetics into two phases: a slow and a rapid phase. The reactants involved influence both stages of the reaction depending on their concentration. This influence can be either positive or negative. The degraded lignin was metabolized by the bacterium P. putida, indicating the potential valorization of this compound for bioproduct production using depolymerized kraft lignin as potential feedstock, adding value chain in pulp and paper industries and promoting a circular economy, along with mitigating environmental pollution.

Data availability

Data is contained within the manuscript.

Author contributions

Conceptualization: A. K. C., L. R. and A. F. S. Methodology: L. R. and G. M. M. Validation: A. F. S. and D. A. S. N. Formal analysis: A. K. C., L. R., A. F. S. and D. A. S. N. Investigation: L. R. and G. M. M. Resources: A. K. C. and D. A. S. N. Data curation: A. F. S. Writing – original draft preparation: L. R. and G. M. M. Writing – review and editing: A. K. C., L. R., G. M. M., A. F. S. and D. A. S. N. Visualization: A. K. C., L. R. and D. A. S. N. Supervision: A. K. C. Project administration: A. K. C. Funding acquisition: A. K. C.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. K. Chandel and L. Ramos gratefully acknowledge São Paulo State Funding Agency-FAPESP, Brazil (grant numbers: 2020/12559-6, 2022/13184-1 and 2023/08226-0), and the National Council for Scientific and Technological Development (CNPq), Brazil (Process Number: 309214/2021-1), for the financial project. We also thank Suzano Papel e Celulose S.A, Limeira – SP, for providing the lignin samples to ReCABS Lab, EEL-USP, Lorena-SP/Brazil. We thank the technician Joaquim Brandão, who has shared his experience in equipment handling to carry out this study.

Notes and references

1. A. Raj, S. Kumar, I. Haq and S. K. Singh, Ecol. Eng., 2014, 71, 355.
2. V. K. Garlapati, A. K. Chandel, S. P. Jeevan-Kumar, S. Sharma, S. Sevda, A. P. Ingle and D. Pant, Renewable and Sustainable Energy Resources, 2020, 130, 109977.
3. A. M. Abdel-Hamid, J. O. Solbiati and I. K. O. Cann, in Insights into Lignin Degradation and its Potential Industrial Applications, ed. S. Sariaslani and G. M. Gadd, Academic Press, United States, 2013, vol. 82, pp. 1–28.
4. R. T. Hilares, L. Ramos, M. A. Ahmed, A. P. Ingle, A. K. Chandel, S. S. Silva, J. W. Choi and J. C. Santos, in Valorization of Lignin Into Value-Added Chemicals and Materials, ed. P. Avinash, A. K. Chandel and S. S. Silva, Wiley-Blackwell, United States, 2020, vol. 11, pp. 247–263.
5. C. Oliveira, A. Alves and L. M. Madeira, Chem. Eng. J., 2014, 241, 190.
6. E. C. Catalkaya and F. Kargi, J. Hazard. Mater., 2007, 139, 244.
7. D. Hermosilla, N. Meravo, R. Ordónez and Á. Blanco, Waste Manage., 2012, 32, 1236.
8. A. A. Kazmi and R. Thul, J. Environ. Sci. Eng., 2007, 49, 189.
9. F. Torrades, S. Saiz and J. A. García-Hortal, Desalination, 2011, 268, 97.
10. A. F. Siqueira, O. L. C. Guimarães, H. J. I. Filho, D. S. Giordani, S. Domingos, I. Oliveira, H. Aquino and M. Silva, Open Chem. Eng. J., 2013, 7, 1.
11. A. F. Siqueira, H. J. I. Filho, M. A. K. Alcântara, C. C. A. Loures, L. A. B. M. Teixeira, O. L. C. Guimarães, A. L. Gabas and D. A. S. Napoleão, Environ. Eng. Sci., 2016, 33, 551.
12. D. A. S. Napoleão, H. J. I. Filho, A. F. Siqueira, E. H. Bredda, L. G. de Aguiar, P. C. M. da Rós and M. K. Alcântara, Ind. Eng. Chem. Res., 2022, 61, 1985.
13. S. Pesakhov, R. Benisty, N. Sikron, Z. Cohen, P. Gomelsky, I. Khozin-Goldberg, R. Dagan and N. Porat, Biochim. Biophys. Acta, Biomembr., 2007, 1768, 590.
14. P. Seesuriyachan, A. Kuntiya, A. Kawee-Ai, C. Techapun, T. Chaiyaso and N. Leksawasdi, Ecol. Eng., 2015, 85, 283.
15. H. Janshekar, C. Brown and A. Fiechter, Anal. Chim. Acta, 1981, 130, 81.
16. N. Tantiwa, A. Kuntiya and P. Seesuriyachan, Chiang Mai J. Sci., 2013, 40, 60.
17. D. M. Stanbury, Dalton Trans., 2022, 51, 2135.
18. P. Dhar, V. Teja and R. Vinu, J. Environ. Chem. Eng., 2020, 8, 104286.
19. A. M. Naguib, S. A. Abdel-Gawad and A. S. Mahmoud, Egypt. J. Pet., 2023, 32, 36.
20. L. Wang, C. Tang, P. Huang, X. Hu and Z. Sun, J. Alloys Compd., 2023, 945, 169263.
21. O. Heinz, J. Rencoret, J. C. del Río and A. Ferraz, ACS Sustainable Chem. Eng., 2022, 10, 7576.
22. G. Zinovyev, I. Sulaeva, S. Podzimek, D. Rössner, I. Kilpeläinen, I. Sumerski, T. Rosenau and A. Potthast, ChemSusChem, 2018, 11, 3259.
23. M. S. Kent, J. Zeng, N. Rader, I. C. Avina, C. T. Simoes, C. K. Brenden, M. L. Busse, J. Watt, N. H. Giron, T. M. Alam, M. D. Allendorf, B. A. Simmons, N. S. Bell and K. L. Sale, Green Chem., 2018, 20, 3024.
24. K. Ninomiya, H. Takamatsu, A. Onishi, K. Takahashi and N. Shimizu, Ultrason. Sonochem., 2013, 20, 1092.
25. I. Arslan-Alaton, G. Tureli and T. Olez-Hanci, Photochem. Photobiol. Sci., 2009, 8, 628.
26. M. Salari, M. R. Nikoo, A. Al-Mamun, G. Rakhshandehroo and M. G. Mooselu, J. Environ. Manage., 2022, 317, 115469.
27. D. Salvachúa, E. M. Karp, C. T. Nimlos, D. R. Vardon and G. T. Beckham, Green Chem., 2015, 17, 4951.
28. N. Kamimura, K. Takahashi, K. Mori, T. Araki, M. Fujita, Y. Higuchi and E. Masai, Environ. Microbiol. Rep., 2017, 9, 679.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4re00401a

---