 Open Access Article
Open Access ArticleFirst-principles investigation of the optical and piezoelectric properties of Janus TiOS monolayers
Jing Tanga,
Kaimin Fan *b and
Kun Wangc
*b and
Kun Wangc
aSchool of Ecology and Environmental Science, Qinghai Institute of Technology, Xining 810016, China
bCenter for General Education, Qinghai Institute of Technology, Xining 810016, China. E-mail: fankm128@163.com
cXingzhi College, Zhejiang Normal University, Jinhua 321004, China
First published on 12th December 2025
Abstract
Using first-principles calculations, we systematically explore the geometric structures, stabilities, electronic structures, optical responses, and piezoelectric properties of Janus TiOS monolayers to assess their suitability for integrated photocatalytic and piezoelectric applications. The stability of both phases was assessed through formation energy calculations, phonon dispersion relations, AIMD simulations, and elastic constant analyses, which collectively confirm their dynamical, thermal, and mechanical stability. Electronic structure calculations reveal that the 1T-TiOS monolayer is a direct-band-gap semiconductor (Eg = 1.27 eV), whereas the 2H phase exhibits an indirect band gap of 1.52 eV. Charge-density analyses indicate that the CBM is mainly contributed by Ti 3d orbitals, while the VBM originates from S 2p states, providing a favourable orbital configuration for efficient charge separation. Both phases exhibit strong visible-light absorption, with absorption coefficients exceeding 1 × 105 cm−1. Remarkably, the 1T- and 2H-TiOS monolayers demonstrate strong potential as solar-driven photocatalysts for water splitting over a broad pH range (0–10). Furthermore, Janus TiOS monolayers show intrinsic and pronounced piezoelectric responses. For the 1T phase, the in-plane and out-of-plane piezoelectric coefficients are 4.99 and 0.32 pm V−1, respectively, while the corresponding values for the 2H phase are 2.38 and 0.27 pm V−1. These results indicate that Janus TiOS monolayers are promising candidates for next-generation materials integrating photocatalytic and piezoelectric functionalities.
1 Introduction
The rutile and anatase phases of TiO2 have been extensively employed in photocatalytic and electrochemical applications owing to their non-toxicity, low cost, and excellent stability.1,2 However, bulk TiO2 suffers from several intrinsic drawbacks, including a relatively small surface area, which limits the number of active sites, and a high recombination rate of photogenerated charge carriers (electrons and holes), thereby reducing catalytic efficiency.3–5 In addition, its wide band gap (3.0–3.2 eV) restricts absorption to the ultraviolet region of the solar spectrum.6 To overcome these limitations, researchers have explored the transformation of TiO2 structures from the bulk to the two-dimensional (2D) scale.7,8 This transition aims to enhance the surface area through a layered structure, shorten the diffusion path of charge carriers, and improve photocatalytic efficiency. Recent studies have shown that 2D TiO2 can exist in several phases, including 1T (octahedral), 2H (hexagonal), LNS (lepidocrocite), ANS (anatase), and HNS (hexagonal nanosheet). Among these, the 1T phase, which can be exfoliated from hexagonal NaTiO2, exhibits a low effective hole mass but still possesses a relatively large band gap of 3.29 eV.9 The band gaps of 1T- and 2H-TiO2 monolayers are calculated to be 3.72 eV and 5.74 eV, respectively, as reported by Rasmussen et al.10 These results demonstrate that wide band gaps are an inherent characteristic of 2D TiO2, which fundamentally limits its photocatalytic applications.Recently, Janus 2D materials have attracted considerable attention as a novel class of layered materials.11–14 Distinct from conventional symmetric 2D structures, these materials exhibit mirror asymmetry and possess an intrinsic vertical dipole moment, which enhances charge-carrier separation and makes them a highly promising platform for high-performance photocatalytic and piezoelectric applications.15,16 Representative examples include Janus MoSSe and WSSe, where the electronegativity difference across the asymmetric surfaces gives rise to unique optical and catalytic properties that surpass those of their symmetric counterparts, MoS2 and WS2.17–19 Dong et al. demonstrated that Janus MXY monolayers (M = Mo or W; X/Y = S, Se, or Te) generate strong in-plane and weak out-of-plane piezoelectric polarizations under uniaxial strain.20 Moreover, the successful synthesis of Janus MoSSe and WSSe monolayers has confirmed their experimental feasibility.21,22 Inspired by these advances, Ti-based Janus materials have also attracted increasing attention. Mogulkoc et al. investigated the structural, mechanical, electronic, thermal, and optical properties of TiXY (X/Y = S, Se, and Te) monolayers using first-principles calculations.23 Yang et al. reported that Janus TiXY (X ≠ Y; X/Y = Cl, Br, I) monolayers exhibit thermal, dynamical, and mechanical stability, together with outstanding in-plane and out-of-plane piezoelectric responses.16 Similarly, Yan et al. found that TiPX (X = F, Cl, Br) monolayers are dynamically and mechanically stable, possess high carrier mobility, and display remarkable flexibility and piezoelectricity.24
Motivated by the exceptional performance of Janus materials, we designed Janus TiOS monolayers derived from the 1T and 2H phases of TiO2 by replacing the oxygen layer on one side with sulfur to form an asymmetric structure. The larger atomic radius and shallower p-orbital energy levels of sulfur effectively narrow the band gap and enhance visible-light absorption. Furthermore, the electronegativity difference between the oxygen and sulfur layers induces vertical polarization, facilitating efficient electron–hole separation. In this work, we systematically explore the electronic, optical, mechanical, and piezoelectric properties of Janus TiOS monolayers using first-principles calculations. The results reveal that Janus TiOS not only mitigates the optical and electronic limitations of 2D TiO2 but also exhibits distinct advantages for photocatalysis and piezoelectric applications, providing theoretical guidance for the development of high-performance Ti-based 2D materials.
2 Computational methods
All first-principles calculations in this study were performed within the framework of density functional theory (DFT) using the Vienna Ab initio Simulation Package (VASP).25,26 The interactions between valence electrons and ionic cores were described by the projector-augmented wave (PAW) method.27,28 To account for van der Waals interactions, the DFT-D3 correction proposed by Grimme was included.29 A plane-wave cutoff energy of 500 eV was adopted, and a vacuum layer of 20 Å was added to eliminate spurious interlayer interactions. The convergence thresholds for energy and forces were set to 10−8 eV and 0.001 eV Å−1, respectively. Geometry optimizations were carried out using the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).30 The Heyd–Scuseria–Ernzerhof hybrid functional (HSE06) was further employed to obtain more accurate electronic band structures.31 A Monkhorst–Pack32 k-point mesh of 10 × 10 × 1 was used for structural optimization, while a denser grid of 20 × 20 × 1 was adopted for the calculations of elastic moduli and piezoelectric coefficients. Phonon dispersion curves were calculated using density functional perturbation theory (DFPT) based on a 4 × 4 × 1 supercell (48 atoms) constructed with the Phonopy package.33 Ab initio molecular dynamics (AIMD) simulations were performed at 300 K for 8 ps with a time step of 2.0 fs under the NVT ensemble.34 The atomic structures were visualized and analyzed using the VESTA code.35 The post-processing of calculation data was carried out using VASPKIT.363 Results and discussion
3.1 Structure and stability
The TiOS monolayers adopt a three-layered structure consisting of Ti, O, and S atomic planes, similar to the TiO2 monolayers in the 1T and 2H phases, as shown in Fig. 1(a) and (b). They can be regarded as TiO2 monolayers in which the top-layer O atoms are replaced by S atoms. The optimized structural parameters are listed in Table 1. The lattice constant (a), Ti–O and Ti–S bond lengths (dTi–O and dTi–S), and monolayer thickness (h) are found to be in good agreement with previously reported values.37–39 Pronounced differences in the Ti–O and Ti–S bond lengths, as well as in the Ti–O–Ti and Ti–S–Ti bond angles, indicate the structural asymmetry of Janus TiOS monolayers. This asymmetry arises from the distinct atomic radii and electro negativities of O and S. | ||
| Fig. 1 Top and side views of (a) 1T- and (b) 2H-TiOS monolayers, with the unit cell marked by a black parallelogram. | ||
| Material | a (Å) | dTi–O (Å) | dTi–S (Å) | h (Å) | ∠Ti–O–Ti (°) | ∠Ti–S–Ti (°) | Ef (eV) | EPBEg (eV) | EHSE06g (eV) |
|---|---|---|---|---|---|---|---|---|---|
| 1T-TiOS | 3.18 | 2.00 | 2.43 | 2.39 | 105.12 | 81.67 | −0.95 | 0.55 | 1.27 |
| 2H-TiOS | 3.08 | 2.00 | 2.45 | 2.59 | 100.91 | 78.20 | −0.88 | 0.62 | 1.52 |
In addition, the formation energies of the two-phase Janus TiOS monolayers were calculated to evaluate their feasibility for experimental synthesis using the following formula:39
| Ef = [ETiOS − (ETiS2 − ES + EO)]/n | (1) |
The phonon dispersion curves presented in Fig. 2(a) show the dynamical stability of Janus TiOS monolayers. Apart from a slight imaginary frequency near the Gamma point, no imaginary modes are present, indicating that both 1T- and 2H-TiOS monolayers are dynamically stable.41 The thermodynamic stability was further evaluated by AIMD simulations. As illustrated in Fig. 2(b), the AIMD simulations performed at 300 K for 8 ps showed only minor energy fluctuations, while the overall lattice structures remained intact without any bond rupture or noticeable distortion. These results indicate that both monolayers are thermally stable at room temperature.42
 | ||
| Fig. 2 (a) Phonon dispersion curves of Janus TiOS monolayers. (b) AIMD simulations of Janus TiOS monolayers at 300 K. | ||
To further elucidate the bonding characteristics, the electron localization function (ELF) was calculated, as shown in Fig. 3(a). The ELF distributions reveal that electrons are mainly localized around O and S atoms, whereas very little electron density is found between Ti and O/S atoms, indicating the predominantly ionic nature of the Ti–O and Ti–S bonds.43 Moreover, the planar-averaged and 3D charge density differences of 1T- and 2H-TiOS monolayers, shown in Fig. 3(b), display clear electron depletion around the Ti sites and electron accumulation near the electronegative O and S atoms. This charge redistribution is consistent with the ELF analysis and provides further evidence for the predominantly ionic character of the Ti–O and Ti–S bonds. This observation is consistent with previous theoretical and experimental results.44,45
3.2 Electronic properties
In this section, the electronic properties of 1T- and 2H-TiOS monolayers are investigated using DFT calculations. The band structure analysis, as illustrated in Fig. 4(a)–(d), reveals distinct differences between the two phases. The 1T-TiOS monolayer exhibits a direct bandgap, where the conduction band minimum (CBM) is primarily derived from Ti atoms, and the valence band maximum (VBM) is predominantly contributed by S atoms. In contrast, the 2H-TiOS monolayer possesses an indirect bandgap. Its CBM is also dominated by Ti states, whereas the VBM is primarily composed of S states with a minor contribution from Ti. The calculated band gaps, as summarized in Table 1, demonstrate noticeable variations depending on the computational methods employed. Specifically, the 1T phase has band gaps of 0.55 eV (PBE) and 1.27 eV (HSE06), while the 2H phase shows corresponding values of 0.62 eV (PBE) and 1.52 eV (HSE06). The HSE06 calculated band gap of 1.27 eV for the 1T phase agrees well with previously reported results, confirming the reliability of the present computational approach.39 Notably, the band gaps of Janus TiOS monolayers are considerably smaller than those of bulk TiO2 (3.2 eV)46 and 1T-TiO2 (3.29 eV),9 yet they remain above the minimum energy required for photocatalytic water splitting (>1.23 eV).47 These findings demonstrate that the band gaps can be effectively tuned through the construction of Janus structures, providing a feasible strategy for designing 2D materials with tailored optoelectronic properties.To gain deeper insights into the electronic structure, the partial density of states (PDOS) of both phases is analyzed, as presented in Fig. 4(e)–(f). The PDOS analysis confirms that, in the 1T phase, the CBM is mainly derived from Ti 3d orbitals, while the VBM is primarily contributed by a combination of S 2p and Ti 3d orbitals. Similarly, in the 2H phase, the CBM is dominated by Ti 3d states, and the VBM originates from the hybridization of S 2p and Ti 3d orbitals. These findings are consistent with the band structure analysis and provide a more comprehensive understanding of the electronic contributions.
Further visualization of the partial charge densities, as shown in Fig. 4(g)–(h), reveals the spatial distribution of the frontier electronic states. In both phases, the CBM is predominantly localized around the Ti atoms, whereas the VBM is primarily concentrated near the S atoms. This distinct spatial separation of photoexcited electrons and holes effectively suppresses their recombination kinetics, which is crucial for enhancing photocatalytic performance. The consistent trends observed in the band structure, density of states, and charge density analyses provide strong evidence for the intrinsic electronic characteristics of Janus TiOS monolayers.
The work function (Φ) is defined as Φ = Ev − Ef, where Ev and Ef are the vacuum level and Fermi level, respectively. Fig. 5(a) and (b) show the calculated work functions and vacuum level differences of 1T- and 2H-TiOS monolayers after applying the dipole correction. A distinct surface potential difference (ΔΦ) arises from the electronegativity contrast between the S and O atoms on the upper and lower surfaces.48 Because O is more electronegative than S, electrons are redistributed from the S layer toward the O layer, generating an intrinsic dipole oriented from the S-terminated surface to the O-terminated surface and a built-in electric field inside the monolayer. This internal field promotes the spatial separation and migration of photoexcited electrons and holes, thereby enhancing the charge-transport efficiency.49
3.3 Optical properties
Understanding the optical properties of 1T- and 2H-TiOS monolayers is crucial for a wide range of applications and experimental investigations. Fig. 6(a) presents the calculated optical absorption spectra, which display a pronounced absorption band in the visible-light region. In this range, the absorption coefficient of the 1T phase reaches 2.37 × 105 cm−1, while that of the 2H phase is 1.95 × 105 cm−1. With both values exceeding 105 cm−1, Janus TiOS monolayers can be considered highly efficient in harvesting solar energy. By contrast, bulk TiO2 exhibits almost no absorption in the visible region, and 1T-TiS2 shows a much lower maximum absorption coefficient of only 4.19 ×104 cm−1.50,51 This comparison clearly demonstrates that Janus TiOS monolayers outperform their symmetric counterparts in visible-light absorption. Furthermore, their absorption coefficient rivals or even surpasses those of previously reported Janus 2D materials, such as MoSSe,52 SnSSe,53 PtSSe,54 and ZrSSe.55 The strong light absorption exhibited by Janus TiOS monolayers further underscores their significant potential as high performance photocatalysts. | ||
| Fig. 6 (a) The optical absorption spectra of Janus TiOS monolayers computed using the HSE06 functional. (b) Band edge positions of Janus TiOS monolayers. (c) Water redox potential with pH. | ||
Based on the band structure analysis, Janus TiOS monolayers exhibit suitable band gaps for photocatalytic water splitting. Besides having a suitable gap, a photocatalyst needs band edges aligned to water redox levels, with the VBM below the oxidation potential and the CBM above the reduction potential. Fig. 6(b) presents the band-edge alignment of Janus TiOS monolayers with respect to the dipole-corrected vacuum levels on their O- and S-terminated surfaces. When the band edges are referenced to the local vacuum level, the intrinsic HSE band gaps of both the 1T and 2H phases are preserved. However, the ΔΦ between the two terminations gives rise to an intrinsic band bending, providing an effective means of band-edge modulation for enhanced photocatalytic activity.56,57 At pH = 0, the VBM of both 1T- and 2H-TiOS on the O-terminated side lie below the water oxidation potential, whereas the CBM on the S-terminated side are located above the water reduction potential. This asymmetric band alignment enhances the oxidation driving force at the O-terminated surface and simultaneously strengthens the reduction driving force at the S-terminated surface.
In addition, the pH dependence of the driving forces for photoexcited electrons and holes is evaluated using the following equations:58
| Ue = ECBM − (0.059 × pH − 4.44) | (2) |
| Uh = −EVBM + (0.059 × pH − 5.67) | (3) |
3.4 Mechanical and piezoelectric properties
The mechanical properties of materials are crucial for assessing their suitability for practical applications. To evaluate the mechanical stability of 1T- and 2H-TiOS monolayers, we applied the Born–Huang criterion. First, we calculated their elastic constants (Cij), from which key mechanical properties such as Young's modulus (Y), and Poisson's ratio (ν) were derived. The results are summarized in Table 2.| Material | C11 (N m−1) | C12 (N m−1) | Y (N m−1) | ν |
|---|---|---|---|---|
| 1T-TiOS | 121.30 | 35.51 | 110.90 | 0.29 |
| 2H-TiOS | 138.78 | 49.91 | 120.84 | 0.36 |
| 2H-TiO2 | 173.7 (ref. 59) | 75.7 (ref. 59) | 141.7 (ref. 59) | 0.44 (ref. 59) |
| 2H-TiS2 | 89.9 (ref. 59) | 28.6 (ref. 59) | 80.8 (ref. 59) | 0.32 (ref. 59) |
| 1T-MoS2 | 132.7 (ref. 59) | 33.0 (ref. 59) | 124.5 (ref. 59) | 0.25 (ref. 59) |
| 2H-MoS2 | 130,60 133.36 (ref. 61) | 32,60 37.05 (ref. 61) | 123.07,61 127.3 (ref. 62) | 0.34,60 0.28 (ref. 61) |
| 2H-MoO2 | 232.92 (ref. 62) | 84.67 (ref. 62) | 202.1 (ref. 62) | 0.36 (ref. 62) |
| 1T-WS2 | 146.5 (ref. 59) | 31.8 (ref. 59) | 139.6 (ref. 59) | 0.22 (ref. 59) |
| 2H-WS2 | 144,60 148.47 (ref. 62) | 31,60 31.20 (ref. 62) | 141.9 (ref. 62) | 0.36,60 0.21 (ref. 62) |
| 2H-WO2 | 261.2 (ref. 59) | 87.8 (ref. 59) | 231.7 (ref. 59) | 0.34 (ref. 59) |
| Ti2C | 137 (ref. 63) | 32 (ref. 63) | 130 (ref. 63) | 0.23,63 0.30 (ref. 64) |
| h-BN | 291 (ref. 60) | 62 (ref. 60) | 271 (ref. 65) | 0.211 (ref. 65) |
| Graphene | 354 (ref. 66) | 60 (ref. 66) | 344 (ref. 66) | 0.19,67 0.169 (ref. 66) |
| 2H-CrSO | 157.86 (ref. 68) | 43.71 (ref. 68) | 145.76 (ref. 68) | 0.28 (ref. 68) |
| 2H-WSO | 196 (ref. 69) | 52 (ref. 69) | 182 (ref. 69) | 0.27 (ref. 69) |
As shown in Table 2, C11 > 0 and C11 > |C12|, which satisfies the structural stability criterion proposed by Born–Huang, indicating the mechanical stability of both 1T- and 2H-TiOS.70 The Young's moduli of the 1T- and 2H-TiOS monolayers fall between those of TiO2 and TiS2.59 Their stiffness is generally lower than that of Janus monolayers with a similar structural phase, such as 2H-CrSO and 2H-WSO, and also lower than that of many widely studied 2D materials, including Ti2C, h-BN, graphene, representative transition-metal dichalcogenides (TMDCs) such as MoS2 and WS2, and transition-metal oxides (TMOs) such as MoO2 and WO2.59–69 The Poisson's ratios of 1T- and 2H-TiOS monolayers are 0.29 and 0.36, respectively, falling within the range 0.25 < ν < 0.5, which indicates predominantly ionic bonding, consistent with the ELF analysis.71 These values are slightly higher than those of Ti2C, h-BN, and graphene, and comparable to those of other Janus monolayers such as WSO and CrSO, together with typical TMDCs and TMOs including MoS2, WS2, MoO2, and WO2.59–69 Overall, owing to their moderate stiffness and favorable ductility, the Janus TiOS monolayers display exceptional mechanical adaptability, rendering them highly promising for strain-engineered modulation of optoelectronic properties.
Due to the lack of mirror symmetry, Janus TiOS monolayers exhibit strong in-plane and significantly weaker out-of-plane piezoelectric polarizations under uniaxial in-plane strain. The piezoelectric coefficients e11 and e31 are computed using DFT. The obtained eij values are then used to determine d11 and d31 through the following relationships:24
 | (4) |
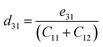 | (5) |
Fig. 7 summarizes the piezoelectric coefficients of Janus TiOS monolayers and compares them with those of other 2D materials. The calculated d11 value for 1T-TiOS is in good agreement with previously reported results.39 As shown in Fig. 7(a), the in-plane piezoelectric response of 1T-TiOS exceeds that of other 1T counterparts, including HfSO, TiSeO, ZrSO, and SnSSe.39,53 For the 2H phase, the in-plane coefficient is slightly smaller than that of other isostructural Ti-based Janus systems such as Ti2O2HF, Ti2O2HCl, and TiBrCl, but remains larger than those of WS2, WSO, WSeO, WSSe, and ZrGeNH3.16,20,60,69,72,73 Meanwhile, Fig. 7(b) illustrates that the out-of-plane piezoelectric coefficients of 1T- and 2H-TiOS (0.32 pm V−1 and 0.27 pm V−1, respectively) exceed those of Janus MoSSe, MoSeTe, MoSTe, WSSe, WSeTe, and WSTe by more than one order of magnitude. Notably, TiOS monolayers demonstrate stronger out-of-plane piezoelectric responses compared to numerous other reported Janus systems, such as Ti2O2HF, Ti2O2HCl, Ga2SSe, In2SSe, ZrGeNH3, ZrGePH3, and ZrGeAsH3.72–74 Overall, both 1T- and 2H-TiOS monolayers exhibit notable piezoelectric performance. The 1T phase, in particular, possesses higher piezoelectric coefficients and pronounced in-plane and out-of-plane responses, rendering it a promising material for integrated photocatalytic–piezoelectric applications.
4 Conclusion
In summary, the structural, electronic, optical, mechanical, and piezoelectric properties of 2D Janus TiOS monolayers (1T and 2H phases) were systematically investigated using first-principles calculations. Janus TiOS monolayers exhibit dynamic, thermal, and mechanical stability. Electronic structure analysis reveals that the 1T-TiOS monolayer behaves as a direct-bandgap semiconductor, while the 2H-TiOS monolayer exhibits an indirect bandgap. The calculated band gaps at the HSE06 level are 1.27 eV for the 1T phase and 1.52 eV for the 2H phase. Additionally, the CBM and VBM of both monolayers are primarily determined by distinct atomic orbital contributions. Both monolayers demonstrate strong optical absorption in the visible spectrum, and their band-edge positions span the water redox potentials over a wide pH range (0–10), making them promising candidates for photocatalytic water splitting. The favorable ductility of the materials is reflected in their Young's modulus and Poisson's ratio. Furthermore, the piezoelectric coefficients of the 1T-TiOS monolayer surpass those of the 2H phase, indicating superior piezoelectric performance. These findings highlight the significant application potential of both the 1T and 2H phases of TiOS in fields such as photocatalysis and piezoelectric devices. This work provides a solid theoretical foundation for the design and application of Janus TiOS monolayers.Author contributions
Jing Tang: conceptualization, data curation, investigation, methodology, validation, writing – original draft, writing – review & editing. Kaimin Fan: conceptualization, funding acquisition, methodology, project administration, resources, writing – review & editing. Kun Wang: writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Data availability
This study did not generate any new datasets. All data analyzed are from publicly available sources, as cited in the manuscript.Acknowledgements
This work was supported by the Scientific Research Project of “Kunlun Elite Talents” Program of Qinghai Province, China (2025-QLGKLYCZX-022).References
- M. Humayun, F. Raziq, A. Khan and W. Luo, Green Chem. Lett. Rev., 2018, 11, 86–102 CrossRef CAS
.
- T. L. Soundarya, T. Jayalakshmi, M. A. Alsaiari, M. Jalalah, A. Abate, F. A. Alharthi, N. Ahmad and G. Nagaraju, Crystals, 2022, 12, 1133 CrossRef CAS
.
- K. Lee, H. Yoon, C. Ahn, J. Park and S. Jeon, Nanoscale, 2019, 11, 7025–7040 RSC
.
- S. Lettieri, M. Pavone, A. Fioravanti, L. Santamaria Amato and P. Maddalena, Materials, 2021, 14, 1645 CrossRef CAS PubMed
.
- V. T. T. Ho, D. H. Chau, K. Q. Bui, N. T. T. Nguyen, T. K. N. Tran, L. G. Bach and S. N. Truong, Inorganics, 2022, 10, 29 CrossRef CAS
.
- D. N. Shvalyuk, M. G. Shelyapina and I. A. Zvereva, Results Chem., 2024, 7, 101296 CrossRef CAS
.
- J. Yang, Y.-L. Jiang, L.-J. Li, E. Muhire and M.-Z. Gao, Nanoscale, 2016, 8, 8170–8177 RSC
.
- H. Zhu, X. Yang, M. Zhang, Q. Li and J. Yang, Mater. Res. Bull., 2020, 125, 110765 CrossRef CAS
.
- I. Kim, G. Lee and M. Choi, Phys. Rev. Mater., 2020, 4, 094001 CrossRef CAS
.
- F. A. Rasmussen and K. S. Thygesen, J. Phys. Chem. C, 2015, 119, 13169–13183 CrossRef CAS
.
- N. Anjum, M. Kashif, A. Shahzad, A. Rasheed and G. Ren, ACS Omega, 2024, 9, 19848–19858 CrossRef CAS PubMed
.
- M. Yagmurcukardes, C. Sevik and F. M. Peeters, Phys. Rev. B, 2019, 100, 045415 CrossRef CAS
.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Phys. Rev. B, 2021, 104, 115410 CrossRef CAS
.
- N. N. Hieu, H. V. Phuc, A. I. Kartamyshev and T. V. Vu, Phys. Rev. B, 2022, 105, 075402 CrossRef CAS
.
- Y. Wang, Y. Tao, Q. Zhang, R. Huang, B. Gao, Z. Li, G. Li and N. Hu, Solid State Commun., 2022, 354, 114893 CrossRef CAS
.
- Q. Yang, T. Zhang, C.-E. Hu, X.-R. Chen and H.-Y. Geng, Phys. Chem. Chem. Phys., 2023, 25, 274–285 RSC
.
- X. Lei, C. Ouyang and K. Huang, Appl. Surf. Sci., 2021, 537, 147919 CrossRef CAS
.
- C. Xia, W. Xiong, J. Du, T. Wang, Y. Peng and J. Li, Phys. Rev. B, 2018, 98, 165424 CrossRef CAS
.
- H. Qu, S. Zhang, J. Cao, Z. Wu, Y. Chai, W. Li, L.-J. Li, W. Ren, X. Wang and H. Zeng, Sci. Bull., 2024, 69, 1427–1436 CrossRef CAS PubMed
.
- L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248 CrossRef CAS PubMed
.
- A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744–749 CrossRef CAS PubMed
.
- T. Zheng, Y.-C. Lin, Y. Yu, P. Valencia-Acuna, A. A. Puretzky, R. Torsi, C. Liu, I. N. Ivanov, G. Duscher, D. B. Geohegan, Z. Ni, K. Xiao and H. Zhao, Nano Lett., 2021, 21, 931–937 CrossRef CAS PubMed
.
- A. Mogulkoc, Y. Mogulkoc, S. Jahangirov and E. Durgun, J. Phys. Chem. C, 2019, 123, 29922–29931 CrossRef CAS
.
- T.-T. Yan, G.-X. Zhou, X.-L. Jiang, X.-C. Qin and J. Li, Phys. Chem. Chem. Phys., 2024, 26, 23998–24007 RSC
.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- G. Kresse, J. Non-Cryst. Solids, 1995, 192, 222–229 CrossRef
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS
.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS
.
- Y.-J. Xiang, S. Gao, C. Wang, H. Fang, X. Duan, Y.-F. Zheng and Y.-Y. Zhang, Chin. Phys. B, 2024, 33, 087101 CrossRef CAS
.
- P. Zhang, S. Fu, C. Pu, X. Tang and D. Zhou, Chin. Phys. B, 2025, 34, 057103 CrossRef CAS
.
- W. Chen, X. Hou, X. Shi and H. Pan, ACS Appl. Mater. Interfaces, 2018, 10, 35289–35295 CrossRef CAS PubMed
.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198 CrossRef CAS PubMed
.
- B. Özdamar, G. Özbal, M. N. Çınar, K. Sevim, G. Kurt, B. Kaya and H. Sevinçli, Phys. Rev. B, 2018, 98, 045431 CrossRef
.
- N. L. P. Andrews, J. Z. Fan, R. L. Forward, M. C. Chen and H.-P. Loock, Phys. Chem. Chem. Phys., 2017, 19, 73–81 RSC
.
- C. Qi, C. Yan, Q. Li, T. Yang, S. Qiu and J. Cai, J. Mater. Chem. C, 2023, 11, 3262–3274 RSC
.
- M. Mizuno, I. Tanaka and H. Adachi, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 15033–15047 CrossRef CAS
.
- B. Jiang, J. M. Zuo, N. Jiang, M. O'Keeffe and J. C. H. Spence, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 341–350 CrossRef CAS PubMed
.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801 CrossRef CAS PubMed
.
- T. Jafari, E. Moharreri, A. Amin, R. Miao, W. Song and S. Suib, Molecules, 2016, 21, 900 CrossRef PubMed
.
- T. Zhao, J. Chen, X. Wang and M. Yao, Appl. Surf. Sci., 2021, 545, 148968 CrossRef CAS
.
- H. Ma, Z. Wang, W. Zhao, H. Ren, H. Zhu, Y. Chi and W. Guo, J. Phys. Chem. Lett., 2022, 13, 8484–8494 CrossRef CAS PubMed
.
- F. Saidi, A. Mahmoudi, K. Laidi, T. Hidouri and S. Nasr, Comput. Condens. Matter, 2021, 28, e00576 CrossRef
.
- H. Liu, L. Yang, Y. Zhao, S. Sun and X. Wei, J. Supercond. Nov. Magn., 2024, 37, 639–655 CrossRef CAS
.
- X. Zuo, K. Chang, J. Zhao, Z. Xie, H. Tang, B. Li and Z. Chang, J. Mater. Chem. A, 2016, 4, 51–58 RSC
.
- S.-D. Guo, X.-S. Guo, R.-Y. Han and Y. Deng, Phys. Chem. Chem. Phys., 2019, 21, 24620–24628 RSC
.
- R. Peng, Y. Ma, B. Huang and Y. Dai, J. Mater. Chem. A, 2019, 7, 603–610 RSC
.
- T. V. Vu, H. D. Tong, D. P. Tran, N. T. T. Binh, C. V. Nguyen, H. V. Phuc, H. M. Do and N. N. Hieu, RSC Adv., 2019, 9, 41058–41065 RSC
.
- Z. Haman, M. Kibbou, N. Khossossi, E. Ouabida, P. Dey, I. Essaoudi and A. Ainane, Int. J. Hydrogen Energy, 2024, 68, 566–574 CrossRef CAS
.
- Y. Ji, M. Yang, H. Lin, T. Hou, L. Wang, Y. Li and S.-T. Lee, J. Phys. Chem. C, 2018, 122, 3123–3129 CrossRef CAS
.
- H. Zhang, C.-Q. Zhou and F.-S. Meng, Solid State Commun., 2023, 370, 115220 CrossRef CAS
.
- M. M. Alyörük, Y. Aierken, D. Çakır, F. M. Peeters and C. Sevik, J. Phys. Chem. C, 2015, 119, 23231–23237 CrossRef
.
- K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876 CrossRef CAS
.
- H. Sun, P. Agrawal and C. V. Singh, Mater. Adv., 2021, 2, 6631–6640 RSC
.
- F. Zeng, W.-B. Zhang and B.-Y. Tang, Chin. Phys. B, 2015, 24, 097103 CrossRef
.
- S. Wang, J.-X. Li, Y.-L. Du and C. Cui, Comput. Mater. Sci., 2014, 83, 290–293 CrossRef CAS
.
- Y.-C. Lu, C.-L. Ren, C.-Y. Wang, Y.-R. Yin, H. Han, W. Zhang and P. Huai, Nucl. Sci. Technol., 2019, 30, 172 CrossRef
.
- K. N. Kudin, G. E. Scuseria and B. I. Yakobson, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 64, 235406 CrossRef
.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef
.
- A. Politano and G. Chiarello, Nano Res., 2015, 8, 1847–1856 CrossRef CAS
.
- T. P. T. Linh, N. N. Hieu, H. V. Phuc, C. Q. Nguyen, P. T. Vinh, N. Q. Thai and N. V. Hieu, RSC Adv., 2021, 11, 39672–39679 RSC
.
- M. J. Varjovi, M. Yagmurcukardes, F. M. Peeters and E. Durgun, Phys. Rev. B, 2021, 103, 195438 CrossRef CAS
.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef
.
- Y. Ö. Çiftci, Can. J. Phys., 2016, 94, 328–333 CrossRef
.
- J. Qiu and J. Liu, Mater. Lett., 2024, 367, 136620 CrossRef CAS
.
- T. V. Vu, V. T. T. Vi, N. T. Hiep, K. V. Hoang, A. I. Kartamyshev, H. V. Phuc and N. N. Hieu, RSC Adv., 2024, 14, 21982–21990 RSC
.
- Y. Guo, S. Zhou, Y. Bai and J. Zhao, Appl. Phys. Lett., 2017, 110, 163102 CrossRef
.
| This journal is © The Royal Society of Chemistry 2025 |




