Open Access Article
Open Access ArticleDensity functional study of PuC and PuC0.75O0.25
Rong Yang *a,
Zhe Zhanga and
Bin Tangb
*a,
Zhe Zhanga and
Bin Tangb
aSchool of Materials Science and Engineering, Chongqing Jiaotong University, Chongqing 400074, PR China. E-mail: cqyr88@126.com
bInstitute of Finance & Trade, Chongqing City Management College, Chongqing 401331, PR China
First published on 8th December 2025
Abstract
We study the structural, magnetic, electronic, thermodynamic and elastic properties of PuC and PuC0.75O0.25 using density-functional theory (DFT) and DFT + U. The nonmagnetic (NM), ferromagnetic (FM) and antiferromagnetic (AFM) configurations are considered in this work. Total energy results obtained with DFT + U indicate that PuC0.75O0.25 has an AFM ground state, matching the AFM nature of stoichiometric PuC. Calculated electronic properties reveal a new density of states peak in PuC0.75O0.25, a consequence of C/O substitution in PuC. Thermodynamically, PuC0.75O0.25 exhibits higher enthalpy difference (HT–H298), entropy difference (ST–S298) and heat capacity (Cv and Cp) than PuC at the same temperature; elastically, it is predicted to be harder, owing to the stronger ionic character of Pu–O versus Pu–C bonds. Crucially, the formation energy of the oxygen-substitution defect is calculated to be highly spontaneous (−5.11 eV), revealing the fundamental driving force for the oxidation and chemical aging of PuC. These results are intended to provide a valuable reference for further theoretical and experimental investigations of PuC and PuC0.75O0.25.
1. Introduction
Nuclear energy attracts wide interest owing to its high efficiency, low pollution, and abundant reserves. However, plutonium (Pu), an important nuclear material, slowly reacts with ambient atmospheric components (e.g., O2, CO, CO2), forming aging products that impact its long-term stability and performance.1 Binary products like Pu oxides, hydrides, and carbides have been extensively studied.2–14 In contrast, investigations into ternary products, such as PuC1−xOx, remain scarce. For PuC1−xOx, experimental observations (via XPS)1,15 and limited theoretical studies (e.g., thermodynamic stability via machine learning,16 lattice constant formulas17) have been reported. Critical gaps remain in understanding its fundamental properties: magnetism, thermodynamics and elasticity. These are essential for application assessment. More importantly, the atomic-scale mechanism of aging is unexplored, particularly the role of O-substituted C defects (the most common defect type). Defect formation energy and its correlation with material properties remain unknown.To address these gaps, this work focuses on PuC1−xOx (x = 0.25). This composition is selected because it contains a medium amount of oxygen, similar to what forms during early stages of aging. At this stage, the competition between Pu–C and Pu–O bonding becomes very clear. This makes it an ideal model system to reveal the initial effects of oxygen incorporation. We systematically investigate the crystal structure, magnetism, electronic structure, thermodynamic properties, and elastic constants of PuC1−xOx (x = 0.25). Notably, to clarify the atomic-scale aging mechanism, we calculate the formation energy of oxygen-substituted carbon defects for the first time and correlate it with the material's fundamental properties.
Since Pu is located at a special site where the transition of 5f electrons from itinerancy to localization occurs,18 it poses a considerable challenge to the theoretical research on PuC1−xOx. In this paper, we use the traditional density functional theory (DFT), DFT plus the Hubbard U (DFT + U) approach to describe PuC1−xOx. As for the value of Ueff parameter, we adopt a value of 4 eV. This value is widely validated in theoretical studies on Pu-based compounds19–21 for reproducing experimental properties reasonably. We thoroughly discuss the sensitivity of key results to Ueff (tested at 3, 4, 5 eV) in the main text, confirming conclusion robustness. Integrating perfect crystal and point defect studies, this work aims to build a fundamental property-aging mechanism correlation for PuC1−xOx, providing theoretical insights for predicting and managing plutonium aging.
The rest of this paper is organized as follows. In Section 2, we give the computational details of this study. In Section 3, we present our results and discussion. First, we validate our method through calculations of the crystal structures and magnetic properties of PuC and PuC0.75O0.25. We then report the electronic structures, thermodynamic properties (from 0 to 1000 K), and elastic constants of both systems. Finally, the formation energies of O-substituted C defects in PuC are analyzed. In Section 4, we summarize some general conclusions.
2. Computational details
All calculations are performed using the Vienna ab initio simulation package (VASP) version 6.3.0 (ref. 22) code. The exchange–correlation functional is used GGA Perdew–Burke–Ernzerhof (PBE) formalism23 and the local spin-density approximation (LSDA).24 These functionals are selected due to their established and widespread application in the first-principles study of plutonium carbides and related compounds.12–14,20,25 The Hubbard model is used to treat strong correlations within the LSDA + U26 and PBE + U methods. We set the parameter Ueff = 4 eV, which is generally used in Pu-based compounds.19–21 The robustness of key results is tested with Ueff values of 3 eV and 5 eV. In the antiferromagnetic (AFM) calculations, we take the 1 − k AFM configuration consisting of alternating spin-up and spin-down ferromagnetic sheets along the [100] direction.We use a 2 × 2 × 1 conventional fcc supercell (containing 4 formula units, 8 atoms) for calculations on the basic bulk properties of PuC and PuC0.75O0.25. The key justifications for selecting this supercell are as follows: first, it preserves PuC's intrinsic fcc symmetry, ensuring an accurate representation of bulk material properties without artificial size effects. Second, it allows for the direct modeling of PuC0.75O0.25 by replacing one C atom with one O atom, achieving the exact x = 0.25 stoichiometry for early-stage oxidation studies. Third, it balances computational cost and accuracy for calculating thermodynamic and elastic properties. For the calculations of defect formation energies in PuC, a larger 2 × 2 × 2 supercell (64 atoms) is used. This larger size reduces spurious interactions between periodic images of the isolated oxygen defect, which is critical for obtaining converged and accurate defect formation energies.
Rigorous convergence tests determine the appropriate plane-wave energy cutoff and k-point meshes, ensuring that total energies are converged to within 1 meV per atom. The results are summarized in Tables 1 and 2. For the 8-atom supercell, a cutoff energy of 500 eV and a 7 × 7 × 7 K-point grid are selected. These settings achieve the following convergence: 0.7 meV per atom (cutoff energy), 0.01 meV per atom (k-point mesh), and ionic forces <0.001 eV Å−1. For the 64-atom defect supercell, a cutoff energy of 400 eV and a 2 × 2 × 2 k-point mesh are sufficient, converging the total energy to within 0.8 meV per atom and 0.3 meV per atom, respectively.
| 8-Atom supercell | 64-Atom supercell | ||
|---|---|---|---|
| Cut-off energy (eV) | E−E600 (meV per atom) | Cut-off energy (eV) | E−E500 (meV per atom) |
| 300 | 21 | 200 | 23 |
| 400 | 7 | 300 | 8 |
| 500 | 0.7 | 400 | 0.8 |
| 600 | 0 | 500 | 0 |
| 8-Atom supercell | 64-Atom supercell | ||
|---|---|---|---|
| k-Point mesh | E−E8×8×8 (meV per atom) | k-Point mesh | E−E3×3×3 (meV per atom) |
| 5 × 5 × 5 | 5.38 | 1 × 1 × 1 | 2.5 |
| 6 × 6 × 6 | 1.31 | 2 × 2 × 2 | 0.3 |
| 7 × 7 × 7 | 0.01 | 3 × 3 × 3 | 0 |
| 8 × 8 × 8 | 0 | — | — |
3. Results and discussion
3.1 Structural and magnetic properties
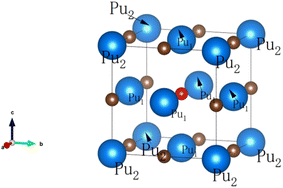
PuC has a NaCl-type structure, in which the 4a Wyckoff positions are occupied by Pu atoms and the 4b ones by C atoms. The known experimental lattice constant of PuC is 4.965 Å.27 Experimental works28,29 indicate that an anti-ferromagnetic transition occurs at 100 K in PuC. Fig. 1 shows the structure of PuC0.75O0.25. For the PuC0.75O0.25 system, Pu atoms are divided into two categories, as illustrated in Fig. 1. We refer to the Pu atoms near the O atom as Pu1, and those far away as Pu2.The reliability of DFT + U calculation is highly sensitive to the choice of the Ueff parameter. To ensure a valid Ueff value, we set Ueff = 4 eV for Pu's 5f orbitals. This choice is justified by theoretical studies on Pu-based compounds,19–21 which show it reasonably reproduce key experimental properties (e.g., lattice constants, magnetic ordering). To confirm the robustness of our results, we systematically test Ueff values of 3, 4 and 5 eV. Details of this analysis, including its impact on the lattice constant (a central structural property), are presented at the end of this section.
Based on the relative total energy values Erel of PuC for the nonmagnetic (NM), ferromagnetic (FM) and antiferromagnetic (AFM) phases given in Table 3, it is evident that the total energies of the FM phase are lower using the LSDA and PBE methods. This suggests that the LSDA and PBE methods predict PuC to be in the FM state, which is not consistent with the available experimental result.28,29 On the other hand, LSDA + U and PBE + U calculations indicate that PuC is AFM, in agreement with experiment. The results imply that strong correlation effects exert a significant influence on the magnetism of PuC. Similarly, the LSDA + U and PBE + U methods predict PuC0.75O0.25 to be in the AFM state, while the LSDA and PBE methods predict it to be in the FM state. Thus, our results indicate that substituting one oxygen for one carbon does not alter the magnetism in PuC.
| Compound | Method | a0/Å | µtot/µB | Erel (eV) | Egap (eV) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NM | FM | AFMa | NM | FM | AFM | NM | FM | AFM | NM | FM | AFM | ||
| a A small tetragonal disorder with a = b ≠ c is found in AFM states. | |||||||||||||
| PuC | LSDA | 4.702 | 4.851 | 4.847 | — | 15.730 | 0.000 | 2.59 | 0.00 | 0.26 | 0.0 | 0.0 | 0.0 |
| LSDA + U | 4.807 | 4.987 | 4.976 | — | 18.023 | 0.000 | 17.73 | 2.44 | 0.00 | 0.0 | 0.0 | 0.0 | |
| PBE | 4.799 | 4.988 | 4.984 | — | 16.481 | 0.000 | 4.75 | 0.00 | 0.45 | 0.0 | 0.0 | 0.0 | |
| PBE + U | 4.916 | 5.129 | 5.117 | — | 18.824 | 0.000 | 21.12 | 3.13 | 0.00 | 0.0 | 0.0 | 0.0 | |
| Expt.27 | 4.965 | — | — | — | |||||||||
| Ref. 20 | — | 5.043 | 5.115 | — | 17.400 | — | — | — | 0.0 | 0.0 | |||
| Ref. 25 | — | — | 4.910 | — | — | — | |||||||
| PuC0.75O0.25 | LSDA | 4.708 | 4.858 | 4.854 | — | 16.606 | 0.000 | 2.95 | 0.00 | 0.13 | 0.0 | 0.0 | 0.0 |
| LSDA + U | 4.868 | 5.008 | 4.987 | — | 18.701 | 0.000 | 14.68 | 0.26 | 0.00 | 0.0 | 0.0 | 0.0 | |
| PBE | 4.809 | 4.998 | 4.991 | — | 17.478 | 0.000 | 5.35 | 0.00 | 0.37 | 0.0 | 0.0 | 0.0 | |
| PBE + U | 5.037 | 5.141 | 5.107 | — | 18.759 | 0.000 | 15.29 | 0.17 | 0.00 | 0.0 | 0.0 | 0.0 | |
| Ref. 17 | 4.968 | — | — | — | |||||||||
| Ref. 16 | 4.979 | — | — | — | |||||||||
As expected, the lattice constant increases when Hubbard U is included. The reason is that the localization of Pu's 5f electrons is enhanced with the introduction of Hubbard U, which weakens the crystal cohesion and thus leads to an increase in the lattice constant. Compared with the experimental data27 for AFM PuC, the discrepancy is merely 0.22% for LSDA + U but reaches 3.06% for PBE + U. This significant discrepancy demonstrates the superiority of LSDA + U over PBE + U for these materials, as PBE + U overestimates the degree of 5f electron localizations. The fundamental difference stem from how the methods handle electron behavior. LSDA + U maintains a balanced description of electron localization and mobility that matches the actual electronic structure of plutonium compounds. In contrast, the PBE functional inherently over-screens 5f electrons. When combined with the Hubbard U correction, this effect is exaggerated, causing excessive electron localization that weakens atomic bonding and leads to excessively large lattice constants. This advantage of LSDA + U is further confirmed by comparing with other theoretical studies. Table 3 shows that the lattice constant of PuC0.75O0.25 predicted by LSDA + U agree well with other theoretical values.16,17 By contrast, PBE and PBE + U consistently overestimate the lattice constants of PuC and PuC0.75O0.25 compared with experimental and theoretical results. This systematic overestimation provides direct evidence that these methods over-localize 5f electrons and underestimate their bonding contributions. Therefore, LSDA + U is more suitable for PuC and PuC0.75O0.25 than PBE + U, at least in terms of predicting lattice constants. In both LSDA + U and PBE + U schemes, our calculated lattice constants of FM states are larger than those of AFM states for both PuC and PuC0.75O0.25. The optimized lattice constants in AFM states are closer to the experimental or other theoretical values, which suggests that the ground states of PuC and PuC0.75O0.25 are likely AFM. Notably, PuC's AFM nature has been confirmed by experimental studies.28,29
Of all the methods, LSDA + U yields very accurate lattice constants. For example, for PuC in the AFM state, its calculated value of 4.976 Å deviates from the experimental value by only 0.011 Å. Additionally, when comparing our results with other theoretical values (HSE20 and SIC-LSD25), we find that the lattice parameters obtained by LSDA + U are much better, suggesting that the present method (LSDA + U) has an advantage over the others in describing PuC. For PuC0.75O0.25, Ganguly et al.17 provide the lattice constant value of 4.968 Å according to Vegard's law, and R. Z. Qiu et al.16 give a value of 4.979 Å using a machine-learning scheme. Our LSDA + U-calculated lattice constant for the AFM state of PuC0.75O0.25 is 4.987 Å, which is close to these results. This suggests that LSDA + U method is also suitable for describing PuC0.75O0.25.
In the sequence PuC → PuC0.75O0.25, the calculated lattice parameters show an expansion in all methods. For instance, the lattice parameter of PuC0.75O0.25 calculated via LSDA + U for the AFM state is expanded by 0.011 Å compared to that of PuC. It means that the substitution of carbon atoms by oxygen atoms leads to lattice expansion. The observed lattice expansion has also been reported by Ganguly et al.17 and R. Z. Qiu et al.16
At the end of this section, Table 4 summarizes the lattice parameters of PuC and PuC0.75O0.25 calculated with Ueff values of 3.0, 4.0, and 5.0 eV. For PuC, the deviation from experimental data is minimized at 4.0 eV (0.22%), compared to 0.54% at 3.0 eV and 0.60% at 5.0 eV. For PuC0.75O0.25, our calculated lattice parameter at 4.0 eV (4.987 Å) is also closest to the previously reported theoretical values.16 This Ueff value is consistent with previous theoretical studies on Pu-based compounds.19–21 For the oxygen-substituted system, which lacks experimental lattice data, we further validate Ueff = 4.0 eV by analyzing the sensitivity of oxygen-induced lattice expansion to Ueff variations. The calculated expansion rates are 0.38% at 3.0 eV, 0.22% at 4.0 eV, and 0.24% at 5.0 eV. This low sensitivity confirms that the structural effect of oxygen substitution remains consistent under small changes in Ueff, reinforcing the reliability of 4.0 eV. We also compare the performance of different exchange–correlation functionals (PBE, PBE + U, LSDA, and LSDA + U). Only LSDA + U with Ueff = 4.0 eV reasonably reproduces experimental lattice constants and magnetic ordering for PuC and PuC0.75O0.25, while other functionals show significant deviations. Therefore, the LSDA + U method with a Ueff parameter of 4.0 eV is employed in all subsequent calculations.
3.2 Electronic properties
The total and partial densities of states for PuC and PuC0.75O0.25 in LSDA + U are depicted in Fig. 2 and 3, with all energy scales uniformly referenced to the Fermi level (EF = 0 eV) for direct comparison. Key features (e.g., peak positions, band edges) are labeled explicitly in the figures to clarify their correspondence with electronic states. The total DOS curves of both systems cross EF with nonzero occupation of Pu 5f electrons. This indicates that both PuC and PuC0.75O0.25 are metals, which is in agreement with the calculated band gaps (Table 3). For PuC and PuC0.75O0.25, the DOS of Pu atoms is mainly dominated by the 5f partial DOS and the Pu d orbits contribute little to the total DOS. The near-Fermi regions of PuC and PuC0.75O0.25 are made up mainly of Pu 5f states, which is similar to the other 5f metal carbides. The experimental valence-band spectra30 of PuC are characterized by the presence of three sharp peaks within 1 eV, located at the Fermi energy EF, and at 0.50 and 0.85 eV. We note that our calculated DOS of PuC also has three sharp peaks located at 0.02 eV, 0.36 eV and 0.66 eV. | ||
| Fig. 2 (Color online) Total and partial densities of states for AFM PuC in LSDA + U (Ueff = 4.0 eV) framework. The Fermi level is the vertical line through E = 0. | ||
 | ||
| Fig. 3 (Color online) Total and partial densities of states for AFM PuC0.75O0.25 in LSDA + U (Ueff = 4.0 eV) framework. The Fermi level is the vertical line through E = 0. | ||
For PuC, peak A is mainly composed of C 2 s states, and peak B is separated from the following C 2p band by a gap of about 2.64 eV. While for PuC0.75O0.25, the band structure of peaks A and B is similar to that of PuC, except for the emergence of a new peak C between them. The new peak is caused by a hybridization between Pu 5f/6d states and O 2p states (Fig. 4). This indicates that the substitution of carbon atoms by oxygen atoms would “break” some Pu–C bonds and “form” some Pu–O bonds. In order to obtain further understanding of the electronic structure and analyze the Pu–O and Pu–C bonds. The difference charge densities along the (010) plane are plotted in Fig. 5. The blue and orange zones represent the loss and the gain of charge. We can observe that the Pu atoms lose charge, the C and O atoms have gained charge. This clearly suggests that there is net charge transfer from the Pu atom to the C and O atom, indicating that the Pu–C and Pu–O bonds have ionic character. The electron transfer observed in the charge density difference plot is quantified by the Bader charge analysis. As shown in Table 5, each Pu atom loses 1.28|e| and this charge is transferred to C atom in the PuC system. From Fig. 1 and Table 5, in the PuC0.75O0.25 system, each Pu atom far from the O atom (Pu2) still loses 1.28|e| (transferred to the C atom), while each Pu atom near the O atom (Pu1) loses 1.38|e| (transferred to the O atom). Thus in the PuC0.75O0.25 system, the ionic character near the O atom is stronger than that in the PuC system.
 | ||
| Fig. 4 Partial densities of states for the Pu 6d/5f and O 2s/2p of AFM PuC0.75O0.25 in LSDA + U (Ueff = 4.0 eV) framework. | ||
 | ||
| Fig. 5 Contour plots of charge density difference along the (010) plane in LSDA + U (Ueff = 4.0 eV) calculations of AFM PuC0.75O0.25. | ||
| Compound | QB (Pu2)/e | QB (Pu1)/e | QB (C)/e | QB (O)/e | VB (Pu2)/Å3 | VB (Pu1)/Å3 | VB (C)/Å3 | VB (O)/Å3 |
|---|---|---|---|---|---|---|---|---|
| PuC | 14.72 | — | 5.28 | — | 19.77 | — | 12.89 | — |
| PuC0.75O0.25 | 14.72 | 14.62 | 5.28 | 7.38 | 18.92 | 18.66 | 12.83 | 11.81 |
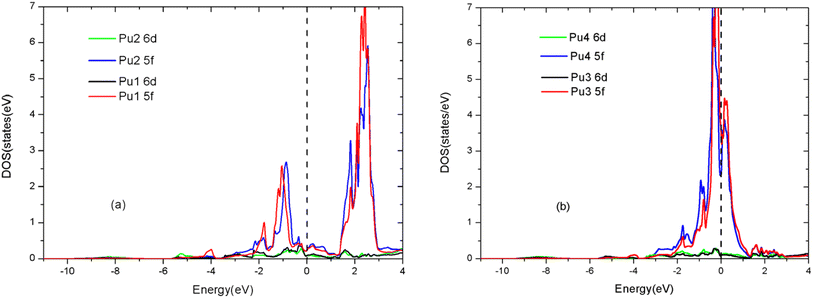
For PuC0.75O0.25, the crystal symmetry is destroyed with the substitution of carbon atoms by oxygen atoms. Thus, we need to distinguish the partial densities of states (PDOSs) of different C atoms and Pu atoms. To provide an unambiguous description defined by the three-dimensional structure, we label the atoms according to their crystallographic coordinates. We assign the labels Pu1, Pu2, Pu3, and Pu4 to the four plutonium atoms at coordinates (0, 0, 0), (0, 0.5, 0.5), (0.5, 0, 0.5), and (0.5, 0.5, 0), respectively. As shown in Fig. 6, the 6d PDOSs of different Pu atoms are similar, while the two main peaks of 5f PDOSs of Pu1 and Pu2 are further separated than those of Pu3 and Pu4. The near-Fermi regions of total DOS are dominated by the 5f PDOS of Pu3 and Pu4. Fig. 7 shows that the 2s and 2p PDOSs of different C atoms are similar.
 | ||
| Fig. 7 (Color online) Partial densities of states of AFM PuC0.75O0.25 for different C atoms in LSDA + U (Ueff = 4.0 eV) framework. The Fermi level is the vertical line through E = 0. | ||
3.3 Thermodynamic properties
For fuel materials, a thorough understanding of their thermodynamic properties is of particular importance. However, available thermodynamic data for plutonium carbides have significant uncertainty due to insufficient experimental data.31 The thermodynamic properties of PuC and PuC0.75O0.25 are investigated herein using phonon density of states obtained via the quasiharmonic approximation (QHA).32 The internal energy ΔE, Helmholtz free energy ΔF, entropy S, and constant-volume specific heat capacity Cv are given, respectively, by33
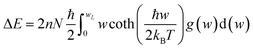 | (1) |
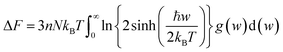 | (2) |
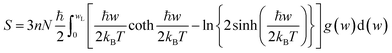 | (3) |
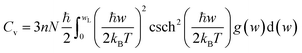 | (4) |
The enthalpy changes (HT–H298) with increasing temperature are presented in Table 6. For PuC, our calculated values are in good agreement with experimental data.35 However, a notable temperature-dependent deviation exists. At 427.6 K, the calculated value is 7% higher than the experimental value, whereas it is 7% lower at 921.7 K. This reverse discrepancy is primarily attributed to the inherent limitations of the QHA, particularly its neglect of electronic thermal contributions and anharmonic phonon effects.36 At a moderate temperature like 427.6 K, the overestimation arises mainly because the model fails to fully reproduce the finite-temperature amplitudes of low-frequency phonons within its T = 0 K harmonic framework. Additionally, the neglect of electronic excitations, though minor, plays a non-negligible role. At 921.7 K, the underestimation is dominated by significant anharmonic effects such as phonon–phonon scattering, beyond the scope of the QHA framework. Thus, it is the temperature-induced emergence of these anharmonic processes that drives the observed breakdown. The deviation is further increased by the growing importance of omitted electronic contributions and higher-order anharmonic effects at high temperature. Volume effects from thermal expansion also contribute to the overall error, but their role is secondary to the effects previously described. Table 6 also lists our calculated values of PuC0.75O0.25 at selected temperatures. Specifically, oxygen substitution in PuC leads to a greater enthalpy difference (HT–H298) at the same temperature relative to pure PuC. This phenomenon can be explained using fundamental thermodynamic relationships: 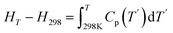 . Since HT–H298 is the integral of Cp, and oxygen substitution increases Cp (as shown in Table 7), the HT–H298 of PuC0.75O0.25 is therefore more significant than that of pure PuC at the same temperature.
. Since HT–H298 is the integral of Cp, and oxygen substitution increases Cp (as shown in Table 7), the HT–H298 of PuC0.75O0.25 is therefore more significant than that of pure PuC at the same temperature.
| Compound | Method | 425.2 K | 427.6 K | 525.2 K | 530.1 K | 628.0 K | 733.2 K | 825.2 K | 830.5 K | 921.7 K |
|---|---|---|---|---|---|---|---|---|---|---|
| PuC | LSDA + U | 6.075 | 6.183 | 10.940 | 11.171 | 15.970 | 21.175 | 25.715 | 25.991 | 30.520 |
| Expt.34 | 5.990 | 5.745 | 11.054 | 11.006 | 16.460 | 22.108 | 28.049 | 27.416 | 32.626 | |
| PuC0.75O0.25 | LSDA + U | 6.999 | 7.110 | 11.826 | 12.032 | 16.844 | 22.786 | 26.631 | 26.858 | 31.425 |
| Compound | T (K) | ST–S298 (J K−1 mol−1) | Heat capacity (J K−1 mol−1) | ||
|---|---|---|---|---|---|
| LSDA + U | Other34 | Cv (LSDA + U) | Cp (other)34 | ||
| PuC | 400 | 13.622 | 13.209 | 48.177 | 48.154 |
| 500 | 24.451 | 24.369 | 48.785 | 51.665 | |
| 600 | 33.377 | 24.369 | 49.163 | 53.797 | |
| 700 | 41.025 | 42.427 | 49.397 | 55.260 | |
| 800 | 47.681 | 49.909 | 49.481 | 56.388 | |
| 900 | 53.462 | 56.514 | 49.572 | 57.308 | |
| 1000 | 58.816 | 62.742 | 49.624 | 58.102 | |
| PuC0.75O0.25 | 400 | 14.047 | — | 48.459 | — |
| 500 | 24.938 | — | 49.048 | — | |
| 600 | 33.992 | — | 49.438 | — | |
| 700 | 41.657 | — | 49.708 | — | |
| 800 | 48.063 | — | 49.799 | — | |
| 900 | 53.855 | — | 49.845 | — | |
| 1000 | 59.277 | — | 49.890 | — | |
Table 7 presents our calculated values of ST–S298 (J K−1 mol−1) and heat capacity (J K−1 mol−1) for PuC and PuC0.75O0.25 using the QHA. Kruger and Savage35 calculated the constant-pressure specific heat capacity (Cp) of PuC using the equation (Cp = 13.08 + 11.44 × 10−4T − 3.232 × 105T−2) proposed by Maier and Kelley.37 The relationship between Cp and Cv is given by the following equation:38
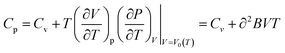 | (5) |
3.4 Elastic properties
The elastic properties are evaluated using the “stress–strain technique” based on the applied strains of ±0.002. The stress is determined as a function of the strain, with internal coordinates optimized for each small strain, and the elastic constants are obtained from the derivatives of stress with respect to strain. Because the structures of PuC and PuC0.75O0.25 belong to cubic symmetry, there are only three independent elastic constants C11, C12 and C44. From the obtained elastic constants, the elastic modulus can be further derived by the Voigt formalism: the shear modulus G = (C11 − C12 + 3C44)/5, Young's modulus Y = 9BG/(G + 3B) and Poisson's ratio σ = (B − 2G/3)/(2B + 2G/3), where B is the bulk modulus defined by B = (C11 + 2C12)/3. Table 8 lists all elastic constants and associated quantities.| System | C11 | C12 | C44 | G | Y | σ | B | G/B |
|---|---|---|---|---|---|---|---|---|
| PuC | 225.72 | 139.94 | 50.72 | 47.59 | 130.49 | 0.37 | 168.53 | 0.28 |
| PuC0.75O0.25 | 228.81 | 126.97 | 66.29 | 60.20 | 160.56 | 0.33 | 160.92 | 0.37 |
For cubic crystals, the necessary conditions for mechanical stability are given by (C11 − C12) > 0, (C11 + 2C12) > 0, C11 > 0 and C44 > 0. Our calculated elastic constants satisfy all these conditions, confirming that PuC and PuC0.75O0.25 are elastically stable. From Table 8, PuC0.75O0.25 exhibits larger G and Y compared to PuC, indicating enhanced hardness. This trend can be explained by the atomic-scale bonding behavior, as shown by Bader charge analysis in Table 2. In PuC, each Pu atom transfers 1.28|e| to the C atom, reflecting the intrinsic ionic character of the Pu–C bond. In PuC0.75O0.25, oxygen substitution leads to differentiated charge transfer. Pu atoms near the O atom (Pu1) lose 1.38|e|, and this is 0.1|e| more than Pu in PuC. The extra charge is transferred to the O atom (QB (O) = 7.38e). Pu atoms far from O (Pu2) retain the same 1.28|e| loss as in PuC, transferred to C atoms. The increased charge transfer for Pu1 confirms stronger ionic character in Pu–O bonds than in Pu–C bonds. This intensifies electrostatic attraction between ions, strengthens bonding, and leads to higher G and Y values. The fact that only Pu1 is affected indicates that hardening is localized around oxygen defects, consistent with the moderate difference in elastic moduli. The reliability of our computational approach is supported by the bulk modulus of PuC. Our calculated result of 168.53 GPa is in reasonable agreement with the previously reported value of 172 GPa (SIC-LSD25). For PuC0.75O0.25, B is slightly lower (160.92 GPa), likely due to local lattice distortion from O substitution. This trend is consistent with Bader volume analysis. Pu1 in PuC0.75O0.25 has a smaller volume (18.66 Å3) than Pu in PuC (19.77 Å3). This compression around the oxygen defect may lead to a lower resistance to volume deformation. The G/B criterion can be used to predict the ductile and brittle behavior. According to Pugh's empirical rule,41 a value higher than the critical G/B ratio of 0.57 is associated with brittleness, while a lower value corresponds to ductility. Our results show that both PuC and PuC0.75O0.25 have G/B ratios below 0.57, confirming they are ductile materials. However, PuC is relatively more ductile compared to PuC0.75O0.25. This difference is also related to bonding nature. The stronger ionic character of Pu–O bonds restricts atomic slip and thus reduces ductility, whereas the more metallic Pu–C bonding facilitates plastic deformation. The calculated Poisson's ratios are between 0.25 and 0.45 for typical metals, further supporting their ductile nature.
3.5 Formation energy of O-substituted C defects
The thermodynamic stability for oxygen substituting in PuC is assessed by calculating the defect formation energy (Eform) within a PuC0.75O0.25 model system. This energy quantifies the energetic cost of replacing a carbon atom with an oxygen atom and reflects the likelihood of defect formation. Eform is given by:| Eform = Edefective − Eperfect + µC − µO, | (6) |
4. Conclusions
This work reveals the initial stage of plutonium carbide aging by investigating PuC and PuC0.75O0.25. We demonstrate that oxygen substitution is thermodynamically inevitable, as evidenced by its large negative formation energy (−5.11 eV). This central result provides the atomic-scale driving force for the degradation process. The oxygen substitution introduces a new peak in the density of states (DOS). The new DOS peak is caused by hybridization between Pu 5f/6d states and O 2p states. Bader charge analysis further demonstrates that Pu ions near the O atom in PuC0.75O0.25 are ionized somewhat stronger than those in the PuC system. At the same temperature, the oxygen substitution in PuC causes greater values of HT–H298, ST–S298, Cp and Cv relative to pure PuC. Furthermore, the calculated elastic properties reveal that PuC0.75O0.25 is anticipated to be harder than PuC, a result consistent with the fact that the Pu–O bond has notably stronger ionic character than the Pu–C bond. Since PuC0.75O0.25 is an important corrosion product of plutonium during chemical aging, we expect that our studies on its structure and physical properties can help evaluate the actual performance of plutonium.Conflicts of interest
There are no conflicts to declare.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Acknowledgements
This work was financially supported by the Natural Science Foundation of Chongqing (Grant No. cstc2021jcyj-msxmX1073).References
- D. C. Hoffman, Advances in Plutonium Chemistry 1967-2000, American Nuclear Society, 2002 Search PubMed.
- H. G. G. Flores, P. Roussel and D. P. Moore, et al., Surf. Sci., 2011, 605, 314–320 CrossRef CAS.
- A. Modin, Y. Yun and M. T. Suzuki, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075113–075120 CrossRef.
- P. Zhang, B. T. Wang and X. G. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144110–144124 CrossRef.
- H. Nakamura, M. Machida and M. Kato, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155131–155137 CrossRef.
- J. M. Haschke and T. H. Allen, J. Alloys Compd., 2001, 320, 58–71 CrossRef CAS.
- G. Cinader, D. Zamir and Z. Hadari, Phys. Rev. B, 1976, 14, 912–920 CrossRef CAS.
- M. T. Butterfield, T. Durakiewicz and E. Guziewicz, et al., Surf. Sci., 2004, 571, 74–82 CrossRef CAS.
- O. Eriksson, Y. G. Hao and B. R. Cooper, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 4590–4597 CrossRef CAS PubMed.
- K. Balasubramanian, T. E. Felter and T. Anklam, et al., J. Alloys Compd., 2007, 444, 447–452 CrossRef.
- L. N. Dinh, J. M. Haschke and C. K. Saw, et al., J. Nucl. Mater., 2014, 408, 171 CrossRef.
- R. Yang, B. Tang, T. Gao and B. Y. Ao, J. Nucl. Mater., 2016, 473, 54–60 CrossRef CAS.
- R. Yang, B. Tang, T. Gao and B. Y. Ao, Eur. Phys. J. B, 2017, 90, 145–154 CrossRef.
- R. Yang, B. Tang, T. Gao and B. Y. Ao, Commun. Theor. Phys., 2016, 66, 447–452 CrossRef CAS.
- L. R. Morss, N. M. Edelstein, and J. Fuger, The Chemistry of the Actinide and Transactinide Elements, Dordrecht: Springer, 2006 Search PubMed.
- R. Z. Qiu, J. Tang, J. F. Chen, P. C. Liu and Q. Wang, Phys. Chem. Chem. Phys., 2024, 26, 14122–14130 RSC.
- C. Ganguly, and D. Vollath, Quantitative Phase Analysis in the U, Pu-C-System by X-Ray Diffraction, Karlsruhe, 1974 Search PubMed.
- S. S. Hecker, Metall. Mater. Trans. A, 2008, 39A, 1585–1592 CrossRef CAS.
- B. Y. Ao, R. Z. Qiu, H. Y. Lu, X. Q. Ye, P. Shi, P. S. Chen and X. L. Wang, J. Phys. Chem. C, 2015, 119, 101–129 CrossRef CAS.
- X. D. Wen, R. L. Martin, G. E. Scueria, S. P. Rudin and E. R. Batista, J. Phys. Chem. C, 2013, 117, 13122–13142 CrossRef CAS.
- B. Sun, P. Zhang and X. G. Zhao, J. Chem. Phys., 2008, 128, 084705–084712 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 773, 865 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- L. Petit, A. Savane, Z. Szotek, W. M. Temmerman and G. M. Stoks, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045124–045132 CrossRef.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 5467–5471 CrossRef PubMed.
- U. Benedict, C. Dufour and O. Scholten, J. Nucl. Mater., 1978, 73, 208–212 CrossRef CAS.
- J. L. Green, G. P. Arnold, J. A. Leary and N. G. Nereson, J. Nucl. Mater., 1967, 23, 231–232 CrossRef CAS.
- J. L. Green, G. P. Arnold, J. A. Leary and N. G. Nereson, J. Nucl. Mater., 1970, 34, 281–289 CrossRef CAS.
- T. Gouder, L. Havela, A. B. Shick, F. Huber, F. Wastin and J. Rebizant, J. Phys.:Condens. Matter, 2007, 19, 476201–476212 CrossRef.
- F. L. Oetting, The Chemical Thermodynamic Properties of Plutonium Compounds, The Dow Company, Rochy Flats Division, Golden, Colorado, 1996, pp. 262–297 Search PubMed.
- A. Siegel, K. Parlinski and U. D. Wdowik, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 104116–104122 CrossRef.
- C. Lee and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 8610–8614 CrossRef CAS PubMed.
- S. Limpijumnong and S. Jungthawan, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 054104–054108 CrossRef.
- O. L. Kruger and H. Savage, J. Chem. Phys., 1964, 40, 3324–3328 CrossRef CAS.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- C. G. Maier and K. K. Kelley, J. Am. Chem. Soc., 1932, 54, 3243–3246 CrossRef CAS.
- R. Wang, S. F. Wang, X. Z. Wu and T. T. Song, Int. J. Thermophys., 2012, 33, 300–310 CrossRef CAS.
- A. T. Petit and P. L. Dulong, Ann. Chem. Phys., 1819, 10, 395 Search PubMed.
- (a) Journée des Actinides, ed. B. Kanellakopulos and L. Manes, Kernforschungszentrum Karlsruhe GmbH, KfK 2840, EUR 5758 e, 1980 Search PubMed; (b) J. W. Yang, T. Gao and L. Y. Guo, Physica B, 2013, 429, 119–126 CrossRef CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
- M. H. Rand and T. L. Markin, Thermodynamics of Nuclear Materials, International Atomic Energy Agency, Vienna, 1968, p. 637 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |