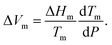DOI:
10.1039/D5RA03931B
(Paper)
RSC Adv., 2025,
15, 25675-25693
Effects of hydrostatic compression and kinetic vitrification on structural relaxation behaviors of amorphous drugs: how to predict them via simple theoretical models?†
Received
3rd June 2025
, Accepted 6th July 2025
First published on 18th July 2025
Abstract
Amorphization is considered one of the most promising strategies for enhancing pharmaceuticals' aqueous solubility and oral bioavailability. However, amorphous systems are susceptible to recrystallization because of their disordered atomic structures and elevated free energies. To resolve this problem, one needs accurate information about molecular mobilities under various physical conditions. Unfortunately, it is difficult to investigate the relaxation processes of amorphous drugs beyond the uncompressed supercooled region. Hence, we aim to develop a simple but effective toolkit to predict pharmaceuticals' relaxation time and dynamic fragility at high pressures and low temperatures. First, we apply the elastically collective nonlinear Langevin equation theory to determine the impact of local and non-local interactions on the motion of drug molecules. Then, based on the similarity between the melting transition of crystalline solids and the glass transition of soft materials, a new chemical mapping is created to connect the hydrostatic pressure, the absolute temperature, and the packing fraction. This combined approach allows us to capture the primary relaxation behaviors of amorphous drugs with minimal computational cost. Our theoretical analyses agree quantitatively well with broadband-dielectric-spectroscopy experiments in both supercooled and glassy states. Therefore, they promise to be valuable for improving the physical stability and the practical applicability of amorphous pharmaceuticals.
1. Introduction
Diseases have long been perceived as the leading threat to human well-being. According to modern studies on ancient pathogen genomics,1 humanity has frequently faced the infection of Yersinia pestis,2 Helicobacter pylori,3 hepatitis B virus,4 and parvovirus B19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 since the Neolithic Age. For thousands of years, numerous catastrophic epidemics and pandemics have been recorded in human history, such as the plague of Justinian,6 the Black Death,7 HIV/AIDS,8 Ebola,9 and COVID-19.10 They have not only claimed the lives of millions of people but also affected all aspects of socio-economic life severely.11–13 In addition to infectious diseases, human health has been threatened by non-communicable ones, including ischaemic heart, stroke, chronic obstructive pulmonary, cancer, Alzheimer's, diabetes, and kidney.14–16 As reported by the World Health Organization,17 cardiovascular problems alone were responsible for more than one-third of global deaths in 2019. Thus, it cannot be denied that disease prevention and treatment have become a deep concern for every individual, organization, and country.18–20
5 since the Neolithic Age. For thousands of years, numerous catastrophic epidemics and pandemics have been recorded in human history, such as the plague of Justinian,6 the Black Death,7 HIV/AIDS,8 Ebola,9 and COVID-19.10 They have not only claimed the lives of millions of people but also affected all aspects of socio-economic life severely.11–13 In addition to infectious diseases, human health has been threatened by non-communicable ones, including ischaemic heart, stroke, chronic obstructive pulmonary, cancer, Alzheimer's, diabetes, and kidney.14–16 As reported by the World Health Organization,17 cardiovascular problems alone were responsible for more than one-third of global deaths in 2019. Thus, it cannot be denied that disease prevention and treatment have become a deep concern for every individual, organization, and country.18–20
In the never-ending struggle against diseases, humanity has invented a crucial weapon called “drug” to deal with structural and functional disorders in living organisms.21–23 Today, about 80% of marketed drugs are prepared in tablet form, and the majority exist in a crystalline state.24 The most prominent advantage of pharmaceutical crystals is their superior physical and chemical stability.25,26 It is feasible to maintain their quality over a prolonged period. Besides, developing synthetic and analytic methods for crystalline drugs is relatively convenient.27,28 However, these pharmaceutical systems have a critical drawback: they are almost insoluble in water.29–31 As an inevitable consequence, they are readily eliminated from the digestive tract before being effectively absorbed into the body.32 In many cases, a large dosage of drugs is necessitated to reach therapeutic levels.33 This burning issue not only occasions undesirable side effects34 but also increases treatment expenses and reduces patient adherence.35
The above predicament leads to an exciting idea of changing the internal structure of pharmaceuticals from a crystalline type with long-range order to an amorphous type with short-range order.36 Fundamentally, amorphous drugs are created by cooling liquids rapidly below their melting points to inhibit nucleation processes.37 Alternative techniques include hot-melt extrusion,38 3D printing,39 crystal dehydration,40 and solvent evaporation.41 It is worth noting that the aqueous solubility of drugs is expected to increase 1.4- to 1668-fold after amorphization.42–45 Accordingly, their oral bioavailability can be markedly improved.46 These enormous benefits promise to open a more fruitful avenue for safeguarding human health. Yet, in practice, the applications of amorphous drugs to disease prevention and treatment remain limited due to their thermodynamic instability. Few amorphous pharmaceutical products are commercialized because recrystallization can readily occur at any stage of drug processing, such as preparation, production, and administration.47–50 It is impracticable to overcome these grand challenges without intimate knowledge of molecular dynamics under different pressure–temperature (P–T) conditions.51
For the reasons above, countless attempts have been made to advance our understanding of relaxation mechanisms in amorphous drugs, particularly α relaxation. On the experimental side, there has been a continuous improvement in the broadband-dielectric-spectroscopy (BDS) technique.52 In the supercooled domain, the α rearrangement of molecules is directly detected via the emergence of high, broad, and asymmetric peaks on dielectric loss spectra.53–57 This approach helps experimentalists measure the structural relaxation time τα, the glass transition temperature Tg, and the dynamic fragility m up to hundreds of megapascals.36 In the glassy domain, since molecular motions are almost frozen, the location of α peaks is indirectly determined by the so-called master plot construction (MPC).58–62 The MPC is considered the most reliable method for predicting the primary relaxation behaviors of amorphous pharmaceuticals at T < Tg.36 However, the MPC will be invalidated if the shape of BDS spectra varies with temperature due to the contribution of excess wing and dc-conductivity.36 Another way to investigate glassy dynamics is to apply the extended Adam-Gibbs model (EAGM)63–65 for the entropy–mobility relationship. The EAGM allows estimating the value of τα(T < Tg) via experimental data for the structural relaxation time at T > Tg and the isobaric heat capacity at T = Tg.66 Nevertheless, accurate information about the isobaric heat capacity of many pharmaceutical systems remains unavailable.51 Besides, it should be noted that the EAGM only works well in the case of freshly generated non-equilibrium samples.67 Consequently, how to evaluate the impact of kinetic vitrification on the structural relaxation of amorphous drugs is still a knotty question for the soft-matter community.
On the computational side, molecular dynamics (MD) simulations have been continuously enhanced to serve drug discovery and development.68 MD studies can yield valuable insights into the microscopic structures, molecular interactions, stabilization mechanisms, and macroscopic properties of single- and multi-component amorphous pharmaceuticals. For instance, one can utilize MD calculations to elucidate how hydrogen-bond networks are established between drugs and polymers, thereby finding innovative ways to design amorphous solid dispersions with high water solubilities and low recrystallization tendencies.69–71 Additionally, it is viable to employ MD outputs to build solid-state descriptors and reinforce machine-learning models in pharmaceutical fields.72 Despite the mentioned positive aspects, MD computations have a severe limitation: they cannot predict τα in a timescale larger than 10−5 s.73–78 This complicated problem principally stems from the selection of simulated temperature and annealing time.79 Recall that the conventional BDS definition of the glass transition point is τα(Tg) = 102 s.51 Currently, there is no reliable method to extrapolate computational results for τα from the MD regime to the BDS one.80 According to Moore's law, it would take until 2048 for the MD-BDS gap to be closed.79 Hence, scientists are still looking forward to the appearance of more powerful computational tools to overcome the MD limit.
One of the most promising strategies for going beyond the MD region is to develop the elastically collective nonlinear Langevin equation (ECNLE) theory.81–83 The ECNLE core idea is to view each amorphous material as a hard-sphere glass former.84 In this reference system, local and non-local excitations can be effortlessly analyzed at various packing fractions ϕ.85 Then, based on available experimental data for bulk quantities (e.g., the dimensionless isothermal compressibility or the glass transition temperature), a chemical mapping is formulated to convert ECNLE results from ϕ to P–T spaces.86,87 This theoretical scheme enables scientists to clarify the physical properties of thermal liquids,88 vdW polymers,89 graphene melts,90 metallic glasses,91 superionic crystals,92 and active pharmaceutical ingredients93 in both MD and BDS timescales without heavy computational processes. Yet, current ECNLE analyses81–93 cannot explain why the temperature dependence of τα switches from non-Arrhenius to Arrhenius-like types near kinetic vitrification.58–62 The consequence is that τα is greatly overestimated in the glassy state.94 In addition, there is a considerable discrepancy between experimental and theoretical results for m at elevated pressures.95 While BDS measurements suggest that most amorphous drugs become stronger during hydrostatic compression, ECNLE calculations predict the opposite. It should be emphasized that the relaxation time, the dynamic fragility, and the recrystallization ability are closely correlated.96–98 Therefore, expanding the ECNLE theory to low-temperature and high-pressure areas remains an appealing problem for research groups in the soft-matter field.
Our ultimate goal in this study is to improve the ECNLE model to capture molecular dynamics in compressed and vitrified amorphous pharmaceuticals with the tiniest computational effort. Overall, it is possible to remove ECNLE restrictions step-by-step by modifying the reference system (microscopic approach)99 or the chemical mapping (macroscopic approach).92 Whereas the microscopic approach can provide novel information about free-energy landscapes,91 the macroscopic approach is time-saving, cost-effective, and user-friendly.100 Thus, to facilitate ECNLE applications in practice, we mainly focus on the intimate relation among bulk quantities in the chemical mapping. The reference system is supposed to be unaffected by pressurization and vitrification. The effectiveness of our ECNLE calculations is demonstrated by comparing them with cutting-edge BDS experiments.
2. Structural relaxation of reference system
Let us start with the ECNLE reference system constructed from an infinite number of rigid spheres with the diameter σ and the density ρ = 6ϕπ−1σ−3 (each sphere is equivalent to an actual molecule). Their spatial arrangement can be rapidly described by applying the well-known Percus–Yevick approximation101–103 to the direct correlation function C(r), the static structure factor S(k), and the radial distribution function g(r), where r is the distance and k is the wavevector. Details about C(r), S(k), and g(r) can be easily found in prior ECNLE reports.90–93 According to Schweizer et al.,104–106 the motion of an arbitrary sphere (the tagged sphere) is strongly affected by its nearest-neighbor interactions, which are characterized by a non-equilibrium quantity Fdyn as| | |
Fdyn = Fideal + Fexcess.
| (1) |
While the first term represents delocalization processes, the second term denotes confinement effects. Their mathematical expressions in real space are explicitly written by104–106| |
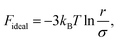 | (2) |
| |
 | (3) |
where kB is the Boltzmann constant.
Overall, there is competition between Fideal and Fexcess in controlling the molecular dynamics of the ECNLE reference system. At ϕ < 0.432, since Fideal gains the upper hand, Fdyn becomes a monotonically decreasing function of r.104–106 That means no kinetic constraints are imposed on the tagged sphere in dilute solutions. However, the situation is reversed in dense fluids. At ϕ > 0.432, Fexcess prevails over Fideal.104–106 Accordingly, a local barrier of height FB appears in the dynamic free–energy plot (Fig. 1). This event causes the tagged sphere to be temporarily trapped in an intermolecular cage of radius rcage. For simplicity, we approximate rcage ≈ 1.5σ instead of solving the minimum condition of g(r). The modulus of FB is deduced from 104–106
| | |
FB = Fdyn(rB) − Fdyn(rL),
| (4) |
where
rB typifies the barrier position, and
rL symbolizes the localization length.
 |
| | Fig. 1 (Color online) Summarizing the prominent features of the ECNLE reference system. Whereas the distribution of hard spheres is described by the Percus–Yevick theory,101–103 their interaction is modeled by the Schweizer free-energy method.104–106 When the tagged sphere breaks out of the nearest neighbor cage, it distorts the first coordination shell and the remaining elastic medium.84,85 | |
Interestingly, the tagged sphere tries to escape confinement by making a thermal jump of amplitude Δr = rB − rL.84,85 Note that Δr can be up to 0.412σ at ϕ = 0.64. This value is quite large on the cage scale. Hence, a long-range deformation field has to be formed in the surroundings to create space for the activated hopping process.84,85 According to the Landau–Lifshitz continuum mechanics,107 the displacement u of hard spheres located at r ≥ rcage is determined by
| |
 | (5) |
where Δ
reff ≈ 0.09375Δ
r2rcage−1 describes how much the first coordination shell expands.
84,85 Eqn (5) shows that
u is considerably shorter than
rL. Thus, we can view each shoved sphere as an Einstein harmonic oscillator having the force constant
KL = (∂
2Fdyn/∂
r2)
r=rL and the energy change Δ
Fdyn =
KLu2/2. This physical picture allows computing the total strain energy
FE stored outside the cage by
84,85| |
 | (6) |
Conspicuously, the diffusion of the tagged sphere is now affected by both local and non-local interactions. Based on the modified Kramers theory,108–110 it is feasible to infer the mean escape time or the structural relaxation time from
| |
 | (7) |
where
τs is the short relaxation timescale and
KB is the absolute curvature of the dynamic free-energy curve at
rB. Numerical results derived from
eqn (4),
(6), and
(7) are presented in
Table 1. At
ϕ < 0.55, because the contribution of
FE is almost negligible, the activated hopping process is mainly governed by cage-scale dynamics. Nevertheless, an opposite trend emerges near the glass transition point (
ϕg ≈ 0.61). At
ϕ > 0.57, the growth rate of
FB becomes much slower than that of
FE. This event results in the dominance of collective dynamics in deeply supercooled and glassy states, consistent with experimental observations on metallic, oxide, vdW, and hydrogen-bonded materials.
111 Unlike MD simulations,
73–79 ECNLE calculations enable us to evaluate molecular mobility at various timescales spanning from picosecond to terasecond and beyond. Therefore, our theoretical data in
Table 1 would be useful for designing and developing amorphous pharmaceuticals. Before applying them to a specific drug, we need to find a way to link the
ϕ space with its
P–
T counterpart.
86,87 This work should be done quickly and accurately. So, how do we meet the above criteria? A detailed answer is revealed in subsequent sections.
Table 1 The local barrier FB, the collective barrier FE, and the structural relaxation time τα of the ECNLE reference system as a function of the packing fraction ϕ. While FB and FE are in the unit of kBT, τα is in the unit of second
| ϕ |
FB |
FE |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τα τα |
| 0.440 |
0.0524 |
0.0002 |
−11.2298 |
| 0.445 |
0.1073 |
0.0007 |
−11.2131 |
| 0.450 |
0.1759 |
0.0018 |
−11.1905 |
| 0.455 |
0.2572 |
0.0034 |
−11.1651 |
| 0.460 |
0.3510 |
0.0059 |
−11.1377 |
| 0.465 |
0.4571 |
0.0095 |
−11.1090 |
| 0.470 |
0.5757 |
0.0143 |
−11.0789 |
| 0.475 |
0.7071 |
0.0207 |
−11.0475 |
| 0.480 |
0.8515 |
0.0290 |
−11.0149 |
| 0.485 |
1.0097 |
0.0396 |
−10.9808 |
| 0.490 |
1.1820 |
0.0531 |
−10.9450 |
| 0.495 |
1.3691 |
0.0700 |
−10.9071 |
| 0.500 |
1.5719 |
0.0912 |
−10.8665 |
| 0.505 |
1.7912 |
0.1177 |
−10.8223 |
| 0.510 |
2.0279 |
0.1507 |
−10.7733 |
| 0.515 |
2.2830 |
0.1919 |
−10.7179 |
| 0.520 |
2.5578 |
0.2433 |
−10.6532 |
| 0.525 |
2.8534 |
0.3078 |
−10.5755 |
| 0.530 |
3.1712 |
0.3889 |
−10.4796 |
| 0.535 |
3.5128 |
0.4913 |
−10.3586 |
| 0.540 |
3.8797 |
0.6188 |
−10.2043 |
| 0.545 |
4.2737 |
0.7863 |
−10.0076 |
| 0.550 |
4.6967 |
0.9973 |
−9.7610 |
| 0.555 |
5.1506 |
1.2678 |
−9.4579 |
| 0.560 |
5.6376 |
1.6155 |
−9.0932 |
| 0.565 |
6.1600 |
2.0632 |
−8.6602 |
| 0.570 |
6.7201 |
2.6403 |
−8.1497 |
| 0.575 |
7.3206 |
3.3851 |
−7.5473 |
| 0.580 |
7.9640 |
4.3449 |
−6.8333 |
| 0.585 |
8.6527 |
5.5653 |
−5.9875 |
| 0.590 |
9.3905 |
7.1086 |
−4.9817 |
| 0.595 |
10.1801 |
9.1287 |
−3.7496 |
| 0.600 |
11.0249 |
11.6169 |
−2.2904 |
| 0.605 |
11.9285 |
14.7202 |
−0.5395 |
| 0.610 |
12.8946 |
18.5606 |
1.5582 |
| 0.61095 |
13.0856 |
19.3847 |
2.0000 |
| 0.612 |
13.2995 |
20.3337 |
2.5082 |
| 0.614 |
13.7153 |
22.2559 |
3.5276 |
| 0.616 |
14.1423 |
24.3369 |
4.6210 |
| 0.618 |
14.5808 |
26.5866 |
5.7927 |
| 0.620 |
15.0311 |
29.0162 |
7.0477 |
| 0.622 |
15.4950 |
31.5123 |
8.3384 |
| 0.624 |
15.9719 |
34.1660 |
9.7036 |
| 0.626 |
16.4613 |
37.0685 |
11.1821 |
| 0.628 |
16.9628 |
40.3109 |
12.8128 |
| 0.630 |
17.4782 |
43.7995 |
14.5565 |
| 0.640 |
20.2701 |
65.4251 |
25.1874 |
3. Effects of hydrostatic compression
Throughout the ECNLE development journey, various strategies have been proposed to associate conceptual hard-sphere fluids with actual glass-forming liquids. Schweizer et al.86 suggested that the ϕ–T relation at zero pressure would be well-quantified by combining theoretical and experimental data for the low-wavevector part of the static structure factor. This pioneering idea was proven to be effective in explaining the glassy dynamics of alkali metals, rare gases, sugar alcohols, nonpolar molecules, and vdW polymers.86,89 Unfortunately, it is very challenging to apply the quasi-universal approach of Schweizer et al.86 to amorphous pharmaceuticals due to the scarcity of equation-of-state data. To address this issue, Phan et al.87 built another chemical mapping from the volumetric expansion of glass formers during isobaric heating. They succeeded in capturing the zero-pressure structural relaxation of unary, binary, and ternary drugs without fitting parameters.87 Inspired by the works of Phan et al.,87 Cuong et al.100 continued to extend the ECNLE model to the high-pressure regime. The chemical mapping of Cuong et al.100 was written by| | |
ϕ = ϕ0βT(Tg − T) + ϕg,
| (8) |
where the initial packing fraction ϕ0 was selected as 0.5 to reproduce the ECNLE outputs of Schweizer et al. for some typical thermal liquids.88 For convenience, Cuong et al.100 expressed the thermal expansivity βT and the glass transition temperature Tg by| |
 | (9) |
| |
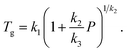 | (10) |
Whereas β0 = 12 × 10−4 K−1 was supposed to be constant for all materials,91–93 the Andersson–Andersson parameters k1, k2, and k3 reflected the distinctive nature of molecular bonds in the disordered state.112 In contrast to S(k), it is easy to look k1, k2, and k3 up in available BDS reports on compressed amorphous drugs.53–55 Hence, Cuong et al.100 successfully calculated the structural relaxation time of indomethacin along different isobars at breakneck speed.
In spite of the mentioned advantages, the macroscopic approach of Cuong et al.100 still suffers from some problems. First, the physical picture behind eqn (9) is unclear. Eqn (9) is only based on the fact that the thermal expansivity and the hydrostatic pressure have a negative correlation.113 We cannot naturally explain why the Andersson–Andersson parameters112 appear in this formula. Second, although a good agreement between theory and experiment is achieved for τα, the chemical mapping of Cuong et al.100 is not strong enough to describe the variation of m at the quantitative level. Take indomethacin as an example. At 0.1 MPa, ECNLE analyses100 give m = 90.1, quite close to m = 82.8 obtained from BDS measurements.114 However, the higher the pressure, the larger the error. At 226 MPa, the ECNLE fragility is about 66.2,100 significantly lower than the BDS counterpart of 75.2.114 The underestimation of m is most likely a consequence of oversimplifying the βT–P–Tg relation.
Herein, we remove these difficulties to gain a better description of supercooled drugs during squeezing. Our key idea is to improve eqn (9) by combining typical expansion techniques in condensed matter physics. Specifically, we begin with the following thermodynamic definition of the thermal expansivity,
| |
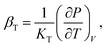 | (11) |
where
V is the molecular volume, and
KT is the isothermal bulk modulus. According to Murnaghan,
115 it is possible to quantify the pressure dependence of
KT via| |
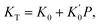 | (12) |
where
K0 and

are the magnitude and derivative of
KT at 0 MPa.
Eqn (12) works best in a compression range 0 ≤
P ≤
PMur ≈ 2
K0.
116 Recent experimental evidence shows that
PMur is in the order of several GPa.
117–119 Meanwhile, the actual production of amorphous drugs is frequently performed at
P < 1 GPa.
51 Thus, the Murnaghan approximation
115 is highly suitable for our study.
Next, we focus on (∂P/∂T)V. In the famed Einstein picture of molecular vibrations, the contribution of thermal excitations to the hydrostatic pressure can be evaluated by120
| |
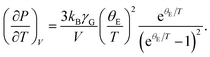 | (13) |
where
θE is the Einstein temperature, and
γG is the Gruneisen parameter. Recall that supercooled liquids primarily exist in a high-temperature region
Tg ≤
T ≤
Tm, where
Tm ≈ 1.362
Tg is the melting point.
93 Previous shock-wave experiments
121 and thermodynamic calculations
122 suggested that
γG would be proportional to
V under these conditions. Moreover, since the studied
T value is far above
θE, we can replace e
θE/T with 1 +
θE/
T. As a result,
eqn (13) is simplified by
| |
 | (14) |
Entering
eqn (12) and
(14) into
eqn (11) provides
| |
 | (15) |
Eqn (15) highlights a close correlation between thermodynamic and mechanical quantities in the supercooled state.
Fascinatingly, we can also connect the elastic responses of materials with their glass-transition behaviors via ECNLE analyses in the ultra-local limit.123 Utilizing the Green–Kubo formula124 for the shear modulus G yields
| |
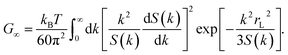 | (16) |
In the high-density regime, because the localization length is much shorter than the particle diameter, the main contributors to instantaneous rigidity are wavevectors with magnitudes larger than π/
σ.
123 This insight enables us to compact
eqn (16) by
| |
 | (17) |
where
Gg and
Vg are the critical values of
G and
V at
Tg, respectively. Our numerical calculations with
τα(
ϕg) = 100 s reveal that
Cg = 1015.6625
kB is a universal constant for all soft-matter systems. This finding is supported by the recent statistics of Shi
et al.125 on metallic glasses.
Eqn (17) can be seen as another definition of kinetic vitrification in the framework of the ECNLE theory. Relying on eqn (17), we can elucidate how the glass transition temperature depends on the hydrostatic pressure via available information about elastic moduli. Indeed, as indicated by Guinan and Steinberg,126 the Gg–P relation can be well described by
| |
 | (18) |
This simple formula is designed to reproduce the Thomas–Fermi picture of shear deformation in the
Vg → 0 limit.
127 Since the Poisson ratio of pharmaceuticals varies slowly during compression,
128 eqn (18) can be rewritten by
| |
 | (19) |
Besides, by integrating
eqn (12), we have
| |
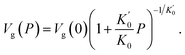 | (20) |
Inserting
eqn (19) and
(20) into
eqn (17) brings
| |
 | (21) |
Now, we can effortlessly associate volumetric dilation with kinetic vitrification. Namely, if the applied pressure is sufficiently low, eqn (21) will be equivalent to
| |
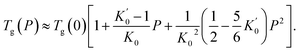 | (22) |
In addition, employing the Taylor expansion
129 to
eqn (10) leads to
| |
 | (23) |
By equating the coefficients of
eqn (22) and
(23), we obtain
| |
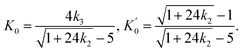 | (24) |
Continuing to combine
eqn (15) and
(24) gives us
| |
 | (25) |
Unlike
eqn (9) and
(25) possesses a solid theoretical background. That is why it can effectively characterize the degree of
βT reduction, as demonstrated in the case of ibuprofen
130 (see
Fig. 2). Furthermore, applying
eqn (25) to practical situations is very convenient thanks to the high availability of Andersson–Andersson parameters.
53–55 For the reasons above, we view it as one of the most crucial factors in deciphering the molecular dynamics of amorphous drugs
via ECNLE calculations.
 |
| | Fig. 2 (Color online) Illustrating the usefulness of eqn (25) in describing the decline of βT. Ibuprofen is selected as a case study with k1 = 234.7 K, k2 = 3.84, and k3 = 970.76 MPa. PVT measurements in ref. 130 are adopted as a benchmark for ECNLE analyses. | |
To further clarify the quality of our chemical mapping [eqn (8), (10), and (25)], we carry out numerical calculations for nine representative active pharmaceutical ingredients, including ketoprofen, probucol, ketoconazole, indomethacin, ticagrelor, fenofibrate, itraconazole, glibenclamide, and ibuprofen. Their Andersson–Andersson parameters are directly deduced from prior BDS measurements114,130–137 and systematically presented in Table 2. More information about them can be found in Section S1 of the ESI.† It should be noted that the glass transition of soft materials is not always defined at τα = 102 s. In some circumstances, experimentalists can determine Tg at a smaller timescale to avoid long extrapolations.135–138 Therefore, depending on the specific BDS definition of Tg, we infer the corresponding value of ϕg from interpolating ECNLE data in Table 1. This treatment ensures a direct comparison between theory and experiment. We also report the critical slope of the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τα plot at ϕg to facilitate the later analyses of the dynamic fragility.
τα plot at ϕg to facilitate the later analyses of the dynamic fragility.
Table 2 Experimental inputs to our newly developed chemical mapping. Here, k1 is in Kelvin, k3 is in megapascal, and τα is in second
| Drug |
k1 |
k2 |
k3 |
τα(Tg) |
ϕg |

|
Reference |
| Ketoprofen |
266.50 |
2.62 |
1344.32 |
100 |
0.61095 |
474.314 |
131 |
| Probucol |
293.80 |
2.08 |
672.32 |
100 |
0.61095 |
474.314 |
132 |
| Ketoconazole |
314.00 |
2.31 |
1366.51 |
100 |
0.61095 |
474.314 |
133 |
| Indomethacin |
315.00 |
3.14 |
1238.00 |
100 |
0.61095 |
474.314 |
114 |
| Ticagrelor |
319.00 |
2.31 |
1954.08 |
100 |
0.61095 |
474.314 |
134 |
| Fenofibrate |
253.60 |
2.46 |
1102.99 |
10 |
0.60875 |
436.008 |
135 |
| Itraconazole |
332.10 |
1.07 |
1743.06 |
1 |
0.60636 |
403.537 |
136 |
| Glibenclamide |
344.36 |
3.86 |
1382.00 |
1 |
0.60636 |
403.537 |
137 |
| Ibuprofen |
234.70 |
3.84 |
970.76 |
0.1 |
0.60377 |
366.294 |
130 |
Fig. 3 shows the structural relaxation time of the selected pharmaceutical systems under various thermodynamic conditions. It is conspicuous that our macroscopic approach helps regenerate most existing experimental data114,131–136,138 without great computational efforts. For a given drug, we only need to spend a few minutes on our personal computer to quantitatively understand the dramatic slowing down of molecular dynamics during isobaric cooling or isothermal squeezing. In particular, no fitting procedures are required to achieve consistency between ECNLE calculations and BDS experiments from microsecond to hectosecond domains. These outstanding advantages distinguish our theory from other methods like EAGM66 or MD.79 Further insights into non-exponential growth in τα are provided in Section S2 of the ESI.†
 |
| | Fig. 3 (Color online) The influences of temperature and pressure on the structural relaxation time of the chosen supercooled drugs: (a) ketoprofen, (b) probucol, (c) ketoconazole, (d) indomethacin, (e) ticagrelor, (f) fenofibrate, (g) itraconazole, (h) glibenclamide, and (i) ibuprofen. While solid lines present our ECNLE calculations, open circles denote prior BDS experiments.114,131–138 | |
Among the studied glass-forming liquids, only glibenclamide presents a marked discrepancy between theoretical and experimental results137 in the supercooled state. From our perspective, this deviation may stem from the effects of tautomerism. It is well-known that glibenclamide samples in practice often contain two tautomeric forms called amide and imidic acid.137 Each tautomer possesses unique physical characteristics, and the tautomer concentration varies with temperature, pressure, and time.139–141 This complexity may result in a non-universal coupling between local and collective dynamics in eqn (7).99 Hence, the reference system and the chemical mapping should be simultaneously improved if we want to capture the structural relaxation of glibenclamide at the quantitative level.
Fig. 4 presents our ECNLE outputs for the dynamic fragility of the chosen glass formers. Fundamentally, this quantity is computed by142
| |
 | (26) |
Eqn (26) confirms a strong connection between
m and
βT, in line with recent experimental observations.
143–147 It also unveils why earlier theoretical studies failed to predict the pressure variation of
m, even at the qualitative level. In ref.
95, researchers only focused on modeling the dynamic free energy of hard-sphere fluids and completely ignored the pressure dependence of
βT. Consequently, they observed a profound contradiction between theory and experiment in
m–
P profiles, although their estimations for
τα in the high-pressure area were quite good.
95
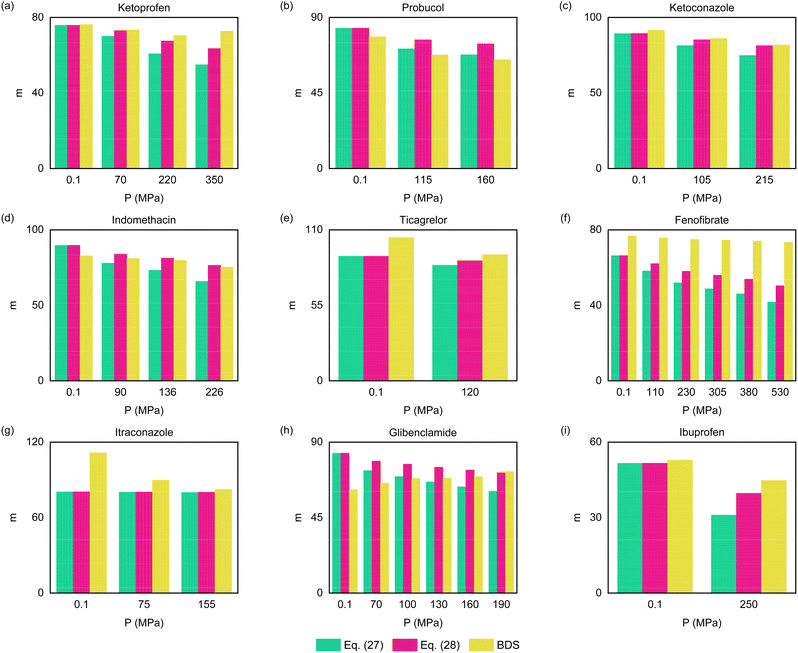 |
| | Fig. 4 (Color online) The correlation between the dynamic fragility and the hydrostatic pressure in the case of (a) ketoprofen, (b) probucol, (c) ketoconazole, (d) indomethacin, (e) ticagrelor, (f) fenofibrate, (g) itraconazole, (h) glibenclamide, and (i) ibuprofen. Whereas green columns are built from eqn (27), pink ones are constructed from eqn (28). Yellow columns indicate BDS data gathered from Ref. 114 and 131–138 (see Table S1 in the ESI†). | |
To further illuminate the underlying correlation between m and P, we rewrite eqn (26) by
| |
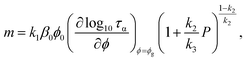 | (27) |
| |
 | (28) |
Whereas
eqn (27) originates from the chemical mapping of Cuong
et al.,
100 eqn (28) stems from our macroscopic approach. Both show a continuous decrease in
m with increasing
P. This tendency is true for the vast majority of amorphous drugs
114,131–136,138 except for glibenclamide,
137 where compression forces may significantly change the tautomeric equilibrium and cause the sample to be more fragile. Yet, it is clear to see that
eqn (28) outperforms
eqn (27) in predicting the magnitude of
m. Replacing
eqn (27) with
(28) can narrow the gap between ECNLE analyses and BDS measurements by a factor of 1.1 to 16.0 while preserving the required computational efficiency. It should be stressed that accurate information about
m is indispensable for controlling the crystallization tendency of pharmaceuticals.
51 Based on the specific value of
m, we can divide amorphous drugs into three principal groups: strong (
m ≤ 30), intermediate (30 <
m < 100), and fragile (
m ≥ 100).
142 Modern experiments and simulations suggest that the smaller the fragility, the greater the stability.
96–98 In that context, our simple but effective toolkit would be practically meaningful for developing tableting processes, where relevant glass-forming systems are often compressed to hundreds of megapascals and forced to undergo dramatic changes in dynamic fragility.
36
Another appealing aspect to discuss is that the difference between ECNLE and BDS data remains relatively large for fenofibrate135 despite a substantial improvement in the chemical mapping of this substance. At P = 530 MPa, we obtain m = 41.75 from eqn (27) and m = 50.32 from eqn (28). Meanwhile, using the BDS technique brings m = 73.3.135 In our opinion, there are two primary reasons behind this problem.
First, accurately determining the dynamic fragility of soft materials is a daunting task for experimentalists.93 The evidence is that the reported experimental results for m are frequently accompanied by enormous error bars due to the non-Arrhenius nature of supercooled liquids.131,137 Moreover, this physical quantity will experience a sharp fluctuation if experimentalists apply different fitting methods to analyze their dataset.135 In the case of fenofibrate, the measured value of m ranges from 76 to 94, even when the applied pressure is merely about 0.1 MPa.148–151 More efforts are necessary to deal with the mentioned predicament.
Second, the hydrogen-bond network of fenofibrate may strongly affect its glassy dynamics.135 As shown by Grzybowska et al.,51 whereas vdW interactions favor the decline of m,152 hydrogen bonds do the opposite.153 That means we should concurrently combine microscopic and macroscopic ECNLE approaches to acquire better predictions of fenofibrate. The combination is expected to occur as follows. If the intermolecular potential of fenofibrate is known, we can derive its radial distribution function and static structure factor from the standard reference interaction site model.154–156 Then, it is possible to recalculate local and collective barriers via the projectionless dynamics theory.157–159 The last step is to add P–T contributions to ECNLE outputs via our newly developed chemical mapping. We believe this is one of the most viable strategies for capturing molecular dynamics in amorphous fenofibrate on the theoretical side. Nevertheless, it would involve a lot of sophisticated computational techniques. Thus, this fascinating subject deserves consideration in a separate ECNLE study.
After obtaining encouraging outcomes for single-component amorphous drugs, a natural question arises: Is our ECNLE theory applicable to more complex pharmaceutical systems? To answer this question, we perform additional calculations for three homogenous solid dispersions constituted of probucol and acetylated saccharide with a molar ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, including PRO-acGLU (k1 = 292.71 K, k2 = 2.99, k3 = 709.81 MPa), PRO-acSUC (k1 = 294.72 K, k2 = 1.97, k3 = 774.68 MPa), and PRO-aibSUC (k1 = 289.43 K, k2 = 1.95, k3 = 744.25 MPa).160,161 The glass transition of these binary mixtures is supposed to happen at ϕg = 0.61095, similar to pure probucol.132 As illustrated in Fig. 5, our theoretical model can quantitatively explain experimental observations160 on the glassy dynamics of PRO-acGLU, PRO-acSUC, and PRO-aibSUC without heavy computational workloads. Regarding the structural relaxation time, ECNLE curves pass through most BDS benchmarks160 regardless of low or high pressures. Regarding the dynamic fragility, the maximum error between eqn (28) and BDS data160 is 2.24% for PRO-acGLU, 9.75% for PRO-acSUC, and 13.57% for PRO-aibSUC. These figures are experimentally acceptable because m is considered the most sensitive quantity in soft-matter physics.93 It is more remarkable that the above agreements do not involve any adjustable parameters. Therefore, our ECNLE theory has great potential for decoding the mystery of multi-component amorphous drugs and extending their practical applicability to health protection and promotion.
1, including PRO-acGLU (k1 = 292.71 K, k2 = 2.99, k3 = 709.81 MPa), PRO-acSUC (k1 = 294.72 K, k2 = 1.97, k3 = 774.68 MPa), and PRO-aibSUC (k1 = 289.43 K, k2 = 1.95, k3 = 744.25 MPa).160,161 The glass transition of these binary mixtures is supposed to happen at ϕg = 0.61095, similar to pure probucol.132 As illustrated in Fig. 5, our theoretical model can quantitatively explain experimental observations160 on the glassy dynamics of PRO-acGLU, PRO-acSUC, and PRO-aibSUC without heavy computational workloads. Regarding the structural relaxation time, ECNLE curves pass through most BDS benchmarks160 regardless of low or high pressures. Regarding the dynamic fragility, the maximum error between eqn (28) and BDS data160 is 2.24% for PRO-acGLU, 9.75% for PRO-acSUC, and 13.57% for PRO-aibSUC. These figures are experimentally acceptable because m is considered the most sensitive quantity in soft-matter physics.93 It is more remarkable that the above agreements do not involve any adjustable parameters. Therefore, our ECNLE theory has great potential for decoding the mystery of multi-component amorphous drugs and extending their practical applicability to health protection and promotion.
 |
| | Fig. 5 (Color online) The first row: ECNLE analyses (solid lines) and BDS measurements160 (open circles) for the structural relaxation time of probucol-based mixtures, including (a) PRO-acGLU, (b) PRO-acSUC, and (c) PRO-aibSUC. The second row: compression effects on the dynamic fragility of (d) PRO-acGLU, (e) PRO-acSUC, and (f) PRO-aibSUC obtained from the previous chemical mapping (green columns), the present macroscopic approach (pink columns), and the BDS experimental method160 (yellow columns). | |
4. Effects of kinetic vitrification
Having successfully explored the high-pressure region, we turn our attention to the low-temperature area. It is well known that the V–T line exhibits an abrupt change in its average steepness at the glass transition point.52 This event implies that we should replace βT with βT − ΔβT in our chemical mapping to appropriately describe the molecular mobility of amorphous drugs at T < Tg. The key parameter here is ΔβT, which characterizes the influences of kinetic vitrification on thermal expansion (ΔβT > 0). So, how is ΔβT determined? The answer lies in a similarity between vitrified and dislocated materials.
A substantial body of evidence shows that crystals tend to behave like glasses when line defects appear in their lattice structures.162–164 For example, Bako et al.165 observed the aging phenomenon – a hallmark of glassy dynamics – in the correlation function and the diffusion coefficient of dislocations via mesoscale simulations. Based on local mechanical perturbation experiments, Gerbode et al.166 found that the relaxation of dislocations in degenerate crystals would undergo two stages – caging and hopping – similar to what happens in glass-forming liquids. A remarkable analogy between defective and glassy dynamics was also recorded in the recent studies of Ispanovity et al.,167 Lehtinen et al.,168 and Ovaska et al.169 on the plastic deformation of crystalline solids in two- and three-dimensional spaces. In particular, Burakovsky et al.170–172 discovered that the melting process of elements could be seen as a defect-meditated structural transformation, where half of the particles were in a dislocation core. This discovery gave them170–172
| |
 | (29) |
where
Cm was a universal constant,
Gm was the shear modulus, and
Vm was the molecular volume at the melting temperature
Tm. Excitingly, the Burakovsky criterion
170–172 for melting transition is identical to our ECNLE criterion for glass transition, even though they have different theoretical backgrounds. The perfect symmetry between
eqn (17) and
(29) reaffirms that vitrified and dislocated materials are strongly correlated. Hence, we can utilize available knowledge of line defects in crystallography to address thorny issues about amorphous drugs in the field of soft matter.
To be more specific, we consider a faulty crystal with physical properties summarized in Fig. 6. Initially, our system exists at the Kauzmann point (VK, TK), where the V–T profiles of solid and liquid phases cross each other.173 Then, it is isobarically heated to the critical location (Vm, Tm) on the V–T diagram. This thermodynamic path is modeled by
| | |
Vm = VK[1 + βm(Tm − TK)],
| (30) |
where
βm is the volumetric expansivity of the crystalline phase. If we continue to supply thermal energy to the sample, it will be liquified. This process is characterized by the fusion volume Δ
Vm and the fusion enthalpy Δ
Hm. These quantities are closely related, as shown by the Clausius–Clapeyron formula,
174,175| |
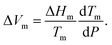 | (31) |
Besides, the liquefaction of lattice spaces is mainly driven by the proliferation of dislocations, so the latent heat of fusion can be straightforwardly estimated
via the enthalpy of defect formation as
170–172| |
 | (32) |
Another thing to note is that the thermal expansion coefficient climbs from
βm to
βm + Δ
βm upon melting. Thus, we have
| | |
Vm + ΔVm = VK[1 + (βm + Δβm)(Tm − TK)].
| (33) |
Combining
eqn (30)–(33) yields
| |
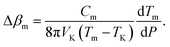 | (34) |
 |
| | Fig. 6 (Color online) The phase diagram of the defective structure used to calculate ΔβT. | |
Relying on the resemblance between melting and glass transitions mentioned earlier, we can expect that Δβm and ΔβT have the same analytical form. Accordingly, when returning to amorphous pharmaceuticals, we obtain.
| |
 | (35) |
It is easy to see from
eqn (8) that
TK is associated with
Tg via| |
 | (36) |
where
ϕK = 0.67233 is determined by parameterizing ECNLE data for
τα in
Table 1 with the Vogel–Fulcher–Tammann function
176 at
ϕ > 0.55. Inserting
eqn (36) into
(35) provides
| |
 | (37) |
Eqn (37) takes a central position in accessing the glassy state
via the ECNLE theory. In the
P → 0 limit, its mathematical expression is simplified by
| |
 | (38) |
To save time and cost, we can approximate
VK as the measured volume of the crystalline phase. The error of this approximation is only a few percent because the thermal expansivity of crystals is quite low
177 (
βm = 10
−6–10
−4 K
−1) and the Kauzmann temperature
178 (
TK = 100–600 K) is not too far from the reported temperature in crystallographic
179 (
T = 100–400 K).
To demonstrate how well our strategy works, we apply eqn (38) to carvedilol (Tg = 310 K), nimesulide (Tg = 291 K), paracetamol (Tg = 297 K), and probucol (Tg = 293.8 K), whose α-relaxation behaviors were unambiguously reported at low temperatures. Their volume can be readily found in the Cambridge Structural Database.179 Note that the parameter VK is affected by polymorphic effects. Based on the melting point reported in the ESI,† we determine VK using nimesulide form I,180 paracetamol form II,181 and probucol form I.182 For carvedilol, we do not know which polymorph was amorphized in earlier BDS experiments.51 Yet, since the VK value of carvedilol weakly depends on its polymorphism,183 we employ form II to construct the chemical mapping. This crystalline structure is widely used in marketed formulations due to its faster dissolution at bio-relevant pH levels.184
In addition, it is practicable to directly extract the initial gradient of glass-liquid boundaries from prior BDS or PVT measurements.132,185,186 For paracetamol, because information about glassy dynamics at elevated pressures is unavailable, we employ the non-equilibrium thermodynamic approximation of Lima et al.187 to the differential-scanning calorimetry data of Ledru et al.188 to infer dTg/dP from dTm/dP. All experimental inputs we require are detailed in Table 3. On that basis, we figure out ΔβT = 4.1232 × 10−4 K−1 for carvedilol, ΔβT = 4.9154 × 10−4 K−1 for nimesulide, ΔβT = 8.7268 × 10−4 K−1 for paracetamol, and ΔβT = 7.7028 × 10−4 K−1 for probucol. These numbers are in good accordance with recent experiments on the equation of state of glass-forming drugs.185
Table 3 The molecular volume and the glass-transition slope of the investigated active pharmaceutical ingredients
| Drug |
VK (Å3) |
dTg/dP (K MPa−1) |
Reference |
| Carvedilol |
2116.8 |
0.16 |
183 and 185 |
| Nimesulide |
2663.4 |
0.24 |
180 and 186 |
| Paracetamol |
1500.2 |
0.24 |
181, 187 and 188 |
| Probucol |
3116.0 |
0.44 |
132 and 182 |
Fig. 7 shows finite-temperature effects on the structural relaxation time of carvedilol and nimesulide. Generally, there is a sudden switch in their molecular dynamics from super-Arrhenius to Arrhenius-like types near the vitrification point. This strange event is called dynamic decoupling – one of the most elusive phenomena in soft-matter physics.189 However, our ECNLE theory can reliably predict complex changes in relaxation maps by updating the chemical mapping with eqn (37) and (38). It is conspicuous that ECNLE calculations perfectly match BDS measurements51,190 in the supercooled region. After adding ΔβT to βT, they can even reproduce MPC results51,190 in the glassy area with considerable accuracy. As far as we know, no theoretical or computational methods can satisfactorily explain the primary relaxation of carvedilol and nimesulide from picosecond to terasecond timescales without fitting parameters, except for the ECNLE. These positive outcomes validate the effectiveness of our strategy.
 |
| | Fig. 7 (Color online) (a) ECNLE and BDS/MPC51 predictions of the α relaxation map of carvedilol in supercooled and vitrified states. (b) The structural relaxation time of nimesulide above and below its glass transition temperature derived from ECNLE and BDS/MPC190 methods. | |
Notably, before introducing a new medicine to the market, one has to check whether its relaxation time exceeds three years under ambient conditions (P = 0.1 MPa and T = 293 K).36 This number is the minimum self-lifetime needed for commercial pharmaceutical products. As illustrated in Fig. 7, none of the studied amorphous drugs meet the above requirement because of the decoupling phenomenon. If we ignore the jump of thermal expansivity near the glass transition, we will overestimate τα by several orders of magnitude and misjudge the practical applicability of carvedilol and nimesulide. More attempts are necessitated to reinforce their physical stability before commercialization. Using polymeric precipitation inhibitors (e.g., cellulose191 or polyvinylpyrrolidone190) may be a fruitful avenue for actualizing the potential of amorphous carvedilol and nimesulide in disease prevention and treatment.
Fig. 8 presents the α relaxation map of paracetamol and probucol. Fundamentally, our ECNLE theory still works very well. All BDS and MPC information132,192,193 is quantitatively decoded regardless of high or low temperatures. In particular, the structural relaxation time τα of paracetamol can be utilized to predict its recrystallization time τcr via194
| |
 | (39) |
At
Tg/
T = 1.0683, recent differential-scanning-calorimetry measurements
194 reveal that amorphous paracetamol samples would recrystallize after 2319 h, comparable to
τcr = 3654 h deduced from ECNLE analyses in the glassy state. This emphasizes the pivotal role of α processes in controlling the physical stability of glass-forming drugs.
 |
| | Fig. 8 (Color online) (a) Theoretical and experimental193,194 outcomes for the structural relaxation process of paracetamol in the amorphous form. (b) Calculated and measured132,192,195 data for the primary relaxation time of probucol after amorphization. | |
Another aspect worth mentioning is that ECNLE calculations markedly differ from aging experiments.194,195 At Tg/T = 1.0255, aging data for probucol is τα = 0.81 h,195 about fivefold longer than the ECNLE counterpart (τα = 0.16 h). That is because we neglect the time dependence of ΔβT. After passing through the vitrification point, the thermal expansivity of amorphous pharmaceuticals abruptly drops from βT to βT − ΔβT.52 Nevertheless, this physical quantity tends to return to its original value during aging.196 In other words, the older the sample gets, the weaker the decoupling becomes. Although the above principle sounds very simple, dealing with aging-related problems is a major challenge for physicists.197–200 One of the most prominent reasons is that aging effects can significantly delay the decoupling event. As shown in the case of paracetamol, old systems begin exhibiting Arrhenius-like behaviors at τα = 1.83 h,194 much later than the commencement of dynamic decoupling in fresh samples (τα = 0.03 h). What is the underlying mechanism behind this enigmatic phenomenon? How do we locate the decoupling position of amorphous drugs on the relaxation diagram over time? Are dislocation glasses the key we are looking for? These intriguing questions will be the subject of ECNLE research in the future.
5. Conclusion
Inspired by the ECNLE theory, we have formulated a time-saving, cost-effective, and user-friendly macroscopic approach to shed light on the influences of hydrostatic compression and kinetic vitrification on the molecular dynamics of amorphous drugs. This free-of-adjustable-parameter method has helped us decipher most BDS and MPC observations on α relaxation processes without computational burdens. Additionally, our ECNLE calculations have unveiled some interesting relations between thermodynamic and elastic properties, between melting and glass transitions, and between crystalline and non-crystalline solids. To facilitate further projects, we have presented all physical pictures, computational steps, and numerical results as clearly as possible. Some viable ideas to extend our theoretical model have also been given. Therefore, we are eager to witness new scientific advances in amorphous drugs in the foreseeable future.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper.
Author contributions
Tran Dinh Cuong: conceptualization, methodology, investigation, writing – original draft, writing – review & editing, visualization. Anh D. Phan: resources, supervision.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This research was funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant No. 103.01-2023.62.
References
- M. A. Spyrou, K. I. Bos, A. Herbig and J. Krause, Ancient pathogen genomics as an emerging tool for infectious disease research, Nat. Rev. Genet., 2019, 20, 323 CrossRef CAS PubMed.
- N. Rascovan, K. G. Sjogren, K. Kristiansen, R. Nielsen, E. Willerslev, C. Desnues and S. Rasmussen, Emergence and spread of basal lineages of Yersinia pestis during the Neolithic decline, Cell, 2019, 176, 295 CrossRef CAS PubMed.
- F. Maixner, B. Krause-Kyora, D. Turaev, A. Herbig, M. R. Hoopmann, J. L. Hallows, U. Kusebauch, E. E. Vigl, P. Malfertheiner, F. Megraud, N. O'Sullivan, G. Cipollini, V. Coia, M. Samadelli, L. Engstrand, B. Linz, R. L. Moritz, R. Grimm, J. Krause and A. Nebel, et al., The 5300-year-old Helicobacter pylori genome of the Iceman, Science, 2016, 351, 162 CrossRef CAS PubMed.
- B. Muhlemann, T. C. Jones, P. D. B. Damgaard, M. E. Allentoft, I. Shevnina, A. Logvin, E. Usmanova, I. P. Panyushkina, B. Boldgiv, T. Bazartseren, K. Tashbaeva, V. Merz, N. Lau, V. Smrcka, D. Voyakin, E. Kitov, A. Epimakhov, D. Pokutta, M. Vicze and T. D. Price, et al., Ancient hepatitis B viruses from the Bronze Age to the Medieval period, Nature, 2018, 557, 418 CrossRef CAS PubMed.
- B. Muhlemann, A. Margaryan, P. D. B. Damgaard, M. E. Allentoft, L. Vinner, A. J. Hansen, A. Weber, V. I. Bazaliiskii, M. Molak, J. Arneborg, W. Bogdanowicz, C. Falys, M. Sablin, V. Smrcka, S. Sten, K. Tashbaeva, N. Lynnerup, M. Sikora, D. J. Smith and R. A. M. Fouchier, et al., Ancient human parvovirus B19 in Eurasia reveals its long-term association with humans, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7557 CrossRef CAS PubMed.
- D. M. Wagner, J. Klunk, M. Harbeck, A. Devault, N. Waglechner, J. W. Sahl, J. Enk, D. N. Birdsell, M. Kuch, C. Lumibao, D. Poinar, T. Pearson, M. Fourment, B. Golding, J. M. Riehm, D. J. D. Earn, S. DeWitte, J. M. Rouillard, G. Grupe and I. Wiechmann, et al., Yersinia pestis and the plague of Justinian 541–543 AD: A genomic analysis, Lancet Infect. Dis., 2014, 14, 319 CrossRef PubMed.
- M. A. Spyrou, L. Musralina, G. A. G. Ruscone, A. Kocher, P. G. Borbone, V. I. Khartanovich, A. Buzhilova, L. Djansugurova, K. I. Bos, D. Kuhnert, W. Haak, P. Slavin and J. Krause, The source of the Black Death in fourteenth-century central Eurasia, Nature, 2022, 606, 718 CrossRef CAS PubMed.
- M. Worobey, T. D. Watts, R. A. McKay, M. A. Suchard, T. Granade, D. E. Teuwen, B. A. Koblin, W. Heneine, P. Lemey and H. W. Jaffe, 1970s and ‘Patient 0’ HIV-1 genomes illuminate early HIV/AIDS history in North America, Nature, 2016, 539, 98 CrossRef CAS.
- E. C. Holmes, G. Dudas, A. Rambaut and K. G. Andersen, The evolution of Ebola virus: Insights from the 2013–2016 epidemic, Nature, 2016, 538, 193 CrossRef CAS PubMed.
- J. Li, S. Lai, G. F. Gao and W. Shi, The emergence, genomic diversity and global spread of SARS-CoV-2, Nature, 2021, 600, 408 CrossRef CAS PubMed.
- P. Piot, M. Bartos, P. D. Ghys, N. Walker and B. Schwartlander, The global impact of HIV/AIDS, Nature, 2001, 410, 968 CrossRef CAS PubMed.
- W. Msemburi, A. Karlinsky, V. Knutson, S. Aleshin-Guendel, S. Chatterji and J. Wakefield, The WHO estimates of excess mortality associated with the COVID-19 pandemic, Nature, 2023, 613, 130 CrossRef CAS PubMed.
- L. Li, A. Taeihagh and S. Y. Tan, A scoping review of the impacts of COVID-19 physical distancing measures on vulnerable population groups, Nat. Commun., 2023, 14, 599 CrossRef CAS PubMed.
- X. Lin, Y. Xu, X. Pan, J. Xu, Y. Ding, X. Sun, X. Song, Y. Ren and P. F. Shan, Global, regional, and national burden and trend of diabetes in 195 countries and territories: An analysis from 1990 to 2025, Sci. Rep., 2020, 10, 14790 CrossRef CAS PubMed.
- G. A. Roth, G. A. Mensah, C. O. Johnson, G. Addolorato, E. Ammirati, L. M. Baddour, N. C. Barengo, A. Z. Beaton, E. J. Benjamin, C. P. Benziger, A. Bonny, M. Brauer, M. Brodmann, T. J. Cahill, J. Carapetis, A. L. Catapano, S. S. Chugh, L. T. Cooper, J. Coresh and M. Criqui, et al., Global burden of cardiovascular diseases and risk factors, 1990–2019: Update from the GBD 2019 study, J. Am. Coll. Cardiol., 2020, 76, 2982 CrossRef PubMed.
- A. Leiter, R. R. Veluswamy and J. P. Wisnivesky, The global burden of lung cancer: Current status and future trends, Nat. Rev. Clin. Oncol., 2023, 20, 624 CrossRef PubMed.
- World Health Organization, Cardiovascular diseases (CVDs), https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds), accessed May 7, 2024.
- S. Mendis and V. Fuster, National policies and strategies for noncommunicable diseases, Nat. Rev. Cardiol., 2009, 6, 723 CrossRef PubMed.
- M. Ezzati, J. Pearson-Stuttard, J. E. Bennett and C. D. Mathers, Acting on non-communicable diseases in low- and middle-income tropical countries, Nature, 2018, 559, 507 CrossRef CAS.
- J. L. Excler, M. Saville, S. Berkley and J. H. Kim, Vaccine development for emerging infectious diseases, Nat. Med., 2021, 27, 591 CrossRef CAS PubMed.
- A. G. Atanasov, S. B. Zotchev, V. M. Dirsch, International Natural Product Sciences Taskforce and C. T. Supuran, Natural products in drug discovery: Advances and opportunities, Nat. Rev. Drug Discovery, 2021, 20, 200 CrossRef CAS PubMed.
- J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. Zhao, Applications of machine learning in drug discovery and development, Nat. Rev. Drug Discovery, 2019, 18, 463 CrossRef CAS PubMed.
- A. R. Kirtane, M. Verma, P. Karandikar, J. Furin, R. Langer and G. Traverso, Nanotechnology approaches for global infectious diseases, Nat. Nanotechnol., 2021, 16, 369 CrossRef CAS PubMed.
- T. Li and A. Mattei, Pharmaceutical Crystals: Science and Engineering, Wiley, Hoboken, 2019 Search PubMed.
- S. R. Vippagunta, H. G. Brittain and D. J. W. Grant, Crystalline solids, Adv. Drug Delivery Rev., 2001, 48, 3 CrossRef CAS PubMed.
- S. Datta and D. J. W. Grant, Crystal structures of drugs: Advances in determination, prediction and engineering, Nat. Rev. Drug Discovery, 2004, 3, 42 CrossRef CAS PubMed.
- D. L. Hughes, Review of synthetic routes and crystalline forms of the antiandrogen oncology
drugs enzalutamide, apalutamide, and darolutamide, Org. Process Res. Dev., 2020, 24, 347 CrossRef CAS.
- D. L. Hughes, Review of synthetic routes and crystalline forms of the oncology drugs capmatinib, selpercatinib, and pralsetinib, Org. Process Res. Dev., 2021, 25, 2192 CrossRef CAS.
- L. Di, P. V. Fish and T. Mano, Bridging solubility between drug discovery and development, Drug Discovery Today, 2012, 17, 486 CrossRef CAS PubMed.
- H. D. Williams, N. L. Trevaskis, S. A. Charman, R. M. Shanker, W. N. Charman, C. W. Pouton and C. J. H. Porter, Strategies to address low drug solubility in discovery and development, Pharmacol. Rev., 2013, 65, 315 CrossRef PubMed.
- S. Kalepu and V. Nekkanti, Insoluble drug delivery strategies: Review of recent advances and business prospects, Acta Pharm. Sin. B, 2015, 5, 442 CrossRef PubMed.
- J. B. Dressman and C. Reppas, Oral Drug Absorption: Prediction and Assessment, CRC Press, Boca Raton, 2016 Search PubMed.
- Q. Ma, C. Wang, X. Li, H. Guo, J. Meng, J. Liu and H. Xu, Fabrication of water-soluble polymer-encapsulated As4S4 to increase oral bioavailability and chemotherapeutic efficacy in AML mice, Sci. Rep., 2016, 6, 29348 CrossRef CAS PubMed.
- J. K. Aronson, Meyler's Side Effects of Drugs: the International Encyclopedia of Adverse Drug Reactions and Interactions, Elsevier, Oxford, 2016 Search PubMed.
- A. O. Iuga and M. J. McGuire, Adherence and health care costs, Risk Manag. Healthc. Policy, 2014, 7, 35 Search PubMed.
- M. Rams-Baron, R. Jachowicz, E. Boldyreva, D. Zhou, W. Jamroz, and M. Paluch, Amorphous Drugs: Benefits and Challenges, Springer, Heidelberg, 2018 Search PubMed.
- J. F. Willart and M. Descamps, Solid state amorphization of pharmaceuticals, Mol. Pharm., 2008, 5, 905 CrossRef CAS PubMed.
- A. Alzahrani, D. Nyavanandi, P. Mandati, A. A. A. Youssef, S. Narala, S. Bandari and M. Repka, A systematic and robust assessment of hot-melt extrusion-based amorphous solid dispersions: Theoretical prediction to practical implementation, Int. J. Pharm., 2022, 624, 121951 CrossRef CAS PubMed.
- S. Qi and D. Craig, Recent developments in micro- and nanofabrication techniques for the preparation of amorphous pharmaceutical dosage forms, Adv. Drug Delivery Rev., 2016, 100, 67 CrossRef CAS PubMed.
- J. F. Willart, A. De Gusseme, S. Hemon, M. Descamps, F. Leveiller and A. Rameau, Vitrification and polymorphism of trehalose induced by dehydration of trehalose dihydrate, J. Phys. Chem. B, 2002, 106, 3365 CrossRef CAS.
- S. J. Dengale, O. P. Ranjan, S. S. Hussen, B. S. M. Krishna, P. B. Musmade, G. G. Shenoy and K. Bhat, Preparation and characterization of co-amorphous ritonavir–indomethacin systems by solvent evaporation technique: Improved dissolution behavior and physical stability without evidence of intermolecular interactions, Eur. J. Pharm. Sci., 2014, 62, 57 CrossRef CAS PubMed.
- B. C. Hancock and M. Parks, What is the true solubility advantage for amorphous pharmaceuticals?, Pharm. Res., 2000, 17, 397 CrossRef CAS PubMed.
- S. B. Murdande, M. J. Pikal, R. M. Shanker and R. H. Bogner, Solubility advantage of amorphous pharmaceuticals: I. A thermodynamic analysis, J. Pharm. Sci., 2010, 99, 1254 CrossRef CAS PubMed.
- S. B. Murdande, M. J. Pikal, R. M. Shanker and R. H. Bogner, Solubility advantage of amorphous pharmaceuticals: II. Application of quantitative thermodynamic relationships for prediction of solubility enhancement in structurally diverse insoluble pharmaceuticals, Pharm. Res., 2010, 27, 2704 CrossRef CAS PubMed.
- R. Paus, Y. Ji, L. Vahle and G. Sadowski, Predicting the solubility advantage of amorphous pharmaceuticals: A novel thermodynamic approach, Mol. Pharm., 2015, 12, 2823 CrossRef CAS PubMed.
- V. H. Thomas, S. Bhattachar, L. Hitchingham, P. Zocharski, M. Naath, N. Surendran, C. L. Stoner and A. El-Kattan, The road map to oral bioavailability: An industrial perspective, Expert Opin. Drug Metab. Toxicol., 2006, 2, 591 CrossRef CAS PubMed.
- C. Bhugra, R. Shmeis, S. L. Krill and M. J. Pikal, Prediction of onset of crystallization from experimental relaxation times. II. Comparison between predicted and experimental onset times, J. Pharm. Sci., 2008, 97, 455 CrossRef CAS PubMed.
- B. V. Eerdenbrugh, J. A. Baird and L. S. Taylor, Crystallization tendency of active pharmaceutical ingredients following rapid solvent evaporation — Classification and comparison with crystallization tendency from under cooled melts, J. Pharm. Sci., 2010, 99, 3826 CrossRef PubMed.
- K. Kawakami, T. Harada, K. Miura, Y. Yoshihashi, E. Yonemochi, K. Terada and H. Moriyama, Relationship between crystallization tendencies during cooling from melt and isothermal storage: Toward a general understanding of physical stability of pharmaceutical glasses, Mol. Pharm., 2014, 11, 1835 CrossRef CAS PubMed.
- J. Sibik, K. Lobmann, T. Rades and J. A. Zeitler, Predicting crystallization of amorphous drugs with terahertz spectroscopy, Mol. Pharm., 2015, 12, 3062 CrossRef CAS PubMed.
- K. Grzybowska, S. Capaccioli and M. Paluch, Recent developments in the experimental investigations of relaxations in pharmaceuticals by dielectric techniques at ambient and elevated pressure, Adv. Drug Delivery Rev., 2016, 100, 158 CrossRef CAS PubMed.
- J. Knapik-Kowalczuk, M. Rams-Baron and M. Paluch, Current research trends in dielectric relaxation studies of amorphous pharmaceuticals: Physical stability, tautomerism, and the role of hydrogen bonding, Trends Anal. Chem., 2021, 134, 116097 CrossRef CAS.
- K. Adrjanowicz, K. Kaminski, Z. Wojnarowska, M. Dulski, L. Hawelek, S. Pawlus, M. Paluch and W. Sawicki, Dielectric relaxation and crystallization kinetics of ibuprofen at ambient and elevated pressure, J. Phys. Chem. B, 2010, 114, 6579 CrossRef CAS PubMed.
- Z. Wojnarowska, L. Hawelek, M. Paluch, W. Sawicki and K. L. Ngai, Molecular dynamics at ambient and elevated pressure of the amorphous pharmaceutical: Nonivamide (pelargonic acid vanillylamide), J. Chem. Phys., 2011, 134, 044517 CrossRef CAS PubMed.
- M. Rams-Baron, J. Pacułt, A. Jedrzejowska, J. Knapik-Kowalczuk and M. Paluch, Changes in physical stability of supercooled etoricoxib after compression, Mol. Pharm., 2018, 15, 3969 CrossRef CAS PubMed.
- A. Minecka, E. Kaminska, D. Heczko, K. Jurkiewicz, K. Wolnica, M. Dulski, B. Hachuła, W. Pisarski, M. Tarnacka, A. Talik, K. Kaminski and M. Paluch, Studying structural and local dynamics in model H-bonded active ingredient — Curcumin in the supercooled and glassy states at various thermodynamic conditions, Eur. J. Pharm. Sci., 2019, 135, 38 CrossRef CAS PubMed.
- K. Chmiel, J. Knapik-Kowalczuk and M. Paluch, How does the high pressure affects the solubility of the drug within the polymer matrix in solid dispersion systems, Eur. J. Pharm. Biopharm., 2019, 143, 8 CrossRef CAS PubMed.
- K. Grzybowska, M. Paluch, A. Grzybowski, Z. Wojnarowska, L. Hawelek, K. Kolodziejczyk and K. L. Ngai, Molecular dynamics and physical stability of amorphous anti-inflammatory drug: Celecoxib, J. Phys. Chem. B, 2010, 114, 12792 CrossRef CAS PubMed.
- K. Adrjanowicz, D. Zakowiecki, K. Kaminski, L. Hawelek, K. Grzybowska, M. Tarnacka, M. Paluch and K. Cal, Molecular dynamics in supercooled liquid and glassy states of antibiotics: Azithromycin, clarithromycin and roxithromycin studied by dielectric spectroscopy. Advantages given by the amorphous state, Mol. Pharm., 2012, 9, 1748 CrossRef CAS PubMed.
- J. Knapik, Z. Wojnarowska, K. Grzybowska, L. Hawelek, W. Sawicki, K. Wlodarski, J. Markowski and M. Paluch, Physical stability of the amorphous anticholesterol agent (ezetimibe): The role of molecular mobility, Mol. Pharm., 2014, 11, 4280 CrossRef CAS PubMed.
- J. Szczurek, M. Rams-Baron, J. Knapik-Kowalczuk, A. Antosik, J. Szafraniec, W. Jamroz, M. Dulski, R. Jachowicz and M. Paluch, Molecular dynamics, recrystallization behavior, and water solubility of the amorphous anticancer agent bicalutamide and its polyvinylpyrrolidone mixtures, Mol. Pharm., 2017, 14, 1071 CrossRef CAS PubMed.
- A. Mansuri, P. Munzner, T. Feuerbach, A. W. P. Vermeer, W. Hoheisel, R. Bohmer, M. Thommes and C. Gainaru, The relaxation behavior of supercooled and glassy imidacloprid, J. Chem. Phys., 2021, 155, 174502 CrossRef CAS PubMed.
- G. Adam and J. H. Gibbs, On the temperature dependence of cooperative relaxation properties in glass-forming liquids, J. Chem. Phys., 1965, 43, 139 CrossRef CAS.
- I. M. Hodge, Strong and fragile liquids — A brief critique, J. Non-Cryst. Solids, 1996, 202, 164 CrossRef CAS.
- S. L. Shamblin, X. Tang, L. Chang, B. C. Hancock and M. J. Pikal, Characterization of the time scales of molecular motion in pharmaceutically important glasses, J. Phys. Chem. B, 1999, 103, 4113 CrossRef CAS.
- B. C. Hancock and S. L. Shamblin, Molecular mobility of amorphous pharmaceuticals determined using differential scanning calorimetry, Thermochim. Acta, 2001, 380, 95 CrossRef CAS.
- K. Adrjanowicz, K. Grzybowska, K. Kaminski, L. Hawelek, M. Paluch and D. Zakowiecki, Comprehensive studies on physical and chemical stability in liquid and glassy states of telmisartan (TEL): Solubility advantages given by cryomilled and quenched material, Philos. Mag., 2011, 91, 1926 CrossRef CAS.
- O. M. H. Salo-Ahen, I. Alanko, R. Bhadane, A. M. J. J. Bonvin, R. V. Honorato, S. Hossain, A. H. Juffer, A. Kabedev, M. Lahtela-Kakkonen, A. S. Larsen, E. Lescrinier, P. Marimuthu, M. U. Mirza, G. Mustafa, A. Nunes-Alves, T. Pantsar, A. Saadabadi, K. Singaravelu and M. Vanmeert, Molecular dynamics simulations in drug discovery and pharmaceutical development, Processes, 2021, 9, 71 CrossRef CAS.
- T. Xiang and B. D. Anderson, Molecular dynamics simulation of amorphous indomethacin-poly (vinylpyrrolidone) glasses: Solubility and hydrogen bonding interactions, J. Pharm. Sci., 2013, 102, 876 CrossRef CAS PubMed.
- T. Xiang and B. D. Anderson, Molecular dynamics simulation of amorphous hydroxypropylmethylcellulose and its mixtures with felodipine and water, J. Pharm. Sci., 2017, 106, 803 CrossRef CAS PubMed.
- T. Xiang and B. D. Anderson, Effects of molecular interactions on miscibility and mobility of ibuprofen in amorphous solid dispersions with various polymers, J. Pharm. Sci., 2019, 108, 178 CrossRef CAS PubMed.
- T. Barnard and G. C. Sosso, Combining machine learning and molecular simulations to predict the stability of amorphous drugs, J. Chem. Phys., 2023, 159, 014503 CrossRef CAS PubMed.
- L. Larini, A. Ottochian, C. De Michele and D. Leporini, Universal scaling between structural relaxation and vibrational dynamics in glass-forming liquids and polymers, Nat. Phys., 2008, 4, 42 Search PubMed.
- P. Z. Hanakata, J. F. Douglas and F. W. Starr, Interfacial mobility scale determines the scale of collective motion and relaxation rate in polymer films, Nat. Commun., 2014, 5, 4163 Search PubMed.
- B. A. P. Betancourt, P. Z. Hanakata, F. W. Starr and J. F. Douglas, Quantitative relations between cooperative motion, emergent elasticity, and free volume in model glass-forming polymer materials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2966 CrossRef PubMed.
- A. Jaiswal, T. Egami and Y. Zhang, Atomic-scale dynamics of a model glass-forming metallic liquid: Dynamical crossover, dynamical decoupling, and dynamical clustering, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 134204 CrossRef.
- A. Ninarello, L. Berthier and D. Coslovich, Models and algorithms for the next generation of glass transition studies, Phys. Rev. X, 2017, 7, 021039 Search PubMed.
- W. Xu, J. F. Douglas and K. F. Freed, Influence of pressure on glass formation in a simulated polymer melt, Macromolecules, 2017, 50, 2585 CrossRef CAS.
- J. Hung, T. K. Patra, V. Meenakshisundaram, J. H. Mangalara and D. S. Simmons, Universal localization transition accompanying glass formation: Insights from efficient molecular dynamics simulations of diverse supercooled liquids, Soft Matter, 2019, 15, 1223 RSC.
- L. Berthier and M. D. Ediger, How to “measure” a structural relaxation time that is too long to be measured?, J. Chem. Phys., 2020, 153, 044501 CrossRef CAS.
- A. Ghanekarade, A. D. Phan, K. S. Schweizer and D. S. Simmons, Nature of dynamic gradients, glass formation, and collective effects in ultrathin freestanding films, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104398118 CrossRef CAS PubMed.
- B. Mei, G. S. Sheridan, C. M. Evans and K. S. Schweizer, Elucidation of the physical factors that control activated transport of penetrants in chemically complex glass-forming liquids, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2210094119 CrossRef CAS.
- A. Ghanekarade, A. D. Phan, K. S. Schweizer and D. S. Simmons, Signature of collective elastic glass physics in surface-induced long-range tails in dynamical gradients, Nat. Phys., 2023, 19, 800 Search PubMed.
- S. Mirigian and K. S. Schweizer, Unified theory of activated relaxation in liquids over 14 decades in time, J. Phys. Chem. Lett., 2013, 4, 3648 CrossRef CAS.
- S. Mirigian and K. S. Schweizer, Elastically cooperative activated barrier hopping theory of relaxation in viscous fluids. I. General formulation and application to hard sphere fluids, J. Chem. Phys., 2014, 140, 194506 CrossRef PubMed.
- S. Mirigian and K. S. Schweizer, Elastically cooperative activated barrier hopping theory of relaxation in viscous fluids. II. Thermal liquids, J. Chem. Phys., 2014, 140, 194507 CrossRef PubMed.
- A. D. Phan, J. Knapik-Kowalczuk, M. Paluch, T. X. Hoang and K. Wakabayashi, Theoretical model for the structural relaxation time in coamorphous drugs, Mol. Pharm., 2019, 16, 2992 CrossRef CAS PubMed.
- A. D. Phan and K. S. Schweizer, Elastically collective nonlinear Langevin equation theory of glass-forming liquids: Transient localization, thermodynamic mapping, and cooperativity, J. Phys. Chem. B, 2018, 122, 8451 CrossRef CAS PubMed.
- S. Mirigian and K. S. Schweizer, Dynamical theory of segmental relaxation and emergent elasticity in supercooled polymer melts, Macromolecules, 2015, 48, 1901 CrossRef CAS.
- T. D. Cuong, A. D. Phan, K. Wakabayashi and P. T. Huy, Structural relaxation time and dynamic shear modulus of glassy graphene, J. Non-Cryst. Solids, 2020, 538, 120024 CrossRef CAS.
- A. D. Phan, A. Zaccone, V. D. Lam and K. Wakabayashi, Theory of pressure-induced rejuvenation and strain hardening in metallic glasses, Phys. Rev. Lett., 2021, 126, 025502 CrossRef CAS PubMed.
- T. D. Cuong and A. D. Phan, Effects of cooperative diffusion on rheological and mechanical behavior of bcc Fe: A combined approach using elastically collective nonlinear Langevin equation theory and statistical moment method, Phys. Rev. B, 2024, 109, 054112 CrossRef CAS.
- A. D. Phan, K. Wakabayashi, M. Paluch and V. D. Lam, Effects of cooling rate on structural relaxation in amorphous drugs: Elastically collective nonlinear Langevin equation theory and machine learning study, RSC Adv., 2019, 9, 40214 RSC.
- D. Chen and G. B. McKenna, Deep glassy state dynamic data challenge glass models: Elastic models, J. Non-Cryst. Solids: X, 2021, 11–12, 100068 CAS.
- A. D. Phan, Determination of Young's modulus of active pharmaceutical ingredients by relaxation dynamics at elevated pressures, J. Phys. Chem. B, 2020, 124, 10500 CrossRef CAS PubMed.
- H. Tanaka, Relationship among glass-forming ability, fragility, and short-range bond ordering of liquids, J. Non-Cryst. Solids, 2005, 351, 678 CrossRef CAS.
- H. Shintani and H. Tanaka, Frustration on the way to crystallization in glass, Nat. Phys., 2006, 2, 200 Search PubMed.
- K. Kawakami, T. Harada, Y. Yoshihashi, E. Yonemochi, K. Terada and H. Moriyama, Correlation between glass-forming ability and fragility of pharmaceutical compounds, J. Phys. Chem. B, 2015, 119, 4873 CrossRef CAS PubMed.
- A. D. Phan and K. Wakabayashi, Theory of structural and secondary relaxation in amorphous drugs under compression, Pharmaceutics, 2020, 12, 177 CrossRef CAS PubMed.
- T. D. Cuong and A. D. Phan, Compression effects on structural relaxation process of amorphous indomethacin, Commun. Phys., 2021, 31, 67 Search PubMed.
- J. K. Percus and G. J. Yevick, Analysis of classical statistical mechanics by means of collective coordinates, Phys. Rev., 1958, 110, 1 CrossRef CAS.
- M. S. Wertheim, Exact solution of the Percus-Yevick integral equation for hard spheres, Phys. Rev. Lett., 1963, 10, 321 CrossRef.
- N. W. Ashcroft and J. Lekner, Structure and resistivity of liquid metals, Phys. Rev., 1966, 145, 83 CrossRef CAS.
- K. S. Schweizer and E. J. Saltzman, Entropic barriers, activated hopping, and the glass transition in colloidal suspensions, J. Chem. Phys., 2003, 119, 1181 CrossRef CAS.
- K. S. Schweizer, Derivation of a microscopic theory of barriers and activated hopping transport in glassy liquids and suspensions, J. Chem. Phys., 2005, 123, 244501 CrossRef PubMed.
- E. J. Saltzman and K. S. Schweizer, Activated hopping and dynamical fluctuation effects in hard sphere suspensions and fluids, J. Chem. Phys., 2006, 125, 044509 CrossRef PubMed.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Permagon Press, London, 1975 Search PubMed.
- H. A. Kramers, Brownian motion in a field of force and the diffusion model of chemical reactions, Physica, 1940, 7, 284 CrossRef CAS.
- P. Hanggi, P. Talkner and M. Borkovec, Reaction-rate theory: Fifty years after Kramers, Rev. Mod. Phys., 1990, 62, 251 CrossRef.
- A. D. Phan, N. K. Ngan, D. T. Nga, N. B. Le and C. V. Ha, Tailoring drug mobility by photothermal heating of graphene plasmons, Phys. Status Solidi RRL, 2022, 16, 2100496 CrossRef CAS.
- T. Hecksher and J. C. Dyre, A review of experiments testing the shoving model, J. Non-Cryst. Solids, 2015, 407, 14 CrossRef CAS.
- S. P. Andersson and O. Andersson, Relaxation studies of poly(propylene glycol) under high pressure, Macromolecules, 1998, 31, 2999 CrossRef CAS.
- I. Avramov, A. Grzybowski and M. Paluch, A new approach to description of the pressure dependence of viscosity, J. Non-Cryst. Solids, 2009, 355, 733 CrossRef CAS.
- Z. Wojnarowska, K. Adrjanowicz, P. Wlodarczyk, E. Kaminska, K. Kaminski, K. Grzybowska, R. Wrzalik, M. Paluch and K. L. Ngai, Broadband dielectric relaxation study at ambient and elevated pressure of molecular dynamics of pharmaceutical: Indomethacin, J. Phys. Chem. B, 2009, 113, 12536 CrossRef CAS PubMed.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244 CrossRef CAS PubMed.
- L. Burakovsky, D. L. Preston and R. R. Silbar, Analysis of dislocation mechanism for melting of elements: Pressure dependence, J. Appl. Phys., 2000, 88, 6294 CrossRef CAS.
- K. L. Kearns, T. Still, G. Fytas and M. D. Ediger, High-modulus organic glasses prepared by physical vapor deposition, Adv. Mater., 2010, 22, 39 CrossRef CAS PubMed.
- M. Tarnacka, O. Madejczyk, K. Adrjanowicz, J. Pionteck, E. Kaminska, K. Kaminski and M. Paluch, Thermodynamic scaling of molecular dynamics in supercooled liquid state of pharmaceuticals: Itraconazole and ketoconazole, J. Chem. Phys., 2015, 142, 224507 CrossRef CAS PubMed.
- G. Szklarz, K. Adrjanowicz, M. Tarnacka, J. Pionteck and M. Paluch, Confinement-induced changes in the glassy dynamics and crystallization behavior of supercooled fenofibrate, J. Phys. Chem. C, 2018, 122, 1384 CrossRef CAS.
- P. I. Dorogokupets, A. M. Dymshits, K. D. Litasov and T. S. Sokolova, Thermodynamics and equations of state of iron to 350 GPa and 6000 K, Sci. Rep., 2017, 7, 41863 CrossRef CAS.
- O. L. Anderson, Equations of State of Solids for Geophysics and Ceramic Science, Oxford University Press, New York, 1995 Search PubMed.
- A. K. Pandey and B. K. Pandey, Rahul, Theoretical prediction
of Grüneisen parameter for bulk metallic glasses, J. Alloys Compd., 2011, 509, 4191 CrossRef CAS.
- K. S. Schweizer and G. Yatsenko, Collisions, caging, thermodynamics, and jamming in the barrier hopping theory of glassy hard sphere fluids, J. Chem. Phys., 2007, 127, 164505 CrossRef PubMed.
- R. Kubo, Statistical–mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems, J. Phys. Soc. Jpn., 1957, 12, 570 CrossRef.
- B. Shi, S. Yang, S. Liu and P. Jin, Lindemann-like rule between average thermal expansion coefficient and glass transition temperature for metallic glasses, J. Non-Cryst. Solids, 2019, 503, 194 CrossRef.
- M. Guinan and D. Steinberg, A simple approach to extrapolating measured polycrystalline shear moduli to very high pressure, J. Phys. Chem. Solids, 1975, 36, 829 CrossRef CAS.
- L. Burakovsky and D. L. Preston, Generalized Guinan-Steinberg formula for the shear modulus at all pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184118 CrossRef.
- V. Mazel, V. Busignies, H. Diarra and P. Tchoreloff, On the links between elastic constants and effective elastic behavior of pharmaceutical compacts: Importance of Poisson's ratio and use of bulk modulus, J. Pharm. Sci., 2013, 102, 4009 CrossRef CAS PubMed.
- G. Arfken, Mathematical Methods for Physicists, Academic Press, Orlando, 1985 Search PubMed.
- K. Adrjanowicz, A. Grzybowski, K. Kaminski and M. Paluch, Temperature and volume effect on the molecular dynamics of supercooled ibuprofen at ambient and elevated pressure, Mol. Pharm., 2011, 8, 1975 CrossRef CAS.
- K. Adrjanowicz, K. Kaminski, M. Paluch and K. Niss, Crystallization behavior and relaxation dynamics of supercooled S-ketoprofen and the racemic mixture along an isochrone, Cryst. Growth Des., 2015, 15, 3257 CrossRef CAS.
- E. Kaminska, A. Minecka, M. Tarnacka, K. Kaminski and M. Paluch, Breakdown of the isochronal structural (α) and secondary (JG β) exact superpositioning in probucol—A low molecular weight pharmaceutical, J. Mol. Liq., 2020, 299, 112169 CrossRef CAS.
- D. Heczko, K. Jurkiewicz, J. Grelska, K. Kaminski, M. Paluch and E. Kaminska, Influence of high pressure on the local order and dynamical properties of the selected azole antifungals, J. Phys. Chem. B, 2020, 124, 11949 CrossRef CAS.
- P. Jesionek, D. Heczko, B. Hachuła, K. Kaminski and E. Kaminska, High-pressure studies in the supercooled and glassy state of the strongly associated active pharmaceutical ingredient—Ticagrelor, Sci. Rep., 2023, 13, 8890 CrossRef CAS PubMed.
- G. Szklarz, K. Adrjanowicz, M. Dulski, J. Knapik and M. Paluch, Dielectric relaxation study at ambient and elevated pressure of the modeled lipophilic drug fenofibrate, J. Phys. Chem. B, 2016, 120, 11298 CrossRef CAS PubMed.
- M. Tarnacka, K. Adrjanowicz, E. Kaminska, K. Kaminski, K. Grzybowska, K. Kolodziejczyk, P. Wlodarczyk, L. Hawelek, G. Garbacz, A. Kocot and M. Paluch, Molecular dynamics of itraconazole at ambient and high pressure, Phys. Chem. Chem. Phys., 2013, 15, 20742 RSC.
- Z. Wojnarowska, K. Adrjanowicz, K. Kaminski, L. Hawelek and M. Paluch, Effect of pressure on tautomers' equilibrium in supercooled glibenclamide drug: Analysis of fragility behavior, J. Phys. Chem. B, 2010, 114, 14815 CrossRef CAS PubMed.
- K. Adrjanowicz, Z. Wojnarowska, M. Paluch and J. Pionteck, Thermodynamic scaling of molecular dynamics in supercooled ibuprofen, J. Phys. Chem. B, 2011, 115, 4559 CrossRef CAS.
- Z. Wojnarowska, K. Grzybowska, K. Adrjanowicz, K. Kaminski, M. Paluch, L. Hawelek, R. Wrzalik, M. Dulski, W. Sawicki, J. Mazgalski, A. Tukalska and T. Bieg, Study of the amorphous glibenclamide drug: Analysis of the molecular dynamics of quenched and cryomilled material, Mol. Pharm., 2010, 7, 1692 CrossRef CAS PubMed.
- Z. Wojnarowska, P. Wlodarczyk, K. Kaminski, K. Grzybowska, L. Hawelek and M. Paluch, On the kinetics of tautomerism in drugs: New application of broadband dielectric spectroscopy, J. Chem. Phys., 2010, 133, 094507 CrossRef CAS PubMed.
- Z. Wojnarowska, M. Paluch and J. Pionteck, The tautomerization phenomenon of glibenclamide drug monitored by means of volumetric measurements, J. Chem. Phys., 2011, 135, 214506 CrossRef CAS.
- C. A. Angell, Relaxation in liquids, polymers and plastic crystals — Strong/fragile patterns and problems, J. Non-Cryst. Solids, 1991, 131, 13 CrossRef.
- C. M. Roland, S. Hensel-Bielowka, M. Paluch and R. Casalini, Supercooled dynamics of glass-forming liquids and polymers under hydrostatic pressure, Rep. Prog. Phys., 2005, 68, 1405 CrossRef CAS.
- R. Casalini and C. M. Roland, Scaling of the supercooled dynamics and its relation to the pressure dependences of the dynamic crossover and the fragility of glass formers, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 014210 CrossRef.
- M. Paluch, E. Masiewicz, A. Grzybowski, S. Pawlus, J. Pionteck and Z. Wojnarowska, General rules prospected for the liquid fragility in various material groups and different thermodynamic conditions, J. Chem. Phys., 2014, 141, 134507 CrossRef CAS PubMed.
- E. Masiewicz, A. Grzybowski, A. P. Sokolov and M. Paluch, Temperature–volume entropic model for viscosities and structural relaxation times of glass formers, J. Phys. Chem. Lett., 2012, 3, 2643 CrossRef CAS PubMed.
- P. Lunkenheimer, A. Loidl, B. Riechers, A. Zaccone and K. Samwer, Thermal expansion and the glass transition, Nat. Phys., 2023, 19, 694 Search PubMed.
- D. Zhou, G. G. Z. Zhang, D. Law, D. J. W. Grant and E. A. Schmitt, Physical stability of amorphous pharmaceuticals: Importance of configurational thermodynamic quantities and molecular mobility, J. Pharm. Sci., 2002, 91, 1863 CrossRef CAS.
- J. A. Baird, B. V. Eerdenbrugh and L. S. Taylor, A classification system to assess the crystallization tendency of organic molecules from undercooled melts, J. Pharm. Sci., 2010, 99, 3787 CrossRef CAS PubMed.
- U. Sailaja, M. S. Thayyil, N. S. K. Kumar and G. Govindaraj, Molecular dynamics of amorphous pharmaceutical fenofibrate studied by broadband dielectric spectroscopy, J. Pharm. Anal., 2016, 6, 165 CrossRef CAS PubMed.
- W. Tu, X. Li, Z. Chen, Y. D. Liu, M. Labardi, S. Capaccioli, M. Paluch and L. M. Wang, Glass formability in medium-sized molecular systems/pharmaceuticals. I. Thermodynamics vs. kinetics, J. Chem. Phys., 2016, 144, 174502 CrossRef.
- R. Casalini, M. Paluch and C. M. Roland, Influence of molecular structure on the dynamics of supercooled van der Waals liquids, Phys. Rev. E, 2003, 67, 031505 CrossRef PubMed.
- K. Grzybowska, M. Paluch, A. Grzybowski, S. Pawlus, S. Ancherbak, D. Prevosto and S. Capaccioli, Dynamic crossover of water relaxation in aqueous mixtures: Effect of pressure, J. Phys. Chem. Lett., 2010, 1, 1170 CrossRef CAS.
- D. Chandler and H. C. Andersen, Optimized cluster expansions for classical fluids. II. Theory of molecular liquids, J. Chem. Phys., 1972, 57, 1930 CrossRef CAS.
- K. S. Schweizer and J. G. Curro, Integral equation theories of the structure, thermodynamics, and phase transitions of polymer fluids, Adv. Chem. Phys., 1997, 98, 1 CrossRef CAS.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, London, 2006 Search PubMed.
- Z. E. Dell and K. S. Schweizer, Microscopic theory for the role of attractive forces in the dynamics of supercooled liquids, Phys. Rev. Lett., 2015, 115, 205702 CrossRef.
- A. Ghosh and K. S. Schweizer, Microscopic theory of the influence of strong attractive forces on the activated dynamics of dense glass and gel forming fluids, J. Chem. Phys., 2019, 151, 244502 CrossRef PubMed.
- A. Ghosh and K. S. Schweizer, Microscopic
theory of onset of decaging and bond-breaking activated dynamics in ultradense fluids with strong short-range attractions, Phys. Rev. E, 2020, 101, 060601(R) CrossRef.
- A. Minecka, B. Hachuła, K. Kaminski, M. Paluch and E. Kaminska, How does pressure affect the molecular dynamics, intramolecular interactions, and the relationship between structural (α) and secondary (JG-β) relaxation above and below the glass transition temperature in binary mixtures of H-bonded API – Probucol and acetylated saccharides?, Eur. J. Pharm. Sci., 2021, 164, 105894 CrossRef CAS PubMed.
- A. Minecka, M. Tarnacka, K. Jurkiewicz, B. Hachula, K. Kaminski, M. Paluch and E. Kaminska, Influence of the internal structure and intermolecular interactions on the correlation between structural (α) and secondary (β-JG) relaxation below the glass transition temperature in neat probucol and its binary mixtures with modified saccharides, J. Phys. Chem. B, 2020, 124, 4821 CrossRef CAS.
- P. D. Ispanovity, I. Groma, G. Gyorgyi, P. Szabo and W. Hoffelner, Criticality of relaxation in dislocation systems, Phys. Rev. Lett., 2011, 107, 085506 CrossRef PubMed.
- J. Rottler, S. S. Schoenholz and A. J. Liu, Predicting plasticity with soft vibrational modes: From dislocations to glasses, Phys. Rev. E, 2014, 89, 042304 CrossRef PubMed.
- X. Wang, F. Maresca and P. Cao, The hierarchical energy landscape of screw dislocation motion in refractory high-entropy alloys, Acta Mater., 2022, 234, 118022 CrossRef CAS.
- B. Bako, I. Groma, G. Gyorgyi and G. T. Zimanyi, Dislocation glasses: Aging during relaxation and coarsening, Phys. Rev. Lett., 2007, 98, 075701 CrossRef CAS PubMed.
- S. J. Gerbode, U. Agarwal, D. C. Ong, C. M. Liddell, F. Escobedo and I. Cohen, Glassy dislocation dynamics in 2D colloidal dimer crystals, Phys. Rev. Lett., 2010, 105, 078301 CrossRef PubMed.
- P. D. Ispanovity, L. Laurson, M. Zaiser, I. Groma, S. Zapperi and M. J. Alava, Avalanches in 2D dislocation systems: Plastic yielding Is not depinning, Phys. Rev. Lett., 2014, 112, 235501 CrossRef PubMed.
- A. Lehtinen, G. Costantini, M. J. Alava, S. Zapperi and L. Laurson, Glassy features of crystal plasticity, Phys. Rev. B, 2016, 94, 064101 CrossRef.
- M. Ovaska, A. Lehtinen, M. J. Alava, L. Laurson and S. Zapperi, Excitation spectra in crystal plasticity, Phys. Rev. Lett., 2017, 119, 265501 CrossRef PubMed.
- L. Burakovsky, D. L. Preston and R. R. Silbar, Melting as a dislocation-mediated phase transition, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 15011 CrossRef CAS.
- L. Gomez, A. Dobry, Ch. Geuting, H. T. Diep and L. Burakovsky, Dislocation lines as the precursor of the melting of crystalline solids observed in Monte Carlo simulations, Phys. Rev. Lett., 2003, 90, 095701 CrossRef CAS PubMed.
- L. Burakovsky, C. W. Greeff and D. L. Preston, Analytic model of the shear modulus at all temperatures and densities, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 094107 CrossRef.
- W. Kauzmann, The nature of the glassy state and the behavior of liquids at low temperatures, Chem. Rev., 1948, 43, 219 CrossRef CAS.
- R. Clausius, Über die bewegende kraft der wärme und die gesetze, welche sich daraus für die wärmelehre selbst ableiten lassen, Ann. Phys., 1850, 155, 368 CrossRef.
- M. C. Clapeyron, Mémoire sur la puissance motrice de la chaleur, J. Ec. Polytech., 1834, 23, 153 Search PubMed.
- C. A. Angell, Formation of glasses from liquids and biopolymers, Science, 1995, 267, 1924 CrossRef CAS PubMed.
- M. Kazmierczak, E. Patyk-Kazmierczak and A. Katrusiak, Compression and thermal expansion in organic and metal–organic crystals: The pressure–temperature correspondence rule, Cryst. Growth Des., 2021, 21, 2196 CrossRef CAS.
- O. N. Senkov and D. B. Miracle, Correlation between thermodynamic and kinetic properties of glass-forming liquids, Mater. Res. Soc. Symp. Proc., 2008, 1048, 10 Search PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- P. Sanphui, B. Sarma and A. Nangia, Phase transformation in conformational polymorphs of nimesulide, J. Pharm. Sci., 2011, 100, 2287 CrossRef CAS PubMed.
- E. J. Chan and D. J. Goossens, Study of the single-crystal X-ray diffuse scattering in paracetamol polymorphs, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 80 CrossRef CAS PubMed.
- J. J. Gerber, M. R. Caira and A. P. Lotter, Structures of two conformational polymorphs of the cholesterol-lowering drug probucol, J. Crystallogr. Spectrosc. Res., 1993, 23, 863 CrossRef CAS.
- L. D. Prado, H. V. A. Rocha, J. A. L. C. Resende, G. B. Ferreira and A. M. R. de Figuereido Teixeira, An insight into carvedilol solid forms: Effect of supramolecular interactions on the dissolution profiles, CrystEngComm, 2014, 16, 3168 RSC.
- D. Csicsak, E. Borbas, S. Kadar, P. Tozser, P. Bagi, H. Pataki, B. Sinko, K. Takacs-Novak and G. Volgyi, Towards more accurate solubility measurements with real time monitoring: a carvedilol case study, New J. Chem., 2021, 45, 11618 RSC.
- K. Koperwas, A. Grzybowski, K. Grzybowska, Z. Wojnarowska and M. Paluch, Effects of dynamic heterogeneity and density scaling of molecular dynamics on the relationship among thermodynamic coefficients at the glass transition, J. Chem. Phys., 2015, 143, 024502 CrossRef CAS PubMed.
- K. Chmiel, J. Knapik-Kowalczuk, E. Kaminska, L. Tajber and M. Paluch, High-pressure dielectric studies—A way to experimentally determine the solubility of a drug in the polymer matrix at low temperatures, Mol. Pharm., 2021, 18, 3050 CrossRef CAS PubMed.
- T. A. Lima, L. F. O. Faria, V. H. Paschoal and M. C. C. Ribeiro, Communication: Glass transition and melting lines of an ionic liquid, J. Chem. Phys., 2018, 148, 171101 CrossRef PubMed.
- J. Ledru, C. T. Imrie, C. R. Pulham, R. Ceolin and J. M. Hutchinson, High pressure differential scanning calorimetry investigations on the pressure dependence of the melting of paracetamol polymorphs I and II, J. Pharm. Sci., 2007, 96, 2784 CrossRef CAS PubMed.
- G. B. McKenna and S. L. Simon, 50th anniversary perspective: Challenges in the dynamics and kinetics of glass-forming polymers, Macromolecules, 2017, 50, 6333 CrossRef CAS.
- J. Knapik, Z. Wojnarowska, K. Grzybowska, L. Tajber, H. Mesallati, K. J. Paluch and M. Paluch, Molecular dynamics and physical stability of amorphous nimesulide drug and its binary drug-polymer systems, Mol. Pharm., 2016, 13, 1937 CrossRef CAS PubMed.
- A. A. Ravikumar, P. K. Kulkarni, R. A. M. Osmani, U. Hani, M. Ghazwani, A. A. Fatease, A. H. Alamri and D. V. Gowda, Carvedilol precipitation inhibition by the incorporation of polymeric precipitation inhibitors using a stable amorphous solid dispersion approach: Formulation, characterization, and in vitro in vivo evaluation, Polymers, 2022, 14, 4977 CrossRef CAS PubMed.
- J. Knapik-Kowalczuk, Z. Wojnarowska, M. Rams-Baron, K. Jurkiewicz, J. Cielecka-Piontek, K. L. Ngai and M. Paluch, Atorvastatin as a promising crystallization inhibitor of amorphous probucol: Dielectric studies at ambient and elevated pressure, Mol. Pharm., 2017, 14, 2670 CrossRef CAS PubMed.
- G. P. Johari, S. Kim and R. M. Shanker, Dielectric studies of molecular motions in amorphous solid and ultraviscous acetaminophen, J. Pharm. Sci., 2005, 94, 2207 CrossRef CAS PubMed.
- K. Yamaguchi, R. Mizoguchi, K. Kawakami and T. Miyazaki, Influence of the crystallization tendencies of pharmaceutical glasses on the applicability of the Adam-Gibbs-Vogel and Vogel-Tammann-Fulcher equations in the prediction of their long-term physical stability, Int. J. Pharm., 2022, 626, 122158 CrossRef CAS PubMed.
- A. Minecka, B. Hachuła, K. Jurkiewicz, K. Kaminski, M. Paluch and E. Kaminska, High pressure aging studies on the low-molecular weight glass-forming pharmaceutical – Probucol, J. Mol. Liq., 2021, 321, 114626 CrossRef CAS.
- P. Lunkenheimer and A. Loidl, Glassy dynamics: From millihertz to terahertz, in The Scaling of Relaxation Processes, ed. F. Kremer and A. Loidl, Springer, Cham, 2018, p. 23 Search PubMed.
- K. Chen and K. S. Schweizer, Molecular theory of physical aging in polymer glasses, Phys. Rev. Lett., 2007, 98, 167802 CrossRef PubMed.
- F. Arceri, F. P. Landes, L. Berthier, and G. Biroli, Glasses and aging, a statistical mechanics perspective on, in Statistical and Nonlinear Physics, ed. B. Chakraborty, Springer, New York, 2022, p. 229 Search PubMed.
- B. Riechers, L. A. Roed, S. Mehri, T. S. Ingebrigtsen, T. Hecksher, J. C. Dyre and K. Niss, Predicting nonlinear physical aging of glasses from equilibrium relaxation via the material time, Sci. Adv., 2022, 8, eabl9809 CrossRef CAS PubMed.
- T. Bohmer, J. P. Gabriel, L. Costigliola, J. N. Kociok, T. Hecksher, J. C. Dyre and T. Blochowicz, Time reversibility during the ageing of materials, Nat. Phys., 2024, 20, 637 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Anh D. Phan
*a and
Anh D. Phan ab
ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 since the Neolithic Age. For thousands of years, numerous catastrophic epidemics and pandemics have been recorded in human history, such as the plague of Justinian,6 the Black Death,7 HIV/AIDS,8 Ebola,9 and COVID-19.10 They have not only claimed the lives of millions of people but also affected all aspects of socio-economic life severely.11–13 In addition to infectious diseases, human health has been threatened by non-communicable ones, including ischaemic heart, stroke, chronic obstructive pulmonary, cancer, Alzheimer's, diabetes, and kidney.14–16 As reported by the World Health Organization,17 cardiovascular problems alone were responsible for more than one-third of global deaths in 2019. Thus, it cannot be denied that disease prevention and treatment have become a deep concern for every individual, organization, and country.18–20
5 since the Neolithic Age. For thousands of years, numerous catastrophic epidemics and pandemics have been recorded in human history, such as the plague of Justinian,6 the Black Death,7 HIV/AIDS,8 Ebola,9 and COVID-19.10 They have not only claimed the lives of millions of people but also affected all aspects of socio-economic life severely.11–13 In addition to infectious diseases, human health has been threatened by non-communicable ones, including ischaemic heart, stroke, chronic obstructive pulmonary, cancer, Alzheimer's, diabetes, and kidney.14–16 As reported by the World Health Organization,17 cardiovascular problems alone were responsible for more than one-third of global deaths in 2019. Thus, it cannot be denied that disease prevention and treatment have become a deep concern for every individual, organization, and country.18–20
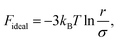





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τα
τα
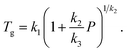
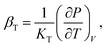
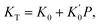
 are the magnitude and derivative of KT at 0 MPa. Eqn (12) works best in a compression range 0 ≤ P ≤ PMur ≈ 2K0.116 Recent experimental evidence shows that PMur is in the order of several GPa.117–119 Meanwhile, the actual production of amorphous drugs is frequently performed at P < 1 GPa.51 Thus, the Murnaghan approximation115 is highly suitable for our study.
are the magnitude and derivative of KT at 0 MPa. Eqn (12) works best in a compression range 0 ≤ P ≤ PMur ≈ 2K0.116 Recent experimental evidence shows that PMur is in the order of several GPa.117–119 Meanwhile, the actual production of amorphous drugs is frequently performed at P < 1 GPa.51 Thus, the Murnaghan approximation115 is highly suitable for our study.
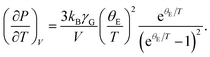


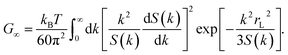



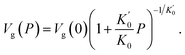

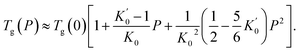

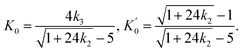


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τα plot at ϕg to facilitate the later analyses of the dynamic fragility.
τα plot at ϕg to facilitate the later analyses of the dynamic fragility.


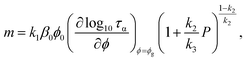

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, including PRO-acGLU (k1 = 292.71 K, k2 = 2.99, k3 = 709.81 MPa), PRO-acSUC (k1 = 294.72 K, k2 = 1.97, k3 = 774.68 MPa), and PRO-aibSUC (k1 = 289.43 K, k2 = 1.95, k3 = 744.25 MPa).160,161 The glass transition of these binary mixtures is supposed to happen at ϕg = 0.61095, similar to pure probucol.132 As illustrated in Fig. 5, our theoretical model can quantitatively explain experimental observations160 on the glassy dynamics of PRO-acGLU, PRO-acSUC, and PRO-aibSUC without heavy computational workloads. Regarding the structural relaxation time, ECNLE curves pass through most BDS benchmarks160 regardless of low or high pressures. Regarding the dynamic fragility, the maximum error between eqn (28) and BDS data160 is 2.24% for PRO-acGLU, 9.75% for PRO-acSUC, and 13.57% for PRO-aibSUC. These figures are experimentally acceptable because m is considered the most sensitive quantity in soft-matter physics.93 It is more remarkable that the above agreements do not involve any adjustable parameters. Therefore, our ECNLE theory has great potential for decoding the mystery of multi-component amorphous drugs and extending their practical applicability to health protection and promotion.
1, including PRO-acGLU (k1 = 292.71 K, k2 = 2.99, k3 = 709.81 MPa), PRO-acSUC (k1 = 294.72 K, k2 = 1.97, k3 = 774.68 MPa), and PRO-aibSUC (k1 = 289.43 K, k2 = 1.95, k3 = 744.25 MPa).160,161 The glass transition of these binary mixtures is supposed to happen at ϕg = 0.61095, similar to pure probucol.132 As illustrated in Fig. 5, our theoretical model can quantitatively explain experimental observations160 on the glassy dynamics of PRO-acGLU, PRO-acSUC, and PRO-aibSUC without heavy computational workloads. Regarding the structural relaxation time, ECNLE curves pass through most BDS benchmarks160 regardless of low or high pressures. Regarding the dynamic fragility, the maximum error between eqn (28) and BDS data160 is 2.24% for PRO-acGLU, 9.75% for PRO-acSUC, and 13.57% for PRO-aibSUC. These figures are experimentally acceptable because m is considered the most sensitive quantity in soft-matter physics.93 It is more remarkable that the above agreements do not involve any adjustable parameters. Therefore, our ECNLE theory has great potential for decoding the mystery of multi-component amorphous drugs and extending their practical applicability to health protection and promotion.