 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New pathways to high-pressure hydrogen enabled by fullerane vibrational modes: an ab initio study
Leonard Constantin Gebac * and
Vasile Bercu
* and
Vasile Bercu
University of Bucharest, Faculty of Physics, 405 Atomistilor Street, Magurele, Romania. E-mail: leonard.gebac@unibuc.ro; Fax: +40 021 457 45 21; Tel: +40 021 457 4419
First published on 7th July 2025
Abstract
The encapsulation of hydrogen within fullerene/fullerane cages offers a promising avenue for studying high pressure hydrogen dynamics. Through ab initio molecular dynamics simulations, we investigate the behavior of a system consisting of hydrogen atoms enclosed in a C20H20 dodecahedrane. Our findings reveal significant structural and dynamical changes as the cage undergoes compression, corresponding to radial symmetric vibration. We analyze geometric, energetic, and thermodynamic parameters, highlighting correlations and observing behavior analogous to high pressure phases of hydrogen. Notably, our study bridges the gap between theory and experiment by proposing a novel approach to achieving high pressures and temperatures experimentally. These results not only contribute to the understanding of hydrogen behavior under extreme conditions but also hold implications for the quest to attain metallic hydrogen. Attaining metallic hydrogen is a widely recognized milestone in materials science with potential applications in various fields.
1 Introduction
Hydrogen, the simplest and most abundant element in the universe, exhibits a rich array of physical behaviors under extreme conditions, particularly at high pressures. At standard ambient conditions, hydrogen predominantly exists in molecular form (H2), with each molecule comprising two hydrogen atoms bonded by a stable covalent bond. However, as pressure increases, hydrogen undergoes dramatic transformations, transitioning through distinct phases with unique properties. Notably, the prospect of metallic hydrogen has captivated scientists for decades, holding implications for various fields ranging from energy production to planetary science.1 Academician V. L. Ginzburg, in his seminal list of significant challenges in physics for the 21st century, ranked metallic hydrogen as the third most pressing challenge.2Experimental observations have revealed a series of distinct phases that hydrogen undergoes under varying pressure and temperature conditions. Under large values of pressures, these include Solid phase I, characterized by a hexagonal close-packed structure,3,4 Phase II,5 known as the “broken-symmetry” phase,6 Phase III7–12 with its hcp structure and intense infrared activity,13 Phase IV marked by alternating layers of six-atom rings and free molecules,9,11,14 and Phase V, a precursor to full atomic and metallic states.15 Recent experimental evidence has also suggested the existence of Phase VI16,17 at extremely high pressures. At even greater pressures, a study claimed to have synthesized metallic hydrogen based on reflectivity measurements at 495 GPa,18 in a good agreement with theoretical predictions,19 but their findings were questioned among the high pressure hydrogen scientific community.20–22 Additionally, hydrogen manifests in two distinct liquid phases: molecular liquid and metallic liquid. The molecular liquid phase occurs at moderate pressures and temperatures and is characterized by the persistence of hydrogen molecules in a fluid state, retaining their molecular identity.23 Conversely, at higher pressures and temperatures, hydrogen undergoes a transition to a metallic liquid phase, where the hydrogen atoms lose their molecular identity.24,25
Nevertheless, uncertainties persist, particularly regarding pressure measurements at such extreme conditions. The need for pressure rescaling has been emphasized in recent studies, acknowledging potential discrepancies of up to −20% at 500 GPa.26 Furthermore, alternative approaches using impurities like argon and silicon-containing compounds to achieve metallization at potentially lower pressures have been conducted, but one study concludes that true metallization of hydrogen has not yet been experimentally realized through these methods. See ref. 27 and references therein.
Considering these experimental results accompanied by uncertainties and even debates, numerical calculations and simulations become essential tools in predicting the structures of the observed phases of solid hydrogen. Previous studies14,28–32 have utilized density functional theory (DFT) and structure search algorithms but have faced difficulties in distinguishing the most stable structures due to small differences in enthalpy values and the choice of exchange–correlation functionals.32–35
Structure search methods show promise in identifying phases at low temperatures with harmonic phonons, but hydrogen's behavior, characterized by pronounced quantum anharmonic effects, even at room temperature, poses challenges for these algorithms.36–38 From this perspective, ab initio molecular dynamics (AIMD) simulations emerge as a suitable approach for exploring this region, contributing to the understanding of the symmetry and the structure at both low and high-temperatures.39 In general, ab initio studies are extremely valuable in examining material properties under high pressure conditions, as demonstrated in several recent studies.40–43 More sophisticated methods,17,44–49 such as quantum Monte Carlo (QMC) and path integral molecular dynamics (PIMD), are used to accurately map the phase diagram of solid hydrogen, taking into account quantum anharmonic effects. However, discrepancies still exist between different calculation methods.50
All the computational methods outlined above, whether based on structure search methods, which are static, following the isothermal-isobaric (NPT) ensemble where pressure is computationally controlled, or molecular dynamics simulations, which are non-static, either ab initio, quantum Monte Carlo, or path integral based, have one thing in common: they seek a structure following computationally imposed pressure or temperature. By contrast, our method does not rely on externally imposed thermodynamic conditions. Instead, we simulate pressure and temperature effects that emerge internally from the vibrational dynamics of a confined system. Specifically, we induce a symmetric radial vibration mode in the C20H20 cage, which transiently compresses and heats the encapsulated hydrogen atoms. This approach allows us to explore analogues of high-pressure hydrogen phases in a dynamic and physically intuitive way. The use of vibrationally driven confinement as a pressure-inducing mechanism represents a conceptual novelty, offering an alternative route to modeling extreme conditions without relying on barostats or pressure constraints.
In this context, our study focuses on AIMD simulations in which the pressures and temperatures are dynamically induced by a C20H20 molecular cage which encapsulates hydrogen atoms. The dodecahedrane was firstly synthesized in 1983 (ref. 51) and is known for it's stability, even when incorporating noble gas atoms.52–54 In addition to its chemical robustness, C20H20 is also computationally advantageous: its relatively small size compared to other fullerene or fullerane cages (e.g., C60) allows for efficient AIMD simulations while still providing sufficient internal volume to encapsulate multiple hydrogen atoms. This makes it an ideal model system for studying nanoscale confinement and pressure-induced behavior in hydrogen systems at atomistic resolution. We investigate the influence of the radial symmetric vibration mode of the C20H20 molecule on the encapsulated hydrogen atoms. Under the immense pressure exerted by the cage, reaching hundreds of gigapascals, we observe a transformation in the behavior of the hydrogen atoms initially grouped as three hydrogen molecules. By utilizing the radial breathing mode of dodecahedrane, we aim to bridge the gap between theory and experiment. Our approach offers insights into the dynamic behavior of hydrogen under extreme pressures. Moreover, we propose a novel method to achieve these extreme pressures and high temperatures experimentally. This method could lead to the formation of metallic hydrogen, whether in its liquid or solid phase. Our study is meant to prove that this goal can be achieved by inducing a symmetric normal mode of vibration in a molecular cage which sequestrates hydrogen atoms. While our investigation acknowledges the potential for further extensions to larger cages such as C60, carbon nanotubes or cages based on other elements, such as boron or hybrid heteroatomic structures, the primary focus of this study is to establish the feasibility of our proposed method. We have chosen to use only six hydrogen atoms enclosed within a C20H20 molecular cage as a demonstrative model. This choice emphasizes the method rather than the number of atoms. Additionally, it reflects findings from other studies, which indicate that hydrogen atoms can adopt a hexagonal close-packed symmetry. This configuration effectively replicates that symmetry. Our simulations reveal intricate correlations between the cage radius, the difference between lowest unoccupied molecular orbital (LUMO) and highest occupied molecular orbital (HOMO) energies, internal H–H distances, and the pressure experienced by the H6 atomic system. These findings not only enhance our understanding of high pressure hydrogen dynamics but also offer valuable insights into the quest for metallic hydrogen and its implications across multiple scientific disciplines, in particularly in the hydrogen energy field and sustainable energy.55–59 While this work focuses on short-timescale pressure dynamics, future studies will investigate extended simulations to assess stability under sustained conditions.
2 Theory and methods
Ab initio molecular dynamics simulations were performed using the TeraChem code.60 The basis set employed is aug-pcseg-1, and the chosen functional is rCAM-B3LYP,61 a functional corrected for long-range interactions with an improved description of systems with fractional number of electrons. This functional has shown very good results compared to other functionals used in calculations where electronic transfer is important.62 Here, it was used in the spin-unrestricted variant. During the simulations, charge transfer between the internal hydrogen atoms and the atoms forming the cage may occur; hence, this functional was chosen for its demonstrated capability in describing such systems accurately.62 The spin-unrestricted variant was selected because, in molecular dynamics, given the initial conditions, the system will evolve over time with considerable variations in interatomic distances, and unrestricted methods provide a more accurate description of the physical behaviour of the system.63 The aug-pcseg-1 basis set was chosen as it is specifically designed to be used with density functional theory methods.64The molecular dynamics simulations were conducted under the microcanonical (NVE) ensemble with a time step of 0.5 fs for a total duration of 500 fs (1000 steps). The extended Lagrangian method65 was employed for motion equation integrator, with initial velocities set to zero and the C20H20 cage initialized in an expanded configuration (1.2× equilibrium dimensions). A grid of 2683 calculation points per atom was used, and geometric, energetic, and thermodynamic quantities were monitored throughout. The short simulation window (0.5 ps) was chosen to capture the critical pressure dynamics during the cage's symmetric vibrational cycles, which induce transient metallic hydrogen signatures.
The input files for the MD simulation, the single-point energy calculation and the results obtained at each time-step are available online.66
2.1 Geometric parameters
One of the geometric parameters studied was the cage radius. This parameter was chosen so that it would show the normal mode of vibration. For this, we used two geometric quantities. The first one is denoted as RC20 and is defined as the average distance between the system's center of mass and the carbon atoms comprising the dodecahedrane. The second one is defined in a similar way by using the average distance to the hydrogen atoms (RH20) of the dodecahedrane.Another geometric parameter, RH6, represents the average distance between the system's center of mass and the encapsulated hydrogen atoms. Concurrently, we calculated the volume enclosed by the hydrogen atoms, denoted as VH6, and the equivalent volume of a sphere with a radius equal to RH6, denoted as  . By comparing these volumes, we can calculate their ratio, which provides valuable insights into the planarity of the instantaneous configuration of the six hydrogen atoms.
. By comparing these volumes, we can calculate their ratio, which provides valuable insights into the planarity of the instantaneous configuration of the six hydrogen atoms.
The volume VH6 was determined using a methodology akin to that described in ref. 67. Initially, the position of the mass center of the H6 system was computed. Subsequently, the total volume VH6 was calculated by summing the volumes of tetrahedra formed by the coordinates of every combination of three points, representing the positions of three hydrogen atoms, with each tetrahedron's apex positioned at the mass center. The volume of a tetrahedron is given by:
 | (1) |
 , are defined by the position differences:
, are defined by the position differences:
 | (2) |
Utilizing  to represent the positions of three points labeled generically as 1, 2, and 3, and
to represent the positions of three points labeled generically as 1, 2, and 3, and  to denote the position of the center of mass of H6, the volume VH6 is computed as:
to denote the position of the center of mass of H6, the volume VH6 is computed as:
 | (3) |
2.2 Energetic parameters
Energetic parameters were defined based on the conservation equation of the total energy:| KC20H20(t) + KH6(t) + QH6@C20H20(t) = const. | (4) |
| QH6@C20H20(t) = QH6(t) + QC20H20(t) + UH6–C20H20(t) | (5) |
Additionally, the energies of the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital), as well as the bandgap were monitored (ΔLUMO,HOMO = ELUMO − EHOMO). This energy levels correspond to the entire system H6@C20H20.
2.3 Thermodynamic parameters
In addition to the geometric and energetic parameters, two thermodynamic physical quantities were also observed and analyzed: pressure and temperature. The pressure is associated with the encapsulated atomic system evolving inside the fullerane, referring to the pressure experienced by the internal hydrogen atoms induced by the C20H20 molecule. It is calculated using the following equation:68,69
 | (6) |
 | (7) |
 and
and  denote the total potential energy and volume, respectively, of the H6 structure following the geometry optimization procedure70 applied to this system. The positions of the hydrogen atoms were geometry optimized, starting from the initial configuration at time step 0. The final optimized configuration was planar, with the hydrogen atoms positioned at considerable distances from each other. In order to be able to apply eqn (7), an intermediate configuration was selected from which variations in the total system energy were negligible (approximately 0.01%). At this point, the values
denote the total potential energy and volume, respectively, of the H6 structure following the geometry optimization procedure70 applied to this system. The positions of the hydrogen atoms were geometry optimized, starting from the initial configuration at time step 0. The final optimized configuration was planar, with the hydrogen atoms positioned at considerable distances from each other. In order to be able to apply eqn (7), an intermediate configuration was selected from which variations in the total system energy were negligible (approximately 0.01%). At this point, the values  and
and 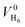 were computed, enabling the calculation of pressure at each time step. Moreover,
were computed, enabling the calculation of pressure at each time step. Moreover,  is considered equal to zero and is omitted from the eqn (7).
is considered equal to zero and is omitted from the eqn (7).
The temperature associated to the H6 system is defined in a classical fashion by the average kinetic energy of the six encapsulated hydrogen atoms:71
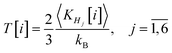 | (8) |
3 Results and discussion
For enhanced clarity in illustrating the correlations between the aforementioned physical parameters, they have been graphically integrated. While the total simulation duration spans 0.5 ps (1000 time steps), only half of this time range is represented to facilitate a more detailed observation of the dependencies and correlations among each quantity.In Fig. 1, the top section illustrates the radii of the dodecahedrane, with RC20 in red and RH20 in blue. It can be observed that the cage begins to compress from the initial time step, as its starting size exceeds its equilibrium size by a factor of k = 1.2. As the system naturally evolves towards a more energetically stable configuration, the cage compresses, resulting in a decrease in RC20. Correspondingly, the radius RH20 also decreases. Notably, within the time interval where RC20 completes one oscillation, RH20 undergoes approximately five variations. This is understandable given that the variation in RH20 is influenced by the characteristic vibration frequency of the C–H bond, which is higher than that of the C–C bond, dictating the variation frequency of RC20. A clear periodicity of this oscillation type is observed over time.
In the bottom section of Fig. 1, the evolution of both pressure and temperature of the encapsulated H6 system over time is shown. The colored portions of the graph highlight the correlations between the quantities represented in the top and bottom sections. It is notable that pressure peaks align with the minimum values of RC20. During these instances of cage compression, the highest pressures within the H6 system are induced, reaching between 400 and 500 GPa. Additionally, except for the initial four time steps, the pressure does not fall below 100 GPa. As depicted in Fig. 1, the temperature ranges between 200 and 2500 K.
In Fig. 2, the time evolution of the volume determined by the six encapsulated hydrogen atoms, VH6 (in red), and the ratio between this volume and the equivalent volume of a sphere with a radius equal to the average distance between the center of mass and the six H atoms,  , is depicted. This representation is instrumental in qualitatively assessing the geometric configuration of the six atoms at various moments in time. Essentially, the system transitions through three well-defined configurations with transitional geometric distributions in between.
, is depicted. This representation is instrumental in qualitatively assessing the geometric configuration of the six atoms at various moments in time. Essentially, the system transitions through three well-defined configurations with transitional geometric distributions in between.
The first configuration is three-dimensional, characterized by large volume ratios (the peaks of the blue curve in Fig. 2) and small volumes VH6. Another encountered configuration is the quasi-molecular one, which features both large volume ratios and large VH6 volumes. The third configuration is the planar-hexagonal one, characterized by very small VH6 volumes and correspondingly small volume ratios. In Fig. 2, these configurations are identifiable where both VH6 and  values are small and overlap.
values are small and overlap.
In Fig. 3, the upper section depicts the variations in energy levels, with the HOMO represented in red and the LUMO in blue. These variations correspond to the entire H6@C20H20 system. The shaded vertical bands, as indicated in Fig. 1, highlight the periods of compression induced by the reduction in the radius RC20. During these compression moments, the HOMO level tends to increase compared to the extension periods, while the LUMO level decreases, reaching its minima. This behavior is further confirmed in the lower section of the Fig. 3, which illustrates the band gap in blue. The band gap narrows to approximately 7 eV during compression, compared to about 9.5 eV during extension, a behavior which was anticipated based on previous studies, for example, in ref. 72, is shown that for dense hydrogen, the band gap decrease linearly with increasing pressure, from 10.9 to 6.57 eV.
Additionally, RH6 is correlated with the pressure increase in the H6 system due to the dodecahedrane's compression (see bottom of Fig. 1). This distance follows the “breathing” mode of the dodecahedrane, showing a decrease in RH6 as the fullerane compresses, thereby compressing the six-atom system.
Fig. 1–3 collectively elucidate the evolution of the H6@C20H20 system and the impact of a radially symmetric vibrational mode on the H6 assembly. The compression of the molecular cage induces significant compression within the H6 system, with pressures surpassing 300 GPa at peak compression points (see bottom of Fig. 1). The geometric configurations associated with these extreme pressures are distinctly three-dimensional, as indicated by the peaks in the volume ratio (see the blue curve of Fig. 2). These high pressure configurations lead to notable changes in the system's energy levels. Additionally, as the cage compresses the H6 system, the band gap of the entire H6@C20H20 structure narrows, highlighting the dynamic interplay between structural and electronic properties under extreme conditions.
At each time-step, the system's classical analogue to a thermodynamic phase, as described in Table 1, can be identified. For the sake of simplicity and ease of reference throughout the text, we will refer to this classical analogue to a thermodynamic phase simply as “phase”. Fig. 4 illustrates the evolution of the six-hydrogen atom system, presenting the phases it traverses alongside the cage radius over time. Notably, during peak compression of the cage, the H6 system transitions into the metallic liquid analogue state, whereas during cage extension, it reverts to the molecular liquid analogue state. Between these extremes, the system exhibits transitions between these two analogues states. To complement this phase evolution plot, Fig. 5 shows the molecular structure of the system at three key moments in time, corresponding to low pressure, peak compression, and partial relaxation. These visualizations73 highlight the dynamic structural rearrangements of the hydrogen atoms induced by the cage's radial vibrational mode and their correlation with internal pressure.
| Phase | Pressure (GPa) | Temperature (K) |
|---|---|---|
| Molecular liquid4,23 | 70–120 | 850–2000 |
| 120–140 | 800–1500 | |
| 140–160 | 750–1300 | |
| 160–180 | 650–1000 | |
| 180–200 | 600–750 | |
| 200–225 | 550–700 | |
| 225–250 | 500–650 | |
| 250–325 | 520–600 | |
| Metallic liquid24,25 | 100–120 | >2000 |
| 120–140 | >1500 | |
| 140–160 | >1300 | |
| 160–180 | >1000 | |
| 180–200 | >750 | |
| 200–225 | >700 | |
| 225–250 | >650 | |
| 250–325 | >600 | |
| 325–425 | >520 | |
| 425–500 | >500 | |
| >500 | >500 | |
| Phase I3,4 | 70–120 | 100–850 |
| 120–140 | 100–800 | |
| 140–160 | 100–750 | |
| 160–180 | 200–650 | |
| 180–200 | 280–600 | |
| 200–225 | 350–550 | |
| 225–250 | 450–500 | |
| Phase II5 | 70–160 | 0–100 |
| Phase III7–12 | 160–180 | 0–200 |
| 180–200 | 0–280 | |
| 200–225 | 0–350 | |
| 225–250 | 0–300 | |
| 250–325 | 0–250 | |
| 325–425 | 0–200 | |
| Phase IV9,11,14 | 225–250 | 300–450 |
| 250–325 | 250–520 | |
| Phase V15 | 325–425 | 200–520 |
| Phase VI16,17 | 425–500 | 0–500 |
| Metallic solid | >500 | 0–500 |
 | ||
| Fig. 4 H6 system evolution across different analogues phases (red) and the dodecahedrane radius (blue) as a function of time. | ||
Table 2 outlines the primary outcomes of the simulation. Here, we introduce the ‘H–H distance’ metric which denotes the average of the six shortest distances between hydrogen atoms. This calculation offers insights into the interatomic distances among neighboring hydrogens, particularly relevant when the H6 system adopts a hexagonal structure geometric configuration, allowing for comparisons with existing literature data.
| Phase | H–H distance [Å] | VH6 [Å3] | P [GPa] | T [K] | |
|---|---|---|---|---|---|
| Molecular Liquid | 0.933 ± 0.075 | 0.496 ± 0.272 | 0.681 ± 0.336 | 210.066 ± 54.027 | 732.694 ± 212.700 |
| Metallic Liquid | 0.904 ± 0.073 | 0.578 ± 0.231 | 0.927 ± 0.301 | 325.259 ± 88.800 | 1680.330 ± 693.512 |
| Solid phase I | 0.966 ± 0.073 | 0.530 ± 0.257 | 0.613 ± 0.199 | 167.763 ± 35.556 | 454.792 ± 118.776 |
| Solid phase II | 1.169 ± — | 1.204 ± — | 0.891 ± — | 74.861 ± — | 46.609 ± — |
| Solid phase IV* | 0.810 ± 0.007 | 0.259 ± 0.030 | 0.511 ± 0.076 | 286.927 ± 24.302 | 445.988 ± 78.162 |
| Solid phase IV | 0.849 ± 0.052 | 0.441 ± 0.223 | 0.811 ± 0.345 | 290.483 ± 26.741 | 417.797 ± 74.687 |
| Solid phase V | 0.833 ± 0.041 | 0.452 ± 0.102 | 0.992 ± 0.192 | 342.816 ± 14.690 | 327.101 ± 55.446 |
| Solid phase VI | 0.775 ± — | 0.445 ± — | 1.201 ± — | 464.146 ± — | 463.448 ± — |
Among the 1000 analyzed data points, only 12 align with phase IV as per the criteria delineated in Table 1. However, 7 of these points exhibit consistent numerical values for volumes and volume ratios. Consequently, these data points have been evaluated, denoted as IV*. Notably, during phase IV*, the average hydrogen–hydrogen distance measures 0.810 Å ± 0.007, closely resembling the 0.82 Å value suggested by ref. 9. Additionally, minimal standard deviations associated with other parameters (volume and volume ratio) further validate the association of these points with phase IV.
For phases II and VI, standard deviation is not applicable, as the system transitions through these phases only once throughout the entire simulation.
Based on the findings outlined in Table 2, it's evident that the disparity in structure between phase I and the molecular liquid phase is minimal. Across the spectrum of states explored in this simulation, these two phases diverge primarily in temperature. Conversely, contrasting structural features emerge between the molecular liquid phase and the metallic liquid phase. In the metallic liquid phase, which is distinguished by higher pressures and temperatures relative to the molecular liquid, the average H–H distances exhibit a reduction. While the volumes of H6 remain approximately constant between the two states, the volume ratio is notably higher in the metallic liquid phase, indicating a denser atomic arrangement that manifests a more pronounced three-dimensional structure compared to the molecular liquid phase.
Noteworthy are the distinctions between phase I and phase IV*. As indicated in the table, hydrogen atom distances are shorter in phase IV*. Despite the system's exploration of states at temperatures akin to those associated with phase IV*, the higher pressure leads to reduced H–H distances (0.810 Å in phase IV* versus 0.966 Å in phase I). Moreover, the average volume in phase IV* is approximately halved compared to phase I. Although the reduction in average distances is not proportional, it suggests a planar configuration in phase IV*. The minimal standard deviation of distances hints at an approximately hexagonal structure, consistent with predictions from previous studies.9,14
In phase V, the inter-atomic distances increase on average by 0.02 Å compared to phase IV*. This transition is marked by a significant rise in the volume ratio and a slight increase in the system volume, suggesting a departure from hexagonal-planar symmetry as the system evolves into phase V. Furthermore, at temperatures close to those associated with phase IV* but at higher pressures, only one data point corresponds to phase VI. In this phase, the H6 system exhibits inter-atomic distances that are 0.058 Å shorter than those in phase V, alongside a moderate increase in volume and a pronounced expansion in the volume ratio. Phase VI represents a distinct three-dimensional configuration for the system.
These findings further reinforce the interpretation that the system dynamically explores different configurations associated with high-pressure hydrogen phases. The variation of RH6, VH6,  , and the volume ratio (Fig. 2 and 3) quantitatively describes the temporal structural evolution of the hydrogen cluster. For example, transitions from low-volume, low-ratio configurations (planar hexagonal) to high-volume, high-ratio ones (three-dimensional) reflect real-time changes in molecular geometry as the system moves between analogues of Phase IV, Phase V, and metallic liquid states. These configurational dynamics are consistent with the observed changes in electronic structure (Fig. 3), particularly the narrowing of the bandgap during compression events. Taken together, the geometric and electronic descriptors trace the full dynamical behavior of the H6 subsystem and its correspondence with known high-pressure hydrogen behavior.
, and the volume ratio (Fig. 2 and 3) quantitatively describes the temporal structural evolution of the hydrogen cluster. For example, transitions from low-volume, low-ratio configurations (planar hexagonal) to high-volume, high-ratio ones (three-dimensional) reflect real-time changes in molecular geometry as the system moves between analogues of Phase IV, Phase V, and metallic liquid states. These configurational dynamics are consistent with the observed changes in electronic structure (Fig. 3), particularly the narrowing of the bandgap during compression events. Taken together, the geometric and electronic descriptors trace the full dynamical behavior of the H6 subsystem and its correspondence with known high-pressure hydrogen behavior.
Finally, we note that the temperature range traversed by the H6 subsystem during the simulation is relatively high, typically between several hundred and over 1000 K (see Fig. 1 and Table 2). At such temperatures, the thermal kinetic energy of the protons is high, resulting in correspondingly short de Broglie wavelengths. Consequently, quantum nuclear effects such as delocalization, tunneling, and exchange are expected to be negligible to first order.25,74
4 Conclusions
In summary, we identified an alternative method for achieving the high pressures and temperatures associated with a hydrogen system. By encapsulating six hydrogen atoms within the C20H20 dodecahedrane, we studied the evolution of the H6@C20H20 system. The C20H20 cage began from an initial configuration extended by a scaling factor of k = 1.2, which initiated a compression corresponding to the symmetric radial vibration mode.We explored the effect of this vibrational mode on the sequestered H6 system by analyzing geometric, energetic, and thermodynamic parameters over a total simulation time of 0.5 ps, using a time step of 0.5 fs. Correlations between the monitored variables showed that as the C20H20 cage compressed, the internal hydrogen atoms underwent structural changes. These changes were reflected in volume variations and led to significant dynamics in the HOMO–LUMO levels and the band gap of the entire system. Additionally, the compression increased the pressure of the encapsulated hydrogen system to hundreds of GPa. The temperature, calculated from the average kinetic energy of the internal hydrogen atoms, also spanned a wide range.
The H6 system explored different thermodynamic analogues states at each time step, covering a wide region in the T–P diagram reported in the literature which includes high pressure hydrogen phases of interest: solid phases I, II, IV, V, and VI, as well as molecular and metallic liquid phases. This novel application of fullerane is significant for the field of high pressure hydrogen research and also in the hydrogen storage field. Further studies involving larger molecular cages or carbon nanotubes with more encapsulated atoms are necessary and also simulations with longer periods of time. This theoretical and computational study may pave the way for a new method of achieving dense hydrogen, potentially making the long-sought goal of room-temperature superconducting metallic hydrogen, first proposed by Wigner and Huntington nearly 90 years ago, a reality.
This study addresses a gap between experimental and theoretical approaches. While previous studies have introduced pressure and temperature as simulation parameters, our approach offers a new method for achieving those pressures and temperatures experimentally. This work not only advances our understanding of hydrogen behavior under extreme conditions but also suggests practical applications for creating metallic hydrogen.
Data availability
Data for this article, including the input files for the MD simulation, the single-point energy calculation and the results obtained at each time-step are available at Zenodo at https://zenodo.org/records/14843440.66Author contributions
Leonard Constantin Gebac: conceptualization, methodology, software, formal analysis, investigation, resources, writing – original draft. Vasile Bercu: conceptualization, validation, writing – original draft, writing – review & editing, supervision, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support provided by the project CNFIS-FDI-2025-F-0364: UB Research Nexus – Transforming Research through Innovation, Digitalization and Exploration at the University of Bucharest.References
- T. Guillot, Annu. Rev. Earth Planet. Sci., 2005, 33, 493–530 CrossRef CAS.
- V. L. Ginzburg, The Physics of a Lifetime: Reflections on the Problems and Personalities of 20th Century Physics, 2001, pp. 149–197 Search PubMed.
- H. K. Mao and P. M. Bell, Science, 1979, 203, 1004–1006 Search PubMed.
- E. Gregoryanz, C. Ji, P. Dalladay-Simpson, B. Li, R. T. Howie and H.-K. Mao, Matter Radiat. Extremes, 2020, 5, 038101 CrossRef CAS.
- X.-D. Liu, R. T. Howie, H.-C. Zhang, X.-J. Chen and E. Gregoryanz, Phys. Rev. Lett., 2017, 119, 065301 Search PubMed.
- I. F. Silvera and R. J. Wijngaarden, Phys. Rev. Lett., 1981, 47, 39 CrossRef CAS.
- R. J. Hemley and H. Mao, Phys. Rev. Lett., 1988, 61, 857 CrossRef CAS PubMed.
- R. T. Howie, T. Scheler, C. L. Guillaume and E. Gregoryanz, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 214104 CrossRef.
- R. T. Howie, C. L. Guillaume, T. Scheler, A. F. Goncharov and E. Gregoryanz, Phys. Rev. Lett., 2012, 108, 125501 CrossRef PubMed.
- M. I. Eremets, A. P. Drozdov, P. Kong and H. Wang, Nat. Phys., 2019, 15, 1246–1249 Search PubMed.
- C. Ji, B. Li, W. Liu, J. S. Smith, A. Majumdar, W. Luo, R. Ahuja, J. Shu, J. Wang and S. Sinogeikin, et al., Nature, 2019, 573, 558–562 CrossRef CAS PubMed.
- Y. Akahama, M. Nishimura, H. Kawamura, N. Hirao, Y. Ohishi and K. Takemura, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 060101 CrossRef.
- M. Hanfland, R. J. Hemley and H.-k. Mao, Phys. Rev. Lett., 1993, 70, 3760 Search PubMed.
- C. J. Pickard and R. J. Needs, Nat. Phys., 2007, 3, 473–476 Search PubMed.
- P. Dalladay-Simpson, R. T. Howie and E. Gregoryanz, Nature, 2016, 529, 63–67 Search PubMed.
- P. Loubeyre, F. Occelli and P. Dumas, Nature, 2020, 577, 631–635 CrossRef CAS PubMed.
- L. Monacelli, M. Casula, K. Nakano, S. Sorella and F. Mauri, Nat. Phys., 2023, 19, 845–850 Search PubMed.
- R. P. Dias and I. F. Silvera, Science, 2017, 355, 715–718 CrossRef CAS PubMed.
- M. Borinaga, J. Ibañez-Azpiroz, A. Bergara and I. Errea, Phys. Rev. Lett., 2018, 120, 057402 CrossRef CAS PubMed.
- A. F. Goncharov and V. V. Struzhkin, Science, 2017, 357, eaam9736 CrossRef PubMed.
- I. F. Silvera and R. Dias, Science, 2017, 357, eaan2671 Search PubMed.
- H. Y. Geng, Matter Radiat. Extremes, 2017, 2, 275–277 CrossRef.
- I. Tamblyn and S. A. Bonev, Phys. Rev. Lett., 2010, 104, 065702 CrossRef PubMed.
- I. F. Silvera, R. Dias, O. Noked, A. Salamat and M. Zaghoo, J. Low Temp. Phys., 2017, 187, 4–19 CrossRef CAS.
- M. A. Morales, C. Pierleoni, E. Schwegler and D. M. Ceperley, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12799–12803 CrossRef PubMed.
- M. Eremets, V. Minkov, P. Kong, A. Drozdov, S. Chariton and V. Prakapenka, Nat. Commun., 2023, 14, 907 CrossRef CAS PubMed.
- D. D. Klug and Y. Yao, Phys. Chem. Chem. Phys., 2011, 13, 16999–17006 RSC.
- H. Nagara and T. Nakamura, Phys. Rev. Lett., 1992, 68, 2468 CrossRef CAS PubMed.
- C. J. Pickard, M. Martinez-Canales and R. J. Needs, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 214114 CrossRef.
- B. Monserrat, R. J. Needs, E. Gregoryanz and C. J. Pickard, Phys. Rev. B, 2016, 94, 134101 CrossRef.
- B. Monserrat, N. D. Drummond, P. Dalladay-Simpson, R. T. Howie, P. L. Ríos, E. Gregoryanz, C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2018, 120, 255701 CrossRef CAS PubMed.
- S. Azadi and G. J. Ackland, Phys. Chem. Chem. Phys., 2017, 19, 21829–21839 RSC.
- S. Azadi and T. D. Kühne, Phys. Rev. B, 2019, 100, 155103 CrossRef CAS.
- S. Azadi and W. Foulkes, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 014115 CrossRef.
- H.-C. Yang, K. Liu, Z.-Y. Lu and H.-Q. Lin, Phys. Rev. B, 2020, 102, 174109 CrossRef CAS.
- R. Singh, S. Azadi and T. D. Kühne, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 014110 CrossRef CAS.
- H. Liu and Y. Ma, Phys. Rev. Lett., 2013, 110, 025903 CrossRef PubMed.
- B. Min, H. Jansen and A. Freeman, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 6383 CrossRef CAS PubMed.
- H. Liu, L. Zhu, W. Cui and Y. Ma, J. Chem. Phys., 2012, 137, 074501 CrossRef PubMed.
- A. Özlem Çetin Karacaoğlan and M. Durandurdu, High Pressure Res., 2024, 1–14 Search PubMed.
- A. Bedjaoui, S. Bin-Omran and A. Bouhemadou, High Pressure Res., 2016, 36, 198–219 CrossRef CAS.
- C. L. Bull, S. A. Barnett, W. G. Marshall and D. R. Allan, High Pressure Res., 2019, 39, 179–184 CrossRef CAS.
- D. L. Y. D. Lun Xiong, L. Huang and J. Zhang, High Pressure Res., 2023, 43, 58–67 CrossRef.
- N. D. Drummond, B. Monserrat, J. H. Lloyd-Williams, P. L. Ríos, C. J. Pickard and R. J. Needs, Nat. Commun., 2015, 6, 7794 CrossRef CAS PubMed.
- S. Azadi, W. Foulkes and T. D. Kühne, New J. Phys., 2013, 15, 113005 CrossRef.
- S. Azadi, B. Monserrat, W. Foulkes and R. Needs, Phys. Rev. Lett., 2014, 112, 165501 CrossRef PubMed.
- H. Y. Geng, Q. Wu and Y. Sun, J. Phys. Chem. Lett., 2017, 8, 223–228 CrossRef CAS PubMed.
- R. Helled, G. Mazzola and R. Redmer, Nat. Rev. Phys., 2020, 2, 562–574 CrossRef CAS.
- J. Chen, X. Ren, X.-Z. Li, D. Alfè and E. Wang, J. Chem. Phys., 2014, 141, 024501 CrossRef PubMed.
- C. Li, J. Chem. Phys., 2024, 160, 144302 CrossRef CAS PubMed.
- L. A. Paquette, R. J. Ternansky, D. W. Balogh and G. Kentgen, J. Am. Chem. Soc., 1983, 105, 5446–5450 CrossRef CAS.
- R. J. Cross, M. Saunders and H. Prinzbach, Org. Lett., 1999, 1, 1479–1481 CrossRef CAS.
- L. C. Gebac, M. Bercu and V. Filip, Fullerenes, Nanotubes Carbon Nanostruct., 2023, 31, 448–458 CrossRef CAS.
- L. C. Gebac and A. Niculescu, Fullerenes, Nanotubes Carbon Nanostruct., 2023, 31, 583–591 CrossRef CAS.
- P. Divya and S. Ramaprabhu, Phys. Chem. Chem. Phys., 2014, 16, 26725–26729 RSC.
- B. H. Kim, W. G. Hong, H. Y. Yu, Y.-K. Han, S. M. Lee, S. J. Chang, H. R. Moon, Y. Jun and H. J. Kim, Phys. Chem. Chem. Phys., 2012, 14, 1480–1484 RSC.
- Y. Song, Phys. Chem. Chem. Phys., 2013, 15, 14524–14547 RSC.
- S. V. Chuvikov, E. A. Berdonosova, A. Krautsou, J. V. Kostina, V. V. Minin, E. A. Ugolkova and S. N. Klyamkin, Phys. Chem. Chem. Phys., 2021, 23, 4277–4286 RSC.
- U. Khalilov, U. Uljayev, K. Mehmonov, P. Nematollahi, M. Yusupov and E. Neyts, Int. J. Hydrogen Energy, 2024, 55, 604–610 CrossRef CAS.
- I. Ufimtsev and T. Martínez, J. Chem. Theory Comput., 2009, 5, 2619 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, J. Chem. Phys., 2007, 126, 191109 CrossRef PubMed.
- A. Malek, D. Peng, W. Yang, R. Balawender and A. Holas, Theor. Chem. Acc., 2014, 133, 1–7 Search PubMed.
- D. Hait, A. Rettig and M. Head-Gordon, J. Chem. Phys., 2019, 150, 094115 CrossRef PubMed.
- F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085 CrossRef CAS PubMed.
- A. M. N. Niklasson, P. Steneteg, A. Odell, N. Bock, M. Challacombe, C. J. Tymczak, E. Holmström, G. Zheng and V. Weber, J. Chem. Phys., 2009, 130, 214109 CrossRef PubMed.
- L. Gebac, Implementation of Molecular Dynamics Simulation for the H6@C20H20 System in TeraChem Software; Results & Video, 2025, DOI:10.5281/zenodo.14843440.
- A. D. Zakirova and D. S. Sabirov, Russ. J. Phys. Chem., 2020, 94, 963–971 CrossRef CAS.
- R. F. W. Bader and M. A. Austen, J. Chem. Phys., 1997, 107, 4271–4285 CrossRef CAS.
- K. Liao, X.-Z. Li, A. Alavi and A. Grüneis, npj Comput. Mater., 2019, 5, 110 CrossRef CAS.
- L.-P. Wang and C. Song, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- G. S. Boltachev and J. W. P. Schmelzer, J. Chem. Phys., 2010, 133, 134509 CrossRef PubMed.
- B. Li, Y. Ding, D. Y. Kim, L. Wang, T.-C. Weng, W. Yang, Z. Yu, C. Ji, J. Wang, J. Shu, J. Chen, K. Yang, Y. Xiao, P. Chow, G. Shen, W. L. Mao and H.-K. Mao, Phys. Rev. Lett., 2021, 126, 036402 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. M. McMahon, M. A. Morales, C. Pierleoni and D. M. Ceperley, Rev. Mod. Phys., 2012, 84, 1607–1653 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |





