DOI:
10.1039/D5RA03088A
(Paper)
RSC Adv., 2025,
15, 25633-25662
Tuning the properties of ASnTe3 (A = Li, Na, K, Rb, Cs) chalcogenide perovskites for optimal solar energy conversion: computational insights
Received
1st May 2025
, Accepted 9th July 2025
First published on 18th July 2025
Abstract
This study explores the structural, electronic, optical, mechanical, and thermodynamic properties of ASnTe3 (A = Li, Na, K, Rb, and Cs) chalcogenide perovskites using density functional theory (DFT). The stability of these materials was assessed by calculating formation energies, Goldschmidt tolerance factors (Tf), Bartel tolerance factor (τ), and phonon dispersion. Electronic structure calculations show indirect band gaps ranging from 0.27 to 1.32 eV, with minimal direct–indirect offsets (0.06–0.23 eV), indicating strong potential for both photovoltaic (Rb, Na, CsSnTe3) and thermoelectric (Li, KSnTe3) applications. Carrier type analysis reveals p-type behavior for Na, K, Rb, and Cs analogues, and n-type for LiSnTe3. Mechanical properties were comprehensively assessed using elastic constants, moduli, Poisson's ratio, Pugh's ratio, machinability index, Vickers hardness, and universal and Zener anisotropy indices, supported by 2D and 3D elastic modulus visualizations. All compounds exhibit elastic anisotropy and good ductility, with NaSnTe3 identified as the most ductile (Poisson's ratio > 0.30, B/G > 1.75). Vickers hardness varies from 0.99 GPa (KSnTe3) to 1.77 GPa (RbSnTe3), and KSnTe3 demonstrates superior machinability (3.05), favoring its practical processability. Thermodynamic parameters—including entropy, enthalpy, free energy, and heat capacity, were derived from phonon dispersion calculations. The materials also exhibit low lattice thermal conductivity (0.27–0.38 W m−1 K−1), high melting points (771–892 K), and favorable Debye temperatures (126–158 K). These results highlight ASnTe3 perovskites as promising, lead-free candidates for multifunctional applications, including solar energy conversion, thermoelectrics, thermal barrier coatings, and flexible electronics.
1. Introduction
Halide perovskites have emerged as a central focus in photovoltaics research over the past decade,1–4 following the pioneering work of Kojima et al., who demonstrated their application as visible-light sensitizers in 2009.5 Subsequent studies have substantiated their exceptional performance in a wide range of optoelectronic applications, including photodetectors,6,7 light-emitting diodes (LEDs),8,9 optical sensors,10,11 and solar cells.12,13 Despite these advances, hybrid lead halide perovskites are hindered by significant challenges, particularly poor ambient stability. The use of small organic cations, such as methylammonium (MA+), contributes to structural degradation upon exposure to moisture, oxygen, or heat. Substitution with larger organic cations, such as formamidinium (FA+), or inorganic cations like cesium, has been shown to partially improve their environmental stability. However, such modifications often introduce phase instability, necessitating complex material compositions and advanced encapsulation strategies.14–19 In addition to stability issues, the presence of lead in these materials raises environmental and health-related concerns. Although there is ongoing debate regarding the trade-off between the toxicity of lead and its performance benefits in photovoltaic devices,20–24 there is a consensus that efficient, stable, and lead-free alternatives are highly desirable. In response, considerable research has been directed toward identifying environmentally benign and structurally robust perovskite analogues. Proposed alternatives include Sn2+- and Ge2+-based halide perovskites,25 halide double perovskites (A2B′B′′X6),26 vacancy-ordered perovskites (A2BX6),27 and chalcogenide perovskites (ABCh3).28–30 Among these, chalcogenide perovskites featuring oxygen, sulfur, or selenium as anionic components are particularly promising due to their composition of earth-abundant and non-toxic elements. A variety of chalcogenide perovskites have demonstrated favorable optoelectronic and structural properties. Compounds such as AHfSe3 and AZrSe3 (A = Ca, Sr, Ba) exhibit suitable electronic and optical characteristics for photovoltaic applications.31,32 The Sr3ZnX3 series (X = S, Se, Te) offers high thermal stability and notable optoelectronic behavior, making them candidates for semiconductors and thermoelectric.33 LaScSe3, with a direct bandgap in the visible spectrum, has further reinforced the potential of chalcogenide perovskites in photonic technologies.34 Promising single-junction solar cell candidates include CaTiS3, BaZrS3, CaZrSe3, and CaHfSe3,35 while ACeTe3 (A = Ca, Sr, Ba) features optimal bandgaps (1.0–1.1 eV) for solar energy absorption.36 Additional candidates such as ABX3 (A = Ba; B = Zr; X = S, Se)37 and Ca6ZrHfS6 (ref. 38) show promising light absorption and detection properties. Further theoretical investigations have identified compounds such as LiScSe2, RbScSe2, and AScS (A = K, Rb) as potential materials for optoelectronic, thermoelectric, and solar absorption applications.39,40 Density functional theory (DFT) studies have also highlighted Al2CdX4 (X = S, Se, Te),41 RbAlTe2, and CsAlTe2 (ref. 42) as strong candidates for photovoltaic deployment. These findings are supported by a growing body of experimental and computational research, underscoring the potential of chalcogenide perovskites in next-generation energy technologies.43–48 Our previous DFT-based investigations into the ABS3 and ABSe3 systems (A = Li, Na, K, Rb, Cs; B = Si, Ge, Sn) have demonstrated their promising properties for solar energy conversion.49–51
Recent experimental efforts have further validated the applicability of chalcogenide perovskites in energy technologies. For instance, Han et al. synthesized EuHfS3, a low-bandgap antiferromagnetic material, for photovoltaic and spintronic applications.52 Jia et al. reported the fabrication of CaSnS3 thin films via sulfurization of CaSnO3, demonstrating favorable characteristics for solar harvesting.53 Pradhan et al. achieved the formation of BaZrS3 and BaHfS3 thin films using single-phase molecular precursors at moderate synthesis temperatures, further highlighting their optoelectronic potential.54 Similarly, BaMS3 compounds (M = Zr, Hf, Ti) have shown great promise in light-based applications.55 Other studies include the synthesis of Rb0.2Ba0.4Cr5Se8, a material exhibiting enhanced thermoelectric performance,56 and investigations into Sr8Ti7S21, which shows potential for lithium–sulfur battery enhancement.57 Perera et al. successfully synthesized BaZrS3, CaZrS3, SrZrS3, and SrTiS3, confirming their suitability for energy harvesting,29 while Nishigaki et al. reported distorted chalcogenide perovskites (e.g., BaZrS3, SrZrS3, BaHfS3, and SrHfS3) with direct bandgaps between 1.94 and 2.41 eV, rendering them ideal absorbers for solar applications.58
Mechanical and thermal properties are critical in determining the practical applicability of perovskite materials, particularly for thin-film technologies in flexible photovoltaic devices.59,60 The elastic modulus plays a vital role in preventing cracking and ensuring mechanical integrity. While high elastic moduli may lead to brittleness and fracture, excessively low values can cause plastic deformation.61 Therefore, a moderate elastic modulus is generally desirable.62 Moreover, appropriate modulus matching between adjacent layers within a device minimizes interfacial stress and promotes adhesion.63
Thermal characteristics, such as the Debye temperature and thermal conductivity, also influence device efficiency.64–66 Lower Debye temperatures correlate with enhanced phonon–phonon scattering due to low-energy phonon modes, leading to reduced thermal conductivity, following the Slack model. This increase in scattering raises the probability of non-radiative relaxation, ultimately lowering the power conversion efficiency (PCE) of photovoltaic devices. Consequently, materials with higher Debye temperatures are typically preferred for high-efficiency solar cells.67 It is, therefore, essential to thoroughly assess the mechanical and thermal behavior of candidate materials before their incorporation into photovoltaic devices.
The tunability of perovskite properties via strategic A-site, B-site, and X-site substitution has greatly expanded their applicability across diverse fields, including solar energy harvesting, optoelectronics, environmental sensing, and photocatalysis. A-site cation substitution, in particular, has been shown to influence both stability and device performance. For example, K3Sb2I9 yields a higher photocurrent density (0.41 mA cm−2) compared to Cs3Sb2I9 and Rb3Sb2I9.68 In the inorganic A3NCl3 (A = Ba, Sr, Ca) perovskite family, Ba-based devices demonstrate the highest PCE (28.81%) compared to their Sr and Ca-based analogues.69 Similarly, the incorporation of Cs+ and Rb+ with MA+ and FA+ has been reported to enhance grain size, carrier lifetime, and device efficiency.70 A-site cation substitution also influences photocatalytic performance, as evidenced in LnTaON2 (Ln = La, Pr), where LaTaON2 exhibits superior H2 and O2 evolution activity.71 Furthermore, Ba2LuTaO6 displays greater photosensitivity than Sr2LuTaO6, suggesting enhanced photocatalytic potential.72
This study addresses the pressing need for stable, lead-free, and tunable semiconducting materials tailored for advanced energy technologies. We hypothesize that systematic substitution of the A-site cation (Li, Na, K, Rb, Cs) in ASnTe3 chalcogenide perovskites (Fig. 1) enables precise control over their band gap, optical absorption, and thermal properties, thereby optimizing them for targeted applications such as photovoltaics and high-temperature thermal management. To evaluate this hypothesis, we conduct a comprehensive first-principles investigation based on density functional theory (DFT). The specific objectives of this work are to: (i) assess the structural stability and phonon dynamics of ASnTe3 compounds; (ii) analyze their electronic band structures and the impact of A-site substitution on band gap tunability; (iii) evaluate their optical properties to determine light-harvesting potential across the solar spectrum; (iv) investigate their mechanical characteristics to ensure structural robustness; and (v) examine their thermodynamic behavior, including lattice thermal conductivity, to assess suitability for thermal barrier coating applications. The findings from this study offer fundamental insights and theoretical guidance for the design and experimental development of next-generation lead-free perovskite materials for sustainable energy solutions.
 |
| | Fig. 1 Schematic of our studied perovskites. | |
Given the absence of experimental data and the novelty of these materials, we employed the Heyd–Scuseria–Ernzerhof hybrid functional (HSE06)73 to enhance the accuracy of electronic structure predictions. HSE06 is well-established for its improved reliability in estimating band gaps, charge transport, and optical properties in perovskite systems. Although computationally demanding, the hybrid functional's accuracy makes it particularly suitable for exploratory studies such as this, where predictive fidelity is critical to guiding future experimental realization. The insights gained provide a foundational understanding and theoretical framework for the development of lead-free perovskite semiconductors in sustainable energy applications. Moreover, although ASnTe3 materials have not yet been synthesized experimentally, structurally and chemically analogous compounds have been successfully fabricated. Liao et al.74 reported the synthesis of various alkali metal tin sulfides, including K2Sn2S8, α-/β-Rb2Sn2S8, and Cs2Sn2S6, via molten salt techniques at moderate temperatures (275–450 °C). These compounds feature Sn(IV) coordination environments and A-site alkali cations similar to those proposed in ASnTe3, reinforcing the feasibility of their synthesis through similar methods.
2. Theoretical methodology
All computational analyses were performed using the CASTEP code within the Materials Studio 2020 software suite (https://www.3ds.com/products/biovia/materials-studio), based on the DFT. The crystal structure of CsSnS3 (triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 2), as provided by the Materials Project database (mp-561710),75 was used as the initial model. Systematic atomic substitutions were carried out to investigate the effects of compositional variations: the A-site Cs atom was replaced with Li, Na, K, and Rb; the B-site Sn atom was substituted with Si and Ge; and the X-site S atoms were replaced with Te. Geometry optimization, as well as electronic and optical property calculations, were conducted using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.73 All exchange–correlation (XC) functionals were evaluated using a kinetic energy cutoff of 650 eV, employing norm-conserving pseudopotentials.76
, 2), as provided by the Materials Project database (mp-561710),75 was used as the initial model. Systematic atomic substitutions were carried out to investigate the effects of compositional variations: the A-site Cs atom was replaced with Li, Na, K, and Rb; the B-site Sn atom was substituted with Si and Ge; and the X-site S atoms were replaced with Te. Geometry optimization, as well as electronic and optical property calculations, were conducted using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.73 All exchange–correlation (XC) functionals were evaluated using a kinetic energy cutoff of 650 eV, employing norm-conserving pseudopotentials.76
The self-consistent field (SCF) convergence criterion was set to 1.0 × 10−6 eV per atom. Geometry optimizations adhered to the following convergence thresholds: a total energy tolerance of 1.0 × 10−5 eV per atom, a maximum Hellmann–Feynman ionic force of 0.03 eV Å−1, and a maximum ionic displacement of 0.001 Å. For Brillouin zone sampling, a dense Monkhorst–Pack k-point mesh of 12 × 12 × 12 was employed.
The optical characteristics have been calculated using the HSE functional and the complex dielectric constant, which is described below:77
| | |
ε(ω) = ε1(ω) + iε2(ω)
| (1) |
The well-established Kramers–Kronig relations connect the real and imaginary components of the complex dielectric function, and can be expressed as follows:78,79
| |
 | (2) |
where,
P denotes the principal value of the integral.
| |
 | (3) |
Here,
u and
e denote the polarization of the incident electric field and the electric charge, respectively.
Ω represent the volume of a unit cell.
ψck and
ψυk signify the wave functions of the valence band and conduction band, respectively, at the position k.
Additional optical parameters, including the reflectivity R(ω), absorption coefficient α(ω), optical conductivity σ(ω), energy loss function L(ω), the real part of the conductivity, and the refractive index n(ω), were calculated as follows.80–82
| |
 | (4) |
| |
 | (5) |
| |
 | (6) |
| |
 | (7) |
| |
 | (8) |
| |
 | (9) |
Mechanical and thermodynamic properties were evaluated using the generalized gradient approximation (GGA) with the PBESOL exchange–correlation functional.83 To assess the mechanical behavior, key parameters such as bulk modulus (B), shear modulus (G), Young's modulus (Y), Poisson's ratio (ν), and machinability index (μm), and Vickers hardness (HV), were investigated. Additionally, elastic anisotropy was characterized using universal anisotropic index (AU), and Zener anisotropy factor (A), based on the computed elastic constants.84 The bulk modulus, shear modulus, and Young's modulus were derived using the Voigt–Reuss–Hill (VRH) averaging scheme,85 which combines the upper and lower bounds of elastic moduli. In this framework, the Voigt model assumes uniform strain throughout the crystal structure,86 whereas the Reuss model assumes uniform stress.87 According to Voigt's theory, the bulk modulus (B) and shear modulus (G) can be calculated as follows:
| |
 | (10) |
| |
 | (11) |
while in the Reuss theory,
| |
 | (12) |
| |
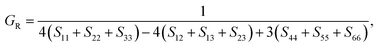 | (13) |
where
Sij is the elastic compliance matrix.
The B, G, B/G, Y, v, μm, HV, AU, and A88–90 can be calculated as:
| |
 | (14) |
| |
 | (15) |
| |
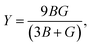 | (16) |
| |
 | (17) |
| |
 | (19) |
| |
 | (20) |
| |
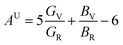 | (21) |
| |
 | (22) |
The Debye temperature (θD) is a fundamental thermal parameter that characterizes the highest temperature associated with a single normal vibrational mode within a crystal. It plays a pivotal role in correlating the mechanical properties of solids with various physical phenomena, including lattice vibrations, thermal expansion, melting point, specific heat capacity, and thermal conductivity. Defined as the temperature corresponding to the maximum phonon frequency, it also marks the lower bound for the onset of lattice vibrations. The Debye model provides an accurate description of the temperature dependence of specific heat at low temperatures, offering significant improvements over the classical Dulong–Petit law. A higher Debye temperature is typically indicative of stronger interatomic bonding and higher acoustic phonon velocities within the material. It is commonly estimated using elastic constants and the average speed of sound in the crystal lattice. The Debye temperature yields critical insights into phonon-mediated thermal transport and is frequently used to predict thermal conductivity. Materials with high Debye temperatures tend to exhibit lower specific heat capacities at low temperatures and enhanced thermal stability. Moreover, θD is a key parameter in understanding the thermodynamic behavior of solids, including their stability, phase transitions, and suitability for high-temperature applications. In the present study, the Debye temperature was calculated using the obtained elastic modulus values and other relevant mechanical parameters. The following equations were employed for this purpose:91
| |
 | (23) |
In this expression,
h and
kB denote the Planck and Boltzmann constants, respectively,
NA is Avogadro's number,
ρ represents the density,
M is the molecular weight, and
n is the number of atoms contained in the unit cell of ASnTe
3.
The average sound velocity (vm) is calculated by using the relation as given in the literature92 as,
| |
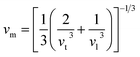 | (24) |
vm can be determined using the values of
vt and
vl, which the transverse and longitudinal sound velocities, respectively
| |
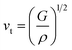 | (25) |
| |
 | (26) |
At the melting temperature (Tm), a substance undergoes a phase transition from solid to liquid under ambient pressure, a process commonly known as melting. Fine et al. proposed the following empirical equation for calculating Tm:93
The minimum thermal conductivity (Kmin) is a critical parameter that quantifies the rate of heat conduction through a material. As temperature increases, the thermal conductivity typically decreases until it reaches a specific threshold, known as the minimum thermal conductivity.94 The value of Kmin can be estimated using the volume fraction (vm), as expressed in the following equation:94
| |
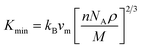 | (28) |
In the CASTEP code, the results of linear response calculations for phonon spectra can be employed to determine various thermodynamic properties, including entropy, enthalpy, free energy, and heat capacity, as functions of temperature. Vibrational analyses performed within CASTEP yield thermodynamic data, which can be visualized using the built-in thermodynamic analysis tools. The temperature dependence of the enthalpy is described by the following equation:
95–97| |
 | (29) |
Here,
Ezp represents the zero-point vibrational energy of the lattice,
kB denotes Boltzmann's constant,
ℏ is the reduced Planck constant, and
F(
ω) corresponds to the phonon density of states. The
Ezp can be computed as:
| |
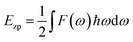 | (30) |
The contribution to the free energy is expressed as:
| |
 | (31) |
The contribution to the entropy is expressed as:
| |
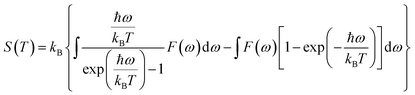 | (32) |
The lattice contribution to the heat capacity is
| |
 | (33) |
3. Results and discussion
3.1. Structure stability
Structural properties are crucial as they influence a system's arrangement and stability. These properties help determine optimal lattice constants, serving as a fundamental basis for analyzing various system characteristics. Fig. 2 illustrates the optimized crystal structure of triclinic ASnTe3 and the Mulliken bond population analysis (MBP) heatmap. As the A-site cation varies from Li+ to Cs+, the progressive increase in ionic radius induces a systematic lattice expansion, resulting in a larger unit cell volume. This volumetric change reflects the structural accommodation required to host the larger alkali ions within the crystal framework (Table 1). Since ASnTe3 compounds have yet to be synthesized, their stability must be evaluated before analyzing other properties. Stability can be inferred from tolerance factor (Tf),98 Bartel tolerance factor (τ),99 formation energy (Eform), and phonon dispersion. Eqn (34–36) are used to determine these Tf, τ, and Eform values.
 |
| | Fig. 2 The optimized structures of the ASnTe3 (a) and the heatmap of MBP (b) in ASnTe3. | |
Table 1 The lattice parameters and unit cell volume (V) for ASnTe3 using HSE06 method
| Perovskite |
Lattice parameter (Å) |
Angle (degree) |
Unit cell volume (Å3) |
| a |
b |
c |
α (degree) |
β (degree) |
γ (degree) |
V |
| LiSnTe3 |
6.747 |
5.646 |
9.146 |
105.719 |
110.500 |
113.817 |
261.725 |
| NaSnTe3 |
6.517 |
6.150 |
8.412 |
89.937 |
117.039 |
109.973 |
288.728 |
| KSnTe3 |
7.115 |
6.412 |
8.4082 |
88.934 |
117.245 |
107.736 |
321.530 |
| RbASnTe3 |
6.823 |
6.597 |
9.427 |
89.820 |
116.927 |
116.730 |
327.076 |
| CsSnTe3 |
7.404 |
6.899 |
8.277 |
88.773 |
116.915 |
106.881 |
357.769 |
To comprehensively evaluate the structural stability of the ASnTe3 perovskites, we employed the classical Goldschmidt tolerance factor (Tf), as given in eqn (34):98
| |
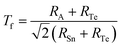 | (34) |
where
RA,
RSn and
RTe are the Shannon ionic radii of
A.
100 The calculated
Tf values are 0.77, 0.88, 0.95, 0.97, and 1.01 for LiSnTe
3, NaSnTe
3, KSnTe
3, RbSnTe
3, and CsSnTe
3, respectively. These values fall within or near the empirically accepted perovskite stability range of 0.8 <
Tf < 1.1, indicating the feasibility of forming distorted yet structurally viable ABX
3 perovskite frameworks. It is well-established that the classical
Tf primarily derived for oxide perovskites, exhibits limitations in accurately predicting the stability of non-oxide systems like chalcogenides, as it does not explicitly account for crucial factors such as bond valence and octahedral distortions prevalent in these materials. To further refine this analysis, we adopted the recently developed Bartel tolerance factor (
τ),
99 as defined in
eqn (35). This factor more effectively captures the impact of ionic radii mismatches and coordination environments, particularly in complex and non-oxide systems.
| |
 | (35) |
where
nA refers to the oxidation state of A. The calculated
τ values are 6.63 (LiSnTe
3), 4.88 (NaSnTe
3), 4.75 (KSnTe
3), 4.73 (RbSnTe
3), and 4.73 (CsSnTe
3), respectively. According to Bartel's model, lower
τ values indicate higher perovskite-forming probability, with
τ < 4.18 indicating high synthesizability and stability. Although our results slightly exceed this threshold, they remain within the extended range where distorted perovskite phases have been reported experimentally, particularly in chalcogenide systems where significant covalency of the Sn–Te bonding and octahedral distortion are present.
101 The decreasing trend as we move down the alkali metal group (from Li to Cs) suggests increasing structural compatibility within the perovskite framework. The combination of these analyses reveals that while geometric descriptors provide useful trends (CsSnTe
3 > RbSnTe
3 > KSnTe
3 > NaSnTe
3 > LiSnTe
3 in stability), the ultimate stability of ASnTe
3 perovskites derives from a balance of covalent bonding and lattice adaptability to distortions. Further insight into the bonding environment was obtained
via MBP, as illustrated
Fig. 2b. This analysis quantifies the shared electron density between atomic pairs, where higher MBP values signify stronger, more covalent bonds, and lower positive values indicate weaker or more ionic interactions. A zero MBP value represents a perfectly ionic bond, while increasing positive values denote a progressively higher degree of covalency. The heatmap reveals distinct trends in the bond character across the ASnTe
3 series, highlighting the tunable nature of the Sn–Te bonds with varying A-site cations. The highest Sn–Te bond populations (0.62–1.43) were observed in LiSnTe
3, signifying strong covalent bonding. In contrast, NaSnTe
3 showed significant bond asymmetry, with several populations dropping (0.09–0.74), highlighting a weaker, more distorted coordination around Sn. From KSnTe
3 to CsSnTe
3, the bond populations became more uniform and moderate (0.22–0.77), suggesting better orbital overlap and reduced strain in the SnTe
6 octahedra. Additionally, Te–Te bonds show significant covalent character, particularly in LiSnTe
3. The total bond populations further reinforce this observation, with LiSnTe
3 having the highest cumulative bonding and NaSnTe
3 the lowest. The total bond populations are 9.92, 4.09, 6.19, 5.99, and 5.94, for LiSnTe
3 to CsSnTe
3, respectively.
It is important to note that geometric tolerance factors serve as preliminary indicators; the ultimate determination of structural and dynamical stability is confirmed through rigorous calculations of negative formation energies (Eform) and the absence of imaginary frequencies in the phonon dispersion curves. The Eform was calculated by eqn (36).
| | |
Eform = EASnTe3 − (EA + ESn + 3ETe)atom
| (36) |
where
EA,
ESn and
ETe represent the energy of A, Sn and Te atoms, respectively;
EASnTe3 represents the energy of ASnTe
3 unit cell.
Fig. 3 illustrates the trends observed in the calculated
Eform for ASnTe
3. The negative values of
Eform also indicate their feasibility for experimental synthesis. The for
Eform of ASnTe
3 compounds is intrinsically linked to the identity of the A-cation and its subsequent impact on the tolerance factor. In perovskite-like structures, the A-cation occupies a large void or “cage” within the framework formed by the B-site (Sn) and anion (Te). As the ionic radius of the A-cation increases, it tends to fill this void more optimally, leading to a more ideal geometric fit. This reduction in structural strain results in a more energetically favorable atomic arrangement, thereby lowering the compound's formation energy. Consequently, a higher tolerance factor (approaching unity) correlates with a lower (more negative) formation energy, indicating enhanced thermodynamic stability. This direct relationship underscores the critical role of the A-cation's identity in dictating both the geometric perfection and the intrinsic thermodynamic stability of these telluride compounds.
 |
| | Fig. 3 Variation of formation energy for ASnTe3. | |
Thermodynamic stability is further confirmed by the absence of imaginary frequencies in the phonon dispersion curves, as shown in Fig. 4. A notable feature in this figure is the phonon band gap. This band gap is evident in KSnTe3, RbSnTe3, and CsSnTe3, whereas it is extremely small for LiSnTe3 and NaSnTe3. The presence of phonon band gap regions in the dispersion where no phonon modes exist can reduce thermal conductivity.102 Therefore, we can conclude that KSnTe3, RbSnTe3 and CsSnTe3 have lower thermal conductivity compared to other studied perovskites.
 |
| | Fig. 4 Phonon dispersion curves for the chalcogenide perovskites ASnTe3 using the GGA/PBEsol method; (a) LiSnTe3, (b) NaSnTe3, (c) KSnTe3, (d) RbSnTe3, and (e) CsSnTe3. | |
3.2. Electronic properties
3.2.1. Electronic properties. The electronic energy band structure is a key tool for understanding the range of energies available to electrons in a material. The band structures of ASnTe3 were computed and are shown in Fig. 5. Table 2 presents the calculated band gap (Eg) values for ASnTe3, comparing them with similar perovskites from previous studies. Additionally, it includes the difference between the indirect and direct band gaps (ΔEg) for each composition. As the A-site cation changes from Li to Cs, the band gap follows the trend: LiSnTe3 < KSnTe3 < CsSnTe3 < NaSnTe3 < RbSnTe3. Prior research indicates that in ABX3 perovskites, the band gap typically decreases with increasing electronegativity of the A-site cation.103–105 Lower electronegativity weakens A-Te interactions, reducing orbital overlap between cations and anions, which in turn leads to a larger Eg. However, as shown in Table 2, NaSnTe3 exhibits a larger Eg than KSnTe3, and RbSnTe3 has a larger Eg than CsSnTe3, despite the fact that Na has a higher electronegativity than K, and Rb has a higher electronegativity than Cs. This suggests that the bonding strength between Te and the A-site cation has a limited influence on the band gap in these materials. The deviation observed in KSnTe3 and CsSnTe3 from the expected electronegativity-band gap relationship mirrors similar inconsistencies reported in previous studies for (NaSnI3 > KSnI3), (NaRhO3 > KRhO3), (RbSnI3 > CsSnI3), and (RbGeI3 > CsGeI3).106,107 The band gap of perovskites decreases when moving from sulfides (S) to selenides (Se) and further to tellurides (Te). This trend is attributed to the upward shift of the valence band edge, which occurs due to the increasing energy of the p-orbitals as one progresses from 4p (selenium) to 5p (tellurium).108,109
 |
| | Fig. 5 Band structure curves for the ASnTe3 perovskites using the HSE06 method; (a) LiSnTe3, (b) NaSnTe3, (c) KSnTe3, (d) RbSnTe3, and (e) CsSnTe3. The colored circles, yellow and red, on the VBM and CBM, respectively. The green arrow indicates the onset of the direct band. | |
Table 2 The Eg and ΔEg values of the studied perovskites using the HSE06 method are compared with similar published perovskites
| Perovskite |
Eg |
ΔEg |
Perovskite |
Eg |
Method |
Ref. |
Perovskite |
Eg |
Method |
Ref. |
Perovskite |
Eg |
Method |
Ref. |
| This work |
| LiSnTe3 |
0.27 |
0.06 |
LiSiCl3 |
0.28 |
TB-mBJ |
113 |
CsGeBr3 |
1.15 |
HSE06 |
114 |
CsGeI3 |
1.19 |
HSE06 |
115 |
| NaSnTe3 |
1.10 |
0.20 |
MASnI3 |
1.15 |
Exp. |
116 |
TlGeBr3 |
1.14 |
TB-mBJ |
117 |
CH3NH3Sn0.5Pb0.5I3 |
1.18 |
Exp. |
118 |
| KSnTe3 |
0.58 |
0.12 |
FASnI3 |
1.15 |
Exp. |
119 |
TlSnCl3 |
1.19 |
TB-mBJ |
117 |
Cu2ZnSnSe4 |
1.15 |
Exp. |
120 |
| RbSnTe3 |
1.32 |
0.23 |
CsSnI3 |
1.15 |
HSE06 |
121 |
RbSnBr3 |
1.10 |
Exp. |
122 |
CsSiCl3 |
0.54 |
TB-mBJ |
113 |
| CsSnTe3 |
0.90 |
0.21 |
Rb2SnI6 |
1.10 |
HSE06 |
123 |
KSiF3 |
1.12 |
HSE06 |
124 |
KGeBr3 |
0.52 |
HSE06 |
127 |
| |
|
|
LiGeI3 |
0.59 |
HSE06 |
125 |
AlCuF3 |
0.54 |
TB-mBJ |
126 |
Rb2TlSbBr6 |
1.34 |
TB-mBJ |
129 |
| |
|
|
Cs2PtI6 |
1.32 |
HSE06 |
123 |
CsSnI3 |
1.30 |
Exp. |
128 |
TlGeCl3 |
1.39 |
TB-mBJ |
116 |
| |
|
|
NaSnCl3 |
1.36 |
HSE06 |
130 |
Rb2SnI6 |
1.32 |
Exp. |
131 |
Cs2CuSnI6 |
0.90 |
TB-mBJ |
132 |
| |
|
|
LiSiF3 |
0.93 |
HSE06 |
124 |
Na2AgAlBr6 |
0.94 |
TB-mBJ. |
133 |
NaSnSe3 |
1.63 |
HSE06 |
51 |
| |
|
|
LiSnS3 |
2.16 |
HSE06 |
50 |
RbSnS3 |
3.11 |
HSE06 |
50 |
KSnSe3 |
2.06 |
HSE06 |
51 |
| |
|
|
NaSnS3 |
2.55 |
HSE06 |
50 |
CsSnS3 |
3.30 |
HSE06 |
50 |
RbSnSe3 |
2.11 |
HSE06 |
51 |
| |
|
|
KSnS3 |
2.78 |
HSE06 |
50 |
LiSnSe3 |
1.5 |
HSE06 |
51 |
CsSnSe3 |
2.27 |
HSE06 |
51 |
In the electronic band structure, the Fermi level (Ef) is set to zero eV, serving as a reference point that distinguishes the conduction band (CB), positioned above Ef, from the valence band (VB), and located below Ef. A material can exhibit either an indirect or a direct band gap, depending on the alignment of its conduction band minimum (CBM) and valence band maximum (VBM). A direct band gap occurs when these two points coincide at the same k-point in the Brillouin zone, whereas an indirect band gap is observed when they do not align. The electronic properties of a material are largely determined by the band structure around Ef. The band structure of ASnTe3 within the energy range of −2 to 6 eV relative to Ef, as shown in Fig. 4. The CBM for KSnTe3, RbSnTe3, and CsSnTe3 is located at the F point in the first Brillouin zone, while for LiSnTe3 and NaSnTe3, it appears at the Ge point. The VBM is positioned at the Q point for LiSnTe3, NaSnTe3, KSnTe3 and CsSnTe3, whereas for RbSnTe3, it is found at the G point. These results confirm that LiSnTe3, NaSnTe3, KSnTe3, RbSnTe3, and CsSnTe3 are indirect band gap semiconductors. Since indirect band gap materials generally exhibit lower efficiency in photovoltaic and photocatalytic applications compared to those with direct band gaps, this characteristic may influence their suitability for such technologies. In direct bandgap materials, electron transitions occur without requiring momentum modification. In contrast, indirect bandgap materials necessitate the involvement of a phonon to conserve momentum during electronic transitions. This additional requirement significantly reduces the efficiency of photon absorption and the generation rate of electron–hole pairs, ultimately affecting the overall performance of devices fabricated from these materials.110 However, some indirect bandgap materials can still exhibit high efficiency in photovoltaic and photocatalytic applications. Specifically, materials with a small ΔEg of less than 0.5 eV have been shown to perform well in these fields.111 A small ΔEg reduces electron–hole separation, mitigating rapid recombination and thereby extending the lifetimes of electron–hole pairs, which is essential for effective photovoltaic processes. The studied perovskites exhibit ΔEg values within a favorable range of 0.06 to 0.23 eV, making them promising candidates for high-efficiency photovoltaic applications.
The bandgap of perovskites for single junction perovskite solar cells, with optimal bandgap values typically ranging from 0.9 to 1.60 eV.112 The bandgap values of LiSnTe3, NaSnTe3, KSnTe3, RbSnTe3, and CsSnTe3, are 0.27, 1.10, 0.58, 1.32, and 0.90 eV, respectively. The tunable bandgap characteristics observed in the studied materials may thus be highly beneficial for optoelectronic applications. Among the investigated perovskite materials, NaSnTe3, RbSnTe3, and CsSnTe3 emerge as the most promising candidates for photovoltaic applications due to their favorable bandgap values of 1.10 eV, 1.32 and 0.90 eV, respectively, which fall within the optimal range of 0.9 to 1.6 eV for single-junction solar cells. Likewise, materials such as RbSnBr3 (ref. 122) and KSiF3 (ref. 124) are currently being explored for their potential in solar cell applications, with reported band gaps of approximately 1.10 eV, which is comparable to that of NaSnTe3. Experimental studies have further demonstrated that CH3NH3Sn0.5Pb0.5I3 (ref. 118) is a viable material for solar cell applications, exhibiting a band gap closely matching that of NaSnTe3. Experimental investigations have also identified Rb2SnI6 (ref. 131) as a promising candidate for optoelectronic applications, demonstrating a band gap comparable to that of RbSnTe3. Additionally, theoretical studies suggest that NaSnCl3 (ref. 130) and Cs2PtI6 (ref. 123) exhibit significant potential for solar cell applications, as their band gaps are closely aligned with that of RbSnTe3. Finally, laboratory-based research has confirmed that Na2AgAlBr6 (ref. 133) possesses optoelectronic properties with a band gap comparable to that of CsSnTe3. In contrast, KSnTe3 (0.58 eV) and LiSnTe3 (0.27 eV) exhibit bandgap values significantly lower than the ideal photovoltaic range, rendering them less suitable for conventional solar cell applications. However, their narrow bandgaps make them attractive for alternative optoelectronic applications such as infrared detectors and thermoelectric devices. Theoretical investigations have identified LiSiCl3 (ref. 113) as a promising candidate for thermoelectric applications, exhibiting a band gap closely aligned with that of LiSnTe3. Moreover, KGeBr3 (ref. 127) has been investigated for its potential use in solar cells and radiation detection, with reported band gaps of approximately 0.5 eV, which is similar to that of KSnTe3.
The effective mass (m*) of charge carriers is a crucial parameter in determining the transport properties of photovoltaic materials. Within the framework of semiclassical transport theory, electrons and holes in semiconductors are characterized by effective masses, denoted as  and
and 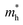 , respectively. These effective masses influence how charge carriers respond to an applied electric field. Consequently, both
, respectively. These effective masses influence how charge carriers respond to an applied electric field. Consequently, both  and
and 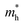 , along with the scattering of charge carriers by phonons, play a fundamental role in governing charge transport properties in photovoltaic materials.134 The m* of charge carriers associated with the VBM and CBM of ASnTe3 were determined through parabolic fitting of the band edges.
, along with the scattering of charge carriers by phonons, play a fundamental role in governing charge transport properties in photovoltaic materials.134 The m* of charge carriers associated with the VBM and CBM of ASnTe3 were determined through parabolic fitting of the band edges.
| m*(k) = ℏ2 × (∂2E(k)/∂k2)−1 |
Here,
ℏ and
E(
k) represent the reduced Planck's constant and the energy of the band edge as a function of the wave vector
k, respectively, which together define the local curvature of the band dispersion. The calculated effective mass values for ASnTe
3 are summarized in
Table 3. The
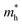
are larger than

, confirming the p-type character
135 of NaSnTe
3, KSnTe
3, RbSnTe
3, and CsSnTe
3 (
Table 3). Meanwhile,

are larger than

, further validating the n-type character
135 of LiSnTe
3. Furthermore,

of KSnTe
3 is found to be smaller than that in LiSnTe
3, NaSnTe
3, RbSnTe
3, and CsSnTe
3, suggesting a higher electron mobility for KSnTe
3.
Table 3 Calculated band gap (Eg) hole  and electron
and electron  effective masses for ASnTe3
effective masses for ASnTe3
| Perovskite |
LiSnTe3 |
NaSnTe3 |
KSnTe3 |
RbSnTe3 |
CsSnTe3 |
 |
0.256 |
1.506 |
2.381 |
3.149 |
1.472 |
 |
1.181 |
0.596 |
0.292 |
0.864 |
0.365 |
3.2.2. Density of states (DOS). The DOS quantifies the number of electronic states available per unit energy within a material, providing a fundamental description of its electronic structure. While the DOS offers a global perspective, it does not delineate the specific atomic orbital contributions to these states. In contrast, the partial density of states (PDOS) resolves the total DOS into contributions from individual atomic orbitals or atoms, enabling the investigation of atomic-level influences on material electronic properties. This is achieved by projecting the total DOS onto specific atomic orbitals (s, p, d) for each constituent atom. To elucidate the origins of observed semiconducting properties, the PDOS was calculated (Fig. 6). Analysis of the PDOS for LiSnTe3, under investigation reveals three distinct energy regions: (1) a region from approximately −16 to −11 eV, dominated by the Te-s states; (2) a region from −10 to 3 eV, primarily characterized by Te-p states; and (3) a region from 2 to 15 eV, exhibiting a complex composition with significant contributions from Li-p and Sn-p states, alongside minor contributions from Li-s, Te-s, Te-p, and Sn-s orbitals. Furthermore, the A-cation s states (Na-s, K-s, Rb-s and Cs-s) reveal the consistent presence of sharp peaks at around −55 eV for NaSnTe3, −32 eV for KSnTe3, −26 eV for RbSnTe3, −21 eV for CsSnTe3. Similarly, the A-cation p states (Na-p, K-p, Rb-p and Cs-p) exhibit sharp peaks around −27 eV for NaSnTe3, −16 eV for KSnTe3, −11 eV for RbSnTe3, −8 eV for CsSnTe3. Notably, a systematic shift of these sharp peaks towards the Fermi level is observed as the A-cation progresses from Na to Cs. The Te-s states consistently display broad peaks within the valence band, spanning approximately −15 to −10 eV for NaSnTe3 and KSnTe3, and −12 to −8 eV for RbSnTe3 and CsSnTe3. The Te-p states, observed in NaSnTe3, KSnTe3, RbSnTe3, and CsSnTe3, exhibit broad peaks within the valence band, ranging from approximately −5 to 0 eV. Finally, the A-cation d states (Na-d, K-d, Rb-d and Cs-d) are observed to contribute broad peaks within the conduction band, extending from approximately 3 to 18 eV for NaSnTe3, KSnTe3, RbSnTe3 and CsSnTe3.
 |
| | Fig. 6 The calculated PDOS of ASnTe3 using the HSE06; (a) LiSnTe3, (b) NaSnTe3, (c) KSnTe3, (d) RbSnTe3, and (e) CsSnTe3. The dashed vertical dashed line represents the Fermi level (EF), the reference point with zero energy. | |
3.3. Optical properties
Fig. 7a illustrates that the real part of the dielectric function, ε1(ω), exhibits both positive and negative values. The propagation of electromagnetic waves corresponds to the positive values, whereas absorption occurs in the negative region, where electromagnetic waves cannot propagate within the material. The ε1(0.01) for LiSnTe3, NaSnTe3, KSnTe3, RbSnTe3, and CsSnTe3 are 16.626, 11.850, 8.028, 7.826, and 6.935, respectively (Fig. 7a). Among these, LiSnTe3 exhibits the highest ε1(0.01), indicating a stronger dielectric response compared to the other studied perovskites. The ε1(ω) curves span an incident photon energy range from 0.0 eV to 50 eV, with maximum positive peaks of 15.03, 13.41, 10.24, 9.22, and 9.157 observed at lower photon energy for LiSnTe3, NaSnTe3, KSnTe3, RbSnTe3 and CsSnTe3, respectively. Beyond this range, ε1(ω) decreases sharply toward zero and reaches negative maximum values of approximately −1.98, −2.03, −1.29, −1.37, and −0.918 for the respective compounds within the 5 eV to 13 eV range. The negative values of ε1(ω) signify the onset of metallic, where the material exhibits complete reflection in these energy ranges. Materials with high ε1(ω) at low photon energies are particularly advantageous for optoelectronic applications, as a high dielectric constant enhances charge separation and transport efficiency. The ASnTe3 compounds exhibit the highest ε1(ω) values at lower energies (∼0.01 to 5.0 eV). Notably, LiSnTe3 and NaSnTe3 demonstrate competitive ε1(ω) values compared to conventional materials, such as silicon (∼11.7),136 CdTe (∼9.5),137 and emerging materials like CH3NHPbI3 (∼6.5).138 Similarly, KSnTe3 exhibits ε1(ω) values comparable to CdTe and CH3NHPbI3, while RbSnTe3 and CsSnTe3 show values competitive with CH3NHPbI3. These findings suggest that ASnTe3 compounds hold promise for photovoltaic applications, although factors such as stability, cost, and scalability must be carefully considered. Furthermore, ASnTe3 materials exhibit higher ε1(ω) values at low energies compared to ASnS3 and ASnSe3, as demonstrated in our previous work.50,51 This further highlights their potential for effective implementation in solar cell technologies.
 |
| | Fig. 7 Calculated spectra for the (a) real dielectric, (b) imaginary dielectric (c), absorption (d), and conductivity of ASnTe3. | |
Understanding the imaginary part of the dielectric function, ε2(ω), is essential for analyzing optical transitions from the valence band to the conduction band. Fig. 7b presents the ε2(ω) spectra for the studied materials, revealing that the maximum values occur within the 2 to 5.5 eV range. This indicates that optical absorption is most pronounced in the UV-vis region. The strong absorption in this range suggests that these perovskites hold significant potential for optoelectronic applications, particularly in devices such as light-emitting diodes.
The optical absorption coefficient quantifies the amount of energy a material absorbs per unit length and serves as a critical parameter for evaluating the potential solar energy conversion efficiency of a material. As shown in Fig. 7c, absorption does not commence at 0 eV, a characteristic attributed to the bandgap of ASnTe3. Notably, absorption in these perovskites begins within the visible spectrum, further supporting their relevance for optoelectronic applications. At an incident photon energy of 8–10 eV, ASnTe3 reaches its maximum absorption, indicating their strong potential for applications in the UV-visible range.
Optical conductivity describes the process of conduction of electrons upon photon absorption and provides valuable insights into the generation of free charge carriers. As shown in Fig. 7d, LiSnTe3 exhibits the highest optical conductivity among the studied perovskites. This behavior is attributed to its lower bandgap, which facilitates the generation of a greater number of electron–hole pairs. The conductivity spectra closely resemble the absorption spectra, as illustrated in Fig. 7d, since the material releases free carriers for conduction upon energy absorption. Notably, all ASnTe3 compounds exhibit favorable optical conductivity at lower energies, highlighting their potential for applications in UV-visible optical devices.
Reflectivity, R(ω), represents a material's ability to reflect incident energy from its surface. Fig. 8a presents the reflectivity spectra for ASnTe3 compounds, with R(0.01) values of 0.36, 0.30, 0.22, 0.23, and 0.20 for LiSnTe3, NaSnTe3, KSnTe3, RbSnTe3 and CsSnTe3, respectively. As photon energy increases, the probability of photon reflection from the material's surface also rises. The studied perovskites exhibit significant reflectivity within the 1.2 eV to 20 eV range, suggesting potential applications in infrared reflectors or coatings. At photon energies above 20 eV, the reflectivity values decline to approximately 0.1 or lower, indicating a reduction in metallic behavior. Small peaks or oscillations observed in the spectra may be attributed to interband transitions or plasma resonance effects. Lower reflectivity is generally desirable for applications in photovoltaics and photocatalysis, as it enhances light absorption rather than reflection.
 |
| | Fig. 8 Calculated spectra for (a) reflectivity, (b) loss function (c) reflectivity (d) extinction coefficient of ASnTe3. | |
For comparison, the reflectivity of commonly used thin-film solar cell materials, such as Cu2ZnSnS4 (20–25% in the visible spectrum),139 SrTiO3 (R around 20–30% in the visible spectrum),140 and CH3NH3PbI3 (5–15% in the visible spectrum),141 is lower than that of ASnTe3, which exhibits a significantly higher reflectivity (∼30–45%) in the low-energy region. This suggests that while ASnTe3 may be less effective for direct solar absorption, it could be advantageous for applications requiring high infrared reflectance, such as thermal barrier coatings or infrared optical devices.
The electron loss energy, L(ω), provides insight into the energy dissipation associated with fast-moving electrons traversing the lattice. The calculated L(ω)values for ASnTe3 are illustrated in Fig. 8b. Notably, no scattering is observed for photon energies below the bandgap, indicating the absence of energy loss in this range. Furthermore, in all cases, L(ω) remains negligible in the visible region. However, the highest values of L(ω) are observed at specific photon energies, corresponding to plasmon losses: 3.895 at 16.990 eV for LiSnTe3, 3.985 at 16.637 eV for NaSnTe3, 2.601 at 15.088 eV for KSnTe3, 2.031 at 14.183 eV for RbSnTe3, and 1.194 at 12.202 eV for CsSnTe3. Lower L(ω) values are advantageous for efficient electronic transport, as they minimize energy dissipation and enhance the photoelectric effect. This characteristic suggests that the studied perovskites exhibit promising potential for photovoltaic and optoelectronic applications, where efficient charge transport and minimal energy loss are crucial.
The suitable materials for optoelectronic applications exhibit refractive index values in the range of n(ω) = 2.0 to 4.0 in the low-energy region.142 As illustrated in Fig. 8c, all studied compounds achieve their highest refractive index within the 0–3.2 eV energy range. The maximum refractive index values are recorded at specific photon energies: 3.912 at 0.123 eV for LiSnTe3, 3.702 at 1.462 eV for NaSnTe3, 3.253 at 1.849 eV for KSnTe3, 3.078 at 2.308 eV for RbSnTe3, and 3.092 at 2.694 eV for CsSnTe3. The refractive index exceeds unity due to the interaction of photons with electrons, which slows down their propagation through the material. Materials with lower refractive indices tend to be more transparent, as they allow more light to pass through with minimal distortion or loss. Among the studied perovskites, RbSnTe3 exhibits the lowest refractive index, indicating greater transparency, whereas LiSnTe3 has the highest refractive index. Notably, around 8 eV, the n(ω) values for ASnTe3 drop below unity, signifying that these perovskites become optically opaque at higher energies. A higher refractive index in solar cell materials enhances internal light reflection within the active layer, improving light trapping and absorption. The refractive index values of LiSnTe3, NaSnTe3, KSnTe3, RbSnTe3, and CsSnTe3 are comparable to those of commonly used materials such as CdTe (∼2.6)143 and CH3NH3PbI3 (∼2.5–3.0).144 This suggests that these perovskites are competitive in terms of light interaction, reinforcing their potential for solar cell and optoelectronic applications.
The extinction coefficient, k(ω), represents the imaginary component of the complex refractive index and provides crucial information regarding light absorption. It characterizes absorption at the band edges, as observed in Fig. 8d, where k(ω) follows a similar trend to the ε2(ω) spectrum. The maximum values of k(ω) are recorded at specific photon energies: 2.178 at 5.418 eV for LiSnTe3, 2.049 at 5.348 eV for NaSnTe3, 1.955 at 5.075 eV for KSnTe3, 1.799 at 6.255 eV for RbSnTe3, and 1.764 at 4.719 eV for CsSnTe3. Notably, a decreasing trend in k(ω) is observed as the A-site cation transitions from Li to Cs. This suggests that LiSnTe3 exhibits the strongest light absorption among the studied perovskites, while CsSnTe3 demonstrates the weakest absorption.
3.4. Mechanical properties
The elastic parameters play a fundamental role in characterizing a material's response to externally applied loads, strains, and pressures. These parameters provide critical insights into the material's ability to withstand external forces and establish the threshold values within which the material maintains its mechanical integrity and functionality. To comprehensively analyze the mechanical properties of ASnTe3, the elastic constants Cij are computed, offering essential information on its mechanical behavior. In the case of triclinic crystals, the stability criteria necessitate the determination of 21 independent elastic constants Cij (C11, C12, C13, C14, C15, C16, C22, C23, C24, C25, C26, C33, C34, C35, C36, C44, C45, C46, C55, C56, and C66) respectively which are calculated based on finite strain theory.145 The values of the elastic constants are given in Table 4. The Born criterion for the stability of a triclinic symmetry crystal structure is that all eigenvalues of the Cij should be positive.146–148 Table 4 show that some elastic constants do not satisfy this criterion for mechanical stability in all directions. This indicates that the triclinic phase is mechanically unstable against the shear deformation along the direction of the C15, C16, C24, C26, C46 elastic tensor at zero temperature for LiSnTe3, along the direction of the C14, C24, C26, C36, C56 for NaSnTe3, along the direction of the C16, C26, C34, C35, C36, C46 for KSnTe3, along the direction of the C14, C15, C16, C24, C26, C34, C36, C45, C46 for RbSnTe3, along the direction of the C15, C24, C26, C34, C36, C45 for CsSnTe3. All the investigated perovskites exhibit higher C11 values compared to C44, indicating a greater resistance to unidirectional compression than to shear deformation. This suggests that the mechanical response of these perovskites is more robust under normal stresses than under shear stresses.
Table 4 The predicted elastic constants Cij (GPa) of ASnTe3
| Cij |
LiSnTe3 |
NaSnTe3 |
KSnTe3 |
RbSnTe3 |
CsSnTe3 |
| C11 |
50.96 |
37.18 |
54.24 |
36.82 |
57.34 |
| C12 |
21.15 |
17.84 |
11.67 |
11.29 |
30.69 |
| C13 |
26.58 |
18.20 |
21.13 |
23.06 |
33.35 |
| C14 |
3.00 |
−1.19 |
4.22 |
−1.23 |
4.66 |
| C15 |
−6.21 |
2.94 |
8.04 |
−2.30 |
−0.70 |
| C16 |
−0.81 |
0.74 |
−2.60 |
−0.83 |
1.22 |
| C22 |
111.58 |
36.93 |
40.95 |
51.30 |
47.84 |
| C23 |
13.88 |
5.54 |
30.26 |
16.45 |
16.29 |
| C24 |
−29.22 |
−7.02 |
1.08 |
−3.99 |
−12.68 |
| C25 |
1.89 |
1.44 |
0.64 |
2.56 |
2.57 |
| C26 |
−4.48 |
−10.85 |
−3.41 |
−10.77 |
−14.87 |
| C33 |
52.88 |
59.34 |
45.87 |
54.51 |
84.83 |
| C34 |
7.96 |
1.97 |
−3.09 |
−1.74 |
−0.79 |
| C35 |
7.36 |
1.17 |
−4.52 |
0.89 |
0.09 |
| C36 |
5.46 |
−0.98 |
−0.73 |
−3.16 |
−4.19 |
| C44 |
22.36 |
11.90 |
9.01 |
8.36 |
12.84 |
| C45 |
4.72 |
1.64 |
1.30 |
−4.19 |
−6.41 |
| C46 |
−1.58 |
2.03 |
−2.22 |
−2.25 |
0.42 |
| C55 |
13.70 |
3.40 |
13.30 |
12.48 |
11.10 |
| C56 |
1.01 |
−1.44 |
3.01 |
1.05 |
−0.37 |
| C66 |
14.61 |
14.54 |
7.44 |
13.96 |
16.16 |
Fig. 9 and Table 5 present the B, G, Y, ν, and Pugh's ratio for the ASnTe3 materials. The B is a critical parameter for assessing the hardness of a material. Among the examined perovskites, LiSnTe3 exhibits the highest B value (Fig. 9a), indicating its superior resistance to volumetric compression. This trend suggests that LiSnTe3 possesses the highest resistance to shape change under pressure compared to the other studied compounds. Interestingly, the bulk B values (Fig. 9a) and total bond populations of these materials reveal a consistent structure–property relationship governed by the A-site cation size and bonding characteristics. LiSnTe3 exhibits both the highest bulk modulus (36.23 GPa) and the largest total bond population (9.92), demonstrating how the small ionic radius of Li+ enhances orbital overlap and strengthens the covalent–ionic bonding network, resulting in superior structural rigidity. In contrast, NaSnTe3 shows the lowest values in both bulk modulus (21.83 GPa) and bond population (4.09), reflecting its reduced resistance to compression due to weaker bonding interactions from the larger Na+ ion. The intermediate compounds (KSnTe3, RbSnTe3, and CsSnTe3) follow a similar trend, with bond populations of 6.19, 5.99, and 5.94, respectively, corresponding to their bulk moduli of 27.44, 24.90, and 24.11 GPa. KSnTe3 displays a slightly higher bond population and B compared to RbSnTe3 and CsSnTe3. The G is a key parameter in describing a material's ability to resist shape deformation caused by shear forces and bond angle distortions. Among the ASnTe3 perovskites, LiSnTe3 exhibits the highest shear modulus (Fig. 9b), consistent with its exceptional bulk modulus and total bond population. In contrast, KSnTe3 shows the lowest G, reflecting its softer lattice. The Y modulus serves as a key indicator of a material's stiffness. As illustrated in Fig. 9c, the calculated Y values for the ASnTe3 series reveal an intriguing mechanical anomaly. Notably, the Rb- and Cs-based compounds exhibit stiffness values comparable to that of LiSnTe3, despite the significantly larger ionic radii of Rb+ and Cs+. This behavior contrasts with the trend observed in the bulk modulus and suggests the presence of cation-specific lattice reinforcement mechanisms. In contrast, NaSnTe3 consistently exhibits the lowest Y, affirming its role as the most deformable member of the series. KSnTe3 occupies an intermediate position. The ν ratio is a critical parameter for predicting the failure behavior of crystalline materials, with values below 0.26 indicating a tendency toward brittle failure, while values exceeding this threshold suggest a higher likelihood of ductile failure.148 The calculated ν values for ASnTe3 indicate a predominantly ductile nature (Fig. 9d). The distinction between ductile and brittle materials can also be assessed using Pugh's ratio.150 According to Pugh's criterion, a Pugh's ratio greater than 1.75 signifies ductility, whereas values below this threshold indicate brittleness. The calculated Pugh's ratio for the ASnTe3 compounds, presented in Table 5 and illustrated in Fig. 9e, confirms the ductile nature of all investigated perovskites. This finding aligns with the conclusions drawn from the analysis of ν. Among the materials, NaSnTe3 demonstrated exceptional ductility with the highest B/G ratio of 3.471. KSnTe3 showed particularly interesting behavior, possessing both a high B/G ratio (2.568) and the highest Poisson's ratio in the series (ν = 0.356), suggesting combination of ductility and toughness. The remaining compounds (LiSnTe3, RbSnTe3, and CsSnTe3) exhibited moderate ductility, with B/G values ranging from 1.847 to 2.025 and ν values between 0.301 and 0.315. These mechanical properties have important implications for potential applications: the remarkable ductility of NaSnTe3 makes it particularly suitable for flexible electronic devices, while the combination of ductility and toughness in KSnTe3 suggests promise for applications requiring fracture resistance, such as durable coatings or impact-resistant components.
 |
| | Fig. 9 Variation of (a) bulk modulus, (b) Shear modulus (c), Young's modulus, (d) ν, and (e) Pugh's ration for ASnTe3. | |
Table 5 The predicted B (GPa), G (GPa), Y (GPa), Pugh's ratio, ν, μm, and HV (GPa) of ASnTe3
| Perovskites |
B |
G |
Y |
B/G |
ν |
μm |
HV |
| LiSnTe3 |
36.23 |
15.22 |
36.224 |
1.847 |
0.315 |
1.620 |
1.698 |
| NaSnTe3 |
21.83 |
9.11 |
27.002 |
3.471 |
0.316 |
1.834 |
1.258 |
| KSnTe3 |
27.44 |
8.68 |
28.248 |
2.568 |
0.356 |
3.045 |
0.999 |
| RbSnTe3 |
24.90 |
11.38 |
34.778 |
2.025 |
0.301 |
2.980 |
1.767 |
| CsSnTe3 |
24.11 |
10.22 |
34.856 |
1.925 |
0.314 |
1.877 |
1.644 |
The mechanical behavior of the ASnTe3 was further evaluated by analyzing their μm and HV. The μm is defined as the ratio of the B to the elastic constant (C44) and serves as a measure of the ease of shaping or processing a material.89 This parameter is widely used to evaluate the industrial applicability of materials, with higher μm values indicating improved machinability. The HV is commonly used to assess the material's hardness, where hard materials (high HV) often show better wear resistance but can be brittle or difficult to shape. A comparison of these values, as presented in Table 5 and Fig. 10a, demonstrates that μm for KSnTe3 is higher than that of the other investigated perovskites. This suggests that KSnTe3 exhibits superior machinability, making it more suitable for industrial applications compared to the other studied compounds. To directly assess a material's hardness, the HV is commonly employed.90 A comparison of these values, as shown in Table 5 and Fig. 10b, indicates that the LiSnTe3 and RbSnTe3 exhibited the highest hardness values of 1.698 and 1.767 GPa, respectively, suggesting superior wear resistance. In contrast, KSnTe3 demonstrated the lowest hardness (0.999 GPa). KSnTe3 and RbSnTe3 showed the highest μm values of 3.045 and 2.980, respectively, indicating their favorable performance in manufacturing or microfabrication processes. These results highlight a trade-off between hardness and machinability, with KSnTe3 offering ease of processing but reduced wear resistance, whereas LiSnTe3 and RbSnTe3 may serve better in applications demanding mechanical durability.
 |
| | Fig. 10 (a) μm, (b) HV, (c) A, and (d) AU for the ASnTe3 perovskites. | |
3.5. Elastic anisotropy
Anisotropy, which refers to the directional dependence of a material's physical properties, is crucial in assessing its suitability for specific technological applications.149 Various physical factors, including plastic deformation, phonon modes, reaction rates, crystal defects, and the incorporation of foreign elements, can significantly influence the degree of anisotropy in a material. The anisotropic behavior of ASnTe3 compounds was assessed using the AU and A indices.89 For isotropic materials, AU is equal to 0 and A is equal to 1, with deviations from these values indicating the extent of anisotropy. Based on the data presented in Table 6, Fig. 10c and d, it is evident that both A and AU values for all the investigated compounds exceed their respective critical values, thereby confirming their anisotropic nature.
Table 6 The minimum and maximum limits of Y (GPa), G (GPa) and ν for ASnTe3
| Perovskite |
Y |
G |
ν |
A |
AU |
| Ymin |
Ymex |
Gmin |
Gmex |
νmin |
νmex |
| LiSnTe3 |
14.548 |
120.17 |
4.472 |
43.983 |
−0.514 |
0.932 |
1.500 |
5.216 |
| NaSnTe3 |
7.217 |
53.642 |
2.479 |
25.434 |
−0.579 |
1.254 |
1.230 |
5.087 |
| KSnTe3 |
12.752 |
73.817 |
4.372 |
31.009 |
−0.1373 |
1.0359 |
0.423 |
4.167 |
| RbSnTe3 |
12.683 |
54.372 |
5.042 |
20.075 |
−0.226 |
0.973 |
0.654 |
1.948 |
| CsSnTe3 |
13.851 |
45.506 |
4.400 |
18.975 |
−0.171 |
0.735 |
0.963 |
1.949 |
To gain a clearer understanding of the anisotropic behavior of ASnTe3, the 2D and 3D plots of the elastic moduli, including Young's modulus, shear modulus, and Poisson's ratio were calculated using the ELATE150 code. The 3D contour plots of E, G, and ν are shown in Fig. 11–13 along the xyz planes, respectively, while Fig. 14–16 display the 2D plots of E, G, and ν along the xy, yz, and zx planes. For an isotropic crystal, these contours are perfectly round, but for an anisotropic material, the contours deviate from this spherical shape.151 The extent of deviation indicates the degree of anisotropy, with more significant deviations suggesting stronger anisotropy. The maximum and minimum deviations from the ideal spherical shape are represented by blue and green colors, respectively. Table 6 presents the maximum and minimum values of E, G, and ν for the studied compounds. The observed sequence of increasing anisotropy follows the trend E < G < v. In Fig. 11, the green surface illustrates the path-dependent Young's modulus of the ABTe3, with the deep green color indicating regions of maximum anisotropy. Similarly, Fig. 12 and 13 depict the shear modulus and Poisson's ratio anisotropy of ABTe3, where deep blue clouds over the solid material indicate the areas with the highest shear modulus and Poisson's ratio, while the blue regions inside the material correspond to the lowest values of these moduli. The 2D plots of E, G, and ν (Fig. 14–16) further confirm the anisotropic nature of the studied phases, as the shapes deviate from the perfect spherical structure. Table 6 summarizes the minimum and maximum values of E, G, and ν.
 |
| | Fig. 11 3D projection of Y for the ASnTe3. | |
 |
| | Fig. 12 3D projection of G for the ASnTe3. | |
 |
| | Fig. 13 3D projection of ν for the ASnTe3. | |
 |
| | Fig. 14 2D projection of Y of the ASnTe3. | |
 |
| | Fig. 15 2D projection of G of the ASnTe3. | |
 |
| | Fig. 16 2D projection of ν of the ASnTe3. | |
3.6. Thermodynamic properties
The predicted vm values for the ASnTe3 are reported in Table 7 and visualized in Fig. 17a. The values exhibit a direct correlation with G of the materials, as established in prior studies.152 Compounds demonstrating elevated G consequently manifest higher vm values, with LiSnTe3 exhibiting the maximum vm among the analyzed systems due to its superior shear modulus. Tm represents a critical parameter for high-temperature applications, as summarized in Table 7 and Fig. 17b. The results indicate that CsSnTe3 possesses a significantly higher Tm compared to other studied perovskites, underscoring its potential utility in high-temperature structural environments. Additionally, the calculated Kmin values for these perovskite systems are presented in Table 7 and graphically represented in Fig. 17c. These findings provide essential insights into the thermal transport characteristics of the materials, informing their suitability for applications requiring controlled heat dissipation.
Table 7 Calculated values of vm, Tm, θD, and Kmin for ASnTe3
| Perovskite |
vm (m s−1) |
θD (K) |
Tm (K) |
kmin (W m−1 K−1) |
| LiSnTe3 |
1588.7 |
158.0 |
854.2 |
0.379 |
| NaSnTe3 |
1316.8 |
127.4 |
772.7 |
0.319 |
| KSnTe3 |
1344.0 |
125.8 |
873.6 |
0.270 |
| RbASnTe3 |
1498.0 |
139.4 |
770.6 |
0.296 |
| CsSnTe3 |
1435.9 |
129.7 |
891.9 |
0.276 |
 |
| | Fig. 17 Variation of (a) vm, (b) Tm, (c) θD, and (d) Kmin for the ASnTe3. | |
The established literature identifies Y4Al2O9 as a promising thermal barrier coating (TBC) material, reporting a minimum thermal conductivity of 1.13 W m−1 K−1.153,154 However, this study demonstrates that the ASnTe3 exhibit substantially lower Kmin values, indicating a potential for enhanced TBC performance. Theoretical models posit an inverse relationship between Debye temperature and minimum thermal conductivity.155 Within the investigated perovskite series, KSnTe3 displays the lowest θD (Fig. 17d), which corresponds to its observed minimal thermal conductivity. This correlation suggests that these materials may offer improved suitability for TBC applications. Furthermore, the correlation between phonon gap and thermal conductivity is well-documented, with larger phonon gaps generally associated with reduced thermal conductivity.102 Analysis of the phonon dispersion curves reveals that LiSnTe3 exhibits the smallest phonon gap, consistent with its comparatively higher thermal conductivity within the series. These results are presented in Table 7 and illustrated in Fig. 17d.
The effect of the A-cation in the series of compounds is evident in their thermal and vibrational properties, which influence their potential applications. LiSnTe3, with the smallest A-cation (Li), exhibits a relatively high mean velocity and melting temperature, along with moderate Debye temperature and thermal conductivity. As the A-cation size increases to Na in NaSnTe3, the mean velocity and melting temperature decrease moderately, while the Debye temperature and thermal conductivity remain moderate. With KSnTe3, the mean velocity and Debye temperature remain moderate, but the melting temperature rises significantly, and thermal conductivity drops to the lowest among the series. RbSnTe3 continues this trend with moderate mean velocity and Debye temperature, a high melting temperature, and relatively low thermal conductivity (though not the lowest). Finally, CsSnTe3, with the largest A-cation, shows moderate mean velocity and Debye temperature but the highest melting temperature in the series and relatively low thermal conductivity. Overall, increasing the size of the A-cation from Li to Cs generally leads to higher melting temperatures and lower thermal conductivities, while mean velocity and Debye temperature remain moderate. This highlights how fine-tuning the A-cation allows for precise material selection for diverse thermal and thermoelectric demands.
Thermodynamic properties of the perovskite series were computed. Entropy, a measure of the disorder within a material system, was analyzed.156 As illustrated in Fig. 18a, the entropy of all investigated perovskites demonstrates a positive correlation with temperature. This trend is attributed to the increased kinetic energy of molecules at elevated temperatures, resulting in enhanced molecular disorder. Notably, the entropy values for all perovskites converge to approximately 2.4 eV at 1000 K, indicating a consistent entropic response across the varied alkali metal cations. Fig. 18b depicts the temperature dependence of enthalpy for the studied perovskites. The enthalpy of the investigated perovskites exhibits a near-linear increase with temperature. Notably, the rate of enthalpy increase is subdued below 100 K, transitioning to a more pronounced rise at temperatures exceeding 100 K. A consistent trend is observed wherein larger alkali metal cations, such as Cs+, correlate with higher enthalpy values. This observation can be attributed to the influence of ionic radii and the nature of cation bonding on the lattice dynamics and, consequently, the thermodynamic stability of the materials. The Gibbs free energy of the studied perovskites demonstrates a decrease with increasing temperature, as illustrated in Fig. 18c for all perovskites. The negative values obtained for the Gibbs free energy are indicative of the thermodynamic stability of the materials.157 Consistent with this, the calculated Gibbs free energy values for all perovskites are negative across the examined temperature range, confirming their thermodynamic stability as also indicated by the formation energy results. Comparative analysis of the Gibbs free energy profiles reveals that KSnTe3 exhibits the lowest free energy values, suggesting a higher degree of thermodynamic stability relative to the other studied perovskites. Specific heat capacity, a fundamental property for characterizing the thermal response of solids, is presented as a function of temperature for the ASnTe3 perovskites in Fig. 18d. An initial rapid increase in specific heat capacity is observed below approximately 200 K, followed by a gradual approach to a plateau at higher temperatures, consistent with the Dulong–Petit limit.158 The pronounced increase in heat capacity within the ∼0–200 K range can be attributed to phonon thermal softening.
 |
| | Fig. 18 Variation of the thermodynamic parameters with temperature for the ASnTe3 perovskites; (a) entropy, (b) enthalpy, (c) free energy, and (d) heat capacity. | |
4. Conclusions
In this study, the structural, electronic, optical, mechanical, thermal, and application-oriented properties of the ASnTe3 (A = Li to Cs) chalcogenide perovskites were systematically explored via DFT calculations. The main findings are summarized as follows: (1) structurally, all ASnTe3 compounds are triclinic, with increasing lattice constants and unit cell volumes from Li to Cs, reflecting A-site size effects. They exhibit negative formation (−2.07 to −3.31 eV per atom) and Gibbs free energies, favorable tolerance factors (Tf = 0.77–1.01; τ = 6.63–4.73), and phonon spectra free of imaginary modes, confirming thermodynamic and dynamical stability. MBP analysis shows LiSnTe3 has the most covalent bonding, NaSnTe3 the weakest, while K–Cs analogues exhibit balanced, stable bonding networks. (2) Electronically, all ASnTe3 compounds exhibit indirect band gaps and their values were 0.27, 1.10, 0.58, 1.32, and 0.90 eV for the Li, Na, K, Rb, and CsSnTe3, respectively, with direct-indirect offsets as low as 0.06–0.23 eV. Rb, Na, and CsSnTe3 are ideally suited for photovoltaic applications, while the narrower gaps of K and LiSnTe3 favor infrared and thermoelectric uses. The PDOS reveals that the valence band near the Fermi level is predominantly composed of Te 5p orbital contributions. Carrier analysis reveals p-type behavior for Na, K, Rb, and Cs, and n-type for LiSnTe3. The  and
and  values span 0.292–1.181 and 0.256–3.149 m0, respectively, with KSnTe3 showing the lowest
values span 0.292–1.181 and 0.256–3.149 m0, respectively, with KSnTe3 showing the lowest  (0.292), suggesting high electron mobility. (3) Optically, they demonstrate strong dielectric response (ε1(0.01) = 6.935–16.626) and high UV-visible absorption. They also display low energy loss, efficient optical conductivity, a desirable refractive index (n(ω) = 3.078–3.912), and moderate reflectivity (∼30–35%) in the low-energy region, all of which affirm their suitability for optoelectronic device applications. (4) Mechanically, the compounds exhibit elastic moduli (B = 21.827–36.227 GPa, G = 8.676–15.224 GPa, Y = 27.002–36.224 GPa). All systems are ductile (ν = 0.301–0.356; B/G = 1.847–3.471), with HV ranging from 0.999 to 1.767 GPa and μm between 1.620 and 3.045. Elastic anisotropy is evident in all materials, increasing in the order E < G < ν. (5) Thermodynamically, these materials are thermally stable with Tm between 770.6 and 891.9 K and θD in the range of 125.8–158.0 K. The κmin = 0.276–0.379 W m−1 K−1. Their thermodynamic functions (Cp, S(T), H(T)) support reliable performance across a broad thermal range. LiSnTe3 has the highest thermal conductivity, while CsSnTe3 has the highest melting point. KSnTe3, has the lowest Debye temperature and thermal conductivity.
(0.292), suggesting high electron mobility. (3) Optically, they demonstrate strong dielectric response (ε1(0.01) = 6.935–16.626) and high UV-visible absorption. They also display low energy loss, efficient optical conductivity, a desirable refractive index (n(ω) = 3.078–3.912), and moderate reflectivity (∼30–35%) in the low-energy region, all of which affirm their suitability for optoelectronic device applications. (4) Mechanically, the compounds exhibit elastic moduli (B = 21.827–36.227 GPa, G = 8.676–15.224 GPa, Y = 27.002–36.224 GPa). All systems are ductile (ν = 0.301–0.356; B/G = 1.847–3.471), with HV ranging from 0.999 to 1.767 GPa and μm between 1.620 and 3.045. Elastic anisotropy is evident in all materials, increasing in the order E < G < ν. (5) Thermodynamically, these materials are thermally stable with Tm between 770.6 and 891.9 K and θD in the range of 125.8–158.0 K. The κmin = 0.276–0.379 W m−1 K−1. Their thermodynamic functions (Cp, S(T), H(T)) support reliable performance across a broad thermal range. LiSnTe3 has the highest thermal conductivity, while CsSnTe3 has the highest melting point. KSnTe3, has the lowest Debye temperature and thermal conductivity.
Overall, these results provide a foundational understanding of ASnTe3 perovskites and highlight their potential in photovoltaics, thermoelectrics, and advanced functional materials. Experimental validation is recommended to confirm these theoretical predictions.
Data availability
The data that support the findings of this study, including all computational input and output files, are available from the corresponding author upon reasonable request.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors extend their appreciation to Northern Border University, Saudi Arabia, for supporting this work through project number(NBU-CRP-2025-2985).
References
- N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Compositional engineering of perovskite materials for high-performance solar cells, Nature, 2015, 517(7535), 476–480 CrossRef CAS PubMed.
- M. Liu, M. B. Johnston and H. J. Snaith, Efficient planar heterojunction perovskite solar cells by vapour deposition, Nature, 2013, 501(7467), 395–398 CrossRef CAS PubMed.
- G. Wang, J. Bi, J. Chang, M. Lei, H. Zheng and Y. Yan, Bandgap tuning of a CsPbBr 3 perovskite with synergistically improved quality via Sn 2+ doping for high-performance carbon-based inorganic perovskite solar cells, Inorg. Chem. Front., 2022, 9(17), 4359–4368 RSC.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Long-range balanced electron-and hole-transport lengths in organic-inorganic CH3NH3PbI3, Science, 2013, 342(6156), 344–347 CrossRef CAS PubMed.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal halide perovskites as visible-light sensitizers for photovoltaic cells, J. Am. Chem. Soc., 2009, 131(17), 6050–6051 CrossRef CAS PubMed.
- Y. H. Lee, I. Song, S. H. Kim, J. H. Park, S. O. Park, J. H. Lee, Y. Won, K. Cho, S. K. Kwak and J. H. Oh, Perovskite Photodetectors: Perovskite Granular Wire Photodetectors with Ultrahigh Photodetectivity (Adv. Mater. 32/2020), Adv. Mater., 2020, 32(32), 2070238 CrossRef.
- W. Tian, H. Zhou and L. Li, Hybrid organic–inorganic perovskite photodetectors, Small, 2017, 13(41), 1702107 CrossRef PubMed.
- Q. Shan, J. Song, Y. Zou, J. Li, L. Xu, J. Xue, Y. Dong, B. Han, J. Chen and H. Zeng, High performance metal halide perovskite light-emitting diode: from material design to device optimization, Small, 2017, 13(45), 1701770 CrossRef PubMed.
- Y. H. Kim, S. Kim, S. H. Jo and T. W. Lee, Metal Halide Perovskites: From Crystal Formations to Light-Emitting-Diode Applications, Small Methods, 2018, 2(11), 1800093 CrossRef.
- C. N. Rao, P. Dua, P. Kuchhal, Y. Lu, S. N. Kale and P. Cao, Enhanced sensitivity of magneto-optical sensor using defect induced perovskite metal oxide nanomaterial, J. Alloys Compd., 2019, 797, 896–901 CrossRef CAS.
- C. Y. Wu, Z. Wang, L. Liang, T. Gui, W. Zhong, R. C. Du, C. Xie, L. Wang and L. B. Luo, Graphene-assisted growth of patterned perovskite films for sensitive light detector and optical image sensor application, Small, 2019, 15(19), 1900730 CrossRef PubMed.
- S. Yang, S. Chen, E. Mosconi, Y. Fang, X. Xiao, C. Wang, Y. Zhou, Z. Yu, J. Zhao, Y. Gao and F. De Angelis, Stabilizing halide perovskite surfaces for solar cell operation with wide-bandgap lead oxysalts, Science, 2019, 365(6452), 473–478 CrossRef CAS PubMed.
- N. Ito, M. A. Kamarudin, D. Hirotani, Y. Zhang, Q. Shen, Y. Ogomi, S. Iikubo, T. Minemoto, K. Yoshino and S. Hayase, Mixed Sn–Ge perovskite for enhanced perovskite solar cell performance in air, J. Phys. Chem. Lett., 2018, 9(7), 1682–1688 CrossRef CAS PubMed.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Semiconducting tin and lead iodide perovskites with organic cations: phase transitions, high mobilities, and near-infrared photoluminescent properties, Inorg. Chem., 2013, 52(15), 9019–9038 CrossRef CAS PubMed.
- G. E. Eperon, G. M. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, Inorganic caesium lead iodide perovskite solar cells, J. Mater. Chem. A, 2015, 3(39), 19688–19695 RSC.
- C. Chen, E. E. Morgan, Y. Liu, J. Chen, R. Seshadri and L. Mao, “Breathing” organic cation to stabilize multiple structures in low-dimensional Ge-, Sn-, and Pb-based hybrid iodide perovskites, Inorg. Chem. Front., 2022, 9(19), 4892–4898 RSC.
- Q. Han, S. H. Bae, P. Sun, Y. T. Hsieh, Y. Yang, Y. S. Rim, H. Zhao, Q. Chen, W. Shi, G. Li and Y. Yang, Single crystal formamidinium lead iodide (FAPbI3): insight into the structural, optical, and electrical properties, Adv. Mater., 2016, 28(11), 2253–2258 CrossRef CAS PubMed.
- Y. Zhou and Y. Zhao, Chemical stability and instability of inorganic halide perovskites, Energy Environ. Sci., 2019, 12(5), 1495–1511 RSC.
- S. Lee, D. B. Kim, J. C. Yu, C. H. Jang, J. H. Park, B. R. Lee and M. H. Song, Versatile defect passivation methods for metal halide perovskite materials and their application to light-emitting devices, Adv. Mater., 2019, 31(20), 1805244 CrossRef PubMed.
- J. Li, H. L. Cao, W. B. Jiao, Q. Wang, M. Wei, I. Cantone, J. Lü and A. Abate, Biological impact of lead from halide perovskites reveals the risk of introducing a safe threshold, Nat. Commun., 2020, 11(1), 310 CrossRef CAS PubMed.
- A. Abate, Perovskite solar cells go lead free, Joule, 2017, 1(4), 659–664 CrossRef CAS.
- P. Billen, E. Leccisi, S. Dastidar, S. Li, L. Lobaton, S. Spatari, A. T. Fafarman, V. M. Fthenakis and J. B. Baxter, Comparative evaluation of lead emissions and toxicity potential in the life cycle of lead halide perovskite photovoltaics, Energy, 2019, 166, 1089–1096 CrossRef CAS.
- I. Celik, Z. Song, A. J. Cimaroli, Y. Yan, M. J. Heben and D. Apul, Life Cycle Assessment (LCA) of perovskite PV cells projected from lab to fab, Sol. Energy Mater. Sol. Cells, 2016, 156, 157–169 CrossRef CAS.
- A. Babayigit, A. Ethirajan, M. Muller and B. Conings, Toxicity of organometal halide perovskite solar cells, Nat. Mater., 2016, 15(3), 247–251 CrossRef CAS PubMed.
- G. Nasti and A. Abate, Tin halide perovskite (ASnX3) solar cells: a comprehensive guide toward the highest power conversion efficiency, Adv. Energy Mater., 2020, 10(13), 1902467 CrossRef CAS.
- W. Yang, W. Li, Q. Liu and Y. Jin, Design and simulation of gradient-structured Cs2AgBiBr6 carbon-based double perovskite solar cell for boosting photovoltaic performance, Sol. Energy, 2025, 290, 113347 CrossRef CAS.
- A. E. Maughan, A. M. Ganose, D. O. Scanlon and J. R. Neilson, Perspectives and design principles of vacancy-ordered double perovskite halide semiconductors, Chem. Mater., 2019, 31(4), 1184–1195 CrossRef CAS.
- N. Chawki, M. Rouchdi, M. Alla and B. Fares, Numerical modeling of a novel solar cell system consisting of electron Transport material (ETM)/CaZrS3-based chalcogenide perovskites using SCAPS-1D software, Sol. Energy, 2024, 274, 112592 CrossRef CAS.
- S. Perera, H. Hui, C. Zhao, H. Xue, F. Sun, C. Deng, N. Gross, C. Milleville, X. Xu, D. F. Watson and B. Weinstein, Chalcogenide perovskites–an emerging class of ionic semiconductors, Nano Energy, 2016, 22, 129–135 CrossRef CAS.
- Q. Sun, W. J. Yin and S. H. Wei, Searching for stable perovskite solar cell materials using materials genome techniques and high-throughput calculations, J. Mater. Chem. C, 2020, 8(35), 12012–12035 RSC.
- D. Liu, H. Peng, J. He and R. Sa, Alloy engineering to tune the optoelectronic properties and photovoltaic performance for Hf-based chalcogenide perovskites, Mater. Sci. Semicond. Process., 2024, 169, 107919 CrossRef CAS.
- D. Liu, H. Zeng, H. Peng and R. Sa, Computational study of the fundamental properties of Zr-based chalcogenide perovskites for optoelectronics, Phys. Chem. Chem. Phys., 2023, 25(19), 13755–13765 RSC.
- V. Chethan and M. Mahendra, Ab initio Investigation of quasi-one-dimensional ternary chalcogenides Sr2ZnX3 (X= S, Se, Te) for efficient photovoltaic and thermoelectric applications, J. Phys. Chem. Solids, 2024, 194, 112222 CrossRef.
- H. Zhang, X. Wu, K. Ding, L. Xie, K. Yang, C. Ming, S. Bai, H. Zeng, S. Zhang and Y. Y. Sun, Prediction and synthesis of a selenide perovskite for optoelectronics, Chem. Mater., 2023, 35(11), 4128–4135 CrossRef CAS.
- Y. Y. Sun, M. L. Agiorgousis, P. Zhang and S. Zhang, Chalcogenide perovskites for photovoltaics, Nano Lett., 2015, 15(1), 581–585 CrossRef CAS PubMed.
- J. Du, J. J. Shi, W. H. Guo, S. M. Liu, Y. He, C. Tian, Y. H. Zhu and H. X. Zhong, Cerium-based lead-free chalcogenide perovskites for photovoltaics, Phys. Rev. B, 2021, 104(23), 235206 CrossRef CAS.
- D. Liu, H. Zeng, H. Peng and R. Sa, Computational study of the fundamental properties of Zr-based chalcogenide perovskites for optoelectronics, Phys. Chem. Chem. Phys., 2023, 25(19), 13755–13765 RSC.
- M. D. Kassa, N. G. Debelo and M. M. Woldemariam, First-principles calculations to investigate small band gap Ca2ZrHfS6 double chalcogenide perovskites for optoelectronic application, Indian J. Phys., 2024, 98(4), 1259–1270 CrossRef CAS.
- R. Fatima, R. A. Khalil, M. I. Hussain and F. Hussain, Computational study of the structural, optoelectronic and thermoelectric properties of scandium-based ternary chalcogenides XScSe2 (X= Li, Rb) for applications in photovoltaic cell, J. Comput. Electron., 2024, 23(1), 82–93 CrossRef CAS.
- M. U. Saeed, T. Usman, S. Pervaiz, Z. Ali, Y. M. Alanazi, A. U. Bacha and Y. Saeed, DFT Analysis of Alkali Scandium Sulfides AScS2 (A= K, Rb): Unveiling Structural, Electronic, and Optical Properties for Enhanced Photocatalysis, ACS Appl. Opt. Mater., 2024, 2(9), 1955–1964 CrossRef CAS.
- A. Alanazi, S. T. Jan, Z. Khan and T. I. Alanazi, Analyzing the hetero-junction compatibility of Al2CdX4 chalcogenides as charge transport layers with lead-free perovskite layer, Opt. Quant. Electron., 2024, 56(8), 1390 CrossRef CAS.
- R. Fatima, R. A. Khalil, M. I. Hussain and F. Hussain, Ultraviolet active novel chalcogenides BAlTe2 (B= Rb, Cs): the structural, optoelectronic, mechanical, and vibrational properties for energy harvesting applications through first principles approach, Opt. Mater. Express, 2024, 14(3), 607–628 CrossRef CAS.
- P. Basera and S. Bhattacharya, Chalcogenide perovskites (ABS3; A= Ba, Ca, Sr; B= Hf, Sn): an emerging class of semiconductors for optoelectronics, J. Phys. Chem. Lett., 2022, 13(28), 6439–6446 CrossRef CAS PubMed.
- M. L. Agiorgousis, Y. Y. Sun, D. H. Choe, D. West and S. Zhang, Machine learning augmented discovery of chalcogenide double perovskites for photovoltaics, Adv. Theory Simul., 2019, 2(5), 1800173 CrossRef.
- K. C. Majhi and M. Yadav, Transition metal-based chalcogenides as electrocatalysts for overall water splitting, ACS Eng. Au, 2023, 3(5), 278–284 CrossRef CAS.
- Y. L. Cen, J. J. Shi, M. Zhang, M. Wu, J. Du, W. H. Guo, S. M. Liu, S. P. Han and Y. H. Zhu, Design of lead-free and stable two-dimensional Dion–Jacobson-type chalcogenide perovskite A′ La2B3S10 (A′= Ba/Sr/Ca; B= Hf/Zr) with optimal band gap, strong optical absorption, and high efficiency for photovoltaics, Chem. Mater., 2020, 32(6), 2450–2460 CrossRef CAS.
- G. M. Mustafa, S. Saba, N. A. Noor, A. Laref, M. Abd El-Rahman, Z. Farooq, R. B. Behram and Z. Ullah, First-principles calculations to investigate HgY2S/Se4 spinel chalcogenides for optoelectronic and thermoelectric applications, J. Mater. Res. Technol., 2023, 22, 97–106 CrossRef CAS.
- G. G. Njema and J. K. Kibet, A review of chalcogenide-based perovskites as the next novel materials: Solar cell and optoelectronic applications, catalysis and future perspectives, Next Nanotechnol., 2025, 7, 100102 CrossRef.
- E. K. Mahmoud, A. A. Farghali, S. I. El-dek and M. Taha, Structural stabilities, mechanical and thermodynamic properties of chalcogenide perovskite ABS3 (A= Li, Na, K, Rb, Cs; B= Si, Ge, Sn) from first-principles study, Eur. Phys. J. Plus, 2022, 137(9), 1006 CrossRef CAS.
- E. K. Mahmoud, S. I. El-dek, A. A. Farghali and M. Taha, Exploring photocatalytic and photovoltaic applications of chalcogenide Perovskites, ABS3 (A= Li, Na, K, Rb, Cs; B= Si, Ge, Sn): A First-Principles investigation using the HSE-06 hybrid functional, Inorg. Chem. Commun., 2025, 172, 113650 CrossRef CAS.
- E. K. Mahmoud, S. I. El-Dek, A. A. Farghali and M. Taha, Investigating the potential of triclinic ABSe3 (A= Li, Na, K, Rb, Cs; B= Si, Ge, Sn) perovskites as a new class of lead-free photovoltaic materials, Sci. Rep., 2024, 14(1), 22691 CrossRef CAS PubMed.
- Y. Han, J. Fang, H. Zhang, Y. Sun, Y. Yuan, X. Chen, M. Jia, X. Li, H. Gao and Z. Shi, Chalcogenide Perovskite EuHfS3 with Low Band Gap and Antiferromagnetic Properties for Photovoltaics, Energy Mater. Adv., 2024, 5, 0116 CrossRef CAS.
- J. T. Jia, X. H. Yang and L. W. Wang, Ultrasonic spray synthesis, photoelectric properties and photovoltaic performances of chalcogenide CaSnS 3, Chalcogenide Lett., 2024, 21(7), 543–556 CrossRef CAS.
- A. A. Pradhan, M. C. Uible, S. Agarwal, J. W. Turnley, S. Khandelwal, J. M. Peterson, D. D. Blach, R. N. Swope, L. Huang, S. C. Bart and R. Agrawal, Synthesis of BaZrS3 and BaHfS3 chalcogenide perovskite films using single-phase molecular precursors at moderate temperatures, Angew. Chem., 2023, 135(15), e202301049 CrossRef.
- J. W. Turnley, K. C. Vincent, A. A. Pradhan, I. Panicker, R. Swope, M. C. Uible, S. C. Bart and R. Agrawal, Solution deposition for chalcogenide perovskites: a low-temperature route to BaMS3 materials (M= Ti, Zr, Hf), J. Am. Chem. Soc., 2022, 144(40), 18234–18239 CrossRef CAS PubMed.
- H. Bouteiller, B. Fontaine, O. Perez, S. Hébert, C. Bourgès, Y. Matsushita, T. Mori, F. Gascoin, J. F. Halet and D. Berthebaud, Enhancement of Thermoelectric Performance through Transport Properties Decorrelation in the Quaternary Pseudo-Hollandite Chalcogenide Rb0. 2Ba0. 4Cr5Se8, Inorg. Chem., 2024, 63(36), 16655–16666 CrossRef CAS PubMed.
- D. Yang, Y. Han, M. Li, C. Li, W. Bi, Q. Gong, J. Zhang, J. Zhang, Y. Zhou, H. Gao and J. Arbiol, Highly Conductive Quasi-1D Hexagonal Chalcogenide Perovskite Sr8Ti7S21 with Efficient Polysulfide Regulation in Lithium-Sulfur Batteries, Adv. Funct. Mater., 2024, 34(42), 2401577 CrossRef CAS.
- Y. Nishigaki, T. Nagai, M. Nishiwaki, T. Aizawa, M. Kozawa, K. Hanzawa, Y. Kato, H. Sai, H. Hiramatsu, H. Hosono and H. Fujiwara, Extraordinary strong band-edge absorption in distorted chalcogenide perovskites, Sol. RRL, 2020, 4(5), 1900555 CrossRef CAS.
- J. Khan, W. Uddin, A. Dutta, I. Boukhris and H. Albalawi, Mapping structural, electronic and optoelectronics features in Na2TlSbY6 (Y= Cl, Br): Implications for next-generation photovoltaics, Polyhedron, 2025, 268, 117381 CrossRef CAS.
- Handbook of Photovoltaic Science and Engineering, ed. A. Luque and S. Hegedus, John Wiley & Sons, 2011, Mar 29 Search PubMed.
- K. W. Böer, Handbook of the Physics of Thin-Film Solar Cells, Springer Science & Business, 2014, Apr 23 Search PubMed.
- K. Fu, A. W. Ho-Baillie, H. K. Mulmudi and P. T. Trang, Perovskite Solar Cells: Technology and Practices, Apple Academic Press, 2019, Mar 19 Search PubMed.
- Z. Zhou, S. Pang, Z. Liu, H. Xu and G. Cui, Interface engineering for high-performance perovskite hybrid solar cells, J. Mater. Chem. A, 2015, 3(38), 19205–19217 RSC.
- S. Berri, Thermoelectric properties of A2BCl6: a first principles study, J. Phys. Chem. Solids, 2022, 170, 110940 CrossRef CAS.
- S. Berri, Theoretical study of physical properties of Ba3B (nb, ta) 2O9 (B= mg, ca, sr, cd, hg, zn, fe, mn, ni, co) perovskites, Comp. Cond. Mat., 2021, 29, e00595 Search PubMed.
- S. Berri, Half-metallic and thermoelectric properties of Sr2EuReO6, Comp. Cond. Mat., 2021, 28, e00586 Search PubMed.
- X. Cai, Y. Zhang, Z. Shi, Y. Chen, Y. Xia, A. Yu, Y. Xu, F. Xie, H. Shao, H. Zhu and D. Fu, Discovery of Lead-Free Perovskites for High-Performance Solar Cells via Machine Learning: Ultrabroadband Absorption, Low Radiative Combination, and Enhanced Thermal Conductivities, Adv. Sci., 2022, 9(4), 2103648 CrossRef CAS PubMed.
- J. P. Correa-Baena, L. Nienhaus, R. C. Kurchin, S. S. Shin, S. Wieghold, N. T. Putri Hartono, M. Layurova, N. D. Klein, J. R. Poindexter, A. Polizzotti and S. Sun, A-site cation in inorganic A 3Sb2I9 perovskite influences structural dimensionality, exciton binding energy, and solar cell performance, Chem. Mater., 2018, 30(11), 3734–3742 CrossRef CAS.
- M. A. Rahman, M. F. Rahman, L. Marasamy, M. Harun-Or-Rashid, A. Ghosh, A. R. Chaudhry and A. Irfan, Impact of A-cations modified on the structural, electronic, optical, mechanical, and solar cell performance of inorganic novel A3NCl3 (A= Ba, Sr, and Ca) perovskites, Energy Fuels, 2024, 38(9), 8199–8217 CrossRef CAS.
- A. Solanki, P. Yadav, S. H. Turren-Cruz, S. S. Lim, M. Saliba and T. C. Sum, Cation influence on carrier dynamics in perovskite solar cells, Nano Energy, 2019, 58, 604–611 CrossRef CAS.
- M. Hojamberdiev, M. F. Bekheet, J. N. Hart, J. J. Vequizo, A. Yamakata, K. Yubuta, A. Gurlo, M. Hasegawa, K. Domen and K. Teshima, Elucidating the impact of A-site cation change on photocatalytic H 2 and O 2 evolution activities of perovskite-type LnTaON 2 (Ln= La and Pr), Phys. Chem. Chem. Phys., 2017, 19(33), 22210–22220 RSC.
- S. Halder, M. S. Sheikh, R. Maity, B. Ghosh and T. P. Sinha, Investigating the optical, photosensitivity and photocatalytic properties of double perovskites A2LuTaO6 (A= Ba, Sr): a combined experimental and density functional theory study, Ceram. Int., 2019, 45(12), 15496–15504 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118(18), 8207–8215 CrossRef CAS.
- J. H. Liao, C. Varotsis and M. G. Kanatzidis, Syntheses, structures, and properties of six novel alkali metal tin sulfides: K2Sn2S8,. alpha.-Rb2Sn2S8,. beta.-Rb2Sn2S8, K2Sn2S5, Cs2Sn2S6, and Cs2SnS14, Inorg. Chem., 1993, 32(11), 2453–2462 CrossRef CAS.
- The Materials Project, https://materialsproject.org/.
- E. L. Shirley, D. C. Allan, R. M. Martin and J. D. Joannopoulos, Extended norm-conserving pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3652 CrossRef PubMed.
- F. Abeles, Optical Properties of Solids, (No Title), 1972 Search PubMed.
- M. D. Segall, P. J. Lindan, M. A. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-principles simulation: ideas, illustrations and the CASTEPcode, J. Phys. Condens. Matter, 2002, 14(11), 2717 CrossRef CAS.
- D. Jana, C. L. Sun, L. C. Chen and K. H. Chen, Effect of chemical doping of boron and nitrogen on the electronic, optical, and electrochemical properties of carbon nanotubes, Prog. Mater. Sci., 2013, 58(5), 565–635 CrossRef CAS.
- S. Saha, T. P. Sinha and A. Mookerjee, Electronic structure, chemical bonding, and optical properties of paraelectric BaTiO 3, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(13), 8828 CrossRef CAS.
- M. Yang, B. Chang, G. Hao, J. Guo, H. Wang and M. Wang, Comparison of optical properties between Wurtzite and zinc-blende Ga0. 75Al0. 25N, Optik, 2014, 125(1), 424–427 CrossRef CAS.
- B. Delley, Fast calculation of electrostatics in crystals and large molecules, J. Phys. Chem., 1996, 100(15), 6107–6110 CrossRef CAS.
- L. He, F. Liu, G. Hautier, M. J. Oliveira, M. A. Marques, F. D. Vila, J. J. Rehr, G. M. Rignanese and A. Zhou, Accuracy of generalized gradient approximation functionals for density-functional perturbation theory calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(6), 064305 CrossRef.
- I. Bourachid, M. Caid, O. Cheref, D. Rached, H. Heireche, B. Abidri, H. Rached and N. Benkhettou, Insight into the structural, electronic, mechanical and optical properties of inorganic lead bromide perovskite APbBr3 (A= Li, Na, K, Rb, and Cs), Comp. Cond. Mat., 2020, 24, e00478 Search PubMed.
- D. H. Chung and W. R. Buessem, The voigt-reuss-hill approximation and elastic moduli of polycrystalline MgO, CaF2, β-ZnS, ZnSe, and CdTe, J. Appl. Phys., 1967, 38(6), 2535–2540 CrossRef CAS.
- M. Dacorogna, J. S. Ashkenazi and M. Peter, Ab initio calculation of the tetragonal shear moduli of the cubic transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26(4), 1527 CrossRef CAS.
- N. E. Christensen, “Force theorem” and elastic constants of solids, Solid State Commun., 1984, 49(7), 701–705 CrossRef CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc. A., 1952, 65(5), 349 CrossRef.
- M. Jubair, A. T. Karim, M. Nuruzzaman, M. Roknuzzaman and M. A. Zilani, Pressure dependent structural, elastic and mechanical properties with ground state electronic and optical properties of half-metallic Heusler compounds Cr2YAl (Y= Mn, Co): first-principles study, Heliyon, 2021, 7(12), e08585 CrossRef CAS PubMed.
- M. H. Rubel, M. A. Hossain, M. K. Hossain, K. M. Hossain, A. A. Khatun, M. M. Rahaman, M. F. Rahman, M. M. Hossain and J. Hossain, First-principles calculations to investigate structural, elastic, electronic, thermodynamic, and thermoelectric properties of CaPd3B4O12 (B= Ti, V) perovskites, Results Phys., 2022, 42, 105977 CrossRef.
- J. C. Wei, H. C. Chen, W. Huang and J. Long, Theoretical investigation of the elastic, Vickers hardness and thermodynamic properties of δ-WN under pressure, Mater. Sci. Semicond. Process., 2014, 27, 883–890 CrossRef CAS.
- M. A. Rahman, W. Hasan, M. Z. Hasan, A. Irfan, S. C. Mouna, M. A. Sarker, M. Z. Rahaman and M. Rahman, Structural, mechanical, electronic, optical and thermodynamic features of lead free oxide perovskites AMnO3 (A= Ca, Sr, Ba): DFT simulation based comparative study, Phys. B, 2023, 668, 415215 CrossRef CAS.
- M. E. Fine, L. D. Brown and H. L. Marcus, Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18(9), 951–956 CrossRef CAS.
- A. Gencer, O. Surucu, G. Surucu and E. Deligoz, Anisotropic mechanical properties of Tl4Ag18Te11 compound with low thermal conductivity, J. Solid State Chem., 2020, 289, 121469 CrossRef CAS.
- S. Lakel, F. Elhamra, K. Almi and H. Meradji, Density functional perturbation theory calculations of vibrational and thermodynamic properties of Zn1− xBexO alloys, Mater. Sci. Semicond. Process., 2015, 40, 209–217 CrossRef CAS.
- M. Yan, X. Shi, H. Wei, Y. Jiang, J. Feng and K. Wang, The influence of Mn content on Fe2B properties and its impact at the αZ-Fe16C2/Fe2B interface, Vacuum, 2024, 222, 113056 CrossRef CAS.
- F. S. Saoud, J. C. Plenet and M. Henini, Structural and elastic stabilities of InN in both B4 and B1 phases under high pressure using density-functional perturbation theory, J. Alloys Compd., 2015, 650, 450–457 CrossRef CAS.
- V. M. Goldschmidt, Die gesetze der krystallochemie, Naturwissenschaften, 1926, 14(21), 477–485 CrossRef CAS.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, New tolerance factor to predict the stability of perovskite oxides and halides, Sci. Adv., 2019, 5(2), eaav0693 CrossRef CAS PubMed.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Found. Crystallogr., 1976, 32(5), 751–767 Search PubMed.
- R. Kondrotas, R. Juškėnas, A. Krotkus, V. Pakštas, A. Suchodolskis, A. Mekys, M. Franckevičius, M. Talaikis, K. Muska, X. Li and M. Kauk-Kuusik, Synthesis and physical characteristics of narrow bandgap chalcogenide SnZrSe 3, Open Res. Eur., 2023, 2, 138 Search PubMed.
- A. Allal, M. Halit, S. Saib, W. Luo and R. Ahuja, Phase stability, phonon, electronic, and optical properties of not-yet-synthesized CsScS2, CsYS2, and APmS2 (A= Li, Na, K, Rb, Cs) materials: Insights from first-principles calculations, Mater. Sci. Semicond. Process., 2022, 150, 106936 CrossRef CAS.
- H. Zhang, M. H. Shang, X. Zheng, Z. Zeng, R. Chen, Y. Zhang, J. Zhang and Y. Zhu, Ba2+ doped CH3NH3PbI3 to tune the energy state and improve the performance of perovskite solar cells, Electrochim. Acta, 2017, 254, 165–171 CrossRef CAS.
- Q. Y. Chen, Y. Huang, P. R. Huang, T. Ma, C. Cao and Y. He, Electronegativity explanation on the efficiency-enhancing mechanism of the hybrid inorganic–organic perovskite ABX3 from first-principles study, Chin. Phys. B, 2015, 25(2), 027104 CrossRef.
- S. Ullah, T. Iqbal, G. Rehman and I. Ahmad, Electronic and optical properties of group IIA-IVB cubic perovskite oxides: Improved TB-mBJ study, Chem. Phys. Lett., 2020, 757, 137887 CrossRef CAS.
- D. Liu, L. Liang and R. Sa, First-principles calculations of structural, electronic, and optical properties of double perovskites Cs2Sn1-xBxI6 (B= Si, Ge; x= 0, 0.25, 0.50, 0.75, 1), Chem. Phys., 2021, 542, 111075 CrossRef CAS.
- M. S. Hayat and R. A. Khalil, A DFT engineering of double halide type perovskites Cs2SiCl6, Cs2GeCl6, Cs2SnCl6 for optoelectronic applications, Solid State Commun., 2023, 361, 115064 CrossRef CAS.
- S. Niu, H. Huyan, Y. Liu, M. Yeung, K. Ye, L. Blankemeier, T. Orvis, D. Sarkar, D. J. Singh, R. Kapadia and J. Ravichandran, Bandgap control via structural and chemical tuning of transition metal perovskite chalcogenides, Adv. Mater., 2017, 29(9), 1604733 CrossRef PubMed.
- T. Tang and Y. Tang, First-principles calculations of orthorhombic chalcogenide ABX3 (A= Ca, Sr, Ba; B= Ge, Sn; X= O, S, Se, Te) perovskites by cation and anion variation, Inorg. Chem. Commun., 2025, 171, 113461 CrossRef CAS.
- K. Villa, J. R. Galán-Mascarós, N. López and E. Palomares, Photocatalytic water splitting: advantages and challenges, Sustain. Energy Fuels, 2021, 5(18), 4560–4569 RSC.
- Q. Sun, H. Chen and W. J. Yin, Do chalcogenide double perovskites work as solar cell absorbers: a first-principles study, Chem. Mater., 2018, 31(1), 244–250 CrossRef.
- S. Wang, C. Chen, S. Shi, Z. Zhang, Y. Cai, S. Gao, W. Chen, S. Guo, E. Abduryim, C. Dong and X. Guan, Flexibility potential of Cs2BX6 (B= Hf, Sn, Pt, Zr, Ti; X= I, Br, Cl) with application in photovoltaic devices and radiation detectors, J. Energy Chem., 2024, 95, 271–287 CrossRef CAS.
- B. Lakhdar, B. Anissa, D. Radouan, N. Al Bouzieh and N. Amrane, Structural, electronic, elastic, optical and thermoelectric properties of ASiCl3 (A= Li, Rb and Cs) chloroperovskites: a DFT study, Opt. Quant. Electron., 2024, 56(3), 313 CrossRef CAS.
- J. Qian, B. Xu and W. Tian, A comprehensive theoretical study of halide perovskites ABX3, Org. Electron., 2016, 37, 61–73 CrossRef CAS.
- S. A. Adalikwu, H. Louis, D. Etiese, U. G. Chukwu and E. C. Agwamba, Density Functional Theory Computation of the Electronic, Elastic, Phonon, X-ray Spectroscopy, and the Optoelectronic Properties of CsXI 3 (X: Si, Ge, Sn) Halide Perovskite Materials, J. Comput. Biophys. Chem., 2023, 22(08), 1081–1095 CrossRef CAS.
- Y. Dang, Y. Zhou, X. Liu, D. Ju, S. Xia, H. Xia and X. Tao, Formation of hybrid perovskite tin iodide single crystals by top-seeded solution growth, Angew. Chem., Int. Ed., 2016, 55(10), 3447–3450 CrossRef CAS PubMed.
- J. K. Rony, M. Islam, M. Saiduzzaman, K. M. Hossain, S. Alam, A. Biswas, M. H. Mia, S. Ahmad and S. K. Mitro, TlBX3 (B= Ge, Sn; X= Cl, Br, I): Promising non-toxic metal halide perovskites for scalable and affordable optoelectronics, J. Mater. Res. Technol., 2024, 29, 897–909 CrossRef CAS.
- Y. Li, W. Sun, W. Yan, S. Ye, H. Rao, H. Peng, Z. Zhao, Z. Bian, Z. Liu, H. Zhou and C. Huang, 50% Sn-based planar perovskite solar cell with power conversion efficiency up to 13.6, Adv. Energy Mater., 2016, 6(24), 1601353 CrossRef.
- S. Kahmann, O. Nazarenko, S. Shao, O. Hordiichuk, M. Kepenekian, J. Even, M. V. Kovalenko, G. R. Blake and M. A. Loi, Negative thermal quenching in FASnI3 perovskite single crystals and thin films, ACS Energy Lett., 2020, 5(8), 2512–2519 CrossRef CAS.
- J. Henry, K. Mohanraj and G. Sivakumar, Photoelectrochemical cell performances of Cu2ZnSnSe4 thin films deposited on various conductive substrates, Vacuum, 2018, 156, 172–180 CrossRef CAS.
- T. Das, G. Di Liberto and G. Pacchioni, Density functional theory estimate of halide perovskite band gap: When spin orbit coupling helps, J. Phys. Chem. C, 2022, 126(4), 2184–2198 CrossRef CAS.
- S. Körbel, M. A. Marques and S. Botti, Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations, J. Mater. Chem. C, 2016, 4(15), 3157–3167 RSC.
- M. Faizan, K. C. Bhamu, G. Murtaza, X. He, N. Kulhari, M. M. AL-Anazy and S. H. Khan, Electronic and optical properties of vacancy ordered double perovskites A2BX6 (A= Rb, Cs; B= Sn, Pd, Pt; and X= Cl, Br, I): a first principles study, Sci. Rep., 2021, 11(1), 6965 CrossRef CAS PubMed.
- Y. Nassah, A. Benmakhlouf, L. Hadjeris, T. Helaimia, R. Khenata, A. Bouhemadou, S. Bin Omran, R. Sharma, S. Goumri Said and V. Srivastava, Electronic band structure, mechanical and optical characteristics of new lead-free halide perovskites for solar cell applications based on DFT computation, Bull. Mater. Sci., 2023, 46(2), 55 CrossRef CAS.
- P. Sharma, P. Ranjan and T. Chakraborty, DFT and TD-DFT studies of perovskite materials LiAX3 (A= Ge, Sn; X= F, Cl, Br, I) in reference to their solar cell applications, Mater. Today Sustain., 2024, 26, 100791 Search PubMed.
- H. Khan, M. Sohail, N. Rahman, M. Hussain, A. Khan and H. H. Hegazy, Theoretical study of different aspects of Al-based Fluoroperovskite AlMF3 (M= Cu, Mn) compounds using TB-MBJ potential approximation method for generation of energy, Results Phys., 2022, 42, 105982 CrossRef.
- M. H. Miah, M. B. Rahman, M. Nur-E-Alam, M. A. Islam, K. A. Naseer, M. Y. Hanfi, H. Osman and M. U. Khandaker, First-principles study of the structural, mechanical, electronic, optical, and elastic properties of non-toxic XGeBr3 (X= K, Rb, and Cs) perovskite for optoelectronic and radiation sensing applications, Mater. Chem. Phys., 2024, 319, 129377 CrossRef CAS.
- K. Shum, Z. Chen, J. Qureshi, C. Yu, J. J. Wang, W. Pfenninger, N. Vockic, J. Midgley and J. T. Kenney, Synthesis and characterization of CsSnI3 thin films, Appl. Phys. Lett., 2010, 96(22), 221903 CrossRef.
- A. Ayyaz, S. Saidi, N. D. Alkhaldi, G. Murtaza, N. Sfina and Q. Mahmood, Lead-free double perovskites Rb2TlSbX6 (X= Cl, Br, and I) as an emerging aspirant for solar cells and green energy applications, Sol. Energy, 2024, 279, 112844 CrossRef CAS.
- T. A. Geleta, D. Behera, N. Bouri, V. J. Rivera and F. M. Gonzalo, First principles insight into the study of the structural, stability, and optoelectronic properties of alkali-based single halide perovskite ZSnCl3 (Z= Na/K) materials for photovoltaic applications, J. Comput. Chem., 2024, 45(30), 2574–2586 CrossRef CAS PubMed.
- A. E. Maughan, A. M. Ganose, M. A. Almaker, D. O. Scanlon and J. R. Neilson, Tolerance factor and cooperative tilting effects in vacancy-ordered double perovskite halides, Chem. Mater., 2018, 30(11), 3909–3919 CrossRef CAS.
- I. A. Shah, M. Imran, F. Hussain, U. Rasheed, A. M. Tighezza, R. M. Khalil, M. Shoaib and M. F. Ehsan, First-principles study of structural, mechanical, optoelectronic and thermoelectric properties of lead-free Cs2BSnX6 (B= Mg, Cu; X= Cl, Br, I) for photo responsive RRAM devices, Opt. Quant. Electron., 2024, 56(8), 1293 CrossRef CAS.
- A. Khan, N. U. Khan, K. Ullah, J. Iqbal, H. Ullah and A. Rehman, DFT-based study of Na2AgAlX6 (X= Cl, Br) halide double perovskites: insights from PBEsol, TB-mBJ, and HSE06 calculations for photovoltaic and photocatalytic applications, Phys. Scr., 2025, 100(5), 055946 CrossRef CAS.
- S. Kukreti, G. K. Gupta and A. Dixit, Theoretical DFT studies of Cu2HgSnS4 absorber material and Al: ZnO/ZnO/CdS/Cu2HgSnS4/Back contact heterojunction solar cell, Sol. Energy, 2021, 225, 802–813 CrossRef CAS.
- A. Mera, T. Zelai, S. A. Rouf, N. A. Kattan and Q. Mahmood, First-principles calculations to investigate mechanical, thermoelectric and optical performance of inorganic double perovskites Rb2AgAlZ6 (Z= Br, I) for energy harvesting, J. Mater. Res. Technol., 2023, 24, 5588–5597 CrossRef CAS.
- S. M. Sze, Y. Li and K. K. Ng, Physics of Semiconductor Devices, John wiley & sons, 2021, Mar 19 Search PubMed.
- S. Adachi, Properties of Semiconductor Alloys: Group-IV, III-V and II-VI Semiconductors, John Wiley & Sons, 2009, Mar 12 Search PubMed.
- P. Umari, E. Mosconi and F. De Angelis, Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 perovskites for solar cell applications, Sci. Rep., 2014, 4(1), 4467 CrossRef PubMed.
- H. Katagiri, N. Ishigaki, T. Ishida and K. Saito, Characterization of Cu2ZnSnS4 thin films prepared by vapor phase sulfurization, Jpn. J. Appl. Phys., 2001, 40(2R), 500 CrossRef CAS.
- M. Cardona, Optical properties and band structure of SrTi O 3 and BaTi O 3, Phys. Rev., 1965, 140(2A), A651 CrossRef.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal halide perovskites as visible-light sensitizers for photovoltaic cells, J. Am. Chem. Soc., 2009, 131(17), 6050–6051 CrossRef CAS PubMed.
- H. H. Hegazy, G. M. Mustafa, A. Nawaz, N. A. Noor, A. Dahshan and I. Boukhris, Tuning of direct bandgap of Rb2ScTlX6 (X= Cl, Br, I) double perovskites through halide ion substitution for solar cell devices, J. Mater. Res. Technol., 2022, 19, 1271–1281 CrossRef CAS.
- P. W. Davis and T. S. Shilliday, Some optical properties of cadmium telluride, Phys. Rev., 1960, 118(4), 1020 CrossRef CAS.
- A. Shukla, V. K. Sharma, S. K. Gupta and A. S. Verma, Investigations of fundamental physical and thermoelectric properties of methylammonium lead iodide (CH3NH3PbI3) perovskites, Mater. Res. Express, 2020, 6(12), 126323 CrossRef.
- Z. L. Liu, High-efficiency calculation of elastic constants enhanced by the optimized strain-matrix sets, A= A, 2020, 500, 5 CrossRef.
- F. Colmenero, A. M. Fernández, V. Timón and J. Cobos, Becquerelite mineral phase: crystal structure and thermodynamic and mechanical stability by using periodic DFT, RSC Adv., 2018, 8(43), 24599–24616 RSC.
- S. Al-Qaisi, M. A. Ali, T. A. Alrebdi, T. V. Vu, M. Morsi, B. U. Haq, R. Ahmed, Q. Mahmood and S. A. Tahir, First-principles investigations of Ba2NaIO6 double perovskite semiconductor: material for low-cost energy technologies, Mater. Chem. Phys., 2022, 275, 125237 CrossRef CAS.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Phil. Mag. J. Sci., 1954, 45(367), 823–843 CrossRef CAS.
- C. F. Yu and Y. L. Liu, DFT Study of Au3In and Au3In2 Intermetallic Compounds: Structural Stability, Fracture Toughness, Anisotropic Elasticity, and Thermophysical Properties for Advanced Applications, Materials, 2025, 18(7), 1561 CrossRef CAS PubMed.
- M. D. Segall, P. J. Lindan, M. A. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-principles simulation: ideas, illustrations and the CASTEPcode, J. Phys. Condens. Matter, 2002, 14(11), 2717 CrossRef CAS.
- Y. H. Duan, Y. Sun, M. J. Peng and S. G. Zhou, Anisotropic elastic properties of the Ca–Pb compounds, J. Alloys Compd., 2014, 595, 14–21 CrossRef CAS.
- S. Daoud, Sound velocities and thermal properties of BX (X= As, Sb) compounds, Int. J. Sci. World, 2015, 3(1), 43–48 CrossRef.
- Y. Zhou, X. Lu, H. Xiang and Z. Feng, Preparation, mechanical, and thermal properties of a promising thermal barrier material: Y 4 Al 2 O 9, J. Adv. Ceram., 2015, 4, 94–102 CrossRef CAS.
- Y. Zhou, H. Xiang, X. Lu, Z. Feng and Z. Li, Theoretical prediction on mechanical and thermal properties of a promising thermal barrier material: Y 4 Al 2 O 9, J. Adv. Ceram., 2015, 4, 83–93 CrossRef CAS.
- S. Al-Qaisi, D. P. Rai, T. Alshahrani, R. Ahmed, B. U. Haq, S. A. Tahir, M. Khuili and Q. Mahmood, Structural, elastic, thermodynamic, electronic, optical and thermoelectric properties of MgLu2X4 (X= S, Se) spinel compounds from ab-initio calculations, Mater. Sci. Semicond. Process., 2021, 128, 105766 CrossRef CAS.
- S. Nawaz, M. Saleem, F. V. Kusmartsev and D. H. Anjum, Major role of multiscale entropy evolution in complex systems and data science, Entropy, 2024, 26(4), 330 CrossRef PubMed.
- A. Ayyaz, G. Murtaza, M. Shafiq, M. Q. Shah, N. Sfina and S. Ali, Exploring structural, thermodynamic, elastic, electro-optic, and thermoelectric characteristics of double perovskites Rb2XInBr6 (X= Na, K) for photovoltaic applications: a DFT approach, Sol. Energy, 2023, 265, 112131 CrossRef CAS.
- S. A. Dar, V. Srivastava, U. K. Sakalle, K. S. Ahmad and D. C. Gupta, A DFT study on structural, electronic
mechanical and thermodynamic properties of 5f-electron system BaAmO 3, J. Supercond. Novel Magn., 2018, 31, 141–149 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
Mohamed Taha
b and
Mohamed Taha *a
*a
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , 2), as provided by the Materials Project database (mp-561710),75 was used as the initial model. Systematic atomic substitutions were carried out to investigate the effects of compositional variations: the A-site Cs atom was replaced with Li, Na, K, and Rb; the B-site Sn atom was substituted with Si and Ge; and the X-site S atoms were replaced with Te. Geometry optimization, as well as electronic and optical property calculations, were conducted using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.73 All exchange–correlation (XC) functionals were evaluated using a kinetic energy cutoff of 650 eV, employing norm-conserving pseudopotentials.76
, 2), as provided by the Materials Project database (mp-561710),75 was used as the initial model. Systematic atomic substitutions were carried out to investigate the effects of compositional variations: the A-site Cs atom was replaced with Li, Na, K, and Rb; the B-site Sn atom was substituted with Si and Ge; and the X-site S atoms were replaced with Te. Geometry optimization, as well as electronic and optical property calculations, were conducted using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional.73 All exchange–correlation (XC) functionals were evaluated using a kinetic energy cutoff of 650 eV, employing norm-conserving pseudopotentials.76











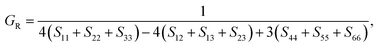


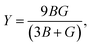



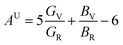


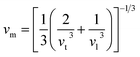
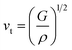

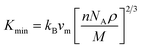

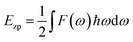

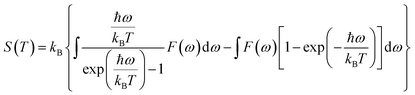

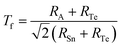


 and
and 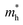 , respectively. These effective masses influence how charge carriers respond to an applied electric field. Consequently, both
, respectively. These effective masses influence how charge carriers respond to an applied electric field. Consequently, both  and
and 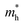 , along with the scattering of charge carriers by phonons, play a fundamental role in governing charge transport properties in photovoltaic materials.134 The m* of charge carriers associated with the VBM and CBM of ASnTe3 were determined through parabolic fitting of the band edges.
, along with the scattering of charge carriers by phonons, play a fundamental role in governing charge transport properties in photovoltaic materials.134 The m* of charge carriers associated with the VBM and CBM of ASnTe3 were determined through parabolic fitting of the band edges.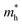 are larger than
are larger than  , confirming the p-type character135 of NaSnTe3, KSnTe3, RbSnTe3, and CsSnTe3 (Table 3). Meanwhile,
, confirming the p-type character135 of NaSnTe3, KSnTe3, RbSnTe3, and CsSnTe3 (Table 3). Meanwhile,  are larger than
are larger than  , further validating the n-type character135 of LiSnTe3. Furthermore,
, further validating the n-type character135 of LiSnTe3. Furthermore,  of KSnTe3 is found to be smaller than that in LiSnTe3, NaSnTe3, RbSnTe3, and CsSnTe3, suggesting a higher electron mobility for KSnTe3.
of KSnTe3 is found to be smaller than that in LiSnTe3, NaSnTe3, RbSnTe3, and CsSnTe3, suggesting a higher electron mobility for KSnTe3.




 and
and  values span 0.292–1.181 and 0.256–3.149 m0, respectively, with KSnTe3 showing the lowest
values span 0.292–1.181 and 0.256–3.149 m0, respectively, with KSnTe3 showing the lowest  (0.292), suggesting high electron mobility. (3) Optically, they demonstrate strong dielectric response (ε1(0.01) = 6.935–16.626) and high UV-visible absorption. They also display low energy loss, efficient optical conductivity, a desirable refractive index (n(ω) = 3.078–3.912), and moderate reflectivity (∼30–35%) in the low-energy region, all of which affirm their suitability for optoelectronic device applications. (4) Mechanically, the compounds exhibit elastic moduli (B = 21.827–36.227 GPa, G = 8.676–15.224 GPa, Y = 27.002–36.224 GPa). All systems are ductile (ν = 0.301–0.356; B/G = 1.847–3.471), with HV ranging from 0.999 to 1.767 GPa and μm between 1.620 and 3.045. Elastic anisotropy is evident in all materials, increasing in the order E < G < ν. (5) Thermodynamically, these materials are thermally stable with Tm between 770.6 and 891.9 K and θD in the range of 125.8–158.0 K. The κmin = 0.276–0.379 W m−1 K−1. Their thermodynamic functions (Cp, S(T), H(T)) support reliable performance across a broad thermal range. LiSnTe3 has the highest thermal conductivity, while CsSnTe3 has the highest melting point. KSnTe3, has the lowest Debye temperature and thermal conductivity.
(0.292), suggesting high electron mobility. (3) Optically, they demonstrate strong dielectric response (ε1(0.01) = 6.935–16.626) and high UV-visible absorption. They also display low energy loss, efficient optical conductivity, a desirable refractive index (n(ω) = 3.078–3.912), and moderate reflectivity (∼30–35%) in the low-energy region, all of which affirm their suitability for optoelectronic device applications. (4) Mechanically, the compounds exhibit elastic moduli (B = 21.827–36.227 GPa, G = 8.676–15.224 GPa, Y = 27.002–36.224 GPa). All systems are ductile (ν = 0.301–0.356; B/G = 1.847–3.471), with HV ranging from 0.999 to 1.767 GPa and μm between 1.620 and 3.045. Elastic anisotropy is evident in all materials, increasing in the order E < G < ν. (5) Thermodynamically, these materials are thermally stable with Tm between 770.6 and 891.9 K and θD in the range of 125.8–158.0 K. The κmin = 0.276–0.379 W m−1 K−1. Their thermodynamic functions (Cp, S(T), H(T)) support reliable performance across a broad thermal range. LiSnTe3 has the highest thermal conductivity, while CsSnTe3 has the highest melting point. KSnTe3, has the lowest Debye temperature and thermal conductivity.

















