Zigzag antiferromagnetic property of two-dimensional NiPX₃ (X = S/Se) monolayers in their pristine structure and Janus phase

Abstract

Transition metal phosphorous trichalcogenides TMPX₃ (TM = transition metal, X = S/Se) with a variety of spin configurations serve as excellent platforms for studying the magnetic properties of two-dimensional systems. As an antiferromagnetic semiconductor, the coexistence of ferromagnetic and antiferromagnetic couplings between the nearest neighboring metal ions of NiPX₃ remains a debatable topic. In this work, the electronic structures and magnetic properties of NiPX₃ monolayers in their pristine structure and Janus phase were systemically investigated using first-principles calculations. It was found that the NiPX₃ system possessed an indirect band gap in the zigzag antiferromagnetic ground state with a sizable Néel temperature, as estimated by Monte Carlo simulations. Electronic structures and crystal orbital Hamilton population analyses revealed that the zigzag antiferromagnetic ordering was primarily driven by superexchange interactions through p–d hybridization. Meanwhile, the coexistence of ferromagnetic and antiferromagnetic couplings was facilitated through a combination of antibonding and bonding states below the Fermi level. This work provides a new approach to explore the diverse and intriguing magnetic properties of two-dimensional materials.

---

1. Introduction

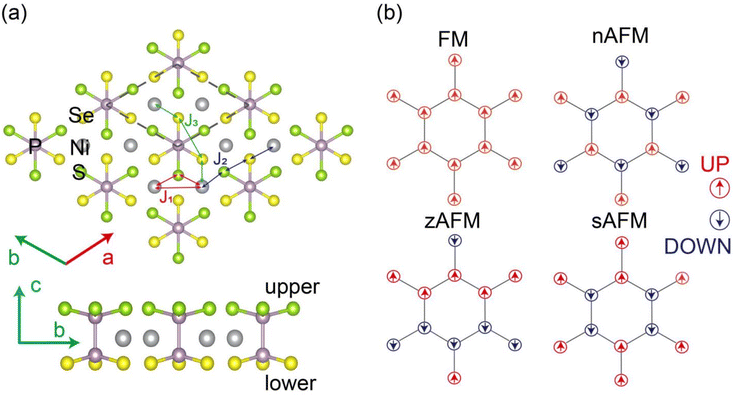
Inspired by the pioneer discovery of an intrinsic magnetic order observed in FePS₃ monolayer,^1,2 transition metal phosphorus trichalcogenides TMPX₃ (TM = transition metals such as Cr, Mn, Fe, Co, and Ni; X = S/Se) have served as excellent platforms to explore two dimensional (2D) magnetism in recent years.³ Most TMPX₃ crystals exhibit an antiferromagnetic (AFM) behavior, with a Néel temperature (T_N) ranging from 82 K to 155 K (ref. 4 and 5); however, some of these crystals, such as MgPS₃ and ZnPSe₃ (ref. 6), exhibit a paramagnetic property owing to the presence of unfilled or fully filled d electrons in the metal ions. Bulk TMPX₃ materials always exhibit a stacking sequence of “ABAB” in C2/m symmetry or “ABC” in R₃ space group and are crystallized by van der Waals (vdW) forces with vdW distances ranging from 3.22 to 3.24 Å (ref. 7); therefore, TMPX₃ monolayer can be mechanically exfoliated from the bulk phase owing to the weak cleavage energy, which is smaller than 0.36 J m⁻² for graphite.⁸ The TMPX₃ monolayer is characterized by a hexagonal honeycomb-like lattice framework formed by TM atoms. Each TM atom is coordinated with six S/Se atoms, which constitute the upper and lower chalcogen layers. These layers are interconnected via P–P pairs. Specifically, the S/Se atoms are sandwiched between P–P pairs both above and below the honeycomb lattice plane. The P–P dimer vertically bisects the center of the hexagonal unit cell, forming a bipyramid-structure of [PX₃⁻]–[PX₃].

While 2D TMPX₃ monolayers typically demonstrate an AFM behavior, the diverse electronic configurations of TM atoms result in diverse magnetic properties and electronic structures. MnPX₃ monolayers exhibit a Néel AFM (nAFM, Fig. 1(b)) configuration as direct band gap semiconductors, while FePX₃ monolayers usually exhibit a zigzag AFM (zAFM, Fig. 1(b)) ordering as indirect band gap semiconductors; moreover, CuPX₃ system displays a paramagnetic metal character.^9,10 In particular, multiple Dirac cones are predicated in paramagnetic NiPX₃, PdPX₃ and PtPX₃ (ref. 11) besides ferromagnetic (FM) CrPSe₃ monolayers.¹² Some strong electron correlations have been experimentally detected, such as the Mott–Hubbard insulation in the NiPX₃ (ref. 13) system and observation of a negative charge transfer in the NiPS₃ monolayer.¹⁴ Magnetic anisotropy energy (MAE) of TMPX₃ monolayers also strongly affects their spin dimensions in Ising, XY and Heisenberg models, which have been observed in FePS₃, MnPS₃ and CoPS₃ monolayers,^1,15,16 respectively. Currently, 2D TMPX₃ systems have attracted considerable attention owing to their fascinating phenomena arising from strong coupling interactions between magnetism and other physical properties. Superconductivity can be driven into some 2D TMPX₃, such as FePS₃, MnPS₃ and NiPSe_3, via a pressure-driven spin-crossover.^17–19 A giant optical linear dichroism has been observed in FePS₃ and NiPSe₃ monolayers using magneto-optical spectroscopy,²⁰ while a second harmonic generation can be produced via polarization-resolved electric quadruple contribution in MnPSe₃ monolayer.²¹ Furthermore, strong electron–phonon coupling in FePS₃ (ref. 22) and magnon–phonon coupling²³ and photon–matter coupling²⁴ in NiPS3 have been directly determined using magneto-Raman spectroscopy, ultrafast spectroscopy and spectroscopic analysis in conjunction with a microscopic theory, respectively.

Fig. 1 (a) Crystal structure of Janus NiPS_3/2Se_3/2 from top and side views; (a)–(c) indicate the lattice vectors along [100], [010] and [001] directions, respectively. The dashed rhombus marks a primitive unit cell. (b) Four magnetic configurations in 2D hexagonal lattice; spin-up (UP) and spin-down (DOWN) magnetic moments are indicated by red and blue arrows, respectively.

Despite extensive research into their unique magnetic properties, diverse electronic structures, and intriguing electromagnetic couplings of 2D TMPX₃ systems, the origin of the zAFM order in some TMPX₃ monolayers remains a subject of ongoing debate. Very recently, the magnetic ground states of NiPS₃ and FePS₃ monolayers have been demonstrated to exhibit a distinct zigzag antiferromagnetic (zAFM) ordering. Specifically, the zAFM state in NiPS₃ is primarily determined by the nearest-neighbor (NN) biquadratic exchange interaction, while in FePS₃, it results from the competition between ferromagnetic (FM) NN and antiferromagnetic (AFM) third-nearest-neighbor (3NN) exchange interactions.²⁵ A small distortion between TM–TM distance has been predicted to result in an zAFM alignment in FePS₃.^9,26 To date, the reason for the co-existence of FM and AFM spin orderings between the NN TM atoms in zAFM systems is unclear. Hence a detailed investigation on the electronic structures is imperative to reveal the mechanism of zAFM spin-ordering, where the adjacent TM chains along the zigzag direction exhibit an opposite orientation in 2D TMPX₃.

Since chalcogen-substituted NiPS_3−xSe_x (0 ≤ x ≤ 1.3) crystal has been successfully synthesized recently,²⁷ in this work, the magnetic properties of 2D NiPX₃ in its pristine structure in conjunction with its Janus phase of NiPS_3/2Se_3/2 were systemically investigated using first-principles calculations and Monte Carlo (MC) simulations, including the magnetic exchange parameters (J), MAE and Néeel temperature (T_N). In addition, the electronic structures combined with crystal orbital Hamilton populations (COHP) and crystal-field splitting were discussed in detail to reveal the magnetic mechanism of zAFM spin ordering.

2 Computational methods

Based on density functional theory (DFT),²⁸ our spin-polarized first-principles calculations were carried out using the Vienna Ab initio simulation package (VASP).²⁹ The ion–electron interactions were characterized using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation potentials within generalized gradient approximation (GGA).³⁰ The GGA+U model was employed to consider the strong electron correlations in 3d orbitals,³¹ where the effective Hubbard parameter U_eff = U − J encompasses both Coulomb repulsion U and Hund's rule-driven exchange interaction J. Electronic functions were described using the projector augmented wave method.³² Kinetic energy cut-off was set at 500 eV to expand the wave functions into a plane-wave basis. A 20 Å thickness vacuum space was set to avoid interlayer interactions caused by periodic boundary conditions. The convergence criteria were set to be 10⁻³ eV Å⁻¹ for the force and 10⁻⁶ eV for the energy, respectively. The Brillouin zone (BZ) was sampled using the Monkhorst–Pack method with a Γ-centered 24 × 24 × 1 k-mesh.³³ The COHP distributions were also employed to understand the chemical bonding using the lobster program based on DFT.³⁴ Phonon dispersion was calculated using the finite displacement method with phonopy program,³⁵ and Nosé–Hoover thermostat method was employed for ab initio molecular dynamics (AIMD) simulations.^36,37 T_N values were simulated using MC methods based on the Metropolis algorithm with boundary conditions.^38,39 Some data related to the pre- and post-processing processes were obtained using the Vesta program⁴⁰ and VASPKIT package,⁴¹ respectively.

3. Results and discussion

3.1. Crystal structure and stability of 2D NiPX₃ and NiPS_3/2Se_3/2

The crystal structure of Janus NiPS_3/2Se_3/2 monolayer with a 60° torsion angle between the upper S and lower Se layers (Fig. 1) has a primitive unit cell containing two formula units. Based on the distinct chalcogen atom arrangements in upper and lower sublayers, the intrinsic NiPX₃monolayer belongs to the D_3d space group, while the Janus NiPS_3/2Se_3/2 exhibits a P3̄1m symmetry. Some lattice parameters of 2D NiPS₃ and NiPSe₃ monolayers in the zAFM state are presented in Table 1. The calculated lattice constant value of a was consistent with the corresponding experimental results.^42,43 The lengths of P–P and P–X bonds indicated a covalent character in a [PS₃]²⁻–[PSe₃]² anion pair. Owing to the larger atomic radius of Se than that of S, the lattice constant, monolayer thickness and bond length of NiPSe₃ were larger than those of NiPS₃. The structure of Janus NiPS_3/2Se_3/2 was also fully optimized, as shown in Table 1. The bond lengths of Ni–X, P–X and P–P were comparable to those of pristine NiPX₃, indicating good structural stability of the Janus monolayer.

Table 1 Lattice constant a (Å), monolayer thickness h (Å), bond-length l (Å) and energy band gap E_g (eV) of NiPS₃, NiPSe₃ and NiPS_3/2Se_3/2 monolayers calculated with U = 4.0 eV, respectively

	a	h	lNi–S	lNi–Se	lP–P	lP–S	lP–Se	Eg
NiPS3	5.83	3.12	2.47	—	2.18	2.04	—	1.72
NiPSe3	6.17	3.25	—	2.58	2.20	—	2.22	1.45
NiPS3/2Se3/2	6.00	3.18	2.48	2.58	2.19	2.05	2.21	1.42

---

As shown in Fig. 1, four different magnetic configurations, namely, FM, nAFM, zAFM and stripy AFM (sAFM), were considered to determine the magnetic ground state of the NiPX₃ and NiPS_3/2Se_3/2 monolayers. The structures were fully relaxed, and total energy was calculated for each magnetic configuration. The calculated energies followed the sequence of E_zAFM < E_nAFM < E_FM < E_sAFM for different U_eff values, as listed in Table 2. Therefore, the pristine NiPX₃ and Janus NiPS_3/2Se_3/2 monolayers were confirmed to be in the zAFM ground state. For the zAFM ordering, each adjacent Ni chain showed an opposite spin orientation along the zigzag direction, while a parallel spin arrangement perpendicular to this direction was displayed in the spin charge density map, as illustrated in Fig. S1.† Here, U = 4.0 eV was chosen for further discussions because at this energy, the calculated T_N and band gap of NiPX₃ monolayer were quantitatively close to the corresponding experimental values, which will be discussed in Section 3.2.

Table 2 Total energy E (eV) at different magnetic configurations and magnetic exchange parameters J_i (i = 1, 2 and 3 meV) of 2D NiPX₃ and NiPS_3/2Se_3/2 with a series of U_eff (eV) values calculated in 2 × 1 × 1 supercells, respectively. Néel temperature T_N (K) was simulated in a 32 × 32 × 1 superlattice

Compound	Ueff	EFM	EnAFM	EzAFM	EsAFM	J1	J2	J3	TN
NiPS3	1.0	−98.12	−98.48	−98.51	−98.06	7.25	0.89	−49.13	384
	2.0	−96.07	−96.34	−94.36	−96.02	5.55	0.72	−32.02	299
	3.0	−94.17	−94.37	−94.39	−94.13	4.22	0.55	−21.84	234
	4.0	−92.41	−92.57	−92.58	−92.38	3.14	0.42	−15.17	186
	5.0	−90.81	−90.92	−90.94	−90.78	2.29	0.32	−10.62	145
	6.0	−89.35	−89.43	−89.44	−89.32	1.60	0.24	−7.40	114
NiPSe3	1.0	−89.31	−89.68	−89.73	−89.25	12.22	0.12	−61.78	351
	2.0	−87.13	−87.42	−87.47	−87.09	7.59	−0.46	−40.42	270
	3.0	−85.12	−85.34	−85.38	−85.08	5.74	−0.16	−27.06	210
	4.0	−83.26	−83.43	−83.46	−83.23	4.33	−0.03	−18.68	160
	5.0	−81.56	−81.69	−81.71	−81.53	3.21	0.04	−12.94	125
	6.0	−80.02	−80.11	−80.13	−79.99	2.30	0.07	−8.88	95
NiPS3/2Se3/2	1.0	−93.49	−93.86	−93.92	−93.45	9.28	−0.59	−55.83	371
	2.0	−91.38	−91.66	−91.71	−91.34	6.81	−0.44	−36.87	291
	3.0	−89.42	−89.63	−89.67	−89.39	5.25	−0.17	−24.94	230
	4.0	−87.61	−87.77	−87.81	−87.58	4.00	−0.03	−17.30	180
	5.0	−85.96	−86.08	−86.10	−85.93	2.95	0.04	−11.99	137
	6.0	−84.45	−84.54	−84.56	−84.43	2.14	0.07	−8.35	110

---

The structural stability of pristine NiPX₃ and Janus NiPS_3/2Se_3/2 monolayers were examined considering the elastic constants, phonon spectra and AIMD for assessing their mechanical, dynamical and thermal performances, respectively. For a hexagonal lattice, the elastic constants C_ij (i, j = 1, 2, and 6) were calculated as C = [∂²E/∂ε²]/S, based on the energy-strain method,⁴⁴ by applying a series of small in-plane strains ε to the monolayers,⁴⁵ where E is the total energy variation with the lattice area S. As listed in Table 3, the elastic constants of C₁₁ and C₁₂, with C₆₆ = (C₁₁ − C₁₂)/2, satisfy the formulas C₁₁ > 0 and C₁₁C₁₂ − C₂₁² > 0 of Born–Huang criterion,⁴⁶ demonstrating that pristine NiPX₃ and Janus NiPS_3/2Se_3/2 exhibit good mechanical stability. Young's modulus Y, shear modulus G and Poisson's ratio v were also calculated, as presented in Table 3; the values for NiPS_3/2Se_3/2 monolayers located between the corresponding values of NiPS₃ and NiPSe₃, respectively. All the Y values were much smaller than that of graphene as Y = 340 ± 40 N m⁻¹. These results confirmed the mechanical flexibility of NiPX₃ monolayers. The phonon spectra are shown in Fig. 2 along with the density of states for each element. All phonon frequencies were positive in the entire energy range for the three monolayers, revealing excellent dynamical stability.^47,48 Clearly, Ni, S/Se and P atoms dominated the low-frequency, mid-frequency and high-frequency branches of the phonon spectra, respectively. During AIMD simulations at 300 K, the total energy curve showed small fluctuations in a narrow range for 10 ps. In addition, the 2D lattice remained in a planar structure after each relaxation for the three monolayers, as shown in Fig. 2.

Table 3 Elastic constants C_ij (N m⁻¹), Young's modulus Y (N m⁻¹), shear modulus G (GPa) and Poisson's ratio v of 2D NiPX₃ and NiPS_3/2Se_3/2

	C11	C12	C66	Y	G	v
NiPS3	93.17	22.97	35.10	87.51	35.10	0.25
NiPSe3	77.36	19.12	29.12	72.64	29.12	0.25
NiPS3/2Se3/2	88.78	21.51	33.64	83.58	33.64	0.24

---

Fig. 2 Phonon spectra along with density of states and total energy oscillations with side views of the relaxed structures after AIMD simulations for (a) NiPS₃, (b) NiPSe₃ and (c) NiPS_3/2Se_3/2.

As a consequence, 2D NiPX₃ and NiPS_3/2Se_3/2 monolayers exhibited good thermal stability at room temperature.

3.2. Magnetic properties of 2D NiPX₃ and NiPS_3/2Se_3/2

The MAE plays a crucial role in stabilizing the long-range magnetic order by preventing spontaneous spin flipping in 2D magnetic materials. Taking the spin–orbit coupling (SOC) effect into account, the MAE was calculated from the energy difference as E_MAE = E₍₁₀₀₎ − E₍₀₀₁₎, with spin orientations in and out of the monolayer plane. The partial components of MAE from different atoms, i.e. E_MAE (Ni) was also calculated. The MAE results of NiPX₃ and NiPS_3/2Se_3/2 monolayers are listed in Table 4. As can be seen, the E_MAE was lower for NiPS₃, while it was higher for NiPSe₃ and NiPS_3/2Se_3/2 in ab-plane (100) than in c-direction [001]. The calculated MAE results reveal distinct magnetic easy axes for the three monolayers: NiPS₃ exhibits an in-plane (ab-plane) easy axis along the a-axis, while NiPSe₃ and NiPS_3/2Se_3/2 show out-of-plane (c-axis) easy axes perpendicular to the ab-plane.²⁷ Furthermore, the absolute E_MAE value was larger in the b [010] direction than in the a [100] direction for the three monolayers owing to their zAFM spin configuration. From the partial component of the E_MAE, the magnetic anisotropy of NiPS₃ was mainly contributed by Ni atoms, whereas, Se atoms dominated the magnetic anisotropy of NiPSe₃ and NiPS_3/2Se_3/2 monolayers.

Table 4 Total E_MAE partial component (i.e. E_MAE (Ni)) of MAE with respect to the value in (001) direction for 2D NiPX₃ and NiPS_3/2Se_3/2 in the unit of meV per u.c. (u.c. indicates a unit cell). Easy axis denotes the MAE-determined spin orientation

Compound	Orientation	EMAE	EMAE (Ni)	EMAE (P)	EMAE (S)	EMAE (Se)	Easy axis
NiPS3	(100)	−87	−82.1	0.7	12.6		ab-Plane
	(010)	−95	−52.5	0.5	1.5
NiPSe3	(100)	344	−6.1	0.05	—	55.3	(001)
	(010)	473	−17.2	10.4		81.1
NiPS3/2Se3/2	(100)	185	−6.6	0.2	1.0	64.9	(001)
	(010)	369	−31.2	5.6	−0.5	140.6

---

In order to describe the magnetic interactions between Ni²⁺ ions for these zAFM monolayers, the magnetic exchange parameters were evaluated using the Heisenberg Hamiltonian as follows_:^9,49

where J₁, J₂ and J₃ represent the magnetic exchange parameters in NN, second-nearest-neighboring (2NN) and 3NN distances, respectively. S_i is the magnetic moment at the atomic site i of Ni²⁺ ions. The calculated magnetic moment was about 1.40μ_B, which was in consistent with previous results for pristine NiPX₃ monolayers.^50,51 The J_i parameters were calculated by mapping the total energies in the four distinct magnetic configurations to the Heisenberg Hamiltonian. The corresponding results for a range of U_eff values are presented in Table 2 for each of the three monolayers, indicating that variations in U_eff values significantly influence the J_i values. A larger U_eff value indicated stronger localization of the d-orbitals, which in turn reduced the magnetic exchange interactions between the Ni ions. In addition, the chalcogen atoms exhibited a notable impact on the magnetic exchange interactions; in particular, NiPS₃ showed smaller J_i values than those of NiPSe₃ and NiPS_3/2Se_3/2. In the case of U = 4.0 eV, the calculated results were J₁ = 3.14 meV, J₂ = 0.42 meV and J₃ = −15.17 meV for NiPS₃ and J₁ = 4.33 meV, J₂ = −0.03 meV and J₃ = −18.68 meV for NiPSe₃, which were in good agreement with previously reported theoretical values.^25,27 For NiPS_3/2Se_3/2, the calculated exchange parameters were J₁ = 4.00 meV, J₂ = −0.03 meV and J₃ = −17.30 meV, which were close to those of NiPSe₃. The positive J₁ value indicated FM interactions between NN Ni²⁺ ions. The 2NN J₂ was very small, indicating a negligible effect. In contrast, 3NN J₃ was negative and exhibited the largest absolute value, which was crucial for determining the ground state of these zAFM monolayers.

The specific heat capacity is definded as where E represents in ternal energy and k_B is the Boltzmann constant; T_N could be calculated from the second-order phase transition variable C_v curve. Using MC simulations, the critical transition temperature was evaluated in a 32 × 32 superlattice, with spin directions flipped randomly about 2 × 10⁹ steps per loop. The simulated C_v and E curves as a function of temperature are plotted in Fig. 3. Under the condition of U_eff = 4.0 eV, calculated T_N values were in good agreement with the experimental results for each pristine NiPX₃ monolayer. In particular, T_N = 160 K was very close to the experimental value of 155 K (ref. 52) for NiPS₃, while T_N = 189 K was slightly lower than 212 K, when measured using temperature-dependent molar susceptibility⁵³ for NiPSe₃. Notably, the T_N of NiPS₃ was lower than that of NiPSe₃, which is attributed to the stronger magnetic exchange interactions of NiPSe₃ than that of NiPS₃. Similarly, the T_N of Janus NiPS_3/2Se_3/2 is predicted to be 180 K, which represents an enhancement compared to 160 K for NiPS₃ but shows a decrease relative to 189 K for NiPSe₃. This feature was consistent with the behavior predicated for Janus MnPS_3/2Se_3/2 monolayer, where the magnetic exchange interactions were dominated by transition metal elements.⁵⁴ The T_N values for a series of U_eff values were also calculated and are presented in Table 2 for each monolayer. As mentioned above, the T_N was much larger than the corresponding experimental value when U > 4.0 eV but much smaller when U < 4.0 eV. These results further confirmed the rationality of selecting U = 4.0 eV for our calculations. Along with the near-room critical temperature, NiPSe₃ and NiPS_3/2Se_3/2 monolayers, which exhibit an out-of-plane magnetization, are suitable for magnetic storage and low-power switching devices, e.g. spin-transfer torque for electrical switching, whereas the in-plane magnetized NiPS₃ monolayer is suited for ultrafast spin information processing, e.g. spin-wave logic circuits.^55,56

Fig. 3 Specific heat capacity C_v and total energy E with respect to temperature T for 2D (a) NiPS₃, (b) NiPSe₃ and (c) NiPS_3/2Se_3/2 calculated using Monte Carlo simulations.

3.3. Electronic structures of 2D NiPX₃ and NiPS_3/2Se_3/2. Band structures were calculated in a 2 × 1 × 1 supercell and then projected into primitive BZ along the high-symmetry line of Γ–M–K–Γ,⁵⁷ as illustrated in Fig. 4(a)–(c) for NiPX₃ and NiPS_3/2Se_3/2, respectively. The three zAFM monolayers behaved as typical semiconductors, with an indirect band gap, valence band (VB) maxima located at the K point and the conduction band (CB) minima in the K–Γ path. Notably, the calculated band gaDp was 1.71 eV for NiPS₃ and 1.44 eV for NiPSe₃ at U = 4.0 eV, and these values were consistent with the previously obtained DFT results.⁵⁰ Furthermore, the calculated value of 1.71 eV in the 2D structure was larger than the experimentally obtained value of 1.66 eV in bulk phase of NiPS₃.⁵⁸ The larger bandgap of NiPS₃ than that of NiPSe₃ can be attributed to the stronger electronegativity of S than Se. Correspondingly, the bandgap of 1.42 eV of NiPS_3/2Se_3/2 was between the bandgap values of NiPS₃ and NiPSe₃ and was much closer to that of NiPSe₃. Beyond the indirect band gap, the band structures of the three monolayers showed similar dispersion patterns; for instance, the four uppermost VBs and four undermost CBs near the Fermi level reached their maximum degeneracy at M point. In addition, the four undermost CBs were almost isolated from the other higher CBs.

Fig. 4 Band structures of 2D (a) NiPS_3, (b) NiPSe₃ and (c) NiPS_3/2Se_3/2. Black arrow points from valence band maxima to conduction band minima.

In order to investigate the electronic structures in detail, the total density of states (DOS) and orbital projected DOS (PDOS) for NiPX₃ and NiPS_3/2Se_3/2 were plotted in Fig. 5(a)–(c). As the NiPX₃ system existed in an AFM ground state, the spin-up channel was symmetrical to the corresponding spin-down channel for each DOS or PDOS. Close to the Fermi level, the uppermost four VBs were mainly contributed by the p_x, p_y, and p_z states of chalcogen atoms, and Ni d orbitals also had some contributions for each zAFM monolayer. The VB maximum was mostly composed of chalcogen p_x and p_y orbitals; hence, NiPS₃ monolayer exhibited a smaller band gap than the NiPSe₃ monolayer as the electronegativity of the S atom was larger than that of the Se atom. It should be noted that just below the Fermi level, the Se p_x and p_y orbitals showed more concentrated contributions than those of the S atom, resulting in a flat band along the K–Γ path for NiPSe₃, especially for NiPS_3/2Se_3/2.

Fig. 5 Total density of states (DOS) and orbital-projected DOS of 2D (a) NiPS₃, (b) NiPSe₃ and (c) NiPS_3/2Se_3/2.

The electron numbers N were calculated by integrating the PDOS in the spin-up channel within the energy range from −0.50 eV to 0.0 eV by the formula of N = κ∫PDOSdE, where κ = 1/2 for pristine structures and κ = 1 for Janus phase, based on their respective molecular formulas. As listed in Table S1,† the electron numbers of the chalcogen elements in their p orbitals were calculated to be N_S = 1.82 e for NiPSe₃ and N_Se = 1.96 e for NiPSe₃, while N_S = 0.94 e and N_Se = 2.33 e for NiPS_3/2Se_3/2. These results clearly indicated that the Se element exhibited more influence on the electronic structures and magnetic properties than the S element for NiPS_3/2Se_3/2. As a consequence, the bandgap, MAE value and magnetic exchange parameters of Janus NiPS_3/2Se_3/2 were much closer to that of NiPSe₃ than that of NiPS₃. Here, Ni d electrons contributed more to the four undermost CBs than to the four uppermost VBs near the Fermi level. These contributions were primarily composed of the d_xz and d_yz states, with some contributions from the d_xy and d_x²−y² orbitals. This feature deviated from that of some other AFM TMPX₃, such as CrPSe₃ and MnPS₃, where d electrons contributed more to the uppermost VBs than to the undermost CBs.^10,12 Throughout the energy range, P p_z orbitals strongly hybridized with those of S/Se atoms, forming the [P₂X₆]⁴⁻ octahedrons that provided excellent mechanical stability for each monolayer. Notably, the Ni d orbitals exhibited pronounced hybridization with the chalcogen p_x and p_y orbitals, facilitating an indirect p–d exchange interaction for Ni ions.

As illustrated in Fig. S1 and S2,† both the spin charge density maps and charge distributions of the Ni hexagonal slide could not provide enough information for the bonding behavior between Ni ions. Here, the electronic structures were further evaluated by extracting the chemical bonding data from COHP diagrams for NiPX₃ and NiPS_3/2Se_3/2 monolayers. The negative diagrams of NN Ni–Ni couplings are plotted in Fig. 6(a)–(c), respectively. In these –COHP diagrams, the bonding and antibonding states were denoted by positive and negative values, respectively. It was evident that there were four negative peak-curves for –COHP below the Fermi level, where the plus/minus signs of –COHP peaks alternated from −6.0 eV to Fermi energy, which was set to 0.0 eV. In particular, the first main peak, situated just under Fermi level, exhibited negative values, which played a vital role in the zAFM configuration.

Fig. 6 –COHP distributions between NN Ni ions in 2D (a) NiPS₃, (b) NiPSe₃ and (c) NiPS_3/2Se_3/2.

The coexistence of FM and AFM couplings between NN Ni ions was discussed by considering both the crystal field effect and electronic structure to clarify the mechanism of zAFM ordering. As shown in Fig. 7(a), each Ni atom was surrounded by six S/Se atoms, forming an octahedral structure with D_3d symmetry.^51,59 Owing to crystal field effect, Ni 3d orbitals could be divided into two parts: one group was named as t_2g of the d_xy, d_x²−y² and d_z² orbitals and the other one was denoted as e_g of d_xz and d_yz orbitals. According to the orbital-projected DOS in Fig. 5, the energy of the t_2g state was lower than that of the e_g state in VBs; thus, the first negative –COHP peak under 0.0 eV was composed of e_g states. Since Ni 3d electrons were in a configuration of 3d⁸ 4s², the t_2g orbitals were fully occupied at the lower energy level, yielding no net magnetic moment. In contrast, the half-filled d_xz/d_yz orbitals had two electrons in the higher energy level with the same-direction spin alignment, resulting in a net magnetic moment with a calculated value about 1.40μ_B for each Ni ion. As illustrated in Fig. 7(b), the AFM exchange interactions could be attributed to the direct hopping between the half-filled e_g orbitals for NN Ni ions, forming some bonding states. Comparatively, in Fig. 7(c), when NN Ni ions formed an FM arrangement, the FM exchange interactions could be realized by some antibonding states according to Hund's rule. As a consequence, the alternation of antibonding and bonding states led to the coexistence of AFM and FM couplings between NN Ni ions in NiPX₃ and NiPS_3/2Se_3/2 monolayers.

Fig. 7 Schematic of (a) octahedral crystal field and 3d electron fillings and (b) AFM, and (c) FM exchange interactions between NN Ni ions.

As discussed above, the first negative –COHP peak could be considered as a result of the FM coupling between e_g orbitals in the antibonding states, resulting in positive J₁ values. In other words, the FM indirect interactions between the NN Ni ions dominated the competition against the AFM direction exchange interactions, as illustrated in Fig. 1. However, the AFM ground states of NiPX₃ and NiPS_3/2Se_3/2 were predominantly determined by the 3NN superexchange interactions mediated via p–d hybridization. Evidently, the absolute value J₃ significantly exceeded J₁, whereas the value of J₂ was negligible. This huge difference between J₂ and J₃ originated from their distinct superexchange pathways. As shown in Fig. 1, the 2NN interactions were mediated by two S/Se atoms residing in different sublayers (one in the upper and the other in the lower), while the 3NN interactions were mediated by two S/Se atoms within the same sublayer. Here, the magnetic mechanism of Janus NiPS_3/2Se_3/2 was consistent with that of the pristine NiPX₃ system; thus, the magnetic properties, including MAE, exchange parameters and T_N values of NiPS_3/2Se_3/2 were similar to those of NiPX₃ in the zAFM state. This stable magnetic feature was consistent with our previous findings on the MnPX₃ system in the nAFM state.¹⁰

4. Conclusion

In summary, the electronic structures and magnetic properties of 2D pristine NiPX₃ and Janus phase NiPS_3/2Se_3/2 were comprehensively investigated using the first-principles calculations. Despite the on-site Coulomb repulsion with a series of U_eff values, both pristine and Janus NiPX₃ systems remained in a zAFM ground state and were characterized as indirect band gap semiconductors. The bandgaps of NiPS₃ and NiPSe₃ were 1.71 eV and 1.44 eV, respectively, while the value of NiPS_3/2Se_3/2 was 1.42 eV. Three 2D monolayers showed excellent structural stability as determined using the elastic coefficients satisfying the Born criterion, phonon spectra with no negative frequency and a planar structure after AIMD relaxation. Calculated MAE values showed that the magnetic easy-magnetization axis was in the z-axis direction for NiPSe₃ and NiPS_3/2Se_3/2, while it was in the xy-plane for NiPS₃. The magnetic exchange parameters for NiPS₃ was J₁ = 3.14 meV, J₂ = 0.42 meV and J₃ = −15.17 meV, for NiPSe₃ was J₁ = 4.33 meV, J₂ = −0.03 meV and J₃ = −18.68 meV and for NiPS_3/2Se_3/2 was J₁ = 4.00 meV, J₂ = −0.03 meV, and J₃ = −17.30 meV. Néel temperatures predicted using Monte Carlo simulations were 160 K for NiPS₃, 189 K for NiPSe_3, and 180 K for NiPS_3/2Se_3/2. The magnetic properties of Janus NiPS_3/2Se_3/2 were more similar to those of pristine NiPSe₃ because the Se p orbitals contributed more to the uppermost valence bands than the S p states for NiPS_3/2Se_3/2. The AFM ground state was determined by evaluating the large superexchange interactions mediated by p–d hybridization for 2D NiPX₃ in both the pristine structure and Janus phase. Furthermore, the coexistence of antibonding and bonding states under the Fermi level led to FM couplings and AFM couplings between NN Ni ions, which could be clearly clarified by the crystal field effect and crystal orbital Hamilton populations.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the programs of Innovation Team in Colleges for Science and Technology of Education Department of Hubei Province (No. T2021012), Doctoral Scientific Research Foundation of HUAT (BK202483, BK202208 and BK202302), Hubei key Laboratory of Energy Storage and Power Battery (No. QCCLSZK2021A06), Open Foundation Project of Hubei Key Laboratory of Optical Information and Pattern Recognition (No. 202403), WIT and College Students' Innovation and Entrepreneurship Training Program (DC2023074 and DC2024087).

References

1. X. Wang, K. Du, Y. Y. F. Liu, P. Hu, J. Zhang, Q. Zhang, M. H. S. Owen, X. Lu, C. K. Gan and P. Sengupta, et al., 2D Mater., 2016, 3, 1.
2. J.-U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C.-H. Park, J.-G. Park and H. Cheong, Nano Lett., 2016, 16, 7433.
3. P. Li, X. Li, J. Feng, J. Ni, Z.-X. Guo and H. Xiang, Phys. Rev. B, 2024, 109, 214418.
4. R. Brec, Solid State Ionics, 1986, 22, 3.
5. A. Wiedenmann, J. Rossat-Mignod, A. Louisy, R. Brec and J. Rouxel, Solid State Commun., 1981, 40, 1067.
6. W. Klingen, R. Ott and H. Hahn, Z. Anorg. Allg. Chem., 1973, 396, 271.
7. F. Wang, T. A. Shifa, P. Yu, P. He, Y. Liu, F. Wang, Z. Wang, X. Zhan, X. Lou and F. Xia, et al., Adv. Funct. Mater., 2018, 28, 1802151.
8. K.-z. Du, X.-z. Wang, Y. Liu, P. Hu, M. I. B. Utama, C. K. Gan, Q. Xiong and C. Kloc, ACS Nano, 2016, 10, 1738.
9. B. L. Chittari, Y. Park, D. Lee, M. Han, A. H. MacDonald, E. Hwang and J. Jung, Phys. Rev. B, 2016, 94, 184428.
10. J.-T. Yang, C.-J. Xu, H.-J. Wang, Q. Min, S.-J. Luo, Y.-C. Xiong, W. Ren and C. Jing, J. Phys.: Condens. Matter., 2023, 35, 395501.
11. Y. Sugita, T. Miyake and Y. Motome, Phys. Rev. B, 2018, 97, 035125.
12. J. Yang, Y. Zhou, Y. Dedkov and E. Voloshina, Adv. Theory Simul., 2020, 2000228.
13. Y. Jin, M. Yan, T. Kremer, E. Voloshina and Y. Dedkov, Sci. Rep., 2022, 12, 735.
14. S. Y. Kim, T. Y. Kim, L. J. Sandilands, S. Sinn, M.-C. Lee, J. Son, S. Lee, K.-Y. Choi, W. Kim and B.-G. Park, et al., Phys. Rev. Lett., 2018, 120, 136402.
15. S. Y. Lim, K. Kim, S. Lee, J.-G. Park and H. Cheong, Curr. Appl. Phys., 2021, 21(1).
16. A. Wildes, B. Fåk, U. Hansen, M. Enderle, J. Stewart, L. Testa, H. Rønnow, C. Kim and J.-G. Park, Phys. Rev. B, 2023, 107, 054438.
17. Y. Wang, Z. Zhou, T. Wen, Y. Zhou, N. Li, F. Han, Y. Xiao, P. Chow, J. Sun and M. Pravica, et al., J. Am. Chem. Soc., 2016, 138, 15751.
18. Y. Wang, J. Ying, Z. Zhou, J. Sun, T. Wen, Y. Zhou, N. Li, Q. Zhang, F. Han and Y. Xiao, et al., Nat. Commun., 2018, 9, 1914.
19. H. Sun, L. Qiu, Y. Han, E. Yi, J. Li, M. Huo, C. Huang, H. Liu, M. Li and W. Wang, et al., Mater. Today Phys., 2023, 36, 101188.
20. Q. Zhang, K. Hwangbo, C. Wang, Q. Jiang, J.-H. Chu, H. Wen, D. Xiao and X. Xu, Nano Lett., 2021, 21, 6938.
21. Z. Ni, A. Haglund, H. Wang, B. Xu, C. Bernhard, D. Mandrus, X. Qian, E. Mele, C. Kane and L. Wu, Nat. Nanotechnol., 2021, 16, 782.
22. A. Ghosh, M. Palit, S. Maity, V. Dwij, S. Rana and S. Datta, Phys. Rev. B, 2021, 103, 064431.
23. E. Ergęcen, B. Ilyas, D. Mao, H. C. Po, M. B. Yilmaz, J. Kim, J.-G. Park, T. Senthil and N. Gedik, Nat. Commun., 2022, 13, 98.
24. F. Dirnberger, R. Bushati, B. Datta, A. Kumar, A. H. MacDonald, E. Baldini and V. M. Menon, Nat. Nanotechnol., 2022, 17, 1060.
25. P. Li, X. Li, J. Feng, J. Ni, Z.-X. Guo and H. Xiang, Phys. Rev. B, 2024, 109, 214418.
26. M. Amirabbasi and P. Kratzer, Phys. Rev. B, 2023, 107, 024401.
27. R. Basnet, K. M. Kotur, M. Rybak, C. Stephenson, S. Bishop, C. Autieri, M. Birowska and J. Hu, Phys. Rev. Res., 2022, 4, 023256.
28. J. Hafner, J. Comput. Chem., 2008, 29, 2044.
29. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
30. L. Matthes, O. Pulci and F. Bechstedt, J. Phys.: Condens. Matter, 2013, 25, 395305.
31. B. Himmetoglu, A. Floris, S. De Gironcoli and M. Cococcioni, Int. J. Quant. Chem., 2014, 114, 14.
32. S. Maintz, V. L. Deringer, A. L. Tchougréeff, and R. Dronskowski, Lobster: A Tool to Extract Chemical Bonding from Plane-Wave based DFT, 2016.
33. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
34. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617.
35. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1.
36. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635.
37. C. Braga and K. P. Travis, J. Chem. Phys., 2005, 123, 134101.
38. R. Blankenbecler, D. Scalapino and R. Sugar, Phys. Rev. D, 1981, 24, 2278.
39. H. Haario, E. Saksman and J. Tamminen, Bernoulli, 2001, 223–242.
40. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272.
41. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
42. A. R. Wildes, V. Simonet, E. Ressouche, G. J. McIntyre, M. Avdeev, E. Suard, S. A. J. Kimber, D. Lançon, G. Pepe and B. Moubaraki, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 224408.
43. G. Le Flem, R. Brec, G. Ouvard, A. Louisy and P. Segransan, J. Phys. Chem. Solids, 1982, 43, 455.
44. F. Knuth, C. Carbogno, V. Atalla, V. Blum and M. Scheffler, Comput. Phys. Commun., 2015, 190, 33.
45. E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235414.
46. R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428.
47. A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001.
48. P. Giannozzi, S. De Gironcoli, P. Pavone and S. Baroni, Phys. Rev. B, 1991, 43, 7231.
49. H. J. Xiang, E. J. Kan, S.-H. Wei, M.-H. Whangbo and X. G. Gong, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 224429.
50. S. Yan, Y. Du, X. Zhang, X. Wan and D. Wang, J. Phys.: Condens. Matter, 2023, 36, 065502.
51. Y. Gu, Q. Zhang, C. Le, Y. Li, T. Xiang and J. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 165405.
52. Y. Lee, C. Kim, S. Son, J. Cui, G. Park, K.-X. Zhang, S. Oh, H. Cheong, A. Kleibert and J.-G. Park, Nano Lett., 2024, 24, 6043.
53. R. Basnet, K. M. Kotur, M. Rybak, C. Stephenson, S. Bishop, C. Autieri, M. Birowska and J. Hu, Phys. Rev. Res., 2022, 4, 023256.
54. J.-T. Yang, C.-J. Xu, H.-J. Wang, Q. Min, S.-J. Luo, Y.-C. Xiong, W. Ren and C. Jing, J. Phys.: Condens. Matter, 2023, 35, 395501.
55. Q. H. Wang, A. Bedoya-Pinto, M. Blei and A. H. Dismukes, et al., ACS Nano, 2022, 16, 6960.
56. S. Toyoda, J. Kruppe, K. Yamakawa, J. Analytis and J. Orenstein, Phys. Rev. B, 2024, 109, 064408.
57. V. Popescu and A. Zunger, Phys. Rev. Lett., 2010, 104, 236403.
58. P. Foot, J. Suradi and P. Lee, Mater. Res. Bull., 1980, 15, 189.
59. C. Autieri, G. Cuono, C. Noce, M. Rybak, K. M. Kotur, C. E. Agrapidis, K. Wohlfeld and M. Birowska, J. Phys. Chem. C, 2022, 126, 6791.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra02861b

---