DOI:
10.1039/D5RA01897H
(Paper)
RSC Adv., 2025,
15, 12964-12981
Cobalt ion-incorporated nanocrystalline spinel cubic zinc ferrite for targeted magnetic hyperthermia and sensing applications†
Received
17th March 2025
, Accepted 4th April 2025
First published on 22nd April 2025
Abstract
To enhance the therapeutic efficacy of magnetic hyperthermia, the effective anisotropy energy barrier of magnetic nanoparticles must be optimized since it affects relaxation dynamics and self-heating capabilities. Tuning the magnetic anisotropy of soft zinc ferrite nanoparticles was achieved in this work via doping of ferromagnetic cobalt ions for controlled hyperthermia therapy. We synthesized four nanocrystalline zinc ferrites doped with cobalt ions of varying concentrations [CoxZn1−xFe2O4 (x = 0.00, 0.10, 0.30, and 0.50)] using the standard chemical co-precipitation method. The role of doping Co2+ ions in modifying the physical properties, including microstructural, electronic, optical and magnetic characteristics, of pure zinc ferrite nanoparticles was thoroughly investigated using several characterization techniques. The obtained TEM images verified good homogeneity in both the size and shape of the studied nanocrystalline ferrites. The optical indirect bandgap was estimated to be 1.55 ± 0.03 eV for the nanosized ferrites. Substitution of ferromagnetic cobalt ions in appropriate amounts improved the magnetic responses of the doped zinc ferrite nanoparticles, and thereby, several magnetic parameters such as coercivity, magnetic anisotropy and magnetization were observed to increase gradually. The tunable magnetic anisotropy energy barrier of pristine ZnFe2O4 nanoparticles was achieved via Co2+ ion doping, and consequently, the induction heating efficiency of the doped ferrite samples improved. Owing to the incorporation of magnetic cobalt ions, the blocking temperature was found to increase, which highly affected the relaxation dynamics and superparamagnetic behavior of the zinc ferrite nanoparticles. The presence of one semicircle in the Cole–Cole plot suggested that the grain boundaries played a more significant role than the conductive grains in determining the dielectric properties of the nanoferrites. The as-synthesized nanomaterials were further explored for the sensing of the herbicide metribuzin. It was observed that the conductivity of the Co2+ ion-doped zinc ferrite nanoparticles decreased in the presence of metribuzin, with 50% cobalt ion-doped zinc ferrite nanoparticles exhibiting a better performance compared with the pristine sample in metribuzin herbicide sensing. The limit of detection (LOD) was determined to be 1 ppm. Hence, it was successfully demonstrated that cobalt ion-incorporated zinc ferrite nanoparticles showed potential for use in magnetic hyperthermia and metribuzin herbicide sensing applications.
1. Introduction
Magnetic hyperthermia therapy has attracted significant interest as an advanced cancer treatment method because of its targeted and less invasive methodology. It involves the use of magnetic nanoparticles for generating localized heat in the presence of an alternating magnetic field.1–4 When placed on cancerous cells, these magnetic nanoparticles produce heat and increase the local temperature to 46 °C in a regulated way, which damages the cancer cell tissues in the presence of an applied alternating magnetic field for a predetermined duration. The required temperature range for diathermy in this thermo-active hyperthermia procedure is between 38 °C and 41 °C, whereas the ideal cell temperature range is between 42 °C and 46 °C, which is sufficient to effectively destroy cancer cells.3 Magnetic nanoparticles in the form of ferrofluid have been found to be highly effective to decorate the targeted medium, enabling the localized generated heat on the target site to be uniform. It was observed that the alternating magnetic field in the radio-frequency region permits fine control of induction heating, while the selection of magnetic nanoparticles offers versatility.4–8 In the case of magnetic nanoparticles to optimize the self-heating efficiency for hyperthermia application, nanocrystalline soft spinel cubic ferrites with a size of less than 20 nm have become the first choice of researchers. This is because of their unique magnetic characteristics together with superparamagnetic behavior at room temperature, making them suitable for controlled magnetic hyperthermia therapy.7–11 In this direction, soft spinel cubic ZnFe2O4 nanoparticles serve as potential systems for magnetic hyperthermia due to the capability to tune their magnetic properties through doping and size variation.2,6,11 Furthermore, coating these ferrite nanomaterials with appropriate bio-friendly polymers can reduce the deleterious effects of the transition metal (TM) ions present in mixed spinel nanoferrites on human cells, which limit their utility in biomedical applications involving hyperthermia. High levels of these doped nanomaterials containing transition metals (TMs) in the human body can cause side effects such as headaches, vomiting, diarrhea, oxidative stress, stomach pain, and immune system impairment. Thus, the modification of magnetic nanoparticles composed of TMs by surface and coating can stop the harmful leakage of TMs and prevent them from accumulating in unwanted places.
Pristine zinc ferrite (ZnFe2O4) belongs to the cubic spinel family, having the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and consisting of two different types of sublattices, i.e., tetrahedral and octahedral coordinated sites. In the unit cell of pure zinc ferrite, where all the Zn2+ ions are located in tetrahedral voids and all the Fe3+ ions occupy octahedral voids, forming a normal spinel cubic crystal structure.11–14 Nanocrystalline zinc ferrite behaves like a soft ferrimagnetic material; therefore, upon doping of suitable magnetic ions and varying the dopant concentration in ZnFe2O4 nanoparticles, the magnetic anisotropy of the system can be controlled, enabling the tunability and optimization of the induction heating efficiency according to the requirement for the magnetic hyperthermia therapy.15,16 In this regard, ferromagnetic cobalt ions having a high Curie temperature, chemical stability and comparable size can ideal dopants for regulating the magnetic anisotropy of zinc ferrite nanoparticles within the percolation limit for optimizing the hyperthermia effect. We chose Co2+ 3d transition metal ions to dope pure zinc ferrite nanoparticles and alter their magnetic properties.17,18 The adequate substitution of ferromagnetic Co2+ ions in the host zinc ferrite nanoparticles is expected to increase the effective anisotropy of the system and improve the induction heating efficiency given that the relaxation losses of magnetic nanoparticles are highly influenced by the anisotropy energy barrier. Due to the superparamagnetic nature of soft undoped and doped ZnFe2O4 nanoparticles at room temperature, relaxation losses contribute more effectively in determining the self-heating efficacy.2,19 Therefore, controlling the effective anisotropy constant of prepared nanoferrite systems is essential to tune the heating efficiency according to the requirements. Tuning the effective anisotropy of the host zinc ferrite system has been performed via doping different concentrations of ferromagnetic Co2+.19,20
m space group and consisting of two different types of sublattices, i.e., tetrahedral and octahedral coordinated sites. In the unit cell of pure zinc ferrite, where all the Zn2+ ions are located in tetrahedral voids and all the Fe3+ ions occupy octahedral voids, forming a normal spinel cubic crystal structure.11–14 Nanocrystalline zinc ferrite behaves like a soft ferrimagnetic material; therefore, upon doping of suitable magnetic ions and varying the dopant concentration in ZnFe2O4 nanoparticles, the magnetic anisotropy of the system can be controlled, enabling the tunability and optimization of the induction heating efficiency according to the requirement for the magnetic hyperthermia therapy.15,16 In this regard, ferromagnetic cobalt ions having a high Curie temperature, chemical stability and comparable size can ideal dopants for regulating the magnetic anisotropy of zinc ferrite nanoparticles within the percolation limit for optimizing the hyperthermia effect. We chose Co2+ 3d transition metal ions to dope pure zinc ferrite nanoparticles and alter their magnetic properties.17,18 The adequate substitution of ferromagnetic Co2+ ions in the host zinc ferrite nanoparticles is expected to increase the effective anisotropy of the system and improve the induction heating efficiency given that the relaxation losses of magnetic nanoparticles are highly influenced by the anisotropy energy barrier. Due to the superparamagnetic nature of soft undoped and doped ZnFe2O4 nanoparticles at room temperature, relaxation losses contribute more effectively in determining the self-heating efficacy.2,19 Therefore, controlling the effective anisotropy constant of prepared nanoferrite systems is essential to tune the heating efficiency according to the requirements. Tuning the effective anisotropy of the host zinc ferrite system has been performed via doping different concentrations of ferromagnetic Co2+.19,20
Magnetic nanoparticles, specially spinel ferrites, can be synthesized using a variety of top-down and bottom-up techniques, each with unique benefits for regulating the particle size, shape, surface morphology, and physical properties. Compared with other preparation methods, the conventional wet chemical co-precipitation route shows a variety of benefits in synthesizing ferrite nanoparticles, including a more accessible and cost-effective approach, enabling more precise control of size, shape, and homogeneity through pH and temperature variations. Thus, it is a widely used technique for the preparation of pure and doped spinel ferrite nanoparticles.6,21
In addition to the hyperthermia application, soft spinel cubic ferrites also show potential as efficient nanomaterials to be used in sensing devices. This is due to their precise selectivity, low response time, affordable cost, and ease of fabrication.22 Soft undoped and doped zinc ferrite nanoparticles display an indirect band gap, are chemically stable, and have good charge carrier mobility through hopping, making them promising nanomaterials for sensing applications.23 In this direction, the detection of commonly used herbicides in agricultural lands is essential given that they can be harmful to humans, plants, animals and the environment when mixed with the groundwater above a certain amount. In India, metribuzin is a common herbicide used to control weeds and grasses in agricultural crops. However, the overuse of this herbicide can seriously harm the ecosystem and contaminate groundwater. Therefore, we thoroughly investigated the metribuzin sensing ability of as-prepared cobalt-doped zinc ferrite nanoparticles.24–26 There are several methods available for examining the sensing capabilities of nanomaterials. Among these methods, the Cole–Cole plot technique to sense toxic elements, which can be obtained via impedance spectroscopy, is the most straightforward and beneficial method.
Our main focus in this current work was to regulate the effective anisotropy of nanocrystalline ZnFe2O4 by varying the percentage of ferromagnetic cobalt dopant, and subsequently controlling the self-heating efficacy according to the requirement for localized magnetic hyperthermia therapy. In this direction, we synthesized a series of cobalt-doped zinc ferrite nanoparticles by varying the Co content, with the composition of CoxZn1−xFe2O4 (x = 0.00, 0.10, 0.30, and 0.50) using the wet chemical co-precipitation method. The impact of Co ion doping in regulating the physical properties of the host nanosized ZnFe2O4 was investigated thoroughly and the corresponding correlations among the physical properties of the doped nanoferrites were established. Due to the superparamagnetic nature of soft-doped zinc nanoferrites at ambient temperature, the relaxation losses, especially the Néel relaxation, actively participate in generating heat through induction heating, which is usually governed by the effective magnetic anisotropy of the system. Controlling the effective anisotropy is necessary to tune the heating efficacy of as-fabricated magnetic nanoparticles.2 For this purpose, cobalt ions were doped in the nanosized zinc ferrite at different contents. Additionally, the synthesized doped nanomaterials are expected to have improved sensing ability to detect herbicides and toxic compounds. Few articles are available on metribuzin sensing and most studies used optical sensing methods for its detection.24–28 Thus, herein, we tested the capability of pure and 50% Co-doped nanoferrites for the detection of metribuzin herbicide at room temperature using the dielectric sensing method (Cole–Cole plot). We observed that the optimal Co ion doping in the zinc ferrite nanoparticles enhanced their detection ability for metribuzin herbicide compared to the undoped system. This study also thoroughly illustrated the role of ferromagnetic cobalt ion doping in regulating the structural, optical, electronic and magnetic properties of ZnFe2O4 (ZNF) nanoparticles for hyperthermia and metribuzin sensing applications.
2. Experimental details
2.1. Synthesis of ferrite nanoparticles
ZnFe2O4 (ZNF) and Co-doped ZNF nanoparticles were prepared using the conventional co-precipitation method.20,21 Four ferrite nanoparticle samples with the generic formula CoxZn1−xFe2O4 (x = 0, 0.10, 0.30, and 0.50) were prepared and labeled as Co-00 (ZNF), Co-10 (ZNF), Co-30 (ZNF), and Co-50 (ZNF) in accordance with the content of Co dopant, respectively. All the details of the synthesis procedure are illustrated in the ESI of this article.†
2.2. Measurement of dielectric properties
Impedance spectroscopy (Novocontrol, Alpha) was employed to measure the AC conductivity and dielectric properties of each sample at room temperature. The dielectric properties were recorded at 300 K in the frequency range of 10 Hz to 10 MHz. For the measurements, the samples were formed into thin circular pellets with a diameter of 13 mm.29 To ensure proper contact, both sides of each pellet were coated with silver paste. Using these prepared pellets, the dielectric properties of the ferrite samples were measured. The Cole–Cole plot was utilized to further determine the sensing of the as-synthesized doped ferrite nanoparticles efficacy for metribuzin. The analyte metribuzin, having a molecular weight of 214.29 g mol−1 and chemical formula C8H14N4OS, was purchased from Merck. The molecular structure of metribuzin, which was used to test the sensing ability of the as-prepared doped nanoferrites is shown in Scheme 1.
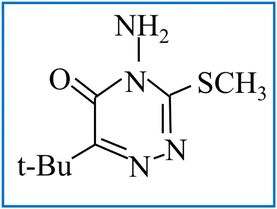 |
| | Scheme 1 Molecular structure of metribuzin. | |
2.3. Induction heating experiment
The effectiveness of the synthesized doped ferrite samples for hyperthermia applications was evaluated via an induction heating experiment. Each sample, prepared at a uniform concentration of 1 mg mL−1, was dispersed in distilled water and placed at the center of a solenoid with a specific diameter and number of turns. The induction heating data for all the samples were recorded at 300 K, using an AC magnetic field with a frequency of 337 kHz and amplitude of 14.91 kA m−1.2,7
2.4. Characterization techniques
The physical properties of the prepared doped ferrite nanoparticles, together with their efficacy for hyperthermia and sensing applications, were thoroughly investigated using several characterization techniques. All the details of the instruments used for the characterization of the ferrite samples are discussed precisely in the ESI of this article.†
3. Results and discussion
3.1. Studies on crystal structure
The room temperature X-ray diffraction patterns of the cobalt-incorporated zinc ferrite nanoparticles consisting of different Co contents are depicted in Fig. 1(a). The diffractograms of these four nanocrystalline ferrites having the composition CoxZn1−xFe2O4 (x = 0.00, 0.10, 0.30, and 0.50) validated the presence of a single-phase spinel cubic crystal structure without impurities having the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The existence of all the characteristic peaks of spinel cubic crystal structure together with an intense (311) peak near 2θ = 35.20° was observed in all the recorded diffractograms, and also perfectly matched JCPDS Card No. 77-0426. It is known that the Rietveld refinement technique is normally used to analyze the diffraction pattern of a crystalline material.17–20 The Rietveld refinement of diffractograms for all the nanocrystalline Co-doped zinc ferrites was conducted with the aid of the GSAS software (General Structure Analysis System) together with the EXPUGI interface. The pseudo-Voigt function was utilized for fitting the profile peaks and the Finger–Cox–Jephcoat asymmetry was used for the correction of the axial divergence. The obtained values of refinement parameters, including goodness of fit (χ2), reliability factors (RP, RWP, and RF2) and unit cell parameters are displayed in Table S1.† The estimated values of the refinement parameters were less than 10% and the goodness of fit (χ2) close to unity for each sample indicated a satisfactory agreement between the experimental diffraction data and standard pattern. Close investigation of the diffractograms revealed that a significant amount of line broadening was present. It is noted that line-broadening in diffractograms is commonly observed in nanocrystalline samples, which is also an inherent property of nanosized crystalline materials.17 It occurs because of the involvement of three fundamental factors, i.e. nanocrystallite size effects, inherent microstrain effects and line-broadening due to instrumental effects. All three factors collectively contribute to broadening the line width of the diffracted peaks in the X-ray diffraction patterns. By recording the diffraction pattern of LaB6 powder in a well-annealed bulk form and keeping all the measurement conditions identical, the instrumental line width was corrected for all the nanoferrite samples. After elimination of the broadening caused by the instrument, the total line width β (FWHM) only contained two contributions, i.e., nanocrystallite size (βsize) and microstrain (βstrain) broadening effects, which can be expressed as follows:6,17,30
m space group. The existence of all the characteristic peaks of spinel cubic crystal structure together with an intense (311) peak near 2θ = 35.20° was observed in all the recorded diffractograms, and also perfectly matched JCPDS Card No. 77-0426. It is known that the Rietveld refinement technique is normally used to analyze the diffraction pattern of a crystalline material.17–20 The Rietveld refinement of diffractograms for all the nanocrystalline Co-doped zinc ferrites was conducted with the aid of the GSAS software (General Structure Analysis System) together with the EXPUGI interface. The pseudo-Voigt function was utilized for fitting the profile peaks and the Finger–Cox–Jephcoat asymmetry was used for the correction of the axial divergence. The obtained values of refinement parameters, including goodness of fit (χ2), reliability factors (RP, RWP, and RF2) and unit cell parameters are displayed in Table S1.† The estimated values of the refinement parameters were less than 10% and the goodness of fit (χ2) close to unity for each sample indicated a satisfactory agreement between the experimental diffraction data and standard pattern. Close investigation of the diffractograms revealed that a significant amount of line broadening was present. It is noted that line-broadening in diffractograms is commonly observed in nanocrystalline samples, which is also an inherent property of nanosized crystalline materials.17 It occurs because of the involvement of three fundamental factors, i.e. nanocrystallite size effects, inherent microstrain effects and line-broadening due to instrumental effects. All three factors collectively contribute to broadening the line width of the diffracted peaks in the X-ray diffraction patterns. By recording the diffraction pattern of LaB6 powder in a well-annealed bulk form and keeping all the measurement conditions identical, the instrumental line width was corrected for all the nanoferrite samples. After elimination of the broadening caused by the instrument, the total line width β (FWHM) only contained two contributions, i.e., nanocrystallite size (βsize) and microstrain (βstrain) broadening effects, which can be expressed as follows:6,17,30| |
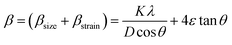 | (1) |
where K represents the sphericity constant (≈0.89 for spherical particles), λ denotes the wavelength of characteristic copper Kα radiation (1.5406 Å), D is the average crystallite size, ε signifies the microstrain present within nanocrystals and θ is the corresponding Bragg's angle. By rearranging eqn (1), we obtain the following equation:17,30| |
 | (2) |
 |
| | Fig. 1 (a) Rietveld refinement of room temperature X-ray diffraction profiles and (b) Williamson–Hall (W–H) plot of all the doped nanocrystalline ferrites. | |
Separation of broadening contributions caused by the nanocrystallite size and microstrain effects in the line width of the diffracted peaks was performed by drawing a graph of is β cos θ against 4 sin θ. This graph is named the Williamson Hall (W–H) plot and is illustrated in Fig. 1(b). The W–H plot forms a straight line and the slope provides the inherent microstrain (ε) in nanocrystals, whereas the intercept on the β cos θ axis is Kλ/D, which is used to calculate the mean crystallite size (D).30 The Williamson–Hall (W–H) method is widely used to determine the microstrain inside nanocrystals by examining the nature of the slope of the straight line, which can be increasing (positive), decreasing (negative), or neutral. Introducing dopants that are relatively larger in size or incorporating Jahn–Teller-active atoms leads to an increase in the (positive) slope in the W–H plot. In contrast, vacancies or doping with comparatively smaller size ions results in a decrease (negative) in the slope, confirming that the existing microstrain has tensile or compressive behavior inside the tiny crystals. It should be noted that the developed microstrain and its nature in the nanocrystals directly influence several physical properties effectively. Generally, it was found that the tensile microstrain increased the lattice constant, whereas compressive microstrain reduced the lattice constant and unit cell volume. We calculated the microstrain and its nature for all the as-fabricated samples using W–H plots (see Table S1†) to understand the effects of Co doping in the crystal structure of the host spinel zinc ferrite matrix. The average crystallite sizes were calculated for all the nanoferrite samples and observed to be in the range of 9.7 nm to 20.1 nm. Compressive microstrain was observed for the low Co-containing Zn-ferrite nanoparticles. Further, with an increase in the Co concentration in the nanosized zinc ferrites, the microstrain turned into a tensile form (see Table S1†). Usually, ZnFe2O4 forms a typical spinel cubic structure, where all the Zn2+ ions occupy the tetrahedral sites, while Fe3+ ions occupy the octahedral voids. Divalent cobalt ions have a tendency to occupy octahedral sites, and therefore the substitution of Co2+ ions resulted in cationic redistribution in the unit cell. Additionally, there is a notable mismatch in ionic radius between Co2+ (0.745 Å) ions and Zn2+ (0.60 Å) ions.20 All these effects also create point defects and vacancies in the spinel cubic lattice structure. This may be responsible for changing the microstrain behavior from compressive to tensile with an increase in the concentration of Co dopant in the host zinc ferrite structure. It was also noted that the lattice parameter decreased with an increase in Co concentration in the host zinc ferrite nanoparticles.17 Cationic rearrangements, point defects, vacancies and the mismatch in ionic radius between the dopant and Zn ions collectively resulted in the observed decrease in the lattice parameter (see Table S1†).
Given that the Zn2+ and Co2+ ions have different preferential sites i.e., tetrahedral and octahedral sites, cationic redistribution occurred inside the lattice. We calculated the average radii of these tetrahedral (A) and octahedral (B) voids for each molecule using the following relations:31,32
| | |
rA = [C(Fe3+)r(Fe3+) + C(Zn2+)r(Zn2+)]
| (3) |
| | |
rB = ½[C(Fe3+)r(Fe3+) + C(Co2+)r(Co2+)]
| (4) |
where
C and
r denote the concentration and ionic radius of the cations for the lattice sites, respectively. Obeying the preference of occupancy with optimal cationic redistribution for Fe
3+ (0.645 Å), Co
2+ (0.745 Å) and Zn
2+ (0.60 Å) ions in the spinel cubic crystal structure, the values of both
rA (in Å) and
rB (in Å) were calculated and shown in Table S2.
† It was observed that the ionic radius (
rB) of the octahedral voids slightly increased due to the incorporation of the relatively large-sized Co ions.
20 In case of the spinel cubic system, the value of the lattice parameter (
ath) can be calculated theoretically using the following equation:
32| |
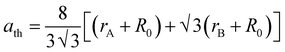 | (5) |
where
R0 (1.32 Å) represents the ionic radius of the O
2− anion. The theoretically obtained lattice constant (
ath) was found to be in agreement with the experimentally obtained lattice constant (
a) for each ferrite sample. An increasing trend in the theoretical lattice constant (
ath) value was noticed due to the incorporation of the Co dopant in the host ZnFe
2O
4 structure (see Table S2
†). In addition, a considerable mismatch in the theoretical and experimental values of lattice parameters for each ferrite sample was observed, which can be ascribed to the conventional concept of atoms, where atoms are considered to be a rigid sphere arranged in a pattern but they contain slightly diffuse boundaries in the actual case. In the calculation of
ath, the ideal arrangement of atoms inside the spinel cubic structure was considered, whereas the effects of point defects, presence of vacancies, and microstrain were not considered, which may be the main reason for the notable mismatch in theoretical and experimental lattice constant. It was also plausible that not all the Co and Zn ions occupied octahedral and tetrahedral positions during cationic rearrangement, which would result in the observation of a discrepancy.
17,31,32
Another commonly used parameter to understand the degree of distortion due to cationic redistribution inside the spinel cubic structure is the oxygen positional parameter (U). It measures the movement of oxygen ions within the spinel cubic structure to adjust the large-sized metal ions. It is noted that the ideal value of U is 0.375 for the spinel cubic system, where the obtained values of U were slightly larger than 0.375, indicating the movement of O2− anions to adjust metal ions and defects towards the 〈111〉 direction. This is because the tetrahedral lattice sites are marginally smaller than the size of the metal ions. No significant difference in the values of U was observed when incorporating Co ions in the host matrix. The existence of vacancies could offset the doping-related change in U (see Table S3†).31–33
Both the bond length and bond angle play a crucial role in determining the strength of magnetic interactions, charge conduction process and transport properties of doped spinel ferrite nanoparticles. In this regard, the hopping length  of the tetrahedral (A) and octahedral (B) sites need to be evaluated to get an idea of the strength of spin interactions and the conduction process of the as-prepared systems. The observed decrease in hopping length with an increase in the concentration of Co ions in the ZnFe2O4 system improved the charge conduction process (see Table S3†). Thereby, the energy requirement for electrons to jump from one cationic site to another decreases, which enhances the conductivity.34
of the tetrahedral (A) and octahedral (B) sites need to be evaluated to get an idea of the strength of spin interactions and the conduction process of the as-prepared systems. The observed decrease in hopping length with an increase in the concentration of Co ions in the ZnFe2O4 system improved the charge conduction process (see Table S3†). Thereby, the energy requirement for electrons to jump from one cationic site to another decreases, which enhances the conductivity.34
3.2. Analysis of TEM micrographs
To examine the size, shape and morphology of the as-synthesized Co-substituted zinc ferrite nanoparticles, we captured TEM images of each sample, as displayed in Fig. 2(a–d). Nearly spherical-shaped nanoparticles together with excellent regularity in size were obtained for all the samples, as evidenced by the recorded TEM micrographs. A significant amount of aggregation among the prepared magnetic nanoparticles was noticed, which can be ascribed to the presence of magnetic dipole–dipole interactions together with van der Waals interactions.6,33 A histogram was drawn to obtain the mean size of the nanoparticles, and also get an elementary idea about the size distribution for each ferrite sample. The obtained histograms for all the nanoferrite samples are presented in the inset of Fig. 2(a–d). Using the histograms, the average sizes of the nanoparticles were obtained and found to be 9.2 ± 0.1 nm, 11.1 ± 0.1 nm, 20.8 ± 0.1 nm and 12.0 ± 0.1 nm for the Co-00 (ZNF), Co-10 (ZNF), Co-30 (ZNF) and Co-50 (ZNF) spinel ferrite samples, respectively. Good agreement was noted between the mean crystallite sizes evaluated using the W–H plot and average particle sizes obtained using TEM images for each sample. In the case of the Co-00 (ZNF) spinel ferrite nanoparticles, the image containing a group of parallel (311) crystal planes was obtained having an interplanar spacing of 0.25 nm.34 The corresponding image of the lattice planes is shown in Fig. 2(e). The selective area electron diffraction pattern (SAED) was recorded for the Co-00 (ZNF) sample to investigate its crystal structure, nanocrystallinity and influence of defects. The obtained SAED pattern of the Co-00 (ZNF) sample is illustrated in Fig. 2(f). Electrons are subatomic particles that can behave like waves and diffract by parallel crystal planes, forming a particular concentric ring pattern. A concentric ring-like structure was observed in the SAED pattern of the Co-00 (ZNF) sample. The presence of several circular rings in the SAED pattern also validated the polycrystalline nature of the Co-00 (ZNF) nanoparticles. All the obtained circular rings were named in accordance with their respective Miller indices. A thorough examination of the captured SAED pattern revealed that circular rings were decorated in a specific manner, where two rings were close, and the third ring was slightly further away, confirming the presence of face-centered cubic lattices in the unit cell of the spinel cubic structure.35
 |
| | Fig. 2 (a–d) TEM micrographs of Co-00 (ZNF), Co-10 (ZNF), Co-30 (ZNF) and Co-50 (ZNF) nanoparticles. (e) HRTEM depicting crystallographic (311) parallel planes with interplanar spacing of the Co-00 (ZNF) sample, and (f) SAED pattern of the Co-00 (ZNF) sample. | |
3.3. Raman spectral analysis
Raman spectroscopy deals with the inelastic scattering of monochromatic light by molecules, which has been extensively used to investigate nanomaterials, crystal structure, phase purity, symmetry, and molecular bonds in modern technologies, making it a versatile characterization tool. We recorded the room-temperature Raman spectra of the pure and doped nanosized zinc ferrites to understand their crystal symmetry, phase purity, and effects of doping on crystal symmetry.17 Normally, bulk zinc ferrite belongs to the spinel cubic family and possesses a normal cubic spinel structure, where all the Zn2+ ions prefer to occupy the tetrahedral coordinated voids and Fe3+ ions occupy the octahedral voids, having an AB2O4-type structure and corresponding to the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. It contains a total of 56 atoms in its unit cell and 14 atoms inside the smallest Bravais cell. Two different types of interpenetrated sublattices, i.e., tetrahedral and octahedral sites, are present in the unit cell of the spinel cubic structure, belonging to the Td and D3d point groups, respectively. There are 42 active modes, including 3 acoustic modes and 39 optical modes in the spinel cubic ZnFe2O4 according to the factor group analysis. A material must have a non-zero change in polarizability against nuclear displacement to be considered Raman active. Usually, five Raman-active modes (A1g + Eg + 3T2g) are found in spinel cubic-structured materials.36 It should be noted that the active modes above 600 cm−1 are associated with the tetrahedral (A) sublattices and below 600 cm−1 are linked to the octahedral (B) sublattices.37 The A1g Raman active mode is associated with the symmetric stretching of oxygen atoms of metal–oxygen bonds in tetrahedral sites. The Eg and T2g(3) active modes are linked with the symmetric and asymmetric bending of Fe–O bonds, respectively. The T2g(2) mode refers to the asymmetric stretching of the M–O (M = Fe or Co) bonds and the T2g(1) Raman-active mode correspond to the translational motion of the FeO4 tetrahedron.17,30
m space group. It contains a total of 56 atoms in its unit cell and 14 atoms inside the smallest Bravais cell. Two different types of interpenetrated sublattices, i.e., tetrahedral and octahedral sites, are present in the unit cell of the spinel cubic structure, belonging to the Td and D3d point groups, respectively. There are 42 active modes, including 3 acoustic modes and 39 optical modes in the spinel cubic ZnFe2O4 according to the factor group analysis. A material must have a non-zero change in polarizability against nuclear displacement to be considered Raman active. Usually, five Raman-active modes (A1g + Eg + 3T2g) are found in spinel cubic-structured materials.36 It should be noted that the active modes above 600 cm−1 are associated with the tetrahedral (A) sublattices and below 600 cm−1 are linked to the octahedral (B) sublattices.37 The A1g Raman active mode is associated with the symmetric stretching of oxygen atoms of metal–oxygen bonds in tetrahedral sites. The Eg and T2g(3) active modes are linked with the symmetric and asymmetric bending of Fe–O bonds, respectively. The T2g(2) mode refers to the asymmetric stretching of the M–O (M = Fe or Co) bonds and the T2g(1) Raman-active mode correspond to the translational motion of the FeO4 tetrahedron.17,30
A monochromatic laser source with a wavelength of 473 nm was used to obtain the Raman spectra in the range of 200–800 cm−1 of the nanosized CoxZn1−xFe2O4 (x = 0.00, 0.10, 0.30, and 0.50) ferrites at room temperature. Lorentzian functions were used to fit the obtained Raman spectra of each nanoferrite sample. The deconvoluted Raman spectra for the pure and doped nanocrystalline zinc ferrites are depicted in Fig. 3. Table S4† lists the deconvoluted Raman active modes for each of the as-synthesized nanoferrite samples. The characteristic Raman active vibrational modes were noticed to exist in all the prepared nanoferrites. The observed A1g(1) + A1g(2) + T2g(3) + T2g(2) + Eg modes are associated with the spinel cubic crystal system, having the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.30 The presence of other two active modes in the Raman spectra, i.e., A1(3) + B2(3), belongs to the P4122 space group. They appeared due to the lowering of the symmetry inside the crystals. Here, the octahedral (B) cubic symmetry of the Fd
m space group.30 The presence of other two active modes in the Raman spectra, i.e., A1(3) + B2(3), belongs to the P4122 space group. They appeared due to the lowering of the symmetry inside the crystals. Here, the octahedral (B) cubic symmetry of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group slightly turns into the tetragonal symmetry of the P4122 space group.17,30 The existence of vacancies due to maintaining the charge valency as well as doping of a relatively larger dopant in the host nanosized ZnFe2O4 matrix resulted in a lowering of the crystal symmetry, as validated by the recorded vibrational Raman spectra. In the case of the nanosized ferrite samples, line broadening of the Raman active modes was observed in their Raman spectra because of the lack of long-range atomic ordering and minute change in bond lengths. Broadening in the active modes was also noticed for our as-synthesized doped ferrite samples. In addition, the bond length, bond strength, size and atomic mass of dopants also determine the shifting in the Raman active modes and alteration of the crystal symmetry of the host system efficiently. Substitution of the comparatively large Co2+ dopant with a lower atomic mass than that of Zn2+ ions led to modified bonds, bond lengths, and their strengths, resulting in a change in the phonon numbers of the active modes for the doped ferrite samples.38
m space group slightly turns into the tetragonal symmetry of the P4122 space group.17,30 The existence of vacancies due to maintaining the charge valency as well as doping of a relatively larger dopant in the host nanosized ZnFe2O4 matrix resulted in a lowering of the crystal symmetry, as validated by the recorded vibrational Raman spectra. In the case of the nanosized ferrite samples, line broadening of the Raman active modes was observed in their Raman spectra because of the lack of long-range atomic ordering and minute change in bond lengths. Broadening in the active modes was also noticed for our as-synthesized doped ferrite samples. In addition, the bond length, bond strength, size and atomic mass of dopants also determine the shifting in the Raman active modes and alteration of the crystal symmetry of the host system efficiently. Substitution of the comparatively large Co2+ dopant with a lower atomic mass than that of Zn2+ ions led to modified bonds, bond lengths, and their strengths, resulting in a change in the phonon numbers of the active modes for the doped ferrite samples.38
 |
| | Fig. 3 Deconvoluted Raman spectra of all the nanosized ferrites. | |
3.4. FT-IR spectroscopy study
Fourier transform infrared (FT-IR) spectroscopy is frequently used to identify various molecular structures, functional groups, and forensic substances and analyze nanomaterials precisely. It is a fingerprint-based method for the identification of materials. The FT-IR spectra of the as-prepared doped ZnFe2O4 nanoparticles are displayed in Fig. S1.† An attentive inspection revealed two zones, which can be used to categorize the spectrum roughly. The first is the fingerprint region of the lattice vibrations of metal oxides at high energies, while the second is the low-energy vibrations of the bonds of organic functional groups.39 The vibrations in the wavenumber range of 535 cm−1 to 555 cm−1 appeared due to the stretching of the metal–oxygen bonds at the tetrahedral sublattices. The vibrations of the octahedral-coordinated Fe–O bonds are located at around 400 cm−1, while that for the tetrahedral coordinated Fe–O bonds is located at 559 cm−1.15,36 The vibrational peak located in the range of 1361 cm−1 to 1382 cm−1 is due to the stretching of C–H bonds. All the H2O molecules present on the surface of the prepared ferrites were revealed by the observed broad band near the wavenumber of 3400 cm−1, which increased due to the O–H bending of the H2O molecule.40 It was noted that the three main parameters, i.e., reduced mass, spring constant of bonds, and bond length, all have a significant impact on the characteristic vibration frequency of the doped spinel ferrites.
3.5. Determination of optical band gap
Both the electrical conductivity and absorption properties of a semiconducting nanomaterial are directly related to its band gap. Therefore, the determination of band gap is essential in understanding the optical properties and charge transport efficacy of nanomaterials. To obtain the optical band gap of all the doped ferrite samples, their room temperature absorption spectra were recorded in the range of 200 nm to 800 nm. Bulk ZnFe2O4 has a normal spinel cubic structure and an indirect optical band gap.40 The Tauc method is the standard technique to determine the optical band gap of a semiconducting nanomaterial. In this regard, the Tauc relation was used, as follows:35,41| | |
α(ν)·hν ≈ C(hν − Eo)n
| (6) |
where ‘C’ is a constant, ‘Eo’ is the indirect optical band gap to be determined for the prepared ferrite nanoparticles, ‘α’ signifies the absorption coefficient and ‘n’ denotes an arbitrary index. In this calculation, an indirect optical band gap of n = 2 was employed and the graph of (αhν)0.5 against photon energy (hν) was drawn for all the Co-substituted zinc ferrite nanoparticles, which is called Tauc plot and shown in Fig. S2.† In this direction, the absorption coefficient (α) values were required to derive the indirect optical band gap at 300 K and they were obtained using the recorded absorbance (A) data of the as-prepared ferrite samples. The following two fundamental relations were used to evaluate the absorption coefficient:41| |
 | (7) |
The absorption coefficient takes the form 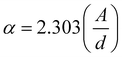 ; where ‘d’ specifies the width of the container holding the sample solution. In the Tauc plot, the value of the indirect optical gap (Eo) can be obtained by extrapolating a straight line along the slope of the curve that intercepts the hν axis. The indirect band gaps were found to be 1.55 ± 0.03 eV for all the nanoferrite samples. No significant difference in band gap was noticed with the incorporation of cobalt ions in the host nanosized zinc ferrites. These synthesized ferrite samples would be promising nanomaterials for a variety of optical applications because they showed an opaque behavior in the near-IR region of the electromagnetic spectrum.40,41
; where ‘d’ specifies the width of the container holding the sample solution. In the Tauc plot, the value of the indirect optical gap (Eo) can be obtained by extrapolating a straight line along the slope of the curve that intercepts the hν axis. The indirect band gaps were found to be 1.55 ± 0.03 eV for all the nanoferrite samples. No significant difference in band gap was noticed with the incorporation of cobalt ions in the host nanosized zinc ferrites. These synthesized ferrite samples would be promising nanomaterials for a variety of optical applications because they showed an opaque behavior in the near-IR region of the electromagnetic spectrum.40,41
3.6. Analysis of magnetic properties
The hysteresis curves of the as-fabricated spinel cubic CoxZn1−xFe2O4 (x = 0.00, 0.10, 0.30, and 0.50) ferrite nanoparticles were recorded at 5 K, as shown in Fig. 4(a). The values of multiple magnetic parameters, such as coercive field (HC), saturation magnetization (MS), magnetic moment (μT) and effective anisotropy constant (KT), were evaluated and listed in Table 1. The recorded M(H) loops at 5 K showed a gradual increase in saturation magnetization as well as coercivity due to the incorporation of magnetic Co2+ ions in the nanocrystalline ZnFe2O4 crystal structure. Two different types of sublattices [tetrahedral (A) and octahedral (B)] are present in the spinel cubic system and the quantum mechanical superexchange interactions (A–O–B) via oxygen anions between A and B sublattices are responsible for the observed ferrimagnetic nature of the system.6,40 Due to the ferrimagnetic behavior, the magnetic moments of both sublattices in a spinel ferrite are oppositely aligned but differ in magnitude. Algebraic subtraction of all the magnetic moments of both sublattices, i.e., μT = (μB − μA), where both μB and μA denote the magnetic moment of the octahedral (B) and tetrahedral (A) coordinated sublattices, respectively, provides the overall magnetic moment of the system.42,43 Substitution of ferromagnetic Co2+ ions having a magnetic moment of 3.87 μB, which is much higher than that of the Zn2+ ions in the host zinc ferrite matrix, resulted in an increase in HC and effectively boosted the ferrimagnetic behavior.17 The strengthening of superexchange interactions (A–O–B) due to magnetic Co ions doping was reflected in the hysteresis loops recorded at 5 K. As seen in Table 1, the Co-50 (ZNF) samples showed a significant coercive field value (4.56 kOe) at 5 K. It should be noted that the overall magnetic moment of the spinel cubic system determines its saturation magnetization, obeying the stated relationship:44| |
 | (8) |
where ρ denotes the density, M is the mass per formula unit and other notations are known. An increase in the net magnetic moment due to the gradual incorporation of magnetic Co2+ dopant led to an increase in MS at 5 K. The effective anisotropy constant (KT) consisting of several contributions such as volume anisotropy, surface anisotropy, shape anisotropy and anisotropy caused by magnetic dipole–dipole interactions can be approximately calculated using the following formula:20| |
 | (9) |
 |
| | Fig. 4 (a) Hysteresis loops obtained at 5 K and (b) room temperature hysteresis curves of all the prepared ferrite nanoparticles. | |
Table 1 Several magnetic parameters obtained at 5 K and 300 K for all the ferrite samples
| Sample id |
Magnetic properties |
| 5 K |
300 K |
| MS (emu g−1) |
HC (kOe) |
KT (emu kOe g−1) |
μT (μB) |
MS (emu g−1) |
Hc (Oe) |
KT (emu kOe g−1) |
μT (μB) |
| Co-00 (ZNF) |
58.2 |
0.52 |
30.8 |
2.51 |
13.6 |
12.1 |
0.16 |
0.58 |
| Co-10 (ZNF) |
68.7 |
1.79 |
125.4 |
2.95 |
18.9 |
20.4 |
0.39 |
0.87 |
| Co-30 (ZNF) |
75.8 |
3.43 |
265.3 |
3.24 |
32.1 |
29.2 |
0.96 |
1.37 |
| Co-50 (ZNF) |
83.5 |
4.56 |
388.5 |
3.55 |
38.7 |
36.6 |
1.44 |
1.64 |
All the obtained values of KT for the as-prepared doped nanoferrites at 5 K are displayed in Table 1 and a systematic enhancement in KT was noted with an increase in the cobalt content in the pure zinc ferrite nanoparticles. This is attributed to the gradual increment in both MS and HC at 5 K for a higher Co ion content in the ferrite samples. In addition, the overall magnetic moments (μT) of the synthesized spinel cubic systems were estimated in terms of Bohr magneton (per formula unit) using the following relation:45
| |
 | (10) |
where
M stands for the mass per formula unit of the system. The progressive increment in the saturation magnetization caused by ferromagnetic Co ion doping in the ZnFe
2O
4 system resulted in the sharp increase in the magnetic moment values at 5 K, as listed in
Table 1.
The room temperature M(H) graphs of the cobalt-doped ZnFe2O4 nanoparticles with varying weight percentages of Co ions are displayed in Fig. 4(b). The room temperature hysteresis loops were used to acquire the values of various magnetic parameters, which are compiled in Table 1. An attentive investigation of the magnetic parameters such as MS and HC revealed that a similar type of trend was followed by these magnetic parameters at room temperature in comparison to the results obtained at 5 K. With the introduction of cobalt ions in the nanosized ZnFe2O4 crystal structure, both MS and HC were found to increase gradually at 300 K due to the ferromagnetic nature of cobalt ions having a Curie temperature of around 1400 K. The undoped zinc ferrite nanoparticles exhibited low coercive field values as well as saturation magnetization at 300 K due to the weakening of superexchange interactions given that Zn ions are diamagnetic.17 The low coercivity at room temperature observed for the undoped nanosized Co-00 (ZNF) sample favored the formation of the superparamagnetic ground state. Therefore, the pure zinc ferrite nanoparticles displayed superparamagnetic behavior at room temperature. With an increase in the content of ferromagnetic Co ions in the host system, the A–O–B superexchange interactions became stronger, and thereby the superparamagnetic characteristics started to decrease gradually. We also computed two additional magnetic factors at 300 K, i.e. effective anisotropy constant and total magnetic moment, for the doped ferrite systems and found that both increased systematically with the incorporation of ferromagnetic cobalt ions into the host nanocrystalline zinc ferrites (see Table 1). The substitution of cobalt ions in the zinc nanoferrites strengthened the magnetic features of the systems at room temperature given that they have a higher magnetic moment than Zn ions and a higher Curie temperature.46–48 This fact was reflected in the recorded hysteresis loops and enabled us to tune the magnetic properties via magnetic ion doping for multiple potential applications. A reduction in the thermal agitation inside the as-prepared magnetic systems due to the reduction in temperature made them magnetically harder.35 Therefore, all the magnetic parameters including coercivity, anisotropy constant and saturation magnetization significantly increased at 5 K for the doped nanoferrites compared with the results obtained at room temperature (see Table 1).
To confirm the superparamagnetic behavior of the undoped and doped nanosized zinc ferrites at 300 K, their temperature-dependent magnetization curves were recorded in the presence of a 200 Oe DC magnetic field. Fig. 5(a) illustrates the zero-field cooled (ZFC) and field-cooled (FC) curves of the M(T) plot for each ferrite sample. All the data for the ZFC and FC protocols and the M(T) plot were collected in the warming cycle by applying a 200 Oe DC magnetic field.34 A maximum in the ZFC curve for each sample was seen and the temperature associated with this maximum is termed the blocking temperature (TB) of magnetic moments for the specific sample containing magnetic nanoparticles.47,48 Both the thermal energy (kBT) and magnetic anisotropy (KTV) barrier energy compete to decide the motion of the net magnetic moment of a magnetic system along two easy axes. These two competing energies are assumed to be equal at TB for a magnetic system and below TB, entire magnetic moments are blocked along the easy axis, and thereby the magnetic system is found to be in a blocked state, in contrast, above TB, the magnetic moments are free to rotate due to having sufficient thermal energy to cross the barrier energy, and thereby coherent flipping of the moments usually occurs. The magnetic state above TB is considered the superparamagnetic ground state for a nanosized magnetic system and can be characterized by the negligible coercivity and negligible remanent field coupled with high saturation magnetization, observed through a hysteresis loop.47 Three main factors, i.e., the mean volume (V) of the magnetic nanoparticles, the effective anisotropy constant (KT), and the device measurement time, strongly influence the blocking temperature (TB) for a magnetic system. The blocking temperature (TB) can be normally described as follows34,48
| |
 | (11) |
where
kB stands for the Boltzmann constant and other notations are known. The values of the blocking temperature for each system were calculated and found to be 31 K [Co-00 (ZNF)], 53 K [Co-10 (ZNF)], 122 K [Co-30 (ZNF)], and 194 K [Co-50 (ZNF)]. The increment in mean diameter (
D), as well as effective anisotropy constant (
KT) with an increase in the percentage of ferromagnetic Co ions in the host ferrite system led to the gradually enhancement in
TB. It was observed that the blocking temperature enhanced and the magnetic properties including coercivity, magnetic moment and magnetic anisotropy, which was strengthened when the Co content in the nanocrystalline zinc ferrites increased. With the introduction of cobalt dopant, the superparamagnetic behavior became weak in the doped ferrite systems.
48 The almost flat nature with respect to the temperature axis observed in the FC curve for the Co-50 (ZNF) sample indicated the existence of strong interparticle interactions among the nanoparticles. In addition, careful observation of the
M(
T) plot showed that the ZFC and FC curves were merged at a temperature that was comparatively higher than
TB for all the nanoferrite samples. This specific temperature is called the thermo-magnetic irreversibility temperature (
Tirr) of a magnetic system. It provides the blocking temperature of the largest-sized ferrite nanoparticles in the system. Given that our studied systems contain a huge number of magnetic nanoparticles, both
TB and
Tirr have an average value. We estimated the values of
Tirr for each magnetic system, which were found to be 36 K [Co-00 (ZNF)], 59 K [Co-10 (ZNF)], 135 K [Co-30 (ZNF)], and 218 K [Co-50 (ZNF)]. The observed increment in the
Tirr value is due to the strong A–O–B superexchange interactions with the Co ion dopant.
34,35 The range of the magnetic anisotropy energy barrier and its behaviour is reflected in the temperature difference between
Tirr and
TB. The observed gradual increment in the temperature difference between
Tirr and
TB reflected the divergence in the particle size distribution and the anisotropy energy barrier. The difference in magnetization between the ZNC-FC curves at low temperatures (say 10 K) can be understood with the aid of the following equation:
49| |
 | (12) |
where
HA represents the applied DC magnetic field (200 Oe) and other symbols are known. The irreversibility of magnetization seen in the ZFC-FC protocols at low temperatures (around 10 K) for the ferrite samples with a higher content of dopant is attributed to the freezing of the magnetic moments along the easy axis.
 |
| | Fig. 5 (a) ZFC and FC curves of M(T) plot at 200 Oe for all the samples and (b) induction heating curves under the application of an alternating magnetic field for each sample. | |
3.7. Studies on hyperthermia properties
Magnetic hyperthermia refers to a heat-generating process that involves elevating the temperature of cancer cell media up to 46 °C using a colloidal suspension of magnetic nanoparticles exposed to an alternating magnetic field for a specific duration to destroy cancer cells. A colloidal suspension of magnetic nanoparticles called ferrofluid is used to target and decorate cancer cells. Upon exposure to an alternating magnetic field, the magnetic nanoparticles inside the colloidal suspension dissipate heat due to the magnetic energy losses.2–9 There are basically three losses that effectively contribute to generating heat energy to destroy cancerous cells, i.e., relaxation loss, hysteresis loss, and eddy current loss. The use of superparamagnetic nanoparticles to form a colloidal suspension enables us to ignore the other two losses, i.e., hysteresis and eddy current. This is due to the infinitesimal remanence and coercivity of superparamagnetic nanoparticles. Therefore, the relaxation loss of superparamagnetic nanoparticles dominates in the heat generation process for hyperthermia application.7 For a colloidal suspension of superparamagnetic nanoparticles under an alternating magnetic field, two distinct relaxation processes, i.e., Néel relaxation loss and Brownian relaxation loss, are engaged in energy loss in heat form. It is known that Brownian relaxation is only present in the relaxation dynamics when magnetic nanoparticles form a colloidal solution, and in the case of solid magnetic nanoparticles, only Néel relaxation dominates. It is well-known that Néel relaxation starts before Brownian relaxation in ferrofluid and that it predominates in a suspension of superparamagnetic nanoparticles with a mean size below 20 nm. In the case of magnetic nanoparticles with a size less than 20 nm, it was observed that the Néel relaxation dominated in the magnetic spin dynamics and a dimensionless factor highly influenced the Néel relaxation time, i.e., KTV/kBT; where KT is the effective anisotropy constant, V is the mean volume of the nanoparticles and the other notations have their usual meaning. By varying the effective anisotropy constant, it is possible to control the Néel-type spin relaxation dynamics. In addition, varying KT via doping not only controls the spin dynamics but also tunes the magnetic anisotropy barrier; therefore, the specific absorption rate (SAR) value of a magnetic system can also be tailored given that it is correlated with KT. This is the most effective way to control the self-heating efficiency of a particular magnetic system when the mean volume of the nanoparticles is fixed. Cobalt is a ferromagnetic metal, and also known for its hard magnetic nature with high magnetic anisotropy. Careful incorporation of Co ions in appropriate amount in the nanosized ZnFe2O4 matrix must tailor the magnetic properties, and also provide appropriate control of the self-heating performance used in targeted magnetic hyperthermia application. Both the self-heating capability and magnetic anisotropy of a magnetic system are interlinked. Here, it is essential to mention that the significant agglomeration of tiny magnetic particles may result in inconsistency in heating effectiveness. The magnetic dipole–dipole interactions and van der Waals attractions are mainly responsible for the agglomeration of magnetic nanoparticles in a fluid when their concentration is high. Therefore, tuning of the magnetic anisotropy and understanding the effects of the dipolar interactions of a magnetic system may open a proper channel to optimize the self-heating efficacy for targeted magnetic hyperthermia application. In this study, we tuned the magnetic anisotropy of spinel cubic-structured ZnFe2O4 nanoparticles via the doping of different amounts of Co ions within the percolation limit, which were used at a low concentration for preparing ferrofluid to avoid their agglomeration, thus optimizing the self-heating efficacy to be used in hyperthermia applications. In this context, a colloidal solution was prepared for all the samples using de-ionized water (pH 7) at a concentration of 1 mg mL−1. The experiment was performed at room temperature and a thermocouple temperature sensor probe was used to record the increase in temperature with time. The heating response was registered for 15 min under varying magnetic fields of amplitude 14.91 kA m−1 for all the as-prepared samples, as displayed in Fig. 5(b). With the addition of cobalt ions, the heating efficacy of the ZnFe2O4 nanoparticles was improved, and the 50% cobalt-doped sample [Co-50(ZNF)] reached 41.4 °C in 900 s. The other as-synthesized ferrite samples, i.e., Co-00 (ZNF), Co-10 (ZNF) and Co-30 (ZNF), attained 37.1 °C, 38.0 °C and 39.7 °C respectively, in 900 s, which indicates that the 50% Co ion-doped ferrite sample is the most suitable for hyperthermia application. The doping of ferromagnetic cobalt ions improved the magnetic properties, which increased the thermal energy dissipation of the host ferrite nanoparticles, as shown in Fig. 5(b). The estimation of dissipated heat for all the as-prepared doped nanoferrites can be done with the aid of a specific absorption rate (SAR). This gives the dissipated power per unit mass sample. By utilizing the following equation and using the beginning slope of curves in Fig. 5(b) under non-adiabatic conditions, we determined the SAR values for each prepared sample:7| |
 | (13) |
where C stands for specific heat (4.186 J g−1 °C−1) of water used as the solvent, ms and mm are the mass of the solution and the ferrite sample, respectively, and  represents the beginning slope of the temperature vs. time graph [see Fig. 5(b)]. To compare the heating abilities among the as-synthesized ferrite samples, the parameter called intrinsic loss power (ILP) was used, as follows:6–10
represents the beginning slope of the temperature vs. time graph [see Fig. 5(b)]. To compare the heating abilities among the as-synthesized ferrite samples, the parameter called intrinsic loss power (ILP) was used, as follows:6–10| |
 | (14) |
where the notations are known. We computed the values of SAR and ILP for all the samples, as displayed in Table 2. Both the SAR and ILP were observed to increase with the addition of ferromagnetic cobalt ions in the host nanoferrites. The self-heating efficacy under an applied field could be adjusted according to the requirement following the Hertz limit via doping of suitable ions. By controlling the anisotropy barrier energy using ferromagnetic Co2+ dopants, the magnetic hyperthermia effect of the zinc ferrite nanoparticles was efficiently controlled obeying biological safety limits. The anisotropy energy barrier (ΔE = KTV); where KT is the effective anisotropy constant (at 300 K) and ‘V’ denotes the mean volume of the as-synthesized nanoparticles, was evaluated to draw the schematic representation of ΔE against cobalt concentration (in wt%). Fig. 6 shows a schematic representation of the anisotropy energy barrier (ΔE) and SAR value with respect to an increase in cobalt concentration (in wt%). Notably, the slow addition of ferromagnetic Co2+ ions to the nanocrystalline ZnFe2O4 matrix, which has relatively high magnetic anisotropy, increased the effective anisotropy (KT) of the system. This, in turn, increased the anisotropy energy barrier, ΔE, and made it more difficult for the magnetic spins to flip between two easy axes, strengthening the magnetic properties of the system, as evidenced by the increase in the blocking temperature (TB). Given that the generation of heat in an induction heating experiment under an applied alternating magnetic field is due to the loss of magnetic energy in terms of heat, the systematic doping of ferromagnetic Co2+ ions gradually increased the SAR values of the doped ferrite systems. The presence of Co2+ ions in suitable amounts successfully modified the hyperthermia efficacy of the host ferrite system, making it useful for cancer theranostics.2 Due to the increment in magnetic Co dopant in the host spinel cubic zinc ferrite system, the effective anisotropy constant KT (see Table 1) was noticed to increase but the average particle size of the Co-30 (ZNF) sample is relatively larger than the others, resulting in a sharp increment in the value of anisotropy energy barrier (ΔE = KTV) of the Co-30 (ZNF) sample at room temperature. Only the SAR values (see Table 2) obtained from the induction heating experiment showed a gradual increment with an increase in concentration of magnetic cobalt dopant in the host ZNF matrix. To demonstrate the capabilities of our synthesized nanomaterials in comparison to other magnetic materials documented in the literature, a comparative table was created (see Table 3).
Table 2 SAR and ILP values of each nanoferrite sample
| Sample id |
SAR (W g−1) |
ILP × 10−4 (nH m2 g−1) |
| Co-00 (CNF) |
55.14 |
7.36 |
| Co-10 (ZNF) |
63.71 |
8.50 |
| Co-30 (ZNF) |
68.73 |
9.17 |
| Co-50 (ZNF) |
70.92 |
9.47 |
 |
| | Fig. 6 Schematic of the anisotropy energy barrier (ΔE) and SAR value with respect to cobalt ion doping. | |
Table 3 Comparison between SAR values reported in the present work and other works available in the literature [1 Oe = 0.08 kA m−1]
| Compound |
Synthesis method |
Size (nm) |
H |
f (kHz) |
SAR (W g−1) |
Reference |
| Ga–Mn ferrites |
Sol–gel method |
13.5–17.4 |
0–15 kA m−1 |
50–1200 |
10–20 |
50 |
| Ca–Zn ferrites |
Sol–gel method |
12–14 |
10.2 kA m−1 |
354 |
24.5 |
51 |
| CoFe2O4 |
Chemical reduction method |
10 |
3.2 kA m−1 |
571 |
22 |
52 |
| Zn0.9Fe2.1O4 |
Precipitation and ultrasonication |
11 |
34.4 Oe |
700 |
36 |
53 |
| Fe3O4 |
Co-precipitation method |
28 |
6.3 kA m−1 |
400 |
36 |
54 |
| Zn–Co ferrites |
Thermal decomposition |
8.1–8.7 |
12 kA m−1 |
183 |
17–36 |
55 |
| Zn–Co ferrite |
Co-precipitation method |
8.6–13 |
288 Oe |
340 |
10 |
56 |
| Cobalt ferrite/hydroxyapatite nanocomposite |
Co-precipitation method |
20–150 |
100–150 Oe |
200 |
28–40 |
57 |
| Zinc ferrite |
Melt-quench method |
76 |
500 Oe |
60 |
4.4 |
58 |
| MWCNT-MnFe2O4 nanocomposite |
Solvothermal method |
3.3–3.8 |
12.89 kA m−1 |
336 |
21.6–28.9 |
7 |
| Cobalt doped ZnFe2O4 nanoparticles |
Co-precipitation method |
9.7–20.1 |
14.91 kA m−1 |
337 |
55–71 |
This work |
3.8. Electrical conductivity studies
Nanosized spinel ferrites with tuned electrical transport properties have the potential to be used in sensor and storage devices. Thus, to understand the potential of the as-synthesized Co-doped ferrite nanomaterials in the direction of sensor application, sufficient knowledge of their electrical conductivity coupled with the mechanism of charge conduction is required. Due to their optical band gap in the range of 1.5–2.0 eV, nanosized spinel ferrites behave as semiconducting materials. Upon exposure to an alternating electric field, electrical conduction through the hopping of electrons typically happens in spinel ferrites, which is a process that involves electrons or holes jumping between ions of the same element in different oxidation states. Electron hopping occurs when the alternating electric field supplies electrons with sufficient energy to overcome the electrostatic barrier.59–61 The electrical conductivity of spinel ferrites is often observed to increase initially when the applied field frequency increases, and then decreases as the hopping frequency of charge carriers lags behind the frequency of the applied field. This type of behavior was also noticed in our synthesized ferrite nanomaterials. It should be noted that the overall conductivity (σt) of spinel ferrites is composed of DC and AC components, as follows:6,60,61| | |
σt (T, ω) = σdc (T) + σac (T, ω)
| (15) |
where the DC component of conductivity (σdc) is only reliant on the temperature, which involves the band conduction of electrons. Alternatively, the AC component of conductivity (σac) depends upon both the frequency and temperature. In the case of spinel ferrites, the AC component of the conductivity usually follows the power law, as follows:60where C(T) becomes a constant when the composition of the substance and the temperature remain unchanged and ‘n’ stands for a dimensionless exponent and is allowed to attain a value between 0 and 1. If the exponent becomes zero, the AC conductivity turns into frequency-independent DC conductivity. The AC conductivity data of all the ferrite nanomaterials were collected at room temperature and plotted against frequency on a logarithmic scale [see Fig. S3(a)†]. As shown in Fig. S3(a),† almost straight-line curves were obtained, and the exponent ‘n’ is usually estimated from the slope of the straight line. It was noticed that the exponent attained values between 0.89 and 0.96, which are less than unity [see Fig. S3(b)†], indicating that the mechanism involved in the conduction of charges is the hopping conduction between metal ions.6,60
3.9. Analysis of dielectric loss
Upon exposure to an external electric field, a dielectric nanomaterial experiences a separation of positive and negative charges probably less than an atomic diameter from their equilibrium position, and thereby a large number of dipoles is formed and the nanomaterial is considered to be polarized. Because of having a band gap above 1.5 eV, spinel ferrites exhibit dielectric properties, which strongly depend on the composition, applied field frequency, and temperature. The electrical energy holding capability of spinel cubic nanoferrites when exposed to an electric field can be understood by analyzing the loss tangent (tan δ). The loss tangent basically measures the polarization loss throughout a nanomaterial because it is directly related to the electrical energy holding capacity of that material.59–61 The loss tangent is expressed by the ratio of the imaginary to real parts of the dielectric constant. In this regard, the applied frequency-dependent loss tangent (tan δ) data was recorded at room temperature for all the doped nanosized ferrites and a graph plotted in the semi-logarithmic scale, which is depicted in Fig. S3(c).† Several primary factors are responsible for the resulting dielectric loss for a nanomaterial including vacancies, point defects, grain boundaries, impurities, and dopants and their content. With an increase in the external field frequency, nanocrystalline spinel ferrites lose their capacity to retain polarization and cannot follow frequency variations, causing dielectric losses.60–63 It was observed that all the nanoferrites exhibited considerable polarization loss at low frequencies up to 1000 Hz. This may be ascribed to the matching of the applied frequencies with the electron hopping frequencies, leading to polarization loss and the appearance of a peak in the loss tangent. With an increase in the content of Co2+ dopant in the pure ZnFe2O4 nanoparticles, the loss tangent was noted to increase, indicating an enhancement in charge conduction through the hopping process. The variation in frequency above 1 kHz was not met with hopping frequencies by any of the nanocrystalline ferrite samples, which significantly decreased the loss tangent value. The synthesized doped ferrite nanomaterials demonstrated negligible dielectric loss in the vicinity of the MHz domain, making them suitable for microwave devices.6
3.10. Studies on Cole–Cole plots
Following Koop's theory, a dielectric material is assumed to be made of grains and grain boundaries, where grains are conductive and grain boundaries are less conductive in nature.64 These conductive grains and resistive grain boundaries collectively participate in determining the dielectric properties of a polycrystalline nanomaterial.18 Grain boundaries are essentially flaws in the lattice planes. The Cole–Cole plot is widely used to separate the contributions of conductive grains and less-conductive grain boundaries to the total conductivity of a dielectric nanomaterial. The dielectric modulus for all the ferrite samples is obtained in this regard by using the real and imaginary parts of the dielectric constant, as follows:18,65| |
 | (17) |
| |
 | (18) |
A graph was created by plotting the real (M′) and imaginary (M′′) parts of the dielectric modulus, which takes the shape of a semicircle and this graph is called the Cole–Cole plot for a dielectric substance. All the obtained Cole–Cole plots for the as-fabricated Co-doped ZnFe2O4 nanoparticles are displayed in Fig. S3(d).† Attentive investigation showed that each sample contained a single semicircular curve, which mainly suggested that the participation of less-conductive grain boundaries was more significant than the conductive grains in deciding the dielectric properties of the as-prepared nanocrystalline ferrites.65 As observed in Fig. S3(d),† a minute decrease in the radius of the semicircles was found with an increase in the concentration of cobalt in the host ferrite system, indicating an enhancement in DC conductivity in the doped nanoferrites.65 Further, the Cole–Cole plot was used to test the metribuzin herbicide sensing ability of prepared samples.
3.11. Studies on metribuzin herbicide sensing
To investigate the sensing capability of the pure and 50% cobalt ion-doped ZnFe2O4 nanoparticles at room temperature for metribuzin herbicide, the Cole–Cole plot was utilized. A notable alteration in the radius of the semicircle was observed upon the addition of metribuzin solution of different concentrations, which instantaneously enabled the sensing of metribuzin. Metribuzin solution having two different concentrations, i.e., 1 ppm and 2 ppm, was prepared and used for sensing application at 300 K. The ability to sense metribuzin solution was tested for the Co-00 (ZNF) and Co-50 (ZNF) nanoferrites at room temperature using the Cole–Cole plot, as displayed in Fig. 7(a and b), respectively. A detailed analysis of the Cole–Cole plots [see Fig. 7(a and b)] showed that when 20 μL metribuzin solution (of 1 ppm and 2 ppm concentrations) was added to the surface of a 13 mm diameter plate made of the as-synthesized nanomaterials, the radius of the semicircle decreased in a systematic way with respect to the control with an increase in the concentration of the metribuzin solution.24–28 The observed decrease in the radius values of the semicircles due to the inclusion of metribuzin solution of different concentrations revealed that the conductivity of the as-prepared nanomaterials gradually decreased, allowing the detection of metribuzin at room temperature. The significant shift in the semicircle radius upon the addition of metribuzin solution indicated that the Co-50 (ZNF) nanoferrites performed relatively better in metribuzin sensing than the pristine sample.66,67 It was established that the undoped and Co2+ ion-substituted zinc ferrite nanomaterials are capable of detecting metribuzin at room temperature; therefore, they have the potential for use in metribuzin sensing devices. We developed a term called “response” represented by the letter “S” to analyse the sensing capabilities of the undoped and 50% cobalt-doped ZnFe2O4 nanoferrite samples, as follows:| |
 | (19) |
where  represent the maximum value of the imaginary part of the dielectric modulus attained by the semicircles of the control and metribuzin-added samples, respectively. It was observed that the calculated values of S were significantly greater for the Co-50 (ZNF) nanoferrite compared with the pure ZnFe2O4 sample in detecting metribuzin of different concentrations at room temperature [see Fig. 7(c)]. Therefore, the nanocrystalline zinc ferrite doped with 50% Co ions was shown to be more sensitive to the presence of metribuzin. When metribuzin solution was added to both nanosized ferrite samples, the radius of the semicircles in the Cole–Cole plot decreased, indicating a decrease in the DC conductivity. This reflected that the metribuzin solution efficiently inhibited the DC conduction of charge carriers in the synthesized nanomaterials.63–65
represent the maximum value of the imaginary part of the dielectric modulus attained by the semicircles of the control and metribuzin-added samples, respectively. It was observed that the calculated values of S were significantly greater for the Co-50 (ZNF) nanoferrite compared with the pure ZnFe2O4 sample in detecting metribuzin of different concentrations at room temperature [see Fig. 7(c)]. Therefore, the nanocrystalline zinc ferrite doped with 50% Co ions was shown to be more sensitive to the presence of metribuzin. When metribuzin solution was added to both nanosized ferrite samples, the radius of the semicircles in the Cole–Cole plot decreased, indicating a decrease in the DC conductivity. This reflected that the metribuzin solution efficiently inhibited the DC conduction of charge carriers in the synthesized nanomaterials.63–65
 |
| | Fig. 7 Metribuzin sensing of (a) Co-00 (ZNF) and (b) Co-50 (ZNF) samples using the Cole–Cole plot, and (c) response of Co-00 (ZNF) and Co-50 (ZNF) samples in metribuzin sensing. | |
For developing an efficient nanomaterial to be used in sensing applications, some crucial factors, such as sensitivity, accuracy, selectivity, response time, working temperature, and detection limit, that need to be precisely determined. Our synthesized nanomaterials manifested a quick response upon the addition of the target analyte (metribuzin solution), and therefore the response time is instantaneous for these nanomaterials. These nanoferrites must be employed effectively at room temperature for metribuzin sensing and are stable throughout a broad temperature range. The as-prepared nanomaterials [Co-00 (ZNF) and Co-50 (ZNF)] were examined for their selectivity to metribuzin solution over other analytes including glyphosate, citric acid, and urea solution.68–72 In this regard, we made 20 μL of 1 ppm solution of the other mentioned analytes to check the selectivity of the prepared nanomaterials. The recorded responses were merged in Fig. S4 and S5,† respectively. There was an insignificant change in the ‘response’ (S) parameter due to the inclusion of the other mentioned analytes compared with the metribuzin solution (see Fig. S4 and S5,† respectively). Table 4 displays a comparative study that compares the metribuzin sensing performance of the as-prepared doped ferrite nanoparticles with recently reported sensing materials. It should be noted that the significantly higher sensitivity of optical sensing compared to dielectric sensing for metribuzin detection is due to the fundamental differences in their detection mechanisms. Optical methods (e.g., fluorescence and SERS) leverage strong light-matter interactions and signal amplification through nanostructures, achieving detection in the nanomolar range.25,27 Additionally, surface functionalization enhances molecular interactions, further lowering the detection limits.26 In contrast, dielectric sensing measures changes in permittivity or impedance, which are inherently weaker effects requiring higher analyte concentrations. The lack of intrinsic amplification and environmental interferences further limit its sensitivity. Herein, we employed a different sensing method to sense metribuzin, which can be useful for less-optically sensitive dielectric nanomaterials. We also tested the efficacy and physical properties of the Co-50 (ZNF) sample before and after five cycles of metribuzin detection and found no significant change [see Fig. S6 (in ESI)†]. To check the integrity of the structural properties of the Co-50 (ZNF) sample, its XRD patterns were recorded before and after five consecutive cycles of metribuzin sensing. No significant change in its structural properties was observed [see Fig. S7 (in ESI)†].
Table 4 Comparison of metribuzin sensing capability between the as-synthesized samples and recently reported sensing materials
| Material |
Detection limit (nM) |
Detection method |
Operation temperature |
Reference |
| CuO NPs/graphene nanocomposite |
7.819 × 105 |
Optical sensing |
RT |
24 |
| Doped carbon/biopolymer complex |
13.04 |
Optical sensing |
RT |
25 |
| Carbon dots |
22.57 |
Optical sensing |
RT |
26 |
| Composite film |
0.682 |
Optical sensing |
RT |
27 |
| Ag-nanocubes/SERS substrate |
0.1 |
Optical sensing |
RT |
28 |
| Cobalt-doped ZnFe2O4 nanoparticles |
4.204 × 103 |
Dielectric sensing |
RT |
This work |
3.12. Analysis of metribuzin sensing mechanism
The cobalt-doped zinc ferrite (ZNF) nanomaterial demonstrated notable changes in its dielectric properties upon interacting with liquid metribuzin analyte, making it suitable as a sensing material. The chemical and electronic interactions between the adsorbed analyte and doped ZNF nanomaterial are pivotal in altering its response as a sensor. Fig. 8 shows a schematic diagram of the metribuzin sensing mechanism. When Co-doped ZNF interacts with atmospheric air and liquid metribuzin, significant changes in its electrical properties occur.68 The interactions with these substances modify the resistance of the prepared nanomaterial for hopping conduction, which are influenced by the formation of superoxide ions and electrochemical processes. Specifically, the interaction with metribuzin resulted in an electrochemical reaction on the nanomaterial surface, causing a decrease in resistance due to the energy released during the bond breaking process.68 This reaction generates electron–hole pairs, impacting the conductivity of the synthesized nanomaterial. In contrast, the response of the doped ZNF sensor to various analytes is influenced by factors such as oxygen adsorption, temperature, crystal structure, grain size, and defect density. For instance, the sensitivity of the doped ZNF nanomaterial to metribuzin is linked to the electrochemical reactions facilitated by surface-adsorbed superoxide, leading to an increase in resistance and decrease in AC conductivity for hopping conduction. These nanomaterials offer a large surface area with numerous active sites for the adsorption of metribuzin, while the Co dopant enhances metribuzin binding to the ZNF surface, facilitating its decomposition. In contrast, because metribuzin has certain functional groups that interact strongly with the ferrite surface and change its electrical characteristics, co-doped zinc ferrite nanoparticles are more sensitive to it. A notable reaction results from the improved adsorption made possible by the molecular structure of metribuzin. Alternatively, urea, citric acid, and glyphosate interact with the surface less specifically or weakly, which reduces the sensitivity. The heightened sensitivity of Co-doped ZNF to metribuzin compared to glyphosate, citric acid, and urea is due to the stronger electron-donating properties of metribuzin, which significantly impacts the surface charge and electronic properties of the sensor, resulting in a more pronounced response. However, in the case of analytes such as glyphosate, citric acid, and urea, the electrochemical reactions do not provide sufficient energy for enhanced electron transport, resulting in a lower sensing response.68,73,74 Introducing dopants, such as Co, into the ZNF system enhances its sensing response towards metribuzin by making charge transfer more feasible. Also, the doping concentration of Co in ZNF influences its electronic properties, ultimately boosting its sensitivity to metribuzin. When metribuzin is applied to the ZNF nanomaterial, the depletion layer of ZNF and energy boundaries become weaker.
 |
| | Fig. 8 Schematic representation of metribuzin herbicide sensing mechanism. | |
4. Conclusion
In summary, the physical properties, including microstructural, dielectric, optical, and magnetic characteristics of nanocrystalline zinc ferrite, were tuned via an appropriate amount of ferromagnetic cobalt ion doping. Four nanosized zinc ferrite samples with varying cobalt contents were prepared using the wet chemical co-precipitation route. The tuneable induction heating performance of the doped ferrite nanoparticles according to the requirement was obtained by regulating the effective magnetic anisotropy of the system to make them suitable for magnetic hyperthermia therapy. The correlations between physical properties and the effects of doping cobalt ions in ZnFe2O4 nanoparticles in modifying physical properties were discussed precisely in this study. Several characterization techniques were employed to study the physical properties and possible applications in the field of magnetic hyperthermia and sensors of cobalt-incorporated zinc ferrite nanoparticles. The formation of the spinel cubic phase in all the as-prepared nanoferrites was validated by their recorded X-ray diffractograms, FTIR spectra and Raman spectra. The average crystallite sizes and intrinsic microstrain were assessed for all the nanoferrites using the Williamson–Hall (W–H) method. The calculated values of mean crystallite sizes ranged from 9.7 nm to 20.1 nm, respectively, and the compressive intrinsic microstrain of the ZnFe2O4 nanoparticles turned to tensile due to the doping of Co ions. The analysis of the Raman spectra revealed the existence of characteristic Raman active modes in each nanoferrite sample and lowering of the crystal symmetry was also detected because of Co ion substitution. A good agreement was observed between the mean crystallite size, as assessed from the W–H plots, for each sample and the average particle size, as estimated from the HRTEM micrographs. Using the Tauc plot, the indirect band gaps were determined to be 1.55 ± 0.03 eV for each of the as-synthesized nanoferrites. Substitution with ferromagnetic cobalt dopants improved the magnetic responses of the ZnFe2O4 nanoparticles, and also enabled the tuning of the magnetic anisotropy constant. A notable increment in magnetic parameters such as coercive field, magnetic moment, anisotropy constant and saturation magnetization in a systematic way was noticed due to the doping of Co in the host matrix. The blocking temperature related to the superparamagnetic state of the prepared doped nanoferrites was improved, favouring the magnetic hyperthermia. The 50% cobalt-doped nanoferrite showed a comparatively better induction heating performance. According to the dielectric analysis, cobalt ion substitution caused the host zinc ferrite to become a lossy dielectric nanomaterial. The loss tangent was shown to increase with an increase in Co2+ dopants in the pure ZnFe2O4 nanoparticles, suggesting an improvement in the hopping conduction. The examination of the Cole–Cole plot revealed that each sample displayed a single semicircular curve, primarily indicating that the dielectric characteristics were determined more by the involvement of less-conductive grain boundaries than by conductive grains. In addition, the sensing ability of the doped and pristine nanoferrites was tested at room temperature for metribuzin herbicide and the Cole–Cole plot was used to identify the sensing performance. When the metribuzin solution was added, there was a noticeable change in the semicircle radius (Cole–Cole plot), which suggested that the Co-50 (ZNF) nanoferrites outperformed the pristine sample in metribuzin herbicide sensing. Based on these findings, it is understood that the synthesized doped nanoferrites are efficient to be utilized in magnetic hyperthermia and metribuzin herbicide sensing applications.
Data availability
The datasets used for this work are made available from the corresponding author upon reasonable request.
Author contributions
MPG: conceptualization , methodology, resources, validation, discussion, writing the original draft, and writing – review and editing. RS: methodology, writing and editing, and formal analysis. GP: methodology and formal analysis. JPB: discussion and methodology. DC: conceptualization, methodology, validation, resources, supervision, discussion, and writing – review and editing.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
The authors thank the SAIC-IASST for providing instrumental facilities. All the authors are also thankful to IISER Bhopal for providing magnetic data of the samples. MPG thanks DST-SERB (ANRF) for the fellowship through the NPDF (PDF/2023/001314) scheme, and RS thanks UGC, New Delhi, for the fellowship. The authors thank IASST, Guwahati, for in-house project.
References
- T. Kaur and D. Sharma, Nanoscale, 2024, 16, 7892–7907 RSC
 .
. - G. Phukan, M. Kar and J. P. Borah, ACS Appl. Mater. Interfaces, 2023, 16, 261–271 CrossRef PubMed
 .
. - G. Nandhini and M. K. Shobana, J. Magn. Magn. Mater., 2022, 552, 169236 CrossRef CAS
 .
. - M. Peiravi, H. Eslami, M. Ansari and H. Zare-Zardini, J. Indian Chem. Soc., 2021, 99, 100269 CrossRef
 .
. - H. Gavilán, S. K. Avugadda, T. Fernández-Cabada, N. Soni, M. Cassani, B. T. Mai, R. Chantrell and T. Pellegrino, Chem. Soc. Rev., 2021, 50, 11614–11667 RSC
 .
. - M. P. Ghosh, N. J. Mondal, R. Sonkar, B. Boro, J. P. Borah and D. Chowdhury, ACS Appl. Nano Mater., 2024, 7, 7028–7042 CrossRef CAS
 .
. - P. Seal, N. Paul, P. D. Babu and J. P. Borah, Appl. Phys. A:Mater. Sci. Process., 2019, 125, 290 CrossRef CAS
 .
. - X. Yu, R. Yang, C. Wu, B. Liu and W. Zhang, Sci. Rep., 2022, 12, 16055 CrossRef CAS PubMed
 .
. - Z. Shaterabadi, G. Nabiyouni and M. Soleymani, Prog. Biophys. Mol. Biol., 2017, 133, 9–19 CrossRef PubMed
 .
. - K. El-Boubbou, O. M. Lemine, S. Algessair, N. Madkhali, B. Al-Najar, E. AlMatri, R. Ali and M. Henini, RSC Adv., 2024, 14, 15664–15679 RSC
 .
. - P. Sahoo, P. Choudhary, S. S. Laha, A. Dixit and O. T. Mefford, Chem. Commun., 2023, 59, 12065–12090 RSC
 .
. - R. Mohan, M. P. Ghosh and S. Mukherjee, Appl. Phys. A:Mater. Sci. Process., 2019, 125, 778 CrossRef
 .
. - C. Yao, Q. Zeng, G. F. Goya, T. Torres, J. Liu, H. Wu, M. Ge, Y. Zeng, Y. Wang and J. Z. Jiang, J. Phys. Chem. C, 2007, 111, 12274–12278 CrossRef CAS
 .
. - P. Guo, L. Cui, Y. Wang, M. Lv, B. Wang and X. S. Zhao, Langmuir, 2013, 29, 8997–9003 CrossRef CAS PubMed
 .
. - P. A. Asogekar, S. K. Gaonkar, A. Kumar and V. M. S. Verenkar, Mater. Res. Bull., 2021, 141, 111330 CrossRef CAS
 .
. - R. Sagayaraj, S. Aravazhi and G. Chandrasekaran, Int. Nano Lett., 2021, 11, 307–319 CrossRef CAS
 .
. - M. P. Ghosh and S. Mukherjee, J. Am. Ceram. Soc., 2019, 102, 7509–7520 CrossRef CAS
 .
. - M. P. Ghosh, S. Kinra, D. Dagur, R. K. Choubey and S. Mukherjee, Phys. Scr., 2020, 95, 095812 CrossRef CAS
 .
. - V. H. Ojha and K. M. Kant, Phys. B, 2019, 567, 87–94 CrossRef CAS
 .
. - M. P. Ghosh and S. Mukherjee, J. Mater. Sci.:Mater. Electron., 2020, 31, 6207–6216 CrossRef CAS
 .
. - M. I. Anik, M. K. Hossain, I. Hossain, A. M. U. B. Mahfuz, M. T. Rahman and I. Ahmed, Nano Sel., 2021, 2, 1146–1186 CrossRef CAS
 .
. - M. K. Shobana, Mater. Sci. Eng., B, 2021, 272, 115344 CrossRef CAS
 .
. - K. Wu, J. Li and C. Zhang, Ceram. Int., 2019, 45, 11143–11157 CrossRef CAS
 .
. - P. Maurya, S. K. Verma, S. K. Srivastava, A. Mishra and R. Verma, Microchem. J., 2024, 207, 112008 CrossRef CAS
 .
. - T. Periyasamy, S. P. Asrafali, S.-C. Kim and J. Lee, Polymers, 2024, 17, 39 CrossRef PubMed
 .
. - F. Y. Vadia, T. R. Potnuru, N. I. Malek, T. J. Park and S. K. Kailasa, J. Cluster Sci., 2023, 34, 2823–2833 CrossRef CAS
 .
. - S. M. Saleh, F. M. Alminderej, R. Ali and O. I. Abdallah, Spectrochim. Acta, Part A, 2019, 229, 117971 CrossRef PubMed
 .
. - K. O. Ay, G. Dikmen and O. Koyuncu, J. Mol. Struct., 2023, 1297, 136869 CrossRef
 .
. - R. Sonkar, N. J. Mondal, S. Thakur, E. Saikia, M. P. Ghosh and D. Chowdhury, Nanoscale Adv., 2023, 5, 7042–7056 RSC
 .
. - A. Aakash, P. Nordblad, N. R. Mohan and S. Mukherjee, J. Magn. Magn. Mater., 2017, 441, 710–717 CrossRef
 .
. - R. Sharma, P. Thakur, M. Kumar, P. B. Barman, P. Sharma and V. Sharma, Ceram. Int., 2017, 43, 13661–13669 CrossRef CAS
 .
. - V. K. Lakhani, T. K. Pathak, N. H. Vasoya and K. B. Modi, Solid State Sci., 2010, 13, 539–547 CrossRef
 .
. - Z. Karimi, Y. Mohammadifar, H. Shokrollahi, Sh. K. Asl, Gh. Yousefi and L. Karimi, J. Magn. Magn. Mater., 2014, 361, 150–156 CrossRef CAS
 .
. - R. Mohan, M. P. Ghosh and S. Mukherjee, J. Magn. Magn. Mater., 2018, 458, 193–199 CrossRef CAS
 .
. - M. P. Ghosh and S. Mukherjee, J. Magn. Magn. Mater., 2019, 489, 165320 CrossRef CAS
 .
. - A. Manohar, C. Krishnamoorthi, K. C. B. Naidu and C. Pavithra, Appl. Phys. A:Mater. Sci. Process., 2019, 125, 477 CrossRef CAS
 .
. - Q.-Y. Xiang, D. Wu, Y. Bai, K. Yan, W.-Q. Yao, L. Zhang, J. Zhang and J.-L. Cao, Ceram. Int., 2016, 42, 16882–16887 CrossRef CAS
 .
. - M. P. Ghosh, S. Mandal and S. Mukherjee, Eur. Phys. J. Plus, 2020, 135, 41 CrossRef CAS
 .
. - A. Makofane, D. E. Motaung and N. C. Hintsho-Mbita, Ceram. Int., 2021, 47, 22615–22626 CrossRef CAS
 .
. - N. J. Mondal, R. Sonkar, B. Boro, M. P. Ghosh and D. Chowdhury, Nanoscale Adv., 2023, 5, 5460–5475 RSC
 .
. - S. Singhal, S. Bhukal, J. Singh, K. Chandra and S. Bansal, J. Nanotechnol., 2011, 2011, 1–6 CrossRef
 .
. - A. Aakash, R. Choubey, D. Das and S. Mukherjee, J. Alloys Compd., 2016, 668, 33–39 CrossRef
 .
. - A. Samavati, M. K. Mustafa, A. F. Ismail, M. H. D. Othman and M. A. Rahman, Mater. Express, 2016, 6, 473–482 CrossRef CAS
 .
. - P. Coppola, F. G. Da Silva, G. Gomide, F. L. O. Paula, A. F. C. Campos, R. Perzynski, C. Kern, J. Depeyrot and R. Aquino, J. Nanopart. Res., 2016, 18, 138 CrossRef
 .
. - R. Sharma, P. Thakur, M. Kumar, P. B. Barman, P. Sharma and V. Sharma, Ceram. Int., 2017, 43, 13661–13669 CrossRef CAS
 .
. - M. D. Hossain, M. A. Hossain and S. S. Sikder, J. Magn. Magn. Mater., 2022, 564, 170095 CrossRef CAS
 .
. - S. B. Darling and S. D. Bader, J. Mater. Chem., 2005, 15, 4189 RSC
 .
. - S. Kumar, V. Singh, S. Aggarwal, U. K. Mandal and R. K. Kotnala, Mater. Sci. Eng., B, 2009, 166, 76–82 CrossRef
 .
. - K. S. Ramakrishna, Ch. Srinivas, C. L. Prajapat, S. S. Meena, M. V. K. Mehar, D. M. Potukuchi and D. L. Sastry, Ceram. Int., 2017, 44, 1193–1200 CrossRef
 .
. - J. Sánchez, D. A. Cortés-Hernández, J. C. Escobedo-Bocardo, J. M. Almanza-Robles, P. Y. Reyes-Rodríguez, R. A. Jasso-Terán, P. Bartolo-Pérez and L. E. De-León-Prado, Ceram. Int., 2016, 42, 13755–13760 CrossRef
 .
. - R. A. Jasso-Terán, D. A. Cortés-Hernández, H. J. Sánchez-Fuentes, P. Y. Reyes-Rodríguez, L. E. De-León-Prado, J. C. Escobedo-Bocardo and J. M. Almanza-Robles, J. Magn. Magn. Mater., 2016, 427, 241–244 CrossRef
 .
. - Ö. Çelik, M. M. Can and T. Firat, J. Nanopart. Res., 2014, 16, 2321 CrossRef
 .
. - A. Hanini, L. Lartigue, J. Gavard, K. Kacem, C. Wilhelm, F. Gazeau, F. Chau and S. Ammar, J. Magn. Magn. Mater., 2016, 416, 315–320 CrossRef CAS
 .
. - B. Samanta, H. Yan, N. O. Fischer, J. Shi, D. J. Jerry and V. M. Rotello, J. Mater. Chem., 2008, 18, 1204 RSC
 .
. - M. Albino, E. Fantechi, C. Innocenti, A. López-Ortega, V. Bonanni, G. Campo, F. Pineider, M. Gurioli, P. Arosio, T. Orlando, G. Bertoni, C. De Julián Fernández, A. Lascialfari and C. Sangregorio, J. Phys. Chem. C, 2019, 123, 6148–6157 CrossRef CAS
 .
. - C. Gómez-Polo, V. Recarte, L. Cervera, J. J. Beato-López, J. López-García, J. A. Rodríguez-Velamazán, M. D. Ugarte, E. C. Mendonça and J. G. S. Duque, J. Magn. Magn. Mater., 2018, 465, 211–219 CrossRef
 .
. - S. A. Hassanzadeh-Tabrizi, H. Norbakhsh, R. Pournajaf and M. Tayebi, Ceram. Int., 2021, 47, 18167–18176 CrossRef CAS
 .
. - S. A. Shah, M. U. Hashmi and S. Alam, Mater. Sci. Eng., C, 2011, 31, 1010–1016 CrossRef CAS
 .
. - Z. Ž. Lazarević, Č. Jovalekić, D. L. Sekulić, A. Milutinović, S. Baloš, M. Slankamenac and N. Ž. Romčević, Mater. Res. Bull., 2013, 48, 4368–4378 CrossRef
 .
. - D. Varshney and K. Verma, Mater. Chem. Phys., 2013, 140, 412–418 CrossRef CAS
 .
. - A. Aakash, M. P. Ghosh and S. Mukherjee, Appl. Phys. A:Mater. Sci. Process., 2019, 125, 853 CrossRef
 .
. - R. K. Panda and D. Behera, J. Alloys Compd., 2013, 587, 481–486 CrossRef
 .
. - N. H. Vasoya, V. K. Lakhani, P. U. Sharma, K. B. Modi, R. Kumar and H. H. Joshi, J. Phys.:Condens. Matter, 2006, 18, 8063–8092 CrossRef CAS
 .
. - C. G. Koops, Phys. Rev., 1951, 83, 121–124 CrossRef CAS
 .
. - H. M. T. Farid, I. Ahmad, I. Ali, A. Mahmood and S. M. Ramay, Eur. Phys. J. Plus, 2018, 133, 41 CrossRef
 .
. - A. Jain, S. K. Gautam and S. Panda, Phys. Scr., 2023, 98, 095909 CrossRef CAS
 .
. - P. Dutta, B. Kalita, B. Gogoi and N. S. Sarma, J. Phys. Chem. C, 2015, 119, 17260–17270 CrossRef CAS
 .
. - W. Tang, J. Wang, Q. Qiao, Z. Liu and X. Li, J. Mater. Sci., 2015, 50, 2605–2615 CrossRef CAS
 .
. - A. Selvapandiyan and R. K. Bhatnagar, Appl. Microbiol. Biotechnol., 1994, 40, 876–882 CrossRef CAS
 .
. - F. Laghrib, M. Bakasse, S. Lahrich and M. A. E. Mhammedi, Mater. Sci. Eng., C, 2019, 107, 110349 CrossRef PubMed
 .
. - L. Janíková, R. Šelešovská, M. Rogozinská, M. Tomášková and J. Chýlková, Monatsh. Chem., 2015, 147, 219–229 CrossRef
 .
. - O. D. Ogunbiyi, D. O. Akamo, E. E. Oluwasanmi, J. Adebanjo, B. A. Isafiade, T. J. Ogunbiyi, Y. A. Alli, D. T. Ayodele and P. O. Oladoye, Groundw. Sustain. Dev., 2023, 22, 100961 CrossRef
 .
. - D. R. Miller, S. A. Akbar and P. A. Morris, Sens. Actuators, B, 2014, 204, 250–272 CrossRef CAS
 .
. - V. Balasubramani, S. Sureshkumar, T. S. Rao and T. M. Sridhar, ACS Omega, 2019, 4, 9976–9982 CrossRef CAS PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Rahul Sonkar
*a,
Rahul Sonkar ab,
Gongotree Phukanc,
Jyoti Prasad Borahc and
Devasish Chowdhury
ab,
Gongotree Phukanc,
Jyoti Prasad Borahc and
Devasish Chowdhury *ab
*ab
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and consisting of two different types of sublattices, i.e., tetrahedral and octahedral coordinated sites. In the unit cell of pure zinc ferrite, where all the Zn2+ ions are located in tetrahedral voids and all the Fe3+ ions occupy octahedral voids, forming a normal spinel cubic crystal structure.11–14 Nanocrystalline zinc ferrite behaves like a soft ferrimagnetic material; therefore, upon doping of suitable magnetic ions and varying the dopant concentration in ZnFe2O4 nanoparticles, the magnetic anisotropy of the system can be controlled, enabling the tunability and optimization of the induction heating efficiency according to the requirement for the magnetic hyperthermia therapy.15,16 In this regard, ferromagnetic cobalt ions having a high Curie temperature, chemical stability and comparable size can ideal dopants for regulating the magnetic anisotropy of zinc ferrite nanoparticles within the percolation limit for optimizing the hyperthermia effect. We chose Co2+ 3d transition metal ions to dope pure zinc ferrite nanoparticles and alter their magnetic properties.17,18 The adequate substitution of ferromagnetic Co2+ ions in the host zinc ferrite nanoparticles is expected to increase the effective anisotropy of the system and improve the induction heating efficiency given that the relaxation losses of magnetic nanoparticles are highly influenced by the anisotropy energy barrier. Due to the superparamagnetic nature of soft undoped and doped ZnFe2O4 nanoparticles at room temperature, relaxation losses contribute more effectively in determining the self-heating efficacy.2,19 Therefore, controlling the effective anisotropy constant of prepared nanoferrite systems is essential to tune the heating efficiency according to the requirements. Tuning the effective anisotropy of the host zinc ferrite system has been performed via doping different concentrations of ferromagnetic Co2+.19,20
m space group and consisting of two different types of sublattices, i.e., tetrahedral and octahedral coordinated sites. In the unit cell of pure zinc ferrite, where all the Zn2+ ions are located in tetrahedral voids and all the Fe3+ ions occupy octahedral voids, forming a normal spinel cubic crystal structure.11–14 Nanocrystalline zinc ferrite behaves like a soft ferrimagnetic material; therefore, upon doping of suitable magnetic ions and varying the dopant concentration in ZnFe2O4 nanoparticles, the magnetic anisotropy of the system can be controlled, enabling the tunability and optimization of the induction heating efficiency according to the requirement for the magnetic hyperthermia therapy.15,16 In this regard, ferromagnetic cobalt ions having a high Curie temperature, chemical stability and comparable size can ideal dopants for regulating the magnetic anisotropy of zinc ferrite nanoparticles within the percolation limit for optimizing the hyperthermia effect. We chose Co2+ 3d transition metal ions to dope pure zinc ferrite nanoparticles and alter their magnetic properties.17,18 The adequate substitution of ferromagnetic Co2+ ions in the host zinc ferrite nanoparticles is expected to increase the effective anisotropy of the system and improve the induction heating efficiency given that the relaxation losses of magnetic nanoparticles are highly influenced by the anisotropy energy barrier. Due to the superparamagnetic nature of soft undoped and doped ZnFe2O4 nanoparticles at room temperature, relaxation losses contribute more effectively in determining the self-heating efficacy.2,19 Therefore, controlling the effective anisotropy constant of prepared nanoferrite systems is essential to tune the heating efficiency according to the requirements. Tuning the effective anisotropy of the host zinc ferrite system has been performed via doping different concentrations of ferromagnetic Co2+.19,20![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The existence of all the characteristic peaks of spinel cubic crystal structure together with an intense (311) peak near 2θ = 35.20° was observed in all the recorded diffractograms, and also perfectly matched JCPDS Card No. 77-0426. It is known that the Rietveld refinement technique is normally used to analyze the diffraction pattern of a crystalline material.17–20 The Rietveld refinement of diffractograms for all the nanocrystalline Co-doped zinc ferrites was conducted with the aid of the GSAS software (General Structure Analysis System) together with the EXPUGI interface. The pseudo-Voigt function was utilized for fitting the profile peaks and the Finger–Cox–Jephcoat asymmetry was used for the correction of the axial divergence. The obtained values of refinement parameters, including goodness of fit (χ2), reliability factors (RP, RWP, and RF2) and unit cell parameters are displayed in Table S1.† The estimated values of the refinement parameters were less than 10% and the goodness of fit (χ2) close to unity for each sample indicated a satisfactory agreement between the experimental diffraction data and standard pattern. Close investigation of the diffractograms revealed that a significant amount of line broadening was present. It is noted that line-broadening in diffractograms is commonly observed in nanocrystalline samples, which is also an inherent property of nanosized crystalline materials.17 It occurs because of the involvement of three fundamental factors, i.e. nanocrystallite size effects, inherent microstrain effects and line-broadening due to instrumental effects. All three factors collectively contribute to broadening the line width of the diffracted peaks in the X-ray diffraction patterns. By recording the diffraction pattern of LaB6 powder in a well-annealed bulk form and keeping all the measurement conditions identical, the instrumental line width was corrected for all the nanoferrite samples. After elimination of the broadening caused by the instrument, the total line width β (FWHM) only contained two contributions, i.e., nanocrystallite size (βsize) and microstrain (βstrain) broadening effects, which can be expressed as follows:6,17,30
m space group. The existence of all the characteristic peaks of spinel cubic crystal structure together with an intense (311) peak near 2θ = 35.20° was observed in all the recorded diffractograms, and also perfectly matched JCPDS Card No. 77-0426. It is known that the Rietveld refinement technique is normally used to analyze the diffraction pattern of a crystalline material.17–20 The Rietveld refinement of diffractograms for all the nanocrystalline Co-doped zinc ferrites was conducted with the aid of the GSAS software (General Structure Analysis System) together with the EXPUGI interface. The pseudo-Voigt function was utilized for fitting the profile peaks and the Finger–Cox–Jephcoat asymmetry was used for the correction of the axial divergence. The obtained values of refinement parameters, including goodness of fit (χ2), reliability factors (RP, RWP, and RF2) and unit cell parameters are displayed in Table S1.† The estimated values of the refinement parameters were less than 10% and the goodness of fit (χ2) close to unity for each sample indicated a satisfactory agreement between the experimental diffraction data and standard pattern. Close investigation of the diffractograms revealed that a significant amount of line broadening was present. It is noted that line-broadening in diffractograms is commonly observed in nanocrystalline samples, which is also an inherent property of nanosized crystalline materials.17 It occurs because of the involvement of three fundamental factors, i.e. nanocrystallite size effects, inherent microstrain effects and line-broadening due to instrumental effects. All three factors collectively contribute to broadening the line width of the diffracted peaks in the X-ray diffraction patterns. By recording the diffraction pattern of LaB6 powder in a well-annealed bulk form and keeping all the measurement conditions identical, the instrumental line width was corrected for all the nanoferrite samples. After elimination of the broadening caused by the instrument, the total line width β (FWHM) only contained two contributions, i.e., nanocrystallite size (βsize) and microstrain (βstrain) broadening effects, which can be expressed as follows:6,17,30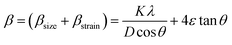


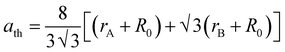
 of the tetrahedral (A) and octahedral (B) sites need to be evaluated to get an idea of the strength of spin interactions and the conduction process of the as-prepared systems. The observed decrease in hopping length with an increase in the concentration of Co ions in the ZnFe2O4 system improved the charge conduction process (see Table S3†). Thereby, the energy requirement for electrons to jump from one cationic site to another decreases, which enhances the conductivity.34
of the tetrahedral (A) and octahedral (B) sites need to be evaluated to get an idea of the strength of spin interactions and the conduction process of the as-prepared systems. The observed decrease in hopping length with an increase in the concentration of Co ions in the ZnFe2O4 system improved the charge conduction process (see Table S3†). Thereby, the energy requirement for electrons to jump from one cationic site to another decreases, which enhances the conductivity.34![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. It contains a total of 56 atoms in its unit cell and 14 atoms inside the smallest Bravais cell. Two different types of interpenetrated sublattices, i.e., tetrahedral and octahedral sites, are present in the unit cell of the spinel cubic structure, belonging to the Td and D3d point groups, respectively. There are 42 active modes, including 3 acoustic modes and 39 optical modes in the spinel cubic ZnFe2O4 according to the factor group analysis. A material must have a non-zero change in polarizability against nuclear displacement to be considered Raman active. Usually, five Raman-active modes (A1g + Eg + 3T2g) are found in spinel cubic-structured materials.36 It should be noted that the active modes above 600 cm−1 are associated with the tetrahedral (A) sublattices and below 600 cm−1 are linked to the octahedral (B) sublattices.37 The A1g Raman active mode is associated with the symmetric stretching of oxygen atoms of metal–oxygen bonds in tetrahedral sites. The Eg and T2g(3) active modes are linked with the symmetric and asymmetric bending of Fe–O bonds, respectively. The T2g(2) mode refers to the asymmetric stretching of the M–O (M = Fe or Co) bonds and the T2g(1) Raman-active mode correspond to the translational motion of the FeO4 tetrahedron.17,30
m space group. It contains a total of 56 atoms in its unit cell and 14 atoms inside the smallest Bravais cell. Two different types of interpenetrated sublattices, i.e., tetrahedral and octahedral sites, are present in the unit cell of the spinel cubic structure, belonging to the Td and D3d point groups, respectively. There are 42 active modes, including 3 acoustic modes and 39 optical modes in the spinel cubic ZnFe2O4 according to the factor group analysis. A material must have a non-zero change in polarizability against nuclear displacement to be considered Raman active. Usually, five Raman-active modes (A1g + Eg + 3T2g) are found in spinel cubic-structured materials.36 It should be noted that the active modes above 600 cm−1 are associated with the tetrahedral (A) sublattices and below 600 cm−1 are linked to the octahedral (B) sublattices.37 The A1g Raman active mode is associated with the symmetric stretching of oxygen atoms of metal–oxygen bonds in tetrahedral sites. The Eg and T2g(3) active modes are linked with the symmetric and asymmetric bending of Fe–O bonds, respectively. The T2g(2) mode refers to the asymmetric stretching of the M–O (M = Fe or Co) bonds and the T2g(1) Raman-active mode correspond to the translational motion of the FeO4 tetrahedron.17,30
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.30 The presence of other two active modes in the Raman spectra, i.e., A1(3) + B2(3), belongs to the P4122 space group. They appeared due to the lowering of the symmetry inside the crystals. Here, the octahedral (B) cubic symmetry of the Fd
m space group.30 The presence of other two active modes in the Raman spectra, i.e., A1(3) + B2(3), belongs to the P4122 space group. They appeared due to the lowering of the symmetry inside the crystals. Here, the octahedral (B) cubic symmetry of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group slightly turns into the tetragonal symmetry of the P4122 space group.17,30 The existence of vacancies due to maintaining the charge valency as well as doping of a relatively larger dopant in the host nanosized ZnFe2O4 matrix resulted in a lowering of the crystal symmetry, as validated by the recorded vibrational Raman spectra. In the case of the nanosized ferrite samples, line broadening of the Raman active modes was observed in their Raman spectra because of the lack of long-range atomic ordering and minute change in bond lengths. Broadening in the active modes was also noticed for our as-synthesized doped ferrite samples. In addition, the bond length, bond strength, size and atomic mass of dopants also determine the shifting in the Raman active modes and alteration of the crystal symmetry of the host system efficiently. Substitution of the comparatively large Co2+ dopant with a lower atomic mass than that of Zn2+ ions led to modified bonds, bond lengths, and their strengths, resulting in a change in the phonon numbers of the active modes for the doped ferrite samples.38
m space group slightly turns into the tetragonal symmetry of the P4122 space group.17,30 The existence of vacancies due to maintaining the charge valency as well as doping of a relatively larger dopant in the host nanosized ZnFe2O4 matrix resulted in a lowering of the crystal symmetry, as validated by the recorded vibrational Raman spectra. In the case of the nanosized ferrite samples, line broadening of the Raman active modes was observed in their Raman spectra because of the lack of long-range atomic ordering and minute change in bond lengths. Broadening in the active modes was also noticed for our as-synthesized doped ferrite samples. In addition, the bond length, bond strength, size and atomic mass of dopants also determine the shifting in the Raman active modes and alteration of the crystal symmetry of the host system efficiently. Substitution of the comparatively large Co2+ dopant with a lower atomic mass than that of Zn2+ ions led to modified bonds, bond lengths, and their strengths, resulting in a change in the phonon numbers of the active modes for the doped ferrite samples.38
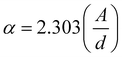 ; where ‘d’ specifies the width of the container holding the sample solution. In the Tauc plot, the value of the indirect optical gap (Eo) can be obtained by extrapolating a straight line along the slope of the curve that intercepts the hν axis. The indirect band gaps were found to be 1.55 ± 0.03 eV for all the nanoferrite samples. No significant difference in band gap was noticed with the incorporation of cobalt ions in the host nanosized zinc ferrites. These synthesized ferrite samples would be promising nanomaterials for a variety of optical applications because they showed an opaque behavior in the near-IR region of the electromagnetic spectrum.40,41
; where ‘d’ specifies the width of the container holding the sample solution. In the Tauc plot, the value of the indirect optical gap (Eo) can be obtained by extrapolating a straight line along the slope of the curve that intercepts the hν axis. The indirect band gaps were found to be 1.55 ± 0.03 eV for all the nanoferrite samples. No significant difference in band gap was noticed with the incorporation of cobalt ions in the host nanosized zinc ferrites. These synthesized ferrite samples would be promising nanomaterials for a variety of optical applications because they showed an opaque behavior in the near-IR region of the electromagnetic spectrum.40,41







 represents the beginning slope of the temperature vs. time graph [see Fig. 5(b)]. To compare the heating abilities among the as-synthesized ferrite samples, the parameter called intrinsic loss power (ILP) was used, as follows:6–10
represents the beginning slope of the temperature vs. time graph [see Fig. 5(b)]. To compare the heating abilities among the as-synthesized ferrite samples, the parameter called intrinsic loss power (ILP) was used, as follows:6–10




 represent the maximum value of the imaginary part of the dielectric modulus attained by the semicircles of the control and metribuzin-added samples, respectively. It was observed that the calculated values of S were significantly greater for the Co-50 (ZNF) nanoferrite compared with the pure ZnFe2O4 sample in detecting metribuzin of different concentrations at room temperature [see Fig. 7(c)]. Therefore, the nanocrystalline zinc ferrite doped with 50% Co ions was shown to be more sensitive to the presence of metribuzin. When metribuzin solution was added to both nanosized ferrite samples, the radius of the semicircles in the Cole–Cole plot decreased, indicating a decrease in the DC conductivity. This reflected that the metribuzin solution efficiently inhibited the DC conduction of charge carriers in the synthesized nanomaterials.63–65
represent the maximum value of the imaginary part of the dielectric modulus attained by the semicircles of the control and metribuzin-added samples, respectively. It was observed that the calculated values of S were significantly greater for the Co-50 (ZNF) nanoferrite compared with the pure ZnFe2O4 sample in detecting metribuzin of different concentrations at room temperature [see Fig. 7(c)]. Therefore, the nanocrystalline zinc ferrite doped with 50% Co ions was shown to be more sensitive to the presence of metribuzin. When metribuzin solution was added to both nanosized ferrite samples, the radius of the semicircles in the Cole–Cole plot decreased, indicating a decrease in the DC conductivity. This reflected that the metribuzin solution efficiently inhibited the DC conduction of charge carriers in the synthesized nanomaterials.63–65

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.




