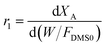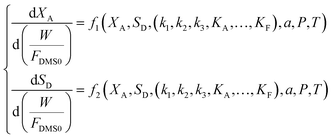Open Access Article
Open Access ArticleKinetic study on the hydrogenation of dimethyl succinate to γ-butyrolactone†
Chenghao Zhao‡
 a,
Chengzhe Du‡b,
Huixia Ma*a,
Rui Jianga,
Huanling Zhanga and
Feng Zhoua
a,
Chengzhe Du‡b,
Huixia Ma*a,
Rui Jianga,
Huanling Zhanga and
Feng Zhoua
aSINOPEC Dalian Research Institute of Petroleum and Petrochemicals Co., Ltd, Dalian 116100, China. E-mail: zhaochenghao.fshy@sinopec.com
bState Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China. E-mail: czdu@ipe.ac.cn
First published on 2nd May 2025
Abstract
The hydrogenation of dimethyl succinate (DMS) to γ-butyrolactone (GBL) is crucial in producing high-value chemicals for pharmaceuticals, agrochemicals, and battery electrolytes. This study utilized a self-developed copper-based catalyst and a micro-fixed bed reactor to systematically investigate the effects of temperature, pressure, and the hydrogen-to-ester ratio on reaction performance. An intrinsic kinetic model was developed based on experimental data, with reaction rate constants and activation energies determined through standard regression techniques. The model correlated well with observed data, providing insights into reaction kinetics. Validation against experimental data indicated fair agreement across various conditions. Sensitivity analysis confirmed the model's robustness, making it useful for process optimization. This kinetic analysis offers insights to enhance the efficiency and cost-effectiveness of industrial GBL production, aiming to improve overall process yield and efficiency.
1 Introduction
γ-Butyrolactone (GBL), also known as 1,4-butyrolactone, is an important chemical intermediate with wide-ranging applications in pharmaceuticals,1,2 solvents,3,4 battery production,5,6 and petrochemicals.7,8 Approximately 70% of GBL's production capacity is utilized for the synthesis of N-methylpyrrolidone (NMP),9 which serves as a key solvent in lithium battery manufacturing. With the rapid development of the new energy vehicle industry in China, the demand for NMP is expected to rise steadily in the future.Currently, the majority of GBL production is derived from the dehydrogenation of 1,4-butanediol (BDO), which is typically produced via the acetylene-based route.10 This method, using calcium carbide as a raw material, falls into the category of “high pollution, high energy consumption, and high carbon emissions”, indicating significant limitations for its future applications. In contrast, the phthalic anhydride esterification and hydrogenation route demonstrates lower emissions, allowing for the co-production of GBL and tetrahydrofuran (THF) alongside BDO.11 Additionally, China's phthalic anhydride production capacity has been continuously increasing, re-sulting in lower raw material costs, thereby presenting a promising application outlook for this route.
Dimethyl succinate (DMS), a product of the hydrogenation of the esterification product dimethyl maleate (DMM), can be further hydrogenated to selectively produce GBL. By modifying the catalyst composition and process conditions, it is possible to achieve either a high yield or a selective production of GBL. The employment of copper-based catalysts for the gas-phase hydrogenation of DMS offers mild operating conditions, a straightforward process, and favorable selectivity and yield.12–14 Many studies have shown that Cu(II)-based catalysts have the following advantages: low cost, environmentally friendly, high selectivity for the cleavage of C–O bonds, low activity for the cleavage of C–C bonds, and excellent activation capability for hydrogen molecules. These characteristics make Cu(II)-based catalysts widely applicable in catalytic reactions, especially in the fields of green chemistry and sustainable development.15–21
Numerous studies have been conducted on the reactors,22,23 catalysts,24,25 processes,26,27 and stability28 associated with the hydrogenation of DMM or DMS, as well as related reaction kinetics.29,30 For example, Chaudhari31 investigated the kinetics of the gas–solid phase reaction of diethyl maleate using a cuprous chromate catalyst, deriving rate constants and activation energies for different reactions within this network. Similarly, Zhang Qi32 examined the gas–solid phase reaction kinetics of diethyl succinate with a copper-based catalyst, obtaining relevant kinetic parameters. However, both studies utilized a power-law kinetic model and operated at pressures exceeding 2 MPa, during which multiple products, including GBL, BDO, THF, and n-butanol, were present.
In contrast, there has been limited intrinsic kinetic research on the selective or multiple production of GBL from DMS under low-pressure conditions. Therefore, this study employs a copper-based catalyst to conduct gas–solid phase catalytic reaction kinetics experiments while eliminating internal and external diffusion limitations. The aim is to elucidate the reaction mechanism for the hydrogenation of DMS to predominantly produce GBL and to derive the parameters for the corresponding hyperbolic intrinsic kinetic model, providing a reference for the reactor design for GBL production via DMS hydrogenation.
2 Materials and methods
2.1 Materials
Dimethyl succinate (DMS, 99%) was obtained from J&K Scientific Technology Co., Ltd; hydrogen gas (99.999%) was sourced from Dalian Special Gases Co., Ltd; methanol, γ-butyrolactone, 1,4-butanediol, and tetrahydrofuran, all of chromatographic purity, were purchased from Shanghai Macklin Biochemical Technology Co., Ltd.2.2 Catalyst
The metal composition of the catalyst consists of Cu, Zn, and Al, referred to as CuZnAl. The specific preparation steps can be found in the ESI.† Additionally, we conducted a systematic characterization of the catalyst, including the crystalline phase structure (Fig. S1†), textural properties (Fig. S2 and Table S1†), the form of copper present (Fig. S3†), reduction properties (Fig. S4†), and morphology (Fig. S5†). Detailed characterization results and analysis are available in the ESI.†2.3 Experimental setup and procedure
The schematic diagram of the micro fixed-bed hydrogenation apparatus used in the experiment is shown in Fig. 1.A fixed-bed reactor with an inner diameter of approximately 8 mm and a length of 120 mm was utilized in this study. The catalyst, after crushing and screening, was uniformly mixed with inert quartz sand and packed in the middle section of the reactor, maintaining a packing height of 50 mm, with inert quartz sand above and below. Hydrogen was introduced into the reactor from the upper end, controlled by a mass flow meter. The fixed bed was then heated to 240 °C according to a programmed schedule and maintained at this temperature for 6 hours to ensure complete activation of the catalyst. Dimethyl succinate (DMS) was delivered into the top of the reactor through a plunger pump along with hydrogen. After passing through a preheater, the DMS came into contact with the catalyst in the fixed bed for the reaction. The reaction pressure was maintained using a backpressure valve. The products were discharged to a constant pressure product tank after passing through a secondary condenser, while the off-gases were directed to the utility venting line.
2.4 Product analysis method
The analysis of reactants and products was conducted using an Agilent 8860 gas chromatograph equipped with a capillary column (50 m × 320 μm × 1.2 μm), featuring a stationary phase of 5% diphenyl-95% dimethyl polysiloxane. Quantitative analysis was performed using the area normalization method. The vaporization chamber temperature was set to 250 °C, and the detector temperature was maintained at 300 °C. The temperature programming for the column was as follows: initial temperature at 100 °C with a hold time of 5 minutes; heating rate of 10 °C min−1 to 160 °C with a hold time of 1 minute; followed by a heating rate of 10 °C min−1 to 280 °C with a hold time of 3 minutes.The calculation formulas for various evaluation indicators of catalyst activity are as follows:
In the expression, nDMS0 represents the number of moles of DMS in the feed; nDMS denotes the number of moles of DMS in the product; and ni indicates the number of moles of DMS converted into product i.
3 Kinetic model development and parameter fitting
3.1 Preliminary experiments
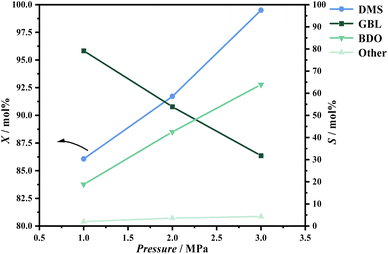
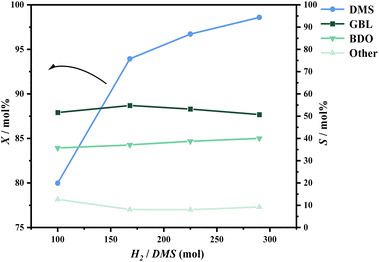
During the hydrogenation of DMS, reaction conditions such as pressure, temperature, and hydrogen-to-ester ratio significantly influence conversion rates and product distribution. To better define the range of experimental conditions for the hydrogenation of DMS to synthesize GBL, preliminary experiments were conducted to investigate the effects of these process parameters on the reaction.Regarding product distribution, as the temperature increased, the selectivity for GBL gradually rose while the selectivity for BDO decreased. This trend can be explained by the endothermic nature of the DMS hydrogenation to GBL and the exothermic reaction of GBL hydrogenation to BDO. The elevation in temperature favors the forward reaction of DMS hydrogenation, which aligns with previously published thermodynamic studies.33
3.2 Assumptions for kinetic pathways and model development
 | ||
| Fig. 5 Schematic representation of the DMS hydrogenation reaction network.((A) DMS; (B) C5H8O3; (C) methanol; (D) GBL; (E) C4H8O2; (F) BDO). | ||
Qin34 noted that most hydrogenation reactions involve the dissociative adsorption of hydrogen on active sites. Li35 also concluded in their kinetic analysis of dimethyl oxalate hydrogenation that hydrogen needs to adsorb dissociatively in order to react with the ester moiety. Consequently, we assume the existence of intermediate product B (C5H8O3) in the pathway from DMS to GBL, and intermediate product E (C4H8O2) in the pathway from GBL to BDO. This assumption aims to make the subsequent mechanistic derivation more aligned with reality and to avoid the occurrence of unreasonable reaction orders in elementary reactions.
 | (1) |
 | (2) |
Using the Langmuir–Hinshelwood (LH) model to describe the adsorption and desorption of reactants, products, and hydrogen, the reaction mechanism is subsequently proposed based on the Hougen–Watson (HW) model, in which hydrogen undergoes dissociative adsorption.36 The main reaction mechanism for the hydrogenation of DMS to GBL is outlined as follows:
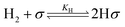 | (3) |
 | (4) |
 | (5) |
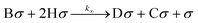 | (6) |
 | (7) |
 | (8) |
Since we did not detect products B and E in our preliminary experiments, we can assume that within the experimental conditions, the rate of the reaction of B to form GBL and MeOH is effectively infinite, indicating that B does not accumulate. Based on this assumption, the elementary reactions (5) and (6) can be considered irreversible processes.31
Similarly, the intermediate product E can be approached with the same approximation. The side reaction mechanism for the further hydrogenation of GBL to BDO is outlined as follows:
 | (9) |
 | (10) |
 | (11) |
Assuming that the surface reaction of DMS hydrogenation in step (5) is the rate-controlling step of the main reaction, the intrinsic rate equation can be expressed as follows:
 | (12) |
Similarly, the rate equation for the reversible hydrogenation of GBL in the side reaction can be expressed as:
 | (13) |
Assuming that the molar flow rate of dimethyl succinate (DMS) in the feed is FDMS0, and that the molar ratio of hydrogen to dimethyl succinate in the feed is a, the molar flow rates of each component Fi and the total molar flow rate FT can be determined based on the conversion of dimethyl succinate (XA) and the selectivity of γ-butyrolactone (SD). The expressions for these molar flow rates are as follows:
| FDMS = FDMS0·(1 − XA) |
| FH2 = FDMS0·[a − 2·XA − 2·(1 − SD)·XA] |
| FGBL = FDMS0·XA·SD |
| FBDO = FDMS0·XA·(1 − SD) |
| FMeOH = 2·FDMS0·XA |
The partial pressures of each component can be calculated using the formula  . For example:
. For example:
Similarly, the partial pressures of the other components can be determined. When considering factors such as temperature, pressure, and the hydrogen-to-ester ratio, the parameter estimation (fitting) problem for the resulting system of nonlinear ordinary differential equations can be expressed as follows:
 ;
;  .
.
| Number of catalyst mesh | W/FDMS0/(g h mol−1) | XA/mol% | SD/mol% |
|---|---|---|---|
| a Reaction conditions: temperature = 220 °C; pressure = 1 MPa; H2/DMS (mol) = 65. | |||
| 10–20 | 42.98 | 78.67 | 94.50 |
| 20–28 | 42.35 | 81.32 | 95.16 |
| 28–35 | 42.53 | 81.75 | 94.97 |
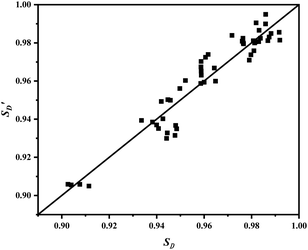
Based on the conclusions from preliminary experiments, we selected reaction temperatures ranging from 210 to 230 °C, pressures from 0.5 to 1.5 MPa, and a hydrogen-to-ester ratio of 40 to 65 for the kinetic experiments. The experimental data were fitted to the derived kinetic model, with the results shown in the figure below, where  and
and  represent the fitted curves.
represent the fitted curves.
At a reaction temperature of 210 °C, the conversion rate of DMS and the distribution of hydrogenation products followed the trends observed in the preliminary experiments. As pressure and the hydrogen-to-ester ratio increased, XA significantly increased, while SD appeared to increase with decreasing pressure. The hydrogen-to-ester ratio seemed to have a minimal impact on the distribution of GBL in the product (Fig. 7).
 | ||
| Fig. 7 Experimental and fitted values of DMS hydrogenation conversion and selectivity at 210 °C (left), 220 °C (middle) and 230 °C (right). | ||
At a reaction temperature of 220 °C and a pressure of 1.1 MPa, the results are similar to those observed at 210 °C; an increase in the hydrogen-to-ester ratio promotes the conversion of DMS, while it has minimal impact on the selectivity for GBL. However, when the hydrogen-to-ester ratio is held constant, a notable effect on conversion rate is observed at pressures below 1.1 MPa. At pressures above 1.1 MPa, the increase in conversion rate is not significant. The selectivity for GBL remains sensitive to changes in pressure, showing a marked increase as pressure decreases.
At a reaction temperature of 230 °C, the conversion rate of DMS and the distribution of products follow a trend similar to that observed at 210 °C. Tables S4–S6† present the experimental conditions and raw data results for chemical reaction kinetics.
The residual sum of squares between the model-calculated values of DMS conversion rate and GBL selectivity and the experimental values was used as the objective function. The fitting was performed using the SLSQP (Sequential Least Squares Programming) method from the Scipy library, applying the continuous least squares approach to estimate the reaction kinetic parameters.39 The reaction rate constants and adsorption equilibrium constants obtained from the fitting at different temperatures are presented in Table 2.
| T/K | 483.15 | 493.15 | 503.15 |
|---|---|---|---|
| k1/(mol g−1 h−1) | 0.6059 | 0.7965 | 1.0358 |
| k2/(mol g−1 h−1) | 0.0504 | 0.1341 | 0.3432 |
| k3/(mol g−1 h−1) | 19.3750 | 40.3571 | 81.6451 |
| KH × 10−2/MPa−0.5 | 2.4072 | 2.1368 | 1.9059 |
| KA × 10−2/MPa−1 | 32.8646 | 23.6396 | 17.2282 |
| KC × 10−2/MPa−1 | 17.3760 | 15.2191 | 13.4004 |
| KD × 10−2/MPa−1 | 6.9455 | 3.7633 | 2.0893 |
| KF × 10−2/MPa−1 | 0.6972 | 0.6553 | 0.6174 |
As shown in Table 2, the reaction rate constants k1, k2 and k3 increase with rising temperature, while the adsorption equilibrium constants KH, KA, KC, KD and KF decrease as the temperature increases. Among these, the rate constant for the dehydrogenation of BDO to GBL is the highest, whereas the rate constant for the hydrogenation of GBL to BDO is the lowest. The adsorption rate constants for DMS and methanol are relatively high, while the adsorption rate constants for GBL and BDO are notably low. This suggests that the adsorption of GBL and BDO on the catalyst is more challenging, allowing them to diffuse out of the solid catalyst's pores more easily, which makes them less likely to be converted to THF or n-butanol through deep hydrogenation, thus resulting in higher selectivity for GBL.
Based on the Arrhenius equation k = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Ea/(RT)], a linear regression of ln
exp[−Ea/(RT)], a linear regression of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k against T was performed to obtain the pre-exponential factor A and the apparent activation energy Ea, with the results presented in Table 3.
k against T was performed to obtain the pre-exponential factor A and the apparent activation energy Ea, with the results presented in Table 3.
| ki | A/(mol g−1 h−1) | Ea/(kJ mol−1) |
|---|---|---|
| k1 | 4.379 × 105 | 54.19 |
| k2 | 4.46 × 1019 | 193.74 |
| k3 | 1.02 × 1017 | 145.36 |
As indicated in Table 3, the activation energy for the hydrogenation of DMS to GBL is significantly lower than that for the further hydrogenation of GBL to BDO. This finding is consistent with the experimental results obtained in this study, suggesting that the hydrogenation of DMS occurs more readily. Under relatively high-temperature and low-pressure conditions, the selectivity for GBL remains above 90%. Additionally, the activation energy for the dehydrogenation of BDO to GBL is also lower than that for the hydrogenation of GBL to BDO. Therefore, it can be concluded that with a moderate increase in temperature, the reverse reaction of BDO dehydrogenation proceeds more easily, favoring the increased or selective production of GBL.
A significance test was conducted on the obtained model to assess its overall capability to represent the experimental data. Given that the kinetic model is nonlinear, statistical methods suitable for nonlinear models were employed for the validation,40 with the results presented in Table 4. It is generally accepted that a coefficient of determination R2 greater than 0.9 and a statistical F-value greater than 10F0.01 indicate a highly suitable model. The results in Table 4 demonstrate that the model is highly suitable and can effectively describe the kinetic characteristics of the DMS hydrogenation reaction.
| Index | R2 | F | F0.01(N,N-M-1) |
|---|---|---|---|
| XA | 0.9854 | 862.14 | 2.97 |
| SD | 0.9141 | 546.37 | 2.97 |
A significance test was conducted on the obtained model to assess its overall capability to represent the experimental data. Given that the kinetic model is nonlinear, statistical methods suitable for nonlinear models were employed for the validation,40 with the results presented in Table 4. It is generally accepted that a coefficient of determination R2 greater than 0.9 and a statistical F-value greater than 10F0.01 indicate a highly suitable model. The results in Table 4 demonstrate that the model is highly suitable and can effectively describe the kinetic characteristics of the DMS hydrogenation reaction.
4 Conclusions
In conclusion, this study provides a detailed kinetic analysis of the hydrogenation of dimethyl succinate (DMS) to γ-butyrolactone (GBL) using a copper-based catalyst. The intrinsic kinetic model developed offers significant insights into the reaction mechanisms and provides essential parameters for process optimization. The study identified the critical factors influencing DMS conversion and GBL selectivity, including temperature, pressure, and the hydrogen-to-ester ratio, which were systematically investigated to develop a reliable kinetic model. The developed model showed good agreement with experimental data, indicating its robustness and applicability for process design.The findings suggest optimal reaction conditions for maximizing GBL yield, providing practical guidelines for industrial-scale production. Future research should focus on broader catalyst ranges, multi-phase reaction environments, long-term stability, and advanced analytical methods to further validate and extend the kinetic model. Overall, this research contributes to the field of catalytic hydrogenation by offering a detailed kinetic understanding and practical insights for the efficient production of γ-butyrolactone (GBL). The derived kinetic parameters and model can serve as valuable references for designing and optimizing industrial reactors, ultimately enhancing the efficiency and cost-effectiveness of GBL production.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Chenghao Zhao: investigation, data curation, writing – original draft. Chengzhe Du: investigation, formal analysis. Huixia Ma: projecet administration, visualization. Rui Jiang and Huanling Zhang: methodology, validation. Feng Zhou: writing – review & editing, supervision, resources, conceptualization.Conflicts of interest
The authors have declared no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22078311) and China Petroleum & Chemical Corporation Enterprise Support Project (223051). The catalyst evaluation apparatus (dual channel catalyst fast evaluation apparatus EMC-1) was provided by the Oushisheng Company.Notes and references
- F. Vandescheur and L. H. Staal, Appl. Catal., A, 1994, 108, 63–83 CrossRef CAS.
- R. A. Kitson, A. Millemaggi and R. K. Taylor, Angew. Chem., Int. Ed., 2009, 48, 9426–9451 CrossRef CAS.
- J. Li, Y. Zhou, J. Tian, L. Peng and W. Chu, J. Mater. Chem. A, 2020, 8, 10386–10394 RSC.
- B. Liang, B. Li, R. Jin and T. Cheng, J. Shanghai Norm. Univ., Nat. Sci., 2021, 50, 629–635 Search PubMed.
- X. Cai, S. Zhang, Y. Fang, Q. Liu and W. Tan, Chem. Reagents, 2019, 41, 767–772 CAS.
- L. Yang and G. Song, Fine Spec. Chem., 2020, 28, 11–14 CAS.
- B. Huang, T. Wang, C. Lei, W. Chen, G. Zeng and F. Maran, J. Catal., 2016, 339, 14–20 CrossRef CAS.
- G. H. M. Rao and F. A. Khan, Synth. Commun., 2018, 48, 1–5 CrossRef.
- X. Cui, Technol. Econ. Petrochem., 2023, 39, 57–62 Search PubMed.
- B. Zhang, F. Bai, P. Shi and J. Gao, Refin. Chem. Ind., 2024, 35, 6–9 Search PubMed.
- J. Huang, C. Chen, C. Wei and C. Zhang, Chem. World, 2023, 64, 409–414 CAS.
- T. Li, T. Zhang, J. Huang, X. Zhang and H. Wang, Appl. Chem. Ind., 2023, 52, 2192–2197+2201 Search PubMed.
- T. Turek, D. L. Trimm, D. S. Black and N. W. Cant, Appl. Catal., A, 1994, 116, 137–150 CrossRef CAS.
- M. Mokhtar, C. Ohlinger, J. H. Schlander and T. Turek, Chem. Eng. Technol., 2001, 24, 423–426 CrossRef CAS.
- A. Dandekar and M. A. Vannice, J. Catal., 1998, 178, 621–639 CrossRef CAS.
- S. S. Acharyya, S. Ghosh and R. Bal, Chem. Commun., 2014, 50, 13311–13314 RSC.
- B. Sarkar, C. Pendem, L. N. S. Konathala, R. Tiwari, T. Sasaki and R. Bal, Chem. Commun., 2014, 50, 9707–9710 RSC.
- M. B. Gawande, A. Goswami, F. O. X. Felpin, T. Asefa, X. Huang, R. Silva, X. Zou, R. Zboril and R. S. Varma, Chem. Rev., 2016, 116, 3722–3811 CrossRef CAS.
- S. Jin, H. Byun and C. H. Lee, J. Catal., 2021, 400, 195–211 CrossRef CAS.
- G. Totarella, R. Beerthuis, N. Masoud, C. Louis, L. Delannoy and P. E. D. Jongh, J. Phys. Chem. C, 2021, 125, 366–375 CrossRef CAS.
- F. A. Rollier, V. Muravev, A. Parastaev, R. C. J. van de Poll, J. M. J. J. Heinrichs, B. Ligt, J. F. M. Simons, M. C. Figueiredo and E. J. M. Hensen, ACS Catal., 2024, 14, 13246–13259 CrossRef CAS PubMed.
- T. Dong, B. Wang, P. Zhou, Y. Wang, J. Guo and X. Han, Chem. Eng. Equip., 2024, 5, 33–35+49 Search PubMed.
- M. Bradac, J. Dudas, M. Kotora and J. Markos, Chem. Zvesti, 2014, 68, 1667–1677 Search PubMed.
- A. L. Figueredo, C. S. Costa, M. L. Gothe, L. M. Rossi, R. C. Bazito, P. Vidinha and C. G. Pereira, Catal. Lett., 2021, 151, 1821–1833 CrossRef CAS.
- H. Wang, G. Gao and Z. Du, Spec. Petrochem., 2017, 34, 36–39 Search PubMed.
- Y. Li, Chem. Ind., 2022, 40, 43–52 Search PubMed.
- X.-Q. Han, Q.-F. Zhang, F. Feng, C.-S. Lu, L. Ma and X.-N. Li, Chin. Chem. Lett., 2015, 26, 1150–1154 CrossRef CAS.
- W. Lei, A. Nuermaimaiti, M. Yubo, Q. Shaojun, G. Zhixian and E. Wumanjiang, React. Kinet. Mech. Catal., 2014, 112, 117–129 CrossRef.
- G. Ding, Y. Zhu, H. Zheng, W. Zhang and Y. Li, Catal. Commun., 2010, 11, 1120–1124 CrossRef CAS.
- M. A. Kohler, M. S. Wainwright, D. L. Trimm and N. W. W. Cant, Ind. Eng. Chem. Res., 1987, 26, 652–656 CrossRef CAS.
- R. V. Chaudhari, R. Jaganathan, S. H. Vaidya, S. T. Chaudhari and C. V. Rode, Chem. Eng. Sci., 1999, 54, 3643–3651 CrossRef CAS.
- Q. Zhang and Z. Wu, Chin. J. Catal., 1991, 12, 346–352 CAS.
- W. Liu, L. Wu and Z. Zhao, Shanghai Chem. Ind., 2007, 32, 12–16 CAS.
- R. Qin, L. Zhou, P. Liu, Y. Gong and N. Zheng, Nat. Catal., 2020, 3, 1–7 CrossRef.
- S. Li, Y. Wang, J. Zhang, S. Wang and X. Ma, Ind. Eng. Chem. Res., 2015, 54, 1243–1250 CrossRef CAS.
- I. B. Ju, W. Jeon, M. J. Park, Y. W. Suh, D. J. Suh and C. H. Lee, Appl. Catal., A, 2010, 387, 100–106 CrossRef CAS.
- C. Perego and S. Peratello, Catal. Today, 1999, 52, 133–145 CrossRef CAS.
- S. A. Shankha, G. Shilpi, T. Ritesh, P. Chandrashekar and S. Takehiko, ACS Catal., 2015, 5, 2850–2858 CrossRef.
- J. Xue, M. Cui, J. Tang, X. Chen and X. Qiao, Chem. React. Eng. Technol., 2010, 26, 296–302 CAS.
- T. Su, X. Zhou, Z. Qin and H. Ji, Chemphyschem, 2017, 18, 299–309 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01226k |
| ‡ Co-first authors. |
| This journal is © The Royal Society of Chemistry 2025 |