Open Access Article
Open Access ArticleHigh sensitivity terahertz metamaterial sensor for trace pesticide detection†
Fardin Ahmed‡
,
Md Ayenul Azim‡ and
Ahmed Zubair *
*
Department of Electrical and Electronic Engineering, Bangladesh University of Engineering and Technology, Dhaka 1205, Bangladesh. E-mail: ahmedzubair@eee.buet.ac.bd
First published on 18th June 2025
Abstract
Pesticides play a vital role in agriculture by protecting crops from pests and diseases and ensuring high yields. However, improper use poses severe risks to human health and the environment, emphasizing the need for the precise detection of pesticide residues. Methods like chromatography and biosensors are commonly used, but each has limitations in stability, selectivity, or applicability. THz metamaterial (MM) sensors offer high sensitivity through changes in spectral response, making them a promising alternative to address many of these challenges. They enable the identification of specific pesticide molecules at extremely low concentrations through resonance frequency shifts. By incorporating innovative design features, these sensors can detect trace pesticide residues with ease, affordability, and rapid response. In this work, we designed an MM sensor with near-perfect absorption at its resonance frequency. The high absorption of 99.43% resulted from impedance matching with the free space. The MM demonstrated an impressive figure of merit, highlighting its effectiveness as a sensing device. This approach has significant potential for food safety and environmental monitoring applications, providing efficient and reliable detection solutions.
1 Introduction
Pesticide use is necessary in agriculture to limit crop damage caused by pests, weeds, and diseases, ensuring high yield and food production.1 Although pesticides are intended to be safe to organisms other than selected pests, they impose a serious threat to the environment and human health.2,3 Improper or excessive pesticide use can lead to poisonous residues on food, which is estimated to be up to five times greater than exposure from other sources, such as air and drinking water.4–6 Pesticide exposure causes diseases such as cancer, Alzheimer's, Parkinson's, and asthma.7,8 As pesticides pose health concerns, there is a maximum residue limit (MRL) on the amount of pesticide residue allowed in food and agricultural products.9 Hence, highly sensitive pesticide detection is essential for ensuring compliance with the MRL standards.Imidacloprid (IMD), carbofuran (CRF), N,N-diethyldithiocarbamate sodium salt trihydrate (DEDT), and N,N-dimethyldithiocarbamate sodium salt hydrate (DMDT) are some of the commonly used pesticides in agricultural practices for the management of insect and fungal pests across diverse crops. IMD is a neonicotinoid, which is used to protect crops such as rice and corn. However, it has raised concerns about its harmful effects on pollinators, particularly bees.10 CRF, a carbamate pesticide, effectively targets soil-dwelling pests, but it presents acute toxicity risks to birds and mammals.11 DMDT and DEDT are commonly employed as fungicides on fruits and vegetables, they exhibit environmental persistence and pose potential human health risks, including neurological effects from extended exposure.12 The presence of these pesticides highlights the necessity for precise detection methods to monitor residue levels and ensure safety accurately.
Numerous methods have been developed for detecting pesticide residues, each with unique advantages and disadvantages. Common separation techniques such as high-performance liquid chromatography (HPLC), gas chromatography (GC), and thin-layer chromatography (TLC) are frequently used to detect trace amounts of pesticides. Among these, gas chromatography-mass spectrometry (GC-MS) and high-performance liquid chromatography ultraviolet/visible spectrometry (HPLC-UV/VIS) are the most prevalent, offering relatively low detection limits and high selectivity when paired with specific detectors.13–17 Enzymatic biosensors have also emerged as popular analytical tools for pesticide detection due to their sensitivity and practicality. However, they face challenges such as low enzyme storage stability, susceptibility to inhibitors, and limited selectivity.18,19 Furthermore, while fluorescence-based methods have various advantages, their application is restricted, as only a few pesticides exhibit strong fluorescence, limiting the effectiveness of these techniques.20 In recent years, advanced techniques like terahertz metamaterial (THz MM) sensors have demonstrated significant potential in sensing applications.
Metamaterials (MMs) are periodically arranged metallic structures whose geometry is at scales smaller than the phenomenon wavelength being influenced. It is possible to regulate the effective permittivity and permeability of the material by engineering the structure of an MM, giving rise to extraordinary properties such as negative refraction, invisible cloaking, superlensing and highly sensitive sensing.21–25 Meanwhile, terahertz technology utilizes the electromagnetic spectrum between microwave and infrared, which ranges from 0.1 to 10 THz. Terahertz waves are extensively studied for their unique characteristics. The terahertz wave, with its low photon energy ranging from 4 to 40 meV, is inherently non-invasive, non-ionizing, and safe for analyzing biological substances. Additionally, its ability to penetrate non-metallic and non-ionizing materials makes it ideal for non-destructive detection and analysis.26,27 Many molecules have characteristic rotational and vibrational modes in the terahertz frequency range, which provides unique spectral fingerprints; making it possible to detect compounds such as amino acids, organisms, melamines, illicit drugs, and pesticides.28–33 By integrating MMs with terahertz detection, we can enhance the sample–wave interaction. This makes THz MM an effective tool for highly sensitive detection. THz MMs have gained attention due to their diverse applications. Research in THz MM sensing has advanced notably in areas such as molecular sensing, biosensing, and microfluidic sensing.34–37
In this paper, we proposed and analyzed a novel MM-based sensor for trace amount pesticide detection operating in the terahertz region. The metastructure consisted of a silicon dioxide dielectric substrate, silver metal wire arrays, and an aluminum backplane. The designed metastructure exhibited near-perfect absorption at the resonant frequency. The high absorbance occurred due to the impedance matching between the MM structure and the surrounding medium. Different key electromagnetic properties in its resonance frequency, such as permittivity, permeability, electric field, magnetic field, and surface current, were analyzed. The MM demonstrated a high Q-factor and exceptional sensitivity, enabling the precise detection of trace amounts of pesticides in wheat flour. These characteristics highlight its potential for real-world pesticide detection and food safety monitoring applications.
2 Design and methodology
The proposed MM structure, shown in Fig. 1, features two circular ring resonators with different radii created on top of a substrate. The outer circular ring was split into two parts and two metal wires couple the rings. The metasurface was intentionally designed with a double split-ring resonator structure to achieve strong localized LC resonances in the THz regime, which are highly sensitive to the dielectric properties of nearby analyte materials. The concentric ring geometry enhances electric field confinement, while the split gaps act as tunable capacitive elements that respond to variations in the surrounding permittivity. The optimal design parameters and their dimensions are listed in Table 1.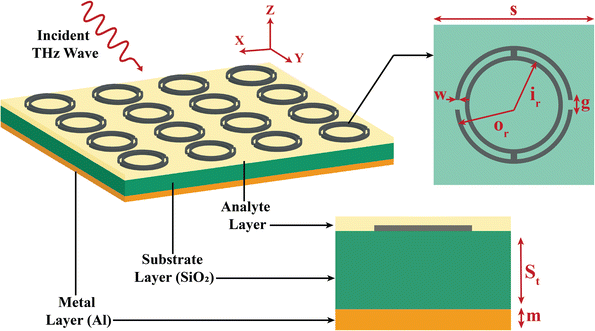 | ||
| Fig. 1 Schematic diagram of the THz MM sensor-based pesticide detection system, including the unit cell structure and cross-section. | ||
| Parameter | Description | Material | Measurement (μm) |
|---|---|---|---|
| m | The thickness of metal layer at the bottom | Al | 2 |
| St | The thickness of substrate layer | SiO2 | 4 |
| t | The thickness of metastructure | Ag | 0.22 |
| s | Periodicity of unit cell | — | 84 |
| or | Outer circle radius of metastructure | — | 28 |
| ir | Inner circle radius of metastructure | — | 14 |
| g | Split gap width of metastructure | — | 1.5 |
| w | Strip width of metastructure | — | 2 |
The structure was made of silver, which has a conductivity of 6.3 × 107 S m−1. The design was implemented on a SiO2 substrate with a relative dielectric constant (εr) of 3.8. The bottom layer consisted of an aluminum plate chosen for its electrical conductivity of 3.56 × 107 S m−1 and relative permeability (μr) of 1. The skin depth of the electromagnetic wave, an important parameter, can be calculated using eqn (1).38
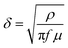 | (1) |
At 0.2 THz, skin depth (δ) is 0.0002 μm. The aluminum backplane had a thickness of 2 μm, which was adequate to block the transmission of the incident wave, as shown in the ESI.† We selected silver for the top layer and aluminum for the bottom layer because their complementing features improve the ability of the MM absorber for sensitive pesticide detection. Silver's high electrical conductivity intensifies the electromagnetic interactions at the surface, hence enhancing the potential for detecting residual pesticides. In addition, aluminum provides excellent conductivity, high reflection, and resistance to oxidation, enhancing the robustness and cost efficiency of the absorber.39
The proposed structure's electromagnetic characteristics, absorption performance, and pesticide sensitivity were analyzed using the CST microwave studio electromagnetic simulator. Each design material's physical properties and parameters were sourced from the materials library of the simulation software (CST). Different amounts of pesticide residue in wheat flour were considered for the analyte layer. The refractive index and absorption characteristics of the pesticides in the terahertz region were collected from.40,41 The optical properties of the pesticide and wheat flour mixture were determined using Maxwell–Garnett effective medium theory,42
 | (2) |
3 Results and discussions
3.1 Absorption analysis
The absorber successively absorbs the electromagnetic (EM) wave according to antireflection criteria. Both magnetic and electric resonances are independently stimulated, potentially confining the wave within the perfect metamaterial absorber (PMA) cell. The wave can then be absorbed by dielectric loss. When the magnetic permittivity is equal to the electric permittivity, it results in complete absorption for incident electromagnetic waves. Absorptivity is defined as,| A(f) = 1 − T(f) − R(f) = 1 − |S21|2 − |S11|2, | (3) |
| A(f) = 1 − |S11|2. | (4) |
When the resonator on the top plane is properly designed, the impedance of the top plane matches that of the free space, ensuring minimum reflection. Fig. 2 shows the absorption, reflection, and transmission spectra of the proposed structure between 1 THz and 2.5 THz.
Observing the simulation results, we found that the structure achieved a narrow absorption peak at 1.8445 THz, and the absorption rate reached 99.43%. The Q-factor was obtained by,
 | (5) |
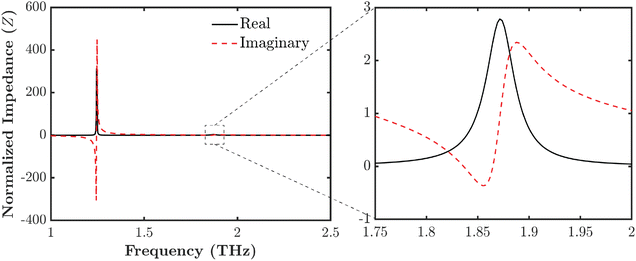
To function as an absorber, the characteristic impedance of an MM must align with the normalized impedance of air; a mismatch of impedance will result in reflection, as indicated by eqn (7). The effective impedance of the absorber can be computed from the S parameters using eqn (6),
 | (6) |
The reflection of PMA at normal incidence is given by,43,44
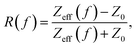 | (7) |
 | (8) |
In a material with thickness d and wave number k0 = 2πf/c, where c is the speed of light and f is the frequency of a microwave signal, permittivity and permeability can be defined as follows.45
 | (9) |
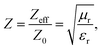 | (10) |
The effective relative permeability and permittivity of the metamaterial are shown in Fig. 4. At the resonant frequency, the effective relative permeability is 22.935 + 37.418 j, and the effective relative permittivity is −1.254 + 42.081 j. As both magnitudes are very close, impedance matching occurs. The large imaginary parts in the complex permittivity and permeability show significant losses of electricity and magnetism. These losses cause electromagnetic energy to spread out, which gives the material its high absorbing properties.47 The negative real part of the complex permittivity at the resonance point suggests that the MM exhibits left-handed or negative index material behavior. This property is crucial for phenomena such as negative refraction, which enhances the absorption performance of the material.48
 | ||
| Fig. 4 The relative permittivity and permeability of the unit cell (a) complex permittivity, (b) complex permeability. | ||
3.2 Surface current, electric field and magnetic field analysis
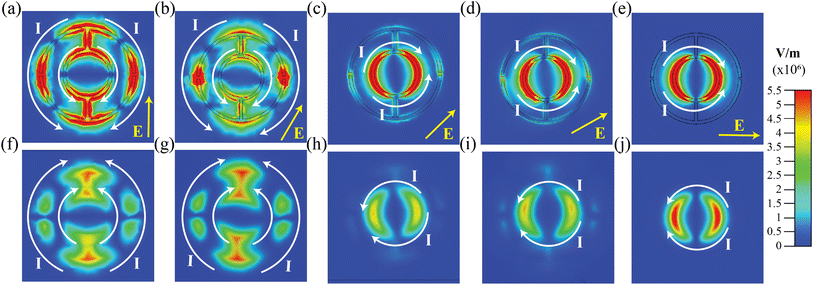
To better understand the mechanism underlying the observed complete absorption, the distributions of the electric field, surface current, and magnetic field within the unit cell structure at the resonant frequencies are presented in Fig. 5. Maxwell's equations determined the electric, magnetic, and surface current distribution within the engineered unit cell, revealing significant resonance behavior. The resonance phenomenon occurs when electric charges oscillate, causing changes in the electric field on both the front and back sides of the PMA, thereby inducing a magnetic field. At the resonant frequency of f = 1.8445 THz, the distribution of the electric field is primarily localized in the upper and lower sections of the structure and at the split gaps, as illustrated in Fig. 5(a). The induced charges are localized at the split gap on the outer circular ring. The split gap functions as a capacitor, storing electric energy when the electric field develops from the potential difference across the gap.Fig. 5(e–f) displays the current distributions on the surfaces of the top and bottom layers, respectively. The current direction on the left side of the structure mirrors that on the right side. Both surface currents parallel the excited electric field, resembling electric dipole resonance. The electric field distribution on the metal backplane demonstrates the induced poles. The electric dipole on the PMA induces an oppositely directed dipole on the metal backplane. This backplane dipole generates an anti-parallel current on the PMA, as shown in Fig. 5(f). The electromagnetic field irradiated by this image dipole undergoes multiple reflections inside the cavity formed by the PMA and backplane.
Moreover, the electric field distribution is relatively low throughout the resonator arms but significantly higher across the split gap, the upper and lower sections of the resonator. The current flow and electric field distributions strongly impact the magnetic characteristics of the MM resonator. When front and back side currents flow in opposing directions, they cause the magnetic flux to interact with the incoming magnetic field, inducing a parallel current that generates magnetic resonance. The magnetic field distribution around the split gap and connector dramatically diminished; this can be attributed to the comparatively large electric field at those locations. The surface currents were diminished in this region as these portions function more as capacitors than conductors, emphasizing energy storage as potential differences rather than enabling sustained current flow. The robust interrelation between electric and magnetic fields, demonstrated by their complementary distribution, signifies impedance matching. This resulted in negligible reflection of the incident wave and optimal absorption. The symmetry of the currents further substantiates that the structure was calibrated to resonate at particular frequencies, resulting in effective absorption. In contrast, no significant electromagnetic behavior was observed at a non-resonant frequency, further explained in the ESI.†
3.3 Dependency on polarization and incident angles
The angle between the x direction and the electric field vector is denoted by the polarization angle (ϕ). The angle formed between the propagation direction and the z direction is known as the angle of incidence (θ). Terahertz waves were incident on the sensor along the negative z direction. Up to a 45° polarization angle, the MM absorber demonstrated polarization insensitivity. The absorber exhibited a steady resonant mode with no discernible change in resonance frequency or amplitude for polarization angles ranging from 0° to 45°, suggesting strong polarization-independent absorption within this range. This behavior can be explained by the structure's half-symmetry, which ensures the same resonant mode is excited irrespective of the polarization direction within this angular range. Fig. 6(a) shows the absorption characteristics at different polarization angles (ϕ).However, a new resonant mode in addition to the original resonance began to arise when the polarization angle increased over 45°. This transition to a higher frequency suggested that the MM's interaction with the incident electromagnetic wave started to be dominated by a new geometric characteristic. The sudden change observed around the polarization angle of 45° arises from the structural asymmetry of the resonator along the x and y directions. Although the geometry may appear visually symmetric, it lacks true symmetry, leading to different interactions between the resonator and the incident electric field at different polarization angles. When the polarization is at 0°, the fields are concentrated along the horizontal arms, while at 90°, the field pattern shifts, indicating the excitation of a different resonant mode. This difference in field distribution results in distinct resonant frequencies for each polarization, and the abrupt transition near 45° is a consequence of this anisotropic behavior, where the response begins to shift between the two modes. We can examine the surface current and electric field in the metal backplane and metastructure surface, shown in Fig. 7 for better understanding. These results were consistent with the previous report.49
Fig. 6(b) shows the characteristics of the reflection coefficient at different oblique incidences (θ). The insensitivity of the MM absorber to incident angles makes it highly beneficial for many practical applications. This property enabled the absorber to operate efficiently without requiring exact control of the incident wave's angle, making it suitable for applications like stealth technology, broadband sensors, radar systems, and electromagnetic interference shielding. This angle insensitivity has practical applications, in which it is not possible to alter the orientation of incoming electromagnetic waves.
3.4 Impact of structural parameter analysis
The absorption behavior of the resonator structure was thoroughly investigated by varying key structural parameters. As shown in Fig. 8, changes in the split gap (g), inner circle radius (ir), and thickness (t) significantly affected the resonance frequencies and absorption coefficients. When the gap size (g) increased, a blue-shift in the resonance frequency was observed, which was attributed to a decrease in capacitance, resulting in higher resonance frequencies. Decreasing gap size increased capacitance, resulting in a red-shift that raised resonance to higher frequencies. Similarly, as the inner radius (ir) varies, resonance shifts occurred because of changes in the inductance and capacitance of the metallic stripes. Additionally, the thickness of the resonator (t) affected absorption. Overall, the study revealed that structural variations can lead to blue- or red-shifts in the resonance frequencies depending on how the capacitance and inductance were altered, and an optimal combination of these parameters was necessary to achieve high absorption performance. | ||
| Fig. 8 Absorption for different (a) split gap, (b) radius of inner circle, and (c) thickness of the MM structure. | ||
3.5 Equivalent circuit model of the sensor
The equivalent circuit model and its simulated reflection coefficient spectra are presented in Fig. 9. The lumped circuit comprised inductors and capacitors derived from the physical structure of the MM. Specifically, the inductor L1 and capacitor C1 in series arose from the silver metal wire and the split in the outer circular ring. The capacitor C2 represented the capacitance between the two concentric circles, while the inductor L2 represented the inner metallic ring. The simulated reflection coefficient (S11) spectra obtained using the Advance Design System (red dashed line) closely match with the simulation results of the CST software (black solid line). This agreement validates the accuracy of the equivalent circuit model in representing the electromagnetic behavior of the MM absorber structure. The polarization angle affects the resonant wavelength by modifying the effective capacitance in the structure. As shown in Fig. 7(c), at a polarization angle of 90°, the electric field intensity at the outer ring's split gap is significantly reduced, indicating a decrease in the overall capacitance. This reduction in effective capacitance leads to a shift in the resonance toward a higher frequency. The analytical calculation of the equivalent circuit model is further detailed in the ESI.† | ||
| Fig. 9 (a) Equivalent circuit design of PMA, (b) reflection coefficient spectra calculated by Advance Design System and simulated by CST software. | ||
3.6 Sensing performance of the terahertz PMA
The THz MM's sensing mechanism is based on the idea that variations in the surrounding permittivity, brought on by analytes with varying refractive indices, will cause resonance frequencies in the relevant transmission spectrum to fluctuate. The refractive index sensitivity (S), the figure of merit (FOM), and the Q-factor are often the three most important metrics to evaluate the sensing capability of a sensor.The refractive index sensitivity is defined as,
 | (11) |
For comparing the sensing characteristics in different frequency regions, the parameter FOM can be introduced as follows,
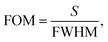 | (12) |
As the refractive index varied, the effective capacitance of the terahertz metasurface sensor varied. The effective capacitance (Ceff) of a sensor is determined by the capacitance of the device (Cres) and the capacitance generated by the addition of the analyte layer (Canalyte).50
 | (13) |
Once the structural properties of the sensor are known, the device's capacitance remains constant. Consequently, changes in the refractive index of the analyte will influence the value of the sensor, thereby altering the resonance characteristics such as resonance frequency and transmission spectra. Since permittivity (ε) is proportional to the refractive index (n), Canalyte increases with the ambient permittivity; thus, the refractive index of the analyte grows as ε = n2. An increase in the refractive index of the tested materials correlates with a notable rise in red-shift, indicating enhanced sensor sensitivity.
The sensing performance of the proposed THz MM sensor was evaluated by varying the refractive index of the analyte layer from 1.0 to 1.25, in increments of 0.05. The analyte thickness was strategically chosen to ensure significant interaction between the terahertz waves and the MM structure. For numerical analysis, a 2 μm thick analyte layer was applied to the top of the MM sensor. Fig. 10(a) displays a red-shift in the resonant peaks as the RI increases. Fig. 10(b), demonstrates a linear relationship between the resonant frequency shift and the RI variations of the analyte layer. The slope of the fitting curves indicates the RI sensitivity of the sensor at the current resonance frequency, which is 208 GHz/RIU, whereas the R2 score was 0.9925.
We used eqn (12) and (5) to calculate the FOM and Q-factor of the designed sensor to obtain a numerical account of its sensing performance. It was found that S is 208 GHz/RIU, FOM was 2.533 RIU−1, and the Q-factor was 22.46.
3.7 Proposed PMA for pesticide detection
We evaluated the sensor's pesticide detection performance by analyzing the absorption characteristics of the metastructure when coated with wheat flour mixtures containing four different pesticides (IMD, CRF, DEDT, and DMDT). For each pesticide, mixtures were prepared with concentrations of 0.1, 0.2, 0.5, and 1 ng per unit cell and deposited uniformly on the MM surface as an analyte layer with a thickness of 2 μm. This layer alters the local dielectric environment of the resonator, changing its effective permittivity and thereby shifting its resonance frequency. As shown in Fig. 11, increasing pesticide concentration resulted in a systematic redshift of the resonance, enabling quantitative detection. In practice, this mechanism can be employed using terahertz time-domain spectroscopy to measure absorption spectra and correlate frequency shifts with pesticide concentration. | ||
| Fig. 11 Absorption spectra for different amounts of (a) IMD, (b) CRF, (c) DEDT, and (d) DMDT per unit cell in wheat flour. | ||
Table 2 summarizes the resonance shifts observed for different amounts of pesticide per unit cell, highlighting that IMD and CRF produce smaller resonance shifts than DEDT and DMDT. This difference in resonance behavior can be attributed to the refractive indices of the pesticides. DEDT and DMDT have higher refractive indices than IMD and CRF. When DEDT or DMDT is introduced at the same concentration as IMD and CRF in wheat flour, their higher refractive indices cause a more substantial change in the overall refractive index of the analyte layer on top of the metasurface. This results in a more pronounced red-shift in the resonance frequency. This characteristic indicates that the sensor was highly responsive to changes in the refractive index of the analyte layer. The method for detecting specific pesticides in wheat flour using resonance and absorbance shifts is described in detail in the ESI.†
| Pesticide type | Resonance red-shift (GHz) | |||
|---|---|---|---|---|
| 0.1 ng | 0.2 ng | 0.5 ng | 1 ng | |
| IMD | 0.3 | 3.0 | 9.1 | 18.8 |
| CRF | 1.2 | 3.5 | 8.3 | 21.3 |
| DEDT | 4.6 | 8.9 | 25.6 | 41.6 |
| DMDT | 3.8 | 7.4 | 21.5 | 32.6 |
Table 3 shows that our THz MM sensor achieves a low detection limit of 0.1 ng and a sensitivity of 208 GHz/RIU at a resonant frequency of 1.85 THz within the 0.2–2.5 THz band. These results highlight the sensor's high sensitivity and suitability for detecting trace pesticide residues, making it ideal for applications in food safety, environmental monitoring, and agricultural quality control.
| Pesticide type | Band (THz) | Resonance (THz) | Sensitivity (THz/RIU) | Limit of detection | Reference |
|---|---|---|---|---|---|
| Phosalone | 0.3–0.8 | 0.574 | — | 0.01 μg mL−1 | 51 |
| Chlorpyrifos | 0.2–2.5 | 0.5, 1.1, 1.7, 2.1 | — | — | 52 |
| Indole-3-acetic acid and tricyclazole | 0.5–1.8 | 0.918, 1.575 | — | 10 ng L−1 | 53 |
| Chlorpyrifos–methyl | 0.2–1.4 | 0.37, 1.13 | 0.09, 0.28 | — | 54 |
| IMD | 0.4–1.2 | 0.88 | 0.22 | 0.0112 mg mL−1 | 55 |
| IMD, CRF, DEDT, and DMDT | 0.2–2.5 | 1.85 | 0.208 | 0.1 ng | This work |
3.8 Proposed fabrication technique
The fabrication of the structure may begin with the preparation of a clean silicon dioxide (SiO2) substrate of 9 μ m−1 thickness using deionized water and anhydrous ethanol, respectively. In the back of the substrate, aluminum can be deposited at room temperature using DC magnetron sputtering at low pressure.56 The sputtering chamber has to be vacuum-pumped for the silver pattern on top to achieve a low base pressure. Then, high-purity argon gas will act as the sputtering medium to remove residual air. Silver films can be deposited onto pre-cleaned glass substrates using a room-temperature radio frequency magnetron sputtering system. Periodic patterns can be created using a laser-localized removal process.574 Conclusion
We designed a unique THz MM sensor composed of silicon dioxide as the substrate, a silver structure array as the metasurface layer, and an aluminum backplane. The structure was analyzed using a finite integration technique. It exhibited a high absorption of 99.43% in the 1.844 THz resonant frequency. The high absorption characteristics were attained by impedance matching. The metastructure demonstrated a sensitivity of 208 GHz/RIU, a Q-factor of 22.46, and a FOM of 2.533 RIU−1, which denotes its capability in sensing applications. It detected 0.1 ng of traces of four different pesticides, such as IMD, CRF, DEDT, and DMDT, in wheat flour. As the pesticide content increases in the wheat flour sample, the resonance frequency undergoes a red-shift, and the absorption peak decreases proportionally. Hence, this THz MM sensor has potential applications in food safety, agricultural quality control, environmental pollution monitoring, and health safety.Data availability
Data for this article are available at GitHub at https://github.com/ahmedzubair003/Trace-Pesticide-Detection.git.Author contributions
Fardin Ahmed: conceptualization, formal analysis, methodology, visualization, software, investigation, writing – original draft, and writing – review & editing. Md Ayenul Azim: conceptualization, formal analysis, methodology, visualization, software, investigation, writing – original draft, and writing – review & editing. Ahmed Zubair: supervision, conceptualization, methodology, visualization, project administration, resources, writing – original draft, and writing – review & editing.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
M. A. A. and F. A. acknowledge the Nanoscale Simulation, Characterization and Fabrication Lab, Department of EEE, BUET, supervised by A. Z., for this work. All the authors thank the Department of EEE, BUET for providing the necessary support. M. A. A. and F. A. acknowledge the funding from the Research and Innovation Centre for Science and Engineering (RISE), BUET.Notes and references
- W. Zhang, Proceedings of the International Academy of Ecology and, Environ. Sci., 2018, 8, 1 Search PubMed.
- I. Mahmood, S. R. Imadi, K. Shazadi, A. Gul and K. R. Hakeem, Plant, soil and microbes: volume 1: implications in crop science, 2016, pp. 253–269 Search PubMed.
- M. H. Hashimi, R. Hashimi and Q. Ryan, Asian Plant Res. J., 2020, 5, 37–47 CrossRef.
- P. Nicolopoulou-Stamati, S. Maipas, C. Kotampasi, P. Stamatis and L. Hens, Front. Public Health, 2016, 4, 148 Search PubMed.
- W. L. Claeys, J.-F. Schmit, C. Bragard, G. Maghuin-Rogister, L. Pussemier and B. Schiffers, Food control, 2011, 22, 508–516 CrossRef.
- Z. Knežević, M. Serdar and M. Ahel, Food Control, 2012, 23, 59–65 CrossRef.
- A. Blair, B. Ritz, C. Wesseling and L. B. Freeman, Occup. Environ. Med., 2015, 72, 81–82 CrossRef PubMed.
- M. Eddleston, L. Karalliedde, N. Buckley, R. Fernando, G. Hutchinson, G. Isbister, F. Konradsen, D. Murray, J. C. Piola and N. Senanayake, et al., Lancet, 2002, 360, 1163–1167 CrossRef PubMed.
- A. Fothergill and A. Abdelghani, WIT Transactions on Ecology and the Environment, 2013, vol. 170, pp. 195–205 Search PubMed.
- Q. Zhang, S. Li, X. Zhang, L. Wang, X. Shi, X. Zhao and X. Wang, Environ. Sci. Pollut. Res., 2018, 25, 3110–3121 Search PubMed.
- P. Mineau and C. Palmer, Environ. Sci. Policy, 2013, 26, 1349–1355 Search PubMed.
- E. D. Caldas, M. C. Miranda, M. H. Conceicao and L. C. De Souza, Food Chem. Toxicol., 2004, 42, 1877–1883 CrossRef CAS PubMed.
- M. Michel and B. Buszewski, J. Liq. Chromatogr. Relat. Technol., 2002, 25, 2293–2306 CrossRef CAS.
- M. Domotorova and E. Matisova, J. Chromatogr. A, 2008, 1207, 1–16 CrossRef PubMed.
- M. F. Kovacs Jr, J. Assoc. Off. Agric. Chem., 1963, 46, 884–893 Search PubMed.
- M. A. Z. Chowdhury, A. Fakhruddin, M. N. Islam, M. Moniruzzaman, S. H. Gan and M. K. Alam, Food control, 2013, 34, 457–465 CrossRef.
- U. S. Handajani, Y. Raharjo and B. Wantoro, J. Chem. Technol. Metall., 2017, 52, 1056–1061 Search PubMed.
- M. Trojanowicz, Electroanalysis, 2002, 14, 1311–1328 CrossRef CAS.
- B. Bucur, F.-D. Munteanu, J.-L. Marty and A. Vasilescu, Biosensors, 2018, 8, 27 CrossRef PubMed.
- A. Coly and J.-J. Aaron, Anal. Chim. Acta, 1998, 360, 129–141 Search PubMed.
- R. A. Shelby, D. R. Smith and S. Schultz, science, 2001, 292, 77–79 CrossRef CAS PubMed.
- D. Schurig, J. J. Mock, B. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr and D. R. Smith, Science, 2006, 314, 977–980 Search PubMed.
- X. Zhou and G. Hu, Appl. Phys. Lett., 2011, 98, 263510 Search PubMed.
- D. Sarker and A. Zubair, Phys. Chem. Chem. Phys., 2024, 26, 10273–10283 Search PubMed.
- D. Sarker and A. Zubair, TENCON 2023 - 2023 IEEE Region 10 Conference (TENCON), 2023, pp. 1–6 Search PubMed.
- B. Ferguson and X.-C. Zhang, Nat. Mater., 2002, 1, 26–33 CrossRef CAS PubMed.
- A. Menikh, R. MacColl, C. A. Mannella and X.-C. Zhang, ChemPhysChem, 2002, 3, 655–658 CrossRef CAS PubMed.
- Z. Zhang, Z. Zhang, Y. Yin, Y. Ueno, R. Rungsawang and K. Ajito, Front. Optoelectron. China, 2009, 2, 239–243 CrossRef.
- J. Liu, J. Luo, P. Li, M. Xion, H. Cao, B. Yang, Y. Jiang and C. Hu, J. Appl. Spectrosc., 2017, 84, 346–350 Search PubMed.
- S. H. Baek, H. B. Lim and H. S. Chun, J. Agric. Food Chem., 2014, 62, 5403–5407 Search PubMed.
- K. Kawase, Y. Ogawa, Y. Watanabe and H. Inoue, Opt. Express, 2003, 11, 2549–2554 Search PubMed.
- Y. Hua and H. Zhang, IEEE Trans. Microwave Theory Tech., 2010, 58, 2064–2070 Search PubMed.
- P. Nie, F. Qu, L. Lin, Y. He, X. Feng, L. Yang, H. Gao, L. Zhao and L. Huang, Int. J. Mol. Sci., 2021, 22, 3425 Search PubMed.
- D.-K. Lee, J.-H. Kang, J.-S. Lee, H.-S. Kim, C. Kim, J. Hun Kim, T. Lee, J.-H. Son, Q.-H. Park and M. Seo, Sci. Rep., 2015, 5, 15459 Search PubMed.
- L. Xie, W. Gao, J. Shu, Y. Ying and J. Kono, Sci. Rep., 2015, 5, 8671 CrossRef PubMed.
- B. You, J.-Y. Lu, T.-A. Liu and J.-L. Peng, Opt. Express, 2013, 21, 21087–21096 Search PubMed.
- B. M. Fischer, M. Walther and P. U. Jepsen, Phys. Med. Biol., 2002, 47, 3807 CrossRef CAS PubMed.
- D. M. Pozar, Microwave Engineering: Theory and Techniques, John wiley & sons, 2021 Search PubMed.
- M. Hao, L. Li, X. Shao, M. Tian, H. Zou, L. Zhang and W. Wang, Polymers, 2022, 14, 2727 Search PubMed.
- I. Maeng, S. H. Baek, H. Y. Kim, G. S. Ok, S. W. Choi and H. S. Chun, J. Food Prot., 2014, 77, 2081–2087 Search PubMed.
- D.-K. Lee, G. Kim and J.-H. Son, Fifth Asia-Pacific Optical Sensors Conference, 2015, pp. 164–167 Search PubMed.
- O. Levy and D. Stroud, Phys. Rev. B, 1997, 56, 8035 CrossRef CAS.
- N. I. Landy, S. Sajuyigbe, J. J. Mock, D. R. Smith and W. J. Padilla, Phys. Rev. Lett., 2008, 100, 207402 CrossRef CAS PubMed.
- S. Li, J. Gao, X. Cao, Z. Zhang, Y. Zheng and C. Zhang, Opt. Express, 2015, 23, 3523–3533 CrossRef CAS PubMed.
- R. Ziolkowski, IEEE Trans. Antenn. Propag., 2003, 51, 1516–1529 CrossRef.
- W. Zhu, Metamaterials and Metasurfaces, IntechOpen, Rijeka, 2018, ch. 7 Search PubMed.
- Y. Abdulkarim, A. Mohanty, O. Acharya, B. Appasani, M. S. Khan, S. K. Mohapatra, F. Muhammadsharif and J. Dong, Front. Phys., 2022, 10, 893791 CrossRef.
- A. Sharma, H. Singh and A. Gupta, J. Supercond. Novel Magn., 2022, 35, 3067–3083 CrossRef CAS.
- D. Wilbert, M. Hokmabadi, P. Kung and S. Kim, IEEE Trans. THz Sci. Technol., 2013, 3, 846–850 Search PubMed.
- M.-R. Nickpay, M. Danaie and A. Shahzadi, Plasmonics, 2022, 17, 237–248 CrossRef CAS.
- T. Lang, M. Xiao and W. Cen, Biosensors, 2023, 13, 560 Search PubMed.
- L. Yue, Y. Wang, Z. Cui, X. Zhang, Y. Zhu, X. Zhang, S. Chen, X. Wang and K. Zhang, Opt. Express, 2021, 29, 13563–13575 Search PubMed.
- Z. Chen, F. Qu, Y. Wang and P. Nie, Spectrochim. Acta Mol. Biomol. Spectrosc., 2021, 263, 120222 Search PubMed.
- D. Wang, S. Luo and K.-D. Xu, ACS Appl. Mater. Interfaces, 2024, 16, 27969–27978 CrossRef CAS PubMed.
- T. Lang, J. Zhang, Y. Qiu, Z. Hong and J. Liu, Opt. Commun., 2023, 537, 129430 Search PubMed.
- M. Kurosawa, T. Sadoh and M. Miyao, J. Appl. Phys., 2014, 116, 173510 CrossRef.
- Y.-y. Wang, B.-j. Li, L.-j. Huang and Q. Xu, Surf. Interfaces, 2022, 31, 102072 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01143d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |