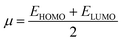DOI:
10.1039/D5RA00864F
(Paper)
RSC Adv., 2025,
15, 8262-8274
Unveiling electronic and remarkable non-linear optical properties of boron–nitrogen carbazole-based compounds via modification of π-linker and donor units: a DFT study†
Received
5th February 2025
, Accepted 11th March 2025
First published on 17th March 2025
Abstract
Boron–nitrogen carbazole (BNCz) based aromatic chromophores have been considered as promising materials in non-linear optical domains due to their distinctive electronic and charge-transfer capabilities. This study presents the electronic and non-linear optical properties of BNCz-based compounds (BTNC–BNPZ). Additionally, a new series of four BNCz-based compounds (BNTP–BNTO) with D–π–A framework was designed by modifying the donors and π-spacer. Structural optimization and optoelectronic properties of BNCz based compounds were determined using density functional theory/time-dependent density functional theory (DFT/TD-DFT) calculations at M06/6-311G(d,p) level. The optimized structures were used to perform frontier molecular orbitals (FMOs), density of states (DOS), transition density matrix (TDM), UV-Visible and non-linear optical (NLO) analyses of examined compounds. The red-shifted absorption spectrum (412.854–566.138 nm) combined with a suitable energy gap (2.784–3.774 eV) facilitates significant charge migration from HOMO to LUMO. The global reactivity descriptors revealed notable softness and significant chemical reactivity in all above-mentioned chromophores. Among all the studied compounds, BNPZ displayed the narrowest band gap (2.784 eV), the highest absorption peak (566.138 nm), and lowest excitation energy (2.190 eV), highlighting its remarkable electronic characteristics. Furthermore, DOS visualizations and TDM heat maps support the FMO findings, confirming the presence of charge densities in a chromophore. All the compounds showed an increased exciton dissociation rate due to their lower exciton binding energy values (Eb = 0.771–0.480 eV). Moreover, NBO analysis revealed that enhanced hyperconjugation and strong intramolecular interactions played a crucial role in stabilizing the studied compounds. Among all the derivatives, BNTP exhibited the highest βtot (74.0 × 10−30 esu) and γtot (81.1 × 10−35 esu) values, suggesting its promising potential as an NLO material.
Introduction
Nonlinear optical (NLO) materials have gained significant strides in recent decades particularly in fiber optics, photonic lasers, and data storage for wireless communication systems.1 These developments have profoundly influenced data processing and related technologies. Both organic and inorganic NLO materials have emerged as crucial and challenging areas of research.2 Inorganic materials have long dominated the commercial NLO applications due to their unique optical properties, high thermal stability, and efficient second-harmonic generation (SHG).3 However, the past fifteen years have witnessed a growing focus on organic systems driven by their structural versatility and tunable properties.4 Organic NLO materials present several advantages, including high absorption efficiency, strong NLO susceptibilities, and excellent thermal stability. Their π–electron delocalization enables rapid response times, contributing to outstanding NLO performance. Initially, organic compounds were often paired with fullerene-derived acceptor units to enhance charge transfer capabilities. However, fullerene-based systems have notable drawbacks, such as high production costs, limited visible-light absorption, challenges in energy-level tuning, and poor photostability.5 Consequently, researchers have shifted toward non-fullerene (NF) chromophores, which offer cost-effective synthesis and enable precise tuning of chemical structures and energy levels.6 Moreover, NF-based compounds offer exceptional stability and allow for easy modulation of electronic and optical properties through structural modifications.7 Therefore, understanding the molecular structure in detail is crucial for uncovering the interconnections between different components of the investigated compounds.8 Key NLO characteristics, such as orbital energy gaps, migration of electrons via π-linkers, dipole moment variations, and excited state transitions, can be optimized through structural modeling.9 Various push pull strategies, including donor–acceptor, donor–π–acceptor, acceptor–π–donor–π–acceptor, donor–π–π–acceptor, and donor–donor–π–acceptor, have been widely explored. Studies demonstrate that organic frameworks exhibit remarkable NLO performance through the push–pull (D–π–A) model, sparking significant interest in such chromophores.10 The nature of donor and acceptor functions along with the extent of π-conjugation also play a crucial role in determining NLO properties, primarily via intramolecular charge transfer (ICT).11 The BNCz core, with its tricoordinate boron atoms, exhibits strong electron-accepting properties, while functionalization with aryl groups stabilizes the structure and fine-tunes electronic properties for enhanced NLO performance.12 Additionally, the phenylthiophene π-spacer is expected to effectively enhance conjugation, further optimizing the charge transfer and NLO efficiency.13
Building on these considerations, this study presents NLO analysis of four boron–nitrogen carbazole (BNCz) based compounds, synthesized via nucleophilic aromatic substitution and electrophilic arene borylation as reported by Hui He and colleagues.14 Additionally, four new BNCz based derivatives, featuring a phenyl thiophene π-spacer and strong phenazine based donor groups were designed. A DFT based investigation was conducted to evaluate the impact of π-linker and donor variations on the NLO properties, assessing the potential of these compounds for practical NLO applications.
Computational procedure
All the calculations for current study were conducted using Gaussian 16 software package.15 DFT and TD-DFT investigations were performed at M06 level 6-311G(d,p) and basis set to explore the electronic and NLO properties of BTNC–BNPZ and BNTP–BNTO. At first, the geometries of these chromophores were optimized at the ground state using abovementioned functional, then these optimized structures were utilized for further analyses. The UV-Visible spectra, frontier molecular orbital, transition density matrix were carried out using the TD-DFT method whereas NBOs, DOS and NLO analyses were conducted at DFT approach. To investigate the stabilization patterns of entitled compounds NBO study was performed. Avogadro software16 was utilized to calculate the FMOs energies and developed their counter surfaces to illustrate the charge transfer in entitled chromophores. The chemical reactivity of BTNC–BNPZ and BNTP–BNTO was assessed by calculating their global reactivity descriptors (GRDs) with the aid of valence and conduction energy gaps. The quantitative assessment of electronic cloud at various parts of studied D–A and D–π–A chromophores was conducted through DOS analysis to support the insights gained from FMOs. Several software tools, i.e., GaussSum,17 Chemcraft,18 Multiwfn,19 and Gauss View 5.0,20 were employed to get the information from the output files. Eqn (1)–(4) were applied to determine values of dipole moment (μ),21 linear polarizability α,22 the first hyperpolarizability (βtotal),23 and second hyperpolarizability (γtotal).24| | |
μ = (μx2 + μy2 + μz2)1/2
| (1) |
| | |
〈α〉 = (axx + ayy + azz)/3
| (2) |
| | |
βtotal = (βx2 + βy2 + βz2)1/2
| (3) |
whereas βx = βxxx + βxyy + βxzz, βy = βyxx + βyyy + βyzz and βz = βzxx + βzyy + βzzz| |
 | (4) |
whereas 
Results and discussion
This study investigates the NLO properties of four previously synthesized boron–nitrogen-based compounds14 (BTNC, BNAC, BNPXZ, and BNPZ) featuring a BNCz acceptor core with various donor units. To optimize computational efficiency and reduce steric hindrance, longer alkyl chains in these compounds were replaced with shorter methyl groups. Additionally, four newly designed BNCz-based derivatives (BNTP, BNTC, BNTA, and BNTO) were also designed, incorporating a D–π–A framework with a 2-phenylthiophene π-bridge and efficient donor groups (Fig. 1). The structures and IUPAC names of the utilized donor groups for entitled compounds are provided in Table S32.† The ground state geometries of the aforesaid compounds are depicted in Fig. 2, with Chemdraw structures in Fig. S1† and cartesian coordinates in Tables S1–S8.† This theoretical study aims to offer valuable insights into the NLO potential of these molecules, paving the way for their practical applications.
 |
| | Fig. 1 Schematic representation of the designed chromophores (BNTP–BNTO). | |
 |
| | Fig. 2 Optimized structures of studied chromophores. | |
Frontier molecular orbitals (FMOS)
The FMOs analysis is key to understanding chromophores' electronic structure and its impact on NLO characteristics.25,26 Among FMOs, the HOMO (ability to donate electrons) and LUMO (capability to accept electrons) played significant role in evaluating a substance's dynamic stability and chemical reactivity.13 Table 1 displays the energies of entitled chromophores calculated at foresaid functional.
Table 1 FMOs energies of studied compoundsa
| Chromophores |
EHOMO |
ELUMO |
ΔE |
| Band gap = ELUMO − EHOMO, units in eV. |
| BTNC |
−5.717 |
−1.943 |
3.774 |
| BNAC |
−5.635 |
−1.987 |
3.648 |
| BNPXZ |
−5.280 |
−2.022 |
3.258 |
| BNPZ |
−4.720 |
−1.936 |
2.784 |
| BNTP |
−5.524 |
−1.964 |
3.56 |
| BNTC |
−5.673 |
−2.021 |
3.652 |
| BNTA |
−5.659 |
−2.006 |
3.653 |
| BNTO |
−5.422 |
2.034 |
3.388 |
The synthesized BTNC–BNPZ14 chromophores exhibit HOMO/LUMO energy levels of −5.717/−1.943, −5.635/−1.987, −5.280/−2.022 and −4.720/−1.936 eV, respectively. Similarly, the HOMO/LUMO energies of designed derivatives (BNTP–BNTO) are −5.524/−1.964, −5.673/−2.021, −5.659/−2.006 and −5.422/2.034 eV, correspondingly. The higher HOMO energy levels and lower LUMO energy levels in all compounds result in reduced band gaps, significantly improving the charge transfer efficiency in these molecules. Among the BTNC–BNPZ, chromophores BNPZ exhibit the smallest ΔE value of 2.784 eV. This narrow band gap might be due to the efficient electronic interaction between the strong donor moiety (dihydrophenazine) and the acceptor (BNCz core), enhancing internal charge transfer. Similarly, BNPXZ, with a smaller energy gap of 3.258 eV compared to BNAC 3.648 eV, demonstrates enhanced electronic properties. This is likely due to the combination of the methyl and p-tolyl groups in dihydrophenazine moiety, which increases its electron-donating capability relative to the single methyl substitution in phenoxazine. BTNC exhibits the highest band gap of 3.774 eV among BTNC–BNPZ, possibly due to the less conjugation in the attached carbazole moiety. It might restrict the charge delocalization, in contrast to the more extensive conjugation in dihydrophenazine and phenoxazine. The ascending sequence of ΔE of these organic chromophores as follows: BNPZ < BNPXZ < BNAC < BTNC. The designed derivative BNTC is observed with reduced energy gap of 3.652 eV than BTNC chromophore due to the incorporation of 2-phenylthiophene (π-bridge). This π-bridge enhances the conjugation, facilitating better charge delocalization. However, designed compound BNTA and chromophore BNAC are observed with comparable band gap values. The designed derivatives exhibit an ascending ΔE sequence as: BNTO < BNTP < BNTC < BNTA.
Fig. 3 illustrates the molecular orbital (MO) surfaces of (BTNC–BNPZ) and (BNTP–BNTO), depicting the charge transfer from donor moiety towards acceptor units via π-spacer. Moreover, Table S9 and Fig. S2† illustrates the energies and counter surfaces of other orbitals (HOMO−1/LUMO+1, HOMO−2/LUMO+2) of studied compounds.
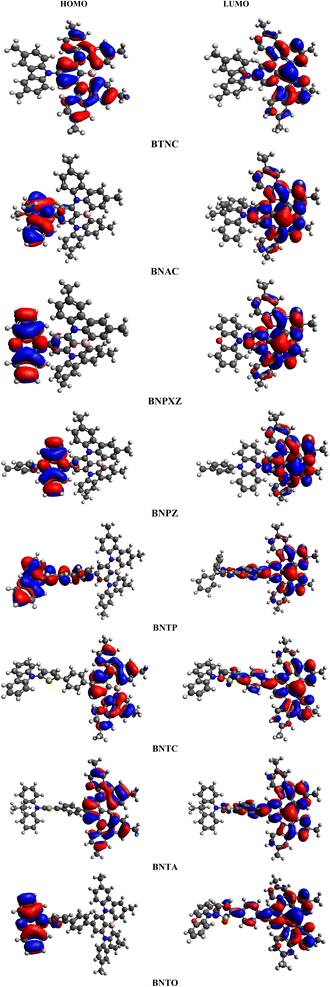 |
| | Fig. 3 HOMOs and LUMOs of BTNC–BNPZ and BNTP–BNTO. | |
Global reactivity parameters
The GRDs are determined with the aid of HOMO–LUMO energy values to assess the chemical properties of the molecules. The global softness (σ),27 electron affinity (EA),28 global hardness (η),27 global electrophilicity index (ω),29 chemical potential (μ), ionization potential (IP),30 and electronegativity (X)31 were calculated using eqn (5)–(11).
Koopmans's theorem32 is used to determine σ, ω, η, μ and X
| |
 | (7) |
| |
 | (8) |
| |
 | (9) |
| |
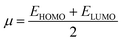 | (10) |
| |
 | (11) |
The capacity of a chromophore to absorb additional electrical charge from its surroundings is represented by ΔNmax33 which is calculated using eqn (12).
The EA and IP values can be used to quantify the ability of a molecule to accept and donate electrons. The results in Table 2 reveal that aforesaid compounds exhibit a higher IP and a low EA. However, among all the compounds studied, BTNC chromophore showed the highest ionization potential, measuring 5.717 eV. The ionization potential decreases in the following order: BTNC (5.717 eV) > BNTC (5.673 eV) > BNTA (5.659 eV) > BNAC (5.635 eV) > BNTP (5.524 eV) > BNTO (5.422 eV) > BNPXZ (5.280 eV) > BNPZ (4.720 eV). The chemical potential is an important parameter in understanding the tendency of electrons to move away from an equilibrium state. The μ values in descending order are: BNTC (−3.847 eV) > BNTA (−3.833 eV) > BTNC (−3.83 eV) > BNAC (−3.811 eV) > BNTP (−3.744 eV) > BNTO (−3.728 eV) > BNPXZ (−3.651 eV) > BNPZ (−3.328 eV). Moreover, BNTC and BNPZ exhibit the highest and lowest electronegativity values of 3.847 eV and 3.328 eV, respectively. Similarly, global softness and hardness measure the extent of chemical reactivity and are inversely correlated. A molecule with a larger bandgap is deemed harder, more stable, and less reactive, while one with a smaller bandgap is softer, more reactive, and less stable. Among the molecules BNPZ shows the highest softness value of 0.359 eV−1 and the lowest band gap (2.784 eV), making it the most reactive and polarizable compound. Similarly, BTNC exhibits the highest hardness value of 1.887 eV and the largest band gap of 3.774 eV, indicating it is the most stable and least reactive compound. The σ values in descending order are: BNPZ (0.359 eV−1) > BNPXZ (0.307 eV−1) > BNTO (0.295 eV−1) > BNTP (0.281 eV−1) > BNAC (0.274 eV−1) = BNTC (0.274 eV−1) = BNTA (0.274 eV−1) > BTNC (0.265 eV−1). Further, BNPZ displays the highest ΔNmax, with a value of 2.391 eV. In conclusion, the GRP results indicate that BNPZ exhibits the highest softness and the lowest band gap (Table 1), demonstrating strongest CT and positioning it as the suitable optoelectronic material for NLO applications.
Table 2 The GRPs of BTNC–BNPZ and BNTP–BNTOa
| Chromophores |
IP |
EA |
X |
η |
μ |
ω |
σ |
ΔNmax |
| Global softness (σ) eV−1, all other units in eV. |
| BTNC |
5.717 |
1.943 |
3.83 |
1.887 |
−3.83 |
3.887 |
0.265 |
2.029 |
| BNAC |
5.635 |
1.987 |
3.811 |
1.824 |
−3.811 |
3.981 |
0.274 |
2.089 |
| BNPXZ |
5.280 |
2.022 |
3.651 |
1.629 |
−3.651 |
4.092 |
0.307 |
2.241 |
| BNPZ |
4.720 |
1.936 |
3.328 |
1.392 |
−3.328 |
3.978 |
0.359 |
2.391 |
| BNTP |
5.524 |
1.964 |
3.744 |
1.78 |
−3.744 |
3.938 |
0.281 |
2.103 |
| BNTC |
5.673 |
2.021 |
3.847 |
1.826 |
−3.847 |
4.053 |
0.274 |
2.107 |
| BNTA |
5.659 |
2.006 |
3.833 |
1.827 |
−3.833 |
4.021 |
0.274 |
2.099 |
| BNTO |
5.422 |
2.034 |
3.728 |
1.694 |
−3.728 |
4.102 |
0.295 |
2.201 |
Optical properties
UV-Vis calculations for BTNC–BNPZ and BNTP–BNTO were performed in gaseous state at M06/6-311G(d,p) to evaluate charge transfer, contributing configurations, and the nature of electronic transitions.34,35 Moreover, the impact of various donor moieties and the inclusion of π-spacer on the optical properties of compounds was also examined. The details of absorption maxima (λmax), excitation energy (ΔE) and oscillator strength (fos), to transitions are provided in Table 3, while the rest of information is presented in Tables S10–S17.†
Table 3 Wavelength (λ), excitation energy (E), oscillator strength (fos) and nature of molecular orbital contributions of compounds (BTNC–BNPZ) and (BNTP–BNTO) in gaseous phasea
| Compounds |
DFT λ (nm) |
E (eV) |
fos |
MO contributions |
| MO = molecular orbital, H=HOMO, L = LUMO, fos = oscillator strength, DFT = density functional theory. |
| BTNC |
412.854 |
3.003 |
0.378 |
H → L (97%) |
| BNAC |
418.286 |
2.964 |
0.375 |
H−1 → L (90%) |
| BNPXZ |
471.369 |
2.630 |
0.039 |
H → L (96%) |
| BNPZ |
566.138 |
2.190 |
0.026 |
H → L (97%) |
| BNTP |
425.565 |
2.913 |
0.365 |
H−1 → L (97%) |
| BNTC |
425.405 |
2.915 |
0.365 |
H → L (97%) |
| BNTA |
425.434 |
2.914 |
0.363 |
H → L (97%) |
| BNTO |
426.326 |
2.908 |
0.358 |
H−1 → L (96%) |
Fig. 4 shows the simulated absorption spectra of the studied chromophores, ranging from 566.138 to 412.854 nm. The absorption spectra are significantly affected by the donor functionalities in the structure due to the push–pull arrangement in the chromophores. The BNPZ chromophore exhibits its maximum absorption peak at 566.138 nm, corresponding to transition energy of 2.190 eV, with 97% contribution from the HOMO to LUMO transition. This peak is likely attributed to the efficient donor moiety, 5-methyl-10-(p-tolyl)-5,10-dihydrophenazine. The introduction of donor (10-methyl-10H-phenoxazine) in BNPXZ has lowered its λmax to 471.369 nm associated with transition energy of 2.630 eV. The λmax further decreases in BNAC and BTNC with the introduction of donors: 9,9,10-trimethyl-9,10-dihydroacridine and 3,6,9-trimethyl-9H-carbazole, resulting in absorption peaks at 418.286 and 412.854 nm, respectively. The compounds are ordered in decreasing absorption peak as follows: BNPZ > BNPXZ > BNAC > BTNC.
 |
| | Fig. 4 Simulated absorption spectra in gas phase of examined chromophores. | |
Among the designed compounds, BNTO featuring a dihydrophenazine donor showed highest absorption at 426.326 nm, the lowest transition energy of 2.908 eV, and 96% H−1 → L contribution. Comparing BTNC and BNTC, both with dihydroacridine donors, BNTC showed a greater red shift at 425.405 nm due to the added π-bridge, which enhances the charge transfer rate. Similarly, by incorporating a phenylthiophene linker in BNTA, compared to BNAC, both containing phenoxazine donor, BNTA showed with higher absorption at 425.434 nm. Overall, the λmax of designed compounds are found to follow this increasing order: BNTO > BNTP > BNTA > BNTC. Hence, all the explored chromophores, particularly BNPZ and BNTO, show promising potential as high-performance optoelectronic materials, owing to their good absorption and charge transfer properties.
Density of states analysis
The density of states analysis confirms the findings shown by FMO study and provides insight into the electronic distribution from HOMO to LUMO.36,37 In DOS graphs, the HOMO corresponds to the valence band, reflecting right side, while the conduction band (LUMO) is represented by left side.38 The partition between the conduction and valence bands represents the energy band gap. The DOS maps for BTNC–BNPZ and BNTP–BNTO were illustrated in Fig. 5. It reveals the contribution of each molecular fragment to the charge transfer. To calculate the density of states, chromophores BTNC–BNPZ were separated into two fragments: the donor and the acceptor (BNCz core), whereas the derivatives: BNTP–BNTO were partitioned into three segments: donor, π-spacer (2-phenylthiophene), and acceptor (BNCz core). In DOS maps, red, green, and blue peaks illustrated the donor, π-spacer, and acceptor, respectively, with the black band indicating the molecule's overall electronic contribution, as shown in Fig. 5.
 |
| | Fig. 5 The DOS plots of the examined chromophores. | |
Table 4 shows that donors contribute 2.1, 0.9, 1.4, and 1.2 to the LUMO, and 0.4, 95.7, 95.8, and 97.4 to the HOMO for BTNC–BNPZ, respectively. While the acceptor contributes 97.9, 99.1, 98.6, and 98.8 to the LUMO, with its HOMO contributions being 99.6, 4.3, 4.2, and 2.6% for BTNC–BNPZ, respectively. For BNTP–BNTO series the acceptor contributes 2.4, 99.8, 99.8, 0.0 to HOMO and 86.1, 84.8, 85.3 and 82.8 to LUMO, respectively (Table 5). Moreover, the charge contribution of the donor to HOMO and LUMO is 55.8, 0.0, 0.0 and 95.9, and 50.1% and 0.5, 0.2, 0.2, 0.2, and 0.2%, respectively. Similarly, π-spacer account to HOMO is 41.8, 0.2, 0.2, and 4.1% while their participation to LUMO is 13.4, 15.0, 14.5 and 17.0% for BNTP–BNTO, respectively.
Table 4 Percentages of acceptor, donor for LUMO and HOMO OF BTNC–BNPZ
| Compounds |
LUMO |
HOMO |
| Acceptor |
Donor |
Acceptor |
Donor |
| BTNC |
97.9 |
2.1 |
99.6 |
0.4 |
| BNAC |
99.1 |
0.9 |
4.3 |
95.7 |
| BNPXZ |
98.6 |
1.4 |
4.2 |
95.8 |
| BNPZ |
98.8 |
1.2 |
2.6 |
97.4 |
Table 5 Percentages of acceptor, donor and π-spacer for LUMO and HOMO of BNTP–BNTO
| Compounds |
LUMO |
HOMO |
| Acceptor |
π-spacer |
Donor |
Acceptor |
π-spacer |
Donor |
| BNTP |
86.1 |
13.4 |
0.5 |
2.4 |
41.8 |
55.8 |
| BNTC |
84.8 |
15.0 |
0.2 |
99.8 |
0.2 |
0.0 |
| BNTA |
85.3 |
14.5 |
0.2 |
99.8 |
0.2 |
0.0 |
| BNTO |
82.8 |
17.0 |
0.2 |
0.0 |
4.1 |
95.9 |
Transition density matrix (TDM) investigation
The TDM study serves as an effective method for evaluating transmission of electronic density between two quantum states.39,40 In molecular systems, TDM analysis generates 3D heat maps that depict charge carrier distribution, and allow the observation of their coherence and delocalization.41,42 Transition density matrix maps of the studied compounds have been calculated in gaseous state and are presented in Fig. 6. It aids in examining the donor–acceptor interaction in the excited state and the localization of electron holes.43 The H atoms are omitted in this study due to their negligible contribution to the transition. To generate TDM maps, the BTNC–BNPZ chromophores were divided into two components: “A” and “D”, while the BNTP–BNTO chromophores were split into three distinct parts: “D”, π-spacer, and “A”. The π-spacer functions as a pathway for CT by enabling relations between the donor and acceptor components. The TDM diagrams show that in BTNC–BNPZ and BNTP–BNTO molecules, an efficient diagonal transfer of charge mobility from donor to the acceptor through the π-spacer. The FMOs study (Fig. 3) reveals that charge transfer occurs significantly towards “A” from “D” through linker, which results in support the TDM heat maps. According to Fig. 6, diagonal charge coherence is observed in BTNC and BNAC from donor to acceptor portions whereas in BNAC and BNPXZ non-diagonal coherence in observed. In designed chromophores (BNTP–BNTO) efficient charge coherence is noted from “D” to “A” regions via the π-spacer.
 |
| | Fig. 6 TDM in the examined compounds (BTNC–BNPZ) and (BNTP–BNTO). | |
Exciton binding energy (Eb)
The Eb is a crucial parameter for evaluating the optoelectronic properties of the studied compounds.44 A lower binding energy leads to enhanced charge mobility, resulting in a stronger NLO response. The Eb of BTNC–BNPZ and BNTP–BNTO were determined by subtracting the first excitation energies (Eopt) from the band gap (Egap) using eqn (13).The values of Eb for BTNC–BNPZ and BNTP–BNTO are computed to be 0.771, 0.684, 0.628, 0.594, 0.647, 0.737, 0.739 eV, respectively (Table 6). Among all the examined chromophores, BNPZ showed the lowest exciton binding energy of 0.594 eV, suggesting superior exciton separation and enhanced charge density potential. To list the compounds in decreasing order of binding energy (Eb) is: BTNC > BNTA > BNTC > BNAC > BNTP > BNPXZ > BNPZ. The least values of Eb illustrated the good CT in entitled chromophores which supported the greater polarity in them resulting good NLO response.
Table 6 Exciton cohesion energies of (BTNC–BNPZ) and (BNTP–BNTO)a
| Compounds |
EH–L |
Eopt |
Eb |
| Units in eV. |
| BTNC |
3.774 |
3.003 |
0.771 |
| BNAC |
3.648 |
2.964 |
0.684 |
| BNPXZ |
3.258 |
2.630 |
0.628 |
| BNPZ |
2.784 |
2.190 |
0.594 |
| BNTP |
3.56 |
2.913 |
0.647 |
| BNTC |
3.652 |
2.915 |
0.737 |
| BNTA |
3.653 |
2.914 |
0.739 |
Natural population analysis (NPA)
The calculation of atomic charges, that reveal the charge distribution across different atoms of a molecule, is essential for predicting changes in bond lengths. These charges are crucial in influencing the dipole moment, electronic structure, molecular polarizability, and other key properties of molecular systems.45
Fig. S3† presents the NPA analysis results; illustrate the natural charge distribution in compounds BTNC–BNPZ and BNTP–BNTO. The distribution of electrical charges on individual atoms significantly influences the arrangement of molecules and their bonding potential. The natural charge analysis indicates that electronegative elements (B, N, O, S) induce uneven electron density redistribution across the heteroatomic rings. Additionally, negative charges on carbon atoms result in hydrogen atoms acquiring positive charges. The NPA graphs reveal that all H, S, and Br atoms carry positive charges, but N and O contain negative charges. Moreover, certain carbon atoms carry a positive charge, while others are assigned a negative charge. The significant negative charge on carbon atoms results from their resonance interaction with adjacent N and O atoms. 11B in BTNC–BNPZ are observed with significant positive charges while 64 N with higher negative charges. Similarly, 11B and 79N display notably positive and negative charges in BNTP–BNTO, respectively. This might be due to the presence of highly negative and positive atoms around them, respectively.
Natural bond orbital (NBO) analysis
NBO analysis is the most accurate method for interpreting electrophilic, nucleophilic and hyper-conjugative interactions, orbitals interactions, and the nature of electronic transitions.46,47 Furthermore, NBO study facilitates the analysis of electron density transfer between unoccupied (A) and occupied (D) molecular orbitals in D–π–A framework.17,46,48 The second-order perturbation method is utilized to assess the reactions that entail delocalization.47 To compute the stabilization energy E(2), for each donor (i) to acceptor (j) interaction which results in i → j delocalization, eqn (14) is used.| |
 | (14) |
The D orbital occupancy is symbolized by qi; the diagonal and off-diagonal NBO Fock matrix elements are signified by Ej − Ei and Fi,j, respectively.49 Orbital overlap leads to various hyperconjugative interactions: σ → σ*, π → π*, LP → σ*, and LP → π*. The π-conjugation in investigated compounds featuring D–A and D–π–A framework facilitates π → π* transitions, making them highly efficient NLO materials. Weak σ → σ* transitions are also observed due to less interactions between donor and acceptor moieties. Table 7 highlights the key transition values for (BTNC–BNPZ) and (BNTP–BNTO), while comprehensive data is provided in Tables S18–S25.†
Table 7 Computed NBO analysis for studied chromophores
| Compounds |
Donor (i) |
Type |
Acceptor (j) |
Type |
E(2) [kcal mol−1] |
| BTNC |
C1–C7 |
π |
C2–C3 |
π* |
28.95 |
| C1–C7 |
π |
C1–C7 |
π* |
0.82 |
| C34–C35 |
σ |
N12–C27 |
σ* |
6.81 |
| N12–C27 |
σ |
C34–C35 |
σ* |
0.97 |
| N12 |
LP1 |
C1–C7 |
π* |
41.16 |
| N64 |
LP1 |
C1–C2 |
σ* |
3.5 |
| BNAC |
C1–C7 |
π |
C2–C3 |
π* |
28.89 |
| C10–C20 |
π |
C10–C20 |
π* |
0.83 |
| C34–C35 |
σ |
N12–C27 |
σ* |
6.79 |
| C16–H19 |
σ |
C16–C17 |
σ* |
0.99 |
| N12 |
LP1 |
C1–C7 |
π* |
40.99 |
| N64 |
LP1 |
C1–C2 |
σ* |
6.76 |
| BNPXZ |
C1–C7 |
π |
C2–C3 |
π* |
29.05 |
| C1–C7 |
π |
C1–C7 |
π* |
0.65 |
| C42–C43 |
σ |
N13–C29 |
σ* |
6.79 |
| C39–C40 |
σ |
C77–H78 |
σ* |
0.51 |
| O83 |
LP2 |
C46–C60 |
π* |
24.72 |
| O83 |
LP1 |
C47–C48 |
σ* |
6.72 |
| BNPZ |
C1–C7 |
π |
C2–C3 |
π* |
29.06 |
| C10–C20 |
π |
C10–C20 |
π* |
0.82 |
| C34–C35 |
σ |
N12–C27 |
σ* |
6.76 |
| N12–C27 |
σ |
C34–C35 |
σ* |
0.97 |
| N12 |
LP1 |
C1–C7 |
π* |
40.48 |
| N83 |
LP1 |
C84–C86 |
σ* |
6.54 |
| BNTP |
C1–C7 |
π |
C2–C3 |
π* |
28.1 |
| C4–C9 |
π |
C4–C9 |
π* |
1.68 |
| C73–C75 |
σ |
C77–N79 |
σ* |
6.9 |
| C24–H25 |
σ |
C22–C24 |
σ* |
0.99 |
| S74 |
LP2 |
C75–C77 |
π* |
24.27 |
| N79 |
LP1 |
C74–C77 |
σ* |
10.31 |
| BNTC |
C1–C7 |
π |
C2–C3 |
π* |
28.31 |
| C10–C20 |
π |
C10–C20 |
π* |
0.83 |
| C73–C75 |
σ |
C77–N79 |
σ* |
6.91 |
| C9–N13 |
σ |
C3–C9 |
σ* |
1.98 |
| S74 |
LP2 |
C72–C73 |
π* |
25.02 |
| N79 |
LP1 |
C74–C77 |
σ* |
13.43 |
| BNTA |
C1–C7 |
π |
C2–C3 |
π* |
28.22 |
| C10–C20 |
π |
C10–C20 |
π* |
0.83 |
| C73–C75 |
σ |
C77–N79 |
σ* |
6.88 |
| C16–H19 |
σ |
C16–C17 |
σ* |
0.99 |
| S74 |
LP2 |
C72–C73 |
π* |
25.04 |
| N79 |
LP1 |
C74–C77 |
σ* |
16.26 |
| BNTO |
C1–C7 |
π |
C2–C3 |
π* |
28.21 |
| C10–C20 |
π |
C10–C20 |
π* |
0.83 |
| C73–C75 |
σ |
C77–N79 |
σ* |
7.04 |
| C24–H25 |
σ |
C22–C24 |
σ* |
0.99 |
| S74 |
LP2 |
C72–C73 |
π* |
25.26 |
| N97 |
LP1 |
S74–C77 |
σ* |
15.89 |
Table 7 shows that in compound BTNC, the most significant π → π* interaction involves π(C1–C7) donating to π*(C2–C3) with E(2) of 28.95 kcal mol−1, while the weakest occurs between π(C1–C7) and its own π* orbital, with an energy of 0.82 kcal mol−1. Among σ → σ* transitions, the strongest is from σ(C34–C35) to σ*(N12–C27) at E(2) of 6.81 kcal mol−1, and the weakest is at 0.97 kcal mol−1 for σ(N12–C27) → σ*(C34–C35) transition. The LP → π* interaction is dominated by LP1(N12) donating to π*(C1–C7), contributing 41.16 kcal mol−1. Meanwhile, for LP → σ* transition, smallest E(2) for LP1(N64) → σ*(C1–C2) is noted at 3.5 kcal mol−1. In BNAC, the most prominent π → π* donation comes from π(C1–C7) to π*(C2–C3), exhibiting an E(2) of 28.89 kcal mol−1, whereas the weakest π interaction is calculated at E(2) = 0.83 kcal mol−1 from π(C10–C20) to π*(C10–C20). The strongest σ → σ* interaction, σ(C34–C35) → σ*(N12–C27), occurs at 6.79 kcal mol−1 stabilization energy, with the weakest being σ(C16–H19) → σ*(C16–C17) at 0.99 kcal mol−1. The leading LP → π* contribution is 40.99 kcal mol−1 for LP1(N12) → π*(C1–C7), while LP1(N64) → σ*(C1–C2) registers the smallest LP → σ* value of 6.76 kcal mol−1. For compound BNPXZ, the highest π → π* interaction involves π(C1–C7) donating to π*(C2–C3), with an energy of 29.05 kcal mol−1, while the lowest is 0.65 kcal mol−1 for π(C1–C7) → π*(C1–C7). The σ → σ* donation from σ(C42–C43) to σ*(N13–C29) is the strongest at 6.79 kcal mol−1, and the weakest, 0.51 kcal mol−1, is from σ(C39–C40) to σ*(C77–H78). LP → π* interactions are led by LP2(O83) → π*(C46–C60) with an energy of 24.72 kcal mol−1, and the smallest LP → σ* interaction comes from LP1(O83) → σ*(C47–C48) at 6.72 kcal mol−1. In BNPZ, the most dominant π → π* transition occurs between π(C1–C7) and π*(C2–C3), showing an energy of 29.06 kcal mol−1, while the weakest π → π* interaction at 0.82 kcal mol−1 involves π(C10–C20) → π*(C10–C20). The σ → σ* transition with the highest energy, 6.76 kcal mol−1, is σ(C34–C35) → σ*(N12–C27), whereas the lowest is 0.97 kcal mol−1 for σ(N12–C27) → σ*(C34–C35). The LP → π* interaction of LP1(N12) → π*(C1–C7) dominates with an energy of 40.48 kcal mol−1, and the weakest LP → σ* transition is LP1(N83) → σ*(C84–C86) at 6.54 kcal mol−1. Moving to the series of designed compounds for BNTP, the highest π → π* transition occurs at 28.1 kcal mol−1 for π(C1–C7) → π*(C2–C3), and the lowest is at 1.68 kcal mol−1 stabilization energy for π(C4–C9) → π*(C4–C9). The highest σ → σ* transition is at 6.9 kcal mol−1 energy for σ(C73–C75) → σ*(C77–N79), and the lowest is at 0.99 kcal mol−1 for σ(C24–H25) → σ*(C22–C24). The highest LP → π* transition occurs at 24.27 kcal mol−1 energy, observed for LP2(S74) → π*(C75–C77), while the lowest is at 10.21 kcal mol−1 stabilization energy for LP1(N79) → σ*(S74–C77). For compound BNTC, the highest π → π* transition is observed at 28.31 kcal mol−1 for π(C1–C7) → π*(C2–C3), with the lowest at 0.83 kcal mol−1 energy for π(C10–C20) → π*(C10–C20). The highest σ → σ* transition energy is 6.91 kcal mol−1 for σ(C73–C75) → σ*(C77–N79), and the lowest is 1.98 kcal mol−1 for σ(C9–N13) → σ*(C3–C9). The highest LP → π* transition energy is 25.02 kcal mol−1 for LP2(S74) → π*(C72–C73), and the lowest is 13.43 kcal mol−1 for LP1(N79) → σ*(S74–C77). For compound BNTA, the maximum π → π* transition occur at stabilization energy of 28.22 kcal mol−1 for π(C1–C7) → π*(C2–C3), while the minimum value of stabilization energy is 0.83 kcal mol−1 for π(C10–C20) → π*(C10–C20). The highest σ → σ* transition occurs at 6.88 kcal mol−1 for σ(C73–C75) → σ*(C77–N79), and the lowest at 0.99 kcal mol−1 for σ(C16–H19) → σ*(C16–C17). The maximum LP → π* transition is noted at 25.04 kcal mol−1 for LP2(S74) → π*(C72–C73), and the minimum is found at 16.26 kcal mol−1 for LP1(N79) → σ*(S74–C77). For compound BNTO, the highest π → π* transition energy is 28.21 kcal mol−1 for π(C1–C7) → π*(C2–C3), with the lowest value at 0.83 kcal mol−1 for π(C10–C20) → π*(C10–C20). The highest σ → σ* transition is 7.04 kcal mol−1 for σ(C73–C75) → σ*(C77–N79), and the lowest is 0.99 kcal mol−1 for σ(C24–H25) → σ*(C22–C24). The highest LP → π* transition energy is 25.26 kcal mol−1 for LP2(S74) → π*(C72–C73), while the lowest is 15.89 kcal mol−1 for LP1(N79) → σ*(S74–C77). Hence, the NBO analysis of the aforementioned molecules indicates that strong intramolecular charge transfer and extensive hyperconjugation significantly contribute to their stabilization and impart remarkable NLO properties.
Non-linear optical (NLO) study
Hyperpolarizability and intramolecular charge transfer (ICT) elucidate the connection between molecular structure and nonlinearity.50,51 High molecular polarizability, significant dipole moment, and hyperpolarizability values collectively enhance NLO performance. The ability of an electric field to distort the electronic distribution within a molecule is referred to as linear polarizability (〈α〉). Hyperpolarizability (β, γ) refers to the atomic and molecular nonlinearity underlying various nonlinear optical phenomena.52 The values of first-order hyperpolarizability (βtot), second-order hyperpolarizability (γtot), linear polarizability (〈α〉), and dipole moment (μtot), along with their respective tensors for BTNC–BNPZ and BNTP–BNTO, are provided in Tables S26–S29† and 8.
Table 8 Computed μtot, 〈α〉, βtot, and γtot for the synthesized moleculesa
| Compounds |
μtot |
〈α〉 × 10−23 |
βtot × 10−30 |
γtot × 10−35 |
| Units in esu. μtot in Debye. |
| BTNC |
1.308 |
9.68 |
19.0 |
24.0 |
| BNAC |
1.110 |
9.55 |
7.11 |
16.5 |
| BNPXZ |
2.046 |
9.16 |
6.42 |
21.4 |
| BNPZ |
1.191 |
10.5 |
18.5 |
29.5 |
| BNTP |
1.000 |
11.9 |
74.0 |
81.1 |
| BNTC |
1.564 |
11.7 |
17.0 |
46.2 |
| BNTA |
1.000 |
12.2 |
18.0 |
47.7 |
| BNTO |
1.952 |
11.7 |
15.0 |
46.9 |
The μ plays a crucial role in evaluating the polarizability of organic chromophores. It is determined by the product of the magnitude of charges and the distance separating them. Table S26† displays the calculated dipole moment values along with the three-dimensional tensor components in the x, y, and z directions. The μtot of the compounds in decreasing order are as follows in Debye: BNPXZ (2.046) > BNTO (1.952) > BNTC > (1.564) > BTNC (1.308) > BNPZ (1.191) > BNAC (1.110) > BNTP (1.000) = BNTA (1.000). Among all the compounds, BNPXZ exhibits the highest μ value (2.046 D), indicating the strongest polarity, while BNTA and BNTP both have the lowest μ (1.000 D), signifying their least polarity. For the studied compounds BTNC, BNAC, BNPXZ, BNPZ, BNTP, BNTC, BNTA, and BNTO, the dominant tensor lies along the μx axis, with values of −1.3084, −1.0776, 0.0307, −1.1899, 0.9027, −1.3190, 0.3779, and 1.6581 D, respectively, indicating it as the primary contribution of polarity. In contrast, BNPXZ shows its highest dipole moment along the μy axis (2.0474 D). The facts from Table S27† reveals that all the studied chromophores exhibit higher linear polarizability along the αxx tensor except BTNC and BNAC, where αyy dominate. The evaluation of average polarizability indicates that BNTA exhibits the highest average polarizability (〈α〉 = 12.2 × 10−23 esu), with tensor components αxx = 1.67 × 10−22, αyy = 1.42 × 10−22, and αzz = 5.57 × 10−23 esu along the x, y, and z axes, respectively. Designing new D–π–A frameworks enable CT between electron accepting and donating parts, reducing the band gap and enhancing first hyperpolarizability (βtot). The calculated first hyperpolarizability values of entitled compounds, along with their respective tensor components, are presented in Table S29.† The investigated chromophores show remarkable βtot values ranging from 6.42 × 10−30 to 74.20 × 10−30 esu, demonstrating strong nonlinear optical responses. Among the designed derivatives, BNTP exhibits the highest βtot value (74.0 × 10−30 esu), likely due to strong electronic communication within its push–pull configuration. In contrast, BNPXZ shows the lowest βtot (6.42 × 10−30 esu) value. The dominant contributing tensor for BTNC, BNTC, BNPZ and BNTP is βxxx, with magnitudes of 3.71× 10−29, 3.61 × 10−29, −3.26 × 10−29 and 9.74 × 10−29, respectively. For BNAC and BNPXZ, the governing tensor is βxxy, with values of −5.01 × 10−31 and 1.35 × 10−29, respectively. In contrast, in BNTA, and BNTO, the dominant contribution comes from βxyy, with values of 2.13 × 10−29, and 2.08 × 10−29, respectively. The total second hyperpolarizability (γtot) values for studied chromophores were also computed, as shown in Table S28.† For BNTP, which exhibits the highest γtot value (81.11 × 10−35 esu) among all the compounds, the dominant contribution originates from the γx tensor (3.59 × 10−34 esu) while the least contribution is attributed to the tensor γz (6.66 × 10−36).
The frequency-dependent NLO properties for the compounds under investigation were calculated at the laser wavelengths of 532 nm (ω = 0.042823 a.u.) and 1064 nm (ω = 0.085645 a.u.) (Tables S30 and S31†). These properties include the electro-optic pockel's effect (EOPE), β(−ω,ω,0), and simple harmonic generation (SHG), β(−2ω,ω,ω), for first hyperpolarizabilities, as well as the electro-optic kerr effect (EOKO), γ(−ω,ω,0,0), and electric field-induced second harmonic generation (ESHG), γ(−2ω,ω,ω,0), for third-order responses. These parameters were evaluated to assess their potential for NLO applications. From the first hyperpolarizability values, summarized in Table S30,† it is evident that the EOPE and SHG are higher at 532 nm for most of the compounds. For example, at 532 nm, BTNC exhibited the first hyperpolarizability of β(−ω,ω,0) = 2.78 × 10−29 esu and β(−2ω,ω,ω) = 7.31 × 10−29 esu. In contrast, BNTP exhibited the highest static values among the synthesized compounds, highlighting its strong NLO response. The third-order responses displayed notable trends as well. BNTP showed the highest EOKO value at 532 nm, with γ(−ω,ω,0,0) = 1.19 × 10−33 esu, indicating its strong potential for third-order NLO applications. Similarly, BNPXZ demonstrated remarkable ESHG values at 1064 nm, with γ(−2ω,ω,ω,0) = 3.89 × 10−33 esu, showing its promise as a high-performance chromophore for second-order NLO processes. At 1064 nm, frequency-dependent properties were consistently enhanced for certain compounds. For instance, BNPXZ exhibited significant third-order NLO responses, with γ(−ω,ω,0,0) = 7.36 × 10−33 esu, indicating its potential as a high-performance third-order NLO chromophore. These results demonstrate the wavelength dependence of NLO properties, suggesting that the compounds can be tailored for specific applications at both 532 nm and 1064 nm. Above data provide understanding of the electro-optic and harmonic generation potential of these molecules for specific applications in optoelectronics, telecommunication, and other advanced technologies.
Conclusion
Herein, the optoelectronic and nonlinear optical (NLO) properties of BNCz based synthesized compounds namely BTNC–BNAC were explored. To explore the effect of π-conjugation (2-phenylthiophene) with various robust donors on the NLO properties, a set of four BNCz compounds (BNTP–BNTO) were designed. The effect of structural tailoring in the designed molecules was assessed for their NLO response using DFT computations. The D–π–A framework in compounds BNTP–BNTO exhibited comparable electronic properties to those of the D–A (BTNC–BNPZ) configuration. The Eg of all the explored compounds is found to be lower (2.784–3.774 eV) accompanied by redshift in absorption (566.138–412.854 nm). The energy order follows the trend: BTNC > BNAC > BNTC ≈ BNTA > BNTP > BNPXZ > BNTO > BNPZ. NBO analysis indicated that strong intramolecular interactions were key factors in stabilizing the studied compounds. Additionally, GRP analysis revealed higher softness, and lower hardness in all the entitled compounds especially in BNPZ and BNTO. These findings support the enhanced polarizability and charge transfer in the studied chromophores, leading to their suitable NLO properties. Among all the studied chromophores, the highest βtot and γtot values were observed for BNTP, measuring (74.0 × 10−30 esu) and γtot (81.1 × 10−35 esu), respectively. This study offers insights into the structure–property relationship of the optoelectronic compounds and may encourage experimental researchers to synthesize them for their notable NLO characteristics.
Data availability
All data generated or analyzed during this study are included in this published article and its ESI Files.†
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP 2503).
References
- F. Brown, R. E. Parks and A. M. Sleeper, Phys. Rev. Lett., 1965, 14, 1029 CrossRef.
- P. Franken, A. E. Hill, C. e. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118 CrossRef.
- J. Lin and C. Chen, Lasers Optron., 1987, 6, 59–63 Search PubMed.
- S. Muhammad, S. Kumar, J. Koh, M. Saravanabhavan, K. Ayub and M. Chaudhary, Mol. Simul., 2018, 44, 1191–1199 CrossRef CAS.
- A. Wadsworth, M. Moser, A. Marks, M. S. Little, N. Gasparini, C. J. Brabec, D. Baran and I. McCulloch, Chem. Soc. Rev., 2019, 48, 1596–1625 RSC.
- N. Liang, W. Jiang, J. Hou and Z. Wang, Mater. Chem. Front., 2017, 1, 1291–1303 Search PubMed.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Nat. Photonics, 2018, 12, 131–142 CrossRef CAS.
- S. R. Marder, J. E. Sohn and G. D. Stucky, Materials for Nonlinear Optics: Chemical Perspectives, ACS Publications, 1991 Search PubMed.
- V. Srinivasan, M. Panneerselvam, N. Pavithra, S. Anandan, K. Sundaravel, M. Jaccob and A. Kathiravan, J. Photochem. Photobiol., A, 2017, 332, 453–464 CrossRef CAS.
- J.-L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664–2668 CrossRef CAS.
- H. Alyar, Rev. Adv. Mater. Sci., 2013, 34, e87 Search PubMed.
- H. Narita, H. Min, N. Kubo, I. Hattori, T. Yasuda and S. Yamaguchi, Angew. Chem., Int. Ed., 2024, e202405412 CAS.
- B. Xerri, F. Labat, K. Guo, S. Yang and C. Adamo, Theor. Chem. Acc., 2016, 135, 1–9 Search PubMed.
- Y.-H. He, F.-M. Xie, H.-Z. Li, K. Zhang, Y. Shen, F. Ding, C.-Y. Wang, Y.-Q. Li and J.-X. Tang, Mater. Chem. Front., 2023, 7, 2454–2463 RSC.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- N. M. O'boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- G. Zhurko, Chemcraft, 2014, http://www.chemcraftprog.com Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. Dennington, T. Keith and J. Millam, GaussView 5.0, Gaussian, Inc., Wallingford, 2008, 20 Search PubMed.
- J. C. Kromann, C. Steinmann and J. H. Jensen, J. Chem. Phys., 2018, 149, 104102 CrossRef PubMed.
- A. Alparone, Chem. Phys., 2013, 410, 90–98 CrossRef CAS.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J.-L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC.
- F. Ullah, K. Ayub and T. Mahmood, New J. Chem., 2020, 44, 9822–9829 RSC.
- S. Haq, M. A. Asghar, I. Shafiq, M. Saeed, W. Anwer, M. Haroon and R. Alotaibi, Comput. Theor. Chem., 2024, 1240, 114788 CrossRef CAS.
- I. Shafiq, M. Khalid, R. Jawaria, Z. Shafiq, M. Haroon and T. Ahamad, J. Mol. Struct., 2025, 1326, 141142 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 Search PubMed.
- A. Luzanov and O. Prezhdo, J. Chem. Phys., 2006, 124, 224109 CrossRef CAS PubMed.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- K. Fukui, Science, 1982, 218, 747–754 Search PubMed.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- T. Koopmans, Physica, 1934, 1, 104–113 Search PubMed.
- J. Padmanabhan, R. Parthasarathi, V. Subramanian and P. Chattaraj, J. Phys. Chem. A, 2007, 111, 1358–1361 CrossRef CAS PubMed.
- M. U. Khan, M. Ibrahim, M. Khalid, S. Jamil, A. A. Al-Saadi and M. R. S. A. Janjua, Chem. Phys. Lett., 2019, 719, 59–66 Search PubMed.
- H. Mehmood, M. Haroon, T. Akhtar, S. Jamal, M. N. Akhtar, M. U. Khan and N. Alhokbany, Synth. Met., 2024, 307, 117701 CrossRef CAS.
- M. Khalid, I. Shafiq, M. Zhu, M. U. Khan, Z. Shafiq, J. Iqbal, M. M. Alam, A. A. C. Braga and M. Imran, J. Saudi Chem. Soc., 2021, 25, 101305 CrossRef CAS.
- N. Boukabcha, A. Djafri, Y. Megrouss, Ö. Tamer, D. Avcı, M. Tuna, N. Dege, A. Chouaih, Y. Atalay and F. Hamzaoui, J. Mol. Struct., 2019, 1194, 112–123 CrossRef CAS.
- I. Shafiq, M. Khalid, M. A. Asghar, M. Adeel, M. F. ur Rehman, A. Syed, A. H. Bahkali, A. M. Elgorban and M. S. Akram, J. Mater. Res. Technol., 2023, 24, 1882–1896 CrossRef CAS.
- M. Ans, J. Iqbal, Z. Ahmad, S. Muhammad, R. Hussain, B. Eliasson and K. Ayub, ChemistrySelect, 2018, 3, 12797–12804 CrossRef CAS.
- N. Tsutsumi, M. Morishima and W. Sakai, Macromolecules, 1998, 31, 7764–7769 CrossRef CAS.
- M. N. Arshad, I. Shafiq, M. Khalid and A. M. Asiri, ACS Omega, 2022, 7, 11606–11617 CrossRef CAS PubMed.
- A. Mahmood, A. Irfan, F. Ahmad and M. R. S. A. Janjua, Comput. Theor. Chem., 2021, 1204, 113387 Search PubMed.
- S. Bibi, R. Jia, H.-X. Zhang and F.-Q. Bai, Sol. Energy, 2019, 186, 311–322 Search PubMed.
- S. Kraner, G. Prampolini and G. Cuniberti, J. Phys. Chem. C, 2017, 121, 17088–17095 CrossRef CAS.
- İ. Sıdır, Y. G. Sıdır, M. Kumalar and E. Taşal, J. Mol. Struct., 2010, 964, 134–151 Search PubMed.
- M. Khalid, M. U. Khan, I. Shafiq, R. Hussain, A. Ali, M. Imran, A. A. Braga, M. Fayyaz ur Rehman and M. S. Akram, R. Soc. Open Sci., 2021, 8, 210570 CrossRef CAS PubMed.
- M. Szafran, A. Komasa and E. Bartoszak-Adamska, J. Mol. Struct., 2007, 827, 101–107 Search PubMed.
- A. Karakas, A. Elmali and H. Unver, Spectrochim. Acta, Part A, 2007, 68, 567–572 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- J. L. Bredas, C. Adant, P. Tackx, A. Persoons and B. Pierce, Chem. Rev., 1994, 94, 243–278 CrossRef CAS.
- V. M. Geskin, C. Lambert and J.-L. Brédas, J. Am. Chem. Soc., 2003, 125, 15651–15658 Search PubMed.
- K. J. Miller, J. Am. Chem. Soc., 1990, 112, 8543–8551 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Ataualpa Albert Carmo Braga
*a and
Ataualpa Albert Carmo Braga c
c