Doping Janus MoSSe monolayer with Al/Ga and P/As atoms, and their clusters: effective methods for the band structure and magnetism engineering

Abstract

In this work, new doping approaches are proposed towards effective band structure and magnetism engineering of Janus MoSSe monolayer. In its pristine form, MoSSe monolayer is a direct gap semiconductor. Magnetic semiconductor nature is obtained by doping with Al/Ga atoms at Mo sublattice and P atom at S sublattice. Herein, overall magnetic moments of 3.00/2.96 and 1.00 μ_B are obtained, respectively. Moreover, the spin-polarized states are produced primarily by the first neighboring Mo atoms from doping site and P impurity, respectively. Meanwhile, As doping metallizes the monolayer, maintaining its nonmagnetic nature. Similarly, no magnetism is induced by doping with AlP₃, AlAs₃, GaP₃, and GaAs₃ binary clusters. However, the substitution of these clusters causes large band gap reduction up to 78.85%, which can be attributed to new mid-gap subands formed mainly by Mo atoms. Further, doping with AlPAs/GaPAs and AlP₃As₃/GaP₃As₃ ternary clusters is also considered. In these cases, magnetic semiconductor and half-metallic natures are obtained, respectively, which are regulated primarily by Mo atoms. Further, Bader charge analysis is carried out to investigate the interactions between impurities/clusters with the host monolayer. Results demonstrate the charge gainer role of Al and Ga atoms, meanwhile P and As impurities act as charge gainer. Our findings may suggest the prospect of the proposed doping approaches to functionalize Janus MoSSe monolayer towards spintronic and optoelectronic applications.

---

1. Introduction

The discovery and successful isolation of graphene¹ has aroused tremendous interest in two-dimensional (2D) materials because of their novel physical and chemical properties. In particular, graphene has high charge migration rates, high carrier mobility, and a half-integer quantum Hall effect.^2,3 However, the semimetal character of pristine graphene hinders considerably its applications in the next-generation electronic devices, which motivates extensive research towards opening the graphene band gap while minimizing the undesired effects to its charge-transport properties. In this regard, tailoring the graphene structure to form nanoribbons with intrinsic band gap has been widely employed.^4,5 Unfortunately, the edge cutting reduces considerably the carrier mobility because of the disappearance of linear energy dispersion (Dirac cone) and scattering effects. Otherwise, the chemical modification through doping and adsorption is also an effective way to adjust the graphene band structure,^6–8 however the carrier recombination centers are introduced simultaneously. Along with modification of graphene electronic properties, the discovery of 2D semiconductor materials analogues of graphene has also attracted no less research attention. Specifically, the transition metal dichalcogenides (TMDs) form one of the most investigated families. Because of their chemical flexibility, diverse electronic natures from metallic (for example, NbS₂ (ref. 9)) to semiconductor. Particularly, MoS₂ and MoSe₂ monolayers are semiconductor with band gap of 1.9 and 1.5 eV,^10,11 respectively. The intrinsic band gap endows these 2D materials promise for photocatalysis,^12,13 electronic devices,^14,15 photovoltaics,^16,17 among others.

It is well known that modifying the chemical composition of materials may induce novel properties. Lu et al.¹⁸ have substituted the top-layer S of MoS₂ monolayer by Se atoms to synthesize successfully Janus MoSSe monolayer. This Janus structure has been also prepared by replacing one Se atomic layer in MoSe₂ monolayer by S atoms in an experiment realized by Zhang et al.¹⁹ Because of the unique geometry, the formation of Janus structure unlocks new physical and chemical properties that MoS₂ or MoSe₂ monolayer may not hold. The structural symmetry breaking generates an intrinsic electrostatic dipole in Janus structure that results in the emergence of a built-in electric field. This feature is of importance for the photocatalytic reactivity by facilitating the separation of the photogenerated carriers.²⁰ The existence of strong in-plane piezoelectric polarization and thickness- and strain-enhanced out-of-plane piezoelectric polarization in MoSSe monolayer has been also verified.²¹ Bifunctional electrocatalysis and harmful gas detection of MoSSe monolayer can be achieved by anchoring with noble metals.²² Further, various research groups have investigated the band structure and magnetism engineering in Janus MoSSe monolayer through doping,^23–25 point defects,^26,27 and surface functionalization.^28,29

Previously, some 2D magnetic Janus structures have been investigated such as FeClF,³⁰ and MnSeTe and MnSTe.³¹ However, MoSSe monolayer has no intrinsic magnetism, therefore functionalization process should be realized in order to open more functionality of this 2D material. Motivated by the huge research effort on developing new 2D magnetic systems towards spintronic applications, we propose the doping with IIIA-group atoms (Al and Ga) and VA-group atoms (P and As) to induce magnetism in Janus MoSSe monolayer. Specifically, Al and Ga atoms are introduced at Mo site because of their metallic nature (similar to Mo atom), meanwhile chalcogen sites are considered for P and As atoms because of their nonmetal characters. Details on the electronic and magnetic properties are provided through band structure, density of states, magnetic moments, and spin density illustration. It is anticipated that the incorporation of impurities in MoSSe monolayer generates new mid-gap states, which in turn make new promising systems for optoelectronic and spintronic applications.

2. Computational details

All calculations are performed using Vienna ab initio simulation package (VASP)^32,33 based on the projector augmented wave (PAW) method within density functional theory (DFT).³⁴ The generalized gradient approximation of Perdew–Burke–Ernzerhof³⁵ (GGA-PBE) is employed to derive the electron exchange–correlation interactions. The plane-wave cutoff energy of 500 eV is adopted. The Monkhorst–Pack k-grids are generated to carry out the Brillouin zone sampling.³⁶ Herein, k-point mesh is set to 20 × 20 × 1 for the pristine MoSSe (studied by a unit cell). The convergence criterion of electronic self-consistent loops is set to 1 × 10⁻⁶ eV. During the processes of structural relaxation, the residual force on each atom is less than 1 × 10⁻² eV per atom. The structural continuity of crystal structure along z-axis is broken by inserting a vacuum gap of more than 16.5 Å between the repeated monolayer images to eliminate their interactions. The Bader charge analysis is adopted to determine final atomic charges that is useful to study the interatomic interactions.^37,38

The doped MoSSe systems are modeled using a 4 × 4 × 1 supercell containing 16 Mo atoms + 16 S atoms + 16 Se atoms, whose Brillouin zone is integrated by a 4 × 4 × 1 Monkhorst–Pack k-point mesh. For the calculation of formation energy E_f, the formula is defined by:

where, E(do@MoSSe) and E(MoSSe) are total energy of the doped and pristine MoSSe monolayer, respectively; n_i and n_j denote number of the replaced host atom (i = Mo, Se, and Se) and number of impurities (j = Al, Ga, P, and As), respectively; μ_i and μ_j refer to chemical potential of atom i and j, respectively, which are calculated from their most stable bulk phase. Then, for the cohesive energy E_c calculation, following expression is used:herein, m_a is number of atom a in the doped MoSSe system (a = Mo, S, Se, Al, Ga, P, and As); E_a is energy of an isolated atom a.

The magnetic anisotropy energy (MAE) is determined through self-consistent spin orbit coupling (SOC) and non-collinear calculations, setting the in-plane magnetization (parallel to x-axis or [100] direction) and out-of-plane magnetization (parallel to z-axis or [001] direction) directions. Herein, total energies are denoted by E_[100] and E_[001], respectively. Then, MAE is given by:

MAE = E_[100] − E_[001] (3)

Note that negative MAE value corresponds to the in-plane magnetization, meanwhile positive value indicates the out-of-plane magnetization.

3. Results and discussions

3.1. Pristine Janus MoSSe monolayer

Fig. 1 shows a 4 × 4 × 1 supercell of Janus MoSSe monolayer that contains 16 Mo atoms + 16 S atoms + 16 Se atoms. The crystal structure is formed by a Mo atomic sublayer sandwiched between a S atomic sublayer and a Se atomic sublayer. This 2D material shares the similar hexagonal honeycomb structure of MoS₂ and MoSe₂ counterparts. From our calculations, Janus MoSSe monolayer has a lattice constant of 3.25 Å. This value is found between that of MoS₂ and MoSe₂ monolayers³⁹ and similar to that of Janus WSSe monolayer,⁴⁰ suggesting its reasonability and reliability. Moreover, some following structural parameters are also obtained: (1) chemical bond lengths: d_Mo–S = 2.42 Å and d_Mo–Se = 2.53 Å; (2) interatomic angles: ∠SMoS = 84.36°, ∠SMoSe = 81.42°, and ∠SeMoSe = 79.73°; and (3) total buckling height: Δ_t = Δ_Mo–S + Δ_Mo–Se = 1.53 + 1.70 = 3.23 Å. In the following, the electronic properties of Janus MoSSe monolayer are calculated using the optimized atomic structure.

Fig. 1 (a) Top-view from S side and (b) side-view of atomic structure of MoSSe monolayer in a 4 × 4 × 1 supercell (Mo atom: grey ball; S atom: yellow ball; Se atom: green ball).

Our spin-polarized calculations demonstrate the spin symmetry of the Janus MoSSe monolayer band structure and projected density of states (PDOS) as seen in Fig. 2. From the figure, it can be noted a K–K direct gap of this 2D material, where the valence band maximum is separated from the conduction band minimum by an energy range of 1.56 eV (E_g). In addition, the hybrid HSE06 functional is also employed⁴¹ that provides a direct gap of 2.02 eV. It is worth mentioning that for MoSSe monolayer, PBE calculations gives a more accurate band gap since an experimental band gap of 1.68 eV has been reported.¹⁸ Moreover, PDOS spectra indicate that Mo-4d, S-3p, and Se-4p orbitals build mainly the band structure. More specifically, Mo-d_eg (d_z²–d_x²−y²) state originates primarily the upper part of valence band and lower part of conduction band close to the Fermi level. It can be also noted small contribution from S-p_z state to the former subband, while S-p_x,y and Se-p_x,y states also contribute to the formation of the latter subband.

Fig. 2 (a) Spin-polarized band structure and (b) projected density of states of Janus MoSSe monolayer.

3.2. Effects of doping with single atoms

In this part, doping with IIIA-group atoms (M = Al and Ga) at Mo sublattice and VA-group atoms (X = P and As) at chalcogen sublattices is proposed to modify the MoSSe monolayer electronic and magnetic properties. Herein, P and As atoms replace S and Se atoms, respectively, considering the similar atomic size of P–S and As–Se pairs. The doped systems are denoted by M@mo and X@mo, respectively. Using eqn (1), E_f values of 3.36, 4.63, 1.57, and 1.43 eV per atom are obtained for Al@mo, Ga@mo, P@mo, and As@mo systems, respectively. Note that doping at chalcogen sites is energetically more favorable than doping at Mo site as suggested by smaller formation energy of X@mo systems as compared to that of M@mo systems. Once formed the doped MoSSe systems, their cohesive energy is calculated to be between −5.00 and −4.87 eV per atom (See Table 1), suggesting their good structural-chemical stability.

Table 1 Formation energy E_f (eV per atom), cohesive energy E_c (eV per atom), electronic band gap E_g (eV; spin-up/spin-down; M: metallic), charge transferred from M/P/As impurity ΔQ (e; positive value: charge losing; negative value: charge gaining), total magnetic moment M_t (μ_B), and magnetic anisotropy energy MAE (μeV) of the doped MoSSe monolayer

	Ef	Ec	Eg	ΔQ	Mt	MAE
Al@mo	3.36	−4.91	1.14/0.57	+2.14/—/—	3.00	−2320
Ga@mo	4.63	−4.87	1.01/0.49	+1.04/—/—	2.96	−620
P@mo	1.57	−5.00	1.51/0.23	—/−0.35/—	1.00	−1.71
As@mo	1.43	−5.00	M/M	—/—/−0.25	0.00	—
AP3@mo	1.77	−4.84	0.35/0.35	+1.95/−0.42/—	0.00	—
AA3@mo	1.30	−4.88	0.37/0.37	+2.02/—/−0.26	0.00	—
GP3@mo	2.00	−4.80	0.36/0.36	+0.78/−0.29/—	0.00	—
GA3@mo	1.58	−4.84	0.33/0.33	+0.98/—/−0.19	0.00	—
APA@mo	1.60	−4.88	0.02/0.27	+2.07/−0.64/−0.01	1.00	850
GPA@mo	1.97	−4.84	0.04/0.25	+0.86/−0.41/0.00	1.00	760
AP3A3@mo	1.41	−4.79	M/0.30	+1.87/−0.71/−0.24	0.79	290
GP3A3@mo	1.46	−4.76	M/0.42	+0.43/−0.31/−0.14	0.77	60

---

Fig. 3 elucidates the spin-polarized band structure of the doped MoSSe systems. It can be noted that Al, Ga, and P doping induces the asymmetric distribution between spin-up and spin-down channels with the appearance of new mid-gap states. Importantly, none of them goes across the Fermi level to determine the semiconductor character in both spin states, such that Al@mo, Ga@mo, and P@mo systems can be classified as 2D magnetic semiconductor systems that could be introduced as promising 2D spintronic candidates.⁴² Our calculations provide energy gaps of 1.14/0.57, 1.01/0.49, and 1.51/0.23 eV for their spin-up/spin-down state, respectively. Meanwhile, the spin-up and spin-down band structures of As@mo system are identical, where the mid-gap states determine its metallic nature. In other word, As doping causes the metallization of Janus MoSSe monolayer.

Fig. 3 Spin-polarized band structure of (a) Al@mo, (b) Ga@mo, (c) P@mo, and (d) As@mo systems (horizontal line: the Fermi level is set to 0 eV).

The asymmetric band structures suggest the emergence of spin-polarized states in Janus MoSSe monolayer upon doping with Al, Ga, and P atoms. The overall magnetic moments of 3.00, 2.96, and 1.00 μ_B are obtained for Al@mo, Ga@mo, and P@mo systems, respectively. The distribution of magnetic moments is now investigated by calculating the spin density defined by: ρ^↑ − ρ^↓, where ρ^↑ and ρ^↓ denote the charge density in spin-up and spin-down channels, respectively. From the results illustrated in Fig. 4, one can see that magnetic moment of M@mo systems is distributed mainly at the first Mo atoms from the doping sites. In other word, these Mo atoms produce primarily the magnetism in M@mo systems. Unlikely, P impurity generates mainly the spin-polarized states in P@mo system considering the highly concentrated spin surfaces at its position. Moreover, our calculations assert the in-plane magnetization of Al@mo, Ga@mo, and P@mo systems considering their negative MAE values of −2320, −620, and −1.71 μeV, respectively. In contrast, As doping at Se sublattice maintains the nonmagnetic nature of Janus MoSSe monolayer as asserted by the spin-symmetrical band structures and zero magnetic moment of As@mo system. Further, Bader charge of metal and pnictogen impurities is calculated to investigate the charge transfer process between them and the host MoSSe monolayer. It is found that Al and Ga metals lose charge, transferring charge quantities of 2.14 and 1.04 e to the host monolayer, respectively. In contrast, P and As atoms attract charge amounts of 0.35 and 0.25 e from the host monolayer, respectively. These charge transfers can be attributed to the environment in which impurities are located. Specifically, Al and Ga impurities are surrounded by more electronegative S/Se atoms, meanwhile the surrounding W atoms are less electronegative than P and As dopant atoms.

Fig. 4 Spin density in (a) Al@mo, (b) Ga@mo, and (c) P@mo systems (iso-surface value: 0.01 e Å⁻³).

PDOS spectra are given in Fig. 5 to provide more detail on the electronic and magnetic properties of the doped MoSSe systems. From the figure, one can see that the magnetic semiconductor nature of Al@mo and Ga@mo systems is regulated mainly by Mo-d_z²–d_x²−y² states since they originate primarily the subbands around the Fermi level, where small contribution from S(Se)-p_x,y,z and Al(Ga)-s states is also observed. Meanwhile, P-p_z state generates mainly the mid-gap states of P@mo system, confirming its key role on the magnetic semiconductor nature. Unlikely, As-p_z state is not observed the vicinity of the Fermi level in the case of As@mo system, whose metallic nature can be attributed mainly to Mo-d_z²–d_x²−y² states and S-p_z state.

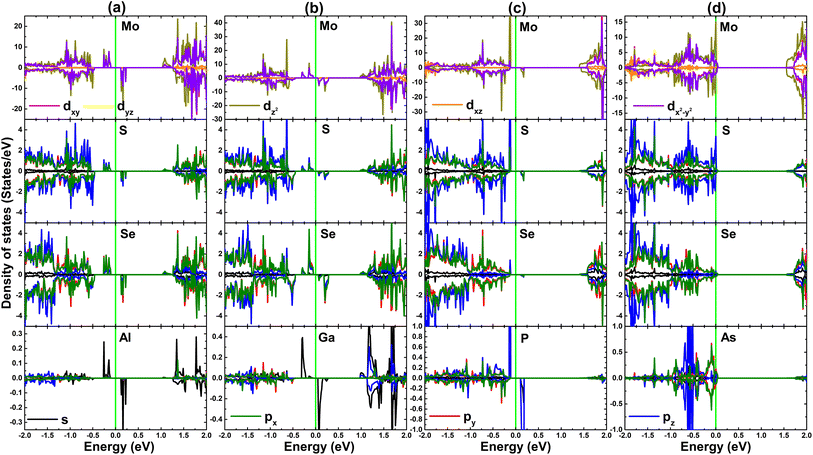Fig. 5 Projected density of states of (a) Al@mo, (b) Ga@mo, (c) P@mo, and (d) As@mo systems (vertical line: the Fermi level is set to 0 eV).

3.3. Effects of doping with MX₃ clusters

Herein, the effects of doping with AlP₃, AlAs₃, GaP₃, and GaAs₃ clusters on the MoSSe electronic and magnetic properties are investigated. The doped systems are denoted by AP3@mo, AA3@mo, GP3@mo, and GA3@mo, respectively. The formation energy of these systems are calculated to be 1.77, 1.30, 2.00, and 1.58 eV per atom, respectively. Note that these values are smaller than those of M@mo systems and slightly larger than those of X@mo systems (except for AA3@mo system, whose E_f is smaller than that of As@mo system). In addition, negative E_c values between −4.88 and −4.80 eV per atom confirm good structural-chemical stability of the considered doped MoSSe systems (see Table 1).

The calculated spin-polarized band structures of the MX₃-doped MoSSe systems are given in Fig. 6. It can be seen clearly two flat subbands above the Fermi level in all cases formed by new doping-induced mid-gap states. Importantly, the spin-up and spin-down states exhibit a perfectly coincident distribution. Moreover, the development of mid-gap state tunes effectively the MoSSe monolayer band gap. Specifically, energy gaps of 0.35, 0.37, 0.36, and 0.33 eV are obtained for AP3@mo, AA3@mo, GP3@mo, and GA3@mo. These results demonstrate that the substitutional incorporation of AlP₃, AlAs₃, GaP₃, and GaAs₃ clusters into MoSSe monolayer lattice causes considerably band gap reduction of the order of 77.56%, 76.28%, 76.72%, and 78.85%, respectively. The band gap reduction may open the working regime (towards infrared regime) of Janus MoSSe monolayer when integrated in optoelectronic devices.

Fig. 6 Spin-polarized band structure of (a) AP3@mo, (b) AA3@mo, (c) GP3@mo, and (d) GA3@mo systems (horizontal line: the Fermi level is set to 0 eV).

The performed Bader charge analysis indicates similar role of metal and pnictogen impurities in comparison with previous cases of single atom doping, that is charge loser role of metals and charge gainer role of pnictogens. Specifically, Al and Ga impurities in AP3@mo/AA3@mo and GP3@mo/GA3@mo systems transfer charge quantities of 1.95/2.02 and 0.78/0.98 e to the host monolayer, respectively. Meanwhile, P/As atoms gain charge amounts of 0.42/0.26 and 0.29/0.19 e from the host monolayer, respectively.

The coincidence of spin-up and spin-down states suggests that no spin-polarized state is produced in Janus MoSSe monolayer upon doping with MX₃ clusters. In other word, its nonmagnetic nature is preserved. This feature is also confirmed by zero magnetic moment of AP3@mo, AA3@mo, GP3@mo, and GA3@mo systems as obtained from our spin-polarized calculations. To further study the band gap reduction, atom-decomposed DOS of these systems are displayed in Fig. 7. Focusing on the subbands around the Fermi level, it can be seen that Mo and pnictogen impurities originate primarily the mid-gap states above the Fermi level, whose interactions are main responsible of the band gap reduction. Moreover, these interactions also regulate the energy gap of AP3@mo, AA3@mo, GP3@mo, and GA3@mo systems since they participate mainly in the formation of the upper part of valence band proximal to the Fermi level.

Fig. 7 Atom-decomposed density of states of (a) AP3@mo, (b) AA3@mo, (c) GP3@mo, and (d) GA3@mo systems (vertical line: the Fermi level is set to 0 eV).

3.4. Effects of doping with MPAs and MP₃As₃ clusters

Now, the band structure and magnetism engineering in Janus MoSSe monolayer is realized by doping with AlPAs, GaPAs, AlP₃As₃, and GaP₃As₃ clusters. In the cases, APA@mo, GPA@mo, AP3A3@mo, and GP3A3@mo notations are employed to denote the doped systems, respectively. Applying eqn (1), it is obtained E_f values between 1.41 and 1.97 eV per atom (see Table 1), respectively. Note that this parameter decreases according to increase the number of pnictogen atoms in the clusters. These results suggest the dual-doping is energetically more favorable than single metal atom doping, that is dual-doping may facilitate the substitution of Al and Ga metals into MoSSe monolayer sublattice. Considering the negative E_c values between −4.88 and −4.76 eV per atom, it can be concluded that the substitution of ternary clusters into Janus MoSSe monolayer leads to the formation of structurally-chemically stable 2D systems.

Fig. 8 displays the spin-polarized band structures for the considered cluster-doped MoSSe systems, in which new subbands are formed to determine diverse spin-polarized electronic properties. Specifically, APA@mo and GPA@mo systems are classified as magnetic semiconductor systems because of the semiconductor character of both spin states. Herein, their spin-up/spin-down states have energy gaps of 0.02/0.27 and 0.04/0.25 eV, respectively. In contrast, the spin-up state is metallized by doping with AlP₃As₃ and GaP₃As₃ clusters, such that the half-metallicity is obtained. In these cases, spin-down energy gaps of 0.30 and 0.42 eV are obtained, respectively. The development of feature-rich electronic properties suggests APA@mo, GPA@mo, AP3A3@mo, and GP3A3@mo as promising 2D materials to generate highly spin-polarized electrons in spintronic devices.⁴³

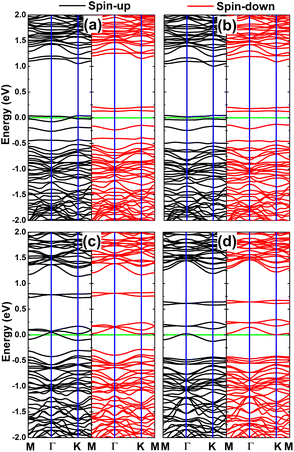Fig. 8 Spin-polarized band structure of (a) APA@mo, (b) GPA@mo, (c) AP3A3@mo, and (d) GP3A3@mo systems (horizontal line: the Fermi level is set to 0 eV).

The spin-asymmetry profile of band structures confirms the generation of magnetic moment in Janus MoSSe monolayer. Our calculations provide overall magnetic moments of 1.00, 0.79, and 0.77 μ_B for APA/GPA@mo, AP3A3@mo, and GP3A3@mo systems, respectively. The spin density in these systems is visualized in Fig. 9. From the figure, one can see high concentration of spin density located at first and second neighboring Mo atoms of P/As impurities in APA@mo and GPA@mo systems. In the latter one, small contribution from pnictogen atoms is also noted. In the cases of doping with P₃As₃ and GaP₃As₃ clusters, the spin-polarized states are produced primarily by first neighboring Mo atoms from doping sites, where the contribution from the substituted clusters is negligible. In addition, the MAE of APA@mo, GPA@mo, AP3A3@mo, and GP3A3@mo systems is calculated to be 850, 760, 290, and 60 μeV, respectively. Positive values suggest the out-of-plane magnetization of these cluster-doped MoSSe systems. Further, the Bader charge analysis asserts the charge transfer of 1.42 and 0.45 e from AlPAs and GaPAs clusters to the host MoSSe monolayer, respectively. In contrast, AlP₃As₃ and GaP₃As₃ clusters act as charge gainers, attracting charge quantities of 0.98 and 0.92 e from the host monolayer. Local Bader charges of each cluster are listed in Table 1.

Fig. 9 Spin density in (a) APA@mo, (b) GPA@mo, (c) AP3A3@mo, and (d) GP3A3@mo systems (iso-surface value: 0.002 e Å⁻³).

Atomic PDOS spectra of APA@mo, GPA@mo, AP3A3@mo, and GP3A3@mo systems are given in Fig. 10. The displayed results indicate that the subbands proximal to the Fermi level are formed mainly by Mo atoms, which regulate the band gap of semiconductor spin states and metallic character of spin-down states. In the cases of AP3A3@mo and GP3A3@mo systems, it can be noted also significant contribution of As atoms in building the subbands above the Fermi level. The degree of spin splitting also demonstrate the key role of Mo atoms in generating the spin-polarized states, which is in agreement with the analysis above.

Fig. 10 Atom-decomposed density of states of (a) APA@mo, (b) GPA@mo, (c) AP3A3@mo, and (d) GP3A3@mo systems (vertical line: the Fermi level is set to 0 eV).

4. Conclusions

In summary, DFT calculations have been performed to investigate systematically the effects of doping with Al/Ga and P/As atoms, and their clusters on the electronic and magnetic properties of Janus MoSSe monolayer. Pristine MoSSe monolayer is a direct gap 2D material, whose band structure is formed by Mo-d, S-p, and Se-p orbitals. The proposed doping makes new mid-gap subbands that determine diverse electronic properties. Specifically, the state transition from nonmagnetic semiconductor to magnetic semiconductor is induced by doping with single Al/Ga and P atom. In Mo-d_z²–d_x²−y² states originate primarily the mid-gap states with strong spin splitting to produce magnetic moment in the first cases, while the spin-polarized states in the latter case can be attributed to P-p_z state. The band structures maintains the spin-symmetric profile when doping with binary MX₃ clusters. Herein, the band gap exhibits significant reduction from that of pristine monolayer because of the appearance of new mid-gap proximal to the Fermi level, which can be attributed to Mo and P/As atoms. Meanwhile, the substitution of ternary MPAs makes new magnetic semiconductors, while the monolayer becomes half-metallic system upon doping with MP₃As₃ clusters. In these cases, the spin splitting and magnetic moment are produced primarily by Mo atoms, where small contribution from P/As atoms is also noted. Bader charge analysis indicates the charge losing of Al/Ga atoms, as well as of AlP₃, AlAs₃, GaAs₃, and MPAs clusters. Meanwhile, P/As atoms, and GaP₃ and MP₃As₃ clusters attract charge from the host monolayer. Our work provide insights into the band structure and magnetism engineering in Janus MoSSe monolayer by doping that are useful to design new promising 2D spintronic and optoelectronic materials.

Data availability

Data will be provided under requesting to authors.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

Calculations were performed in DGCTIC-UNAM Supercomputing Center (projects LANCAD-UNAM-DGTIC-368).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-e. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306(5696), 666–669.
2. C. Soldano, A. Mahmood and E. Dujardin, Production, properties and potential of graphene, Carbon, 2010, 48(8), 2127–2150.
3. D. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, Properties of graphene: a theoretical perspective, Adv. Phys., 2010, 59(4), 261–482.
4. Y.-W. Son, M. L. Cohen and S. G. Louie, Energy gaps in graphene nanoribbons, Phys. Rev. Lett., 2006, 97(21), 216803.
5. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Energy band-gap engineering of graphene nanoribbons, Phys. Rev. Lett., 2007, 98(20), 206805.
6. C.-H. Chang, X. Fan, L.-J. Li and J.-L. Kuo, Band gap tuning of graphene by adsorption of aromatic molecules, J. Phys. Chem. C, 2012, 116(25), 13788–13794.
7. X. Fan, Z. Shen, A. Liu and J.-L. Kuo, Band gap opening of graphene by doping small boron nitride domains, Nanoscale, 2012, 4(6), 2157–2165.
8. R. Balog, B. Jørgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Lægsgaard, A. Baraldi and S. Lizzit, et al., Bandgap opening in graphene induced by patterned hydrogen adsorption, Nat. Mater., 2010, 9(4), 315–319.
9. S. Zhao, T. Hotta, T. Koretsune, K. Watanabe, T. Taniguchi, K. Sugawara, T. Takahashi, H. Shinohara and R. Kitaura, Two-dimensional metallic NbS₂: growth, optical identification and transport properties, 2D Materials, 2016, 3(2), 025027.
10. X. Wang, Y. Gong, G. Shi, W. L. Chow, K. Keyshar, G. Ye, R. Vajtai, J. Lou, Z. Liu and E. Ringe, et al., Chemical vapor deposition growth of crystalline monolayer MoSe₂, ACS Nano, 2014, 8(5), 5125–5131.
11. N. Singh, G. Jabbour and U. Schwingenschlögl, Optical and photocatalytic properties of two-dimensional MoS₂, Eur. Phys. J. B, 2012, 85, 1–4.
12. R. Yang, Y. Fan, Y. Zhang, L. Mei, R. Zhu, J. Qin, J. Hu, Z. Chen, Y. Hau Ng and D. Voiry, et al., 2D transition metal dichalcogenides for photocatalysis, Angew. Chem., 2023, 135(13), e202218016.
13. W. Peng, Y. Li, F. Zhang, G. Zhang and X. Fan, Roles of two-dimensional transition metal dichalcogenides as cocatalysts in photocatalytic hydrogen evolution and environmental remediation, Ind. Eng. Chem. Res., 2017, 56(16), 4611–4626.
14. X. Song, Z. Guo, Q. Zhang, P. Zhou, W. Bao and D. W. Zhang, Progress of large-scale synthesis and electronic device application of two-dimensional transition metal dichalcogenides, Small, 2017, 13(35), 1700098.
15. X. Chen, C. Liu and S. Mao, Environmental analysis with 2D transition-metal dichalcogenide-based field-effect transistors, Nano-Micro Lett., 2020, 12, 1–24.
16. X. Yu and K. Sivula, Toward large-area solar energy conversion with semiconducting 2D transition metal dichalcogenides, ACS Energy Lett., 2016, 1(1), 315–322.
17. Z. Zhou, J. Lv, C. Tan, L. Yang and Z. Wang, Emerging frontiers of 2D transition metal dichalcogenides in photovoltaics solar cell, Adv. Funct. Mater., 2024, 2316175.
18. A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei and Y. Yang, et al., Janus monolayers of transition metal dichalcogenides, Nat. Nanotechnol., 2017, 12(8), 744–749.
19. J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy and L. Shi, et al., Janus monolayer transition-metal dichalcogenides, ACS Nano, 2017, 11(8), 8192–8198.
20. X. Ma, X. Wu, H. Wang and Y. Wang, A Janus MoSSe monolayer: a potential wide solar-spectrum water-splitting photocatalyst with a low carrier recombination rate, J. Mater. Chem. A, 2018, 6(5), 2295–2301.
21. L. Dong, J. Lou and V. B. Shenoy, Large in-plane and vertical piezoelectricity in Janus transition metal dichalchogenides, ACS Nano, 2017, 11(8), 8242–8248.
22. J.-X. Guo, S.-Y. Wu, G.-J. Zhang, L. Yan, J.-G. Hu and X.-Y. Li, Single noble metals (Pd, Pt and Ir) anchored Janus MoSSe monolayers: Efficient oxygen reduction/evolution reaction bifunctional electrocatalysts and harmful gas detectors, J. Colloid Interface Sci., 2022, 616, 177–188.
23. T.-N. Do, C. Nguyen, L. V. Tan, M. Idrees, B. Amin, N. V. Hieu, N. T. Hoai, L. T. Hoa, N. N. Hieu and H. V. Phuc, Effects of La and Ce doping on electronic structure and optical properties of Janus MoSSe monolayer, Superlattices Microstruct., 2021, 151, 106841.
24. R. Peng, Y. Ma, S. Zhang, B. Huang and Y. Dai, Valley polarization in Janus single-layer MoSSe via magnetic doping, J. Phys. Chem. Lett., 2018, 9(13), 3612–3617.
25. S.-S. Guan, S.-S. Ke, F.-F. Yu, H.-X. Deng, Y. Guo and H.-F. Lü, Controlling magnetism of monolayer Janus MoSSe by embedding transition-metal atoms, Appl. Surf. Sci., 2019, 496, 143692.
26. C. Long, Y. Dai and H. Jin, Effect of point defects on electronic and excitonic properties in Janus-MoSSe monolayer, Phys. Rev. B, 2021, 104(12), 125306.
27. M. Meng, T. Li, S. Li and K. Liu, Ferromagnetism induced by point defect in Janus monolayer MoSSe regulated by strain engineering, J. Phys. D: Appl. Phys., 2018, 51(10), 105004.
28. Z. Cui, N. Lyu, Y. Ding and K. Bai, Noncovalently functionalization of Janus MoSSe monolayer with organic molecules, Phys. E, 2021, 127, 114503.
29. X. Zhang, Y. Song, F. Zhang, Q. Fan, H. Jin, S. Chen, Y. Jin, S. Gao, Y. Xiao and N. Mwankemwa, et al., The electronic properties of hydrogenated Janus MoSSe monolayer: a first principles investigation, Mater. Res. Express, 2019, 6(10), 105055.
30. L. Zhang, Y. Liu, M. Wu and G. Gao, Electric-field-and stacking-tuned antiferromagnetic FeClF bilayer: The coexistence of bipolar magnetic semiconductor and anomalous valley hall effect, Adv. Funct. Mater., 2024, 2417857.
31. L. Zhang, Y. Zhao, Y. Liu and G. Gao, High spin polarization, large perpendicular magnetic anisotropy and room-temperature ferromagnetism by biaxial strain and carrier doping in Janus MnSeTe and MnSTe, Nanoscale, 2023, 15(46), 18910–18919.
32. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50.
33. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54(16), 11169.
34. W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140(4A), A1133.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
36. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B:Condens. Matter Mater. Phys., 1976, 13(12), 5188.
37. W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21(8), 084204.
38. M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134(6), 064111.
39. A. Kandemir, H. Yapicioglu, A. Kinaci, T. Çağın and C. Sevik, Thermal transport properties of MoS₂ and MoSe₂ monolayers, Nanotechnology, 2016, 27(5), 055703.
40. A. Patel, D. Singh, Y. Sonvane, P. Thakor and R. Ahuja, High thermoelectric performance in two-dimensional Janus monolayer material WS-X (X= Se and Te), ACS Appl. Mater. Interfaces, 2020, 12(41), 46212–46219.
41. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106.
42. K. Sato and H. Katayama-Yoshida, First principles materials design for semiconductor spintronics, Semicond. Sci. Technol., 2002, 17(4), 367.
43. X. Li and J. Yang, First-principles design of spintronics materials, Natl. Sci. Rev., 2016, 3(3), 365–381.

---