Novel insights into nanoscale surface displacement detection in polystyrene thin films using photothermal mirror- and atomic force microscopy-mid-IR spectroscopy

Abstract

Photothermal spectroscopy techniques operating at single wavelengths in the vis-NIR range have been widely used to measure optical absorption and thermal characteristics of materials owing to their high sensitivity. We introduced photothermal mirror spectroscopy employing a highly tunable mid-IR pump laser (PTM-IR) for the chemical analysis of thin film polystyrene samples on IR transparent calcium fluoride substrates. PTM-IR spectroscopy surpasses conventional PTM spectroscopy as it provides chemical specificity through molecule-specific absorption via the detection of the magnitude of the PTM signal as a function of the excitation wavelength. We compared the obtained spectra with those measured using atomic force microscopy-infrared spectroscopy (AFM-IR), an already well-established photothermal technique also operating in the mid-IR range, and standard Fourier-transform infrared (FT-IR) spectroscopy. Numerical simulations using finite element analysis were employed to estimate the expected increase in temperature and surface deformation induced by the laser pulse train in each photothermal technique. Excellent agreement was obtained across the studied techniques in terms of qualitative mid-IR spectra and thickness determination.

---

Introduction

The chemical and mechanical properties of polymer thin films can be tailored by changing their chemical composition, enabling them to address the specific needs stemming from a wide range of application areas, such as flexible electronics,^1,2 the energy sector for solar cells³ and batteries,⁴ as well as the biomedical field for targeted drug delivery,⁵ tissue engineering,⁶ or development of biosensors.⁷ These films are characterised by their physical properties and chemical composition, which need to be determined and controlled when using them either in research or industrial applications. Parameters of interest often include the thickness of the films and their uniformity in terms of their molecular composition and structural phase, such as crystallinity or amorphous regions.

The chemical composition of molecules is typically analysed using vibrational spectroscopy techniques, such as infrared spectroscopy or Raman spectroscopy. When infrared (IR) light is absorbed by the molecule of interest, vibrational modes are stimulated, thus allowing the identification of functional groups. Notably, the mid-infrared (mid-IR) spectral region between 4000 and 400 cm⁻¹ holds great significance because it covers fundamental molecular vibrations that can be associated with specific molecular features. Arguably, the most known technique for thin film characterisation is spectroscopic ellipsometry. In recent years, developments in quantum cascade laser-based mid-IR spectroscopic ellipsometry have been demonstrated.⁸ Grazing angle reflectance spectroscopy is also an established technique allowing thin film analysis utilising FT-IR instrumentation. Notable indirect techniques are time domain thermoreflectance (TDTR),⁹ infrared reflection-adsorption spectroscopy (IRRAS), and polarisation modulation IRRAS (PM-IRRAS).^10,11 TDTR is a pump-probe technique where an ultra-fast laser, e.g., a mode-locked Ti:sapphire laser oscillator, is split and used as a pump and probe beam through a polarising beam splitter. Then, the pump laser is used to heat the material surface, where the delayed probe laser measures the change in reflectivity caused by temperature changes.⁹ However, measurements require a fairly complex setup, highly reflective surfaces, e.g., a thin metallic transducer film applied over the sample of interest, and ultrafast lasers in the femto- and pico-second regimes. (PM-)IRRAS measurements equally rely on substrates of high reflectivity, where, after absorption of light by the thin film, a change in reflection occurs, which can be used for the direct measurement of the film thickness. This limits the substrates and scenarios where this technique can be used. Another method for analysing thin polymer films is attenuated total reflection Fourier transform infrared (ATR-FTIR) spectroscopy.¹² Here, the developed evanescent field at the crystal/sample interface interacts with the thin film sample. However, this means that the thin film needs to be fixed on the ATR crystal, which limits the number of samples that can be studied. Another limitation is that the film thickness in relation to the depth of penetration effectively limits the range of suitable film thicknesses.

In this work, we applied two notable techniques for the chemical analysis and thickness determination of thin polymer films: photothermal mirror-infrared (PTM-IR) spectroscopy and atomic force microscopy-infrared (AFM-IR) spectroscopy.

PTM-IR spectroscopy is a non-destructive, all-optical pump-probe method that can measure the thermo-optical and mechanical properties of materials. In this method, a modulated mid-IR laser beam is used for the photothermal excitation of the sample. This periodic excitation causes surface deformation of the sample, which induces a phase shift to the probe beam reflected off the sample surface. The probe beam is placed collinear to the excitation beam and detected in the far-field region by monitoring its intensity signal. The time evolution of the laser-induced surface deformation depends on thermal diffusivity, and the amplitude of the deformation is directly related to the optical absorption and thermal expansion coefficients.^13–15 The PTM method has already been successfully applied for material characterisation using visible laser excitation and for glasses,^13–17 polymers,¹⁸ metals,^19–22 and semiconductors,²³ providing insights into the thermal diffusivity, optical absorption, and linear thermal expansion coefficients of the sample.

AFM-IR spectroscopy—another indirect photothermal method—combines high-spatial resolution beyond the diffraction limit^24–27 with the chemical specificity of mid-IR spectroscopy. This allows morphology and chemical composition analyses at the nanoscale, which have been demonstrated with various materials.^28–33 Characterisation beyond the diffraction limit is achieved by a sharp probe, where a pulsed, tuneable mid-IR laser causes a local, short-lived photothermal expansion upon absorption of IR light and thermal expansion of the sample, which pushes the cantilever upwards. This expansion then resolves in a damped oscillatory motion of the cantilever. As demonstrated by Dazzi et al., this ring down is proportional to the absorption coefficient of the sample.^25,34 Thus, by keeping the cantilever tip in position and tuning the IR excitation laser, absorbance infrared spectra are generated, resembling conventional FT-IR spectra. In contrast, keeping the wavelength fixed and scanning the sample, a chemical image at a specific absorption wavelength can be recorded.

The experimental capabilities of the PTM method were extended to investigate thin polystyrene films using an external cavity quantum cascade laser (EC-QCL). This is the first time the method was applied to characterise thin films, and a mid-IR pump laser was introduced, allowing chemical analysis of the thin films. The results were found to be in excellent agreement with AFM-IR and FT-IR measurements. The dependence of the photothermal signal was evaluated for different powers and thin film thicknesses. The theoretical model presented describes the temperature change and surface displacement, considering the heat transfer effect from the thin film to the surrounding air and substrate. The dependence of temperature and surface displacement was investigated for different substrates and film thicknesses. The PTM-IR method presented here can be a valuable tool for in situ characterisation of thin films on non-absorbing substrates, where fast, remote, and non-destructive measurements are required. The advantages and disadvantages of each method are also presented to evaluate different tools that can be used to investigate thin film materials as we move toward technological advancements fuelled by nanomaterials.

Results

Mid-infrared spectroscopy

Measurements of the polystyrene (PS) thin films were performed with PTM-IR and AFM-IR, and as a control, state-of-the-art FT-IR was used as described in Methods.

The spectral coverages differ for the techniques used (see also Methods). The EC-QCL pump source used in the PTM-IR technique allows a coverage of 1798–1488 cm⁻¹. Thus, as we investigate polystyrene thin films, we focus on the aromatic ring stretching vibration at 1601 cm⁻¹. The additional aromatic ring modes at 1492 cm⁻¹ and 1451 cm⁻¹ are not plotted in Fig. 1 for either technique to maintain consistency and allow direct comparison of the three techniques investigated.

Fig. 1 Polystyrene thin film spectra with varying film thicknesses (1080 nm, 742 nm, 370 nm, 340 nm, 208 nm, and 113 nm) compared with PTM-IR, AFM-IR and FT-IR. Each spectrum is an average of 10 spectra. Spectra are normalized, smoothed, and baseline corrected (see Methods). The insets show (a) PTM-IR and (b) AFM-IR signal amplitude at 1601 cm⁻¹ for the PS thin film on CaF₂ optical window for different thicknesses.

The infrared spectra of the polystyrene thin films (with film thicknesses from 113 nm to 1080 nm) are shown in Fig. 1. Using the three techniques, characteristic bands at 1601 cm⁻¹ and 1583 cm⁻¹ were reproduced, which can be assigned to the aromatic ring stretching of polystyrene. A further band appears at 1540 cm⁻¹, which also corresponds to the stretching vibration of the phenyl ring. However, these bands are clearly visible in the PTM-IR and FT-IR spectra although only observable for films with greater thickness. In the AFM-IR spectra, the shape of the band is only barely recognisable, often lost in noise. However, it is worth noting that AFM-IR examines a nanoscopic part of the sample, while the other two techniques average millimetre ranges over a longer period of time.

The band positions as well as the band shapes obtained are comparable for all the three techniques (see Fig. 1 and S1†). The PTM-IR spectra were recorded in the reflection mode on a sample surface area of a few millimetres square. The FT-IR measurements were recorded in transmission, where the probed area is approximately the same as that in PTM-IR, whereas the spectra obtained using AFM-IR are limited by the size of the cantilever tip, with a tip radius <25 nm. Thus, the AFM-IR technique has a much higher spatial resolution, and the effect is measured locally. In comparison, the results obtained by PTM-IR and FT-IR provide an average value of a much larger (millimetre range) probed region. By selecting the marker band of polystyrene at 1601 cm⁻¹, it is possible to plot the signal intensity of the respective technique against the thickness; see insets Fig. 1a and b. Note that the used signal value is an average of 10 recorded spectra of each thin polymer film ranging from 113 nm to 1080 nm (see Table 1). The relationship between signal intensity and film thickness is clearly evident across all three techniques (FT-IR data, see Fig. S2†). The optical absorption coefficient of (540 ± 30) cm⁻¹ for polystyrene thin films at 1601 cm⁻¹ was obtained from the linear fit of absorbance versus thickness by multiplying the slope by ln(10) and used in the simulations of temperature change and surface deformation presented in the next section. The obtained optical absorption coefficient agrees with the literature data.³⁵

Table 1 Actual concentrations and measured thicknesses of the polystyrene thin films

Concentration (wt%)	Film thickness (nm)
1.71	113
1.88	208
4.06	340
4.39	370
5.98	742
7.76	1080

---

Photothermal effect is induced by optical absorption and subsequent temperature variation and thermal expansion. Fig. 2 shows the PTM signal obtained from detector D₂ (as shown in Fig. 5) and demodulated by a lock-in amplifier at a frequency of 80 Hz and duty cycle of 50% (detailed description in Methods). A linear relationship between the photothermal signal and peak excitation power was observed as expected.

Fig. 2 (a) PTM-IR spectra for excitation at different peak powers for polystyrene thin film with thickness of 742 nm on the CaF₂ substrate. (b) PTM-IR amplitude signal power dependence at 1601 cm⁻¹.

Temperature change and surface deformation induced by laser

The temperature change, T_i(r,z,t), in the PS thin film (i = film) on a CaF₂ optical window (i = ow) surrounded by air (i = air) caused by laser absorption can be calculated using the heat diffusion equation:²⁰where, ρ_i is mass density, c_pi is specific heat, k_i is thermal conductivity, α_i is the optical absorption coefficient at the excitation wavenumber, ω_e is the radius of the excitation beam in the thin film, and t is time. Since the problem is circularly symmetric, temperature and displacement depend only on the normal z- and radial r-coordinates. z_i is the position of the first interface of each material. Assuming that the origin of the coordinate system is at the air/film interface, z_film = 0 and z_ow = L_film. The amplitude of the heat source (Q_film) = 2P_eϕ/πω_e². The optical absorption in the fluid and substrate can be neglected, i.e., α_air = α_ow = 0. P_e is the excitation beam peak power, and ϕ accounts for the fraction of the absorbed energy converted into heat. When the absorbed energy is completely converted into heat, ϕ = 1. The temporal distribution of the laser source is represented by F(t). In this work, we considered three cases for the time-dependence source term:where, f_R is pulse repetition frequency, τ is laser pulse width, the duty cycle is defined by D = τf, and sgn(x) refers to the sign function.

Surface displacement in the thin film and substrate, u_i(r,z,t), induced by the non-uniform temperature distribution can be calculated using the thermoelastic equation.^19,20

ν is Poisson's ratio, α_T is linear thermal expansion coefficient, and E is Young's modulus. The last term on the right side of eqn (3) is known as inertia term. For continuous excitation and low modulation frequency, the inertia term can be neglected, and the displacement is governed by temperature change. This assumption is known as quasistatic approximation. However, for pulsed laser excitation with a pulse width of a few nanoseconds, the inertia term yields elastic wave motion.²² We applied finite element analysis (FEA) to solve eqn (1) and (3) (see Methods). A complete FEA description, physical properties, and experimental parameters used for the simulations are presented in the Methods section, Tables 2 and 3. Fig. 3 shows the time-dependent temperature and axial surface deformation at the interface air/thin film (z = 0) and centre of the laser beam (r = 0), considering the experimental parameters related to the spatial and temporal profile of the mid-IR laser in the PTM-IR (Fig. 3a and c) and AFM-IR (Fig. 3b and d) for the PS thin film with different thicknesses on CaF₂ optical window. For thicker films, more energy is absorbed, inducing a greater temperature change and, consequently, a more significant thermal deformation.

Table 2 The thermal and mechanical properties used for the simulations. The parameters listed below are associated with characteristic values found in the literature. The optical absorption coefficient (α) of PS used in the simulations was 540 cm⁻¹ (measured in this work at 1601 cm⁻¹)

Properties (units)	k (W m^−1 K^−1)	ρ (kg m^−3)	cp (J kg^−1 K^−1)	αT (10^−6 K^−1)	ν	E (10^9 Pa)
Air^37	0.026	1.18	1007	—	—	—
PS^38	0.12	1050	1300	70	0.38	3.25
CaF2 ^39	9.71	3180	854	18.85	0.26	75.8
ZnSe^39	18	5270	339	7.1	0.28	67.2
ZnS^39	27.2	4090	515	6.5	0.28	74.5
Silicon^39	163.3	2330	703	2.6	0.266	131

---

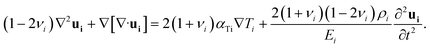Table 3 Parameters used in simulations related to the spatial and temporal profile of the excitation beam in the PTM-IR and AFM-IR techniques

Parameters	Units	PTM-IR	AFM-IR
ωe	μm	400	40
fR	Hz	80	200 k
τ	μs	6250	0.200
D	%	50	4.0
Pe (at 1601 cm^−1)	mW	70	130

---

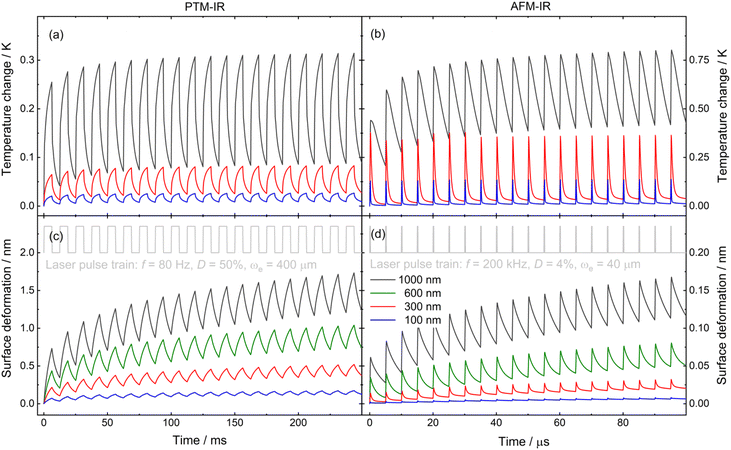Fig. 3 Time-dependent (a and b) temperature change and (c and d) axial surface displacement at the interface air/thin film (z = 0 and r = 0) for the PS thin film with different thicknesses on the CaF₂ optical window. The result was obtained using FEA considering the parameters related to the spatial and temporal laser profile in (a and c) PTM-IR and (b and d) AFM-IR, presented in Table 2 and 3.

PTM-IR and AFM-IR used different laser repetition frequencies, pulse widths, and laser beam dimensions, leading to different behaviours for temperature change and deformation in the sample. For PTM-IR, a modulation frequency of 80 Hz, duty cycle of 50%, peak power of 70 mW (average power of 35 mW), and excitation beam radius on the sample of 400 μm were used. For a film thickness of 1000 nm, after 20 pulses, a temperature increase of approximately 300 mK and surface deformation of 1.7 nm were observed, as shown in Fig. 3a and c. For samples with smaller film thicknesses, a sub-nanometre surface deformation was observed. In contrast, AFM-IR, operating at a higher modulation frequency of 200 kHz with a duty cycle of 4%, peak power of 130 mW, and a beam radius of 40 μm, resulted in a larger temperature increase of 800 mK but a smaller surface deformation of 0.17 nm, as shown in Fig. 3b and d. The greater local temperature change obtained for the AFM-IR technique is mainly related to the laser beam being more focused, with a diameter 10× smaller than that in PTM-IR. The greater surface deformation for PTM-IR is due to the lower modulation frequency and longer time required to perform the measurement. Since PTM-IR was performed at low frequency, the time required to perform the measurement at each wavelength is in the order of milliseconds. After the train of laser pulses and heat diffusion from the thin film to the substrate and air, the temperature oscillation did not change significantly. However, the surface deformation continued to increase due to the continuous heat transfer to the substrate, which increases the depth at which heat reaches the substrate, thus contributing significantly to surface deformation. Thus, for low frequencies, the majority of the surface deformation contribution is induced by the expansion of the substrate, with the thin film acting as the optical absorber on the surface. A similar effect is observed for the parameters used in AFM-IR; however, as the measurement is performed faster (shorter time), the heating is localised and the substrate contributes less to the deformation observed at the thin film interface. The dynamics of temperature distribution and surface deformation over time for the PS thin film on CaF₂ substrate can be observed in animations S1–S4 presented in the ESI.† In both cases, it is observed that there is not enough time for complete thermal relaxation between subsequent pulses. Thus, there is heat accumulation due to the laser pulse train. Using higher frequencies and shorter time measurements favors more significant contribution of the measured deformation induced by the thermal expansion of the thin film.

The effect of different substrates on temperature change and surface displacement of the film was evaluated (Fig. 4). Transparent materials commonly used in the mid-infrared range were considered (CaF₂, ZnSe, ZnS, and silicon). It was observed that for high modulation frequencies (such as those used in AFM-IR), temperature change does not differ much between the substrates; however, more significant surface displacement is observed using CaF₂ as the substrate (see Fig. 4c and d). For low modulation frequencies (such as those used in PTM-IR), the effect of the substrate on temperature increase is considerably higher. Substrates with lower thermal conductivity dissipate less heat and reach greater temperature change around the laser excitation region. For surface displacement, the variation can be two orders of magnitude for different substrates. Substrates with lower thermal conductivity and higher coefficient of thermal expansion (such as CaF₂) will have more significant thermal expansion, amplifying the photothermal signal measured using PTM-IR and AFM-IR techniques, while substrates with higher thermal conductivity and lower coefficient of thermal expansion (such as silicon) will expand less. Furthermore, specifically for the PTM-IR method, silicon is unsuitable owing to its high optical absorption in the visible spectrum (wavelength range of the probe beam laser). Additionally, ZnSe and ZnS substrates have higher optical absorption coefficients in the visible region than CaF₂, possibly inducing a permanent temperature gradient in the substrate and thin film. Consequently, the wedged CaF₂ optical window was the ideal candidate for this proof-of-principle study as a substrate for thin films. Simulation results presented herein offer valuable insights into temperature variations and surface displacement, thereby enhancing the understanding of alternative methods involving laser beam interactions with absorber films.

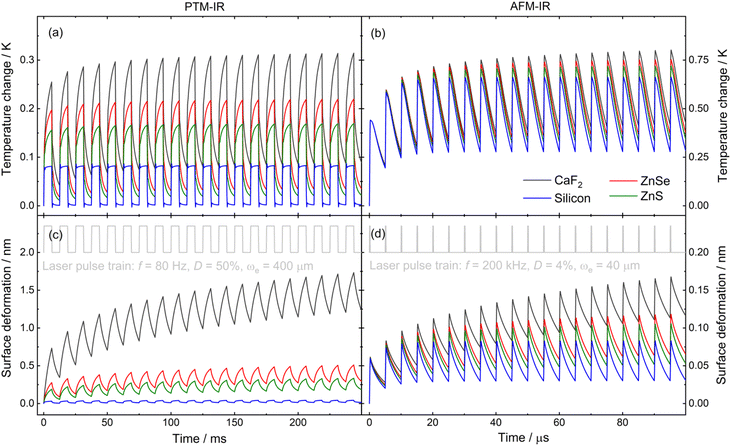Fig. 4 Time-dependent (a and b) temperature and (c and d) axial surface deformation at (z = 0) and (r = 0) considering a PS film with a thickness of 1000 nm on different substrates (CaF₂, ZnSe, ZnS, and silicon) and the spatial and temporal profile of the excitation laser used in each technique. The result was obtained using FEA considering the parameters presented in Tables 2 and 3, related to the spatial and temporal laser profile in the (a and c) PTM-IR and (b and d) AFM-IR methods.

Discussion

We measured sub-nanoscale surface displacements in polymer thin films using PTM-IR and AFM-IR techniques. Herein, the thin-film samples were on a transparent substrate and illuminated by mid-IR incident pulses. The mid-infrared spectra recorded with these techniques showed excellent agreement with FT-IR measurements. A linear relationship between absorbance, PTM-IR, AFM-IR signals, and film thickness was observed. Despite the high optical absorption coefficient of polystyrene at 1601 cm⁻¹, light attenuation in the thin film was minimal owing to their small thickness, ranging from approximately 0.5% for 113 nm films to 6% for 1080 nm films. Thus, following the Beer–Lambert law, a linear relationship between absorbance and film thickness was observed. There is also a linear dependence of the absorbed light intensity and film thickness for α_filmL_film ≪ 1, e^{−α_filmL_film} ≈ 1 − α_filmL_film.

Our findings demonstrate that silicon is unsuitable for the PTM-IR method. While ZnSe and ZnS are potential alternatives, they show higher optical absorption coefficients in the visible region compared to CaF₂. Thus, we selected the wedged CaF₂ optical window as an ideal candidate for this study. The simulations performed to validate this choice provide valuable insights into temperature variations and surface displacement across various substrates.

A notable advantage of the PTM-IR technique is its ability to remotely detect subtle changes in optical absorption, thus making it highly sensitive and a valuable tool for in situ characterisation, where fast and non-contacting measurements are required. Using a larger spot of the excitation and probe beams at the sample position, it is possible to keep the optical components, such as lenses and mirrors, far from the sample while maintaining good sensitivity of infrared spectrum measurement for remote sensing; however, at the cost of spatial resolution. Additionally, it is a non-contact, non-destructive technique, meaning that the sample remains intact during measurements. However, as the PTM-IR measurements are conducted in the reflection mode, the surface roughness of the sample surfaces investigated can affect the result. This can have two causes: high roughness results in poor quality of the probe beam reflected on the photodetector, possibly affecting the signal intensity recorded. Furthermore, a rough surface can affect mid-IR optical absorption due to slight changes in the film thickness, thus influencing the signal intensity in all methods that use optical absorption to characterise thin films. In addition, in this proof-of-concept study, the PTM-IR setup relies on manual adjustments. This means that the reflected probing beam needs to be realigned for each sample to guarantee that the centre of the beam reaches the pinhole-photodetector assembly (as described in Methods), which affects measurement time; however, it can be fully automated. The measurement of the PTM signal as a function of time allows the fit with the theoretical model to obtain the thermo-optical properties of the sample.^13–15 However, it should be noted that for the samples studied in this work, the measured PTM signal corresponds to the same order of magnitude of the noise (RMS) as the probe laser used. Therefore, it was not possible to obtain a transient PTM signal with good SNR to fit the experimental data with the theoretical model. The lock-in amplifier was used to measure the tiny photothermal mirror signal and thus obtain the mid-IR spectrum. For the time-domain PTM signal, a probe beam with higher optical power (to increase the light intensity reflected on the thin film–air interface) and with lower noise would be necessary. As previously mentioned, for continuous-wave excitation, the thin film behaves as a surface absorber, and the dominant contribution to the PTM signal is induced by the thermal expansion of the substrate. Thus, the theoretical fit of the transients would be mainly related to the optical absorption of the thin film as well as the thermal and mechanical properties of the substrate. Furthermore, photothermal lens-infrared (PTL-IR) spectroscopy measurements were conducted. Nevertheless, the probe beam passing through the thin film and substrate yielded no detectable signal (data not shown here). This clearly indicates that in this particular case, the phase shift induced by surface deformation in the reflected beam dominates over the thermal lens effect in the transmitted beam.

AFM-IR, when compared as an indirect photothermal technique, is also non-destructive, allowing for multiple measurements on the same sample. In AFM-IR, similar to PTM-IR, surface deformation allows for signal generation. Although the main advantage of AFM-IR, its high spatial resolution, is not utilised in this work, it is precisely this characteristic that needs to be discussed. Local photothermal excitation causes thermal expansion, which is then detected by a cantilever with a tip diameter >25 nm. This means that AFM-IR, similar to PTM-IR, relies on sample preparation, because signal generation occurs in a very small sample area. While thin films are ideal for measurement, rough sample surfaces can result in varying signal intensities, as the tip is fixed at one location while recording a spectrum. This issue was addressed by recording spectra at different locations on the sample. Furthermore, AFM-IR signal quality is highly dependent on the focus of the IR beam and its position relative to the tip; however, by keeping the cantilever used the same and not changing the focus, good comparability between samples can be achieved.

Methods

Materials

All reagents in this work were used as received. Polystyrene (Mw = 250.000) was purchased from Sigma Aldrich. Toluene (AnalaR Normapur) was purchased from VWR Chemicals. Calcium fluoride wedged windows (30 arcminute wedge) were purchased from Crystran Ltd.

Film preparation

Polymer thin films were created by spin-coating polystyrene (PS) from solution. PS was dissolved in toluene via magnetic stirring without heating. Upon complete dissolution, 90 μL of the solution was immediately spin-coated (Spin150i Tabletop, APF Automation) on a cleaned wedged CaF₂ optical window. Spin coating parameters were selected as follows: 2000 rpm for a duration of 60 s using 2 s acceleration. Using the same parameters, a total of six thin-film samples with concentrations ranging from 1.7 wt% to 8 wt% were prepared. No further annealing was conducted.

Thin film thickness measurement

Film thicknesses were determined using a profilometer (Bruker Dektak XT), resulting in 113 nm, 208 nm, 340 nm, 370 nm, 742 nm and 1080 nm thickness.

Furthermore, using the profilometer, surface roughness measurements were conducted by acquiring three sample line-scans in the sample area of interest. Each line was 400 μm for 60 s using a 3 mg force. Arithmetic mean roughness (R_a) and arithmetic mean waviness (W_a) were recorded. Surface roughness measurement results are listed in the ESI† (Table S7).

PTM-IR

The experimental diagram for PTM-IR measurements is shown in Fig. 5. A tuneable, continuous wave (cw) external cavity quantum cascade laser (HEDGEHOG, DRS Daylight Solutions Inc., model 41062-HHG-UT) with a spectral coverage of 1798 cm⁻¹ to 1488 cm⁻¹ was used to pump the sample. A mechanical shutter (Stanford Research Systems, Model SR475) was used to modulate the continuous excitation with a frequency of 80 Hz and a duty cycle of 50%. The excitation beam was split in the ratio of 50 : 50 (R : T) by means of a ZnSe beam splitter (Thorlabs, model BSW711). The reflected beam was measured by an infrared photodetector D₁ (VIGO Photonics, model LabM-I-10.6) connected to a thermoelectric cooler controller (VIGO Photonics, model PTCC-01-ADV) and a lock-in amplifier (Zurich Instruments, model MFLI 500 kHz) and used as a reference for excitation power. The transmitted beam was focused on the sample position using a ZnSe lens (L₃) with a focal length f = 0.20 m (Thorlabs, model LA7228-E2). A 10 mW continuous TEM₀₀ He–Ne laser at 632.8 nm (Thorlabs, model HNL100RB), almost collinear to the excitation beam (γ < 2°), focused by lens L₄ (f = 0.15 m), was used to probe the periodic deformation of the sample surface induced by the modulated excitation beam. The sample was located close to the waist of the excitation beam at a position where the change in the radius of the excitation beam is minimal with respect to the change in the wavelength of the infrared excitation laser. Laser beam profiles were analysed by a dual scanning slit beam profiler (Thorlabs, BP209IR1/M) and a pyroelectric array laser beam profiler (Spiricon, Pyrocam III HR) operating in the mid-IR range. The intensity of the probe beam centre after reflection on the sample surface was maximised by adjusting mirror M₄ and detected by a pinhole photodetector D₂ (Thorlabs, model PDA100A2) assembly. The lock-in amplifier (LIA) demodulates the probe (D₂) and the excitation (D₁) signals using the optical shutter frequency as a reference. The acquisition and storage of signals were performed by means of an in-house-developed LabVIEW GUI. A black-walled housing continuously flushed with dry air was used to prevent ambient light from being detected by the photodetectors and reduce water vapor contribution as a source of noise in the spectral region under investigation. For each sample, an average of 10 spectra was taken. Each spectrum was recorded with the step & measure tuning mode of the EC-QCL controller with a resolution of 1 cm⁻¹ and stabilisation time of 335 ms, followed by an acquisition time of 40 ms per wavenumber. A time constant of 20 ms and filter order 6 were used as parameters for the LIA. Data acquisition used the signal amplitude from the two photodetectors (D₂ and D₁) to compute the probe signal normalised by the excitation power (D₂/D₁) as a function of the wavenumber. Finally, the PTM-IR signal was obtained by the ratio of the power-normalised probe signal by the initial intensity measured on detector D₂.

Fig. 5 Schematic of the experimental PTM-IR measurements. Red laser is an He–Ne laser (632.8 nm). Blue laser is a tuneable cw EC-QCL. L₁ and L₂ (f = 5 cm), L₃ (f = 20 cm) and L₄ (f = 15 cm) are lenses, S stands for shutter, B is a beam splitter, M₁–M₄ are mirrors. D₁ is a mercury cadmium telluride (MCT) detector and D₂ is a silicon (Si) amplified photodiode. Enclosed in a black-walled housing, continuously flushed with dry air. Experimental parameters are ω_e = 400 μm, ω_p = 836 μm, z_c = 3.86 cm, z₁ = 37.1 cm, and z₂ = 240 cm, where ω_p is the radius of the probe beam at the sample surface, z_c is the confocal distance of the probe beam, z₁ is the distance from the probe beam waist to the sample, and z₂ is the distance from the sample to the photodetector.

AFM-IR

AFM-IR data was collected on a nanoIR3s system (Bruker, Santa Barbara) using an overall gold-coated contact mode cantilever (ContGB-G, BudgetSensors Innovative Solutions Bulgaria Ltd.) with a typical first resonance frequency at (13 ± 4) kHz and a nominal spring constant between 0.07 Nm⁻¹ and 0.40 Nm⁻¹. The nanoIR3s was coupled to a pulsed, tuneable EC-QCL (MIRcat-QT, DRS Daylight Solutions Inc.) with a spectral coverage of 1985 cm⁻¹ to 900 cm⁻¹.

Data acquisition was performed using Analysis Studio (v3.15, Anasys Instruments). For measurements, a mid-IR laser was used in s-polarisation. Spectra were recorded at three different locations on each sample. In each location, the cantilever was held in a fixed position, and the laser was tuned to the local contact resonance of the cantilever. Hence, by sweeping through the EC-QCL wavelength range, a spectrum was recorded. The sweeping speed was 100 cm⁻¹ s⁻¹. Per position, 10 single spectra were collected. The laser repetition rate was set to match the eigenmode of the cantilever at 200 kHz utilising resonance-enhanced AFM-IR. The laser pulse width was set to 200 ns, which corresponds to 4% duty cycle. Peak pulse power for the measurements was set to 130 mW. Throughout all measurements, the peak pulse power and focus were constant. The data was imported in Python3 using the native NanoIR file format and exported to a generic data format (xarray.Data set) with the ansys-python-tools library.³⁶ The unprocessed spectra were then collected and exported and combined with other measurement data for processing and plotting. This was achieved using Origin Pro 2024 (OriginLab, USA), and the spectra were smoothed using the Savitzky–Golay algorithm with 2nd-order polynomial and 7 smoothing points. For baseline correction, a polynomial fit of 2nd-order, with three baseline points, was applied. The experimental diagram for AFM-IR measurements is shown in Fig. 6.

Fig. 6 Schematic of the AFM-IR measurements. Blue laser is a pulsed, tuneable EC-QCL. C is the cantilever. DL is the deflection laser, and PD is a 4-quadrant photodetector registering the cantilever deflection. The sample sits on an xyz-stage, where the pulsed excitation beam is focused on the sample under the cantilever tip.

FT-IR

FT-IR measurements were conducted with a Bruker Vertex 70v (Bruker, Germany), employing a globar source and a liquid nitrogen-cooled MCT detector. The thin film samples on CaF₂ were fixed vertically on a mount and placed in the sample chamber centred around the IR beam. Spectra were recorded in the frequency range of 4000 cm⁻¹ to 400 cm⁻¹. For each sample, the average of 10 spectra was recorded with a total of 256 scans per spectrum, resulting in an acquisition time of 57 s per spectrum. Spectra were recorded with a resolution of 2 cm⁻¹. Measurements were performed at ambient temperature. Prior to each measurement, the instrument was purged with dry air for at least 10 minutes to minimise water vapor absorption.

Initial evaluation of spectra was done with OPUS 8.5 (Bruker, Germany). The absorbance of the PS thin film was calculated against the CaF₂ optical window. Final evaluation and processing were done with Origin Pro 2024 (OriginLab, USA). The spectra were smoothed using the Savitzky–Golay algorithm with 2nd-order polynomial and 7 smoothing points and a baseline correction 2nd-order polynomial using three baseline points.

Finite element analysis

The FEA software provides numerical solutions to the heat diffusion and thermoelastic equations with realistic boundary conditions imposed by the experimental geometry. The model was built with 2D axisymmetric geometry using the software Comsol Multiphysics 5.6. ‘Heat Transfer in Solids’ and ‘Solid Mechanics’ modules were used to obtain the temperature and normal component of the surface displacement in the thin film, air and CaF₂ optical window. The values of the thermal, mechanical, and optical properties used for the FEA modelling simulations are shown in Table 2. Table 3 shows the experimental parameters related to the spatial and temporal profile of the excitation beam in the PTM-IR and AFM-IR techniques used for FEA simulations. Realistic sample geometry was considered, i.e., a substrate with 2 mm thickness and 12.7 mm radius, with 10 mm air thickness surrounding the sample. The heat diffusion equation (eqn (1)) was solved for all the domains, considering the heat source defined in eqn (2). The thermoelastic equation (eqn (3)) was solved for the thin film and substrate domain. There are four types of boundaries in the model. One boundary represents the axis of symmetry (at r = 0), which coincides with the centre of the excitation laser beam. The external boundaries are defined as thermal insulation. The thin film–air interface is free, with no loads or constraints. The lateral and back surfaces of the substrate are defined as fixed constraints.

Conclusions

In this work, the nanoscale surface displacement on thin films induced by mid-IR laser heating was measured using PTM-IR and AFM-IR techniques. The photothermal mirror technique was successfully applied for the first time for polymer thin film characterisation within this work. Furthermore, it was the first demonstration of the PTM technique by taking advantage of mid-IR excitation. Temperature change and thermoelastic displacement were modelled using finite element analysis, taking thermal coupling between the fluid, thin film, and substrate into account. The main characteristics of each measurement technique were evaluated, and the mid-infrared spectra showed excellent agreement with state-of-the-art FT-IR measurements.

Despite these advancements, further engineering improvements are required to enhance the optical setup, particularly in the automating the alignment processes to ensure repeatability without the need for manual adjustments and focusing. Additionally, using a probe beam with higher optical power and reduced noise could significantly improve the sensitivity and accuracy of the technique.

Looking forward, optimisation and automatisation of the system could pave the way for developing a more compact and robust system capable of conducting chemical analysis and thickness measurements in a range of applications. Furthermore, the possibility of transient analysis can offer valuable insights into the quantitative properties of different materials.

Abbreviations

PTM-IR	Photothermal mirror-infrared spectroscopy
AFM-IR	Atomic force microscopy-infrared spectroscopy
FT-IR	Fourier transform-infrared spectroscopy
FEA	Finite element analysis
PS	Polystyrene
CaF2	Calcium fluoride
ZnSe	Zinc selenide
ZnS	Zinc sulfide
EC-QCL	External cavity quantum cascade laser
PM-IRRAS	Polarization modulation infrared reflection-absorption spectroscopy
TDTR	Time domain thermo-reflectance
ATR	Attenuated total reflectance
SNR	Signal to noise ratio

Symbols

k	Thermal conductivity
ρ	Density
cp	Specific heat capacity
αT	Thermal expansion coefficient
ν	Poisson's ratio
E	Young's modulus
ωe	Excitation beam radius
fR	Repetition rate
τ	Pulse duration
D	Duty cycle
Pe	Excitation power

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

U. Y. and G. V. B. L. prepared samples and drafted the manuscript. U. Y. performed the AFM-IR and thickness measurements. G. V. B. L. and E. S. performed the PTM-IR and FT-IR measurements. G. V. B. L., Y. Z., and N. G. C. A. performed FEA simulations. U. Y., G. R., and G. V. B. L. conceptualised the study. B. L. secured funding of this work. All the authors have read and revised the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This study has received funding from the European Union's Horizon 2020 research and innovation programme. U. Y. and G. R. acknowledge PeroCUBE (grant agreement No. 861985) and Tumor-LN-oC (grant agreement No. 953234). Y. Z., B. L., and G. R. acknowledge Optaphi (grant agreement No. 860808). G. R. gratefully acknowledges financial support by the Austrian Federal Ministry for Labour and Economy and the National Foundation for Research, Technology and Development and the Christian Doppler Research Association. G. V. B. L., E. S. and N. G. C. A. acknowledge support from CNPq (grant agreement No. 307415/2022-8 and 305333/2023-2), CAPES (Finance Code 001), and Fundação Araucária. N. G. C. A. acknowledges financial support through the Competence Centers for Excellent Technologies (COMET) Centre CHASE, funded within the COMET programme by the BMK, the BMDW and the Federal Provinces of Upper Austria and Vienna. The COMET programme is managed by the Austrian Research Promotion Agency (FFG). The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme. We are grateful to S. E. Bialkowski, L. C. Malacarne and M. L. Baesso for illuminating discussions.

References

1. K. Fukuda, Y. Takeda, Y. Yoshimura, R. Shiwaku, L. T. Tran, T. Sekine, M. Mizukami, D. Kumaki and S. Tokito, Fully-Printed High-Performance Organic Thin-Film Transistors and Circuitry on One-Micron-Thick Polymer Films, Nat. Commun., 2014, 5(1), 4147,  DOI:10.1038/ncomms5147.
2. A. Malik and B. Kandasubramanian, Flexible Polymeric Substrates for Electronic Applications, Polym. Rev., 2018, 58(4), 630–667,  DOI:10.1080/15583724.2018.1473424.
3. C. Sun, F. Pan, H. Bin, J. Zhang, L. Xue, B. Qiu, Z. Wei, Z.-G. Zhang and Y. Li, A Low Cost and High Performance Polymer Donor Material for Polymer Solar Cells, Nat. Commun., 2018, 9(1), 743,  DOI:10.1038/s41467-018-03207-x.
4. J. Lopez, D. G. Mackanic, Y. Cui and Z. Bao, Designing Polymers for Advanced Battery Chemistries, Nat. Rev. Mater., 2019, 4(5), 312–330,  DOI:10.1038/s41578-019-0103-6.
5. A. Ullah, M. Jang, H. Khan, H. J. Choi, S. An, D. Kim, Y.-R. Kim, U.-K. Kim and G. M. Kim, Microneedle Array with a pH-Responsive Polymer Coating and Its Application in Smart Drug Delivery for Wound Healing, Sens. Actuators, B, 2021, 345, 130441,  DOI:10.1016/j.snb.2021.130441.
6. Y. M. Elkasabi, J. Lahann and P. H. Krebsbach, Cellular Transduction Gradients via Vapor-Deposited Polymer Coatings, Biomaterials, 2011, 32(7), 1809–1815,  DOI:10.1016/j.biomaterials.2010.10.046.
7. P. Mohankumar, J. Ajayan, T. Mohanraj and R. Yasodharan, Recent Developments in Biosensors for Healthcare and Biomedical Applications: A Review, Measurement, 2021, 167, 108293,  DOI:10.1016/j.measurement.2020.108293.
8. A. Ebner, R. Zimmerleiter, K. Hingerl and M. Brandstetter, Towards Real-Time In-Situ Mid-Infrared Spectroscopic Ellipsometry in Polymer Processing, Polymers, 2021, 14(1), 7,  DOI:10.3390/polym14010007.
9. P. Jiang, X. Qian and R. Yang, Tutorial: Time-Domain Thermoreflectance (TDTR) for Thermal Property Characterization of Bulk and Thin Film Materials, J. Appl. Phys., 2018, 124(16), 161103,  DOI:10.1063/1.5046944.
10. A. H. Kycia, K. Koczkur, J. J. Leitch, J. Lipkowski, V. Zamlynny and M. W. P. Petryk, Application of PM-IRRAS to Study Thin Films on Industrial and Environmental Samples, Anal. Bioanal. Chem., 2013, 405(5), 1537–1546,  DOI:10.1007/s00216-012-6469-6.
11. M. Djak, E. Gilli, E. Kontturi and R. Schennach, Thickness Dependence of Reflection−Absorption Infrared Spectra of Supported Thin Polymer Films, Macromolecules, 2011, 44(7), 1775–1778,  DOI:10.1021/ma102905v.
12. P. Luan and G. S. Oehrlein, Characterization of Ultrathin Polymer Films Using P-Polarized ATR-FTIR and Its Comparison with XPS, Langmuir, 2019, 35(12), 4270–4277,  DOI:10.1021/acs.langmuir.9b00316.
13. N. G. C. Astrath, L. C. Malacarne, P. R. B. Pedreira, A. C. Bento, M. L. Baesso and J. Shen, Time-Resolved Thermal Mirror for Nanoscale Surface Displacement Detection in Low Absorbing Solids, Appl. Phys. Lett., 2007, 91(19), 191908,  DOI:10.1063/1.2812542.
14. G. V. B. Lukasievicz, N. G. C. Astrath, L. C. Malacarne, L. S. Herculano, V. S. Zanuto, M. L. Baesso and S. E. Bialkowski, Pulsed-Laser Time-Resolved Thermal Mirror Technique in Low-Absorbance Homogeneous Linear Elastic Materials, Appl. Spectrosc., 2013, 67(10), 1111–1116,  DOI:10.1366/13-07068.
15. V. S. Zanuto, L. S. Herculano, M. L. Baesso, G. V. B. Lukasievicz, C. Jacinto, L. C. Malacarne and N. G. C. Astrath, Thermal Mirror Spectrometry: An Experimental Investigation of Optical Glasses, Opt. Mater., 2013, 35(5), 1129–1133,  DOI:10.1016/j.optmat.2013.01.003.
16. S. T. Souza, E. J. S. Fonseca, C. Jacinto, N. G. C. Astrath, T. P. Rodrigues and L. C. Malacarne, Direct Measurement of Photo-Induced Nanoscale Surface Displacement in Solids Using Atomic Force Microscopy, Opt. Mater., 2015, 48, 71–74,  DOI:10.1016/j.optmat.2015.07.028.
17. T. V. Moreno, V. S. Zanuto, N. G. C. Astrath, G. R. Silva, E. J. S. Fonseca, S. T. Souza, D. Zhao, H. Jain and L. C. Malacarne, In Situ Measurements of Photoexpansion in A s 2 S 3 Bulk Glass by Atomic Force Microscopy, Opt. Mater., 2019, 94, 9–14,  DOI:10.1016/j.optmat.2019.05.016.
18. O. S. Aréstegui, P. Y. N. Poma, L. S. Herculano, G. V. B. Lukasievicz, F. B. Guimarães, L. C. Malacarne, M. L. Baesso, S. E. Bialkowski and N. G. C. Astrath, Combined Photothermal Lens and Photothermal Mirror Characterization of Polymers, Appl. Spectrosc., 2014, 68(7), 777–783,  DOI:10.1366/13-07404.
19. L. C. Malacarne, F. Sato, P. R. B. Pedreira, A. C. Bento, R. S. Mendes, M. L. Baesso, N. G. C. Astrath and J. Shen, Nanoscale Surface Displacement Detection in High Absorbing Solids by Time-Resolved Thermal Mirror, Appl. Phys. Lett., 2008, 92(13), 131903,  DOI:10.1063/1.2905261.
20. G. V. B. Lukasievicz, L. C. Malacarne, N. G. C. Astrath, V. S. Zanuto, L. S. Herculano and S. E. Bialkowski, A Theoretical and Experimental Study of Time-Resolved Thermal Mirror with Non-Absorbing Heat-Coupling Fluids, Appl. Spectrosc., 2012, 66(12), 1461–1467,  DOI:10.1366/12-06743.
21. O. A. Capeloto, G. V. B. Lukasievicz, V. S. Zanuto, L. S. Herculano, N. E. Souza Filho, A. Novatski, L. C. Malacarne, S. E. Bialkowski, M. L. Baesso and N. G. C. Astrath, Pulsed Photothermal Mirror Technique: Characterization of Opaque Materials, Appl. Opt., 2014, 53(33), 7985–7991,  DOI:10.1364/AO.53.007985.
22. O. A. Capeloto, V. S. Zanuto, G. V. B. Lukasievicz, L. C. Malacarne, S. E. Bialkowski, T. Požar and N. G. C. Astrath, Generation and Detection of Thermoelastic Waves in Metals by a Photothermal Mirror Method, Appl. Phys. Lett., 2016, 109(19), 191908,  DOI:10.1063/1.4967530.
23. P. P. González-Borrero, G. V. B. Lukasievicz, V. S. Zanuto, N. G. C. Astrath and L. C. Malacarne, Accessing Thermo-Mechanical Properties of Semiconductors Using a Pump-Probe Surface Displacement Method, J. Appl. Phys., 2017, 121(19), 195101,  DOI:10.1063/1.4983451.
24. A. Dazzi, C. B. Prater, Q. Hu, D. B. Chase, J. F. Rabolt and C. A. F. M. -I. R. Marcott, Combining Atomic Force Microscopy and Infrared Spectroscopy for Nanoscale Chemical Characterization, Appl. Spectrosc., 2012, 66(12), 1365–1384,  DOI:10.1366/12-06804.
25. A. Dazzi and C. B. Prater, AFM-IR: Technology and Applications in Nanoscale Infrared Spectroscopy and Chemical Imaging, Chem. Rev., 2017, 117(7), 5146–5173,  DOI:10.1021/acs.chemrev.6b00448.
26. A. Centrone, Infrared Imaging and Spectroscopy Beyond the Diffraction Limit, Annu. Rev. Anal. Chem., 2015, 8, 101–126,  DOI:10.1146/annurev-anchem-071114-040435.
27. A. M. Katzenmeyer, G. Holland, J. Chae, A. Band, K. Kjoller and A. Centrone, Mid-Infrared Spectroscopy beyond the Diffraction Limit via Direct Measurement of the Photothermal Effect, Nanoscale, 2015, 7(42), 17637–17641,  10.1039/C5NR04854K.
28. J. Li, B. Huang, E. Nasr Esfahani, L. Wei, J. Yao, J. Zhao and W. Chen, Touching Is Believing: Interrogating Halide Perovskite Solar Cells at the Nanoscale via Scanning Probe Microscopy, npj Quantum Mater., 2017, 2(1), 1–7,  DOI:10.1038/s41535-017-0061-4.
29. A. C. V. D. dos Santos, B. Lendl and G. Ramer, Systematic Analysis and Nanoscale Chemical Imaging of Polymers Using Photothermal-Induced Resonance (AFM-IR) Infrared Spectroscopy, Polym. Test., 2022, 106, 107443,  DOI:10.1016/j.polymertesting.2021.107443.
30. U. Yilmaz, S. Sam, B. Lendl and G. Ramer, Bottom-Illuminated Photothermal Nanoscale Chemical Imaging with a Flat Silicon ATR in Air and Liquid, Anal. Chem., 2024, 96(11), 4410–4418,  DOI:10.1021/acs.analchem.3c04348.
31. J. Mathurin, E. Pancani, A. Deniset-Besseau, K. Kjoller, C. B. Prater, R. Gref and A. Dazzi, How to Unravel the Chemical Structure and Component Localization of Individual Drug-Loaded Polymeric Nanoparticles by Using Tapping AFM-IR, Analyst, 2018, 143(24), 5940–5949,  10.1039/C8AN01239C.
32. K. Hinrichs and T. Shaykhutdinov, Polarization-Dependent Atomic Force Microscopy–Infrared Spectroscopy (AFM-IR): Infrared Nanopolarimetric Analysis of Structure and Anisotropy of Thin Films and Surfaces, Appl. Spectrosc., 2018, 72(6), 817–832,  DOI:10.1177/0003702818763604.
33. M. Kelchtermans, M. Lo, E. Dillon, K. Kjoller and C. Marcott, Characterization of a Polyethylene–Polyamide Multilayer Film Using Nanoscale Infrared Spectroscopy and Imaging, Vib. Spectrosc., 2016, 82, 10–15,  DOI:10.1016/j.vibspec.2015.11.004.
34. A. Dazzi, F. Glotin and R. Carminati, Theory of Infrared Nanospectroscopy by Photothermal Induced Resonance, J. Appl. Phys., 2010, 107(12), 124519,  DOI:10.1063/1.3429214.
35. T. L. Myers, R. G. Tonkyn, T. O. Danby, M. S. Taubman, B. E. Bernacki, J. C. Birnbaum, S. W. Sharpe and T. J. Johnson, Accurate Measurement of the Optical Constants n and k for a Series of 57 Inorganic and Organic Liquids for Optical Modeling and Detection, Appl. Spectrosc., 2018, 72(4), 535–550,  DOI:10.1177/0003702817742848.
36. G. Ramer, Anasyspythontools: A Suite of Python Tools for Use with Analysis Studio AFM-IR Files, https://github.com/GeorgRamer/anasys-python-tools, accessed 2023-05-02.
37. W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 2014.
38. G. Wypych, PS Polystyrene, in Handbook of Polymers, ed. Wypych, G., ChemTec Publishing, 2nd edn, 2016, pp 560–566,  DOI:10.1016/B978-1-895198-92-8.50175-0.
39. The Crystran Handbook of Infra-red and Ultra-violet Optical Materials, Crystran Ltd, Poole, UK, 5th edn, 2023, https://www.crystran.com/handbook.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra00555h

---