Open Access Article
Open Access ArticleInvestigating Li2Mg2(WO4)3: structure, morphology, and electrical properties with ultra-low dielectric loss for optimizing laser host materials
Mehdi Akermi*a,
Ines Mbarekb,
Rym Hassanic,
Saber Nasri b and
Abderrazek Oueslati
b and
Abderrazek Oueslati *b
*b
aNanotechnology research unit, Jazan University, P.O. Box. 114, Jazan 45142, Kingdom of Saudi Arabia. E-mail: makermi@jazanu.edu.sa
bLaboratory for Spectroscopic Characterization and Optics of Materials, Faculty of Sciences, University of Sfax, B.P. 1171, 3000 Sfax, Tunisia. E-mail: oueslatiabderrazek@yahoo.fr
cEnvironment and Nature Research Centre, Jazan University, P.O. Box. 114, Jazan 45142, Kingdom of Saudi Arabia
First published on 23rd April 2025
Abstract
With technological advancements driving the demand for innovative materials, triple tungstate compounds, like Li2Mg2(WO4)3 (LMWO), offer exceptional properties for optoelectronic technologies. To investigate these potential outcomes, the LMWO compound was prepared via the solid-state reaction approach. The X-ray diffraction analysis revealed a single-phase material crystallizing in the orthorhombic structure, belonging to the Pnma space group. The crystallite size of the material was determined to be 58.32 nm, which played a significant role in enhancing its electrical performance. Scanning electron microscopy (SEM) revealed prismatic or rod-shaped particles with an average grain size of approximately 2.83 μm. Additionally, EDX confirmed the elemental composition, verifying the presence of Mg, W, and O, and ensuring the material's purity. Nyquist plots indicated non-Debye type relaxation, and further analysis of the relaxation frequency confirmed long-range motion of charge carriers. The temperature dependence of dielectric relaxation followed the Arrhenius law, yielding an activation energy of 0.84 eV. The frequency dependent behavior of M′′ and Z′′ at various temperatures indicated a shift from short-range to long-range mobility of charge carriers. The conductivity of the material increased with both temperature and frequency, demonstrating its semiconducting behavior. The temperature dependence of Jonscher's exponent suggests that conduction follows the non-overlapping small polaron tunneling (NSPT) model. This compound exhibited a high dielectric constant (ε ∼ 105) and low dielectric loss at high frequencies, making it promising for applications in laser host materials and energy storage.
Introduction
Tungstate oxides are highly promising materials thanks to their excellent ionic and electronic conductivity, as well as their ferroelectric, piezoelectric, and catalytic properties.1–3 They are particularly appealing as solid-state laser host materials due to their high capacity for rare earth ion incorporation.4–6 These compounds have a broad range of applications, including use as scintillation detectors and laser host materials, and in optical fibers.7,8Transition metal oxides have recently gained significant attention as pseudo-capacitive materials because of their ability to exhibit multiple oxidation states, with examples including Ni,9 Mo,10 Co,11 Mn,12 W,12 Cu,12 and V.12 However, single metal oxides still face issues such as toxicity, high cost, and low cycle life. In contrast, mixed metal oxides,13 binary metal oxides,14 and ternary metal oxides15 often exhibit superior performance compared to their single-metal counterparts, owing to their varied oxidation states16 and higher electrical conductivity.17 Among the various double tungstates, the Li-based tungstates, LixMy(XO4)z where M = Al, In, Sc, Cr, Bi, Fe, Mg rare earth ion and X = Mo, W., are distinguished by their unique ionic conductivity and structural characteristics, making them pivotal materials for advancing energy storage and electrochemical devices.18 The studies revealed that only four elements Cu, Fe, Mg, and Zn form double tungstates. Among these, the tetrahedral coordination of tungsten atoms was observed in Li2Mg2(WO4)3,19 Na4Mg(WO4)3,20 Na4Zn(WO4)3,21 and K4Zn(WO4)3,22 while a wolframite-like structure was suggested for Li2Fe(WO4)2 (ref. 23) and Li2Cu(WO4)2.24 Magnesium has been reported to form two double tungstates though with different stoichiometry Li2Mg2(WO4)3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3)25 and Na4Mg(WO4)3 (2
3)25 and Na4Mg(WO4)3 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3).26 Following a comprehensive review of the literature, we have selected Li2Mg2(WO4)3 to synthesize in this study. The crystal structure of Li2Mg2(WO4)3 projected onto the (100) plane is depicted in Fig. 1. As shown, WO4 units form tetrahedra with W atoms at their centers. The (1/3Li + 2/3Mg)O6 units adopt an octahedral coordination, where (1/3Li + 2/3Mg) occupy the central position. Additionally, LiO6 forms a prismatic structure with Li positioned at its center.27
3).26 Following a comprehensive review of the literature, we have selected Li2Mg2(WO4)3 to synthesize in this study. The crystal structure of Li2Mg2(WO4)3 projected onto the (100) plane is depicted in Fig. 1. As shown, WO4 units form tetrahedra with W atoms at their centers. The (1/3Li + 2/3Mg)O6 units adopt an octahedral coordination, where (1/3Li + 2/3Mg) occupy the central position. Additionally, LiO6 forms a prismatic structure with Li positioned at its center.27
This article aims to explore the morphological structure and electrical properties of a newly developed tungstate material. By examining its microstructural features and analyzing its conductivity, this study seeks to provide insights into how the material's composition and arrangement at the microscopic level influence its overall electrical behavior. Understanding these characteristics is essential for assessing the material's potential applications in advanced electronic devices and improving its performance for specific industrial purposes.
Experimental details
In this investigation, Li2Mg2(WO4)3 was prepared through a solid-state reaction technique. The starting materials consisted of ultra-pure WO3, Li2CO3, and MgO. These materials were mixed in a molar ratio of WO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li2CO3
Li2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgO = 3
MgO = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and pressed into a pellet. To compensate for lithium loss due to volatilization, an additional 2 mol% of Li2CO3 was added. The prepared mixture was first calcined at 750 °C for 35 h and was subjected to solid-state sintering at 900 °C for 120 hours in air, leading to the formation of the Li2Mg2(WO4)3 compound.
2 and pressed into a pellet. To compensate for lithium loss due to volatilization, an additional 2 mol% of Li2CO3 was added. The prepared mixture was first calcined at 750 °C for 35 h and was subjected to solid-state sintering at 900 °C for 120 hours in air, leading to the formation of the Li2Mg2(WO4)3 compound.
This extended sintering time was chosen to ensure complete phase formation, optimal crystallinity, and improved material properties. The prolonged sintering period allows the sample to undergo thorough structural refinement, reducing defects and promoting homogeneity. The furnace was maintained at a constant temperature throughout the 120-hour process, ensuring stable conditions for the sample during the entire sintering duration. Compounds in this family are commonly prepared at this temperature to achieve the desired material properties such as Li2Ni(WO4)2, Li2Cu(WO4)2, Li2Co(WO4)2 which are prepared in 700 °C for 160 hours.28 Also our compound under study is already studied with the same method.27
The crystal structure of the synthesized samples was examined using a Philips X'Pert X-ray powder diffractometer (XRD) with Cu Kα radiation (λ = 1.5418 Å). Data collection was conducted over a Bragg angle range of 10–60° at a scan rate of 0.05°/min. The structural refinement was performed through Rietveld analysis of the X-ray diffraction data, utilizing the FULLPROF software29,30
The microstructural features and elemental composition of the samples were examined using a FEI Nova NanoSEM 200 scanning electron microscope, integrated with an energy-dispersive X-ray spectroscopy (EDXS) analyzer.
Electrical measurements were conducted using two silver electrodes in an Ag/electrolyte/Ag configuration. The powder samples were pressed into tablets (8 mm in diameter and 1 mm in thickness) under a uniaxial pressure of 3 t cm−2, with a silver conductive layer applied to both surfaces to serve as electrodes. Impedance measurements were performed across frequencies ranging from 0.1 Hz to 5 MHz using a 1260 Solartron Impedance Analyzer, controlled by a microcomputer, and carried out at temperatures between 473 and 673 K.
Results and discussion
Structural study
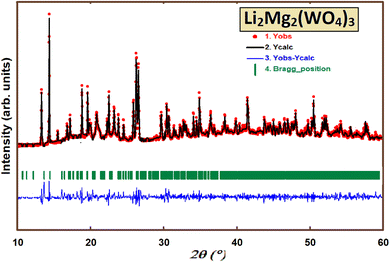
The X-ray diffraction (XRD) pattern of Li2Mg2(WO4)3, presented in Fig. 2, indicates that the sample is single-phase. All detected peaks correspond to an orthorhombic unit cell, belonging to the Pnma space group.The crystal structure of Li2Mg2(WO4)3 was refined using the Rietveld method, with the refinement results summarized in Table 1 which are in good agreement with those determined from the published crystallographic data of Li2Mg2(WO4)3.27 Considering the lattice parameters and the space group, the crystal structure of Li2Mg2(WO4)3 may be considered to be similar to that of Li2Fe2(MoO4)3 (ref. 31) and Li3Fe(MoO4)3 (ref. 19) with W6+ tetrahedrally coordinated to four oxygen atoms.
| Li2Mg2(WO4)3 compound at room temperature | |
| System | Orthorhombic |
| Space group | Pnma |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Lattice parameters | |
| a | 5.120 (±0.005) |
| b | 10.502 (±0.006) |
| c | 17.591 (±0.006) |
| α | 90 |
| β | 90 |
| γ | 90 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Reliability factors | |
| RP/RwP/Rexp | 5.8%/7.9%/11.89% |
| χ2 | 1.44 |
| Crystallite size | 58.32 nm |
As presented in Table 1, the reliability factors (Rwp and Rp) show excellent consistency between the experimental results and the theoretical calculations.
XRD analysis is utilized to calculate crystallite size. The average crystallite size (D) based on Debye–Scherrer equation can be calculated by32,33
 | (1) |
The D value is listed in Table 1. For double tungstate compounds, crystallite sizes in the nanometer range can lead to enhanced electrical properties, as well as improved conductivity and catalytic performance, often due to the increased surface area and quantum effects associated with nanostructured materials. As a result, we decided to conduct a comprehensive electrical study.
Morphology analysis
Scanning electron microscopy (SEM) was employed to primarily examine the structural morphology of our material. In Fig. 3(a), SEM image presents the microstructure of the ceramic compound Li2Mg2(WO4)3, a lithium magnesium tungstate material. The morphology shows prismatic or rod-shaped particles in various sizes, with one measured at 4.90 μm in length, while others are smaller, measuring approximately 2.8 μm and 1.26 μm. These variations in size may indicate different growth orientations of the phase.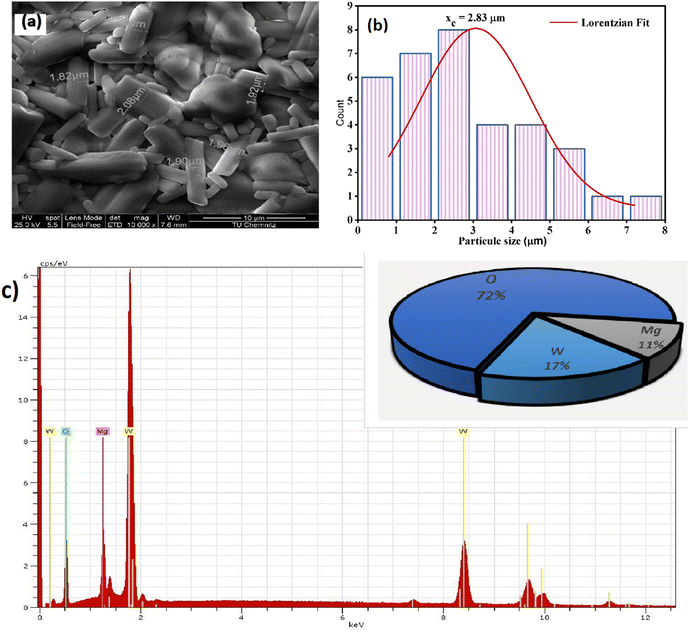 | ||
| Fig. 3 (a) Scanning electron microscopy images, (b) distribution histogram of grains. (c) EDX spectrum of the compound LMWO. | ||
Fig. 3(b) depicts the grain count plotted against particle size (μm). The particle size distribution, obtained through ImageJ software, closely followed a Lorentzian fitting curve. Based on SEM analysis, the average grain size was determined to be 2.83 μm.
Energy dispersive X-ray microanalysis (EDX), as shown in Fig. 3(c), was employed to confirm the qualitative composition and assess the purity of the synthesized material. The identification of Mg, W, and O throughout the synthesis process confirmed that no elements were lost as the compound formed. Interestingly, lithium is not detected because its atomic number overlaps with that of the reference element used for this compound, beryllium. This study illustrates the uniformity of the synthesized Li2Mg2(WO4)3 sample.
Electrical properties
To gain insights into the electrical processes and conduction mechanisms within the Li2Mg2(WO4)3 compound, its electrical properties were investigated using complex impedance spectroscopy over a temperature range of 473–673 K. The Nyquist plot illustrates the relationship between the imaginary part of impedance (Z′′) and the real part (Z′). Fig. 4 presents Nyquist plots for the Li2Mg2(WO4)3 ceramic at various temperatures. All spectra exhibit two semicircular arcs, with their centers positioned below the Z′ axis. This indicates a relaxation behavior that deviates from the classical Debye model.34The Nyquist plot of LMWO reveals two distinct arcs, which correspond to the responses of grain boundaries at lower temperatures and grains at higher temperatures, respectively.
The spectra were successfully modeled using a two-cell circuit model, consisting of two parallel combinations. The first component consists of a resistance (Rg) paired with a capacitance (Cg), whereas the second component includes a resistance (Rgb) in parallel with a constant phase element (CPE) and an additional capacitance (Cgb).35
The impedance of the fractal interface capacitance CPE is calculated as follows36
 | (2) |
Based on the equivalent electrical circuit, the real part (Z′) and the imaginary part (Z′′) of the complex impedance can be expressed using the equations provided below:
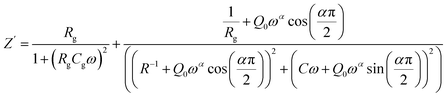 | (3) |
 | (4) |
Fig. 5(a and b) illustrate the frequency-dependent relationship between the real part (Z′) and the imaginary part (Z′′) of the impedance within the temperature range of 473–673 K.
 | ||
| Fig. 5 (a): Frequency dependence of Z′ at different temperatures. (b) Frequency dependence of Z′′ at different temperatures. | ||
At each temperature point, the experimental (scatter) and theoretical (line) curves for both real and imaginary impedances closely align, indicating that the proposed circuit model accurately represents the behavior across the entire temperature range. Fig. 5(a) demonstrates that Z′ decreases as both frequency and temperature increase, indicating that the material possesses negative temperature coefficient of resistance (NTCR) behavior.37,38
This behavior suggests that improving AC conductivity in Li2Mg2(WO4)3 could be achieved by increasing charge carrier mobility and decreasing trapped charge density. At high frequencies, Z′ becomes less sensitive to temperature, indicating the presence of space charge within the material. As the frequency increases, the reduced relaxation time of the space charge leads to the convergence of the curves. This merging is attributed to a decrease in space charge polarization.39
In contrast, the fluctuations observed in the imaginary part Z′′ (Fig. 5(b)) provide insights into the fundamental charge transport mechanism and the temperature-dependent relaxation process in Li2Mg2(WO4)3 .At lower temperatures, the relaxation process appears to be influenced by stationary species or electrons, while defects or vacancies play a more significant role at higher temperatures. Each spectrum shows a distinct peak known as the “relaxation frequency”, which has a broad shape that deviates notably from ideal Debye behavior. At frequencies higher than the relaxation frequency, the movement of localized carriers is influenced by the extended transport of charge carriers, which primarily governs conduction processes below the loss peak frequency.
As the temperature increases, the relaxation peak shifts to higher frequencies, indicating a thermally activated relaxation process. Furthermore, the reduction in peak height with increasing temperature implies a decrease in the resistance of both the grains and grain boundaries.
The behavior of Z′ and Z′′ across the frequency range in our sample aligns with observations made in other ceramic systems reported in the existing literature.40–42
In Fig. 6, we present plots of  and
and  and for a temperature of 633 K to accurately determine the relaxation frequency Z′′. The analysis reveals a shift in the relaxation frequency between the peak of the normalized impedance and the peak of its derivative. This shift confirms that the relaxation mechanism of our sample is non-Debye in nature.43 Additionally, the relaxation model indicates that the behavior of the charge carriers is consistent with the temperature-dependent characteristics of the material.
and for a temperature of 633 K to accurately determine the relaxation frequency Z′′. The analysis reveals a shift in the relaxation frequency between the peak of the normalized impedance and the peak of its derivative. This shift confirms that the relaxation mechanism of our sample is non-Debye in nature.43 Additionally, the relaxation model indicates that the behavior of the charge carriers is consistent with the temperature-dependent characteristics of the material.
Modulus analysis
A comprehensive analysis of the dielectric modulus offers a valuable method for investigating electrical transport phenomena in ceramics and for elucidating the microscopic mechanisms underlying dielectric relaxation44The complex dielectric modulus, M*, is expressed as the inverse of the complex dielectric constant.
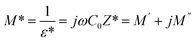 | (5) |
 denotes the geometric capacitance (where ε0 = vacuum permittivity, A = surface, d = thickness).
denotes the geometric capacitance (where ε0 = vacuum permittivity, A = surface, d = thickness).
The complex modulus is expressed in terms of its real and imaginary components, as shown in the following expression
 | (6) |
 | (7) |
Fig. 7 shows the variation of the real part of the modulus (M′) with frequency at different temperatures. At lower frequencies, M′ is nearly zero. As the frequency increases, M′ steadily rises and eventually reaches a saturation point beyond a specific frequency. This characteristic frequency is temperature-dependent, and the amplitude of M′ reaches a higher saturation level as the temperature rises. The phenomenon of saturation in M′ is linked to charge transport behavior, which is governed by the mobility of available charge carriers. As temperature increases, the enhanced mobility of the charge carriers leads to a higher overall saturation of M′.45 Nevertheless, as the temperature rises, the movement of charge carriers is enhanced, leading to an increase in the overall saturation of M′ with temperature.46
At a fixed temperature, the maximum of M′′ and minimum tangent points of M′ coincide (Fig. 8), which agrees well with Bergman's fit.
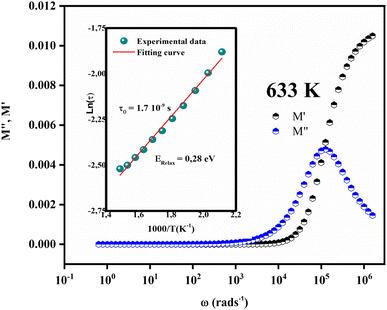 | ||
| Fig. 8 Variation of M′ and M′′ as a function of ω at a fixed temperature (T = 633 K). (insert) The plot of ln(ωmax) versus 1000/T. | ||
In this context, the relaxation frequency corresponding to the M′ peak signifies the transition between long-range and short-range dynamics as the frequency rises. The variation in temperature on the low-frequency side of the dielectric relaxation can be characterized using the Arrhenius equation. As a result, the activation energy (Erelax) is determined from:
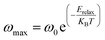 | (8) |
 are 0.82 eV and 1.7 × 10−9 s, respectively.
are 0.82 eV and 1.7 × 10−9 s, respectively.
Fig. 9 illustrates the variation of the imaginary part of the modulus (M′′) as a function of frequency, revealing three distinct regions. The first region occurs at low frequencies, below the peak maximum of M′′  , where charge carriers exhibit long-range mobility, suggesting that ions can hop between adjacent sites. The second region corresponds to the high-frequency range, beyond the peak maximum of the M′′ modulus
, where charge carriers exhibit long-range mobility, suggesting that ions can hop between adjacent sites. The second region corresponds to the high-frequency range, beyond the peak maximum of the M′′ modulus  , where the majority of charge carriers remain confined within their potential wells. In this region, charge carriers are restricted to short-range movement, demonstrating only localized motion within the potential well.47 The final region corresponds to the peak of
, where the majority of charge carriers remain confined within their potential wells. In this region, charge carriers are restricted to short-range movement, demonstrating only localized motion within the potential well.47 The final region corresponds to the peak of  , where the transition from long-range to short-range mobility occurs. The imaginary part of M′′ is fitted using the modified Kohlrausch–Williams–Watts (KWW) function, as proposed by Bergman.48
, where the transition from long-range to short-range mobility occurs. The imaginary part of M′′ is fitted using the modified Kohlrausch–Williams–Watts (KWW) function, as proposed by Bergman.48
 | (9) |
 represents the maximum value of M′′, and ωmax denotes the corresponding maximum frequency.
represents the maximum value of M′′, and ωmax denotes the corresponding maximum frequency.
The modulus deconvolution presented in Fig. 10 clearly reveals two contributions: one from the grain and the other from the grain boundary at the selected temperature of 473 K. We have chosen this temperature because at low temperatures, the deconvolution can be shown more clearly.
The complex modulus spectrum (M′′ vs. M′) for the Li2Mg2(WO4)3 compound displays semicircular arcs, as shown in Fig. 11. The spectrum clearly shows two prominent semicircles: the first at lower frequencies, attributed to grain effects, and the second at higher frequencies, corresponding to grain boundary effects. Additionally, a smaller semicircle appears at even higher frequencies, indicating the electrode effect. This behavior, depicted in the Nyquist plot in Fig. 4, supports the choice of the equivalent circuit model.
Fig. 12 illustrates the combined variation of M′′ and Z′′ with frequency at two different temperatures, 473 K and 673 K. Analyzing such curves is important because it provides information about the presence of the smallest capacitance and the largest resistance.49 Additionally, the combined curve helps determine whether the relaxation process is associated with either short-range or long-range motion of charge carriers. If the peaks of Z′′ and M′′ are observed at different frequencies, the relaxation is linked to a short-range process. Conversely, for long-range motion, the peaks will coincide at the same frequency.50 In the compound under investigation, the correspondence of the peaks at different temperatures suggests the presence of long-range motion of charge carriers and a deviation from non-Debye behavior50 the variation of  and
and  with
with  at both the lowest and highest temperatures for Li2Mg2(WO4)3 ceramics. The peaks of
at both the lowest and highest temperatures for Li2Mg2(WO4)3 ceramics. The peaks of  and
and  do not coincide, confirming the non-Debye type relaxation behavior evident in the frequency-dependent results of the imaginary part of the modulus (Fig. 9). This same trend is observed at all other temperatures.51
do not coincide, confirming the non-Debye type relaxation behavior evident in the frequency-dependent results of the imaginary part of the modulus (Fig. 9). This same trend is observed at all other temperatures.51
AC conductivity
In Fig. 13 illustrates the variation of AC conductivity with frequency over a temperature range of 473 K to 673 K.The DC conductivity, observed at low frequencies, remains relatively stable and is not significantly influenced by frequency changes. In contrast, conductivity shows a frequency-dependent dispersion at high frequencies primarily attributed to AC conductivity. At low frequencies, charge carriers undergo activated hopping, leading to random diffusion and thus contributing to DC conductivity (σdc). During this frequency-dispersive region, ions move back and forth in a coordinated manner. Funke and Hoppe's jump relaxation model12 explains the observed frequency-independent DC conductivity and the frequency-dependent AC conductivity. At lower frequencies, successful hops are the main contributors to conductivity, enabling long-distance ionic motion. The dispersion observed in the conductivity spectra is governed by the ratio of successful to failed hops. In the high-frequency range, an increase in failed hops results in greater dispersion.
The AC conductivity curve is modeled using the Jonscher power law:52–55
| σAC = σdc + Aωs | (10) |
This curve follows Arrhenius' law, which is expressed as:61
 | (11) |
This plot enables the determination of the activation energy, which is found to be 0.84 eV. The activation energy of the current substance seems to be within a range similar to that of the compounds previously studied,62,63 which fall within the typical range of values characteristic of semiconductors.64
Insert Fig. 16 illustrates how the AC conductivity (σac) changes with reciprocal temperature (1000/T) at constant frequencies for the compound under investigation. A linear segment is observed for each frequency. The data clearly show that the conductivity rises with both increasing frequency and temperature, which suggests that the sample exhibits semiconducting behavior. The higher value of the thermal activation energy for conduction, Ea, calculated from the slope of the curve, is observed in the low-frequency domain, whereas it is lower in the high-frequency domain (see Fig. 16). In the low-frequency region, the transport of charge carriers over longer distances requires less energy,65 contributing to higher conductivity. In contrast, phenomena such as relaxation or orientation require more energy.66 Additionally, the mobilities of vacancies (such as oxygen) along with cations at the grain boundaries can increase the activation energy at higher temperatures.
 | ||
| Fig. 16 Variation of the activation energy as a function of the frequency. (insert) Variation of the exponent s as a function of the temperature. | ||
Dielectric
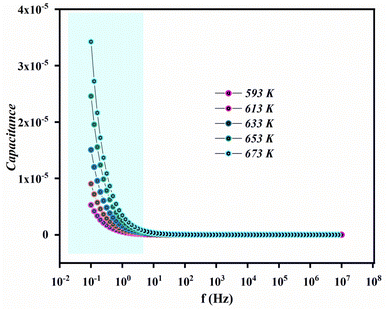
Fig. 17 depicts the change in capacitance as a function of angular frequency at various temperatures. The relationship between frequency and capacitance is clear, with capacitance decreasing as frequency increases. At lower frequencies, capacitance reaches its highest values, indicating the formation of inhomogeneous barriers at the interface due to interface states, which can generate an interfacial space charge. As seen in permittivity studies, capacitance initially decreases and then stabilizes. At 593 K, the capacitance values at lower frequencies are around 10−5 F. Consequently, higher capacitance could potentially enhance the performance of field-effect transistor (FET) devices.Dielectric permittivity provides critical information about the properties of the material under study. It signifies the material's capacity to become polarized in response to an applied electric field. The dielectric behavior of a material is described by the complex dielectric constant:
 | (12) |
Additionally, the dielectric loss factor is defined as the quotient of the imaginary part (ε′′) and the real part (ε′) of the complex permittivity (ε*).
 | (13) |
The study examines the variation of ε′(ω) and tan δ with frequency across the temperature range of 473–673 K. In Fig. 18, the frequency-dependent ε′ values are shown at different temperatures. The sample exhibited higher ε′ values at low frequencies, indicating their potential for low-frequency energy storage. As frequency increases, ε′ values decrease, leading to a reduction in energy storage capacity. Additionally, at a given frequency, ε′ values increase with temperature, indicating the thermal activation of charge carriers that affects polarization. This behavior is associated with four primary types of polarization: ionic, electronic, orientational, and interfacial. The polarizability of the system comprises relaxation components such as orientation and interfacial polarizations, along with resonance components that include ionic and electronic polarizations.
In contrast, for materials intended for optoelectronic applications, it is important to consider the “dissipation factor”, represented as tan(δ) in Fig. 19. In this context, δ is the angle between the voltage and the charging current, often termed the “loss angle”.67 Dielectric loss results from several physical processes, including conduction, dielectric relaxation, molecular dipole moments, and interfacial polarization.68 In the low-frequency range, more energy is needed to move charge carriers, resulting in higher tan(δ) values in this range. As the frequency increases, the material's resistivity decreases, allowing charge carriers to move more efficiently with less energy.69 This characteristic leads to a reduction in dielectric loss at higher frequencies, underscoring the potential of these materials for electrical device applications. Furthermore, higher temperatures and lower frequencies contribute to increased dielectric loss, suggesting an improvement in the material's conductivity.70
Conclusion
With growing interest in double tungstate materials, we explore the structural, morphological, and electrical characteristics of the Li2Mg2(WO4)3 compound, synthesized using the solid-state reaction method. XRD analysis confirms the high crystallinity of the particles, identifying an orthorhombic structure with a Pnma space group. EDS elemental mapping demonstrates a homogeneous distribution of the constituent elements.The influence of temperature on the relaxation and electronic transport processes in Li2Mg2(WO4)3 has been studied. In the study of AC conductivity, the universal power law model was utilized to examine the frequency-dependent behavior of the electrical data.
With its high dielectric constant (ε ∼ 105) and low dielectric loss at high frequencies, this compound demonstrates strong potential for applications in laser host materials and energy storage.
Data availability
The authors confirm that the data used to support the findings of this study are included within the article and are available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This article is derived from a research grant funded by the Research, Development, and Innovation Authority (RDIA) of the Kingdom of Saudi Arabia, with grant number 12894-JAZZAN-2023-JZU-R-2-1-SE.References
- X. Xu, et al., Harvesting vibration energy to piezo-catalytically generate hydrogen through Bi2WO6 layered-perovskite, Nano Energy, 2020, 78, 105351 CrossRef CAS.
- S. S. Hota, D. Panda and R. N. P. Choudhary, Structural, topological, dielectric, and electrical properties of a novel calcium bismuth tungstate ceramic for some device applications, J. Mater. Sci.: Mater. Electron., 2023, 34(10), 900 CrossRef CAS.
- F. Ahmad and S. Ahmad, 2D Metal Oxide Nanosheets—Electronic Applications Recent Developments and Future Prospects, Advanced Applications of 2D Nanostructures: Emerging Research and Opportunities, 2021, pp. 121–181 Search PubMed.
- Z. Chen, et al., Emerging and perspectives in microlasers based on rare-earth ions activated micro-/nanomaterials, Prog. Mater. Sci., 2021, 121, 100814 CrossRef CAS.
- S. E. Crawford, P. R. Ohodnicki and J. P. Baltrus, Materials for the photoluminescent sensing of rare earth elements: challenges and opportunities, J. Mater. Chem. C, 2020, 8(24), 7975–8006 RSC.
- X. Xia, et al., Quantum point defects for solid-state laser refrigeration, Adv. Mater., 2021, 33(23), 1905406 CrossRef CAS PubMed.
- C. Kim, et al., A review of inorganic scintillation crystals for extreme environments, Crystals, 2021, 11(6), 669 CrossRef CAS.
- B. Rekik, et al., Optical properties of 2 at%(Ln3+) doped LiGd (WO4) 2 with Ln; Eu, Er and Tm, grown by μ-pulling down technique, J. Alloys Compd., 2020, 830, 154165 CrossRef CAS.
- X. Ge, et al., Li2Ni (WO4) 2/C: a potential tungstate anode material for lithium ion batteries, J. Alloys Compd., 2021, 888, 161535 CrossRef CAS.
- N. Matskevich, et al., Crystal growth and heat capacity of lithium molybdate tungstates, Russ. J. Inorg. Chem., 2022, 67(10), 1521–1526 CrossRef CAS.
- I. P. Muthuselvam, et al., Two-step antiferromagnetic transition and moderate triangular frustration in Li 2 Co (WO 4) 2, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(17), 174430 CrossRef.
- B. Wanklyn, F. Wondre and W. Davison, Flux growth of crystals of some magnetic oxide materials: Mn 7 SiO 12, CuO, MCr 2 O 4, MTiO 3, Ni 2 NbBO 6, MMoO 4 and Li 2 M 2 (MoO 4) 3,(M= Mn, Co, Ni), J. Mater. Sci., 1976, 11, 1607–1614 CrossRef CAS.
- X. Liu, et al., Noble metal–metal oxide nanohybrids with tailored nanostructures for efficient solar energy conversion, photocatalysis and environmental remediation, Energy Environ. Sci., 2017, 10(2), 402–434 RSC.
- Y. Zhang, et al., Binary metal oxide: advanced energy storage materials in supercapacitors, J. Mater. Chem. A, 2015, 3(1), 43–59 RSC.
- A. Walsh, et al., Oxidation states and ionicity, Nat. Mater., 2018, 17(11), 958–964 CrossRef CAS PubMed.
- M. B. Schütz, et al., Microwave-assisted synthesis of nanocrystalline binary and ternary metal oxides, Int. Mater. Rev., 2018, 63(6), 341–374 CrossRef.
- F. Hong, et al., Significant improvement in Mn2O3 transition metal oxide electrical conductivity via high pressure, Sci. Rep., 2017, 7(1), 44078 CrossRef PubMed.
- K. S. Dhindsa, Enhancement in Electrochemical Performance of LiFePO4-Carbon Nano Composite Materials for Lithium Ion Batteries, Wayne State University, 2015 Search PubMed.
- S. Chen, et al., Lithiated bimetallic oxide, Li3Fe (MoO4) 3, as a high-performance anode material for lithium-ion batteries and its multielectron reaction mechanism, J. Power Sources, 2020, 476, 228656 CrossRef CAS.
- Y. Xiao, D. Yan and D. Wu, Comment on “Bandshift luminescence thermometry using Mn4+: Na4Mg (WO4) 3 phosphors”, Chem. Mater., 2020, 32(22), 9813–9816 CrossRef CAS.
- A. Buzlukov, et al., Revealing sodium-ion diffusion in alluaudite-type Na4–2xM1+ x (MoO4) 3 (M= Mg, Zn, Cd) from 23Na MAS NMR and ab initio studies, J. Solid State Chem., 2021, 293, 121800 CrossRef CAS.
- R. Klevtsova, N. Ivannikova and P. Klevtsov, Crystal structure and polymorphism of potassium zinc tungstate K 4 Zn (WO 4) 3, Kristallografiya, 1979, 24(2), 257–264 CAS.
- P. Klevtsov, N. Novgorodtseva and L. Y. Kharchenko, Hydrothermal Synthesis of the Tungstates Li 2 Fe (WO 4) 2 and Li 2 WO 4 and Their Thermographic and X-Ray Investigation, in Soviet Physics Doklady, 1969 Search PubMed.
- A. Mahieddine, et al., Synthesis, characterization, and effect of electrolyte concentration on the electrochemical performance of Li2Cu (WO4) 2 as a high-performance positive electrode for hybrid supercapacitors, J. Energy Storage, 2022, 56, 106011 CrossRef.
- H. Zhu, et al., Photoluminescence properties of Li2Mg2 (WO4) 3: Eu3+ red phosphor with high color purity for white LEDs applications, J. Lumin., 2016, 172, 180–184 CrossRef CAS.
- D. K. Amarasinghe and F. A. Rabuffetti, Bandshift luminescence thermometry using Mn4+: Na4Mg (WO4) 3 phosphors, Chem. Mater., 2019, 31(24), 10197–10204 CrossRef CAS.
- Z. Fu and W. Li, Crystal structure of a new compound Li2Mg2 (WO4) 3, Powder Diffr., 1994, 9(3), 158–160 CrossRef CAS.
- K. Karoui, et al., Electrical and electrochemical properties of Li 2 M (WO 4) 2 (M= Ni, Co and Cu) compounds, RSC Adv., 2019, 9(12), 6785–6792 RSC.
- H. M. Rietveld, A profile refinement method for nuclear and magnetic structures, J. Appl. Crystallogr., 1969, 2(2), 65–71 CrossRef CAS.
- R. Bandyopadhyay, et al., Application of powder X-ray diffraction in studying the compaction behavior of bulk pharmaceutical powders, J. Pharmaceut. Sci., 2005, 94(11), 2520–2530 CrossRef CAS PubMed.
- C. Torardi and E. Prince, Structure of the lithium insertion compound Li2Fe2 (MoO4) 3 from neutron powder diffraction data, Mater. Res. Bull., 1986, 21(6), 719–726 CrossRef CAS.
- S. Yousefi, B. Ghasemi and M. P. Nikolova, Morpho/Opto-structural characterizations and XRD-assisted estimation of crystallite size and strain in MgO nanoparticles by applying Williamson–Hall and size–strain techniques, J. Cluster Sci., 2022, 33(5), 2197–2207 CrossRef CAS.
- N. Rani, et al., Role of oxygen vacancies for mediating ferromagnetic ordering in La-doped MgO nanoparticles, J. Supercond. Novel Magn., 2020, 33, 1473–1480 CrossRef CAS.
- S. Chaouachi, B. Hamdi and R. Zouari, Crystal structure, electrical study and dielectric behavior of a new centrosymmetric hybrid material, Synth. Met., 2017, 223, 122–131 CrossRef CAS.
- P. Aswathy, R. Ganga and D. N. Rajendran, Impact of A-site calcium on structural and electrical properties of samarium cobaltite perovskites, Solid State Commun., 2022, 350, 114748 CrossRef CAS.
- P. Córdoba-Torres, T. J. Mesquita and R. P. Nogueira, Relationship between the origin of constant-phase element behavior in electrochemical impedance spectroscopy and electrode surface structure, J. Phys. Chem. C, 2015, 119(8), 4136–4147 CrossRef.
- D. Panda, S. S. Hota and R. Choudhary, Synthesis of a scheelite barium molybdate: Structural, topological, electrical, and transport properties for negative temperature coefficient thermistor application, J. Solid State Chem., 2024, 331, 124531 CrossRef CAS.
- B. K. Das, T. Das and D. Das, Structural and electrical properties of mechanically alloyed ZnO nanoceramic for NTC thermistor application, J. Mater. Sci.: Mater. Electron., 2023, 34(3), 230 CrossRef CAS.
- G. Fang, et al., Determining the preferable polarization loss for magnetoelectric microwave absorbers by strategy of controllably regulating defects, Chem. Eng. J., 2023, 463, 142440 CrossRef CAS.
- X. Lin, H. Gong and Z. Chen, Fabrication of SiCN (Fe)/Al2O3 wave-absorbing ceramics with enhanced electromagnetic performance, Ceram. Int., 2023, 49(14), 23851–23863 CrossRef CAS.
- J. Su, et al., Thin La doped CaMnO3 ceramics for attenuation− impedance balance to facilitate excellent microwave absorption, Ceram. Int., 2023, 49(19), 32049–32057 CrossRef CAS.
- Z. Lu, et al., Energy storage properties in Nd-doped AgNbTaO3 lead-free antiferroelectric ceramics with Nb-site vacancies, J. Adv. Dielectr., 2023, 13(01), 2242006 CrossRef CAS.
- M. Javed, et al., Charge conduction mechanism and non-debye type relaxation in LaCrO3 perovskite orthochromite, Mater. Chem. Phys., 2022, 290, 126522 CrossRef CAS.
- S. Patil, et al., Molecular mechanism of the Debye relaxation in monohydroxy alcohols revealed from rheo-dielectric spectroscopy, Phys. Rev. Lett., 2023, 130(9), 098201 CrossRef CAS PubMed.
- S. Anirban, R. Roy and A. Dutta, Microstructure, charge carrier conduction mechanism model, dielectric properties and leakage current analysis of Dy2FeMnO6 nanomaterial, Ceram. Int., 2023, 49(8), 12334–12347 CrossRef CAS.
- A. S. Jbara, et al., Density functional theory study of mixed halide influence on structures and optoelectronic attributes of CsPb (I/Br) 3, Appl. Opt., 2020, 59(12), 3751–3759 CrossRef CAS PubMed.
- S. K. Barik, R. Choudhary and A. Singh, Ac impedance spectroscopy and conductivity studies of Ba0. 8Sr0. 2TiO3 ceramics, Adv. Mater. Lett., 2011, 2(6), 419–424 CrossRef CAS.
- R. Bergman, General susceptibility functions for relaxations in disordered systems, J. Appl. Phys., 2000, 88(3), 1356–1365 CrossRef CAS.
- D. C. Sinclair and A. R. West, Impedance and modulus spectroscopy of semiconducting BaTiO3 showing positive temperature coefficient of resistance, J. Appl. Phys., 1989, 66(8), 3850–3856 CrossRef CAS.
- N. Panda, et al., Structural, dielectric and electrical properties of the Ba 2 BiNbO 6 double perovskite, J. Mater. Sci.: Mater. Electron., 2015, 26, 3797–3804 CrossRef CAS.
- S. Brahma, R. Choudhary and A. K. Thakur, AC impedance analysis of LaLiMo2O8 electroceramics, Phys. B, 2005, 355(1–4), 188–201 CrossRef CAS.
- K. Funke and R. Hoppe, Jump-relaxation model yields Kohlrausch-Williams-Watts behaviour, Solid State Ionics, 1990, 40, 200–204 CrossRef.
- I. Garoui, et al., Lead-Free Halide Perovskites for optoelectronic application: Investigation of Structural, Optical, Electric and Dielectric behaviors, Opt. Mater., 2024, 115664 Search PubMed.
- K. Krishna, et al., Mg2+-induced luminescence enrichment and dielectric investigations on Ca (WO4): Tm3+/Yb3+, Opt. Mater., 2024, 154, 115623 CrossRef CAS.
- A. Al-Muntaser, et al., Tuning the structural, optical, electrical, and dielectric properties of PVA/PVP/CMC ternary polymer blend using ZnO nanoparticles for nanodielectric and optoelectronic devices, Opt. Mater., 2023, 140, 113901 CrossRef CAS.
- I. Kammoun, et al., Investigation of structural, optical and electrical conductivity of a new organic inorganic bromide:[C 12 H 17 N 2] 2 ZnBr 4, RSC Adv., 2023, 13(12), 8034–8042 RSC.
- M. Rani, R. C. Pawar and N. Panwar, Exploring the comparison of optical, dielectric and photocatalytic performance of Yb3+ and Gd3+ half-doped DyCrO3 nanostructures, Mater. Chem. Phys., 2024, 314, 128848 CrossRef CAS.
- M. Krichen, et al., Structural, optical and electrical properties of NiMO4 (M= W and Mo), J. Mol. Struct., 2024, 1298, 137116 CrossRef CAS.
- M. L. Bouazizi, et al., Sol-gel synthesis and property studies of Cu0. 4Mg0. 4Co0. 2FeCrO4 spinel ferrite for optoelectronic, magnetic, and electrical applications, Opt. Mater., 2024, 149, 115059 CrossRef.
- M. Abdel-baki, S. Ibrahim and G. M. Turky, Role of SnO2 on the structural, optical, thermal conductivity, and electrical characteristics of multicomponent borate glasses, Opt. Mater., 2024, 149, 115048 CrossRef CAS.
- J. Zhang, et al., Impact of non-bridging oxygens on the thermal, electrical and optical properties of germanate glasses and exploration of the germanate anomaly, Ceram. Int., 2024, 50(9), 14020–14030 CrossRef CAS.
- N. Yadav and A. Khare, Minimization of carrier recombination in La2NiMnO6 double perovskite solar cells by optimizing defects and band offsets, Phys. Scr., 2023, 98(7), 075917 CrossRef CAS.
- D. S. GT and R. Bhowmik, Doping of large amount tetravalent Ge ions into Fe2O3 structure and experimental results on modified structural, optical and electronic properties, Mater. Sci. Semicond. Process., 2024, 170, 107949 CrossRef.
- M. Naher, et al., A comprehensive ab-initio insights into the pressure dependent mechanical, phonon, bonding, electronic, optical, and thermal properties of CsV3Sb5 Kagome compound, Results Phys., 2023, 51, 106742 CrossRef.
- A. Páez, et al., Comparing distance, time, and metabolic energy cost functions for walking accessibility in infrastructure-poor regions, J. Transport Geogr., 2020, 82, 102564 CrossRef.
- C. E. Jackson, et al., A reaction-coordinate perspective of magnetic relaxation, Chem. Soc. Rev., 2021, 50(12), 6684–6699 RSC.
- D. Nayak, et al., Effect of Nanofillers-Reinforced Polymer Blends for Dielectric Applications, in Emerging Nanodielectric Materials for Energy Storage: from Bench to Field, Springer, 2023, pp. 151–187 Search PubMed.
- L. Zhu, Exploring strategies for high dielectric constant and low loss polymer dielectrics, J. Phys. Chem. Lett., 2014, 5(21), 3677–3687 CrossRef CAS PubMed.
- H. F. Haneef, A. M. Zeidell and O. D. Jurchescu, Charge carrier traps in organic semiconductors: a review on the underlying physics and impact on electronic devices, J. Mater. Chem. C, 2020, 8(3), 759–787 RSC.
- R. Li, et al., Review on polymer composites with high thermal conductivity and low dielectric properties for electronic packaging, Mater. Today Phys., 2022, 22, 100594 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |