DOI:
10.1039/D4RA08877H
(Paper)
RSC Adv., 2025,
15, 10691-10699
Transport properties of dissolved [O] in the (LiF–CaF2)eut.–NdOF molten salt system
Received
19th December 2024
, Accepted 24th March 2025
First published on 7th April 2025
Abstract
The transport properties of [O] in dissolved rare-earth oxyfluorides provide an important theoretical basis for optimizing anode reactions during molten salt electrolysis in fluoride systems for rare-earth metal production. In this study, the solubility of NdOF in (LiF–CaF2)eut. was investigated, and the electrical conductivity and density of the saturated NdOF system were measured. The self-diffusion coefficients and radial distribution functions of the ions in the system were analyzed using first-principles molecular dynamics. The transport number of dissolved O*(II) ions in the saturated (LiF–CaF2)eut.–NdOF system was determined using the coulometric method, providing a comprehensive analysis of the variation in the migration rate and diffusion coefficients of dissolved O*(II) ions. The results showed that the solubility of NdOF in the (LiF–CaF2)eut. System, along with the electrical conductivity and density of the saturated system, exhibited linear variations in the temperature range of 1123–1373 K. The transport number, migration rate, and diffusion coefficient of dissolved O*(II) ions underwent non-linear changes with increasing potential within the range of 3.0–4.5 V, reaching a maximum in the range of 3.75–4.25 V, while still increasing linearly with temperature. When the [temperature-potential] was in the [1200 K↑–3.5 V↑] range, the migration rate and diffusion coefficient of O*(II) ions were the highest, with the potential playing a dominant role in the diffusion coefficient of O*(II) ions. The radial distribution function values of the ions in the system indicated that Nd*(III) ions had the strongest restraining effect on the dissolved O*(II) ions during the diffusion process.
1. Introduction
The application of rare-earth functional metal materials continues to expand, with market demand increasing every year.1 Pr–Nd alloys, as raw materials for NdFeB magnetic materials, have become the main product in rare-earth metal applications.2 Currently, molten salt electrolysis is the main method for the industrial preparation of Pr–Nd alloys, and the carrier for electrolysis is the fluoride-rare earth oxide molten salt system. According to statistics, the current efficiency of Pr-Nd alloys prepared by molten salt electrolysis generally ranges from 85% to 90%. The main factor affecting the current efficiency is the anodic gas generated by the reaction between oxygen ions and the carbon anode during anodic oxidation in the electrolysis process, which leads to anodic effects and anodic degradation.3 E. Stefanidaki et al.4,5 studied the Nd–F–O complex ions and anodic process of the LiF–NdF3–Nd2O3 system. The results indicate that NdOFx(x−1)− and Nd2OFx+3(x−1)– might be formed, with the most reasonable mononuclear complex ions being NdOF43− and NdOF54− and the binuclear ones being Nd2OF106− and Nd2OF84−, as identified through Raman spectroscopy. Meanwhile, neodymium oxyfluorides and Nd–F–O complex ions were oxidised at the anode to oxygen, which was evolved before the oxidation of F− ions. In this work, NdOF and Nd–F–O complex ions, which are involved in the anodic reaction process in the LiF–NdF3–NdOF system during electrolysis, are presented as O*(II) ions. According to the research results in (ref. 6 and 7), it is indicated that the low solubility of NdOF can lead to a decrease in current efficiency and the formation of electrolytic cell sludge.
Therefore, the study of the transport characteristics of O*(II) ions in the (LiF–CaF2)eut.–NdOF system has important guiding significance for controlling the anode effect, improving current efficiency and optimizing the anodic process.8,9 However, due to the complexity and diversity of dissolved O*(II) ion groups in high-temperature molten salt systems, the established models of O*(II) ion transport behaviour still need to be continuously improved to enhance accuracy and practicality.10 The main purpose of this work is to systematically investigate the nature of dissolved O*(II) ion transport in the (LiF–CaF2)eut.–NdOF molten salt system and to provide a new scheme for analyzing the transport and migration laws of dissolved O*(II) ions. In this study, the solubility, conductivity, density, and ion mobility number of the (LiF–CaF2)eut.–NdOF molten salt system were determined experimentally, and the mobility and diffusion coefficients of O*(II) ions in the solvated state of the system were calculated using Einstein's equation.11 Based on the first-principles molecular dynamics method,12,13 the interaction laws and self-diffusion coefficients of the dissolved ions M* in the system were analyzed. The results of the study can elucidate the variation patterns of the transport number, migration rate, and diffusion coefficient of complex O*(II) ions with temperature and potential coupling in the (LiF–CaF2)eut.–NdOF system, providing a more comprehensive theoretical basis for the optimisation of the transport process of O*(II) ions.
2. Materials and methods
2.1 Solubility–conductivity–density measurement methods
Analytically pure LiF (99.99% metals basis, CAS No. 7789-24-4, Macklin) and CaF2 (99.99% metals basis, CAS No. 7789-75-5, Macklin) were dried at 423 K for 36 h to remove water under an argon-protected atmosphere. A mixture of 50 mol% Nd2O3 (99.99% metals basis, CAS 1313-97-9, Macklin) and 50 mol% NdF3 (99.99% metals basis, CAS 13709-42-7, Macklin) was ground in a glove box, then placed in a BN crucible and vacuum dried at 673 K for 24 h. Subsequently, the mixed powder was heated at 1123 K for 6 h under argon protection and cooled with liquid nitrogen to obtain NdOF powder.
Under argon protection, dehydrated LiF and CaF2 were uniformly mixed according to a molar ratio of LiF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaF2 = 79
CaF2 = 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 and then heated to a set melting temperature. NdOF was subsequently added to form a supersaturated (LiF–CaF2)eut.–NdOF molten salt. Samples of the saturated molten salt supernatant were drawn using a tungsten capillary and cooled. The solubility of NdOF was determined by analyzing the Nd content of the samples using inductively coupled plasma-optical emission spectroscopy (ICP-OES).
21 and then heated to a set melting temperature. NdOF was subsequently added to form a supersaturated (LiF–CaF2)eut.–NdOF molten salt. Samples of the saturated molten salt supernatant were drawn using a tungsten capillary and cooled. The solubility of NdOF was determined by analyzing the Nd content of the samples using inductively coupled plasma-optical emission spectroscopy (ICP-OES).
The conductivity meter was calibrated using a standard resistance solution. The molten salt was heated to a set temperature after being placed in a boron nitride conductivity cell. A molybdenum probe connected to the conductivity meter was then inserted into the molten salt and calibrated for depth. The resistance of the molten salt was measured by performing the probe lifting procedure at a constant temperature, and the conductivity of the molten salt system was calculated according to eqn (1).
The density of the molten salt system was determined using the Archimedes method. A precision electronic balance was used to measure the mass M1 (g) of the molybdenum probe in air and the mass M2 (g) after immersion in the molten salt, from which the density of the molten salt was calculated using eqn (2). The molybdenum probe was connected to a steel wire and suspended on a precision electronic balance, with the center position adjusted to test the pure water density at 293 K to calibrate the measurement system. The sample to be measured in the crucible was heated to a predetermined temperature and then maintained at a constant temperature for 20 min, with the molybdenum probe position kept the same as that of the calibration experiment. The density measurement program was then run to perform the measurement.
| |
 | (1) |
where
σ is the electrical conductivity (s cm
−1),
A is the internal cross-sectional area of the conductivity cell (cm
2),
Z is the total circuit resistance (Ω),
L is the length of the conductivity cell (cm),
ρ is the density of the molten salt (g cm
−3), and
V is the volume of the calibrated molybdenum measuring head (cm
3).
2.2 Migration count measurement methods
The transport number t[0] of the O*(II) ions is defined as the ratio of the charge current II of the O*(II) ions to the total current I passing through the electrolyte, which is equivalent to the ratio of the total charge Q[0] released during the oxidation of the O*(II) ions to the total charge Q passing through the electrolyte, as shown in eqn (3).
The measurement device is shown in Fig. 1. The main structure consists of a two-chamber slot separated by a porous boron nitride plate to isolate the cathode and anode chambers. Excess NdOF was added to a tungsten crucible in the cathode chamber to ensure that the molten (LiF–CaF2)eut. was saturated. The W cathode was introduced into the cathode chamber after melting the molten salt at an elevated temperature under argon protection and held for 30 min, whereas the high-purity graphite anode was introduced into the anode chamber after the mass (M1) was determined using an electronic balance. The anode and cathode were connected to a DC power supply, setting a constant-pressure electrolysis and real-time plotting of the potential–current curve. According to the data provided in the literature,14 the emission of perfluorocarbons (CF4, C2F6) and the concentration of NdOF in anode chamber were managed to stay between 0.5 and 1.5%. Meanwhile, the critical voltage and anode current density were maintained at less than 0.3 A cm−2 and 4.5 V, respectively. After 2 h of electrolysis, the graphite anode was cooled, and the mass was remeasured (M2). The total electric charge Q of the electrolyte was obtained by integrating the potential–current curve, while the total electric charge Q[0] released by the O*(II) ions was calculated by accounting for the consumption of the high-purity graphite anode (M1–M2) in the reaction to produce CO/CO2. Referring to the results of the literature,15,16 the reaction of generating CO and CO2 gases mainly occurred at the anode in the experiment, and the proportional relationship of CO/CO2 changed with variations in temperature and potential during the experiment. The off-gas from the anode chamber was continuously analyzed by taking 1 L min−1 from the cell atmosphere and pumping it at 353 K through the FT-IR spectrometer (Gasmet, Ansyco), which was calibrated for the proportion of CO/CO2 gases.
 |
| | Fig. 1 Schematic representation of the transport number measuring device. | |
2.3 Principles and methods of molecular dynamics calculations
The main process and parameter settings for molecular dynamics calculations are as follows:
(1) Based on Gaussian 16 software package, the LiF, CaF2, and NdOF molecules were optimized using the B3LYP method and mixed basis sets (i.e., Li, Ca, O, and F using the 6-311G* basis set from Pople17,18 and Nd using the SDD pseudopotential basis set).
(2) Packmol software19 was utilized to randomly populate a cubic box of length 145.0 nm with the optimized 79 LiF, 21CaF2 and two NdOF molecules, serving as a (LiF–CaF2)eut.–NdOF preprocessing model.20 Periodic boundary conditions were applied, and an NPT ensemble was enforced, employing a Nosé–Hoover thermostat to maintain the target temperature. The pressure was set at 1.013 × 105 Pa.
(3) The ab initio molecular dynamics (AIMD) calculation was performed using the CP2K software package.21,22 All atoms in the system were described using the DZVP-MOLOPT-SR-GTH basis set.23,24 Li and F valence electrons were treated as outer electrons, Nd atomic 3d/4f/6 s orbital electrons were considered to be valence electrons, and the remaining core electrons were described using Perdew–Burke–Ernzerhof pseudopotentials. All electrons were treated using the Grimme-D3 dispersion correction.25 Self-consistent field convergence was achieved using the orbital transformation method with an accuracy of 10−6 Hartree. Geometric optimisation was performed using the L-BFGS minimisation algorithm with the convergence criteria shown in Table 1, with a step size of 1 fs (TIMESTEP), running for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps (STEP), and an operation time of 10 ps. The maximum value of the grid precision cutoff was set to 600 Ry, and the REL_cutoff was set to 60 Ry.26,27
000 steps (STEP), and an operation time of 10 ps. The maximum value of the grid precision cutoff was set to 600 Ry, and the REL_cutoff was set to 60 Ry.26,27
Table 1 Convergence criterion of geometric optimization (unit a.u.)
| Convergence terms |
MAX_DR |
RMS_DR |
MAX_FORCE |
RMS_FORCE |
| Convergence criteria values |
3 × 10−3 |
1.5 × 10−3 |
4.5 × 10−4 |
3 × 10−4 |
(4) The radial distribution function (RDF) is the ratio of the particle number density function between A–B particles and the average particle number density, as shown in eqn (4).
| |
 | (4) |
where
ρB(
r) is the density of particles B at a distance
r from particle A and

is the average density of particles B within a shell of radius
rmax centered at particle A. The
rmax value was considered as half the box length, with the time averaged in the calculations.
(5) Post-processing analyses were performed using VMD software and VASTA software.
3. Results and discussion
3.1 Solubility–conductivity–density patterns of the (LiF–CaF2)eut.–NdOF system
The solubility of NdOF in the (LiF–CaF2)eut. molten salt system in the range of 1123–1373 K and the change rule in density and conductivity of the (LiF–CaF2)eut. system in the saturated state of NdOF are shown in Fig. 2. The results of linear fitting of the mean values of the data obtained from three parallel experiments corresponding to solubility, density and conductivity tests are shown in Fig. 2(a)–(c), respectively, corresponding to descriptive statistics with mean errors of 1.77%, 1.25% and 2.54%, respectively. The relatively high measurement error of conductivity is mainly attributed to the expansion of the molybdenum probe at high temperatures, resulting in an error in the length of the conductivity cell during the measurement process. Additionally, the difference in conductivity of the molybdenum probe at high temperatures compared to ambient temperatures also has an effect on the measurement results. Fig. 2(a) shows that the solubility of NdOF (SNdOF) in the (LiF–CaF2)eut. molten salt system is in the interval of 2.27–3.82 wt% in the temperature range of 1123–1373 K, which is in accordance with the linear increasing relationship eqn (5). Fig. 2(b) and (c) show that the density (ρ) of the saturated (LiF–CaF2)eut.–NdOF molten salt system conforms to the linear decreasing relationship eqn (6) in the interval of 2.33–2.88 g m3 in the temperature range of 1123–1373 K, whereas the conductivity (σ) conforms to the linear increasing relationship eqn (7) in the interval of 6.87–7.88 S cm−1.| | |
SNdOF = 6.28 × 10−5 T − 4.38
| (5) |
| | |
ρNdOF = −3.65 × 10−5 T + 5.21
| (6) |
| | |
σNdOF = 2.78 × 10−5 T + 2.61
| (7) |
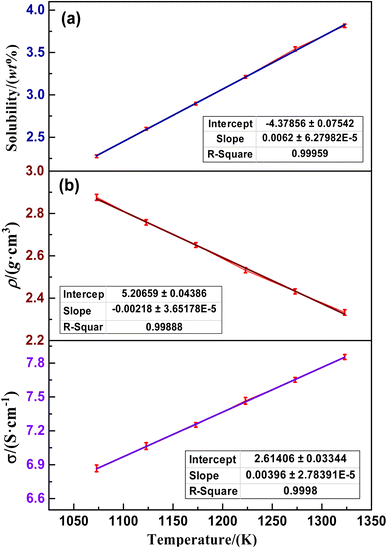 |
| | Fig. 2 Variation in (a) solubility of NdOF in (LiF–CaF2)eut. molten salt and (b) density and (c) conductivity of the saturated system with increasing temperature. | |
3.2 Patterns of changes in transport number and migration rate of O*(II) ions
The transport number of active O*(II) ions in the saturated (LiF–CaF2)eut.–NdOF system under varying potential (3.0–4.5 V) and temperature (1073–1323 K) conditions is presented in Table 2. The corresponding transport number of O*(II) ions is converted into migration rate under the corresponding potential–temperature conditions through eqn (8), as shown in Fig. 3. The curves in Fig. 3(a) show that the active O*(II) ion migration rate of the saturated (LiF–CaF2)eut.–NdOF system in the temperature range of 1073–1373 K varies nonlinearly with potential in the range of 3.0–4.5 V. The potential reaches a maximum value of O*(II) ion migration rate in the range of 3.75–4.25 V and the potential beyond this range causes the O*(II) ion migration rate to decrease. In the 3.0–3.75 V range, the active O*(II) ions in the system are subjected to a stronger electric field, while the rate of electrode reduction on the surface of the graphite electrode continues to increase, and both the transport number and migration rate of the active O*(II) ions increase as the potential increases. When the voltage is 3.75–4.25 V, the electric reduction of O*(II) ions on the graphite anode surface reaches equilibrium, and the Faraday current reaches an extreme value (i.e., the O*(II) ion migration rate and transport number are extremely high). When the potential exceeds 4.25 V, the non-Faraday current in the system increases, and the free F(I) ions and Li(I)/Ca(II) ions become carriers, which leads to a decrease in the transport number and migration rate of O*(II) ions. Additionally, as the potential increases, the anodic current density increases, and the desorption resistance of CO/CO2 gas molecules formed after the reduction of active O*(II) ions on the carbon graphite electrode surface increases. The concentration polarization and electrochemical reaction polarization on the electrode surface are enhanced, and more inactive ions in the system participate in the charge-transfer process, further decreasing the transport number and migration rate of the O*(II) ions.
Table 2 Transport number of dissolved O*(II) ions under varying temperature–potential conditions
| Temperature (K) |
Potential (V) |
| 3 V |
3.25 V |
3.5 V |
3.75 V |
4 V |
4.25 V |
4.5 V |
| 1073 |
0.179 |
0.219 |
0.295 |
0.319 |
0.352 |
0.338 |
0.260 |
| 1123 |
0.218 |
0.256 |
0.331 |
0.356 |
0.391 |
0.377 |
0.296 |
| 1173 |
0.261 |
0.296 |
0.362 |
0.388 |
0.424 |
0.409 |
0.331 |
| 1223 |
0.299 |
0.337 |
0.395 |
0.418 |
0.455 |
0.441 |
0.366 |
| 1273 |
0.343 |
0.382 |
0.431 |
0.452 |
0.488 |
0.477 |
0.407 |
| 1323 |
0.385 |
0.428 |
0.462 |
0.481 |
0.513 |
0.499 |
0.446 |
 |
| | Fig. 3 Change in dissolved state O*(II) ion migration rate (a) with increasing potential and (b) temperature–potential fitting projections. | |
The coupling law projection diagram of the migration rate of active O*(II) ions in the saturated (LiF–CaF2)eut.–NdOF system at 1073–1323 K and 3.0–4.5 V can be obtained by differential fitting of the data in Fig. 3(a), as shown in Fig. 3(b). It can be observed that when the temperature–potential is in the [1200 K↑–3.5 V↑] region, the migration rate of O*(II) ions is at its maximum. The high temperature accelerates volatilization of the molten salt medium and disrupts the equilibrium of the electrolytic system. Simultaneously, when the potential exceeds 5.0 V, the (LiF–CaF2)eut. base medium approaches the decomposition potential and loses its stability. Therefore, the continued application of higher potentials drastically reduces the current efficiency.
Therefore, by controlling the system potential in the range of 3.75–4.25 V while constraining the temperature at 1250–1350 K, the O*(II) ion migration rate can be controlled in the ideal range of 7.0 × 10−8 m2 V−1·s.
where
μi is the migration rate of O*(
II) ions (m
2 V
−1·s),
σ is the conductivity (S m
−1),
F is Faraday's constant (96
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
485 C mol
−1),
ci is the concentration of O*(
II) ions (mol m
−3), and
ti is the transport number of O*(
II) ions.
The fitted relationships and kinetic parameters of O*(II) ion migration rate according to temperature under varying potentials are listed in Table 3, indicating that the active O*(II) ion migration rate of the system increases linearly in the range of 1073–1323 K at 3.0–4.5 V. Since an increase in temperature directly increases the kinetic energy of O*(II) ions, the ion migration rate increases. Through logarithmic fitting analysis, the activation energy for O*(II) ion migration at varying potentials was calculated. It can be seen that as the potential increases from 3.0 V → 3.25 V → 3.5 V → 3.75 V → 4.0 V, the corresponding migration activation energy gradually decreases. As the potential increases from 4.0 V → 4.25 V → 4.5 V, the corresponding migration activation energy also decreases with increasing potential, consistent with the trend in the migration rate.
Table 3 Linear fitting relationship of migration rate–temperature of O(II) ions at varying potentials
| Potential (V) |
Diffusion coefficient |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μi – 1/T μi – 1/T |
Prefactor (J mol−1) |
MEA (J mol−1) |
| 3.0 |
μi = –9.19 × 10−8 + 1.19 × 10−10 T |
Y = −13.95 – 3428.32X |
8.74 × 10−7 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503.05 503.05 |
| 3.25 |
μi = −8.19 × 10−8 + 1.16 × 10−10 T |
Y = −14.27 – 2893.47X |
6.35 × 10−7 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056.31 056.31 |
| 3.50 |
μi = −2.59 × 10−8 + 7.85 × 10−11 T |
Y = −15.14 – 1628.87X |
2.66 × 10−7 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542.43 542.43 |
| 3.75 |
μi = −1.37 × 10−8 + 7.18 × 10−11 T |
Y = −15.27 – 1405.19X |
2.34 × 10−7 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682.75 682.75 |
| 4.00 |
μi = −2.65 × 10−9 + 6.78 × 10−11 T |
Y = −15.33 – 1224.78X |
2.20 × 10−7 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182.82 182.82 |
| 4.25 |
μi = −8.25 × 10−9 + 7.04 × 10−11 T |
Y = −15.29 – 1314.64X |
2.29 × 10−7 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 929.92 929.92 |
| 4.50 |
μi = −5.11 × 10−8 + 9.52 × 10−11 T |
Y = −14.79 – 2139.55X |
3.77 × 10−7 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 788.22 788.22 |
Overall, the transport number and migration rate of O*(II) ions are synchronized with the changes of temperature and potential, and the trends are consistent. The migration rate of O*(II) ions is closely correlated with the conductivity of the system, which in turn is strongly correlated with the temperature of the system and the microforms and states of the O*(II) ionic groups, as well as the interactions between the ions of the system. From the coupling relationship of O*(II) ion migration rate with temperature and potential, it can be seen that the O*(II) ions in the system are in a dynamic process. Therefore, dynamic control of the temperature-potential-concentration-component composition to drive the decomposition and miniaturization of the complex O*(II) ion clusters during the electroreduction process is the key to ensuring that the transport number and migration rate of O*(II) ions are in an optimized state.
3.3 Change law of self-diffusion coefficient of ions in the system
Fig. 4(a) shows the optimized electron density localization function planar filling of the structure of the saturated (LiF–CaF2)eut.–NdOF system calculated using AIMD, indicating no obvious electron density around the Li/Ca/Nd/O/F atoms in the system and no stable ionic bonds between the metallic elements (Li/Ca/Nd) and the non-metallic elements (O/F), which exist as discrete ions (denoted as M*, where M = Li/Ca/O/Nd/F).
 |
| | Fig. 4 Patterns of variation in (a) ELF planar color-filling diagrams and (b) M* ion self-diffusion coefficients for the saturated (LiF–CaF2)eut.–NdOF system. | |
Based on the data obtained from the AIMD calculations, the coordinates of motion of the system M* ions corresponding to time can be tracked, and the root-mean-square displacements (MSD), corresponding with the extent of change in the position of the atoms over time with respect to the reference point, can be calculated using eqn (9). Subsequently, the self-diffusion coefficient of M* ions in the (LiF–CaF2)eut.–NdOF system can be calculated using the limiting expression of the Einstein formula in eqn (10). The calculated results are shown in Fig. 4(b) and indicate that the self-diffusion coefficient of the M* ions in the system increases linearly with temperature. At the same temperature, in descending order, the self-diffusion coefficients are D(Li) > D(F) > D(Ca) > D(O) > D(Nd), where D(O) and D(Nd) are significantly lower than D(Li)/D(Ca)/D(F) in the molten salt medium. Since the diffusion coefficient–diffusion activation energy is in accordance with the Arrhenius equation (eqn (11)), which is transformed into the logarithmic relationship (eqn (12)) and then linearly fitted to ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D – (1/T), the diffusion activation energies and prefactors of the various M* ions in the system can be obtained; the results are shown in Table 4. The diffusion activation energies of the Nd(III) and O*(II) ions in the system are similar and relatively high, while those of Ca(II) and F(I) are similar. Li(I) exhibits the lowest migration barrier.
D – (1/T), the diffusion activation energies and prefactors of the various M* ions in the system can be obtained; the results are shown in Table 4. The diffusion activation energies of the Nd(III) and O*(II) ions in the system are similar and relatively high, while those of Ca(II) and F(I) are similar. Li(I) exhibits the lowest migration barrier.
| |
 | (9) |
| |
 | (10) |
| |
 | (11) |
| |
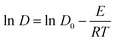 | (12) |
where
d is the MSD dimension, which is 3 in this study;
t is time (
s);

is the mean square displacement;
D is the diffusion coefficient of ions (cm
2 s
−1);
E is the activation energy for ion diffusion (J mol
−1); and
R is the ideal gas constant (8.314 J mol
−1 K
−1).
Table 4 Linear fitting relationship and relevant parameters of diffusion coefficients of M* ions
| Ions |
Diffusion coefficient |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D – 1/T D – 1/T |
Prefactor (J mol−1) |
DEA (J mol−1) |
| Li(I) |
DLi = −2.08 × 10−4 + 2.33 × 10−7 T |
Y = −5.46 – 4928.08X |
4.25 × 10−3 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972.06 972.06 |
| Ca(II) |
DCa = −1.31 × 10−4 + 1.43 × 10−7 T |
Y = −5.67 – 5378.31X |
3.45 × 10−3 |
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715.27 715.27 |
| Nd(III) |
DNd = −5.56 × 10−5 + 5.69 × 10−8 T |
Y = −5.49 – 7005.16X |
4.13 × 10−3 |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240.90 240.90 |
| O(II) |
DO = −8.29 × 10−5 + 8.59 × 10−8 T |
Y = −5.32 – 6642.99X |
4.89 × 10−3 |
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229.82 229.82 |
| F(I) |
DF = −1.18 × 10−4 + 1.98 × 10−7 T |
Y = −5.38 – 5314.39X |
4.61 × 10−3 |
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183.84 183.84 |
3.4 Change pattern of O*(II) ion diffusion coefficient
Based on the migration rate data of O*(II) ions in the saturated (LiF–CaF2)eut.–NdOF system, the diffusion coefficients of the O*(II) ions under varying potential-temperature conditions can be calculated from the Einstein equation (eqn (13)). Combined with the O*(II) ion self-diffusion coefficient data in Fig. 4(b), the O*(II) ion diffusion coefficient of the saturated (LiF–CaF2)eut.–NdOF system can be obtained by varying the temperature and potential, as shown in Fig. 5(a). It can be observed that the O*(II) ion diffusion coefficient increased nonlinearly with increasing potential between 3 and 3.75 V in the temperature range of 1123–1373 K. After reaching a maximum at 3.75–4.25 V, the diffusion coefficient tended to decrease as the potential increased. The data in Fig. 5(a) can be differentially fitted to obtain the variation rule of the O*(II) ion diffusion coefficient under the coupling conditions of temperature and potential, as shown in Fig. 5(b). Under a potential not lower than ≈3.50 V and temperature not lower than ≈1223 K, O*(II) ions exhibit a higher diffusion rate with diffusion coefficients that are more sensitive to potential changes. Fitting the data in Fig. 5(a) from the perspective of temperature–diffusion coefficients at corresponding potentials reveals that under 3.0–4.5 V, the diffusion coefficients of the O*(II) ions linearly increase within the temperature range of 1123–1373 K. Table 5 presents the linear expressions. Furthermore, by fitting D − (1/T) and performing logarithmic transformation, the trend in the activation energy change of O*(II) ions under varying potentials is E3.0V > E3.25V > E3.5V > E3.75V > E4.0V < E3.25V < E4.5V, further indicating the existence of a minimum value in the diffusion barrier of O*(II) ions between the potentials of 3.75–4.25 V.
 |
| | Fig. 5 (a) Relationship between temperature and potential and (b) projection of temperature–potential coupling of O*(II) ion diffusion coefficients in (LiF–CaF2)eut.–NdOF system. | |
Table 5 Linear fitting relationship and related parameters of diffusion coefficient–temperature for O(II)* ions in the system at varying potentials
| Potential (V) |
Diffusion coefficient fits |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D – 1/T fit D – 1/T fit |
Prefactor (J mol−1) |
MEA (J mol−1) |
| 3.0 |
D = −7.31 × 10−5 + 8.29 × 10−8 T |
Y = −6.71 – 4617.05X |
1.22 × 10−3 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386.15 386.15 |
| 3.25 |
D = −7.17 × 10−5 + 8.48 × 10−8 T |
Y = −7.02 – 4082.19X |
8.94 × 10−4 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.33 939.33 |
| 3.50 |
D = −4.85 × 10−5 + 7.00 × 10−8 T |
Y = −7.90 – 2817.60X |
3.71 × 10−4 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 425.53 425.53 |
| 3.75 |
D = −4.43 × 10−5 + 6.83 × 10−8 T |
Y = −8.03 – 2593.91X |
3.26 × 10−4 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565.77 565.77 |
| 4.00 |
D = −4.18 × 10−5 + 6.89 × 10−8 T |
Y = −8.09 – 2413.51X |
3.07 × 10−4 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065.92 065.92 |
| 4.25 |
D = −4.34 × 10−5 + 6.91 × 10−8 T |
Y = −8.05 – 2503.36X |
3.19 × 1 0−4 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 812.94 812.94 |
| 4.50 |
D = −5.89 × 10−5+7.65 × 10−8 T |
Y = −7.55 – 3328.27X |
5.26 × 10−4 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 671.24 671.24 |
In summary, the diffusion coefficients and mobilities of dissolved O*(II) ions are covariant at certain temperatures, and the diffusion of O*(II) ions is more sensitive to potential changes. This is mainly attributed to the increase in the concentration gradient due to the directional motion of O*(II) ions under the action of the electric field, and the increase of the polarization rate and the dipole distance of O*(II) ion clusters induced by the external electric field, which results in the activation and decomposition of complex O*(II) ion clusters to form smaller groups.
where
D is the diffusion coefficient of ions (m
2 s
−1),
kB is the Boltzmann constant (1.38 × 10
−23 J K
−1),
T is the absolute temperature (K),
q is the ionic charge (
C), and
ui is the migration rate of O*(
II) ions (m
2 V
−1·s).
3.5 Analysis of O*(II)–M* radial distribution function of the system
The radial distribution function [RDF, g(rM*)] between O*(II)–M* ions in the system can be calculated from the M* ion motion trajectory data in the saturated (LiF–CaF2)eut.–NdOF system using AIMD, which in turn allows the average first coordination radius (RM*) and truncation radius (rM*) between M*–O*(II) ions in the system to be determined. The O*(II)–M* interion migration energy barrier V(M*) can be obtained using eqn (14); the results are listed in Table 6.
Table 6 Data on the radial distribution function of the saturated (LiF–CaF2)eut.–NdOF system
| M*–O* |
Average coordination radius/Å |
Cut-off radius/Å |
V(r)/kJ mol−1 |
| Li–O |
1.85 |
2.95 |
23.47 |
| Ca–O |
2.25 |
3.35 |
34.54 |
| F–O |
3.05 |
4.55 |
8.95 |
| Nd–O |
2.05 |
3.55 |
53.53 |
Fig. 6(a) and (b) show the RDF curves (mean) and migration energy barriers V(M*), respectively, between O*(II)–M* ions in the 1123–1373 K range for the saturated (LiF–CaF2)eut.–NdOF system. Combined with the data in Table 5, it can be observed that the average coordination radius between O*(II) ions and cations in the [Nd*(III)/Ca*(II)/Li*(I)] system is close to the value of the truncation radius. Owing to the small radius of Li*(I), the first coordination layer between O*(II) and Li*(I) is tighter. Although the radius of the Ca*(II) ion is smaller than that of Nd*(III), the electrostatic interactions between O*(II)–Nd*(III) and O*(II)–Ca*(II) are stronger, resulting in a slightly tighter first coordination layer between O*(II)–Nd*(III) and O*(II)–Ca*(II).
 |
| | Fig. 6 (a) Mean values of radial distribution functions and (b) migration energy barriers V(M*) for O*(II)–M* in the saturated (LiF–CaF2)eut.–NdOF system. | |
Overall, owing to the electrostatic repulsion between the [O*(II)/F*(I)] and O*(II) ions, the first coordination radius and truncation radius between the system cations [Nd*(III)/Ca*(II)/Li*(I)] and O*(II) are larger than that between the anions [O*(II)/F*(I)] and O*(II), and the first coordination layer is looser. The average migration energy barriers Vr between the O*(II)–M* ion pairs are in the order V(Nd*) > V(O*) > V(Ca*) > V(Li*) > V(F*), indicating that Nd*(III) has the strongest hold on the diffusive migration of O*(II), whereas the hold of F*(I) is the weakest. It is noteworthy that the interactions between the O*(II) ions are much stronger than those between the F*(I) and O*(II) anions owing to the stronger nucleoelectric repulsion between O*(II) and O*(II), as well as the stronger interactions between Nd*(III) and O*(II) during solvation and dissociation of the NdOF molecule; the F*(I) ions have a weaker direct interaction on O*(II) in the system.
| |
V(r) = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(r) g(r)
| (14) |
where
R is the ideal gas constant (8.314 J mol
−1 K
1),
T is the absolute temperature (K), and
g(
r) is the ion pair radial distribution function value.
4. Conclusion
In the temperature range of 1123–1373 K, the solubility of NdOF in the (LiF–CaF2)eut. system increases linearly within the range of 2.27–3.82 wt%. The density (ρ) of the saturated (LiF–CaF2)eut.–NdOF system decreases linearly with increasing temperature in the range of 2.33–2.88 g m3, while the conductivity increases linearly with increasing temperature in the range of 6.87–7.88 S cm−1. The mobility number/mobility/diffusion coefficient of active O*(II) ions in the saturated (LiF–CaF2)eut.–NdOF system varies nonlinearly with potential in the 3.0–4.5 V/1073–1323 K range, where the O*(II) ion mobility reaches a maximum at 3.75–4.25 V. At a certain potential, the migration number/migration rate/diffusion coefficient of O*(II) ions in the saturated (LiF–CaF2)eut.–NdOF system increased linearly in the temperature range of 1073–1323 K and is more sensitive to potential changes. When the temperature and potential exceeded 1200 K and 3.5 V, respectively, the migration rate of O*(II) ions reached its maximum. The values of the radial distribution function between ions in the saturated (LiF–CaF2)eut.–NdOF system indicate that the Nd*(IIi) ions have the strongest hold on the migration and diffusion of the solvated O*(II) ions.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 52474328 and No. 52074134).
References
- Z. Zuo, Y. Liu, X. Yang and F. Liu, PrF3-NdF3-DyF3-LiF electrolyte system for preparation of Pr-Nd-Dy alloy by electrolysis, J. Rare Earths, 2022, 40, 996–1001 CAS.
- H. Zhu, Rare earth metal production by molten salt electrolysis, Encyclopedia of Applied, Electrochemistry, 2014, pp. 1765–1772 Search PubMed.
- C. Liao, L. Que and Z. Fu, et al., Research Status of Electrolytic Preparation of Rare Earth Metals and Alloys in Fluoride Molten Salt System: A Mini Review of China, Metals, 2024, 14(4), 27 Search PubMed.
- E. Stefanidaki, G. M. Photiadis and C. G. Kontoyannis, et al., Oxide solubility and Raman spectra of NdF3-LiF-KF-MgF2-Nd2O3 melts, J. Chem. Soc., Dalton Trans., 2002, 11, 2302–2307 Search PubMed.
- E. Stefanidaki, C. Hasiotis and C. Kontoyannis, Electrodeposition of neodymium from LiF–NdF3–Nd2O3 melts, Electrochim. Acta, 2001, 46, 2665–2670 Search PubMed.
- H. Sun and Y. Yang, Molten salt synthesis of neodynium oxyfluoride with tetragonal structure, Ceram. Int., 2021, 47, 432–437 Search PubMed.
- C. M. Fan, S. Z. Liu, J. J. Gu, S. Y. Guan, J. H. Zhao and B. Li, Electrochemical investigation of the anode processes in LiF–NdF3 melt with low oxygen content, Int. J. Miner., Metall. Mater., 2021, 28, 398–403 CrossRef CAS.
- A. Zhadan, V. Sarou-Kanian, L. Del Campo, L. Cosson, M. Malki and C. Bessada, Transport properties in molten carbonates: self-diffusion and conductivity measurements at high temperature, Int. J. Hydrogen Energy, 2021, 46, 15059–15065 CrossRef CAS.
- X. Li, Y. Zhang, B. Yue, L. Yan, T. Jiang and S. Peng, Unifying the diffusion coefficients of lanthanides and actinides in binary molten salt mixtures: a data review, J. Mol. Liq., 2020, 297, 112106 CrossRef CAS.
- Y. Xie, M. Bu, Y. Zhang and G. Lu, Effect of composition and temperature on microstructure and thermophysical properties of LiCl–CaCl2 molten salt based on machine learning potentials, J. Mol. Liq., 2023, 383, 2112 CrossRef.
- E. L. Shreve, Theoretical Derivation of Atmospheric Ion Concentrations, Conductivity, Space Charge Density, Electric Field and Generation Rate from 0 to 60 km, J. Atmos. Sci., 1970, 27, 1186–1194 CrossRef.
- J. Wang, J. Wu, G. Lu, Y. Jianguo and J. Yu, Molecular dynamics study of the transport properties and local structures of molten alkali metal chlorides, J. Mol. Liq., 2017, 238, 236–247 CrossRef CAS.
- C. Chen, J. Li, R. Luo and H. Zhang, Ab initio Molecular Dynamics Study on microstructure and Diffusion Properties of CaF2–2.2NaF–AlF3 System, Chem. Phys., 2021, 550, 1294 CrossRef.
- H. Vogel and B. Friedrich, Reducing Greenhouse Gas Emission from the Neodymium Oxide Electrolysis. Part II: Basics of a Process Control Avoiding PFC Emission, Int. J. Nonferrous Metall., 2017, 6, 27–46 CrossRef CAS.
- H. Vogel, B. Flerus, F. Stoffner and B. Friedrich, Reducing Greenhouse Gas Emission from the Neodymium Oxide Electrolysis. Part I: Analysis of the Anodic Gas Formation, J. Sustain. Met., 2017, 3, 99–107 CrossRef.
- S. Liu, L. Chen, B. Li, L. Wang, B. Yan and M. Liu, Anode processes for Nd electrowinning from LiF-NdF3-Nd2O3 melt, Electrochim. Acta, 2014, 147, 82–86 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient diffuse function-augmented basis sets for anion calculations. III. The 3–21+ G basis set for first-row elements, Li–F, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, Packmol: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef.
- A. Bengtson, H. O. Nam, S. Saha, R. Sakidja and D. Morgan, First-principles molecular dynamics modeling of the LiCl–KCl molten salt system, Comput. Mater. Sci., 2014, 83, 362–370 CrossRef CAS.
- H. Jürg, I. Marcella, S. Florian and J. Vandevondele, cp2k: Atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2014, 4, 15–25 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- C. Can, L. Jie, R. Luo and H. Zhang, Ab initio Molecular Dynamics Study on microstructure and Diffusion Properties of CaF2–2.2NaF–AlF3 System, Chem. Phys., 2021, 11, 1294 Search PubMed.
- M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi and M. Del Ben, CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103 Search PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128 CAS.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaF2 = 79
CaF2 = 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 and then heated to a set melting temperature. NdOF was subsequently added to form a supersaturated (LiF–CaF2)eut.–NdOF molten salt. Samples of the saturated molten salt supernatant were drawn using a tungsten capillary and cooled. The solubility of NdOF was determined by analyzing the Nd content of the samples using inductively coupled plasma-optical emission spectroscopy (ICP-OES).
21 and then heated to a set melting temperature. NdOF was subsequently added to form a supersaturated (LiF–CaF2)eut.–NdOF molten salt. Samples of the saturated molten salt supernatant were drawn using a tungsten capillary and cooled. The solubility of NdOF was determined by analyzing the Nd content of the samples using inductively coupled plasma-optical emission spectroscopy (ICP-OES).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps (STEP), and an operation time of 10 ps. The maximum value of the grid precision cutoff was set to 600 Ry, and the REL_cutoff was set to 60 Ry.26,27
000 steps (STEP), and an operation time of 10 ps. The maximum value of the grid precision cutoff was set to 600 Ry, and the REL_cutoff was set to 60 Ry.26,27
 is the average density of particles B within a shell of radius rmax centered at particle A. The rmax value was considered as half the box length, with the time averaged in the calculations.
is the average density of particles B within a shell of radius rmax centered at particle A. The rmax value was considered as half the box length, with the time averaged in the calculations.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), ci is the concentration of O*(II) ions (mol m−3), and ti is the transport number of O*(II) ions.
485 C mol−1), ci is the concentration of O*(II) ions (mol m−3), and ti is the transport number of O*(II) ions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μi – 1/T
μi – 1/T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503.05
503.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056.31
056.31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542.43
542.43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682.75
682.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182.82
182.82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 929.92
929.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 788.22
788.22
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D – (1/T), the diffusion activation energies and prefactors of the various M* ions in the system can be obtained; the results are shown in Table 4. The diffusion activation energies of the Nd(III) and O*(II) ions in the system are similar and relatively high, while those of Ca(II) and F(I) are similar. Li(I) exhibits the lowest migration barrier.
D – (1/T), the diffusion activation energies and prefactors of the various M* ions in the system can be obtained; the results are shown in Table 4. The diffusion activation energies of the Nd(III) and O*(II) ions in the system are similar and relatively high, while those of Ca(II) and F(I) are similar. Li(I) exhibits the lowest migration barrier.


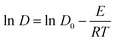
 is the mean square displacement; D is the diffusion coefficient of ions (cm2 s−1); E is the activation energy for ion diffusion (J mol−1); and R is the ideal gas constant (8.314 J mol−1 K−1).
is the mean square displacement; D is the diffusion coefficient of ions (cm2 s−1); E is the activation energy for ion diffusion (J mol−1); and R is the ideal gas constant (8.314 J mol−1 K−1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D – 1/T
D – 1/T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972.06
972.06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715.27
715.27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240.90
240.90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229.82
229.82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183.84
183.84
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D – 1/T fit
D – 1/T fit![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386.15
386.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.33
939.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 425.53
425.53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565.77
565.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065.92
065.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 812.94
812.94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 671.24
671.24
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(r)
g(r)

