 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ga-doping in Li0.33La0.56TiO3: a promising approach to boost ionic conductivity in solid electrolytes for high-performance all-solid-state lithium-ion batteries†
Md. Nagib Mahfuz‡
 a,
Appy Feroz Nura‡
a,
Appy Feroz Nura‡ a,
Md Shafayatul Islamb,
Tomal Sahaa,
Koushik Roy Chowdhurya,
Sheikh Manjura Hoque
a,
Md Shafayatul Islamb,
Tomal Sahaa,
Koushik Roy Chowdhurya,
Sheikh Manjura Hoque d,
Md Abdul Gafurc,
Aninda Nafis Ahmed*c and
Ahmed Sharif
d,
Md Abdul Gafurc,
Aninda Nafis Ahmed*c and
Ahmed Sharif *a
*a
aDepartment of Materials and Metallurgical Engineering, Bangladesh University of Engineering & Technology (BUET), Dhaka, Bangladesh. E-mail: asharif@mme.buet.ac.bd
bDepartment of Materials Science and Engineering, University of Illinois Urbana Champaign, Urbana, Illinois 61801, USA
cPilot Plant and Process Development Centre, Bangladesh Council of Scientific and Industrial Research (BCSIR), Dhaka 1205, Bangladesh. E-mail: a_nafis_ahmed@bcsir.gov.bd
dMaterials Science Division, Atomic Energy Centre, Dhaka 1000, Bangladesh
First published on 13th January 2025
Abstract
All-solid-state lithium-ion batteries (ASSLBs) are the next advancement in battery technology which is expected to power the next generation of electronics, particularly electric vehicles due to their high energy density and superior safety. ASSLBs require solid electrolytes with high ionic conductivity to serve as a Li-ion battery, driving extensive research efforts to enhance the ionic conductivity of the existing solid electrolytes. Keeping this in view, the B-site of Li0.33La0.56TiO3 (LLTO) solid electrolyte has been partially substituted with Ga and novel Ga-doped LLTO (Li0.33+xLa0.56Ti1−xGaxO3) solid-electrolytes are fabricated using the solid-state reaction method, followed by sintering at 1100 °C for 2 h. The effects of Ga substitution on the structural changes, chemical states, ionic conductivity, and electrochemical stability of LLTO are systematically analyzed. The XRD analysis of the LLTO samples confirms the formation of a tetragonal perovskite structure and increasing bottleneck size up to 3% Ga-doped samples. XPS results have further confirmed the successful substitution of Ti4+ by Ga3+. The Ga3+ substitution has successfully enhanced the conductivity of LLTO solid electrolytes and the highest conductivity of 4.15 × 10−3 S cm−1 is found in Li0.36La0.56Ti0.97Ga0.03O3 (x = 0.03), which is an order of magnitude higher than that of pristine LLTO. This increase in ionic conductivity is a synergistic effect of B–O bond stretching resulting from the size difference between Ga3+ and Ti4+ and the increase in grain size. Moreover, the synthesized solid electrolytes are stable within the range of 2.28 to 3.78 V against Li/Li+, making them potential candidates for all-solid-state lithium-ion batteries.
1 Introduction
Rechargeable batteries have been an exclusive choice for researchers over the past few decades. Phones, laptops, pacemakers, electric vehicles, and many other devices used in our daily lives rely heavily on these batteries. Lithium-ion batteries (LIBs) are commonly used in these devices and they are popular due to their higher energy storage and longer lifespans.1,2 However, LIBs have safety limitations due to their highly flammable organic liquid electrolytes, mostly cobalt oxide. Upon heating, these liquid electrolytes can cause fires and explosions.3,4 As a potential solution, researchers are now exploring all-solid-state lithium-ion batteries (ASSLBs), which use non-flammable ceramic solid electrolytes.5 The solid nature of these solid electrolytes (SEs) offers various advantages over traditional LIBs. For example, conventional liquid electrolytes start evaporating at 70 °C,6,7 causing expansion and fires, whereas most ASSLBs remain stable even above 200 °C,8 eliminating the fire risks. Moreover, ASSLBs have better electrochemical stability, higher energy and power density, and simpler battery design.9–12Various kinds of solid electrolytes, such as NASICON, garnet, perovskite, LISICON, sulfide, anti-perovskite, and many more types have been studied in the past few years.13 The sulfide-based SEs has the highest ionic conductivity of the order 10−2 S cm−1.14 Also, they are soft and deformable, which allows them to be densely packed under medium pressure (100–700 MPa) and room temperature,15 and this dense packing results in lower grain boundary resistance.16,17 However, their chemical instability and sensitivity to moisture are their major drawbacks.18,19 NASICON-type SEs are good ionic conductors and have good electrochemical stability but they are very costly due to one of their precursors, GeO2, being expensive.13 Garnet-type LLZO has high ionic conductivity but it is unstable against moisture and CO2.18 Perovskite-type SEs have a broad tolerance factor t, (where t = 0.75–1.0), allowing them to be doped with most of the ions, a wide electrochemical window allowing the use of high-voltage positive materials and have high bulk Li-ion conductivity (10−3 S cm−1) in LLTO.20 For these reasons, Perovskite-type SEs have become a leading candidate for solid-state batteries.18,20
Most of the Li-ion solid electrolytes are generally A-site-deficient materials. One such electrolyte is LLTO having a general formula Li3xLa2/3−xTiO3 with (1/3-2x) A-site vacancy per chemical formula which has gained significant research interest in the past decades. La0.57Li0.30TiO3, La0.56Li0.33TiO3, La0.55Li0.35TiO3, and La0.50Li0.50TiO3 are more commonly researched materials in the Li3xLa2/3−xTiO3 family.21–24 Two different perovskite structures were observed for Li3xLa2/3−xTiO3 with varying Li concentrations. For low Li content (x < 0.08), the perovskite structure consists of an orthorhombic unit cell with Pmmm space group, and for higher Li content (x > 0.1), the structure consists of a tetragonal unit cell with P4/mmm space group.25 A disordered structure with a cubic unit cell can also be produced by quenching the LLTO solid electrolytes in liquid nitrogen from sintering temperature and this quenched cubic structure showed greater conductivity compared to the ordered tetragonal structure.26 Li-ion conductivity in LLTO is attributed to the movement of Li-ion from one vacancy to another through octahedral channels.27 The conductivity of LLTO ceramics has the contribution of both bulk and grain boundary resistance where grain boundary resistance is always higher than the bulk grain resistance.28,29 Sintering temperature affects the grain size which in turn affects the conductivity as the volume of bulk grain and grain boundary changes with grain size. Smaller grain size constitutes an increased number of grains with a higher volume fraction of grain boundary, leading to more mismatch in the conduction pathway, which lowers ion conduction.30 With increasing grain size, the grain boundary resistance itself decreases, which can also contribute to increasing conductivity.31
High ionic conductivity was found in A-site substituted La2/3−xM3xTiO3 (M = Li, Na, K) materials. The high lithium-ion conductivity in LLTOs was attributed to the small ionic radius of Li+ not bound to the rigid lattice framework and the size of structural channels and the cavities formed by TiO6 octahedron which indicated that Li+ needs an appropriate channel size to migrate.32 The effect of B site substitution on LLTO was studied by doping with various metal ions with different valence (Mg, Al, Mn, Ge, Ru, W). Al (trivalent) substituted LLTO exhibited increased ionic conductivity for 0.05% Al doping, and it was attributed to the weakening of the A–O bond and strengthening of the B–O bond due to more negative free energy of Al2O3.33 Al-doped LLTO material prepared via radio-frequency magnetron sputtering technology also showed higher ionic conductivity than that of pure LLTO.34 However, substituting the B-site with ions of higher valence than Ti4+, for instance, pentavalent ions (Ta5+ and Nb5+) did not result in increased ionic conductivity. Among the Li3xLa2/3−xTiO3 family, maximum conductivity was found in the composition with x = 0.11 sintered at 1350 °C.30 Li3xLa2/3−xTiO3 with x = 0.11 or La0.56Li0.33TiO3 was also found to be relatively stable in air. The phase of the La0.56Li0.33TiO3 did not change even after storage in contact with lithium for 24 h.35 Hu et al.36 studied Ge-doped LLTO materials which showed improved conductivity up to a certain percentage of doping as a result of increased crystallinity and densification. The bigger ionic radius of Ge2+ compared to that of Ti4+ may have also favored Li+ migration to improve Li ion conductivity.
In this study, we synthesized a novel Ga-doped LLTO with the chemical formula Li0.33+xLa0.56Ti1−xGaxO3 (x = 0.01, 0.03, and 0.05) to analyze the effect of B-site substitution on La0.56Li0.33TiO3 with tri-valent Ga ion. Ga was chosen as the dopant ion for two key reasons. The first one is the slightly larger ionic radius of Ga3+ compared to Ti4+, which is expected to promote the Li-ion migration. The other reason is its lower valence state compared to Ti (3+ vs. 4+), which will introduce oxygen vacancy in the structure. After substituting with Ga, we successfully achieved an increased conductivity of 4.15 × 10−3 S cm−1 in Li0.36La0.56Ti0.97Ga0.03O3, which is significantly higher than the minimum conductivity required (>10−4 S cm−1) for a functioning solid electrolyte in ASSBs.37 Furthermore, only a few studies have reported conductivity of LLTO in the 10−3 S cm−1 range, making our Ga-LLTO a more promising solid-electrolyte for the ASSLBs.
2 Experimental
2.1 Material synthesis
The pure Li0.33La0.56TiO3 and Ga-doped Li0.33+xLa0.56Ti1−xGaxO3 samples were synthesized through the solid-state reaction method (Fig. 1). Stoichiometric quantities of as received Li2CO3 (Merck kGaA, 99.93%), La2O3 (Merck kGaA, 99.99%), TiO2 (Research-lab, 99%), and Ga2O3 (Merck kGaA, 99.6%) powders were carefully weighed according to the formula Li0.33+xLa0.56Ti1−xGaxO3 (x = 0.00, 0.01, 0.03, 0.05). Lithium being volatile, excess Li2CO3 powder of about 10 wt% was added to compensate for the lithium loss during high-temperature processes like calcination and sintering. The powders of raw materials were fully mixed using a planetary ball mill with ethanol at 200 rpm for 16 h. The mixture was dried at 120 °C for 2 h to remove the ethanol. The dried mixture was ground into fine powders using a mortar and a pestle. The homogeneous mixture was calcined at 800 °C for 2 h in alumina crucibles. The calcined powders were grounded with 5% polyvinyl alcohol (PVA) addition and then pressed into pellets with uniaxial pressure. The pellets were sintered at 1100 °C for 2 h after a ramp of 2 °C min−1. To avoid any contamination from the alumina crucible and any by-product formation, the pellets were placed and sintered on the alumina powder bed. Finally, the pellets were polished to smooth the surface for further characterization.2.2 Material characterization
The crystallographic characterization and phase identification of the sintered samples were done by X-ray diffraction (XRD, 3040-X′′Pert PRO, Philips) with Cu Kα radiation of wavelength, λ = 1.5418 Å with 2θ from 10° to 80°. Further, the Rietveld refinement was done to assess the lattice parameters. X-ray photoelectron spectroscopy (XPS) was carried out using the Thermo Fisher Scientific Escalab Xi+ with Al Kα radiation to confirm the elemental composition and chemical states of the samples. The morphology and grain size of the pellet samples were observed using a scanning electron microscope (FE-SEM: JEOL JSM 7600F) with an acceleration voltage of 5 kV. One side of the pellets was coated with silver before performing SEM analysis. Energy Dispersive X-ray Spectroscopy (EDX) was done to assess the elemental composition of the samples. Transmission electron microscopy (HR-TEM) was done with the Talos F200X (Thermo Fisher Scientific) to analyze the microscopic nature and d-spacing of the samples. To prepare samples for TEM, the LLTO powders were sonicated for 25 minutes in 2 mL of ethanol, and then placed on a carbon-coated Cu grid. The conductivity of the LLTO ceramics was calculated from the impedance spectra obtained over the 10−1 to 106 Hz frequency range using the Reference 3000 Gamry electrochemical workstation at room temperature. LLTO powders were mixed with 5% PVA as binder and ethanol to prepare a slurry which was then dip-coated onto a carbon rod (ESI Fig. S1†). Electrochemical Impedance Spectroscopy (EIS) was performed using a three-electrode system in 1 M LiOH solution. A carbon rod coated with LLTO ceramic was the working electrode. The Pt electrode and saturated calomel electrode (SCE) were used as the counter and reference electrode, respectively. Cyclic voltammetry was done to investigate the electrochemical stability of the solid electrolytes within the voltage range −1 to 0.5 V against SCE at scan rates of 10 mV s−1 and 50 mV s−1 and then the potential window was referred to the Li/Li+ couple.3 Results and discussion
3.1 Structural characterization
Fig. 2(a) presents the XRD patterns of the LLTO and Ga-doped LLTO samples sintered at 1100 °C for 2 h. The base LLTO sample shows diffraction peaks at 11.46°, 25.72°, 32.70°, 40.32°, 46.88°, 48.42°, 52.82°, 54.22°, 58.32°, 68.45°, 73.24° and 77.92° corresponding to the crystallographic planes (001), (101), (110), (112), (200), (201), (202), (211), (212), (220), (300) and (310) respectively. The positions of the peaks and their associated planes match well with the JCPDS card no. 01-087-0935 (Li0.33 La0.56 TiO3).38 The Ga-doped samples also show the same crystallographic planes with negligible variations in position. Thus, it affirms the perovskite tetragonal crystalline structure with the P4/mmm space group of the synthesized undoped and doped-LLTO samples Fig. 2(b). The tetragonal structure is further validated by the Raman spectroscopy analysis (ESI Fig. S2†). However, two additional peaks (marked with a diamond, ♦) were found in the XRD patterns at 2θ values of [31.9° and 43.5°] for the 5% Ga-LLTO sample. These impurity peaks were identified as TiO2 [JCPDS card no. 98-018-9327].39 Additionally, no peaks corresponding to Ga-containing compounds were found in any of the samples. This indicates that Ga3+ has successfully replaced Ti4+ at the B site without introducing any additional phases. | ||
| Fig. 2 (a) XRD patterns of Li0.33+xLa0.56Ti1−xGaxO3 sintered at 1100 °C for 2 h, (b) tetragonal perovskite structure of LLTO. | ||
The observation of multiple sharp peaks in the XRD pattern of the synthesized samples indicates that they are polycrystalline in nature.40 Among them, the most intense peak is attributed to the crystal plane (110) at 32.70°. The sharp peaks indicate that the material has high crystallinity (data provided in ESI Table S1†). The Rietveld Refinement method was performed to analyze the XRD spectra to determine the unit cell parameters & volume and is depicted in Fig. 3(a–d). The unit cell parameters and volumes are listed in Table 1. The formula used in Rietveld refinement to determine the lattice parameters (a = b & c) of the tetragonal unit cell is:
 | (1) |
 | ||
| Fig. 3 Rietveld refinement (a–d) and Williamson–Hall plot (e–h) of LLTO and Ga-LLTO solid electrolytes. | ||
| Base LLTO | 1% Ga-LLTO | 3% Ga-LLTO | 5% Ga-LLTO | ||
|---|---|---|---|---|---|
| Unit cell parameters | a (Å) | 3.87552 | 3.874 | 3.8724 | 3.87767 |
| b (Å) | 3.87552 | 3.874 | 3.8724 | 3.87767 | |
| c (Å) | 7.74304 | 7.746 | 7.7556 | 7.74169 | |
| Volume (Å3) | 116.298 | 116.251 | 116.2992 | 116.4063 |
The findings, along with the agreement indices, are tabulated in ESI Table S1.† Since the goodness-of-fit values for the LLTO samples were between 1.36 and 1.61, the refinement is reliable and valid. In addition, the crystallite size and microstrain of the synthesized samples were determined from the Williamson–Hall plot41 Fig. 3(e–h), and the obtained values are tabulated in ESI Table S2.† The change of microstrain, dislocation density and crystallite size with different Ga content are shown in ESI Fig. S3.†
3.2 Chemical state and bond weakening
Fig. 4(a) shows the survey plots of pristine LLTO and Ga-LLTO with x = 0.03 with their main peaks assigned to Li 1s, La 3p, La 3d, La 4p, Ti 2p, O 1s, C 1s, and an additional Ga 2p in Ga-LLTO. The peaks are calibrated with respect to the peak of C 1s having a binding energy of 284.8 eV. Fig. 4(b–e) represents the XPS spectra of the elements present in 3% Ga-LLTO. The Li region shows the core peak of Li 1s at a binding energy of 55.18 eV, confirming the valence of +1 of Li-ion in the perovskite Ga-LLTO. The La 3d spectrum shows separated components of 3d3/2 and 3d5/2 corresponding to binding energies 851.08 eV and 834.28 eV due to spin–orbit splitting. The two spin–orbit doublets of La 3d are 18.8 eV energy apart. Additionally, both 3d3/2 and 3d5/2 components show satellite peaks at higher energy separated by 4.5 eV from the main peaks (851.08 eV and 834.28 eV respectively). These satellite peaks are attributed to the shake-up process due to monopole excitations of valence electrons upon core electron ejection.42 The Ti 2p spectrum shows a spin–orbit doublet with a large narrow peak of Ti 2p3/2 is at 458.27 eV having a full-width half maximum (FWHM) of 1.17 eV and a smaller peak of Ti 2p1/2 at a higher energy of 464.18 eV, separated from the Ti 2p3/2 peak by 5.9 eV. The Ti 2p peaks imply Ti–O bond with octahedrally coordinated Ti4+ ions.43 No peaks corresponding to the Ti3+ ions are seen in the spectra, implying the only valence state of Ti4+ exists in the sample. Moving on to the Ga 2p, the two doublets Ga 2p1/2 and Ga 2p3/2 are positioned at 1144.68 eV and 1117.78 eV with a separation of 26.9 eV, confirming the presence of Ga3+ in the doped sample. An additional peak in between the Ga 2p doublets is seen in the spectrum at a binding energy of 1128.1 eV (ESI Fig. S4†). It is identified as a characteristic peak of La 3p3/2.44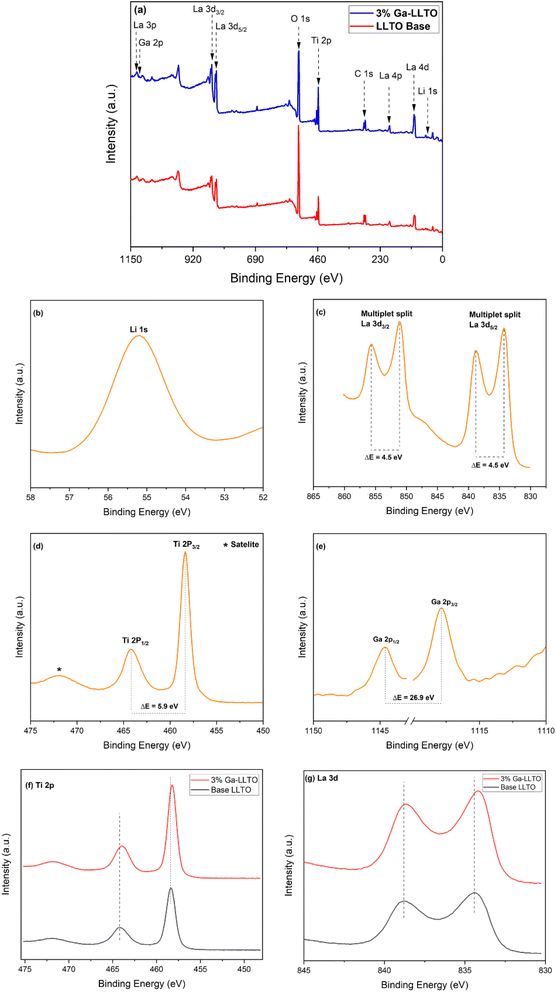 | ||
| Fig. 4 XPS survey spectra of base LLTO and 3% Ga-LLTO (a), XPS spectra of Li 1s, La 3d, Ti 2p, and Ga 2p for 3% Ga-LLTO (b–e), and peak shifting comparison of base LLTO and 3% Ga-LLTO (f and g). | ||
Fig. 4(f and g) shows the shifting of peak positions of 3% Ga-doped LLTO with respect to the pristine LLTO sample. After Ga substitution in the B site, the peak positions shifted towards the lower binding energies. A lower binding energy corresponds to a weakening of the bond strength which is a consequence of increased bond length. The lower binding energy of Ti after substituting Ti4+ (0.61 Å) with a larger Ga3+ (0.62 Å) ion, is a result of stretching of Ti–O bond length which effectively enlarged the bottleneck for Li-ion migration.45,46 The shifting of the binding energy of La towards lower energy can be referred to the stretching of the c-axis, as previously confirmed by the Rietveld analysis (Table 1).
3.3 Morphological analysis
Fig. 5 shows the particle surface morphology of LLTO ceramics with varying Ga contents. Most of the grains are seen to be in good contact with considerable porosity. The pore volume increased with increasing Ga content from x = 0.00 to x = 0.05. The grain shapes are somewhat uniform in Ga-LLTO with x = 0 and x = 0.01. With the increasing amount of Ga, from x = 0.01 to x = 0.03, the particles gradually lost their shape and became larger in size. The grain size distribution of all the samples is shown in ESI Fig. S5.† The average grain size is 575 ± 15 nm in pure LLTO (Li0.33La0.56TiO3), which gradually increased in Ga-LLTO (Li0.33+xLa0.56Ti1−xGaxO3) up to x = 0.03, decreasing the grain boundary area. This indicates that Ga substitution in LLTO has affected the grain size. The average grain sizes in the Ga-LLTOs are 634 ± 8 nm, 709 ± 27 nm, and 559 ± 40 nm for x = 0.01, x = 0.03 and x = 0.05 respectively. The decrease in average grain size of the 5% Ga-LLTO leads to a higher volume fraction of grain boundary area, resulting in increased grain boundary resistance. | ||
| Fig. 5 SEM images of Ga-LLTO with different Ga concentrations, (a) x = 0.00, (b) x = 0.01, (c) x = 0.03, and (d) x = 0.05. | ||
3.4 TEM analysis
Fig. 6(a–d) represents the selected area electron diffraction (SAED) patterns of the base and Ga-LLTO samples. The concentric rings of bright spots with different orientations in these patterns indicate the polycrystalline nature of the samples, which was previously confirmed by the XRD analysis. The ImageJ tool was used to estimate the ring diameters and to measure the d-spacing values. The measured interplanar distances for LLTO solid-electrolytes, d1 = 0.2726 nm, d2 = 0.2236 nm, d3 = 0.1923 nm, and d4 = 0.1588 nm correspond to the crystal planes (110), (112), (200), and (212), respectively, as indexed by the previously mentioned JCPDS card number. Additionally, in the SAED pattern of 5% Ga-LLTO, two additional rings with interplanar distances d1 = 0.2790 nm and d2 = 0.2081 nm were identified, indicating the presence of (111) and (211) planes of TiO2. | ||
| Fig. 6 SAED patterns of base LLTO, 1% Ga-LLTO, 3% Ga-LLTO, 5% Ga-LLTO (a–d) respectively, TEM images, and lattice fringes of 1% Ga-LLTO (e and f), and 3% Ga-LLTO (g and h). | ||
Fig. 6(e–h) shows the typical TEM images of Ga-LLTO, along with visible lattice fringes. The Digital Micrograph tool was used to analyze the HR-TEM images by employing the Fast Fourier Transform (FFT) technique. The interplanar distances were calculated from the resulting FFT images, and several planes were indexed according to the JCPDS card number (ESI Fig. S6†). These indexed planes are also consistent with the corresponding SAED patterns.
3.5 Electrochemical characterization
The Nyquist plots of the LLTO and Ga-LLTO ceramics are shown in Fig. 7(a) and individual plots are given in ESI Fig. S7† (real and imaginary parts of the impedance are normalized by multiplying with A/L). All of these spectra comprise a semi-circle that was observed at a high-frequency region and their first intercept on the X-axis indicates the solution resistance. The semicircle is related to the migration of Li+ ions in grain interior and across grain boundaries.36 Constant Phase Element (CPE) is due to the capacitance at low frequency. The curves were fitted using the circuit shown in the inset of Fig. 7(a) and they match well with the measured data. A detailed explanation of the circuit is provided in the ESI file (ESI Fig. S8†). The ionic conductivity of the samples was measured by the following equation:
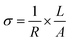 | (2) |
| Composition | Doping amount (X) | Resistance, R (Ω) | Conductivity σ (S cm−1) |
|---|---|---|---|
| 0.00 | 194.4 | 2.04 × 10−4 | |
| Li0.33+xLa0.56Ti1−xGaxO3 | 0.01 | 109.3 | 2.46 × 10−4 |
| 0.03 | 68.8 | 4.15 × 10−3 | |
| 0.05 | 264.5 | 1.65 × 10−4 |
Variations in the grain size of LLTO and Ga-LLTO samples could be another factor affecting the ionic conductivity. The grain size of Li0.33+xLa0.56Ti1−xGaxO3 with Ga content x = 0.03 is larger compared to pure LLTO and other compositions of Ga-LLTO. This increase in grain size results in a lower grain boundary volume fraction in the x = 0.03 sample. Since grain boundary resistance is higher and more dominant than grain resistance28 and conductivity increases with increasing grain size,31 the larger grains further enhanced the Li-ion conductivity in the mentioned sample. The highest conductivity in the Li0.33+xLa0.56Ti1−xGaxO3 with x = 0.03 indicates that the optimum doping amount is about x = 0.03 for Ga as a higher amount of Ga doping produces a secondary impurity phase which affects ionic conductivity.
The conventional method for performing the EIS tests on solid electrolytes involves using an ion-blocking electrode on both sides of a pellet. However, due to the unavailability of certain facilities, a different method was used in this study employing a three-electrode system with liquid electrolytes, which resulted in slightly higher conductivity compared to the other reported values of LLTO solid electrolytes (ESI Table S5†). This can be easily attributed to different testing setups and the significantly lesser contact resistance at the LiOH solution/electrode interface.49 However, as all the tests were done in the same method, the observed trend of increased conductivity with Ga substitution in LLTO remains consistent and valid.
Fig. 7(b and c) represents the cyclic voltammetry curves of the LLTO and Ga-LLTO samples obtained at two different scanning rates of 10 and 50 mV s−1 in the voltage range −1 to 0.5 V against the SCE. The potential values were then referred to as the Li/Li+ couple (ELi/Li+ = –3.28 V vs. SCE) and the translated potential window became 2.28 to 3.78 V against Li. No redox peaks were observed within this voltage range, indicating the stability of the solid electrolyte in this potential window. This absence of redox peaks also indicates a constant-rate reversible electrochemical reaction occurring in the materials.50 The symmetry of the curves further confirms the successful charging and discharging of the electrolytes. A rectangular and symmetric CV curve indicates an electrical double-layer capacitance (EDLC) charge storage mechanism whereas deviation from the rectangular shape indicates a faradaic pseudocapacitive charge storage mechanism.51 The CV curves obtained from our sample appear to be quasi-rectangular in shape, proposing a mixture of EDLC and pseudocapacitive behavior. During the EDLC mechanism, Li ions from the electrolyte (LiOH) adsorb or desorb onto the LLTO electrode surfaces and facilitate the following reaction:
| (LLTO)surface + Li+ + e− ↔ (LLTO Li)surface | (i) |
The pseudocapacitive charge storage mechanism involves the intercalation or extraction of cations (Li+) from the liquid electrolyte into bulk LLTO electrodes such as:
| LLTO + Li+ + e− ↔ (LLTOLi)intercalation | (ii) |
The integral area of the CV curve (ESI Table S6†) shows an increase with a higher doping concentration, achieving the highest value at 3% Ga doping, followed by a decrease in the 5% Ga-LLTO. This trend is similar to what we found in the XRD analysis and EIS measurement. The decrease in the integral area might be a consequence of the previously mentioned TiO2 impurity and this will lead to a lower charge storage capability of the 5% Ga-LLTO compared to the pristine and other doped LLTO solid electrolytes.
Fig. 7(d and e) demonstrates the effect of scan rate on the output current as well as the shape of the curves. The output current depends on the diffusion layer formed at the electrode/electrolyte interfaces and changes proportionately with scan rates. At lower scan rates, the ions get more time to diffuse toward the electrode interface and can easily enter the activation sites on the LLTO solid electrolyte, increasing the charge storage capacity. On the other hand, at higher scan rates, due to slower diffusion, only a limited number of ions can reach the micropores of the material, leaving a large number of underutilized activation sites inside. This lowers the charge storage capacity of the solid electrolytes.52
The analysis above indicates that the LLTO and Ga-LLTO solid electrolytes can also function as solid-state supercapacitors.
4 Conclusion
In this work, the novel Ga-LLTO solid electrolyte was successfully synthesized using the solid-state reaction method, with varying amounts of Ga (x = 0.01, 0.03, and 0.05). Both Li0.33La0.56TiO3 and Ga-LLTO exhibit a tetragonal perovskite structure with P4/mmm space group. The shifting of peaks in XPS spectra towards lower binding energy indicated an increase in the B–O bond length of Ga-LLTO with x = 0.03. Li0.36La0.56Ti0.97Ga0.03O3 showed the highest conductivity of 4.15 × 10−3 S cm−1, which is about one order higher than that of the pristine LLTO. The enhancement in conductivity is mainly attributed to the stretching of B–O bonds which enlarged the bottleneck size for lithium-ion diffusion. Additionally, the larger grain size contributed to the conductivity enhancement by lowering the grain boundary resistance. The solid electrolytes are stable within the voltage range of 2.28 to 3.78 V against Li/Li+ suggesting potential applications not only in ASSBs but also in solid-state supercapacitors. Therefore, the Li0.36La0.56Ti0.97Ga0.03O3 is identified as a promising candidate for the next generation of solid-state lithium-ion batteries.Data availability
The data that support the finding of this study are available from the corresponding author upon reasonable request.Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript. Md. Nagib Mahfuz: conceptualization, methodology, investigation, formal analysis, writing – original draft. Appy Feroz Nura: conceptualization, methodology, investigation, formal analysis, writing – original draft. Md Shafayatul Islam: methodology, formal analysis, writing – review & editing. Koushik Roy Chowdhury: investigation, formal analysis. Tomal Saha: investigation, formal analysis. Aninda Nafis Ahmed: methodology, investigation, formal analysis. Sheikh Manjura Hoque: investigation, formal analysis. Md Abdul Gafur: investigation, formal analysis. Ahmed Sharif: conceptualization, resources allocation, supervision, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to express their appreciation to the Research and Innovation Centre for Science and Engineering (RISE), Bangladesh University of Engineering and Technology (BUET), Dhaka-1000, Bangladesh for funding through the RISE Student Research Grant. The authors would also like to express their gratitude to department of Materials and Metallurgical Engineering, BUET; Bangladesh Council of Scientific and Industrial Research (BCSIR), Dhaka and Materials science division, Atomic Energy Centre, Dhaka, for their assistance with synthesis and characterization. The authors declare that they have no use of AI and AI-assisted technologies in the writing process.References
- Q. Zhang, Z. Gao, X. Shi, C. Zhang, K. Liu, J. Zhang, L. Zhou, C. Ma and Y. Du, J. Rare Earths, 2021, 39, 1–10 CrossRef CAS.
- M. Bertrand, S. Rousselot, D. Aymé-Perrot and M. Dollé, Mater. Adv., 2021, 2, 2989–2999 RSC.
- Q. Wang, J. Sun and G. Chu, Fire Saf. Sci., 2005, 8, 375–382 Search PubMed.
- J. Lu and Y. Li, J. Mater. Sci.: Mater. Electron., 2021, 32, 9736–9754 CrossRef CAS.
- C. Yu, S. Ganapathy, E. R. H. Van Eck, L. Van Eijck, S. Basak, Y. Liu, L. Zhang, H. W. Zandbergen and M. Wagemaker, J. Mater. Chem. A, 2017, 5, 21178–21188 RSC.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS.
- S. Troy, A. Schreiber, T. Reppert, H. G. Gehrke, M. Finsterbusch, S. Uhlenbruck and P. Stenzel, Appl. Energy, 2016, 169, 757–767 CrossRef.
- J. W. Fergus, J. Power Sources, 2010, 195, 939–954 CrossRef CAS.
- S. Chen, D. Xie, G. Liu, J. P. Mwizerwa, Q. Zhang, Y. Zhao, X. Xu and X. Yao, Energy Storage Mater., 2018, 14, 58–74 CrossRef.
- A. Hayashi, Y. Nishio, H. Kitaura and M. Tatsumisago, Electrochem. Commun., 2008, 10, 1860–1863 CrossRef CAS.
- U. Ulissi, M. Agostini, S. Ito, Y. Aihara and J. Hassoun, Solid State Ionics, 2016, 296, 13–17 CrossRef CAS.
- D. H. Kim, D. Y. Oh, K. H. Park, Y. E. Choi, Y. J. Nam, H. A. Lee, S. M. Lee and Y. S. Jung, Nano Lett., 2017, 17, 3013–3020 CrossRef CAS PubMed.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- N. Thi Minh Nguyet, T. V. Toan, L. T. Anh, L. Thi Quynh Anh, T. A. Tu and N. H. H. Phuc, Mater. Adv., 2024, 5, 7222–7229 RSC.
- K. Takada, J. Power Sources, 2018, 394, 74–85 CrossRef CAS.
- K. Takada and S. Kondo, Ionics, 1998, 4, 42–47 CrossRef CAS.
- B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430 CrossRef CAS.
- H. Muramatsu, A. Hayashi, T. Ohtomo, S. Hama and M. Tatsumisago, Solid State Ionics, 2011, 182, 116–119 CrossRef CAS.
- J. Lu and Y. Li, J. Mater. Sci.: Mater. Electron., 2021, 32(8), 9736–9754 CrossRef CAS.
- J. F. Wu and X. Guo, Solid State Ionics, 2017, 310, 38–43 CrossRef CAS.
- S. Sasano, R. Ishikawa, I. Sugiyama, T. Higashi, T. Kimura, Y. H. Ikuhara, N. Shibata and Y. Ikuhara, Appl. Phys. Express, 2017, 10, 061102 CrossRef.
- B. Antoniassi, A. H. M. González, S. L. Fernandes and C. F. O. Graeff, Mater. Chem. Phys., 2011, 127, 51–55 CrossRef CAS.
- M. Kotobuki, H. Munakata and K. Kanamura, J. Power Sources, 2011, 196, 6947–6950 CrossRef CAS.
- X. Guo, P. S. Maram and A. Navrotsky, J. Mater. Chem. A, 2017, 5, 12951–12957 RSC.
- Y. Harada, T. Ishigaki, H. Kawai and J. Kuwano, Solid State Ionics, 1998, 108, 407–413 CrossRef CAS.
- S. Stramare, V. Thangadurai and W. Weppner, Chem. Mater., 2003, 15, 3974–3990 CrossRef CAS.
- Y. Inaguma, C. Liquan, M. Itoh, T. Nakamura, T. Uchida, H. Ikuta and M. Wakihara, Solid State Commun., 1993, 86, 689–693 CrossRef CAS.
- J. F. Wu and X. Guo, Solid State Ionics, 2017, 310, 38–43 CrossRef CAS.
- H. Geng, J. Lan, A. Mei, Y. Lin and C. W. Nan, Electrochim. Acta, 2011, 56, 3406–3414 CrossRef CAS.
- C. W. Ban and G. M. Choi, Solid State Ionics, 2001, 140, 285–292 CrossRef CAS.
- A. G. Belous, J. Eur. Ceram. Soc., 2001, 21, 1797–1800 CrossRef CAS.
- V. Thangadurai and W. Weppner, Ionics, 2000, 6, 70–77 CrossRef CAS.
- S. Ulusoy, S. Gulen, G. Aygun, L. Ozyuzer and M. Ozdemir, Solid State Ionics, 2018, 324, 226–232 CrossRef CAS.
- K. Y. Yang, I. C. Leu, K. Z. Fung, M. H. Hon, M. C. Hsu, Y. J. Hsiao and M. C. Wang, J. Mater. Res., 2008, 23, 1813–1825 CrossRef CAS.
- Z. Hu, J. Sheng, J. Chen, G. Sheng, Y. Li, X. Z. Fu, L. Wang, R. Sun and C. P. Wong, New J. Chem., 2018, 42, 9074–9079 RSC.
- J. Lu and Y. Li, J. Mater. Sci.: Mater. Electron., 2021, 32(8), 9736–9754 CrossRef CAS.
- H. T. T. Le, R. S. Kalubarme, D. T. Ngo, S. Y. Jang, K. N. Jung, K. H. Shin and C. J. Park, J. Power Sources, 2015, 274, 1188–1199 CrossRef CAS.
- Z. Fu, Y. Liang, S. Wang and Z. Zhong, Phys. Status Solidi B, 2013, 250, 2206–2214 CrossRef CAS.
- M. S. Islam, K. R. Chowdhury, S. M. Hoque and A. Sharif, Mater. Adv., 2024, 5, 2946–2967 RSC.
- J. O. Bonsu, A. Bhadra and D. Kundu, Adv. Sci., 2024, 11, 2403208 CrossRef CAS PubMed.
- K. Y. Yang, I. C. Leu, K. Z. Fung, M. H. Hon, M. C. Hsu, Y. J. Hsiao and M. C. Wang, J. Mater. Res., 2008, 23, 1813–1825 CrossRef CAS.
- C. R. Onyeagba, M. Valashani, H. Wang, C. Brown, P. Yarlagadda and T. Tesfamichael, Surf. Interfaces, 2023, 40, 103090 CrossRef CAS.
- M. Rawlence, A. N. Filippin, A. Wäckerlin, T. Y. Lin, E. Cuervo-Reyes, A. Remhof, C. Battaglia, J. L. M. Rupp and S. Buecheler, ACS Appl. Mater. Interfaces, 2018, 10, 13720–13728 CrossRef CAS PubMed.
- L. X. He and H. I. Yoo, Electrochim. Acta, 2003, 48, 1357–1366 CrossRef CAS.
- K. Yu, L. Jin, Y. Li, G. Liu, X. Wei and Y. Yan, Ceram. Int., 2019, 45, 23941–23947 CrossRef.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- T. Katsumata, Y. Matsui, Y. Inaguma and M. Itoh, Solid State Ionics, 1996, 86–88, 165–169 CrossRef CAS.
- P. Braun, C. Uhlmann, A. Weber, H. Störmer, D. Gerthsen and E. Ivers-Tiffée, J. Electroceram., 2017, 38, 157–167 CrossRef CAS.
- J. Zhi, O. Reiser and F. Huang, ACS Appl. Mater. Interfaces, 2016, 8, 8452–8459 CrossRef CAS.
- Q. Wu, T. He, Y. Zhang, J. Zhang, Z. Wang, Y. Liu, L. Zhao, Y. Wu and F. Ran, J. Mater. Chem. A, 2021, 9, 24094–24147 RSC.
- D. Sahoo, J. Shakya, S. Choudhury, S. S. Roy, L. Devi, B. Singh, S. Ghosh and B. Kaviraj, ACS Omega, 2022, 7, 16895–16905 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra08811e |
| ‡ Md. Nagib Mahfuz and Appy Feroz Nura contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |



