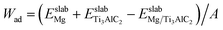Insight into the heterogeneous nucleation mechanism of Ti₃AlC₂/Mg interface doped with alloying elements by using first principle calculation

Abstract

In the present study, a comprehensive investigation has been conducted on the work of adhesion, interfacial energy, and electronic structure of both pristine and hybrid Ti₃AlC₂(0001)/Mg(0001) interfaces. This examination aims to elucidate the conceptual framework of the interface and explain the heterogeneous nucleation mechanism of Ti₃AlC₂ particles within the Mg matrix composites. Our research reveals a notable discovery: the C(TiC)-terminated Ti₃AlC₂(0001)/Mg(0001) interface, arranged in HCP stacking, demonstrates remarkable interfacial stability. This stability is attributed to the formation of a strong Mg–C covalent bond, which reinforces interfacial bonding strength and durability. Therefore, our findings affirm the potential of Ti₃AlC₂ particles as an effective substrate for heterogeneous nucleation of magnesium grains, ultimately enhancing the strength and ductility of Mg matrix composites. It's worth highlighting that the introduction of specific elements in the layer adjacent to the interface produces significant effects. The incorporation of Fe, Mn, Si, Al, and Ni into the C(TiC)-terminated Ti₃AlC₂(0001)/Mg(0001) interface with HCP stacking significantly boosts adhesion and simultaneously lowers interfacial energy. This beneficial outcome contributes positively to the nucleation process within the Mg matrix. Conversely, the addition of Cu to the interface diminishes adhesion, thereby impeding the nucleation of Ti₃AlC₂ on Mg matrices. Regarding adhesion energy at the alloyed Ti₃AlC₂(0001)/Mg(0001) interface, our analysis ranks the effectiveness of various elements as follows: Fe surpasses Mn, which precedes Si, then Al, succeeded by Ni, and finally Cu. This study significantly advances our comprehension of the distinctive attributes of Ti₃AlC₂(0001)/Mg(0001) interfaces and the fundamental nucleation mechanisms. These insights hold promising potential for advancing the development of innovative magnesium-based composite materials.

---

1. Introduction

Magnesium alloys rank among the lightest structural materials in engineering.¹ Their relatively lower density, a higher relative strength, and a higher particular stiffness have made them increasingly attractive for applications in the aerospace, defense, and automotive industries.^2–4 Among these, AZ91 alloy stands out as the most widely used cast magnesium alloy due to its excellent casting properties, efficient forming process, and low assembly costs.^5–7 However, during casting, AZ91 alloy is prone to forming large grains and eutectic phases, which diminish its mechanical properties and limit its further development and application.⁸ Consequently, researchers are focusing on developing high-performance new AZ91 alloys.

To enhance the microstructure and properties of AZ91 alloy, alloying treatments and particle reinforcement have proven effective.^9,10 In recent years, numerous studies have explored the modification of AZ91 by adding various alloying elements such as alkaline earth metals,¹¹ transition metals,¹² light rare earth elements,¹³ and heavy rare earth elements,¹⁴ along with different reinforcing particles. These efforts have led to a series of significant research achievements.^15,16 Metal matrix composites have garnered considerable attention in the research community due to their superior strength, heightened wear resistance, and better fatigue and creep characteristics when compared with conventional materials.^17,18 Among the various types of composites, those reinforced with particles offer distinct advantages, including low densities, high modulus of elasticity, superior anti-oxidation properties, corrosion resistance, good wettability, and strong interfacial bonding with magnesium.^19,20 Ceramic particles, known for their high strength, hardness, and wear resistance, are particularly effective in enhancing the mechanical properties of magnesium alloys when incorporated into them.²¹

Ti₃AlC₂, a composite from the MAX phase family, is distinguished by its layered ternary structure, which exhibits outstanding electrical conductivity and oxidation resistance. This makes it an ideal candidate for innovative electrical contact materials.²² Moreover, Ti₃AlC₂ integrates remarkable characteristics of both metals and ceramics, such as minimal density, reduced friction coefficient, elevated modulus and strength, along with superior electrical and thermal conductivity and enhanced oxidation resistance.^23–25 Ameur Chouket et al.²⁶ fabricated a Ti₃AlC₂/AZ91 composites by insulated Spark Plasma Sintering technology and powder metallurgy method, and revealed that raising the content of Ti₃AlC₂ in AZ91 remarkably enhanced the hardness and tensile strength of the compound. In the meantime, Ti₃AlC₂ shows excellent strengthening properties in various different substrate alloys, such as Cu matrix alloys,²⁷ Ag matrix alloys,²⁸ and Al matrix alloys.²⁹ However, the interfacial stability and component of the above specimens were observed by scanning and high resolution transmissive electronic microscopy, which is difficult to completely understand the interfacial stability between Ti₃AlC₂ particle and matrix alloy through experimental methods. Consequently, comprehending the interfacial characteristics of Ti₃AlC₂/Mg composites, including adhesion work, interfacial energy, and electronic attributes, is essential for the fabrication of high-performance composites.

Over recent years, the elastic, thermodynamic, and electronic properties of bulk materials have been rigorously analyzed through first-principles studies.^30–32 Many researchers both internationally and domestically have developed interfacial models via a first-principles approach, elucidating the mechanisms of interfacial bonding.^33–35 In examining the bonding dynamics at interfaces between metals and nonmetals, it is observed that a predominant number of these bonds are characterized by the establishment of robust covalent interactions involving metal and nonmetal atoms. These interactions notably enhance both the stability of the interfaces and their bonding efficacy, as exemplified in the Al/Al₃BC interface, Ti₂AlC/TiAl interface, and Mg/Al₃BC interfaces.^36–38 Besides, Ti₃AlC₂ has a hexagonal crystal structure and widely used for high-temperature structural components, thermal shock-resistant materials and electrical contact materials due to its unique combination of metallic and ceramic properties.³⁹ Conversely, the mechanisms underlying the reinforcing effect of Ti₃AlC₂ particles within the AZ91 alloy, along with the influence of alloying elements on Ti₃AlC₂ particles in the same alloy, have not been sufficiently explored in a theoretical context. Consequently, leveraging first-principles-based analyses to corroborate adhesion work and doping simulations could furnish a theoretical underpinning for the interfacial engineering of Ti₃AlC₂/Mg composites, thereby serving as an effective theoretical adjunct to empirical investigations.

To elucidate the fundamental bonding mechanisms at the interfaces of magnesium matrix composites, particularly those doped with elements such as Mn, Al, Cu, Ni, Fe, and Si in AZ91 alloys. The study focuses on the composite interface formed by Mg/Ti₃AlC₂ and its doped variations. Through atomic-scale analysis, it investigates the bonding scenarios at the composite material interfaces and the segregation of doping elements. Additionally, it examines the essential reasons for atomic interactions between interfaces by analyzing the differential charge density and density of states. This comprehensive approach provides a theoretical foundation for understanding the bonding mechanisms at composite material interfaces. Besides, first-principles calculations are further utilized to predict and analyze the interface energy and structure between heterogeneous nuclei and primary phases during the solidification process. Given that Ti₃AlC₂ is commonly used as a grain refiner nucleating agent for magnesium alloys, this study incorporates first-principles calculations to discuss the nucleation mechanism of magnesium induced by Ti₃AlC₂ particles, underpinned by thermodynamic theory.

2. Calculation methods and models

2.1. Calculational methodology

In conducting our computational analysis, the density functional theory (DFT)-based CASTEP software^40–42 with periodic boundary conditions was employed. Furthermore, the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional, along with the utilization of plane wave ultra-soft pseudo-potentials (USPPs), were applied to delineate the exchange–correlation energy as well as the interactions between ion cores and valence electrons. These computation strategies facilitated the examination of the interfacial characteristics of the Ti₃AlC₂(0001)/Mg(0001) interface in our research. This calculation considers the valence electron configurations of Ti, Al, and C atoms are 3d²4s², 3s²3p¹ and 2s²2p², respectively. The k-point grid of the Brillouin zone uses the Monkhorst Pack scheme for special k-point sampling.⁴³ Moreover, the k point of the Ti₃AlC₂ bulk, surface structure, and interfacial structure were selected as 10 × 10 × 1, 14 × 14 × 1, and 14 × 14 × 1 respectively. Following assessments of convergence, a cutoff energy for plane waves was established at 500 eV for all the analyses in this project. The accuracy threshold for self-consistent convergence was maintained at 5.0 × 10⁻⁷ eV per atom. Additionally, we set the convergence criterion for interatomic forces at 0.01 eV Å⁻¹, with the peak force capped at 0.02 GP, and the upper limit for displacement fixed at 5.0 × 10⁻⁴ Å.

2.2. Calculational models

Fig. 1 displays the crystal configurations of Ti₃AlC₂ and Mg in bulk form, showing their shared hexagonal crystal framework, with each classified under the space group P6/mmc. To establish the precision and validity of our computational approach and findings, Table 1 outlines the lattice parameters, enthalpy of formation, and volume for the bulk form of Ti₃AlC₂, drawing on data from both theoretical calculations and empirical studies. As indicated in Table 1, there is a strong correlation between our computed values and those obtained from experiments and simulations as cited in existing literature,⁴⁴ thus verifying the dependability of our calculation techniques for future investigations.

Fig. 1 (a) Crystal structure of Mg bulk; (b) crystal structure of Ti₃AlC₂ bulk.

Table 1 Structural parameters (a, c, and V) and formation enthalpy (ΔH_f) of Ti₃AlC₂

Structures	a = b	c	c/a	Volume (Å^3)	ΔHf (eV)	Ref.
Ti3AlC2	3.081	18.679	6.062	153.55	−7.1187	24
	3.075	18.578	6.041			44
	3.072	18.624	6.063	152.21	−7.103	Present

---

In constructing the Ti₃AlC₂(0001)/Mg(0001) interface, we positioned an Mg(0001) layer on top of Ti₃AlC₂(0001) layers, as illustrated in Fig. 2. Additionally, we conducted thorough calculations and analyses on how the thickness of the vacuum layers influences the interface's energy, with detailed outcomes presented in Fig. 2. These findings reveal a gradual reduction in interface energy as the vacuum layer's thickness increases, with the energy reaching stability at a vacuum thickness of 12 Å. Therefore, to construct surface and interface models with periodic boundary conditions and improve the calculation precision, a 15 Å vacuum layer was applied to eliminate the influence between the top and bottom surfaces. By adopting this structure, we effectively mitigate the impact of interlayer interactions, thereby ensuring the fidelity of the interface properties' portrayal.

Fig. 2 (a) Atomic structure diagram of the Mg(0001)/Ti₃AlC₂(0001) interface; (b) variation of the interfacial energy with the thickness of vacuum layer.

3. Results and discussion

3.1. Surface properties

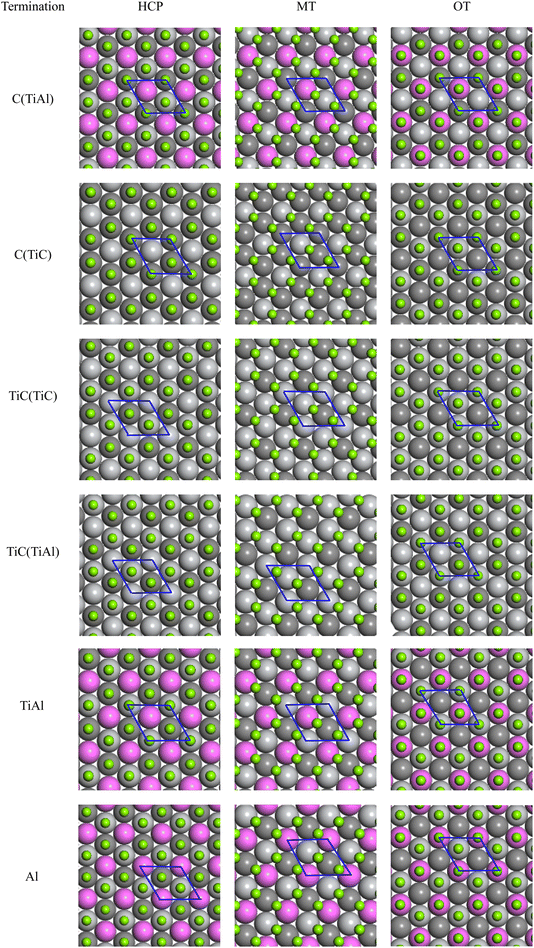
For the Mg(0001) and Ti₃AlC₂(0001) slabs, a bulk-like character within the interior is exhibited when the number of atomic layers is sufficiently large. Therefore, an initial surface convergence test is conducted. According to existing studies,⁴⁵ the Mg(0001) surface demonstrates convergence when it comprises five or more atomic layers. As a result, we opted to use five atomic layers for the Mg(0001) surface in our study.

The Ti₃AlC₂(0001) surface can be divided into six surface models of TiAl, C(TiC), Al, TiC(TiAl), C(TiAl), and TiC(TiC) according to different atomic terminals, as shown in Fig. 3. Given the substantial number of models that occupy a significant amount of space, a specific representative surface model featuring a distinct number of atomic layers is designated for various terminal surfaces. Consequently, each surface model with varying atomic layer counts is excluded from this document.

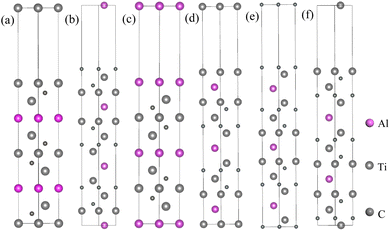Fig. 3 Schematic of different terminated Ti₃AlC₂(0001) surfaces: (a) TiC(TiAl), (b) C(TiC), (c) Al, (d) TiAl, (e) C(TiAl), (f) TiC(TiC).

Considering the relative simplicity of the surface model of Ti₃AlC₂(0001), the calculation of the convergence of the surface energy with the layer thickness can be approximated to choose a suitable number of surface layers:⁴⁶

In this setting, E_slab(N) signifies the comprehensive energy associated with the surface configuration, whereas E_bulk signifies the enhanced energy per atom within the bulk. N signifies the number of layers on the surface, and A_surface signifies the surface area. Table 2 illustrates the surface energies corresponding to six distinct terminations of Ti₃AlC₂(0001) surfaces, featuring varying counts of atomic layers. It is noted from Table 2 that the surface energy progressively stabilizes with an increase in the number of surface layers. Notably, for the C(TiAl), C(TiC), TiC(TiC), TiC(TiAl), TiAl, and Al-terminated Ti₃AlC₂(0001) surface, the energy can quickly converge to 6.67 J m⁻², 8.13 J m⁻², 3.66 J m⁻², 2.06 J m⁻², 1.32 J m⁻², and 0.24 J m⁻², when the surface layers reach to 17, 17, 17, 15, 13, and 13 layers, respectively.

Table 2 The variation of four Ti₃AlC₂(0001) surface energy with the different number of layers

Number of layer	Surface energy (J m^−2)
	9	11	13	15	17	19
Ti3AlC2(0001)-C(TiAl)	6.39	6.48	6.55	6.59	6.66	6.66
Ti3AlC2(0001)-C(TiC)	8.01	8.08	8.10	8.12	8.13	8.13
Ti3AlC2(0001)-TiC(TiC)	3.49	3.57	3.59	3.63	3.66	3.65
Ti3AlC2(0001)-TiC(TiAl)	1.98	2.00	2.04	2.06	2.05	2.06
Ti3AlC2(0001)-TiAl	1.26	1.29	1.33	1.33	1.34	1.33
Ti3AlC2(0001)-Al	0.20	0.21	0.24	0.24	0.25	0.24

---

From Table 2, Al-terminated surfaces of Ti₃AlC₂(0001) manifest as the most stable slabs, due to the smallest surface energy. On the other hand, C(TiC)- and C(TiAl)-terminated Ti₃AlC₂(0001) are prone to forming unstable structures, due to their higher surface energy. This is in high agreement with the results reported in the literature⁴⁷ about the calculation of the Ti₃AlC₂.

Based on the outcomes of the bulk and surface convergence assessments, it has been determined that the lattice dimensions for the Mg(0001) surface slab measure: a = b = 3.209 Å, α = 120°. Conversely, the Ti₃AlC₂(0001) surface slab registers dimensions at a = b = 3.071 Å and α = 120°. Consequently, the interface between Mg(0001) and Ti₃AlC₂(0001) exemplifies a common semi-coherent type with a lattice mismatch of 4.3%, remaining under 5%. This reveals that the structural configuration at the interface between Mg(0001) and Ti₃AlC₂(0001) maintains considerable stability and exhibits appropriate physicochemical properties at the interface. Hence, layers of Ti₃AlC₂ were positioned beneath the Mg(0001) slabs, accompanied by a vacuum layer of 15 Å atop the Mg(0001) slabs to reduce interactions within the Mg(0001) slabs across periodic representations.

3.2. Interface properties

Based on the convergence assessment results mentioned previously, we constructed the interface models by superimposing differently terminated Ti₃AlC₂(0001) surfaces onto Mg(0001) surface with five atomic layers. Therefore, to save computational cost and time, we chose the smallest lattice parameter among Ti₃AlC₂(0001) surfaces and Mg(0001) surface. And the interface calculations were modeled using the Ti₃AlC₂(0001) surface with the optimal number of layers for the 1 × 1 cell geometry and the 5-layer Mg(0001) surface based on the results of the surface stability calculations, which had a mismatch of about 4.3%. The coherent interface approximation is used in the calculations to preserve the periodic boundary conditions.

To minimize periodic disturbances during interactions of the atoms, the vacuum layer of 15 Å was introduced upon the designed interface. When the interface is assembled with the model, we investigated three unique methods for aligning each termination with the opposing surface within the Ti₃AlC₂(0001)/Mg(0001) interface. As illustrated in Fig. 4, a total of eighteen interfacial models were created to enable a comprehensive analysis of the interfaces. In Fig. 4, “OT” denotes the Ti₃AlC₂(0001) surface atom aligned directly over Mg atoms, “MT” indicates the Ti₃AlC₂(0001) surface atom situated centrally among four neighboring Mg atoms, and “HCP” identifies the Ti₃AlC₂(0001) surface atom placed centrally among three neighboring Mg atoms.

Fig. 4 The locations of interfacial atoms in the OT, MT, and HCP stackings before relaxation of the Ti₃AlC₂(0001)/Mg(0001) interface (green spheres: Mg atoms; light gray: Ti atoms; red spheres: Al atoms; heavy gray spheres: C atoms).

The interfacial bonding energy is defined as the amount of energy necessary to separate a unit area of an interface into two distinct surfaces, ignoring the degrees of freedom related to plasticity and diffusion. Alternatively, it can be described as the energy required to divide a unit area of the interface into two separate slabs, disregarding any degrees of freedom pertaining to diffusion and plasticity. This measure effectively represents the atomic binding strength at the interface, thereby facilitating the evaluation of its stability. The computation of interfacial binding energy is conducted according to the following formula:

Here, and E^slab_Mg implies the surface energy of Ti₃AlC₂(0001) slab and Mg(0001) slab, respectively. denotes the interfacial energy of the Ti₃AlC₂(0001)/Mg(0001) interface, A represents the interface area formed by Mg(0001) slab and Ti₃AlC₂(0001) slab.

The W_ad of the Ti₃AlC₂(0001)/Mg(0001) interface can be obtained by a step-by-step method using both the unrelaxed and relaxed geometry. The first approach is to calculate the total energy of unrelaxed interfaces with different interfacial separations d₀ by fitting the data to the Universal Binding Energy Relationship (UBER) to obtain the optimized W_ad and d₀. It represents the preparatory stage leading to the attainment of the ultimate outcome, while offering the benefits of superior computational efficacy and reduced expenses. Therefore, the UBER curves of the Ti₃AlC₂(0001)/Mg(0001) interface across eighteen distinct stacking configurations are shown in Fig. 5. Typically, reduced spacing at the interface correlates with enhanced atomic connections and greater bonding energy at the interface, which suggests improved stability of the interface. Clearly, as depicted in Fig. 5, among the three stacking arrangements, the HCP stacking sequence's optimized interface demonstrates the minimal interfacial gap and the highest interfacial binding energy. Consequently, interfaces arranged in the HCP sequence exhibit the greatest stability for the Ti₃AlC₂(0001)/Mg(0001) pairing, with the MT sequence ranking next in terms of stability, and interfaces configured in the OT sequence showing the least stability. This suggests a preference for the Mg(0001) surface to align its atoms in an HCP sequence when interfacing with the Ti₃AlC₂(0001) surface.

Fig. 5 UBER curves of eighteen Ti₃AlC₂(0001)/Mg(0001) interfaces with various interfacial distance and stacking method: (a) C(TiAl)-terminated, (b) C(TiC)-terminated, (c) TiC(TiC)-terminated, (d) TiC(TiAl)-terminated, (e) TiAl-terminated, (f) Al-terminated.

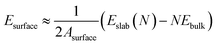
To deepen our understanding of the interfacial thermal and mechanical stability, we computed the interfacial energies (γ_int) for Ti₃AlC₂(0001)/Mg(0001) interface. The presence of interface strain at the semi-coherent Ti₃AlC₂(0001)/Mg(0001) boundary results in a positive interfacial energy. Typically, an interface characterized by negative energy suggests thermodynamic instability, prompting atom diffusion at the interface and potentially leading to the organization of the formation of intermetallic compounds (IMCs). In contrast, an interface displaying a positive and smaller interfacial energy indicates higher stability. An exceedingly negative or large interfacial energy indicates that the interface is thermodynamically unstable. Since the Ti₃AlC₂(0001) surface possesses polarity, the interfacial energy can be ascertained by evaluating the chemical potential of the individual phases that comprise the interface. The interfacial energy of Ti₃AlC₂(0001)/Mg(0001) interface can be calculated from ref. 45:

γ_Mg/Ti3AlC2 = σ_Mg + σ_Ti3AlC2 − W_ad

Representing the surface energy of Ti₃AlC₂(0001) as σ_Ti3AlC2 and the surface energy of Mg(0001) as σ_Mg, we calculate the adhesion work denoted as W_ad. The results obtained for interface energy are presented in Table 3. Upon comparing the unrelaxed interface with the structurally relaxed one, a notable enhancement in the adhesion of all interfaces is evident. Furthermore, Table 3 reveals that the adhesion work and dispersion distance at the Mg(0001)/Ti₃AlC₂(0001) interface are comparable for both the MT and HCP configurations. Among all the terminations, the OT stacked interface displays the largest interatomic distance and the least working adhesion, while the HCP stacked interface shows the smallest interatomic distance and the greatest working adhesion. These results are consistent with the adhesion work presented in Fig. 5. Furthermore, the interfacial energy of the interface of C(TiC) termination is notably lower compared to other terminations, indicating its enhanced stability.

Table 3 The best interface distance and adhesion work of different Ti₃AlC₂(0001)/Mg(0001) interface model

Termination	Stacking	Unrelaxed		Relaxed
		d0/Å	Wad (J m^−2)	d0/Å	Wad (J m^−2)	γ (J m^−2)
C(TiAl)	OT	2.05	3.53	1.98	3.86	2.95
	MT	1.62	5.18	1.54	5.64	1.87
	HCP	1.42	5.16	1.40	5.98	−0.15
C(TiC)	OT	2.20	3.55	2.16	4.06	4.23
	MT	1.65	5.45	1.58	6.12	3.17
	HCP	1.43	8.66	1.38	9.57	−0.68
TiC(TiC)	OT	3.21	1.80	3.15	1.95	2.87
	MT	2.75	2.51	2.69	2.74	2.08
	HCP	2.56	2.64	2.50	3.89	0.06
TiC(TiAl)	OT	2.98	1.51	2.93	1.76	1.46
	MT	2.76	2.28	2.74	2.43	0.78
	HCP	2.55	2.41	2.51	2.65	0.57
TiAl	OT	2.93	1.53	2.91	1.79	0.69
	MT	2.70	2.28	2.65	2.48	0.15
	HCP	2.41	2.47	2.35	2.71	0.24
Al	OT	2.85	0.95	2.83	1.15	0.25
	MT	2.45	1.35	2.39	1.56	0.19
	HCP	2.36	1.55	2.32	1.86	0.26

---

Drawing from the findings of bonding strength calculations, the C(TiC)-terminated interfaces were selected for a more comprehensive examination of the bonding properties at the Mg/Ti₃AlC₂ interface. To delve deeper into these characteristics, computations were conducted for partial density of states (PDOS) and electron density difference. Illustrated in Fig. 6 is the PDOS obtained for the HCP-stacked Ti₃AlC₂(0001)/Mg(0001) interface, where vertical dashed lines denote the Fermi level. Upon close inspection of Fig. 6, it becomes evident that the PDOS at the interface diverges significantly from that observed in the inner layers, signifying a redistribution of electrons at the interface. More specifically, Fig. 6(a) reveals that in the case of the OT configuration interface, there is an overlap between the Mg-2p orbital of the first-layer Mg atom within the Mg(0001) slab and the C-2p orbital of the first-layer C atom in the Ti₃AlC₂(0001) slab. This overlap is characterized by higher occupied states proximal to the Fermi level, facilitating orbital hybridization, and particularly, the formation of covalent bonds between Mg-2p and C-2p.

Fig. 6 PDOS for C(TiC)-terminated Mg(0001)/Ti₃AlC₂(0001) interface: (a) OT stacking, (b) MT stacking, (c) HCP stacking. The dotted line refers to the Fermi level.

It is noteworthy that the PDOS patterns observed in both the HCP and MT configurations bear similarities, potentially attributed to the instability of the MT configuration and its tendency to transition towards the HCP arrangement upon relaxation. As illustrated in Fig. 6(b) and (c), for the HCP-stacked Ti₃AlC₂(0001)/Mg(0001) interface, a clear hybridization occurs between the Mg-2p orbital of the Mg(0001) slab and the C-2p orbital of the topmost layer in the Ti₃AlC₂(0001) slab, resulting in the formation of covalent bonds. Furthermore, within the energy range spanning from 4.6 eV to 9.5 eV, there is an overlap between the Mg-2p orbital of the Mg(0001) slab and the Ti-3d orbital located in the second layer of the Ti₃AlC₂(0001) slab, indicating the establishment of Mg–Ti metallic bonds at the interface. Taken together, these findings underscore the exceptional stability exhibited by the C(TiC)-terminated Ti₃AlC₂(0001)/Mg(0001) interface, which is predominantly attributed to the formation of both C–Mg covalent bonds and strong Mg–Ti metallic bonds.

To obtain a comprehensive understanding of the interfacial binding properties, an investigation into the charge density difference was conducted for the Ti₃AlC₂(0001)/Mg(0001) interface model after complete relaxation, as depicted in Fig. 7. Within this illustration, the interface area between Ti₃AlC₂ slab and Mg slab is denoted by a dashed line. Notably, the colors red and blue represent the highest localization and maximum de-localization of electrons, respectively. Moreover, it becomes apparent that the positioning of atoms on different terminations plays a significant role in determining the movement and allocation of electrons across all interfacial models.

Fig. 7 The electron density differences of C(TiC) termination of the Mg(0001)/Ti₃AlC₂(0001) interface with (a) OT stacking, (b) MT stacking, (c) HCP stacking.

Upon a thorough examination of Fig. 7, it is evident that there is a notable variation in charge accumulation at the interface between Mg atoms and C atoms in the initial layer of the Mg(0001) slab and Ti₃AlC₂(0001) slab respectively. This observation provides compelling evidence for the coexistence of both covalent bonds and metal bonds at the Ti₃AlC₂(0001)/Mg(0001) interface. Furthermore, a significant charge transfer is discernible between C atoms and Ti atoms in Ti₃AlC₂(0001) slab, reinforcing the existence of robust C–Ti covalent bonds. These discoveries are consistent with prior computations and bolster the assertion that the C(TiC) termination interfacial model exhibits superior stability compared to all other interfacial models under consideration.

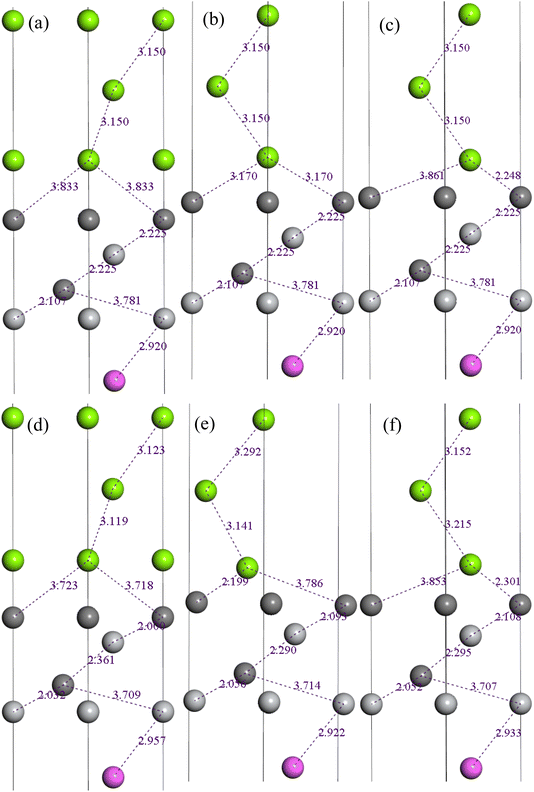
In the following process of relaxation, we permitted three layers adjacent to the interface of both Mg(0001) and Ti₃AlC₂(0001) slabs to undergo unconstrained relaxation, while maintaining the positions of the remaining atoms. Fig. 8 depicts the structural transformations of the C(TiC) termination of the Ti₃AlC₂(0001)/Mg(0001) interface pre- and post-relaxation. In the case of the OT stacking interface, we observed a reduction in the interatomic distance between the interfacial Mg atoms in Mg(0001) slab and C atoms in Ti₃AlC₂(0001) slab, with Mg atoms shifting to the Ti₃AlC₂(0001) surface. These behavior indicates the formation of robust bonds between Mg and C atoms at the interface. For the MT stacking interface, a distinct migration pattern emerged among the interfacial Mg atoms. These atoms also moved closer to the Ti₃AlC₂(0001) surface, resulting in enhanced bonding strength. Regarding the HCP stacking interface, the interfacial distance between Mg and C atoms remained largely unchanged. However, a notable movement of Ti atoms on the Ti₃AlC₂(0001) surface towards the Mg(0001) surface was observed. This shift indicates a pronounced bonding characteristic between Mg and Ti atoms.

Fig. 8 Interface configurations of the C(TiC)-terminated Ti₃AlC₂(0001)/Mg(0001) interface before and after relaxed. (a) OT stacking interface before relaxation, (b) MT stacking interface before relaxation, (c) HCP stacking interface before relaxation, (d) OT stacking interface after relaxation, (e) MT stacking interface after relaxation, and (f) HCP stacking interface after relaxation.

3.3. The doped Mg(0001)/Ti₃AlC₂(0001) interfaces

Based on the above findings, it is evident that the C(TiC) termination of HCP stacked Ti₃AlC₂(0001)/Mg(0001) interface emerges as the most stable interfacial structure. Consequently, this particular interface was chosen for further investigation, specifically to explore the impact of doping elements on its interfacial properties. Since the energy required for interstitial doping is much larger than that of replacement doping when doping atoms on the Mg side, therefore, the doping of alloying elements is directly selected as replacement doping. Additionally, during the subsequent relaxation process, only three layers of Mg(0001) slab and Ti₃AlC₂(0001) slab adjacent to the interface were permitted to undergo free relaxation, while the remaining atoms were kept fixed. Fig. 9 illustrates the six interfaces following relaxation, each incorporating a single doped active atom. In addition, since the calculations are performed in a simulation box with periodic conditions for the single cell, therefore the atom replacement in the manuscript is actually replacing a single layer of Mg atoms at the interface, and we chose only the single cell for the simulation in order to save computational cost.

Fig. 9 Interface configurations after relaxation doped with (b) Al, (b) Ni, (c) Cu, (d) Fe, (e) Mn, and (f) Si atoms.

From Fig. 9, one can seen that the distance between the C atoms and the dopant atoms shown in Fig. 9 is shorter than that between the C atoms and the magnesium atoms shown in Fig. 8(f), which indicates that the doped atoms moved towards the surface of Ti₃AlC₂(0001), and the interfacial C atoms have strong attachment to the doped atoms and form a strong bond at the interface. Besides, the optimized interface spacing between the interfacial C atoms in Ti₃AlC₂(0001) slab and the doped atoms in Mg(0001) slab can be ranged as: Fe < Si < Mn < Ni < Cu < Al < clean interface, and therefore the strong covalent bonds may have formed between the interfacial C atoms in Ti₃AlC₂(0001) slab and the doped atoms in Mg(0001) slab at the interface after doping, the bond strength can be ranged as: Fe > Si > Mn > Ni > Cu > Al > clean interface. However, the interatomic distance between the C atoms in first layer of Ti₃AlC₂(0001) slab and Ti atoms in second layer of Ti₃AlC₂(0001) slab increased after doping the atoms, indicating that the inner bonding strength is reduced. In summary, the doped interfaces exhibit greater stability in all cases, that is, the doped atoms and the interfacial C atoms are separated to the middle of the interface and perform the role of an interfacial binder.

To evaluate the impact of reacting components on both institutional properties and the stability of the interfaces, the W_ad value along with the segregation enthalpy (ΔG_seg) post-relaxation were determined. The calculation of ΔG_seg is facilitated through the following equation:⁴⁵

In this section, both the aggregate energy of the clean and doped interfaces are presented. Here, n represents the count of doping atoms, and μ signifies the chemistry potential of each of these atoms. And and denotes the energies of initial interfaces and the doped interface respectively. As detailed in Table 4, the segregation energy (ΔG_seg), W_ad, and total energy for various interfaces post-relaxation are documented. Notably, the W_ad for the pristine interface reaches 9.57 J m⁻² after relaxation. In contrast, for the Cu-doped interfaces, this value slightly reduces to 9.46 J m⁻², and the corresponding ΔG_seg registers at 0.14 eV, indicating thermodynamic instability. On the other hand, introducing Fe, Mn, Si, Al, or Ni atoms results in increased W_ad of 12.42 J m⁻², 10.96 J m⁻², 10.35 J m⁻², 9.66 J m⁻², and 9.64 J m⁻², respectively, with respective ΔG_seg values of −2.36 eV, −1.87 eV, −1.75 eV, −0.15 eV, and −0.11 eV. These negative ΔG_seg values signify a thermodynamically stable state, suggesting superior stability in Fe-, Mn-, Si-, Al-, and Ni-doped interfaces compared to those doped with Cu.

Table 4 The interfacial total energy (eV), ΔG_seg (eV), and W_ad (J m⁻²) of the relaxed doping interfacial models

Doping elements	Wad (J m^−2)	ΔGseg (eV)
None	9.57	—
Al	9.66	−0.15
Ni	9.64	−0.11
Cu	9.46	0.14
Fe	12.42	−2.36
Mn	10.96	−1.87
Si	10.35	−1.75

---

Due to the maximum adhesion work and minimal segregation energy observed at the Fe-doped interfaces, these interfaces were chosen for optimizing the atomic doping locations. The stabilization effects of Fe atoms at the interface were evaluated by introducing dopants at various positions, with the specific doping locations, adhesion values, and segregation energies depicted in Fig. 10. The doping site 1 represents the interfacial located, site 2 represents the sub-interface located, and site 3 within the Mg slab. For the Fe dopant, the Gibbs free energy of segregation (ΔG_seg) values are −2.36 eV, −2.06 eV, and −1.89 eV at positions 1, 2, and 3, respectively. Similarly, the adhesion energy (W_ad) values at these positions are 12.42 J m⁻², 11.86 J m⁻², and 11.43 J m⁻², respectively. This suggests a heightened stability at the interface when doping occurs near it. Thus, it is evident that Fe atoms serve as effective stabilizers at these interfacial regions.

Fig. 10 The heat of segregation and working adhesion at different doping position.

Fig. 11 depicts the changes in differential charge density of the C(TiC) termination of HCP stacked Ti₃AlC₂(0001)/Mg(0001) interface before and after doping. The figure illustrates a notable charge transfer, highlighting an electronic structural reorganization at the interface with visual accumulation and depletion of charge in the vicinity of interfacial atoms. In the undoped interface, illustrated in Fig. 7(c), the C atoms are encompassed by a red region, signifying electron loss from these atoms, with electrons migrating towards a more electronegative dopant and resulting in a blue region around the doping atoms. This leads to significant charge concentration, thereby promoting a strong covalent bond formation across the boundary line. For the Cu-doped interface, an enlarged blue region indicates a reduced charge transfer compared to other doped interfaces, suggesting a weakening of the interfacial bond strength post doping with Cu atoms. Conversely, in the interfaces doped with Fe, Mn, Si, Al, and Ni, an expanded red region indicates an increase in electron gain after doping, which enhances the interfacial bonding strength.

Fig. 11 Charge density difference of interfaces doped with (a) Al, (b) Ni, (c) Cu, (d) Fe, (e) Mn, and (f) Si atoms.

To gain an in-depth comprehension of the binding attributes of doping atoms on the C(TiC) termination of the HCP stacked Ti₃AlC₂(0001)/Mg(0001) interface, we examine the PDOS diagrams post-doping, illustrated in Fig. 12. Here, the Fermi level is demarcated by a black dashed line. In terms of the original interface, as depicted in Fig. 6(c), an amalgamation of the Mg-2p and C-2p orbitals occur, creating Mg–C covalent linkages. Additionally, the fusion of Mg-2p and Ti-3d orbitals between 4.6 eV and 9.5 eV indicates the Mg–Ti metallic bonds may formed. With Al doping, the interface exhibits similar orbital overlapping between C and Al atoms as seen in the original Ti₃AlC₂(0001)/Mg(0001) interface, yet a diminished PDOS for C-p states on Fermi scale indicates a reduction in bond strength.

Fig. 12 Partial density of states (PDOS) curves of interfaces doped with (a) Al, (b) Ni, (c) Cu, (d) Fe, (e) Mn, and (f) Si atoms.

For the Cu-doped interface, a notable lack of considerable overlap between C atoms and the doping elements at the interface infers a significant diminishment in both covalent and ionic bond strengths. Conversely, interfaces doped with Fe, Mn, Ni, and Si show substantial overlap between Fe-d, Mn-d, Ni-d, Si-p, and C-p states between −7.5 eV and −2.5 eV, with the overlap of Ti-d states occurring between 0.5 eV and 5.5 eV, denoting the presence of stronger covalent connections. Furthermore, among these, the interface doped with Ti and Mn exhibits the lowest PDOS at the Fermi level for C atoms, suggesting the formation of the most robust covalent and ionic linkages at the Fe, Ni, Mn, and Si doped interfaces. Thus, these doped interfaces demonstrate superior interfacial stability, corroborating findings from preceding adsorption studies.

4. Conclusion

This study harnesses density functional theory to evaluate the structural integrity and the influence of various alloying additives such as Al, Cu, Fe, Ni, Mn, and Si on the heterogeneous nucleation behaviors of the Ti₃AlC₂(0001)/Mg(0001) interface. The findings from this investigation reveal critical insights:

(1) Relative to other interface terminations with identical stacking configurations, the C(TiC) termination of the Ti₃AlC₂(0001)/Mg(0001) interface shows superior adhesion energy and reduced segregation heat. Additionally, within the same termination category, configurations positioned at hollow sites present the greatest adhesion energy and minimal segregation heat across all stacking types evaluated.

(2) The adhesion energy at the C(TiC) termination of HCP stacked Ti₃AlC₂(0001)/Mg(0001) interface surpasses that observed at the Mg/Mg boundary. This outcome underscores the efficacy of Ti₃AlC₂ as a durable foundation for facilitating heterogeneous Mg grain nucleation, both from crystallographic and thermodynamic viewpoints. Moreover, the chemical bonds at the C(TiC) termination of HCP stacked Ti₃AlC₂(0001)/Mg(0001) interface display notable covalent traits, especially in the Mg-p and C-s orbital interactions.

(3) The presence of alloying components Fe, Ni, Mn, Al, and Si beneficially augments the adhesion energy at the Ti₃AlC₂(0001)/Mg(0001) interface, thus bolstering the bond strength at the Mg/Ti₃AlC₂ boundary. In contrast, introducing Cu reduces the adhesion energy, adversely affecting the Mg/Ti₃AlC₂ interface's stability. Consequently, considering their effects on the working adhesion at the doping Ti₃AlC₂(0001)/Mg(0001) interface, the active elements can be ranked as follows: Fe > Mn > Si > Al > Ni > Cu.

Data availability

Some or all data, models, or code generated or used during the study are proprietary or confidential in nature and may only be provided with restrictions.

Author contributions

Mingjie Wang: writing, reviewing and editing, methodology, and software. Ding Wei, Luya Wang, Ben Wang and Hongxing Zheng: visualization, investigation, and supervision. Meiping Liu and Yijie Zhang: investigation. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

Authors Mingjie Wang, Ding Wei, Luya Wang, Meiping Liu, Ben Wang, Hongxing Zheng, and Yijie Zhang have all received research grants from Huanghuai University, Shanghai University and Dongliang Aluminum Industry Co., Ltd. The authors declare that they have no financial or personal relationships with other people or organizations that could inappropriately influence their work, and the authors declare that they have no conflict of interest.

Acknowledgements

This research received financial support from the National Natural Science Foundation of China (No. 52371033, and 52071299), and the Natural Science Foundation of Shanxi Province (202303021211158), and Henan Provincial Science and Technology Tackling Project (242102210164, and 242102220085), and the Institutions of Higher Learning Key Scientific Research Project of Henan Province (25B430020).

References

1. X. X. Mi, L. L. Dai, X. R. Jing, J. She, B. Holmedal, A. T. Tang and F. S. Pan, J. Magnesium Alloys, 2024, 12(2), 750–766,  DOI:10.1016/j.jma.2024.01.005.
2. J. L. Ning, B. S. Gao, X. Y. Yuan, J. L. Zhou, G. Z. Tang and L. S. Chen, J. Mater. Res. Technol., 2024, 28, 3781–3793,  DOI:10.1016/j.jmrt.2023.12.275.
3. J. Y. Bai, Y. Yang, C. Wen, J. Chen, G. Zhou, B. Jiang, X. D. Peng and F. S. Pan, J. Magnesium Alloys, 2023, 11(10), 3609–3619,  DOI:10.1016/j.jma.2023.09.015.
4. P. Peng, H. S. Xue, J. She, J. Y. Zhang, A. T. Tang, S. Long, C. Zhang, Q. S. Yang and F. S. Pan, J. Mater. Res. Technol., 2015, 29, 4480–4504,  DOI:10.1016/j.jmrt.2024.02.131.
5. P. Siahmard, R. A. Najafabadi, A. Meysami, M. Meysami and T. Isfahani, Results Eng., 2023, 18, 101138,  DOI:10.1016/j.rineng.2023.101138.
6. S. G. Shabestari and E. Ghaniabadi, Trans. Nonferrous Met. Soc. China, 2023, 33(2), 396–408,  DOI:10.1016/S1003-6326(22)66115-6.
7. S. Ganguly, A. K. Chaubey, R. Gope, A. Kushwaha, A. Basu and M. Gupta, Compos. Commun., 2023, 996, 171203,  DOI:10.1016/j.jallcom.2023.171203.
8. D. X. Wang, Y. Jing, B. S. Lin, J. P. Li, Y. Shi and R. D. K. Misra, Mater. Charact., 2023, 194, 112444,  DOI:10.1016/j.matchar.2022.112444.
9. B. Zhang, C. L. Yang, Y. X. Sun, J. Li and F. Liu, Mater. Today Commun., 2020, 24, 101023,  DOI:10.1016/j.mtcomm.2020.101023.
10. C. Vasu, A. B. Andhare and R. Dumpala, Int. J. Refract. Met. Hard Mater., 2024, 48, 10941–10951,  DOI:10.1016/j.ijrmhm.2023.106538.
11. W. Qiu, Y. W. Li, G. Huang, J. Chen, Y. J. Ren, W. Y. Huang, W. Chen, T. Q. Wu, M. H. Yao and A. H. Xiong, Trans. Nonferrous Met. Soc. China, 2023, 33(5), 1398–1410,  DOI:10.1016/S1003-6326(23)66191-6.
12. B. Wang, X. Liu, Y. J. Wang, J. Ding, S. C. Wei, X. C. Xia, M. Liu and B. S. Xu, J. Mater. Res. Technol., 2022, 21, 2730–2742,  DOI:10.1016/j.jmrt.2022.10.086.
13. P. X. Cui, M. L. Hu, Z. S. Ji, Y. Wang, Y. Guo and H. Y. Xu, Trans. Nonferrous Met. Soc. China, 2024, 34(5), 1456–1469,  DOI:10.1016/S1003-6326(24)66483-6.
14. J. H. Zhang, X. D. Niu, X. Qiu, K. Liu, C. M. Nan, D. X. Tang and J. Meng, J. Alloys Compd., 2024, 471(1–2), 322–330,  DOI:10.1016/j.jallcom.2008.03.089.
15. Z. Q. Liu, W. L. Yang, X. X. He, T. C. Cheng, H. L. Huang, J. Xiong and G. L. Huang, Mater. Charact., 2022, 30, 101870,  DOI:10.1016/j.surfin.2022.101870.
16. D. D. Zhuang, X. L. Lian, T. Y. Zhou, S. H. Zhang, X. C. Wang, J. Li, H. S. Ding and C. L. Wang, Surf. Coat. Technol., 2022, 479, 130541,  DOI:10.1016/j.surfcoat.2024.130541.
17. A. Gnanavelbabu, E. Vinothkumar, N. S. Ross, M. K. Gupta and M. Jamil, Tribol. Int., 2023, 178(B), 108054,  DOI:10.1016/j.triboint.2022.108054.
18. P. Kumar, A. K. Mondal, S. G. Chowdhury, G. Krishna and A. K. Ray, Mater. Sci. Eng., A, 2017, 683, 37–45,  DOI:10.1016/j.msea.2016.12.006.
19. L. Pezzato, L. Lorenzetti, L. Tonelli, G. Bragaggia, M. Dabalà, C. Martini and K. Brunelli, Surf. Coat. Technol., 2023, 428, 127901,  DOI:10.1016/j.surfcoat.2021.127901.
20. J. L. Shang, L. M. Ke, F. C. Liu, F. Y. Lv and L. Xing, J. Alloys Compd., 2019, 797, 1240–1248,  DOI:10.1016/j.jallcom.2019.04.280.
21. G. H. Meng, X. Lin, H. Xie, C. Wang, S. Q. Wang and X. Ding, J. Alloys Compd., 2019, 672, 660–667,  DOI:10.1016/j.jallcom.2016.02.191.
22. Y. H. Nian, Z. Y. Zhang, S. N. Yang, M. M. Liu, K. H. Zhang and X. L. Zhou, Vacuum, 2024, 224, 113158,  DOI:10.1016/j.vacuum.2024.113158.
23. Z. X. Zhang, W. L. Wang, Y. X. Li, J. T. Zhang, Z. Y. Zhang, Q. Zhang, H. Liu, G. F. Han and W. B. Zhang, Ceram. Int., 2024, 50(11), 20694–20705,  DOI:10.1016/j.ceramint.2024.03.191.
24. C. Magnus, D. Cooper, C. Jantzen, H. Lambert, T. Abram and M. Rainforth, Corros. Sci., 2020, 182, 109193,  DOI:10.1016/j.corsci.2020.109193.
25. H. Zhang, B. T. Hu, B. Dai, L. S. Chu, Q. G. Feng and C. F. Hu, J. Eur. Ceram. Soc., 2023, 44(3), 1436–1444,  DOI:10.1016/j.jeurceramsoc.2023.10.064.
26. A. Chouket, P. Montmitonnet, K. Frances, C. Pradille, R. Chmielowski and I. Lahouij, J. Alloys Compd., 2024, 990, 174403,  DOI:10.1016/j.jallcom.2024.174403.
27. X. Liu, X. J. Cao, X. Y. Yi, H. Z. Wang, J. Guo and J. Yang, Mater. Today Commun., 2024, 38, 108421,  DOI:10.1016/j.mtcomm.2024.108421.
28. K. K. Ding, J. X. Ding, K. G. Zhang, L. M. Chen, C. J. Ma, Z. C. Bai, P. G. Zhang and Z. M. Sun, Ceram. Int., 2022, 48(22), 33670–33681,  DOI:10.1016/j.ceramint.2022.07.313.
29. V. Desai, V. Badheka, T. Parekh and N. I. Jamnapara, Tribol. Int., 2024, 195, 109594,  DOI:10.1016/j.triboint.2024.109594.
30. M. J. Wang, H. M. Han, G. W. Zhang, H. Xu, Z. Yin, Y. Dong and Y. Z. Fu, Results Phys., 2022, 38, 105659,  DOI:10.1016/j.rinp.2022.105659.
31. M. J. Wang, J. W. Sun, Y. C. Meng, S. Y. Li, H. G. Shou, G. W. Zhang, Z. Yin, Y. Dong, H. X. Zheng and Y. J. Zhang, J. Alloys Compd., 2024, 1002, 175290,  DOI:10.1016/j.jallcom.2024.175290.
32. B. Chen, M. P. Liu, M. J. Wang and C. H. Zhang, Mater. Today Commun., 2024, 39, 109169,  DOI:10.1016/j.mtcomm.2024.109169.
33. J. L. Li, D. C. Chen, T. Fan, X. H. Hu, H. B. Rong, Z. M. Zheng, H. X. Zheng and C. Y. Liu, Appl. Surf. Sci., 2022, 605, 154713,  DOI:10.1016/j.apsusc.2022.154713.
34. K. Zhang and Y. Z. Zhan, Vacuum, 2019, 165, 215–222,  DOI:10.1016/j.vacuum.2019.04.028.
35. W. B. Guo, Z. Y. She, H. T. Xue and X. M. Zhang, Ceram. Int., 2019, 46(4), 5430–5435,  DOI:10.1016/j.ceramint.2019.10.301.
36. M. J. Wang, J. W. Sun, S. Y. Li, Y. C. Meng, H. X. Zheng, Z. Yin, Y. Z. Fu and Y. J. Zhang, Surf. Interfaces, 2024, 46, 104040,  DOI:10.1016/j.surfin.2024.104040.
37. M. J. Peng, R. F. Wang, L. K. Bao and Y. H. Duan, Appl. Surf. Sci., 2021, 569, 150996,  DOI:10.1016/j.apsusc.2021.150996.
38. X. Pei, M. N. Yuan, P. F. Zhou, J. W. Zhu, W. Yang, X. S. Zhou, Y. H. Zhao and X. Q. Shen, J. Mater. Res. Technol., 2023, 27, 3424–3435,  DOI:10.1016/j.jmrt.2023.10.122.
39. S. R. G. Christopoulos, P. P. Filippatos, M. A. Hadi, N. Kelaidis, M. E. Fitzpatrick and A. Chroneos, J. Appl. Phys., 2018, 123(2), 025103,  DOI:10.1063/1.5011374.
40. A. Mattsson, P. Schultz and M. Desjarlais, Modell. Simul. Mater. Sci. Eng., 2005, 13, R1–R30,  DOI:10.1088/0965-0393/13/1/R01.
41. L. Cao, J. Shen and N. X. Chen, J. Alloys Compd., 2002, 336, 18–28,  DOI:10.1016/S0925-8388(01)01863-1.
42. D. Vanderbilt, Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 41, 7892–7895,  DOI:10.1103/PhysRevB.41.7892.
43. H. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
44. W. Jeitschko and H. Nowotny, Monatsh. Chem., 1967, 98, 329–337.
45. X. H. Li, Y. Li, J. H. Xu, J. J. Gong, Y. X. Wang and Z. Chen, Comput. Mater. Sci., 2023, 232, 112630,  DOI:10.1016/j.commatsci.2023.112630.
46. J. Yang, Y. Wang, J. H. Huang, Z. Ye, X. Sun, S. H. Chen and Y. Zhao, Appl. Surf. Sci., 2019, 475, 906–916,  DOI:10.1016/j.apsusc.2019.01.047.
47. H. Z. Zhang and S. Q. Wang, Acta Mater., 2007, 55, 4645–4655,  DOI:10.1016/j.actamat.2007.04.033.

---