Viscoelasticity of a single poly-protein probed step-by-step during its mechanical unfolding and refolding under the force-clamp conditions

Abstract

One of still outstanding issues in protein folding is to be able to directly observe structural changes occurring along the folding pathway. Herein, we report on changes of the viscoelastic properties for a single protein molecule measured along its mechanically-induced unfolding and refolding trajectories. We use a model system, the I27 poly-protein, and investigate its conformational changes via force-clamp AFM (FC-AFM) spectroscopy. Typically only protein's length and force have been measured using this approach. By applying Euler–Bernoulli model of the AFM cantilever with properly accounted hydrodynamic damping we show how to access – from the same measurements – related changes of two additional observables such as molecular stiffness and molecular friction coefficient. Our results are compared to recent analytical models and experimental results. These findings are expected to lead to proper identification of the intermediate folding states from the knowledge of their mechanical properties.

---

Introduction

Protein folding is the key biophysical process related to sustaining life as well as to many diseases.^1–3 Despite maturity of this field of research, there have been many experimental advancements in protein folding lately, including novel NMR experimental methods,⁴ fast micro-fluidic methods with fluorescence⁵ and surface-enhanced Raman detection⁶ as well as cryo-EM methods.^7,8 In addition, novel molecular dynamics methods⁹ and entirely new computational approaches such as Alpha-Fold^10,11 have been developed. Despite being described already sufficiently well on the grounds of statistical physics,³ its many intricate mechanistic details are still unknown. In particular, being able to directly observe structural changes occurring along the folding pathway is still a holy-grail of the folding problem. Current methods for probing of such structural changes in situ are limited pretty much to the NMR studies, but truly single molecule resolution is still missing therein. Another strategy is to use single molecule force spectroscopy (SMFS). In particular, in the force-clamp studies with atomic force microscopy (FC-AFM), a single protein molecule is stretched at a well-described force, which slows down typical (un)folding times from μs to fractions of the second.¹²

The force-quench experiments (FQ-AFM) are a variant of the FC-AFM, where the clamping force acting on the single protein molecule is initially increased to allow its unfolding and later quenched to initiate refolding. Rate constants obtained from the FQ-AFM studies are measured directly at each clamping force and without any need to use any additional constants or approximations. However, physiological aspects of the SMFS methods are still discussed, particularly in the context of altered, non-physiological unfolding pathways explored during mechanically-forced (un)folding.^13–15 And indeed careful FQ-AFM experiments showed force-induced changes in the folding and refolding energy landscapes.¹⁶ Yet, the SMSF measurements approximated to zero force often, and particularly in the context of proteins with mechanical function, relate to their thermal or chemical unfolding experiments. Thus, it makes them a reasonable avenue to study intricate details of the (un)folding processes.

Temporal resolution of the FC-AFM studies as well as other types of SMFS-AFM experiments is often too large and detection of the end-to-end protein length changes are often too ambiguous to uniquely decipher minuscule structural changes occurring along the folding pathways. Therefore, other observables are dearly desired. One advancement has been to probe at the same time protein stiffness calculated either via a Hooke's law,¹⁷ or via polymer-based elasticity models such as the worm-like chain (WLC) model.^18,19 Another advancement is to monitor additional mechanical parameters such as (internal) friction coefficient. Such friction coefficients represent energy dissipation, with a separation into solvent–polymer friction and internal friction arising from intra-polymer interactions, i.e., obtained at a limit of vanishing solvent viscosity.

Recent analytical modelling of internal friction coefficients from molecular dynamics studies showed that already small α-helical peptides display size-dependant internal friction and their internal friction coefficients depend substantially on the given media.^20–22 Furthermore, proteins exhibit distinctively different stiffness along various force-application directions.^23,24 Thus, mechanical signatures consisting of two stiffnesses and two dissipation factors measured along two orthogonal directions, i.e., pulling and its orthogonal direction, would provide additional four experimental observables to trace in situ local structural changes of the (un)folding protein. Knowledge of such observables is expected to sufficiently improve modelling of the possible intermediate structures visited by the (un)folding protein, and consequently to bring us closer to deciphering small structural changes occurring along the folding pathways, at least in the cases of simple proteins to start with.

I27 is the 27th domain of a human cardiac titin. It has 89 residues and contains two β patches within an immunoglobulin-like fold, which is one of the most common structural motifs in the pdb protein database.^13,25 Over last 25 years it has become the model system for single molecule unfolding studies at various conditions.^12,26–29 In addition, it has been thoroughly studied through MD simulations as well as in ensemble.^13,19,30,31 Throughout all these studies, a dominant I27 unfolding pathway has been settled to proceed through an intermediate state, where a short A strand at the N-terminus is detached from the rest of the β-sandwich. This event is followed by a major rupture of the A′G sheet, which requires substantial energy and/or stretching force of up to 200 pN to occur. However, so-far its viscoelastic properties have been assessed at the approximate, simplified lever, i.e., via FX-SMFS-AFM and using simplified models of a cantilever as a dampened harmonic oscillator under a stochastic thermal force.^18,29,32

Therefore, I27 is a good model system for the proposed above in situ studies of mechanical signatures. To do so, we propose here to use a complete, distributed-mass Euler–Bernoulli description of the AFM cantilever with hydrodynamic damping. Simple cantilever models were insufficient to quantify mechanical properties of typical arbitrary substrates, let alone the proteins.^18,33–35 Furthermore, molecular stiffness and internal friction coefficients for single proteins, such as I27, are of the same orders of magnitude as the relevant viscoelastic properties for the AFM cantilevers used to measure them.³² Thus, it is easy to introduce errors, when the respective viscoelastic properties of the cantilevers are only estimated. Finally, hydrodynamic damping plays a significant role not only in liquids, but also in air, and its proper description is expected provide an excellent agreement between experiments and theory.³⁶

Consequently, herein we report on two major advancements. First, we develop a model for obtaining the viscoelastic properties of the protein from a detailed, 3D beam description of the AFM cantilever interacting with the protein. The protein is described by two orthogonal stiffnesses and their respective energy dissipation factor. Second, we apply this model to elucidate stiffness and internal friction coefficient of the I27 along its single unfolding and refolding trajectory studied with FQ-SMFS-AFM. We discuss obtained results in the light of the polymer physics models¹⁸ as well as recently produced models of internal friction for simple alpha-helical peptides.^21,22 While our current FQ-AFM study does not yet produce its full potential to uniquely determine any of the proposed short-lived transient structures along the folding trajectories, they provide an important step forward towards a complete structural description of folding at the single molecule level.

Materials and methods

For fingerprinting single I27 units in FQ-AFM, a recombinant protein comprising four identical I27 molecules (pdb 1TIT) connected in tandem has been used. I27₄ cloning and expression, sample preparation, and details on FQ-AFM experiments using our custom AFM setup have been described in ref. 37. The I27₄ gene was obtained from a I27 DNA after several rounds of its in-cloning into the pQE30 plasmid. The final construct had 378 residues, which amounts to four 89 residue long I27s units connected via two extra residues (–R–S–) in between, 12 residue long his-tag at the N-terminus (M–R–G–S–H₆–G–S–) and four additional residues (with two cysteins) at C-terminus (–R–S–C–C). The I27₄ was expressed in E. coli XL1-Blue cells, purified in Talon-Co²⁺ gravity column, dialysed into Dulbecco phosphate-buffered saline buffer (DPBS), and stored at 4 °C at a concentration of 1 mg ml⁻¹. The quality of purified protein was verified by SDS-PAGE. A protein sample for each FQ-AFM experiment was prepared by depositing several μL of a protein solution on a gold evaporated glass slide.

For all reported here FQ-AFM traces the BL-RC-150VB-C1 type B cantilever from Olympus has been used with a thermally calibrated spring constant of 7.36 pN nm⁻¹ (±5%), which was calibrated like in the ref. 37. Igor Pro software from Wavemetrics, USA, was used for data acquisition and processing using custom written procedures. The FQ-AFM experiments report changes in a stretched protein length and force acting on the protein as a function of time. These are obtained from raw cantilever deflection and externally calibrated piezo displacement data adjusted for the calibrated cantilever displacement. For optimal AFM feedback the FQ-AFM data are low-pass filtered at sub-kHz frequencies.³⁷ In addition, the so-called “fast” FQ-AFM force traces have been recorded here at 166.6 kSamples per second, which was our maximum available data acquisition speed. For anti-aliasing, fast FQ-AFM force signals were low-pass filtered at a Nyquist frequency of 83.3 kHz. Fast Fourier transforms (FFTs) were then obtained from the fast FQ-AFM force traces for each data segment being 4098 points long. Next, 20 of such consecutive FFTs were averaged to get the FFT spectrum out of which the cantilever's resonance frequencies were read and compared with their fitted values obtained from the model. Thus, considering 6 μs spacing between consecutive data points a total time of ca. 0.5 s (=20 × 4098 × 6 μs) was necessary per one reading of stiffness and internal friction coefficients. Usage of shorter data fragments or less averaging resulted in larger errors in determination of resonance frequencies for the AFM cantilever. Fitting errors in liquid were up to 10% for the 1st resonance frequency at ca. 1 kHz, and only up to 1% for 2nd and 3rd resonances between 13–18 kHz and 46–53 kHz, respectively. In air even smaller errors were obtained – cumulatively less than 3% over three fitted resonances.

The cantilever's resonance frequencies in air and water have been calculated from a distributed-mass Euler–Bernoulli model describing hydrodynamically dampened vibrations of rectangular beams (here: cantilevers) with a small aspect ratio. The model described an AFM cantilever through its length L, width b and thickness t, tip height h_tip, and tip mass m_tip. The cantilever has been tilted at an angle α (manufacturer specifications) with respect to the normal to the substrate. The tip was attached at a point βL along the beam. One beam end was clamped by a support spring with an elastic spring constant k_S estimated with dynamometer. The other end was either left free or in contact – via the tip – with a protein. Using the manufacturer's scanning electron microscopy (SEM) measurements, the cantilever's thickness was fitted in air and constrained between 0.15 and 0.20 μm. The values of L, b, h_tip and β were obtained from optical and SEM imaging. The values of β were fitted in air and constrained between 0.90 and 0.95. The value of m_tip has been calculated using the formula introduced in the ref. 36 The cantilever density ρ was obtained from a weighted average of three layers amounting to its thickness. These are: silicon nitride with density ρ_SiNx = 3100 kg m⁻³,³⁸ 10 nm Cr layer with density ρ_Cr = 7140 kg m⁻³, and 50 nm gold layer with density ρ_Au = 19 320 kg m⁻³. The Young modulus of the cantilever E was fitted in air and constrained between 170 and 210 GPa. Other parameters of the model were: a position of the AFM laser beam along the cantilever εL and an arbitrary cantilever excitation amplitude amp. Additional values utilized in calculations were air density ρ_air = 1.18 kg m⁻³ and viscosity η_air = 1.86 × 10⁻⁵, both calculated at 25 °C, as well as PBS density ρ_PBS = 998 kg m⁻³ and viscosity η_PBS = 0.91 × 10⁻³, both taken for water at 23 °C.

To model the cantilever resonance frequencies in air, an explicit introduction of air damping within the wave vector κ_air was applied as in ref. 36 and with f being frequency:

While applying the model to PBS, a different form of the hydrodynamic function (now: ) was utilized. It was developed in ref. 36 as: Herein, the Reynolds number Re is (2πfρ_PBSb²)/(4η_PBS). The new parameters A₀, a₁ and a₂ have been fitted from the shifts of the respective resonance frequencies with respect to air and constrained within ±20% of the analogous values of A₀, a₁ and a₂ derived in ref. 36. A complete formula for κ_PBS was:

After performing the fits in air, in PBS and in the proximity to the substrate (also in PBS), the following set of parameters has been obtained: L = 100 μm, b = 30 μm, t = 0.160 ± 0.005 μm (was fitted in air), h_tip = 7.1 μm, m_tip = 76.3 pg, β = 0.932 ± 0.001 (was fitted in air), α = 20.5 deg, k_S = 520 N m⁻¹, ρ = 8420 kg m⁻³, E = 290 ± 5 GPa (was fitted in air), ε = 0.885, amp = 10⁻³⁰, A₀ = 7.20 ± 0.01 (was fitted in PBS), a₁ = −0.580 ± 0.005 (was fitted in PBS), a₂ = 0.076 ± 0.001 (was fitted in PBS) and an additional parameter to model the cantilever's behavior in PBS near substrate: s = 1.0450 ± 0.0005.

Results and discussion

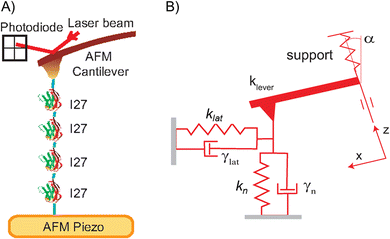
Fig. 1(A) shows an overview of our FQ-AFM setup to (un)fold single I27 molecules and infer associated changes of their viscoelastic properties along the unfolding and refolding trajectories. The protein is clamped between an AFM tip and a gold substrate. Its his-tag at N-terminus preferentially sticks to an AFM cantilever and cystein residues at its C-end preferentially stick to gold. Since this cannot be visually verified the polyprotein construct was necessary, and only selected FQ-AFM traces were utilized to fingerprint stretching of the properly surface attached I27 units, which will be described later.

Fig. 1 Principles of the AFM force spectroscopy and a Kelvin–Voight model abstracting the protein as two dissipative springs. (A) The AFM tip grabs and manipulates the protein molecule (here: I27₄) from the substrate (here: gold). Force exerted by a cantilever is monitored by deflection of a laser beam and changed by piezo displacements. (B) To infer its visco-elastic properties the protein is described by a Kelvin–Voight model using a normal (and lateral) spring constants, k_n (and k_lat), in parallel with associated normal (and lateral) energy dissipation factors γ_n (and γ_lat).

Fig. 1(B) shows how the protein is abstracted through by a rheological Kelvin–Voight model. It is described as two connected dissipative springs with spring constants k and mechanical energy dissipation factors γ along two orthogonal directions. In the case of our AFM experiments the normal spring with k_n and γ_n will naturally correspond to the protein pulling/compressing direction, which is normal to the substrate, while the values of k_lat and γ_lat correspond to a generalized lateral stretching direction being in plane with the substrate.³⁶ The energy dissipation factors relate to the molecular friction coefficients of the stretched protein molecules along the described directions.²² Consequently, the four parameter model yields a quite accurate description of the protein molecule along its mechanical unfolding and refolding trajectory.

The measurements of k and γ are obtained from the shifts of several resonance frequencies of the AFM cantilever interacting with the protein. To start with, the cantilever displacement, x, is measured for certain time and transformed into a frequency domain. To model the values of x we utilized a distributed mass Euler–Bernoulli model with explicit hydrodynamic damping. The model needs many parameters, see Materials and methods, which are adjusted to a great precision from the measurements of flexural resonance modes for thermally exited cantilevers at several calibration stages. Our fitting procedure seeks to minimize a cumulative error between experimentally measured and analytically calculated positions of the cantilever respective resonance frequencies. Only several parameters are fitted at each calibration stage and three calibration stages have been used in this work.

First, the model was applied to fit resonance frequencies of the cantilever in air. To describe vibrations of rectangular cantilevers with a small aspect ratio, like the BL-RC-150 used here, the model – developed originally for vacuum³⁵ – needed an explicit introduction of air damping to account on behavior of higher resonance modes.³⁶ The key idea was developed in the ref. 36. It dwelled on changing the wave vector κ in vacuum – needed for the solution – towards an appropriate wave vector in air κ_air.³⁶ Due to our experimental bandwidth, we could access reliably only three cantilever resonance modes in air, at ca. 10, 90 and 270 kHz. Thus, only three, most critical, cantilever properties (t, Eβ) have been fitted and within certain realistic constraints, see Materials and methods. After fitting, an excellent agreement with model was obtained with a relative error of less than 3%.

In the next step, the cantilever frequency response in a PBS buffer, but far away from any substrate with proteins was fitted. To do so, we utilized another previously developed equation for the corresponding wave vector, now κ_PBS, with an appropriate hydrodynamic damping function in water 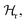³⁶ see Materials and methods.

However, in order to analytically calculate resonance frequencies of an AFM cantilever stretching a single protein molecule, the final upgrade is needed, which we develop herein. The model fitted very well all the resonance frequencies far away from the substrate in PBS, but it failed while the cantilever was brought to the vicinity of the substrate. This happened due to additional downshifts of the resonance frequencies observed in the contact proximity. Similar frequency shifts for the same kind of AFM cantilevers have been also observed recently by Mori et al.³² and attributed mostly to a modified hydrodynamic damping at the proximity of the surface.³⁹ In particular, we observed that the second detectable resonance frequency in liquid (at roughly 17 kHz) has decreased by a factor of 0.85 when compared the situations of being several hundreds of μm, i.e., “far away” from the substrate, and 200 nm from the substrate. Analogously, a third detectable resonance frequency (at roughly 55 kHz) has decreased by a factor 0.91. Furthermore, these resonance frequencies stayed at fairly the same values between 200 nm away and several tens of nm from the substrate (within 1–2 percent relative error). A mere introduction of an additional parameter “s” multiplying the values of the wave vector κ_PBS for the cantilever being “far away” modelled well our observations, i.e., within 5–10% relative error. Consequently, we introduce the following equation for the wave vector at ca. 200 nm above the substrate κ_nearSurface:

κ_nearSurface = κ_PBS × s (3)

Having prepared the stage via subsequent calibration steps we became ready to estimate the minuscule changes of the mechanical signatures, i.e., stiffnesses and internal friction coefficients of the single protein molecules along their mechanical unfolding and refolding trajectories. Fig. 2 explains how these variables are obtained for single I27₄ molecules during their mechanical unfolding and refolding processes. First, the I27₄ molecule is grabbed and stretched by an AFM tip as presented in Fig. 2(A). Initially, the cantilever is brought to contact with the substrate with adsorbed single protein molecules using 100 pN contact compressive forces. If the protein attaches to the tip, it will be stretched in the next phase, when the force is changed from compression to tension. Upon a prolonged tensile force of 195 ± 5 pN the protein and linkers extend elastically by several nanometers and then the protein units unfold in a stepwise increase of its end-to-end length x with time. Initial elastic extension of the linkers and protein modules connected with their later unfolding steps was a necessary ingredient to observe therein, since only such behavior fingerprints the protein molecules attached to the cantilever and the substrate in a proper manner. Next, the force is quenched and I27₄ first collapses entropically and then tries to refold. An increase of force after 15 s produces a stepwise unfolding again implying that all four modules of I27₄ refolded upon the force quench. Fig. 2(B) presents selected averaged fast Fourier transforms obtained for the fast force FQ-AFM trace at three selected points p₁ to p₃ along the protein's folding trajectory. One can clearly distinguish three mechanical resonances of the AFM cantilever coupled with the protein, but in some cases we had some uncertainties with its first resonance at ca. 1 kHz. Therefore, due to limitations of our “not-so-fast” FQ-AFM spectrometer, we reduce our model to two parameters and approximate k_protein = k_n = k_lat as well as γ_protein = γ_n = γ_lat. These approximation are expected to be corrected later and will become the subject of our future investigations utilizing much faster FQ-AFM setups. Consequently, the FFT traces in Fig. 2(B) are then fitted with respective Lorentzians³⁷ to obtain their resonance frequencies. Such resonance frequencies are then compared with their analytically derived analogues obtained from our calibrated Euler–Bernoulli cantilever model, but now with only two new parameters: the values of k_protein and γ_protein.

Fig. 2 Typical FQ-AFM results in time (A) and frequency domains (B). (A) An example of the FQ-AFM trace showing mechanically induced refolding of the I27₄ molecule. First, the cantilever is brought to contact at 100 pN compressive forces with the protein molecule on the substrate. Then, the molecule is quickly unfolded using a tensile force of −195 pN. Inset shows initial four I27₄ unfolding events. Then, the force is slowly relaxed, and the molecule refolds abruptly after ca. 10 s, which is observed in its abrupt length contraction. After several seconds in the refolded state, the molecule is once again re-unfolded, but slowly, which is observed as clear steps in its length. (B) Portions of the FQ-AFM trajectory can be selected and Fourier transformed into a frequency domain to visualize mechanical resonances of the cantilever in contact with the protein. Herein, three random portions (0.5 s each) “p1”, “p2” and “p3” were selected in the FQ-AFM trajectory and are showed in the frequency domain. Next, mechanical resonances of the cantilever (marked by red double arrows) are read and their frequencies (here roughly at 1, 17 and 55 kHz) are fitted with the Euler–Bernoulli cantilever model with hydrodynamic damping to obtain the visco-elastic properties of the protein.

By repeating the aforementioned procedure along an entire protein unfolding/refolding trajectory, stiffness and friction coefficients for the protein are elucidated at each temporal segment chosen along the FQ-AFM trajectory. In this work, however, instead of fitting both stiffness and friction coefficients, we decided to estimate analytically molecular stiffness using the WLC model,^12,14 so that to fit only the values of γ_protein.

The WLC model connects the protein extended length x with an applied force F:

F = (k_BT/p)[0.25(1 − x/L_o)⁻² − 0.25 + x/L_o], (4)

so that the elastic stiffness of a protein along its force-application directions becomes:

k_protein = ∂F/∂x = (k_BT/(2 × p × L_o))[(1 − x/L_o)⁻³ + 2], (5)

where k_B is the Boltzmann's constant, T is the absolute temperature, p is the persistance length (or the length of each chain unit) and L_o is the protein contour length (or a maximum chain length).

For example, from eqn (5) the elastic spring constant k_unf of ca. 22 pN nm⁻¹ is obtained for our entirely unfolded I27₄ protein, which is stretched by the 195 pN tensile force. To calculate this value, we utilized a standard value of p = 0.36 nm as well as the total number of 378 residues within our protein construct, so that L_o = 378 × p = 136.8 nm. Very similar condition is reflected in the initial phase of our FQ-AFM experiments presented in Fig. 3(A). In this case, the unfolded protein's L_o was obtained from the protein's length vs. time trace to be 131 nm. Noteworthy, such value amounted to stretching only 364 out of 378 residues, i.e., all modules and their linkers but only six additional residues at the N and C termini out of a maximum of 16, see Materials and methods. Determination of an actual value of L_o is performed at the initial phase of the FQ-AFM measurements, i.e., at times of 0.3–0.5 s, where an initially stretched protein length L must follow eqn (4) for a given applied force. As verified in Fig. 3(A) in the re-unfolding phase starting at times of ca. 16 s, exactly four I27 modules have unfolded and then refolded and then re-unfolded again in the presented case.

Fig. 3 Two examples for obtaining visco-elastic properties of I27 from the FQ-AFM experiments. Vertical lines at roughly 11 and 16 seconds mark on onset of the collapsing and re-unfolding zones, respectively. (A) The results showing unfolding, proper folding and re-unfolding of four I27 modules. (B) Resulting protein stiffness (in blue) and internal friction coefficient (in red). (C and D) Analogous results for two I27 modules, which initially unfolded, then partially collapsed, but did not fully refold.

For the calculations of L_o in the case of an entirely folded I27₄ protein, we used the value of 18 nm, since an end-to-end distance between N to C ends of each folded I27₄ module together with their two additional linking residues is 4.5 nm.¹⁷

Different situation is presented in Fig. 3(C). Therein, an original extended length and precisely two major unfolding steps strongly suggested that the molecule has been grabbed by the AFM cantilever at the end of the second I27 module, or at its end, but then the first two modules adhered strongly to the substrate. By similar reasoning as earlier, i.e., from the observation of initially unfolded length, we obtained L_o of 64.8 nm, which amounts to 180 residues, i.e., two I27 modules, their linkers and two additional residues from either their N or C ends. Furthermore, this particular protein did not refold, since on the re-unfolding phase (starting after 15 s) no clear re-unfolding steps were observed.

Next, we use the obtained values of L_o as well as measured mean values of the protein extended length x, to estimate molecular stiffness of the protein molecule using eqn (5) within each 0.5 s long data point, see Materials and methods. We continue this approach till an onset of the collapsed region at ca. 11 s. Within a collapsed zone we start to use L_o of 18 nm for the case of the I27₄ molecules, which refold, see Fig. 3(A) and (B). We also continue to use L_o of 64.8 nm in the case of the I27₂ molecules, which did not refold. For the re-unfolding case in Fig. 3(A), after 16 s, L_o is gradually increased to 65.5, 98.25 and 131 nm after each re-unfolding step in Fig. 3(A). However, the non-re-unfolding case in Fig. 3(C), the value of L_o is continuously kept at 64.8 nm. The resulting molecular stiffness values calculated in these cases are plotted in Fig. 3(B) and (D), respectively, in blue.

In the last step, using calculated molecular stiffness values, the friction coefficients are obtained once again from our Euler–Bernoulli model of the cantilever in the vicinity of the substrate, i.e., with κ_nearSurface, and from the miniscule shifts of the resonance frequencies of the cantilever in contact with the protein at each temporal periods along the FQ-AFM trajectories. These friction coefficients are then plotted in Fig. 3(C) and (D), respectively, in red. Consequently, molecular stiffness and friction coefficients are obtained independently, but along the same (un)folding trajectory.

Obtained here values of molecular stiffness in the case of folded I27₄ are as low as 0.2 pN nm⁻¹ and increase up to roughly 5 pN nm⁻¹. Due to our sequential fitting procedure it is the easiest to estimate their errors from the variations of the minimum stiffness, which varies between 0.2 and 0.5 pN nm⁻¹ in Fig. 3(B). In the case of the collapsed I27₂ their minimum stiffness variations are between 0.4 and 1.8 pN nm⁻¹ in Fig. 3(D). In the latter case, we have no additional experimental means to verify any partial folding of the collapsed I27₂. However, a minimum collapsed length in Fig. 3(C) is ca. 30 nm, which is much larger then a folded length of ca. 10 nm, which would have been obtained for two folded I27 modules with linkers. Furthermore, only an entropic extension of the polymer chain is visible during the last, re-unfolding experimental stage.

We notice that larger molecular stiffness values obtained in the stretched and unfolded regimes are connected with substantially larger friction coefficients. This is expected, since the same power-law dependence on force, via F^3/2, has been predicted for molecular stiffness and internal friction coefficients at high stretching force for the polymers described via the WLC chain model with bending friction, i.e., the friction described by local curvature fluctuations of the chain.¹⁸ In WLC model applied to proteins, the chain links have the size p, which corresponds to a size of an amino acid along the protein backbone. The peptide bond is known to be between single and double bond, and consequently it is stiffer than any carbon–carbon bonds. Thus, stiff areas around the peptide bonds are connected through α-carbons (C_α) along the protein backbone and curvature fluctuations of the backbone arise mostly from the motion of the side chains. However, vibrations of each C_α are bound by the limiting dihedral angles for each type of the secondary and tertiary structures within folded proteins and by dihedral angle isomerisations within unfolded structures. Consequently, as also expected from other models, such as Rouse models with internal friction, the time scales for dihedral angle isomerisations sets the bound on the internal friction. Interestingly, Khatri et al. have derived as well that pure bending of the WLC chain at the linking points would lead to a weaker force dependence of internal friction, i.e., via F^1/2, than in the case of chain stiffness proportional to F^3/2. An appropriate force-dependence can be verified by extending our work to highly stretched proteins.

Excluding high stretching zones, our molecular stiffness values agree with previously observed results. In particular, the elastic spring constant for a folded I27₄ has been previously measured to be between several pN nm⁻¹ to a few tens of pN nm⁻¹.^18,40,41 Noteworthy, these values are of the same order of magnitude as the spring constant of the cantilever, here: ca. 7 pN nm⁻¹, which – due to chosen model – did not interfere within the calculations, apart of protein length calibration, where the cantilever's displacement had to be subtracted from the measured piezo extension.

Friction coefficients of I27₅ proteins have been estimated so-far from the FX-SMFS measurements by Kawakami et al. using a simple harmonic oscillator model.²⁷ Values between almost zero to 100 × 10⁻⁹ kg s⁻¹ has been obtained therein within the folded regime, and up to 300 × 10⁻⁹ kg s⁻¹ has been observed in the highly stretched regime. These are very similar values as the ones we observe, but herein, we can calculate them very precisely and associate them with a particular position along the unfolding and refolding trajectory, which is a major advancement. Based on earlier developments these authors suggested that internal friction coefficients in the stretched regime are expected to be smaller than in the folded regime. If true, this is contrary to our observations. Consequently, it is an indicator that the friction coefficients we observe are in most parts originating from the protein–solvent interactions. This is because solvent–protein interactions are expected to be less within the collapsed states than in the stretched state due to smaller solvent-accessible surface area in the collapsed state.

Dihedral angle isomerisations have been found as the main source of internal friction in the case of helical peptides.²² Supposing that similar mechanisms would contribute to measured here friction coefficients, at least in the unfolded states, one can estimate roughly such a contribution from the following assumptions. Global friction coefficients calculated in water for ALA4 and ALA21 peptides from their equilibrium (un)folding molecular dynamics simulations yielded values of γ_g of 1.76 and 47.0 × 10⁻⁹ kg s⁻¹, respectively. These coefficients did not scale straightforwardly with the backbone length, but observing roughly the same factor of contour lengths between stretched ALA21 and ALA4 as between stretched I27 and ALA21, one obtains about 110 × 10⁻⁹ kg s⁻¹ of friction coefficient for a mechanically extended I27 molecule. Stretching this argument further one would expect about four times more in the unfolded region of I27₄ in Fig. 3(B) and about two times more in the unfolded region of I27₂ presented in Fig. 3(D). This is pretty much what is observed in our data in the unfolded zones, which suggests similar origins of friction coefficients in the unfolded parts for the compared cases, and points out again towards contributions from the solvent–protein friction. Solvent–protein friction in the case of α-helical peptides in water has been estimated to produce up to 100% difference between the values of internal friction and (global) friction coefficient in water.²² However, if one would like to estimate the global friction coefficient in the case of I27₄ using an analytical approach derived in the case of α-helical peptides^21,22 one obtains a value of 2.23 × 10⁻⁴ kg s⁻¹.⁴² This is three orders of magnitude larger than values observed herein. Consequently, the meaning of γ_g is not clear yet in the case of β-type proteins, and its calculations derived in the case of α-helical peptides cannot be applied in our current study. However, future measurements of friction coefficient in solvents of different viscosities, such as osmolytes interacting with I27 folding to the least extent, are expected to yield contributions originating from the solvent–protein interactions.

From our data on the I27 tetramer, see Fig. 3(A) and (B), and dimer, Fig. 3(C) and (D), one can also draw useful conclusions about a monomer. Excluding a highly stretched regime one readily finds that stiffness for a fully unfolded I27₄ within a tensile force range 50–150 pN – being between 3 and 12 pN nm⁻¹ (mean of 7.5 pN nm⁻¹) is almost half of that for a fully unfolded I27₂ – being between 10 and 30 pN nm⁻¹ (mean of 20 pN nm⁻¹). This suggests that stiffnesses of the modules add up like capacitances connected in series, i.e., via their inverses. Thus, a particular stiffness of an individual module is estimated to be between 20 and 40 pN nm⁻¹. All of these depend on an actual applied force, as exemplified by eqn (5). In the contact region, for a folded I27₄ one gets less than 1 pN nm⁻¹, for a collapsed I27₂ less than 2 pN nm⁻¹, so that for a monomer one expects less than 4 pN nm⁻¹. However, I27₂ is not fully folded within this regime. Similar observations relate to friction coefficients. In the vicinity of 100 pN tensile force, its values are between 50 and 150 μg s⁻¹ for I27₄ and between 100 and 300 μg s⁻¹ for I27₂. Thus, values between 200 and 600 μg s⁻¹ are expected for an unfolded I27 monomer. It is less evident – due to uncertainties – to conduct such an analysis within the folded case, but one gets values around 50 μg s⁻¹ for I27₄ and around 100 μg s⁻¹ for I27₂, which suggests values around 200 μg s⁻¹ for a single I27 molecule.

The estimates for the folded I27 monomer can be compared with the recent results of Deopa et al.²⁹ performed under a force-extension mode, where actual force had to be integrated and reconstructed. To do so they used interferometry together with small amplitude off-resonance measurements. An expected stiffness of the folded I27 monomer at 15 pN stretching forces was estimated here to be around 4 pN nm⁻¹, which is at least 10× less than the results obtained by Deopa et al. being between 50 and 150 pN nm⁻¹. In the case of internal friction coefficients Deopa et al. obtained values between 1000 and 4000 μg s⁻¹, while we estimated it to be around 200 μg s⁻¹. However, Deopa et al. calculated their values of stiffness and internal friction coefficient for a single I27 domain at much higher tensile forces ranging between 120 and 190 pN than us. Stiffness depends non-linearly on force, and at their high tensile forces, stiffness can indeed reach values of 10× more (and larger) than the one estimated from our results at 15 pN stretching forces. Regarding friction coefficients, already dihedral angle isomerisation events alone dissipate much more energy at large tensile forces than at low tensile forces. Therefore, it is expected that Deopa et al. obtained much larger values of internal friction coefficients for the folded state at high stretch than in our work.

Finally, we observed some fluctuations of stiffness and friction along the folding trajectories. Ensemble of transient, random-coiled states RC_f, present during force-quenched I27 refolding was predicted from the coarse-grained folding simulations of I27 molecule by Li et al.⁴³ Thus, spikes in friction coefficient observed along the folding trajectories might relate to these states. More studies are needed, however, to relate elastic properties of the RC_f ensemble to the results of our study.^44–48

Conclusions

Herein, a complete distributed mass AFM cantilever model introduced by Dupas et al.³⁵ has been adopted and coupled with a Kelvin–Voight description of the protein to measure viscoelastic properties of single protein molecules in FQ-AFM studies of their mechanical unfolding and refolding. Next we applied this model to report changes of the protein stiffness and friction coefficients for the single unfolding and refolding trajectories of I27_x molecules. This has been performed using the FQ-AFM experiments with ca. 0.5 s temporal resolution for each reading of molecular stiffness and friction coefficients. We used the WLC model to calculate independently molecular stiffness values, so that to fit only the values of friction coefficients.

Within a tensile force range 50–150 pN we obtained molecular stiffness to be between 1 and 5 pN nm⁻¹ for a fully unfolded I27₄ and between 10 and 20 pN nm⁻¹ for a fully unfolded I27₂. In the vicinity of 100 pN tensile force, the values of friction coefficients were between 50 and 150 μg s⁻¹ for I27₄ and between 100 and 300 μg s⁻¹ for I27₂. Molecular stiffness in the folded region of I27₄ was less than 2 pN nm⁻¹ with one spike at around 6 pN nm⁻¹; and in the collapsed region of I27₂ its values were between 2 and 5 pN nm⁻¹. Related values of friction coefficients in the folded/collapsed zones were around 50 μg s⁻¹ for I27₄ (with one spike at around 130 μg s⁻¹) and around 100 μg s⁻¹ for I27₂.

By comparing these results with predictions based on polymer models and with recent calculations of internal friction in the case of α-helical peptides, we suggested that obtained here values of friction coefficients are dominated by water–protein interactions rather than by the internal protein friction. This would need to be addressed via high-bandwidth FQ-AFM measurements at various concentrations of osmolytes.

Our derivations are expected to provoke additional developments, such as validations of the polymer physics models describing highly stretched proteins. The analysis can also readily be expanded to include more AFM cantilever resonances, and thus to probe mechanical signature of a folding protein in a greater detail, i.e., to yield its normal and lateral dissipation properties. This is within the current technological reach, but higher resonance modes are more noisy and such measurements would hinge on faster and less noisy SMFS spectrometers.

Data availability

The data accompanying this paper will be available at the institutional repository at the University of Warsaw.

Author contributions

RS was the sole author of this paper.

Conflicts of interest

There are no competing interests to declare.

Acknowledgements

The work was supported by the National Science Center, Poland, with a grant number 2018/30/M/ST4/00005. The open access payment was supported by the UW Statuary Funds from the IDUB programme. The author thanks a former group of Prof. J. Fernandez for a gift of a pQE30-I27 gene and Dr Nicoletta Ploscariu for experimental help.

Notes and references

1. F. Chiti and C. M. Dobson, Protein misfolding, functional amyloid, and human disease, Annu. Rev. Biochem., 2006, 75, 333–366.
2. D. Thirumalai, D. K. Klimov and R. I. Dima, Emerging ideas on the molecular basis of protein and peptide aggregation, Curr. Opin. Struct. Biol., 2003, 13, 146–159.
3. C. D. Kocher and K. A. Dill, Origins of life: The Protein Folding Problem all over again?, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(34), e2315000121,  DOI:10.1073/pnas.2315000121.
4. L. E. Kay, NMR studies of protein structure and dynamics, J. Magn. Reson., 2011, 213(2), 477–491.
5. H. Roder, K. Maki and H. Cheng, Early Events in Protein Folding Explored by Rapid Mixing Methods, Chem. Rev., 2006, 106(5), 1836–1861,  DOI:10.1021/cr040430y , pMID: 16683757..
6. A. K. Dhillon, et al., Raman spectroscopy and its plasmon-enhanced counterparts: a toolbox to probe protein dynamics and aggregation, Wiley Interdiscip. Rev.:Nanomed. Nanobiotechnol., 2023, e1917,  DOI:10.1002/wnan.1917.
7. L. A. Earl, V. Falconieri, J. L. Milne and S. Subramaniam, Cryo-EM: beyond the microscope, Curr. Opin. Struct. Biol., 2017, 46, 71–78.
8. H. Ma, X. Jia, K. Zhang and Z. Su, Cryo-EM advances in RNA structure determination, Signal Transduction Targeted Ther., 2022, 7(1), 1–6,  DOI:10.1038/s41392-022-00916-0 , https://www.nature.com/articles/s41392-022-00916-0.
9. S. A. Hollingsworth and R. O. Dror, Molecular Dynamics Simulation for All, Neuron, 2018, 99(6), 1129–1143,  DOI:10.1016/j.neuron.2018.08.011 , https://linkinghub.elsevier.com/retrieve/pii/S0896627318306846.
10. J. Jumper, et al., Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596(7873), 583–589,  DOI:10.1038/s41586-021-03819-2 , https://www.nature.com/articles/s41586-021-03819-2.
11. S.-J. Chen, et al., Protein folds vs. protein folding: differing questions, different challenges, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(1), e2214423119,  DOI:10.1073/pnas.2214423119.
12. J. M. Fernandez and H. Li, Force-Clamp Spectroscopy Monitors the Folding Trajectory of a Single Protein, Science, 2004, 303(5664), 1674–1678,  DOI:10.1126/science.1092497.
13. J.-H. Han, S. Batey, A. A. Nickson, S. A. Teichmann and J. Clarke, The folding and evolution of multidomain proteins, Nat. Rev. Mol. Cell Biol., 2007, 8, 321–330.
14. M. Carrion-Vazquez, et al., Mechanical design of proteins studied by single-molecule force spectroscopy and protein engineering, Prog. Biophys. Mol. Biol., 2000, 74(1), 63–91,  DOI:10.1016/S0079-6107(00)00017-1 , https://www.sciencedirect.com/science/article/pii/S0079610700000171.
15. S. B. Fowler, et al., Mechanical Unfolding of a Titin Ig Domain: Structure of Unfolding Intermediate Revealed by Combining AFM, Molecular Dynamics Simulations, NMR and Protein Engineering, J. Mol. Biol., 2002, 322(4), 841–849,  DOI:10.1016/S0022-2836(02)00805-7 , https://www.sciencedirect.com/science/article/pii/S0022283602008057.
16. H. Chen, et al., Dynamics of Equilibrium Folding and Unfolding Transitions of Titin Immunoglobulin Domain under Constant Forces, J. Am. Chem. Soc., 2015, 137(10), 3540–3546,  DOI:10.1021/ja5119368 , pMID: 25726700..
17. K. Małek and R. Szoszkiewicz, Changes of protein stiffness during folding detect protein folding intermediates, J. Biol. Phys., 2014, 40, 15–23,  DOI:10.1007/s10867-013-9331-y.
18. B. S. Khatri, et al., Internal friction of single polypeptide chains at high stretch, Faraday Discuss., 2008, 139, 35–51.
19. A. Borgia, P. M. Williams and J. Clarke, Single-molecule studies of protein folding, Annu. Rev. Biochem., 2008, 77, 101–125.
20. D. de Sancho, A. Sirur and R. B. Best, Molecular origins of internal friction effects on protein-folding rates, Nat. Commun., 2014, 5(1), 4307,  DOI:10.1038/ncomms5307 , https://www.nature.com/articles/ncomms5307.
21. A. Wosztyl, K. Kuczera and R. Szoszkiewicz, Analytical Approaches for Deriving Friction Coefficients for Selected α-Helical Peptides Based Entirely on Molecular Dynamics Simulations, J. Phys. Chem. B, 2022, 126(44), 8901–8912,  DOI:10.1021/acs.jpcb.2c03076.
22. A. Świątek, K. Kuczera and R. Szoszkiewicz, Effects of Proline on Internal Friction in Simulated Folding Dynamics of Several Alanine-Based α-Helical Peptides, J. Phys. Chem. B, 2024, 128, 3856–3869,  DOI:10.1021/acs.jpcb.4c00623.
23. M. Carrion-Vazquez, et al., Mechanical design of proteins-studied by single-molecule force spectroscopy and protein engineering, Prog. Biophys. Mol. Biol., 2000, 74, 63–91.
24. H. Dietz, F. Berkemeier, M. Bertz and M. Rief, Anisotropic deformation response of single protein molecules, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12724–12728.
25. S. Improta, A. S. Politou and A. Pastore, Immunoglobulin-like modules from titin I-band: extensible components of muscle elasticity, Structure, 1996, 4, 323–337.
26. H. Lu, B. Isralewitz, A. Krammer, V. Vogel and K. Schulten, Unfolding of Titin Immunoglobulin Domains by Steered Molecular Dynamics Simulation, Biophys. J., 1998, 75(2), 662–671,  DOI:10.1016/S0006-3495(98)77556-3 , https://www.sciencedirect.com/science/article/pii/S0006349598775563.
27. M. Kawakami, K. Byrne, D. J. Brockwell, S. E. Radford and D. A. Smith, Viscoelastic Study of the Mechanical Unfolding of a Protein by AFM, Biophys. J., 2006, 91(2), L16–L18,  DOI:10.1529/biophysj.106.085019 , https://www.sciencedirect.com/science/article/pii/S0006349506717398.
28. M. Muddassir, et al., Single-molecule force-unfolding of titin I27 reveals a correlation between the size of the surrounding anions and its mechanical stability, Chem. Commun., 2018, 54, 9635–9638,  10.1039/C8CC05557B.
29. S. Deopa, S. Rajput, A. Kumar and S. Patil, Direct and Simultaneous Measurement of the Stiffness and Internal Friction of a Single Folded Protein, J. Phys. Chem. Lett., 2022, 13, 9473–9479,  DOI:10.1021/acs.jpclett.2c02257.
30. J. M. Fernandez and H. B. Li, Force-clamp spectroscopy monitors the folding trajectory of a single protein, Science, 2004, 303, 1674–1678.
31. I. Herrada, et al., Monitoring Unfolding of Titin I27 Single and Bi Domain with High-Pressure NMR Spectroscopy, Biophys. J., 2018, 115, 341–352.
32. M. Mori, X. Liang and K. Nakajima, Application of Thermal Noise Analysis to Viscoelasticity Measurements of Single Polymer Chains using AFM with High-Tip Cantilever, e-J. Surf. Sci. Nanotechnol., 2023, 21, 224–230.
33. U. Rabe, K. Janser and W. Arnold, Vibrations of free and surface-coupled atomic force microscope cantilevers: theory and experiment, Rev. Sci. Instrum., 1996, 67, 3281–3293.
34. P.-E. Mazeran and J.-L. Loubet, Normal and lateral modulation with a scanning force microscope, an analysis: implication in quantitative elastic and friction imaging, Tribol. Lett., 1999, 7, 199–212.
35. E. Dupas, G. Gremaud, A. Kulik and J. L. Loubet, High-frequency mechanical spectroscopy with an atomic force microscope, Rev. Sci. Instrum., 2001, 72, 3891–3897.
36. N. Ploscariu and R. Szoszkiewicz, A method to measure nanomechanical properties of biological objects, Appl. Phys. Lett., 2013, 103(26), 263702,  DOI:10.1063/1.4858411.
37. A. Dey and R. Szoszkiewicz, Complete noise analysis of a simple force spectroscopy AFM setup and its applications to study nanomechanics of mammalian Notch 1 protein, Nanotechnology, 2012, 23, 175101–175115.
38. A. Khan, J. Philip and P. Hess, Young's modulus of silicon nitride used in scanning force microscope cantilevers, J. Appl. Phys., 2004, 95, 1667–1672.
39. Electrostatic forces are greatly reduced in water and double layer forces start to play a role at very short distances of several nanometers.
40. M. Rief, M. Gautel, F. Oesterhelt, J. M. Fernandez and H. E. Gaub, Reversible unfolding of individual titin immunoglobulin domains by AFM, Science, 1997, 267, 1109–1112.
41. Y. Taniguchi, B. S. Khatri, D. J. Brockwell, E. Paci and M. Kawakami, Dynamics of the coiled-coil unfolding transition of myosin rod probed by, Biophys. J., 2010, 99, 257–262.
42. See ESI†.
43. M. S. Li, C. K. Hu, D. K. Klimov and D. Thirumalai, Multiple stepwise refolding of immunoglobulin domain I27 upon force quench depends on initial conditions, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 93–98.
44. Y. Taniguchi, D. J. Brockwell and M. Kawakami, The Effect of Temperature on Mechanical Resistance of the Native and Intermediate States of I27, Biophys. J., 2008, 95(11), 5296–5305,  DOI:10.1529/biophysj.108.141275 , https://www.cell.com/biophysj/abstract/S0006-3495(08)78954–9.
45. M. Carrion-Vazquez, et al., Mechanical and chemical unfolding of a single protein: a comparison, Proc. Natl. Acad. Sci. U. S. A., 1999, 96(7), 3694–3699,  DOI:10.1073/pnas.96.7.3694.
46. S. B. Fowler and J. Clarke, Mapping the Folding Pathway of an Immunoglobulin Domain: Structural Detail from Phi Value Analysis and Movement of the Transition State, Structure, 2001, 9(5), 355–366,  DOI:10.1016/S0969-2126(01)00596-2 , https://www.cell.com/structure/abstract/S0969-2126(01)00596-2.
47. P. E. Marszalek, et al., Mechanical unfolding intermediates in titin modules, Nature, 1999, 402(6757), 100–103,  DOI:10.1038/47083 , https://www.nature.com/articles/47083.
48. F. Rico, L. Gonzalez, I. Casuso, M. Puig-Vidal and S. Scheuring, High-Speed Force SpectroscopyUnfolds Titin at theVelocity of Molecular Dynamics Simulations, Science, 2013, 342(6159), 741–743,  DOI:10.1126/science.1239764.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary text and Fig. S1. See DOI: https://doi.org/10.1039/d4ra08047e

---