Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First principles study of double perovskites Li2AgAsX6 (X = Cl, Br, I) for optoelectronic and thermoelectric applications
Ghulam M. Mustafa a,
Bisma Younas
a,
Bisma Younas *b,
Ahmad Ayyaz
*b,
Ahmad Ayyaz c,
A. I. Aljameeld,
Saud Alotaibi*e,
S. Bouzgarroufg,
Syed Kashif Alih,
Q. Mahmoodij,
Imed Boukhrisk and
M. S. Al-Buriahil
c,
A. I. Aljameeld,
Saud Alotaibi*e,
S. Bouzgarroufg,
Syed Kashif Alih,
Q. Mahmoodij,
Imed Boukhrisk and
M. S. Al-Buriahil
aDepartment of Physics, Division of Science and Technology, University of Education, Lahore, Punjab 54770, Pakistan
bDepartment of Physics, The University of Lahore, Lahore, Pakistan. E-mail: bismayounas55@gmail.com
cCentre for Advanced Studies in Physics, GC University, Lahore, 54000, Pakistan
dDepartment of Physics, College of Science, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh 11623, Saudi Arabia
ePhysics Department, Faculty of Science and Humanities in Ad-Dawadmi, Shaqra University, Shaqra 11911, Saudi Arabia. E-mail: Saud@su.edu.sa
fDepartment of Physics, College of Science, Qassim University, P. O. 64, Buraidah, Saudi Arabia
gLaboratoire de Microélectronique et Instrumentation (UR03/13-04), Faculté des Sciences de Monastir, Avenue de l’Environnement, 5000 Monastir, Tunisia
hDepartment of Physical Sciences, Chemistry Division, College of Science, Jazan University, P.O. Box. 114, Jazan 45142, Saudi Arabia
iDepartment of Physics, College of Science, Imam Abdulrahman Bin Faisal University, P. O. Box 1982, Dammam, 31441, Saudi Arabia
jBasic and Applied Scientific Research Center, Imam Abdulrahman Bin Faisal University, P. O. Box 1982, Dammam, 31441, Saudi Arabia
kDepartment of Physics, Faculty of Science, King Khalid University, P. O. Box 9004, Abha, Saudi Arabia
lDepartment of Physics, Sakarya University, Sakarya, Turkey
First published on 17th February 2025
Abstract
The present communication aims to provide a theoretical examination of the structural, electronic, optical, transport, and mechanical characteristics of Li2AgAsX6 (X = Cl, Br, I) to check their potential for optoelectronic and thermoelectric applications. The structural analysis reveals their cubic symmetry, and their structural and thermodynamic stability is verified through assessments of their tolerance factors (0.96, 0.94, and 0.93) and formation energies (−3.63, −3.10, and −2.16 eV). Their mechanical stability and ductile nature are confirmed using elastic constants, Poisson's ratio, and Pugh's criterion. Analysis of the band structure exhibits bandgaps of 0.86, 0.56, and 0.22 eV for Cl-, Br- and I-based compositions. Analysis of their optical behavior is carried out in terms of complex dielectric constant, complex refractive index, optical conductivity, reflectivity, and loss, providing better insight into material characteristics. The highest absorption in the infrared region underscores their prospects as infrared detectors. Additionally, the materials exhibit high electrical conductivity, and ultra-low lattice thermal conductivity with a considerable figure of merit, highlighting their feasibility for thermoelectric devices.
1. Introduction
Optoelectronic devices have the potential to transform different aspects of civilization and modern industry by improving energy production, healthcare, and scientific research.1 Their ability to manipulate light with high precision is a gateway to innovation and revolution in different fields. Optoelectronics is key to advancing renewable energy solutions and storage systems. Optoelectronic devices in the IR range represent the most crucial element. This spectral domain includes wavelengths longer than visible light and is useful in various applications due to its properties and abilities.2 Furthermore, IR optoelectronic devices are good candidates for new applications, for instance, photonics and quantum computing, which will stimulate the creation of new technologies and products and the development of technologies based on IR spectroscopy. Overall, the technical advances signify that the role and application of IR optoelectronic devices will increasingly find their niche, establish new trends, and pave a brand-new path in the future. In IR optoelectronics, double perovskite materials showed signs of stimulation and potentiality.3,4 These materials have great potential to enhance the efficiency and operation of devices working in the IR region of the electromagnetic spectrum because of their unique band structure and optoelectronic properties.5Double perovskite materials are highly flexible in terms of their structures and they possess several interesting characteristics, suggesting they may be promising candidates for use in optoelectronics.6 These compounds have the formula A2BB′X6, where A is often a large cation, B and B′ are various transition metal cations, and X is an anion that may be oxygen or a halogen. These materials have amazing structural characteristics, which are correlatively connected with different physical characteristics. They can vary their behavior due to their chemical nature, allowing researchers to adapt their characteristics to fit the intended purpose. The optical properties of double perovskites revolve around their flexibility in capturing one of the most stimulating elements.7 These materials exhibit a wide range of optical properties, including photoluminescence, absorption, and emission, that can be modified by doping level, composition, or crystal structure.8,9 The optical properties of these materials are a key starting point for advancing new multi-functional optoelectronic applications, including photodetectors, solar cells, and light-emitting diodes (LEDs). In addition, double perovskites show remarkable thermoelectric performance, enabling them to efficiently convert heat into electrical power.10 To be a good thermoelectric contender, a material must have low thermal conductivity, high electrical conductivity, and a high Seebeck coefficient.11 Due to these materials having such characteristics, they can be used in waste heat recovery, solid-state cooling, and power generation, which is pivotal in the search for a sustainable energy source.12
Researchers are investing significant time studying the prospects of using double perovskites in optoelectronics because of their adjustable bandgap properties and prospects for application in LEDs, photodetectors, and solar cells. These materials represent several opportunities for the development of optoelectronics, as they present unique behavior to solve the challenges related to efficient light emission, absorption, and energy conversion. For instance, Abbas et al. studied Li2AgGaX6 (X = Cl, Br, and I) double perovskites, focusing on their mechanical, optical, and transport properties, as characterized by first-principles calculations. Their work offered detailed investigations of the materials and their interactions with the environment, enhancing the understanding of several potential applications.13 In addition, Zafar et al. used DFT to analyze the transport and optoelectrical properties of K2NaTlX6 (X= Cl, Br, I) compounds for renewable energy applications. The results have provided useful information to create an integrated platform for advancing renewable energy technologies.14 Rehman et al. used DFT to analyze the structural, optoelectronic, mechanical, and thermal properties of Cs2AgBiX6 (X = Cl, Br, I) DPs for photovoltaic application. They conducted extensive studies on these materials, highlighting their inherent characteristics and ability to convert energy from sunlight. Their findings presented important information for designing and optimizing photovoltaic devices.15 Likewise, Iqbal et al. conducted DFT-based computations to observe the electrical and thermal attributes of K2AgSbX6 (X = Cl, Br) and explored their capacity for solar cell applications. Their research was fundamental for unraveling the effect of the material's behavior when subjected to different compositions, thereby providing a basis for improving solar energy conversion efficiency. The results obtained have given an excellent indication of ways to improve high-efficiency and stable solar cells with K2AgSbX6 materials.16 In their research paper, Soni et al. studied Cs2ZSbX6 (Z = Ag, Cu and X = Cl, Br, I) as possible candidates for photovoltaic devices, emphasizing their mechanical stability and light absorption properties. Their examination showed that the most prominent feature of these materials is their pronounced mechanical resistance and huge light absorption value, which establish them as prospective photovoltaic tuning samples. Their results were the building blocks for factors such as efficiency and durability for designing and developing solar energy harvesting devices.17
The current report holds enormous significance for developing optoelectronics technology, using density functional theory (DFT) to comprehensively explore the structural, electronic, optical, thermoelectric, and mechanical parameters of Li2AgAsX6 (X = Cl, Br, I) double perovskites. Integrating theoretical approximations offers significant understanding of key mechanisms leading to the performance of these materials in several optoelectronic device applications. Such holistic insight is crucial for the rational design and optimization of next-generation devices with improved functionality and efficiency.
2. Computational methodology
In the current study, we applied the density functional theory (DFT)-centered FP-LAPW process available in WIEN2k to investigate the electronic and transport response of Li2AgAsX6 (X = Cl, Br, I).18–20 Initially, lattice parameters and bulk moduli were optimized before examining the band structure with the PBEsol approximation. This approximation calculates the structural properties correctly, but fails to evaluate the bandgap accurately. Therefore, for the accuracy of the bandgap, the most versatile approach of TB-mBJ has been adopted. The energy released during optimization was applied to the Murnaghan equation of state to ascertain their ground-state properties, employing the PBEsol approach.21 Initially calculated using the mBJ potential, the optical properties were further refined using the Trans-Blaha (TB-mBJ) extension.22,23 During the initialization process, RMT × Kmax and Gmax were set to 8 and 12, respectively, with a K-mesh of 20 × 20 × 20. Energy convergence criteria were established at 10−4 Ry for self-consistent field computation. The optical response was calculated using the Kramer–Kronig expression,24 while thermoelectric properties were evaluated with BoltzTraP code.253. Results and discussion
3.1. Structural properties
To measure the ground-state parameters and ground-state energy, the crystal structures of these materials were optimized, which belong to the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space-group (no. 225).26 The optimization graphs for all these compositions are presented in Fig. 1(a–c). Each unit cell comprises ten atoms, and the structural parameters were determined by optimizing the geometry using the GGA method proposed by Perdew, Burke, and Ernzerhof.27 This optimization involves minimizing the unit cell energy relative to its volume. The figure demonstrates that increasing the volume to a certain value reduces the unit cell energy. Beyond this volume, any further increase in volume results in higher energy, indicating instability.28 The unit cell's most stable state, corresponding to minimum energy, is used for calculating the ground-state lattice parameter (ao) and bulk modulus (Bo), which are listed in Table 1.29 Table 1 shows that ao increases when X is replaced by Cl to I in Li2AgAsX6, probably because of the increasing atomic radius of X atoms from Cl to I. Similarly, Bo reduces from Cl to I because of an inverse relationship between ao and Bo. The unit cell of Li2AgAsX6 is presented in Fig. 1(d). For the thermodynamic analysis, the energy of formation (ΔHf) was computed by utilizing the following equation:
m space-group (no. 225).26 The optimization graphs for all these compositions are presented in Fig. 1(a–c). Each unit cell comprises ten atoms, and the structural parameters were determined by optimizing the geometry using the GGA method proposed by Perdew, Burke, and Ernzerhof.27 This optimization involves minimizing the unit cell energy relative to its volume. The figure demonstrates that increasing the volume to a certain value reduces the unit cell energy. Beyond this volume, any further increase in volume results in higher energy, indicating instability.28 The unit cell's most stable state, corresponding to minimum energy, is used for calculating the ground-state lattice parameter (ao) and bulk modulus (Bo), which are listed in Table 1.29 Table 1 shows that ao increases when X is replaced by Cl to I in Li2AgAsX6, probably because of the increasing atomic radius of X atoms from Cl to I. Similarly, Bo reduces from Cl to I because of an inverse relationship between ao and Bo. The unit cell of Li2AgAsX6 is presented in Fig. 1(d). For the thermodynamic analysis, the energy of formation (ΔHf) was computed by utilizing the following equation:| ΔHf = E(LiaAgbAscXd) − aELi − bEAg − cEAs − dEX | (1) |
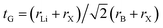 | (2) |
 | ||
| Fig. 1 Energy–volume plots for (a) Li2AgAsCl6, (b) Li2AgAsBr6, (c) Li2AgAsI6. (d) Cubic unit cell of Li2AgAsX6 (X = Cl, Br, I). | ||
| Parameter | Li2AgAsCl6 | Li2AgAsBr6 | Li2AgAsI6 |
|---|---|---|---|
| ao (Å) | 10.40 | 10.96 | 11.78 |
| B (GPa) | 33.10 | 24.99 | 25.40 |
| ΔH (eV) | −3.63 | −3.10 | −2.16 |
| tF | 0.96 | 0.94 | 0.93 |
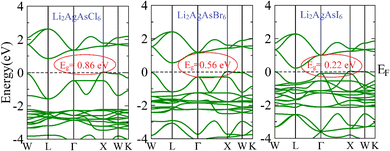
| Eg (eV) | 0.86 | 0.56 | 0.22 |
| ε1(0) | 7.50 | 9.00 | 13.12 |
| n(0) | 2.73 | 3.00 | 3.63 |
| R(0) | 0.216 | 0.250 | 0.323 |
3.2. Electronic properties
The electronic properties of the investigated compositions are analyzed through their band structures to determine the nature and value of their bandgaps and density of states (DOS) to identify their potential for electronic transitions.32 The computed band structures are shown in Fig. 2. It is observed that the edge of the valence band (VB) is positioned at the X point. In contrast, the edge of the conduction band (CB) lies at the L symmetry point, indicating the indirect bandgap nature of these semiconductors. The bandgap value for Li2AgAsCl6 is seen to be 0.86 eV, decreasing to 0.56 eV for Li2AgAsBr6 and 0.22 eV for Li2AgAsI6.33 This reduction in bandgap value can be understood based on an increase in atomic size, a decrease in electronegativity, a reduction in orbital overlap, and strong spin–orbit coupling. The small bandgap values exhibit the potential of these compositions in optoelectronic devices operating in the infrared region. The density of states (DOS) plots provide insight into the role of various elemental states in band formation and bandgap tuning. Near the Fermi level (EF), the formation of VB maxima involves primarily the d-state of Ag and the p-states of As and halides.34 In this band, the highest density of states is that of the d-states of Ag. Conversely, CB minima result from the hybridization of the d-states of Ag and the p-states of As and halogens, with the dominant contribution from the p-states of As. It is also evident from the PDOS spectra that the substitution of larger-sized halogen atoms pushes the CB minima toward the Fermi level, leading to a reduction in the bandgap of Br and I-based compositions.35 This decrease in bandgap is attributed to the increased covalent character of halide atoms surrounding B-site atoms (Fig. 3).3.3. Optical properties
The dielectric characteristics of Li2AgAsX6 (X = Cl, Br, I) are analyzed using the complex dielectric constant ε(ω) = ε1(ω) + iε2(ω) and related features. The real ε1(ω) and imaginary ε2(ω) components of these parameters probe the polarization of the material and dispersion of incident light during the interaction of light with the material.36 The computed values of all optical parameters are plotted against the energy of the incident light in Fig. 4 and 5. In Fig. 4(a), the value of ε1(ω) is plotted against the energy of incident photons, showcasing peak values at 1.73 eV for Li2AgAsCl6, 1.50 eV for Li2AgAsBr6 and 1.24 eV for Li2AgAsI6. The positions of these peaks are determined by the resonance frequency of the relaxation phenomenon present in the material. The shifting of peaks towards lower frequency with the increasing size of the halogens shows that heavier materials move slowly and have a smaller resonance frequency. In contrast, the peak height increased with an increase in the size of the halogen, which is attributed to the greater polarizability of larger-sized halogens. The static value of the real part of the dielectric constant ε1(0) is linked to the optical bandgap (Eg) via Penn's model, where ε(0) ≈ (ℏωp/Eg)2.37 Furthermore, trends observed in ε1(ω) mirror those in n(ω), indicating similar dispersive behavior and material transparency, as depicted in Fig. 4(b). The static ε1(0) and n(0) values are connected through the expression , as illustrated in Table 1.38 The peaks of n(ω) appear for Li2AgAsCl6 at 1.81 eV, for Li2AgAsBr6 at 1.50 eV, and for Li2AgAsI6 at 1.15 eV, signifying their importance in optoelectronic applications. The absorption attributes of a material are delineated by ε2(ω), as graphed in Fig. 4(c). The determination of Eg is facilitated by identifying the threshold values of ε2(ω). Notably, absorption bands within the ranges of 1.61–2.51 eV for Li2AgAsCl6, 1.46–2.30 eV for Li2AgAsBr6, and 1.0–2.1 eV for Li2AgAsI6 confirm light absorption in the infrared spectra. Substituting Cl with Br and I induce a shift in absorption bands towards lower energies, leading to a red shift from the visible to the infrared region.39 Additionally, a reduction in light energy is quantified by the absorption coefficient α(ω), as portrayed in Fig. 4(d). The absorption profile provides a wealth of information regarding the electronic and optical responses of a material and serves as a decisive parameter from the perspective of applications.40
, as illustrated in Table 1.38 The peaks of n(ω) appear for Li2AgAsCl6 at 1.81 eV, for Li2AgAsBr6 at 1.50 eV, and for Li2AgAsI6 at 1.15 eV, signifying their importance in optoelectronic applications. The absorption attributes of a material are delineated by ε2(ω), as graphed in Fig. 4(c). The determination of Eg is facilitated by identifying the threshold values of ε2(ω). Notably, absorption bands within the ranges of 1.61–2.51 eV for Li2AgAsCl6, 1.46–2.30 eV for Li2AgAsBr6, and 1.0–2.1 eV for Li2AgAsI6 confirm light absorption in the infrared spectra. Substituting Cl with Br and I induce a shift in absorption bands towards lower energies, leading to a red shift from the visible to the infrared region.39 Additionally, a reduction in light energy is quantified by the absorption coefficient α(ω), as portrayed in Fig. 4(d). The absorption profile provides a wealth of information regarding the electronic and optical responses of a material and serves as a decisive parameter from the perspective of applications.40
Fig. 5(a) presents a graph of the energy-dependent extinction coefficient k(ω), highlighting the ratio of maximum to minimum transmission energy at specific energy levels. This graph mirrors the behavior of ε2(ω) due to their connection through the Kramer–Kronig relation. Optical conductivity σ(ω), shown in Fig. 5(b), represents the electron flow within optical materials as a result of light–matter interactions.41 The pattern of σ(ω) aligns with that of α(ω) because greater absorption of energy leads to more excited electrons, leading to increased σ(ω). The plot of reflectivity R(ω), depicted in Fig. 5(c), reveals surface characteristics. According to Table 1, R(ω) values at zero energy rise when Cl is substituted by Br or I, which is attributed to their greater size and the higher number of Br and I electrons than for Cl. This results in enhanced reflectivity in the visible spectrum, indicating the compound's suitability for optoelectronic applications.42 Some energy is lost during light–material interactions through scattering, heating, and thermal agitation. This energy loss is represented by the loss function L(ω), illustrated in Fig. 5(d). Comprehensive analysis of the optical spectrum confirms that these materials exhibit maximum absorption and minimal energy loss in the visible region, making the investigated compositions highly promising for renewable energy devices.43
3.4. Thermoelectric properties
One critical parameter for assessing a material's energy harvesting capabilities is its suitable bandgap, essential in energy conversion devices. A thermoelectric material has attracted significant attention in the past due to its capability to convert waste heat into electrical energy.44 The thermoelectric characteristics of materials can be determined by utilizing the BoltzTraP code within WIEN2k software. The properties involving electrical conductivity (σ), thermal conductivity (κe), Seebeck coefficient (S), power factor (PF), specific heat capacity (Cv), κe/σ ratio, lattice thermal conductivity (κL), and figure of merit (ZT) are elaborated with BoltzTraP code. The relaxation time typically ranges between 10−13 and 10−14 s for most semiconductor materials. In this study, a value of 10−14 s is used. For an effective thermoelectric material, high values of σ and S and low values of κe are desirable.45 Fig. 6(a) illustrates the variation in electrical conductivity with temperature, showing a linear increase from 2.08/2.41/2.59 × 105 at 200 K to 2.50/2.92/3.25 × 105 (Ω m)−1 at 600 K for Li2AgAsX6 (X = Cl, Br, I). The increase in temperature provides more carriers in the CB, enhancing σ. Notably, Li2AgAsCl6 exhibits lower σ values than Li2AgAsBr6 or Li2AgAsI6 due to the smaller ionic radius and higher electronegativity of Cl, leading to stronger interactions and less mobility for charge carriers. Thermal conduction occurs through two modes: one is electrons and the other is phonons, represented by the relation κ = κe + κph, where κph and κe are the phononic and electronic thermal conductivities, respectively.46 Since BoltzTraP does not account for lattice vibration, only the electronic component of κe is considered in the present report. As demonstrated in Fig. 6(b), there is a rise in thermal conductivity (κe) with temperature. At 600 K, the observed κe values are 5.1 for Li2AgAsCl6, 5.95 for Li2AgAsBr6, and 6.92 W m−1 K−1 for Li2AgAsI6. The value of κe is smaller for Li2AgAsCl6 than for Li2AgAsBr6 or Li2AgAsI6, which is likely due to the stronger phonon scattering caused by the smaller ionic radius of Cl ions, which limits the enhancement in thermal conductivity.47 The thermal-to-electrical conductivity ratio, κe/σ, remains small at 10−5. Consequently, our calculated parameters indicate that the investigated compounds suit thermoelectric applications. The Seebeck coefficient (S) gauges potential differences relative to the temperature variance among connections between two different metals. Its plot is portrayed in Fig. 6(c). A positive value of S indicates that holes constitute the majority carriers, characterizing the studied materials as p-type semiconductors.48 At 600 K, the observed S values are 0.129, 0.120, and 0.112 for Li2AgAsCl6, Li2AgAsBr6, and Li2AgAsI6, respectively. The higher S of Li2AgAsCl6 compared to Li2AgAsBr6 or Li2AgAsI6 is attributed to the higher carrier concentration and lower electrical conductivity due to the smaller ionic radius and higher electronegativity of Cl, leading to enhanced thermoelectric performance. The power factor (PF) determines the performance of thermoelectric devices, and is reliant on σ and S2, as depicted in Fig. 6(d) with varying temperature. The PF values steadily rise from 200 K and reach peak values of 4.7/5.2/5.8 W m−1 K−2 for Li2AgAsCl6, Li2AgAsBr6, and Li2AgAsI6, respectively, at 600 K, showcasing the significance of these materials for thermoelectric devices.49The capacity of a material to endure heat is quantified by its specific heat at constant volume (CV), portrayed against temperature in Fig. 7(a). The CV value steadily increases from 0.411, 0.501, and 0.752 J mol−1 K−1 at 200 K to 0.821, 1.235, and 2.22 J mol−1 K−1 at 600 K for Li2AgAsCl6, Li2AgAsBr6, and Li2AgAsI6, respectively, underscoring their potential for future-oriented devices.50 Understanding the complex interaction of σ and κe is facilitated by the thermal-to-electrical conductivity (κe/σ) ratio, as it is challenging to disentangle the electronic component of κe from the total. The conduction of heat includes both charge carriers and lattice vibration. This ratio can be expressed as a polynomial with coefficients A0, A1, A2, A3 and A4:
| κe/σ = A0 + A1T + A2T2 + A3T3 + A4T4 | (3) |
Notably, the A1 coefficient of the linear term aligns with the Weidman–Franz law51 κe/σ = L0T where L0 = 2.44 × 10−8 (a.u.). Hence, the κe/σ ratio is exceedingly minute, of the order of 10−5, enhancing the appeal of these compounds for thermoelectric devices, as demonstrated in Fig. 7(b). To evaluate the contribution of lattice vibration to κe, values of κL are calculated and presented in Fig. 7(c). The negligible values of κL for the studied compounds confirm a minimal contribution, auguring well for the superior performance of these materials.52 At 200 K, the κL values are noted to be 0.163, 0.147, and 0.17 W m−1 K−1 for Li2AgAsCl6, Li2AgAsBr6, and Li2AgAsI6, respectively, decreasing to 0.06, 0.04, and 0.02 W m−1 K−1 at 600 K, highlighting the importance of the studied materials for futuristic thermoelectric devices.53 The figure of merit (ZT) delineates the efficiency scale of the investigated compositions for practical applications. The computed values, illustrated in Fig. 7(d) against temperature, indicate ZT values of 0.43/0.53/0.62 for Li2AgAsCl6, Li2AgAsBr6, and Li2AgAsI6, respectively, at 300 K, diminishing with increasing temperature and reaching 0.27/0.32/0.41 at 600 K. Hence, the investigated compounds exhibit exceptional thermoelectric performance at low and ambient temperatures.
3.5. Mechanical properties
The mechanical features of Li2AgAsX6 (X = Cl, Br, I) were analyzed utilizing the Chapin approach. For cubic symmetry, three elastic constants (C11, C12, and C44) are appropriate to depict mechanical response.54 The calculated elastic constant satisfies Born's conditions: C11 − C12 > 0, C44 > 0, C11 + 2C12 > 0, and C12 < Bo < C11.38 The elastic constants for Li2AgAsI6 are lower than those for Li2AgAsCl6 and Li2AgAsBr6, indicating that Li2AgAsCl6 and Li2AgAsBr6 are mechanically more stable than Li2AgAsI6. The computed bulk (B), shear (G), and Young's (Y) moduli are shown in Table 2, revealing higher values for Li2AgAsCl6, which suggests greater rigidity. The Pugh (B/G) ratio is used to differentiate between brittle (Pugh ratio less than 1.75) and ductile (Pugh ratio greater than 1.75) natures.55 The values in Table 2 indicate that the investigated compounds exhibit ductile behavior, as verified by the Poisson (ν) ratio, i.e., ν > 0.26. Comparatively, Li2AgAsBr6 is more ductile than Li2AgAsCl6 or Li2AgAsI6, as reflected in its higher Pugh and Poisson ratios. A value of A = 1 indicates the isotropic nature of a material, while deviations indicate anisotropic behavior.56 According to the values in Table 2, Li2AgAsCl6 is more anisotropic than Li2AgAsBr6 or Li2AgAsI6. The Navier equations are also scrutinized to determine the average sound velocity (vm) by separating its transverse and longitudinal components using the equations provided in ref. 57. The Debye temperature (θD) is then computed based on vm using the formula:
 | (4) |
| Tm = 553 + 5.91C11/GPa | (5) |
| Parameter | Li2AgAsCl6 | Li2AgAsBr6 | Li2AgAsI6 |
|---|---|---|---|
| C11 (GPa) | 75.35 | 50.20 | 37.96 |
| C12 (GPa) | 26.14 | 17.66 | 11.40 |
| C44 (GPa) | 21.00 | 13.20 | 8.92 |
| B (GPa) | 42.67 | 28.50 | 20.25 |
| G (GPa) | 22.44 | 14.35 | 10.46 |
| E (GPa) | 57.29 | 36.87 | 26.78 |
| B/G | 1.90 | 1.98 | 1.94 |
| ν | 0.276 | 0.284 | 0.279 |
| A | 0.84 | 0.81 | 0.67 |
| Vl (km s−1) | 4.93 | 3.47 | 2.78 |
| Vt (km s−1) | 2.74 | 1.90 | 1.54 |
| Vm (km s−1) | 3.05 | 2.12 | 1.72 |
| θD (K) | 267 | 177 | 133 |
| Tm (K) | 1000 | 850 | 777 |
| Ha (GPa) | 9.44 × 106 | 6.54 × 106 | 5.39 × 106 |
| Kmin (W m−1 K−1) | 0.197 | 0.125 | 0.088 |
The calculated Tm suggests that the investigated compositions can be fabricated at RT (Table 2). The investigation reveals that Tm is higher for Li2AgAsCl6 than for Li2AgAsBr6 or Li2AgAsI6, suggesting stronger bonding in Li2AgAsCl6 compared to the rest of the compositions. This is because of the larger ionic radius of Br and I. Moreover, the hardness of the investigated compounds is determined using the expression:
| Hv = 0.92(G/B)1.137G0.708 | (6) |
This hardness value accounts for changes in compound formation and their directional parameters, as described by Tian et al.59 for a cubic structure. The hardness values are presented in Table 2, confirming that Li2AgAsCl6 is harder than Li2AgAsBr6 or Li2AgAsI6, due to its larger shear modulus and stronger bonding. To understand the lattice dynamics, the minimum lattice conductivity Kmin of the investigated compounds is calculated using the Cahill criterion:60,61
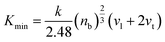 | (7) |
The Kmin values are tabulated in Table 2, indicating very low values for the investigated compounds, in agreement with κL calculated using ShengBTE code. Consequently, the lower κL and higher ZT and light energy absorption in the visible-IR range make these materials excellent contenders for renewable energy applications.
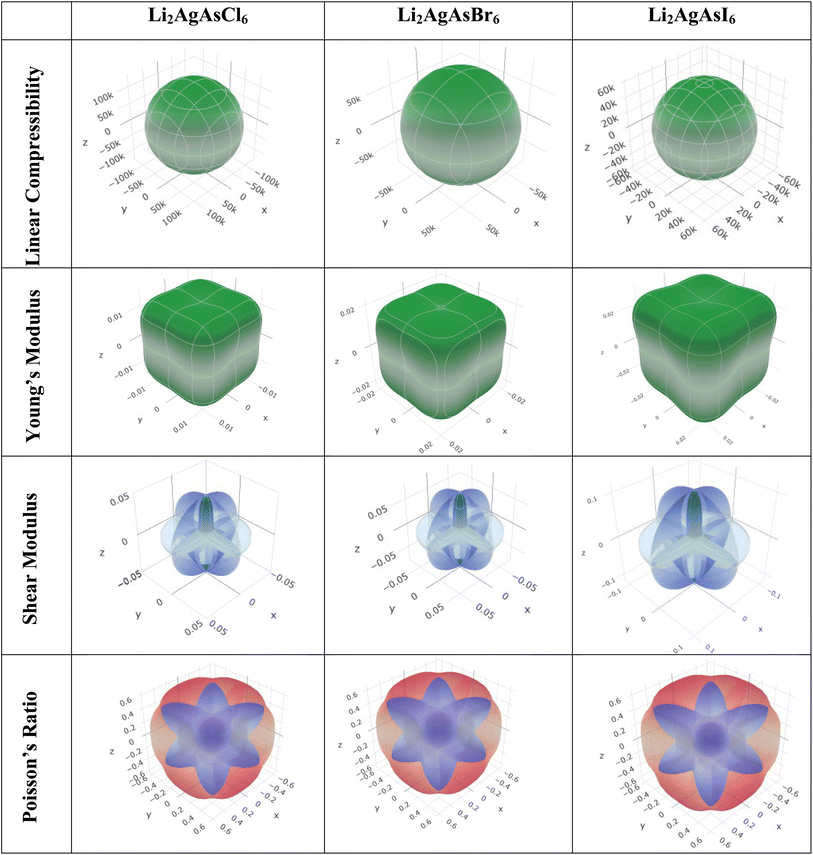
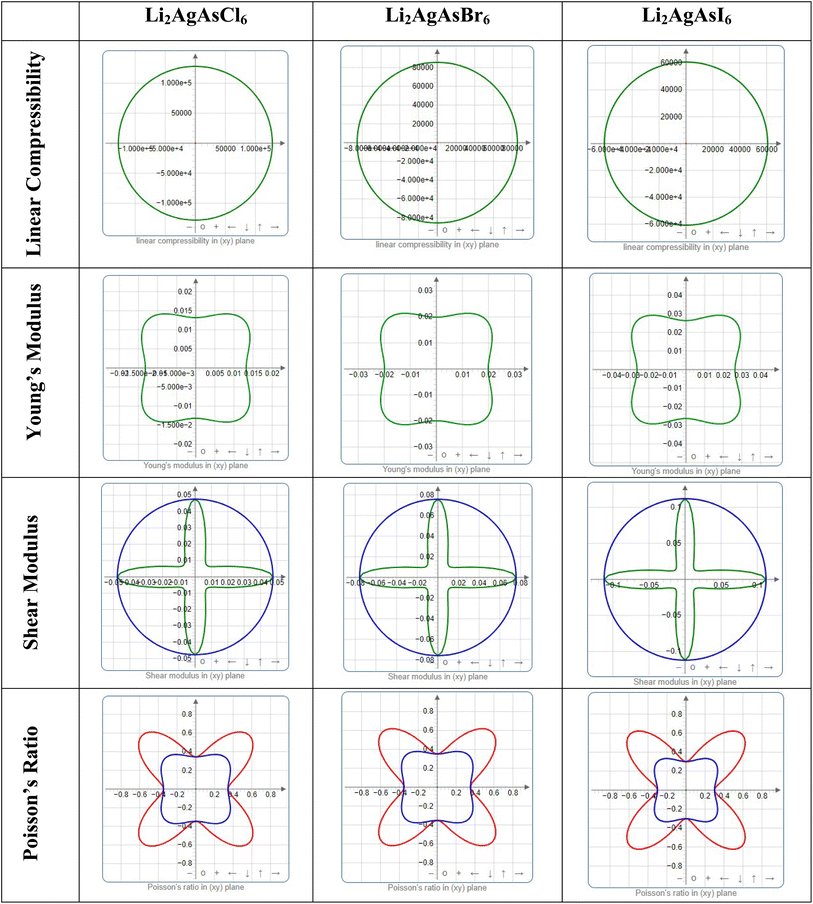
3.6. Elastic anisotropy
Elastic anisotropy represents a crucial physical attribute of a material. Anisotropic materials demonstrate variations in their chemical and physical properties with directional changes, displaying discrepancies across axes.62 In contrast, an isotropic material shows reliable performance irrespective of the direction of measurement. Fig. 8 and 9 depict 3D plots and 2D representations of linear compressibility (β), Young's (Y) and shear (G) moduli, and Poisson's (ν) ratio for Li2AgAsX6 (X = Cl, Br, I).63 A spherical 3D surface structure indicates isotropy, while deviations from a sphere indicate anisotropy, with greater deviations indicating stronger anisotropy.64 The 3D figures for Li2AgAsI6 do not resemble spheres, indicating anisotropy. Further insights into the elastic anisotropy of Li2AgAsI6 are obtained by examining the values of βmax, βmin, Ymax, Ymin, Gmax, Gmin, νmax, and νmin, with (βmax/βmin, Ymax/Ymin, Gmax/Gmin, and νmax/νmin) ratios presented in Table 3. For an isotropic material, these ratios equal 1, while for anisotropic materials, they deviate from 1, with higher ratios indicating stronger anisotropy.65 For Li2AgAsI6, βmax/βmin = 1, Ymax/Ymin = 1.6, Gmax/Gmin = 5.9, and νmax/νmin = 0.3, indicating greater anisotropy compared to Li2AgAsCl6 or Li2AgAsBr6.66| Compound | Young's modulus (Y) (GPa) | Linear compressibility (β) | Shear modulus (G) (GPa) | Poisson's ratio (ν) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ymin | Ymax | A | βmin | βmax | A | Gmin | Gmax | A | νmin | νmax | A | |
| Li2AgAsCl6 | 0.013 | 0.020 | 1.5 | 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
1 | 0.01 | 0.05 | 4.7 | −0.8 | −0.3 | 0.4 |
| Li2AgAsBr6 | 0.019 | 0.030 | 1.5 | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 520 |
85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 520 |
1 | 0.01 | 0.07 | 4.9 | −0.8 | −0.3 | 0.4 |
| Li2AgAsI6 | 0.026 | 0.43 | 1.6 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 760 |
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760 760 |
1 | 0.02 | 0.11 | 5.9 | −0.9 | −0.3 | 0.3 |
4. Conclusion
The current report investigates the structural, electronic, optical, thermoelectric, and mechanical characteristics of Li2AgAsX6 (X = Cl, Br, I) DPs utilizing WIEN2k simulation. We employed the mBJ potential within the FP-LAPW method to ensure precise calculations. The structural and thermodynamic stability of the studied compositions was confirmed by formation enthalpy values ranging from −3.63 to −2.16 eV and tolerance factors between 0.96 and 0.93. The Born's stability conditions also confirmed the structural stability of these compounds. The bandgap decreased from 0.86 eV, to 0.56 eV, and 0.22 eV when Br and I replaced Cl. This bandgap tuning within the infrared region makes Li2AgAsX6 (X = Cl, Br, I) favorable for infrared photodetector applications and as an alternative to inorganic/organic materials. Moreover, Li2AgAsI6 exhibits extensive span absorption with negligible optical loss in the visible range; as the temperature increases, σ and κe rise linearly, aligning with the observed trend in bandgap. A high S, with a low κe/σ ratio and ZT close to unity, indicate that Li2AgAsX6 (X = Cl, Br, I) show significant promise for thermoelectric power generation applications.Data availability
All data included in this study will be available on request.Conflicts of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.Acknowledgements
The author would like to thank the Deanship of Scientific Research at Shaqra University for supporting this work. The author extends their appreciation to the Deanship of Research and Graduate Studies at King Khalid University, Saudi Arabia for funding this work through Large Groups Project under grant number RGP2/518/45.References
- A. Bibi, I. Lee, Y. Nah, O. Allam, H. Kim and L. N. Quan, et al., Lead-free halide double perovskites: Toward stable and sustainable optoelectronic devices, Mater. Today, 2021, 49, 123–144 CrossRef CAS.
- T. Zuo, F. Qi, C. Yam and L. Meng, Lead-free all-inorganic halide double perovskite materials for optoelectronic applications: progress, performance and design, Phys. Chem. Chem. Phys., 2022, 24(44), 26948–26961 RSC.
- S. Ghosh, H. Shankar and P. Kar, Recent developments of lead-free halide double perovskites: a new superstar in the optoelectronic field, Mater. Adv., 2022, 3(9), 3742–3765 RSC.
- M. M. Al-Anazy, M. A. Ali, S. Bouzgarrou, G. Murtaza, T. I. Al-Muhimeed and A. A. AlObaid, et al., Study of optoelectronic and thermoelectric properties of double perovskites for renewable energy, Phys. Scr., 2021, 96(12), 125828 CrossRef.
- C. J. Bartel, J. M. Clary, C. Sutton, D. Vigil-Fowler, B. R. Goldsmith and A. M. Holder, et al., Inorganic halide double perovskites with optoelectronic properties modulated by sublattice mixing, J. Am. Chem. Soc., 2020, 142(11), 5135–5145 CrossRef CAS PubMed.
- A. Hanif, S. A. Aldaghfag, A. Aziz, M. Yaseen and A. Murtaza, Theoretical investigation of physical properties of Sr2XNbO6 (X= La, Lu) double perovskite oxides for optoelectronic and thermoelectric applications, Int. J. Energy Res., 2022, 46(8), 10633–10643 CrossRef CAS.
- H. Chen, C. R. Zhang, Z. J. Liu, J. J. Gong, W. Wang and Y. Z. Wu, et al., Vacancy defects on optoelectronic properties of double perovskite Cs2AgBiBr6, Mater. Sci. Semicond. Process., 2021, 123, 105541 CrossRef CAS.
- Z. Zhang, J. Su, J. Hou, Z. Lin, Z. Hu and J. Chang, et al., Potential applications of halide double perovskite Cs2AgInX6 (X= Cl, Br) in flexible optoelectronics: unusual effects of uniaxial strains, J. Phys. Chem. Lett., 2019, 10(5), 1120–1125 CrossRef CAS PubMed.
- A. M. Mebed, S. Al-Qaisi and M. A. Ali, Study of optoelectronic and thermoelectric properties of double perovskites Rb2AgBiX6 (X= Br, I): by DFT approach, Eur. Phys. J. Plus, 2022, 137(8), 1–8 CrossRef.
- D. Y. Hu, X. H. Zhao, T. Y. Tang, L. M. Lu, L. Li and L. K. Gao, et al., Study on the structural, electronic and optical properties of double-perovskite halides Cs2AgSbX6 (X= I, Br, Cl) based on first-principles, Mater. Sci. Semicond. Process., 2022, 152, 107077 CrossRef CAS.
- M. Saeed, I. U. Haq, S. U. Rehman, A. Ali, W. A. Shah and Z. Ali, et al., Optoelectronic and elastic properties of metal halides double perovskites Cs2InBiX6 (X= F, Cl, Br, I), Chin. Opt. Lett., 2021, 19(3), 030004 CrossRef.
- Z. Abbas, N. Iram, M. Aslam, A. Parveen, S. Al-Qaisi and S. Muhammad, et al., DFT insights for structural, opto-electronic, thermodynamic and transport characteristics of Tl2TeX6 (X= At, Br, Cl, I) double perovskites for low-cost solar cell applications, Inorg. Chem. Commun., 2024, 163, 112293 CrossRef CAS.
- S. A. Abbas, W. Tanveer, N. A. Noor, M. Aslam and A. Mahmood, Investigating the physical properties of Li2AgGaX6 (X= Cl, Br, I) double perovskites using ab initio calculations, Phys. Scr., 2024, 99(2), 025970 CrossRef CAS.
- R. Zafar, S. Naseem, S. Riaz, N. A. Noor, A. Mahmood and K. Shahzad, DFT calculations of optoelectronic and thermoelectric properties of K2NaTlX6 (X= Cl, Br, I) halide double perovskites for energy harvesting applications, Phys. Scr., 2023, 98(11), 115914 CrossRef CAS.
- M. A. Rehman, J. ur Rehman and M. B. Tahir, Density functional theory study of structural, electronic, optical, mechanical, and thermodynamic properties of halide double perovskites Cs2AgBiX6 (X= Cl, Br, I) for photovoltaic applications, J. Phys. Chem. Solids, 2023, 181, 111443 CrossRef CAS.
- M. W. Iqbal, M. Manzoor, S. Gouadria, M. Asghar, M. Zainab and N. N. Ahamd, et al., DFT insights on the opto-electronic and thermoelectric properties of double perovskites K2AgSbX6 (X= Cl, Br) via halides substitutions for solar cell applications, Mater. Sci. Eng., B, 2023, 290, 116338 CrossRef CAS.
- Y. Soni, U. Rani, A. Shukla, T. K. Joshi and A. S. Verma, Transition metal-based halides double Cs2ZSbX6 (Z= Ag, Cu, and X= Cl, Br, I) perovskites: a mechanically stable and highly absorptive materials for photovoltaic devices, J. Solid State Chem., 2022, 314, 123420 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kuasnicke and J. Luitz, Introduction to WIEN2K. An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, 2001 Search PubMed.
- P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Full-potential, linearized augmented plane wave programs for crystalline systems, Comput. Phys. Commun., 1990, 59(2), 399–415 CrossRef CAS.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- K. Fuchizaki, Murnaghan's equation of state revisited, J. Phys. Soc. Jpn., 2006, 75(3), 034601 CrossRef.
- D. Koller, F. Tran and P. Blaha, Merits and limits of the modified Becke-Johnson exchange potential, Phys. Rev. B, 2011, 83(19), 195134 CrossRef.
- S. Jiang, Y. Fang, R. Li, H. Xiao, J. Crowley and C. Wang, et al., Pressure-dependent polymorphism and band-gap tuning of methylammonium lead iodide perovskite, Angew. Chem., Int. Ed., 2016, 55(22), 6540–6544 CrossRef CAS PubMed.
- N. Singh, D. Anjum, G. Das, I. Qattan, S. Patole and M. Sajjad, Phonon dynamics and transport properties of copper thiocyanate and copper selenocyanate pseudohalides, ACS Omega, 2020, 5(44), 28637–28642 CrossRef CAS PubMed.
- D. Singh, M. Sajjad, J. A. Larsson and R. Ahuja, Promising high-temperature thermoelectric response of bismuth oxybromide, Results Phys., 2020, 19, 103584 CrossRef.
- M. Tariq, M. A. Ali, A. Laref and G. Murtaza, Anion replacement effect on the physical properties of metal halide double perovskites Cs2AgInX6 (X= F, Cl, Br, I), Solid State Commun., 2020, 314, 113929 CrossRef.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B, 1992, 45(23), 13244 CrossRef PubMed.
- R. Ullah, M. A. Ali, S. Murad, A. Khan, S. A. Dar and I. Mahmood, et al., Structural, electronic and optical properties of cubic perovskite RbYbF3 under pressure: A first principles study, Mater. Res. Express, 2019, 6(12), 125901 CrossRef CAS.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244–247 CrossRef CAS PubMed.
- B. Sabir, G. Murtaza, Q. Mahmood, R. Ahmad and K. C. Bhamu, First principles investigations of electronics, magnetic, and thermoelectric properties of rare earth based PrYO3 (Y= Cr, V) perovskites, Curr. Appl. Phys., 2017, 17(11), 1539–1546 CrossRef.
- A. E. Fedorovskiy, N. A. Drigo and M. K. Nazeeruddin, The role of Goldschmidt's tolerance factor in the formation of A2BX6 double halide perovskites and its optimal range, Small Methods, 2020, 4(5), 1900426 CrossRef CAS.
- N. H. Alotaibi, First principle study of double perovskites Cs2AgSbX6 (X= Cl, Br, I) for solar cell and renewable energy applications, J. Phys. Chem. Solids, 2022, 171, 110984 CrossRef CAS.
- Q. Mahmood, G. M. Mustafa, N. A. Kattan, T. Alshahrani, N. Sfina and A. Mera, et al., Tuning of band gap of double perovskites halides Rb2CuSbX6 (X= Cl, Br, I) for solar cells and energy harvesting, Mater. Sci. Eng., B, 2022, 286, 116088 CrossRef CAS.
- W. Shi, T. Cai, Z. Wang and O. Chen, The effects of monovalent metal cations on the crystal and electronic structures of Cs2MBiCl6 (M= Ag, Cu, Na, K, Rb, and Cs) perovskites, J. Chem. Phys., 2020, 153(14), 144704 CrossRef PubMed.
- L. Boudad, M. Taibi, A. Belayachi and M. Abd-Lefdil, Structural, morphological, dielectric, and optical properties of double perovskites RBaFeTiO6 (R= La, Eu), RSC Adv., 2021, 11(63), 40205–40215 RSC.
- Q. Mahmood, G. Nazir, S. Bouzgarrou, A. I. Aljameel, A. Rehman and H. Albalawi, et al., Study of new lead-free double perovskites halides Tl2TiX6 (X= Cl, Br, I) for solar cells and renewable energy devices, J. Solid State Chem., 2022, 308, 122887 CrossRef CAS.
- D. R. Penn, Wave-number-dependent dielectric function of semiconductors, Phys. Rev., 1962, 128(5), 2093–2097 CrossRef CAS.
- T. Zelai, S. A. Rouf, Q. Mahmood, S. Bouzgarrou, M. A. Amin and A. I. Aljameel, et al., First-principles study of lead-free double perovskites Ga2PdX6 (X= Cl, Br, and I) for solar cells and renewable energy, J. Mater. Res. Technol., 2022, 16, 631–639 CrossRef CAS.
- N. Alaal and I. S. Roqan, Tuning the electronic properties of hexagonal two-dimensional GaN monolayers via doping for enhanced optoelectronic applications, ACS Appl. Nano Mater., 2018, 2(1), 202–213 CrossRef.
- Q. Mahmood, M. H. Alhossainy, M. S. Rashid, T. H. Flemban, H. Althib and T. Alshahrani, et al., First-principles study of lead-free double perovskites Rb2TeX6 (X= Cl, Br, and I) for solar cells and renewable energy, Mater. Sci. Eng., B, 2021, 266, 115064 CrossRef CAS.
- N. A. Noor, Q. Mahmood, M. Rashid, B. U. Haq and A. Laref, The pressure-induced mechanical and optoelectronic behavior of cubic perovskite PbSnO3 via ab-initio investigations, Ceram. Int., 2018, 44(12), 13750–13756 CrossRef CAS.
- Q. Mahmood, M. Hassan, T. H. Flemban, B. U. Haq, S. AlFaify and N. A. Kattan, et al., Optoelectronic and thermoelectric properties of double perovskite Rb2PtX6 (X= Cl, Br) for energy harvesting: first-principles investigations, J. Phys. Chem. Solids, 2021, 148, 109665 CrossRef CAS.
- Y. Zhang, L. Li, W. Bai, B. Shen, J. Zhai and B. Li, Effect of CaZrO3 on phase structure and electrical properties of KNN-based lead-free ceramics, RSC Adv., 2015, 5(25), 19647–19651 RSC.
- B. U. Haq, S. AlFaify, A. Laref, R. Ahmed, F. K. Butt and A. R. Chaudhry, et al., Optoelectronic properties of new direct bandgap polymorphs of single-layered Germanium sulfide, Ceram. Int., 2019, 45(14), 18073–18078 CrossRef.
- S. Zhao, K. Yamamoto, S. Iikubo, S. Hayase and T. Ma, First-principles study of electronic and optical properties of lead-free double perovskites Cs2NaBX6 (B= Sb, Bi; X= Cl, Br, I), J. Phys. Chem. Solids, 2018, 117, 117–121 CrossRef CAS.
- M. Sajjad, Q. Mahmood, N. Singh and J. A. Larsson, Ultralow lattice thermal conductivity in double perovskite Cs2PtI6: A promising thermoelectric material, ACS Appl. Energy Mater., 2020, 3(11), 11293–11299 CrossRef CAS.
- G. Murtaza, T. Alshahrani, R. A. Khalil, Q. Mahmood, T. H. Flemban and H. Althib, et al., Lead-free double perovskites halides X2AgTlCl6 (X= Rb, Cs) for solar cells and renewable energy applications, J. Solid State Chem., 2021, 297, 121988 CrossRef CAS.
- F. Aslam, B. Sabir and M. Hassan, Structural, electronic, optical, thermoelectric, and transport properties of indium-based double perovskite halides Cs2InAgX6 (X= Cl, Br, I) for energy applications, Appl. Phys. A:Mater. Sci. Process., 2021, 127, 1–12 CrossRef.
- R. Anbarasan, M. Srinivasan, R. Suriakarthick, H. Albalawi, J. K. Sundar and P. Ramasamy, et al., Exploring the structural, mechanical, electronic, and optical properties of double perovskites of Cs2AgInX6 (X= Cl, Br, I) by first-principles calculations, J. Solid State Chem., 2022, 310, 123025 CrossRef CAS.
- M. Zanib, M. W. Iqbal, M. Manzoor, M. Asghar, R. Sharma and N. N. Ahmad, et al., A DFT investigation of mechanical, optical and thermoelectric properties of double perovskites K2AgAsX6 (X= Cl, Br) halides, Mater. Sci. Eng., B, 2023, 295, 116604 CrossRef CAS.
- Q. Mahmood, M. Hassan, M. Rashid, B. U. Haq and A. Laref, The systematic study of mechanical, thermoelectric and optical properties of lead-based halides by first-principle approach, Phys. B, 2019, 571, 87–92 CrossRef CAS.
- M. A. Khan, H. A. Alburaih, N. A. Noor and A. Dahshan, Comprehensive investigation of optoelectronic and transport properties of Cs2ScAgX6 (X= Cl, Br, I) for solar cells and thermoelectric applications, Sol. Energy, 2021, 225, 122–128 CrossRef.
- A. A. AlObaid, S. A. Rouf, T. I. Al-Muhimeed, A. I. Aljameel, S. Bouzgarrou and H. H. Hegazy, et al., New lead-free double perovskites (Rb2GeCl/Br)6; a promising material for renewable energy applications, Mater. Chem. Phys., 2021, 271, 124876 CrossRef CAS.
- Q. Mahmood, M. Rashid, M. Hassan, M. Yaseen, A. Laref and B. U. Haq, Engineering of the band gap and optical properties of InxGa1−x(As/Sb) via across composition alloying for solar cell applications using density functional theory-based approaches, Phys. Scr., 2019, 94(10), 105812 CrossRef CAS.
- X. Ji, Y. Yu, J. Ji, J. Long, J. Chen and D. Liu, Theoretical studies of the pressure-induced phase transition and elastic properties of BeS, J. Alloys Compd., 2015, 623, 304–310 CrossRef CAS.
- M. Roknuzzaman, K. Ostrikov, H. Wang, A. Du and T. Tesfamichael, Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations, Sci. Rep., 2017, 7(1), 14025 CrossRef PubMed.
- Y. J. Hao, X. R. Chen, H. L. Cui and Y. L. Bai, First-principles calculations of elastic constants of c-BN, Phys. B, 2006, 382(1–2), 118–122 CrossRef CAS.
- R. Singh and G. Balasubramanian, Impeding phonon transport through superlattices of organic–inorganic halide perovskites, RSC Adv., 2017, 7(59), 37015–37020 RSC.
- Y. Tian, B. Xu and Z. Zhao, Microscopic theory of hardness and design of novel superhard crystals, Int. J. Refract. Hard Met., 2012, 33, 93–106 CrossRef CAS.
- M. Marathe, A. Grünebohm, T. Nishimatsu, P. Entel and C. Ederer, First-principles-based calculation of the electrocaloric effect in BaTiO3: A comparison of direct and indirect methods, Phys. Rev. B, 2016, 93(5), 054110 CrossRef.
- S. Tariq, M. I. Jamil, A. Sharif, S. M. Ramay, H. Ahmad and N. Ul Qamar, et al., Exploring structural, electronic and thermo-elastic properties of metallic AMoO3 (A= Pb, Ba, Sr) molybdates, Appl. Phys. A:Mater. Sci. Process., 2018, 124, 1–8 CrossRef CAS.
- L. Qiao, Z. Jin, G. Yan, P. Li, L. Hang and L. Li, Density-functional-studying of oP8–, tI16–, and tP4–B2CO physical properties under pressure, J. Solid State Chem., 2019, 270, 642–650 CrossRef CAS.
- Z. Ma, J. Zuo, C. Tang, P. Wang and C. Shi, Physical properties of a novel phase of boron nitride and its potential applications, Mater. Chem. Phys., 2020, 252, 123245 CrossRef CAS.
- X. Li and M. Xing, Novel carbon-rich nitride C3N: A superhard phase in monoclinic symmetry, Comput. Mater. Sci., 2019, 158, 170–177 CrossRef CAS.
- Q. Fan, W. Zhang, S. Yun, J. Xu and Y. Song, III-nitride polymorphs: XN (X= Al, Ga, In) in the Pnma phase, Chem. - Eur. J., 2018, 24(65), 17280–17287 CrossRef CAS PubMed.
- W. Zhang, C. Chai, Q. Fan, Y. Song and Y. Yang, Six novel carbon and silicon allotropes with their potential application in photovoltaic field, J. Phys.: Condens. Matter, 2020, 32(35), 355701 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |