Open Access Article
Open Access ArticleDeciphering allosteric mechanisms in KRAS activation: insights from GTP-induced conformational dynamics and interaction network reorganization†
De-Rui Zhao abc,
Ji-Tong Yangd,
Meng-Ting Liu
abc,
Ji-Tong Yangd,
Meng-Ting Liu ab,
Li-Quan Yang
ab,
Li-Quan Yang *abc and
Peng Sang
*abc and
Peng Sang *abc
*abc
aCollege of Agriculture and Biological Science, Dali University, Dali 671000, China. E-mail: ylqbioinfo@gmail.com; speng431@163.com
bKey Laboratory of Bioinformatics and Computational Biology of the Department of Education of Yunnan Province, Dali University, Dali 671000, China
cCo-Innovation Center for Cangshan Mountain and Erhai Lake Integrated Protection and Green Development of Yunnan Province, Dali University, Dali 671000, China
dCollege of Basic Medical Sciences, Kunming Medical University, Kunming 650500, China
First published on 23rd January 2025
Abstract
The conformational dynamics and activation mechanisms of KRAS proteins are of great importance for targeted cancer therapy. However, the detailed molecular mechanics of KRAS activation induced by GTP binding remains unclear. In this study, we systematically investigated how GTP/GDP exchange affects the thermodynamic and kinetic properties of KRAS and explored the activation mechanism using molecular dynamics (MD) simulations, Markov state models (MSMs), and neural relational inference (NRI) models. Our MD simulation results show that GTP binding significantly enhances the conformational flexibility of KRAS, and thus promotes its transition to an active conformation with more open switch I and II regions. MSMs analyses show that KRAS in the GTP-bound state can be transitioned to the active state more efficiently during the simulation than in the GDP-bound state. In addition, NRI model calculations showed that GTP binding enhanced residue–residue interactions within the KRAS protein, especially when the long-range interactions were significantly enhanced. Furthermore, the allosteric signaling pathways from the P-loop to switch I and II as well as the key amino acid sites along the pathways were obtained using a graph-based shortest path analysis. Our results can contribute to a deeper understanding of the mechanism of KRAS allosteric activation and provide a foundation for the development of targeted therapeutic drugs to regulate KRAS activity.
1. Introduction
The small GTPase family of RAS proteins includes three major classes: KRAS, HRAS, and NRAS, which act as molecular switches to control many important cellular signaling pathways, and thus play a significant role in the regulation of cell growth, differentiation, and apoptosis.1,2 RAS proteins are active only when bound to GTP, but their intrinsic GTPase activity can hydrolyze GTP to GDP at the appropriate time, thus changing their conformation to an inactive state. On the other hand, when the RAS protein is inactive, the guanine exchange factor (GEF) can facilitate the exchange of GDP with GTP, thereby reactivating RAS by replacing GDP with GTP (Fig. 1a).3,4 The cycle of GTP hydrolysis and GDP-GTP exchange is important for maintaining the equilibrium between the active and inactive conformations of the RAS protein as well as for stabilizing the cellular pathway. However, current studies have shown that certain mutations in RAS proteins can disrupt this balance between their active and inactive states, and these mutations often result in RAS being in a persistently active state, which can lead to completely uncontrolled cell proliferation and apoptosis. To date, mutations in the RAS gene have been identified in more than 30% of human cancers, with a particularly high prevalence in pancreatic, colorectal, and lung cancers.5 Among them, KRAS has a significantly higher mutation rate than HRAS and NRAS, making it a key target for cancer therapy.6Crystallographic studies have shown that the structure of KRAS mainly consists of two parts: the effector lobe (residues 1–86) and the allosteric lobe (residues 87–166) (Fig. 1b).7 The effector lobe consists of three parts: switch I, switch II, and the P-loop (phosphate-binding loop), in which the P-loop (residues 10–17) is mainly responsible for binding to the β-phosphate of GDP or GTP, whereas switch I (residues 25–40) and switch II (residues 57–76) are essential for effector binding, and all three of them undergo a significant conformational change when nucleotides are exchanged.3,8,9 The main role of the allosteric lobe is mainly to maintain the overall stability of the protein and its interaction with regulatory proteins such as GEF and GAP, thus regulating the conformational transition between the active and inactive states of KRAS. The static structures of KRAS in the GTP-bound and GDP-bound states are distinctly different (Fig. 1c). The GTP-bound state is usually characterized by a more “open” conformation at the nucleotide binding site, a conformational feature that facilitates its interaction with downstream effectors such as RAF kinase and PI3K.10 In contrast, after hydrolysis of GTP into GDP, the switch region and P-loop rearrange the conformation to a “closed” character due to the lack of γ-phosphate groups in the switch region and the P-loop, thus reducing the ability to interact with effector proteins.10 Although the structures of KRAS in both the active (GTP-bound) and inactive (GDP-bound) states have been resolved,11,12 which can provide some static structural basis for probing the conformational state of the protein, the exact molecular mechanism by which GTP binding induces conformational changes leading to KRAS activation is still unclear.
In recent years, MD simulations have been widely used to study the conformational change of KRAS activation,13–15 and KRAS mutations, particularly at positions 12, 13, and 61, have been extensively studied due to their significant impact on KRAS dynamics. Nayak et al. demonstrated that mutations such as G12C, G12D, and G13D disrupt the normal cycling between active and inactive states, leading to persistent activation of KRAS.16 Chen et al. revealed that mutations like G12V and D33E increase the flexibility of switch I and switch II regions and alter correlated motions, affecting their interactions with GDP and GTP.17 Similarly, Jani et al. reported that mutations in the P-loop region, such as G12D and G13D, induce rigidity in KRAS and restrict its ability to transition between intermediate and active states.18 These findings highlight how oncogenic mutations perturb the structural dynamics and regulatory mechanisms of KRAS, emphasizing its critical role in cancer progression.
Although these studies have provided valuable insights for understanding its activation mechanism, the thermodynamic (conformational state distributions) and kinetic properties (rates of transitions between conformations) of KRAS during activation, as well as key molecular mechanics involved and residue networks, especially the long-range interactions and allosteric signaling pathways to switches I and II, still remain to inadequately understood.8 Exploring which amino acids play a major role in KRAS activation and how they affect the activation process is of significant importance for the development of targeted therapies against KRAS activation, especially those acting at allosteric sites.19,20
Markov state models (MSMs) are now widely used to analyze the thermodynamic and kinetic properties of conformational transitions in biomolecular systems.21–24 MSMs can decompose continuous trajectories obtained from molecular dynamics (MD) simulations into discrete states, which makes it possible to study the long-term behaviors of the system and to compute the probabilities of distributions of these states and the rates of transitions between states.25 In addition, with the development of machine learning techniques, neural relational inference (NRI) based on graph neural networks provides a new way of thinking for exploring complex biological systems.26 NRI can predict patterns of interactions by modeling relationships between entities (e.g., residues) as edges in a graph to infer dynamic relationships that are difficult to detect by traditional methods, and thus is well suited for analyzing biological complex interaction networks within macromolecules. NRI is particularly effective in identifying long-range interactions and metastable communication pathways within proteins and can help provide insight into how long-distance interactions between residues can affect the overall conformational changes of proteins through interactions.
In this study, we performed MD simulations and MSMs analyses on the GDP- and GTP-bound states of KRAS, and compared them in terms of conformational flexibility, molecular motion, thermodynamic and kinetic properties. The long-range interaction network between residues in KRAS during activation was explored by using the NRI model, and the shortest path algorithm was further used to identify the key allosteric signaling pathways during activation and the key residue sites along the pathways. Our study could provide new insights into the allosteric mechanism of KRAS activation and aid in the development of anticancer drugs targeting activation-related alias sites on KRAS.
2. Materials and methods
2.1 Structure preparation and MD simulation
The X-ray crystallographic structure of the GDP-bound KRAS was obtained from the Protein Data Bank (http://www.pdb.org/) with PDB ID 4OBE.11 It is noted that 4OBE was chosen because it represents the wild-type KRAS protein with a nearly complete sequence and possesses the highest resolution among all available GDP-bound KRAS crystal structures. Additionally, 4OBE has been widely used as a reference structure in KRAS-related studies, highlighting its reliability and suitability for comparative analysis. The structure of the GTP-bound KRAS was obtained by substituting the GDP molecule with GTP.All simulations were carried out using the GROMACS 2021.5 software package27 with the CHARMM36 force field.28 The initial structures of GDP-bound KRAS and GTP-bound KRAS were utilized as the starting configurations. Parameters for the GDP and GTP molecules were generated via the CHARMM General Force Field (CGenFF) server.29,30 The structures were then solvated using the TIP3P water model31 and placed in a dodecahedral box, ensuring a minimum distance of 1.2 nm between any protein atom and the box edge. To mimic physiological conditions, the systems were neutralized and brought to a 150 mM NaCl concentration. Energy minimization of the systems was performed using the steepest descent algorithm, followed by two phases of equilibration: a 500 ps NVT equilibration and a 300 ps NPT equilibration, both with harmonic position restraints applied to the heavy atoms of the protein using a force constant of 1000 kJ mol−1 nm−2. To enhance sampling and avoid biased conclusions,32 each system underwent 3 independent 3-μs production MD simulations. Each replica was initialized with different atomic velocities drawn from a Maxwell distribution at 300 K, totaling 9 μs of simulation time per system.
The production MD simulations were conducted with the following parameters: bond lengths were constrained using the LINCS algorithm with a 2 fs integration time step;33 long-range electrostatic interactions were computed using the particle-mesh Ewald (PME) method34 with a Fourier grid spacing of 0.135 nm and a Coulomb cut-off of 1.0 nm; van der Waals interactions were treated with the cut-off scheme at 1 nm; the temperature was maintained at 300 K using the v-rescale thermostat35 with a 0.1 ps time constant; pressure was kept at 1 atm using the Parrinello–Rahman barostat36 with a 0.5 ps time constant; and structural snapshots were saved every 10 ps.
To further investigate the role of GDP and GTP in stabilizing KRAS conformational dynamics, we performed additional MD simulations on the apo KRAS system (without GDP or GTP ligands). The initial structure of the apo KRAS was obtained by removing the GDP molecule from 4OBE. Three independent 3-μs simulations were conducted, totaling 9 μs of simulation time, under the same simulation conditions as described for the GDP- and GTP-bound systems.
2.2 Structural flexibility and molecular motion analysis
We used the following GROMACS tools to perform structural and geometrical analyses of MD trajectories: ‘gmx rms’ to determine backbone root mean square deviation (RMSD) relative to the starting structure, ‘gmx rmsf’ to determine per-residue Cα root mean square fluctuation (RMSF), ‘gmx sasa’ to determine contact area, ‘gmx mindist’ to calculate the number of native contacts (NNC), ‘gmx hbond’ to determine hbonds (HBs), and gmx energy’ to calculate the potential energy.Essential Dynamics (ED), also known as the principal component analysis (PCA) in mathematics, is widely used to extract the largest amplitude protein motions (also called collective motions or large-scale concerted motions) from an MD trajectory. A detailed mathematical description of the ED method can be found in the literature.37
In this study, ED analyses were performed on the concatenated trajectories of KRAS using the GROMACS tools gmx covar and gmx anaeig. Only the Cα atoms were included in the ED analyses. The MD trajectories were projected onto the first principal component to visualize the primary conformational changes. Porcupine plots were generated to visually represent the direction and magnitude of atomic displacements along the principal components using PyMOL.
2.3 Conformational sampling and Markov state models
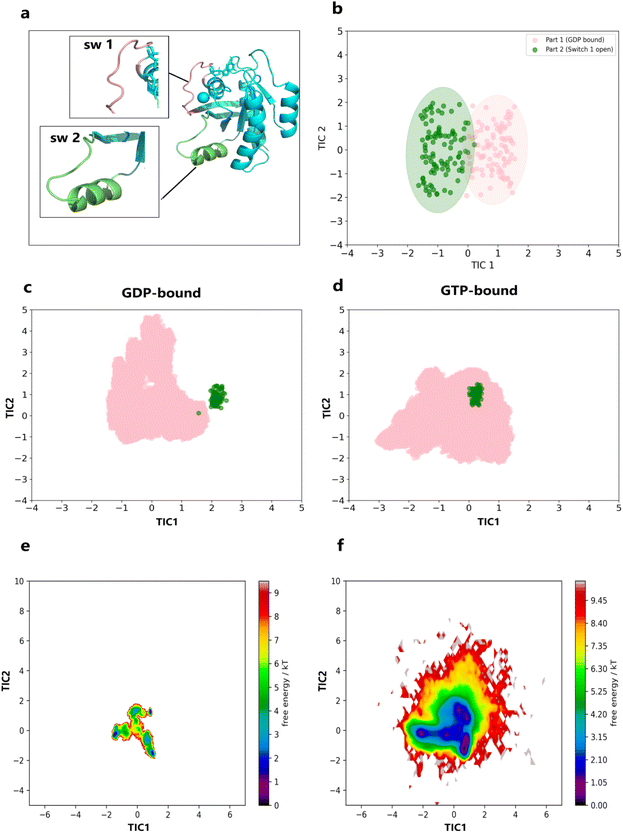
We employed the Python library PyEMMA38 to estimate conformational sampling and analyze MSMs from MD simulations. The trajectories were first featured using Cα–Cα distances between residues in the switch I and switch II regions, and dimensionality reduction was performed using Time-lagged Independent Component Analysis (TICA) with a 0.1 ns lag time to capture slow dynamics.To evaluate and compare the conformational sampling of KRAS, the combined trajectories from any two simulations were processed using TICA, and projection scatter plots were generated by projecting the structures onto the first two independent components. This method provides a visualization of the conformational state distribution, facilitating the comparison of different structural states for further analysis. It is worth noting that the reference trajectories for the inactive and active states were generated through 1 ns MD simulations of the inactive (PDB ID: 4OBE) and active (PDB ID: 6M9W) structures under the same conditions as the main simulations. The short simulation time was chosen to ensure that the resulting structures remained close to their respective inactive and active conformations.
In contrast to the conformational sampling analysis, the reduced data from TICA were further used for standard MSM analysis. The reduced data from TICA were clustered into microstates using the K-means clustering algorithm, representing distinct conformational states of KRAS. A transition matrix was constructed by calculating the transition probabilities between microstates over the selected lag time, describing the kinetics of the conformational transitions in KRAS. The microstates were further lumped into a smaller number of macrostates using the PCCA+ (Perron Cluster Cluster Analysis) algorithm,39 aiding in the identification of metastable states and their transition pathways. Validation of the constructed MSM was performed using implied timescales and the Chapman–Kolmogorov test40 to ensure that the chosen lag time and clustering scheme accurately captured the system's dynamics. The MSM was then utilized to analyze the thermodynamic and kinetic properties of the KRAS conformational transitions. Free energy landscapes41 were constructed using the first two independent components from TICA.
2.4 Neural relational inference
Neural Relational Inference (NRI)26,42 was employed to analyze the long-range interactions and allosteric communication pathways within KRAS. The NRI framework is based on neural network models designed to infer the latent interaction structure within dynamic systems. It consists of an encoder to infer a probabilistic graph of interactions from input trajectories and a decoder to predict future states of the system based on this inferred graph. The NRI python framework code used in this study was provided by Zhu et al.26,42The MD simulation trajectories, which included the three-dimensional coordinates and velocities of the Cα atoms, were used as input data. Each 3 μs trajectory, originally containing 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames, was subsampled to 5000 frames to manage computational load, ensuring uniform coverage. Each simulation system provided three independent 3 μs trajectories, treated as three separate experiments, resulting in a comprehensive dataset. To prepare the input data for the NRI model, the trajectories were featurized using the 3D coordinates and velocities of Cα atoms. The position and velocity features were standardized to a maximum absolute value of 1 to ensure consistent scaling across all input data. The featurized data were segmented into timesteps of 50 frames, with an interval of 100 frames between segments. This segmentation was crucial for capturing both short-term and long-term dynamics. The Cα atom of each residue in the KRAS protein was treated as a node in the graph neural network, with the standardized coordinates and velocities of the Cα atoms serving as input features. The interaction networks inferred by the NRI model were represented as interaction matrices, where interaction strengths (weights) between residues were identified and quantified.
000 frames, was subsampled to 5000 frames to manage computational load, ensuring uniform coverage. Each simulation system provided three independent 3 μs trajectories, treated as three separate experiments, resulting in a comprehensive dataset. To prepare the input data for the NRI model, the trajectories were featurized using the 3D coordinates and velocities of Cα atoms. The position and velocity features were standardized to a maximum absolute value of 1 to ensure consistent scaling across all input data. The featurized data were segmented into timesteps of 50 frames, with an interval of 100 frames between segments. This segmentation was crucial for capturing both short-term and long-term dynamics. The Cα atom of each residue in the KRAS protein was treated as a node in the graph neural network, with the standardized coordinates and velocities of the Cα atoms serving as input features. The interaction networks inferred by the NRI model were represented as interaction matrices, where interaction strengths (weights) between residues were identified and quantified.
The NRI model was trained using the Adam optimizer with a learning rate of 0.0005 and a batch size of 1. The learning rate was reduced by a factor of 0.5 every 200 epochs. Each model was trained for 500 epochs, with the best-performing model saved based on validation set performance. The training objective was to minimize the reconstruction error between the predicted and actual trajectories, using the mean squared error (MSE) loss function. After training, the NRI model was used to analyze the interaction networks within KRAS.
The resulting inter-domain interaction matrices were used as input data for network visualization and analysis in Cytoscape software version.43 The Py4Cytoscape package was utilized to process the network data within Cytoscape, where transparency mapping was calculated and applied based on the weight of each edge, and colors were assigned to the edges according to the color attributes of the nodes. During the network mapping process, each domain of the KRAS protein was represented as a node, while the interaction strengths (weights) between domains were defined as edges. To filter insignificant interactions, we applied a threshold of 0.2, retaining only edges with interaction strengths above this value. This threshold was chosen to balance network sparsity and information completeness. For pathway analysis, we employed Dijkstra's algorithm44 to identify the shortest paths between specified residues.The shortest paths were mapped using a combination of self-written Python scripts and visualization in PyMOL software.
3. Results
3.1 Structural flexibility and molecular motion analysis
The stability of our simulations was assessed by calculating the time-dependent backbone root mean square deviation (RMSD) values for each replica of the simulation systems (3 × 3 μs). The RMSD curves for the GDP- and GTP-bound KRAS are presented in ESI Fig. S1.† As shown in the figure, the RMSD curves indicate that both systems reached equilibrium after approximately 500 ns of simulation. To further illustrate the RMSD trends and address potential deviations between replicates, we additionally plotted the average RMSD values for each simulation group (ESI Fig. S2†). As shown in ESI Fig. S2,† the average RMSD values confirm that the GDP-bound systems exhibit lower overall fluctuations compared to the GTP-bound systems, highlighting the increased conformational flexibility induced by GTP binding.To further ensure the reliability and equilibration of the MD simulations, we performed a potential energy analysis for the GDP- and GTP-bound KRAS systems (ESI Fig. S3†). The potential energy profiles of both systems show an initial rapid decrease within the first 300 ns, reflecting the equilibration process as the systems transition to a thermodynamically stable state. After 300 ns, the energy profiles stabilize and exhibit small fluctuations around their respective mean values, indicating that both systems have reached equilibrium. Interestingly, the GTP-bound KRAS system displays slightly lower average potential energy compared to the GDP-bound system, suggesting enhanced stabilization due to the additional polar interactions introduced by the γ-phosphate group of GTP. However, the GTP-bound system also exhibits larger energy fluctuations compared to the GDP-bound state. These energy fluctuations may arise from the increased conformational flexibility observed in the GTP-bound state, particularly in the switch I and switch II regions, as revealed by following RMSF analysis.
To compare the structural flexibility of KRAS in GDP-bound and GTP-bound states, we calculated the per-residue Cα atom root mean square fluctuation (RMSF) values for the different replicas during simulations (Fig. 2a). As shown in Fig. 2a, the GTP-bound KRAS exhibits higher RMSF values across several regions, particularly in switch I, switch II, and P-loop. The overall higher flexibility for the GTP-bound state suggests that it possesses greater conformational freedom compared to the GDP-bound state, facilitating the structural changes necessary for activation. To further investigate the conformational flexibility observed in the RMSF analysis, we analyzed the secondary structure variations of KRAS residues in both GDP-bound and GTP-bound states. The results (ESI Fig. S4†) show that while the overall secondary structure remains largely stable, significant changes occur in critical regions such as switch I, switch II, and the P-loop. In the GDP-bound state, these regions maintain a more stable α-helix and β-sheet structure, consistent with a rigid conformation. In contrast, the GTP-bound state exhibits increased occurrences of turns and loop elements, particularly in the switch I and switch II regions, suggesting a transition to a more flexible and dynamic conformation. These observations are in agreement with the higher RMSF values seen in these regions, highlighting the role of GTP binding in promoting structural flexibility required for KRAS activation.
Essential dynamics (ED) analysis, also known as principal component analysis (PCA), was performed on the Cα atoms' 3D coordinates to further investigate the molecular motion patterns. The analysis revealed distinct differences between the GDP- and GTP-bound states. The motion along the first principal component (Fig. 2c) for the GTP-bound KRAS showed a tendency for the switch I and switch II regions to move apart, promoting an open conformation. In contrast, the GDP-bound KRAS exhibited movements towards a closed conformation (Fig. 2b). These results indicate that the GTP-bound KRAS favors transitions towards the active form, whereas the GDP-bound state remains in an inactive conformation.
Intramolecular interactions play a significant role in determining the conformational flexibility of proteins. To investigate the mechanism underlying the increased flexibility observed upon GTP binding, we evaluated the intramolecular interactions within the protein by calculating hydrogen bonds, native contacts, van der Waals interactions, and electrostatic energies. As shown in Table 1, the number of native contacts (NNC) and hydrogen bonds (NHB) are reduced in the GTP-bound state, indicating a more relaxed and less tightly packed structure. Additionally, the analysis of short-range electrostatic and van der Waals potential energies reveals slight increases in the GTP-bound state (Table 1). This suggests that the average distance between interacting atoms might be greater, leading to weaker interactions and a more flexible overall structure.
| Protein | NNCa | NHBb | Energy (KJ mol−1) | ||
|---|---|---|---|---|---|
| Coul-SRc | LJ-SRd | Totale | |||
| a Number of native contacts. A native contact is considered to exist if the distance between two atoms is less than 6 Å.b Number of hydrogen bonds.c Short-range electrostatic potential energy.d Short-range van der Waals potential energy.e Total potential energy. | |||||
| GDP-bound | 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017(15.6) 017(15.6) |
112(0.043) | −48880.2 | −4384.18 | −53264.38 |
| GTP-bound | 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121(3.2) 121(3.2) |
109(0.040) | −48827.3 | −4321.31 | −53148.61 |
The weakened intramolecular interactions of KRAS upon GTP binding can be attributed to the introduction of a polar phosphate group in GTP. To further explore the molecular mechanics of the conformational increase upon GTP binding, we calculated the contact area between GDP and GTP, respectively, and the KRAS. As shown in ESI Fig. S5,† GTP binding resulted in a significant increase in the total contact area compared with GDP binding, especially in the nonpolar region. Specifically, the nonpolar contact area increased from 7.165 Å2 for GDP binding to 9.865 Å2 for GTP binding, while the total contact area increased from 12.496 Å2 for GDP binding to 13.549 Å2 for GTP binding. The increase in contact area suggests that the phosphate groups in GTP cover the otherwise exposed hydrophobic regions of the KRAS surface, resulting in a weakening of the hydrophobic forces on the KRAS protein, leading to structural instability and increased conformational flexibility.
We note that using the crystal structure of the GDP-bound state directly and constructing the GTP-bound state by replacing GDP may introduce some bias. This is due to the intrinsic differences in the initial conditions of the GDP and GTP states, which may affect the direct comparison of conformational flexibility. To further validate this issue, we performed a systematic analysis of the KRAS crystal structures available in the PDB database, including 12 GDP-bound and 3 GTP-bound states, and additionally included the structures of 19 GNP (GTP analog) bound states. In addition, we supplemented the HRAS and NRAS proteins with 1 crystal structure each of the GDP- and GTP-bound states, resulting in a total of 28 crystal structures (14 GDP-bound states, 14 GTP/GNP-bound states). We performed 1 μs MD simulations of each of these structures and systematically analyzed their conformational flexibility differences. The results show that the crystal structures of the GTP-bound states do not exhibit significantly higher conformational flexibility than that of the GDP-bound states in the simulations, and some of them even show lower flexibility (ESI Fig. S6–S8†). We hypothesize that this result occurs mainly because the crystal structure represents a conformation of the protein in a low-energy steady state, where the overall structure is already more stable. In addition, the γ-phosphate group on the GTP molecule further enhances the stability of the GTP-bound state by forming additional polar interactions (e.g., hydrogen bonding and electrostatic interactions) with the P-loop, switch I, and switch II regions, leading to its overall reduced flexibility. Notably, our previous simulation results of constructing the GTP-bound state by replacing GDP actually reflect the dynamic activation process of KRAS after GTP replacement of GDP. This biological process involves a transient structural perturbation that leads to an increase in conformational flexibility and contributes to the transition of KRAS from the inactive state to the active conformation. However, this increase in flexibility is transient and the overall flexibility decreases as KRAS gradually transitions to a stable active state. Thus, our simulations capture the dynamics of a transient increase in conformational flexibility during GTP replacement of GDP, whereas the crystal structure reflects the stabilized state after activation. This difference emphasizes the dynamic nature of conformational flexibility on different time scales, rather than the “naturally” higher flexibility of the GTP-bound state.
To further validate the stabilizing effects of GDP and GTP binding on KRAS and to provide a more comprehensive comparison, we also performed MD simulations on the apo KRAS system (without GDP or GTP ligands) as a control. RMSD analysis (ESI Fig. S9†) shows that the apo KRAS system reaches a stable equilibrium during the simulations. However, RMSF analysis (ESI Fig. S10†) reveals that the apo KRAS exhibits the lowest conformational flexibility compared to the GDP- and GTP-bound systems, particularly in the switch I and switch II regions. These results suggest that both GDP and GTP binding increase KRAS flexibility, likely by destabilizing specific intramolecular interactions.
3.2 Conformational sampling and distribution
While the structural flexibility and molecular motion analyses indicated that replacing GDP with GTP in KRAS promotes a transition towards a more open, active conformation, it remains uncertain whether the GTP-bound KRAS simulations conclusively sampled active state structures. To clarify this, we generated Time-lagged Independent Component Analysis (TICA) based conformational distribution scatter plots to examine the conformational sampling and distribution of KRAS upon GTP binding (details in Methods). The active-state KRAS structure (PDB ID: 6M9W) was used as a reference for the active conformation. As described in the introduction, the primary distinction between the active and inactive states of KRAS lies in the conformational differences in the switch I and switch II regions, which are responsible for the open and closed conformations. Therefore, we selected Cα–Cα distances between residues in the switch I and switch II regions as features for our analysis (Fig. 3a). As shown in Fig. 3b, the conformational distribution scatter plot generated from the first two TICA components separates the active and inactive conformations, confirming that the selected features effectively distinguish between these two states.Given the validated effectiveness of the chosen features, the main 3 × 3 μs MD simulation trajectories were combined with the active-state structures. The projection scatter plots (Fig. 3d) revealed that the GTP-bound KRAS simulations exhibited substantial overlap with the active-state reference structures, indicating effective sampling of the active conformations. Conversely, the GDP-bound KRAS simulations showed no significant overlap with the active-state structures (Fig. 3c), demonstrating that the GDP-bound KRAS remained predominantly in the inactive state throughout the simulations. Our results indicate that the replacement of GDP with GTP in KRAS effectively promotes the transition to its active conformation. This observation is consistent with our earlier results from the structural flexibility and molecular motion analysis, which indicated higher conformational flexibility and a tendency toward the active state in the GTP-bound KRAS.
In order to gain a deeper understanding of the conformational state distribution of KRAS in the GDP-bound and GTP-bound states, we selected the first two TICA components to construct the free energy landscape (FEL) of KRAS (Fig. 3e and f). Fig. 3e shows the FEL of KRAS in the GDP-bound state, which is a narrow and deep energy basin, and it can be seen that the conformational diversity of KRAS is lower and the structure is more stable in this state. In contrast, the FEL of GTP-bound KRAS (Fig. 3f) presents a wider and shallower energy landscape, reflecting the rich conformational diversity and lower structural stability of the protein in this state.
3.3 Thermodynamics and kinetics of conformational transitions
In order to further elucidate the thermodynamic and kinetic properties of KRAS conformational transitions, we constructed MSMs for the MD trajectories of GDP- and GTP-bound KRAS, respectively. We first used the VAMP-2 score to determine the appropriate number of microstate clusters and found that the tethering equilibrium was optimal when the conformational clustering was 1000 microstates (ESI Fig. S11†). We chose the implied time scale to guide the determination of the lag time of the MSMs, and finally determined the lag time to be 3 ns, which maximizes the likelihood of capturing detailed information about the slow motion of the system while ensuring Markovianity (ESI Fig. S12†). The microstates of the two simulated systems were grouped into four macrostates using PCCA+ (Perron Cluster Cluster Analysis) as shown in Fig. 4a and b.As shown in Fig. 4, there are significant differences in the equilibrium distributions of the GDP- and GTP-bound KRAS conformational states. For example, in the GDP-bound state, the representative structure of state 4 is very similar to the simulated initial structure of the inactive conformational state, and it dominates all conformational groups, with its conformational proportion as high as 97.38%, while states 1, 2 and 3, which are more similar to the active state, together account for less than 2.5% (Fig. 4c), which suggests that the KRAS of the GDP-bound state basically maintains the inactive conformational state during the whole simulation. This conclusion is further confirmed by the mean first passage time (MFPT) analysis of the GDP-bound states, as shown in Fig. 4c, the transition times from states 1, 2, and 3 to state 4 are very short, i.e., the three conformations converging to the active state can be easily converted to the inactive state 4, whereas the corresponding inverse transition times (state 4 to the other three states) are significantly longer than those of the other three states. The corresponding reverse transition (state 4 to the other three states) time is significantly slower, i.e., the GDP-bound state of KRAS is very difficult to convert to the active state during the simulation. In contrast, the distribution of KRAS in the GTP-bound state is more balanced among multiple states, with 15.59%, 20.38%, 31.03%, and 32.99% of conformations in states 1, 2, 3, and 4, respectively (Fig. 4d), and all of them converge to the relatively open active state. Further MFPT analysis of KRAS in GTP-bound state also showed that the transition time between different states was relatively short, and the states could be easily converted to each other, indicating that GTP-bound KRAS had high conformational flexibility and conformational diversity during the simulation process, and that the binding of GTP obviously promoted the transition of KRAS to the activated state conformation.
To further compare the conformational state distributions and dynamics, we performed MSM analysis on the apo KRAS system. The apo KRAS system was decomposed into four major conformational states, with nearly equal distributions (11.69%, 20.57%, 31.12%, and 36.61%) as shown in Table S1.† Mean first passage time (MFPT) analysis revealed that the apo system exhibits significantly faster conformational transitions compared to the GDP- and GTP-bound systems, reflecting its higher dynamic transition efficiency. Notably, representative structures of the four states closely resemble the initial apo structure (derived from PDB ID 4OBE without GDP), indicating that apo KRAS predominantly adopts a non-active conformation similar to the GDP-bound state (ESI Fig. S13†).
3.4 Interaction network and allosteric pathway analysis
Although the above MSMs analyses indicate that KRAS in the GTP-bound state is more inclined to adopt an active conformation during the simulation, yet it remains unclear how the GTP replacement of GDP activates KRAS through allosteric signaling to the switch region. To further investigate the molecular mechanics of KRAS activation by GTP, we used the neural inference relationship (NRI) method to analyze the changes in the internal residue–residue and domain–domain (Fig. 5a) interaction network of KRAS after the replacement of GDP by GTP, as well as the pathways of allosteric signaling from the P-loop to the switch I and switch II regions.Fig. 5b and c show the residue–residue and domain–domain interaction network of KRAS in both the GDP- and GTP-bound states as represented by the NRI-derived interaction matrix, where the color shades represent the interaction strengths (weights). As shown in Fig. 5b and c, the interaction strength of the GTP-bound state is significantly higher than that of the GDP-bound state, especially around the P-loop and the switch region, suggesting that the replacement of GDP by GTP significantly enhances the internal interactions of the KRAS. We further quantitatively compared the residue–residue interaction networks of the GTP- and GDP-bound states using several commonly used graph theoretic metrics (ESI Fig. S14–S18†), and the results showed that the network of the GTP-bound state had a shorter average path length, larger average weight, and larger centrality measure, thus suggesting that the replacement of GDP by GTP rendered the residue–residue communication network of KRAS more associative and efficient. Notably, a focused analysis on the region spanning residues 40–75 (ESI Fig. S14–S18†), which includes the switch I and switch II regions, revealed distinct patterns in network properties. In the GDP-bound state, residues within the 40–55 range exhibited slightly higher centrality and connectivity values compared to the GTP-bound state. However, the switch II region (residues 57–70) displayed significantly greater centrality measures under GDP binding, indicating tighter residue–residue communication in this region. In contrast, the GTP-bound state exhibited higher clustering coefficients across this region, suggesting the formation of a tighter local interaction network that likely facilitates KRAS activation by stabilizing dynamic communication between critical regions.
The network diagrams (Fig. 5d and e) provide a more visual representation of the inferred domain–domain interactions and their directionalities. In the GDP-bound state, the network is sparser with localized connections. In contrast, the GTP-bound state shows a denser network, with stronger interactions from the P-loop to switch I (sw1), and switch II (sw2), and extending to distal regions (r1, r2, r3). This suggests that GTP binding reorganizes the interaction network, propagating activation signals through specific allosteric pathways. Notably, the P-loop exhibits increased outbound interactions (out-degree), reinforcing its role as a signal initiator. The enhanced signal reception by switch I highlight its critical role in KRAS activation, while switch II also shows increased signal emission, though to a lesser extent. Overall, these results support the P-loop's role as a signal relay center, facilitating communication to the switch regions.
We further used the shortest path method (Dijkstra algorithm) to analyze and compare the allosteric signaling paths from the P-loop to reach switch I and switch II, respectively, in the interaction network of GDP- and GTP-bound binding states of KRAS. Since all three structural regions contain a high number of residues, we selected the three nodes with the highest centrality values as the representative nodes of each region (if there were more than three nodes with the highest centrality values, the three nodes with the highest weights were filtered according to the weight values), and thus nine possible signaling paths each for the P-loop-switch I and the P-loop-switch II were generated for both states (ESI Tables S1 and S2†), and the paths with the highest probability among the nine paths for each were subsequently selected and displayed in the concentric circle network diagrams (Fig. 6a and b) and molecular surface diagrams (Fig. 6c and d), respectively. It is worth mentioning that the concentric circle network diagrams Fig. 6c and d show all the nodes (all residues) of the whole protein system and are arranged according to the centrality (importance) of the nodes in descending order from the center outwards.
In the GDP-bound state (Fig. 6a, c and ESI Table S2†), there are no intermediate nodes in the shortest paths from the P-loop to switches I and II, which suggests that the interactions between the signal departure and arrival regions are more direct and relatively simpler. In addition, as shown in Fig. 6a, KRAS has more nodes closer to the center (larger centrality values) in the GDP-bound state for switches I and II compared to the GTP-bound state, suggesting that these regions are more centralized and structurally rigid in the GDP-bound state, thus limiting the functional activity of the protein. In contrast, in the GTP-bound state (Fig. 6b, d and ESI Table S3†), the shortest paths from the P-loop to switches I and II contained intermediate nodes, suggesting that the replacement of GDP by GTP in KRAS is associated with greater structural flexibility and a wider range of dynamic interactions (enhanced complexity of the network). For example, the two paths with the highest probability leading from the P-loop to switch I and switch II, respectively, in the GTP-bound state are [11, 69, 28] and [11, 107, 74], both of which contain intermediate nodes. The increase in intermediate nodes reflects the increase in network complexity, which is crucial for allosteric signaling. In the GDP-bound state, although the connection between the P-loop and the switching region is more direct, this direct connection may limit the signaling efficiency because of the lack of a complex intermediate network to efficiently amplify and transmit the signal. In the GTP-bound state, the increase of intermediate nodes provides more transmission paths and “transit stations” for the signal, which not only helps the signal to be transmitted from the P-loop to the switch I and switch II regions, but also amplifies the signal through the complex network to promote the activation of KRAS more effectively. It is worth mentioning that this pathway ending at switch I also passes through residue 69 of switch II, suggesting that when GTP replaces GDP, it also increases the interaction between switch I and switch II, which is crucial for the activation of the KRAS protein. In addition, in the GTP-bound state, the node positions of switch I and switch II were more dispersed in the concentric circle network graph compared to the GDP-bound state (Fig. 6b), suggesting that the node centrality of these two regions decreased compared to the GDP-bound state, and thus similarly reflecting that GTP replacement of GDP increased the complexity the KRAS residue interaction network, which in turn enhanced the efficiency of allosteric signaling to facilitate the transition of KRAS from the inactive to the active state.
4. Discussion
Despite extensive studies, the precise molecular mechanisms by which GTP binding induces conformational changes leading to KRAS activation remain incompletely understood.45,46 Investigating these activation mechanisms is of significant importance for developing targeted cancer therapies.20,47 In this study, we utilized molecular dynamics (MD) simulations,48 Markov State Models (MSMs),21,22 and Neural Relational Inference (NRI)42 to elucidate the molecular mechanics of KRAS activation, focusing on conformational dynamics, residue interactions, particularly long-range interactions, and the pathways of GTP-mediated allosteric signal transduction within the molecule.Our RMSD and RMSF analyses demonstrate that GTP binding significantly enhances the conformational flexibility of KRAS, particularly in the switch I and switch II regions. This increased flexibility enables KRAS to explore a wider range of conformations, providing the structural foundation for activation. Free Energy Landscapes (FELs) further support these findings, showing that the GTP-bound state occupies a broader, shallower energy basin, reflecting greater conformational diversity. In contrast, the GDP-bound state remains confined to a narrow, deep energy basin, indicative of a stable, inactive conformation. These results suggest that GTP binding increases KRAS's ability to sample various conformational states, enhancing its activation potential. Essential Dynamics (ED) analysis further confirms that GTP binding promotes structural changes toward an active-like conformation, with the switch regions moving apart into an open configuration, unlike the more closed GDP-bound form. These observations align with the allosteric mechanisms proposed in recent studies.49,50 For instance, Yang et al. highlighted that the switch-II region plays a pivotal role in KRAS oncogenic activation through dynamic allosteric regulation, which involves conformational reorganization to accommodate functional changes.49 Weng et al. (2024) conducted a systematic energy analysis and mutation study, identifying multiple allosteric sites in the KRAS protein, including the switch-II and P-loop regions, and highlighting their potential importance in inhibitor design.50 Furthermore, current studies have shown that many mutations can influence the activation process of KRAS by affecting the conformational flexibility of the switch regions and the P-loop.16–18,51–53
The increased conformational flexibility of KRAS in the GTP-bound state can be attributed to the reduction of its intramolecular stabilizing interactions, such as a decrease in the number of hydrogen bonds and natural contacts compared to the GDP-bound state, as well as an increase in van der Waals' energy and electrostatic energy, which suggests that KRAS becomes structurally looser and more unstable after the substitution of GTP for GDP, and therefore possesses increased conformational flexibility as well as conformational switching potential. To investigate the molecular mechanic behind the increased flexibility and reduced interactions, we calculated the contact area between GTP/GDP and KRAS. Calculations show that GTP, upon replacing GDP, covers the previously exposed hydrophobic surface of KRAS due to the addition of a polar phosphate group to the molecule, resulting in a weakening of the hydrophobic force, which leads to a looser structure as well as an increase in conformational flexibility. The weakened hydrophobic force further enhances the desolvation effect and entropy increases as water molecules are repelled from the hydrophobic region, leading to a decrease in the free energy of the system and further contributing to the increased flexibility of KRAS. In addition, the increased phosphate groups after the exchange of GTP and GDP may also generate new polar non-covalent interactions with some groups on the surface of the KRAS protein, and such interactions may disrupt the equilibrium of the original interaction network within the protein, i.e., produce the effect of pulling one hair and affecting the whole body through the so-called 'butterfly effect', leading to the formation and breakage of non-covalent bonds within the protein, and accompanied by significant enthalpy changes, thus increasing the flexibility of the protein's conformation. This disruption and reorganization of the interaction network accompanied by enthalpy changes lays the foundation for KRAS allosteric activation signaling, as analyzed in the NRI results.
Although the above analyses on protein conformational flexibility and molecular motion patterns indicate the potential and motion trend of KRAS to shift to the active state after GTP substitution for GDP, however, whether KRAS in the GTP-bound state is realistically sampled to the activated state conformation during simulation as well as the thermodynamic and kinetic properties of KRAS during activation need to be further analyzed and elucidated. Our TICA-based conformational sampling scatter plot shows that the sampled conformations of GTP-bound KRAS during the simulation highly overlap with the control conformations of the active state we selected, while the sampling of GDP-bound KRAS is restricted to the inactive state only, which suggests that GTP replaces GDP to efficiently activate the KRAS.MSM-based cluster analysis can further reveal the specific conformational state distribution (thermodynamic properties) during activation. We calculated that more than 97% of the conformations are in the inactive state. However, the GTP-bound protein shows a much broader conformational distribution and a large proportion of conformations are in the active-like state, suggesting that GTP binding allows for a broader conformational sampling of KRAS, which greatly increases the likelihood of a transition to the active state. Kinetic analyses also revealed to us significant differences between the two states. In the GDP-bound state, the transition to the active-like state is both infrequent and slow, whereas in the GTP-bound state, the transition is much more rapid and frequent. This dynamic change reflects the increased flexibility of the GTP-bound state, which favors the transition of KRAS to its active form.
Our results further highlight the role of GDP and GTP in modulating KRAS dynamics by comparing with the apo KRAS system. While the apo KRAS system exhibits the lowest conformational flexibility, its dynamic transitions are significantly faster than those observed in the nucleotide-bound systems. These findings suggest that both GDP and GTP binding stabilize KRAS structure but with distinct effects: GDP-bound KRAS remains in a non-active conformation, whereas GTP binding promotes transitions toward the active state. Structural analysis of the apo system further confirms that, in the absence of nucleotide binding, KRAS predominantly adopts a conformation similar to the GDP-bound state, reinforcing the hypothesis that GTP binding plays a unique role in driving KRAS activation.
While increased flexibility provides the potential for KRAS to sample various conformations, which has been demonstrated by MSM analysis, it does not fully explain why KRAS specifically transitions into its active state. To investigate how GTP binding directs KRAS toward activation, we conducted an NRI analysis to examine the reorganization of the interaction network and how long-range interactions facilitate allosteric signaling. The results of our NRI analyses show that the complexity of the residue–residue interaction network is greatly increased upon GTP binding, and in particular the long-range interactions between the P-loop and the switch I and switch II regions become more pronounced, while the reorganization of these interactions effectively facilitates the delivery of the allosteric signals triggered by GTP binding and directs the regions of switches I and II to the active conformation. In addition, our NRI analysis identified pathways by which the allosteric effects of GTP binding are transmitted through the protein's internal interaction network, and these pathways involve key intermediate residues that ensure efficient signaling from the P-loop to the switch I and switch II regions to activate KRAS. The dynamic interplay between the P-loop and switch regions, as observed in our shortest-path analyses, corroborates findings from kinetic and thermodynamic allostery studies in Ras proteins, which emphasize the importance of long-range allosteric communication in regulating protein function.54
In summary, our study presents a mechanistic model of KRAS activation driven by GTP binding. The introduction of a polar phosphate group disrupts hydrophobic interactions and increases the contact area with KRAS, particularly in nonpolar regions. These changes reduce hydrophobic forces, destabilizing the compact structure and promoting higher conformational flexibility. The combined entropic and enthalpic effects, along with the reorganization of the interaction network observed in NRI analysis, enhance KRAS's ability to sample active-like conformations. The allosteric signals initiated by GTP binding propagate from the phosphate group to key regions, including switch I and switch II, driving them into an open, active conformation. This network reorganization provides new insights into KRAS's allosteric regulation and presents potential therapeutic targets for modulating its activation pathways. The specific residues involved in signal transmission between the P-loop and switch regions represent key nodes within this network. These residues could serve as potential targets for allosteric inhibitors designed to modulate KRAS activity. By targeting these critical interaction points, it may be possible to disrupt the activation process, providing a novel approach for developing therapies aimed at KRAS-driven cancers.
Data availability
MD trajectories for this article are available at https://pan.quark.cn/s/1c292c4b57eb#/list/share.Author contributions
D.-R. Z., J.-T. Y. and M.-T. L. performed the MD simulation, analyzed the data, and participated in designing the study and drafting the manuscript. P. S. and L.-Q. Y. designed the study, coordinated the work, and wrote and revised the manuscript. All authors contributed to and approved the final version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study was funded by the Xingdian Talents Support Program of Yunnan Province (YNWR-QNBJ-2020-086), and grants (31860243 and 31960198) from the National Natural Sciences Foundation of China.References
- A. Rio-Vilarino, L. del Puerto-Nevado, J. Garcia-Foncillas and A. Cebrian, Cancers, 2021, 13, 3757 CrossRef PubMed.
- R. Nussinov, H. Jang, C.-J. Tsai, T.-J. Liao, S. Li, D. Fushman and J. Zhang, Cell. Mol. Life Sci., 2017, 74, 3245–3261 Search PubMed.
- L. Shaoyong, J. Hyunbum, M. Serena, G. Attila, K. Ozlem, N. Ruth and Z. Jian, Chem. Rev., 2016, 116, 6607–6665 CrossRef PubMed.
- Z. Moghadamchargari, J. Huddleston, M. Shirzadeh, X. Zheng, D. E. Clemmer, F. M. Raushel, D. H. Russell and A. Laganowsky, Biochemistry, 2019, 58, 3396–3405 CrossRef PubMed.
- M. E. Bahar, H. J. Kim and D. R. Kim, Signal Transduction Targeted Ther., 2023, 8, 455 CrossRef PubMed.
- L. Huang, Z. Guo, F. Wang and L. Fu, Signal Transduction Targeted Ther., 2021, 6, 386 CrossRef.
- J. Chen, J. Wang, W. Yang, L. Zhao, J. Zhao and G. Hu, Molecules, 2024, 29, 2317 CrossRef PubMed.
- T. Pantsar, Comput. Struct. Biotechnol. J., 2020, 18, 189–198 CrossRef.
- D. K. Menyhárd, G. Pálfy, Z. Orgován, I. Vida, G. M. Keserű and A. Perczel, Chem. Sci., 2020, 11, 9272–9289 RSC.
- Y. Wang, D. Ji, C. Lei, Y. Chen, Y. Qiu, X. Li, M. Li, D. Ni, J. Pu and J. Zhang, Comput. Struct. Biotechnol. J., 2021, 19, 1184–1199 CrossRef.
- J. C. Hunter, D. Gurbani, S. B. Ficarro, M. A. Carrasco, S. M. Lim, H. G. Choi, T. Xie, J. A. Marto, Z. Chen and N. S. Gray, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8895–8900 CrossRef PubMed.
- S. Xu, B. N. Long, G. H. Boris, A. Chen, S. Ni and M. A. Kennedy, Acta Crystallogr., Sect. D:Struct. Biol., 2017, 73, 970–984 CrossRef.
- B. J. Grant, A. A. Gorfe and J. A. McCammon, PLoS Comput. Biol., 2009, 5, e1000325 CrossRef.
- S. Vatansever, Z. H. Gümüş and B. Erman, Sci. Rep., 2016, 6, 37012 CrossRef CAS PubMed.
- S. Roet, F. Hooft, P. G. Bolhuis, D. W. Swenson and J. Vreede, J. Phys. Chem. B, 2022, 126, 10034–10044 CrossRef CAS PubMed.
- S. A. Mir, B. Nayak, N. H. Aljarba, V. Kumarasamy, V. Subramaniyan and B. Dhara, ACS Omega, 2024, 9, 30665–30674 CrossRef CAS.
- J. Chen, S. Zhang, W. Wang, L. Pang, Q. Zhang and X. Liu, J. Chem. Inf. Model., 2021, 61, 1954–1969 CrossRef CAS.
- V. Jani, U. Sonavane and R. Joshi, Heliyon, 2024, 10, e36161 CrossRef CAS PubMed.
- B. Papke and C. J. Der, Science, 2017, 355, 1158–1163 CrossRef CAS PubMed.
- A. D. Cox, S. W. Fesik, A. C. Kimmelman, J. Luo and C. J. Der, Nat. Rev. Drug Discovery, 2014, 13, 828–851 CrossRef CAS.
- B. E. Husic and V. S. Pande, J. Am. Chem. Soc., 2018, 140, 2386–2396 CrossRef CAS PubMed.
- K. A. Konovalov, I. C. Unarta, S. Cao, E. C. Goonetilleke and X. Huang, JACS Au, 2021, 1, 1330–1341 CrossRef CAS PubMed.
- X. Li, Z. Qi, D. Ni, S. Lu, L. Chen and X. Chen, Molecules, 2021, 26, 5647 CrossRef CAS PubMed.
- I. C. Unarta, S. Cao, S. Kubo, W. Wang, P. P.-H. Cheung, X. Gao, S. Takada and X. Huang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024324118 CrossRef CAS.
- J. D. Chodera and F. Noé, Curr. Opin. Struct. Biol., 2014, 25, 135–144 CrossRef CAS PubMed.
- J. Zhu, J. Wang, W. Han and D. Xu, Nat. Commun., 2022, 13, 1661 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- J. Huang and A. D. MacKerell Jr, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, J. Comput. Chem., 2010, 31, 671–690 CrossRef PubMed.
- W. Yu, X. He, K. Vanommeslaeghe and A. D. MacKerell Jr, J. Comput. Chem., 2012, 33, 2451–2468 CrossRef PubMed.
- D. J. Price and C. L. Brooks III, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef PubMed.
- B. Knapp, L. Ospina and C. M. Deane, J. Chem. Theory Comput., 2018, 14, 6127–6138 CrossRef PubMed.
- B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef.
- A. Amadei, A. B. Linssen and H. J. Berendsen, Proteins: Struct., Funct., Bioinf., 1993, 17, 412–425 CrossRef PubMed.
- M. K. Scherer, B. Trendelkamp-Schroer, F. Paul, G. Pérez-Hernández, M. Hoffmann, N. Plattner, C. Wehmeyer, J.-H. Prinz and F. Noé, J. Chem. Theory Comput., 2015, 11, 5525–5542 CrossRef PubMed.
- P. Deuflhard and M. Weber, Linear Algebra Appl., 2005, 398, 161–184 CrossRef.
- G. R. Bowman, V. S. Pande and F. Noé, An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation, Springer Science & Business Media, 2013 Search PubMed.
- L.-Q. Yang, X.-L. Ji and S.-Q. Liu, J. Biomol. Struct. Dyn., 2013, 31, 982–992 CrossRef CAS PubMed.
- J. Zhu, J. Wang, W. Han and D. Xu, bioRxiv, 2021, preprint, DOI:10.1101/2021.01.20.427459.
- P. Shannon, A. Markiel, O. Ozier, N. S. Baliga, J. T. Wang, D. Ramage, N. Amin, B. Schwikowski and T. Ideker, Genome Res., 2003, 13, 2498–2504 CrossRef CAS.
- A. Javaid, SSRN Electron. J., 2013, 2340905 Search PubMed.
- D. K. Simanshu, D. V. Nissley and F. McCormick, Cell, 2017, 170, 17–33 CrossRef CAS PubMed.
- B. R. Dandekar, N. Ahalawat, S. Sinha and J. Mondal, JACS Au, 2023, 3, 1728–1741 CrossRef CAS PubMed.
- F. McCormick, Clin. Cancer Res., 2015, 21, 1797–1801 CrossRef CAS.
- M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652 CrossRef CAS PubMed.
- M. H. Yang, T. H. Tran, B. Hunt, R. Agnor, C. W. Johnson, B. Shui, T. J. Waybright, J. A. Nowak, A. G. Stephen and D. K. Simanshu, Cancer Res., 2023, 83, 3176–3183 CrossRef CAS PubMed.
- C. Weng, A. J. Faure, A. Escobedo and B. Lehner, Nature, 2024, 626, 643–652 CrossRef CAS.
- P. Grudzien, H. Jang, N. Leschinsky, R. Nussinov and V. Gaponenko, J. Mol. Biol., 2022, 434, 167695 CrossRef CAS PubMed.
- Z. Yu, Z. Wang, X. Cui, Z. Cao, W. Zhang, K. Sun and G. Hu, Molecules, 2024, 29, 645 CrossRef CAS.
- A. Cuevas-Navarro, Y. Pourfarjam, F. Hu, D. J. Rodriguez, A. Vides, B. Sang, S. Fan, Y. Goldgur, E. de Stanchina and P. Lito, Nature, 2024, 1–3 Search PubMed.
- L. J. Manley and M. M. Lin, Biophys. J., 2023, 122, 3882–3893 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra07924h |
| This journal is © The Royal Society of Chemistry 2025 |