Insights into the specific capacitance of CNT-based supercapacitor electrodes using artificial intelligence

Abstract

In this study, the specific capacitance characteristics of a carbon nanotube (CNT) supercapacitor was predicted using different machine learning algorithms, such as artificial neural network (ANN), random forest regression (RFR), k-nearest neighbors regression (KNN), and decision tree regression (DTR), based on experimental studies. The results of the simulation verified the accuracy of the ANN algorithm with respect to the data derived from the specific capacitance of the supercapacitor module. It was observed that there was a strong correlation between the experimental results and the predictions made by the ANN algorithm. Comparative analysis showed that the developed ANN algorithm was consistently superior over other algorithms in terms of different metrics, as indicated by the lowest root mean square error (RMSE) value of roughly 26.24 and the highest R² value of approximately 0.91. In contrast, the DTR model recorded the least reliable results in the accuracy analysis, as indicated by the highest RMSE value of about 53.46 and the lowest R² value of roughly 0.63. To further explore the impact of independent input parameters including pore structure, specific surface area, and I_D/I_G ratio on a single output parameter (particularly, the specific capacitance) the sensitivity analysis was also conducted using the SHapley Additive exPlanations (SHAP) framework. This investigation sheds light on the relative significance and effects of different input variables on the specific capacitance of supercapacitors based on CNTs. The results indicated that the ANN algorithm accurately predicted the capacitance of the CNT-based supercapacitor, demonstrating the feasibility and significance of neural network algorithms in the design of energy storage devices.

---

1. Introduction

With the rapid development of the economy, information technology has become one of the most important corresponding fields.^1,2 Recently, the specific requirements for many technological applications, including sensor networks and portable microelectronic devices, have attracted attention globally.^3–6 Nevertheless, the demand for compact energy storage devices with a high energy and power density is one of the biggest challenges encountered by these technological applications.^7,8 In this case, supercapacitors have demonstrated their feasibility as top-notch storage components owing to their superior power density, long cycle life, quick charge/discharge rates, maintenance-free traits, simplified packaging techniques, and compatibility with integrated circuits. Owing to their ability to retain substantially more electrical charge than regular capacitors, supercapacitors are capable of having high capacitance values. Consequently, supercapacitors have found a wide range of uses in creating self-powered systems, especially in numerous sensing applications and portable electronic devices.⁹ However, the structural traits and physiochemical qualities of the used electrode materials significantly influence the performance of supercapacitors. Therefore, numerous carbon nanostructured materials have been explored as electrode materials in supercapacitors, including activated carbon, carbon nanowires, carbon nanotubes (multi- and single-walled CNTs), one- to few-layered graphene structures, and spherical carbon nanoparticles.^10–15 Owing to the outstanding properties of carbon-based materials such as large specific surface area, low cost, high porosity, easy availability, high conductivity, and environmental friendliness, they have been widely used as supercapacitor electrodes.^16,17 Among the various potential carbon-based electrode materials, carbon nanotubes (CNTs) are considered superior candidates for the fabrication of supercapacitor electrodes due to their high mechanical strength, large theoretical surface area, chemical stability, and adaptable electronic structure.^18,19 Accordingly, the development of high-performance supercapacitors with CNT and CNT nanocomposite-based electrodes has been the focus of numerous investigations.^20–24 Recently, conducting polymers and transitional metal oxides have been successfully incorporated in the structure of CNTs to improve their capacitance performance; however, more research is required to increase the efficiency of the corresponding supercapacitors devices.^25–28 Also, despite the fact that the process of modifying the electrode of a capacitor only relies on a few empirical calculations or rough theoretical models, there is no recognized theory that systematically describes how to increase the specific capacitance. Thus, to predict the electrochemical capacitance based on various input features and optimize the effective parameters, machine learning algorithms have been utilized. This can speed up the development of CNT-based electrodes.

Machine learning algorithms describe the intricate interaction between dependent and independent variables by using learning algorithms based on available data. Every experiment in the dataset, with its input characteristics (for example, physiochemical) and output characteristics (specific capacitance), can be considered a single data point. Additionally, machine learning algorithms may perform better if they have access to additional data points. Thus, with reliable, long-lasting experimental data sets, machine learning can produce results that are accurate, reproducible, and consistent.

The accuracy of the data collected and supplied to the training and testing process determines the accuracy of machine learning algorithms. Researchers depend on the rigor of the analytical process and the repeatability of the experimental study findings to guarantee the accuracy of the data points supplied for machine learning algorithms. In this case, the intricate electrochemical processes found in supercapacitors make precise modeling extremely difficult.^29–33 Numerous research groups have made significant contributions to the field of energy storage devices based on machine learning.^34–40

Herein, upon examining numerous research articles, we created a database to simulate the capacitance of CNT-based supercapacitors. The capacitance can be affected by a variety of physiochemical features, including pore size, specific surface area, I_D/I_G ratio, nitrogen content, and atomic oxygen percentage. The electrochemical test characteristics including electrolyte concentration, electrolyte material, and applied voltage window also affect the specific capacitance, which are derived from galvanostatic charge/discharge tests. By integrating these features into a machine learning model, predictive models can be developed, which not only predict the specific capacitance accurately but also offer insights into the underlying factors influencing the energy storage performance. The selection of these features reflects a holistic approach to understanding and predicting the behavior of energy storage materials in practical applications. The machine learning algorithms were fed electrochemical and physicochemical properties as inputs, and their output was the specific capacitance of CNT-based electrodes. The main goal of our study was to develop specialized machine learning algorithms that can quickly, precisely, and accurately forecast a particular subset of material-based supercapacitor electrodes. Subclassifying the supercapacitor electrode materials and creating specialized machine learning algorithms with improved prediction power within their respective subspaces were crucial to achieving this goal. We developed these machine learning algorithms using the open-source scikit-learn Python library.⁴⁰ Using this package, it was easier to build machine learning algorithms that could input values related to CNT electrodes and use a simple, effective method to forecast the electrode performance with a high degree of accuracy. These machine learning algorithms allow the prediction of capacitance performance by analyzing large amounts of experimental data, which eliminates the need for laborious trial-and-error tests. Thus, the contributions of this investigation are as follows: (i) collecting a dataset for CNT-based electrodes from an extensive review of numerous academic publications, (ii) analyzing and preprocessing the collected dataset; selecting the feature to be tuned for training and testing the machine learning algorithms, and (iii) modeling the CNT-based electrodes dataset; four machine learning algorithms were compared in terms of performance, and the best method was selected. Therefore, this paper is organized as follows: Section 2 introduces the prior research conducted by numerous publishers; Section 3 discusses the strategies employed to accomplish the goal of this study; Section 4 presents and discusses the outcomes produced by machine learning algorithms; and Section 5 presents the conclusion and future directions.

2. Literature review

Because of the complexity of the variables in carbon-based supercapacitors, machine learning techniques are required, which provide the ideal solution for the prediction of multi-structure/single-property interactions. Machine learning is a type of science that helps researchers make predictions accurately and efficiently as well as helps in introducing explanations for the relationships between variables. Recently, machine learning techniques have been successfully employed to investigate several chemical engineering problems, which motivated us to investigate how carbon factors affect the capacitance of supercapacitors using the machine learning method. As a result, data was obtained through published research publications prior to several model-based supercapacitor implementations. Machine learning-based energy storage systems have benefited greatly from the work by Zhu et al.,³³ Su et al.,³⁵ Zhou et al.,³⁶ Zhou et al.,³⁷ Gheytanzadeh et al.,³⁸ Liu et al.,³⁹ Saad et al.,⁴⁰ and Tawfik et al.⁴¹ Zhu et al. examined the impacts of five variables (specific surface area, I_D/I_G ratio, voltage window, N-doping quantity, and projected pore size) using the ANN approach for carbon-based electrodes.³³ Their results demonstrated that the ANN approach has superior accuracy and a higher correlation coefficient. The authors compared the results of the ANN model with that of the Lasso and linear regression models as reference models. Using SSA, pore size, surface area of micropores, % pore volume of mesopores, and surface area of micropores, Liu et al.³⁹ experimented with six models with varying properties. One machine learning technique that has been used to estimate the capacitance of carbon-based supercapacitors is the artificial neural network (ANN). Saad et al.⁴⁰ predicted the specific capacitance of graphene-based supercapacitor electrodes using the electrochemical and physiochemical properties of 12 input features through four ML models including KNN, DTR, Bayesian ridge regression (BRR), and ANN. To forecast the performance of SCs with CNT electrodes for nine variables, Tawfik et al. used a variety of models, including stochastic gradient descent (SGD) model, ridge regression (RR), Bayesian regression (BR), and gradient boosting regression (GBR).⁴¹ This allowed them to identify the optimal model. In this investigation, the specific capacitance characteristics of CNT-based supercapacitor electrodes were predicted via various machine learning algorithms including ANN, RFR, KNN, and DTR. In a subclass of electrodes based on supercapacitors, our work aimed to create more specific machine learning models with straightforward, quick, and accurate prediction power. Therefore, specific machine learning models with higher prediction ability in their subspace should be used to classify and model different electrode material classes for supercapacitors.

3. Materials and methods

In this work, machine learning algorithms were developed using data gathered from an extensive survey of many published publications. The input features of this study included indicators of the structural characteristics and the electrochemical test features of the electrode. The atomic percentages of nitrogen and oxygen doping, pore size, specific surface area, and I_D/I_G ratio are a few characteristics that describe the structural features. Nonetheless, the ionic conductivity, concentration, material, and voltage window of the electrolyte were included in the electrochemical test features. The specific capacitance, in farads per gram (F g⁻¹), was used to assess the performance of the CNT-based electrode. Specific capacitance represents the total ability of the device to store electrical charge. However, our future work will explore other relevant performance metrics. Although we learned a lot from the papers we investigated, only a few of them had comprehensive numerical data for every attribute we were looking for. The completeness and quality of the input features have a big impact on the accuracy of the machine learning algorithms. All the points in the dataset were employed to build the machine learning algorithms. For testing and training purposes, parts of the data were divided into separate sets. Eighty percent of the datasets was used for algorithm generation training, while the remaining twenty percent was used for testing to assess the performance of the developed models (Fig. 1). The goal of this work was to gather and use a variety of distinct electrode characteristics that have not been used to train machine learning algorithms before.

Fig. 1 Schematic of all machine learning algorithms employed to simulate the capacitance behavior of CNT-based supercapacitor electrodes.

3.1. Machine learning algorithm development

Scikit-learn, an open-source machine learning software, was used to create machine learning algorithms that can forecast the electrode performance with a high degree of accuracy and provide input values related to CNT electrodes. The sequential process of using machine learning algorithms and data processing techniques to predict the performance of supercapacitors is outlined visually in Fig. 2. The dataset had nine input features making up the machine learning algorithms including voltage window, specific surface area, electrolyte materials, concentration, ionic conductivity, I_D/I_G ratio, pore size, and N/O-doping elements (at%), and specific capacitance (F g⁻¹) was the only output variable. The I_D/I_G ratio is a measure of the relative intensity of the D-band (defect-induced band) to the G-band (graphitic band) in the Raman spectra of carbon materials, such as graphene or CNTs. The dataset was first subjected to feature engineering to prepare the variables for efficient modeling. To prepare the dataset for analysis, some data points with unusual capacitance measurements were first eliminated. This step focused on the majority of data points that showed more consistent and dependable capacitance values in an effort to improve the resilience and generalizability of the machine learning algorithms. For instance, data points with fewer than nine attributes were eliminated from the dataset, together with those with particular capacitance values higher than 300 F g⁻¹, which were only found in a small number of research publications. As a result, there were fewer high specific capacitance data points in the dataset, which may have made it more challenging for the machine learning algorithms to identify and predict these values. Further, although the removal of data points greatly decreased the size of our dataset, records with less data points than the nine selected attributes were also eliminated. Additionally, we were unable to get features including specific capacitance, voltage window, specific surface area, and pore size for the units we selected, i.e., F g⁻¹, V, m² g⁻¹, and nm, respectively. Subsequently, the machine learning algorithms were constructed using 146 data points that were collected from different papers. The dataset is accessible in the ESI.† Decision trees were employed in the feature selection procedure of this study to account for feature importance. Feature selection lowers the chance of overfitting and produces a more effective, interpretable, and resilient model that generalizes better to new data. To ensure stable model prediction and generalization, feature scaling was also employed to ensure that the scale of features falls between −1 and 1. Feature scaling enhances the numerical stability, convergence, and performance of the model, particularly for gradient-based and distance-based optimization techniques. It guarantees equal contribution from each feature, avoids bias, and improves the interpretability of the model. Notably, the predictive power of a model may be severely limited when working with small datasets. Overfitting, a lack of generalization, excessive variation, poor feature representation, bias, trouble choosing features, model complexity, and difficulties with validation and assessment are a few of the main drawbacks. Methods such as regularization, data augmentation, and transfer learning can be used to lessen these restrictions. Furthermore, when working with a limited dataset, increasing the amount of data collected or utilizing methods such as synthetic data generation can assist enhance the predictive power of the model, which will be discussed in our future work.

Fig. 2 Flowchart of the implementation of a machine learning algorithm and data processing for supercapacitor performance prediction.

To create and validate the performance of the model, these data points were split into two groups, i.e., the training set and the test set. The training set contained 110 data points, while the test set contained 30 data points, or 80% and 20% of the total data, respectively. Several machine learning algorithms such as artificial neural network (ANN), random forest regression (RFR), k-nearest neighbors regression (KNN), and decision tree regression (DTR) were used to predict the capacity of the CNT-based supercapacitors. By altering the number of hidden layers (i.e., one, two, and three) as well as the neurons in the hidden layer, the prefect architecture was discovered. The optimum architecture in this investigation was composed of two hidden layers with a 10 × 35 configuration. The hyperparameters of each model were chosen by a method of trial and error to determine which was best. The structure of the ANN model is 10 → 35 → 1, with the following parameters: loss = RMSE, optimizer = adam, epochs = 50, regulation = L2. RFR model, min samples split at 2 and max features at 1.0, with max depth of 17 and n estimators of 325. KNN model, weights = distance, n_neighbors = 7. Model DTR, criterion = friedman_mse, max_depth = 5, min_samples_leaf = 4, min_samples_split = 2. In this investigation, a trial-and-error method was used for hyperparameter tuning given that the preliminary tests showed that the special features of our dataset made it difficult to define ideal settings. Our trial-and-error strategy allowed us to repeatedly alter the hyperparameters with a more practical resource investment than automated methods such as grid search or Bayesian optimization, which can demand significant computer resources and may also result in overfitting. Employing this strategy, we could enhance the model performance without using the substantial computational resources usually required for thorough or automated tuning methods.

The correlation coefficient (R²) values and the minimum root mean square error (RMSE) were used to evaluate the performance of the machine learning algorithm on the test split.⁴² The R², as depicted in eqn (1), provides a thorough and precise assessment of the model performance, offering insightful information free from restrictions in interpretability. R² values nearer 1 suggest increased predictive accuracy and are frequently employed in the evaluation of regression algorithms. Furthermore, as shown in eqn (2), RMSE enhances the evaluation of the model performance.^41,42

When evaluating predictive performance, y_i stands for the true rating in a testing dataset and ŷ_i for the predicted rating. The mean of all the collected data point outputs is ȳ. The number of rating the prediction pairs between the testing data and the predicted results is indicated by the symbol n. A better fit between the model and the dataset is shown by a smaller RMSE and R² values move closer to 1. To improve the predicted accuracy, the regression algorithm with the lowest RMSE and the highest R² is given priority when comparing different algorithms.

Generally, in regression problems, R² is the counter-representative of accuracy. Because of its sensitivity to large errors, RMSE is the method of choice. It is computed by taking the square root of the squared differences between the actual and forecasted values. Larger errors have a disproportionately big impact on the RMSE given that errors are squared. Although RMSE and R² were chosen for their suitability in handling large continuous values and evaluating model fit, we acknowledge that including MAE and MBD could improve the evaluation by providing additional insights into the model performance, particularly regarding outlier sensitivity and bias. This means that if the model has a few very large errors, they will significantly increase the RMSE, making it higher even if other errors are small. Thus, in our future investigation, we will consider including these indicators in subsequent analyses to provide a more comprehensive evaluation of the resilience of our model.

4. Results and discussion

4.1. Correlation analysis

The intensity and direction of the linear link between two features are measured by the Pearson correlation coefficient, commonly referred to as the correlation coefficient. The degree of correlation between the variables is represented by a value that falls between −1 and 1. An effective statistical tool for determining the linearity relationship between two parameters in a dataset is the correlation coefficient. Fig. 3 displays a heatmap that shows the Pearson correlation coefficient between each input parameter and the color intensity. Each square in this heatmap has a numerical representation of the Pearson correlation coefficient, which indicates the degree of the linearity relationship between two crossing parameters. The intensity of the linear correlation between the two variables is shown by the color of the square. A positive (+ve) correlation coefficient indicates a propensity for both traits to increase or fall together. Conversely, inverse relationships are indicated by negative (−ve) correlation coefficient values, whereby a drop in one trait leads to an increase in the other, and vice versa. According to the heatmap, specific surface area (SSA), electrolyte ionic conductivity, electrolyte concentration, I_D/I_G, and N (at%) are the features that have the highest association with capacitance based on the data. Generally, the capacitance in energy storage devices is greatly influenced by the SSA of their materials because it increases the number of active sites for charge storage, increases the charge storage capacity, improves the electrolyte accessibility, lowers the resistance, and enables the properties of the materials to be tailored to maximize their energy storage performance. Therefore, the SSA is an important consideration in the design of CNT-based electrodes for supercapacitors.³⁹ Additionally, in the case of weak correlation, features such as O (at%), pore size, electrolyte chemical composition, and voltage window are arranged in descending order. The capacity of the machine learning algorithms to recognize and take advantage of the intricate connections between different parameters and specific capacitance enables improved specific capacitance prediction. To improve the prediction accuracy, the machine learning algorithms take advantage of the complex interactions that exist between a given capacitance and its electrochemical and physiochemical properties. The machine learning algorithms may be able to estimate the specific capacitance more accurately by leveraging these correlations, which will enhance their performance in tasks requiring capacitance prediction.

Fig. 3 Correlation map showing the intensity of each color for each feature in the algorithm.

Fig. 4 displays the scatter distribution curve of all the features that were used to build the machine learning algorithms. The mean and standard deviation (STD) values for all the feature distributions are listed in Table 1. The scatter distribution curves of the dataset offer a number of interesting findings. A useful way to understand the properties and distribution of the dataset is to consider both the mean and STD. They are frequently used in machine learning to comprehend and measure the characteristics of the data and draw conclusions or predictions from them. In our instance, the STD value of 0.83 and mean value of 1.33 V for the voltage window reflect that numerous of the research papers surveyed had voltage windows larger than 1.0 V. A high-voltage window improves the specific capacitance and energy density of supercapacitors.⁴³ The energy density (E) of a supercapacitor is proportional to the square of the voltage window (V), according to the equation E = 1/2CV². Therefore, the voltage window is an important metric for assessing the overall performance of devices. As is known, the type of electrolyte largely affects the voltage window of devices. The primary characteristic of the CNTs that make up the supercapacitor electrodes is their specific surface area (SSA). It is necessary to increase the SSA to improve the capacitance (C) according to the relationship between them, C = εε₀A/d, where A is the specific surface area, ε is the electrolyte dielectric constant, ε₀ is the vacuum permittivity, and d is the distance between the ion center and the CNT surface. The STD value associated with the SSA in this study illustrates the great variation of the surface morphologies across the CNT-based electrode materials under investigation. This variety shows how these materials exhibit a wide range of surface properties. The variety in the SSA values throughout the dataset is reflected in the high value of STD, which highlights the diversity of the surface structures and attributes. Additionally, the pore size of the electrode has an impact on the accessibility of the electrolyte ions. The vast surface morphology range observed in the examined data is further demonstrated by the comparatively significant STD values for the pore size in comparison to its low mean value. Furthermore, the influence of crystallinity on the electrical conductivity of carbon materials can be examined using Raman spectroscopy. The D and G-bands located at roughly 1360 and 1570 cm⁻¹ correspond to the defects and sp²-hybridized carbon, respectively. Besides the structural characteristics, the individual constituents have a noteworthy influence on the capacitive performance. The mean and STD of the I_D/I_G ratio are 0.97 and 0.41, respectively. Increased I_D/I_G values (>0.97) show the dominance of the sp² C=C sites, which can lower the specific capacitance of supercapacitors.^44–46 In addition to optimal architectures, carbonaceous materials for capacitive applications require appropriate components. Among the elements, the two most often added heteroatoms in the carbon matrix are nitrogen and oxygen. Through the addition of extra pseudocapacitance and quantum capacitance, the nitrogen and oxygen-content functional groups significantly improve the capacitive characteristics of CNT-based materials. In supercapacitor devices, pseudocapacitance is a type of charge storage mechanism that takes place at the electrode–electrolyte interface. To make machine learning algorithms more flexible, features with non-numeric values such as the chemical formula of the electrolyte were represented as categorical data. Given that label encoding is a straightforward method, it was utilized to encode the non-numerical categories as numerical values. Every distinct non-numeric category was given a unique numerical integer value. We could convert the various electrolyte composition classification forms into numerical numbers by ranking each one based on the degree of ionic conductivity. From the highest to lowest ionic conductivity, the electrolyte components of all the data points were arranged, starting with Li₂SO₄, then LiPF₆, EMIMBF₄, Et₄NBF₄, H₂SO₄, KOH, and finally TEABF₄/PC. In fact, the type of electrolyte utilized in electrochemical systems can significantly affect a number of characteristics, including ionic conductivity, voltage window, and capacity. For instance, conventional liquid electrolytes can provide comparatively high ionic conductivity. Effective charge transfer is made possible by the ion mobility in the liquid phase. Additionally, the voltage windows of various electrolyte types vary according to their stability and chemical composition, which affects the capacity.

Fig. 4 Scatter curves showing the input and output characteristic density distributions.

Table 1 Statistical features of the dataset used, including input feature classifications, mean, standard deviation (STD), minimum values, and maximum values of all feature distributions

Input feature classifications		Input features	Mean	Standard deviation	Min. value	Max. value
Electrochemical features	Electrolyte properties	Electrolyte chemical formula	5.88	3.29	0	15
		Electrolyte concentration	2.46	2.24	0.1	6
		Electrolyte ionic conductivity	4.82	2.79	0	7
	Operational parameters	Potential window (V)	1.33	0.83	0.6	3.5
Physiochemical features	Electrode characteristics	Specific surface area (m^2 g^−1)	508.42	597.34	0.99	3160
		Pore size (nm)	2.67	4.79	0.34	23.89
		ID/IG	0.97	0.41	0.09	2.9
		N (at%)	1.34	3.27	0.1	15.8
		O (at%)	1.67	3.13	0.3	13.5

---

4.2. Algorithms assessment

Table 2 lists the evaluation criteria that were applied to each of the machine learning algorithms that were used to evaluate the predictions. The computation of the RMSE and R² values, which are used to measure the effectiveness of the machine learning algorithms, is a prerequisite for the evaluation criteria. It is clear from examining the evaluation data that for the expected capacitance, the ANN algorithm has the best R² value and the lowest RMSE value. This shows that compared to the other machine learning algorithms considered, the ANN algorithm with the given architecture generates the most accurate predictions. The cross diagrams in Fig. 5 illustrate the performance of all the machine learning algorithms by comparing the predicted and experimental values of a specific capacitance based on the test dataset. The diagonal line in each panel represents the ideal correlation between the values that were predicted and the experimental values. The value of R² is in the range of −1 to 1 based on the degree of connection between the variables and whether they move in the same direction (+ve correlation) or the other way (−ve correlation). The considerable deviations in the numerous data points from the diagonal line, as well as the lowest R² and highest RMSE values demonstrate that among the four machine learning techniques examined in this paper, DTR produces the worst statistics. It appears that the correlation between several input parameters cannot be adequately captured by multiplying separate characteristics or using the quadratic approximation. Given that RFR and KNN both have significantly higher R² and lower RMSE values, they can both offer significantly superior fits to the experimental data. However, when the capacitance becomes close to zero, they are unable to replicate the experimental findings. Given that ANN yielded the highest R² and lowest RMSE values, it offered the best fitting overall and showed a much better accuracy. Generally, ANNs have become highly effective machine learning tools because of their exceptional capacity to represent intricate nonlinear interactions in a wide range of data types. Their architecture, which is made up of linked layers of nodes (neurons), makes it possible to catch complex patterns that are frequently missed by conventional machine learning models. Because of their adaptability, ANNs are especially well-suited for jobs requiring big, multidimensional datasets, such as image identification and natural language processing. However, this flexibility comes at a price, where the increased danger of overfitting is one of the most important issues associated with ANNs. When a model learns the noise in the training data as well as the underlying patterns, it is considered to be overfitted, which results in poor generalization to new, unseen data. Small datasets or highly complicated models can make this especially problematic because the model may become unduly adapted to the training set. Because of this, even when an ANN performs admirably on training data, its effectiveness may drastically decline when used on validation datasets or in real-world applications. The computational complexity of ANNs is another drawback. It can take a lot of computing power and memory to train these models, especially when working with huge datasets or complex designs such as deep neural networks (Table 3).

Table 2 Comparison of the evaluation criteria of each machine learning algorithm

Machine learning algorithm	R^2	RMSE
ANN	0.91	26.24
RFR	0.79	39.01
KNN	0.71	46.38
DTR	0.63	53.46

---

Fig. 5 (a–d) Assessment of the performance of all the machine learning algorithms. Comparing the true versus predicted specific capacitance values of CNT-based supercapacitor electrodes for all the machine learning algorithms.

Table 3 Comparison of our models with earlier ML algorithms that predicted the specific capacitance of carbon material-based supercapacitor electrodes

References	Electrode materials	ML algorithms	Input features		RMSE
			No.	Details
35	Carbon-based	RT	7	PW, SSA, PS, PV, ID/IG ratio, N, and O (at%)	67.62
36	Carbon-based	ANN	8	Scan rate, micropores SSA, mesopores SSA, O (at%), nN-5 (at%), nN-6 (at%), nN-Q (at%), and other nitrogen types (at%)	31.54
37	Carbon-based	ANN	3	Scan rate, micropores SSA, mesopores SSA	36.4
38	Carbon-based	GWO-SVM	5	PW, SSA, PS, ID/IG ratio, and N (at%)	39.22
39	Carbon-based	XGBoost	11	SSA, PS, PV, Smicropores, Smesopores, Vmicropores, Vmesopores, ratio of Vmicro/Vmeso, ratio of Vmeso/PV, ratio of Smicro/Smeso, ratio of Smicro/SSA	25.5
40	Graphene-based	ANN	12	Current density, PW, SSA, PS, PV, ID/IG ratio, N (at%), O (at%), C (at%), electrode material, electrolyte material, electrolyte concent.	60.42
41	CNT-based	GBR	9	PW, SSA, PS, ID/IG ratio, N (at%), O (at%), electrolyte ionic conductivity, electrolyte material, electrolyte concent.	36.31
	CNT-based	Bayesian regression	9		44.38
	CNT-based	RR	9		50.34
	CNT-based	(SGD)	9		55.33
This work	CNT-based	ANN	9	PW, SSA, PS, ID/IG ratio, N (at%), O (at%), electrolyte ionic conductivity, electrolyte material, electrolyte concent.	26.24
	CNT-based	RFR	9		39.01
	CNT-based	KNN	9		46.38
	CNT-based	DTR	9		53.46

---

In our ANN model, various strategies to counteract the overfitting problem were implemented. The main method used was L2 regularization, which penalizes large weight values and adds a penalty term to the loss function to deter excessively complex models. L2 regularization efficiently reduces the magnitude of the weights by including this penalty, leading to simpler models that are less likely to overfit. This strategy not only promotes generalization efficiency but also improves the model interpretability by minimizing the complexity. In addition to L2 regularization, dropout approaches during training were employed, which randomly deactivate a subset of neurons in each iteration. This stochastic technique helps to prevent co-adaptation of neurons, hence fostering a more robust representation of the data. Dropout can further mitigate overfitting risks by improving the ability of the network to generalize to new data by lowering the reliance on specific neurons.

The relative significance of several variables in affecting capacitance can be ascertained. The relative feature importance can provide a way to rank the features based on their contribution to the predictive power of the model. Features with higher importance are considered more influential in making predictions or decisions. As can be seen in Fig. 6, the column graph clearly illustrates the weight of the nine features. The two most crucial factors are the pore size and I_D/I_G ratio. Lower weights are caused by the voltage window, SSA, electrolyte concentration, and N-doping percentage (at%). The formula for the electrolyte and the percentage of O-doping (at%) had the least impact on the capacitive results.

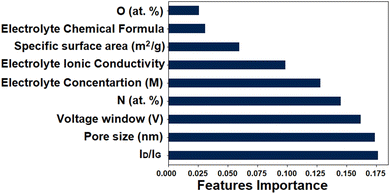Fig. 6 Predictive supercapacitor capacitance and the relative significance of the nine input features.

4.3. ANN algorithm SHAP values

Employing SHAP (SHapley Additive exPlanations) data, better knowledge of the internal workings of the constructed ANN algorithm may be obtained. These SHAP values shed light on how each input attribute contributes to the predictions made for particular data points.⁴⁰ The significance values of each feature can be determined by computing the SHAP values for individual predictions. The SHAP values are calculated for each input feature for a given data point, explaining how each feature contributes to the prediction by the model based on that particular data point. Averaging the predictions made on the test data points yields the base value, which serves as a benchmark. A characteristic that increases the prediction from the basis value is indicated by a positive SHAP value, whilst a feature that decreases the prediction from the base value is shown by a negative value. In this investigation, the SHAP values were calculated for each test split prediction that the ANN algorithm supplied. The goal of this investigation was to provide important new light on the underlying mechanisms and decision-making procedures of the ANN algorithm. A detailed summary of the SHAP values acquired for each feature is shown in Fig. 7. Low and high feature values in this visualization are represented as light blue and dark red, respectively. A better understanding of the relationship between the feature value and the SHAP value that matches it can be achieved by taking a closer look at the horizontal distribution of the positive and negative SHAP values for each feature. Based on their relative relevance, the traits are arranged from top to bottom in descending order to make analysis easier. The relative importance of each attribute is recorded by taking the average of its absolute SHAP values. This organization of the features makes it easier to comprehend the importance and influence of each one on the predictions by the model, which makes it easier to identify the main contributing components. Fig. 7 displays the three key characteristics for the ANN prediction results including the voltage window, SSA, and I_D/I_G ratio. Significantly, as shown by the dark red dots, the increased SSA levels in the electrode composite are linked to the SHAP values, which show a strongly positive trend. Conversely, lower levels of SSA are linked to negative SHAP values, which are shown by the dots with light blue color. This implies that when the ANN algorithm comes across a data point with a higher SSA level, it tends to increase its specific capacitance prediction. Comparably, larger I_D/I_G ratios are linked to positive SHAP values, whereas lower I_D/I_G ratios are linked to negative SHAP values. In contrast to the SHAP values of the SSA feature, the I_D/I_G ratio feature SHAP values exhibit more subdued impacts in both the positive and negative directions. This suggests that the I_D/I_G ratio has a relatively small effect on changing the prediction outcomes. Alternatively, the prediction accuracy of the ANN algorithm decreases with an increase in the voltage window levels. This implies that the specific capacitance prediction of the ANN algorithm is less affected by high voltage windows.

Fig. 7 SHAP diagram values showing how the features affect the ANN algorithm.

Finally, this extensive investigation is essential for the future screening, design, optimization, and synthesis of high-quality CNT-based electrodes. Furthermore, the machine learning approach developed in this work can be expanded to methodically and consistently examine the effectiveness of various surface modification methods in CNT-based electrodes, which is anticipated to be crucial for the experimental realization of high-performance supercapacitors in the near future.

5. Conclusion

In conclusion, the goal of this study was to evaluate how well various machine learning (ML) algorithms predicted the specific capacitance of CNT-based supercapacitor electrodes. To evaluate the capacitance of a CNT-based supercapacitor, four machine learning algorithms were studied including artificial neural network (ANN), random forest regression (RFR), k-nearest neighbors regression (KNN), and decision tree regression (DTR). As input variables, nine features were employed including voltage window, electrolyte composition, its concentration, and its ionic conductivity, pore size, its specific surface area (SSA), its percentage of nitrogen atoms (N at%), its percentage of oxygen atoms (O at%), and its I_D/I_G ratio. One of the key findings of this study is that the ANN algorithm performs the best among these algorithms in terms of RMSE and correlation coefficient (R²), with the lowest RMSE of 26.24 and the highest R² value of 0.91. Further, the performance of the different machine learning algorithms was ranked as follows: ANN > RFR > KNN > DTR. In addition, a study employing the SHAP framework was carried out to gain insights into the relative significance of the input features. The findings showed that the most important characteristics that had a significant impact on the predictions made by the ANN algorithm were the SSA and I_D/I_G ratio. Supercapacitors and other electronic and electrical equipment may be able to store more energy owing to the use of CNTs, which can advance sustainability and energy management technology. As the need for more sophisticated energy solutions increases, this research finding will be very helpful in guiding the development of next-generation supercapacitors that are more potent and environmentally friendly. Thus, we will address every issue that surfaced during this inquiry in our next study, including enhancing the generalization by adding more data, simplifying the model, and facilitating the model assessment process by employing a variety of evaluation criteria, such as accuracy. Additional experimental validation will be obtained as part of our plan to strengthen our subsequent research.

Data availability

All data are available within the manuscript and its ESI.†

Author contributions

Wael Z. Tawfik: conceptualization, data curation, visualization, investigation, writing – reviewing & editing. Mohamed Shaban: methodology, software, validation, writing – original draft. Athira Raveendran: writing – reviewing & editing. June Key Lee: data curation and investigation. Abdullah M. Al-Enizi: formal analysis, methodology, writing – review and editing. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors extend their sincere appreciation to the Researchers Supporting Project Number (RSP2025R55), King Saud University, Riyadh, Saudi Arabia for the support.

References

1. P. Thakkar, S. Khatri, D. Dobariya, D. Patel, B. Dey and A. K. Singh, Advances in materials and machine learning techniques for energy storage devices: a comprehensive review, J. Energy Storage, 2024, 81, 110452,  DOI:10.1016/j.est.2024.110452.
2. X. Liu, K. Fan, X. Huang, J. Ge, Y. Liu and H. Kang, Recent advances in artificial intelligence boosting materials design for electrochemical energy storage, Chem. Eng. J., 2024, 490, 151625,  DOI:10.1016/j.cej.2024.151625.
3. J. Wang, X. Zhang, Z. Li, Y. Ma and L. Ma, Recent progress of biomass-derived carbon materials for supercapacitors, J. Power Sources, 2020, 451, 227794,  DOI:10.1016/j.jpowsour.2020.227794.
4. Y. Cao, S. Li, C. Xu, X. Ma, G. Huang, C. Lu and Z. Li, Mechanisms of porous carbon based supercapacitors, ChemNanoMat, 2021, 7, 1273–1290,  DOI:10.1002/cnma.202100261.
5. G. J. Adekoya, O. C. Adekoya, U. K. Ugo, E. R. Sadiku, Y. Hamam and S. S. Ray, A minireview of artificial intelligence techniques for predicting the performance of supercapacitors, Mater. Today: Proc., 2022, 62, S184–S188,  DOI:10.1016/j.matpr.2022.05.079.
6. Y. Qin, L. Miao, M. Mansuer, C. Hu, Y. Lv, L. Gan and M. Liu, Spatial confinement strategy for micelle-size-mediated modulation of mesopores in hierarchical porous carbon nanosheets with an efficient capacitive response, ACS Appl. Mater. Interfaces, 2022, 14, 33328–33339,  DOI:10.1021/acsami.2c08342.
7. K. Wickramaarachchi, M. Minakshi, S. A. Aravindh, R. Dabare, X. Gao, Z.-T. Jiang and K. W. Wong, Repurposing N-doped grape marc for the fabrication of supercapacitors with theoretical and machine learning models, Nanomaterials, 2022, 12, 1847,  DOI:10.3390/nano12111847.
8. L. Qu, P. Wang, B. Motevalli, Q. Liang, K. Wang, W.-J. Jiang, J. Z. Liu and D. Li, New Engineering Science Insights into the Electrode Materials Pairing of Electrochemical Energy Storage Devices, Adv. Energy, 2024, 36, 2404232,  DOI:10.1002/adma.202404232.
9. S. Mathew, P. B. Karandikar and N. R. Kulkarni, Modeling and optimization of a jackfruit seed-based supercapacitor electrode using machine learning, Chem. Eng. Technol., 2020, 43, 1765–1773,  DOI:10.1002/ceat.201900616.
10. Z. Zhang, L. Feng, P. Jing, X. Hou, G. Suo, X. Ye, L. Zhang, Y. Yang and C. Zhai, In situ construction of hierarchical polyaniline/SnS₂@carbon nanotubes on carbon fibers for high-performance supercapacitors, J. Colloid Interface Sci., 2021, 588, 84–93,  DOI:10.1016/j.jcis.2020.12.055.
11. X. Li, X. Chen, Y. Zhao, Y. Deng, J. Zhu, S. Jiang and R. Wang, Flexible all-solid-state supercapacitors based on an integrated electrode of hollow N-doped carbon nanofibers embedded with graphene nanosheets, Electrochim. Acta, 2020, 332, 135398,  DOI:10.1016/j.electacta.2019.135398.
12. S. K. Shim, W. Z. Tawfik, C. M. M. Kumar, S. Liu, X. Wang, N. Lee and J. K. Lee, Nanopatterned sapphire substrate to enhance the efficiency of AlGaN-based UVC light source tube with CNT electron-beam, J. Mater. Chem. C, 2020, 8, 17336–17341,  10.1039/D0TC04597G.
13. K. Deshsorn, K. Payakkachon, T. Chaisrithong, K. Jitapunkul, L. Lawtrakul and P. Iamprasertkun, Unlocking the Full Potential of Heteroatom-Doped Graphene-Based Supercapacitors through Stacking Models and SHAP-Guided Optimization, J. Chem. Inf. Model., 2023, 63, 5077–5088,  DOI:10.1021/acs.jcim.3c00670.
14. A. Ehsani, M. K. Moftakhar and F. Karimi, Lignin-derived carbon as a high efficient active material for enhancing pseudocapacitance performance of p-type conductive polymer, J. Energy Storage, 2021, 35, 102291,  DOI:10.1016/j.est.2021.102291.
15. J. S. Gao, Z. Liu, Y. Lin, Y. Tang, T. Lian and Y. He, NiCo₂O₄ nanofeathers derived from prussian blue analogues with enhanced electrochemical performance for supercapacitor, Chem. Eng. J., 2020, 388, 124368,  DOI:10.1016/j.cej.2020.124368.
16. A. Ghosh and Y. H. Lee, Carbon-based electrochemical capacitors, ChemSusChem, 2012, 5(3), 480–499,  DOI:10.1002/cssc.201100645.
17. Y. Zhai, Y. Dou, D. Zhao, P. F. Fulvio, R. T. Mayes and S. Dai, Carbon materials for chemical capacitive energy storage, Adv. Mater., 2011, 23(42), 4828–4850,  DOI:10.1002/adma.201100984.
18. Z. Z. Chang, B. J. Yu and C. Y. Wang, Lignin-derived hierarchical porous carbon for high-performance supercapacitors, J. Solid State Electrochem., 2016, 20, 1405–1412,  DOI:10.1007/s10008-016-3146-2.
19. M. A. Bissett, I. A. Kinloch and R. A. W. Dryfe, Characterization of MoS₂-graphene composites for high-performance coin cell supercapacitors, ACS Appl. Mater. Interfaces, 2015, 7, 17388–17398,  DOI:10.1021/acsami.5b04672.
20. A. Dang, T. Li, C. Xiong, T. Zhao, Y. Shang, H. Liu, X. Chen, H. Li, Q. Zhuang and S. Zhang, Long-life electrochemical supercapacitor based on a novel hierarchically carbon foam templated carbon nanotube electrode, Composites, Part B, 2018, 141, 250–257,  DOI:10.1016/j.compositesb.2017.12.049.
21. J. Li, J. Tang, J. Yuan, K. Zhang, X. Yu, Y. Sun, H. Zhang and L. C. Qin, Porous carbon nanotube/graphene composites for high-performance supercapacitors, Chem. Phys. Lett., 2018, 693, 60–65,  DOI:10.1016/j.cplett.2017.12.052.
22. G. D. Park, J. K. Lee and Y. C. Kang, Three-dimensional macroporous CNTs microspheres highly loaded with NiCo₂O₄ hollow nanospheres showing excellent lithium-ion storage performances, Carbon, 2018, 128, 191–200,  DOI:10.1016/j.carbon.2017.11.088.
23. L. W. Taylor, O. S. Dewey, R. J. Headrick, N. Komatsu, N. M. Peraca, G. Wehmeyer, J. Kono and M. Pasquali, Improved properties, increased production, and the path to broad adoption of carbon nanotube fibers, Carbon, 2021, 171, 689–694,  DOI:10.1016/j.carbon.2020.07.058.
24. S. Shalini, T. B. Naveen, D. Durgalakshmi, S. Balakumar and R. A. Rakkesh, Progress in flexible supercapacitors for wearable electronics using graphene-based organic frameworks, J. Energy Storage, 2024, 86, 111260,  DOI:10.1016/j.est.2024.111260.
25. P. Tiwari, D. Janas and R. Chandra, Self-standing MoS₂/CNT and MnO₂/CNT one dimensional core shell heterostructures for asymmetric supercapacitor application, Carbon, 2021, 177, 291–303,  DOI:10.1016/j.carbon.2021.02.080.
26. M. Bibi, Y. Yu, A. Nisar, A. Zafar, Y. Liu, S. Karim, S. Mehboob, Y. Faiz, H. Sun, T. Ali, A. Khalid, A. Safdar, F. Faiz and M. Ahmad, NiCo₂O₄@SnS₂ nanosheets on carbon cloth as efficient bi-functional material for high performance supercapacitor and sensor applications, Nanotechnology, 2024, 35, 255701,  DOI:10.1088/1361-6528/ad3219.
27. H. Liu, J. Zhu, Z. Li, Z. Shi, J. Zhu and H. Mei, Fe₂O₃/N doped rGO anode hybridized with NiCo LDH/Co(OH)₂ cathode for battery-like supercapacitor, Chem. Eng. J., 2021, 403, 126325,  DOI:10.1016/j.cej.2020.126325.
28. S. Sahoo and J. J. Shim, Facile Synthesis of Three-Dimensional Ternary ZnCo₂O₄/Reduced Graphene Oxide/NiO Composite Film on Nickel Foam for Next Generation Supercapacitor Electrodes, ACS Sustain. Chem. Eng., 2017, 5, 241–251,  DOI:10.1021/acssuschemeng.6b01367.
29. D. Li, S. Li, S. Zhang, J. Sun, L. Wang and K. Wang, Aging state prediction for supercapacitors based on heuristic Kalman filter optimization extreme learning machine, Energy, 2022, 250, 123773,  DOI:10.1016/j.energy.2022.123773.
30. K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555,  DOI:10.1038/s41586-018-0337-2.
31. M. Rahimi, M. H. Abbaspour-Fard and A. Rohani, Synergetic effect of N/O functional groups and microstructures of activated carbon on supercapacitor performance by machine learning, J. Power Sources, 2022, 521, 230968,  DOI:10.1016/j.jpowsour.2021.230968.
32. A. Eddahech, O. Briat, M. Ayadi and J. M. Vinassa, Modeling and adaptive control for supercapacitor in automotive applications based on artificial neural networks, Electr. Power Syst. Res., 2014, 106, 134–141,  DOI:10.1016/j.epsr.2013.08.016.
33. S. Zhu, J. Li, L. Ma, C. He, E. Liu, F. He, C. Shi and N. Zhao, Artificial neural network enabled capacitance prediction for carbon-based supercapacitors, Mater. Lett., 2018, 233, 294–297,  DOI:10.1016/j.matlet.2018.09.028.
34. T. Gao and W. Lu, Machine learning toward advanced energy storage devices and systems, iScience, 2021, 24, 101936,  DOI:10.1016/j.isupercapacitori.2020.101936.
35. H. Su, S. Lin, S. Deng, C. Lian, Y. Shang and H. Liu, Predicting the capacitance of carbon-based electric double layer capacitors by machine learning, Nanoscale Adv., 2019, 1, 2162–2166,  10.1039/c9na00105k.
36. M. Zhou, A. Vassallo and J. Wu, Data-driven approach to understanding the inoperando performance of heteroatom-doped carbon electrodes, ACS Appl. Energy Mater., 2020, 3, 5993–6000,  DOI:10.1021/acsaem.0c01059.
37. M. Zhou, A. Gallegos, K. Liu, S. Dai and J. Wu, Insights from machine learning of carbon electrodes for electric double layer capacitors, Carbon, 2020, 157, 147–152,  DOI:10.1016/j.carbon.2019.08.090.
38. M. Gheytanzadeh, A. Baghban, S. Habibzadeh, A. Mohaddespour and O. Abida, Insights into the estimation of capacitance for carbon-based supercapacitors, RSC Adv., 2021, 11, 5479–5486,  10.1039/D0RA09837J.
39. P. Liu, Y. Wen, L. Huang, X. Zhu, R. Wu, S. Ai, T. Xue and Y. Ge, An emerging machine learning strategy for the assisted-design of high-performance supercapacitor materials by mining the relationship between capacitance and structural features of porous carbon, J. Electroanal. Chem., 2021, 899, 115684,  DOI:10.1016/j.jelechem.2021.115684.
40. A. G. Saad, A. Emad-Eldeen, W. Z. Tawfik and A. G. El-Deen, Data-driven machine learning approach for predicting the capacitance of graphene-based supercapacitor electrodes, J. Energy Storage, 2022, 55, 105411,  DOI:10.1016/j.est.2022.105411.
41. W. Z. Tawfik, M. S. Abdel-wahab, J. K. Lee, A. Al-Enizi and R. Y. Youssef, Modeling Specific Capacitance of Carbon Nanotube-Based Supercapacitor Electrodes by Machine Learning Algorithms, Phys. Scr., 2024, 99, 066011,  DOI:10.1088/1402-4896/ad4df3.
42. W. Z. Tawfik, S. N. Mohammad, K. H. Rahouma, E. Tammam and G. M. Salama, An artificial neural network model for capacitance prediction of porous carbon-based supercapacitor electrodes, J. Energy Storage, 2023, 73, 108830,  DOI:10.1016/j.est.2023.108830.
43. L. Zhang, Z. Meng, Q. Qi, W. Yan, N. Lin and X. Y. Liu, Aqueous supercapacitors based on carbonized silk electrodes, RSC Adv., 2018, 8, 22146–22153,  10.1039/C8RA01988F.
44. B. S. Reddy, P. L. Narayana, A. K. Maurya, U. M. R. Paturi, J. Sung, H. J. Ahn, K. K. Cho and N. S. Reddy, Modeling capacitance of carbon-based supercapacitors by artificial neural networks, J. Energy Storage, 2023, 72, 108537,  DOI:10.1016/j.est.2023.108537.
45. Z. Kavaliauskas, L. Marcinauskas and V. Valincius, Influence of the oxygen plasma treatment on carbon electrode and capacity of supercapacitors, Acta Phys. Pol. A, 2014, 125, 1316–1318,  DOI:10.12693/aphyspola.125.1316.
46. W. Z. Tawfik, S. N. Mohammad, K. H. Rahouma, G. M. Salama and E. Tammam, Machine learning models for capacitance prediction of porous carbon-based supercapacitor electrodes, Phys. Scr., 2024, 99, 026001,  DOI:10.1088/1402-4896/ad190c.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra05546b

---