Understanding the reaction mechanism of anti-addition of (NHC)Au(I)–H and (NHC)Au(I)–F across alkyne

Abstract

The experimentally observed anti-addition reactions of (NHC)Au(I)–H with dimethyl acetylenedicarboxylate (DMAD) MeOOCC≡CCOOMe and (NHC)Au(I)–F with phenylacetylene MeC≡CPh are intriguing and deserve more in-depth study. In this work, with the aid of density functional theory (DFT) calculations and intrinsic bond orbital (IBO) analysis, we systematically investigated the addition reactions of (NHC)Au(I)–X (X = H, Me and halides) with different alkynes. We found that the nature of the two anti-addition reactions is different. The addition of (NHC)Au(I)–H is initiated by a direct nucleophilic hydride attack from (NHC)Au(I)–H, followed by migration of the [(NHC)Au(I)]⁺ moiety to the diagonally opposite side with the aid of the out-of-plane π-bond of the alkyne. However, in the addition of (NHC)Au(I)–F, the [(NHC)Au(I)]⁺ moiety functions as a Lewis acid to initially activate the alkyne, followed by the fluoride attack.

---

Introduction

The utilization of gold catalysts, characterized by their ease of use and typically mild reaction conditions, has significantly advanced gold catalysis as a prominent field of study in chemical research since the onset of the 21st century. Gold catalysis is renowned for its diverse applications, encompassing redox transformations,¹ photoredox reactions,² coupling reactions,³ and the nucleophilic additions of unsaturated C–C bonds.⁴ Traditionally gold complexes are considered as Lewis acids, effectively activating π-systems and facilitating the nucleophilic addition of unsaturated C–C bonds. Numerous reports have demonstrated that nucleophile attacks on gold-coordinated alkynes display anti-stereoselectivity rather than syn-stereoselectivity. However, in the majority of these studies, the nucleophiles are not constituents of the gold metal complexes themselves.⁴

Recently, researchers have increasingly explored how gold complexes differ in reactivity from other transition metal complexes.⁵ Like most transition metal complexes, which undergo migratory insertion with alkynes in a syn fashion,⁶ gold complexes also exhibit similar stereoselectivity.⁷ However, the interesting studies reported in 2007 and 2008 revealed that (NHC)Au(I)–F and (NHC)Au(I)–H complexes can add across alkyne triple bonds stoichiometrically to yield anti-addition products (Scheme 1),^8,9 contradicting to the results observed in reactions of many transition metal complexes. Remarkably, despite being reported 17 years ago and attracting significant citations and attention since then due to its relevance in catalysis,¹⁰ the unusual anti-addition phenomenon has yet to be addressed by any theoretical work attempting to explain it. Hence, this unusual anti-addition underscores the need for comprehensive computational studies to decode the mechanisms for the reactions of Au(I)–F and Au(I)–H complexes with alkynes, especially considering the thermodynamically challenging cleavage of the Au–H bond. Thus, in this work, we aim to puzzle out and understand the reaction mechanism of the addition reactions of Au(I)–F and Au(I)–H complexes with alkynes, with the aids of density functional theory (DFT) calculations, followed by intrinsic bond orbital (IBO) analysis¹¹ to visualize the changes in orbital interactions along the reaction coordinates. To our knowledge, there exists no prior literature that delves into this specific aspect. We hope this work could enrich our understanding of the chemistry and catalysis of gold(I) complexes.

Scheme 1 Stoichiometric Addition of (NHC)Au(I)–F/H across alkyne.

Results and discussion

To gain insight into the reaction mechanism for the two reactions shown in Scheme 1, we conducted DFT calculations at the ωB97X-D level of theory¹² (see Computational details) using the actual gold complexes and alkynes employed in the experiments. We compare the crystal structures^8,9 and the corresponding optimized structures of L′Au–F, revealing a striking similarity between the two with the largest difference in bond length being no more than 0.02 Å. Fig. 1 shows the energy profiles calculated for the addition reactions of LAu–H and L′Au–F with the alkynes. In our DFT calculations, we considered both syn- and anti-additions, and the calculation results clearly show that for both reactions, anti-addition is the most favorable pathway.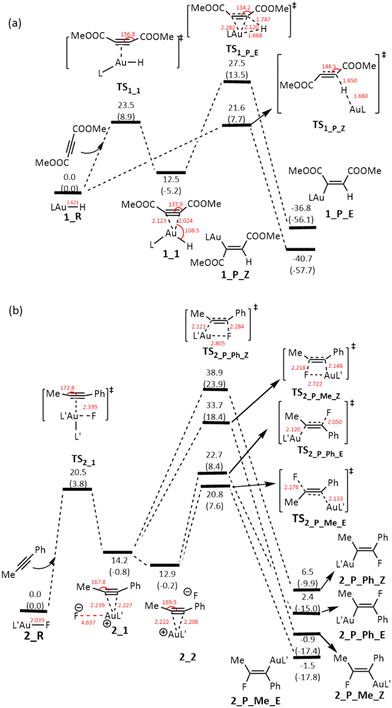

Fig. 1 Gibbs energy profiles calculated for the additions of (a) LAu–H and (b) L′Au–F across alkyne. The relative free energies and electronic energies (in parentheses) are given in kcal mol⁻¹.

For the addition of LAu–H across the alkyne MeOOCC≡CCOOMe (Fig. 1a), the most favorable pathway involves the hydride approaching one of the two alkyne carbons from a direction that is approximately perpendicular to the triple bond. The calculated Gibbs free energy barrier for this pathway is 21.6 kcal mol⁻¹, occurring at the transition state TS_{1_P_Z}, which features a hydride-bridged configuration as observed in the hydride transfer process from a silane to a Au(I) metal center.¹³ Subsequently, a new C–H bond is formed, leading to the breaking of the Au–H bond. Simultaneously, the [LAu]⁺ fragment gradually migrates to the opposite side of the C≡C moiety, ultimately forming the Z-isomeric product (1_P_Z). Further discussion on the feasibility of the [LAu]⁺ fragment migrating along such an extended pathway to the opposite side of the C≡C moiety will be presented later within the context of our analysis of the IBO plots.

Alternatively, the LAu–H complex functions as a Lewis acid to activate the alkyne through coordination. This activation process leads to the formation of a three-coordinated Au complex intermediate (1_1). During this coordination, both the ∠C(sp)–C(sp)–C(sp²) angles are bent to around 140°, achieved by overcoming a Gibbs free energy barrier of 23.5 kcal mol⁻¹. Subsequently, a 1,2-hydride migration occurs, resulting in the formation of the E-isomeric species (1_P_E). However, this pathway requires overcoming a much higher Gibbs free energy barrier of 27.5 kcal mol⁻¹ through the transition state TS_{1_P_E}, rendering this syn-addition pathway kinetically less favorable. The higher Gibbs free energy barrier of syn-addition compared to the favorable anti-addition discussed above arises likely due to the electronic repulsion between the Au–alkyne bond and hydride during the hydride addition and the steric repulsion between the ligand and the alkyne COOMe substituent.

In the addition of L′Au–F across the alkyne PhC≡CMe (Fig. 1b), notably, we do not observe the fluoride approaching an alkyne carbon, as seen in the LAu–H scenario. Instead, we only observe that L′Au–F functions as a Lewis acid. However, no three-coordinated gold complex intermediate was formed, distinguishing it from the behavior observed in the reaction of the LAu–H complex. Computational findings reveal that the initial step involves the substitution of the fluoride in the L′Au–F complex by the alkyne. Due to the high electronegativity of F, the substitution yields an alkyne-coordinated linear cationic Au complex intermediate alongside a non- or weakly-coordinated fluoride anion (2_1). Coordination of alkyne on the Au(I) metal center leads to a slight bending of the alkyne. The interaction between the fluoride anion and the cation Au(I) complex intermediate is predominantly ionic, allowing the fluoride anion to freely position itself from the same side of the AuL′ fragment (2_1) to the opposite side of the AuL′ fragment (2_2), with the latter configuration exhibiting slightly greater stability (ΔΔG = −1.3 kcal mol⁻¹) owing to reduced steric repulsion. To substantiate that movement of the fluoride ion incurs minimal energy expenditure, we simulated the displacement of the fluoride anion to distances of 6 Å and 8 Å from the Au(I) metal center. The resulting energy changes were found to be within 1 kcal mol⁻¹, indicating that the transition from 2_1 to 2_2 is energetically very plausible.

Given the asymmetry of the alkyne PhC≡CMe, starting from 2_1 or 2_2, the mobile fluoride anion nucleophilically attacks an alkyne carbon, leading to four different addition products. The energy profiles shown in Fig. 1b clearly indicate that the two syn-addition pathways starting from 2_1 are noticeably less favorable kinetically than the two anti-addition pathways starting from 2_2, suggesting that the repulsion between the fluoride anion and the Au-alkyne bonding electrons in the transition states of both the syn-addition pathways is very significant. In line with the experimental findings, the preferred addition product 2_P_Me_E results from the fluoride addition to the Me-substituted alkyne carbon. This aligns with the understanding that in PhC≡CMe the Me-substituted alkyne carbon is less π-electron rich, promoting the addition of the fluoride anion.

When comparing the two reactions, the reaction involving LAu–H is notably exergonic at −40.7 kcal mol⁻¹, whereas the reaction involving L′Au–F is only slightly exergonic at −1.5 kcal mol⁻¹. This can be explained as follows. An Au–H bond is reactive and its addition reaction with an alkyne gives a stronger C–H bond. In the case of L′Au–F, the Au–F bond is highly ionic and its addition gives a relatively weaker C–F bond when compared with the Au–F bond. Based on the bond dissociation energy (BDE) analysis as reported by Zhu and co-workers,¹⁴ we calculated that the BDE of the Au–F bond is 140.3 kcal mol⁻¹ whereas the BDE of the C–F bond is 125.2 kcal mol⁻¹.

To have a clear view of the electron flows for the addition reactions, we carried out intrinsic bond orbital (IBO) analysis,¹¹ which is a powerful tool that allows visualization of electron flows and trace the active IBOs along the reaction coordinate. Fig. 2 shows the results of the IBO analysis for the most kinetically favorable pathways concerning the additions of LAu–H and L′Au–F across alkyne. The key structures for the IBO analysis are obtained from the intrinsic reaction coordinates (IRC) calculations¹⁵ of the respective transition states. In the case of the LAu–H system, an additional structure exemplifying the interaction between [AuL]⁺ and the out-of-plane π-bond of the C≡C moiety was included. For the L′Au–F system, an intermediate structure illustrating the Au–F bond formation was also chosen.

Fig. 2 IBO analysis of the most kinetically favorable pathways of the additions of (a) LAu–H and (b) L′Au–F across alkynes MeOOCC≡CCOOMe and MeC≡CPh, respectively. In the case of LAu-H, the IBO plots show the transformation of Au–H σ /alkyne π to C–H σ /Au–C σ bond. In the case of L′Au–F, the IBO plots illustrate the transformation of fluoride lone pair/alkyne π to C–F σ /Au–C σ bond. Substituents on the NHC ligand are omitted for better visualization.

For LAu–H (Fig. 2a), the IBO plots in the first row show the gradual formation of the C–H bond (in purple color) along the reaction coordinate as the hydride approaches one of the two alkyne carbons. In the second row of the IBO plots, we observed a progressive shift of electron density associated with the in-plane π-bond of the alkyne (in green color) towards the other alkyne carbon, reaching maximum density on the diagonally opposite side relative to the newly formed C–H bond. In the third row of the IBO plots (in orange color), it is evident that the out-of-plane π-bond of the alkyne plays a crucial role in guiding the migration of the [AuL]⁺ moiety. Initially, this process involves the dissociation of the [AuL]⁺ moiety from the hydride, followed by its interaction with the out-of-plane π-bond, and ultimately leads to bonding with maximum electron density on the diagonally opposite side relative to the newly formed C–H bond. It is noted that the interaction between the [AuL]⁺ moiety and the out-of-plane π-bond is insufficient to establish this species as a local minimum based on the IRC calculation.

For L′Au–F (Fig. 2b), the IBO plots in the first row show the C–F bond formation (in purple/blue color) while the IBO plots in the second row (in green color) show the Au–C bond formation along the reaction coordinate.

The analysis above reveals the distinct nature of the two addition reactions: In the addition of LAu–H, the favorable addition pathway is initiated by a direct hydride attack from LAu–H, followed by migration of the [AuL]⁺ moiety. Conversely, in the addition of L′Au–F, the [AuL′]⁺ moiety functions as a Lewis acid to initially activate the alkyne, followed by the fluoride attack.

To support and further elaborate on our conclusions from the IBO analysis, we examined the effect of different alkynes on the reaction pathways. To do this, we first examined the hypothetical addition reactions of LAu–H with PhC≡CPh and MeC≡CMe. Interestingly, both additions maintain an anti-selectivity as the most favorable pathway (see Fig. S1 and S2† for the detailed energy profiles). However, the reaction barriers (ΔG^‡ = 26.7 kcal mol⁻¹ and 43.7 kcal mol⁻¹, respectively) are significantly higher than that calculated for the reaction with MeOOCC≡CCOOMe. The significantly elevated barriers for the reactions of these two alkynes are in line with the expectation that reactions of LAu–H are triggered by a direct nucleophilic hydride attack. In comparison to MeOOCC≡CCOOMe, both PhC≡CPh and MeC≡CMe are π electron-richer, impeding the nucleophilic attack. Notably, MeC≡CMe, being even π electron-richer in the alkyne bond than PhC≡CPh, results in the inaccessible barrier of 43.7 kcal mol⁻¹.

Then we examined the hypothetical addition reaction of L′Au–F with MeOOCC≡CCOOMe. Again, an anti-selectivity is maintained as the most favorable pathway (see Fig. S3† for the detailed energy profile). Moreover, the reaction energy barrier (ΔG^‡ = 22.5 kcal mol⁻¹) is only slightly higher than that for the reaction with PhC≡CMe. Clearly, the relative stability of the C–F bond formation transition state is not very sensitive to the π electron-richness of the alkyne bond.

We also examined the hypothetical addition reactions of LAu–H and L′Au–F with ArC≡CAr (Ar = C₆H₄-p-NO₂, C₆H₄-p-CN, C₆H₄-p-OMe, C₆H₄-p-NMe₂) and compared the reaction barriers (Tables S1 and S2†). The results obtained also align well with what we observed and discussed above. For LAu–H, the reaction barrier is much higher for an electron-rich alkyne (ΔG^‡ = 32.9 kcal mol⁻¹ for the Ar = C₆H₄-p-OMe and 33.5 kcal mol⁻¹ for Ar = C₆H₄-p-NMe₂) than that of an electron-deficient alkyne (ΔG^‡ = 19.7 kcal mol⁻¹ for C₆H₄-p-CN and 18.2 kcal mol⁻¹ for C₆H₄-p-NO₂). For L′Au–F, while the stability of 2_2 is higher with electron-rich alkynes, the energy barriers are roughly the same for both electron-rich and electron-deficient alkynes (ΔG^‡ = 17.4–19.6 kcal mol⁻¹).

We also explored whether other similar gold complexes can add across alkynes and studied the hypothetical addition reactions of LAu–Me with MeOOCC≡CCOOMe and L′Au–X (X = Cl, Br, I) with MeC≡CPh (Fig. S4 and Table S3†). For LAu–Me, the addition shows anti-stereoselectivity, similar to that of LAu–H. However, the reaction barriers of both syn-addition and anti-addition are significantly higher (ΔG^‡ = 40.5 kcal mol⁻¹ for syn-addition and ΔG^‡ = 38.4 kcal mol⁻¹ for anti-addition). We also calculated the reaction barriers for an S_E2 pathway, which can also yield the anti-addition product, and the barrier is even greater (ΔG^‡ = 44.6 kcal mol⁻¹). The increased reaction barriers can be explained as follows. In order for the addition to occur, a significant cleavage of the Au(I)–Me bond is needed, leading to inaccessible barriers. In the Au(I)–H bond, the spherical nature of the H 1s orbital allows the hydride acts as a bridge when nucleophilically attacking an alkyne carbon, leading to a small energy cost. For L′Au–X (X = Cl, Br, I), the addition reactions become highly thermodynamically unfavorable (ΔG° > 15 kcal mol⁻¹) due to the weak C–X bond formed upon addition, thus also leading to much higher reaction barriers (ΔG^‡ = 25.8–27.8 kcal mol⁻¹).

Finally, we examined the ligand effect by calculating the addition reactions of (Ligand)Au(I)–H (Ligand = ^AdCAAC¹⁶ and PPh₃) with MeOOCC≡CCOOMe and (Ligand)Au(I)–F (Ligand = ^AdCAAC¹⁶ and PPh₃) with MeC≡CPh. Comparing the reaction barriers and the reaction energies (Tables S4 and S5†) with those presented in Fig. 1, we found that the ligand effect is weak. The selectivity remains unchanged, and both the reaction barriers and the reaction energies do not vary significantly.

Conclusions

The reaction mechanisms of anti-addition reactions of (NHC)Au(I)–H across dimethyl acetylenedicarboxylate (DMAD) MeOOCC≡CCOOMe and (NHC)Au(I)–F across phenylacetylene MeC≡CPh have been investigated with the aid of DFT calculations and IBO analysis. Although both reactions show anti-selectivity, the nature of the two addition reactions is different. In the addition of (NHC)Au(I)–H, the favorable addition pathway is initiated by a direct nucleophilic hydride attack from (NHC)Au(I)–H, followed by migration of the [(NHC)Au(I)]⁺ moiety to the diagonally opposite side with the aid of the out-of-plane π-bond of the alkyne. Conversely, in the addition of (NHC)Au(I)–F, the [(NHC)Au(I)]⁺ moiety functions as a Lewis acid to initially activate the alkyne, followed by the fluoride attack and the key event of the addition reaction is the distortion of alkynes during alkyne coordination to the Au(I) metal center, thus insensitive to the electron-richness of the alkyne substrate.

Theoretical examination on the hypothetical addition reactions of (NHC)Au(I)–Me and (NHC)Au(I)–X (X = Cl, Br and I) leads to the following findings. In these reactions, anti-addition is favored over syn-addition. However, the addition reactions of (NHC)Au(I)–Me require significant cleavage of the Au(I)–Me bond in order to facilitate a direct nucleophilic attack, and therefore, inaccessible barriers have been calculated. In the addition reactions of (NHC)Au(I)–X (X = Cl, Br and I), the reactions are thermodynamically not favorable due to the weak C–X bonds formed in the addition products.

As a final note, it is noteworthy that syn-additions of Au(I)-silyl and -boryl complexes across alkynes have been also well documented in the literature,⁷ whereas anti-additions of Au(III)–OAc and Au(III)–H across acetylene has been observed.^17,18 Ongoing investigations into the mechanisms of these reactions are currently underway, with the aim of a systematic understanding of the factors that influence the stereoselectivity inherent to gold chemistry.

Computational details

DFT calculations were performed using the Gaussian 16 package.¹⁹ All structures were optimized using the ωB97X-D functional¹² with the basis set def2TZVP,²⁰ which includes effective core potentials for Au and I along with polarization functions for I only. Additionally, a 6-311+G** basis set²¹ was used for F, Cl and Br, and a 6-31G** basis set²² was employed for other elements. The calculations were performed with the SMD solvation model.²³ Benzene was used as the solvent for calculations involving LAu–H and LAu–Me, while dichloromethane was utilized as the solvent for calculations involving L′Au–F and L′Au–X (X = Cl, Br and I), considering the solvents used for the reactions shown in Scheme 1. Keyword “int = superfine” was also employed. Frequency calculations were performed to ensure intermediates have no imaginary frequencies and the transition state structures have only one imaginary frequency. Intrinsic reaction coordinate (IRC) calculations¹⁴ were also performed to ensure transition state structures connect appropriate reactants and products.

IBO (intrinsic bond orbital) analysis was conducted using the IBOview program.¹¹ The input .molden files were generated through the following steps: first, single point energy calculations were performed using Gaussian 16 program¹⁸ with the basis set def2TZVP¹⁹ for all elements, which resulted in the generation of .chk files. Subsequently, the .chk files were converted to .molden files using the multiwave function (Multiwfn) program²⁴ and ORCA 5.0.2 program.²⁵

In our DFT calculations, we used an implicit solvent model, which is justified for the following reason. The transition state structures involve bond formation and cleavage, which are key steps in the reaction mechanism. IRC calculations show that ion migrations (e.g., [NHC–Au]⁺ or F⁻) around the alkyne occur before or after the transition states, indicating that these migrations are not rate-determining or energetically demanding compared to the bond changes in the transition states.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Research Grants Council of Hong Kong (HKUST 16302222).

References

1. B. Huang, M. Hu and F. D. Toste, Homogeneous gold redox chemistry: organometallics, catalysis, and beyond, Trends Chem., 2020, 2, 707–720.
2. M. N. Hopkinson, A. Tlahuext-Aca and F. Glorius, Merging visible light photoredox and gold catalysis, Acc. Chem. Res., 2016, 49, 2261–2272.
3. M. N. Hopkinson, A. D. Gee and V. Gouverneur, AuI/AuIII Catalysis: An Alternative Approach for C-C Oxidative Coupling, Chem. – Eur. J., 2011, 17, 8248–8262.
4. (a) D. Campeau, D. F. L. Rayo, K. Muratov and F. Gagosz, Gold-catalyzed reactions of specially activated alkynes, allenes, and alkenes, Chem. Rev., 2021, 121, 8756–8867; (b) D. Zuccaccia, L. Belpassi, A. Macchioni and F. Tarantelli, Ligand effects on bonding and ion pairing in cationic gold(I) catalysts bearing unsaturated hydrocarbons, Eur. J. Inorg. Chem., 2013, 4121–4135; (c) M. Trinchillo, P. Belanzoni, L. Belpassi, L. Biasiolo, V. Busico, A. D′Amora, L. D′Amore, A. Del Zotto, F. Tarantelli, A. Tuzi and D. Zuccaccia, Extensive experimental and computational study of counterion effect in the reaction mechanism of NHC-gold(I)-catalyzed alkoxylation of alkynes, Organometallics, 2016, 35, 641–654.
5. C. C. Chintawar, A. K. Yadav, A. Kumar, S. P. Sancheti and N. T. Patil, Divergent gold catalysis: unlocking molecular diversity through catalyst control, Chem. Rev., 2021, 121, 8478–8558.
6. (a) Hydrofunctionalization, ed. V. P. Ananikov and M. Tanaka, Springer, Berlin, 2011; (b) P. S. Hanley and J. F. Hartwig, Migratory insertion of alkenes into metal–oxygen and metal–nitrogen bonds, Angew. Chem., Int. Ed., 2013, 52, 8510–8525.
7. (a) M. Joost, P. Gualco, S. Mallet-Ladeira, A. Amgoune and D. Bourissou, Direct syn Insertion of Alkynes and Allenes into Au-Si Bonds, Angew. Chem., Int. Ed., 2013, 52, 7160–7163; (b) M. Joost, L. Estévez, S. Mallet-Ladeira, K. Miqueu, A. Amgoune and D. Bourissou, Mechanisms of syn-Insertion of Alkynes and Allenes into Gold–Silicon Bonds: A Comprehensive Experimental/Theoretical Study, J. Am. Chem. Soc., 2014, 136, 10373–10382; (c) M. Joost, N. S. Merceron, A. Amgoune and D. Bourissou, Synthesis, Structure, and Reactivity of an NHC Silyl Gold(I) Complex, Organometallics, 2019, 38, 3494–3497; (d) H. Kuniyasu, T. Nakajima, T. Tamaki, T. Iwasaki and N. Kambe, Regioselective Cis Insertion of DMAD into Au–P Bonds: Effect of Auxiliary Ligands on the Reaction Mechanism, Organometallics, 2015, 34, 1373–1376; (e) A. Suzuki, L. Wu, Z. Lin and M. Yamashita, Isomerization of a cis–(2−Borylalkenyl)Gold Complex via a Retro–1,2−Metalate Shift: Cleavage of a C-C/C-Si Bond trans to a C−Au Bond, Angew. Chem., Int. Ed., 2021, 60, 21007–21013.
8. J. A. Akana, K. X. Bhattacharyya, P. Müller and J. P. Sadighi, Reversible C-F bond formation and the Au-catalyzed hydrofluorination of alkynes, J. Am. Chem. Soc., 2007, 129, 7736–7737.
9. E. Y. Tsui, P. Müller and J. P. Sadighi, Reactions of a stable monomeric gold(I) hydride complex, Angew. Chem., Int. Ed., 2008, 47, 8937–8940.
10. (a) T. Zhou, P. Gao, R. Lalancette, R. Szostak and M. Szostak, Gold-catalysed amine synthesis by reductive hydroamination of alkynes with nitroarenes, Nat. Chem., 2024, 16, 2025–2035; (b) P. H. M. Budzelaar, M. Bochmann, M. Landrini and L. Landrini, Electronic Effects of Bidentate P,N-Ligands on the Elementary Steps of Au(I)/Au(III) Reactions Relevant to Cross-Coupling Chemistry, Angew. Chem., Int. Ed., 2024, 63, e202317774; (c) M. Longuet, K. Vitse, A. Martin-Mingot, B. Michelet, F. Guégan and S. Thibaudeau, Determination of the Hammett Acidity of HF/Base Reagents, J. Am. Chem. Soc., 2024, 146, 12167–12173; (d) S. P. Sancheti, D. J. Mondal and N. T. Patil, Fluorination of α-Imino Gold Carbenes to Access C₃-Fluorinated Aza-Heterocycles, ACS Catal., 2023, 13, 4391–4397; (e) H. Yang, J. Wang, C. Jin, X. Li and X. Xu, Au(I)-Catalyzed Regioselective Hydrofluorination of Propargylamines Using Aqueous HF, J. Org. Chem., 2023, 88, 12074–12078.
11. G. Knizia and J. E. M. N. Klein, Electron flow in reaction mechanisms—revealed from first principles, Angew. Chem., Int. Ed., 2015, 54, 5518–5522.
12. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom = atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
13. S. Labouille, A. Escalle-Lewis, Y. Jean, N. Mezailles and P. Le Floch, Mechanism of the Dehydrogenative Silylation of Alcohols Catalyzed by Cationic Gold Complexes: An Experimental and Theoretical Study, Chem. – Eur. J., 2011, 17, 2256–2265.
14. Y. Li and J. Zhu, Achieving a favorable activation of the C-F bond over the C-H bond in five-and six-membered ring complexes by a coordination and aromaticity dually driven strategy, Organometallics, 2021, 40, 3397–3407.
15. K. Fukui, The path of chemical reactions-the IRC approach, Acc. Chem. Res., 1981, 14, 363–368.
16. A. S. Romanov and M. Bochmann, Organometallics, 2015, 34, 2439–2454.
17. (a) M. S. M. Holmsen, A. Nova, D. Balcells, E. Langseth, S. Øien-Ødegaard, R. H. Heyn, M. Tilset and G. Laurenczy, trans-Mutation at Gold(III): A Mechanistic Study of a Catalytic Acetylene Functionalization via a Double Insertion Pathway, ACS Catal., 2017, 7, 5023–5034; (b) M. S. M. Holmsen, A. Nova, K. Hylland, D. S. Wragg, S. Øien-Ødegaard, R. H. Heyn and M. Tilset, Synthesis of a (N,C,C) Au (iii) pincer complex via C sp³−H bond activation: increasing catalyst robustness by rational catalyst design, Chem. Commun., 2018, 54, 11104–11107; (c) M. S. M. Holmsen, A. Nova and M. Tilset, Cyclometalated (N,C) Au(III) Complexes: The Impact of Trans Effects on Their Synthesis, Structure, and Reactivity, Acc. Chem. Res., 2023, 56, 3654–3664.
18. (a) A. Pintus, L. Rocchigiani, J. Fernandez-Cestau, P. H. M. Budzelaar and M. Bochmann, Stereo–and Regioselective Alkyne Hydrometallation with Gold(III) Hydrides, Angew. Chem., Int. Ed., 2016, 55, 12321–12324; (b) L. Rocchigiani, J. Fernandez-Cestau, I. Chambrier, P. Hrobárik and M. Bochmann, Unlocking Structural Diversity in Gold(III) Hydrides: Unexpected Interplay of cis/trans-Influence on Stability, Insertion Chemistry, and NMR Chemical Shifts, J. Am. Chem. Soc., 2018, 140, 8287–8302.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
20. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
21. A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835.
22. A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577.
23. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Generalized born solvation model SM12, J. Chem. Theory Comput., 2013, 9, 609–620.
24. (a) T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592; (b) T. Lu, A comprehensive electron wavefunction analysis toolbox for chemists, Multiwfn, J. Chem. Phys., 2024, 161, 082503.
25. (a) F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78; (b) F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5qo00432b

---