Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An air-stable high-performance single-molecule magnet operating as a luminescent thermometer below its blocking temperature†
Julio
Corredoira-Vázquez
 abc,
Cristina
González-Barreira
abc,
Cristina
González-Barreira
 a,
Matilde
Fondo
a,
Matilde
Fondo
 *a,
Ana M.
García-Deibe
*a,
Ana M.
García-Deibe
 a,
Jesús
Sanmartín-Matalobos
a,
Jesús
Sanmartín-Matalobos
 ab,
Silvia
Gómez-Coca
ab,
Silvia
Gómez-Coca
 d,
Eliseo
Ruiz
d,
Eliseo
Ruiz
 d,
Carlos D. S.
Brites
d,
Carlos D. S.
Brites
 c and
Luís D.
Carlos
c and
Luís D.
Carlos
 *c
*c
aDepartamento de Química Inorgánica, Facultade de Química, Universidade de Santiago de Compostela, 15782, Santiago de Compostela, Spain. E-mail: matilde.fondo@usc.es
bInstitute of Materials (iMATUS), Universidade de Santiago de Compostela, 15782, Santiago de Compostela, Spain
cPhantom-g, CICECO – Aveiro Institute of Materials, Physics Department University of Aveiro, 3810-193, Aveiro, Portugal. E-mail: lcarlos@ua.pt
dDepartament de Química Inorgànica i Orgànica and Institut de Recerca de Química Teòrica i Computacional, Universitat de Barcelona, Diagonal 645, 08028, Barcelona, Spain
First published on 3rd June 2025
Abstract
The field of molecule magnets has advanced significantly in recent years. Yet, key challenges persist for their practical applications, such as achieving higher blocking temperatures and maintaining precise temperature control in air-stable magnets. This work addresses aspects related to both challenges. Thus, it presents the air-stable hexagonal bipyramidal compound {[Dy(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1·1.5CH2Cl2) and its diluted analogue {[Dy0.1Y0.9(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1@Y·1.5CH2Cl2). Their high axiality, achieved by reducing equatorial charge, enables magnetic behaviour with energy barriers higher than 1500 K and blocking temperatures based on hysteresis (THB) of 12 and 40 K, respectively. Hence, 1@Y·1.5CH2Cl2 is the SMM with the highest THB reported among air-stable uncapsulated molecule magnets. Besides, both complexes show temperature-dependent luminescence. Remarkably, 1@Y·1.5CH2Cl2 stands out as the pioneering example of a bifunctional molecule magnet and luminescent thermometer with both functionalities active below its THB. This breakthrough makes it possible to monitor the temperature of a molecule in the range where it exhibits remanent magnetization for the first time. Moreover, this molecular material presents by far the best magnetic characteristics (Ueff and THB) of any SMM luminescent thermometer reported to date. Experimental magnetic and luminescent data are analysed using theoretical calculations. Notably, luminescence is interpreted via coupled cluster methods, offering a more sophisticated alternative to the traditional time-dependent DFT approach.
Introduction
Multifunctionality is the future goal of new smart materials. In this context, the development of magneto-luminescent molecular materials is a scientific field of growing interest. Single molecule magnets (SMMs) are very promising due to its potential applications in technologically significant areas such as magnetic storage1 and quantum computing.2,3 However, one of the primary challenges to overcome before such technological applications become feasible is attaining their precise temperature control, which is essential for maintaining the magnetized state and preserving magnetic memory. Nevertheless, conventional thermometers are not suitable for measuring temperature at the nanoscale. Therefore, constructing microdevices based on SMMs with integrated thermometric capabilities could overcome this limitation. In this regard, obtaining SMMs with temperature-dependent luminescence represents a key issue.4,5 Achieving this end will allow SMMs to function as in situ thermometers, enabling continuous self-monitoring of their temperature, thus avoiding the loss of magnetic behaviour resulting from excessive heating. Since the first compounds displaying dual SMM and luminescent thermometer characteristics, described in 2019,6–9 the number of additional compounds with such bifunctional nature reported to date remains relative low.10–29 Since then, there have been substantial enhancements in the magnetic and thermometric properties of these molecular nanomaterials. Accordingly, a few compounds have been described that show thermometric character in part of the temperature range where they present slow relaxation of magnetization in the absence of an external field.7,14–16,21–23 However, it is worth noting that none of these complexes behaves as a luminescent thermometer below the blocking temperature of the SMM.Consequently, another major challenge in this research field is the obtaining of air-stable SMMs of high blocking temperature. In this regard, it should be noted that the blocking temperature based on magnetic hysteresis (THB) of 80 K, established with an organometallic mononuclear SMM,30 has not been surpassed, but matched with another dinuclear mixed valent dysprosium metallocene.31 Nevertheless, the air instability of these organometallic compounds is challenging for their practical utility. This inconvenience has led to an active search for air-stable SMMs with improved properties. In this way, a dysprosium azafullerene with a 100-seconds blocking temperature of 45 K (THB = 39 K) was recently reported,32 but the current record of THB for unencapsulated SMMs is 36 K, which is held by a dysprosium complex with pentagonal bipyramid geometry.33 In recent years, other air-stable mononuclear SMMs with hexagonal bipyramid geometry have been obtained, with energy barriers exceeding 2400 K,34 and blocking temperatures up to 20 K.35 However, within SMMs that in turn behave as luminescent thermometers, the energy barriers and blocking temperatures do not exceed 944 K and 8 K, respectively.23
Developing lanthanoid luminescent thermometers with exceptionally high-energy barriers, leading to substantial crystal field (CF) splitting of both ground and excited state multiplets, presents a significant challenge. This arises because the thermal sensitivity of Boltzmann-type luminescent thermometers hinges on the energy gap between the thermally coupled excited states. Large energy gaps can compromise high relative thermal sensitivity across the entire temperature range where slow relaxation occurs.36 Consequently, a fundamental obstacle remains in the development of molecular magnets that function as luminescent thermometers within their operational regime.
One potential way to circumvent this theoretical limitation would be to base the luminescent thermometric behaviour of the magnet not on the metal, but on the ligand. This would involve designing lanthanoid complexes with luminescent ligands that in turn predetermine a suitable geometry to favour high anisotropy. This strategy could lead to the improvement of the parameters Ueff and THB in SMMs with luminescence thermometry, as well as to the achievement of the performance of both mentioned magnetic and optical properties in the same temperature range.
Building on these assumptions, we analyse the thermometric properties of the high-performance SMM {[Dy(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1·1.5CH2Cl2). This analysis is based on ligand triplet emission coupled with Dy3+ luminescence. In addition, we also present here the bifunctional analogue {[Dy0.1Y0.9(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1@Y·1.5CH2Cl2), which exhibits Dy3+-based slow relaxation of the magnetization and ligand-based luminescence thermometry. Both compounds are molecule magnets that function as optical thermometers, with magnetic properties surpassing those of any SMM with luminescence thermometry described so far. Notably, 1@Y·1.5CH2Cl2 is the first SMM capable of operating as a luminescent thermometer below its blocking temperature. Thus, 1@Y·1.5CH2Cl2 shows bifunctionality up to 40 K.
Results and discussion, experimental
Synthesis and structural characterization
{[Dy(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1·1.5CH2Cl2) was isolated from previously reported {[Dy(LN6en)(CH3COO)2](NO3)}·2H2O,25 through a modified version of a published method,37,38 as illustrated in Fig. 1. | ||
| Fig. 1 Reaction scheme for the isolation of 1 from related {[Dy(LN6en)(CH3COO)2](NO3)}. Solvate molecules are omitted for clarity. | ||
Recrystallisation of the isolated solid by diffusion of diethyl ether into a dichloromethane solution of the complex at ca. 5 °C allowed to collection of colourless single crystals of {[Dy(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1·1.5CH2Cl2). This compound is stable in air, as no significant changes were observed in the experimental powder X-ray diffractogram (Fig. S1†) or in its elemental analyses after one year. Moreover, no noticeable changes in colour or appearance were observed upon exposure to air over the same period.
The diluted {[Dy0.1Y0.9(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1@Y·1.5CH2Cl2) complex was similarly obtained, by mixing dysprosium and yttrium species in the adequate ratios (see ESI†). The composition and purity of the yttrium species was checked by elemental analysis and 1H NMR spectroscopy (ESI†). The Dy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y proportion for 1@Y·1.5CH2Cl2 was corroborated by micro X-ray fluorescence techniques.
Y proportion for 1@Y·1.5CH2Cl2 was corroborated by micro X-ray fluorescence techniques.
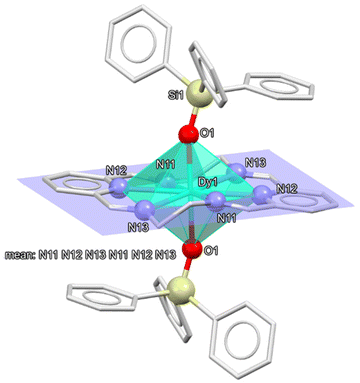
The experimental data for the X-ray diffraction studies of 1·1.5CH2Cl2 are summarised in Table S1.† The asymmetric unit of 1·1.5CH2Cl2 contains two crystallographically different, but chemically equivalent, halves of the cationic complex [Dy(LN6en)(OSiPh3)2]+, whose metal atoms are sited on inversion centres, and a whole [BPh4]− anion. Consequently, the two whole complex molecules, which will be called 1a and 1b, are respectively generated by the symmetry operations (−x + 2, −y + 2, −z) and (−x + 1, −y + 1, −z + 1). Ellipsoid diagrams of the cations of these two molecules are shown in Fig. 2 and S2,† respectively. Moreover, the asymmetric unit includes disordered molecules of dichloromethane as solvate, summing up to 1.5 molecules per complex unit. In addition to the disorder shown by the solvates, for cation 1b (which contains Dy2), some atoms (N21, N23 and the contiguous ethylene chains) are also disordered on two sites (occupation sites 0.51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.49).
0.49).
The cationic complex [Dy(LN6en)(OSiPh3)2]+ displays an N6O2 coordination environment, similar to those observed for other octacoordinated dysprosium complexes derived from N6 macrocycles (Table S2†),39 with {[Dy(L8)(Ph3SiO)2](BPh4)}38 (L8 = (2E,6E,9E,13E)-2,7,9,14-tetramethyl-3,6,10,13-tetraaza-1,8(2,6)-dipyridinacyclotetradecaphane-2,6,9,13-tetraene) being particularly alike, since the main difference with 1 is the presence of methyl groups on the imine carbon atoms of L8. Calculations of the degree of distortion of the DyN6O2 core relative to an ideal polyhedron of eight vertexes made for 1 with the SHAPE program40,41 (Table S3†), reveal a hexagonal bipyramid (hbp) geometry. The neutral N6 donor macrocycle lies in the equatorial plane, with both triphenylsilanolate anions occupying opposite apical positions with a perfect O-Dy-O angle of 180°. With such low distortion of the polyhedron, Dy1 is contained in the calculated plane formed by the six N-donor atoms, while these latter ones only protrude ca. 0.15 Å from the calculated plane. It is remarkable that the deviation from an ideal hbp is also notably smaller for 1 (Table S2†) than for the mentioned {[Dy(L8)(Ph3SiO)2](BPh4)},38 since its ChSM value is 2.163, while this value is between 1.12 and 1.44 for 1. The main geometric parameters of this compound are listed in Table S4,† with typical values, including both coordination Dy–O and Dy–N distances, which are within the usual ranges found for other related compounds.39
Powder X-ray diffraction measurements for 1·1.5CH2Cl2 (Fig. S1†) reveal that the isolated product was obtained with high purity, as no additional peaks were observed in the experimental diffractogram. Furthermore, the diffractogram of the complex was remeasured after one year, demonstrating that both patterns are equal. These results confirm the air stability of the compound, without detecting any sign of decomposition.
In addition, the powder X-ray diffractogram for the diluted analogue 1@Y·1.5CH2Cl2 (Fig. S3†) agrees with a very similar structure to that of 1·1.5CH2Cl2.
Magnetic studies
Direct-current (dc) magnetic susceptibility measurements for 1·1.5CH2Cl2 were recorded in the 2–300 K temperature range. The χMT vs. T graph is shown in Fig. S4.† The χMT value at 300 K is 14.4 cm3 K mol−1, which is close to the expected one for an uncoupled Dy3+ ion at room temperature (14.17 cm3 K mol−1). The experimental curve remains basically constant up to 15 K, and then it drops sharply, to reach a value of 4.8 cm3 K mol−1 at 2 K. This great drop seems to indicate magnetic blocking more than the presence of large crystal field splitting.35 In fact, ab initio calculations (vide infra), which take into account the large crystal field, do not show such sharp drop at low T (Fig. S4†). The field dependence of the reduced magnetisation at 2 K at the maximum applied field of 5 T tends to 5.5 Nμβ, suggesting a highly anisotropic Dy3+ ion with an Ising-like ground doublet.42 Moreover, the magnetisation graph shows a sigmoidal shape at low field, which is often found for high-performance SMMs.35,43The dynamic magnetic properties of 1·1.5CH2Cl2 were also studied, and they show out-of-phase frequency dependence of the susceptibility  as a function of the temperature up to 100 K (Fig. 3).
as a function of the temperature up to 100 K (Fig. 3).
 | ||
Fig. 3 Frequency dependence of  for 1·1.5CH2Cl2 at Hdc = 0 at frequencies ranging from: (a) 0.1 to 1500 Hz; (b) 50 to 10 for 1·1.5CH2Cl2 at Hdc = 0 at frequencies ranging from: (a) 0.1 to 1500 Hz; (b) 50 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz. Solid lines are fits to the data. 000 Hz. Solid lines are fits to the data. | ||
In addition, the Cole–Cole plots (Fig. S5†) display curves with α parameters in the range 0.3–0.1 (Table S5†), indicative of various relaxation processes.37,44 The presence of multiple relaxation mechanisms is also supported by the dependence of the relaxation time τ with temperature in the 2–100 K range (Fig. 4), which shows varying behaviour across different temperature ranges. Thus, below 10 K, the relaxation is almost independent of temperature and this behaviour points out to a quantum tunnelling of magnetisation (QTM) mechanism. Above this temperature, the shape of the curve is in agreement with the presence of thermally activated processes.32
Hence, attempts were made to fit this plot considering all the possible relaxation mechanisms except the Direct one (Orbach, Raman, and QTM), according to eqn (1), individually or grouped.
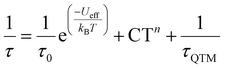 | (1) |
The best fit of the data (Fig. 4) is obtained considering the three relaxation processes, and this renders the parameters Ueff = (1528 ± 6) K [(1062 ± 4) cm−1], τ0 = (6.9 ± 0.3) × 10−11 s, C = (8.5 ± 0.1) × 10−4 s−1 K−n, n = (3.2 ± 0.2) and τQTM = (0.2 ± 0.1) s. The n value can seem quite low, but considerations of both the acoustic and optical phonons in magnetic dynamics can explain the deviation from the predicted value for the Kramers ion (n = 9).45,46
The comparison of these data with those obtained for some magneto-structurally characterised mononuclear dysprosium SMMs with N6 macrocycles and triphenylsilanolate as ligands (Table S2†)35,38,43,47 allows to draw some conclusions. Thus, comparison between 1·1.5CH2Cl2 and {[Dy(L8)(Ph3SiO)2](BPh4)}38 clearly shows that removing an electron-donating group from the N6 macrocyclic ligand, such as the methyl one, significantly improves the energy barrier for the spin reversal. From this, 1·1.5CH2Cl2 has a barrier of ca. 1500 K, while for {[Dy(L8)(Ph3SiO)2](BPh4)} Ueff is ca. 1100 K.38 The absence of the methyl groups in 1·1.5CH2Cl2 results in a more perfect hbp polyhedron. However, this less deviated geometry does not explain by itself the improved results, as Table S2† evidences. Accordingly, this work deepens in the fact that the elimination of electron-donating substituents in the equatorial plane is a key factor in enhancing the behaviour of SMMs, as previously inferred.39
Variable-field magnetisation measurements revealed the trends in magnetic relaxation behaviour. The data were recorded by scanning the field between −3 and 3 T, employing an average sweep rate of 10 mT s−1. At low temperatures, the magnetisation value experiences a steep decline close to H = 0 (Fig. 5a) but with open curves, which also suggests the existence of fast QTM relaxation. This relaxation mechanism is common among dysprosium hexagonal bipyramidal SMMs (Table S2†). In spite of this, the complex shows open thin hysteresis till 12 K (Fig. 5a and b). The blocking temperature THB was established by observing the last temperature at which the remanent magnetisation decreases, a criterion commonly used32,48 to establish the THB values in different SMMs. The low values of magnetisation and coercive field cannot be attributed to artefacts due to errors in measures, given that the field was corrected using a palladium standard measured under the same conditions.
In addition, zero-field-cooled (ZFC) and field-cooled (FC) magnetic susceptibility curves show divergence up to 10 K (Fig. S6†), supporting the hysteresis results.
An yttrium magnetically diluted mixed compound {[Dy0.1Y0.9(LN6en)(OSiPh3)2](BPh4)}·1.5CH2Cl2 (1@Y·1.5CH2Cl2) was also synthesized in order to improve the magnetic blocking. The relaxation times (Fig. 4) extracted from the  vs. ν graph (Fig. S7†) for 1@Y·1.5CH2Cl2 closely overlap with those of 1·1.5CH2Cl2 above 20 K (Fig. 4). However, below 20 K, both curves differ significatively and the one for 1@Y·1.5CH2Cl2 shows a gradual but more pronunced drop of the τ−1 values with temperature compared to 1·1.5CH2Cl2. This could suggets a reduction of the QTM. Nevertheless, the Cole–Cole plots (Fig. S8†) and the dependence of τ with temperature still agree with various relaxations mechanism. Thus, the best fitting of the relaxation times for the diluted complex renders the parameters Ueff = (1531 ± 5) K [(1064 ± 2) cm−1], τ0 = (4.3 ± 0.1) × 10−12 s, C = (5.7 ± 0.5) × 10−5 s−1 K−n, n = (3.8 ± 0.2) and τQTM = (0.6 ± 0.2) s. Accordingly, it seems that the dilution partially suppresses the QTM.49
vs. ν graph (Fig. S7†) for 1@Y·1.5CH2Cl2 closely overlap with those of 1·1.5CH2Cl2 above 20 K (Fig. 4). However, below 20 K, both curves differ significatively and the one for 1@Y·1.5CH2Cl2 shows a gradual but more pronunced drop of the τ−1 values with temperature compared to 1·1.5CH2Cl2. This could suggets a reduction of the QTM. Nevertheless, the Cole–Cole plots (Fig. S8†) and the dependence of τ with temperature still agree with various relaxations mechanism. Thus, the best fitting of the relaxation times for the diluted complex renders the parameters Ueff = (1531 ± 5) K [(1064 ± 2) cm−1], τ0 = (4.3 ± 0.1) × 10−12 s, C = (5.7 ± 0.5) × 10−5 s−1 K−n, n = (3.8 ± 0.2) and τQTM = (0.6 ± 0.2) s. Accordingly, it seems that the dilution partially suppresses the QTM.49
The hysteresis cycles recorded for 1@Y·1.5CH2Cl2 also show thin hysteresis, with open loops up to 40 K (Fig. 5c and d). Consequently, the diminishment of the QTM in the diluted sample seems to result in a significant improvement in the blocking temperature. However, the observed enhancement might also be partly driven by changes in the Raman relaxation mechanism, the mitigation of which generally leads to an improvement in the magnetic properties.50
FC/ZFC measurements for 1@Y·1.5CH2Cl2 also reveal divergences in the curves up to 40 K (Fig. S9†), though no clear peaks are present. A similar absence of peaks was noted by Coronado in the encapsulated stable molecule magnet with THB of 39 K, which also exhibits thin magnetic hysteresis.32
Therefore, the FC/ZFC measurements also support the hysteresis results. Consequently, to the best of our knowledge, the blocking temperature for 1@Y·1.5CH2Cl2 exceeds the reported highest THB of 36 K (sweep rate 20 mT s−1) for uncapsulated, air-stable SMMs, establishing a new record.
Ab initio calculations
Multiconfigurational SA-CASSCF calculations51 with the SINGLE_ANISO code,52 as implemented in Orca 5.0.3,53–55 have been performed to gain more insight into the magnetic properties of 1. The atom coordinates of both complex units present in the crystal structure have been employed. In the case of 1b, due to the disorder of the experimental geometry, two models have been created (1b_1 and 1b_2, see computational details in ESI and Fig. S10†). The results obtained for the three independent calculated molecules are similar, so we have included here only the results for 1a. Meanwhile, 1b results are collected in the ESI.† For the Dy3+ ion, the ground state 6H15/2 is formed by eight Kramers Doublets (KDs). For 1a the KDs span in an energy range of about 1450 cm−1 (Table 1). Analysis of the KDs and their g-factors reveals a very large easy-axis anisotropy in the complex (Tables 1, S6 and S7†).| Energy (cm−1) | g xx | g yy | g zz | θ (°) |
|---|---|---|---|---|
| 0 | 0.00025 | 0.00027 | 19.883 | |
| 519.9 | 0.066 | 0.068 | 16.973 | 4.712 |
| 941.6 | 0.007 | 0.081 | 14.004 | 7.198 |
| 1206.6 | 1.343 | 1.532 | 9.238 | 12.346 |
| 1296.3 | 1.597 | 8.440 | 10.993 | 85.867 |
| 1323.6 | 1.148 | 6.988 | 11.265 | 86.580 |
| 1375.9 | 1.315 | 2.223 | 7.640 | 88.050 |
| 1443.1 | 0.563 | 7.319 | 12.239 | 80.777 |
The ground state KD is mJ = |± 15/2〉, which is highly anisotropic, and it is characterised by a large axial g component and a small transverse one. The anisotropy gzz axis for 1a lies mostly along the O–Dy–O direction, as shown in Fig. 6a.
The first and second excited KDs are also highly anisotropic with large axial g components. Additionally, for the first and second excited KDs, the gzz axis are aligned close (tilting angles smaller than 8°) to the ground state one, decreasing the probability of relaxation through those states. Moreover, the ab initio blocking barrier has been computed (Fig. 6b), suggesting that relaxation occurs through the third excited state, located around 1200 cm−1, close to the experimental value of 1062 cm−1.
Quite similar results were observed for 1b (see Tables S6, S7, Fig. S11 and S12†), demonstrating that ab initio calculations support the experimentally found energy barrier.
Photoluminescence and luminescence thermometry
To assess the potential of the prepared SMMs as thermographic materials, the temperature-dependent solid-state emission spectra of 1·1.5CH2Cl2 and 1@Y·1.5CH2Cl2 were acquired upon excitation at 364 and 461 nm, respectively (corresponding to the maxima observed in their excitation spectra, Fig. S13†). A significant influence of dilution on the luminescence was observed, as discussed below.For 1·1.5CH2Cl2, the emission spectrum (Fig. S14a†) exhibits characteristic Dy3+ intra-4f transitions (4F9/2 → 6H11/2, 4F9/2 → 6H13/2, and 4F9/2 → 6H15/2) at approximately 659, 590, and 488 nm, respectively. These transitions, however, display low relative intensity and are only observed up to 145 K. Additionally, a broad band in the UV-visible spectral range (380–550 nm) attributed to ligand-based emission25 dominates the spectra across the entire temperature range. At low temperatures, this band is significantly intense and quenches as the temperature rises (Fig. S14a†).
To explore this temperature-dependent behaviour for luminescence thermometry, the ratio of the integrated areas I1 (ligand), I2 (4F9/2 → 6H15/2), and I3 (4F9/2 → 6H13/2), Δ1 = (I2 + I3)/I1, was employed as the thermometric parameter (Fig. S14b and c†). As temperature increases, Δ1 decreases, indicating the potential of 1·1.5CH2Cl2 as a luminescent thermometer in the 13–120 K range. A phenomenological linear calibration curve was fitted to the data (Fig. S14c†), with the corresponding parameters summarized in Table S8.† The thermometric performance was further evaluated using the relative thermal sensitivity (Sr) and temperature uncertainty (δT), the standard figures of merit for luminescent thermometers (see ESI for details†).56 A maximum Sr of 3.5% K−1 and a minimum δT of 3.0 K at 120 K were obtained (Fig. S14d, e and Table S8†). These results show a modest thermometric performance. However, they also validate the viability of 1·1.5CH2Cl2 as a functional luminescent thermometer, capable of providing approximate temperature monitoring within the studied range, despite this range being above the magnetic blocking temperature of 1·1.5CH2Cl2, 12 K (as it occurs for all reported SMMs). Even so, this is the SMM with the highest effective energy barrier and blocking temperature for which luminescent thermometry has been observed, the previous records being at 994 K and 8 K, respectively.23
Since 1@Y·1.5CH2Cl2 exhibits a blocking temperature of 40 K, its temperature-dependent luminescence was also evaluated and, as discussed below, the results demonstrate that it is the first SMM operating as a luminescent thermometer below its blocking temperature.
The emission spectra of 1@Y·1.5CH2Cl2 show a broad emission band centred at 575 nm (Fig. 7a), indicative of ligand-based luminescence. Although this band may appear red-shifted compared to that of the undiluted complex 1·1.5CH2Cl2, the shift arises from the use of a different excitation wavelength (461 nm) to maximize emission. When both spectra are recorded under identical excitation conditions (364 nm), the broad emission bands are centred at the same wavelength (Fig. S15†), confirming that no actual red shift occurs upon dilution.
 | ||
| Fig. 7 (a) Temperature-dependent emission spectra of 1@Y·1.5CH2Cl2 excited at 461 nm. (b) Temperature dependence of the thermometric parameter (Δ2) for 1@Y·1.5CH2Cl2. The line represents the best linear fit (r2 > 0.98) to the experimental data (fit details provided in Table S8†). (c) Temperature dependence of Sr for 1@Y·1.5CH2Cl2. (d) Temperature dependence of δT for 1@Y·1.5CH2Cl2. | ||
In the diluted sample, with only 10% of the metal ion being Dy3+, the signal from Dy3+ completely vanishes, thus leaving only the ligand emission observable.13 Therefore, as the spectra are dominated by a ligand-band emission, the signal is not expected to be influenced by the coercive magnetic field retained in the sample once it is magnetized. Furthermore, excitation at 461 nm prevents efficient energy transfer from the ligand to the Dy3+ ion. As a result, the electronic energy levels of the Dy3+ centre should remain unaffected by the irradiation, preserving the single-molecule magnet behaviour. Consequently, this selective excitation is particularly advantageous, as it allows for luminescence thermometry to be performed without disturbing the magnetic relaxation dynamics. In contrast to systems where excitation can lead to changes in the population of the 4f electronic states of the lanthanoid ion -thus potentially altering its magnetic anisotropy or inducing changes in the relaxation processes-, this approach minimizes such risks by avoiding direct excitation of Dy3+. Hence, the separation of optical and magnetic pathways in 1@Y·1.5CH2Cl2 supports the potential for simultaneous operation of both functionalities.
In an effort to elucidate the underlying mechanism of the emission spectra, time-dependent density functional theory (TDDFT) calculations were performed on the X-ray structure of 1·1.5CH2Cl2 using hybrid correlation and exchange functionals like B3LYP57 or PBE0.58 However, these functionals, commonly used for such studies, yielded unrealistic results, indicating degeneracy of the excited singlet and triplet states.59 This well-documented issue is often encountered in systems exhibiting long-range charge transfer excitations.59,60 To better describe long-range interactions, long-range corrected functionals (e.g. CAM-B3LYP61) or double-hybrid functionals (e.g. SCS/SOS-wB2PLYP62) are often employed. While these functionals partially alleviate the degeneracy issue for some optimised geometries of the first and fundamental excited states, they still yield unreasonable excitation energies significantly higher than experimental values.
To overcome these limitations, coupled-cluster calculations were performed using the STEOM-DLPNO-CCSD (similarity transformed equation of motion approach combined with the domain-based local pair orbital implementation of coupled-cluster singles and doubles) method54,63–68 implemented in Orca 5.0.3.53–55 This methodology does not present the problems of the TDDFT with the charge transfer excitations but is computationally demanding, limiting its applicability to smaller systems, preventing the calculation of the complete lanthanoid complex. Thus, the ligands LN6en, Ph3SiO− and the counterion BPh4− were analysed separately. The STEOM-DLPNO-CCSD results (Table S9†) show that the lowest singlet excitation originates from the axial Ph3SiO− ligand (309 nm), while the lowest-energy triplet emission arises from the equatorial ligand (423 nm). These results qualitatively agree with experimental observations, suggesting a possible charge transfer between the two ligands, consistent with the difficulties encountered in TDDFT calculations. They also suggest that BPh4− is unlikely to participate directly in a charge transfer process with the ligands, given that its first singlet excited state appears at significantly higher energy (261 nm). While the STEOM-DLPNO-CCSD calculations provide a reasonable description, considering the limitations of calculating the complete system, a quantitative reproduction of experimental data remains challenging. Accordingly, the temperature dependence of the emission spectra of 1@Y·1.5CH2Cl2 can be explained by two distinct ligand-based components. To quantify these contributions, we employed a deconvolution technique with two Gaussian components (Fig. S16a†). The resulting fitting parameters (peak energy, width, and integrated area) are summarized in Table S10 in ESI.† Notably, while peak energy and width remain constant, the integrated area of each component (A1 and A2) decreases with increasing temperature (Fig. S16b†). This suggests a temperature-dependent variation in the relative intensities of these ligand-based emissions. Therefore, to demonstrate the applicability of 1@Y·1.5CH2Cl2 as a ratiometric luminescent thermometer, we employed the ratio of the integrated areas of the two Gaussian components (Δ2 = A1/A2, Fig. 7b). In the absence of a theoretical framework for this ratio, a phenomenological linear calibration curve was established (parameters in Table S8 of the ESI†) and the thermometric performance was evaluated using Sr and δT values. 1@Y·1.5CH2Cl2 operates as a luminescent thermometer in the 13–325 K temperature range. While the maximum Sr (0.2% K−1) and minimum δT (1.0 K), both at 325 K, are not exceptional (Fig. 7c and d), they are comparable to other broadband emission materials.56
Despite this, the relatively low uncertainty (below 1.7 K across the entire temperature range) allows for temperature monitoring of cryogenic magnets, indicating that 1@Y·1.5CH2Cl2 is a luminescent thermometer below its THB (40 K). Thus, 1@Y·1.5CH2Cl2 represents a dual magneto-optical molecule, capable of self-monitoring its temperature, and this advancement helps address the challenge of temperature monitoring in molecular magnetic nanomaterials where conventional thermometers are impractical, in order to avoid their loss of magnetization.
Conclusions
This work, which reports a high-performance mononuclear SMM (1·1.5CH2Cl2) and its yttrium diluted analogue (1@Y·1.5CH2Cl2), unveils the first SMM capable of self-monitoring temperature within the range where it acts as a magnet. Significantly, 1@Y·1.5CH2Cl2 is an air-stable SMM that exhibits a blocking temperature of 40 K, the highest THB among uncapsulated air-stable molecule magnets reported to date. The integration of luminescence thermometry and magnet performance in this diluted material, with a high energy barrier (>1000 cm−1), is achieved through a meticulous design that separates the origin of the magnetic properties, which relies on Dy3+ ions, from the luminescence, that is based on the emitting ligands. This approach diverges from conventional SMMs, where the lanthanoid ion contributes to both functions, often limiting the potential for high-performance luminescent magnets. Our strategy, exemplified by 1@Y·1.5CH2Cl2, overcomes this limitation, and provides a route for non-invasive optical interrogation of the material, enabling temperature readout without compromising the magnetic state. This separation of optical and magnetic pathways supports the simultaneous operation of both functionalities. Besides, 1@Y·1.5CH2Cl2 holds the distinction of being the SMM with the highest energy barrier and blocking temperature reported to date while simultaneously enabling self-temperature monitoring through luminescence thermometry.Rigorous theoretical calculations, including innovative coupled cluster methods for luminescence analysis (instead of the more commonly used time-dependent DFT ones), provide robust support for the experimental magnetic and luminescent data.
As a result, this work sets a new standard for designing SMMs with enhanced integrated luminescence thermometry. Future research will focus on refining this strategy through ligand optimization to achieve even higher operational temperatures. Subtle modifications to the ligand can influence the coordination environment of the lanthanoid ions, resulting in increased magnetic anisotropy, and the material's luminescent properties, enhancing overall performance and functionality.
Author contributions
Conceptualization: M. F., J. C.-V., E. R., L. D. C.; methodology: J. C.-V., C. G.-B., J. S.-M., S. G.-C.; validation: M. F., E. R., L. D. C.; formal analysis: J. C.-V., M. F., A. M. G.-D., S. G.-C., E. R., C. D. S. B.; investigation: J. C.-V., C. G.-B.; resources: M. F., E. R., L. D. C.; visualization: J. C.-V., C. G.-B., S. G.-C., C. D. S. B.; data curation and supervision: M. F., E. R., L. D. C.; writing – original draft preparation: M. F., J. C.-V., E. R., S. G.-C., L. D. C.; project administration: M. F., L. D. C.; funding acquisition: M. F., E. R., L. D. C.Data availability
The data supporting this article have been included as part of the ESI.†Crystallographic data for 1·1.5CH2Cl2 have been deposited with The Cambridge Crystallographic Data Centre (CCDC 2262113†).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Universidade de Santiago de Compostela (2024-PU027-1), Consellería de Cultura, Educación, Formación Profesional e Universidades, Xunta de Galicia (convenio 2023-1298), by Portuguese funds through the FCT/MCTES (PIDDAC) (UIDB/50011/2020, https://doi.org/10.54499/UIDB/50011/2020; UIDP/50011/2020, https://doi.org/10.54499/UIDP/50011/2020; and LA/P/0006/2020, https://doi.org/10.54499/LA/P/0006/2020 projects of the CICECO-Aveiro Institute of Materials), and by Ministerio de Ciencia, Innovación y Universidades (PID2021-122464NB-I00 and Maria de Maeztu CEX2021-001202-M). This article is based upon work from COST Action CA22131, supported by COST (European Cooperation in Science and Technology). J. C. V. also thanks Xunta de Galicia for his postdoctoral fellowship (ED481B-2022-068). We also acknowledge the Generalitat de Catalunya for the 2021-SGR-00286 grant and E. R. for an ICREA Academia grant. We thank CSUC and BSC supercomputer centres for the computational resources.References
- R. Sessoli, Single-atom data storage, Nature, 2017, 543, 189–190 CrossRef CAS.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Molecular spins for quantum computation, Nat. Chem., 2019, 11, 301–309 CrossRef.
- M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS.
- R. Marin, G. Brunet and M. Murugesu, Shining New Light on Multifunctional Lanthanide Single-Molecule Magnets, Angew. Chem., Int. Ed., 2021, 60, 1728–1746 CrossRef CAS.
- A. G. Bispo-Jr, Multifunctional lanthanide(III) single-molecule magnets displaying luminescence thermometry: Progress, challenges, and future directions, Coord. Chem. Rev., 2025, 537, 216685 Search PubMed.
- G. Brunet, R. Marin, M.-J. Monk, U. Resch-Genger, D. A. Gálico, F. A. Sigoli, E. A. Suturina, E. Hemmer and M. Murugesu, Exploring the dual functionality of an ytterbium complex for luminescence thermometry and slow magnetic relaxation, Chem. Sci., 2019, 10, 6799–6808 RSC.
- D. Errulat, R. Marin, D. A. Gálico, K. L. M. Harriman, A. Pialat, B. Gabidullin, F. Iikawa, O. D. D. Couto Jr., J. O. Moilanen, E. Hemmer, F. A. Sigoli and M. Murugesu, A luminescent thermometer exhibiting slow relaxation of the magnetization: toward self-monitored building blocks for next-generation optomagnetic devices, ACS Cent. Sci., 2019, 5, 1187–1198 CrossRef CAS.
- D. A. Gálico, R. Marin, G. Brunet, D. Errulat, E. Hemmer, F. A. Sigoli, J. O. Moilanen and M. Murugesu, Triplet-State Position and Crystal-Field Tuning in Opto-Magnetic Lanthanide Complexes: Two Sides of the Same Coin, Chem. – Eur. J., 2019, 25, 14625–14637 CrossRef.
- K. Kumar, D. Abe, K. Komori-Orisaku, O. Stefańczyk, K. Nakabayashi, J. R. Shakirova, S. P. Tunik and S.-I. Ohkoshi, Neodymium β-diketonate showing slow magnetic relaxation and acting as a ratiometric thermometer based on near-infrared emission, RSC Adv., 2019, 9, 23444–23449 RSC.
- J. Wang, J. J. Zakrzewski, M. Heczko, M. Zychowicz, K. Nakagawa, K. Nakabayashi, B. Sieklucka, S. Chorazy and S.-I. Ohkoshi, Proton conductive luminescent thermometer based on near-infrared emissive {YbCo2} molecular nanomagnets, J. Am. Chem. Soc., 2020, 142, 3970–3979 CrossRef CAS.
- M. Fondo, J. Corredoira-Vázquez, A. M. García-Deibe, J. Sanmartín-Matalobos, M. Amoza, A. M. P. Botas, R. A. S. Ferreira, L. D. Carlos and E. Colacio, Field-induced slow magnetic relaxation and luminescence thermometry in a mononuclear ytterbium complex, Inorg. Chem. Front., 2020, 7, 3019–3029 RSC.
- J. Wang, J. J. Zakrzewski, M. Zychowicz, V. Vieru, L. F. Chibotaru, K. Nakabayashi, S. Chorazy and S.-I. Ohkoshi, Holmium(III) molecular nanomagnets for optical thermometry exploring the luminescence re-absorption effect, Chem. Sci., 2021, 12, 730–741 Search PubMed.
- S. Ma, T. Zhang, J.-P. Zhao, Z.-Y. Liu and F.-C. Liu, A magnetic site dilution approach to achieve bifunctional fluorescent thermometers and single-ion magnets, Dalton Trans., 2021, 50, 1307–1312 RSC.
- A. A. Kitos, D. A. Gálico, N. Mavragani, R. Castañeda, J. O. Moilanen, J. L. Brusso and M. Murugesu, Probing optical and magnetic properties via subtle stereoelectronic effects in mononuclear DyIII-complexes, Chem. Commun., 2021, 57, 7818–7821 Search PubMed.
- R. A. S. Ferreira, E. Mamontova, A. M. P. Botas, M. Shestakov, J. Vanacken, V. Moshchalkov, Y. Guari, L. F. Chibotaru, D. Luneau, P. S. André, J. Larionova, J. Long and L. D. Carlos, Synchronous temperature and magnetic field dual-sensing by luminescence in a dysprosium single-molecule magnet, Adv. Opt. Mater., 2021, 9, 2101495 CrossRef CAS.
- R. Marin, D. A. Gálico, R. Gayfullina, J. O. Moilanen, L. D. Carlos, D. Jaque and M. Murugesu, A zero-field single-molecule magnet with luminescence thermometry capabilities containing soft donors, J. Mater. Chem. C, 2022, 10, 13946–13953 Search PubMed.
- V. Tangoulis, V. Nastopoulos, N. Panagiotou, A. Tasiopoulos, G. Itskos, M. Athanasiou, E. Moreno-Pineda, W. Wernsdorfer, M. Schulze and O. Malina, High-performance luminescence thermometer with field-induced slow magnetic relaxation based on a heterometallic cyanido-bridged 3d–4f complex, Inorg. Chem., 2022, 61, 2546–2557 Search PubMed.
- K. Karachousos-Spiliotakopoulos, V. Tangoulis, N. Panagiotou, A. Tasiopoulos, V. Nastopoulos, E. Moreno-Pineda, W. Wernsdorfer, M. Schulze, A. M. P. Botas and L. D. Carlos, Lanthanide luminescence thermometry and slow magnetic relaxation in 3-D polycyanidometallate-based materials, Inorg. Chem., 2022, 61, 18629–18639 CrossRef CAS PubMed.
- K. Kumar, O. Stefanczyk, K. Nakabayashi, K. Imoto, Y. Oki and S.-I. Ohkoshi, Detection of sub-terahertz Raman response and nonlinear optical effects for luminescent Yb(III) complexes, Adv. Opt. Mater., 2022, 10, 2101721 CrossRef CAS.
- K. Karachousos-Spiliotakopoulos, V. Tangoulis, N. Panagiotou, A. Tasiopoulos, E. Moreno-Pineda, W. Wernsdorfer, M. Schulze, A. M. P. Botas and L. D. Carlos, Luminescence thermometry and field induced slow magnetic relaxation based on a near infrared emissive heterometallic complex, Dalton Trans., 2022, 51, 8208–8216 RSC.
- J. Corredoira-Vázquez, C. González-Barreira, M. Fondo, A. M. García-Deibe, J. Sanmartín-Matalobos, M. A. Hernández-Rodríguez and L. D. Carlos, Luminescence thermometry in a Dy4 single molecule magnet, Dalton Trans., 2022, 51, 15593–15600 RSC.
- J. Wang, J. J. Zakrzewski, M. Zychowicz, Y. Xin, H. Tokoro, S. Chorazy and S.-I. Ohkoshi, Desolvation-induced highly symmetrical terbium(III) single-molecule magnet exhibiting luminescent self-monitoring of temperature, Angew. Chem., Int. Ed., 2023, 62, e202306372 Search PubMed.
- S. Zanella, M. Aragon-Alberti, C. D. S. Brite, F. Salles, L. D. Carlos and J. Long, Luminescent single-molecule magnets as dual magneto-optical molecular thermometers, Angew. Chem., Int. Ed., 2023, 62, e202306970 CrossRef CAS PubMed.
- A. G. Bispo-Jr, L. Yeh, D. Errulat, D. A. Gálico, F. A. Sigoli and M. Murugesu, Improving the performance of β-diketonate-based DyIII single-molecule magnets displaying luminescence thermometry, Chem. Commun., 2023, 59, 8723–8726 RSC.
- J. Corredoira-Vázquez, C. González-Barreira, A. M. García-Deibe, J. Sanmartín-Matalobos, M. A. Hernández-Rodríguez, C. D. S. Brites, L. D. Carlos and M. Fondo, Harnessing ligand design to develop primary and self-calibrated luminescent thermometers with field-induced single ion magnet behaviour in Dy3+ complexes, Inorg. Chem. Front., 2024, 11, 1087–1098 RSC.
- G. Félix, S. Sene, A. Kulakova, A. N. Bilyachenko, V. N. Khrustalev, E. S. Shubina, Y. Guari and J. Larionova, Tetranuclear lanthanide-based silsesquioxanes: towards a combination of a slow relaxation of the magnetization and a luminescent thermometry, RSC Adv., 2023, 13, 26302–26312 RSC.
- A. G. Bispo-Jr, D. A. Gálico, R. M. Diaz-Rodriguez, J. S. Ovens, F. A. Sigoli and M. Murugesu, The role of terminal ligands in the slow relaxation of magnetisation and luminescence thermometry of dinuclear NdIII complexes, Inorg. Chem. Front., 2023, 10, 3929–3939 RSC.
- A. G. Bispo-Jr, D. A. Gálico, J. S. Ovens, F. A. Sigoli and M. Murugesu, Impacts of β-diketonate terminal ligands on slow magnetic relaxation and luminescence thermometry in dinuclear DyIII single-molecule magnets, Dalton Trans., 2025, 54, 4876–4887 RSC.
- S. Shome, N. C. Maurya, M. Mukherjee, K. V. Adarsh and S. Konar, Leveraging ligand conjugation to improve luminescence thermometry in Dy-single-molecule magnets, Chem. Commun., 2025, 61, 2337–2340 RSC.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403 CrossRef CAS.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding, Science, 2022, 375, 198–202 CrossRef CAS.
- Z. Hu, Y. Wang, A. Ullah, G. M. Gutiérrez-Finol, A. Bedoya-Pinto, P. Gargiani, D. Shi, S. Yang, Z. Shi, A. Gaita-Ariño and E. Coronado, High-temperature magnetic blocking in a monometallic dysprosium azafullerene single-molecule magnet, Chem, 2023, 9, 3613–3622 CAS.
- L. Zhu, Y. Dong, B. Yin, P. Ma and D. Li, Improving the single-molecule magnet properties of two pentagonal bipyramidal Dy3+ compounds by the introduction of both electron-withdrawing and -donating groups, Dalton Trans., 2021, 50, 12607–12618 RSC.
- W.-J. Xu, Q.-C. Luo, Z.-H. Li, Y.-Q. Zhai and Y.-Z. Zheng, Bis-alkoxide dysprosium(III) crown ether complexes exhibit tunable air stability and record energy barrier, Adv. Sci., 2024, 11, 2308548 CrossRef CAS.
- Z. Zhu, C. Zhao, T. Feng, X. Liu, X. Ying, X.-L. Li, Y.-Q. Zhang and J. Tang, Air-stable chiral single-molecule magnets with record anisotropy barrier exceeding 1800 K, J. Am. Chem. Soc., 2021, 143, 10077–10082 CrossRef CAS.
- M. Suta and A. Meijerink, A Theoretical Framework for Ratiometric Single Ion Luminescent Thermometers—Thermodynamic and Kinetic Guidelines for Optimized Performance, Adv. Theory Simul., 2020, 3, 2000176 CrossRef CAS.
- Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Y.-S. Ding and Y.-Z. Zheng, Air-stable hexagonal bipyramidal dysprosium(III) single-ion magnets with nearly perfect D6h local symmetry, Chem. – Eur. J., 2019, 25, 16219–16224 CrossRef CAS PubMed.
- A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Insight into D6h symmetry: targeting strong axiality in stable dysprosium(III) hexagonal bipyramidal single-ion magnets, Angew. Chem., Int. Ed., 2019, 58, 14146–14151 CrossRef CAS.
- J. Corredoira-Vázquez, C. González-Barreira, P. Oreiro-Martínez, A. M. García-Deibe, J. Sanmartín-Matalobos and M. Fondo, Synthesis and applications of lanthanoid complexes of pentadentate and hexadentate N5 and N6 macrocycles: A review, J. Rare Earths, 2024, 42, 1–15 CrossRef.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE, version 2.1, Universitat de Barcelona, Barcelona, Spain, 2013 Search PubMed.
- A. Ruiz-Martínez, D. Casanova and S. Alvarez, Polyhedral structures with an odd number of vertices: nine-coordinate metal compounds, Chem. – Eur. J., 2008, 14, 1291–1303 CrossRef.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- S. Liu, Y. Gil, C. Zhao, J. Wu, Z. Zhu, X.-L. Li, D. Aravena and J. Tang, A conjugated Schiff-base macrocycle weakens the transverse crystal field of air-stable dysprosium single-molecule magnets, Inorg. Chem. Front., 2022, 9, 4982–4989 RSC.
- Y. Guo, K. Liu, Y. Qin, Q. Wu, K. Hu, L. Mei, Z. Chai, X. Liu, J. Yu and W. Shi, Role of molecular symmetry in the magnetic relaxation dynamics of five-coordinate Dy(III) complexes, Dalton Trans., 2023, 52, 2703–2711 Search PubMed.
- A. Singh and K. N. Shrivastava, Optical-acoustic two-phonon relaxation in spin systems, Phys. Status Solidi B, 1979, 95, 273–277 Search PubMed.
- K. N. Shrivastava, Theory of spin–lattice relaxation, Phys. Status Solidi B, 1983, 117, 437–458 CrossRef CAS.
- Z. Zhu, C. Zhao, Q. Zhou, S. Liu, X.-L. Li, A. Mansikkamäki and J. Tang, Air-Stable Dy(III)-Macrocycle Enantiomers: From Chiral to Polar Space Group, CCS Chem., 2022, 4, 3762–3771 CrossRef CAS.
- S. C. Corner, W. J. A. Blackmore, G. K. Gransbury, A. Mattioni, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, A fluorobenzene-bound dysprosium half-sandwich dication single-molecule magnet, Chem. Sci., 2025, 16, 610–620 Search PubMed.
- D. S. Krylov, F. Liu, A. Brandenburg, L. Spree, V. Bon, S. Kaskel, A. U. B. Wolter, B. Büchner, S. M. Avdoshenko and A. A. Popov, Magnetization relaxation in the single-ion magnet DySc2N@C80: quantum tunneling, magnetic dilution, and unconventional temperature dependence, Phys. Chem. Chem. Phys., 2018, 20, 11656–11672 Search PubMed.
- Q.-C. Luo and Y.-Z. Zheng, Mitigating Raman relaxation for high-temperature single-molecule magnets, Trends Chem., 2023, 5, 869–872 CrossRef CAS.
- P.-Å. Malmqvist and B. O. Roos, The CASSCF state interaction method, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- L. F. Chibotaru and L. Ungur, Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Thermometry at the nanoscale, Nanoscale, 2012, 4, 4799–4829 Search PubMed.
- A. D. Becke, Density–functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- D. Mester and M. Kállay, Charge-transfer excitations within density functional theory: how accurate are the most recommended approaches?, J. Chem. Theory Comput., 2022, 18, 1646–1662 CrossRef CAS.
- P.-F. Loos, M. Comin, X. Blase and D. Jacquemin, Reference energies for intramolecular charge-transfer excitations, J. Chem. Theory Comput., 2021, 17, 3666–3686 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- M. Casanova-Páez and L. Goerigk, Time-dependent long-range-corrected double-hybrid density functionals with spin-component and spin-opposite scaling: a comprehensive analysis of singlet-singlet and singlet-triplet excitation energies, ChemRxiv, 2021 DOI:10.26434/chemrxiv.14706042.
- A. K. Dutta, F. Neese and R. Izsák, Towards a pair natural orbital coupled cluster method for excited states, J. Chem. Phys., 2016, 145, 034102 CrossRef.
- A. K. Dutta, M. Nooijen, F. Neese and R. Izsák, Automatic active space selection for the similarity transformed equations of motion coupled cluster method, J. Chem. Phys., 2017, 146, 074103 CrossRef PubMed.
- A. K. Dutta, M. Nooijen, F. Neese and R. Izsák, Exploring the accuracy of a low scaling similarity transformed equation of motion method for vertical excitation energies, J. Chem. Theory Comput., 2017, 14, 72–91 CrossRef PubMed.
- M. Nooijen and R. J. Bartlett, Similarity transformed equation-of-motion coupled-cluster theory: details, examples, and comparisons, J. Chem. Phys., 1997, 107, 6812–6830 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, A new method for excited states: similarity transformed equation-of-motion coupled-cluster theory, J. Chem. Phys., 1997, 106, 6441–6448 CrossRef CAS.
- J. Sous, P. Goel and M. Nooijen, Similarity transformed equation of motion coupled cluster theory revisited: a benchmark study of valence excited states, Mol. Phys., 2013, 112, 616–638 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2262113. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5qi01113b |
| This journal is © the Partner Organisations 2025 |