Magneto-chiral dichroism in a chiral twistacene ytterbium(III) one-dimensional assembly of single-molecule magnets

Abstract

Here we report on one-dimensional nano objects of formula [Yb(hfac)₃(M-or P-Ant-C8)]_n where the Ant-C8 moiety refers to enantiopure M- and P-twistacenes decorated at positions 2,6 with 4-pyridyl-ethynyl units and helically locked into an end-to-end twist by an octyl tether. The crystal structure analysis reveals intertwined 1D nano-chains featuring two crystallographically independent Yb(III) ions. Under applied magnetic fields these systems show slow relaxation of the magnetization. The optical properties show the expected contributions of the ²F_7/2 ← ²F_5/2 electronic transition of the Yb(III) ions split by the crystal field. Magnetic field and temperature dependent Magneto-Chiral Dichroism (MChD) studies reveal contributions of opposite sign and similar intensity for the two crystallographically independent ions that cancel out for the 0–0′ and 0–2′ absorptions but not for the 0–1′. These findings, supported by ab intio theoretical calculations, demonstrate the important role of the structural arrangement of MChD-active ions when designing chiral magneto-optical materials responsive to light and magnetic fields.

---

Introduction

Magneto-Chiral Dichroism (MChD), a phenomenon which manifests as a differential absorption of light that chiral systems might exhibit when irradiated collinearly with a magnetic field, was theoretically predicted in 1984¹ and experimentally demonstrated in 1997 for an emissive chiral Eu(III) complex.² MChD arises from an enantioselective light–matter interaction in magnetic and optically-active molecular materials. It offers practical technological advantages since it is independent of the state of light polarization, thus it can be observed without requiring polarized light irradiation. This characteristic opens potential applications, such as optical readout of magnetic data using unpolarized light.³ As highlighted in recent reviews, MChD can be studied through UV-vis-NIR light emission or via UV-vis-NIR light and hard X-ray absorption.⁴ Another important feature of MChD is its proportionality to the magnetization of the materials.⁵ Consequently, most studies have focused on chiral molecular complexes involving paramagnetic transition metals^6–9 and lanthanide ions.^10,11 Lanthanide ions have recently become the most studied, as both a significant magnetic moment and strong spin–orbit coupling are prerequisites for observing strong MChD effects.¹² In the field of molecular magnetism, lanthanide ions are renowned for their high magnetic moments and strong magnetic anisotropy, making them ideal candidates for designing high-performance Single-Molecule Magnets (SMMs).^13,14 In this context, some of us demonstrated that promoting axial magnetic anisotropy in one-dimensional nano-objects enables the observation of slow magnetic relaxation and MChD signals up to room temperature.¹⁵ It is essential to note, however, that while the presence of SMM behaviour in lanthanide complexes is a prerequisite, it does not guarantee a strong MChD signal. Magnetic-dipole allowed f–f transitions are also required.^16,17 Finally, recent advancements have demonstrated the potential for optically detecting magnetic bistability in SMMs using unpolarized light through MChD.³

While the role of f–f transitions and magnetic properties (such as magnetization, spin–orbit coupling, and magnetic anisotropy) have been demonstrated – the former within the broader framework of the Richardson's theory of optical activity¹⁸ – the role of the type of chirality into the resulting MChD response is still unclear.

One of the few reported examples of room-temperature MChD was observed in an Yb(III) SMM complex involving chiral helicene-based ligands decorated with two 4-pyridyl-ethynyl units.¹⁵ This study proposes to replace the helicene moiety with their linearly-fused analogs, twisted acene (twistacene). Acenes, a subclass of polycyclic aromatic hydrocarbons, consist of linearly fused benzene rings and can be considered as 1D nanographenes.¹⁹ Chemists can design nanocarbons with defined sizes and shapes to fine-tune their electronic, magnetic and optical properties.

The degree of dihedral twisting can be controlled through chemical substitution,²⁰ and this twisting significantly influences (chir)optical properties such as natural circular dichroism and circularly polarized luminescence (CPL).²¹

In the present work, enantiopure M- and P-twistacenes, decorated at positions 2,6 with 4-pyridyl-ethynyl units and sterically locked into an end-to-end twist by an octyl tether (referred to as M- or P-Ant-C8) were reacted with the Yb(hfac)₃(H₂O)₂ building block. This result in the formation of one-dimensional nano objects of formula [Yb(hfac)₃(M- or P-Ant-C8)]_n (M- or P-1), which were successfully isolated as single-crystals suitable for X-ray diffraction analysis. This study highlights the combination of SMM behavior and unprecedented MChD within a twistacene-based system. These findings are further detailed and rationalized through ab initio calculations.

Results and discussion

Synthesis and structural analysis

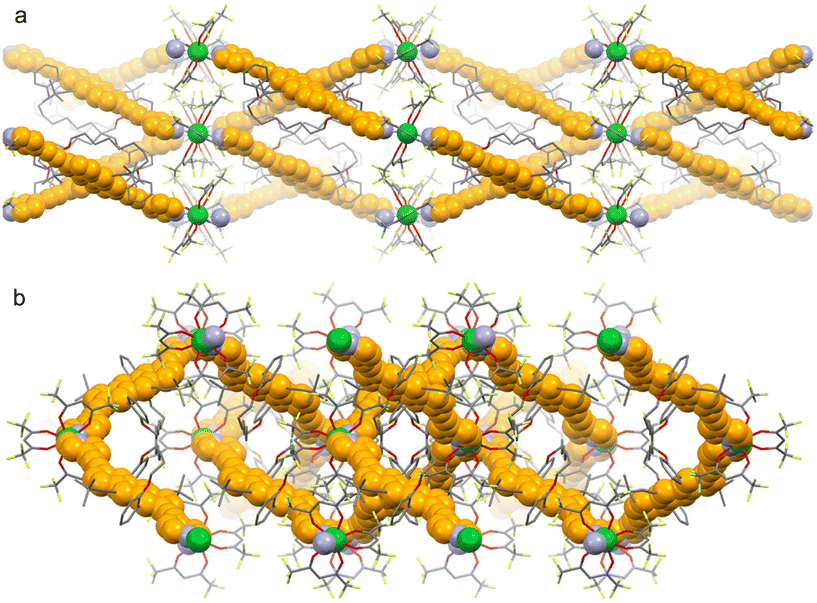
It has been previously demonstrated that Yb(III) ion is a promising candidate for exhibiting remarkable optical and chiroptical properties, including CPL^15,22–27 and MChD^4,11,28 activities, as well as field-induced SMM behavior. Enantiopure M- and P-twistacenes, decorated at positions 2,6 with 4-pyridyl-ethynyl units, are helically locked to a specific handedness by an octyl tether (M or P-Ant-C8) (Fig. 1b). By analogy with M- and P-carbo[6]helicenes, similarly decorated (Fig. 1a),¹⁵ M or P-Ant-C8 appears suitable for the preparation of polymeric nanomolecular objects. Enantiopure twistacene ligands M- or P-Ant-C8 were synthesized by Sonogashira coupling of M- or P-twistacene-C8 with 4-iodopyridine in 55–60% yield (see ESI for synthetic and characterization details†).¹⁹ ECD spectra display the expected mirror image with the typical vibronic pattern of the anthracene p-band at 420–490 nm (Fig. S7†).

Fig. 1 (a) Molecular structure of [H₆(Py)₂Yb(hfac)₃]_n (2), (b) chemical reaction for the formation of [Yb(hfac)₃(Ant-C8)]_n (1), (c) X-ray structure of M-1 (up) and P-1 (down) along the b axis with part of M or P-Ant-C8 and Yb(hfac)₃ with pyridyl-ethynyl drawn in spacefill and wireframe representations.

Refluxing an equimolar mixture of M or P-Ant-C8 and Yb(hfac)₃(H₂O)₂ (hfac⁻ = 1,1,1,5,5,5-hexafluoroacethylacetonate) for 2 hours in toluene yielded single crystals of [Yb(hfac)₃(M or P-Ant-C8)]_n (M or P-1) suitable for X-ray diffraction after diffusion with n-pentane. Enantiopure compounds M-1 and P-1 crystallize in the non-centrosymmetric orthorhombic C222 space group (No. 21) (Table S1†). The asymmetric unit consists of one Ant-C8 chiral ligand and two half Yb(hfac)₃ units, that is, two crystallographically independent Yb(III) ions are present. Single-crystal X-ray diffraction revealed the formation of chiral one-dimensional nano-assemblies, where each Yb(III) centre is eight-coordinated with six oxygen atoms coming from three bischelating hfac⁻ anions and two nitrogen atoms from the pyridine rings of the Ant-C8 chiral ligand (Fig. 2). The Yb–O and Yb–N bond lengths range from 2.508(12) to 2.567(11) Å and 2.249(10) to 2.316(9) Å, respectively. Furthermore, the N–Yb–N angles range from 141.3(3) to 142.9(3)°. SHAPE analysis²⁹ indicates that the Yb(III) coordination sphere adopts a slightly distorted D_4d square antiprismatic symmetry in both enantiomers (Table S2†). The bond lengths and angles involving the first neighbouring atoms around the Yb(III) centre are comparable to those observed in the chiral 1D polymeric structures obtained with helicene ligands (M- and P-2).¹⁵ However, the arrangement of the ligands results in an increase in symmetry from D_2d for M- and P-2 to D_4d for M- and P-1. With such chiral ligands, it is well-established that the tether length strongly influences the degree of twisting, which in turn governs the chiroptical properties of the ligand.²⁰ In M- and P-1, the anthracene core is nearly flat, resulting in an end-to-end dihedral angle of 175.9(4)°, similar to that observed for the free twistacene with an octyltether.²⁰ The shortest intra- and inter-chain Yb–Yb distances are 8.439 Å and 25.711 Å, respectively. The crystal packing revealed intertwined 1D nano-chains, resulting in the formation of cavities in the (011) and (110) planes. Nevertheless, the various substitutions with tert-butyl and octyltether groups effectively prevent any π–π stacking between the π-extended systems. Instead, the crystal packing is stabilized by F⋯F and F⋯H short contacts.

Fig. 2 Representation of the crystal packing for M-1 along the a axis (a) and the b axis (b).

Magnetic measurements analysis

Crunched single crystals of M-1 were immobilized in a Teflon pellet to investigate their magnetic properties through SQUID magnetometry. The temperature dependence of the molar magnetic susceptibility displays an experimental room temperature value of 2.38 cm³ K mol⁻¹, which is consistent with the expected value for an isolated Yb(III) ion (2.57 cm³ K mol⁻¹ for ground-state multiplet ²F_7/2 with g_J = 8/7) per formula unit (Fig. S10†).³⁰ The depopulation of the M_J doublets results in a monotonic decay down to 1.21 cm³ K mol⁻¹ at 2 K. The field dependence of the magnetization measured at 2 K reaches 1.75Nβ under a magnetic field of 5 T, significantly lower than the expected saturation value of 4.0Nβ for isolated Yb(III) ions in the absence of magnetic anisotropy (Inset of Fig. S10†). The g tensors and corresponding calculated wavefunction energies for the ground state multiplet ²F_7/2 are reported in Tables S3 and S4† highlighting a |± m_J〉 = |± 7/2〉 dominant Kramers doublet (KD) for the ground state. The ab initio simulated temperature dependence of the magnetic susceptibility and field dependence of the magnetization are in fair agreement with the experimental data (Fig. S10†).

The slow magnetic relaxation of M-1 was probed by measuring the magnetic susceptibility in a 5 Oe alternating field. At 2 K, no significant frequency dependence of the out-of-phase magnetic susceptibility was observed in the 100–10 000 Hz frequency range under zero applied DC field. This behavior is likely due to fast magnetic relaxation through Quantum Tunneling of the magnetization (QTM), as usually observed for Yb(III) with non-zero transverse component in the g tensor. However, QTM could be suppressed by applying an external DC field. Indeed, field-dependent magnetic susceptibility revealed frequency-dependent behavior at 2 K (Fig. 3a and S11†). The relaxation times (τ) were extracted with an extended Debye model^31–33 fitting simultaneously the in-phase and out-of-phase components of the magnetic susceptibility (eqn (S1) and Table S5†). The best fit for the field dependence of the relaxation time at 2 K (Fig. 3b) was obtained using eqn (1).

Fig. 3 (a) Frequency dependence of the for M-1 at 2 K in the 0–2800 Oe magnetic field range. (b) Magnetic field dependence of the relaxation time (τ) (black dots) with the best fit (full red line) obtained with eqn (S1†). The dashed black and blue lines represent the QTM and Raman + Orbach processes contributions, respectively. (c) Frequency dependence of for M-1 in the 2–6.5 K temperature range under an applied magnetic field of 1400 Oe. (d) Thermal dependence of log(τ) for M-1 (black dots) in the 2–6.5 K temperature range under an applied magnetic field of 1400 Oe with the best fit (full red line) obtained with eqn (S1†) (see text for parameter values). Raman and Orbach contributions are drawn in dashed blue and black lines respectively.

From left to right, the terms represent the contributions of QTM, direct and field independent, possibly thermally activated (Orbach + Raman) processes. The best-fitted parameters for m fixed to 4 are: B₁ = 6.92(3) × 10⁴ s⁻¹, B₂ = 1.60(10) × 10⁻⁵ Oe⁻², B₃ = 1.89(2) × 10⁻¹² s⁻¹ K⁻¹ Oe⁻⁴ and B₄ = 6.75(6) × 10³ s⁻¹. The fitting results indicate that the QTM process dominates for μ₀H < 750 Oe, while field-independent processes (Orbach + Raman) are predominant in the range 750 < μ₀H < 3000 Oe. The direct process does not dominate for μ₀H < 3000 Oe. The optimal field for investigating the thermal dependence of the magnetic susceptibility was chosen as a compromise between the relaxation time and the amplitude of . M-1 exhibits frequency dependence of under an applied DC magnetic field of 1400 Oe (Fig. 3c), which can be analyzed in the framework of the extended Debye model (Table S5 and Fig. S12†).^31–33 The temperature dependence of the relaxation time is plotted in Fig. 3d. The log(τ) vs. T curve was fitted using eqn (2) accounting for a combination of Raman and Orbach processes.

The best fit was obtained with C = 136.0(61) K⁻ⁿ s⁻¹, n = 0.87(15), τ₀ = 3.45(13) × 10⁻⁷ s⁻¹ and Δ = 26.2(3) K, where C and n are the constant and exponent factor of the Raman process, τ₀ and Δ are the relaxation time and energy barrier of the Orbach relaxation process, respectively. The expected n value for Kramers ions should be 9;³⁴ however, it is well known that in molecular systems, the presence of both acoustic and optical phonons can result in lower n values, typically between 2 and 7.^35–37 In some cases, especially in organometallic complexes and when phonon bottleneck process is involved, n can be even lower than 2.³⁸ Finally, the normalized Argand diagram (Fig. S13†) shows that 90% of the sample experiences slow magnetic relaxation under the selected applied DC magnetic field.

A comparison between the polymeric structures 1 and 2 revealed slow magnetic relaxation under similar applied DC magnetic fields, with magnetization relaxation occurring through a combination of Raman and Orbach processes. The energy barriers for both compounds are comparable, accounting for 14.8(9) K for 2 and 26.2(3) K for 1. The main difference between 1 and 2 relies in the nature of the ground KD, which was constructed of an admixture of |± m_J〉 states (68% |± 7/2〉, 13% |± 1/2〉, 12% |± 3/2〉 and 7% |± 5/2〉) for 2 whereas,¹⁵ for 1 the ground state reveals purer |± 7/2〉 composition (Table S4†). This directly affects the magnetization dynamics as well as the magneto-chiral optical properties (see below).

Magneto-chiral dichroism spectroscopy

To get insights into the electronic transitions of the investigated compound, single crystals of M-1 and P-1 were used to record temperature-dependent (4.0–290 K) absorption spectra in the 900–1000 nm range, with unpolarized light k propagating parallel to the b crystallographic axis. The absorption spectra for M-1 are presented in Fig. 4. Three distinct absorption bands, centred at ca. 928, 950 and 976 nm are observed (Fig. 4). These bands are associated with the ²F_7/2 → ²F_5/2 electronic transition of the Yb(III) ion. The three main components arise from the crystal field splitting of the ²F_7/2 ground and ²F_5/2 excited multiplets (Fig. 4b). The peak at λ = ca. 976 nm, associated with the lowest energy 0–0′ absorption, represents the sharpest contribution. However, it is worth noting that its full width at half maximum of 3 nm is broader than typically observed in similar Yb(III) complexes,^11,15,28 and its shape deviates from a symmetric Gaussian profile, exhibiting asymmetric features (inset of Fig. 4). This suggests inhomogeneous broadening due to non-equivalent Yb(III) sites. The contributions at λ = ca. 950 nm and λ = ca. 928 nm, associated with the 0–1′ and 0–2′ transitions, respectively, increase in intensity as the temperature decreases and become well-defined at T = 4.0 K. These contributions are notably broader than what is commonly observed.^11,15,28 These spectral features can be attributed to the presence of two crystallographically independent Yb(III) ions within the unit cell, each with distinct crystallographic parameters (see above). While these structural differences are insufficient to render the ions fully optically distinguishable, they appear to contribute at different energies to the optical spectrum. Indeed, ab initio theoretical calculation at the SA-CAS(13,7)PT2/RASSI-SO level on the two crystallographically independent Yb(III) sites show that they contribute differently to the optical spectrum in agreement with the experimental findings. Furthermore, the calculated energy differences between the 0′, 1′ and 2′ excited state sublevels are in good agreement with what is experimentally observed (Fig. 4 and Table S3†).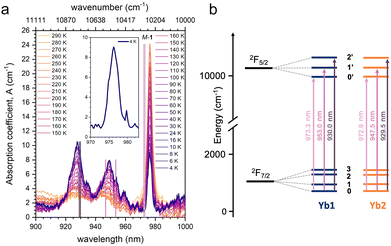

Fig. 4 (a) Thermal variation of the absorption coefficient for a single crystal of M-1 (k//b) in the 900–1000 nm range. Vertical sticks are the calculated energy (rescaled of 10 nm) of the m_J doublets of the excited ²F_5/2 multiplet states for the two Yb(III) ions. (b) Energy diagram for the ²F_7/2 → ²F_5/2 transition split by the crystal field parameters in three main components and calculated values for the two crystallographically independent Yb(III) ions in the crystal structure (rescaled of 10 nm). The calculated values are reported in Table S3.†

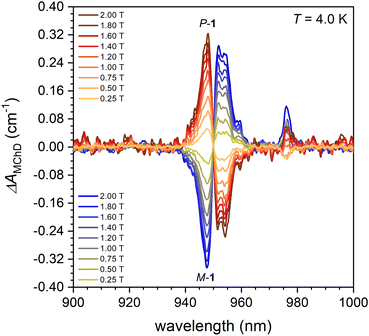
Magnetic field dependent MChD measurements were conducted on M-1 and P-1 at T = 4.0 K, with alternating magnetic fields B applied along k from 0.0 to 2.0 T. The results are presented in Fig. 5. The B dependence of the MChD spectra for the two enantiomers show mirror-image spectral profiles with opposite signs and similar intensities, which increase as the magnetic field intensity increases (Fig. 5). At T = 4.0 K, a distinct, strong, and fine-structured MChD signal associated with the 0–1′ transition is observed between 940 and 960 nm. Additionally, a sharp but weak MChD signal is observed at λ = 976 nm (0–0′ transition), while the 0–2′ transition does not provide a MChD signal above the detection limits of our setup (Fig. 5).

Fig. 5 Magnetic field dependence of ΔA_MChD for M-1 and P-1 at T = 4.0 K in the 900–1000 nm range.

The MChD spectra of compound 1 are unusual. First, while an intense and sharp contribution to the MChD spectrum is typically observed for the 0–0′ transition, only a weak signal is detected here. Second, low-temperature MChD spectra of Yb(III) chiral complexes generally display a weak MChD contribution for the 0–2′ transition, which is absent here. Third, the MChD contribution associated with the 0–1′ transition at λ = 950 nm appears, at first glance, to have a derivative-type lineshape, which contrasts with the expectations from the microscopic theory of MChD.¹ Derivative-type signals are associated with MChD A-terms, which are temperature-independent and arise from the Zeeman splitting of the ground state induced by the magnetic field. For paramagnetic systems, these terms usually become noticeable only at T > 100 K.^11,15,26 At lower temperatures, absorptive-type MChD C-terms, which reflect the Boltzmann population changes of the ground state split by the magnetic field, typically dominate due to their temperature dependence, which follows the magnetization of the system.

Based on these considerations and the findings reported above for the experimental absorption spectra, the MChD results can be rationalized as follows: The MChD signal at λ = 950 nm is more likely attributed to the contributions of two crystallographically independent Yb(III) ions. These ions produce MChD responses of similar intensity but opposite signs at slightly different wavelengths: one at λ = ca. 948 nm and one at λ = ca. 953 nm, in agreement with ab initio theoretical calculations and not a unique derivative-type signal (Fig. 5). Therefore, each contribution should be regarded as an independent temperature-dependent C-term (vide infra). The MChD dissymmetry factor |g_MChD| (eqn (S2)†) at λ = 948.0 and 952.0 nm (T = 4.0 K and B = 1.0 T) are 0.025(1) T⁻¹ and 0.024(1) T⁻¹, respectively. Applying similar reasoning to the 0–0′ and 0–2′ transitions explain why these transitions do not produce a detectable MChD signal. In general, the MChD contribution to the 0–2′ transition of Yb(III) chiral complexes is weak and broad.^11,15,28 Two broad signals of weak intensity and opposite sign, originating from two crystallographically independent Yb(III) ions, centred at slightly different wavelengths (see above), are expected to average to zero. This likely explains why no MChD signal is observed for this transition. For the 0–0′ transition, the two Yb(III) ions are expected to produce signals of similar intensity but opposite sign. However, due to the very small energy difference between the two contributions (see above), the observed weak MChD at T = 4 K can be ascribed to the residual non-compensated average of the two contributions.

An important consideration relates to the magnitude of the ΔA_MChD signals at λ = ca. 948 and ca. 953 nm. At these wavelengths, ΔA_MChD is strong and comparable to the values observed for compound 2 for the same transition. In both compounds 1 and 2, the coordination sphere consists of 6 oxygen atoms in the equatorial plane and 2 nitrogen atoms in axial positions, with the magnetic easy axis aligned along the 2 axial nitrogen atoms. Furthermore, the MChD properties were investigated in both case with k and B oriented along the crystallographic direction (k, B || to b and c axes for 1 and 2, respectively) that minimize the angle between and the magnetic easy axis. Therefore, (i) it is not surprising that ΔA_MChD is strong for the 0–1′ transition, and (ii) this supports the hypothesis that the absence of a MChD signal for the 0–0′ transition arises from the presence of two distinct Yb(III) sites, rather than from a lack of the physico-chemical conditions necessary to produce a strong MChD signal in 1.

Temperature dependent MChD measurements were carried out on M-1 and P-1 in the T = 4.0–290 K range with an alternating magnetic field = 1.0 T applied along. The results are presented in Fig. 6. The MChD signals at λ = ca. 948 and ca. 953 nm decrease in intensity as the temperature increases, falling below the detection limits of our setup above ca. 50 K.

Fig. 6 Temperature dependence of ΔA_MChD for M-1 and P-1 at B = 1.0 T in the 900–1000 nm range.

Within this temperature range, the signal intensity changes significantly, while the spectral shape remains largely unaffected. These observations support the assignment of these two contributions to independent MChD C-terms. The temperature at which the signals become undetectable is consistent with previous findings. The MChD signal associated with the (0–2′) transition, which is absent at 4.0 K, remains undetectable at higher temperatures, as expected. In contrast, the MChD signal at λ = 976 nm (0–0′ transition) exhibits a non-monotonic behaviour with T, differing slightly between opposite enantiomers. Additionally, the signal intensities are not mirror-symmetric for M-1 and P-1. This further corroborates the hypothesis that the observed MChD signal represents an average of two contributions with comparable intensities and opposite signs, arising from crystallographically independent Yb(III) ions. A residual MChD signal is indeed detectable at temperatures close to room temperature (Fig. S14†), further supporting the hypothesis that a strong MChD can potentially be observed for 1 at this wavelength.

Finally, the thermal variations of the MChD signal at λ = 947.7 and ca. 952.0 nm were compared to the corresponding variations in sample magnetization measured at = 1.0 T (Fig. 7a). The data show good agreement with those obtained through magnetometry for both enantiomers. The magnetic field dependence of the MChD signal at the same wavelengths between 0 and 2 T shows a linear behaviour, as observed through magnetometry in the same magnetic field range (Fig. 7b).

Fig. 7 Temperature (a) and magnetic field (b) dependence of ΔA_MChD (λ = 948, 952 nm) compared to magnetization data recorded in the same conditions on a microcrystalline sample of M-1.

Conclusions

In conclusion, we have investigated enantiopure one-dimensional assemblies of ytterbium(III)-based single-molecule magnets where the chirality is provided by M and P-twistacenes decorated at positions 2,6 with 4-pyridyl-ethynyl units and helically locked to a specific handedness by an octyl tether. The magnetic and optical properties are in good agreement with ab initio theoretical calculations. Magnetic measurements under an AC magnetic field show slow relaxation of the magnetization at low temperature. The optical spectrum is characterized by unusually broad absorptions associated with ²F_7/2 → ²F_5/2 electronic transition split by the crystal field. The origin of the broad absorptions is associated with two crystallographically independent Yb(III) ions in the crystal structure. The energy of the optical transitions for the two ions is slightly different for the 0–0′ and 0–2′ transitions. Therefore, the resulting MChD signals, which are expected to be of similar intensity and opposite sign for the two Yb(III), are averaged to zero. The 0–1′ optical transition instead is associated with two contributions well separated in energy for the two Yb(III) ions. As a result, the MChD signal is intense, as it can be expected by the magnetic-dipole allowed character of the transition, and follows the expected magnetic and temperature-dependent behaviour. These findings clearly demonstrate the important role of the structural arrangement of MChD-active ions when designing chiral magneto-optical materials responsive to light and magnetic fields.

Author contributions

I. S. takes care of the syntheses; L. C. A., M. A., C. T. and G. L. J. A. R. performed the MChD measurements and the interpretations; V. D. realised the single crystal X-ray diffraction; O. C. and F. P. carried out the magnetic measurements and their treatment; B. L. G. performed the computational investigation; J. C. and O. G. are at the initiative of the collaboration; F. P., J. C. and O. G. conceived, oversaw and directed the project. F. P. and M. A. prepared the initial draft of the paper. All authors contributed to manuscript editing and discussion.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for the structures reported in this paper have been deposited at the Cambridge Crystallographic Data Center under the deposition number 2390931 (for P-1) and 2390932 (for M-1).† The authors will supply the relevant data in response to reasonable requests.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The French National Research Agency (ANR) is acknowledged for financial support through the SWITCH-MChD (ANR-23-CE07-0003) and PRINCIPE (ANR-23-CE07-0015) projects. This project has received financial support from the CNRS through the MITI interdisciplinary programs through its exploratory research program. The French GENCI/IDRIS-CINES centers for high-performance computing resources are also acknowledged. O. G. acknowledges European Union's Horizon 2020 research and innovation program (grant agreement no. 850836, ERC Starting Grant “PolyHelix”) and the Israel Science Foundation (grant no. 3085/21).

References

1. L. D. Barron and J. Vrbancich, Magneto-chiral birefringence and dichroism, Mol. Phys., 1984, 51, 715–730.
2. G. L. J. A. Rikken and E. Raupach, Observation of Magneto-Chiral Dichroism, Nature, 1997, 390, 493–494.
3. M. S. Raju, K. Paillot, I. Breslavetz, G. Novitchi, G. L. J. A. Rikken, C. Train and M. Atzori, Optical readout of Single-Molecule Magnets magnetic memories with Unpolarized Light, J. Am. Chem. Soc., 2024, 146, 23616–23624.
4. F. Pointillart, M. Atzori and C. Train, Magneto-chiral dichroism of chiral lanthanide complexes, Inorg. Chem. Front., 2024, 11, 1313–1321.
5. C. Train, R. Gheorghe, V. Krstic, L.-M. Chamoreau, N. S. Ovanesyan, G. L. J. A. Rikken, M. Gruselle and M. Verdaguer, Strong magneto-chiral dichroism in enantiopure chiral ferromagnets, Nat. Mater., 2008, 7, 729–734.
6. R. Sessoli, M.-E. Boulon, A. Caneschi, M. Mannini, L. Poggini, F. Wilhelm and A. Rogalev, Strong magneto-chiral dichroism in a paramagnetic molecular helix observed by hard X-ray, Nat. Phys., 2015, 11, 69–74.
7. M. Atzori, I. Breslavetz, K. Paillot, K. Inoue, G. L. J. A. Rikken and C. Train, A Chiral Prussian Blue Analogue Pushes Magneto-Chiral Dichroism Limits, J. Am. Chem. Soc., 2019, 141, 20022–20025.
8. M. Atzori, I. Breslavetz, K. Paillot, G. L. J. A. Rikken and C. Train, Role of structural dimensionality in the magneto-chiral dichroism of chiral molecular ferrimagnets, J. Mater. Chem. C, 2022, 10, 13939–13945.
9. B. Sun, X.-F. Liu, X.-Y. Li, Y. Zhang, X. Shao, D. Yang and H.-L. Zhang, Two-Dimensional Perovskite Chiral Ferromagnets, Chem. Mater., 2020, 32, 8914–8920.
10. X. Wang, S.-Q. Wang, J.-N. Chen, J.-H. Jia, C. Wang, K. Paillot, I. Breslavetz, L.-S. Long, L. Zheng, G. L. J. A. Rikken, C. Train, X.-J. Kong and M. Atzori, Magnetic Anisotropy Drives Magnetochiral Dichroism in a Chiral Molecular Helix Probed with Visible Light, J. Am. Chem. Soc., 2022, 144, 8837–8847.
11. M. Atzori, K. Dhbaibi, H. Douib, M. Grasser, V. Dorcet, I. Breslavetz, K. Paillot, O. Cador, G. L. J. A. Rikken, B. Le Guennic, J. Crassous, F. Pointillart and C. Train, Helicene-Based Ligands Enable Strong Magneto-Chiral Dichroism in a Chiral Ytterbium Complex, J. Am. Chem. Soc., 2021, 143, 2671–2675.
12. M. Atzori, H. D. Ludowieg, A. Valentin-Pérez, M. Cortijo, I. Breslavetz, K. Paillot, P. Rosa, C. Train, J. Autschbach, E. A. Hillard and G. L. J. A. Rikken, validation of microscopic magnetochiral dichroism theory, Sci. Adv., 2021, 7, eabg2859.
13. C. Benelli and D. Gatteschi, Introduction to Molecular Magnetism: From Transition Metals to Lanthanides, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015.
14. R. A. Layfield, M.-L. Tong, B. M. Day, Y.-C. Chen, F.-S. Guo and A. Mansikkamaki, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403.
15. K. Dhbaibi, M. Grasser, H. Douib, V. Dorcet, O. Cador, N. Vanthuyne, F. Riobé, O. Maury, S. Guy, A. Bensalah-Ledoux, B. Baguenard, G. L. J. A. Rikken, C. Train, B. Le Guennic, M. Atzori, F. Pointillart and J. Crassous, Multifunctionnal Helicene-Based ytterbium Coordination Polymer Displaying Circularly Polarized Luminescence, Slow Magnetic Relaxation and Room temperature Magneto-Chiral Dichroism, Angew. Chem., Int. Ed., 2023, 135, e202215558.
16. M. S. Raju, K. Dhbaibi, M. Grasser, V. Dorcet, I. Breslavetz, K. Paillot, N. Vanthuyne, O. Cador, G. L. J. A. Rikken, B. Le Guennic, J. Crassous, F. Pointillart, C. Train and M. Atzori, Magneto-Chiral Dichroism in a One-Dimensional Assembly of Helical Dysprosium(III) Single-Molecule Magnets, Inorg. Chem., 2023, 62, 17583–17587.
17. C.-Y. Li, L. C. Adi, K. Paillot, I. Breslavetz, L.-S. Long, L.-S. Zheng, G. L. J. A. Rikken, C. Train, X.-J. Kong and M. Atzori, Enhancement of Magneto-Chiral Dichroism Intensity by Chemical Design: The Key Role of Magnetic-Dipole Allowed Transitions, J. Am. Chem. Soc., 2024, 146, 16389–16393.
18. L. C. Adi, O. G. Willis, A. Gabbani, G. L. J. A. Rikken, L. Di Bari, C. Train, F. Pineider, F. Zinna and M. Atzori, Magneto-Chiral Dichroism of Chiral Lanthanide Complexes in the Context of Richardson’s Theory of Optical Activity, Angew. Chem., Int. Ed., 2024, 63, e202412521.
19. J. E. Anthony, The larger Acenes: Versatile Organic Semiconductors, Angew. Chem., Int. Ed., 2008, 47, 452–483.
20. A. Bedi, A. M. Armon, Y. Diskin-Posner, B. Bogoslavsky and O. Gidron, Controlling the helicity of π-conjugated oligomers by tuning the aromatic backbone twist, Nat. Commun., 2022, 13, 451–458.
21. A. Bedi, G. Schwartz, U. Hananel, A. M. Armon, I. Shioukhi, G. Markovich and O. Gidron, The effect of axial and helical chirality on circularly polarized luminescence: lessons learned from tethered twistacenes, Chem. Commun., 2023, 59, 2011–2014.
22. B. Lefeuvre, C. A. Mattei, J. Flores Gonzalez, F. Gendron, V. Dorcet, F. Riobé, C. Lalli, B. Le Guennic, O. Cador, O. Maury, S. Guy, A. bensalah-Ledoux, B. Baguenard and F. Pointillart, Solid-State Near-Infrared Circularly Polarized Luminescence from Chiral YbIII-Single-Molecule Magnet, Chem. – Eur. J., 2021, 27, 7362–7366.
23. C. A. Mattei, V. Montigaud, B. Lefeuvre, V. Dorcet, G. Argouarch, O. Cador, B. Le Guennic, O. Maury, C. Lalli, Y. Guyot, S. Guy, C. Gindre, A. Bensalah-Ledoux, F. Riobé, B. Baguenard and F. Pointillart, Circularly polarized luminescence in the one-dimensional assembly of binaphtyl-based Yb(III) single-molecule magnets, J. Mater. Chem. C, 2023, 11, 7299–7310.
24. A. Sickinger, M. Grasser, B. Baguenard, A. Bensalah-Ledoux, L. Guy, A. T. Bui, Y. Guyot, V. Dorcet, F. Pointillart, O. Cador, S. Guy, O. Maury, B. Le Guennic and F. Riobé, Temperature-dependent NIR-CPL spectra of chiral Yb(III) complexes, Phys. Chem. Chem. Phys., 2024, 26, 15776–15783.
25. O. G. Willis, F. Zinna, G. Pescitelli, C. Micheletti and L. Di Bari, Remarkable near-infrared chiroptical properties of chiral Yb, Tm and Er complexes, Dalton Trans., 2022, 51, 518–523.
26. X.-L. Li, A. Wang, Y. Li, C. Gao, M. Cui, H.-P. Xiao and L. Zhou, Two Chiral YbIII Enantiomeric Pairs with Distinct Enantiomerically Pure N-Donor Ligands Presenting Significant Differences in Photoluminescence, Circularly Polarized Luminescence, and Second-Harmonic Generation, Inorg. Chem., 2023, 62, 4351–4360.
27. X. Du, Z. Zhang, C. Gao, F. Li and X.-L. Li, Two pairs of chiral YbIII enantiomers presenting distinct NIR luminescence and circularly polarized luminescence performances with giant differences in second-harmonic generation responses, Dalton Trans., 2023, 52, 17758–17766.
28. L. C. Adi, M. Aragon-Alberti, J. Rouquette, G. L. J. A. Rikken, C. Train, J. Long and M. Atzori, Coexistence of room temperature magneto-chiral dichroism and magneto-electric coupling in a chiral nanomagnet, Nanoscale, 2025, 17, 1954–1958.
29. M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, in SHAPE Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools, Departament de Quimica Fisica, Departament de Quimica Inorganica, and Institut de Quimica Teorica i Computacional – Universitat dè Barcelona, Barcelona, Spain, 2013.
30. O. Kahn, in Molecular Magnetism, VCH, Weinhem, 1993.
31. K. S. Cole and R. H. Cole, Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics, J. Chem. Phys., 1941, 9, 341–351.
32. R. Orbach, Spin-lattice relaxation in rare-earth salts, Proc. R. Soc. London, Ser. A, 1961, 264, 458–484.
33. R. Orbach, On the theory of spin-lattice relaxation in paramagnetic salts, Proc. Phys. Soc, 1961, 77, 821–826.
34. C. Dekker, A. F. M. Arts, H. W. de Wijn, A. J. van Duyneveldt and J. A. Mydosh, Activated dynamics in a two-dimensional Ising spin glass: Rb₂Cu_1-xCo_xF₄, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 11243–11251.
35. J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer, Berlin, Germany, 2015.
36. P. Evans, D. Reta, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, Bis-Monophospholyl Dysprosium Cation Showing Magnetic Hysteresis at 48 K, J. Am. Chem. Soc., 2019, 141, 19935–19940.
37. D. Reta and N. F. Chilton, Uncertainty estimates for magnetic relaxation times and magnetic relaxation parameters, Phys. Chem. Chem. Phys., 2019, 21, 23567–23575.
38. K. N. Shrivastava, Theory of Spin-Lattice Relaxation, Phys. Status Solidi B, 1983, 117, 437–458.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2390931 and 2390932. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5qi00832h

---