Synthesis and characterization of neutral and cationic 1-tris(pyrazolyl)borate organo-beryllium complexes

Abstract

The neutral and cationic 1-tris(pyrazolyl)borate (Tp) organo-beryllium complexes TpBe(R) (R = Ph, nBu, Me, Cp, Cp*) and [TpBe(carbene)]⁺ (carbene = IMe, IiPr, IDipp, CAAC(Dipp)) have been synthesized. These compounds were analyzed via NMR and IR spectroscopy, mass spectrometry as well as X-ray diffraction. A comparison of the Be–C bonds in solution and the solid state revealed no significant differences in the nature of this bond. Extensive quantum chemical evaluation of the bonding within the DFT framework showed that the Be–C bonds in all cases are dative covalent.

---

Introduction

The first organo-beryllium compounds were synthesized and investigated almost a century ago, yet this class of chemistry has been the subject of limited research.^1,2 This is due to the health hazards associated with the second-lightest metal in the periodic table and its compounds.^3–6 Apart from the perceived toxicity, the production of the starting materials was also dangerous and unreliable.⁷ However, in recent years there has been a resurgence of interest in the organometallic chemistry of this almost-forgotten metal,^8–14 and a considerable number of novel organo-beryllium compounds have been prepared and characterized.^15–22 It is difficult to compare these compounds and derive general trends of their structures, properties, and reactivity as these systems are structurally highly diverse and various donors are coordinated to the central atom. For example, the bond lengths and the ⁹Be NMR chemical shifts of the compounds in Fig. 1 ^{2,15–19,23–27} differ greatly (see also below and Fig. 3). However, for a rational design of organo-beryllium complexes and their directed application in low valent main group chemistry, bond activation, catalysis or material synthesis, a profound knowledge on the nature of Be–C bonds is mandatory.²⁸ For this reason, beryllium complexes are needed, where only one coordination site is vacant, which can be occupied by the C-donor ligand of choice. We have already used beryllium complexes with the monoanionic scorpionate tris(pyrazolyl)borate (Tp)^29,30 successfully to compare the properties of pseudo-halido ligands.³¹ We, therefore, prepared neutral and cationic organo-beryllium complexes, in which three coordination sites at the small beryllium atom are occupied by the Tp ligand, so that at the fourth site the C-donor ligand can be varied. This ensures good comparability between different systems.

Fig. 1 Example of organo-beryllium compounds (Dipp = 2,6-diisopropylphenyl).^{2,15–19,23–27}

Results and discussion

The neutral TpBe-organyl complexes (1–4, Fig. 2a and b) were synthesized analogously to the TpBe-pseudo-halides,³¹ with the exception of TpBe(Me) (3), which was synthesized via the reaction of dimethylberyllium (BeMe₂) with potassium tris(pyrazolyl)borate (TpK), in accordance to the literature.³²1, 2 and 4 were synthesized through reaction of either the beryllium Grignard compounds^26,33 or the beryllium half-sandwich complexes²⁰ with TpK. Of the heteroleptic starting materials, chlorides or bromides were the most suitable, as the iodides often led to the formation of byproducts. The realization of cyclopentadienyl (Cp) derivate TpBe(η¹-Cp) (5) was difficult because the products TpBeBr and 5 are in competition and always form in equal proportions (Fig. S43†). The reaction could not be controlled by different stoichiometries or solvent variation (Fig. 2c). The cationic TpBe-organyls 6–9[pf] were obtained by removal of the chloride ligand from TpBeCl with a lithium perfluoro-alkoxyaluminate ([Al(OC(CF₃)₃)₄]⁻ = [pf])^34,35 and simultaneously providing carbenes to occupy the in situ generated vacant coordination site at the beryllium atom (Fig. 2d). In this one-pot approach, the target compounds are separated from the reaction mixture as oily residues.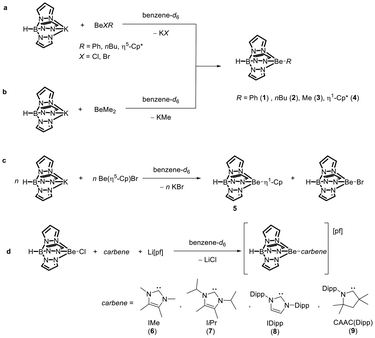

Fig. 2 Synthetic routes towards TpBe(R) (1–5) and [TpBe(R)][pf] (6–9[pf]) (n = 1, 2; Dipp = 2,6-diisopropylphenyl).

The neutral and cationic compounds could be distinguished not only by their physical state, but also by their chemical shifts in the ⁹Be NMR spectra.^36,37 Shifts in the range of 4.76–7.18 ppm were observed for the neutral species (Table 1). 3 has the highest resonance frequency with a chemical shift of 7.18 ppm. The lowest resonance frequencies were observed for the pentamethylcyclopentadienyl (Cp*) and Cp derivatives TpBe(η¹-Cp*) (4) and 5. In the literature, high upfield shifts in the range of −17 to −18 ppm have been reported for beryllium cyclopentadiene species.²⁰ These exceptional upfield shifts are caused by anisotropic shielding of the ⁹Be nuclei, which are in the center of the π-system of the cyclopentadienyl ligands. For this reason, ⁹Be NMR chemical shifts are a direct indicator of the coordination mode of the Cp ligands. Therefore, the ⁹Be NMR chemical shift of 4.76 ppm in 4 is indicative for η¹-coordination. Considering only four orbitals of the Be atom are energetically accessible for molecular bonding, of which three are occupied by the Tp-ligand, this coordination mode is expected. TpBe(η¹-Cp) also showed a downfield shift to 4.02 ppm compared to Be(η⁵-Cp)Br (−18 ppm), illustrating the different hapticities.²⁰ However, in the ¹H and ¹³C NMR spectra of 4 and 5, all CH₃ or CH groups, as well as ring carbon nuclei of the cyclopentadienyl ligands are equivalent. We assume that a fast (on the NMR timescale) sigmatropic and/or haptotropic rearrangement is accountable for this observation. Though, low temperature NMR spectroscopy did not freeze this tautomerism (Fig. S37†). The ⁹Be NMR signals of 4 and 5 are also more upfield shifted than the phenyl and nBu compounds 1 and 2.

Table 1 Observed ⁹Be NMR spectra shifts (C₆D₆ or C₆D₆ : oDFB|3 : 2) and Be–C atomic distances derived from single crystal X-ray diffraction

	^9Be NMR [ppm]	Be–C [Å]
TpBe(Ph) (1)	5.83 (ω1/2 = 16.2 Hz)	1.7442(9)
TpBe(nBu) (2)	6.87 (ω1/2 = 40.9 Hz)	—
TpBe(Me) (3)	7.18 (ω1/2 = 20.2 Hz)	1.708(6) ^38
TpBe(η^1-Cp*) (4)	4.76 (ω1/2 = 23.1 Hz)	1.8294(2)
TpBe(η^1-Cp) (5)	4.02 (ω1/2 = 5.4 Hz)	—
[TpBe(IMe)][pf] (6[pf])	3.78 (ω1/2 = 16.3 Hz)	—
[TpBe(IiPr)][pf] (7[pf])	3.94 (ω1/2 = 19.4 Hz)	1.8021(6)
[TpBe(IDipp)][pf] (8[pf])	3.59 (ω1/2 = 14.2 Hz)	1.8231(1)
[TpBe(CAAC(Dipp))][pf] (9[pf])	5.18 (ω1/2 = 21.5 Hz)	—

---

Compared to the neutral TpBe-organyls, the cationic compounds exhibit significantly poorer solubility. A mixture of 1,2-difluorobenzene (oDFB) and benzene-d₆ had to be used to dissolve these complexes. Within these cationic compounds, a downfield shift of 3.59–5.18 ppm can be observed from [TpBe(IDipp)][pf] (8[pf]) to [TpBe(CAAC(Dipp))][pf] (9[pf]). Among the carbenes used, cyclic(alkyl)(amino)carbene (CAAC) shows the largest deviation from the other carbenes with a ⁹Be NMR chemical shift of 5.18 ppm. Fig. 3 summarizes the ⁹Be NMR properties of various organo-beryllium compounds.^15–19 As described in the literature, the double- and triple-coordinated organo-beryllium compounds are the most downfield shifted.³⁷ The κ²N coordinated beryllates²⁵ and the neutral beryllium organyls^15,25 are easily distinguished from the κ³N-species of this study. The exception is the [κ²N-Be(carbene)] compounds of Gilliard et al., which are found in a similar shift range. This might be due to the π-electron interactions found in these systems.²⁷

Fig. 3 Observed ⁹Be NMR chemical shifts of 1–9 (orange) in comparison to the literature compounds from Fig. 1 (green).

In the ¹³C NMR spectra, the carbene C atoms were detected with an upfield shift compared to the free carbenes (Table 2). The chemical shifts in the ¹¹B NMR spectra of 1–5 and 6–9[pf] vary slightly (−4.43 to −5.11 ppm), as do the chemical shifts for the aluminate anion in their ²⁷Al and ¹⁹F NMR spectra (35.11–35.51 ppm |−75.08 to −75.16 ppm) for the cationic Be compounds 6–9[pf].

Table 2 ¹³C NMR spectra shifts [ppm] of coordinated and free carbene carbon atoms in 6–9[pf] (C₆D₆ : oDFB|3 : 2)

	[TpBe(R)][pf]	Free ligand R
[TpBe(IMe)][pf] (6[pf])	164.98	212.7 (C6D6)^39
[TpBe(IiPr)][pf] (7[pf])	164.31	205.9 (C6D6)^39
[TpBe(IDipp)][pf] (8[pf])	173.52	220.3 (CDCl3)^40
[TpBe(CAAC(Dipp))][pf] (9[pf])	272.81	313.6 (C6D6)^41

---

Comparison of the neutral and cationic compounds shows no significant difference in the ⁹Be and ¹³C NMR chemical shifts of the beryllium nuclei (Table 1) or the beryllium coordinated carbon nuclei (Table 2), respectively. This indicates that no differences between formally dative or covalent/ionic Be–C bonds can be detected NMR spectroscopically. This is in line with solid state bond parameters and quantum chemical calculations (see below). This observation is further supported by the good agreement between the NMR spectroscopic parameters determined for the investigated compounds and previously described organo-beryllium species.²⁶

The molecule structures of 1, 4, 7[pf] and 8[pf] were verified by single crystal X-ray diffraction experiments. Attempts to obtain single crystal data of the other complexes failed due to intergrowth or data completeness issues. The single crystals of 1 and 4 were obtained from a concentrated benzene solution at ambient temperature. 1 crystallizes in the monoclinic space group C2/c with eight formula units per unit cell, while 4 crystallizes in the orthorhombic space group P2₁2₁2₁ with four formula units per unit cell. An ellipsoid representation of the molecular structure of 1 in the solid state is shown in Fig. 4. The complex 7[pf] crystallized in the monoclinic space group P2₁/c with four formula units per unit cell and was obtained from a pentane layered benzene solution. The solid state structure of the [TpBe(IiPr)]⁺ cation is shown in Fig. 4. Single crystals of 8[pf] were obtained by freezing the oily reaction residue at −36 °C and subsequent thawing, which was repeated two more times. The molecular structures of 1 and 8[pf] in the solid state are depicted in Fig. S1 and S4.† All crystal data and details of the structure determination are summarized in ESI Tables S1 and S2.† In the solid state the metal center in neutral and cationic TpBe-organyl complexes 1, 4, 7[pf] and 8[pf] is pseudo tetrahedrally coordinated, as expected. Three of the coordination sites are occupied by N-atoms from the Tp ligand and the fourth is occupied by the C-donor ligand. The η¹-coordination of the Cp* group in complex 4 was confirmed by the single crystal X-ray structure (Fig. 4 left site). The Be–C atomic distances become smaller with decreasing steric bulk of the residue R (Table 1). The N–N, N–C, C–C and B–N separations of the Tp ligand 1, 4, 7[pf] and 8[pf] are in the range of 1.362(2)–1.375(4), 1.335(2)–1.460(2), 1.389(3)–1.394(5) and 1.542(2)–1.548(2) Å, respectively. These are within the standard uncertainty identical to other tris(pyrazolyl)borate beryllium complexes.^31,42,43 The Be–N pyrazole distances 1.749(2) to 1.787(2) Å are slightly longer than those previously described for beryllium Tp complexes^31,42,43 and comparable to other Be–N separations in amine complexes.^44–47

Fig. 4 Top: Molecular structures of TpBe(η¹-Cp*) (4) (left) and of the [TpBe(IiPr)]⁺ cation 7 (right) in the solid state. Bottom: Molecular structures of 1, 4, 7 and 8 along the bonding axis B–Be–C. Displacement ellipsoids are shown at 70% probability at 100 K. Hydrogen atoms are shown at arbitrary radii, carbon bound hydrogen atoms are omitted and selected carbon atoms shown as wireframe for clarity.

Large deviations can be observed in the Be–N and Be–C bond lengths. The larger the C-donor ligand on the Be atom, the shorter two Be–N bonds are, while the third Be–N bond is elongated. This leads to a reduction of two N–Be–N angles, while the third is widened. In these compounds, the B–Be–C atoms no longer lie on a straight line and the angle moves further away from 180° (Fig. 4). The Be–C atomic distances overlap for the neutral and the cationic TpBe-organic compounds. The decisive factor here is also the steric requirement of the C-donor. The more space is occupied, the larger the distances between these two atoms become.

The cationic TpBe organyls 6[pf], 7[pf], and 9[pf] were also analyzed by electrospray-ionization mass-spectrometry (ESI-MS). Upon collision-induced dissociation (CID), the Be–C bond is broken more easily for the more bulky carbene ligands. For the smallest congener, [TpBe(IMe)]⁺ (6) (m/z = 346, Fig. 5), the loss of pyrazole is observed at lower collision energies than the loss of the IMe ligand, and the latter process requires a very high normalized collision energy (NCE) of 40.

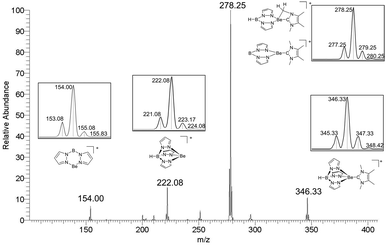Fig. 5 CID mass spectrum of the mass-selected cation [TpBe(IMe)]⁺ (6) at a normalized collision energy of 40 together with the expected isotopologue distributions.

By contrast, for the cations [TpBe(IiPr)]⁺ (7) and [TpBe(CAAC(Dipp))]⁺ (9), carbene loss is easier than pyrazole loss. While the pyrazole loss from 6 causes the formation of a cation at m/z = 278, it is not unequivocal if the necessary hydrogen atom stems from the boron atom of the Tp ligand or if C–H-bond activation of the CH₃ group of the NHC ligand takes place. However, CID of the formed cation ([(pz₂B)Be(IMe)]⁺ or [(pz₂BH)Be(IMe–H)]⁺) causes the release of a neutral fragment with 124 u, which corresponds to intact IMe, and thus the formation of [(pz₂B)Be]⁺ (m/z = 154). This observation indicates that the initial pyrazole loss probably causes the formation of [(pz₂B)Be(IMe)]⁺ rather than C–H-bond activation of the carbene ligand. In contrast to [TpBe(IMe)]⁺, CID of 7 (m/z = 346) causes the elimination of an iso-propyl group as an additional fragmentation channel followed by further fragmentation of the carbene unit into a fragment with m/z = 292 (Fig. S62†). Also [TpBe]⁺ and [(pz₂B)Be]⁺ are formed (Fig. S62†). CID of 9 (m/z = 507) mainly causes the generations of [TpBe]⁺ and [(pz₂B)Be]⁺ as well as the elimination of 1,1,2,2-tetramethylcyclopropane. As a minor fragmentation product, the formation of [(pz₂B)Be(CAAC(Dipp))]⁺ (m/z = 439) is observed (Fig. S78†).

Theoretical results

Quantum chemical calculations at the BP86-D3(BJ)/def2-TZVPP level^48–51 were carried out to study the structures, stability, and bonding in the title complexes. Fig. S79† shows the minimum energy geometries of [TpBeR]^q (q = 0, +1) complexes in the singlet spin state. It is found that in all cases triplet spin state is significantly higher in energy (by 74–86 kcal mol⁻¹) than the corresponding singlet electronic state. [TpBeR]^q for R = Ph, nBu, Cp*, Cp and IiPr has a C_s symmetry and ¹A′ electronic ground state, whereas TpBeMe has a C_3v symmetry and ¹A₁ electronic state. On the other hand, [TpBeR]⁺ (R = CAAC(Dipp), IDipp and IMe) lacks any symmetry. The computed geometrical parameters match closely with the experimental values, which indicates the suitability of the chosen level of theory to analyze the stability and bonding of the studied complexes. The computed Be–C_R bond distances (Table 3) in these complexes match quite well with the typical Be–C single bond, computed from the sum of their covalent radii reported by Pyykkö and Atsumi.⁵² In all investigated compounds the formal oxidation state of beryllium is +2. Calculated natural charges of 1.58–1.60 on Be in these complexes also support the assignment of +2 oxidation state of Be. However, there is significant debate on how oxidation states should be interpreted in beryllium organic compounds.^53–55 Therefore, it is important to gain an in depth insight into the nature of the Be–C bond with neutral and anionic C-ligands to assess this interpretation problem. Thus, we investigated this Be–C interaction in detail.

Table 3 TpBe–R bond dissociation energy at 0 K (D₀, kcal mol⁻¹) and 298 K (ΔG^{298 K}, kcal mol⁻¹) for the process, TpBeR^q (q = 0, +1) → TpBe^q + R, the HOMO–LUMO energy gap (Δ_H–L, eV), Wiberg (WBO) and Mayer (MBO) bond order (P) of Be–C_R bond, the net natural charge on R (q_R, e) and the bond length (r(Be–C_R), Å) computed at the BP86-D3(BJ)/def2-TZVPP level

Complex	TpBeR → TpBe + R		TpBeR → TpBe^+ + R^−		Δ H–L	P(Be–CR)		q R	r(Be–CR)
	D 0	ΔG^298 K	D 0	ΔG^298 K		WBO	MBO
TpBe(Ph) (1)	101.8	90.0	180.9	169.8	3.89	0.28	1.01	−0.80	1.740
TpBe(nBu) (2)	84.4	71.9	188.9	178.0	3.48	0.29	0.87	−0.81	1.745
TpBe(Me) (3)	88.8	78.5	193.8	184.3	3.93	0.32	0.82	−0.79	1.741
TpBe(η^1-Cp*) (4)	74.3	58.8	145.3	132.1	2.21	0.19	0.39	−0.84	1.823
TpBe(η^1-Cp) (5)	84.9	71.6	146.1	134.2	2.70	0.19	0.47	−0.83	1.818
	[TpBeR]^+ → TpBe^+ + R		[TpBeR]^+ → TpBe + R^+
[TpBe(IMe)]^+ (6)	76.9	64.8	142.0	128.5	4.40	0.27	0.81	0.19	1.787
[TpBe(IiPr)]^+ (7)	79.4	65.9	139.0	124.7	4.23	0.27	0.85	0.18	1.795
[TpBe(IDipp)]^+ (8)	86.4	71.7	148.2	135.6	4.05	0.25	1.07	0.16	1.798
[TpBe(CAAC(Dipp))]^+ (9)	81.7	66.2	132.1	114.7	3.31	0.22	1.08	0.13	1.810

---

We computed the zero-point energy corrected bond dissociation energies (BDE) at 0 K (D₀) and free energy changes at 298 K (ΔG^{298 K}) for two alternative dissociation processes: TpBeR → TpBe + R and TpBeR → TpBe⁺ + R⁻ for neutral complexes, and [TpBeR]⁺ → TpBe⁺ + R and [TpBeR]⁺ → TpBe + R⁺ for cationic complexes (Table 3). For all these complexes, both types of dissociation processes are highly unlikely as reflected by the very high D₀ and ΔG^{298 K} values. These values justify the high thermal stability of the reported complexes. Competitively, for neutral systems, the homolytic cleavage leading to TpBeR → TpBe + R is energetically less expensive than the heterolytic cleavage, TpBeR → TpBe⁺ + R⁻, whereas for cationic complexes, the fragmentation leading to a positive charge on more electropositive Be center, [TpBeR]⁺ → TpBe⁺ + R is energetically more favorable than the one, imposing the positive charge on R, [TpBeR]⁺ → TpBe + R⁺. The BDE value in neutral systems is the maximum for R = Ph (D₀ = 101.8 kcal mol⁻¹) and the minimum for R = Cp* (D₀ = 74.3 kcal mol⁻¹), following the order as Ph > Me > nBu ≈ Cp > Cp*. For the cationic compounds, the BDE value is the largest for R = IDipp (D₀ = 86.4 kcal mol⁻¹), followed by CAAC(Dipp), IiPr and IMe.

The electronic stability of the title complexes can also be roughly understood by the energy gap (Δ_H–L) between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). In general, a compound with a high Δ_H–L value shows high electronic stability and low reactivity according to the maximum hardness principle.^56–59 In the present cases, Δ_H–L values are quite large, ranging within 3.31–4.40 eV, except for TpBeR (R = Cp and Cp*) (Table 3). Even in the latter two cases, the Δ_H–L value is reasonably high, being 2.70 (Cp) and 2.21 (Cp*) eV. But on a comparative note, TpBeR (R = Cp and Cp*) is expected to show higher reactivity than the other complexes. Lower electronic stability of TpBeR (R = Cp and Cp*) can be understood by examining the related MOs. Fig. S80† displays the shape of the LUMO, HOMO and other MOs that are responsible for the Be–C_R interactions in these complexes. In the neutral complexes, LUMO mainly reflects N⋯N interaction in the Tp moiety. HOMO−2 for TpBe(Ph), HOMO for TpBe(Me) and TpBe(Bu) and HOMO−1 for TpBeR (R = Cp and Cp*) are responsible for the TpBe-R σ-interaction. A closer look on the shape of the HOMO−1 for TpBeR (R = Cp and Cp*) reveals that this is actually a π-orbital of six π-electronic aromatic Cp⁻ and Cp*-fragments. Therefore, the electronic donation from one such π orbital of Cp and Cp* to TpBe moiety disturbs the aromaticity, and therefore, makes these complexes less electronic stable which is reflected from their corresponding low Δ_H–L values. In the cationic complexes, LUMO in 8 and 9 is a π-orbital on the ligand, while for 6 and 7, it is located mainly on the Tp moiety. In these complexes, HOMO−8 represents the TpBe-R σ-bonding, except for complex 8 where it is located quite deep in energy (HOMO−22). The other relevant MOs responsible for weak TpBe-R π-interactions are also shown in Fig. S80.†

Table 3 also provides Wiberg (WBO)⁶⁰ and Mayer bond order (MBO)⁶¹ for the Be–C_R bonds. WBO values of Be–C_R bonds are quite small, ranging within 0.19–0.32, which contradicts with high orbital involvement in σ MOs and the obtained Be–C_R bond lengths matching with the single Be–C covalent bond distance. On the other hand, the MBO for the Be–C_R bond has a significantly higher value than the corresponding WBO value. MBO values are almost close to 1 for all cases, except for TpBeR (R = Cp and Cp*). Somewhat smaller MBO values for the latter two cases (0.4–0.5) can be associated with the obtained longest Be–C_R bond distances in these complexes among the neutral systems. Nonetheless, the present results indicate that the MBO suits better than the WBO to describe the bond order for the polar Be–C bonds. This observation also corroborates the previously reported conclusion that the MBO is a more reliable descriptor of bond order than the WBO.^62–64 In fact, the major shortcoming of the WBO is that it neglects the overlap of atomic orbitals completely, whereas the MBO considers the overlap matrix.

The very polar nature of the Be–C_R bond can also be understood from the natural partial charge distribution, which reveals that the apparently neutral complexes, in reality, exist as charge-separated complexes, [TpBe]⁺[R]⁻ (Table 3). On the other hand, the cationic complexes can be represented as [TpBe]⁺[R] with a net electron donation of 0.13–0.19 e from R to TpBe. Such high charge separation leads us to examine the topology of the electron density distribution by quantum theory of atoms-in-molecules (QTAIM) analysis.⁶⁵ The contour plots of the Laplacian of electron density, ∇²ρ(r) at the N–Be–C_R plane of the studied complexes are provided in Fig. 6 and Fig. S81.† The solid blue lines show the electron density depleted region, and the red dotted lines reveal the electron density accumulated region. In all these complexes, there is a large electron density accumulated region in between Be and C_R centers which reflects the covalent character. However, because of the polarity of the bond, the bond critical point (BCP) is located very close to the Be center and at the outside of the electron concentrated region. This makes ∇²ρ(r_c) for Be–C_R bond positive in all cases. In fact, for polar covalent bonds, the negative ∇²ρ(r_c) criterion is not essentially valid.^66,67 The total energy density, H(r_c) is a more reliable descriptor in these cases where it is negative and positive for covalent and non-covalent bonds, respectively.⁶⁸ In all cases, H(r_c) values are negative, revealing the covalent character in the Be–C_R bonds, and the covalent character is somewhat larger in neutral complexes than in the cationic ones as understood from the relative size of H(r_c) values.

Fig. 6 The contour plots of the Laplacian of electron density, ∇²ρ(r) at the N–Be–C_R plane of the complexes at the BP86-D3(BJ)/def2-TZVPP level. The blue solid lines indicate the region of ∇²ρ(r) > 0 and red dotted lines show ∇²ρ(r) < 0 region. The blue dots indicate the bond critical points.

To get more information about the Be–C_R bonding, we have carried out energy decomposition analysis (EDA)⁶⁹ in combination with natural orbital for chemical valence (NOCV) theory.^70,71 The numerical values of different energy terms obtained in EDA-NOCV depend largely on the chosen fragments. Since for neutral complexes, the charge distribution indicates the ionic description, [TpBe]⁺[R]⁻ but the BDE value for neutral fragmentation is smaller than the ionic one, we have carried out EDA using both schemes: (1) [TpBe]⁺ + [R]⁻ and (2) [TpBe] + [R] (Table S3†). In EDA, the prescribed way to choose the best fragmentation scheme to describe a bond is the one that yields the smallest orbital interaction (ΔE_orb) absolute value as it indicates that the electronic distribution in the chosen fragments matches most nearly to those in the complex.^72–75 Table S3† shows that in all neutral systems, the ionic scheme, [TpBe]⁺ + [R]⁻ gives the smallest ΔE_orb value, corroborating with the charge analysis. Therefore, the bonding situation in TpBeR is akin to the LiF molecule which gets dissociated into the neutral Li and F but in the molecule, the bonding can be represented as a polar covalent dative bond Li⁺ ← F⁻.^66,76

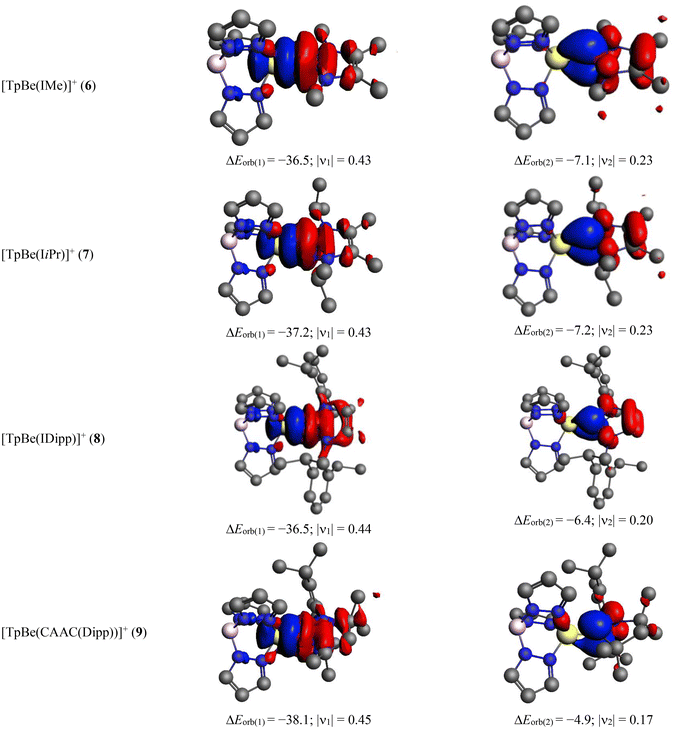
The detailed numerical results for the EDA-NOCV calculations for TpBeR using the ionic scheme are provided in Table 4. As expected from the ionic description, the electrostatic interaction energy (ΔE_elstat) is the most dominating term which accounts for 59–73% of the total attraction. The covalent interaction is also quite significant which is responsible for 25–33% of total attractive energy. The dispersion interaction makes up 1–7% of total stabilization. The most important information comes from the decomposition of the total covalent term into pair-wise orbital interactions, ΔE_orb(n). The nature of such interactions can be understood from the corresponding deformation densities depicted in Fig. 7 where the electron density shifts from red to blue region. The strongest orbital term, ΔE_orb(1) originates from the TpBe⁺ ← R⁻σ donation which is alone responsible for 59–67% of the total covalent interaction. The remaining two weak orbital terms, ΔE_orb(2) and ΔE_orb(3) come from the TpBe⁺ → R⁻ π backdonation, except for ΔE_orb(2) of TpBe(Ph), which develops from the π-polarization in the Ph unit followed by slight electron transfer to Be. Rather large rest of the orbital interaction term, ΔE_orb(rest) comes from the several small intra- and inter-fragment polarization terms.

Fig. 7 The plot of the deformation densities corresponding to ΔE_orb(1)–(3) for TpBeR complexes at the BP86-D3(BJ)/TZ2P level. The isosurface value is 0.0006 au. Electron density moves from red to blue region.

Table 4 EDA-NOCV results of TpBeR complex at the BP86-D3(BJ)/TZ2P//BP86-D3(BJ)/def2-TZVPP level using the fragments TpBe⁺ (S) and R⁻ (S). Energy values are given in kcal mol⁻¹

Energies	Interaction	1 TpBe^+ (S) + Ph^− (S)	2 TpBe^+ (S) + nBu^− (S)	3 TpBe^+ (S) + Me^− (S)	4 TpBe^+ (S) + (Cp*)^− (S)	5 TpBe^+ (S) + (Cp)^− (S)
a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb.
ΔEint		−198.3	−207.3	−211.3	−174.9	−166.0
ΔEPauli		90.2	95.2	96.2	70.5	60.0
ΔEdisp ^a		−8.6 (3.0%)	−7.0 (2.3%)	−4.4 (1.4%)	−18.0 (7.3%)	−10.8 (4.8%)
ΔEelstat ^a		−203.9 (70.7%)	−213.3 (70.5%)	−224.5 (73.0%)	−146.3 (59.6%)	−141.5 (62.6%)
ΔEorb ^a		−75.9 (26.3%)	−82.2 (27.2%)	−78.5 (25.5%)	−81.1 (33.0%)	−73.7 (32.6%)
ΔEorb(1) ^b	TpBe^+ ← R^− σ donation	−45.2 (59.6%)	−53.4 (65.0%)	−50.0 (63.7%)	−51.8 (63.9%)	−49.0 (66.5%)
ΔEorb(2) ^b	TpBe^+ → R^− π backdonation	−8.1 (10.7%)	−4.7 (5.7%)	−5.0 (6.4%)	−4.6 (5.7%)	−4.8 (6.5%)
ΔEorb(3) ^b	TpBe^+ → R^− π backdonation	−3.0 (4.0%)	−4.7 (5.7%)	−5.0 (6.4%)	−3.3 (4.1%)	−3.3 (4.5%)
ΔEorb(rest) ^b		−19.6 (25.8%)	−19.4 (23.6%)	−18.5 (23.6%)	−21.4 (26.4%)	−16.6 (22.5%)

---

In cases of the cationic complexes, we have found that [TpBe]⁺ + [R] is a more reasonable scheme than [TpBe] + [R]⁺ (Table S4†). Table 5 presents the results of the EDA-NOCV data for the cationic systems and the related deformation densities are depicted in Fig. 8. In these cases, the electrostatics contribute is around 48–58% and the covalent is around 34–35% of total attraction. The strongest orbital term comes from the TpBe⁺ ← R σ donation which is accountable for 56–65% of total covalent character. There is another small contribution that originates from the π-polarization in R followed by the donation to some extent to the TpBe moiety. Therefore, the present bonding analysis reveals that both neutral and cationic complexes possess Be ← C_R dative covalent bonds.

Fig. 8 The plot of the deformation densities corresponding to ΔE_orb(1)–(2) for [TpBeR]⁺ complexes at the BP86-D3(BJ)/TZ2P level. The isosurface value is 0.0006 au. Electron density moves from red to blue region.

Table 5 EDA-NOCV results of [TpBe–R]⁺ complex at the BP86-D3(BJ)/TZ2P//BP86-D3(BJ)/def2-TZVPP level using the fragments TpBe⁺ (S) and R (S). Energy values are given in kcal mol⁻¹

Energies	Interaction	6 TpBe^+ (S) + IMe (S)	7 TpBe^+ (S) + IiPr (S)	8 TpBe^+ (S) + IDipp (S)	9 TpBe^+ (S) + CAAC(Dipp) (S)
a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb.
ΔEint		−91.6	−95.8	−105.6	−99.8
ΔEPauli		70.1	76.8	86.9	86.5
ΔEdisp		−12.0 (7.4%)	−16.1 (9.3%)	−34.2 (17.8%)	−27.9 (15.0%)
ΔEelstat ^a		−93.8 (58.0%)	−96.2 (55.8%)	−92.9 (48.3%)	−94.2 (50.6%)
ΔEorb ^a		−55.9 (34.6%)	−60.2 (34.9%)	−65.4 (34.0%)	−64.1 (34.4%)
ΔEorb(1) ^b	TpBe^+ ← R σ donation	−36.5 (65.3%)	−37.2 (61.8%)	−36.5 (55.8%)	−38.1 (59.4%)
ΔEorb(2) ^b	π polarization/TpBe^+ ← R π donation	−7.1 (12.7%)	−7.2 (12.0%)	−6.4 (9.8%)	−4.9 (7.6%)
ΔEorb(rest) ^b		−12.3 (22.0%)	−15.8 (26.2%)	−22.5 (34.4%)	−21.1 (32.9%)

---

Conclusions

In summary, we have prepared a set of neutral and cationic Tp-beryllium complexes to evaluate the influence of anionic and neutral C-donor ligands onto the Be–C bond. Neither in solution via NMR spectroscopy nor in the solid state via X-ray diffractometry could significant differences be observed between the two types of complexes. Extensive computational analyses of the Be–C bonds in the studied compounds also reveal that in all cases the bond should be described as a Be ← C_R dative covalent bond and confirm the experimental finding. Therefore, the distinction into covalent, ionic or dative bonds is a pure formalism, which is no longer warranted by experimental or theoretical techniques. The findings of this case study should be applicable at least to most main group metals and hopefully help in rationalizing synthetic procedures for metal–organic compounds.

Author contributions

C. B. synthesized the compounds and collected the vibrational spectra. I.-A. B. synthesized the CAAC ligand. C. B. and M. R. B. performed the NMR spectroscopic measurements. C.B., G. S. and B. B. collected the MS spectrometric data. C. B. carried out the X-ray single crystal analysis. S. P. and C. D. performed the quantum chemical calculations. M. R. B. devised the central idea and coordinated the work. C. B., B. B., A. S., S. P. and M. R. B. analyzed the data and wrote the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. R. B. thanks Prof. F. Kraus for moral and financial support as well as the provision of laboratory space. The DFG is gratefully acknowledged for financial support (BU2725/8-1).

References

1. H. Gilman and F. Schulze, CCCLIII.-Beryllium dialkyls, J. Chem. Soc., 1927, 2663–2669.
2. A. I. Snow and R. E. Rundle, The structure of dimethylberyllium, Acta Crystallogr., 1951, 4, 348–352.
3. M. R. Buchner and M. Müller, Handling Beryllium, the Safe Way, ACS Chem. Health Saf., 2023, 30, 36–43.
4. J. Elguero and I. Alkorta, The dubious origin of beryllium toxicity, Struct. Chem., 2023, 34, 391–398.
5. M. R. Buchner, Beryllium coordination chemistry and its implications on the understanding of metal induced immune responses, Chem. Commun., 2020, 56, 8895–8907.
6. M. R. Buchner, Beryllium-associated diseases from a chemist's point of view, Z. Naturforsch., B: Chem. Sci., 2020, 75, 405–412.
7. H. Gilman, Studies Concerning the Direct Preparation of Organoberyllium Halides, J. Am. Chem. Soc., 1923, 45, 2693–2695.
8. M. Arrowsmith, H. Braunschweig, M. A. Celik, T. Dellermann, R. D. Dewhurst, W. C. Ewing, K. Hammond, T. Kramer, I. Krummenacher, J. Mies, K. Radacki and J. K. Schuster, Neutral zero-valent s-block complexes with strong multiple bonding, Nat. Chem., 2016, 8, 638–642.
9. T. Tröster, F. Endres, M. Arrowsmith, L. Endres, F. Fantuzzi and H. Braunschweig, Dibenzoberylloles: antiaromatic s-block fluorene analogues, Chem. Commun., 2023, 59, 9199–9202.
10. J. T. Boronski, L. R. Thomas-Hargreaves, M. A. Ellwanger, A. E. Crumpton, J. Hicks, D. F. Bekiş, S. Aldridge and M. R. Buchner, Inducing Nucleophilic Reactivity at Beryllium with an Aluminyl Ligand, J. Am. Chem. Soc., 2023, 145, 4408–4413.
11. J. T. Boronski, A. E. Crumpton, L. L. Wales and S. Aldridge, Diberyllocene, a stable compound of Be(I) with a Be-Be bond, Science, 2023, 380, 1147–1149.
12. C. Czernetzki, M. Arrowsmith, F. Fantuzzi, A. Gärtner, T. Tröster, I. Krummenacher, F. Schorr and H. Braunschweig, A Neutral Beryllium(I) Radical, Angew. Chem., Int. Ed., 2021, 60, 20776–20780.
13. J. T. Boronski, A. E. Crumpton, A. F. Roper and S. Aldridge, A nucleophilic beryllyl complex via metathesis at [Be-Be]²⁺, Nat. Chem., 2024, 16, 1295–1300.
14. C. Berthold, J. Maurer, L. Klerner, S. Harder and M. R. Buchner, Formation, Structure and Reactivity of a Beryllium(0) Complex with Mgδ⁺Beδ⁻ Bond Polarization, Angew. Chem., Int. Ed., 2024, 63, e202408422.
15. L. R. Thomas-Hargreaves, M. Müller, N. Spang, S. I. Ivlev and M. R. Buchner, Behavior of Lewis Bases toward Diphenylberyllium, Organometallics, 2021, 40, 3797–3807.
16. M. Arrowsmith, M. S. Hill, G. Kociok-Köhn, D. J. MacDougall and M. F. Mahon, Beryllium-Induced C-N Bond Activation and Ring Opening of an N-Heterocyclic Carbene, Angew. Chem., Int. Ed., 2012, 51, 2098–2100.
17. J. Gottfriedsen and S. Blaurock, The First Carbene Complex of a Diorganoberyllium: Synthesis and Structural Characterization of Ph₂Be(i-Pr-carbene) and Ph₂Be(n-Bu₂O), Organometallics, 2006, 25, 3784–3786.
18. M. Müller and M. R. Buchner, Diphenylberyllium Reinvestigated: Structure, Properties and Reactivity of BePh₂, [(12-crown-4)BePh]⁺ and [BePh₃]⁻, Chem. – Eur. J., 2020, 26, 9915–9922.
19. M. Del Mar Conejo, R. Fernández, D. Del Río, E. Carmona, A. Monge, C. Ruiz, A. M. Márquez and J. F. Sanz, Synthesis, Solid-State Structure, and Bonding Analysis of the Beryllocenes [Be(C₅Me₄H)₂], [Be(C₅Me₅)₂], and [Be(C₅Me₅)(C₅Me₄H)], Chem. – Eur. J., 2003, 9, 4452–4461.
20. D. Naglav, B. Tobey, A. Neumann, D. Bläser, C. Wölper and S. Schulz, Synthesis, Solid-State Structures, and Computational Studies of Half-Sandwich Cp*BeX (X = Cl, Br, I) Compounds, Organometallics, 2015, 34, 3072–3078.
21. M. Bayram, D. Naglav, C. Wölper and S. Schulz, Synthesis and Structure of Bis(diphenylphosphinimino)methanide and Bis(diphenylphosphinimino)methanediide Beryllium Complexes, Organometallics, 2016, 35, 2378–2383.
22. M. Bayram, D. Naglav, C. Wölper and S. Schulz, Syntheses and Structures of Homo- and Heteroleptic Beryllium Complexes Containing N,N-Chelating Ligands, Organometallics, 2017, 36, 467–473.
23. F. Lindl, A. Lamprecht, M. Arrowsmith, E. Khitro, A. Rempel, M. Dietz, T. Wellnitz, G. Bélanger-Chabot, A. Stoy, V. Paprocki, D. Prieschl, C. Lenczyk, J. Ramler, C. Lichtenberg and H. Braunschweig, Aromatic 1,2-Azaborinin-1-yls as Electron-Withdrawing Anionic Nitrogen Ligands for Main Group Elements, Chem. – Eur. J., 2023, 29, e202203345.
24. M. Arrowsmith, M. S. Hill and G. Kociok-Köhn, Activation of N-Heterocyclic Carbenes by BeH₂ and Be(H)(Me) Fragments, Organometallics, 2015, 34, 653–662.
25. A. Paparo, S. P. Best, K. Yuvaraj and C. Jones, Neutral, Anionic, and Paramagnetic 1,3,2-Diazaberyllacyles Derived from Reduced 1,4-Diazabutadienes, Organometallics, 2020, 39, 4208–4213.
26. M. R. Buchner, L. R. Thomas-Hargreaves, C. Berthold, D. F. Bekiş and S. I. Ivlev, A Preference for Heterolepticity - Schlenk Type Equilibria in Organometallic Beryllium Systems, Chem. – Eur. J., 2023, 29, e202302495.
27. L. A. Freeman, J. E. Walley, A. D. Obi, G. Wang, D. A. Dickie, A. Molino, D. J. D. Wilson and R. J. Gilliard, Stepwise Reduction at Magnesium and Beryllium: Cooperative Effects of Carbenes with Redox Non-Innocent α-Diimines, Inorg. Chem., 2019, 58, 10554–10568.
28. R. Fernández and E. Carmona, Recent Developments in the Chemistry of Beryllocenes, Eur. J. Inorg. Chem., 2005, 3197–3206.
29. S. Trofimenko, Boron-Pyrazole Chemistry, J. Am. Chem. Soc., 1966, 88, 1842–1844.
30. S. Trofimenko, Boron-pyrazole chemistry. II. Poly(1-pyrazolyl)-borates, J. Am. Chem. Soc., 1967, 89, 3170–3177.
31. C. Berthold, M. Müller, S. I. Ivlev, D. M. Andrada and M. R. Buchner, Gauging ambiphilicity of pseudo-halides via beryllium-trispyrazolylborato compounds, Dalton Trans., 2023, 52, 13547–13554.
32. R. Han, A. Looney and G. Parkin, Tris(pyrazolyl)hydroboratomagnesium and aluminum alkyl derivatives: alkyl exchange with methyl iodide and enolate formation with acetone, J. Am. Chem. Soc., 1989, 111, 7276–7278.
33. C. Helling and C. Jones, Schlenk-Type Equilibria of Grignard-Analogous Arylberyllium Complexes: Steric Effects, Chem. – Eur. J., 2023, 29, e202302222.
34. I. Krossing and A. Reisinger, Chemistry with weakly-coordinating fluorinated alkoxyaluminate anions: Gas phase cations in condensed phases?, Coord. Chem. Rev., 2006, 250, 2721–2744.
35. D. Himmel, H. Scherer, D. Kratzert and I. Krossing, Synthesis and Characterization of Cp*Be-F-Al(ORF)₃, Z. Anorg. Allg. Chem., 2015, 641, 655–659.
36. P. G. Plieger, K. D. John, T. S. Keizer, T. M. McCleskey, A. K. Burrell and R. L. Martin, Predicting ⁹Be Nuclear Magnetic Resonance Chemical Shielding Tensors Utilizing Density Functional Theory, J. Am. Chem. Soc., 2004, 126, 14651–14658.
37. J. K. Buchanan and P. G. Plieger, ⁹Be nuclear magnetic resonance spectroscopy trends in discrete complexes: an update, Z. Naturforsch., B: J. Chem. Sci., 2020, 75, 459–472.
38. R. Han and G. Parkin, Synthesis, structure, and reactivity of η³-HB(3-tert-Bupz)₃BeCH₃, a terminal beryllium alkyl complex supported by tris(3-tert-butylpyrazolyl)hydroborato ligation, Inorg. Chem., 1993, 32, 4968–4970.
39. N. Kuhn and T. Kratz, Synthesis of Imidazol-2-ylidenes by Reduction of Imidazole-2(3H)-thiones, Synthesis, 1993, 561–562.
40. X. Bantreil and S. P. Nolan, Synthesis of N-heterocyclic carbene ligands and derived ruthenium olefin metathesis catalysts, Nat. Protoc., 2011, 6, 69–77.
41. C. Müller, D. M. Andrada, I.-A. Bischoff, M. Zimmer, V. Huch, N. Steinbrück and A. Schäfer, Synthesis, Structure, and Bonding Analysis of Tin(II) Dihalide and Cyclopentadienyltin(II) Halide (Alkyl)(amino)carbene Complexes, Organometallics, 2019, 38, 1052–1061.
42. D. Naglav, D. Bläser, C. Wölper and S. Schulz, Synthesis and Characterization of Heteroleptic 1-Tris(pyrazolyl)borate Beryllium Complexes, Inorg. Chem., 2014, 53, 1241–1249.
43. D. Naglav-Hansen, K. Dzialkowski, B. Tobey, C. Wölper, G. Jansen and S. Schulz, Hungry for charge – how a beryllium scorpionate complex “eats” a weakly coordinating anion, Z. Naturforsch., B: J. Chem. Sci., 2020, 75, 503–508.
44. A. Paparo and C. Jones, Beryllium Halide Complexes Incorporating Neutral or Anionic Ligands: Potential Precursors for Beryllium Chemistry, Chem. – Asian J., 2019, 14, 486–490.
45. M. Müller and M. R. Buchner, Preparation and crystal structures of the beryllium ammines [Be(NH₃)₄]X₂ (X = Br, I, CN, SCN, N₃) and Be(NH3)₂X’₂ (X′ = Cl, Br, I), Chem. Commun., 2019, 55, 13649–13652.
46. M. Müller, A. J. Karttunen and M. R. Buchner, Speciation of Be²⁺ in acidic liquid ammonia and formation of tetra- and octanuclear beryllium amido clusters, Chem. Sci., 2020, 11, 5415–5422.
47. A. Paparo, C. D. Smith and C. Jones, Diagonally Related s- and p-Block Metals Join Forces: Synthesis and Characterization of Complexes with Covalent Beryllium-Aluminum Bonds, Angew. Chem., Int. Ed., 2019, 58, 11459–11463.
48. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100.
49. L. Goerigk and S. Grimme, A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
50. J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
51. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
52. P. Pyykkö and M. Atsumi, Molecular Single-Bond Covalent Radii for Elements 1-118, Chem. – Eur. J., 2009, 15, 186–197.
53. M. Gimferrer, S. Danés, E. Vos, C. B. Yildiz, I. Corral, A. Jana, P. Salvador and D. M. Andrada, The oxidation state in low-valent beryllium and magnesium compounds, Chem. Sci., 2022, 13, 6583–6591.
54. S. Pan and G. Frenking, Comment on “The oxidation state in low-valent beryllium and magnesium compounds” by M. Gimferrer, S. Danés, E. Vos, C. B. Yildiz, I. Corral, A. Jana, P. Salvador and D. M. Andrada, Chem. Sci. 2022, 13, 6583, Chem. Sci., 2023, 14, 379–383.
55. M. Gimferrer, S. Danés, E. Vos, C. B. Yildiz, I. Corral, A. Jana, P. Salvador and D. M. Andrada, Reply to the “Comment on The oxidation state in low-valent beryllium and magnesium compounds” by S. Pan and G. Frenking, Chem. Sci., 2022, 13, DOI: 10.1039/D2SC04231B, Chem. Sci., 2023, 14, 384–392.
56. R. G. Pearson, The principle of maximum hardness, Acc. Chem. Res., 1993, 26, 250–255.
57. R. G. Parr and P. K. Chattaraj, Principle of maximum hardness, J. Am. Chem. Soc., 1991, 113, 1854–1855.
58. S. Pan, M. Sola and P. K. Chattaraj, On the Validity of the Maximum Hardness Principle and the Minimum Electrophilicity Principle during Chemical Reactions, J. Phys. Chem. A, 2013, 117, 1843–1852.
59. W. Grochala, The generalized maximum hardness principle revisited and applied to atoms and molecules, Phys. Chem. Chem. Phys., 2017, 19, 30964–30983.
60. K. B. Wiberg, Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083–1096.
61. I. Mayer, Charge, bond order and valence in the AB initio SCF theory, Chem. Phys. Lett., 1983, 97, 270–274.
62. R. Liu, L. Qin, Z. Zhang, L. Zhao, F. Sagan, M. Mitoraj and G. Frenking, Genuine quadruple bonds between two main-group atoms. Chemical bonding in AeF− (Ae = Be–Ba) and isoelectronic EF (E = B–Tl) and the particular role of d orbitals in covalent interactions of heavier alkaline-earth atoms, Chem. Sci., 2023, 14, 4872–4887.
63. Y.-Q. Liu, M.-H. Wang, B. Yan, L. Li, S. Pan, Z.-H. Cui and G. Frenking, Quest of Quadruple Bonding Between Two Main-Group Atoms in AeB− and AeC (Ae=Ca, Sr, Ba) and the Role of d Orbitals of Heavier Alkaline-Earth Atoms in Covalent Interactions, Chem. – Eur. J., 2023, 29, e202300446.
64. L. Qin, Y.-Q. Liu, R. Liu, X. Yang, Z.-H. Cui, L. Zhao, S. Pan, S. Fau and G. Frenking, Analysis of the Unusual Chemical Bonds and Dipole Moments of AeF− (Ae=Be−Ba): A Lesson in Covalent Bonding, Chem. – Eur. J., 2024, 30, e202304136.
65. R. F. W. Bader, Atoms in molecules. A quantum theory, Oxford University Press, Oxford, 1990.
66. L. Zhao, S. Pan and G. Frenking, The nature of the polar covalent bond, J. Chem. Phys., 2022, 157, 34105.
67. S. Pan and G. Frenking, Comment on “Realization of Lewis Basic Sodium Anion in the NaBH₃− Cluster”, Angew. Chem., Int. Ed., 2020, 59, 8756–8759.
68. D. Cremer and E. Kraka, Chemical bonds without bonding electron density–Does the difference electron-density analysis suffice for a description of the chemicadensity, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628.
69. T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chem. Acc., 1977, 46, 1–10.
70. M. Mitoraj and A. Michalak, Donor-acceptor properties of ligands from the natural orbitals for chemical valence, Organometallics, 2007, 26, 6576–6580.
71. M. Mitoraj and A. Michalak, Applications of natural orbitals for chemical valence in a description of bonding in conjugated molecules, J. Mol. Model., 2008, 14, 681–687.
72. C. Chi, S. Pan, L. Meng, M. Luo, L. Zhao, M. Zhou and G. Frenking, Alkali Metal Covalent Bonding in Nickel Carbonyl Complexes ENi(CO)₃⁻, Angew. Chem., Int. Ed., 2019, 58, 1732–1738.
73. R. Saha, S. Pan, P. K. Chattaraj and G. Merino, Filling the void: controlled donor–acceptor interaction facilitates the formation of an M–M single bond in the zero oxidation state of M (M = Zn, Cd, Hg), Dalton Trans., 2020, 49, 1056–1064.
74. G. Wang, J. E. Walley, D. A. Dickie, S. Pan, G. Frenking and R. J. Gilliard, A Stable, Crystalline Beryllium Radical Cation, J. Am. Chem. Soc., 2020, 142, 4560–4564.
75. W. Yang, K. E. Krantz, L. A. Freeman, D. A. Dickie, A. Molino, G. Frenking, S. Pan, D. J. D. Wilson and R. J. Gilliard, Persistent Borafluorene Radicals, Angew. Chem., Int. Ed., 2020, 59, 3850–3854.
76. L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chemical Bonding and Bonding Models of Main-Group Compounds, Chem. Rev., 2019, 119, 8781–8845.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, extended crystallographic data, IR, NMR and mass spectra. CCDC 2385384–2385387. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi03234a

---