 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluoride binding in unlikely partners: the formation of anion–anion complexes with [M(EGTA)]− and [M(OBETA)]− (M = Gd3+, Y3+)†
Lorenzo
Risolo
 a,
Marco
Ricci
a,
Marco
Ricci
 a,
Daniela
Lalli
a,
Daniela
Lalli
 *ab,
Carlos
Platas-Iglesias
*ab,
Carlos
Platas-Iglesias
 c and
Mauro
Botta
c and
Mauro
Botta
 *ab
*ab
aDipartimento di Scienze e Innovazione Tecnologica, Università del Piemonte Orientale “A. Avogadro”, Viale T. Michel 11, 15121 Alessandria, Italy. E-mail: mauro.botta@uniupo.it
bMagnetic Resonance Platform (PRISMA-UPO), Università del Piemonte Orientale “A. Avogadro”, Viale T. Michel 11, 15121 Alessandria, Italy
cUniversidade da Coruña, Centro de Investigacións Científicas Avanzadas (CICA) and Departamento de Química, Facultade de Ciencias, 15071, A Coruña, Galicia, Spain
First published on 24th December 2024
Abstract
Anionic metal complexes (M = Gd3+, Y3+) with two homologous acyclic aminopolycarboxylate ligands, heptadentate (OBETA) and octadentate (EGTA), were prepared and characterized using both relaxometric NMR (for Gd3+) and high-resolution NMR (for Y3+) techniques. The addition of fluoride to aqueous solutions of these complexes led to the formation of ternary complexes where F− displaces a coordinated water molecule from the metal ion's inner coordination sphere. In the Gd3+ complexes, this exchange process was tracked by monitoring changes in the nuclear magnetic relaxation rate of water protons, allowing calculation of the binding affinity. For the diamagnetic Y3+ complexes, the exchange was followed through variable-temperature high-resolution 19F NMR experiments. Calculated enthalpic and entropic contributions to the activation free energy suggest a dissociative exchange mechanism for the monohydrated [M(EGTA)(H2O)]− and an associative mechanism for the dihydrated [M(OBETA)(H2O)2]−. Additionally, an unusual dimeric structure was observed for the dihydrated complexes, where two anionic complexes are bridged by fluoride. Detailed DFT calculations confirmed the presence of the dimer, showing a Y–F bond length of 2.33 Å and a 1JY–F NMR coupling constant of 38.0 Hz, in excellent agreement with the experimental value.
Introduction
Anion recognition by metal ions is of great importance in coordination chemistry, as it underlies key processes in both inorganic and biological chemistry. The interaction between metal centres and anions, with varying degrees of selectivity, is central to processes such as catalysis, molecular recognition, and ion transport.1 In biological systems, metal ion–anion binding plays a crucial role in enzyme function, ion transport, and cellular signalling pathways.2Expanding our knowledge of metal ion–anion interactions, and the factors that influence their strength and selectivity, is also essential for the design and development of advanced inorganic materials for applications in environmental, energy, pharmaceutical, and sensing technologies.3 Moreover, the study of anion coordination is particularly relevant for understanding the mechanisms of action of contrast agents (CAs) used in magnetic resonance imaging (MRI), with the goal of optimizing their efficacy (relaxivity, r1) and maintaining stability in vivo.4–6
Relaxivity depends on several factors, including molecular tumbling, hydration number (q), water exchange rate (kex), and electronic relaxation time, all of which must be optimized to maximize CAs effectiveness.7,8 One strategy previously explored has been to design Gd3+ complexes with two water molecules in the metal ion's inner coordination sphere. For decades, all approved Gd-based contrast agents (GBCAs) had only one inner-sphere water molecule (q = 1). Moving to q = 2 complexes can increase r1 by approximately 50%, assuming all other factors remain constant. However, progress along this direction has been constrained by two main challenges: (a) the propensity of such complexes to form ternary compounds with oxyanions present in biological fluids (e.g., carbonate, oxalate, phosphate, and lactate), which displace coordinated water molecules;9–11 and (b) the significant reduction in thermodynamic stability and kinetic inertness of the complex when reducing the chelating agent's denticity.12,13 However, these characteristics are not entirely universal. Examples of Ln(III) complexes with q > 1 have been designed and reported that either exhibit high stability, show no tendency to form ternary complexes with anions, or possess both qualities. Notable examples include Ln(III) complexes with HOPO-based chelators, AAZTA, aDO3A, and CyPic3A.9,11,14,15
Only recently has the first Gd3+ complex with q = 2, Gadopiclenol, been approved for clinical use and entered the market. This macrocyclic ligand is heptadentate, and the complex demonstrates stability and inertness under physiological conditions.16 Clearly, there is significant room for improving our understanding of the details governing the anion–metal ion interactions. Gaining deeper insight into these interactions could aid in designing more effective systems for selective recognition or in developing new MRI diagnostic probes with enhanced efficiency, where the binding interaction is minimized.
In the broader context of advancing our understanding of interactions between Ln3+ complexes and anions, the binding of halide ions has drawn considerable interest in recent years, although relatively few studies have been reported. Around three decades ago, significant changes in the 1H NMR spectra of paramagnetic macrocyclic complexes [Ln(DOTA)]− were observed with increasing additions of fluoride ions (H4DOTA = 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid).17 More recently, Faulkner et al. investigated fluoride binding in DOTA tetraamide and tetrapicolyl Ln3+ complexes using both NMR and photophysical techniques.18,19 Charbonnière and coworkers further demonstrated the formation of supramolecular adducts featuring a fluoride bridge in Ln3+ complexes with a DOTA derivative containing two indazolyl groups at the 1,7 positions.20 Butler developed a Eu3+ complex with a strong affinity for F− compared to other anions, enabling fluoride detection in water at environmentally relevant concentrations.21 For obvious reasons, most reported studies have involved cationic or neutral Ln3+ complexes, which are characterized by relatively high affinity constants. In fact, examples of fluoride binding to metal centres in anionic complexes are very rare.22,23 In contrast, fluoride interactions with metal ions other than lanthanides have been extensively studied, particularly in the context of PET applications.24 For instance, the {Al18F}2+ complex has attracted considerable interest for its role in enhancing radiofluorination techniques, providing a straightforward and efficient way to attach the positron-emitting 18F isotope to biomolecules.25 It is also worth noting that some lanthanides, such as Tb isotopes, are utilized in PET/SPECT imaging and targeted radiotherapy. Fluoride complexes have the potential to offer improved stability and biodistribution profiles, further broadening their applicability.
In this work, we present the results of our study on the interaction between the fluoride anion and negatively charged complexes (M = Gd3+, Y3+) with H4EGTA (ethylene glycol bis(2-aminoethyl ether) N,N,N′,N′-tetraacetic acid) and H4OBETA (2,2′-oxobis(ethylamine) N,N,N′,N′-tetraacetic acid) (Scheme 1). These structurally related complexes – OBETA being the lower homolog of the well-known EGTA – exhibit different hydration states (q = 1 and q = 2).26
The goals of this study are threefold: (a) to establish the strength of the interaction and its dependence on hydration state in structurally correlated complexes; (b) to determine relaxivity changes following coordinated water molecule substitution; and (c) to assess the effect of F− binding on water exchange rate for the bishydrated complex. Thus, we employed a combination of high- and low-resolution NMR techniques in both frequency and time domains, enabling a detailed characterization of the kinetics and thermodynamics underlying the fluoride-binding event. Proton relaxometry is a highly suitable technique, as the displacement of a coordinated water molecule results in a decrease in the longitudinal nuclear magnetic relaxation rate of solvent protons (R1). This decrease can be precisely monitored throughout a titration of a dilute solution of the paramagnetic Gd3+ complex.7 On the other hand, established high-resolution NMR techniques allow for direct measurement of the 19F nucleus in a solution of the diamagnetic Y3+ complex, providing valuable kinetic insights into exchange dynamics.
Results and discussion
Relaxometric characterization
Paramagnetic molecules undergoing Brownian motions in solution can generate oscillating local magnetic fields, which induce relaxation of the nuclei of nearby water molecules. The water molecules interacting with such complexes are classified as: inner sphere (IS) molecules, directly coordinated to the metal ion and in exchange with the bulk water; second sphere (SS) molecules, involved in hydrogen bonds with the polar groups of the complex; and outer sphere (OS) molecules, diffusing close to the chelate.4,8 Each contributes to the relaxivity as follows:| r1 = rIS1 + rSS1 + rOS1 | (1) |
 | (2) |
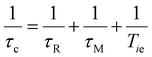 | (3) |
Our procedure begins by measuring the dependence of relaxivity on the proton Larmor frequency across a wide range (0.01–120 MHz) at three different temperatures (283, 298, and 310 K) (Fig. S1†). The resulting data are 1H NMRD (Nuclear Magnetic Relaxation Dispersion) profiles, which can be analysed to determine the molecular parameters governing relaxation (Fig. 1).28 The profiles show two plateaux at low and high frequencies, spaced out by a single dispersion at ∼4 MHz, characteristic of low molecular weight Gd3+ complexes tumbling rapidly in solution. The increased relaxivity values with decreasing temperatures are consistent with systems in fast exchange regime (τM < T1M). The profiles were analysed using the SBM equations27 and the Freed equation,29 with the latter specifically accounting for the outer-sphere contributions to relaxation.
 | ||
| Fig. 1 1H NMRD profiles (top panel) of an aqueous solution of [Gd(OBETA)(H2O)2]− (2.9 mM and pH = 7.15) and [Gd(EGTA)(H2O)]− (5.2 mM and pH = 7.15) recorded at 298 K. 17O transverse reduced relaxation rates (bottom) as a function of the temperature of an aqueous solution of [Gd(OBETA)(H2O)2]− (7.0 mM and pH = 7.0)26 and [Gd(EGTA)(H2O)]− (32 mM and pH = 7.0) measured at 11.75 T. The solid lines correspond to the fits of the data, as described in the text. | ||
Exchange rates of the IS water molecule(s) (kex) were obtained by measuring the 17O chemical shift (Δωr) and reduced transverse relaxation rates (R2r = 1/T2r) of the isotopically enriched bulk-water as a function of temperature (280–350 K), at high field (11.75 T) (Fig. S2†).30 The 17O R2 data of the investigated complexes exhibit a bell-shaped curve, characterized by relatively broad maxima below 300 K, typical of fast exchange regimes (Fig. S2†). The data were analysed with the Swift–Connick equations,31 which describe the water exchange process between two-site characterized by different populations and relaxation times. A global analysis of the experimental 1H NMRD and 17O NMR data was performed simultaneously, to obtain results that are more reliable. Following an established procedure, some parameters were fixed to standard values reported in the literature, including hydration number (q = 2 for [Gd(OBETA)]− and q = 1 for [Gd(EGTA)]−), the M–H distance between the IS water molecule(s) and Gd3+ (rM–H = 3.0 Å), the M–H distance involving the OS water molecules (a = 4.0 Å), the relative diffusion coefficient of OS water molecules and the complex at 298 K (298D = 2.24 × 105 cm2 s−1), and the activation energy for the modulation of the zero-field splitting interaction (EV = 1.0 kJ mol−1). The analysis yielded an excellent fit of the data, providing parameter values consistent with those already published. This set of parameters was then used as a reliable starting point for further analysis and comparisons (Table 1 and Table S1†).
Affinity constant of the fluoride anion for the Gd complexes
It is known that fluoride can coordinate the metal centre of lanthanide complexes so efficiently to replace one or more labile IS water molecules.10,18 Of course, we expect the strength of the interaction to be closely dependent on the overall charge of the host, resulting in a significantly weaker interaction for anionic complexes, especially those with octadentate ligands. The hydration loss results in a relaxivity drop that can be readily detected by 1H NMR relaxometric analysis. Measuring R1 variation of the water protons as a function of increasing additions of fluoride in dilute Gd3+ complexes aqueous solutions (ca. 0.5–1 mM), at a fixed frequency (32 MHz), allow access to the affinity constant (KA) of the molecular interaction (Scheme 2) and the relaxivity of the F-bound complex (rbound1), given the number of independent interaction sites (n).Solutions of [Gd(OBETA)(H2O)2]− and [Gd(EGTA)(H2O)]− were titrated with increasing amounts of NaF until the observed change in R1 became negligible, i.e. in the presence of a halide excess approximately three orders of magnitude greater than that of the complexes (Fig. 2). The obtained titration curves can be analysed using the well-established proton relaxation enhancement (PRE) method.7 The low affinity constants (KA = 13.6 ± 2.0 M−1 for [Gd(OBETA)(H2O)2]− and KA = 14.5 ± 2.7 M−1 for [Gd(EGTA)(H2O)]−) are consistent with binding interactions weakened by the strong electrostatic repulsion between the negatively charged complexes and the anions, and comparable to that found for the anionic [Gd(AAZTA)(H2O)2]− chelate (KA = 8.8 ± 0.8 M−1).22
The relaxivity values of the ternary adducts suggests that fluoride displaces only one water molecule from the coordination sphere of both Gd3+ ions. In fact, the rbound1 = 5.60 ± 0.05 mM−1 s−1 of [Gd(OBETA)(H2O)F]2− is consistent with that of a monohydrated complex, while that of [Gd(EGTA)F]2− (rbound1 = 3.36 ± 0.03 mM−1 s−1) is only slightly higher than that of a q = 0 species (Table 2).
It is worth noting that knowing KA enables calculating the relative populations of binary and ternary complexes present in solution for any given concentration of fluoride ions (Scheme 2). This information is essential to analyse the relaxometric properties of pure ternary species in the absence of binary complexes, since the latter, being endowed with a higher degree of IS hydration, can substantially alter r1 even at very low concentrations. This effect is especially evident in the case of weak halide-complex interactions, where the use of F− concentrations <0.6 M, such as to keep the water microviscosity and relaxometric properties of the complexes’ unaltered, inevitably generates mixtures of binary and ternary species. Therefore, KA allows deriving the relative concentration of the two adducts, and subtracting the relaxometric contribution of the binary species, to obtain the relaxometric properties of the ternary complex alone, as explained in the next paragraph.
Relaxometric characterization of the Gd3+ ternary complexes
The substitution of a water molecule by a fluoride anion has a significant impact on the relaxometric properties of Gd3+ complexes. For [Gd(EGTA)F]2−, such substitution results in a shift from q = 1 to q = 0, theoretically reducing the relaxivity to the OS contribution (rOS1) only. However, F− ions are well-known for their capacity to promote strong hydrogen bonding interactions with surrounding water molecules, suggesting the likely presence of an extra-contribution of SS (rSS1).10,32 This effect is also relevant for [Gd(OBETA)(H2O)F]2−, which, additionally, holds one metal-bound water molecule with exchange rate modulated by the presence of fluoride in the inner coordination sphere.To characterize the ternary complexes and elucidate the effects associated with F− binding, we collected a full set of 1H NMRD profiles for both complexes, complemented by variable-temperature 17O NMR data for the [Gd(OBETA)(H2O)F]2− adduct (Fig. 3A and Fig. S3†). Solutions were prepared with known stoichiometric mixtures of binary and ternary complexes. Under these conditions, the paramagnetic contribution to the relaxation rate in a solution with a total Gd3+ concentration of 1 mM corresponds to the sum of the relaxivities of the binary (rfree1) and ternary (rbound1) complexes, each weighted by its respective molar fraction:
| r1 = rfree1 × χfree + rbound1 × χbound | (4) |
To account for the high ionic strength, the relaxation rate contribution from the binary complex, prepared under identical ionic strength conditions employing NaCl (see Fig. S4 and S5†), was subtracted from the 1H NMRD and 17O profiles, following previously reported methodologies.22 A simultaneous analysis of the 1H NMRD profiles and 17O NMR data acquired for [Gd(OBETA)(H2O)F]2−, and the fit of the 1H NMRD profiles recorded for [Gd(EGTA)F]2− were performed (Fig. 3), following the same approach described above.
Kinetics and thermodynamics of the fluoride exchange with Y3+ complexes
To gain insight into the structure of the ternary adducts and the kinetic and thermodynamic parameters of the chemical exchange reaction between the metal-bound (F−bound) and the free fluoride (F−free) ensembles, high-resolution 19F NMR studies were performed. Such analyses are feasible only if the spectral resolution is high enough to allow observing the 19F signals and measuring their linewidths with appropriate accuracy. However, this is not the case for paramagnetic Gd3+ systems, whose unpaired electrons cause a strong relaxation enhancement of the neighbouring nuclei, thus generating extremely broad lines. Therefore, Gd3+ has been replaced with the diamagnetic analogue Y3+ characterized by: (i) a similar ionic radius, which preserves coordination geometries and exchange dynamics, and (ii) sharp lines, which allow for high-resolution NMR techniques to be applied. The formation of the ternary complexes was followed by NMR titrations of the Y3+ complexes with increasing amounts of NaF (B0 = 11.75 T, T = 275 K). After each addition, proton-decoupled 1D 19F NMR spectra were acquired to quantify the relative concentration of the F−bound and F−free species, until equal populations of the exchange sites were reached (Fig. S6†). Under these conditions, two 19F signals are observed for the [Y(EGTA)F]2− complex, which, based on their chemical shifts, can be attributed to the F−bound (−70.6 ppm) and F−free (−119 ppm) forms in slow exchange on the NMR timescale (Fig. S6†).18,22 Surprisingly, three signals are observable in the proton-decoupled 19F NMR spectra in the case of [Y(OBETA)]− after the addition of fluoride: one resonating at −61.4 ppm, with a narrow line and spin multiplicity of a triplet (J ≈ 40 Hz), and the others at −76.2 and −119 ppm, with broad lines indicative of the presence of an exchange reaction (Fig. S6†). The first signal (−61.4 ppm) most probably arises from the scalar coupling between F− and two identical NMR active nuclei with nuclear spin-½ and 100% natural abundance, such as 89Y. This evidence suggests the formation of a dimeric complex composed of two monohydrated Y3+-adducts bridged by a metal-bound-fluoride [F⊂(YOBETA)2]3−, which does not exchange with the other species present in solution at low temperatures. To support this hypothesis, DFT calculations were performed, as reported below. On the other hand, the other two signals resemble those observed for [Gd(EGTA)F]2− and can be attributed to F−bound (−76 ppm) and F−free (−119 ppm) ensembles in slow chemical exchange.To access the kinetic information on the exchange rates of the chemical reactions, and therefore the thermodynamic parameters associated with the activation energy, line-shape analysis at variable temperature was performed on [Y(EGTA)F]2− and [Y(OBETA)(H2O)F]2− (Fig. 4). As chemical exchange processes produce readily detectable effects on the shapes of NMR signals, variations of the 19F line shapes induced upon temperature changes were monitored for a quantitative evaluation of the pseudo-first order rate constants for fluoride exchange (kF), which characterize the two-site exchange involving F−bound and F−free. For both the investigated complexes, significant line-broadening is observed at increasing temperatures due to the acceleration of the fluoride kF, until coalescence is reached just above 310 K (Fig. 4A and C). A quantitative evaluation of the fluoride exchange rate constants was obtained by fitting the integrals and linewidths of the F−bound and F−free signals over the entire set of analysed temperatures (Fig. 4B and D) by using the Dynamic NMR (DNMR) Lineshape Analysis tool (version 1.1.2) implemented in Bruker's Topspin 3.2 software.
The exchange rates calculated at 290 K for the [Y(EGTA)F]2− and [Y(OBETA)(H2O)F]2− complexes are similar (Table 3) and much faster than those reported in literature for tricationic Y(DOTA)-tetraamide derivatives,18 indicating that the electrostatic repulsion between the fluoride anion and the negatively charged complex, significantly accelerates the dissociation reaction with respect to positively charged adducts.
| Ligands | 290 k F (103 s−1) | ΔH‡ (kJ mol−1) | ΔS‡ (J mol−1 K−1) | 290ΔG‡ (kJ mol−1) |
|---|---|---|---|---|
| EGTA | 4.57 | 53.1 ± 0.3 | 7.9 ± 0.9 | 50.8 ± 0.9 |
| OBETA | 9.76 | 42.1 ± 0.1 | −23.3 ± 0.4 | 48.8 ± 0.4 |
Plotting ln(kF/T) as a function of 1/T provides a straight line, whose slope and intercept afford the variations of activation enthalpy (ΔH‡) and entropy (ΔS‡), respectively (Fig. 5). From the so obtained ΔH‡ and ΔS‡ it is possible to determine the changes of the Gibbs free activation energy (ΔG‡) associated with the exchange process (Table 3). The signs of ΔS‡ are different for the two complexes, suggesting different exchange mechanisms. The slightly positive value of ΔS‡ obtained for [Y(EGTA)F]2− suggests that F− exchange follows a dissociatively activated mechanisms, in which the Y–F bond involving the leaving ligand elongates significantly before the entering F− ion approaches the metal ion.33 The relatively large value of ΔS‡ obtained for [Y(OBETA)(H2O)F]2− is likely related to an associative exchange process, most likely favoured by the heptadentate nature of the ligand, which leaves room for the simultaneous coordination of both the entering and leaving F− anions in the transition state. The different mechanisms are also supported by the values of ΔH‡, as dissociative mechanisms are generally characterized by higher enthalpy barriers, as the rate determining step is associated to the rupture of the bond between the metal ion and the leaving ligand.33 However, these conclusions should be interpreted with caution, as the disruption and rearrangement of the fluoride anion's hydration sphere upon metal complexation may significantly contribute to ΔS‡.34
 | ||
| Fig. 5 Eyring plots for the exchange rates of the fluoride-free with (A) [Y(OBETA)(H2O)F]2− and (B) [Y(EGTA)F]2−. Dashed lines represent the fitted data. | ||
DFT calculations
To support the hypothesis of the dimeric structure formation [F⊂(YOBETA)2]3−, a comprehensive computational study of the fluoro-adducts described in this work was carried out. DFT geometry optimization were performed on [Y(OBETA)(H2O)2]− and [Y(EGTA)(H2O)]−, along with corresponding structures where one (or two, in the case of OBETA) inner-sphere water molecules were substituted by fluoride anions. The optimised geometry of the [Y(OBETA)(H2O)F]2− adduct was used as a starting point for the optimization of the [F⊂(YOBETA)2]3− structure. All structures included explicit second-sphere water molecules, while bulk solvent effects were considered using a polarized continuum model (PCM). Various computational studies have demonstrated that this combined cluster/continuum approach is necessary for achieving an accurate description of the Ln–Ow and Ln–F bonds.35 These optimized structures were crucial in supporting the high-resolution 19F NMR spectra through targeted computational analysis, aimed to obtain theoretical chemical shifts for all studied structures and, in the case of [F⊂(YOBETA)2]3−, also the 1JY–F coupling constant. DFT calculations were performed on these structures to obtain the 19F isotropic nuclear shielding values (σ), which were then used to predict the corresponding 19F chemical shift. This computational methodology is well established in the literature and is based on the linear correlation between experimental and computationally calculated chemical shifts.36 Briefly, the absolute shielding constants for the different systems were obtained using scalar relativistic DFT calculations at the TPSSh/ZORA/Def2-TZVPP level. The calculated chemical shift values were obtained by subtracting these absolute shielding constants (σi) from that of CCl3F, used as the 19F NMR reference:| δcalc = σCCl3F − σi | (5) |
The δcalc values were subsequently plotted against the experimental chemical shift values, as shown in Fig. 6, revealing a notable linear correlation. To minimize systematic errors in the computational method, the predicted chemical shift values were scaled through linear regression analysis:
 | (6) |
Here δscal are the scaled chemical shifts obtained with DFT and A and B are the intercept and slope of the plot of δexpversus δcalc.
It is important to note that the absolute shielding constants are highly dependent on the coordination and chemical environment of the 19F ion. For instance, when assessing the absolute shielding of the fluoride in aqueous solution, it is crucial to include an explicit hydration sphere alongside the implicit solvation model. The predicted chemical shift value for fluoride, calculated without this explicit hydration, is −273.8 ppm, deviating by 115.0 ppm from the experimental value (−118.8 ppm). The predicted chemical shift improves significantly to −118.6 ppm, perfectly matching the experimental data, when six water molecules are incorporated to form hydrogen bonds with fluoride. The number of the hydrogen bonded water molecules incorporated in the model was guided by calculations of the electrostatic potential derived from the self-consistent field electron density of the anion. This finding highlights the substantial influence of the surrounding chemical environment on the 19F absolute shielding values, emphasizing the necessity of accurate structural modelling to achieve reliable chemical shift predictions.
These considerations are particularly critical for the [F⊂(YOBETA)2]3− dimer. DFT geometry optimization revealed a bent nature of the Y–F–Y bond, with an angle of approximately 152.6°; second-sphere water molecules that form hydrogen bonds between the two complexes stabilize this conformation. The potential energy surface was further explored by changing the O–Y–F–Y dihedral angle involving a carboxylate oxygen atom (Fig. S7†), which identified two energy minima at −31.1° and 104.7°. The first one is the most stable, with a 13 kcal mol−1 difference in energy. The Y–F distance is a critical parameter, closely affecting the 1JY–F scalar-coupling constant in the 19F NMR data. An initial geometry optimization yielded a Y–F distance of 2.26 Å, corresponding to a DFT calculated 1JY–F coupling of 56.7 Hz, which differs considerably from the experimental value ≈40.0 Hz. This discrepancy suggests that the computational model may overestimate the strength of the Y–F bonds, likely due to challenges in accurately describing the complex solvation environment, which significantly affects the chemical environment of the fluoride anion. To address this, several geometry optimizations were performed, fixing the Y–F bond lengths to values ranging from 2.26 to 2.35 Å and subsequently calculating the corresponding 1JY–F coupling values. As expected, a rather good linear correlation was obtained. The dimer structure with a Y–F bond length of 2.33 Å shows a 1JY–F coupling of 38.0 Hz, closely matching the experimental value (≈40.0 Hz). For this structure, as well as the others studied in this work (Table 4), the predicted chemical shift values are consistent with the experimental data, with a maximum discrepancy of 3.9 ppm observed for [Y(EGTA)F]2−.
| σ | δ calc | δ scal | δ exp | |
|---|---|---|---|---|
| a Absolute shielding constants obtained with DFT at the TPSSh/ZORA/Def2-TZVPP level. Experimental values determined at 275 K. b Not observed. | ||||
| CCl3F | 167.0 | 0.0 | 0.0 | 0.0 |
| F− | 481.0 | −314.0 | −273.8 | −118.8 |
| F−·6H2O | 303.2 | −136.25 | −118.6 | −118.8 |
| [Y(OBETA)F]2− | 251.1 | −84.2 | −73.2 | −76.2 |
| [F⊂Y(OBETA)2]3− | 237.2 | −70.2 | −61.0 | −61.4 |
| [Y(OBETA)F2]3− | 276.6 | −109.6 | −95.4 | |
| 263.1 | 96.1 | −83.6 | ||
| [Y(EGTA)F]2− | 252.7 | −85.7 | −74.5 | −70.6 |
The comparison of the experimental and DFT data reported in Table 4: (i) provides strong support for the hypothesis that the [F⊂(YOBETA)2]3− dimer forms with a geometry similar to that obtained computationally, as evidenced by the excellent match of the experimental and calculated values of both the 19F chemical shifts and 1JY–F values; (ii) suggest that [Y(OBETA)F2]3− species is not form in significant concentrations under our experimental conditions, as indicated by the absence of the 19F NMR signal in the experimental spectra within the range of the DFT-predicted chemical shift.
Experimental
Characterization techniques
1H, 13C and 2D NMR spectra of the ligands and the complexes were recorded using a Bruker 500 UltraShield™ spectrometer equipped with a 5 mm double resonance TXI probe. Electrospray ionization mass spectra (ESI MS) were recorded using an SQD 3100 Mass Detector (Waters), operating in positive- or negative-ion mode, with 1% v/v formic acid in methanol as the carrier solvent.Preparation of the [M(OBETA)(H2O)2]− and [M(EGTA)(H2O)]− complexes
The OBETA ligand (336.30 g mol−1) was provided by CAGE Chemicals S.r.l. while EGTA (380.35 g mol−1) was purchased from Fluka (purity >99.0%). As a source of metal ions, we used nitrate salts produced by Sigma Aldrich.The complexes were prepared by adding a slight excess of Gd3+ or Y3+ in the form of pentahydrate nitrate salts to an aqueous solution containing the ligand. This approach was taken to prevent the potential presence of excess ligand, which could interfere with studies on fluoride interaction. After adjusting the pH to 6.0 with dilute NaOH, the solution was stirred at room temperature (r.t.) for 2 h. Then, the pH was raised to 8/8.5 with NaOH (1 M) and the solution was stirred for 2 h to allow the precipitation of the uncomplexed metal ions as insoluble hydroxides. The solution was centrifuged (4000 rpm, 15 min, r.t.), the supernatant was filtered twice (using 0.22 μm NYL filters) and neutralized with dilute HNO3. The concentration of the paramagnetic complexes was evaluated by 1H NMR measurements, using Evans’ method. The 1D 1H NMR spectra of the diamagnetic [Y(OBETA)(H2O)2]− and [Y(EGTA)(H2O)]− complexes demonstrate quantitative complexation. The 89Y NMR chemical shift obtained for [Y(EGTA)(H2O)]− (68.6 ppm) using 1H,89Y-HMQC spectroscopy is in excellent agreement with the literature. For [Y(OBETA)(H2O)2]−, the 89Y NMR signal at 55.5 ppm is more shielded in comparison with [Y(EGTA)(H2O)]−, as expected by the larger shielding contribution estimated for a coordinated water molecule (107.6 ppm) than for an ether oxygen atom (95.7 ppm).37
The assigned NMR spectra of the Y3+ complexes are reported in the ESI (Fig. S8–S11†).
[Y(OBETA)(H2O)2]−
1H NMR (D2O, 500 MHz, 300 K): δH = 2.81 ppm (t, 3J = 5.2 Hz, 4H, 2), 3.33 (d, 2J = 16.7 Hz, 4H, 3), 3.46 (d, 2J = 16.7 Hz, 4H, 3), 3.72 (t, 3J = 5.2 Hz, 4H, 1). 13C NMR (D2O, 500 MHz, 300 K): δC = 180.3 ppm (4C, 4), 69.4 (2C, 1), 61.8 (4C, 3), 57.2 (2C, 2). MS ESI+ (m/z) = 444.17 [M− + Na+ + H+] and 460.13 [M− + K+ + H+]; calculated for [YC12H16N2O9]− = 420.99.[Y(EGTA)(H2O)]−
1H NMR (H2O/D2O, 500 MHz, 275 K): δH = 2.45 (d, 2H, 9′,12′), 2.88 ppm (t, 2H, 9,12), 3.05 (d, 2J = 17.7 Hz, 2H, 6,7), 3.15 (d, 2J = 17.7 Hz, 2H, 6′,7′), 3.20 (s, 4H, 5,8), 3.46 (d, 2H, 10,11), 3.64 (d, 4H, 10′,11′,13′,14′), 3.74 (d, 2J = 7.0 Hz, 2H, 13,14). 13C NMR (H2O/D2O, 500 MHz, 275 K): δC = 180.1 ppm (4C, 1–4), 70.8 (2C, 13–14), 70.1 (2C, 10–11), 63.8 (2C, 5,8), 62.2 (2C, 6,7), 57.6 (2C, 9,12). MS ESI+ (m/z) = 467.02 [M− + 2H+]; calculated for [YC14H20N2O10]− = 465.02.Fluoride affinities for the [Gd(OBETA)(H2O)2]− and [Gd(EGTA)(H2O)]− complexes
Association constants (KA) and longitudinal relaxivities (r1) of [Gd(OBETA)(H2O)F]2− and [Gd(EGTA)F]2− were determined by relaxometric titrations. The titrations were performed at 32 MHz and 298 K by adding increasing amounts of NaF salt to aqueous solutions of the complexes. Specifically, a solution of [Gd(OBETA)(H2O)2]− (0.48 mM, pH = 7.5, [HEPES] = 10 mM) was titrated with NaF until the change in the longitudinal relaxation rate (Robs1) became negligible, corresponding to an 1000-fold molar excess of the anion. Similarly, a solution of [Gd(EGTA)(H2O)]− (0.85 mM, pH = 7.4, [HEPES] = 10 mM) was titrated with NaF until reaching a fluoride concentration of 0.11 M. Above this concentration, an increase turbidity of the solution was noticed and an unexpected drop in the relaxation rate was measured. Probably, at high concentrations, fluoride begins to compete with the EGTA ligand for the complexation of Gd3+, which precipitates as GdF3.For the relaxometric characterization, 1H NMRD profiles (from 0.01 to 120 MHz) were acquired on the ternary [Gd(OBETA)(H2O)F]2− complex prepared by adding 0.5 mM NaF salt to a 0.51 mM [Gd(OBETA)(H2O)2]− solution at pH = 7.5 buffered with HEPES (10 mM). For each measurement, the relaxation contribution of the binary complex was subtracted, considering the respective mole fractions in solution calculated. The binary [Gd(OBETA)(H2O)2]− complex solution was prepared in a similar manner, using NaCl to ensure the same ionic strength and microviscosity conditions (Fig. S5†).
1H NMRD profiles were acquired also on the [Gd(EGTA)F]2− complex, prepared by adding 0.1 mM NaF salt to a 0.83 mM [Gd(EGTA)(H2O)]− solution at pH = 7.4 in HEPES (10 mM). For each measurement, the relaxation contribution of the binary complex, prepared by adding 0.1 mM NaCl, was subtracted (Fig. S4†).
Fluoride exchange in the [Y(OBETA)(H2O)F]2− and [Y(EGTA)F]2− complexes
The rates of fluoride exchange were determined by 19F high-resolution NMR measurements. The complexes were prepared by adding 175 mM of NaF to 180 mM [Y(OBETA)(H2O)2]− solution and 50 mM of NaF to a 200 mM [Y(EGTA)(H2O)]− solution. The salt concentrations were chosen so that the integrated signal intensities of the F−free and F−bound species were approximately in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. 1D 19F NMR spectra were acquired by varying the temperature. The rates of exchange of fluoride were calculated by fitting the 19F line shapes of the F−free and F−bound species at various temperatures through the dynamic NMR (DNMR) LineShape Analysis module (version 1.1.2) implemented using Bruker's Topspin 3.2 (Fig. 4).
1 ratio. 1D 19F NMR spectra were acquired by varying the temperature. The rates of exchange of fluoride were calculated by fitting the 19F line shapes of the F−free and F−bound species at various temperatures through the dynamic NMR (DNMR) LineShape Analysis module (version 1.1.2) implemented using Bruker's Topspin 3.2 (Fig. 4).
Relaxometric measurements
1H Nuclear Magnetic Relaxation Dispersion (NMRD) profiles were acquired using two different instruments, one operating at lower field (0.01–10 MHz) and the other at higher field strengths (20–120 MHz). Low field data were measured using a fast-field cycling (FFC) Stelar SMARTracer relaxometer (Stelar S.r.l., Mede (PV), Italy) equipped with a silver magnet. High-field measurements were collected with a high-field relaxometer (Stelar) equipped with an HTS-110 3 T Metrology cryogen-free superconducting magnet. The measurements were performed using the standard inversion recovery sequence (20 experiments and 2 scans) with a typical 90° pulse width of 3.5 μs and the reproducibility of the data was within ±0.5%. The temperature was controlled with a Stelar VTC-91 airflow heater equipped with a copper–constantan thermocouple (uncertainty of ±0.1 K).Variable temperature 17O NMR measurements
Variable-temperature 17O NMR measurements were recorded on a Bruker 500 UltraShield™ spectrometer (11.75 T, 67.8 MHz for 17O) equipped with a 5 mm probe and standard temperature control unit. An aqueous solution of the complexes containing 2.0% of the 17O isotope (Cambridge Isotope) was used. Transverse relaxation rates were measured from the signal width at half-height as a function of temperature in the range 275–350 K. The bulk magnetic susceptibility contribution was subtracted from the 17O NMR shift data using the 1H NMR shifts of the t-BuOH signal as internal reference.Computational details
Geometry optimizations of the Y3+ complexes and the corresponding F− adducts were performed with the Gaussian 16 program package (Rev C.01)38 using restricted calculations with the TPSSh39 functional and the Def2-TZVP basis set40 for F, C, H, N and O atoms. The Stuttgart–Bonn ECP28MDF small-core relativistic effective core potential was used for Y3+ in combination with the ECP28MDF_VTZ 41s37p25d2f1g/5s5p4d2f1g valence basis set.41 Solvent effects were incorporated with a polarized continuum model using the default settings [scrf = (pcm, solvent = water)] implemented in Gaussian 16.42 The integration grid was increased using the integral = ultrafine keyword. Frequency calculations were used to confirm that the optimized structures corresponded to stationary points. For the [F⊂(YOBETA)2]3− dimer calculations, the same method was applied but using the dispersion-corrected wB97XD functional43 and the smaller Def2-SV basis set.40 Optimized cartesian coordinates of the studied structures are reported from Tables S2–S7.†19F NMR shielding tensors were calculated with the ORCA44 suite (version 5.0.4), which uses the SHARK integral package.45 Scalar relativistic effects were considered with the ZORA method46 using the all-electron ZORA-Def2-TZVPP basis set for the ligand atoms, which is a recontracted version of the Def2-TZVPP basis set,40 and the SARC-ZORA-TZVPP basis set for Y.47 We selected the TPSSh functional39 for NMR shielding calculations, as it was shown in previous studies to provide good results for yttrium complexes.48 Shielding tensors were obtained with the gauge-including atomic orbitals (GIAO) method.49 The resolution of identity and chain of spheres exchange (RIJCOSX)50 approximation was used in these calculations, using the def2/J and SARC/J auxiliary basis sets.51 The sizes of the DFT and COSX grids were set with DefGrid3 keyword. Bulk solvent effects (water) were considered with a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions (SMD).52
Conclusions
In conclusion, a combination of low- and high-resolution NMR techniques and DFT calculations have been employed to investigate the interaction between the fluoride anion and two negatively charged acyclic M3+ complexes with OBETA and EGTA, which are characterized by different denticity (hepta- and octadentate), resulting in different coordination geometries, and hydration numbers (q = 1, 2).Relaxometric titrations enabled to monitor the formation of ternary adducts, which occurs by substitution of a single IS water molecule with F−, and to estimate the affinity constant. Interestingly, the binding affinity between the halide and the anionic Gd3+ chelates is relatively high for both homologues, despite the interaction being disfavoured by electrostatic repulsions. A complete relaxometric characterization indicates the presence of SS water molecule(s) (qSS = 1 for OBETA, qSS = 2 for EGTA) in strong hydrogen bonding interactions with the halide, which substantially contribute to the relaxivity of the ternary adducts. In the case of OBETA, additional 17O NMR analyses unveiled water exchange dynamics accelerated by F− binding, which destabilizes the remaining coordinated water molecule, as expected.
Furthermore, the high-resolution NMR technique allowed access to the structure of the ternary species. While in the case of EGTA the formation of a single ternary complex is observed ([Y(EGTA)F]2−), for OBETA we surprisingly notice the simultaneous presence of two fluoride adducts, comprising one monomeric ([Y(OBETA)(H2O)F]2−) and one homonuclear dimeric ([F⊂(YOBETA)2]3−) species. Supramolecular lanthanide dimers have already been observed for positively charged DOTA derivatives, where the assembly of two positively charged complexes is stabilized by a fluoride-bridging species.53–55 However, to the best of our knowledge, this is the first observation of a fluoride-bridged dimeric adduct where two negatively charged units are stabilized by one fluoride anion. DFT calculations supported our findings providing a structural model of the dimeric complex, where the bridging fluoride coordinates the two Y3+ chelates with an angle of ∼152.6°, which is in good agreement with the chemical shift values and the 1JY–F coupling constant experimentally measured.
To complete the picture, high-resolution NMR line shape analyses enabled us to describe the kinetic and thermodynamic parameters associated with the fluoride chemical exchange reaction. While the fluoride-ion exchange kinetics is similar for the ternary monomeric adducts of OBETA and EGTA, the thermodynamic parameters vary substantially, suggesting two different exchange processes: a dissociative activated mechanisms for EGTA, and an associative driven pathway for OBETA.
The methodology here presented can be widely applicable to characterize the molecular interactions between paramagnetic complexes and NMR active ions. This provides the basis for the rational design of new systems capable of recognizing anions with increased affinity, which is of large interest in technological and biomedical fields and represents a significant challenge for coordination chemistry.
Author contributions
L. R.: synthesis, purification, and characterization of the complexes, NMRD profiles, manuscript preparation. M. R.: 17O NMR data, DFT calculations and manuscript preparation. D. L.: 19F NMR data and line shape analysis, conceptualization and manuscript preparation. C. P.-I.: DFT calculations, relaxometric data analyses and manuscript preparation. M. B.: project supervision, conceptualization and manuscript preparation; relaxometric data analyses.Data availability
The data supporting this article have been included in the main article and as a part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. B. acknowledges the project NODES, which has received funding from the Ministero dell'Università e della Ricerca (MUR–M4C2 1.5 of PNRR with grant agreement no. ECS00000036). C. P.-I. thanks Ministerio de Ciencia e Innovación (Grant PID2022-138335NB-I00) and Xunta de Galicia (ED431C 2023/33) for generous financial support and Centro de Supercomputación de Galicia (CESGA) for providing supercomputer facilities.References
- J. L. Sessler, P. A. Gale and W.-S. Cho, Anion Receptor Chemistry, Royal Society of Chemistry, Cambridge, 2006 Search PubMed.
- (a) V. Král, O. Rusin, T. Shishkanova, R. Volf, P. Matějka and K. Volka, Anion Binding: from Supramolecules to Sensors, Chem. Listy, 1999, 93, 546–553 Search PubMed; (b) E. N. Baker, B. F. Anderson, H. M. Baker, M. Haridas, G. E. Norris, S. V. Rumball and C. A. Smith, Metal and anion binding sites in lactoferrin and related proteins, Pure Appl. Chem., 1990, 62, 1067–1070 CrossRef CAS; (c) P. Aisen and I. Listowsky, Iron transport and storage proteins, Annu. Rev. Biochem., 1980, 49, 357–393 CrossRef CAS PubMed; (d) S. Markússon, J. G. Hjorleifsson, P. Kursula and B. Ásgeirsson, Structural characterization of functionally important chloride binding sites in the marine Vibrio alkaline phosphatase, Biochemistry, 2022, 61, 2248–2260 CrossRef PubMed; (e) M. Guo, I. Harvey, W. Yang, L. Coghill, D. J. Campopiano, J. A. Parkinson, R. T. A. MacGillivray, W. R. Harris and P. J. Sadler, Synergistic Anion and Metal Binding to the Ferric Ion-binding Protein from Neisseria gonorrhoeae, J. Biol. Chem., 2003, 278, 2490–2502 CrossRef CAS PubMed.
- (a) A. B. Aletti, D. M. Gillen and T. Gunnlaugsson, Luminescent/colorimetric probes and (chemo-) sensors for detecting anions based on transition and lanthanide ion receptor/binding complexes, Coord. Chem. Rev., 2018, 354, 98–120 CrossRef CAS; (b) L. Fabbrizzi and A. Poggi, Anion recognition by coordinative interactions: metal–amine complexes as receptors, Chem. Soc. Rev., 2013, 42, 1681–1699 RSC; (c) T. L. Martinon, The urgent recognition of phosphate resource scarcity and pollution, RSC Sustainability, 2023, 1, 1594–1598 RSC; (d) V. C. Pierre and R. K. Wilharm, Design principles and applications of selective lanthanide-based receptors for inorganic phosphate, Front. Chem., 2022, 10, 821020 CrossRef CAS PubMed.
- A. Merbach, L. Helm and É. Tóth, The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, John Wiley & Sons, New York, 2nd edn, 2013 Search PubMed.
- L. Burai, V. Hietapelto, R. Király, E. Tóth and E. Brücher, Stability constants and 1H relaxation effects of ternary complexes formed between Gd-DTPA, Gd-DTPA-BMA, Gd-DOTA, and Gd-EDTA and citrate, phosphate, and carbonate ions, Magn. Reson. Med., 1997, 38, 146–150 CrossRef CAS PubMed.
- R. M. Supkowski and W. D. Horrocks, Displacement of Inner Sphere Water Molecules from Eu3+ Analogues of Gd3+ MRI Contrast Agents by Carbonate and Phosphate Anions: Dissociation Constants from Luminescence Data in the Rapid-Exchange Limit, Inorg. Chem., 1999, 38, 5616–5619 CrossRef CAS PubMed.
- L. Helm, J. R. Morrow, C. J. Bond, F. Carniato, M. Botta, M. Braun, Z. Baranyai, R. Pujales-Paradel, M. Regueiro-Figuero, D. Esteban-Gómez, C. Platas-Iglesias and T. J. Scholl, in Contrast Agents for MRI: Experimental Methods, ed. V. C. Pierre and M. J. Allen, Royal Society of Chemistry, Cambridge, 2017, pp. 121–242 Search PubMed.
- J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chemistry of MRI contrast agents: current challenges and new frontiers, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS PubMed.
- D. Messeri, M. P. Lowe, D. Parker and M. Botta, A stable, high relaxivity, diaqua gadolinium complex that suppresses anion and protein binding, Chem. Commun., 2001, 2742–2743 RSC.
- M. Botta, S. Aime, A. Barge, G. Bobba, R. S. Dickins, D. Parker and E. Terreno, Ternary Complexes between Cationic GdIII Chelates and Anionic Metabolites in Aqueous Solution: An NMR Relaxometric Study, Chem. – Eur. J., 2003, 9, 2102–2109 CrossRef CAS PubMed.
- E. M. Gale, N. Kenton and P. Caravan, [Gd(CyPic3A)(H2O)2]−: a stable, bis(aquated) and high-relaxivity Gd(III) complex, Chem. Commun., 2013, 49, 8060–8062 RSC.
- E. Brücher, G. Tircso, Z. Baranyai, Z. Kovács and A. D. Sherry, Stability and Toxicity of Contrast Agents, in The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, ed. A. Merbach, L. Helm and E. Toth, John Wiley & Sons, Ltd, 2013 Search PubMed.
- A. Bianchi, L. Calabi, C. Giorgi, P. Losi, P. Mariani, P. Paoli, P. Rossi, B. Valtancoli and M. Virtuani, Thermodynamic and structural properties of Gd3+ complexes with functionalized macrocyclic ligands based upon 1,4,7,10-tetraazacyclododecane, J. Chem. Soc., Dalton Trans., 2000, 697–705 RSC.
- E. J. Werner, A. Datta, C. J. Jocher and K. N. Raymond, High-Relaxivity MRI Contrast Agents: Where Coordination Chemistry Meets Medical Imaging, Angew. Chem., Int. Ed., 2008, 47, 8568–8580 CrossRef CAS PubMed.
- F. Travagin, L. Lattuada and G. B. Giovenzana, AAZTA: The rise of mesocyclic chelating agents for metal coordination in medicine, Coord. Chem. Rev., 2021, 438, 213908 CrossRef CAS.
- I. Maimouni, C. Henoumont, M.-C. De Goltstein, J.-F. Mayer, A. Dehimi, Y. Boubeguira, C. Kattenbeck, T. J. Maas, N. Decout, I. Strzeminska, G. Bazin, C. Medina, C. Factor, O. Rousseaux, U. Karst, S. Laurent and S. Catoen, Gadopiclenol: A q = 2 Gadolinium-Based MRI Contrast Agent Combining High Stability and Efficacy, Investig. Radiol., 2024 DOI:10.1097/RLI.0000000000001121.
- S. Aime, M. Botta, M. Fasano, M. P. M. Marques, C. F. G. C. Geraldes, D. Pubanz and A. E. Merbach, Conformational and Coordination Equilibria on DOTA Complexes of Lanthanide Metal Ions in Aqueous Solution Studied by 1H-NMR Spectroscopy, Inorg. Chem., 1997, 36, 2059–2068 CrossRef CAS PubMed.
- O. A. Blackburn, A. M. Kenwright, P. D. Beera and S. Faulkner, Axial fluoride binding by lanthanide DTMA complexes alters the local crystal field, resulting in dramatic spectroscopic changes, Dalton Trans., 2015, 44, 19509–19517 RSC.
- O. A. Blackburn, A. M. Kenwright, A. R. Jupp, J. M. Goicoechea, P. D. Beer and S. Faulkner, Fluoride Binding and Crystal-Field Analysis of Lanthanide Complexes of Tetrapicolyl-Appended Cyclen, Chem. – Eur. J., 2016, 22, 8929–8936 CrossRef CAS PubMed.
- T. Liu, A. Nonat, M. Beyler, M. Regueiro-Figueroa, K. Nchimi Nono, O. Jeannin, F. Camerel, F. Debaene, S. Cianférani-Sanglier, R. Tripier, C. Platas-Iglesias and L. J. Charbonnière, Supramolecular Luminescent Lanthanide Dimers for Fluoride Sequestering and Sensing, Angew. Chem., Int. Ed., 2014, 53, 7387–7391 CrossRef.
- S. J. Butler, Quantitative determination of fluoride in pure water using luminescent europium complexes, Chem. Commun., 2015, 51, 10879–10882 RSC.
- D. Lalli, F. Carniato, L. Tei, C. Platas-Iglesias and M. Botta, Surprising Complexity of the [Gd(AAZTA)(H2O)2]− Chelate Revealed by NMR in the Frequency and Time Domains, Inorg. Chem., 2022, 61, 496–506 CrossRef CAS PubMed.
- S. Karimi, G. Hunter, L. Moriggi, C. Platas-Iglesias and L. Helm, Complexation of [Gd (DTTA–Me)(H2O)2]− by Fluoride and Its Consequences to Water Exchange, Inorg. Chem., 2016, 55, 6231–6239 CrossRef CAS PubMed.
- P. J. Blower, W. Levason, S. K. Luthra, G. McRobbie, F. M. Monzittu, T. O. Mules, G. Reid and M. Nadeem Subhan, Exploring transition metal fluoride chelates – synthesis, properties and prospects towards potential PET probes, Dalton Trans., 2019, 48, 6767–6776 RSC.
- S. J. Archibald and L. Allott, The aluminium-[18F]fluoride revolution: simple radiochemistry with a big impact for radiolabelled biomolecules, EJNMMI Radiopharm. Chem., 2021, 6, 30 CrossRef PubMed.
- (a) R. Negri, Z. Baranyai, L. Tei, G. B. Giovenzana, C. Platas-Iglesias, A. C. Bényei, J. Bodnár, A. Vágner and M. Botta, Lower Denticity Leading to Higher Stability: Structural and Solution Studies of Ln(III)–OBETA Complexes, Inorg. Chem., 2014, 53, 12499–12511 CrossRef CAS PubMed; (b) S. Aime, A. Barge, A. Borel, M. Botta, S. Chemerisov, A. E. Merbach, U. Müller and D. Pubanz, A Multinuclear NMR Study on the Structure and Dynamics of Lanthanide(III) Complexes of the Poly(amino carboxylate) EGTA4− in Aqueous Solution, Inorg. Chem., 1997, 36, 5104–5112 CrossRef CAS.
- (a) I. Solomon, Relaxation Processes in a System of Two Spins, Phys. Rev., 1955, 99, 559–565 CrossRef CAS; (b) N. Bloembergen, Proton Relaxation Times in Paramagnetic Solutions, J. Chem. Phys., 1957, 27, 572–573 CrossRef CAS; (c) N. Bloembergen and L. O. Morgan, Proton Relaxation Times in Paramagnetic Solutions. Effects of Electron Spin Relaxation, J. Chem. Phys., 1961, 34, 842–850 CrossRef CAS.
- S. Aime, M. Botta, D. Esteban-Gómez and C. Platas-Iglesias, Characterisation of magnetic resonance imaging (MRI) contrast agents using NMR relaxometry, Mol. Phys., 2018, 117, 898–909 CrossRef.
- J. H. Freed, Dynamic effects of pair correlation functions on spin relaxation by translational diffusion in liquids. II. Finite jumps and independent T1 processes, J. Chem. Phys., 1978, 68, 4034–4037 CrossRef CAS.
- J. A. Peters, The reliability of parameters obtained by fitting of 1H NMRD profiles and 17O NMR data of potential Gd3+-based MRI contrast agents, Contrast Media Mol. Imaging, 2016, 11, 160–168 CrossRef CAS PubMed.
- (a) T. J. Swift and R. E. Connick, NMR–Relaxation Mechanisms of 17O in Aqueous Solutions of Paramagnetic Cations and the Lifetime of Water Molecules in the First Coordination Sphere, J. Chem. Phys., 1962, 37, 307–320 CrossRef CAS; (b) T. J. Swift and R. E. Connick, Erratum: NMR–Relaxation Mechanisms of 17O in Aqueous Solutions of Paramagnetic Cations and the Lifetime of Water Molecules in the First Coordination Sphere, J. Chem. Phys., 1964, 41, 2553–2554 CrossRef CAS.
- M. Botta, Second Coordination Sphere Water Molecules and Relaxivity of Gadolinium(III) Complexes: Implications for MRI Contrast Agents, Eur. J. Inorg. Chem., 2000, 3, 399–407 CrossRef.
- L. Helm and A. E. Merbach, Inorganic and Bioinorganic Solvent Exchange Mechanisms, Chem. Rev., 2005, 105, 1923–1959 CrossRef CAS PubMed.
- S. J. Butler and D. Parker, Anion binding in water at lanthanide centres: from structure and selectivity to signalling and sensing, Chem. Soc. Rev., 2013, 42, 1652–1666 RSC.
- (a) D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas, L. Helm and C. Platas-Iglesias, Hyperfine Coupling Constants on Inner-Sphere Water Molecules of GdIII-Based MRI Contrast Agents, ChemPhysChem, 2012, 13, 3640–3650 CrossRef PubMed; (b) A. Rodríguez-Rodríguez, Á. Arnosa-PrietoIsabel Brandariz, D. Esteban-Gómez and C. Platas-Iglesias, Axial Ligation in Ytterbium(III) DOTAM Complexes Rationalized with Multireference and Ligand-Field ab Initio Calculations, J. Phys. Chem. A, 2020, 124, 1362–1371 CrossRef.
- (a) G. Barone, L. Gomez-Paloma, D. Duca, A. Silvestre, R. Riccio and G. Bifulco, Structure Validation of Natural Products by Quantum-Mechanical GIAO Calculations of 13C NMR Chemical Shifts, Chem. – Eur. J., 2002, 8, 3233–3239 CrossRef CAS; (b) S. K. Latypov, F. M. Polyancev, D. G. Yakhvarov and O. G. Sinyashin, Quantum chemical calculations of 31P NMR chemical shifts: scopes and limitations, Phys. Chem. Chem. Phys., 2015, 17, 6976–6987 RSC.
- Y. Xing, A. K. Jindal, M. Regueiro-Figueroa, M. Le Fur, N. Kervarec, P. Zhao, Z. Kovacs, L. Valencia, P. Pérez-Lourido, R. Tripier, D. Esteban-Gómez, C. Platas-Iglesias and A. D. Sherry, The Relationship between NMR Chemical Shifts of Thermally Polarized and Hyperpolarized 89Y Complexes and Their Solution Structures, Chem. – Eur. J., 2016, 22, 16657–16667 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, revision C.01, Gaussian, Inc., Wallingford CT, 2019 Search PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, Energy-consistent relativistic pseudopotentials and correlation consistent basis sets for the elements Y–Pd, J. Chem. Phys., 2007, 126, 124101 CrossRef.
- J. Tomasi, B. Mennucci and E. Cancès, The IEF Version of the PCM Solvation Method: An Overview of a New Method Addressed to Study Molecular Solutes at the QM Ab Initio Level, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- (a) F. Neese, Software update: the ORCA program system, version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed; (b) F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, The SHARK Integral Generation and Digestion System, J. Comput. Chem., 2023, 44, 381–396 CrossRef CAS PubMed.
- C. van Wüllen, Molecular density functional calculations in the regular relativistic approximation: Method, application to coinage metal diatomics, hydrides, fluorides and chlorides, and comparison with first-order relativistic calculations, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- J. D. Rolfes, F. Neese and D. A. Pantazis, All-electron scalar relativistic basis sets for the elements Rb–Xe, J. Comput. Chem., 2020, 41, 1842–1849 CrossRef CAS PubMed.
- R. C. Knighton, L. K. Soro, L. Francés-Soriano, A. Rodríguez-Rodríguez, G. Pilet, M. Lenertz, C. Platas-Iglesias, N. Hildebrandt and L. J. Charbonnière, Cooperative Luminescence and Cooperative Sensitisation Upconversion of Lanthanide Complexes in Solution, Angew. Chem., Int. Ed., 2022, 61, e202113114 CrossRef CAS PubMed.
- G. L. Stoychev, A. A. Auer, R. Izsák and F. Neese, Self-Consistent Field Calculation of Nuclear Magnetic Resonance Chemical Shielding Constants Using Gauge-Including Atomic Orbitals and Approximate Two-Electron Integrals, J. Chem. Theory Comput., 2018, 14, 619–637 CrossRef CAS.
- (a) F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree-Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS; (b) B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, An improved chain of spheres for exchange algorithm, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed; (c) R. Izsák and F. Neese, An overlap fitted chain of spheres exchange method, J. Chem. Phys., 2011, 135, 144105 CrossRef; (d) R. Izsák, F. Neese and W. Klopper, Robust fitting techniques in the chain of spheres approximation to the Fock exchange: The role of the complementary space, J. Chem. Phys., 2013, 139, 094111 CrossRef.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- (a) A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed; (b) M. Garcia-Rates and F. Neese, Effect of the Solute Cavity on the Solvation Energy and its Derivatives within the Framework of the Gaussian Charge Scheme, J. Comput. Chem., 2020, 41, 922–939 CrossRef CAS PubMed.
- R. Tripier, C. Platas-Iglesias, A. Boos, J.-F. Morfin and L. Charbonnière, Towards Fluoride Sensing with Positively Charged Lanthanide Complexes, Eur. J. Inorg. Chem., 2010, 2735–2745 CrossRef CAS.
- A. Nonat, C. Chan, T. Liu, C. Platas-Iglesias, Z. Liu, W.-T. Wong, W.-K. Wong, K.-L. Wong and L. J. Charbonnière, Room temperature molecular up conversion in solution, Nat. Commun., 2016, 7, 11978 CrossRef CAS PubMed.
- A. Nonat, T. Liu, O. Jeannin, F. Camerel and L. J. Charbonnière, Energy Transfer in Supramolecular Heteronuclear Lanthanide Dimers and Application to Fluoride Sensing in Water, Chem. – Eur. J., 2018, 24, 3784–3792 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 1H NMRD profiles, 17O NMR data, 1H, 13C, 19F NMR spectra, 2D NMR: 1H–1H COSY, 1H–13C HSQC, 1H–89Y HMBC spectra and DFT optimized cartesian coordinated of the complexes under investigation. See DOI: https://doi.org/10.1039/d4qi02908a |
| This journal is © the Partner Organisations 2025 |






