Exploring the substitution effect on the magnetic coupling of tetrazinyl-bridged Ln₂ single-molecule magnets

Abstract

The design of new radical bridging ligands that can effectively promote strong magnetic coupling with Ln^III ions needs to focus on radicals that are susceptible to synthetic modifications and bear diffuse spin density on their donor atoms. To probe this, we introduced various substituents possessing different electron-withdrawing/donating capabilities into the redox-active s-tetrazinyl centre. This allowed for the systematic tuning of the redox and optoelectronic properties of the tetrazinyl ring. The effect of substitution on the strength of Ln–rad magnetic coupling was investigated on a series of radical-bridged Ln metallocene complexes featuring the 3,6-dimethyl-1,2,4,5-tetrazine (dmtz) and the 3,6-dimethoxy-1,2,4,5-tetrazine (dmeotz) ligands; [(Cp*₂Ln)₂(dmtz˙⁻)(THF)₂][BPh₄]·THF (Ln = Gd (1-Gd) or Dy (1-Dy); Cp* = pentamethylcyclopentadienyl; THF = tetrahydrofuran) and [(Cp*₂Ln)₂(dmeotz˙⁻)(THF)][BPh₄] (Ln = Gd (2-Gd) or Dy (2-Dy)). Cyclic voltammetry, UV-Vis absorption spectroscopy, SQUID magnetometry and ab initio as well as density functional theory (DFT) calculations are combined to underline the trends observed in this study, while comparisons with the unsubstituted 1,2,4,5-tetrazine (tz) and the 3,6-dichloro-1,2,4,5-tetrazine (dctz) are made. Notably, an intricate interplay between orbital overlap, ligand substituent effects and changes in the coordination environment is found to collectively dictate the magnitude of J_Gd–rad in the investigated systems. The strong magnetic coupling combined with highly anisotropic Dy^III ions makes 1-Dy and 2-Dy exhibit slow magnetic relaxation in the absence of an external applied field. For 1-Dy, an opening of the hysteresis loop is observed with H_c = ∼5000 Oe, one of the highest coercivities for a dinuclear organic radical-bridged single-molecule magnet.

---

Introduction

Redox-active ligands are highly sought-after in areas such as catalysis,¹ conductivity,^2,3 magnetism,^4–6 as well as energy generation and storage.^7,8 These types of compounds have more energetically accessible levels that allow them to participate in redox-active reactions by altering their charge state.⁹ Furthermore, their intrinsic electronic properties can be fine-tuned through the introduction of substituents. Depending on the electron-donating/withdrawing nature of these substituents, the energy level of the ligand's frontier molecular orbitals (FMOs) can be modulated. Of special interest are ligands that can stabilize radical species, as these are often highly reactive.¹⁰ However, some heteroatomic organic ligands can house unpaired electrons and maintain their open shell nature while coordinating with metal ions.¹¹ This has successfully led to the isolation of complexes^12,13 and extended networks^14,15 with extraordinary chemical and physical properties.

Regarding the latter, open shell ligands have proved to be valuable building blocks in the targeted design of a specific class of complexes. These complexes exhibit bulk magnetic properties at the molecular scale such as slow magnetic relaxation and magnetic hysteresis and hence are termed single-molecule magnets (SMMs).¹⁶ Combined with the highly anisotropic lanthanides (Ln), the incorporation of open shell bridges can lead to enhanced magnetic properties^17,18 (i.e. high blocking temperatures and large magnetic hysteresis), which is the ultimate goal for potential applications of SMMs in high-density information storage and spin-based computing.¹⁹ This is because the introduction of a paramagnetic linker into Ln-based SMMs surpasses the otherwise weak magnetic coupling, which characterizes polynuclear Ln systems²⁰ and usually introduces through-barrier magnetic relaxation, i.e. quantum tunnelling of magnetization (QTM).^21–23 Therefore, the search for bridging redox-active ligands with diffuse molecular orbitals (MOs) that can penetrate the shielded 4f orbitals is an ongoing challenge.

Several types of inorganic and organic radicals have been explored to this extent.²⁴ The use of diatomic p-block radicals has yielded impressive magnetic performance in dinuclear Ln metallocene complexes.^17,25 However, the strategic incorporation of such radicals into complexes is rather scarce and challenging, while synthetic modifications of such ligands are, to this date, unknown. On the other hand, organic radicals offer a more accessible alternative. Amongst the various radical ligands, nitroxide,²⁶ oxazolidine-N-oxide,²⁷ verdazyl,²⁸ tetraoxolene,²⁹ N-heterocyclic carbene³⁰ and other radicals^31–34 have been used in the synthesis of SMMs without however surpassing the N₂˙³⁻ system. The strength of the Ln–rad coupling is of unparalleled importance as it needs to be stronger than the anisotropy of the individual Ln ions in order to lead to improvement in the magnetic performance. Thus, the design of new radical bridges calls for ligands that can be rationally incorporated into a reaction, are susceptible to synthetic modifications and can promote strong magnetic coupling with the Ln ions.

One class of ligands that fulfills the aforementioned criteria is 3,6-R₂-1,2,4,5-tetrazines (Chart 1). In these ligands the four sp² nitrogen atoms provide an easily accessible π* low energy LUMO (lowest unoccupied molecular orbital), which facilitates the formation and stabilization of a radical anion.^35,36 Recently we have demonstrated how the diffuse spin density of the unsubstituted 1,2,4,5-tetrazine (tz) ligand can promote significantly strong Ln–rad magnetic coupling in both dinuclear³⁷ [(Cp*₂Ln)₂(tz˙⁻)(THF)₂](BPh₄) (“Ln₂-tz˙⁻”; Ln = Gd, Tb or Dy; Cp* = pentamethylcyclopentadienyl; THF = tetrahydrofuran) and tetranuclear^38,39 lanthanocene complexes. We have also investigated the use of a tetrazine bearing 3,5-dimethyl-pyrazolyl groups in the 3- and 6-positions of the tetrazine ring, where, thanks to the trans coordination mode of the ligand, one of the highest Ln–rad exchange couplings was achieved in dinuclear lanthanocene complexes [(Cp*₂Ln)₂(bpytz˙⁻)](BPh₄) (“Ln₂-bpytz˙⁻”; Ln = Gd, Tb, Dy or Y; bpytz = 3,6-bis(3,5-dimethyl-pyrazolyl)-1,2,4,5-tetrazine).⁴⁰ However, the true influence of the substituents in the 3- and 6-positions of the tetrazinyl ring has yet to be determined. In principle, altering the electron distribution of the tetrazine ring by inserting different groups with electron-donating or -withdrawing nature should, in turn, affect the strength of the Ln–rad magnetic coupling.

Chart 1 The 3,6-R₂-tetrazine derivatives explored in this work. The substituents (R) can be either electron-donating or electron-withdrawing groups, which can significantly impact the electron density of the tetrazine ring.

With this in mind, we introduced various substituents with different electron-withdrawing/donating capabilities into the s-tetrazine ring to systematically tune its redox properties and explore the effect of the substitution of the tetrazine ring on the Ln–rad magnetic coupling. Two series of radical-bridged Ln metallocene complexes were isolated featuring the 3,6-dimethyl-1,2,4,5-tetrazine (dmtz) and the 3,6-dimethoxy-1,2,4,5-tetrazine (dmeotz); [(Cp*₂Ln)₂(dmtz˙⁻)(THF)₂][BPh₄]·THF (Ln = Gd (1-Gd) or Dy (1-Dy)) and [(Cp*₂Ln)₂(dmeotz˙⁻)(THF)][BPh₄] (Ln = Gd (2-Gd) or Dy (2-Dy)), respectively. The introduction of the electron-donating methyl and methoxy groups significantly enhances the magnetic exchange coupling between the Ln^III ions and the radical. Cyclic voltammetry, UV-Vis absorption spectroscopy, SQUID magnetometry and ab initio as well as density functional theory (DFT) calculations are combined to underline the observed trends, while comparisons with the tz and 3,6-dichloro-1,2,4,5-tetrazine (dctz) are made. These studies reveal that the interplay between orbital overlap, ligand substituent effects and changes in the coordination environment of the Ln centres collectively dictates the magnitude of the obtained J_Gd–rad in the investigated systems. The strong magnetic coupling combined with the highly anisotropic Dy^III ions leads complexes 1-Dy and 2-Dy exhibiting slow magnetic relaxation in the absence of an external applied field. In the case of 1-Dy, an opening of the hysteresis loop is observed with H_c = ∼5000 Oe, one of the highest coercivities for a dinuclear organic radical-bridged SMM.

Results and discussion

Synthesis and optoelectronic features of the tetrazine ligands

The synthesis of 1,2,4,5-tetrazines was first reported by Pinner, at the end of the 19^th century.⁴¹ In general, depending on the substituents of the tetrazine ring two synthetic approaches can be used. Tetrazines can be synthesized either by reacting hydrazine with the respective nitrile or by using a pre-synthesized tetrazine as a starting material and replacing the functional groups at the 3- and 6-positions through nucleophilic substitution.⁴² The synthesis of tz⁴³ and dmtz⁴⁴ involves the reaction of hydrazine with formamidine acetate or acetamidine hydrochloride, respectively, to produce the dihydrotetrazine intermediates which can afford the fully aromatic tetrazines upon oxidation. For the syntheses of dctz and dmeotz, bis(3,5-dimethyl-pyrazolyl)-1,2,4,5-tetrazine⁴⁵ (bpytz) was used as a starting material where the pyrazolyl groups act as soft leaving groups. In further detail, the reaction of bpytz with hydrazine produces the 3,6-dihydrazino-1,2,4,5-tetrazine, which upon treatment with trichloroisocyanuric acid yields dctz as an orange crystalline solid.⁴⁶ On the other hand, the reaction of bpytz with dry MeOH in the presence of triethylamine affords dmeotz as a vivid red crystalline solid.⁴⁷

In order to probe the substituent effect on the redox and optoelectronic properties of the aforementioned s-tetrazines electrochemical, optical and computational studies were performed. The redox behavior of dmtz, dmeotz, tz and dctz was probed by cyclic voltammetry (CV; Fig. 1A and S1–S4†) in dichloromethane (DCM) solutions with 0.1 M tetrabutylammonium hexafluorophosphate as the supporting electrolyte. In all cases, the cathodic CV scans revealed a quasi-reversible one-electron reduction vs. Fc/Fc⁺, occurring at −1.71 V, −1.51 V, −1.20 V and −0.91 V for dmtz, dmeotz, tz and dctz, respectively. The LUMO energy levels were obtained based on the formal potential of the Fc/Fc⁺ in DCM and are given in Table S1 (see the ESI for further details).† The redox potentials highlight the role played by the substituents: strong electron-withdrawing groups like chlorine shift the standard potential towards less negative values, whereas electron-donating substituents like methyl or methoxide shift it to the opposite direction.

Fig. 1 (A) Cyclic voltammograms of dmtz (pink), dmeotz (purple), tz (blue) and dctz (light blue), measured in DCM at room temperature with [Bu₄N][PF₆] (0.1 M) as the supporting electrolyte at a scan rate of 0.1 V s⁻¹. (B) UV/Vis absorption spectra for dmtz (pink), dmeotz (purple), tz (blue) and dctz (light blue), measured in DCM at room temperature. (C) Frontier molecular orbitals (FMOs) and energy level diagram of these FMOs for dmtz, dmeotz, tz and dctz, respectively.

Being able to determine both the highest occupied molecular orbital (HOMO) and LUMO levels of the tetrazines’ FMOs using only CV is a fairly rare occurrence. In this case, the energy of the HOMO level can be deduced from the electrochemically obtained MO energy and the optically measured energy gap (E_gap)_. Subsequently, the photophysical properties of all tetrazines were investigated via UV-Vis absorption spectroscopy in DCM solutions (Fig. 1B and S5–S8†). In all cases the UV-Vis absorption spectra show two characteristic bands. The first broadband is in the visible region of the spectra with maxima at around 540 nm for dmtz, 520 nm for dmeotz, 530 nm for tz and 515 nm for dctz. A second broadband is observed in the UV region with the maxima at around 273 nm for dmtz, 345 nm for dmeotz, 253 nm for tz and 307 nm for dctz, respectively. These values are consistent with those reported in the literature.³⁵ As shown in Fig. 1B no obvious trend can be observed for the UV-Vis absorption spectra which is further evident from the similar values of the E_gap extracted from the onset wavelength of the lowest energy absorption band in the visible region (Table S1†).

Additionally, single point TDDFT (time-dependent density-functional theory) calculations were performed at the CAM-B3LYP⁴⁸/def2-TZVPP levels of theory for the B3LYP^49–51/def2-TZVPP⁵² optimized geometries of the aforementioned tetrazines (Fig. S17†) to obtain the calculated optical energy gaps (Table S1†). Thus, these energy gaps present an energy difference of the ground and the first excited state and can be compared with the experimental ones, which were determined from UV-Vis absorption data. Both the computationally and the experimentally determined E_gap values are in very good agreement (Table S1†), providing mutual validation of the E_gap. Constructing the energy level diagram based on the experimentally determined E_gap values, a shift is observed in the position of the tetrazines’ HOMO–LUMO gap (Fig. 1C). For the electron-withdrawing groups, like chlorine (dctz), the HOMO–LUMO gap is shifted towards lower energies, whereas for the electron-donating substituents, like methyl (dmtz), it is shifted towards higher energies.⁵³

Synthesis and structural description of 1-Ln and 2-Ln

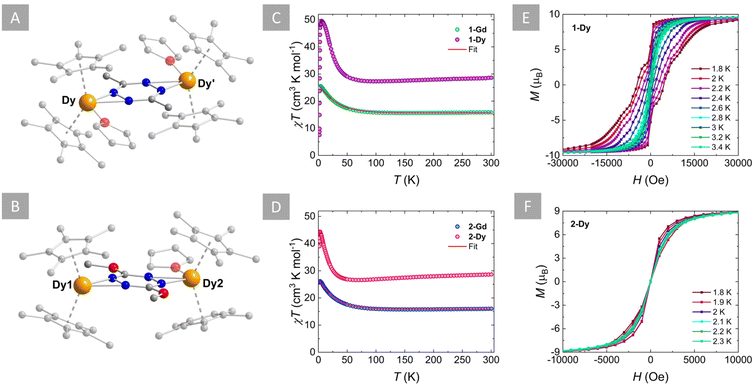
The incorporation of the aforementioned tetrazines as radical bridges into {Cp*₂Ln}⁺ complexes was attempted both for the electron-donating (R = Me and MeO) and electron-withdrawing substituents (R = Cl). Unfortunately, despite our best efforts, the isolation of complexes featuring the dctz˙⁻ was not successful. This can probably be explained by the electron-deficient nature of the chloro-substituted ligand as well as the reactive nature of the dctz ring, which has been shown to be incredibly versatile.⁵⁴ The equimolar reaction of dmtz and [Cp*₂Ln][BPh₄] (Ln = Gd or Dy) in THF leads to the isolation of 1-Ln as purple crystals upon vapor diffusion with Et₂O at low temperature. Attempts to add a reducing agent such as KC₈ or Cp₂Co did not lead to the isolation of the desired complexes. On the other hand, the synthesis of analogous complexes featuring dmeotz˙⁻ involved the reaction of dmeotz and Cp₂Co in THF and the subsequent addition of two parts of [Cp*₂Ln][BPh₄] (Ln = Gd or Dy) in THF. Stirring, filtration and vapor diffusion with Et₂O at room temperature afforded 2-Ln as dark red-green (dichroic) crystals over a period of one week. Infrared (IR) spectroscopy revealed an excellent agreement for the spectra of the Gd and Dy congeners in both cationic families (Fig. S9 and S10†).

The solid-state crystal structures of all complexes were determined through single-crystal X-ray diffraction (SCXRD) analysis. X-ray data and refinement details of all complexes are summarized in Table S2,† while selected bond distances and angles are given in Tables S3 for 1-Ln and S4† for 2-Ln. SCXRD analysis reveals that 1-Gd and 1-Dy are isostructural and crystallize in P2/c as centrosymmetric dinuclear complexes, with one crystallographically independent Ln^III centre (Fig. S11†). Given their structural similarities only 1-Dy was chosen as a representative example to describe the salient structural features of these complexes (Fig. 2A). The complex consists of two {Cp*₂Dy^III}⁺ moieties, bridged by a μ-dmtz˙⁻ ligand. Two THF solvent molecules complete the coordination sphere of each Dy^III centre, while a BPh₄⁻ counter ion and one THF solvent molecule are found in the crystal lattice. The average Dy–C_Cp* and Dy–Cp*_cent (cent = the centroid of the Cp* ligand) bond distances are 2.681(8) Å and 2.408(7) Å, respectively, while the Cp*_cent–Dy–Cp*_cent angle is 137.5(2)°. These, bond distances and angles are slightly larger than the respective distances and angles in the “Dy₂-tz˙⁻” system (2.678(1) Å, 2.395(4) Å and 136.6(2)°, respectively).³⁷ This can be explained by the electron-donating nature of the methyl groups, which enhances the electron density of the tetrazinyl ring and in turn increases the attraction between the dmtz˙⁻ and the positively charged Dy^III ion. This is further evident from the difference in the average Dy–N_dmtz bond distance of 2.395(6) Å, which is slightly shorter than the respective average bond distance of 2.460(2) Å in the “Dy₂-tz˙⁻” system. In addition to the longer Dy–O_THF bond distance of 2.433(4) Å in 1-Dy (2.389(2) Å in the “Dy₂-tz˙⁻” system), this signifies that a higher affinity with the dmtz˙⁻ is achieved thanks to its richer electron density compared to tz˙⁻.

Fig. 2 Left: molecular structures of 1-Dy (A) and 2-Dy (B). For clarity, partial transparency, labeling, omission of the BPh₄⁻ moieties, H-atoms, solvent molecules and disorder conformers have been employed. Color code: C: light grey; N: blue; O: red; Dy: orange. Middle: variable temperature χT plots of (C) 1-Gd (green circles), 1-Dy (purple circles) and (D) 2-Gd (blue circles), 2-Dy (pink circles) under an applied static field of 1000 Oe. The solid red line represents the fit as determined by applying the −2J formalism. Right: hysteresis sweep for 1-Dy (E) and 2-Dy (F) at the indicated temperatures with an average sweep rate of 30 Oe s⁻¹.

On the other hand, the isostructural complexes 2-Gd and 2-Dy crystallize in the P1̄ space group with two crystallographically independent Ln^III centres. Similarly to 1-Dy, complex 2-Dy is also cationic, featuring two {Cp*₂Dy^III}⁺ units bridged by a μ-dmeotz˙⁻ ligand and stabilized by a BPh₄⁻ anion in the crystal lattice (Fig. 2B and S12†). Unlike 1-Dy, in 2-Dy only one THF solvent molecule is coordinated to one of the two Dy^III centres (Dy2). This difference occurs due to the orientation of the bulky methoxy groups in the cis-fashion, which in turn blocks the addition of a second THF molecule to Dy1. Notably, these equatorially coordinated THF(s) affect the value of the exchange coupling constants (vide infra). However, efforts to promote the alignment of the methoxy groups in a trans-fashion,⁵⁵ which would ultimately exclude the coordination of the THF solvent, were unsuccessful. The average Dy–C_Cp* bond distances are slightly shorter for Dy1 (2.644(1) Å) than Dy2 (2.678(2) Å), due to the presence of the coordinated THF molecule in the latter (Dy2–O_THF: 2.432(2) Å). This is further evident from the shorter Dy–Cp*_cent distances and larger Cp*_cent–Dy–Cp*_cent angles for Dy1 (av. 2.356(5) Å; 139.60(2)°), compared to Dy2 (2.396(5) Å; 136.72(2)°). It is evident, that the presence of the coordinated THF molecule in Dy2 greatly impacts the axiality imposed by the Cp* ligands by introducing further equatorial ligand contributions compared to Dy1, which only coordinates to dmeotz˙⁻. Interestingly, the Dy–N_dmeotz bond distances are on average 2.394(5) Å for Dy1 and 2.442(5) Å for Dy2 and are still shorter than the respective distances for the “Dy₂-tz˙⁻” system.³⁷ This corroborates the trend observed for 1-Dy, i.e. the electron-donating nature of the MeO groups enhances the electron density of the tetrazinyl radical and thus higher affinity with the Ln^III centres can be achieved (vide infra).

The formation of the tetrazinyl radicals in both 1-Dy and 2-Dy was confirmed by charge balance considerations, as well as the clear elongation of the N–N bonds. In 1-Dy, the N1–N2 bond distance of 1.382(7) Å, as well as the C1–N1 and C1–N2 bond distances of 1.332(8) Å and 1.333(7) Å, respectively, confirm the formation of the dmtz˙⁻ ligand. Despite the absence of a reducing agent in the reaction conditions, the spontaneous formation of dmtz˙⁻ is not surprising. As has been previously shown in the literature, the BPh₄⁻ moiety of the [Cp*₂Ln][BPh₄] starting material is able to provide an electron to reduce redox-active ligands.^56,57 Thus, in its presence, dmtz could potentially undergo a one e⁻ reduction to form the radical species. Similar bond distances are observed for the dmeotz˙⁻ ligand, where the N1–N2 and N3–N4 bond distances are 1.401(3) Å and 1.373(3) Å, respectively, while the C1–N1, C2–N2, C2–N3 and C1–N4 bond distances are 1.326(5) Å, 1.315(5) Å, 1.334(5) Å and 1.328(5) Å, respectively. These N–N and C–N bond distances are in agreement with the previously reported values for other tetrazinyl-based radical ligands.^{37,38,40,58,59}

Static magnetic susceptibility behaviour and magnetic coupling

The direct current (dc) magnetic susceptibilities of all complexes were measured between 300 and 1.8 K at 1000 Oe, to probe their magnetic behaviour (Fig. 2C and D). The χT products of 15.84 cm³ K mol⁻¹ for 1-Gd, 16.02 cm³ K mol⁻¹ for 2-Gd, 28.62 cm³ K mol⁻¹ for 1-Dy and 28.64 cm³ K mol⁻¹ for 2-Dy are in good agreement with the theoretical values of 16.13 cm³ K mol⁻¹ and 28.71 cm³ K mol⁻¹, respectively, for two Ln^III ions (Gd: S = 7/2, ⁸S_7/2, g = 2, C = 7.88 cm³ K mol⁻¹; Dy: S = 5/2, L = 5, ⁶H_15/2, g = 4/3, C = 14.17 cm³ K mol⁻¹) and one radical (S = ½, C = 0.37 cm³ K mol⁻¹) species. Upon lowering of the temperature, a slight decrease of the χT value is observed until ∼155 K for 1-Gd and 2-Gd, 95 K for 1-Dy and 70 K for 2-Dy, reaching shallow minima of 15.63, 15.76, 27.29 and 26.58 cm³ K mol⁻¹, respectively. Below these temperatures, a rapid increase of the χT is observed with maxima of 25.52 cm³ K mol⁻¹ at 3.5 K for 1-Gd, 28.15 cm³ K mol⁻¹ at 2.8 K for 2-Gd, 49.56 cm³ K mol⁻¹ at 5.5 K for 1-Dy and 44.36 cm³ K mol⁻¹ at 3 K for 2-Dy. This behavior can be attributed to the parallel spin alignment of the Ln^III ions as a consequence of the strong antiferromagnetic coupling between the Ln^III centres and the radical ligand. The antiferromagnetic Ln–rad coupling leads to a ferrimagnetic ground state where the magnetic moments of the Ln^III ions are aligned in the same direction, thus leading to an increase of the χT product at low temperatures.^25,34,60,61 Further lowering of the temperature leads to a slight decrease of the χT for 1-Gd and 2-Gd, with values of 24.88 cm³ K mol⁻¹ and 25.84 cm³ K mol⁻¹ at 1.8 K, respectively. In contrast, for 1-Dy and 2-Dy, below 3 and 2.8 K, respectively, the drop of the χT is abrupt, yielding values of 7.54 cm³ K mol⁻¹ and 39.03 cm³ K mol⁻¹ at 1.8 K. For the latter, this downturn in the low-temperature region is indicative of magnetic blocking, as has been observed in other tetrazinyl-bridged Ln complexes.^37,38,40

A direct correlation between the effect of the substituent groups on the tetrazine ring and the strength of the Ln–rad magnetic coupling can be drawn by fitting the dc susceptibility data. In contrast to the rest of the lanthanide series, Gd^III ions allow for this quantification thanks to their isotropic 4f⁷ electron configuration. Thus, using PHI software,⁶² the dc magnetic susceptibility data of 1-Gd and 2-Gd can be fit to the spin-only Hamiltonian: Ĥ = −2J_Gd–radŜ_rad(Ŝ_Gd1 + Ŝ_Gd2) − 2J_Gd–GdŜ_Gd1Ŝ_Gd2 − zJ′_Gd–Gd〈Ŝ_z〉Ŝ_z, where J_Gd–rad represents the Gd^III–radical exchange coupling, J_Gd–Gd represents the intramolecular Gd^III–Gd^III exchange coupling, Ŝ_Gd and Ŝ_rad are the spin operators for each paramagnetic centre, 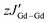represents weak intermolecular magnetic interactions and 〈Ŝ_z〉 is the mean value of the Ŝ_z component of the spin operator. Indeed, for 1-Gd, the best-fit afforded J_Gd–rad = −9.42 cm⁻¹, J_Gd–Gd = 0.22 cm⁻¹ and , while for 2-Gd the best-fit yielded J_Gd–rad = −8.54 cm⁻¹, J_Gd–Gd = 0.30 cm⁻¹ and 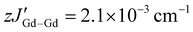. The latter, although small, was necessary to accurately fit the data, which can most likely be explained by the close intermolecular Ln⋯Ln distances (Fig. S13 and S14†). These values are among the highest Ln–rad exchange couplings for organic radical-bridged Ln SMMs. Within the small family of tetrazinyl-based radicals the values of −9.42 cm⁻¹ for 1-Gd and −8.54 cm⁻¹ for 2-Gd are higher than the respective value of −7.20 cm⁻¹ for “Gd₂-tz˙⁻”³⁷ and are only surpassed by the “Gd₂-bpytz˙⁻” system (−14.0 cm⁻¹).⁴⁰

From the aforementioned Hamiltonian, due to the very strong antiferromagnetic Ln–rad coupling, small ferromagnetic exchange couplings between the Ln^III centres can be extracted; J_Gd–Gd = 0.22 cm⁻¹ for 1-Gd and 0.30 cm⁻¹ for 2-Gd. This is further validated by the field dependence of the magnetization for both complexes at low temperatures (Fig. S15†). Indeed, the magnetization increases with the increase of the applied field, reaching saturation at values of 13.57 Nμ_B and 13.78 Nμ_B for 1-Gd and 2-Gd, respectively, which further support a S = 13/2.

The relative strength of the experimentally determined Gd–radical exchange coupling constants in 1-Gd, 2-Gd as well as the respective “Gd₂-tz˙⁻” ³⁷ system follows a trend: R = Me > MeO > H. This trend was further investigated by calculating the exchange coupling constant J_Gd–rad for 1-Gd, 2-Gd and nine (hypothetical) tetrazinyl-bridged Gd complexes – 1-GdMe^THF, 1-GdMe, 2-^cisGdMeO^THF, 2-^cisGdMeO, 2-^transGdMeO, 3-GdCl^THF, 3-GdCl, 4-GdOH^THF and 5-GdNH₂^THF – using the broken symmetry density functional theory (BS-DFT) (see the ESI for details; Fig. S18 and Tables S5–S10†). Both electron-donating and -withdrawing groups were introduced into the hypothetical complexes to evaluate whether resonance and inductive effects of the substituents could alter the spin density distribution on the coordinating atoms of the tetrazinyl ligands and affect the strength of the Ln–rad exchange coupling. The effects of the coordinating THF molecules on the exchange coupling constant were also investigated through calculations.

The relative strength of the calculated J_Gd–rad amongst the gas-phase optimized structures with coordinated THF molecules followed a trend: Me > MeO > NH₂ > OH > Cl > H in agreement with the experimental results (Tables 1 and S11†). However, in the case of the non-optimized structures of 1-Gd and 2-Gd the trend was the opposite (MeO > Me) by a small margin. Here, the non-optimized structures refer to the complexes 1-Gd and 2-Gd where only the positions of hydrogen atoms were optimized in the gas phase, while the positions of heavy atoms were fixed to their respective crystal structure coordinates. The calculated J_Gd–rad values also show that the removal of the coordinated THF molecules increases the magnitude of J_Gd–rad in the investigated complexes (Table 1 and S11;†1-GdMe^THF, 2-^cisGdMeO^THF and 3-GdCl^THFvs.1-GdMe, 2-^cisGdMeO and 3-GdCl), while stereoisomerism of the substituent plays only a minor role in the magnitude of J_Gd–rad (Tables 1 and S11;†2-^cisGdMeO^THFvs.2-^transGdMeO^THF).

Table 1 Coupling parameters for the J_Gd–rad and J_Gd–Gd of 1-Gd, 2-Gd, Gd₂-tz˙⁻ and nine hypothetical complexes. For 1-Gd, 2-Gd and Gd₂-tz˙⁻ both the calculated and the experimentally determined values are given

	J Gd–rad (cm^−1)	J Gd–Gd (cm^−1)
a Extracted from the fit of the χT vs. T plots. b Calculated. c Ref. 37.
With THF
1-Gd	−9.42	0.22
2-Gd	−8.54	0.30
Gd2-tz˙^− ^,	−7.20	0.32
1-Gd	−11.86	−0.03
2-Gd	−13.35	−0.27
Gd2-tz˙^− ^,	−6.20	—
1-GdMe^THF	−12.69	−0.03
2-^cisGdMeO^THF	−11.96	−0.14
3-GdCl^THF	−8.12	−0.02
4-GdOH^THF	−11.80	−0.02
5-GdNH2^THF	−11.93	−0.02
Without THF
1-GdMe	−14.07	−0.04
2-^cisGdMeO	−13.84	0.10
2-^transGdMeO	−14.57	−0.03
3-GdCl	−11.87	−0.03

---

Interestingly, the trends observed herein, are opposite to those observed for the 5,5′-R₂bpym˙⁻ (bpym = 2,2′-bipirymidine) ligands in a work presented previously by Long and coworkers.⁶³ In the case of 5,5′-R₂bpym˙⁻ complexes, the introduction of substituents that were electron donating by resonance at the 5 and 5′ carbons of the bpym ligand framework resulted in a decrease in the magnitude of the exchange coupling constant due to the decrease of the spin density at the 2 and 2′ carbons, as well as the nitrogen atoms, whereas the electron-withdrawing substituents showed the opposite effect. However, this is not the case for the tetrazinyl-derived (3,6-R₂tz˙⁻) ligands simply because their spin density distributions differ from 5,5′-R₂bpym˙⁻ (Fig. S19†). In particular, the spin density is accumulated more on the nitrogen atoms in 3,6-R₂tz˙⁻ than in 5,5′-R₂bpym˙⁻ as indicated by the calculated spin populations (Tables S12 and S13†). A closer look at the calculated spin populations for 5,5′-R₂bpym˙⁻ shows that the spin populations of the nitrogen and carbon (2 and 2′) atoms follow the proposed trend (F > Me₂ > OEt₂ > NMe₂) for the most part, but there are also some discrepancies in the trend. For instance, both Mulliken population analysis (MPA) and atom in molecules (AIM) population analysis predict smaller spin populations for the nitrogen atoms of Me₂bpym˙⁻ (AIM = 0.096; MPA = 0.093) than for the nitrogen atoms of NMe₂bpym˙⁻ (AIM = 0.098; MPA = 0.101). Additionally, the spin populations of the nitrogen atoms of OEt₂bpym˙⁻ (AIM = 0.134; MPA = 0.138) are higher than those of F₂bpym˙⁻ (AIM = 0.110; MPA = 0.110). For 3,6-R₂tz˙⁻, considering only the highest value of each nitrogen atom, the AIM spin populations predict that the order of exchange coupling constants is as follows: Me > MeO > OH > Cl > H > NH₂ based on the respective values of spin populations: 0.341, 0.300, 0.2851, 0.2826, 0.2815 and 0.2780. Thus, only the order of NH₂tz˙⁻ is incorrectly predicted by the spin population analysis, if the electron-donating substituent by resonance led to a stronger J_Gd–rad for 3,6-R₂tz˙⁻. On the other hand, if the total spin populations of the coordinating nitrogen atoms across different substituents and radicals are considered, then the electron-donating and withdrawing substituents have only little effect on the overall spin density at the nitrogen sites as the differences in total AIM (MPA) spin populations are within 0.05 (0.04) and 0.05 (0.07) for 5,5′-R₂bpym˙⁻ and 3,6-R₂tz˙⁻, respectively. Moreover, the total spin populations at the nitrogen sites do not predict the correct order of the exchange coupling constants for 5,5′-R₂bpym˙⁻ and 3,6-R₂tz˙⁻ (Tables S12 and S13†). Given that the total spin density of an unpaired electron must sum up to 1, the above values mean that the investigated electron-donating and -withdrawing substituents contribute ∼4–7% to the total spin densities of the nitrogen atoms, although individual nitrogen sites might experience larger local changes. These results suggest that the primary radical character and the spin density distribution are determined by the core structure of the radical unit rather than the nature of the substituents, although the latter can also have some influence. Additionally, the spin density distributions of 5,5′-R₂bpym˙⁻ and 3,6-R₂tz˙⁻ are different and, thus, the order of magnitude for J_Gd–rad cannot be inferred solely from the spin density, as had been previously stated in the literature.⁶³

Other factors affecting the strength of the coupling constants of tetrazine-based radical complexes were further investigated by performing a fragment orbital analysis for 1-GdMe^THF, 1-GdMe, 2-^cisGdMeO^THF, 2-^cisGdMeO, 3-GdCl^THF and 3-GdCl (see the ESI† for details). Previous studies have shown that the singly occupied molecular orbital (SOMO) of a tetrazine radical transforms according to the same presentation as the 4f_xyz orbital.⁶⁴ This means that there is at least one significant 4f-SOMO interaction that contributes to the antiferromagnetic exchange interaction via a 4f-radical kinetic exchange mechanism^65,66 in the investigated complexes. However, the total value of J_Gd–rad is determined by several factors,^67,68 and previous studies have shown that ferromagnetic 5d-radical Goodenough's exchange^69,70 can also contribute to the value of J_Gd–rad in Gd–radical complexes through orbital mixing.^70–73 The order of magnitude of the latter is usually much smaller than that of the 4f-radical kinetic exchange mechanism.⁷⁰ Orbital analysis indicates that the SOMO of the tetrazine radical does not directly interact with the half-filled 4f orbitals of the Gd ions. However, there is a mixing between the SOMO of the radical and the vacant 5d orbitals of the Gd ions (Fig. S20–25†). The radical contribution to the metal–ligand bond orbitals varies from 9% to 49%, whereas the metal contribution is between 2% and 10%. The other mixing is observed between occupied π-orbitals of the radical ligand and the 4f or 5d orbitals of Gd ions. Here contributions of the metal and ligand to the metal–ligand bonding vary from 2% to 80% and from 3% to 90%, respectively. Interestingly, the observed mixings are less pronounced in 3-GdCl^THF and 3-GdCl than in 1-GdMe^THF, 1-GdMe, 2-^cisGdMeO^THF and 2-^cisGdMeO. These results indicate that electron-withdrawing substituents, such as chlorine atoms, introduce an inductive effect that pulls electron density away from the tetrazine ring, rendering it more electron deficient. This is in agreement with the CV studies of the dctz ligand, where a lower redox potential of the dctz ligand compared to the dmtz, dmeotz and tz ligands is indicative of its higher electron deficiency. This reduction in electron density at the tetrazine ligand limits its orbital overlap with the orbitals of Gd^III ions and leads to weaker metal–radical interactions. The opposite effect is observed for electron-donating substituents like Me and MeO, which increase the electron density on the tetrazine ring through the resonance effect. This is also evident from the Ln–N bond distances which are shorter in 1-Ln and 2-Ln compared to the “Ln₂-tz˙⁻” complexes pointing towards a higher affinity of the dmtz˙⁻ and dmeotz˙⁻ with the Ln ions. Furthermore, the orbital analysis reveals that the orbital mixing between the orbitals of the tetrazine and Gd ions increases upon removal of the equatorially coordinated THF molecules (Fig. S20–25;†1-GdMe, 2-^cisGdMeO and 3-GdClvs.1-GdMe^THF, 2-^cisGdMeO^THF and 3-GdCl^THF, respectively). This effect explains why THF-free complexes show larger J_Gd–rad than the ones with coordinated THF. A small mixing between the vacant 6s orbitals of Gd^III ions and the occupied π orbitals of the tetrazine is also observed for 2-^cisGdMeO^THF and 2-^cisGdMeO, but its effect on the coupling constant is most likely very small.

The above data demonstrate that an intricate interplay between orbital overlap, ligand substituent effects and changes in the coordination environment collectively dictates the magnitude of J_Gd–rad in the investigated systems. Given that the substituent effects in 1-Ln and 2-Ln arise from the substituent at a remote, nonmetal binding site, the magnitude of the exchange coupling constant in tetrazinyl-bridged complexes can be tuned simply through a ligand modification to some extent, without significant perturbation of the lanthanide's coordination environment.

Magnetic hysteresis

The field dependence of the magnetization at low temperatures for 1-Dy and 2-Dy was investigated to probe the presence of magnetic blocking as seen by the χT vs. T plots. For 1-Dy a clear s-shape of the magnetization was observed at 1.9 K, indicating the presence of magnetic blocking at that temperature (Fig. S15†). To validate this, hysteresis measurements were performed between ±70 kOe and 1.8–3.4 K with an average sweep rate of 30 Oe s⁻¹ (Fig. 2E). Indeed, at 1.8 K the opening of the hysteresis loop revealed a coercive field of H_c = 5000 Oe. This is amongst the highest coercive fields within the family of dinuclear organic radical-bridged SMMs and it is comparable to the Ln₂-bpym˙⁻,⁷⁴ Ln₂-Bpim˙^− 34 and Ln₂-pyz˙^− 64 examples (where bpym = bipyrimidyl, Bpim = 2,2′-bisbenzimidazole and pyz = pyrazine), which exhibit similar coercive fields of 6000, 5400 and 5000 Oe, respectively. As the temperature increases a gradual close of the loop is observed until 3.4 K, above which it is no longer open. This temperature agrees with the temperature of 3.2 K, where a clear divergence between the zero-field-cooled and field-cooled (ZFC/FC) susceptibility is observed (Fig. S16A†).

On the other hand, for 2-Dy the magnetization curves (Fig. S15†) exhibit a field-dependent increase without reaching saturation even at low temperatures and high fields (10.16 Nμ_B at 1.9 K; 70 kOe). This lack of saturation and the non-superposition of the reduced magnetization curves are indicative of the high anisotropy of the system. However, no s-shape of the magnetization is observed for 2-Dy, in contrast to the 1-Dy and “Dy₂-tz˙⁻” complexes. Hysteresis measurements were also performed for 2-Dy between ±70 kOe with an average sweep rate of 30 Oe s⁻¹. At 1.8 K a small opening of a waist-restricted hysteresis loop is observed. The loop gradually closes with the increase of the temperature until 2.3 K above which it is no longer open. This trend agrees with the ZFC/FC susceptibility measurements which showed a small divergence of the two data sets below 2.2 K (Fig. S16B†).

The vast difference between the hysteresis of 1-Dy and 2-Dy must be of molecular origin, as confirmed by ab initio calculations (see the ESI† for further details). An investigation of the calculated g tensors of the local ground KDs of the Dy ions in 1-Dy and 2-Dy reveals that the Dy1 ion in 2-Dy, without the coordinated THF molecule, exhibits the most axial g tensors, albeit by a very small margin (Tables S14 and S15†). The g tensors of the first excited KDs are also similar, but differences are observed in the higher-lying KDs. The ground KDs consist of an almost pure M_J = ±15/2 state for 2-Dy, whereas for 1-Dy, the mixing of states is already visible in the ground KD (Tables S16–S18†). The local Dy sites in 1-Dy and 2-Dy also exhibit slightly different orientations of the main magnetic axes, depending on the absence or presence of the coordinated THF molecules (Fig. S26†). As variations in the orientations of the main magnetic axes are small, it is likely that their orientation is primarily influenced by the terminal Cp* ligands. The most striking difference is seen in the crystal field splitting of the ground multiplet ⁶H_15/2 of the Dy ions. For the Dy ions with coordinated THF molecules in 1-Dy and 2-Dy, the crystal field splitting is approximately 400–500 cm⁻¹, but for the Dy1 ion in 2-Dy it is over 1000 cm⁻¹ and this is accompanied by larger anisotropy (Tables S14 and S15†). This can be attributed to the different ligand fields acting on the Dy ions in 1-Dy and 2-Dy. Indeed, the investigation of calculated crystal field parameters with the leading-order rank k = 2 reveals that the diagonal B₂₀ parameter is larger for the Dy1 ion in 2-Dy compared to the Dy ions with coordinated THF molecules in 1-Dy and 2-Dy (Table S19†). Also, the off-diagonal B_2±1 parameter of 2-Dy is smaller than that of 1-Dy. The result indicates stronger axiality for the Dy1 ion in 2-Dy, which is, however, partially compensated by the high value of the off-diagonal parameter B_2±2. The higher-order rank (≥4) parameters are more uniform for all Dy ions. All the above differences between 1-Dy and 2-Dy, as well as the two distinct metal sites in 2-Dy, are expected to introduce competing effects on their magnetic performance.

Open, waist-restricted, hysteresis loops were also observed for the “Dy₂-tz˙⁻” system in the temperature range of 1.8 to 3.5 K. The blocking temperatures of 3.8, 3.5 and 2.2 K for 1-Dy, “Dy₂-tz˙⁻” and 2-Dy seem to follow a trend: R = Me > H > MeO. However, in contrast to the trend observed for the magnetic coupling, where more electron-donating substituents seem to directly affect the Ln–rad magnetic coupling, similar correlations with magnetic blocking seem to be rather difficult to make.

Dynamic magnetic susceptibility properties

To probe the potential SMM behaviour of 1-Dy and 2-Dy, alternating current (ac) magnetic susceptibility measurements were performed in the 0.1–1500 Hz frequency range. For both complexes a temperature-dependent signal was observed in the absence of a static magnetic field (H_dc = 0 Oe). For 1-Dy both the in-phase (χ′; Fig. S28†) and out-of-phase (χ′′; Fig. 3A) ac susceptibilities exhibit a frequency-dependent behavior between 8 and 2.8 K, indicative of a thermally activated magnetic relaxation. Similarly, for 2-Dy when H_dc = 0 Oe, a frequency-dependent signal of the ac susceptibility was observed in a lower temperature range of 5.4–4 K (Fig. 3B and S29†). However, below this temperature region a second frequency-dependent process appears as a distinct second peak of the χ′′ between 3.8 and 2 K. Accordingly, the relaxation times (τ) were extracted for both complexes by fitting both the χ′ and χ′′ using the CCFit-2 software⁷⁵ (Tables S20–S22†).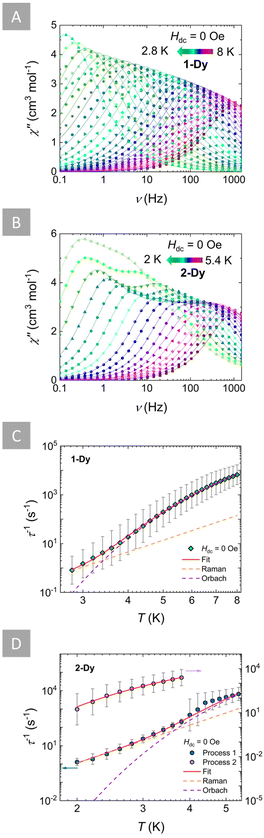

Fig. 3 Top: frequency-dependence of the out-of-phase (χ”) magnetic susceptibilities of 1-Dy (A) and 2-Dy (B) in the absence of an applied dc field (H_dc = 0 Oe) at the respective temperature regions. Solid lines represent fits to the generalized Debye model. Bottom: temperature-dependence of relaxation times (τ⁻¹) for 1-Dy (C) and 2-Dy (D) with the respective estimated standard deviations (grey bars). These estimated standard deviations of τ⁻¹ have been calculated from the α-parameters of the generalized Debye fits with the log–normal distribution.⁷⁵ The solid red lines represent the best-fit based on eqn (1) for 1-Dy (teal diamonds) and Process 1 of 2-Dy (blue hexagons), while the dashed orange and purple lines represent the individual components of the magnetic relaxation for Raman and Orbach processes, respectively. For Process 2 of 2-Dy (pink circles), the solid red line represents the best-fit to eqn (2).

Insights into the magnetic relaxation dynamics of these complexes were gained by the analysis and fit of the τ⁻¹vs. T plots. For 1-Dy a combination of Raman and Orbach mechanisms was used to accurately fit the τ based on eqn (1):

τ⁻¹ = CTⁿ + τ₀⁻¹ exp(−U_eff/k_BT), (1)

yielding the following best-fit parameters: C = 4.08 × 10⁻³ s⁻¹ K⁻ⁿ, n = 5.13, τ₀ = 3.30 × 10⁻⁷ s and U_eff = 34 cm⁻¹ (Fig. 3C). For 2-Dy, the τ values for two distinct processes were analyzed (Fig. 3D). The τ values of the first process (Process 1) were also fitted based on eqn (1) resulting in the following best-fit parameters: C = 9.62 × 10⁻³ s⁻¹ K⁻ⁿ, n = 6.88, τ₀ = 1.48 × 10⁻⁸ s and U_eff = 35 cm⁻¹. For the second process (Process 2), the τ values exhibited a clearly exponential temperature-dependent trend and were fit to an Orbach-only process based on eqn (2):

τ⁻¹ = τ₀⁻¹ exp(−U_eff/k_BT), (2)

yielding the following best-fit parameters: τ₀ = 2.10 × 10⁻⁶ s and U_eff = 14 cm⁻¹. The best-fit parameters for the temperature-dependent magnetic relaxation of 1-Dy and 2-Dy are summarized in Table S23.† The obtained U_eff values surpass the previously reported U_eff value for the “Dy₂-tz˙⁻” system (25 cm⁻¹).³⁷ Consequently, for the U_eff values of the primary relaxation processes a trend can be observed: Me ≈ MeO > H. This trend can be rationalized by the increasingly stronger Ln–rad magnetic coupling in 1-Ln and 2-Ln, compared to the “Ln₂-tz˙⁻” system, which is induced by the electron-donating nature of the methyl and methoxy groups on the tetrazinyl ring (vide supra). Additionally, the ab initio calculated local first-excited KDs for 1-Dy and 2-Dy are above 160 cm⁻¹ (Tables S14 and S15†). Thus, the small heights of the obtained experimental U_eff suggest that the magnetic relaxation should occur through a coupled exchanged state instead of the local exited states of Dy ions.^37–40,64 Further evidence for this was obtained from the simulated low-lying exchange-coupled states of 1-Dy and 2-Dy, indicating that their relaxation could occur via the second or third exchange doublet (Fig. S27†).

To study the effect of the applied dc field on the magnetic relaxation of these complexes, ac susceptibility measurements at varying fields up to 3000 Oe were undertaken at 3.5 K for 1-Dy (Fig. S30†) and 3 K for 2-Dy (Fig. S31†). A common observation for both complexes was that despite the continuous increase of the applied dc field, the overall ac susceptibility signal showed no improvement, while the position of the χ′′ maxima did not shift significantly even at higher fields. This is expected since the magnetic relaxation in both complexes is thermally-activated via Raman and Orbach contributions. Consequently, upon extracting the τ values (Tables S24 and S25†) it is evident that they remain relatively unaffected by the applied dc field and overall remain constant (Fig. S32 and S33†). To further probe the relaxation dynamics that dictate the magnetic relaxation of these complexes, the τ⁻¹vs. H plots for both complexes were fit (see ESI† for further details). For 1-Dy a combination of Raman and Orbach mechanisms was able to accurately fit the data. For 2-Dy, the relaxation times of Process 1 were fit to a combination of Raman and Orbach, while for Process 2 an Orbach-only process was used to provide a satisfactory fit. Efforts to account for the presence of QTM or direct mechanisms, which are strongly field-dependent processes, did not improve the fit or provided any meaningful parameters and were therefore excluded. This further corroborates the observed trends from both the field and temperature-dependent ac susceptibility studies, where for both 1-Dy and 2-Dy the relaxation of the magnetization is clearly dominated by the same combination of thermally-activated processes (Raman and Orbach). Best-fit parameters for the field-dependent magnetic relaxation of 1-Dy and 2-Dy are given in Table S26.†

Conclusion

In summary, the present study demonstrates that introducing substituent groups in the 3- and 6-positions of the s-tetrazine ring can have an immediate impact on the electronic structure of the tetrazinyl bridge, which in turn affects the strength of the Ln–rad magnetic exchange coupling. Electron-withdrawing substituents, such as chlorine atoms, introduce an inductive effect that pulls electron density away from the tetrazine ring, rendering it more electron deficient. The opposite effect is observed for electron-donating substituents, such as Me and MeO, which increase the electron density on the tetrazine ring through resonance as seen for 1-Gd (−9.42 cm⁻¹) and 2-Gd (−8.54 cm⁻¹) compared to the previously published “Gd₂-tz˙⁻” complex (−7.2 cm⁻¹).³⁷ DFT calculations reveal that the Ln–rad magnetic coupling does not solely depend on the spin density of the radical ligands but it is a rather intricate interplay between orbital overlap, ligand substituent effects and changes in the coordination environment of the Ln^III ions. In the case of 1-Dy and 2-Dy, SMM behaviour is observed at zero field, while the slow magnetic relaxation is mediated by purely thermally-activated pathways. For 1-Dy, a coercive field of 5000 Oe rates this complex amongst the highest performing dinuclear radical-bridged Dy^III lanthanocenes.

From the work presented herein, it is clear that the designing principles for improved SMMs of this type depend on a number of factors. While previous research had suggested that the magnetic exchange coupling is directly correlated with the spin density distribution of the radical ligands, it is evident that this is far more complicated. Since the substituent effects in 1-Ln and 2-Ln arise from the substituent at a remote, nonmetal binding site, the magnitude of the exchange coupling constant in tetrazinyl-bridged complexes can be tuned simply through a ligand modification to some extent, without significant perturbation of the lanthanide's coordination environment. Thus, an in-depth understanding of the origin of magnetic exchange coupling is key to harnessing the magnetic properties of strongly coupled SMMs. Excitingly, the observed trends for the magnetic coupling mediated by the tetrazinyl ligands can potentially extend to other paramagnetic Ln^III ions, given their similar physical and chemical properties across the series and thus can lead to the development of new high-performing radical-bridged Ln^III SMMs.

Author contributions

The manuscript was written through the contributions of all authors.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

N. M., A. A. K. and M. M. thank the University of Ottawa, the Canada Foundation for Innovation (CFI) and the Natural Sciences and Engineering Research Council of Canada (NSERC) for the financial support of this work. N. M. acknowledges the Stavros Niarchos Foundation for financial support through scholarships. The authors thank Prof. Jaclyn L. Brusso (University of Ottawa) for providing access to the IR and UV/Vis spectrometers, as well as for useful discussions regarding the CV and UV-Vis measurements and data interpretation. A. M. acknowledges funding provided by the Academy of Finland (grant no. 332294) and the University of Oulu (Kvantum Institute). J. O. M. and R. G. acknowledge the Academy of Finland (projects 315829, 345484 and 338733) for the financial support. Computational resources were provided by Prof. H. M. Tuononen (University of Jyväskylä) and CSC-IT Center for Science in Finland and the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533).

References

1. T. Hashimoto, Y. Kawamata and K. Maruoka, An organic thiyl radical catalyst for enantioselective cyclization, Nat. Chem., 2014, 6, 702–705.
2. D. Yuan, W. Liu and X. Zhu, Design and Applications of Single-Component Radical Conductors, Chem, 2021, 7, 333–357.
3. P. Perlepe, I. Oyarzabal, L. Voigt, M. Kubus, D. N. Woodruff, S. E. Reyes-Lillo, M. L. Aubrey, P. Négrier, M. Rouzières, F. Wilhelm, A. Rogalev, J. B. Neaton, J. R. Long, C. Mathonière, B. Vignolle, K. S. Pedersen and R. Clérac, From an antiferromagnetic insulator to a strongly correlated metal in square-lattice MCl₂(pyrazine)₂ coordination solids, Nat. Commun., 2022, 13, 5766.
4. P. Perlepe, I. Oyarzabal, A. Mailman, M. Yquel, M. Platunov, I. Dovgaliuk, M. Rouzières, P. Négrier, D. Mondieig, E. A. Suturina, M.-A. Dourges, S. Bonhommeau, R. A. Musgrave, K. S. Pedersen, D. Chernyshov, F. Wilhelm, A. Rogalev, C. Mathonière and R. Clérac, Metal-organic magnets with large coercivity and ordering temperatures up to 242 °C, Science, 2020, 370, 587–592.
5. T. Morita, M. Damjanović, K. Katoh, Y. Kitagawa, N. Yasuda, Y. Lan, W. Wernsdorfer, B. K. Breedlove, M. Enders and M. Yamashita, Comparison of the Magnetic Anisotropy and Spin Relaxation Phenomenon of Dinuclear Terbium(III) Phthalocyaninato Single-Molecule Magnets Using the Geometric Spin Arrangement, J. Am. Chem. Soc., 2018, 140, 2995–3007.
6. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level, J. Am. Chem. Soc., 2003, 125, 8694–8695.
7. F. Alkhayri and C. A. Dyker, A Two-Electron Bispyridinylidene Anolyte for Non-Aqueous Organic Redox Flow Batteries, J. Electrochem. Soc., 2020, 167, 160548.
8. M. Al Raihan and C. A. Dyker, Ester-Substituted Bispyridinylidenes: Double Concerted Two-Electron Bipolar Molecules for Symmetric Organic Redox Flow Batteries, ACS Energy Lett., 2023, 8, 3314–3322.
9. P. J. Chirik and K. Wieghardt, Radical Ligands Confer Nobility on Base-Metal Catalysts, Science, 2010, 327, 794–795.
10. A. Studer and D. P. Curran, Catalysis of Radical Reactions: A Radical Chemistry Perspective, Angew. Chem., Int. Ed., 2016, 55, 58–102.
11. J. O. Moilanen, N. F. Chilton, B. M. Day, T. Pugh and R. A. Layfield, Strong Exchange Coupling in a Trimetallic Radical-Bridged Cobalt(II)-Hexaazatrinaphthylene Complex, Angew. Chem., 2016, 128, 5611–5615.
12. X. Ma, E. A. Suturina, S. De, P. Négrier, M. Rouzières, R. Clérac and P. Dechambenoit, A Redox-Active Bridging Ligand to Promote Spin Delocalization, High-Spin Complexes, and Magnetic Multi-Switchability, Angew. Chem., Int. Ed., 2018, 57, 7841–7845.
13. X. Ma, E. A. Suturina, M. Rouzières, M. Platunov, F. Wilhelm, A. Rogalev, R. Clérac and P. Dechambenoit, Using Redox-Active π Bridging Ligand as a Control Switch of Intramolecular Magnetic Interactions, J. Am. Chem. Soc., 2019, 141, 7721–7725.
14. H. Chen, L. Voigt, M. Kubus, D. Mihrin, S. Mossin, R. W. Larsen, S. Kegnæs, S. Piligkos and K. S. Pedersen, Magnetic Archimedean Tessellations in Metal–Organic Frameworks, J. Am. Chem. Soc., 2021, 143, 14041–14045.
15. H. Chen, A. S. Manvell, M. Kubus, M. A. Dunstan, G. Lorusso, D. Gracia, M. S. B. Jørgensen, S. Kegnæs, F. Wilhelm, A. Rogalev, M. Evangelisti and K. S. Pedersen, Towards frustration in Eu(II) Archimedean tessellations, Chem. Commun., 2023, 59, 1609–1612.
16. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984.
17. S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Giant coercivity and high magnetic blocking temperatures for N₂³⁻ radical-bridged dilanthanide complexes upon ligand dissociation, Nat. Commun., 2017, 8, 2144.
18. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding, Science, 2022, 375, 198–202.
19. E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2020, 5, 87–104.
20. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide Single-Molecule Magnets, Chem. Rev., 2013, 113, 5110–5148.
21. J.-T. Chen, H. Yan, T.-T. Wang, T.-D. Zhou and W.-B. Sun, Di- and Tetranuclear Dysprosium Single-Molecule Magnets Bridged by Unprecedentedly Disassembled Nitrogen-Enriched Tetrazine Derivatives, Inorg. Chem., 2022, 61, 19097–19105.
22. J. Goura, J. P. S. Walsh, F. Tuna and V. Chandrasekhar, Tetranuclear Lanthanide(III) Complexes in a Seesaw Geometry: Synthesis, Structure, and Magnetism, Inorg. Chem., 2014, 53, 3385–3391.
23. D. I. Alexandropoulos, S. Mukherjee, C. Papatriantafyllopoulou, C. P. Raptopoulou, V. Psycharis, V. Bekiari, G. Christou and T. C. Stamatatos, A New Family of Nonanuclear Lanthanide Clusters Displaying Magnetic and Optical Properties, Inorg. Chem., 2011, 50, 11276–11278.
24. H.-D. Li, S.-G. Wu and M.-L. Tong, Lanthanide–radical single-molecule magnets: current status and future challenges, Chem. Commun., 2023, 59, 6159–6170.
25. P. Zhang, R. Nabi, J. K. Staab, N. F. Chilton and S. Demir, Taming Super-Reduced Bi₂^3– Radicals with Rare Earth Cations, J. Am. Chem. Soc., 2023, 145, 9152–9163.
26. S. Calancea, L. Carrella, T. Mocanu, V. Sadohin, M. Raduca, I. Gutu, J. C. da Rocha, M. G. F. Vaz, E. Rentschler and M. Andruh, Magnetic Molecular Rectangles Constructed from Functionalized Nitronyl-Nitroxide Ligands and Lanthanide(III) Ions, Eur. J. Inorg. Chem., 2021, 2021, 567–577.
27. P. Rey, A. Caneschi, T. S. Sukhikh and K. E. Vostrikova, Tripodal Oxazolidine-N-Oxyl Diradical Complexes of Dy³⁺ and Eu³⁺, Inorganics, 2021, 9, 91.
28. L. Norel, L.-M. Chamoreau, Y. Journaux, O. Oms, G. Chastanet and C. Train, Verdazyl-lanthanide(III) one dimensional compounds: synthesis, structure and magnetic properties, Chem. Commun., 2009, 2381–2383.
29. P. Zhang, M. Perfetti, M. Kern, P. P. Hallmen, L. Ungur, S. Lenz, M. R. Ringenberg, W. Frey, H. Stoll, G. Rauhut and J. van Slageren, Exchange coupling and single molecule magnetism in redox-active tetraoxolene-bridged dilanthanide complexes, Chem. Sci., 2018, 9, 1221–1230.
30. J. Long, D. M. Lyubov, G. A. Gurina, Y. V. Nelyubina, F. Salles, Y. Guari, J. Larionova and A. A. Trifonov, Using N-Heterocyclic Carbenes as Weak Equatorial Ligands to Design Single-Molecule Magnets: Zero-Field Slow Relaxation in Two Octahedral Dysprosium(III) Complexes, Inorg. Chem., 2022, 61, 1264–1269.
31. G. Huang, C. Daiguebonne, G. Calvez, Y. Suffren, O. Guillou, T. Guizouarn, B. Le Guennic, O. Cador and K. Bernot, Strong Magnetic Coupling and Single-Molecule-Magnet Behavior in Lanthanide-TEMPO Radical Chains, Inorg. Chem., 2018, 57, 11044–11057.
32. E. M. Fatila, M. Rouzières, M. C. Jennings, A. J. Lough, R. Clérac and K. E. Preuss, Fine-Tuning the Single-Molecule Magnet Properties of a [Dy(III)-Radical]₂ Pair, J. Am. Chem. Soc., 2013, 135, 9596–9599.
33. I. S. Morgan, A. Mansikkamäki, M. Rouzières, R. Clérac and H. M. Tuononen, Coexistence of long-range antiferromagnetic order and slow relaxation of the magnetization in the first lanthanide complex of a 1,2,4-benzotriazinyl radical, Dalton Trans., 2017, 46, 12790–12793.
34. F. Benner, L. L. Droitte, O. Cador, B. L. Guennic and S. Demir, Magnetic hysteresis and large coercivity in bisbenzimidazole radical-bridged dilanthanide complexes, Chem. Sci., 2023, 14, 5577–5592.
35. G. Clavier and P. Audebert, s-Tetrazines as Building Blocks for New Functional Molecules and Molecular Materials, Chem. Rev., 2010, 110, 3299–3314.
36. O. Stetsiuk, A. Abhervé and N. Avarvari, 1,2,4,5-Tetrazine based ligands and complexes, Dalton Trans., 2020, 49, 5759–5777.
37. N. Mavragani, A. A. Kitos, A. Mansikkamäki and M. Murugesu, New members of radical bridged Ln₂ metallocene single-molecule magnets based on the unsubstituted 1,2,4,5-tetrazine ligand, Inorg. Chem. Front., 2023, 10, 259–266.
38. N. Mavragani, D. Errulat, D. A. Gálico, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Radical-Bridged Ln₄ Metallocene Complexes with Strong Magnetic Coupling and a Large Coercive Field, Angew. Chem., Int. Ed., 2021, 60, 24206–24213.
39. N. Mavragani, A. A. Kitos, D. A. Gálico, A. Mansikkamäki and M. Murugesu, Probing the magnetic and magneto-optical properties of a radical-bridged Tb₄ single-molecule magnet, Chem. Commun., 2023, 59, 13970–13973.
40. N. Mavragani, A. A. Kitos, J. Hrubý, S. Hill, A. Mansikkamäki, J. O. Moilanen and M. Murugesu, Strong magnetic exchange coupling in Ln₂ metallocenes attained by the trans-coordination of a tetrazinyl radical ligand, Inorg. Chem. Front., 2023, 10, 4197–4208.
41. A. Pinner, Ueber die Einwirkung von Hydrazin auf Imidoäther, Ber. Dtsch. Chem. Ges., 1893, 26, 2126–2135.
42. N. Mavragani, A. A. Kitos, J. L. Brusso and M. Murugesu, Enhancing Magnetic Communication between Metal Centres: The Role of s-Tetrazine Based Radicals as Ligands, Chem. – Eur. J., 2021, 27, 5091–5106.
43. K. V. Domasevitch, I. A. Gural'skiy, P. V. Solntsev, E. B. Rusanov, H. Krautscheid, J. A. K. Howard and A. N. Chernega, 4,4′-Bipyridazine: a new twist for the synthesis of coordination polymers, Dalton Trans., 2007, 3140–3148.
44. R. M. Versteegen, R. Rossin, W. ten Hoeve, H. M. Janssen and M. S. Robillard, Click to Release: Instantaneous Doxorubicin Elimination upon Tetrazine Ligation, Angew. Chem., Int. Ed., 2013, 52, 14112–14116.
45. M. D. Coburn, G. A. Buntain, B. W. Harris, M. A. Hiskey, K.-Y. Lee and D. G. Ott, An improved synthesis of 3,6-diamino-1,2,4,5-tetrazine. II. From triaminoguanidine and 2,4-pentanedione, J. Heterocycl. Chem., 1991, 28, 2049–2050.
46. M. D. Helm, A. Plant and J. P. A. Harrity, A novel approach to functionalised pyridazinone arrays, Org. Biomol. Chem., 2006, 4, 4278–4280.
47. R. I. Ishmetova, N. I. Latosh, I. N. Ganebnykh, N. K. Ignatenko, S. G. Tolshchina and G. L. Rusinov, Replacement of dimethylpyrazolyl group in 1,2,4,5-tetrazines by aliphatic alcohols and water, Russ. J. Org. Chem., 2009, 45, 1102–1107.
48. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
49. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789.
50. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100.
51. A. D. Becke, Density–functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
52. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
53. D. J. Min, K. Lee, H. Park, J. E. Kwon and S. Y. Park, Redox Potential Tuning of s-Tetrazine by Substitution of Electron-Withdrawing/Donating Groups for Organic Electrode Materials, Molecules, 2021, 26, 894.
54. N. Saracoglu, Recent advances and applications in 1,2,4,5-tetrazine chemistry, Tetrahedron, 2007, 63, 4199–4236.
55. P. Kang, S. Jung, J. Lee, H. J. Kang, H. Lee and M.-G. Choi, Anion induced structural transformation in silver-(3,6-dimethoxy-1,2,4,5-tetrazine) coordination polymers under mechanochemical conditions, Dalton Trans., 2016, 45, 11949–11952.
56. F. Benner and S. Demir, From unprecedented 2,2′-bisimidazole-bridged rare earth organometallics to magnetic hysteresis in the dysprosium congener, Inorg. Chem. Front., 2023, 10, 4981–4992.
57. M. R. MacDonald, J. W. Ziller and W. J. Evans, Coordination and Reductive Chemistry of Tetraphenylborate Complexes of Trivalent Rare Earth Metallocene Cations, [(C₅Me₅)₂Ln][(μ-Ph)₂BPh₂], Inorg. Chem., 2011, 50, 4092–4106.
58. B. S. Dolinar, D. I. Alexandropoulos, K. R. Vignesh, T. James and K. R. Dunbar, Lanthanide Triangles Supported by Radical Bridging Ligands, J. Am. Chem. Soc., 2018, 140, 908–911.
59. B. S. Dolinar, S. Gómez-Coca, D. I. Alexandropoulos and K. R. Dunbar, An air stable radical-bridged dysprosium single molecule magnet and its neutral counterpart: redox switching of magnetic relaxation dynamics, Chem. Commun., 2017, 53, 2283–2286.
60. F.-S. Guo and R. A. Layfield, Strong direct exchange coupling and single-molecule magnetism in indigo-bridged lanthanide dimers, Chem. Commun., 2017, 53, 3130–3133.
61. C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, A Trinuclear Radical-Bridged Lanthanide Single-Molecule Magnet, Angew. Chem., Int. Ed., 2017, 56, 10103–10107.
62. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: a powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175.
63. C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, Substituent Effects on Exchange Coupling and Magnetic Relaxation in 2,2′-Bipyrimidine Radical-Bridged Dilanthanide Complexes, J. Am. Chem. Soc., 2020, 142, 21197–21209.
64. N. Bajaj, N. Mavragani, A. A. Kitos, D. Chartrand, T. Maris, A. Mansikkamäki and M. Murugesu, Hard single-molecule magnet behavior and strong magnetic coupling in pyrazinyl radical-bridged lanthanide metallocenes, Chem, 2024, 10, 2484–2499.
65. P. W. Anderson, New Approach to the Theory of Superexchange Interactions, Phys. Rev., 1959, 115, 2–13.
66. N. Iwahara and L. F. Chibotaru, Exchange interaction between J multiplets, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 91, 174438.
67. J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Magnetic Interactions in Molecules and Highly Correlated Materials: Physical Content, Analytical Derivation, and Rigorous Extraction of Magnetic Hamiltonians, Chem. Rev., 2014, 114, 429–492.
68. J. J. Novoa, M. Deumal and J. Jornet-Somoza, Calculation of microscopic exchange interactions and modelling of macroscopic magnetic properties in molecule-based magnets, Chem. Soc. Rev., 2011, 40, 3182–3212.
69. J. B. Goodenough, Magnetism and the Chemical Bond, in Interscience Monographs on Chemistry, John Wiley & Sons, Ltd, New York, NY, 1963, vol. I.
70. V. Vieru, N. Iwahara, L. Ungur and L. F. Chibotaru, Giant exchange interaction in mixed lanthanides, Sci. Rep., 2016, 6, 24046.
71. T. Nakamura, T. Kanetomo and T. Ishida, Strong Antiferromagnetic Interaction in a Gadolinium(III) Complex with Methoxy-TEMPO Radical: A Relation between the Coupling and the Gd–O–N Angle, Inorg. Chem., 2021, 60, 535–539.
72. T. Kanetomo, T. Yoshitake and T. Ishida, Strongest Ferromagnetic Coupling in Designed Gadolinium(III)–Nitroxide Coordination Compounds, Inorg. Chem., 2016, 55, 8140–8146.
73. T. Gupta, T. Rajeshkumar and G. Rajaraman, Magnetic exchange in {Gd^III–radical} complexes: method assessment, mechanism of coupling and magneto-structural correlations, Phys. Chem. Chem. Phys., 2014, 16, 14568–14577.
74. S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, Exchange Coupling and Magnetic Blocking in Bipyrimidyl Radical-Bridged Dilanthanide Complexes, J. Am. Chem. Soc., 2012, 134, 18546–18549.
75. D. Reta and N. F. Chilton, Uncertainty estimates for magnetic relaxation times and magnetic relaxation parameters, Phys. Chem. Chem. Phys., 2019, 21, 23567–23575.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, single-crystal X-ray diffraction data, additional CV, and spectroscopic, magnetic and computational data. CCDC 2373023, 2373024, 2373025 and 2373026. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qi02796e

---