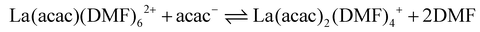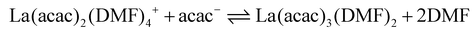DOI:
10.1039/D4QI02530J
(Research Article)
Inorg. Chem. Front., 2025,
12, 1890-1899
Unravelling the formation pathway and energetic landscape of lanthanide cages based on bis-β-diketonato ligands†
Received
9th October 2024
, Accepted 27th November 2024
First published on 29th November 2024
Abstract
This study focuses on the self-assembly mechanisms of triple- and quadruple-stranded lanthanide cages and their solution behaviour, particularly concerning equilibrium and cage interconversion. A systematic investigation was conducted to unravel the formation process of lanthanide cages based on bis-β-diketonato ligands. By employing diamagnetic La3+ ions, NMR spectroscopy coupled with ESI-MS analyses revealed the consecutive and competitive formation of four different species: [La2L]4+, [La2L2]2+, [La2L3], and [La2L4]2−. Moreover, stepwise and overall stability constants were derived. Further studies on the energetics of the equilibrium between the two most stable species, the triple-stranded [La2L3] and quadruple-stranded [La2L4]2− cages, were conducted through variable temperature analyses, indicating that the interconversion is exergonic, endothermic and mainly entropy driven. DFT thermochemical calculations involving an explicitly coordinated solvent allowed for a better evaluation of the role of enthalpic and entropic factors in step-by-step ligand association.
Introduction
Supramolecular self-assembly entails the spontaneous arrangement of molecular constituents into higher-order structures. Understanding the precise mechanisms driving this assembly process is essential for effectively controlling and maximizing system functionalities. Metallo-supramolecular coordination assemblies, particularly those leading to cage architectures, have emerged as significant systems for both foundational research and practical applications.1 Despite extensive exploration of coordination-driven supramolecular cages over the past two decades, in-depth molecular-level comprehension of the self-assembly process of these cages is still scarce and has primarily focused on systems involving Pd(II)/Pt(II) ions and multi-topic pyridine ligands. This understanding has been facilitated by a combination of computational approaches2–4 and experimental techniques, including the QASAP method (quantitative analysis of self-assembly process) proposed by Hiraoka.5 However, the complexity in understanding this process is further increased by the fact that coordination-driven systems are dynamic owing to the nature of metal–ligand bonds. Arguably, the first and most commonly reported example involves the self-assembly of linear ligands and 90° metal corners with Pd(II) and Pt(II) ions to form triangular and square molecular polygons.6–9 Even supramolecular cages constructed from other metal ions can undergo interconversion, which may be controlled by external stimuli, including physical10–13 and chemical14–18 triggers. However, if we consider ions different from Pd(II)/Pt(II), the study of the interconversion mechanism19–21 is very rare. Lanthanide-based assemblies have recently gained attention owing to their unique electronic and coordination properties, which offer new opportunities to construct intricate supramolecular architectures.22,23 These features make lanthanide systems suitable for applications in areas such as sensing, imaging, and information storage. However, lanthanide architectures are challenging considering the variable coordination numbers and coordination geometries of these ions. In the context of Ln-based cages, we have recently reported on [Ln2L4]2− systems based on bis-β-diketonate ligands, which exhibit intriguing supramolecular characteristics. Oligo-β-diketone ligands allow access to a wide range of metallo-supramolecular systems. In view of the seminal work of Saalfrank24 and the extensive study by Lindoy,25 these ligands can be used to prepare metallocycles, cages, MOFs,15,26–29 and even interlocked structures.30–33 Although less common, oligo-β-diketones allow access to Ln based architectures. For instance, we demonstrated that [Ln2L4]2− quadruple-stranded helicates and their host–guest properties allow dynamic and adaptive helicity reorganization due to guest-to-host chirality transfer.34 Helicate-mesocate isomerism in [Ln2L4]2− cages is strongly affected by the guest size and ligand flexibility.35 Moreover, these cages show Ln3+ ion exchange,36 leading to the formation of heterometallic systems. These systems can also serve as luminophore with high brightness to realize transparent luminescent solar concentrators.37 The reaction between a Ln3+ ion and a bis-β-diketonate can easily lead to [Ln2L3] triple- or [Ln2L4]2− quadruple-stranded helicates.34,38–46 [Ln2L3] and [Ln2L4]2− architectures feature different behaviours in terms of host–guest, luminescence and magnetic properties. Hence it is paramount to fully understand the formation pathway and energetic landscapes governing the self-assembly and the possible interconversion of these two systems. In the case of Ln cages, previous studies47–51 have taken advantage of Eu and Tb systems through spectrophotometric titrations usually coupled with factor analyses to rationalize spectroscopic data in terms of possible species and infer their formation constants. Mass spectrometry can also provide valuable insights into the formation of lanthanide-based systems, as demonstrated in studies investigating the self-assembly of high-nuclearity Ln clusters.52–56
Herein, a systematic study was conducted through NMR, ESI-MS and DFT calculations to unravel the self-assembly of [La2L3] and [La2L4]2− systems considering three different bis-β-diketonate ligands in terms of the central scaffold. Four different species were found to be involved in the self-assembly between La3+ ions and bis-β-diketonate ligands, namely, [La2L]4+, [La2L2]2+, [La2L3], and [La2L4]2−. The stepwise and overall formation constants were determined, and particular attention was devoted to the equilibrium between the triple-stranded [La2L3] and quadruple-stranded [La2L4]2− cages and its energetics.
Results and discussion
Formation studies
We previously reported that pure [Ln2L4]2− cages, based on three different bis-β-diketonate ligands (LA, LB, and LM: Fig. 1), are straightforwardly prepared by employing stoichiometric ligand excess (Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 1
L ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5).34,36,37 Using a Ln
2.5).34,36,37 Using a Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, [Ln2L3] triple-stranded helicate is formed. The possibility to control the formation of the two different systems [Ln2L3] and [Ln2L4]2− by simply tuning the Ln
3, [Ln2L3] triple-stranded helicate is formed. The possibility to control the formation of the two different systems [Ln2L3] and [Ln2L4]2− by simply tuning the Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio prompted us to undertake a systematic study of cage formation, with the aim of investigating, not only qualitatively but also quantitatively, the different species and steps leading to their self-assembly.
L ratio prompted us to undertake a systematic study of cage formation, with the aim of investigating, not only qualitatively but also quantitatively, the different species and steps leading to their self-assembly.
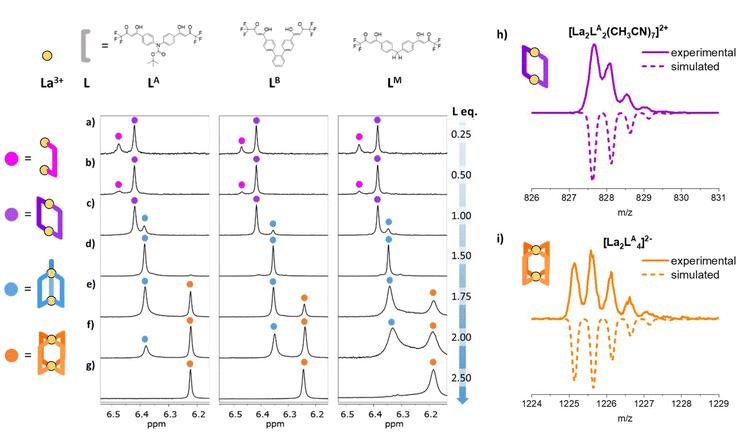 |
| | Fig. 1 (a–g) 1H-NMR spectra (25 °C, 300 MHz, DMF-d7) in the α-proton region of [La2LAy]n, [La2LBy]n and [La2LMy]n (where y = 1, 2, 3, and 4 and n = 4+, 2+, 0, and 2−, respectively) following ligand addition. The different species are marked as follow: [La2L]4+ = magenta, [La2L2]2+ = purple, [La2L3] = blue, and [La2L4]2− = orange. (h) and (i) ESI-MS isotopic patterns for [La2LA2]2+ and [La2LA4]2− species. | |
The formation of [Ln2L3] and [Ln2L4]2− can be readily monitored through 1H-NMR using La3+ ions34,36,37 since the β-diketonate α proton is very diagnostic and easily allows to differentiate the species present in solution. For instance, in the case of LA, the α proton is at 7.12 ppm for the free ligand, 6.00 ppm for the deprotonated ligand, 6.38 ppm for [La2LA3] and 6.22 ppm for [La2LA4]2−.
To an La3+ solution of known concentration, prepared by dissolving La(NO3)3·6H2O in DMF-d7, different aliquots of a deprotonated ligand solution of known concentration were added stepwise. 1H-NMR spectra were recorded immediately after each ligand addition and again after three days to ensure equilibration, revealing no significant differences. It is important to note that all NMR investigations were conducted in DMF-d7 to have a good coordinating solvent capable of effectively competing with the strong chelating ligands. In this way, La3+-ligand association constants are reduced to fall within an appropriate NMR range (i.e., K up to or slightly above 106). Formation studies were carried out on the three ligands LA, LB and LM. The obtained full 1H-NMR spectra are reported in Fig. S8–S10,† while Fig. 1 shows the region relative to the diagnostic α-proton. After the addition of 0.25 ligand equivalents (La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5), two singlets (6.43–6.48 ppm and 6.36–6.42 ppm, given as a magenta and purple circle, respectively, in Fig. 1a) are visible at lower fields as compared to the signals relative to [La2L3] and [La2L4]2− cages. By further adding 0.25 equivalents (La
0.5), two singlets (6.43–6.48 ppm and 6.36–6.42 ppm, given as a magenta and purple circle, respectively, in Fig. 1a) are visible at lower fields as compared to the signals relative to [La2L3] and [La2L4]2− cages. By further adding 0.25 equivalents (La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the relative intensity of the two singlets changes toward the peak at a lower ppm value (Fig. 1b). Considering 1.00 ligand equivalent (La
1), the relative intensity of the two singlets changes toward the peak at a lower ppm value (Fig. 1b). Considering 1.00 ligand equivalent (La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), there are still two singlets, but the one at 6.43–6.48 ppm disappears, while the [La2L3] cage signal (6.30–6.38 ppm, blue circle in Fig. 1c) appears. [La2L3] species is the only one present at a 2
2), there are still two singlets, but the one at 6.43–6.48 ppm disappears, while the [La2L3] cage signal (6.30–6.38 ppm, blue circle in Fig. 1c) appears. [La2L3] species is the only one present at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 La
3 La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio (Fig. 1d). Next, with 1.75 equivalents of ligand (La
L ratio (Fig. 1d). Next, with 1.75 equivalents of ligand (La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.5), the signal at 6.15–6.24 ppm relative to [La2L4]2− species (orange circle in Fig. 1e), appears, confirming the presence of an equilibrium between the 2
3.5), the signal at 6.15–6.24 ppm relative to [La2L4]2− species (orange circle in Fig. 1e), appears, confirming the presence of an equilibrium between the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2
3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 cages. Both cages were still present after the addition of 2.0 equivalents of the ligand (Fig. 1f). Finally, the [La2L4]2− cage is the sole species present when an excess of ligand was added (2.50 equivalents, Fig. 1g). These experiments highlighted two new species at La
4 cages. Both cages were still present after the addition of 2.0 equivalents of the ligand (Fig. 1f). Finally, the [La2L4]2− cage is the sole species present when an excess of ligand was added (2.50 equivalents, Fig. 1g). These experiments highlighted two new species at La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratios lower than 2
L ratios lower than 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. These species are systems with a lower number of coordinated ligands. In particular, the predominant species, as shown in Fig. 1c (purple), when the La
2. These species are systems with a lower number of coordinated ligands. In particular, the predominant species, as shown in Fig. 1c (purple), when the La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio is 2
L ratio is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, may be the [La2L2]2+ system, whereas the secondary species (magenta) observed in the first two spectra (Fig. 1a and b) appears only at an La
2, may be the [La2L2]2+ system, whereas the secondary species (magenta) observed in the first two spectra (Fig. 1a and b) appears only at an La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio below 2
L ratio below 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, i.e. when the La3+ ion is in strong excess compared to the ligand, suggesting that this species may be the [La2L]4+ complex. This [La2L]4+ species, because of its higher positive charge, appears at lower fields. As the positive charge decreases, the α proton shifts to higher fields. DOSY-NMR spectra of the solutions with La
1, i.e. when the La3+ ion is in strong excess compared to the ligand, suggesting that this species may be the [La2L]4+ complex. This [La2L]4+ species, because of its higher positive charge, appears at lower fields. As the positive charge decreases, the α proton shifts to higher fields. DOSY-NMR spectra of the solutions with La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LA ratios of 2
LA ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, 2
0.5, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2
3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 are reported in Fig. 2. The observed diffusion coefficients are all very similar (ca. 2.5 × 10−10 m2 s−1, Table S1†), i.e., the [La2LA]4+, [La2LA2]2+, [La2LA3] and [La2LA4]2− species possess similar hydrodynamic radii. This similarity can be explained by the fact that the Ln⋯Ln distance is mainly governed by the size of the ligand.
4 are reported in Fig. 2. The observed diffusion coefficients are all very similar (ca. 2.5 × 10−10 m2 s−1, Table S1†), i.e., the [La2LA]4+, [La2LA2]2+, [La2LA3] and [La2LA4]2− species possess similar hydrodynamic radii. This similarity can be explained by the fact that the Ln⋯Ln distance is mainly governed by the size of the ligand.
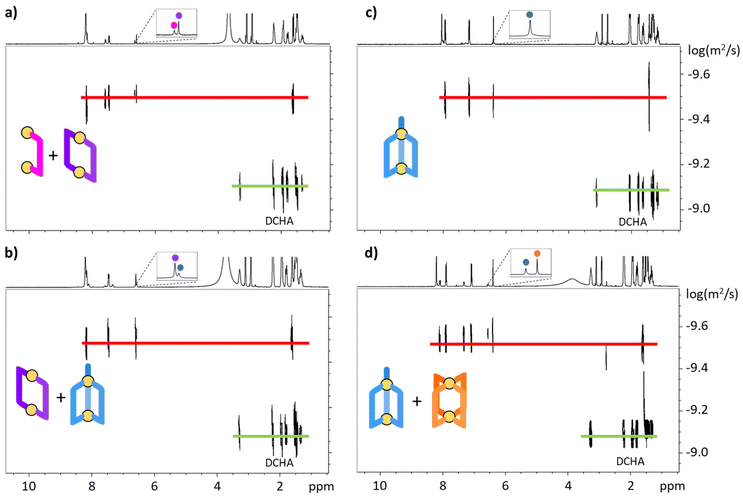 |
| | Fig. 2 DOSY-NMR spectra (25 °C, 400 MHz, DMF-d7) at an La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LA ratio of (a) 2 LA ratio of (a) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, (b) 2 0.5, (b) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, (c) 2 2, (c) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and (d) 2 3 and (d) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. DCHA is the dicyclohexylammonium cation. 4. DCHA is the dicyclohexylammonium cation. | |
In a similar manner, we conducted analyses using electrospray mass spectrometry (ESI-MS) in both positive and negative modes after adding 0.25, 0.5, 1.0, 1.5, 2.0, and 2.5 equivalents of the ligand LA, (Fig. S11†). Across all scenarios, a single prominent peak at 828 m/z was observed in positive mode. In negative mode, a peak at 1226 m/z was discernible only when 1.5, 2.0 and 2.5 equivalents were added. The agreement between experimental and simulated isotopic patterns confirms that the 828 m/z peak corresponds to the solvated species [La2LA2]2+ (Fig. 1h), whereas the negative mode peak is attributed to the quadruple-stranded cage [La2LA4]2− (Fig. 1i). Under conditions induced by the electrospray process, only these two species were detected, indicating that the other species identified through NMR likely undergo conversion into these two assemblies during the ionization process.
1H-NMR experiments allowed for the addition of one ligand at a time to the forming cage, starting from [La2L]4+ species and concluding with the [La2L4]2− cage. Fig. 3 summarizes the species present in solution at different La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LA ratios and their relative percentages. Fig. S12† reports the same quantities for LB and LM. A La
LA ratios and their relative percentages. Fig. S12† reports the same quantities for LB and LM. A La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 leads to the pure triple-stranded [La2L3], while a La
3 leads to the pure triple-stranded [La2L3], while a La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 gives a mixture of [La2L3] and [La2L4]2−. The pure quadruple-stranded cage can be obtained only in the presence of ligand excess. The stepwise formation constant (K) and overall stability constant (β) of each [La2LXy]n species were hence derived. In the presence of a slow equilibrium57 between the species, as in this case, formation constants can be obtained from 1H-NMR spectra via integration of peaks relative to the single species. Once the relative concentration of the species was obtained, these values were converted into concentrations by exploiting an internal standard (4-(4-formylphenoxy) benzaldehyde) according to eqn (1) and (2). The dialdehyde was chosen as internal standard in order to have a stable compound that does not react with the investigated systems and whose NMR signals do not overlap with those of the cages. This assures the presence of easily integrable signals, which reduce possible errors in area integration and, hence, in the formation constants determination. Concentrations at the equilibrium of the free ligand ([L2−]eq) and La3+ ions ([La3+]eq) were derived by considering the mass balance described in eqn (3) and (4), respectively:
4 gives a mixture of [La2L3] and [La2L4]2−. The pure quadruple-stranded cage can be obtained only in the presence of ligand excess. The stepwise formation constant (K) and overall stability constant (β) of each [La2LXy]n species were hence derived. In the presence of a slow equilibrium57 between the species, as in this case, formation constants can be obtained from 1H-NMR spectra via integration of peaks relative to the single species. Once the relative concentration of the species was obtained, these values were converted into concentrations by exploiting an internal standard (4-(4-formylphenoxy) benzaldehyde) according to eqn (1) and (2). The dialdehyde was chosen as internal standard in order to have a stable compound that does not react with the investigated systems and whose NMR signals do not overlap with those of the cages. This assures the presence of easily integrable signals, which reduce possible errors in area integration and, hence, in the formation constants determination. Concentrations at the equilibrium of the free ligand ([L2−]eq) and La3+ ions ([La3+]eq) were derived by considering the mass balance described in eqn (3) and (4), respectively:
| | 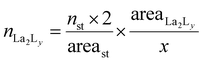 | (1) |
| | 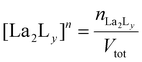 | (2) |
| | 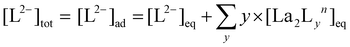 | (3) |
| | 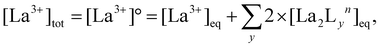 | (4) |
where
nLa2Ly is the number of moles of [La
2L
y]
n species;
nst is the number of moles of the standard; area
La2Ly is the area of the α-proton peak for the [La
2L
y]
n system; area
st is the area of the dialdehyde singlet due to proton H1 (Fig. S7
†);
y is the number of coordinated ligands and the values in square brackets are initial (°), added (ad) and equilibrium (eq) concentrations. Cage formation can be described stepwise,
i.e. considering the addition of a ligand at a time according to
eqn (5)–(8), as described in
Fig. 4.
| | 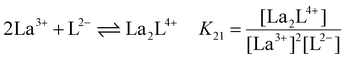 | (5) |
| | 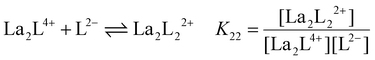 | (6) |
| | 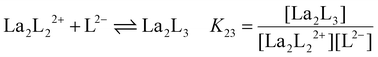 | (7) |
| | 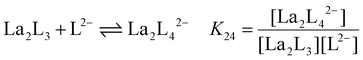 | (8) |
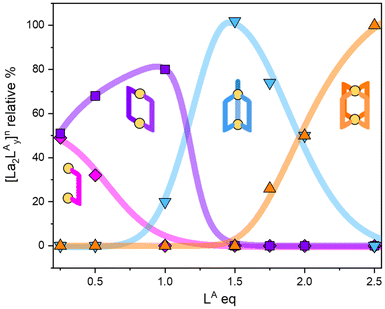 |
| | Fig. 3 Relative percentage of [La2LAy]n species (where y = 1, 2, 3, and 4 and n = 4+, 2+, 0, and 2−, respectively) as derived from 1H-NMR analyses following LA ligand additions. | |
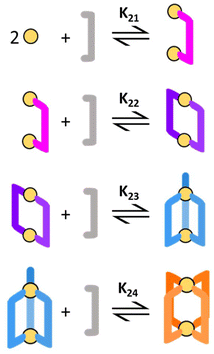 |
| | Fig. 4 Schematic of the stepwise formation process. | |
The stepwise (K2y) and overall (β2y) formation constants are reported in Table 1. The order of magnitude of the constants for the three different systems [La2LAy]n, [La2LBy]n and [La2LMy]n is nearly the same. Nevertheless, both constants are generally higher for [La2LAy]n. As is usually observed,58,59K2y decreases from the first to the final step. Indeed, the coordination of the first ligand to the metal ion is strongly favoured, while the coordination of successive ligands becomes more difficult with every step because of steric hindrance and charge effect considerations. Nevertheless, the overall formation constants β23 and β24 for the [La2L3] and [La2L4]2− cages are relatively high (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β23 = 15.0–16.7 and log
β23 = 15.0–16.7 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β24 = 17.8–19.8). For example, for mononuclear complexes such as Ln3+ tetrakis- and tris-(acetylacetonate), general overall values (in water) are log
β24 = 17.8–19.8). For example, for mononuclear complexes such as Ln3+ tetrakis- and tris-(acetylacetonate), general overall values (in water) are log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βLnL3 ≈ 13 and log
βLnL3 ≈ 13 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βLnL4 ≈ 15.60–63 Moreover, it has to be noted that the constants have been obtained in DMF, a highly coordinating solvent that can compete with the ligand in coordinating the La3+ ion.
βLnL4 ≈ 15.60–63 Moreover, it has to be noted that the constants have been obtained in DMF, a highly coordinating solvent that can compete with the ligand in coordinating the La3+ ion.
Table 1 Stepwise (K2y) and overall (β2y) formation constants for [La2Ly]n cages with ligands LA, LB and LM (where y = 1, 2, 3, and 4 and n = 4+, 2+, 0, and 2−, respectively)
| Constanta |
Equilibrium |
LA |
LB |
LM |
|
Values determined in DMF-d7 at 25 °C.
|
|
K
21
|
2La3+ + L2− ⇌ La2L4+ |
2.99 × 107 |
1.55 × 106 |
8.97 × 106 |
|
K
22
|
La2L4+ + L2− ⇌ La2L22+ |
3.62 × 105 |
6.36 × 104 |
1.35 × 105 |
|
K
23
|
La2L22+ + L2− ⇌ La2L3 |
4.60 × 103 |
1.33 × 104 |
9.26 × 102 |
|
K
24
|
La2L3 + L2− ⇌ La2L42− |
1.33 × 103 |
1.29 × 103 |
5.73 × 102 |
|
β
21
|
2La3+ + L2− ⇌ La2L4+ |
2.99 × 107 |
1.55 × 106 |
8.97 × 106 |
|
β
22
|
2La3+ + 2L2− ⇌ La2L22+ |
1.08 × 1013 |
9.86 × 1010 |
1.21 × 1012 |
|
β
23
|
2La3+ + 3L2− ⇌ La2L3 |
4.97 × 1016 |
1.31 × 1015 |
1.12 × 1015 |
|
β
24
|
2La3+ + 4L2− ⇌ La2L42− |
6.58 × 1019 |
1.27 × 1018 |
6.40 × 1017 |
Thermochemical analyses of the triple- versus quadruple-stranded cage equilibrium
Since the triple- and quadruple-stranded cages [La2LA3] and [La2LA4]2− are the species that have potential applications and the two systems that can be easily isolated by tuning the La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio, we focused on the thermochemical analysis of the equilibrium between these two cages. Using variable temperature 1H-NMR studies (VT-NMR), we determined the Gibbs free energy (ΔG), enthalpy (ΔH) and entropy (ΔS) differences of the equilibrium between [La2L3] and [La2L4]2− (eqn (8)) for the three ligands LA, LB and LM. A series of 1H-NMR spectra were recorded between 313 and 233 K (Fig. S14–S16†) with a La
L ratio, we focused on the thermochemical analysis of the equilibrium between these two cages. Using variable temperature 1H-NMR studies (VT-NMR), we determined the Gibbs free energy (ΔG), enthalpy (ΔH) and entropy (ΔS) differences of the equilibrium between [La2L3] and [La2L4]2− (eqn (8)) for the three ligands LA, LB and LM. A series of 1H-NMR spectra were recorded between 313 and 233 K (Fig. S14–S16†) with a La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. The equilibrium constant K24 at different temperatures was determined using eqn (1)–(4). K24 values were plotted as a function of the inverse of temperature (1/T) (Fig. 5a) and fitted with an expanded van't Hoff model64 (see ESI† for more details) to derive ΔH and ΔS. The ΔG, ΔH and TΔS of the reaction are reported in Fig. 5b. In all the three cases (LA, LB, and LM), over the range of studied temperatures, the addition of a fourth ligand to [La2L3] affording [La2L4]2− is endothermic, entropy driven and exergonic. Hence, the formation of a quadruple-stranded helicate from a triple-stranded one is a spontaneous process stabilized by the favourable entropy factor, which predominates over the unfavourable enthalpy effect. Indeed, in this case, the high entropy value could be mainly associated with the displacement of solvent molecules.
4. The equilibrium constant K24 at different temperatures was determined using eqn (1)–(4). K24 values were plotted as a function of the inverse of temperature (1/T) (Fig. 5a) and fitted with an expanded van't Hoff model64 (see ESI† for more details) to derive ΔH and ΔS. The ΔG, ΔH and TΔS of the reaction are reported in Fig. 5b. In all the three cases (LA, LB, and LM), over the range of studied temperatures, the addition of a fourth ligand to [La2L3] affording [La2L4]2− is endothermic, entropy driven and exergonic. Hence, the formation of a quadruple-stranded helicate from a triple-stranded one is a spontaneous process stabilized by the favourable entropy factor, which predominates over the unfavourable enthalpy effect. Indeed, in this case, the high entropy value could be mainly associated with the displacement of solvent molecules.
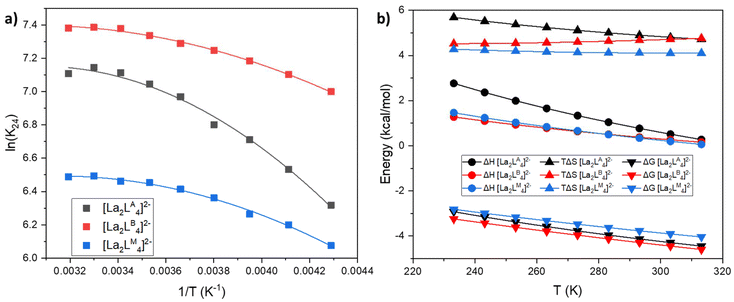 |
| | Fig. 5 (a) van't Hoff plot of K24 (eqn (8)) for the three cages fitted with the expanded van't Hoff model. (b) ΔG, ΔH and TΔS. | |
First, the coordination of the chelating bis-β-diketonate ligand releases two solvent molecules for each ligand, increasing the entropy of the system (chelate effect). Secondly, it has been reported that solvent molecules bound to the metal ion experience reduced conformational, rotational, and translational degrees of freedom, resulting in lower entropy.65,66 Thus any process which releases solvent molecules from this type of strain results in an entropy increase. On the contrary, enthalpic contribution is positive within the investigated temperature range. These results are in line with the idea of the displacement of tightly bound solvent molecules around Ln ions. Indeed, DMF is a well-known coordinating solvent that requires energy input for displacement from the coordination sphere of the metal ion by a ligand. Hence, although the reaction requires an input of energy in the form of heat (positive ΔH), the increase in disorder (positive ΔS) makes the overall process energetically favourable.
DFT thermochemical analyses of step-by-step ligand association
In coordination-driven self-assembly, the formation of metallo-supramolecular ensembles is typically explained by the enthalpic stabilization resulting from the formation of metal–ligand bonds.1 However, in the [La2L3] to [La2L4]2− equilibrium (eqn (8)), the enthalpic factor is unfavourable, making the reaction primarily entropy-driven. As a matter of fact, gas-phase studies on Pd(II) coupled with pyridine-based ligands have shown that enthalpic stabilization decreases as the number of ligands coordinated to the metal increases, favouring the formation of unsaturated structures.67 To better evaluate the roles of the enthalpic and entropic factors in step-by-step ligand coordination, we performed DFT thermochemical calculations involving the explicitly coordinated DMF solvent. Fig. 6 reports the DFT optimized structures of four DMF solvated [La2LAy(DMF)16−4y]n species (where y = 1, 2, 3, and 4 and n = 4+, 2+, 0, and 2−, respectively), see ESI† for computational details. The DFT optimized structures of [La2LBy(DMF)16−4y]n and [La2LMy(DMF)16−4y]n are reported in Fig. S18.† We considered only 8-coordinated species. This is supported by the fact that in Ln3+ DMF solutions, the dominant species is the Ln(DMF)83+ complex, although it must be outlined that for lighter Ln3+ ions, a solvation equilibrium involving Ln(DMF)93+ takes place.68 In fact, we previously isolated and characterized single crystal XRD [Eu2L4]2− cages with different coordination environments: a first structure with both Eu ions 8-coordinated by four ligands,34 a second structure with both Eu ions 9-coordinated by four ligands and one solvent molecule,36 and a third structure with one Eu ion 8-coordinated by four ligands while the other 9-coordinated by four ligands and one solvent molecule.37 Moreover, previous DFT calculations36 showed that this extra solvent molecule has a binding energy close to 8 kcal mol−1, suggesting that it can be easily lost in solution. Fig. 6b illustrates that for the solvated [La2L2(DMF)8]2+ species, two different isomers are possible: cis-[La2L2(DMF)8]2+ with a saddle shape and trans-[La2L2(DMF)8]2+ with the two ligands almost lying on the same plane. Calculations showed that for the LA ligand, cis-[La2L2(DMF)8]2+ is more stable (4.5 kcal mol−1), while for the LM and LB ligands, the stabilization of the cis isomer is below 2 kcal mol−1. Consequently, it can be inferred that both isomers coexist in solution at least for the systems based on LM and LB. Unfortunately, [La2Ly(DMF)16−4y]n structures contain too many atoms to perform DFT thermochemical analyses in terms of Hessian computational cost. Therefore, we used a smaller model system of a mononuclear complex with acetylacetonate (acac). [La(acac)y(DMF)8−2y]n complexes were optimized using PBE functional with the inclusion of implicit solvent effects (COSMO model) and dispersion corrections (Grimme model). Thermodynamic parameters (H, S and G) were calculated for each optimized species involved in eqn (9)–(12). ΔH, ΔS and ΔG associated with a specific reaction were obtained in accordance with Hess's law. Additional computational details are reported in the ESI.†| | | La(DMF)83+ + acac− ⇌ La(acac)(DMF)62+ + 2DMF | (9) |
| | 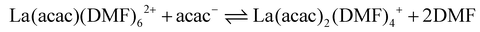 | (10) |
| | 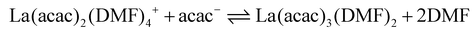 | (11) |
| | | La(acac)3(DMF)2 + acac− ⇌ La(acac)4− + 2DMF | (12) |
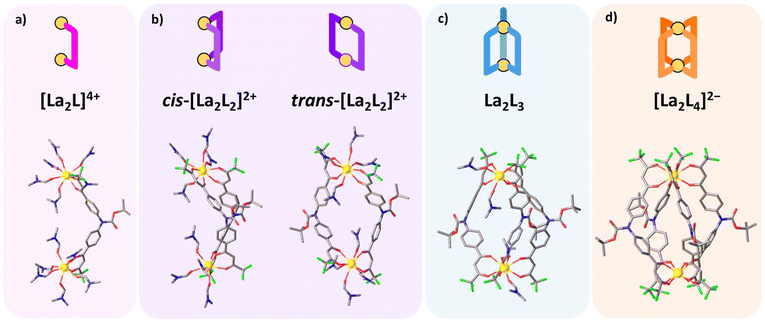 |
| | Fig. 6 DFT optimized structures for DMF solvated [La2LAy(DMF)16−4y]n species (where y = 1, 2, 3, and 4 and n = 4+, 2+, 0, and 2−, respectively). (a) [La2LA(DMF)12]4+, (b) cis-[La2LA2(DMF)8]2+ and trans-[La2LA2(DMF)8]2+, (c) [La2LA3(DMF)4], (d) [La2L4]2−. Red, blue, grey and green sticks represent O, N, C, and F atoms, respectively. The yellow spheres are La atoms. H atoms are omitted for clarity. | |
First, we applied the model to the equilibrium between the tris- and the tetrakis-chelate (eqn (12)), the analogue of eqn (8) that describes the equilibrium between the triple- and quadruple-stranded cages. Fig. 7a shows the calculated values of TΔS, ΔH and ΔG of the reaction in eqn (12) within the analysed temperature range. The reaction is energetically favoured. As the studied model is different from the experimental one, the numerical values differ, but the trend of the three quantities (Fig. 7a) follow the experimental models, as shown in Fig. 5: by increasing the temperature, their values smoothly decrease. Moreover, as experimentally found, the main driving force for negative ΔG is the entropic factor. These findings confirm that the smaller model system satisfactorily reproduces the experimental trends. Hence, the same calculations have been extended to other equilibria (eqn (9)–(11)). Fig. 7b–d depict the values of TΔS, ΔH and ΔG for the four reactions (eqn (9)–(12)), detailing the step-by-step association of the acac ligand with solvated La(DMF)83+. The trends observed in ΔG indicate a decrease in stepwise formation constants from the first to the final ligand association, as experimentally observed (Table 1). Additionally, as previously discussed, enthalpic gain decreases as the number of ligands coordinated to the metal increases. The trends in ΔH and TΔS further illustrate that for the first ligand association, enthalpic stabilization plays a more significant role than the entropic factor. However, starting from the second ligand association, entropic contribution becomes comparable to ΔH, and finally, it becomes the dominant stabilizing factor for both the third and fourth ligand associations.
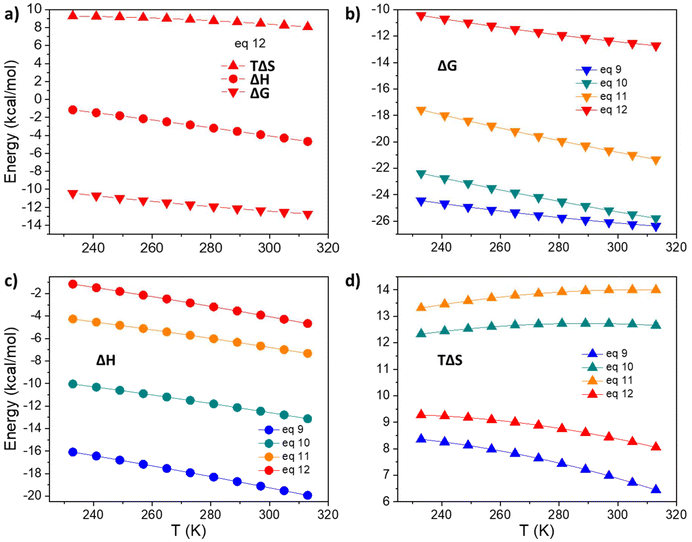 |
| | Fig. 7 Thermochemical parameters derived from the DFT calculations. (a) TΔS, ΔH and ΔG for the equilibrium of eqn (12). (b) ΔG for the four equilibria of eqn (9)–(12). (c) ΔH for the four equilibria of eqn (9)–(12). (d) TΔS for the four equilibria of eqn (9)–(12). | |
Experimental
See ESI.†
Conclusions
The systematic study of three different triple- and quadruple-stranded cages with the general formula [La2L3] and [La2L4]2− provided valuable insights into the formation process of these metallo-supramolecular systems and interconversion between the triple- and quadruple-stranded cages. The study involved tracking the different species formed during the self-assembly pathway through 1H-NMR analyses, which led to the identification of four species: [La2L]4+, [La2L2]2+, [La2L3], and [La2L4]2−. The subsequent determination of association constants for each chemical system revealed that [La2L3] and [La2L4]2− are the most stable. Variable temperature 1H-NMR studies provided valuable thermodynamic data, showing that the transition from the triple-stranded to the quadruple-stranded cage is endothermic, entropy-driven, and energetically favourable. The obtained high entropy values were attributed to the displacement of solvent molecules, emphasizing the importance of the coordination environment. To delve deeper into this aspect, DFT thermochemical calculations were performed on smaller model systems, which successfully reproduced experimental trends and provided insights into the contributions of enthalpic and entropic stabilization in stepwise ligand association.
Author contributions
Maria Rando: investigation, formal analysis, original draft, writing – review and editing. Alice Carlotto: investigation, formal analysis, writing – review and editing. Silvia Carlotto: investigation, formal analysis, writing – review and editing. Roberta Seraglia: investigation, formal analysis, writing – review and editing. Marzio Rancan: conceptualization, investigation, formal analysis, funding acquisition, writing – original draft, review and editing. Lidia Armelao: conceptualization, funding acquisition, supervision, writing – review and editing.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
M. R. thanks the National Research Council for “PROGETTI@CNR P@CNR_01_TerMoSmart”, “FOE2020 Capitale naturale e risorse per il futuro dell'Italia”, “FOE2022 FuturRaw” and the research project “nuovi Concetti, mAteriali e tecnologie per l'iNtegrazione del fotoVoltAico negli edifici in uno scenario di generazione diffuSa” (CANVAS), funded by the Italian Ministry of Environment and Energy Security, through the research fund for the Italian Electrical System (type-A call, published in G. U. R. I. no. 192 on 18-08-2022). L. A. thanks the University of Padova P-DiSC#01-BIRD2021 for financial support. M. Rando thanks the Department of Chemical Sciences and Materials Technologies of the National Research Council for providing financial support through a Ph.D. scholarship.
References
- S. Pullen, J. Tessarolo and G. H. Clever, Increasing structural and functional complexity in self-assembled coordination cages, Chem. Sci., 2021, 12, 7269–7293 RSC.
- D. A. Poole, E. O. Bobylev, S. Mathew and J. N. H. Reek, Entropy directs the self-assembly of supramolecular palladium coordination macrocycles and cages, Chem. Sci., 2022, 13, 10141–10148 RSC.
- S. Takahashi, S. Iuchi, S. Hiraoka and H. Sato, Theoretical and computational methodologies for understanding coordination self-assembly complexes, Phys. Chem. Chem. Phys., 2023, 25, 14659–14671 RSC.
- M. Yoneya, T. Yamaguchi, S. Sato and M. Fujita, Simulation of metal-ligand self-assembly into spherical complex M 6L 8, J. Am. Chem. Soc., 2012, 134, 14401–14407 CrossRef CAS PubMed.
- Y. Tsujimoto, T. Kojima and S. Hiraoka, Rate-determining step in the self-assembly process of supramolecular coordination capsules, Chem. Sci., 2014, 5, 4167–4172 RSC.
- K. Uehara, K. Kasai and N. Mizuno, Syntheses and characterizations of palladium-based molecular triangle/square compounds and hybrid composites with polyoxometalates, Inorg. Chem., 2007, 46, 2563–2570 CrossRef CAS.
- M. Schweiger, S. R. Seidel, A. M. Arif and P. J. Stang, Solution and solid state studies of a triangle-square equilibrium: Anion-induced selective crystallization in supramolecular self-assembly, Inorg. Chem., 2002, 41, 2556–2559 CrossRef CAS.
- M. Fujita,
et al., On the structure of transition-metal-linked molecular squares, Chem. Commun., 1996, 1535–1536, 10.1039/CC9960001535.
- T. Weilandt, R. W. Troff, H. Saxell, K. Rissanen and C. A. Schalley, Metallo-supramolecular self-assembly: The case of triangle-square equilibria, Inorg. Chem., 2008, 47, 7588–7598 CrossRef CAS PubMed.
- M. Han,
et al., Light-Controlled Interconversion between a Self-Assembled Triangle and a Rhombicuboctahedral Sphere, Angew. Chem., Int. Ed., 2016, 55, 445–449 CrossRef CAS PubMed.
- R. G. DiNardi,
et al., Visible-Light-Responsive Self-Assembled Complexes: Improved Photoswitching Properties by Metal Ion Coordination, Angew. Chem., 2022, 134, e202205701 CrossRef.
- A. Stephenson, S. P. Argent, T. Riis-Johannessen, I. S. Tidmarsh and M. D. Ward, Structures and dynamic behavior of large polyhedral coordination cages: An unusual cage-to-cage interconversion, J. Am. Chem. Soc., 2011, 133, 858–870 CrossRef CAS.
- M. Rancan,
et al., Self-assembly of a constitutional dynamic library of Cu(II) coordination polygons and reversible sorting by crystallization, Dalton Trans., 2013, 42, 7534–7538 RSC.
- M. Scherer, D. L. Caulder, D. W. Johnson and K. N. Raymond, Triple Helicate—Tetrahedral Cluster Interconversion Controlled by Host–Guest Interactions, Angew. Chem., Int. Ed., 1999, 38, 1587–1592 CrossRef PubMed.
- M. Rancan,
et al., Double level selection in a constitutional dynamic library of coordination driven supramolecular polygons, Inorg. Chem., 2014, 53, 7276–7287 CrossRef CAS PubMed.
- V. Sivalingam, M. Parbin, S. Krishnaswamy and D. K. Chand, Cage-To-Cage Transformations in Self-Assembled Coordination Cages Using “Acid/Base” or “Guest Binding-Induced Strain” as Stimuli, Angew. Chem., Int. Ed., 2024, 63, e202403711 CrossRef CAS PubMed.
- B. Kilbas, S. Mirtschin, R. Scopelliti and K. Severin, A solvent-responsive coordination cage, Chem. Sci., 2012, 3, 701–704 CAS.
- E. Benchimol, B. N. T. Nguyen, T. K. Ronson and J. R. Nitschke, Transformation networks of metal–organic cages controlled by chemical stimuli, Chem. Soc. Rev., 2022, 51, 5101–5135 CAS.
- R. G. Siddique,
et al., The kinetics and mechanism of interconversion within a system of [Fe2L3]4+ helicates and [Fe4L6]8+ cages, Chem. Commun., 2021, 57, 4918–4921 CAS.
- R. G. Siddique,
et al., Controlling the Complexity and Interconversion Mechanisms in Self-Assembled [Fe2L3]4+ Helicates and [Fe4L6]8+ Cages, Angew. Chem., Int. Ed., 2022, 61, e202115555 CAS.
- K. H. Yim,
et al., Helicate-to-tetrahedron transformation of chiral lanthanide supramolecular complexes
induced by ionic radii effect and linker length, Commun. Chem., 2021, 4(1), 1–10 Search PubMed.
- D. J. Bell, L. S. Natrajan and I. A. Riddell, Design of lanthanide based metal–organic polyhedral cages for application in catalysis, sensing, separation and magnetism, Coord. Chem. Rev., 2022, 472, 214786 CAS.
- X. Z. Li, C. B. Tian and Q. F. Sun, Coordination-Directed Self-Assembly of Functional Polynuclear Lanthanide Supramolecular Architectures, Chem. Rev., 2022, 122, 6374–6458 CrossRef CAS PubMed.
- R. W. Saalfrank, H. Maid and A. Scheurer, Supramolecular Coordination Chemistry: The Synergistic Effect of Serendipity and Rational Design, Angew. Chem., Int. Ed., 2008, 47, 8794–8824 CrossRef CAS.
- J. K. Clegg, F. Li and L. F. Lindoy, Oligo-β-diketones as versatile ligands for use in metallo-supramolecular chemistry: Recent progress and perspectives, Coord. Chem. Rev., 2022, 455, 214355 CrossRef CAS.
- J. K. Clegg,
et al., New discrete and polymeric supramolecular architectures derived from dinuclear (bis-β-diketonato)copper(II) metallocycles, Dalton Trans., 2006, 3977–3984, 10.1039/B606523F.
- J. K. Clegg,
et al., Hierarchical Self-Assembly of a Chiral Metal–Organic Framework Displaying Pronounced Porosity, Angew. Chem., Int. Ed., 2010, 49, 1075–1078 CrossRef CAS PubMed.
- M. Rancan,
et al., A templating guest sorts out a molecular triangle from a dimer–trimer constitutional dynamic library, Chem. Commun., 2012, 48, 3115–3117 RSC.
- J. K. Clegg,
et al., Hierarchical assembly of discrete copper(II) metallo-structures from pre-assembled dinuclear (bis-β-diketonato)metallocycles and flexible difunctional co-ligands, Dalton Trans., 2013, 42, 14315–14323 RSC.
- F. Li, J. K. Clegg, L. F. Lindoy, R. B. MacQuart and G. V. Meehan, Metallosupramolecular self-assembly of a universal 3-ravel, Nat. Commun., 2011, 2(1), 1–5 Search PubMed.
- M. Rancan, G. Truccolo, A. Carlotto, S. Quici and L. Armelao, A Zn(II) Metallocycle as Platform to Assemble a 1D + 1D → 1D Polyrotaxane via π⋯π Stacking of an Ancillary Ligand, Inorganics, 2019, 7, 137 CAS.
- G. Truccolo,
et al., A Cu(II) metallocycle for the reversible self-assembly of coordination-driven polyrotaxane-like architectures, Dalton Trans., 2018, 47, 12079–12084 CAS.
- H. Ju, J. K. Clegg, K. M. Park, L. F. Lindoy and S. S. Lee, Formation of a dicopper platform based polyrotaxane whose string and bead are constructed from the same components, J. Am. Chem. Soc., 2015, 137, 9535–9538 CAS.
- M. Rancan,
et al., Adaptive helicity and chiral recognition in bright europium quadruple-stranded helicates induced by host-guest interaction, Cell Rep. Phys. Sci., 2022, 3, 100692 CAS.
- S. Carlotto, L. Armelao and M. Rancan, Helicate versus Mesocate in Quadruple-Stranded Lanthanide Cages: A Computational Insight, Int. J. Mol. Sci., 2022, 23, 10619 CrossRef CAS PubMed.
- M. Rancan,
et al., Dynamic lanthanide exchange between quadruple-stranded cages: the effect of ionic radius differences on kinetics and thermodynamics, Inorg. Chem. Front., 2022, 9, 4495–4505 RSC.
- I. Motta,
et al., Transparent and colour-neutral luminescent solar concentrators using bright Eu3+ supramolecular cages towards photovoltaic windows, J. Mater. Chem. A, 2024, 12, 22516–22527 RSC.
- G. Han,
et al., Preorganized helical chirality controlled homochiral self-assembly and circularly polarized luminescence of a quadruple-stranded Eu2L4 helicate, Dalton Trans., 2020, 49, 3312–3320 RSC.
- Y. B. Tan,
et al., Visible Circularly Polarized Luminescence of Octanuclear Circular Eu(III) Helicate, J. Am. Chem. Soc., 2020, 142, 17653–17661 CrossRef CAS PubMed.
- N. Suko, H. Itamoto, Y. Okayasu, N. Okura and J. Yuasa, Helix-mediated over 1 nm-range chirality recognition by ligand-to-ligand interactions of dinuclear helicates, Chem. Sci., 2021, 12, 8746–8754 RSC.
- A. P. Bassett,
et al., Highly luminescent, triple- and quadruple-stranded, dinuclear Eu, Nd, and Sm(III) lanthanide complexes based on bis-diketonate ligands, J. Am. Chem. Soc., 2004, 126, 9413–9424 CrossRef CAS.
- A. J. Brock, I. M. Etchells, E. G. Moore and J. K. Clegg, Dinuclear triple stranded phenyl-spaced 1,3-bis-β-diketonato lanthanide(III) complexes:
synthesis, structures and spectroscopy, Dalton Trans., 2021, 50, 4874–4879 RSC.
- R. Chen,
et al., Dinuclear helicate or mononuclear pincer lanthanide complexes from one ligand: stereo-controlled assembly and catalysis, Org. Chem. Front., 2021, 8, 2576–2582 RSC.
- X. Gao, H. Li, P. Chen, W. Sun and P. Yan, A series of triple-stranded lanthanide(III) helicates: Syntheses, structures and single molecular magnets, Polyhedron, 2017, 126, 1–7 CrossRef CAS.
- P. Chen,
et al., Crystallization of triple- and quadruple-stranded dinuclear bis-β-diketonate-Dy(III) helicates: single molecule magnetic behavior, CrystEngComm, 2015, 17, 7227–7232 RSC.
- H. Li, P. Chen, W. Sun, L. Zhang and P. Yan, Solvent triggered structural diversity of triple-stranded helicates: single molecular magnets, Dalton Trans., 2016, 45, 3175–3181 RSC.
- Y. Zhou,
et al., Point Chirality Controlled Diastereoselective Self-Assembly and Circularly Polarized Luminescence in Quadruple-Stranded Europium(III) Helicates, Inorg. Chem., 2020, 59, 12850–12857 CrossRef CAS.
- B. Li,
et al., Insight into the roles of structures and energy levels of mono- and bis-β-diketones on sensitizing Nd(III) NIR-luminescence, Dalton Trans., 2016, 45, 11459–11470 RSC.
- D. E. Barry,
et al., Chiral luminescent lanthanide complexes possessing strong (samarium, SmIII) circularly polarised luminescence (CPL), and their self-assembly into Langmuir–Blodgett films, Dalton Trans., 2019, 48, 11317–11325 RSC.
- N. Klangwart, C. Ruijs, C. S. Hawes, T. Gunnlaugsson and O. Kotova, Tripodal 1,3,5-benzenetricarboxamide ligand with dipicolinic acid units and its binding with Eu(III) ions, Supramol. Chem., 2022, 34, 10–19 CrossRef CAS.
- I. N. Hegarty, D. E. Barry, J. P. Byrne, O. Kotova and T. Gunnlaugsson, Formation of lanthanide luminescent di-metallic helicates in solution using a bis-tridentate (1,2,3-triazol-4-yl)-picolinamide (tzpa) ligand, Chem. Commun., 2023, 59, 6044–6047 RSC.
- Z. R. Luo,
et al., Assembly of Dy60 and Dy30 cage-shaped nanoclusters, Commun. Chem., 2020, 3(1), 1–9 CrossRef.
- Z. H. Zhu, J. M. Peng, H. L. Wang, H. H. Zou and F. P. Liang, Assembly Mechanism and Heavy Metal Ion Sensing of Cage-Shaped Lanthanide Nanoclusters, Cell Rep. Phys. Sci., 2020, 1, 100165 CrossRef CAS.
- H. L. Wang,
et al., Tracking the Stepwise Formation of the Dysprosium Cluster (Dy10) with Multiple Relaxation Behavior, Inorg. Chem., 2019, 58, 9169–9174 CrossRef CAS.
- M. H. Du,
et al., Counterintuitive Lanthanide Hydrolysis-Induced Assembly Mechanism, J. Am. Chem. Soc., 2022, 144, 5653–5660 CrossRef CAS.
- Y. L. Li, H. L. Wang, Z. H. Zhu, F. P. Liang and H. H. Zou, Recent advances in the structural design and regulation of lanthanide clusters: Formation and self-assembly mechanisms, Coord. Chem. Rev., 2023, 493, 215322 CrossRef CAS.
- I. R. Kleckner and M. P. Foster, An introduction to NMR-based approaches for measuring protein dynamics, Biochim. Biophys. Acta, Proteins Proteomics, 2011, 1814, 942–968 CrossRef CAS.
- M. A. Mir and M. W. Ashraf, Chelate formation and stability analysis of cobalt, nickel and copper with lomatiol, Arabian J. Chem., 2021, 14, 102930 CrossRef CAS.
- A. A. Amindzhanov, F. D. Dzhamoliddinov, S. M. Safarmamadov and D. A. Davlatshoeva, Renium(V) complexation with N-ethylthiourea, Russ. J. Inorg. Chem., 2017, 62, 1544–1547 CrossRef CAS.
- N. K. Dutt and P. Banyopadhyay, Chemistry of the lanthanons—XIII: The stabilities of the acetylacetonates, propionylacetonates and benzoylacetonates of La, Pr, Nd and Y, J. Inorg. Nucl. Chem., 1964, 26, 729–736 CrossRef CAS.
- Y. Albinsson,
et al., Solvent Extraction Studies of Lanthanide Acetylacetonates. Part III. Complexes formed by Tb, Ho, Tm and Lu, Acta Chem. Scand., 1989, 43, 919–925 CrossRef CAS.
- S. Misumi and N. Iwasaki, The Infrared Spectra and Some Properties of Tris-(acetylacetonato) Lanthanide(III) Complexes, Bull. Chem. Soc. Jpn., 1967, 40, 550–554 CrossRef CAS.
- R. M. Izatt, W. C. Fernelius, C. G. Haas and B. P. Block, Studies on coordination compounds.
XI. Formation constants of some tervalent ions and the thorium(IV) ion with the acetylacetonate ion, J. Phys. Chem., 1955, 59, 170–174 CrossRef CAS.
- C. G. Maier and K. K. Kelley, An equation for the representation of high-temperature heat content data, J. Am. Chem. Soc., 1932, 54, 3243–3246 CrossRef CAS.
- R. J. P. Williams, The stability of complex ions with special reference to hydration, J. Phys. Chem., 1954, 58, 121–126 CrossRef CAS.
- E. G. Moschetta, K. M. Gans and R. M. Rioux, Elucidating the roles of enthalpy, entropy, and donor atom in the chelate effect for binding different bidentate ligands on the same metal center, J. Catal., 2014, 309, 11–20 CrossRef CAS.
- S. Hiraoka, Unresolved Issues that Remain in Molecular Self-Assembly, Bull. Chem. Soc. Jpn., 2018, 91, 957–978 CrossRef CAS.
- C. Cossy and A. E. Merbach, Recent developments in solvation and dynamics of the lanthanide(III) ions, Pure Appl. Chem., 1988, 60, 1785–1796 CrossRef CAS.
|
| This journal is © the Partner Organisations 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Alice
Carlotto
a,
Alice
Carlotto
 a,
Silvia
Carlotto
a,
Silvia
Carlotto
 ab,
Roberta
Seraglia
ab,
Roberta
Seraglia
 c,
Marzio
Rancan
c,
Marzio
Rancan
 *b and
Lidia
Armelao
*b and
Lidia
Armelao
 ad
ad
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 1
L ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5).34,36,37 Using a Ln
2.5).34,36,37 Using a Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, [Ln2L3] triple-stranded helicate is formed. The possibility to control the formation of the two different systems [Ln2L3] and [Ln2L4]2− by simply tuning the Ln
3, [Ln2L3] triple-stranded helicate is formed. The possibility to control the formation of the two different systems [Ln2L3] and [Ln2L4]2− by simply tuning the Ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio prompted us to undertake a systematic study of cage formation, with the aim of investigating, not only qualitatively but also quantitatively, the different species and steps leading to their self-assembly.
L ratio prompted us to undertake a systematic study of cage formation, with the aim of investigating, not only qualitatively but also quantitatively, the different species and steps leading to their self-assembly.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5), two singlets (6.43–6.48 ppm and 6.36–6.42 ppm, given as a magenta and purple circle, respectively, in Fig. 1a) are visible at lower fields as compared to the signals relative to [La2L3] and [La2L4]2− cages. By further adding 0.25 equivalents (La
0.5), two singlets (6.43–6.48 ppm and 6.36–6.42 ppm, given as a magenta and purple circle, respectively, in Fig. 1a) are visible at lower fields as compared to the signals relative to [La2L3] and [La2L4]2− cages. By further adding 0.25 equivalents (La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the relative intensity of the two singlets changes toward the peak at a lower ppm value (Fig. 1b). Considering 1.00 ligand equivalent (La
1), the relative intensity of the two singlets changes toward the peak at a lower ppm value (Fig. 1b). Considering 1.00 ligand equivalent (La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), there are still two singlets, but the one at 6.43–6.48 ppm disappears, while the [La2L3] cage signal (6.30–6.38 ppm, blue circle in Fig. 1c) appears. [La2L3] species is the only one present at a 2
2), there are still two singlets, but the one at 6.43–6.48 ppm disappears, while the [La2L3] cage signal (6.30–6.38 ppm, blue circle in Fig. 1c) appears. [La2L3] species is the only one present at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 La
3 La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio (Fig. 1d). Next, with 1.75 equivalents of ligand (La
L ratio (Fig. 1d). Next, with 1.75 equivalents of ligand (La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L = 2
L = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.5), the signal at 6.15–6.24 ppm relative to [La2L4]2− species (orange circle in Fig. 1e), appears, confirming the presence of an equilibrium between the 2
3.5), the signal at 6.15–6.24 ppm relative to [La2L4]2− species (orange circle in Fig. 1e), appears, confirming the presence of an equilibrium between the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2
3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 cages. Both cages were still present after the addition of 2.0 equivalents of the ligand (Fig. 1f). Finally, the [La2L4]2− cage is the sole species present when an excess of ligand was added (2.50 equivalents, Fig. 1g). These experiments highlighted two new species at La
4 cages. Both cages were still present after the addition of 2.0 equivalents of the ligand (Fig. 1f). Finally, the [La2L4]2− cage is the sole species present when an excess of ligand was added (2.50 equivalents, Fig. 1g). These experiments highlighted two new species at La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratios lower than 2
L ratios lower than 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. These species are systems with a lower number of coordinated ligands. In particular, the predominant species, as shown in Fig. 1c (purple), when the La
2. These species are systems with a lower number of coordinated ligands. In particular, the predominant species, as shown in Fig. 1c (purple), when the La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio is 2
L ratio is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, may be the [La2L2]2+ system, whereas the secondary species (magenta) observed in the first two spectra (Fig. 1a and b) appears only at an La
2, may be the [La2L2]2+ system, whereas the secondary species (magenta) observed in the first two spectra (Fig. 1a and b) appears only at an La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio below 2
L ratio below 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, i.e. when the La3+ ion is in strong excess compared to the ligand, suggesting that this species may be the [La2L]4+ complex. This [La2L]4+ species, because of its higher positive charge, appears at lower fields. As the positive charge decreases, the α proton shifts to higher fields. DOSY-NMR spectra of the solutions with La
1, i.e. when the La3+ ion is in strong excess compared to the ligand, suggesting that this species may be the [La2L]4+ complex. This [La2L]4+ species, because of its higher positive charge, appears at lower fields. As the positive charge decreases, the α proton shifts to higher fields. DOSY-NMR spectra of the solutions with La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LA ratios of 2
LA ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, 2
0.5, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2
3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 are reported in Fig. 2. The observed diffusion coefficients are all very similar (ca. 2.5 × 10−10 m2 s−1, Table S1†), i.e., the [La2LA]4+, [La2LA2]2+, [La2LA3] and [La2LA4]2− species possess similar hydrodynamic radii. This similarity can be explained by the fact that the Ln⋯Ln distance is mainly governed by the size of the ligand.
4 are reported in Fig. 2. The observed diffusion coefficients are all very similar (ca. 2.5 × 10−10 m2 s−1, Table S1†), i.e., the [La2LA]4+, [La2LA2]2+, [La2LA3] and [La2LA4]2− species possess similar hydrodynamic radii. This similarity can be explained by the fact that the Ln⋯Ln distance is mainly governed by the size of the ligand.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LA ratio of (a) 2
LA ratio of (a) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, (b) 2
0.5, (b) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, (c) 2
2, (c) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and (d) 2
3 and (d) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. DCHA is the dicyclohexylammonium cation.
4. DCHA is the dicyclohexylammonium cation.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LA ratios and their relative percentages. Fig. S12† reports the same quantities for LB and LM. A La
LA ratios and their relative percentages. Fig. S12† reports the same quantities for LB and LM. A La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 leads to the pure triple-stranded [La2L3], while a La
3 leads to the pure triple-stranded [La2L3], while a La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 gives a mixture of [La2L3] and [La2L4]2−. The pure quadruple-stranded cage can be obtained only in the presence of ligand excess. The stepwise formation constant (K) and overall stability constant (β) of each [La2LXy]n species were hence derived. In the presence of a slow equilibrium57 between the species, as in this case, formation constants can be obtained from 1H-NMR spectra via integration of peaks relative to the single species. Once the relative concentration of the species was obtained, these values were converted into concentrations by exploiting an internal standard (4-(4-formylphenoxy) benzaldehyde) according to eqn (1) and (2). The dialdehyde was chosen as internal standard in order to have a stable compound that does not react with the investigated systems and whose NMR signals do not overlap with those of the cages. This assures the presence of easily integrable signals, which reduce possible errors in area integration and, hence, in the formation constants determination. Concentrations at the equilibrium of the free ligand ([L2−]eq) and La3+ ions ([La3+]eq) were derived by considering the mass balance described in eqn (3) and (4), respectively:
4 gives a mixture of [La2L3] and [La2L4]2−. The pure quadruple-stranded cage can be obtained only in the presence of ligand excess. The stepwise formation constant (K) and overall stability constant (β) of each [La2LXy]n species were hence derived. In the presence of a slow equilibrium57 between the species, as in this case, formation constants can be obtained from 1H-NMR spectra via integration of peaks relative to the single species. Once the relative concentration of the species was obtained, these values were converted into concentrations by exploiting an internal standard (4-(4-formylphenoxy) benzaldehyde) according to eqn (1) and (2). The dialdehyde was chosen as internal standard in order to have a stable compound that does not react with the investigated systems and whose NMR signals do not overlap with those of the cages. This assures the presence of easily integrable signals, which reduce possible errors in area integration and, hence, in the formation constants determination. Concentrations at the equilibrium of the free ligand ([L2−]eq) and La3+ ions ([La3+]eq) were derived by considering the mass balance described in eqn (3) and (4), respectively: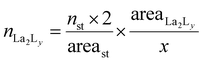
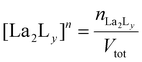
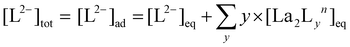
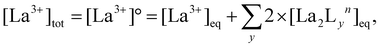
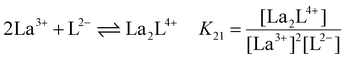
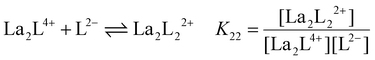
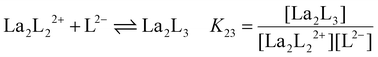
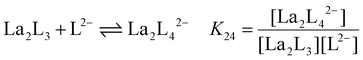

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β23 = 15.0–16.7 and log
β23 = 15.0–16.7 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β24 = 17.8–19.8). For example, for mononuclear complexes such as Ln3+ tetrakis- and tris-(acetylacetonate), general overall values (in water) are log
β24 = 17.8–19.8). For example, for mononuclear complexes such as Ln3+ tetrakis- and tris-(acetylacetonate), general overall values (in water) are log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βLnL3 ≈ 13 and log
βLnL3 ≈ 13 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βLnL4 ≈ 15.60–63 Moreover, it has to be noted that the constants have been obtained in DMF, a highly coordinating solvent that can compete with the ligand in coordinating the La3+ ion.
βLnL4 ≈ 15.60–63 Moreover, it has to be noted that the constants have been obtained in DMF, a highly coordinating solvent that can compete with the ligand in coordinating the La3+ ion.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio, we focused on the thermochemical analysis of the equilibrium between these two cages. Using variable temperature 1H-NMR studies (VT-NMR), we determined the Gibbs free energy (ΔG), enthalpy (ΔH) and entropy (ΔS) differences of the equilibrium between [La2L3] and [La2L4]2− (eqn (8)) for the three ligands LA, LB and LM. A series of 1H-NMR spectra were recorded between 313 and 233 K (Fig. S14–S16†) with a La
L ratio, we focused on the thermochemical analysis of the equilibrium between these two cages. Using variable temperature 1H-NMR studies (VT-NMR), we determined the Gibbs free energy (ΔG), enthalpy (ΔH) and entropy (ΔS) differences of the equilibrium between [La2L3] and [La2L4]2− (eqn (8)) for the three ligands LA, LB and LM. A series of 1H-NMR spectra were recorded between 313 and 233 K (Fig. S14–S16†) with a La![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L ratio of 2
L ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. The equilibrium constant K24 at different temperatures was determined using eqn (1)–(4). K24 values were plotted as a function of the inverse of temperature (1/T) (Fig. 5a) and fitted with an expanded van't Hoff model64 (see ESI† for more details) to derive ΔH and ΔS. The ΔG, ΔH and TΔS of the reaction are reported in Fig. 5b. In all the three cases (LA, LB, and LM), over the range of studied temperatures, the addition of a fourth ligand to [La2L3] affording [La2L4]2− is endothermic, entropy driven and exergonic. Hence, the formation of a quadruple-stranded helicate from a triple-stranded one is a spontaneous process stabilized by the favourable entropy factor, which predominates over the unfavourable enthalpy effect. Indeed, in this case, the high entropy value could be mainly associated with the displacement of solvent molecules.
4. The equilibrium constant K24 at different temperatures was determined using eqn (1)–(4). K24 values were plotted as a function of the inverse of temperature (1/T) (Fig. 5a) and fitted with an expanded van't Hoff model64 (see ESI† for more details) to derive ΔH and ΔS. The ΔG, ΔH and TΔS of the reaction are reported in Fig. 5b. In all the three cases (LA, LB, and LM), over the range of studied temperatures, the addition of a fourth ligand to [La2L3] affording [La2L4]2− is endothermic, entropy driven and exergonic. Hence, the formation of a quadruple-stranded helicate from a triple-stranded one is a spontaneous process stabilized by the favourable entropy factor, which predominates over the unfavourable enthalpy effect. Indeed, in this case, the high entropy value could be mainly associated with the displacement of solvent molecules.