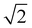DOI:
10.1039/D4QI01475H
(Research Article)
Inorg. Chem. Front., 2025,
12, 1257-1272
Aqueous phase synthesis and electronic spectroscopy of nanostructured layered double hydroxides †
Received
17th June 2024
, Accepted 5th December 2024
First published on 13th December 2024
Abstract
Herein, we proposed a green synthetic route based on coordination chemistry to produce nanostructured layered double hydroxides (LDHs). The synthesized NiAl-, NiFe- and ZnAl-LDHs exhibited similar morphologies and crystal structures. A possible mechanism for LDH formation was proposed based on pH-potentiometric titrations. Extensive electronic spectroscopy analyses, interpreted through the lens of ligand field theory, provided key insights into the formation mechanism of NiFe-LDH.
1. Introduction
Layered double hydroxides (LDHs), also known as hydrotalcite-like compounds, are a class of natural1 or synthetic2 two-dimensional materials3,4 that find many applications as ion exchangers, plastic additives, flame retardants and catalysts for steam reforming, since the last century.2 Nowadays, transition-metal-based LDHs have garnered significant research attention due to their promising electrochemical properties for energy storage and conversion applications.5–7 Furthermore, recent hypotheses suggest their potential role in the origins of life on Earth.8,9 Layered double hydroxide compounds are structurally derived from layered divalent metal hydroxides (e.g., Mg(OH)2) through the isomorphous substitution of a fraction of divalent metal species with trivalent ones.2 The resulting lattice consists of stacked positively charged metal hydroxide layers separated by charge-counterbalancing anions and water molecules.2 Hence, LDHs represent a broad family of layered materials with a common chemical composition, which can be summarized as follows:| | | [M1−x2+Mx3+(OH)2]x+A(x/n)n−·yH2O | (1) |
Here, M2+ (e.g., Mg2+, Ca2+, Fe2+, Ni2+, …) and M3+ (e.g., Al3+, Cr3+, Fe3+, …) represent divalent and trivalent metal species, respectively, which make up the hydroxide layers, while An− refers to inorganic or organic anions (e.g., Cl−, NO3−, CO32−, R-COO−, …) that are intercalated in the interlayer space.2 The coefficient x is defined as M3+/(M2+ + M3+) and typically takes values in the range of 0.2 to 0.33.2,10 For simplicity, in this study, we refer to these compounds as M2+ M3+-LDHs. The significant flexibility in the chemical composition of LDHs has led to the development of several synthetic approaches.2,11–19 However, the most commonly exploited chemical pathway for the synthesis of LHDs involves the slow reaction between a trivalent metal hydroxide (i.e., M(OH)3) and M2+ cations dissolved in an aqueous solution.11–14,19 Both the “urea hydrolysis” and co-precipitation methods are frequently used for this synthesis route.11–14,19 However, these procedures often require the use of autoclaves to achieve sufficiently high temperatures (typically around 150 °C) to ensure the complete conversion of M(OH)3 into LDHs.11–14 Moreover, the addition of chelating agents to the reaction mixture is pivotal for forming pure transition-metal LDH phases.12 Another common method for LDH synthesis involves conducting the reaction at a constant pH (usually pH ≈ 9 or 10) at which both metal ions precipitate simultaneously.2 Nanostructured LDH materials (i.e., single- or few-layer nanosheets) can eventually be obtained through a top-down approach by delaminating the bulk LDH material synthetized using one of the aforementioned procedures.6 The top-down approach involves the liquid phase-exfoliation4,20,21 of bulk LDH materials into an appropriate solvent. The most suitable delaminating solvent for LDHs is the toxic formamide.6,22,23 Alternatively, several bottom-up approaches have been proposed for the direct synthesis of nanostructured LDH materials.15–18,24 More specifically, the reverse microemulsion route has been used to synthesize nanostructured MgAl-LDHs, which can be easily incorporated into polymer matrices.15 However, the use of a water–isooctane emulsion raises concerns from both safety and environmental standpoints for practical applications. Tokudome et al. proposed a synthetic route for nanostructured NiAl- and NiFe-LDHs from an ethanol–water solution,17,18 but 1-chloro-2-propanol is produced as a byproduct,17,18,25 thus requiring a proper disposal being a halogenated compound. The aqueous miscible organic solvent treatment (AMOST) procedure yields nanostructured MgAl- and ZnAl-LDHs dispersible into non-polar hydrocarbons.16 However, AMOST is only limited to tetraborate anions in the LDH interlayer space. Noteworthily, Hibino and Kobayashi reported the synthesis and delamination in the water of lactate-intercalated LDHs.24 On the flip side, a massive amount of lactate (more than 20-fold the stoichiometric ratio) is required to achieve the synthesis of lactate-intercalated LDHs.24 Herein, we propose a fully aqueous and direct precipitation of nanostructured LDH compounds by exploiting the coordination chemistry of citric acid through an alternative synthetic route. Our synthetic approach is inspired by chemical bath deposition processes (CBD),26,27 which are widely utilized for metal oxide and sulphide film deposition for optoelectronic applications. Hence, our LDH synthesis process could be exploited for future production of mixed metal oxide films. The main advantage of our synthesis approach is that it is one-pot. In addition, different from other one-pot LDH synthesis approaches, the availability of metal cations, resulting from the hydrolysis of metal–citrate complexes, is the rate-limiting factor in the LDH formation process. This means that the stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) of metal–citrate complexes dictate the availability of cations, influencing the nucleation of LDH nanosheets. Hence, this study focuses on the formation mechanism of citrate intercalated LDHs probed by pH-potentiometric titrations coupled to ligand field analysis of the electronic transitions. We demonstrate that our method is straightforwardly applicable to nickel-based LDHs, and can also be applied to ZnAl-LDHs, with some restrictions. So far, the formation mechanism of LDHs has been probed through pH titrations exclusively for all-inorganic syntheses.11,13,19 Jaśkaniec et al.12 and Tokudome et al.17 performed pH vs. time characterizations of their LDH synthesis procedures, both of which exploit coordination chemistry. However, pH vs. time characterizations provide information only on the hydrolysis rate of the ammonium (or hydroxide) releasing agent used during the synthesis, and not on the actual formation mechanism of LDH materials. On the contrary, a pH titration allows external control of the equivalents of hydroxide ions supplied to the reaction environment, and therefore, provides insights into the reaction mechanism. These understandings can be useful in designing new or improving the existing synthetic processes. Herein, we report how citrate anions alter the formation mechanism of LDHs from the classical precipitation pathway to a hydrolytic polymerization of metal–citrate complexes. Lastly, by interpreting the electronic spectra of the reaction environment and the final LDH product through the lens of the ligand field theory, we report the values of ligand field strength and Racah parameters of Ni2+ and Fe3+ in LDH crystal lattices. Then, we critically discuss the obtained results and possible implications by considering the current knowledge on electronic spectroscopy of nickel hydroxides, ferric oxides, and related materials.28–42
β) of metal–citrate complexes dictate the availability of cations, influencing the nucleation of LDH nanosheets. Hence, this study focuses on the formation mechanism of citrate intercalated LDHs probed by pH-potentiometric titrations coupled to ligand field analysis of the electronic transitions. We demonstrate that our method is straightforwardly applicable to nickel-based LDHs, and can also be applied to ZnAl-LDHs, with some restrictions. So far, the formation mechanism of LDHs has been probed through pH titrations exclusively for all-inorganic syntheses.11,13,19 Jaśkaniec et al.12 and Tokudome et al.17 performed pH vs. time characterizations of their LDH synthesis procedures, both of which exploit coordination chemistry. However, pH vs. time characterizations provide information only on the hydrolysis rate of the ammonium (or hydroxide) releasing agent used during the synthesis, and not on the actual formation mechanism of LDH materials. On the contrary, a pH titration allows external control of the equivalents of hydroxide ions supplied to the reaction environment, and therefore, provides insights into the reaction mechanism. These understandings can be useful in designing new or improving the existing synthetic processes. Herein, we report how citrate anions alter the formation mechanism of LDHs from the classical precipitation pathway to a hydrolytic polymerization of metal–citrate complexes. Lastly, by interpreting the electronic spectra of the reaction environment and the final LDH product through the lens of the ligand field theory, we report the values of ligand field strength and Racah parameters of Ni2+ and Fe3+ in LDH crystal lattices. Then, we critically discuss the obtained results and possible implications by considering the current knowledge on electronic spectroscopy of nickel hydroxides, ferric oxides, and related materials.28–42
2. Results and discussion
2.1. Morphology and crystal structure
We investigated the particle morphology of NiFe-, NiAl- and ZnAl-LDHs synthesized from metal–citrate complexes and then dispersed them in water. All dispersions were made up of lamellar particles (i.e., nanosheets) that are ∼5–20 nm wide in the case of NiFe-LDH (Fig. 1a), ∼5 nm wide in the case of NiAl-LDH (Fig. S1a†) and ∼200–500 nm wide in the case of ZnAl-LDH (Fig. S1b†). The nanosheets are rarely found isolated, since they form micron-sized structures also visible under scanning electron microscopy imaging (Fig. 1b and c). The presence of vertically aligned nanosheets NiFe-LDH and ZnAl-LDH in the HRTEM image (Fig. S1c†) enabled us to estimate their thickness, which is in the 1–2 nm range, in agreement with our previous work, in which we produced citrate-intercalated NiFe-LDH nanosheets by coprecipitation.43 On the contrary, the NiAl-LDH sample does not present vertically aligned nanosheets. The detailed study of the dependence of the morphology of LDHs on the synthetic conditions lies beyond the scope of this work. The X-ray diffraction patterns of the citrate-intercalated NiAl- and NiFe-LDH powders are presented in Fig. 1d. Analogous diffraction patterns of NiAl- and NiFe-LDHs with variable metal ratios are presented in Fig. S2,† showing that our synthesis technique allows for a wide range of compositions in nickel-based LDH in the 0.14–0.33 range of x, being consistent with what was previously reported by B. Grégoire et al.10 On the flip side, the ZnAl-LDH phase appears to be feasible only for the x equal to 0.33, with some incidental ZnO contamination, as illustrated in Fig. 1e. While, as illustrated in Fig. 1f, the synthesis of ZnAl-LDH with an x value lower than 0.25, mainly leads to the formation of wurtzite type ZnO. For the sake of clarity, in LDH XRD patterns, we refer to the Miller indices of the hydrotalcite crystal structure (i.e., natural carbonate-intercalated MgAl-LDH, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group). This indexing allows an easier comparison with the past literature patterns of the synthetic LDH materials and LDH minerals (Table S3†).1,44–46 The LDH diffraction patterns can be divided into three different regions. At scattering angles (2θ) below 30°, the “basal reflections” appear. These reflections are ascribed to the (00l) crystallographic planes, i.e., planes parallel to the hydroxide layers and perpendicular to the unit cell c axis.47 Thus, the 2θ position of the basal reflections reveals the unit cell c axis of LDHs (by the weighted mean of d00l lattice parameters, as described in ESI section 4†). Our analyses provide the following c axis lengths for the citrate-intercalated LDHs: 3.669 nm for NiAl-LDH, 3.680 nm for NiFe-LDH, and 3.665 nm for ZnAl-LDH. The thickness of one hydroxide layer plus one interlayered distance, called “basal spacing”, is equal to one third the length of the c axis (in the, R
m space group). This indexing allows an easier comparison with the past literature patterns of the synthetic LDH materials and LDH minerals (Table S3†).1,44–46 The LDH diffraction patterns can be divided into three different regions. At scattering angles (2θ) below 30°, the “basal reflections” appear. These reflections are ascribed to the (00l) crystallographic planes, i.e., planes parallel to the hydroxide layers and perpendicular to the unit cell c axis.47 Thus, the 2θ position of the basal reflections reveals the unit cell c axis of LDHs (by the weighted mean of d00l lattice parameters, as described in ESI section 4†). Our analyses provide the following c axis lengths for the citrate-intercalated LDHs: 3.669 nm for NiAl-LDH, 3.680 nm for NiFe-LDH, and 3.665 nm for ZnAl-LDH. The thickness of one hydroxide layer plus one interlayered distance, called “basal spacing”, is equal to one third the length of the c axis (in the, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group).2 These results are consistent with those from the past literature on citrate-intercalated MgAl-, NiAl- and ZnAl-LDHs synthetized by the anion exchange or the dissolution/precipitation routes.44–46 Instead, the second region, in the 2θ range of 30° to 55°, displays reflections from (0kl) and (h0l) crystallographic planes.
m space group).2 These results are consistent with those from the past literature on citrate-intercalated MgAl-, NiAl- and ZnAl-LDHs synthetized by the anion exchange or the dissolution/precipitation routes.44–46 Instead, the second region, in the 2θ range of 30° to 55°, displays reflections from (0kl) and (h0l) crystallographic planes.
 |
| | Fig. 1 (a) High resolution transmission electron microscopy image of citrate-intercalated NiFe-LDH nanosheets. (b) Transmission electron microscopy image of the citrate-intercalated NiFe-LDH aggregates of nanosheets (a few isolated nanosheets are visible in the top left corner). (c) Scanning electron microscopy image of the lamellar micron-sized structures in a NiFe-LDH powder. (d) Powder X-ray diffraction pattern of the citrate-intercalated NiAl- and NiFe-LDH pellets. (e) Powder X-ray diffraction pattern of the citrate-intercalated ZnAl-LDH pellet synthesized with an initial Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio of 2 Al ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. (f) Powder X-ray diffraction pattern of the citrate-intercalated ZnAl-LDH pellet synthesized with an initial Zn 1. (f) Powder X-ray diffraction pattern of the citrate-intercalated ZnAl-LDH pellet synthesized with an initial Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio of 3 Al ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Reflection marker with an asterisk refers to wurtzite type ZnO (PANISC: 98-002-6170, P63mc space group). The incident X-ray radiation used in XRD pattern is Cu Kα. 1. Reflection marker with an asterisk refers to wurtzite type ZnO (PANISC: 98-002-6170, P63mc space group). The incident X-ray radiation used in XRD pattern is Cu Kα. | |
The shape of these reflections is indicative of faults in the layer stacking.48 In fact, sharp and well-defined reflections in this region are characteristics of highly crystalline LDHs.48 On the contrary, our LDHs show an asymmetric broad reflection covering the whole 30–55°, 2θ region. This feature is indicative of a turbostratic disorder, i.e., randomly slid and twisted layers, also visible in Fig. 1a, in which two NiFe-LDH nanosheets are stacked on top of each other. Turbostraticity is a characteristic property of α-Ni(OH)2,29 LDHs intercalated with bulky anions,44,45,48–50 as well as other defective two-dimensional materials.51,52 The third region in the LDHs diffraction pattern is located at 2θ angles above 55°. This region contains the (110) reflection, from which the unit cell parameter a is obtained2 (ESI section 4†). Crystallographic parameters of the citrate-intercalated LDHs are summarized in Table 1.
Table 1 Basal spacing and unit cell parameter dimensions of citrate-intercalated LDHs calculated according to Bragg's law
| Sample |
x
|
Basal spacing (nm) |
a axis (nm) |
c axis (nm) |
| NiAl-LDH |
0.25 |
1.223 |
0.3019 |
3.669 |
| NiFe-LDH |
0.25 |
1.227 |
0.3053 |
3.680 |
| ZnAl-LDH |
0.33 |
1.222 |
0.3056 |
3.665 |
2.2. pH-potentiometric titrations
In this section, we describe the hydrolytic behaviour of monometallic and bimetallic solutions, with and without dissolved citrate, studied using pH-potentiometric titrations. Titration curves are expressed as a function of the hydroxylation rate (R), i.e., the added moles of hydroxide with respect to the total moles of metal cations. The total metal/citrate molar ratio is set to 1/1, whereas the ratio between metals of bimetallic solutions was chosen to reflect the stoichiometry of the corresponding hydroxide-carbonate minerals (i.e., natural LDHs):1 1/3 for aluminium–nickel solutions, 1/3 for iron–nickel solutions and 1/2 for aluminium–zinc solutions, corresponding to takovite, reevesite and zaccagnaite minerals, respectively.1 We also deliberately chose not to add any amount of strong acid, since it can bring an unnecessary source of error in the R determination from titration profiles, while also making less straightforward the comparison with previously published literature.11,13,53 Hence the initial pH in the titration profiles will be determined by the Lewis acidity of the metal cations involved.
2.2.1. Hydrolytic behaviour of Al3+, Fe3+, Ni2+, Zn2+ and their bimetallic solutions.
The hydrolytic behaviour of monometallic and bimetallic solutions has been extensively characterized in the past.11,13,19 However, we decided to briefly report our results since they serve as baselines for titrations of metal–citrate solutions and as validation experiments. The titration profile of the Al(NO3)3 solution presents three equivalent points, located at 0.04, 2.65 and 2.97 RAl3+, related to the formation of [Al2(OH)2]4+, Keggin's clusters, and the complete precipitation of Al(OH)3, respectively.54–56 The titration profile of the Fe(NO3)3 solution presents three closely spaced equivalent points, averaged at 2.97 RFe3+, related to the complete precipitation of ferric oxyhydroxides. Furthermore, the three different equivalent points are located at 2.90, 2.97 and 3.05 RFe3+ and are related to β-FeOOH, ferrihydrite (i.e., FeOOH·xH2O) and α-FeOOH, respectively.13,57,58 The titration profile of the Ni(CH3CO2) solution presents two equivalent points located at 0.06 and 1.89 RNi2+ related to the condensation of [Ni(H2O)6]2+ cations into dimers and tetramers, and the precipitation α-Ni(OH)2 phase, respectively.13,29,59,60 The titration profile of the Zn(NO3)2 solution presents one equivalent point located at 2.01 RZn2+, confirming the precipitation of the stoichiometric Zn(OH)2, probably present in its most insoluble polymorph (ε-Zn(OH)2).61 All titration profiles of bimetallic solutions present two equivalent points, namely E1 and E2, separated by a buffer region. As illustrated in Table 2, E1 is always delayed compared to its expected RM3+ value, whereas E2 precedes its expected RM2+ value, as previously described by Braterman's and Carteret's groups, regarding the formation mechanism of LDHs.11,13,53 Moreover, the more the LDH phase is favoured, the more E1 is delayed and less sharp.11,13,53 Titration profiles of the monometallic and bimetallic solutions without dissolved citrate are presented in Fig. S3.†
Table 2 Hydroxylation ratios (R) of equivalent points observed in metal-citrate solutions
| Cations |
Mole ratio |
E
1
|
E
2
|
| Al3+ |
— |
2.97 RAl3+ |
— |
| Fe3+ |
— |
2.97 RFe3+ |
— |
| Ni2+ |
— |
— |
1.89 RNi2+ |
| Zn2+ |
— |
— |
2.01 RZn2+ |
| Al3+, Ni2+ |
1/3 |
∼1.1 R |
2.11 R |
| Normalized |
|
∼4.4 RAl3+ |
∼1.3 RNi2+ |
| Fe3+, Ni2+ |
1/3 |
0.79 R |
2.16 R |
| Normalized |
|
3.16 RFe3+ |
1.82 RNi2+ |
| Al3+, Zn2+ |
1/2 |
1.05 R |
2.28 R |
| Normalized |
|
3.15 RAl3+ |
1.84 RZn2+ |
2.2.2. Hydrolytic behaviour of metal–citrate solutions.
When citrate anions are present, metal–citrate coordination compounds are formed. The nature of such metal–citrate complexes depends both on the solution pH and on the metal/citrate ratio.61–85 In the following titrations and speciation models, citric acid (i.e., C6H8O7) is considered as tetraprotic (i.e., H4Cit), having the following acidity constants:86 pKa1 = 3.13, pKa2 = 4.76, pKa3 = 6.40 and pKa4 = 14.4. This means that the three carboxylic groups of citric acid are readily deprotonated in water, whereas the alcoholic group may only deprotonate in the complex formation or under concentrated alkali conditions. Hence, we denote free citrate anions originating from the dissolution of trisodium citrate (i.e., Na3HCit) as HCit3−. Fig. 2 reports the titration profiles of the trivalent metal–citrate solutions in the 1st column, divalent metal–citrate solutions in the 2nd column, and mixed metal–citrate solutions in the 3rd column. In the aluminium–citrate titration profile, the equivalent point, EL1, at 1.39 RAl3+ is related to the formation of [Al3Cit3OH]4−, according to the following equilibrium:| |  | (2) |
which predicts a 1.33 RAl3+ value. Moreover, the asymmetric 1st derivative profile of EL1 is related to the [Al2Cit2]2− formation, as follows:| | | 2Al3+ + 2HCit3− + 2OH− ⇌ [Al2Cit2]2− + 2H2O, | (3) |
in agreement with our speciation model presented in Fig. 3a. The titration profile of the iron–citrate solution is similar to the aluminium–citrate one. However, in contrast to aluminium, two equivalent points related to iron–citrate complexes, namely EL1a and EL1b, are clearly resolved and located at ∼1.3 and 1.52 RFe3+, respectively. Our simulation is based on Silva et al.65 iron–citrate stability constants, and predicts the existence of two iron–citrate complexes (i.e., [Fe2Cit2]2− and [FeCit]−) that are predominant at acidic and neutral pH values, as shown in Fig. 3b. However, the observed position of EL1a and EL1b in Fig. 2d is not accurately predicted, because Silva et al.65 could not account for acid–base equilibria of the coordinated water molecules and hydroxide ions, due to constraints of the electrospray ionization mass spectrometry used to determine the iron–citrate stability constants. Hence, oligomeric [Fe2Cit2OH]n3n− species (with n of few units), produced by the condensation of [Fe2Cit2]2− and [FeCit]−, represent a more plausible picture of the iron–citrate speciation, as previously proposed by Spiro et al.,68,69 but without providing stability constants. More in detail, the 1.52 RFe3+ value of EL1b is consistent with the following formation equilibrium:| |  | (4) |
which predicted a theoretical 1.5 RFe3+, whereas a theoretical 1.3 RFe3+ value of EL1a is yielded from the formation equilibrium:| |  | (5) |
which is the iron analogous of (2). Lastly, EHyd corresponds to ferrihydrite nucleation from the partial hydrolysis of iron–citrate complexes.68,69 Since EHyd is located at ∼2.7 RFe3+ it means that less than three hydroxide ions are consumed per iron ion, being consistent with the observations of Spiro et al., concerning the progressive hydrolysis of [Fe2Cit2OH]n3n− into ∼8 nm ferrihydrite clusters capped with citrate anions.68,69 We also stress that EHyd appears as a broad peak in the 1st derivative profile, which indicates that the kinetics of the [Fe2Cit2OH]n3n− hydrolysis into ferrihydrite is slower than the titration speed of 2.8 R h−1. An analogous EHyd at ∼2.5 RAl3+ is also present in the titration profile of the aluminium citrate solution. Overall, as shown in Fig. 2g, the aluminium- and iron-citrate hydrolytic behaviour are similar. Both metals form 1/1 oligomeric citrate complexes that are stable in the 1.3–2.5 RM3+ range and up to ∼9.5 pH. The nickel–citrate titration profile presents one equivalent, namely EL2, located at 1.02 RNi2+ prior to hydroxide saturation. In addition to this, the solution remained clear of any precipitate even at the end of the titration, suggesting the stability of nickel–citrate complexes up to ∼12.5 pH. In literature, several polynuclear nickel–citrate compounds have been reported.67,72–76 However, to the best of our knowledge, speciation studies that account for the hydroxyl group deprotonation in nickel–citrate complexes are scarce.67 For this reason, the speciation model presented in Fig. 3c predicts the formation of a solid phase that is not experimentally observed. As expected from Fig. 3c, at 0.00 RNi2+ and neutral pH, the formation of the [NiHCit]− complex is predominant, as follows:| | | Ni2+ + HCit3− ⇌ [NiHCit]−. | (6) |
 |
| | Fig. 2 Potentiometric titration profiles and their respective 1st derivative of metal/citrate solutions with 1/1 molar ratio, as follows: (a) Al3+, (b) Ni2+, and (c) Al3+–Ni2+ with 1/3 ratio, (d) Fe3+, (e) Zn2+, and (f) Fe3+–Ni2+ with a 1/3 ratio, (i) Al3+–Zn2+ with a 1/2 ratio. Comparison of titration curves in the presence of citrate (continuous line) and without citrate (dotted line) of: (g) trivalent metals, and (h) divalent metals. EL1 refers to Al3+ and Fe3+ complex formations, EL2 refers to Ni2+ and Zn2+complex formation. EHyd refers to the hydrolysis of complexes that leads to the formation of the respective hydroxides. | |
 |
| | Fig. 3 Speciation models of (a) Al–citrate, (b) Fe–citrate, (c) Ni–citrate and (d) Zn–citrate systems, with a metal/citrate molar ratio of 1/1. Speciation models are based on data from ref. 61–67, 81 and 86 We accounted for the solubility products of freshly formed precipitates; the solubility products of the aged precipitates are not considered. | |
Then, the consumption of one equivalent of hydroxide leads to the formation of [Ni2Cit2]4−, as follows:
| | | 2[NiHCit]− + 2OH− ⇌ [Ni2(Cit)2]4− + 2H2O. | (7) |
However, according to E. Still et al.,67 the formation of a hydroxylated tetramer is more plausible according to the equilibrium:
| |  | (8) |
In any case, according to both (7) and (8), an equivalent point at 1.00 RNi2+ is predicted; while considering the formation of [Ni4Cit3OH]5− instead of [Ni2(Cit)2]4−, has a negligible impact on our simulation results, since the aforementioned complexes have similar stability constants (Table S4†). To explain the absence of a precipitate, we refer to studies of Güdel and co-workers in which they reported the crystal structure of several different complexes containing 7, 8 and 21 nickel atoms coordinated with citrates, hydroxides, and water molecules,73–75 with the latter having the following chemical composition: [Ni21(Cit)12(OH)10(H2O)10]16−. Moreover, by considering the overall formation equilibrium of Ni21 as follows:
| |  | (9) |
a theoretical 1.05
RNi2+ is yielded, being in line with the experimental value of 1.02
RNi2+ for
EL2 in
Fig. 2b. Noteworthily, this Ni
21 complex contains a cluster of nickel atoms with a structure that resembles a Ni(OH)
2 nucleation seed.
60,75 Reasonably, large nickel–citrate complexes, such as Ni
21, are the result of the hydrolytic polymerization of smaller species originating from either
(7) or
(8), while residual bound citrates hinder the further growth of the Ni(OH)
2 solid phase,
75 explaining the absence of a precipitate. The zinc–citrate titration profile shows similarities with the nickel–citrate one, displaying an
EL2 at 1.06
RZn2+.
According to our speciation model, this equivalent point is related to the complete formation of [Zn2(HCit)2(OH)2]4− as follows:
| | | 2[ZnHCit]− + 2OH− ⇌ [Zn2(HCit)2(OH)2]4− | (10) |
that yields a theoretical 1.00
RZn2+. In addition, the zinc–citrate system shows an
EHyd at 2.28
RZn2+ that corresponds to the slow hydrolysis of [Zn
2(HCit)
2(OH)
2]
4− as follows:
| |  | (11) |
consuming a second hydroxide equivalent to produce Zn(OH)
2, which is clearly visible as a precipitate. In summary, divalent metal–citrate solutions behave similarly, according to the following generalized equilibria:
| |  | (12a) |
or
| | 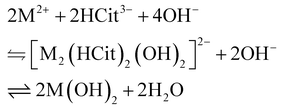 | (12b) |
From literature on nickel- and zinc–citrate complexes crystal structure73–75,79,80 and speciations,61,67,81–85 the nickel–citrate system follows (12a), whereas the zinc–citrate system follows (12b) equilibria. The titration profiles of aluminium–nickel, iron–nickel, and aluminium–zinc solution, in the presence of citrates, are reported in the 3rd column of Fig. 2. All three titration profiles present two equivalent points related to the formation of complexes that are analogous to the respective monometallic–citrate solutions. However, by normalizing EL1 by its trivalent metal ratio, it follows that EL1 is always delayed compared to the corresponding monometallic solution (Table 3), with the aluminium–zinc–citrate system showing the largest EL1 delay of 0.35 R compared to the aluminium–citrate solution. We ascribe the delay of EL1 to the progressive formation of mixed metal–citrate complexes by consuming trivalent metal–citrate complexes as reactants. In the aluminium- and iron–nickel systems, EL2 is also delayed by 0.16 RNi2+ compared to the nickel–citrate system. On the contrary, EL2 of the aluminium–zinc–citrate solution precedes the equivalent point expected for the zinc–citrate solution by 0.16 RZn2+. The reason behind this discrepancy is not yet clear to us and may be worth further investigation. However, it is reasonably related to the different speciation of nickel- and zinc–citrate systems as inferable from eqn (12). Eventually, the increased hydroxylation of citrate complexes leads to their hydrolysis, as apparent from the translucent aspect of the titrated bimetallic solutions beyond pH ∼12.
Table 3 Hydroxylation ratios (R) of equivalent points observed in metal–citrate solutions
| Cations |
Mole ratio |
E
L1
|
E
L2
|
E
Hyd
|
| Al3+ |
— |
1.39 RAl3+ |
— |
∼2.5 RAl3+ |
| Fe3+ |
— |
∼1.3 RFe3+ |
— |
∼2.7 RFe3+ |
| 1.52 RFe3+ |
| Ni2+ |
— |
— |
1.02 RNi2+ |
— |
| Zn2+ |
— |
— |
1.06 RZn2+ |
2.28 RZn2+ |
| Al3+, Ni2+ |
1/3 |
0.38 R |
1.28 R |
— |
| Normalized |
1.53 RAl3+ |
1.19 RNi2+ |
|
|
| Fe3+, Ni2+ |
1/3 |
0.40 R |
1.28 R |
∼1.9 R |
| Normalized |
1.60 RFe3+ |
1.18 RNi2+ |
|
|
| Al3+, Zn2+ |
1/2 |
0.58 R |
1.18 R |
2.10 R |
| Normalized |
1.74 RAl3+ |
0.90 RZn2+ |
|
|
2.3. Electronic spectroscopy
2.3.1. Nickel.
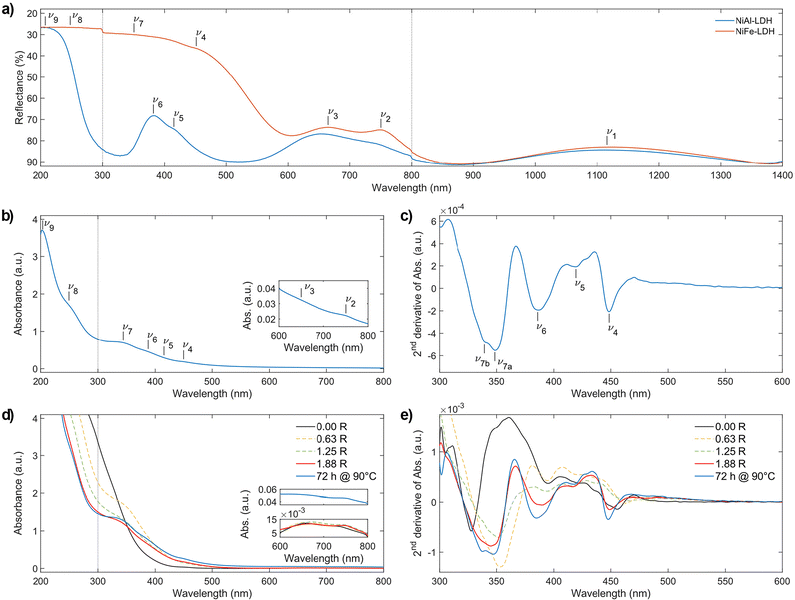
This section describes the nature of Ni2+ related features observed in the electronic spectra of NiAl- and NiFe-LDHs, as shown in Fig. 4. The 3A2g(3F) → 3T2g(3F), the 3A2g(3F) → 3T1g(3F) and the 3A2g(3F) → 3T1g(3P) transitions are characteristic features of the electronic spectra of nickel-based compounds;28–38 for the sake of simplicity, we labelled the aforementioned transitions as ν1, ν3 and ν6, respectively. We also point out that the ν3 is often accompanied by the 3A2g(3F) → 1Eg(1D) “spin–flip” transition, due to the state mixing between 3T1g and 1Eg, in the case of their energy proximity.34–36 We labelled 3A2g(3F) → 1Eg(1D) as ν2; nevertheless, several authors prefer to report a single average transition as 3A2g(3F) → 3T1g(3F), 1Eg(1D).32,37,38,87 Interestingly, ν2 results in enhancing the NiFe-LDH electronic spectra due to super-exchange interactions in Fe3+–O–Ni2+ bonds (see section 2.3.3). Eventually, we also detected the contribution to the absorbance of the 3A2g(3F) → 1T2g(1D), 1A1g(1G) spin-forbidden transition, labelled as ν5. The wavelength positions of the observed Ni2+ electronic transitions are reported in Table 4 and visualized in the Tanabe–Sugano diagram for d8 configuration (Scheme 1a). A straightforward comparison with other nickel-based minerals and synthetic compounds is shown in Table S5.†
Table 4 Electronic transitions observed in the electronic spectra of NiFe-LDHs
| Band |
Wavelength (nm) |
Type |
Transition |
|
Spin-forbidden transitions. dd = Ligand Field Transitions (parity-forbidden). LMCT = Ligand-to-metal charge transfer. MO = molecular orbital. HOMO and LUMO = Highest occupied MO and lowest unoccupied MO.
6A1g(6S) → 4Eg(4D) contribution to the absorbance.
6A1g(6S) → 4T1g(4P) contribution to the absorbance.
|
|
ν
1
|
1120 |
dd (Ni2+) |
3A2g(3F) → 3T2g(3F) |
|
ν
2
|
750 |
dd (Ni2+)a |
3A2g(3F) → 1Eg(1D) |
|
ν
3
|
665 |
dd (Ni2+) |
3A2g(3F) → 3T1g(3F) |
|
ν
4
|
448 |
dd (Fe3+)a |
Ni2+ 6A1g(6S) → 4Eg, 4A1g(4G) |
|
ν
5
|
420 |
dd (Ni2+)a |
3A2g(3F) → 1T2g(1D), 1A1g(1G) |
|
ν
6
|
386 |
dd (Ni2+) |
3A2g(3F) → 3T1g(3P) |
| dd (Fe3+)a |
6A1g(6S) → 4T2g(4D) |
|
ν
7
|
348b, 338c |
dd (Fe3+)a |
6A1g(6S) → 4Eg(4D), 4T1g(4P) |
|
ν
8
|
250 |
LMCT |
t1uβ → t2gβ (Fe(III)) |
|
ν
9
|
210 |
LMCTs |
t1uβ → egβ (Fe(III)Ni(II)) |
| MOs of RCOO− |
n → π* (HOMO → LUMO) |
 |
| | Fig. 4 Electronic spectra of: (a) citrate intercalated NiAl- and NiFe-LDHs powders, (b) carbonate-intercalated NiFe-LDH dispersed in ethanol according to ref. 12 and taken as reference material, (c) second derivative of (b), (d) synthesis solution of citrate-intercalated NiFe-LDH at different R values, (e) second derivative of (d). Dotted vertical lines at 300 and 800 nm indicate the switch of lamp and detector, respectively. Inset to (b) and (d) is the magnification of the electronic spectra in the 600–800 nm range. | |
 |
| | Scheme 1 Tanabe-Sugano diagrams of: (a) d8 octahedral configuration, and (b) high-spin d5 octahedral configuration. The abscissae report the ligand field strength (10Dq) normalized by the Racah parameter B, whereas the ordinates report the energies, normalized by B, of ligand field states. In each diagram, the abscissae axis always corresponds to the ground state. Here, energy states are colour-coded according to their spin–orbit terms which are reported on the left (i.e., black for S, cyan for P, orange for D, violet for F and green for G). Moreover, energy states with the same spin multiplicity as the ground state are represented with a plain line, while energy states with a spin multiplicity different from the ground state are represented with a dashed line. The symmetry term of each energy state is reported on the top-right of the diagrams according to the Mulliken nomenclature. The red vertical lines indicate the 10Dq/B ratios we computed for NiAl- and NiFe-LDHs (Table 5). Racah parameters used: (a) B = 887 cm−1, C = 4075 cm−1; (b) B = 916 cm−1, C = 2632 cm−1. ESI section 6.3† for computation details. | |
2.3.2. Iron.
In the NiFe-LDH electronic spectrum, we observed, the 6A1g(6S) → 4Eg, 4A1g(4G) and 6A1g(6S) → 4Eg(4D) spin-forbidden transitions of Fe3+, labelled as ν4 and ν7, at 448 and 348 nm (Fig. 4a–c) by means of second derivative spectrophotometry. Moreover, ν7 presents an asymmetric shape due to the absorbance contribution of 6A1g(6S) → 4T1g(4P) at 338 nm (i.e., ν7b in Fig. 4c). Eventually, the two absorbance bands ascribed to ligand-to-metal charge transfer transitions (LMCT) are located at 250 and 210 nm and are labelled as ν8 and ν9, respectively. For the sake of completeness, we also include in ν9, the absorbance contribution of the n → π* transition of the carboxylic groups that falls at ∼210 nm. The wavelength positions of these Fe3+ electronic transitions are reported in Table 4 and visualized in the Tanabe–Sugano diagram for high-spin d5 configuration (Scheme 1b). For a straightforward comparison with other ferric compounds see Table S5.†
2.3.3. Ligand field analysis.
The electronic spectroscopy of transition-metal-based LDHs is a topic often disregarded in current literature. In fact, only a few studies analysed LDHs electronic spectra, merely assigning the ligand field transitions.28,43,88 Previously, we proved how second derivative spectrophotometry is effective in resolving multiple ligand field transitions in NiFe-LDH electronic spectra.43 Here, by means of second derivative spectrophotometry, we computed the magnitude of the ligand field strength (10Dq), B and C Racah parameters related to Ni2+ and Fe3+ located within NiAl- and NiFe-LDH materials. From the Racah parameters, the nephelauxetic effect can be estimated. The nephelauxetic effect is the reduction of interelectronic repulsion of d electrons, with respect to the isolated ions, due to a coordination environment. This directly translates into an estimation of the ionic degree of ligand–metal bonds,89 given by the nephelauxetic ratio historically defined as:| |  | (13) |
Here Bgas is the tabulated value of B for ions in the gas phase. During the years, the nephelauxetic effect has been further revisited.90–92 For our purposes, we used the (13) revisited version of Brik et al.,91,92 which also accounts for C and Cgas, as follows:
| | 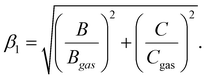 | (14) |
We point out that a proper comparison between β values reported in the literature, β1 should be obtained by normalizing the latter by 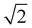 . The ligand field analysis results are reported in Table 5. For Ni2+, located LDH crystal lattices, typical 10Dq values of ∼9000 cm−1, B values of ∼890 cm−1 and C values of ∼4000 cm−1 were computed, and these consistent with those from the past literature concerning nickel hydroxides and related materials.28,37,42 This indicates that the nature of trivalent metals in nickel-based LDHs has a negligible influence on the ligand field parameters of Ni2+. In addition, Ni2+, in both NiAl- and NiFe-LDH crystal lattices, has a
. The ligand field analysis results are reported in Table 5. For Ni2+, located LDH crystal lattices, typical 10Dq values of ∼9000 cm−1, B values of ∼890 cm−1 and C values of ∼4000 cm−1 were computed, and these consistent with those from the past literature concerning nickel hydroxides and related materials.28,37,42 This indicates that the nature of trivalent metals in nickel-based LDHs has a negligible influence on the ligand field parameters of Ni2+. In addition, Ni2+, in both NiAl- and NiFe-LDH crystal lattices, has a  of 0.849. By comparison, we performed the same ligand field analysis on the spectroscopic data published by Oliver-Tolentino et al.28 yielding a
of 0.849. By comparison, we performed the same ligand field analysis on the spectroscopic data published by Oliver-Tolentino et al.28 yielding a  of 0.862 for carbonate-intercalated nickel-based LDHs, whereas the data published by Poul et al.42 yielded a
of 0.862 for carbonate-intercalated nickel-based LDHs, whereas the data published by Poul et al.42 yielded a  of 0.860 for nickel hydroxide-acetate (which is isomorphous to LDHs). Hence, we conclude that the nephelauxetic ratio in nickel-based LDHs is neither significantly influenced by the nature of the trivalent metal cation hosted in the hydroxide layers nor by the nature of the anions amid them. In high-spin Fe3+, all possible ligand field transitions are spin-forbidden. However, in correlated materials, the spin restrictions are lifted because of super-exchange interactions, making formally spin-forbidden transitions observable.33,40,41,93–97 The 6A1g(6S) → 4Eg, 4A1g(4G) and 6A1g(6S) → 4Eg(4D) transitions, which are 10Dq-independent,39–41 directly provide the Fe3+ values of B and C, which are 916 and 2632 cm−1, respectively. To have a proper comparison, we also performed the same ligand field analysis on the spectroscopic data reported by Sherman et al.40,41 It follows that, according to (14), Fe3+ experiences a
of 0.860 for nickel hydroxide-acetate (which is isomorphous to LDHs). Hence, we conclude that the nephelauxetic ratio in nickel-based LDHs is neither significantly influenced by the nature of the trivalent metal cation hosted in the hydroxide layers nor by the nature of the anions amid them. In high-spin Fe3+, all possible ligand field transitions are spin-forbidden. However, in correlated materials, the spin restrictions are lifted because of super-exchange interactions, making formally spin-forbidden transitions observable.33,40,41,93–97 The 6A1g(6S) → 4Eg, 4A1g(4G) and 6A1g(6S) → 4Eg(4D) transitions, which are 10Dq-independent,39–41 directly provide the Fe3+ values of B and C, which are 916 and 2632 cm−1, respectively. To have a proper comparison, we also performed the same ligand field analysis on the spectroscopic data reported by Sherman et al.40,41 It follows that, according to (14), Fe3+ experiences a 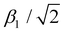 value of 0.747 in NiFe-LDH. This means that the nephelauxetic ratio of Fe3+ in NiFe-LDH is comparable to the 0.75 value of [Fe(H2O)6]3+ reported in literature,98,99 whereas the expected nephelauxetic ratio of Fe3+ in metal–oxide lattices ranges between 0.6 and 0.7, as shown in Fig. 5. In our opinion, these nephelauxetic similarities between Fe3+ in LDHs and [Fe(H2O)6]3+ are related to the performance of the NiFe-LDHs as catalysts in water-splitting applications.100–102 In ferric compounds, the magnitude of 10Dq is usually obtained from the energy of 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) transitions. However, we have not detected any contribution to the absorbance spectrum ascribable to the aforementioned transitions. According to the Tanabe mechanism, the interaction between super-exchanged ions and incident light involves only orbitals that are partially filled,33,94,96,97 and is described by the following Hamiltonian:
value of 0.747 in NiFe-LDH. This means that the nephelauxetic ratio of Fe3+ in NiFe-LDH is comparable to the 0.75 value of [Fe(H2O)6]3+ reported in literature,98,99 whereas the expected nephelauxetic ratio of Fe3+ in metal–oxide lattices ranges between 0.6 and 0.7, as shown in Fig. 5. In our opinion, these nephelauxetic similarities between Fe3+ in LDHs and [Fe(H2O)6]3+ are related to the performance of the NiFe-LDHs as catalysts in water-splitting applications.100–102 In ferric compounds, the magnitude of 10Dq is usually obtained from the energy of 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) transitions. However, we have not detected any contribution to the absorbance spectrum ascribable to the aforementioned transitions. According to the Tanabe mechanism, the interaction between super-exchanged ions and incident light involves only orbitals that are partially filled,33,94,96,97 and is described by the following Hamiltonian:
| |  | (15) |
where
i and
j are the half-filled d orbitals of a and b ions, respectively,
s are the corresponding spin vectors, and
E is the electric vector of the incident light.

represents the partial derivative of exchange constants between a
i and b
j with respect to E coordinates. Since the t
2g orbitals of Ni
2+ are full, they do not bring any contribution to
(15), relegating the enhancement of ligand field transitions to the super-exchange interactions in Fe
3+–O–Ni
2+ bonds through e
g orbitals. This explains the observed intensity of
6A
1g(
6S) →
4A
1g(
4G) and
6A
1g(
6S) →
4E
g(
4D), since the former transition is related to the spin canting of e
g orbitals, whereas the latter is related to a spin–flip in e
g orbitals of Fe
3+ (see tables of the matrix elements of Coulomb interactions in ref.
103 and
104). On the contrary,
6A
1g(
6S) →
4T
1g(
4G) and
6A
1g(
6S) →
4T
2g(
4G) do not benefit from
(15) since both transitions involve an electron transfer from e
g to t
2g orbitals of Fe
3+ with a concomitant spin–flip. The same phenomenon has been observed and described in the past for Ni
2+-doped manganese halide perovskites.
33,95 Given this, we could only rely on the energy of
6A
1g(
6S) →
4T
1g(
4P) for the 10
Dq of Fe
3+, which turns out to be 7049 cm
−1. By comparison, this 10
Dq value is approximatively half of the ∼15
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 cm
−1 expected for Fe
3+ in oxide crystal lattices,
39–41 being consistent with the linear relationship between
Dq and the effective charge of the ligands.
104 With known
Dq,
B and
C values, the expected positions of the unobserved Fe
3+ ligand field transitions are obtained from the Tanabe–Sugano diagram for high-spin d
5 configurations (
Scheme 1b). The
6A
1g(
6S) →
4T
1g(
4G) and
6A
1g(
6S) →
4T
2g(
4G) transitions are expected to fall at ∼590 and ∼480 nm, respectively.
 |
| | Fig. 5 Scatter plot of the energy of the 6A1g(6S) → 4Eg(4D) transitions in ferric compounds vs. their respective nephelauxetic ratios. Empty triangles indicate the classical nephelauxetic ratio, i.e., β = B/B0. Filled circles resent the new nephelauxetic ratio91,92 divided by  , i.e., , i.e.,  . The dashed lines represent the expected range of . The dashed lines represent the expected range of  in ferric compounds. Apart from NiFe-LDH, the nephelauxetic ratios were computed from the spectroscopic data reported in ref. 40 and 41. in ferric compounds. Apart from NiFe-LDH, the nephelauxetic ratios were computed from the spectroscopic data reported in ref. 40 and 41. | |
Table 5 Results of ligand field analysis of the electronic spectra of NiAl- and NiFe-LDHs
| Ion |
Material |
10Dq (cm−1) |
B (cm−1) |
C (cm−1) |
10 Dq/B |
C/B |
β
|
β
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
Defined as: 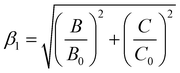 , see ref. 91 for details.
Computed from the ν7 contribution to the absorbance of 6A1g(6S) → 4T1g(4P). , see ref. 91 for details.
Computed from the ν7 contribution to the absorbance of 6A1g(6S) → 4T1g(4P).
|
| Ni2+ |
NiAl-LDH |
9009 |
892 |
4054 |
10.1 |
4.54 |
0.857 |
1.200 |
| NiFe-LDH |
8929 |
887 |
4075 |
10.1 |
4.59 |
0.852 |
1.199 |
| Gas phase89 |
— |
1041 |
4831 |
— |
4.64 |
1 |

|
| Fe3+ |
NiFe-LDH |
7049b |
916 |
2632 |
7.7 |
2.87 |
0.903 |
1.056 |
| Gas phase90 |
— |
1015 |
4800 |
— |
4.73 |
1 |
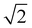
|
However, it is evident from the second derivative electronic spectra in Fig. 4c and e that the contribution of those transitions, if any, is below our limit of detection, being consistent with the previous statement about super-exchange interactions in Fe3+–O–Ni2+ bonds. Eventually, the 6A1g(6S) → 4T2g(4D) transition is predicted to fall at ∼370 nm, overlapping with the absorbance contribution of Ni2+ to ν6. We also stress that ν7 has been assigned, in the past, to the 6A1g(6S) → 4Eg, 4T2g(4D) transition.28,43 We deem this assignment incorrect for two reasons. Firstly, the assignment is inconsistent with the electronic spectra of ferric oxides.40,41 Secondly, by considering the literature ν7 assignment, our ligand field analysis yields improbable values of 10Dq close to zero. However, it is evident from the second derivative electronic spectra in Fig. 4c and e that the contribution of those transitions, if any, is below our limit of detection, being consistent with the previous statement about super-exchange interactions in Fe3+–O–Ni2+ bonds.
2.3.4. Formation mechanism of NiFe-LDH.
The electronic spectra, and their 2nd derivative, of subsequent aliquots collected during the citrate-intercalated NiFe-LDH synthesis are displayed in Fig. 4d and e. Prior to the addition of any hydroxide equivalent (0.00 R), the solution appears green. This green colour is caused by three absorbance bands at 740, 660, and ∼450 nm. As described earlier, the two bands at 740 and 660 nm are related to Ni2+ ligand field transitions, ν2 and ν3, respectively, while the absorbance band at ∼450 nm is related to Fe3+, i.e., ν4. However, we cannot exclude possible contributions from ν5 and ν6. The LMCT absorbance edge begins at 400 nm saturating our detector at 290 nm. During the addition of NaOH, the solution turns from green to yellow after EL1 at 0.4 R is passed. Thereafter, a progressive increase in the absorbance intensity is observed in the 350–500 nm region. This observation confirms our interpretation of the potentiometric titration profiles. In fact, the progressive formation of bimetallic–citrate compounds implies an increasing number of possible super-exchange interactions in Fe3+–O–Ni2+ bonds, and therefore an increasing intensity of Fe3+ related spin-forbidden transitions (namely, ν4 and ν7) by the Tanabe mechanism. At the same time, as R increases, the LMCT absorbance edge shifts by ∼100 nm to lower wavelengths. This shift can be explained by the hydrolysis of chemical bonds between transition metals and citrate carboxylic groups forming complexes. In fact, the increase of the photon energy required for a LMCT fits well with the alteration of the Fe3+ or Ni2+ coordination environment. In addition, it is consistent with a shift from a ligand electron-rich environment constituted by carboxylic groups to a ligand electron-poor environment constituted by hydroxide ions. After 1.88 R (ESI section 2†), the reaction mixture still appears clear of any precipitate, while its absorbance spectrum (red line in Fig. 4d) resembles that of carbonate-intercalated NiFe-LDH (Fig. 4b). Then, after performing the aging treatment at 90 °C, the reaction mixture became opaque due to suspended LDH particles, while its absorbance spectrum shows a further increase in the absorbance related to ligand field transitions (blue line in Fig. 4d).
3. Conclusions and perspectives
In summary, we developed an aqueous, coordination-chemistry-based synthetic procedure that yields nanostructured layered double hydroxides (LDHs) without using any anion exchange process, avoiding the use of organic solvents. We successfully synthetized nanostructured citrate-intercalated NiAl-, NiFe- and ZnAl-LDH materials, which possess a turbostratic disorder arising from the restacking of nanosheets ranging from 5 to 500 nm wide, depending on their chemical composition. The presence of vertically aligned nanosheets in the transmission electron microscopy images of NiFe- and ZnAl-LDH samples allowed us to estimate their thicknesses, which are in the 1–2 nm range. The LDH formation mechanism is a two-step process, as revealed by pH-potentiometric titrations and electronic spectroscopy investigations. The first step consists of forming bimetallic–citrate coordination compounds that occur by increasing the reaction environment pH. The second step consists of heating the reaction environment that causes the complete hydrolysis of the metal–citrate compounds, leading to the formation of LDH nanosheets. By means of electronic spectroscopy, we have shown a progressive enhancement of Fe3+ spin-forbidden ligand field transitions during the NiFe-LDH synthesis. This enhancement is due to super-exchange interactions in the increasing number of Fe3+–O–Ni2+ bonds formed during the LDH synthesis process. In addition, our ligand field analysis reveals that Ni2+ in NiAl- and NiFe-LDH crystal lattices behaves similarly to that in nickel hydroxide and other related materials. On the contrary, Fe3+ in NiFe-LDH behaves similarly to that in [Fe(H2O)6]3+, rather than in its ferric oxide counterparts, suggesting a correlation with the water-splitting electrocatalytic activity of NiFe-LDHs. Our approach and insights gained on the coordination chemistry of LDH synthesis may be useful to synthesize nanoparticles via coprecipitation and fabricate functional films for optoelectronics via electroplating or chemical bath deposition.26,27,105 Our ligand field analysis results may help to fully understand the electronic structure of transition metal-based LDHs, which constitute a valid option in the field of two-dimensional correlated insulators for future spintronic devices.106–108
Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
FB is the co-founder and Scientific Director of BeDimensional S.p.A., a company producing and commercializing 2D materials. The other authors have no conflicts to declare.
Acknowledgements
DC and CR acknowledge the Italian Ministry of University and Research for funding through the LEGACY (healing wide-gap chalcopyrite, grant no. 20223ZP4WP) project of national relevance (PRIN 2022), under the ERC PE3 Condensed Matter Physics sector.
For the acquisition of HRTEM images, we acknowledge “Laboratorio di microscopia elettronica avanzata ELEMENTAL” at Dipartimento di Chimica e Chimica Industriale, Università degli Studi di Genova, via Dodecaneso 31, 16146 Genoa, Italy.
References
- S. J. Mills, A. G. Christy, J.-M. R. Génin, T. Kameda and F. Colombo, Nomenclature of the hydrotalcite supergroup: natural layered double hydroxides, Mineral. Mag., 2012, 76, 1289–1336 CrossRef CAS.
- F. Cavani, F. Trifirò and A. Vaccari, Hydrotalcite-type anionic clays: Preparation, properties and applications, Catal. Today, 1991, 11, 173–301 CrossRef CAS.
- A. C. Ferrari, F. Bonaccorso, V. Fal'ko, K. S. Novoselov, S. Roche, P. Bøggild, S. Borini, F. H. L. Koppens, V. Palermo, N. Pugno, J. A. Garrido, R. Sordan, A. Bianco, L. Ballerini, M. Prato, E. Lidorikis, J. Kivioja, C. Marinelli, T. Ryhänen, A. Morpurgo, J. N. Coleman, V. Nicolosi, L. Colombo, A. Fert, M. Garcia-Hernandez, A. Bachtold, G. F. Schneider, F. Guinea, C. Dekker, M. Barbone, Z. Sun, C. Galiotis, A. N. Grigorenko, G. Konstantatos, A. Kis, M. Katsnelson, L. Vandersypen, A. Loiseau, V. Morandi, D. Neumaier, E. Treossi, V. Pellegrini, M. Polini, A. Tredicucci, G. M. Williams, B. Hee Hong, J. H. Ahn, J. Min Kim, H. Zirath, B. J. van Wees, H. van der Zant, L. Occhipinti, A. di Matteo, I. A. Kinloch, T. Seyller, E. Quesnel, X. Feng, K. Teo, N. Rupesinghe, P. Hakonen, S. R. T. Neil, Q. Tannock, T. Löfwander and J. Kinaret, Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems, Nanoscale, 2015, 7, 4598–4810 RSC.
- V. Nicolosi, M. Chhowalla, M. G. Kanatzidis, M. S. Strano and J. N. Coleman, Liquid exfoliation of layered materials, Science, 2013, 340, 72–75 CrossRef.
- M. Shao, R. Zhang, Z. Li, M. Wei, D. G. Evans and X. Duan, Layered double hydroxides toward electrochemical energy storage and conversion: design, synthesis and applications, Chem. Commun., 2015, 51, 15880–15893 RSC.
- Q. Wang and D. Ohare, Recent advances in the synthesis and application of layered double hydroxide (LDH) nanosheets, Chem. Rev., 2012, 112, 4124–4155 CrossRef CAS PubMed.
- F. Song, L. Bai, A. Moysiadou, S. Lee, C. Hu, L. Liardet and X. Hu, Transition Metal Oxides as Electrocatalysts for the Oxygen Evolution Reaction in Alkaline Solutions: An Application-Inspired Renaissance, J. Am. Chem. Soc., 2018, 140, 7748–7759 CrossRef CAS PubMed.
- S. Duval, F. Baymann, B. Schoepp-Cothenet, F. Trolard, G. Bourrié, O. Grauby, E. Branscomb, M. J. Russell and W. Nitschke, Fougerite: the not so simple progenitor of the first cells, Interface Focus, 2019, 9, 20190063 CrossRef PubMed.
- S. Duval, E. Branscomb, F. Trolard, G. Bourrié, O. Grauby, V. Heresanu, B. Schoepp-Cothenet, K. Zuchan, M. J. Russell and W. Nitschke, On the why's and how's of clay minerals’ importance in life's emergence, Appl. Clay Sci., 2020, 195, 105737 CrossRef CAS.
- B. Grégoire, C. Ruby and C. Carteret, Structural cohesion of M II-M III layered double hydroxides crystals: Electrostatic forces and cationic polarizing power, Cryst. Growth Des., 2012, 12, 4324–4333 CrossRef.
- J. W. Boclair and P. S. Braterman, Layered double hydroxide stability. 1. Relative stabilities of layered double hydroxides and their simple counterparts, Chem. Mater., 1999, 11, 298–302 CrossRef CAS PubMed.
- S. Jaśkaniec, C. Hobbs, A. Seral-Ascaso, J. Coelho, M. P. Browne, D. Tyndall, T. Sasaki and V. Nicolosi, Low-temperature synthesis and investigation into the formation mechanism of high quality Ni-Fe layered double hydroxides hexagonal platelets, Sci. Rep., 2018, 8, 4–11 CrossRef PubMed.
- B. Grégoire, C. Ruby and C. Carteret, Hydrolysis of mixed Ni2+–Fe3+ and Mg2+–Fe3+ solutions and mechanism of formation of layered double hydroxides, J. Chem. Soc., Dalton Trans., 2013, 42, 15687–15698 RSC.
- S. S. C. Pushparaj, C. Forano, V. Prevot, A. S. Lipton, G. J. Rees, J. v. Hanna and U. G. Nielsen, How the Method of Synthesis Governs the Local and Global Structure of Zinc Aluminum Layered Double Hydroxides, J. Phys. Chem. C, 2015, 119, 27695–27707 CrossRef CAS.
- G. Hu and D. O'Hare, Unique layered double hydroxide morphologies using reverse microemulsion synthesis, J. Am. Chem. Soc., 2005, 127, 17808–17813 CrossRef CAS PubMed.
- Q. Wang and D. O′hare, Large-scale synthesis of highly dispersed layered double hydroxide powders containing delaminated single layer nanosheets, Chem. Commun., 2013, 49, 6301–6303 RSC.
- Y. Tokudome, T. Morimoto, N. Tarutani, P. D. Vaz, C. D. Nunes, V. Prevot, G. B. G. Stenning and M. Takahashi, Layered Double Hydroxide Nanoclusters: Aqueous, Concentrated, Stable, and Catalytically Active Colloids toward Green Chemistry, ACS Nano, 2016, 10, 5550–5559 CrossRef CAS PubMed.
- H. Koshikawa, H. Murase, T. Hayashi, K. Nakajima, H. Mashiko, S. Shiraishi and Y. Tsuji, Single Nanometer-Sized NiFe-Layered Double Hydroxides as Anode Catalyst in Anion Exchange Membrane Water Electrolysis Cell with Energy Conversion Efficiency of 74.7% at 1.0 A cm-2, ACS Catal., 2020, 10, 1886–1893 CrossRef CAS.
- D. Tichit, G. Layrac, M. G. Alvarez and I.-C. Marcu, Formation pathways of MII/MIII layered double hydroxides: A review, Appl. Clay Sci., 2024, 248, 107234 CrossRef CAS.
- C. Backes, A. M. Abdelkader, C. Alonso, A. Andrieux-Ledier, R. Arenal, J. Azpeitia, N. Balakrishnan, L. Banszerus, J. Barjon, R. Bartali, S. Bellani, C. Berger, R. Berger, M. M. B. Ortega, C. Bernard, P. H. Beton, A. Beyer, A. Bianco, P. Bøggild, F. Bonaccorso, G. B. Barin, C. Botas, R. A. Bueno, D. Carriazo, A. Castellanos-Gomez, M. Christian, A. Ciesielski, T. Ciuk, M. T. Cole, J. Coleman, C. Coletti, L. Crema, H. Cun, D. Dasler, D. De Fazio, N. Díez, S. Drieschner, G. S. Duesberg, R. Fasel, X. Feng, A. Fina, S. Forti, C. Galiotis, G. Garberoglio, J. M. García, J. A. Garrido, M. Gibertini, A. Gölzhäuser, J. Gómez, T. Greber, F. Hauke, A. Hemmi, I. Hernandez-Rodriguez, A. Hirsch, S. A. Hodge, Y. Huttel, P. U. Jepsen, I. Jimenez, U. Kaiser, T. Kaplas, H. Kim, A. Kis, K. Papagelis, K. Kostarelos, A. Krajewska, K. Lee, C. Li, H. Lipsanen, A. Liscio, M. R. Lohe, A. Loiseau, L. Lombardi, M. Francisca López, O. Martin, C. Martín, L. Martínez, J. A. Martin-Gago, J. Ignacio Martínez, N. Marzari, Á. Mayoral, J. McManus, M. Melucci, J. Méndez, C. Merino, P. Merino, A. P. Meyer, E. Miniussi, V. Miseikis, N. Mishra, V. Morandi, C. Munuera, R. Muñoz, H. Nolan, L. Ortolani, A. K. Ott, I. Palacio, V. Palermo, J. Parthenios, I. Pasternak, A. Patane, M. Prato, H. Prevost, V. Prudkovskiy, N. Pugno, T. Rojo, A. Rossi, P. Ruffieux, P. Samorì, L. Schué, E. Setijadi, T. Seyller, G. Speranza, C. Stampfer, I. Stenger, W. Strupinski, Y. Svirko, S. Taioli, K. B. K. Teo, M. Testi, F. Tomarchio, M. Tortello, E. Treossi, A. Turchanin, E. Vazquez, E. Villaro, P. R. Whelan, Z. Xia, R. Yakimova, S. Yang, G. R. Yazdi, C. Yim, D. Yoon, X. Zhang, X. Zhuang, L. Colombo, A. C. Ferrari and M. Garcia-Hernandez, Production and processing of graphene and related materials, 2D Mater., 2020, 7, 022001 CrossRef CAS.
- F. Bonaccorso, A. Lombardo, T. Hasan, Z. Sun, L. Colombo and A. C. Ferrari, Production and processing of graphene and 2d crystals, Mater. Today, 2012, 15, 564–589 CrossRef CAS.
- Z. Liu, R. Ma, M. Osada, N. Iyi, Y. Ebina, K. Takada and T. Sasaki, Synthesis, anion exchange, and delamination of Co-Al layered double hydroxide: Assembly of the exfoliated nanosheet/polyanion composite films and magneto-optical studies, J. Am. Chem. Soc., 2006, 128, 4872–4880 CrossRef CAS PubMed.
- W. Yu, H. Li, N. Du and W. Hou, Estimation of surface free energy and solubility parameters of Mg–Al layered double hydroxides, J. Colloid Interface Sci., 2019, 546, 361–370 CrossRef CAS PubMed.
- T. Hibino and M. Kobayashi, Delamination of layered double hydroxides in water, J. Mater. Chem., 2005, 15, 653–656 RSC.
- A. E. Gash, T. M. Tillotson, J. H. Satcher, J. F. Poco, L. W. Hrubesh and R. L. Simpson, Use of epoxides in the sol-gel synthesis of porous iron(III) oxide monoliths from Fe(III) salts, Chem. Mater., 2001, 13, 999–1007 CrossRef CAS.
- G. Hodes, Semiconductor and ceramic nanoparticle films deposited by chemical bath deposition, Phys. Chem. Chem. Phys., 2007, 9, 2181 RSC.
- D. A. Garzón, C. Rossi, I. Khatri, F. Soggia, I. Çaha, F. L. Deepak, D. Colombara and S. Sadewasser, Chemical Bath Deposition of Zn1−x Snx Oy Films as Buffer Layers for Cu(In,Ga)Se2 Solar Cells, Sol. RRL, 2023, 7, 2300173 CrossRef.
- M. A. Oliver-Tolentino, J. Vázquez-Samperio, A. Manzo-Robledo, R. D. G. González-Huerta, J. L. Flores-Moreno, D. Ramírez-Rosales and A. Guzmán-Vargas, An approach to understanding the electrocatalytic activity enhancement by superexchange interaction toward OER in alkaline media of Ni-Fe LDH, J. Phys. Chem. C, 2014, 118, 22432–22438 CrossRef CAS.
- D. S. Hall, D. J. Lockwood, C. Bock and B. R. MacDougall, Nickel hydroxides and related materials: a review of their structures, synthesis and properties, Proc. R. Soc. A, 2015, 471, 20140792 CrossRef PubMed.
- N. V. Kuleshov, V. G. Shcherbitsky, V. P. Mikhailov, S. Kück, J. Koetke, K. Petermann and G. Huber, Spectroscopy and excited-state absorption of Ni2+-doped MgAl2O4, J. Lumin., 1997, 71, 265–268 CrossRef CAS.
- N. Mironova-Ulmane, M. G. Brik and I. Sildos, Crystal field calculations of energy levels of the Ni2+ ions in MgO, J. Lumin., 2013, 135, 74–78 CrossRef CAS.
- A. C. Scheinost, R. G. Ford and D. L. Sparks, The role of Al in the formation of secondary Ni precipitates on pyrophyllite, gibbsite, talc, and amorphous silica: A DRS study, Geochim. Cosmochim. Acta, 1999, 63, 3193–3203 CrossRef CAS.
- O. S. Wenger, R. Valiente, H. U. Güdel and R. Valiente, Optical spectroscopy of the Ni2+-doped layer perovskites Rb2MCl4 (M=Cd,Mn): Effects of Ni2+-Mn2+ exchange interactions on the Ni2+ absorption, luminescence, and upconversion properties, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 64, 1–8 CrossRef.
- E. González, A. Rodrigue-Witchel and C. Reber, Absorption spectroscopy of octahedral nickel(II) complexes: A case study of interactions between multiple electronic excited states, Coord. Chem. Rev., 2007, 251, 351–363 CrossRef.
- G. Bussière and C. Reber, Coupled Excited States in Nickel(II) Complexes Probed by Polarized Absorption Spectroscopy, J. Am. Chem. Soc., 1998, 120, 6306–6315 CrossRef.
- J. Reedijk, P. W. N. M. van Leeuwen and W. L. Groeneveld, A semi-empirical energy-level diagram for octahedral, Nickel(II) Complexes, Recl. Trav. Chim. Pays-Bas, 2010, 87, 129–143 CrossRef.
- A. Harvey, X. He, I. J. Godwin, C. Backes, D. McAteer, N. C. Berner, N. McEvoy, A. Ferguson, A. Shmeliov, M. E. G. Lyons, V. Nicolosi, G. S. Duesberg, J. F. Donegan and J. N. Coleman, Production of Ni(OH)2 nanosheets by liquid phase exfoliation: From optical properties to electrochemical applications, J. Mater. Chem. A, 2016, 4, 11046–11059 RSC.
- Y. Qi, H. Qi, J. Li and C. Lu, Synthesis, microstructures and UV-vis absorption properties of β-Ni(OH)2 nanoplates and NiO nanostructures, J. Cryst. Growth, 2008, 310, 4221–4225 CrossRef CAS.
- J. J. Krebs and W. G. Maisch, Exchange Effects in the Optical-Absorption Spectrum of Fe3+ in Al2O3, Phys. Rev. B, 1971, 4, 757–769 CrossRef.
- D. M. Sherman, The electronic structures of Fe3+ coordination sites in iron oxides: Applications to spectra, bonding, and magnetism, Phys. Chem. Miner., 1985, 12, 161–175 CrossRef CAS.
- D. M. Sherman and T. D. Waite, Electronic spectra of Fe3+ oxides and oxide hydroxides in the near IR to near UV., Am. Mineral., 1985, 70, 1262–1269 CAS.
- L. Poul, N. Jouini and F. Fievet, Layered hydroxide metal acetates (metal = zinc, cobalt, and nickel): Elaboration via hydrolysis in polyol medium and comparative study, Chem. Mater., 2000, 12, 3123–3132 CrossRef CAS.
- M. Piccinni, S. Bellani, G. Bianca and F. Bonaccorso, Nickel–Iron Layered Double Hydroxide Dispersions in Ethanol Stabilized by Acetate Anions, Inorg. Chem., 2022, 61, 4598–4608 CrossRef CAS PubMed.
- J. Tronto, M. J. dos Reis, F. Silvério, V. R. Balbo, J. M. Marchetti and J. B. Valim, In vitro release of citrate anions intercalated in magnesium aluminium layered double hydroxides, J. Phys. Chem. Solids, 2004, 65, 475–480 CrossRef CAS.
- J. Zhang, F. Zhang, L. Ren, D. G. Evans and X. Duan, Synthesis of layered double hydroxide anionic clays intercalated by carboxylate anions, Mater. Chem. Phys., 2004, 85, 207–214 CrossRef CAS.
- M. Meyn, K. Beneke and G. Lagaly, Anion-Exchange Reactions of Layered Double Hydroxides, Inorg. Chem., 1990, 29, 5201–5207 CrossRef CAS.
- A. v. Radha, P. V. Kamath and C. Shivakumara, Conservation of order, disorder, and ‘crystallinity’ during anion-exchange reactions among Layered Double Hydroxides (LDHs) of Zn with Al, J. Phys. Chem. B, 2007, 111, 3411–3418 CrossRef CAS PubMed.
- W. A. Slawiński, A. O. Sjåstad and H. Fjellvåg, Stacking Faults and Polytypes for Layered Double Hydroxides: What Can We Learn from Simulated and Experimental X-ray Powder Diffraction Data?, Inorg. Chem., 2016, 55, 12881–12889 CrossRef PubMed.
- D. R. Hines, G. T. Seidler, M. M. J. Treacy and S. A. Solin, Random stacking of a commensurate guest layer in an ordered host: Ni/Al layer-double-hydroxides, Solid State Commun., 1997, 101, 835–839 CrossRef CAS.
- F. Malherbe, L. Bigey, C. Forano, A. de Roy and J. P. Besse, Structural aspects and thermal properties of takovite-like layered double hydroxides pillared with chromium oxo-anions, J. Chem. Soc., Dalton Trans., 1999, 3831–3839 RSC.
- Z. Q. Li, C. J. Lu, Z. P. Xia, Y. Zhou and Z. Luo, X-ray diffraction patterns of graphite and turbostratic carbon, Carbon, 2007, 45, 1686–1695 CrossRef CAS.
- K. J. Putman, M. R. Rowles, N. A. Marks and I. Suarez-Martinez, The role of the 2D-to-3D transition in X-ray diffraction analysis of crystallite size, J. Phys.: Condens. Matter, 2021, 33, 294002 CrossRef CAS PubMed.
- J. W. Boclair, P. S. Braterman, J. Jiang, S. Lou and F. Yarberry, Layered double hydroxide stability. 2. Formation of Cr(III)-containing layered double hydroxides directly from solution, Chem. Mater., 1999, 11, 303–307 CrossRef CAS PubMed.
- J. Y. Bottero, D. Tchoubar, J. M. Cases and F. Fiessinger, Investigation of the hydrolysis of aqueous solutions of aluminum chloride. 2. Nature and structure by small-angle X-ray scattering, J. Phys. Chem., 1982, 86, 3667–3673 CrossRef CAS.
- J. Y. Bottero, J. M. Cases, F. Fiessinger and J. E. Poirier, Studies of hydrolyzed aluminum chloride solutions. 1. Nature of aluminum species and composition of aqueous solutions, J. Phys. Chem., 1980, 84, 2933–2939 CrossRef CAS.
- J. Y. Bottero, M. Axelos, D. Tchoubar, J. M. Cases, J. J. Fripiat and F. Fiessinger, Mechanism of formation of aluminum trihydroxide from keggin Al13 polymers, J. Colloid Interface Sci., 1987, 117, 47–57 CrossRef CAS.
- C. M. Flynn, Hydrolysis of inorganic iron(III) salts, Chem. Rev., 1984, 84, 31–41 CrossRef CAS.
- J. L. Jambor and J. E. Dutrizac, Occurrence and constitution of natural and synthetic ferrihydrite, a widespread iron oxyhydroxide, Chem. Rev., 1998, 98, 2549–2585 CrossRef CAS PubMed.
- P. V. Kamath, G. H. Annal Therese and J. Gopalakrishnan, On the Existence of Hydrotalcite-Like Phases in the Absence of Trivalent Cations, J. Solid State Chem., 1997, 128, 38–41 CrossRef CAS.
- G. Defontaine, L. J. Michot, I. Bihannic, J. Ghanbaja and V. Briois, Synthesis of NiGa layered double hydroxides. A combined extended X-ray absorption fine structure, small-angle X-ray scattering, and transmission electron microscopy study. 1. Hydrolysis in the pure Ni2 + system, Langmuir, 2003, 19, 10588–10600 CrossRef CAS.
-
D. R. Burgess, Critically Selected Stability Constants of Metal Complexes: Version 8.0 for Windows, National Institute of Standards and Technology, https://data.nist.gov/od/id/mds2-2154, (accessed 1 March 2024) Search PubMed.
- K. Mech, Influence of organic ligands on electrodeposition and surface properties of nickel films, Surf. Coat. Technol., 2017, 315, 232–239 CrossRef CAS.
- N. V. Plyasunova, Y. Zhang and M. Muhammed, Critical evaluation of thermodynamics of complex formation of metal ions in aqueous solutions. IV. Hydrolysis and hydroxo-complexes of Ni2+ at 298.15 K, Hydrometallurgy, 1998, 48, 43–63 CrossRef CAS.
- E. Konig, P. Hemmerich, C. K. Jorgensen, J. B. Neilands, R. S. Nybolm, D. Reinen and R. J. P. Williams, The nephelauxetic effect, Struct. Bonding, 1971, 9, 175–212 CrossRef.
- A. M. N. Silva, X. Kong, M. C. Parkin, R. Cammack and R. C. Hider, Iron(III) citrate speciation in aqueous solution, Dalton Trans., 2009, 8616–8625 RSC.
- C. F. Timberlake, 975. Iron–malate and iron–citrate complexes, J. Chem. Soc., 1964, 5078–5085 RSC.
- E. R. Still and P. Wikberg, Solution studies of systems with polynuclear complex formation. 2. The nickel(II) citrate system, Inorg. Chim Acta, 1980, 46, 153–155 CrossRef CAS.
- T. G. Spiro, L. Pape and P. Saltman, The Hydrolytic Polymerization of Ferric Citrate. I. The Chemistry of the Polymer, J. Am. Chem. Soc., 1967, 89, 5555–5559 CrossRef CAS.
- T. G. Spiro, G. Bates and P. Saltman, Hydrolytic polymerization of ferric citrate. II. Influence of excess citrate, J. Am. Chem. Soc., 1967, 89, 5559–5562 CrossRef CAS.
- I. Shweky, A. Bino, D. P. Goldberg and S. J. Lippard, Syntheses, Structures, and Magnetic Properties of Two Dinuclear Iron(III) Citrate Complexes, Inorg. Chem., 1994, 33, 5161–5162 CrossRef CAS.
- A. Bino, I. Shweky, S. Cohen, E. R. Bauminger and S. J. Lippard, A Novel Nonairon(III) Citrate Complex: A ‘Ferric Triple-Decker’, Inorg. Chem., 1998, 37, 5168–5172 CrossRef CAS.
- E. N. Baker, H. M. Baker, B. F. Anderson and R. D. Reeves, Chelation of nickel(II) by citrate. The crystal structure of a nickel-citrate complex, K2[Ni(C6H5O7)(H2O)2]2·4H2O, Inorg. Chim Acta, 1983, 78, 281–285 CrossRef CAS.
- M. Murrie, H. Stoeckli-Evans and H. U. Güdel, Assembly of Ni7 and Ni21 molecular clusters by using citric acid, Angew. Chem., Int. Ed., 2001, 40, 1957–1960 CrossRef CAS PubMed.
- M. Murrie, D. Biner, H. Stœckli-Evans and H. U. Güdel, Increasing the crystallisation temperature to access new spin clusters: Conversion of [Ni8(cit)6(OH)2(H2O) 2]10- to [Ni8(cit)6(OH)2]10-, Chem. Commun., 2003, 230–231 RSC.
- S. T. Ochsenbeln, M. Murrie, E. Rusanov, H. Stoeckli-Evans, C. Sekine and H. U. Gudel, Synthesis, structure, and magnetic properties of the single-molecule magnet [Ni21(cit)12(OH)10 (H2O)10]16-, Inorg. Chem., 2002, 41, 5133–5140 CrossRef PubMed.
- J. Strouse, S. W. Layten and C. E. Strouse, Structural Studies of Transition Metal Complexes of Triionized and Tetraionized Citrate. Models for the Coordination of the Citrate Ion to Transition Metal Ions in Solution and at the Active Site of Aconitase, J. Am. Chem. Soc., 1977, 99, 562–572 CrossRef CAS PubMed.
- E. Marklund, L.-O. Öhman, K. Grjotheim, L. V. Vilkov, H. V. Volden, K. Maartmann-Moe and S. Wold, Equilibrium and Structural Studies of Silicon(IV) and Aluminium(III) in Aqueous Solution. XXV. Composition and Stability of Aluminium Complexes with Methylmalonic Acid and Alanine, Acta Chem. Scand., 1990, 44, 353–357 CrossRef CAS.
- T. L. Feng, P. L. Gurian, M. D. Healy and A. R. Barron, Aluminum Citrate: Isolation and Structural Characterization of a Stable Trinuclear Complex, Inorg. Chem., 1990, 29, 408–411 CrossRef CAS.
- I. H. Hwang, P.-G. Kim, C. Kim and Y. Kim, Bis(μ-3-carboxy-2-hydroxypropane-1,2-dicarboxylato)bis(diaquazinc)–1,2-bis(pyridin-4-yl)ethene–water (1/1/2), Acta Crystallogr., Sect. E:Struct. Rep. Online, 2012, 68, m1305–m1306 CrossRef CAS PubMed.
- M. T. M. Al-Dajani, H. H. Abdallah, N. Mohamed, C. S. Yeap and H.-K. Fun, Diguanidinium bis(μ-2-hydroxypropane-1,2,3-tricarboxylato)bis[diaquazincate(II)] dihydrate, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2010, 66, m109–m110 CrossRef CAS PubMed.
- S. Capone, A. De Robertis, C. De Stefano and S. Sammartano, Formation and stability of zinc(II) and cadmium(II) citrate complexes in aqueous solution at various temperatures, Talanta, 1986, 33, 763–767 CrossRef CAS PubMed.
- G. H. R. Northover, Y. Mao, S. Blasco, R. Vilar, E. Garcia-España, C. Rocco, M. Hanif and D. J. Weiss, Synergistic use of siderophores and weak organic ligands during zinc transport in the rhizosphere controlled by pH and ion strength gradients, Sci. Rep., 2022, 12, 6774 CrossRef CAS PubMed.
- Y. F. Deng and Z. H. Zhou, Synthesis and crystal structure of a zinc citrate complex [Zn(H 2cit)(H 2O)] n, J. Coord. Chem., 2009, 62, 1484–1491 CrossRef CAS.
- P. Che, D. Fang, D. Zhang, J. Feng, J. Wang, N. Hu and J. Meng, Hydrothermal synthesis and crystal structure of a new two-dimensional zinc citrate complex, J. Coord. Chem., 2005, 58, 1581–1588 CrossRef CAS.
- I. A. Farbun, I. V. Romanova, T. E. Terikovskaya, D. I. Dzanashvili and S. A. Kirillov, Complex formation in the course of synthesis of zinc oxide from citrate solutions, Russ. J. Appl. Chem., 2007, 80, 1798–1803 CrossRef CAS.
- A. M. N. Silva, X. Kong and R. C. Hider, Determination of the pKa value of the hydroxyl group in the α-hydroxycarboxylates citrate, malate and lactate by 13C NMR: Implications for metal coordination in biological systems, BioMetals, 2009, 22, 771–778 CrossRef CAS PubMed.
- A. P. de Moura, R. C. Lima, E. C. Paris, M. S. Li, J. A. Varela and E. Longo, Formation of β-nickel hydroxide plate-like structures under mild conditions and their optical properties, J. Solid State Chem., 2011, 184, 2818–2823 CrossRef CAS.
- C. Rudolf, B. Dragoi, A. Ungureanu, A. Chirieac, S. Royer, A. Nastro and E. Dumitriu, NiAl and CoAl materials derived from takovite-like LDHs and related structures as efficient chemoselective hydrogenation catalysts, Catal. Sci. Technol., 2014, 4, 179–189 RSC.
-
J. E. Huheey, E. A. Keiter and R. L. Keiter, Inorganic Chemistry: Principles of Structure and Reactivity, Pearson College Div, 1993 Search PubMed.
- A. L. Tchougréeff and R. Dronskowski, Nephelauxetic effect revisited, Int. J. Quantum Chem., 2009, 109, 2606–2621 CrossRef.
- M. G. Brik, S. J. Camardello, A. M. Srivastava, N. M. Avram and A. Suchocki, Spin-Forbidden Transitions in the Spectra of Transition Metal Ions and Nephelauxetic Effect, ECS J. Solid State Sci. Technol., 2016, 5, R3067–R3077 CrossRef CAS.
- M. G. Brik, N. M. Avram and C. N. Avram, Comparative crystal field study of Ni2+ energy levels in NiCl2, NiBr2, and NiI2 crystals, Phys. B, 2006, 371, 43–49 CrossRef CAS.
- P. J. McCarthy and H. U. Güdel, Optical spectroscopy of exchange-coupled transition metal complexes, Coord. Chem. Rev., 1988, 88, 69–131 CrossRef CAS.
- J. Ferguson, H. J. Guggenheim and Y. Tanabe, The Effects of Exchange Interactions in the Spectra of Octahedral Manganese. II. Compounds, J. Phys. Soc. Jpn., 1966, 21, 692–704 CrossRef CAS.
- J. Ferguson, H. J. Guggenheim and Y. Tanabe, Absorption of Light by Pairs of Like and Unlike Transition-Metal Ions, Phys. Rev. Lett., 1965, 14, 737–738 CrossRef CAS.
- L. R. Bradshaw, J. W. May, J. L. Dempsey, X. Li and D. R. Gamelin, Ferromagnetic excited-state Mn2+ dimers in Zn1−xMnxSe quantum dots observed by time-resolved magnetophotoluminescence, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 115312 CrossRef.
- K.-I. Gondaira and Y. Tanabe, A Note on the Theory of Superexchange Interaction, J. Phys. Soc. Jpn., 1966, 21, 1527–1548 CrossRef CAS.
-
C. K. Jørgensen, in Progress in Inorganic Chemistry, 1962, vol. 4, pp. 73–124 Search PubMed.
-
C. K. Jørgensen, in Advance in Chemical Physics, 1963, vol. 5, pp. 33–146 Search PubMed.
- L. Trotochaud, S. L. Young, J. K. Ranney and S. W. Boettcher, Nickel-Iron oxyhydroxide oxygen-evolution electrocatalysts: The role of intentional and incidental iron incorporation, J. Am. Chem. Soc., 2014, 136, 6744–6753 CrossRef CAS PubMed.
- M. W. Louie and A. T. Bell, An investigation of thin-film Ni-Fe oxide catalysts for the electrochemical evolution of oxygen, J. Am. Chem. Soc., 2013, 135, 12329–12337 CrossRef CAS PubMed.
- G. Młynarek, M. Paszkiewicz and A. Radniecka, The effect of ferric ions on the behaviour of a nickelous hydroxide electrode, J. Appl. Electrochem., 1984, 14, 145–149 CrossRef.
- Y. Tanabe and S. Sugano, On the Absorption Spectra of Complex Ions. I, J. Phys. Soc. Jpn., 1954, 9, 753–766 CrossRef CAS.
-
S. Sugano, Y. Tanabe and H. Kamimura, in Pure and applied physics v. 33, 1970, vol. 33, pp. 332–333 Search PubMed.
- D. Di Girolamo, F. Matteocci, M. Piccinni, A. Di Carlo and D. Dini, Anodically electrodeposited NiO nanoflakes as hole selective contact in efficient air processed p-i-n perovskite solar cells, Sol. Energy Mater. Sol. Cells, 2020, 205, 110288 CrossRef CAS.
- X. Song, F. Yuan and L. M. Schoop, The properties and prospects of chemically exfoliated nanosheets for quantum materials in two dimensions, Appl. Phys. Rev., 2021, 8, 011312 CAS.
- Y. Li, B. Yang, S. Xu, B. Huang and W. Duan, Emergent Phenomena in Magnetic Two-Dimensional Materials and van der Waals Heterostructures, ACS Appl. Electron. Mater., 2022, 4, 3278–3302 CrossRef CAS.
- D. Soriano, M. I. Katsnelson and J. Fernández-Rossier, Magnetic Two-Dimensional Chromium Trihalides: A Theoretical Perspective, Nano Lett., 2020, 20, 6225–6234 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Chemicals used, synthesis procedure and experimental details, samples compositions, supplementary TEM images, supplementary XRD patterns and crystallographic data, supplementary pH-potentiometric titration profiles, speciation insights and affinity constants with references, ligand field analysis details and MATLAB code, comparison tables. See DOI: https://doi.org/10.1039/d4qi01475h |
|
| This journal is © the Partner Organisations 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Christian
Rossi
a,
Diego
Colombara
*ab and
Francesco
Bonaccorso
ab,
Christian
Rossi
a,
Diego
Colombara
*ab and
Francesco
Bonaccorso
 *bc
*bc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) of metal–citrate complexes dictate the availability of cations, influencing the nucleation of LDH nanosheets. Hence, this study focuses on the formation mechanism of citrate intercalated LDHs probed by pH-potentiometric titrations coupled to ligand field analysis of the electronic transitions. We demonstrate that our method is straightforwardly applicable to nickel-based LDHs, and can also be applied to ZnAl-LDHs, with some restrictions. So far, the formation mechanism of LDHs has been probed through pH titrations exclusively for all-inorganic syntheses.11,13,19 Jaśkaniec et al.12 and Tokudome et al.17 performed pH vs. time characterizations of their LDH synthesis procedures, both of which exploit coordination chemistry. However, pH vs. time characterizations provide information only on the hydrolysis rate of the ammonium (or hydroxide) releasing agent used during the synthesis, and not on the actual formation mechanism of LDH materials. On the contrary, a pH titration allows external control of the equivalents of hydroxide ions supplied to the reaction environment, and therefore, provides insights into the reaction mechanism. These understandings can be useful in designing new or improving the existing synthetic processes. Herein, we report how citrate anions alter the formation mechanism of LDHs from the classical precipitation pathway to a hydrolytic polymerization of metal–citrate complexes. Lastly, by interpreting the electronic spectra of the reaction environment and the final LDH product through the lens of the ligand field theory, we report the values of ligand field strength and Racah parameters of Ni2+ and Fe3+ in LDH crystal lattices. Then, we critically discuss the obtained results and possible implications by considering the current knowledge on electronic spectroscopy of nickel hydroxides, ferric oxides, and related materials.28–42
β) of metal–citrate complexes dictate the availability of cations, influencing the nucleation of LDH nanosheets. Hence, this study focuses on the formation mechanism of citrate intercalated LDHs probed by pH-potentiometric titrations coupled to ligand field analysis of the electronic transitions. We demonstrate that our method is straightforwardly applicable to nickel-based LDHs, and can also be applied to ZnAl-LDHs, with some restrictions. So far, the formation mechanism of LDHs has been probed through pH titrations exclusively for all-inorganic syntheses.11,13,19 Jaśkaniec et al.12 and Tokudome et al.17 performed pH vs. time characterizations of their LDH synthesis procedures, both of which exploit coordination chemistry. However, pH vs. time characterizations provide information only on the hydrolysis rate of the ammonium (or hydroxide) releasing agent used during the synthesis, and not on the actual formation mechanism of LDH materials. On the contrary, a pH titration allows external control of the equivalents of hydroxide ions supplied to the reaction environment, and therefore, provides insights into the reaction mechanism. These understandings can be useful in designing new or improving the existing synthetic processes. Herein, we report how citrate anions alter the formation mechanism of LDHs from the classical precipitation pathway to a hydrolytic polymerization of metal–citrate complexes. Lastly, by interpreting the electronic spectra of the reaction environment and the final LDH product through the lens of the ligand field theory, we report the values of ligand field strength and Racah parameters of Ni2+ and Fe3+ in LDH crystal lattices. Then, we critically discuss the obtained results and possible implications by considering the current knowledge on electronic spectroscopy of nickel hydroxides, ferric oxides, and related materials.28–42![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group). This indexing allows an easier comparison with the past literature patterns of the synthetic LDH materials and LDH minerals (Table S3†).1,44–46 The LDH diffraction patterns can be divided into three different regions. At scattering angles (2θ) below 30°, the “basal reflections” appear. These reflections are ascribed to the (00l) crystallographic planes, i.e., planes parallel to the hydroxide layers and perpendicular to the unit cell c axis.47 Thus, the 2θ position of the basal reflections reveals the unit cell c axis of LDHs (by the weighted mean of d00l lattice parameters, as described in ESI section 4†). Our analyses provide the following c axis lengths for the citrate-intercalated LDHs: 3.669 nm for NiAl-LDH, 3.680 nm for NiFe-LDH, and 3.665 nm for ZnAl-LDH. The thickness of one hydroxide layer plus one interlayered distance, called “basal spacing”, is equal to one third the length of the c axis (in the, R
m space group). This indexing allows an easier comparison with the past literature patterns of the synthetic LDH materials and LDH minerals (Table S3†).1,44–46 The LDH diffraction patterns can be divided into three different regions. At scattering angles (2θ) below 30°, the “basal reflections” appear. These reflections are ascribed to the (00l) crystallographic planes, i.e., planes parallel to the hydroxide layers and perpendicular to the unit cell c axis.47 Thus, the 2θ position of the basal reflections reveals the unit cell c axis of LDHs (by the weighted mean of d00l lattice parameters, as described in ESI section 4†). Our analyses provide the following c axis lengths for the citrate-intercalated LDHs: 3.669 nm for NiAl-LDH, 3.680 nm for NiFe-LDH, and 3.665 nm for ZnAl-LDH. The thickness of one hydroxide layer plus one interlayered distance, called “basal spacing”, is equal to one third the length of the c axis (in the, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group).2 These results are consistent with those from the past literature on citrate-intercalated MgAl-, NiAl- and ZnAl-LDHs synthetized by the anion exchange or the dissolution/precipitation routes.44–46 Instead, the second region, in the 2θ range of 30° to 55°, displays reflections from (0kl) and (h0l) crystallographic planes.
m space group).2 These results are consistent with those from the past literature on citrate-intercalated MgAl-, NiAl- and ZnAl-LDHs synthetized by the anion exchange or the dissolution/precipitation routes.44–46 Instead, the second region, in the 2θ range of 30° to 55°, displays reflections from (0kl) and (h0l) crystallographic planes.








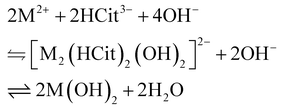



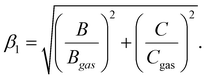
 . The ligand field analysis results are reported in Table 5. For Ni2+, located LDH crystal lattices, typical 10Dq values of ∼9000 cm−1, B values of ∼890 cm−1 and C values of ∼4000 cm−1 were computed, and these consistent with those from the past literature concerning nickel hydroxides and related materials.28,37,42 This indicates that the nature of trivalent metals in nickel-based LDHs has a negligible influence on the ligand field parameters of Ni2+. In addition, Ni2+, in both NiAl- and NiFe-LDH crystal lattices, has a
. The ligand field analysis results are reported in Table 5. For Ni2+, located LDH crystal lattices, typical 10Dq values of ∼9000 cm−1, B values of ∼890 cm−1 and C values of ∼4000 cm−1 were computed, and these consistent with those from the past literature concerning nickel hydroxides and related materials.28,37,42 This indicates that the nature of trivalent metals in nickel-based LDHs has a negligible influence on the ligand field parameters of Ni2+. In addition, Ni2+, in both NiAl- and NiFe-LDH crystal lattices, has a  of 0.849. By comparison, we performed the same ligand field analysis on the spectroscopic data published by Oliver-Tolentino et al.28 yielding a
of 0.849. By comparison, we performed the same ligand field analysis on the spectroscopic data published by Oliver-Tolentino et al.28 yielding a  of 0.862 for carbonate-intercalated nickel-based LDHs, whereas the data published by Poul et al.42 yielded a
of 0.862 for carbonate-intercalated nickel-based LDHs, whereas the data published by Poul et al.42 yielded a  of 0.860 for nickel hydroxide-acetate (which is isomorphous to LDHs). Hence, we conclude that the nephelauxetic ratio in nickel-based LDHs is neither significantly influenced by the nature of the trivalent metal cation hosted in the hydroxide layers nor by the nature of the anions amid them. In high-spin Fe3+, all possible ligand field transitions are spin-forbidden. However, in correlated materials, the spin restrictions are lifted because of super-exchange interactions, making formally spin-forbidden transitions observable.33,40,41,93–97 The 6A1g(6S) → 4Eg, 4A1g(4G) and 6A1g(6S) → 4Eg(4D) transitions, which are 10Dq-independent,39–41 directly provide the Fe3+ values of B and C, which are 916 and 2632 cm−1, respectively. To have a proper comparison, we also performed the same ligand field analysis on the spectroscopic data reported by Sherman et al.40,41 It follows that, according to (14), Fe3+ experiences a
of 0.860 for nickel hydroxide-acetate (which is isomorphous to LDHs). Hence, we conclude that the nephelauxetic ratio in nickel-based LDHs is neither significantly influenced by the nature of the trivalent metal cation hosted in the hydroxide layers nor by the nature of the anions amid them. In high-spin Fe3+, all possible ligand field transitions are spin-forbidden. However, in correlated materials, the spin restrictions are lifted because of super-exchange interactions, making formally spin-forbidden transitions observable.33,40,41,93–97 The 6A1g(6S) → 4Eg, 4A1g(4G) and 6A1g(6S) → 4Eg(4D) transitions, which are 10Dq-independent,39–41 directly provide the Fe3+ values of B and C, which are 916 and 2632 cm−1, respectively. To have a proper comparison, we also performed the same ligand field analysis on the spectroscopic data reported by Sherman et al.40,41 It follows that, according to (14), Fe3+ experiences a 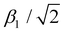 value of 0.747 in NiFe-LDH. This means that the nephelauxetic ratio of Fe3+ in NiFe-LDH is comparable to the 0.75 value of [Fe(H2O)6]3+ reported in literature,98,99 whereas the expected nephelauxetic ratio of Fe3+ in metal–oxide lattices ranges between 0.6 and 0.7, as shown in Fig. 5. In our opinion, these nephelauxetic similarities between Fe3+ in LDHs and [Fe(H2O)6]3+ are related to the performance of the NiFe-LDHs as catalysts in water-splitting applications.100–102 In ferric compounds, the magnitude of 10Dq is usually obtained from the energy of 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) transitions. However, we have not detected any contribution to the absorbance spectrum ascribable to the aforementioned transitions. According to the Tanabe mechanism, the interaction between super-exchanged ions and incident light involves only orbitals that are partially filled,33,94,96,97 and is described by the following Hamiltonian:
value of 0.747 in NiFe-LDH. This means that the nephelauxetic ratio of Fe3+ in NiFe-LDH is comparable to the 0.75 value of [Fe(H2O)6]3+ reported in literature,98,99 whereas the expected nephelauxetic ratio of Fe3+ in metal–oxide lattices ranges between 0.6 and 0.7, as shown in Fig. 5. In our opinion, these nephelauxetic similarities between Fe3+ in LDHs and [Fe(H2O)6]3+ are related to the performance of the NiFe-LDHs as catalysts in water-splitting applications.100–102 In ferric compounds, the magnitude of 10Dq is usually obtained from the energy of 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) transitions. However, we have not detected any contribution to the absorbance spectrum ascribable to the aforementioned transitions. According to the Tanabe mechanism, the interaction between super-exchanged ions and incident light involves only orbitals that are partially filled,33,94,96,97 and is described by the following Hamiltonian:
 represents the partial derivative of exchange constants between ai and bj with respect to E coordinates. Since the t2g orbitals of Ni2+ are full, they do not bring any contribution to (15), relegating the enhancement of ligand field transitions to the super-exchange interactions in Fe3+–O–Ni2+ bonds through eg orbitals. This explains the observed intensity of 6A1g(6S) → 4A1g(4G) and 6A1g(6S) → 4Eg(4D), since the former transition is related to the spin canting of eg orbitals, whereas the latter is related to a spin–flip in eg orbitals of Fe3+ (see tables of the matrix elements of Coulomb interactions in ref. 103 and 104). On the contrary, 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) do not benefit from (15) since both transitions involve an electron transfer from eg to t2g orbitals of Fe3+ with a concomitant spin–flip. The same phenomenon has been observed and described in the past for Ni2+-doped manganese halide perovskites.33,95 Given this, we could only rely on the energy of 6A1g(6S) → 4T1g(4P) for the 10Dq of Fe3+, which turns out to be 7049 cm−1. By comparison, this 10Dq value is approximatively half of the ∼15
represents the partial derivative of exchange constants between ai and bj with respect to E coordinates. Since the t2g orbitals of Ni2+ are full, they do not bring any contribution to (15), relegating the enhancement of ligand field transitions to the super-exchange interactions in Fe3+–O–Ni2+ bonds through eg orbitals. This explains the observed intensity of 6A1g(6S) → 4A1g(4G) and 6A1g(6S) → 4Eg(4D), since the former transition is related to the spin canting of eg orbitals, whereas the latter is related to a spin–flip in eg orbitals of Fe3+ (see tables of the matrix elements of Coulomb interactions in ref. 103 and 104). On the contrary, 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) do not benefit from (15) since both transitions involve an electron transfer from eg to t2g orbitals of Fe3+ with a concomitant spin–flip. The same phenomenon has been observed and described in the past for Ni2+-doped manganese halide perovskites.33,95 Given this, we could only rely on the energy of 6A1g(6S) → 4T1g(4P) for the 10Dq of Fe3+, which turns out to be 7049 cm−1. By comparison, this 10Dq value is approximatively half of the ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 expected for Fe3+ in oxide crystal lattices,39–41 being consistent with the linear relationship between Dq and the effective charge of the ligands.104 With known Dq, B and C values, the expected positions of the unobserved Fe3+ ligand field transitions are obtained from the Tanabe–Sugano diagram for high-spin d5 configurations (Scheme 1b). The 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) transitions are expected to fall at ∼590 and ∼480 nm, respectively.
000 cm−1 expected for Fe3+ in oxide crystal lattices,39–41 being consistent with the linear relationship between Dq and the effective charge of the ligands.104 With known Dq, B and C values, the expected positions of the unobserved Fe3+ ligand field transitions are obtained from the Tanabe–Sugano diagram for high-spin d5 configurations (Scheme 1b). The 6A1g(6S) → 4T1g(4G) and 6A1g(6S) → 4T2g(4G) transitions are expected to fall at ∼590 and ∼480 nm, respectively.

 , i.e.,
, i.e.,  . The dashed lines represent the expected range of
. The dashed lines represent the expected range of  in ferric compounds. Apart from NiFe-LDH, the nephelauxetic ratios were computed from the spectroscopic data reported in ref. 40 and 41.
in ferric compounds. Apart from NiFe-LDH, the nephelauxetic ratios were computed from the spectroscopic data reported in ref. 40 and 41.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
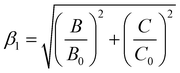 , see ref. 91 for details.
b Computed from the ν7 contribution to the absorbance of 6A1g(6S) → 4T1g(4P).
, see ref. 91 for details.
b Computed from the ν7 contribution to the absorbance of 6A1g(6S) → 4T1g(4P).