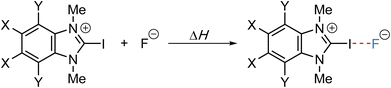A computational analysis of substituent effects in pnictogen-, chalcogen-, and halogen-bond donors

Abstract

The interaction enthalpies of differently substituted cationic pnictogen-, chalcogen-, and halogen-bond donors with the fluoride anion have been analyzed computationally. In general, electron-withdrawing substituents increase the binding strength of the Lewis acid, but the precise location of a given substituent (e.g., within the benzimidazolium group or within the aryl group) has only little influence on the reaction enthalpies. While no single parameter could be identified that describes all Lewis acids across the periodic table, both electrostatic (V_s,max) and charge-transfer approaches (LUMO energies) can be used to predict the binding enthalpies for structurally related compounds. The computational analysis eventually led to the synthesis of a new selenium-based catalyst with an improved catalytic activity in a transfer hydrogenation of imines.

---

Introduction

Noncovalent interactions like halogen, chalcogen, and pnictogen bonding have become increasingly popular over the last decades in various areas of chemistry and biology.¹ Amongst those, halogen bonding has been extensively studied with numerous applications in organocatalysis,^1,2 crystal engineering,³ material science,⁴ or pharmaceutical studies.⁵ The related chalcogen bond has been known in the solid state for more than 60 years.⁶ Most likely due to the success of halogen bonding, recent investigations also highlight the potential of chalcogen bonding in solution.^1a,c,d,6c,7 In contrast, the analogous pnictogen bond is still less explored.^1a,d,8

A typical explanation for these “unconventional” interactions relies on the σ-hole concept initially introduced by Clark, Murray, and Politzer in 2007.⁹ In this context, the σ-hole originates from an anisotropic distribution of the electron density around the respective halogen, chalcogen, or pnictogen atom that can be visualized on the electrostatic potential surface (Fig. 1). While halogen-bond donors possess only one σ-hole, chalcogen-bond donors display two and pnictogen-bond donors three σ-holes in elongation of the respective σ-bonds. Lewis bases can now interact with those areas to form the corresponding noncovalent interactions.

Fig. 1 Schematic representation of electrostatic contributions (in kJ mol^–1) through σ-holes for typical pnictogen-, chalcogen-, and halogen-bond donors (BzIm: 1,3-dimethylbenzimidazolium).

Besides the electrostatic explanation, n → σ* orbital interactions (i.e., Mulliken charge-transfer contributions)¹⁰ are often very important to describe the bonding interaction (Fig. 2).¹¹ Similar results have also been proposed involving π → π* interactions.¹² In line with the importance of charge transfer, “anti-electrostatic” halogen bonds between anions have been reported and benefit substantially from those charge-transfer contributions.¹³

Fig. 2 (A) Schematic representation of orbital contributions to noncovalent interactions via n → σ* and n/π → π* charge transfer (Z: central pnictogen, chalcogen or halogen atom of the Lewis acid); (B) representative lowest-unoccupied molecular orbitals for the chalcogen-bond donor BzImTeC₆F₅.

As the nature of these noncovalent interactions remains an ongoing discussion,^11c,14 researchers have wondered which parameters can be used to describe and predict the strengths of these interactions. In this context, the maximal values of the electrostatic potential (V_s,max) are often employed to correlate the observed effects with electrostatics.¹⁵ In contrast, the LUMO energies for the anti-bonding orbital are typically used to probe the influence of charge transfer on these noncovalent interactions.^15b,16 In 2020, Huber and colleagues introduced a new empirical parameter (Ω_σ*) to describe the Lewis acidity of 17 different halogen-bond donors.^16b The best predictions were obtained when both the depth of the σ-hole and the LUMO energy (σ*_C–I) were considered.

Based on calculated atomic polarizabilities,¹⁷ it is typically expected that the strength of the noncovalent interaction increases from top to bottom and from right to left within the periodic table (Table 1). Furthermore, electron-withdrawing groups in the vicinity of the respective central atom should generally lead to an increase in the interaction energies.^3c,18 While numerous studies confirmed the increasing interaction energies within one period,¹ comparisons between different periods (i.e., between the different noncovalent interactions) turned out to be less clear. Over the last decade, several computational and experimental studies tried to rationalize and predict the binding strengths of these noncovalent interactions and came up with different suggestions.¹⁹

Table 1 Calculated atomic polarizabilities (in a.u.) for elements of group 15–17

Group 15 (pnictogens)	Group 16 (chalcogens)	Group 17 (halogens)
a Calculated with MP2/aug-cc-pVTZ from ref. 17. b Calculated with GFN2 (this work).
N	O	F
7.1^a (7.5)^b	4.9^a (5.2)^b	3.4^a (3.6)^b
P	S	Cl
25.0^a (25.9)^b	19.3^a (19.6)^b	14.3^a (14.7)^b
As	Se	Br
29.7^a (31.0)^b	25.4^a (25.7)^b	20.5^a (20.8)^b
Sb	Te	I
43.3^a (44.8)^b	38.3^a (38.8)^b	32.3^a (32.5)^b

---

Frontera and colleagues compared the interaction energies of different halogen-, chalcogen-, and pnictogen-bonded complexes in 2013.²⁰ From crystallographic and computational data, the authors concluded that the reference Lewis base has a substantial influence on the relative interaction energies. While halogen bonding led to the energetically most stable complex for an amine base as reaction partner, pnictogen-bonded complexes were found to be most stable for the Lewis base benzene.

Dong, Li, and Scheiner later computationally studied very small model Lewis acids containing As, Se, and Br.²¹ The computed CCSD(T)-interaction energies for the fully hydrogenated acids (e.g., AsH₃, H₂Se, HBr) with the Lewis base NH₃ decreased in the series chalcogen > halogen > pnictogen. In contrast, an interaction strength halogen > chalcogen > pnictogen was determined for the mono-fluorinated acids.

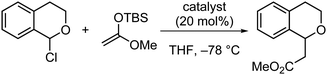
Eventually, Matile and colleagues experimentally determined the interaction energies of neutral C₆F₅-substituted Lewis acids with NBu₄Cl in THF (Table 2).^15a The interaction energies calculated from the experimental dissociation constants followed the expectations from atom polarizabilities (Table 1): Sb(C₆F₅)₃ binds chloride much stronger than the analogous As(C₆F₅)₃, Te(C₆F₅)₂, or I(C₆F₅). Computational investigations by Lu and colleagues confirmed these results shortly after.²² More importantly, the Matile group could also show that these trends carry over to the catalytic activities in model chloride-abstraction reactions. For the reaction involving 1-chloroisochromane with a silyl ketene acetal, the largest rate enhancement was observed for the strongest Lewis acid – the antimony catalyst (Table 2).^15a

Table 2 Comparison of chloride-binding energies (reported dissociation constants K_D and derived ΔG_int) and catalytic effects (k_cat/k_uncat) for different noncovalent catalysts in the chloride-abstraction reaction of chloroisochromane^15a

Catalyst	K D (M)	ΔGint (kJ mol^−1)	k cat/kuncat
Sb(C6F5)3	1.90 × 10^−5	−26.9	99
Te(C6F5)2	4.70 × 10^−4	−19.0	39
I(C6F5)	1.37 × 10^−3	−16.3	5

---

As most of the highly active catalysts bear at least one positive charge,^1,2 we now wondered about the influence of substituents on the Lewis acidities of structures featuring a cationic benzimidazolium substituent. The latter was chosen as it is a common structural motif in many catalysts.^1,2 To compare the relative strengths, we first calculated the reaction enthalpies (ΔH) for the reaction of each Lewis acid with the fluoride anion as reference Lewis base (eqn (1)) in CH₂Cl₂. We then tried to correlate the resulting enthalpies with different electronic properties to allow for the prediction of more active catalysts. The fluoride anion is similar to the halide anions, which are often used in experimental binding studies. However, as F⁻ is substantially smaller, steric effects should be less pronounced and the calculations procced slightly faster. Furthermore, this combination allows comparisons with other Lewis acids through fluoride anion affinities (FIA).²³

Results and discussion

Choice of the computational method

As described in more detail below, we relied on a computational method that was previously employed for related studies on noncovalent interactions.²⁴ Based on different benchmarks,²⁵ the chosen functionals M06-2X²⁶ and B2-PLYP²⁷ are generally expected to describe the underlying noncovalent interactions reasonably well. We decided to model the reactions in dichloromethane solutions to at least partially account solvation effects and to allow for a better comparison with solution-phase data. Additionally, the use of a continuum model also substantially reduces competing interactions arising from hydrogen bonds involving polarized C–H bond within cations, which can occur in the gas phase.²⁸ We, furthermore, considered interactions with all potential σ-holes of the catalyst (cf.Fig. 1). As the interaction energies often fall in a rather small energy range, we will only discuss reaction enthalpies (ΔH) in the manuscript and show the corresponding free energies (ΔG) in the SI. This should also reduce potential errors that arise from the calculation of entropy changes.²⁹

Comparison within the periodic table

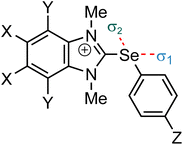
We started our analysis by comparing structurally related pnictogen-, chalcogen-, and halogen-bond donors that bear one cationic benzimidazolium (BzIm) substituent. For pnictogen and chalcogen atoms, both phenyl (C₆H₅) and perfluorophenyl (C₆F₅) groups were chosen as the remaining substituents (R², R³ in Fig. 1). While the former is a simpler synthetic target, the latter should be substantially more electron-withdrawing.³⁰ We further considered that the fluoride anion can coordinate to different positions (or σ-holes, see Fig. 1). In all cases, a coordination opposite the cationic benzimidazolium group is possible (σ₁ in Table 3), while an additional interaction opposite to the aryl substituent (C₆H₅ or C₆F₅) is also conceivable for chalcogen- and pnictogen-bond donors (σ₂ in Table 3). For symmetry reasons, however, σ-holes σ₂ and σ₃ of Fig. 1 lead to identical structures for the pnictogen-bond donors. Representative structures of the fluoride adducts are also depicted in Fig. 3. In line with expectations, the bonding angle for the halogen bond is linear (179.9°), while deviations are observed for the tellurium (σ₁: 163°; σ₂: 161°) and antimony compound (σ₁:160°; σ₂: 156°). While this could be an indication for an additional anion–π interaction, natural population analyses indicate that these interactions are substantially smaller compared to the charge-transfer contribution discussed above. Furthermore, similar energetic contributions have been calculated for the anion–π interaction for both coordination modes. Thus, we conclude that these additional interactions should only play a minor role for this investigation. Table 3 summarizes the calculated enthalpies for the reactions of those Lewis acids with the fluoride anion (eqn (1)).

Fig. 3 Graphical representations of the most stable fluoride-anion adducts of for a pnictogen-bond, chalcogen-bond, and halogen-bond donor with selected bond lengths (BzIm: 1,3-dimethylbenzimidazolium).

Table 3 Calculated enthalpies (ΔH, in kJ mol⁻¹) for the reactions of different noncovalent Lewis acids bearing one benzimidazolium substituent and the fluoride anion in CH₂Cl₂ with calculated V_s,max values (0.001 a.u. surface, in kJ mol⁻¹), and LUMO energies (in eV)

X	R	ΔH (σ1)	V s,max (σ1)	E LUMO (σ1)	ΔH (σ2)	V s,max (σ2)	E LUMO (σ2)
Cl	—	−46	407	1.17	—	—	—
Br	—	−64	434	−0.29	—	—	—
I	—	−106	455	−1.45	—	—	—

---

Ch	R	ΔH (σ1)	V s,max (σ1)	E LUMO (σ1)	ΔH (σ2)	V s,max (σ2)	E LUMO (σ2)
S	C6H5	−37	351	2.45	−50	411	2.41
Se	C6H5	−55	379	0.78	−54	421	1.08
Te	C6H5	−94	414	−0.49	−78	423	0.14
S	C6F5	−55	400	1.73	−67	441	1.74
Se	C6F5	−71	428	0.04	−76	462	0.27
Te	C6F5	−113	460	−1.15	−113	486	−0.69

---

Pn	R	ΔH (σ1)	V s,max (σ1)	E LUMO (σ1)	ΔH (σ2)	V s,max (σ2)	E LUMO (σ2)
P	C6H5	−52	312	2.63	−44	357	3.91
As	C6H5	−62	336	0.93	−49	362	2.15
Sb	C6H5	−111	379	−0.35	−83	391	1.17
P	C6F5	−93	345	1.81	−91	433	2.25
As	C6F5	−94	356	−0.01	−91	429	0.78
Sb	C6F5	−136	402	−1.03	−133	472	−0.16

---

In line with the general expectations (see above),^15a,17,21 our calculations show that the interaction energies are generally getting more favorable when moving down within a group. Replacing the additional C₆H₅ substituent with the electron-withdrawing C₆F₅ group results in stronger interactions for chalcogen and pnictogen bonds. This effect is particularly pronounced for the coordination opposite to this aryl group (σ₂) and leads to a substantial stabilization of up to 50 kJ mol⁻¹ (e.g., −83 vs. −133 kJ mol⁻¹ for the Sb compound). The electron-withdrawing nature of the additional fluorine atoms strongly influences both the electrostatic nature of the central atom as well as the charge-transfer contributions involving this group and consequently results in stronger interactions. Interestingly, a weaker but still substantial stabilization is also observed for the alternate coordination opposite to the BzIm group (σ₁; e.g., −111 vs. −136 kJ mol⁻¹ for the Sb compound). Thus, the calculations again highlight the general importance of electron-deficient substituents for strong noncovalent interactions.

When next comparing the interaction energies for both coordination sites (σ₁ and σ₂), our calculations do not provide a clear picture regarding any preferential binding site. While the interaction with the BzIm substituent via σ₁ seems to be slightly preferred within the C₆H₅ series, comparable interaction energies for σ₁ and σ₂ have been determined for the C₆F₅-substituted Lewis acids. This indicates that the neutral perfluorophenyl group has a similar influence on the interaction strength as the cationic benzimidazolium substituent.

To better understand these effects and to identify potential predictors for future analyses of related systems, we probed different parameters in correlations with the calculated reaction enthalpies. While more details are provided in the SI, only selected correlations are shown here for the sake of clarity.

We initially employed the atomic polarizabilities α of Table 1 as the most general predictor, which resulted in a modest correlation (r² = 0.61) when all values of Table 3 were considered (not shown in Fig. 4). Slightly better correlations were observed, when the analysis was restricted to the interaction with σ-hole σ₁ (r² = 0.77). Excellent correlations were eventually determined, when the different series (C₆H₅vs. C₆F₅) were treated separately (Fig. 4A). Similar observations were also made for the other σ-hole σ₂. The atomic polarizabilities α calculated for the actual structures of Table 3, however, resulted in slightly worse correlations.

Fig. 4 Correlations of the calculated reaction enthalpies ΔH for the complexation of a fluoride anion with (A) the atomic polarizability a; (B) the value of the electrostatic potential V_s,max (on the 0.001 a.u. surface); (C) the value of the electrostatic potential V_s,max (on the 0.01 a.u. surface); (D) the LUMO energy; and (E) the NBO charge on the central atom (X, Ch, or Pn).

We subsequently selected the magnitude of the corresponding σ-holes (V_s,max values) as another possible predictor. However, applying the typical isodensity value of 0.001 a.u. for the determination of the V_s,max values^3c,16b,31 generally resulted in very poor correlations. This predictor completely fails, when all reaction enthalpies of Table 3 are considered (r² = 0.22, see the SI) and no substantial improvement is observed for the different series (Fig. 4B). Interestingly, increasing the isodensity value to 0.01 a.u. resulted in a much better correlation (for all ΔH values: r² = 0.91), but scattering is observed particularly for the interaction with σ-hole σ₁ (Fig. 4C). As a consequence, our investigations indicate that V_s,max values might only work reliably for closely related structures and can be problematic when applied to structurally diverse compounds.

As charge transfer frequently contributes substantially to these noncovalent interactions,¹¹ we also tested, if the LUMO energies of the σ*-orbitals can be employed to predict the reaction enthalpies. Again, only a mediocre correlation (r² = 0.54) was observed for all reaction enthalpies. Here, no substantial improvement was observed for different subsets of the data (Fig. 4D). Similar to the V_s,max values, our investigations indicate that the LUMO energies might also be problematic for comparisons across the periodic table.

Finally, we considered different NBO charges³² (e.g., on the central atom Z of the Lewis acid) as a potential measure for the interaction energies, but those again resulted in poor correlations (Fig. 4E) and do not qualify as a suitable predictor.

In summary, our calculations indicate that it might be difficult to identify a unique parameter for the prediction of binding energies for comparisons across the periodic table. We also attempted to employ multiple regression analysis, but the results were not encouraging (see the SI). Although rather high adjusted r² values (0.86) were obtained, the statistical analysis also revealed a substantial multicollinearity (as indicated by variance inflation factors >8). This is most likely due to the fact that there already is at least some correlation between the different predictors (0.16 < r² < 0.78).

Overall, the electrostatic potential (V_s,max) resulted in the best correlations, but still suffered from substantial deviations. For a series of closely related compounds, the atomic polarizabilities α seem to work reasonably well across the periodic table and comes with the additional advantage that they can be determined very quickly.

Substituent effects in halogen-bond donors

As a general prediction for all noncovalent interactions seems to be more complex, we next wondered if better predictions are possible for closely related structures. Therefore, we next studied how substituents influence the interaction of different halogen-bond donors with the reference Lewis base F⁻. We selected the well-studied iodinated benzimidazolium motif as a representative example. These structures are conformationally rigid and only allow for one noncovalent interaction. Furthermore, they can serve as a simple benchmark for substituent effects. To reduce the number of potential conformers, we only included symmetrical structures with substituents in the 5,6- (X) or the 4,7-positions (Y) of the benzimidazole part. The substituents were chosen to include both strongly electron-donating and -withdrawing substituents and possess different Hammett substitution constants σ (OH: −0.37,³³ OMe: −0.27,³³ CH₃: −0.17,³³ H: 0.00, F: 0.06,³³ SH: 0.15,³³ I: 0.18,³³ Br: 0.23,³³ Cl: 0.23,³³ CBr₃: 0.29,³⁴ CCl₃: 0.46,³⁵ CF₃: 0.54,³³ CN: 0.66).³⁶ Substituents that could easily lead to self-aggregation (e.g., NR₂) were excluded from the analysis.³⁷ The calculated reaction enthalpies ΔH are summarized in Table 4 together with the respective V_s,max values and LUMO energies as potential predictors.

Table 4 Calculated enthalpies (ΔH, in kJ mol⁻¹) for the reactions of differently substituted iodine-based Lewis acids and the fluoride anion in CH₂Cl₂ with calculated V_s,max values (0.001 a.u. surface, in kJ mol⁻¹) and LUMO energy (in eV)

X	Y	ΔH	V s,max	E LUMO	X	Y	ΔH	V s,max	E LUMO
OH	H	−102	447	−1.35	H	OH	−105	445	−1.37
OMe	H	−100	437	−1.17	H	OMe	−103	434	−1.28
CH3	H	−102	444	−1.25	H	CH3	−104	449	−1.45
H	H	−106	455	−1.45	H	H	−106	455	−1.45
F	H	−110	473	−1.66	H	F	−113	475	−1.74
SH	H	−108	456	−1.43	H	SH	−110	453	−1.55
I	H	−111	460	−1.50	H	I	−114	458	−1.64
Br	H	−113	464	−1.53	H	Br	−115	463	−1.69
Cl	H	−112	472	−1.62	H	Cl	−117	471	−1.72
CBr3	H	−114	463	−1.48	H	CBr3	−115	453	−1.43
CCl3	H	−115	476	−1.69	H	CCl3	−115	466	−1.62
CF3	H	−117	490	−1.84	H	CF3	−117	483	−1.86
CN	H	−120	500	−1.93	H	CN	−121	491	−1.91

---

The reaction enthalpies for substituted halogen-bond donors fall in the range of −121 < ΔH < −100 kJ mol⁻¹, covering an energy window of almost 21 kJ mol⁻¹. This implies that the strongest Lewis acid will bind to the fluoride anion approx. four orders of magnitude stronger than the weakest representative. At a first glance, the positions of the substituents (5,6 vs. 4,7) only cause small differences in ΔH, with the 4,7-substituted halogen-bond donors being slightly stronger. As summarized in Fig. 5, we again analyzed which parameters are suitable for the prediction of the reaction enthalpies. For all tested parameters, much better correlations are obtained for the 5,6-disubstituted series and a lot of scattering is observed for the 4,7-disubstituted compounds. This can probably be attributed to additional steric interactions between the substituent Y and the additional N-CH₃ groups that result in partial distortion form planarity, which partially overrides the trends within the noncovalent interaction. The best single predictors for the 5,6-disubstituted systems are the substituent constant σ_p (r² = 0.94, Fig. 5A) and the calculated NBO-charge on the iodine atom (r² = 0.92, Fig. 5E). The other parameters (atomic polarizability α, V_s,max values, LUMO energies) result in worse correlations. Here, a change of the isosurface (see above) did not result in an improved result and very similar r²-values were obtained.

Fig. 5 Correlations of the calculated reaction enthalpies ΔH for the reaction of differently substituted halogen-bond donors with the fluoride anion with (A) Hammett's substituent constant σ_p; (B) the atomic polarizability α; (C) the value of the electrostatic potential V_s,max (on the 0.001 a.u. surface); (D) the LUMO energy; and (E) the NBO charge on the iodine atom.

In summary, for simple halogen-bond donors, substituent constants σ_p allow for a reasonable a priori prediction of the interaction strengths, while NBO charges can be used in an a posteriori fashion.

Substituent effects in chalcogen-bond donors

We next focused our analysis on related cationic selenium-based chalcogen-bond donors. One the one hand, those structures allow for an additional substituent in the para-position of the Se-phenyl group (Z), which adds another possibility to tune the reactivity of the Lewis acid. On the other hand, these chalcogen-bond donors also feature two coordination modes (σ₁ and σ₂, Fig. 1), which could be exploited for the future design of polydentate structures. Table 5 summarizes the calculated enthalpies for the reactions of these selenium-based Lewis acids with the fluoride anion (eqn (1)) as well as selected predictor values.

Table 5 Calculated enthalpies (ΔH, in kJ mol⁻¹) for the reactions of differently substituted selenium-based Lewis acids and the fluoride anion in CH₂Cl₂ with calculated V_s,max values (0.001 a.u. surface, in kJ mol⁻¹), and LUMO energy (in eV)

X	Y	Z	ΔH (σ1)	V s,max (σ1)	E LUMO (σ1)	ΔH (σ2)	V s,max (σ2)	E LUMO (σ2)
H	H	OH	−53	370	0.82	−52	417	1.26
H	H	OMe	−53	365	0.91	−52	410	1.34
H	H	CH3	−53	369	0.87	−53	413	1.23
H	H	H	−55	378	0.78	−54	421	1.08
H	H	F	−56	390	0.64	−56	430	0.98
H	H	SH	−56	375	0.81	−56	420	1.17
H	H	I	−59	383	0.72	−58	425	1.03
H	H	Br	−60	388	0.68	−59	429	0.96
H	H	Cl	−59	389	0.68	−59	430	0.96
H	H	CBr3	−61	389	0.68	−60	427	0.99
H	H	CCl3	−61	394	0.62	−60	432	0.94
H	H	CF3	−62	406	0.52	−61	437	0.73
H	H	CN	−64	411	0.45	−62	447	0.67
OH	H	H	−53	370	0.89	−53	401	1.18
OMe	H	H	−52	362	1.07	−52	399	1.27
CH3	H	H	−53	366	0.94	−53	406	1.22
H	H	H	−55	378	0.78	−54	421	1.08
F	H	H	−59	393	0.55	−59	439	0.91
SH	H	H	−57	378	0.78	−57	416	1.07
I	H	H	−59	381	0.73	−59	426	1.03
Br	H	H	−60	385	0.67	−60	431	0.99
Cl	H	H	−60	390	0.63	−60	428	0.94
CBr3	H	H	−61	386	0.70	−61	429	0.99
CCl3	H	H	−62	395	0.57	−62	439	0.89
CF3	H	H	−64	408	0.37	−63	453	0.73
CN	H	H	−66	416	0.27	−66	469	0.63
H	OH	H	−53	368	0.87	−53	402	1.21
H	OMe	H	−53	358	1.00	−53	388	1.31
H	CH3	H	−53	373	0.84	−54	405	1.16
H	H	H	−55	378	0.78	−54	421	1.08
H	F	H	−60	390	0.52	−59	433	0.90
H	SH	H	−57	375	0.75	−57	416	1.12
H	I	H	−60	380	0.69	−59	420	1.06
H	Br	H	−61	384	0.62	−60	424	1.03
H	Cl	H	−61	388	0.57	−59	429	0.98
H	CBr3	H	−65	376	0.78	−63	397	1.16
H	CCl3	H	−61	390	0.75	−60	417	1.02
H	CF3	H	−62	399	0.46	−61	436	0.85
H	CN	H	−64	408	0.32	−64	457	0.76

---

The reaction enthalpies for these chalcogen-bond donors fall in the range of −66 < ΔH < −52 kJ mol⁻¹. This energy window (14 kJ mol⁻¹) as well as the overall enthalpies are substantially smaller compared to the halogen-bond donor discussed above indicating that selenium-based chalcogen-bond donors are weaker Lewis acids compared to their iodinated analogues and also less influenced by substituent effects. Although electron-deficient substituents lead to stronger interactions, the substituent effect within the selenium compounds covers only three orders of magnitude in association constants. This finding generally agrees with the smaller polarizability of selenium compared to iodine (Table 1).

We furthermore noticed that the calculated enthalpies seem to be almost independent from the location of the substituent and the coordination of the fluoride anion. Generally, the enthalpies for different series correlate very well with each other (0.95 < r² < 0.99). As observed before for halogen-bond donors, slightly worse correlations were again obtained when 4,7-disubstituted systems were involved (Fig. 6A). The high correlation between the different series furthermore implies that a single substituent within the phenyl ring (position Z) has a comparable effect as two substituents within the benzimidazolium subunit (X or Y). This information could turn out useful for the future design of chalcogen-bond donors (e.g., as organocatalysts), as the same effect in terms of binding can be achieved from different structures.

Fig. 6 Correlations of the calculated reaction enthalpies ΔH for the reaction of differently substituted chalcogen-bond donors with the fluoride anion with (A) each other; (B) the atomic polarizability α; (C) the value of the electrostatic potential V_s,max; (D) the LUMO energy; and (E) the NBO charge on the selenium atom.

In line with the calculations described above, the interaction energies for both orientations (σ₁ and σ₂) are almost identical. This seems to be in contrast to earlier studies by Erdelyi, Huber, and colleagues on the interaction of related imidazolium systems with the bromide anion.^30a For the selenium-based Lewis acid, the authors find a substantial preference (ΔΔG = −13 kJ mol⁻¹) in favor of the interaction opposite to neutral substituent (σ₂ of Fig. 1). One explanation for the different interaction energies could result from the different azolium substituent, as benzimidazolium-containing structures are typically better catalysts compared to their imidazolium analogues.³⁸ Generally, the small energetic differences between the different binding modes highlights the structural diversity that could be associated with these structures and complicates the design of future catalysts.

As shown in Fig. 6, our attempts to identify a single predictor for all interactions within Table 5 failed. As the atomic polarizability α of the selenium ion does not change significantly for different substituents (Δα = 0.15), rather scattered correlations are observed with no general trend. Interestingly, positive correlations were found for Y- (purple symbols in Fig. 6) and Z-substitutions (orange), a negative correlation was observed for X-substituent (blue). The other predictors (V_s,max, E_LUMO, NBO charge) resulted in moderate correlations for all selenium compounds (Fig. 6C–E). Exclusion of the 4,7-disubstituted Lewis acids and separation of the different interaction modes (σ₁vs. σ₂) eventually resulted in improved correlations. As already observed before, multivariant regression analysis provided no further improvement (see the SI for details).

In summary, the DFT calculations provided valuable insights into the influence of the nature and location of different substituents in noncovalent organocatalysts. However, no single parameter could be identified in this study to predict the interaction energies across all studied Lewis acids. For structurally related compounds, both V_s,max values as well as LUMO energies resulted in useful correlations that could have predictive character. These findings are reminiscent of the use of pK_a values to predict the nucleophilicity, which also only work well for a series of related compounds.³⁹

Application in catalysis

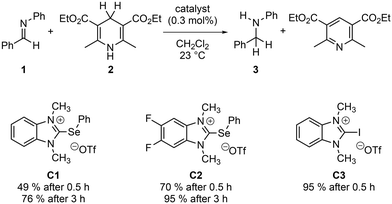
Finally, we wanted to probe the computational results in a catalytic reaction. Therefore, we selected the 5,6-difluoro substituted selenium Lewis acid C2 as synthetically accessible target. To our knowledge, this motive has not been used in catalysis so far and should be more Lewis acidic compared to the unsubstituted analog C1 based on our calculations. The synthesis routes for both C1 and C2 are summarized in Scheme 1 and follow modified literature procedures.^30a,40

Scheme 1 Synthesis of the chalcogen-bond donors C1 and C2 following literature protocols.^30a,40

For both salts, suitable crystals could be isolated that allow a characterization of the solid-state structure by X-ray diffraction. In line with a previous report in the literature at 170 K,^30a we found for C1 two crystallographically independent molecules in the asymmetric unit denoted as C1a and C1b. The molecular structures of C1a and C1b are shown in Fig. 7 and display both the feature of the classical Se⋯O noncovalent interaction of the triflate anion with the selenium atom (3.065(1) and 3.132(1) Å) as well as a contribution from an anion–π interaction (3.036(2) and 2.977(2) Å), albeit in different strengths. Interestingly, no obvious comparable interaction between cation and anion was observed within the solid-state structure of C2. Instead, two-dimensional layers can be observed that are dominated by noncovalent interactions between the selenium atom and the aromatic rings of another molecule (see the SI).

Fig. 7 Crystal structures of C1 (2492387, top) and C2 (2492388, bottom); displacement ellipsoids are drawn at the 50% probability level.

As thermodynamics do not necessarily correlate with kinetic effects, we wanted to at least briefly assess the catalytic performance of these structures. For comparison, we also selected the monodentate halogen-bond donor C3. The catalysts were employed in the reduction of an typical imine 1 with the Hantzsch ester (2) in dichloromethane. These and related transfer hydrogenation reactions have already been studied in the context of noncovalent catalysis (Scheme 2).⁴¹ While no background reaction (yield <1%) was observed in the absence of any catalyst, all Lewis acids are highly active in this reaction. In line with the computational results from above, the catalytic performance increases in the series C1 < C2 < C3. This nicely illustrates that the thermodynamic findings discussed above also carry over to the catalytic activities and eventually allow for the design of improved catalysts.

Scheme 2 Catalytic performance of noncovalent catalysts C1–3 in a model transfer hydrogenation.

Conclusions

This work aimed for a better understanding of the influence of substituents within cationic pnictogen-, chalcogen-, and halogen-bond donors. Therefore, the interaction enthalpies with the fluoride anion have been calculated for a large selection of different Lewis acids. In general, our analysis implies again that electron-withdrawing substituents result in the strongest interactions. However, the calculations also reveal that the position of the substituent (e.g., on the charged benzimidazolium system or within the additional aryl substituent) is less important. Furthermore, our DFT study indicates that the different coordination sites (i.e., the different σ-holes) result in comparable interaction strengths. Based on our analysis, there is no general single parameter that could be used to reliably predict the binding strengths. While atomic polarizabilities α resulted in reasonable correlations for comparisons across the periodic table (r² around 0.95), electrostatic (V_s,max) and charge-transfer (E_LUMO) parameters behaved almost equally for halogen- and chalcogen-bond donors (r² around 0.85). Following the suggestions of the calculations, we were subsequently able to identify a selenium-based catalyst for the hydrogenation of imines with an improved performance. This underlines the broader applicability of our analysis for the future development of noncovalent organocatalysts.

Computational details

The conformational space for each structure was explored with the meta-dynamics package Conformer Rotamer Ensemble Sampling Tool (CREST).⁴² The default parameters were used in combination with GFN2-xTB.⁴³ All structures were subsequently fully optimized with the meta-hybrid M06-2X functional,²⁶ the triple-ζ basis set 6-311+G(d,p) for H–Ge, and the aug-cc-pVTZ basis set with the corresponding pseudopotential (commonly called aug-cc-pVTZ-PP) for As–I.⁴⁴ Vibrational analysis verified that each structure was a minimum. Thermal corrections were calculated from unscaled harmonic vibrational frequencies at the same level of theory. Entropic contributions to free energies were obtained from partition functions evaluated with Grimme's quasi-harmonic approximation.^29b This method employs the free-rotor approximation for all frequencies below 100 cm⁻¹, the rigid-rotor-harmonic-oscillator (RRHO) approximation for all frequencies above 100 cm⁻¹, and a damping function to interpolate between the two expressions. Energies were subsequently calculated with single-point calculations employing the double-hybrid B2PLYP functional,²⁷ Grimme's D3 correction with Becke–Johnson damping,⁴⁵ the large quadruple-ζ basis set def2-QZVPP with the associated pseudopotential for I and corresponding auxiliary basis sets,⁴⁶ and the modified SMD solvation model for dichloromethane.⁴⁷ All calculations involving M06-2X were performed with Gaussian 16,⁴⁸ while all B2PLYP calculations were performed with ORCA 5.⁴⁹

Conflicts of interest

There are no conflicts to declare.

Data availability

The primary research data have been included as part of the supplementary information (SI). Supplementary information: computational and experimental investigations. See DOI: https://doi.org/10.1039/d5ob01575h.

CCDC 2492387 (C1) and 2492388 (C2) contain the supplementary crystallographic data for this paper.^50a,b

Acknowledgements

We gratefully acknowledge financial support by the Deutsche Forschungsgemeinschaft (BR 5154/4-1, BR 5154/6-1) and Chemnitz University of Technology. We thank Patrick Weber (University of Cologne) for helpful discussions. We are also thankful to the DFG for supporting the research infrastructure at Chemnitz University of Technology via projects 317545327, 432922437, and 530103110.

References

1. (a) D. Jovanovic, M. Poliyodath Mohanan and S. M. Huber, Angew. Chem., Int. Ed., 2024, e202404823; (b) Y. Li, C. Zhao, Z. Wang and Y. Zeng, J. Phys. Chem. A, 2024, 128, 507–527; (c) G. Sekar, V. V. Nair and J. Zhu, Chem. Soc. Rev., 2024, 53, 586–605; (d) M. Breugst and J. J. Koenig, Eur. J. Org. Chem., 2020, 5473–5487; (e) J. Bamberger, F. Ostler and O. G. Mancheño, ChemCatChem, 2019, 11, 5198–5211; (f) M. Breugst, D. von der Heiden and J. Schmauck, Synthesis, 2017, 3224–3236.
2. (a) R. L. Sutar and S. M. Huber, ACS Catal., 2019, 9, 9622–9639; (b) D. Bulfield and S. M. Huber, Chem. – Eur. J., 2016, 22, 14434–14450.
3. (a) J. Teyssandier, K. S. Mali and S. De Feyter, ChemistryOpen, 2020, 9, 225–241; (b) M. Saccone and L. Catalano, J. Phys. Chem. B, 2019, 123, 9281–9290; (c) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601; (d) A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524.
4. (a) A. Liu and Y.-W. Yang, Coord. Chem. Rev., 2025, 530, 216488; (b) R. Kampes, S. Zechel, M. D. Hager and U. S. Schubert, Chem. Sci., 2021, 12, 9275–9286; (c) L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195.
5. (a) S. Vaas, M. O. Zimmermann, D. Schollmeyer, J. Stahlecker, M. U. Engelhardt, J. Rheinganz, B. Drotleff, M. Olfert, M. Lämmerhofer, M. Kramer, T. Stehle and F. M. Boeckler, J. Med. Chem., 2023, 66, 10202–10225; (b) M. R. Scholfield, C. M. V. Zanden, M. Carter and P. S. Ho, Protein Sci., 2013, 22, 139–152; (c) P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794.
6. (a) P. C. Ho, J. Z. Wang, F. Meloni and I. Vargas-Baca, Coord. Chem. Rev., 2020, 422, 213464; (b) P. Scilabra, G. Terraneo and G. Resnati, Acc. Chem. Res., 2019, 52, 1313–1324; (c) L. Vogel, P. Wonner and S. M. Huber, Angew. Chem., Int. Ed., 2018, 58, 1880–1891; (d) R. E. Rosenfield Jr., R. Parthasarathy and J. D. Dunitz, J. Am. Chem. Soc., 1977, 99, 4860–4862; (e) R. Weiss, C. Schlierf and K. Schloter, J. Am. Chem. Soc., 1976, 98, 4668–4669; (f) N. W. Alcock, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1972, vol. 15, pp. 1–58; (g) H. Steeple, Acta Crystallogr., 1961, 14, 847–853.
7. (a) G. Gao, D. Xie and P.-P. Zhou, Asian J. Org. Chem., 2025, 14, e202500098; (b) K. T. Mahmudov, M. N. Kopylovich, M. F. C. Guedes da Silva and A. J. L. Pombeiro, Dalton Trans., 2017, 46, 10121–10138.
8. S. Scheiner, Acc. Chem. Res., 2012, 46, 280–288.
9. (a) J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2007, 107, 2286–2292; (b) T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296; (c) J. Murray, P. Lane and P. Politzer, J. Mol. Model, 2009, 15, 723–729.
10. R. S. Mulliken, J. Am. Chem. Soc., 1950, 72, 600–608.
11. (a) H. A. Bent, Chem. Rev., 1968, 68, 587–648; (b) C. Wang, D. Danovich, Y. Mo and S. Shaik, J. Chem. Theory Comput., 2014, 10, 3726–3737; (c) L. de Azevedo Santos, T. C. Ramalho, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Eur. J., 2023, 29, e202203791.
12. C. W. Kellett, P. Kennepohl and C. P. Berlinguette, Nat. Commun., 2020, 11, 3310.
13. (a) J. Holthoff, E. Engelage, R. Weiss and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 11150–11157; (b) C. Loy, J. M. Holthoff, R. Weiss, S. M. Huber and S. V. Rosokha, Chem. Sci., 2021, 12, 8246–8251.
14. (a) T. Brinck and A. N. Borrfors, J. Mol. Model., 2022, 28, 275; (b) J. Řezáč and A. de la Lande, Phys. Chem. Chem. Phys., 2017, 19, 791–803; (c) S. M. Huber, E. Jimenez-Izal, J. M. Ugalde and I. Infante, Chem. Commun., 2012, 48, 7708–7710.
15. (a) S. Benz, A. I. Poblador-Bahamonde, N. Low-Ders and S. Matile, Angew. Chem., Int. Ed., 2018, 57, 5408–5412; (b) X. Li, Y. Liu, W. Wang and Y. Wang, J. Am. Chem. Soc., 2025, 147, 3233–3242.
16. (a) T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2019, 58, 8922–8926; (b) E. Engelage, D. Reinhard and S. M. Huber, Chem. – Eur. J., 2020, 26, 3843–3861.
17. A. Bauzá, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517.
18. (a) A. Bauzá, D. Quiñonero, A. Frontera and P. M. Deyà, Phys. Chem. Chem. Phys., 2011, 13, 20371–20379; (b) S. Portela, J. J. Cabrera-Trujillo and I. Fernández, J. Org. Chem., 2021, 86, 5317–5326.
19. (a) S. Scheiner, Faraday Discuss., 2017, 203, 213–226; (b) K. J. Donald, N. Pham and P. Ravichandran, J. Phys. Chem. A, 2023, 127, 10147–10158; (c) L. E. Bickerton, A. Docker, A. J. Sterling, H. Kuhn, F. Duarte, P. D. Beer and M. J. Langton, Chem. – Eur. J., 2021, 27, 11738–11745.
20. A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, CrystEngComm, 2013, 15, 3137–3144.
21. W. Dong, Q. Li and S. Scheiner, Molecules, 2018, 23, 1681.
22. L. Lu, Y. Lu, Z. Zhu and H. Liu, J. Mol. Model., 2020, 26, 16.
23. (a) K. O. Christe, D. A. Dixon, D. McLemore, W. W. Wilson, J. A. Sheehy and J. A. Boatz, J. Fluorine Chem., 2000, 101, 151–153; (b) T. E. Mallouk, G. L. Rosenthal, G. Mueller, R. Brusasco and N. Bartlett, Inorg. Chem., 1984, 23, 3167–3173; (c) P. Erdmann, J. Leitner, J. Schwarz and L. Greb, ChemPhysChem, 2020, 21, 987–994; (d) P. Erdmann, M. Schmitt, L. M. Sigmund, F. Krämer, F. Breher and L. Greb, Angew. Chem., Int. Ed., 2024, 63, e202403356.
24. (a) T. Arndt, P. K. Wagner, J. J. Koenig and M. Breugst, ChemCatChem, 2021, 13, 2922–2930; (b) J. J. Koenig, T. Arndt, N. Gildemeister, J.-M. Neudörfl and M. Breugst, J. Org. Chem., 2019, 84, 7587–7605; (c) M. Breugst, E. Detmar and D. von der Heiden, ACS Catal., 2016, 6, 3203–3212.
25. (a) S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918–1931; (b) B. Brauer, M. K. Kesharwani, S. Kozuch and J. M. Martin, Phys. Chem. Chem. Phys., 2016, 18, 20905–20925.
26. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
27. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
28. (a) C. E. Cannizzaro and K. N. Houk, J. Am. Chem. Soc., 2002, 124, 7163–7169; (b) S. Ghosh, P. Chopra and S. Wategaonkar, Phys. Chem. Chem. Phys., 2020, 22, 17482–17493.
29. (a) S.-C. Liu, X.-R. Zhu, D.-Y. Liu and D.-C. Fang, Phys. Chem. Chem. Phys., 2023, 25, 913–931; (b) S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964; (c) R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2011, 115, 14556–14562.
30. (a) S. Akbaba, T. Steinke, L. Vogel, E. Engelage, M. Erdelyi and S. M. Huber, Chem. – Eur. J., 2024, 30, e202400608; (b) D. Pal, T. Steinke, L. Vogel, E. Engelage, S. Heinrich, D. Kutzinski and S. M. Huber, Adv. Synth. Catal., 2023, 365, 2718–2723; (c) L. Bao, X. Kong and Y. Wang, Asian J. Org. Chem., 2020, 9, 757–760.
31. (a) R. Weiss, E. Aubert, P. Pale and V. Mamane, Angew. Chem., Int. Ed., 2021, 60, 19281–19286; (b) M. Kolář, J. Hostaš and P. Hobza, Phys. Chem. Chem. Phys., 2014, 16, 9987–9996; (c) B. Zhou and F. P. Gabbaï, Organometallics, 2021, 40, 2371–2374.
32. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7, 2018.
33. D. H. McDaniel and H. C. Brown, J. Org. Chem., 1958, 23, 420–427.
34. W. A. Sheppard, Trans. N. Y. Acad. Sci., 1967, 29, 700–710.
35. O. Exner, Collect. Czech. Chem. Commun., 1966, 31, 65–89.
36. J. D. Roberts and E. A. McElhill, J. Am. Chem. Soc., 1950, 72, 628.
37. (a) E. Uran, L. Fotović, N. Bedeković, V. Stilinović and D. Cinčić, Crystals, 2021, 11, 529; (b) V. Nemec and D. Cinčić, CrystEngComm, 2016, 18, 7425–7429.
38. S. H. Jungbauer and S. M. Huber, J. Am. Chem. Soc., 2015, 137, 12110–12120.
39. F. G. Bordwell, T. A. Cripe and D. L. Hughes, in Nucleophilicity, American Chemical Society, 1987, vol. 215, ch. 9, pp. 137–153.
40. N. E. Kanitz, M. Fresia, P. G. Jones and T. Lindel, Eur. J. Org. Chem., 2021, 3573–3578.
41. (a) J. Zhang, J. Wei, W.-Y. Ding, S. Li, S.-H. Xiang and B. Tan, J. Am. Chem. Soc., 2021, 143, 6382–6387; (b) M. Yang, D. Tofan, C.-H. Chen, K. M. Jack and F. P. Gabbaï, Angew. Chem., Int. Ed., 2018, 57, 13868–13872; (c) S. Benz, J. Mareda, C. Besnard, N. Sakai and S. Matile, Chem. Sci., 2017, 8, 8164–8169; (d) S. Benz, J. López-Andarias, J. Mareda, N. Sakai and S. Matile, Angew. Chem., Int. Ed., 2017, 56, 812–815.
42. (a) S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862; (b) P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
43. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
44. (a) R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806; (b) K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
45. (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
46. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065; (c) A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597.
47. (a) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396; (b) E. Engelage, N. Schulz, F. Heinen, S. M. Huber, D. G. Truhlar and C. J. Cramer, Chem. – Eur. J., 2018, 24, 15983–15987.
48. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016.
49. (a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327; (c) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
50. (a) CCDC 2492387: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2pnjlh; (b) CCDC 2492388: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2pnjmj.

---