Computational analysis of energetic features and intermolecular interactions in protein-inhibitor USP7 complexes

Abstract

Ubiquitin-specific proteases (USPs) play crucial roles in cellular processes and have emerged as promising therapeutic targets for various diseases, including cancer. This study utilizes a multi-faceted computational approach to investigate the binding mechanisms of small molecule inhibitors to USP7, a key member of the USP family. We combine transferable aspherical atom model (TAAM) calculations, density functional theory (DFT) analysis, and other computational tools to elucidate the electrostatic landscapes and non-covalent interactions in selected USP7-inhibitor complexes. Our findings demonstrate that electrostatic interactions are the dominant force in USP7-inhibitor binding, with charged residues contributing significantly to binding energies. Furthermore, the TAAM-based UBDB + EPMM method accurately captured the overall charge distribution, showing strong agreement with DFT calculations. We identified key residues involved in inhibitor binding, including previously overlooked contributors such as E298 and M407. The use of Hirshfeld surfaces and electrostatic potential (ESP) mapping provided detailed insights into the charge distribution and complementarity between USP7 and its inhibitors. Our results revealed that compounds with more concentrated positive charge distributions exhibited higher affinities Additionally, reduced density gradient (RDG) analysis offered further insight into the various non-covalent interactions at play. This study underscores the importance of long-range electrostatic interactions that extend beyond the immediate binding pocket. The insights gained from this work advance our understanding of USP7 inhibition and provide a valuable framework for the design of selective inhibitors targeting other members of the USP family.

---

1. Introduction

The ubiquitin-proteasome system (UPS) regulates a variety of cellular processes, including DNA repair, stress responses, and cell proliferation.^1,2 In the UPS, proteins are tagged for degradation with ubiquitin through a cascade of enzymatic reactions involving ubiquitin-activating (E1), ubiquitin-conjugating (E2), and ubiquitin ligase (E3) enzymes.³ Ubiquitinated proteins are processed by the 26S proteasome, which controls their cellular levels and eliminates misfolded or damaged protein molecules.⁴ Dysregulation of UPS is implicated in the pathogenesis of numerous diseases, including cancer, neurodegenerative disorders, and inflammation.^5,6 Within the UPS, a key role is played by deubiquitinating enzymes (DUBs), a diverse group of proteases responsible for the removal of ubiquitin.^7,8 DUBs regulate protein stability, activity, and subcellular localization of their targets, thereby providing an additional level of control over cellular processes including protein half-life, signal transduction, stress response, genome integrity, and cell cycle control.^7,9,10 DUBs are classified into several distinct families based on their functions, catalytic mechanisms and structural features. The main families include ubiquitin-specific proteases (USPs), ubiquitin C-terminal hydrolases (UCHs) and ovarian tumour proteases (OTUs), among others.^7,11 The USP family, the largest among DUBs, is characterized by a conserved catalytic domain comprising fingers, thumb, and palm motifs, with a cysteine–histidine–aspartate/asparagine catalytic triad.¹² USP7's catalytic domain switches between active and inactive conformations, with ubiquitin binding triggering the realignment of its catalytic triad.^13–15 Additional domains, such as DUSP and UBL (ubiquitin-like), regulate activity, mediate protein interactions, and determine substrate specificity.¹⁶ Dysregulation of USPs is linked to various diseases, particularly cancer and neurodegenerative disorders.^16,17 USP7, also known as herpesvirus-associated ubiquitin-specific protease (HAUSP), has emerged as a promising therapeutic target due to its role in cancer progression through stabilization of MDM2, which promotes p53 degradation and suppresses apoptosis.¹⁸ USP7 also regulates other cancer-related proteins, such as FOXO4,¹⁹ PTEN²⁰ and FOXP3,²¹ and plays a role in Parkinson's disease.²²

The first generation of deubiquitinase inhibitors (e.g., b-AP15, P5091, P22077, PR-619 and HBX41108) had limited selectivity and weak potency, with IC₅₀ values in the micromolar range.²³ The second generation of the inhibitors is characterised by superior selectivity and affinity to their targets including USP1 (ML323,²⁴ pimozide²⁵), USP2 (ML364²⁶), USP7 (FT671,¹⁴ GNE-6776²⁷ and XL188²⁸) and USP14 (IU1 series²⁹). Chemotypes and structural formulae of selected USP inhibitors relevant for this study are provided in Fig. 1 and Table S1.† Despite sharing a conserved catalytic domain, most USPs exhibit unique allosteric sites and distinct conformational dynamics (e.g., USP7's higher flexibility compared to USP14).^13,18 These structural differences enable selective inhibition, offering promising therapeutic strategies for cancer and neurodegenerative disorders.³⁰ The most potent inhibitors exhibited binding affinity as low as 0.2 nM and blocked USP7 activity at sub-micromolar concentrations in cellular experiments (see Table 1 and Table S1†).³¹ Tested compounds induced tumour cell death and enhanced the cytotoxicity of other therapeutic agents such as PIM kinase inhibitors and DNA-damaging agents.¹⁶ Most inhibitors bind to a hydrophobic, ubiquitin-binding pocket near the thumb-palm cleft of USP7, distant from the catalytic cysteine.^16,18 Upon binding, the inhibitor molecule locks USP7 in an inactive apo state, preventing its transition to the active conformation. These inhibitors primarily interact with specific acidic residues of USP7, modulating its preference for ubiquitin chains with free Lys48 side chains. Key residues involved in USP7 binding include D295, V296, Q297, Q351, F409, K420, H456, N460, H461, Y465 and Y514. A distinct family of inhibitors was found to target an alternative binding cavity in USP7; however, these compounds showed lower affinity, with the best IC₅₀ value of 0.75 μM.^27,32 The inhibitory effects of these compounds stem from specific interactions and conformational changes in USP7. Geometric analysis of USP7-inhibitor complexes revealed multiple binding contributions, including Coulomb interactions, hydrogen bonding, hydrophobic effects and π–π stacking. Despite available experimental structures, comprehensive computational studies of USP-inhibitor complexes remain scarce, highlighting a significant gap in current understanding of this topic. Elucidating the intricate binding mechanisms of inhibitors to USP7 is paramount for the development of more efficacious therapeutic agents. This study aims to provide a more nuanced characterization of binding site residues and their interactions with inhibitors, utilizing state-of-the-art computational tools. Such an approach offers valuable insights that can inform the rational design of novel USP7 inhibitors, potentially leading to improved therapeutic outcomes.

Fig. 1 Structures of selected USP inhibitors. Black rectangular indicated protonation sites. Fragments displaying very high similarity across different chemical scaffolds are highlighted using green. Fragments highly specific for a given inhibitors are highlighted in red. Each compounds is labelled to indicate its PDB entry.

Table 1 Selected properties of the studied ligands extracted from the literature and PDB database as well as electrostatic energies from the UBDB + EPMM method

PDB entry	Ligand entry	Resolution [Å]	IC50	K d	Total energy [kcal mol^−1]	Binding site energy [kcal mol^−1]	Binding to total site energy ratio [%]	Ref.
6VN3	R3Y	2.73	1.2 nM	—	−283.50	−170.73	60.2	30
6VN4	R4D	2.69	8.2 μM	—	−90.50	−74.38	82.2	30
6M1K	EZF	2.25	40.8 nM	78 nM	−246.35	−149.34	60.6	67
6F5H	CQ5	2.84		90 nM	−295.45	−160.32	54.3	68
5N9T	8QQ	1.73	—	—	−277.01	−174.19	62.9	31
5VS6	9QD	2.27	22 nM	—	−223.42	−95.80	42.9	29
5WHC	AJJ	2.55	90 nM	—	−172.22	−137.35	79.8	32
5UQW	8JM	2.84	79 μM	—	−174.44	−150.09	86.0	26
			750 nM

---

Charge-density studies of biological molecules provide insights into chemical bonds, molecular interactions, and reactivity through electron density (ED) analysis.^33,34 The electrostatic potential (ESP) distribution, which visualises and quantifies molecular charge distribution, is crucial in determining the specificity and strength of intermolecular interactions in biomolecules.^35,36 Analysis of ESP facilitates rational drug design by identifying regions of complementary charge distribution and optimising electrostatic interactions.^37–39 Quantum chemical methods, particularly density functional theory (DFT), generate high-quality maps of ED and its derivatives, enabling prediction of electronic properties and protein–ligand interaction energies.^40,41 Nonetheless, while providing highly accurate electronic structure descriptions, full quantum calculations remain computationally prohibitive for large biomolecular systems.^42,43 Simplified approaches, such as the multipole model (MM) of the ED offer practical alternatives while maintaining acceptable accuracy.⁴⁴ The MM provides a compact and efficient representation of the electron density distribution, capturing the essential features of the charge distribution without the need for expensive quantum calculations.³⁴ By partitioning the ED into atomic multipole functions and their moments, MM allows for the rapid calculation of electrostatic potentials, electric fields, and interaction energies, offering a convenient framework for quantitative studies of intermolecular interactions.⁴⁵ The inclusion of higher-order multipole moments captures the anisotropic ED properties, allowing for a more precise description of directional interactions, including hydrogen bonding, π–π stacking, and halogen bonding.⁴⁶ The TAAM (transferable aspherical atom model) method is a specific approach to MM that aims to simplify charge-density studies of macromolecules by offering transferable multipole parameters which can be applied to similar chemical environments across different molecules. Up to now, different flavours of the TAAM method have been successfully applied to various molecular systems, including proteins,^47–49 nucleic acids,⁵⁰ and organic compounds.^51,52 Transferability has been achieved by developing libraries of pre-computed multipole parameters and assuming that ED distribution around an atom is primarily determined by its local chemical environment.⁴⁵ Several multipole parameters databases have been created, including ELMAM2,⁵³ GID⁵⁴ and UBDB,^55,56 the last one has found a number of practical applications in computational biochemistry^48,57 and medicinal chemistry.⁵⁸ The University at Buffalo Databank (UBDB) is a comprehensive repository of aspherical atomic electron densities derived through Fourier-space fitting of the Hansen–Coppens multipole model (HCMM) of pseudoatoms to molecular electron densities obtained from DFT calculations. Based on analysis of thousands of experimental crystal structures, pseudoatoms are categorised according to their electron density parameters and structural topology. UBDB has been recently restructured into the MATTS (multipolar atom types from theory and statistical clustering) database.⁵⁹ The resulting HCMM parameters provide a framework for modelling electron density distributions in molecular systems. TAAM/UBDB implementation in packages such as XD2016⁶⁰ or MoPro allows the calculation of electrostatic energy, ED and its derivatives for large molecular systems.

We employed the UBDB + EPMM method, which utilises a continuous aspherical model of charge density,^48,61 offering advantages over conventional point-charge force fields through incorporation of charge penetration effects. This method achieves accuracy comparable to quantum chemistry methods across diverse interaction types and distances, while requiring significantly fewer computational resources than full-quantum methods, including linear-scaling approaches such as ONETEP⁶² or BigDFT.⁶³ TAAM, despite its computational advantages, has limitations stemming from multipole parameters transferability, which are not able to emulate subtle quantum effects, particularly in systems dominated by polarisation or dispersion effects.⁴⁵ In contrast, DFT calculations provide accurate electronic structure descriptions by implicitly accounting for electronic polarisation, charge transfer, and dispersion forces.^43,64 Its flexibility enables investigation of diverse molecular systems without pre-defined multipole parameters,^65,66 while its molecular wavefunction facilitates charge-density studies and topological analysis. DFT calculations on system fragments enable quantitative analysis of non-covalent interactions through reduced density gradient (RDG) methods, including non-covalent index (NCI)⁶⁷ and interaction region indicator (IRI).⁶⁸

This study employs advanced computational tools to analyse ligand–protein interactions in selected USP-inhibitor X-ray-derived structural models. The combination of UBDB + EPMM and DFT calculations, alongside other computational methods, provides detailed insights into electronic properties and molecular interaction mechanisms. These findings aim to guide the rational design of selective USP7 inhibitors, contributing to therapeutic strategies for diseases linked to its dysregulation.

2. Materials and methods

2.1 Structure preparation

17 structures of USP7-inhibitor complexes were extracted from protein data bank (PDB) in September 2023. The PDB codes of investigated complexes, the protein names, inhibitor codes, and literature references can be found in Table S1.† An initial quality check was conducted using MolProbity,⁸¹ including addition of hydrogen atoms using nuclear position option, for each protein chain separately. Chains with a low MolProbity score (below 2.50) and clash score (below 16.00) were selected for EP/MM calculations (8 structures: 6VN3, 6VN4, 6M1K, 6F5H, 5N9T, 5VS6, 5WHC, 5UQV; resolution between 1.73 and 2.84 Å). Addition of missing hydrogen atoms and further geometry inspection were performed in ChimeraX. Missing fragments of residue sidechains were reconstructed in ChimeraX using the Dunbrack rotamer library.⁸² The formal charge of most inhibitors was set to +1, the only exception was 6VN4 with zero charge. All X-ray structures were processed by removing water molecules, organic compounds (except studied inhibitors) and inorganic ions. All H–X bond lengths were adjusted to experimental values from neutron diffraction experiments⁶⁹ before preparing input files for XD2016 program suite.

2.2 Conformational analysis of USP7 protein

To distinguish between crystal packing effects and ligand-induced conformational changes in USP7 complexes, we analysed protein flexibility using CABS-Flex, a coarse-grained simulation tool that generates structural ensembles which well correlate with NMR data.⁷⁰ We use the same 8 structures, selected for EP/MM calculations, which were mentioned in paragraph 2.1. Modelling of conformational flexibility was performed using CABS-Flex method via CABS-Flex 2.0 server applying default parameters.⁷¹ Further structural analysis and visualisations were prepared using UCSF ChimeraX (versions 1.17 and 1.18).⁷²

2.3 Hirshfeld surface calculations

Hirshfeld surfaces (HS) partition electron density (ED) equally between a molecule's atoms (promolecule) and its surroundings (procrystal). These surfaces are characterised by d_i and d_e, metrics representing shortest distances from surface points to internal and external atomic nuclei, respectively. Two-dimensional fingerprint plots of d_iversus d_e visualise intermolecular contacts and quantify interatomic interactions, highlighting structural differences. Only residues in the vicinity of an inhibitor (around 4 Å) were used. Atomic coordinates used in the calculations were extracted from previously prepared PDB files, or in the case of other complexes prepared in the same way (hydrogen atoms were added in Chimera, waters and other non-protein fragments were removed), and converted to suitable .cif files using CCDC Mercury⁷³ and Microsoft Excel 2016 programs. Hirshfeld surfaces and two-dimensional fingerprint plots were calculated using Koga–Kanayama–Watanabe–Imai–Thakkar atomic wavefunction in CrystalExplorer21 program.⁷⁴ The detailed information including PDB codes is available in Table S1.†

2.4. Multipole model (EP/MM) calculations

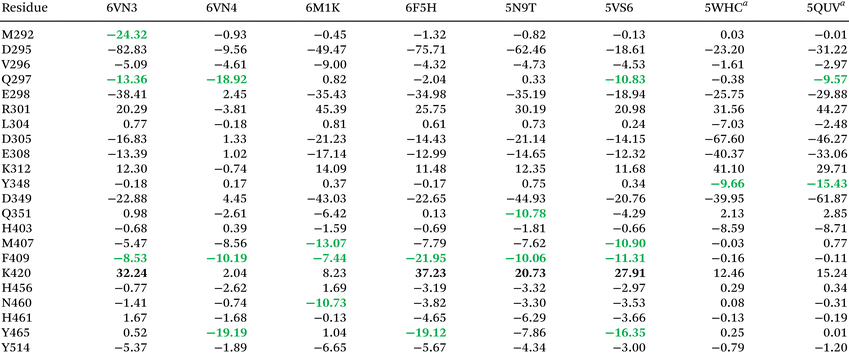
Input files for XD2016 suite were prepared in CCDC Mercury program and edited in Notepad++ text editor. We employed TAAM-based UBDB + EPMM method (later referred to as TAAM for the sake of brevity) to compute pairwise residues-ligand electrostatic energies in selected USP7-inhibitor complexes. At neutral pH, USP7 carries a −6 total charge, with protonated basic and deprotonated acidic residues, consistent with reported experimental conditions. The latest version of UBDB was used to reconstruct the distribution of electron density for all protein-inhibitor complexes,⁷⁵ the ED parameters were transferred using the LSDB program. UBDB provides a set of aspherical atomic electron density distributions for light elements commonly present in organic molecules. Some of the potentially interesting structures deposited in the PDB (e.g., 6VN2 and 5NGE) contain atoms in inhibitor molecules for which there are no atom types in the UBDB, and hence were not subjected to detailed studies, apart from HS analysis described earlier. To obtain the pairwise electrostatic interaction energies (E_el) between residues and inhibitor, the exact potential and multipole model (EP/MM) method was applied, which allowed computation of E_el between two molecular charge distributions represented within the Hansen–Coppens ED formalism. It combines a numerical evaluation of the exact Coulomb integral for short-range interatomic interactions (less than 4.5 Å) with a Buckingham-type multipole approximation for the long-range contacts. After generating charge density distributions of selected complexes, the EP/MM calculations were carried out in the XDPROP module of the XD2016 package.⁶⁰ Spherical core and valence electron densities were based on atomic wave functions from Clementi and Roetti.⁷⁶ Default integration parameters were used (iqt = 2, Nrad = 50 and Nang = 194), the exact potential zone radius (rcrit1) was set to 5 Å and atomic multipoles zone radius (rcrit2) to 200 Å. Electron density, molecular electrostatic potential (MEP) and Hirshfeld surface maps, derived from UBDB electron densities, were also calculated in XDPROP. Cubic grids for these maps were generated with specific dimensions (box 500 × 500 × 500 Å and voxel size 0.1 Å) with the origin point around the centre of mass. The raw results were then processed using home-made scripts. We distinguished the total electrostatic binding energy of all amino acid residues (E_el,T), and electrostatic binding energies for selected residues within 5 Å of the ligand binding site (E_el,S). For the sake of clarity, the set of residues belonging to the binding site was identical for each complex: M292, D295, V296, Q297, E298, R301, L304, D305, E308, K312, Y348, D349, Q351, H403, R407, F409, K420, H456, N460, H461, Y465, and Y514. All computed maps were visualised using the MoleCoolQt64 program. Values of electrostatic residue-ligand interaction energies were mapped on molecular surfaces of USP7 complexes using ChimeraX.

2.5. Statistical analysis of EP/MM results

Statistical analyses and data visualisation were conducted using Python programming environment. The pandas⁷⁷ and seaborn⁷⁸ libraries were employed for generating correlation matrices, heat maps, and analysing correlations between IC₅₀ values and electrostatic energies. Linear regression models were computed using the statsmodels.api module.⁷⁹ K-means clustering was performed utilising the sklearn.cluster module from the scikit-learn library.⁸⁰ All charts and plots were created using matplotlib.pyplot module.⁸¹

2.6. DFT calculations

We employed the R²SCAN-3c composite DFT method, known for reliable description of non-covalent interactions in organic systems.⁸² This method has built-in D4 dispersion correction, gCP (geometrical counterpoise) correction, and modified def2-mTZVPP basis set providing comparable results to ωB97-M-V and related range-separated functionals with triple-zeta basis sets. From the following complexes: 6VN3, 6F5H, 6M1K, 5N9T, 5VS6 and 5WHC we arbitrarily selected a set of residues having important stabilising/destabilising electrostatic contribution to binding. Each amino acid residue was treat as a separate molecule, peptide bonds were removed and corresponding side chains were capped by a methyl group. Composite DFT calculations were performed in ORCA 5.0^83,84 using ChimeraX SEQCROW bundle⁸⁵ as a graphical interface. Geometry optimisation preceded energy calculations to address dispersion forces’ sensitivity to hydrogen positioning, all optimizations were performed using the R²SCAN-3c composite method with implicit SMD water solvent model and Tight SCF setting.⁸² To avoid significant changes in the geometry of the binding sites, all atoms except of hydrogens were frozen during the optimization. We performed single point energy calculations for 6VN3, 6F5H, 6M1K and 5N9T complexes. To allow direct comparison between electrostatic energies obtained from UBDB + EPMM, which do not include solvation effects, all single point energies of residue-ligand heterodimers as well as separated ligand and capped amino acid molecules were calculated in vacuo using the R²SCAN-3c method. The interaction energies of residue-ligand heterodimers were computed using supermolecule approach (eqn (1)), where E_Int, E_super, E_R, E_L are energies of interactions, a supermolecule and isolated subsystems (here an amino acid residue and a ligand) respectively.

E_Int = E_super − (E_P + E_L) (1)

2.7. Wavefunction analysis and intermolecular interactions

Methods based on reduced density gradient (RDG) enable visualisation of non-covalent interactions in 3D space. The sign of λ₂ (second eigenvalue of ED Hessian), hereafter sign(λ₂), distinguishes between attractive (λ₂ < 0) and repulsive (λ₂ > 0) interactions. The interaction region indicator (IRI), derived from RDG, simultaneously reveals multiple interaction types (covalent bonds, hydrogen bonds, van der Waals forces), making it valuable for complex chemical system analysis.⁶⁸ Visualisation typically employs colour-coded isosurfaces or scatter plots based on sign(λ₂) values, where blue represents strong attractive interactions, red indicates strong repulsive interactions, and green shows weak van der Waals (vdW) interactions. Low IRI values indicate non-covalent interactions, while covalent bonds manifest as high-density spikes. Wavefunction files for the previously optimised fragments of protein–ligand complexes were calculated in ORCA 5.0 with implicit SMD water solvent model using R²SCAN-3c method. Calculations of ED, electrostatic potential (ESP) and IRI maps as well as quantitative analysis of ESP isosurfaces were performed in Multiwfn program (version 3.8).⁸⁶ ESP distributions were calculated using the GTO regrouping algorithm implemented in Multiwfn and then mapped on vdW (0.001 a.u. ED) isosurfaces and analysed using Marching Tetrahedra algorithm implemented in Multiwfn. Scatter plots of IRI distribution were calculated in Gnuplot 6.0 program using previously existing scripts (https://www.gnuplot.info). All other visualisations were created using ChimeraX.

3. Results

3.1. USP7 inhibitor properties

For the sake of clarity, we reference USP7 inhibitors by their PDB structure entries rather than chemical names or ligand entry abbreviations (Fig. 1 and Table 1). These inhibitors comprise diverse heterocyclic scaffolds with varying substituents that significantly influence binding (Fig. 1 and Table S1†). Within certain inhibitor sets (e.g., 6VN2, 6VN3, 6VN6), the core scaffold position remains conserved, though variable fragments show conformational flexibility. This binding pocket adaptability accommodates diverse chemical structures, offering advantages for drug design (Fig. 2). Interestingly, inhibitor 5VS6 features a piperazine ring that extends beyond the binding cavity to interact with external acidic residues. Most ligands bind to the same hydrophobic pocket outside the catalytic centre, except 5WHC and 5UQV, which target an alternative smaller binding site located in close proximity to the main binding site (Fig. 2C). All inhibitors induce conformational changes that inactivate the catalytic centre, with binding affinities ranging from nanomolar to micromolar (typically <1 μM).

Fig. 2 Binding of selected USP7 inhibitors. (A) Superposition of ligands in the complexes. Ligands binding to the main cavity are depicted in black (right), ligands binding to the secondary cavity are depicted in light colours (left). (B) Position of the binding cavities on the molecular surface of USP7 with superimposed ligands. (C) Focus on main binding cavity. Compound 5VS6 (coloured white) contains piperazine ring extending from the cavity. (D) Focus on the secondary binding cavity.

3.2. Intrinsic flexibility of USP7 catalytic domains

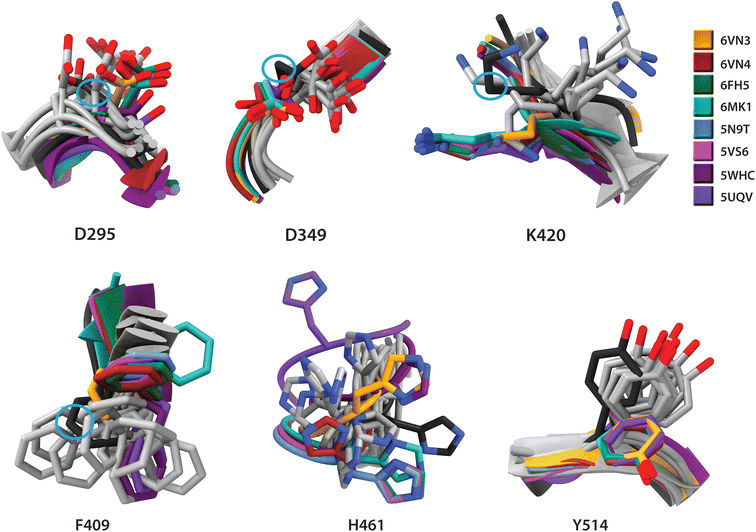
The results of CABS-Flex simulations indicate that the USP7 catalytic domain exhibits overall rigidity, with low C-α root-mean-square fluctuation (RMSF) values, except in disordered loops that may facilitate ligand-induced conformational changes (Fig. S1 and Table S2†). Selected residues which directly participate in inhibitor binding and show side-chain flexibility with cluster arrangements differing from crystallographic observations, were selected for detailed discussion (Table 2 and Fig. 3).

Fig. 3 Flexibility of selected residues of USP7. The apo form is coloured black, models from CABS-Flex are coloured grey and structures of protein–ligand complexes are depicted in various colours indicated in the legend. Blue ovals indicate the position of the apo form residues in cases of reduced visibility.

Table 2 Conformational analysis of selected residues important for binding of the inhibitors

Residue	Conformational changes
D295	Considerable variation in side chain orientation between X-ray and CABS structures, with simulations showing a wider range of conformations.
D349	Similar overall orientation in both X-ray and CABS structures, with minor variations in side chain positioning. In the apo form, residue is positioned between CABS and X-ray clusters
F409	Computed structures display wide range of conformations and apo form falls in this cluster. Protein–ligand complexes have different conformations which depend upon the ligand.
K420	CABS structures show a broader range of conformations compared to clustered experimental structures. The conformation of the apo form is similar to the computed structures.
H461	CABS structures show more variability compared to the X-ray ones, with 5UQW being an outlier with considerable different coordinates
Y514	In all protein–ligand X-ray structures, residues are clustered in virtually the same conformation different from the apo form, with the apo form within the CABS cluster.

---

Key structural differences between experimental and computed conformations occur in residues D295, F409, K420, and H461, primarily in side-chain orientations (Fig. 3). F409 exhibits the most pronounced variations in computed conformations, including backbone conformational changes. While experimental coordinates generally fall within simulated ensembles (Fig. S2 and S3†), observed discrepancies suggest inhibitor-induced conformational changes beyond the intrinsic flexibility of the apo form. Residues Y348, Q351, R408 and Y465 show experimental structures clustering separately from the simulated ensemble, indicating possible crystal packing effects. In summary, our conformational analysis supported by the literature evidence indicates that inhibitor-binding residues maintain stable local and global dynamics, validating crystal structures as suitable models for further computational studies.

3.3. Hirshfeld surfaces of the USP7 inhibitors

While HS analysis can examine protein–ligand complexes by treating the ligand as promolecule and the binding cavity as procrystal, USP7 inhibitors’ partial exposure to solvent limits quantitative analysis using crystal explorer's computations which rely on simple atomic wavefunctions on an incomplete model (e.g. missing solvent molecules). Consequently, our analysis focuses on qualitative assessment of protein-inhibitor intermolecular interactions. Analysis revealed diverse interaction patterns (Table S3 and Fig. S4†), predominantly H⋯H, H⋯O, and H⋯N contacts, with varying distributions across complexes. While structures 6VN2 and 6VN3 show balanced interatomic contact distributions, 5N9T, 5VS6, and 5VSK exhibit numerous close H⋯H contacts. These H⋯H interactions warrant careful interpretation, as they may indicate steric clashes from imperfect binding or experimental artefacts. Notably, high-affinity compounds like 6VN3 lack such close interatomic contacts. Hirshfeld surfaces show greater sensitivity to steric clashes in solid state and packed biomolecules than conventional vdW surfaces.⁸⁷ Structures exhibiting numerous close H⋯H contacts may require additional refinement to minimise steric clashes. Other contacts such as H⋯O and H⋯N contribute consistently to binding through strong hydrogen bonds while C⋯H contacts play a minor role through weak hydrogen bonds and dispersion forces. Fluorinated compounds (5NGE and 5N9T) exhibit close H⋯F contacts, relatively common for such ligand–protein complexes,^88,89 while the Br atom in 5N9R contributes through a long hydrogen bond. Despite its limitations, Hirshfeld surface analysis identifies key interaction sites, including hydrogen bonds and potential steric clashes. For complexes selected for TAAM-based calculations, including 5VS6, potential clashes are minimal. Moreover, electrostatic-focused multipole models remain reliable due to their long-range nature and directional character, being less sensitive to close H⋯H contacts.

3.4. Global picture of TAAM electrostatic interaction energies

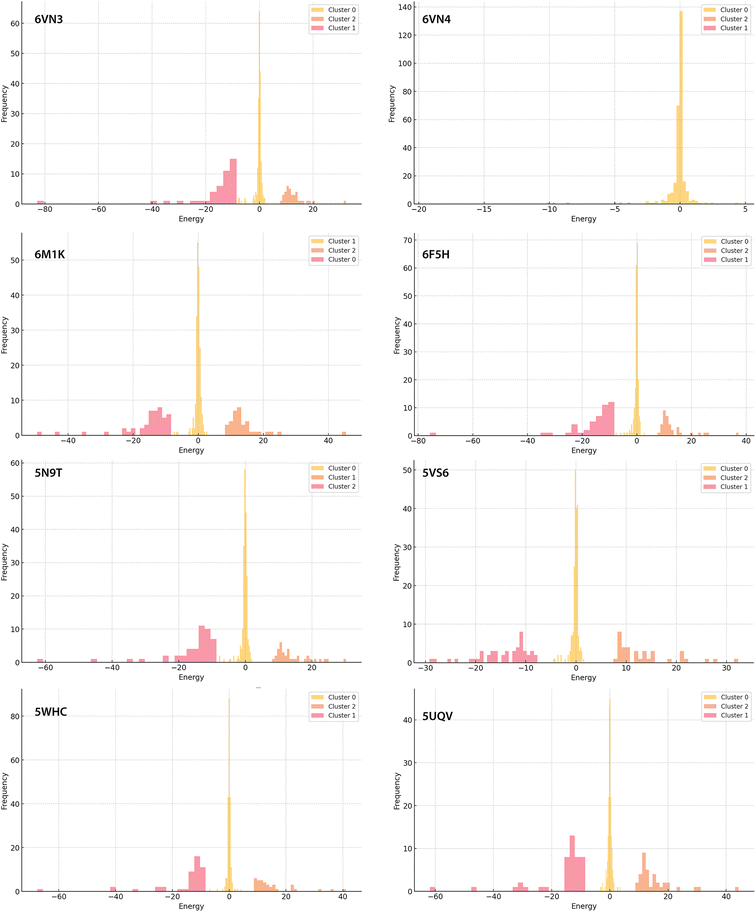
Total electrostatic binding energies (E_el,T) range from −300 kcal mol⁻¹ to −100 kcal mol⁻¹ approximately. Complexes 6MK1 and 6VN3 exhibit the strongest binding (most negative energy), while 6VN4 exhibits the weakest binding (Fig. 5). K-clustering analysis of all pair-wise electrostatic binding energies (Fig. 4 and Fig. S5†; raw data available in ESI†) reveals a relatively similar pattern across all complexes except 6VN4: Cluster 0 displays a sharp peak near 0 kcal mol⁻¹, Cluster 1 shows a broader negative energy distribution (usually −20 to −40 kcal mol⁻¹), and Cluster 2 presents a smaller positive energy distribution. Cluster 0 comprises predominantly neutral residues within binding cavities that minimally impact direct binding but stabilise protein-inhibitor interactions through hydrogen bonding and dispersion forces. Cluster 1 contains mainly negatively charged residues, both proximal to the inhibitor (showing most negative energies) and across the protein surface, contributing to bulk electrostatic interactions. The broad energy distribution in Cluster 1 reflects complex electrostatic interactions that deviate from simple r⁻² distance dependence due to higher multipole moments, penetration energy effects, and protein-inhibitor interface complexity. Cluster 2 encompasses positively charged residues, with interaction energies similarly modulated by inhibitor-residue distances. The lower frequency and magnitude of positive contributions are outweighed by favourable negative interactions. While this general pattern is observed across most complexes, notable variations exist. Complex 6VN4 shows a prominent Cluster 0 peak without strong positive or negative contributors, consistent with a neutral inhibitor lacking charge–charge interactions. Complexes 6MK1 and 6VN3 demonstrate stronger binding through pronounced negative energy contributions, the latter also displays greatly reduced contribution from Cluster 2. On the other hand, 5VS6 and 5UQV exhibit broader Cluster 2 distributions, indicating more complex interaction profiles with more pronounced unfavourable contacts.

Fig. 4 K-clustering of pairwise residue-ligand energies for USP7 complexes. Frequency indicates the number of residues within a structure, all energies values are in kcal mol⁻¹. Cluster 0 (yellow) represents residues with small positive or negative contribution to overall binding energy (approximately −5 to +5 kcal mol⁻¹). Cluster 1 (red) represent residues with high positive contribution to binding energy whilst cluster 2 (orange) represent residues with negative contribution to binding.

Fig. 5 Statistical analysis of electrostatic energies, only inhibitors from the main binding site are presented. (A) Values of E_el,T for USP7 complexes (left) and values of E_el,S for USP7 complexes (right). (B) Heat maps for correlation matrices of E_el,T (left) and E_el,S (right). Positive Pearson correlation is coloured red and negative is blue. (C) Log-linear regression of IC₅₀ as a function of E_el,T (left) and E_el,S (right).

Given the long-range nature of electrostatic interactions, total protein-inhibitor binding energy may not accurately reflect affinity. We therefore analysed both total electrostatic binding energy (E_el,T) and electrostatic binding energies for the sum of selected residues within 5 Å of the ligand binding site (E_el,S). These proximal residues contribute significantly to overall binding, with E_el,S ranging from approximately −175 kcal mol⁻¹ to −75 kcal mol⁻¹_. The contribution is most substantial in complexes 5N9T, 6VN3, and 6VN4, suggesting more specific binding, notably in 6VN4 despite its lack of charge–charge interactions. Correlation matrices computed for both E_el,T and E_el,S, for each complex, were visualised as heat maps (Fig. 5B). Complex 6VN4 emerges as an outlier due to its neutral ligand's reduced interactions with charged residues. For other complexes, both heat maps show strong similarity, indicating that selected residues effectively represent the overall binding energy profile of USP7's catalytic domain. These selected residues play key roles in binding interactions, and their energy profiles are strongly correlated with the overall protein–ligand interaction landscape.

The strong correlations observed in complexes 5N9T and 6MK1 (0.98, 0.95 for E_el,T and E_el,S, respectively) might reflect a potential connection between the structural features of ligands and their binding patterns. However, this relationship is only superficial, as demonstrated by complexes 6VN3 and 6F5H, which exhibit similarly high correlations (0.96, 0.93 for E_el,T and E_el,S respectively) despite having structurally distinct ligands. Similarly, 5WHC and 5UQV correlate well with other complexes despite distinct binding sites, primarily due to strategically positioned charged residues (D295, E298, R301, D349, K420) near both binding sites. Even higher E_el,T correlations among the remaining complexes reflect long-range interactions with evenly distributed charged residues, suggesting that ligand positive charge positioning relative to protein carboxylic groups primarily determines electrostatic binding energy. Moreover, USP7's conserved core structure maintains stable energy profiles across different binding cavities. Excluding charged residues significantly alters both E_el,S values and correlation patterns, revealing greater complex-specific variations (Fig. S6†). Neutral residues contribute over 50% to E_el,S in most complexes except 5VS6, where charged residues dominate (−71.82 vs. −23.98 kcal mol⁻¹). Complexes 5UQV and 5WHC show particularly low non-charged contributions (−34.53 and −18.57 kcal mol⁻¹, respectively), potentially explaining their reduced USP7 affinity through limited specific recognition and shape complementarity. Structure–activity correlations become more evident when considering neutral residues: structurally similar compounds 5VS6 and 6VN4 (differing by a small substituent) show high correlation (R = 0.93), while 5VS6–6F5H and 5N9T–6F5H pairs exhibit lower correlations (R = 0.79 and 0.62, respectively), despite some structural similarity in the first pair. Complex 6VN3 shows no significant correlation with others, likely due to its ligand's distinct structure and high rigidity. Correlation between electrostatic energy profiles does not necessarily indicate similar binding mechanisms or affinities. While high correlations suggest comparable electrostatic environments, local structural variations can yield distinct binding modes. Directional interactions, such as hydrogen bonds and dipole–dipole forces, critically influence binding specificity and strength, particularly within well-defined protein structural environments. In aqueous solution, these local interactions become paramount for ligand stabilisation,^90,91 as water's high dielectric constant and counter-ions screen long-range charge–charge interactions, emphasising the importance of short-range forces for binding affinity and specificity. Although charge–charge interactions facilitate initial ligand attraction and orientation, they may not primarily determine binding affinity. Local interactions, while weaker, resist solvent screening more effectively within the binding pocket's microenvironment, where bulk solvent effects are minimised.^92,93 The non-charged 6VN4 exemplifies this principle, relying predominantly on site-specific electrostatic interactions, including hydrogen bonds and van der Waals forces, which show greater resistance to aqueous environment interference.

To examine the correlation between ligand-residue pairwise electrostatic energy and ligand affinity, we applied an approximate log-linear model, which is expressed as log(IC₅₀) = β₀ + β₁(E_el) + ε, where β_i are regression coefficients and ε is the error term. This model assumes an exponential relationship between IC₅₀ (half maximal inhibitory concentration) and electrostatic energy, based on (i) the exponential relationship between binding free energy ΔG, and binding affinity K_a, where log(IC₅₀) ∝ ΔG, since the inhibitors are non-competitive it may be assumed that K_i ≈ IC₅₀ for a given experimental setup; (ii) linear free energy relationships (LFER), commonly used in organic chemistry, linking logarithmic equilibrium constants to molecular parameters such as substituent effects,⁹⁴ and (iii) the significant contribution of electrostatic interactions to protein–ligand binding. While log-linear models effectively handle wide affinity ranges and skewed distributions,⁹⁵ they may oversimplify complex systems by assuming electrostatic dominance and neglecting cooperative interactions. This simplified approach remains valid for our study given the predominantly charged nature of inhibitors and significant electrostatic interactions at ligand–protein interfaces, evidenced by strong hydrogen bonds. We analysed only compounds binding to the main cavity to minimise confounding variables. Regression analysis indicated moderate correlations between experimental affinities and both E_el,T and E_el,S (R = 0.73 and 0.66, respectively). The log(E_el,T)-affinity relationship is virtually linear for most compounds except 6VN3 and 6F5H, suggesting additional binding factors unique to these inhibitors. The E_el,S correlation, while positive, is less clear and shows high residual errors, warranting cautious interpretation of quantitative analyses. The multipole model-based E_el calculations provide partial insight into USP7-ligand interactions, with moderate correlations (R = 0.73 for E_el,T and R = 0.66 for E_el,S) indicating significant contributions from other factors, including hydrophobic effects, conformational entropy, and dispersion interactions. The model's limitations include: (i) potential underestimation of quantum effects including electronic polarisation, charge transfer, and electron correlation; (ii) lack of entropic contribution such as hydrophobic effects and conformational dynamics in E_el,S calculations; (iii) IC₅₀ variability due to kinetic rates, solubility, and inter-study differences. Nevertheless, the linear E_el,T-log(IC₅₀) relationship suggests utility for rapid affinity estimation of novel USP7 inhibitors, particularly when complemented by DFT calculations and experimental validation.

3.5. Structural insight into electrostatic interactions

The USP7 catalytic domain surface displays complex electrostatic interaction patterns with bound ligands (Fig. 6A), featuring distinct regions of stabilising (red) and destabilising (blue) contributions. Stabilising interactions concentrate inside the ligand binding cavity and surrounding residues, while charged residues distribute more randomly across other surface regions. Under physiological conditions, counter-ion screening reduces the contribution of distant charged residues to ligand binding. Detailed analyses of 6VN3 and 6M1K complexes illustrate these patterns (Fig. 6B, C and Table 4). Complexes 6VN3 and 6M1K were selected for their contrasting ligand properties: 6VN3's rigid, compact ligand forms fewer but stronger intermolecular interactions, while 6M1K's extended ligand establishes numerous weaker contacts. Both complexes share key interacting residues: D295, E298, and F409 provide stabilising contributions, while residues such as R301, K357, and K420 show destabilising effects. The binding involves both aromatic (F409, Y514) and charged residues (D295, E298), with charged residues contributing more significantly to binding energy. The complexes differ in their electrostatic landscapes: 6VN3 shows distinct strong pairwise interactions, including unique contacts either strong (M292) or weak (H294), while 6M1K exhibits a more distributed pattern. These differences reflect their contrasting conformations: 6VN3's compact, centrally positioned ligand versus6M1K's extended conformation engaging a broader residue range. Other complex interaction maps (Fig. S7, ESI†) reveal distinct patterns. Complex 5N9T shows multiple stabilising contacts, particularly with D295, E298, D305, and D349, resulting in favourable electrostatic interactions comparable to 6VN3 and reflected in high E_el,S values (Fig. 5). The 5VS6 binding pocket exhibits an asymmetric interaction pattern: one cavity side shows pronounced destabilising effects from proximal positive charges, suggesting suboptimal charge alignment and insufficient compensatory interactions, leading to reduced E_el,S. However, its extended ligand conformation enables additional stabilisation through piperazine ring interactions with anionic residues (E345, E371, D380) in the finger subdomain, outside the binding cavity, which explains the substantial difference between E_el,T and E_el,S (−223.42 vs. −95.80 kcal mol⁻¹). Complex 6F5H's binding cavity exhibits a nuanced interaction pattern combining favourable and unfavourable contacts. Similar patterns characterise 5WHC and 5UQV ligands in the secondary binding site, where 5WHC features a key stabilising anchor through D305, while 5UQV shows stronger overall stabilising interactions across multiple residues, potentially explaining its lower IC₅₀. Despite cavity structural similarities, USP7 complexes display distinct electrostatic landscapes arising from varied ligand conformations and positions. The differences between total (E_el,T) and site-specific (E_el,S) energies highlight the complementary roles of local and extended interactions in binding strength.

Fig. 6 Electrostatic pairwise residue-ligand electrostatic energies mapped onto molecular surface of whole catalytic domain of USP7. Some residues missing in the experimental structures were added to show whole molecular surface of the protein (grey colour). A red-white-blue gradient scheme is applied, where residues with highest stabilising contribution (negative energy sign) are coloured red while residues with highest destabilising contribution (positive energy sign) are deep blue. (A) Global map of showing pairwise interaction on the whole surface of USP7 in 6VN3 complex. Pairwise interactions in the binding cavity of 6VN3 (B) and 6M1K (C) complexes. Three different orientation were chosen to show both location of the inhibitors on the protein surface (top) and inside of the binding cavity (middle, bottom).

3.6. DFT calculations of the binding energies

DFT calculations provide a benchmark for assessing the accuracy of electrostatic energies derived from multipole model approximations. While TAAM offers greater computational efficiency for large systems, its simpler approach may introduce inaccuracies, particularly in handling dispersion forces. Modern composite DFT methods provide more rigorous electronic structure calculations, including electron correlation effects and empirical dispersion corrections, allowing a more accurate description of non-covalent interactions than pure electrostatic portrait offered by multipole models.^96,97 We selected four complexes (6VN3, 6M1K, 6F5H and 5N9T) with similar values of E_el,S for DFT calculations. Comparison of DFT and TAAM energies (E_DFT and E_TAAM, respectively) reveals TAAM's tendency to underestimate both positive residue repulsion and anionic residue stabilising interactions (Fig. 8, panels A, B; Table S4†). The discrepancy is particularly notable for D295 and E459, where differences often exceed 100 kJ mol⁻¹ (Fig. 7C), suggesting superior accuracy for charge-dense systems where polarisation and electron correlation start to play a more vital role in direct charge–charge interactions.⁷⁸ On the other hand, DFT and TAAM energies generally agree well for neutral residues, including aromatic moieties, with notable complex-specific exceptions (Table S4†): (i) 6F5H complex: TAAM overestimates F409 (E_DFT = −36.42 vs. E_TAAM = −91.77 kJ mol⁻¹) and Y465 (E_DFT = −29.89 vs. E_TAAM = −79.91 kJ mol⁻¹); (ii) 6M1K complex: significant discrepancies for N351 (E_DFT = −70.10 vs. E_TAAM = −26.82 kJ mol⁻¹) and M407 (E_DFT = −10.13 vs. E_TAAM = −54.62 kJ mol⁻¹). These complex-specific variations likely stem from local electrostatic environment differences and subtle differences in hydrogen atom positions rather than systematic TAAM limitations. For instance, methionine's highly polarisable sulfur may be underestimated by fixed multipoles, particularly in S⋯π stacking, while asparagine's polar side chain interactions may be overestimated by the multipole model approximation. The F409 and Y465 discrepancies in the 6F5H complex may reflect DFT's higher sensitivity to geometric distortions in the experimental model. Despite good structural quality (MolProbity scores 1.22–1.96), the medium-resolution crystallographic data suggest potential local structural errors. These variations emphasise the need for cautious TAAM interpretation, particularly for charged and aromatic residues. Despite these local incongruences, TAAM and DFT energies show strong positive linear correlations (e.g., R² = 0.98 and R² = 0.93 for 6VN3 and 5N9T respectively) across four USP7 complexes (Fig. 7D, Table 3 and Fig. S8†), with correlation strength maintained across different regression analyses including MM-regression and other robust methods (Table S5†).

Fig. 7 Comparison of DFT and TAAM pairwise electrostatic energies. (A) Scatter plot of DFT and TAAM energies for selected residue-ligand heterodimers. Negatively charged residues are labelled (e.g., D295) or indicated by the red oval, positively charged residues are indicated by the blue ellipsoid. (B) Focus on the middle fragment of the scatter plot. (C) Discrepancies between DFT and TAAM energies for the selected residues. (D) MM-estimated linear fitting between DFT and TAAM energies for 6VN3 complex.

Fig. 8 Ligand ESP mapped onto Hirshfeld surfaces for selected inhibitors. A rainbow gradient scheme is applied where violet indicates most positive regions and red most negative (ESP is expressed in e Å⁻¹). Notable charge–charge interactions are highlighted by black ovals, a region of slightly positive charge around chlorine is highlighted by green oval, and stacking interactions as tan ovals. The right panel shows a cross-section through these HS providing an inward look into ESP distribution over a given HS.

Table 3 TAAM electrostatic pair-wise interactions for selected residues [kcal mol⁻¹]. Green colour indicate neutral residues having significant contribution to binding

a Different binding site.

---

3.7. Analysis of the electrostatic potentials mapped onto VdW and Hirshfeld surfaces

The XD2016 program employs source function calculations for Hirshfeld surface (HS) generation, rather than atomic wave functions, enabling analysis of partially exposed molecular fragments such as cavity-bound ligands. This HS-based approach provides more accurate intermolecular interaction descriptions than van der Waals surfaces, through ED-based molecular partitioning that prevents neighbouring molecule overlap and associated ESP mapping artefacts. Analysis of selected USP7 inhibitors across varied IC₅₀ values (Fig. 8) reveals distinct ESP patterns. Complex 6VN3's ligand shows exclusively positive ESP (+0.553 to +0.046 e Å⁻¹⁾ with broader, more localised charge distribution compared to other compounds. Key features include: (i) charge–charge interaction between D295 and the ligand's secondary amino group (black oval, Fig. 8); (ii) strong spot of positive charge (+0.5 e Å⁻¹) indicating amino group-carbonyl hydrogen bonding; (iii) slight positive region near the chlorine atom interacting with adjacent residue hydrogens; (iv) T-stacking between F409 and the chlorinated benzyl ring. The ligand's ESP distribution facilitates attraction to D/E residues, while its compact HS suggests optimal cavity fit for charge–charge interactions. Complex 6VN4, lacking positive charge, shows a mixed electrostatic profile. Its HS features: (i) a positive protrusion forming F409 stacking interaction; (ii) a negative region stabilising Q297 interactions but repelling D/E residues; (iii) non-uniform positive charge distribution reducing electrostatic complementarity with the negative binding cavity.

The 5VS6 ligand's extended conformation forms a larger HS volume with predominantly positive charge, particularly near cavity-external D/E residues and M407. Compared to 6VN3, its larger, elongated HS enables more numerous but diffuse electrostatic interactions, potentially compromising precise binding site alignment. The increased HS volume suggests greater desolvation requirements and higher entropic penalties, particularly disadvantageous for flexible ligands like 5VS6. Complex 5WHC exhibits distinct ESP characteristics, with uneven ED distribution along its molecular axis and polar charge concentration at opposite ends. Unlike other compounds’ extensive positive charge regions, 5WHC shows only localised positive charge near the D305-amine salt bridge. These varying electrostatic profiles correlate with binding affinities: compounds with concentrated positive charge distributions (e.g., 6VN3) achieve optimal electrostatic complementarity with the negative binding cavity, while larger or heterogeneous profiles may compromise binding through suboptimal interactions or increased entropic costs.

Composite DFT calculations, while computationally intensive, provide a more comprehensive ESP representation than multipole models by incorporating full electronic structure and correlation effects. Due to both high-quality crystal structure and high affinity of the ligand, we selected the 6VN3 complex for ESP analysis (Fig. 9A). This analysis maps ESP onto an ED isosurface (0.001 a.u., equal to van der Waals surface), revealing charge distributions similar to multipole model results (Fig. S9B†). Despite different computational methods, Hirshfeld and van der Waals (vdW) surfaces often exhibit comparable geometric features, enabling relatively straightforward comparative analysis of these molecular boundaries. The minor discrepancies between these surfaces primarily arise from their different approaches to representing the ligand–protein molecular boundary and peripheral electron density regions.

Fig. 9 DFT-based ESP analysis for 6VN3 binding site. (A) ED isosurface of the ligand (yellow, 0.001 a.u.) has ESP extrema depicted as spheres embedded into the ED isosurface (kcal mol⁻¹). ESP extrema of the binding cavity are depicted as small dots (left, centre). Red labels indicates local maxima and blue labels local minima. The right panel also show ED isosurface of the protein (blue). Here larger dots indicate local extrema of the free ligand (labels are underscored) and small dots indicate local extrema of the complex upon binding. (B) ESP mapped on ED isosurface (0.001 a.u). The rainbow gradient scheme was applied and the highest ESP values are +0.2 (violet) and −0.2 (red, expressed in a.u.). ESP maps are as follow free ligand (left), free protein (centre) and protein–ligand complex (right).

Topological analysis of ESP local extrema on vdW surfaces provides insights into ligand–protein electrostatic compatibility. In ESP maps, regions of local minima and maxima can correspond to sites of favourable or unfavourable electrostatic interactions, respectively. These features can complement specific electron density topological features identified through QTAIM analysis. ESP topology often provides a more straightforward visualisation of electrostatic features, particularly for electrostatically dominated interactions.^36,98 While points near nuclei typically represent maxima and inter-atomic or low-ED regions correspond to minima, even positively charged groups show non-uniform ED distribution (Fig. 9A, left). Local ESP minima can arise in areas of higher electron density due to electron lone pairs or regions of negative potential created by electron-rich groups. These minima can facilitate favourable electrostatic interactions with positively charged or electron-deficient regions of a binding partner. The complementary positioning of positive and negative ESP extrema on the ligand and the binding cavity surfaces, respectively, indicates strong electrostatic compatibility, enhancing binding affinity and specificity. The 6VN3 ligand's most positive ESP region (near the amino group) shows complementarity with the free binding cavity, promoting stable complex formation (Fig. 9B, centre). Upon complexation, ESP extrema on the ligand's solvent-exposed ED isosurface diminish, demonstrating high potential complementarity. The unbound protein's vdW surface displays an amphipathic ESP landscape, with negative regions near D/E residues and positive regions near R/K residues. Complex formation induces charge redistribution in the binding region (Fig. 9B), moderating extreme ESP values through partial charge neutralisation. ESP maps (Fig. S10†) confirm these observations: (i) the free ligand shows expanded positive isosurface near the amine group; (ii) the unbound USP7 displays complementary negative isosurface at the binding centre; (iii) the complex formation reduces positive charge through partial neutralisation.

3.8. Analysis of non-covalent interactions using RDG approach

The IRI (interaction region indicator) surface analysis of USP7 complexes shows an interplay of different non-covalent interaction types, from classical hydrogen bonds to less common sulfur-π contacts. Here, we focus on selected non-covalent interactions in USP7 binding cavities (Fig. 10). The extensive green surfaces surrounding the 5WHC ligand indicate predominant vdW interactions, characteristic of favourable non-polar contacts in the binding pocket. These broad, continuous basins suggest good shape complementarity between the ligand and the protein surface (Fig. 9A). The highlighted hydrogen bond with H407 represents a key anchoring point, indicating the dual nature of the binding mode combining specific directional interactions with non-specific vdW contacts. Ligand 6VN3 interacts with USP7 via various non-covalent interactions. The distinct interaction region reveals a strong hydrogen bond between the ligand and an amide hydrogen (Fig. 9B). The sharpness and intensity of this feature in the IRI surface suggests a well-oriented H-bond with optimal geometry, which is expected to be the crucial determinant of binding specificity and orientation. The thieno[3,2-b]bipyridine ring system exhibits multiple stabilising interactions with surrounding residues (Fig. 9C). The IRI surface pattern suggests a combination of π–π stacking and CH–π interactions, which contribute significantly to binding affinity through both electrostatic and dispersion components. Interactions between M407 and 6VN3 demonstrate a relatively rare sulfur-π stacking arrangement (Fig. 9D). The IRI surface characteristics in this region indicate a favourable electronic interaction, despite the unusual nature of this contact. Ligand 5NT9 participates in stabilising F⋯H interactions via its CF₃ group, which forms multiple weak but overall significant contacts with adjacent residues. The IRI surface features suggest a combination of F⋯H–C interactions and possible multipolar effects. The presence of fluorine atoms appears to optimise local interaction geometry while contributing to the overall binding energy through multipolar effects.

Fig. 10 Examples of IRI surfaces. (A) Overall view of IRI surface for 5WHC ligand. A red oval indicate a strong H-bond between the ligand and H407 residue. (B) Strong H-bond (indicated by a red oval) between 6VN3 ligand and an amide hydrogen atom. (C) Stabilising interactions between thieno[3,2-b]bipyridine ring of 6VN3 ligand and adjacent residues (red ovals). (D) Sulfur-π stacking between M407 and 6VN3 ligand (red ovals). (E) Contribution of CF₃ group of 5NT9 ligand to noncovalent interactions (red ovals) with adjacent residues.

Additionally, IRI scatter plots show global interaction patterns across USP7 complexes (Fig. S11†), revealing distributions of non-covalent interactions. Complexes exhibit distinct features: enhanced hydrogen bonding in 5VS6 and 5N9T, localised steric clashes in 6F5H, reduced stabilising interactions in 5WHC correlating with its lower affinity, and a specific bimodal distribution of strong interactions in 6VN3 (see ESI† for detailed analysis). While IRI plots aid in visualisation of interaction distributions, they do not offer direct measures of interaction quality or specificity, as precisely positioned high-energy interactions often dominate binding affinity compared to numerous dispersed contacts (Fig. 10).

3.9. Most important residues and their contribution to inhibitor binding

In the final paragraph we take a closer look at several selected residues that have a certain impact on USP7-inhibitor complexes. Table 4 provides a brief summary of the pairwise interactions between these residues and the ligands whereas some of them are presented in Fig. 11. Unless mentioned otherwise, all electrostatic binding energies were derived from TAAM calculations.

Fig. 11 Selected intermolecular interactions with USP7 inhibitors. Some residues that do not participate were removed for the sake of clarity, ligand molecules are coloured black. (A) Acidic residues (coloured orange), from left to right: H-bonds between D295 and 6VN4; and 5VS6; charge–charge interaction between E298 and 6FH5; H-bond between D349 and 6VN4. (B) H-bonds with V296 (orange) and 6VN4 (left), 6M1K (right). (C) H-bonding between Q297 (orange) and 6VN3 (black), and 6VN4 (green). (D) H-bond between Q351 (orange) and 5UQV. (E) Interactions between M292 and 6VN3, structural scheme (left) and IRI map (right). On IRI map H-bond is highlighted by red oval, green blobs represents weak interaction. (F) Cation-sulfur and S⋯π stacking between M407 (orange) and 6M1K; nearby hydrogen and charged amino group are highlighted by red ovals. (G) Interactions with F409, from left to right: superposition of F409 conformations for different complexes, outliers are 6VN3 (tan) and 6M1K (light cyan); S⋯π stacking with 6VN3; H-bonds and S⋯π stacking with 5VS6. (H) H-bonds with Y residues: Y348 with 5UQV (right), Y465 with 6VN4 (left) (I) H-bonding between H403 and 5UQV.

Table 4 Intermolecular interactions of selected residues

Residue	Binding properties
M292	Strong H-bond with 6VN3 and dispersion interactions with chlorine and oxygen atoms.
D295	Strongly attractive charge–charge electrostatic interactions and H-bonds (ligands in the main binding cavity).
V296	Weak H-bonds with 6VN3 and 6VN4, strong H-bonds with 6M1K
Q297	Strong H-bonds with 6VN3, 6VN4 and 5VS6 heterocyclic rings. Interacts with 5WHC and 5UQVvia combination of weak H-bonds and dispersion interactions.
E298	Long-range electrostatic interactions (except 6VN4).
R301	Strong charge–charge repulsion for ligands (except 6VN4, which is stabilised)
L304	Relatively weak electrostatic interactions with 5WHC and 5UQV
D305	Strongly attractive charge–charge electrostatic interactions with 5WHC and 5UQV
E308	Strongly attractive charge–charge electrostatic interactions with 5WHC and 5UQV
K312	Strong charge–charge repulsion for 5WHC and 5UQV
Y348	H-bonds and stacking interactions with 5WHC and 5UQV
D349	Strongly attractive charge–charge electrostatic interactions with 6M1K, 5WHC, 5UQV and 5N9T, 6M1K
Q351	Strong H-bonds with charged amino group of 5N9T and 6M1K
H403	Strong H-bonds with OH groups of 5WHC and 5UQV
M407	S⋯π stacking and cation-sulfur interaction with heterocyclic rings (6VN3, 6VN4, 5N9T, 5VS6), strong H-bond between aromatic ring and carbonyl oxygen in 6F5H
F409	Forms both weak C–H⋯O H-bonds and T-shape π⋯π stacking with 6VN3 (S⋯π), 6VN4 and 5VS6 (π⋯π). Offset stacking with 6M1K. Mostly dispersion interactions with 6F5H and 5N9T.
K420	Strong charge–charge repulsion for ligands in the main binding cavity (except 6VN4, moderate for 6M1K, 5WHC and 5QUV)
N460	Strong H-bonds between hydrogen in the peptide bond and ether oxygen in 6M1K
H461	Weak C–H⋯π and dispersion interactions with 5N9T
Y465	Strong H-bonds with oxygen atoms of the ligands (6VN3, 6VN4, 6M1K, 5VS6)
Y514	Weak dipole–dipole interactions and π⋯π stacking (often inclined)

---

Residue D295 plays a central role in main cavity inhibitor binding through charge–charge interactions and, for 6VN4, hydrogen bonding (Fig. 11A). It shows the highest binding energies (E_el from −82.83 to −49.47 kcal mol⁻¹) for all charged ligands except 5VS6, where cavity-external charge positioning reduces E_el to only −18.61 kcal mol⁻¹. In the secondary cavity, D305, E309, and E349 serve analogous functions with E_el ranging from −33.06 to −67.60 kcal mol⁻¹. Previously overlooked residues E298 and D349 contribute significantly to complex stability (E_el < −20 kcal mol⁻¹), through long-range electrostatic interactions with ligand NH₃⁺ groups in the main binding cavity. This particular finding emphasises the importance of comprehensive binding site analysis, including surrounding residues, for understanding ligand affinity and specificity determinants. R301 exhibits complex interaction patterns: its guanidinium group generally destabilises positively charged ligands in both binding cavities through electrostatic repulsion (E_el 20.29 to 45.39 kcal mol⁻¹). This repulsion arises from electrostatic interactions between the positively charged guanidinium group of arginine and charged amine groups of the ligands. However, with complex 6VN4, R301 provides slight stabilisation (−3.81 kcal mol⁻¹) through interactions with the ligand's hydroxyl and carbonyl groups. K420, by contrast, consistently destabilises main cavity binding through its ε-amino group's electrostatic repulsion with ligands and competition for interactions with negative or polar binding site groups. Among the aliphatic neutral residues, M292 demonstrates unique binding characteristics in the 6VN3 complex (Fig. 11E), stabilising the ligand through strong hydrogen bonding (E_el −24.32 kcal mol⁻¹). This interaction, observed only in highest-affinity complexes 6VN3 and 6VN2, suggests a correlation between the specific conformation of M292 in these complexes and the binding strength. M407 contributes through previously undiscussed S⋯π stacking and sulfur-cation interactions (Fig. 11F),³¹ notably with 6M1K and 6VS5 (E_el −13.07 and −10.90 kcal mol⁻¹, respectively). V296's contribution to 6VN3 and 6VN4 binding proves to be less significant than previously proposed on the basis of simple structural assessments (Fig. 11B). Computed energies (E_el −5.09 and −4.61 kcal mol⁻¹, respectively) are relatively low, suggesting only a minor contribution. Amide residues show diverse binding roles (Fig. 11C and D): Q297 forms hydrogen bonds across both binding cavities, indicating its versatility in the ligand recognition (E_el −18.92 to −9.57 kcal mol⁻¹), Q351 interacts with NH₃⁺ groups of 6M1K and 5N9T (E_el −6.42 and −10.78 kcal mol⁻¹, respectively), while N460 specifically binds 6M1K through a main-chain carbonyl oxygen (E_el −10.73 kcal mol⁻¹). Aromatic residues show distinctive binding behaviours, particularly F409, which adopts a solvent-exposed conformation upon inhibitor binding. F409 maintains consistent interaction modes across main cavity inhibitors through T-shaped stacking, weak C–H⋯O bonds (and C–H⋯F for 5N9T), and dispersion interactions (Fig. 11G). While TAAM suggests significant F409 contributions (E_el −7.44 to −21.95 kcal mol⁻¹), DFT calculations indicate lower absolute values (< −10 kcal mol⁻¹). Y465 contributes through hydroxyl group hydrogen bonding, notably with 6VN4, 6F5H, and 5VS6 (E_el −19.19, −19.12 and −16.35 kcal mol⁻¹, respectively). Similarly, Y348 stabilises 5WHC and 5UQV complexes (E_el −9.66 and −15.43 kcal mol⁻¹, respectively), while Y514 provides modest stabilisation through dipole–dipole and dispersion interactions (E_el −1.89 to −6.65 kcal mol⁻¹). Collectively, these aromatic residues shape the binding pocket and enhance stability through π-stacking and dispersion interactions (Fig. 11H). This short survey of residue-specific interactions in USP7 complexes reveals intricate interaction networks involving both known and newly identified residues (e.g., M407 and D349). The significant role of previously overlooked acidic residues E298 and D349 in long-range interactions emphasises the importance of comprehensive binding site analysis beyond the immediate pocket. Less common interactions, such as M407's S⋯π stacking, highlight the diverse molecular mechanisms contributing to USP7-ligand binding and suggest expanded strategies for charged ligand design.

4. Discussion

Our multi-method computational analysis reveals several key insights into USP7-inhibitor interactions and provides a comprehensive framework for understanding binding mechanisms and future drug design. The findings can be organized into several interconnected themes:

4.1. Electrostatic landscape and binding mechanisms

The dominant role of electrostatics in USP7-inhibitor binding emerges consistently across our analyses. TAAM calculations reveal total electrostatic binding energies ranging from −300 to −100 kcal mol⁻¹, with binding site energies contributing 40–80% of total interactions. This finding aligns with the ESP mapping results showing distinct charge complementarity between USP7's negatively charged binding cavity and the predominantly positive inhibitor surfaces. The previously identified electrostatic network (H294, W285, E298, Y224)⁹⁹ maintaining the inactive conformation appears to work synergistically with inhibitor binding, particularly through E298's newly recognised contribution to long-range interactions. The correlation between electrostatic energy profiles and binding affinity suggests that optimising charge distribution of novel inhibitors could improve their potency. Notably, compounds with concentrated regions of the positive charge (e.g., 6VN3) demonstrate superior binding through optimal electrostatic complementarity. However, the moderate correlation strength indicates that other factors, including hydrophobic effects and conformational entropy, significantly influence binding affinity. This is particularly evident in the case of neutral compound 6VN4, which achieves fairly strong binding through specific short-range interactions rather than charge–charge attractions. We identified significant contributions from previously underappreciated residues, particularly E298 and D349 for long-range interactions, and M407 for S⋯π stacking. The complementary results from TAAM and DFT calculations validate these observations, though TAAM's slight tendency to underestimate charged residue interactions implies a cautious approach to highly charged systems. On the other hand, some of these differences may stem from slightly different positions of hydrogen atoms upon geometry optimisation and residual contribution of main polypeptide chain. While CABS-flex simulations confirm the overall rigidity of USP7's catalytic domain, they also reveal specific flexible regions that may facilitate inhibitor binding through induced-fit mechanisms. This dynamic perspective helps reconcile the apparent contradiction between the protein's structural stability and its ability to accommodate diverse inhibitors. The previously identified allosteric communication pathway involving residues G215, D481-D484, and S486 suggests potential for alternative inhibition strategies.¹⁰⁰

4.2. Implications for drug design

The predominant role of electrostatic complementarity suggests that future inhibitor design should carefully consider charge distribution optimisation. This can be achieved through strategic placement of ionisable groups and fine-tuning of electron-withdrawing or electron-donating substituents to create optimal charge patterns matching the binding site's electrostatic landscape. The identification of previously overlooked interaction sites, particularly the contributions of E298 and D349, opens new avenues for structure-based drug design since these residues could be better targeted through extended inhibitor scaffolds. Furthermore, the possibility of developing dual-site binders that simultaneously engage both the primary and secondary binding pockets presents an intriguing opportunity for achieving higher specificity and potency. Fragment-based drug design approaches could be particularly valuable in this context, allowing systematic exploration of both the main binding pocket and the newly identified interaction sites.^101,102 The observed flexibility in certain protein regions, mentioned in the literature, suggests that fragment growing and linking strategies should also account for potential induced-fit effects. The moderate correlation between electrostatic energy and binding affinity indicates the importance of optimising multiple binding determinants simultaneously. This includes traditional pharmacophores’ elements such as hydrogen bonding networks and hydrophobic contacts, as well as less common interactions such as S⋯π stacking with M407. Moreover, the dynamic nature of protein–ligand interactions, as highlighted by our analysis, suggests that further incorporation of protein flexibility in TAAM methods could improve their results.¹⁰³ For instance, our recent study on cyclooxygenase inhibitors indicates that even small differences in X-ray structures may lead to significant changes in ligand-residue electrostatic interactions.⁴⁹

4.3. Methodological considerations

The integration of multiple computational approaches in our study reveals both the strengths and limitations of some methodologies in protein–ligand interaction analysis. The complementarity between TAAM and DFT calculations provides a robust computational framework, yet several important methodological aspects warrant careful consideration. The UBDB + EPMM and related multipole-based approaches demonstrate particular strength in initial evaluation of electrostatic interactions, offering computational efficiency crucial for inhibitor screening. However, the treatment of non-electrostatic interactions, particularly π-π stacking and hydrophobic effect, present a considerable methodological challenge. The selection of DFT methodology for treating dispersion interactions represents a practical compromise between computational feasibility and theoretical rigour. The so-called 3c composite methods offer a balanced approach to address three critical deficiencies in lower-cost electronic structure calculations: basis set superposition error (BSSE), insufficient description of dispersion interactions, and short-range functional inadequacies.^104,105 Through the incorporation of D3/D4 dispersion corrections, geometric counterpoise corrections, and short-range basis set modifications, these methods usually offer good cost–benefit ratio when applied to most organic systems.^65,106 Nevertheless, the handling of dispersion effects in common DFT methods is still limited. The dispersion corrections are largely empirical and lack clear physical foundation.¹⁰⁷ Their dependence on the choice of functional introduces an element of arbitrariness that could affect the reliability of binding energy predictions, especially in systems where dispersion forces play a crucial role.¹⁰⁸ Recent literature has highlighted the limitations of conventional DFT dispersion corrections when compared to more rigorous approaches like symmetry adapted perturbation theory (SAPT) with complete basis sets.¹⁰⁹ SAPT offers theoretically sound treatment of dispersion forces; hence provides intermolecular interaction energies possessing clear physical meaning. However, the computational demands of SAPT calculations make them impractical for routine analysis of large protein–ligand complexes such as USP7-inhibitor systems.¹¹⁰ On the other hand, atom-atom dispersion correction functions (D_as) offer an alternative approach to handle this problem. Due to better scaling, with square number of atoms O(A²), they are considerably less expensive if compared to SAPT (which exhibits scaling between O(N⁸) – O(N⁵)), and also provide physical meaning in contrast to conventional DFT dispersion corrections.¹⁰⁹ The selected composite DFT approach represents a pragmatic choice that balances theoretical accuracy with computational efficiency, enabling the relatively fast analysis of multiple protein-inhibitor complexes.

The treatment of protein flexibility and conformational entropy presents another methodological challenge. While CABS-flex simulations provide insights into protein dynamics, the integration of these dynamic effects into binding energy calculations remains incomplete. More sophisticated approaches combining multiple conformational states with accurate energy evaluations might be necessary for fully capturing the complexity of USP7-ligand interactions. Furthermore, water-mediated interactions represent a particularly challenging aspect of our computational framework. The current implementations of TAAM method do not take into account solvation due to the lack of reliable estimates for the position of hydrogen atoms in water molecules, potentially missing important specific water-mediated contacts. Explicit consideration of key water molecules, possibly through hybrid quantum mechanical/molecular mechanical (QM/MM) approaches, could provide more accurate representations of the binding interface. Nevertheless, they require significant computational resources and have their own potential caveats such as boundary artefacts and slow convergence. The hierarchical nature of our computational pipeline – from relatively fast TAAM calculations to more detailed DFT analysis – offers a practical framework for drug discovery applications. Looking forward, the integration of emerging methodological advances could further enhance our computational framework. This might include the use of polarisable force fields such as AMOEBA,¹¹¹ more rigorous treatment of entropy effects, and improved sampling of protein–ligand conformational space.

5. Summary and conclusion

Our findings demonstrate the crucial role of electrostatic interactions in USP7-inhibitor binding, with the TAAM-based UBDB + EPMM method effectively capturing electrostatic landscapes that correlate well with DFT calculations, suggesting its utility for rapid interaction screening. We identified key binding residues, including previously overlooked E298 and D349, while emphasising the significance of long-range electrostatic interactions beyond the immediate binding pocket. This broader perspective on protein surface interactions could enhance inhibitor design strategies. Hirshfeld surface analysis and ESP mapping reveal charge distribution patterns and USP7-inhibitor complementarity, correlating with binding affinity and specificity. Additionally, RDG analysis through the IRI method provides detailed insights into non-covalent interaction networks, demonstrating the combined effects of hydrogen bonding, van der Waals forces, and other weak interactions in inhibitor binding. Compounds with concentrated positive charge distributions (e.g., 6VN3) demonstrate higher affinities through optimal electrostatic complementarity with the negative binding cavity. TAAM results generally agree with DFT calculations, with only small differences for selected residues. CABS-Flex simulations confirm the USP7 catalytic domain's general rigidity while identifying key flexible residues that facilitate diverse ligand accommodation through induced-fit binding mechanisms. These complementary computational approaches provide comprehensive insights into protein–ligand interactions, offering valuable guidance for rational USP7 inhibitor design. We suggest that strategic optimisation of electrostatic complementarity through charged group positioning offers promising avenues for enhancing inhibitor potency and selectivity. The detailed understanding of USP7's main and secondary binding sites provides opportunities for dual-site inhibitor design and alternative binding strategies, potentially extending to other USP family members. Future work should focus on experimental validation of computational predictions, molecular dynamics exploration of protein–ligand interactions, and application of this integrated computational approach to other challenging drug targets.

Data availability

Detailed raw computational results of UBDB + EPMM method are available in ESI† in the following file: USP7-electrostatic-energies.xlsx.

Detailed raw results of DFT calculations (pairwise binding energies) are available in ESI† in the following file: Supplementary-information.

Both files were uploaded during the submission process.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by National Science Centre in Poland (grant no. UMO-2017/24/C/NZ1/00366). The research was carried out at the Biological and Chemical Research Centre, University of Warsaw, established within the project co-financed by European Union from the European Regional Development Fund under the Operational Programme Innovative Economy, 2007–2013. Authors UAB and PMD received computing resources and storage from the PL-Grid Infrastructure through grant ubdb2018. Molecular graphics and analyses performed with UCSF ChimeraX, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from National Institutes of Health R01-GM129325 and the Office of Cyber Infrastructure and Computational Biology, National Institute of Allergy and Infectious Diseases.

References

1. J. Park, J. Cho and E. J. Song, Arch. Pharmacal Res., 2020, 43, 1144–1161.
2. E. N. Tsakiri and I. P. Trougakos, International Review of Cell and Molecular Biology, Elsevier, 2015, vol. 314, pp. 171–237.
3. C. M. Pickart, Annu. Rev. Biochem., 2001, 70, 503–533.
4. A. Folger and Y. Wang, Cells, 2021, 10, 2835.
5. C. Pla-Prats and N. H. Thomä, Trends Cell Biol., 2022, 32, 696–706.
6. S. A. Bhat, Z. Vasi, R. Adhikari, A. Gudur, A. Ali, L. Jiang, R. Ferguson, D. Liang and S. Kuchay, Curr. Opin. Pharmacol., 2022, 67, 102310.
7. M. E. Sowa, E. J. Bennett, S. P. Gygi and J. W. Harper, Cell, 2009, 138, 389–403.
8. N. A. Snyder and G. M. Silva, J. Biol. Chem., 2021, 297, 101077.
9. D. Komander and M. Rape, Annu. Rev. Biochem., 2012, 81, 203–229.
10. Y. Li and D. Reverter, Int. J. Mol. Sci., 2021, 22, 986.
11. H. G. Suresh, N. Pascoe and B. Andrews, Open Biol., 2020, 10, 200279.
12. M. Hu, P. Li, M. Li, W. Li, T. Yao, J.-W. Wu, W. Gu, R. E. Cohen and Y. Shi, Cell, 2002, 111, 1041–1054.
13. N. Keijzer, A. Priyanka, Y. Stijf-Bultsma, A. Fish, M. Gersch and T. K. Sixma, Life Sci. Alliance, 2024, 7, e202302533.
14. A. P. Turnbull, S. Ioannidis, W. W. Krajewski, A. Pinto-Fernandez, C. Heride, A. C. L. Martin, L. M. Tonkin, E. C. Townsend, S. M. Buker, D. R. Lancia, J. A. Caravella, A. V. Toms, T. M. Charlton, J. Lahdenranta, E. Wilker, B. C. Follows, N. J. Evans, L. Stead, C. Alli, V. V. Zarayskiy, A. C. Talbot, A. J. Buckmelter, M. Wang, C. L. McKinnon, F. Saab, J. F. McGouran, H. Century, M. Gersch, M. S. Pittman, C. G. Marshall, T. M. Raynham, M. Simcox, L. M. D. Stewart, S. B. McLoughlin, J. A. Escobedo, K. W. Bair, C. J. Dinsmore, T. R. Hammonds, S. Kim, S. Urbé, M. J. Clague, B. M. Kessler and D. Komander, Nature, 2017, 550, 481–486.
15. G. Gavory, C. R. O'Dowd, M. D. Helm, J. Flasz, E. Arkoudis, A. Dossang, C. Hughes, E. Cassidy, K. McClelland, E. Odrzywol, N. Page, O. Barker, H. Miel and T. Harrison, Nat. Chem. Biol., 2018, 14, 118–125.
16. L.-L. Zheng, L.-T. Wang, Y.-W. Pang, L.-P. Sun and L. Shi, Eur. J. Med. Chem., 2024, 266, 116161.
17. M. Rape, Nat. Rev. Mol. Cell Biol., 2018, 19, 59–70.
18. A. Pozhidaeva and I. Bezsonova, DNA Repair, 2019, 76, 30–39.
19. A. Van Der Horst, A. M. M. De Vries-Smits, A. B. Brenkman, M. H. Van Triest, N. Van Den Broek, F. Colland, M. M. Maurice and B. M. T. Burgering, Nat. Cell Biol., 2006, 8, 1064–1073.
20. A. Christine, M. K. Park, S. J. Song and M. S. Song, Exp. Mol. Med., 2022, 54, 1814–1821.
21. J. van Loosdregt, V. Fleskens, J. Fu, A. B. Brenkman, C. P. J. Bekker, C. E. G. M. Pals, J. Meerding, C. R. Berkers, J. Barbi, A. Gröne, A. J. A. M. Sijts, M. M. Maurice, E. Kalkhoven, B. J. Prakken, H. Ovaa, F. Pan, D. M. W. Zaiss and P. J. Coffer, Immunity, 2013, 39, 259–271.
22. X.-W. Zhang, N. Feng, Y.-C. Liu, Q. Guo, J.-K. Wang, Y.-Z. Bai, X.-M. Ye, Z. Yang, H. Yang, Y. Liu, M.-M. Yang, Y.-H. Wang, X.-M. Shi, D. Liu, P.-F. Tu and K.-W. Zeng, Sci. Adv., 2022, 8, eabo0789.
23. A. M. Montagut, M. Armengol, G. G. De Pablo, R. Estrada-Tejedor, J. I. Borrell and G. Roué, Semin. Cell Dev. Biol., 2022, 132, 213–229.
24. Q. Liang, T. S. Dexheimer, P. Zhang, A. S. Rosenthal, M. A. Villamil, C. You, Q. Zhang, J. Chen, C. A. Ott, H. Sun, D. K. Luci, B. Yuan, A. Simeonov, A. Jadhav, H. Xiao, Y. Wang, D. J. Maloney and Z. Zhuang, Nat. Chem. Biol., 2014, 10, 298–304.
25. H. Mistry, G. Hsieh, S. J. Buhrlage, M. Huang, E. Park, G. D. Cuny, I. Galinsky, R. M. Stone, N. S. Gray, A. D. D'Andrea and K. Parmar, Mol. Cancer Ther., 2013, 12, 2651–2662.
26. M. I. Davis, R. Pragani, J. T. Fox, M. Shen, K. Parmar, E. F. Gaudiano, L. Liu, C. Tanega, L. McGee, M. D. Hall, C. McKnight, P. Shinn, H. Nelson, D. Chattopadhyay, A. D. D'Andrea, D. S. Auld, L. J. DeLucas, Z. Li, M. B. Boxer and A. Simeonov, J. Biol. Chem., 2016, 291, 24628–24640.
27. L. Kategaya, P. Di Lello, L. Rougé, R. Pastor, K. R. Clark, J. Drummond, T. Kleinheinz, E. Lin, J.-P. Upton, S. Prakash, J. Heideker, M. McCleland, M. S. Ritorto, D. R. Alessi, M. Trost, T. W. Bainbridge, M. C. M. Kwok, T. P. Ma, Z. Stiffler, B. Brasher, Y. Tang, P. Jaishankar, B. R. Hearn, A. R. Renslo, M. R. Arkin, F. Cohen, K. Yu, F. Peale, F. Gnad, M. T. Chang, C. Klijn, E. Blackwood, S. E. Martin, W. F. Forrest, J. A. Ernst, C. Ndubaku, X. Wang, M. H. Beresini, V. Tsui, C. Schwerdtfeger, R. A. Blake, J. Murray, T. Maurer and I. E. Wertz, Nature, 2017, 550, 534–538.
28. I. Lamberto, X. Liu, H.-S. Seo, N. J. Schauer, R. E. Iacob, W. Hu, D. Das, T. Mikhailova, E. L. Weisberg, J. R. Engen, K. C. Anderson, D. Chauhan, S. Dhe-Paganon and S. J. Buhrlage, Cell Chem. Biol., 2017, 24, 1490–1500.
29. Y. Wang, Y. Jiang, S. Ding, J. Li, N. Song, Y. Ren, D. Hong, C. Wu, B. Li, F. Wang, W. He, J. Wang and Z. Mei, Cell Res., 2018, 28, 1186–1194.
30. J. A. Harrigan, X. Jacq, N. M. Martin and S. P. Jackson, Nat. Rev. Drug Discovery, 2018, 17, 57–78.
31. P. R. Leger, D. X. Hu, B. Biannic, M. Bui, X. Han, E. Karbarz, J. Maung, A. Okano, M. Osipov, G. M. Shibuya, K. Young, C. Higgs, B. Abraham, D. Bradford, C. Cho, C. Colas, S. Jacobson, Y. M. Ohol, D. Pookot, P. Rana, J. Sanchez, N. Shah, M. Sun, S. Wong, D. G. Brockstedt, P. D. Kassner, J. B. Schwarz and D. J. Wustrow, J. Med. Chem., 2020, 63, 5398–5420.
32. P. Di Lello, R. Pastor, J. M. Murray, R. A. Blake, F. Cohen, T. D. Crawford, J. Drobnick, J. Drummond, L. Kategaya, T. Kleinheinz, T. Maurer, L. Rougé, X. Zhao, I. Wertz, C. Ndubaku and V. Tsui, J. Med. Chem., 2017, 60, 10056–10070.
33. B. Dittrich and C. F. Matta, IUCrJ, 2014, 1, 457–469.
34. P. Macchi, J.-M. Gillet, F. Taulelle, J. Campo, N. Claiser and C. Lecomte, IUCrJ, 2015, 2, 441–451.
35. S. Mebs, A. Lüth and P. Luger, Bioorg. Med. Chem., 2010, 18, 5965–5974.
36. C. H. Suresh, G. S. Remya and P. K. Anjalikrishna, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1601.
37. M. R. Bauer and M. D. Mackey, J. Med. Chem., 2019, 62, 3036–3050.
38. A. A. Korlyukov, M. Malinska, A. V. Vologzhanina, M. S. Goizman, D. Trzybinski and K. Wozniak, IUCrJ, 2020, 7, 71–82.
39. M. Malińska, K. N. Jarzembska, A. M. Goral, A. Kutner, K. Woźniak and P. M. Dominiak, Acta Crystallogr., D: Biol. Crystallogr., 2014, 70, 1257–1270.
40. N. Ye, Z. Yang and Y. Liu, Drug Discovery Today, 2022, 27, 1411–1419.
41. S. El Rhabori, A. El Aissouq, O. Daoui, S. Elkhattabi, S. Chtita and F. Khalil, Heliyon, 2024, 10, e24551.
42. N. Yilmazer and M. Korth, Int. J. Mol. Sci., 2016, 17, 742.
43. L. Gundelach, T. Fox, C. S. Tautermann and C.-K. Skylaris, Phys. Chem. Chem. Phys., 2021, 23, 9381–9393.
44. N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A, 1978, 34, 909–921.
45. M. Kulik and P. M. Dominiak, Comput. Struct. Biotechnol. J., 2022, 20, 6237–6243.
46. S. P. Thomas, A. G. Dikundwar, S. Sarkar, M. S. Pavan, R. Pal, V. R. Hathwar and T. N. G. Row, Molecules, 2022, 27, 3690.
47. B. Guillot, C. Jelsch, A. Podjarny and C. Lecomte, Acta Crystallogr., D: Biol. Crystallogr., 2008, 64, 567–588.
48. U. A. Budniak, N. K. Karolak, M. Kulik, K. Młynarczyk, M. W. Górna and P. M. Dominiak, J. Phys. Chem. B, 2022, 126, 9152–9167.
49. S. Pawlędzio, M. Ziemniak, X. Wang, K. Woźniak and M. Malinska, IUCrJ, 2025, 12(2), 208–222.
50. M. Malinska and Z. Dauter, Acta Crystallogr., Sect. D:Struct. Biol., 2016, 72, 770–779.
51. B. Gruza, M. L. Chodkiewicz, J. Krzeszczakowska and P. M. Dominiak, Acta Crystallogr., Sect. A:Found. Adv., 2020, 76, 92–109.
52. K. K. Jha, F. Kleemiss, M. L. Chodkiewicz and P. M. Dominiak, J. Appl. Crystallogr., 2023, 56, 116–127.
53. S. Domagała, B. Fournier, D. Liebschner, B. Guillot and C. Jelsch, Acta Crystallogr., Sect. A:Found. Crystallogr., 2012, 68, 337–351.
54. B. Dittrich, C. B. Hübschle, K. Pröpper, F. Dietrich, T. Stolper and J. J. Holstein, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2013, 69, 91–104.
55. P. M. Dominiak, A. Volkov, X. Li, M. Messerschmidt and P. Coppens, J. Chem. Theory Comput., 2007, 3, 232–247.
56. K. N. Jarzembska and P. M. Dominiak, Acta Crystallogr., Sect. A:Found. Crystallogr., 2012, 68, 139–147.
57. M. Ziemniak, A. Zawadzka-Kazimierczuk, S. Pawlędzio, M. Malinska, M. Sołtyka, D. Trzybiński, W. Koźmiński, S. Skora, R. Zieliński, I. Fokt, W. Priebe, K. Woźniak and B. Pająk, Int. J. Mol. Sci., 2021, 22, 3720.
58. M. Wanat, M. Malinska, A. Kutner and K. Woźniak, Molecules, 2022, 27, 1757.
59. P. M. Rybicka, M. Kulik, M. L. Chodkiewicz and P. M. Dominiak, J. Chem. Inf. Model., 2022, 62, 3766–3783.
60. XD2016 home page, https://www.chem.gla.ac.uk/~louis/xd-home/, (accessed 30 August 2024).
61. A. Volkov, T. Koritsanszky and P. Coppens, Chem. Phys. Lett., 2004, 391, 170–175.
62. C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119.
63. S. Mohr, L. E. Ratcliff, P. Boulanger, L. Genovese, D. Caliste, T. Deutsch and S. Goedecker, J. Chem. Phys., 2014, 140, 204110.
64. S. Ehrlich, A. H. Göller and S. Grimme, ChemPhysChem, 2017, 18, 898–905.
65. M. Bursch, J. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735.
66. U. Ryde and P. Söderhjelm, Chem. Rev., 2016, 116, 5520–5566.
67. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
68. T. Lu and Q. Chen, Chem.:Methods, 2021, 1, 231–239.
69. F. H. Allen and I. J. Bruno, Acta Crystallogr., Sect. B, 2010, 66, 380–386.
70. M. Jamroz, A. Kolinski and S. Kmiecik, Nucleic Acids Res., 2013, 41, W427–W431.
71. A. Kuriata, A. M. Gierut, T. Oleniecki, M. P. Ciemny, A. Kolinski, M. Kurcinski and S. Kmiecik, Nucleic Acids Res., 2018, 46, W338–W343.
72. T. D. Goddard, C. C. Huang, E. C. Meng, E. F. Pettersen, G. S. Couch, J. H. Morris and T. E. Ferrin, Protein Sci., 2018, 27, 14–25.
73. C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
74. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011.
75. P. Kumar, B. Gruza, S. A. Bojarowski and P. M. Dominiak, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 398–408.
76. E. Clementi and C. Roetti, At. Data Nucl. Data Tables, 1974, 14, 177–478.
77. W. McKinney, Data Structures for Statistical Computing in Python, Austin, Texas, 2010, pp. 56–61.
78. M. Waskom, J. Open Source Softw., 2021, 6, 3021.
79. S. Seabold and J. Perktold, Statsmodels: Econometric and Statistical Modeling with Python, Austin, Texas, 2010, pp. 92–96.
80. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, A. Müller, J. Nothman, G. Louppe, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
81. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
82. S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103.
83. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
84. F. Neese, WIREs Comput. Mol. Sci., 2022, 12(5), e1606.
85. A. J. Schaefer, V. M. Ingman and S. E. Wheeler, J. Comput. Chem., 2021, 42, 1750–1754.
86. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
87. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
88. P. Zhou, J. Zou, F. Tian and Z. Shang, J. Chem. Inf. Model., 2009, 49, 2344–2355.
89. W. Pietruś, R. Kafel, A. J. Bojarski and R. Kurczab, Molecules, 2022, 27, 1005.
90. S. K. Panigrahi and G. R. Desiraju, Proteins: Struct., Funct., Bioinf., 2007, 67, 128–141.
91. A. Erbaş, M. O. de la Cruz and J. F. Marko, Phys. Rev. E, 2018, 97, 022405.
92. M. Majewski, S. Ruiz-Carmona and X. Barril, Commun. Chem., 2019, 2, 110.
93. G. Bitencourt-Ferreira, M. Veit-Acosta and W. F. De Azevedo, in Docking Screens for Drug Discovery, ed. W. F. De Azevedo, Springer New York, New York, NY, 2019, vol. 2053, pp. 67–77.
94. J. Shorter, The correlation analysis of organic reactivity: with particular reference to multiple regression, Research Studies Pr, Chichester u.a, 1982.
95. C. Feng, H. Wang, N. Lu and X. M. Tu, Stat. Med., 2013, 32, 230–239.
96. W. Hujo and S. Grimme, J. Chem. Theory Comput., 2013, 9, 308–315.
97. M. Cafiero, J. Phys. Chem. A, 2024, 128, 8777–8786.
98. C. H. Suresh and S. Anila, Acc. Chem. Res., 2023, 56, 1884–1895.
99. A. Özen, L. Rougé, C. Bashore, B. R. Hearn, N. J. Skelton and E. C. Dueber, Structure, 2018, 26, 72–84.
100. J. Xu, Y. Wang, J. Zhang, A. A. Abdelmoneim, Z. Liang, L. Wang, J. Jin, Q. Dai and F. Ye, Comput. Biol. Med., 2023, 162, 107068.
101. Y. Chen, Y. Zheng, Q. Jiang, F. Qin, Y. Zhang, L. Fu and G. He, Eur. J. Med. Chem., 2017, 127, 997–1011.
102. S. Chen, J. Xie, R. Ye, D. D. Xu and Y. Yang, Chem. Sci., 2024, 15, 10366–10380.
103. P. Kumar and P. M. Dominiak, Molecules, 2021, 26, 3872.
104. E. Caldeweyher and J. G. Brandenburg, J. Phys.: Condens. Matter, 2018, 30, 213001.
105. J. Hostaš and J. Řezáč, J. Chem. Theory Comput., 2017, 13, 3575–3585.
106. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
107. D. G. Truhlar, J. Chem. Educ., 2019, 96, 1671–1675.
108. J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
109. W. Jedwabny, E. Dyguda-Kazimierowicz, K. Pernal, K. Szalewicz and K. Patkowski, J. Phys. Chem. A, 2021, 125, 1787–1799.
110. K. Patkowski, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1452.
111. J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ob01953a

---