Interplay of geometry and magnetic coupling in ferromagnetic nanorings

Abstract

We present a systematic study of angular-dependent magnetization reversal in circular and rounded rectangular Permalloy (Ni₈₁Fe₁₉) nanorings, examining both isolated and strongly interacting arrays using magneto-optical Kerr effect measurements and micromagnetic simulations. Magnetic reversal behavior was analyzed by determining the magnetic fields required for vortex state (VS) nucleation (H_VS1) and vortex state annihilation (H_VS2). For circular rings, increased magnetostatic coupling in more closely spaced nanostructures increased H_VS1 and decreased H_VS2, with the most significant effects observed with applied field aligned with the inter-ring spacing. Rectangular rings exhibit pronounced configurational anisotropy, particularly with field applied near their short axis, where both isolated and coupled arrays display three-step switching behavior and a distinct, angle-dependent enhancement of the VS stable field range. This enhancement spans a broader angular range in coupled arrays and is likely facilitated by the nucleation of vortex core states in areas of high flux curvature and ring width. These findings provide new insights into geometry- and angle-dependent switching in nanorings and highlight their potential in applications such as neuromorphic computing.

---

Introduction

Ferromagnetic nanostructures are foundational elements in a wide range of emerging technological applications, including data storage,^1,2 magnetic sensors,^3,4 logic devices,^5,6 and magnonics.^7,8 Recently, Vidamour et al.⁹ showed that the dynamics of magnetic domain walls in interconnected Ni₈₀Fe₂₀ nanoring arrays can be directly used for reservoir computing. By encoding information in the amplitude of rotating magnetic fields, they triggered emergent domain wall interactions that created the necessary nonlinearity and fading memory. This method achieved state-of-the-art performance on key benchmark tasks, including signal transformation, spoken digit recognition, and time-series prediction, highlighting the potential of magnetic nanorings for neuromorphic computing. In arrays of nanomagnets, the magnetization configurations and their transitions are highly sensitive to factors such as the shape, thickness, and material composition of the nanomagnets,^10–12 as well as the geometry of the array and inter-element spacing^12,13via shape anisotropy and magnetostatic interactions between neighboring nanomagnets.

Nanorings (NRs) are particularly interesting among various geometries because of their ability to support a vortex state – a closed loop magnetization configuration that eliminates stray magnetic fields, while avoiding the singularity of a vortex core.¹⁴ A typical circular NR exhibits two primary magnetization states: a bi-domain “onion state” (OS) under high external magnetic fields and a circulating vortex state (VS) at low fields.^10,15 By reducing the field, OS transitions to VS as one domain wall depins, propagates and ultimately annihilates the other wall.¹² Further increasing the applied field distorts the circulating magnetization of VS, leading to nucleation of two domains and domain walls in the reverse onion state (ROS).¹² This results in a two-step switching process: OS → VS → ROS.

Modifying structural parameters, such as ring thickness and width, significantly alters these magnetization transitions. An increase in thickness leads to a change from transverse to vortex domain walls,¹⁶ which exhibit distinct dynamic behaviors.¹⁷ Similarly, variations in ring width influence the stability and type of magnetization states. For instance, wider rings can support the vortex core state (VCS) – a circulating configuration with a vortex core – while narrower rings may stabilize a twisted state.^{10,15,18–20}

Further control over magnetization states can be achieved by deviating from the symmetric circular NR geometry. Introducing asymmetry, such as by displacing the central hole,²¹ incorporating notches,²² or integrating additional structural elements,²³ can enhance control over the VS chirality under specific field orientations. Non-circular geometries, such as rectangular or elliptical NRs, can exhibit anisotropic reversal behavior that depends on the axis of applied magnetic field (e.g., along the long or short axis).^11,24–27 This directional dependence can benefit device applications requiring distinct read and write pathways.

Additionally, reducing the spacing between adjacent nanorings enhances magnetostatic interactions, which can induce collective magnetization behavior across the array.²⁸ Such collective dynamics open new avenues for designing highly responsive and energy-efficient magnetic systems.

Previous studies have significantly advanced our understanding of nanoring magnetization behavior, including non-circular rings. However, in the latter case they have primarily focused on magnetic field orientations along, or close to, the principal axes – namely, the long axis (ϕ = 0°) and short axes (ϕ = 90°).^{11,13,21,28,29} Investigations of non-circular NRs at other angles have often used coarse angular increments (e.g., 15°)^27,30 or have been limited to fine sampling over narrow angular ranges.²⁶ Consequently, a comprehensive understanding of the angular dependence of magnetization reversal across various nanoring geometries remains incomplete.

A comprehensive angular characterization is essential for several reasons. First, in practical applications, magnetic elements are seldom exposed to perfectly aligned external fields, making it crucial to understand off-axis responses for reliable and predictable device performance. Second, intermediate angles can reveal unexpected switching behaviors or new magnetization states, presenting opportunities for novel functionalities, as our results demonstrate. A thorough angular analysis may also uncover fundamental symmetry-breaking mechanisms inherent to confined magnetic systems that are not visible when considering only the principal structural axes.

In this work, we systematically investigate the magnetization reversal behavior of circular and rounded rectangular Ni₈₁Fe₁₉ nanorings under two distinct conditions: effectively isolated and strongly interacting arrays. We conduct a comprehensive angular study, examining how the switching fields, specifically the fields at which the vortex state is nucleated (H_VS1) and annihilated (H_VS2), evolve as a function of the angle of the applied magnetic field. These critical fields, along with the stable field range of the vortex state, serve as key metrics for characterizing nanoring behavior and assessing their suitability for various applications.

By comparing circular and rectangular geometries, we explore how field orientation influences vortex state stability and how magnetostatic interactions modify angle-dependent reversal dynamics. This study fills key gaps in our understanding of angular dependence in nanoring systems and provides insights relevant for fundamental research and device design.

We identify a region of enhanced VS stability in rectangular nanorings, where the VS is well-established before remanence when the magnetic field is applied near the short axis (ϕ ≈ 90°). While similar transitions have been noted in previous studies,^26–28 the onset of this behavior and the range of angles over which it occurs have not been reported before. Notably, while strongly coupled nanorings exhibit a broader angular range of VS stability (13° vs. 2°), the field required to nucleate the VS is lower than in isolated rings (85 Oe vs. 130 Oe).

Micromagnetic simulations support our experimental findings and offer further insights into the mechanisms driving this behavior. These results highlight the potential of angularly tunable nanorings for use in neuromorphic computing systems, where multiple stable magnetic states can be exploited to control the hysteresis and non-linearity of the system.

Method

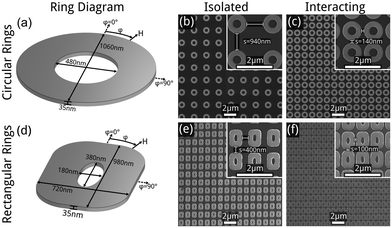
Arrays of nanoscale ring structures were fabricated using deep ultraviolet (DUV) lithography over a large resist-coated area (4 mm × 4 mm) on silicon substrates, following the methodology described by Adeyeye and Singh.³¹ A 35 nm-thick layer of Permalloy (in this work Ni₈₁Fe₁₉ was used, though Ni₈₀Fe₂₀ is also standard) was deposited onto the patterned resist via sputtering from a single target, under a chamber pressure of 1.88 × 10⁻³ Torr and from a base pressure of the order of ×10⁻⁷ Torr. The photoresist was subsequently removed via ultrasonic lift-off using OK73 resist thinner, followed by rinsing with deionized water. Scanning electron microscopy (SEM) imaging confirmed the success of the lift-off process.

Two nanoring geometries were investigated: circular and rounded rectangular, with corresponding schematics and dimensions shown in Fig. 1(a) and (d). The circular rings had an outer diameter of 1060 nm and inner diameter of 480 nm. The rounded rectangular rings had outer dimensions of 720 nm × 980 nm and hole dimensions of 180 nm × 380 nm. Two regimes of edge-to-edge spacing (s) were analyzed for each geometry to differentiate between effectively isolated and strongly interacting configurations. For circular rings, spacings of s = 940 nm and s = 140 nm were examined as shown in Fig. 1(b) and (c). For rectangular rings, spacings of s = 400 nm and s = 100 nm were studied, as shown in Fig. 1(e) and (f).

Fig. 1 Schematic illustrations of (a) circular and (d) rectangular rings, with dimensions and field-angle orientations labeled. SEM images of (b) widely and (c) tightly packed arrays of circular rings. SEM images of (e) widely spaced and (f) tightly spaced arrays of rectangular rings with rounded corners. Insets show magnified images with corresponding edge-to-edge spacings s.

Magnetization reversal was characterized using a custom-built longitudinal magneto-optical Kerr effect (MOKE) magnetometer. Measurements were conducted with the magnetic field applied in-plane, sweeping through a range of ±560 Oe. Angular dependence was studied by rotating the sample with a precision rotation stage. For rectangular nanorings, magnetization reversal was measured through the full angular range (ϕ = 0°–360°) in 5° increments. For circular nanorings, due to their symmetry, measurements were taken from ϕ = 0° to 180° in 15° steps. Additionally, finer angular resolution of 1° steps was employed within the range ϕ = 80°–100° (and ϕ = 260°–280° for rectangular rings) to capture details of the vortex state transitions. A gradient correction was applied to all hysteresis loops to account for a linear background caused by the magnetic response of the silicon substrate. The switching fields corresponding to nucleation into (H_VS1), and annihilation (H_VS2), of the vortex state were extracted from these loops.

Micromagnetic simulations were carried out using both the LLG Micromagnetics Simulator³² and MuMax3.³³ Hysteresis loop simulations were performed with the LLG Micromagnetics Simulator, while simulations of demagnetizing fields and equilibrium magnetization states were conducted using MuMax3. Standard material parameters for Permalloy were employed: an exchange stiffness constant of A = 1.30 × 10⁻¹¹ J m⁻¹, saturation magnetization M_sat = 8.6 × 10⁵A m⁻¹, damping parameter α = 0.008 and zero magnetocrystalline anisotropy. A uniform micromagnetic cell size of 5 nm × 5 nm × 5 nm was used throughout the simulations. Structural dimensions were based on values extracted from SEM images of the fabricated NRs. Hysteresis simulations were performed on 2 × 2 grids of elements with corresponding spacings and periodic boundary conditions, except for isolated circular NRs which were simulated as a single element. Demagnetising field simulations were performed using single elements.

Results and discussion

Circular rings

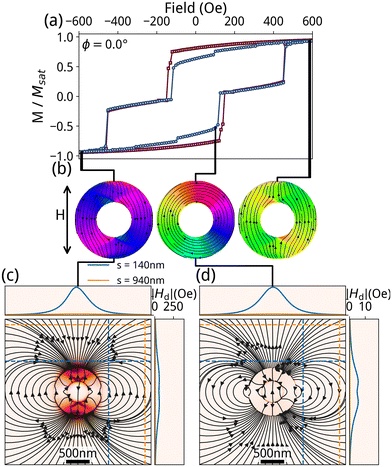
We examine first the magnetization reversal behavior of isotropic circular nanorings (NRs) to clarify the interplay between ring geometry and magnetostatic coupling. Fig. 2 presents the reversal characteristics of isolated circular NRs with an edge-to-edge spacing of s = 940 nm. Representative hysteresis loops measured at field orientations of ϕ = 0°, ϕ = 45° and ϕ = 90° are shown in Fig. 2(a), where the fields corresponding to nucleation of the VS (H_VS1, orange) and annihilation of the VS (H_VS2, light blue) are indicated. Throughout this work, these are defined for the field sweep from −ve to +ve applied field, as indicated by the arrow of the field H. At all angles, the nanorings exhibit the characteristic two-step switching transition sequence: OS → VS → ROS. Notably, H_VS1 at ϕ = 0° is slightly higher than at ϕ = 45° and ϕ = 90°, while H_VS2 remains approximately constant across all angles. The angular dependence of H_VS1 and H_VS2 is summarized in the polar plot shown in Fig. 2(b). Here, H_VS1 varies between −5 Oe and 35 Oe with an average of 10 Oe, peaking near 150°, while H_VS2 remains largely constant, ranging from 315 Oe to 335 Oe with a mean of 320 Oe. This angular variation in H_VS1 is unexpected, as neither the isotropic geometry of the NRs nor the negligible array interactions at this spacing are expected to produce such anisotropy. Further investigation, including measurements of continuous films (see SI), indicates that this anisotropy originates from the deposition process.

Fig. 2 Experimental measurements of isolated circular rings with s = 940 nm. (a) MOKE measurements with field along ϕ = 0°45° and 90°. Transitions into and out of vortex state are shown in orange and light blue respectively. (b) Polar plot of transitions into and out of vortex state at varied ϕ. Centre SEM image acts as a guide for field direction.

Next, we examine the effect of magnetostatic coupling by studying the magnetization reversal of interacting circular nanorings with a reduced edge-to-edge spacing of s = 140 nm, as presented in Fig. 3. The hysteresis loops shown in Fig. 3(a) reveal that all samples maintain the characteristic two-step switching transition. Notably, at ϕ = 45°, the magnetization decreases significantly more prior to the onset of the vortex state, compared to other angles. The vortex state switching fields remain largely consistent, with H_VS1 slightly reduced at ϕ = 45°. The angular dependence of the switching fields is summarized in the polar plot of Fig. 3(b), where H_VS1 ranges from 35 Oe to 60 Oe, averaging 50 Oe, and H_VS2 varies between 290 Oe and 315 Oe, with a mean value of 305 Oe. Both switching fields display maxima near ϕ = 90° and minima around ϕ = 45° and ϕ = 135°.

Fig. 3 Experimental measurements of interacting circular rings with s = 140 nm. (a) MOKE measurements with field along ϕ = 0°, 45° and 90°. Transitions into and out of vortex state are shown in orange and light blue respectively. (b) Polar plot of transitions into and out of vortex state at varied ϕ. Centre SEM image acts as a guide for field direction.

Comparing the isolated and interacting ring structures, the results show that magnetostatic coupling increases the average H_VS1 by approximately 40 Oe, while reducing the average H_VS2 by 20 Oe. Consequently, the overall stable range of the vortex state decreases by 60 Oe. To further understand these observations, micromagnetic simulations were conducted, as shown in Fig. 4. In Fig. 4(a), both isolated and interacting configurations display the characteristic two-step switching transition, with the increase in H_VS1 being more pronounced than the decrease in H_VS2, in line with the experimental trends. Fig. 4(b) presents the corresponding magnetization states, where the magnetization directions are indicated by arrows, clearly indicating the OS, VS, and ROS as expected.

Fig. 4 Simulation of circular rings with field applied along ϕ = 0° (a) Hysteresis loop of isolated (interacting) circular rings in dark blue (dark red) with ϕ = 0°. (b) Magnetization states of simulation at labeled field. (c). Demagnetizing field plots of OS (left) and VS (right). Dashed line indicates a slice of the demagnetizing field away from the edge: blue – 140 nm, orange – 940 nm. Adjacent plots show the magnitude of the demagnetizing field at each slice. Note the large difference in the magnitude of the fields in (c) and (d).

The demagnetizing fields associated with OS and VS of a single nanoring are depicted in Fig. 4(c) and (d), respectively. The side and top views show the magnitude of the stray fields at edge-to-edge spacings of 140 nm and 940 nm. For the OS, the stray field is strongest along the direction of the applied field, reaching a maximum of 370 Oe at s = 140 nm, while perpendicular to the applied field direction, the stray field peaks at only 60 Oe. This anisotropic stray field distribution explains the increased H_VS1 near ϕ = 0° and 90° compared to intermediate angles such as ϕ = 45° and ϕ = 135°, where the effective edge-to-edge spacing is larger, resulting in weaker magnetostatic coupling and correspondingly smaller enhancements in H_VS1. Notably, demagnetizing field strength is significantly reduced at s = 940 nm, illustrating the isolation of the NRs.

In Fig. 4(d), the demagnetizing field of the VS shows that stray field is once again strongest along the direction of the applied field, primarily due to twisting of magnetization. However, the maximum stray field in this direction is only 15 Oe, which is significantly lower than that observed in The Onion state. This reduced stray field magnitude clarifies why the decrease in H_VS2 is less pronounced compared to the increase in H_VS1, reflecting the weaker magnetostatic coupling present during the VS transition.

Rectangular rings

The magnetization reversal behavior of isotropic circular nanorings exhibited the expected characteristics. For both isolated and interacting arrays, the switching fields H_VS1 and H_VS2 showed limited angular variation, with magnetostatic coupling leading to an increase in H_VS1 and a decrease in H_VS2. We now turn to the magnetization reversal of rectangular nanorings with rounded corners, beginning with the isolated configuration with an edge-to-edge spacing of 400 nm shown in Fig. 5. The effective isolation has been verified through hysteresis simulations of different spacings (see SI). The hysteresis loops presented in Fig. 5 reveal a pronounced angular dependence in both the shape of the loops and the switching fields. At ϕ = 0° and ϕ = 91°, a three-step switching is observed, in contrast to the two-step switching seen at ϕ = 45°. The additional intermediate state at ϕ = 0° appears before the formation of the vortex state. This metastable state is unique to the ϕ = 0° (and ϕ = 180°) axis; it is absent at ϕ = 5°, where only the typical two-step switching transition occurs. In contrast, at ϕ = 90°, a metastable state emerges between the VS and ROS configurations. Despite these variations, the vortex state is consistently observed across all angles. However, both the switching fields and the stable range of the vortex state exhibit significant angular dependence, with the narrowest stable range of the three occurring at ϕ = 45°.

Fig. 5 Experimental measurements of isolated rectangular rings with s = 400 nm. (a) MOKE measurements with field along ϕ = 0°45° and 91°. Transitions into and out of vortex state are shown in orange and light blue respectively. (b) Polar plot of transitions into and out of vortex state at varied ϕ. Centre SEM image acts as a guide for field direction. (c) MOKE bottom half-loops at ϕ = 80°–100° with transitions shown.

The angular dependence of the fields H_VS1 and H_VS2 is summarized in the polar plot shown in Fig. 5(b). Neglecting the behavior near ϕ = 90° for now, H_VS1 ranges from 65 Oe to 130 Oe with an average value of 95 Oe. It exhibits local maxima at ϕ = 60° (and ϕ = 120°), with minima near ϕ = 0° and before the transition near ϕ = 90°. The angular trend of H_VS1 displays mirror symmetry about ϕ = 0° and ϕ = 90°, as well as two-fold rotational symmetry, which is consistent with the symmetry expected from the geometry of the rectangular rings. H_VS2, on the other hand, decreases monotonically from its maximum at ϕ = 0° to its minimum at ϕ = 90°, ranging between 175 Oe and 265 Oe respectively, with a mean value of 205 Oe. This variation is more pronounced than that observed for H_VS1, highlighting a stronger angular sensitivity in the exit transition from the vortex state.

Finally, we examine the behavior near ϕ = 91°–92°, where a sharp change in vortex state entry is observed. In Fig. 5(b), this is marked by a sudden drop in H_VS1 that is more clearly visualized in Fig. 5(c), showing the lower half of the hysteresis loops between ϕ = 80° and ϕ = 100°. As the angle increases from ϕ = 80°, H_VS1 decreases steadily before exhibiting a dramatic drop from 65 Oe at ϕ = 90° to −60 Oe at ϕ = 91°–92°. In contrast, H_VS2 remains largely unchanged across this range, consistently measuring 175 Oe.

We now examine the magnetization reversal in the array of coupled rectangular NRs with reduced spacing (s = 100 nm), see Fig. 6. The hysteresis loops in Fig. 6(a) exhibit a similar angular dependence to the isolated NRs: a two-step switching transition at ϕ = 0° and three-step switching at ϕ = 45° and ϕ = 91°. However, notable differences arise. At ϕ = 0°, the metastable state observed in the isolated NRs is absent in the coupled NRs. At ϕ = 45°, the metastable state appears only briefly, which may reflect the switching field distribution seen in interacting rings and that the vortex state is less stable. The behavior at ϕ = 45° closely resembles that of the isolated case. The behavior at ϕ = 91° also closely resembles that of the isolated case.

Fig. 6 Experimental measurements of interacting rectangular rings with s = 100 nm. (a) MOKE measurements with field along ϕ = 0°45° and 91°. Transitions into and out of vortex state are shown in orange and light blue respectively. (b) Polar plot of transitions into and out of vortex state at varied ϕ. Centre SEM image acts as a guide for field direction. (c) MOKE bottom half-loops at ϕ = 80°–100° with transitions shown.

The polar plot, Fig. 6(b), highlights the angular dependence of the switching fields in the interacting NRs. Excluding the sharp drop near ϕ = 90°, the influence of deposition-related anisotropy – previously observed in circular rings – is again evident. A gradual increase in H_VS1 is noted near ϕ = 160°, while a corresponding rise in H_VS2 appears near ϕ = 5°, diverging from the behavior seen in isolated rectangular rings. This added anisotropy complicates the direct interpretation of the angular dependence of H_VS1. Nonetheless, H_VS1 ranges from 30Oe–70 Oe, with an average of 50 Oe. H_VS2 exhibits a similar monotonic decrease from a peak near ϕ = 0° to a minimum at ϕ = 90°, consistent with the isolated NRs. It spans a range of 105 Oe to 205 Oe, with a mean of 135 Oe – indicating a significantly broader variation than that of H_VS1.

By comparing the switching fields of isolated and interacting rectangular NRs, we find a reduction in H_VS1 of −45 Oe and H_VS2 of −70 Oe. The reduction in H_VS2 is larger than that of H_VS1, unlike the circular rings, where the magnetostatic interactions increased H_VS1 and decreased H_VS2. Importantly, these reductions are not uniformly distributed across angles, emphasizing the complexity of angular-dependent magnetization behavior under strong coupling conditions.

Focusing on the angular region between ϕ = 80° and ϕ = 100°, in Fig. 6(b) and the magnified view in Fig. 6(c), a distinct regime of enhanced vortex state stability is observed. The expanded VS range spans ϕ = 83° to ϕ = 95°, within which H_VS2 remains constant at around 105 Oe, while H_VS1 gradually decreases, then drops sharply from 30 Oe to between −65 Oe and −50 Oe with an average of −55 Oe. Comparing this transition to that observed in the isolated ring array shows notable differences. In the interacting system, the extended VS region covers a wider angular range of 13°, compared to just 2° in the isolated case. However, the change in H_VS1 is less abrupt in the coupled NRs, decreasing by only 85 Oe compared to 130 Oe in the isolated NRs. Interestingly, the post-transition H_VS1 values are similar in both configurations, suggesting that this lower limit may be predominantly determined by the intrinsic ring geometry, rather than coupling effects.

To further explore these observations, micromagnetic simulations were conducted for isolated and interacting NRs with spacings of 400 nm and 100 nm, respectively, along ϕ = 0° and ϕ = 90°, as shown in Fig. 7(a) and (b). At ϕ = 0°, both configurations exhibit two-step switching behavior, while at ϕ = 90°, a three-step switching sequence is observed – both in agreement with experimental results. However, discrepancies emerge when examining switching fields at ϕ = 90°. In simulations, H_VS1 is higher and H_VS2 is lower for the interacting rings, a trend not observed in experimental data. This suggests that additional complexities in the experimental system, such as imperfections or non-uniformities, may influence the magnetization dynamics beyond what is captured in idealized simulations.

Fig. 7 Micromagnetic simulation results for rectangular nanorings with field applied along ϕ = 0° and ϕ = 90°. (a) Hysteresis loops for isolated (dark blue) and interacting (dark red) rings with field applied along ϕ = 0°. (b) Hysteresis loops for isolated and interacting rings with field applied along ϕ = 90°. (c and d) Magnetization states at key field values showing the evolution through different states for ϕ = 0° (c) and ϕ = 90° (d). Note the formation of onion state (OS), vortex state (VS), vortex core state (VCS) and reverse onion state (ROS). (e–h) Demagnetizing field distributions with accompanying magnitude plots for: (e) onion state at ϕ = 0°, (f) onion state at ϕ = 90°, (g) vortex state at ϕ = 90°, and (h) vortex core state at ϕ = 90°. Colored lines in the adjacent plots represent field magnitudes at distances of 100 nm (blue), and 400 nm (orange) from the ring edge. Note the large difference in magnitudes of the fields.

Fig. 7(c) and (d) present the simulated magnetization configurations during the reversal for ϕ = 0° and ϕ = 90° respectively. At ϕ = 0°, the expected sequence of states – OS, VS and ROS – is observed. In contrast, reversal at ϕ = 90° proceeds via four distinct configurations: OS, VS, VCS, and ROS.

A notable difference in the OS structure is evident between the two angles. At ϕ = 0°, the magnetization primarily aligns with the applied field and follows the elongated geometry of the ring, requiring minimal curvature around the hole. This alignment is aided by the fact that the long axes of both the outer ring and the inner elliptical hole are parallel to the applied field. As a result, the magnetization on the left and right sides of the hole remains largely aligned. At ϕ = 90°, the applied field is perpendicular to the hole's long axis, necessitating significant distortion of the magnetization around the hole's boundary. This reduced alignment with the field direction results in a higher energy configuration. For both cases, magnetization cants at the edges along the field axis – reducing, but not eliminating, stray field. Prior studies have shown that the direction of magnetization canting at these ends, whether symmetric or antisymmetric, can influence reversal dynamics in rectangular structures,³⁴ and a similar effect may be relevant here. At low applied fields, both VS configurations appear visually similar, but for ϕ = 90° a transition into VCS is also observed. This behavior is consistent with previous findings in circular nanorings, where the VCS tends to emerge in regions of high curvature that enhance edge twisting of the magnetization.^10,15

We now examine the distributions of demagnetizing fields shown in Fig. 7(e)–(h). Fig. 7(e) illustrates the demagnetizing field of the OS for a rectangular NR with the applied field along ϕ = 0°. The field distribution is distinctly asymmetric, arising from the canting in the magnetization configuration. The stray field concentrates in the direction of the applied field, with a magnitude of approximately 500 Oe measured 100 nm away from the long axis of the ring, compared to just 100 Oe at the same distance from the short axis. This directional disparity supports previous findings that magnetostatic coupling – and thus collective switching – are strongest when the external field is aligned with the long axis of rectangular NRs.²⁸Fig. 7(f) shows the OS configuration for the field applied at ϕ = 90°. Similar to the ϕ = 0° case, the stray field is mainly aligned with the direction of the applied field. Notably, there is a higher density of magnetostatic field along the lower domain walls compared to the upper ones. This asymmetry suggests a greater likelihood for the lower walls to develop into vortex domain walls, which aligns with prior observations of domain wall behavior in confined geometries. In Fig. 7(g), the demagnetizing field of the VS at ϕ = 90° is presented. As expected for a VS, the stray field is significantly reduced, with a maximum magnitude of around 70 Oe. Finally, Fig. 7(h) shows the field distribution in the VCS. Although the presence of the vortex core induces localized magnetizaton out of plane, it does not dramatically increase the stray field in plane: the peak field near the core reaches approximately 200 Oe, compared to 120 Oe in adjacent regions of circulating magnetization. Instead of increasing magnetostatic energy, the vortex core reduces the Zeeman energy by locally minimizing the magnetization component that is anti-parallel to the applied field. This energy trade-off plays a role in stabilizing the VCS during reversal.

We therefore propose that the experimentally observed transition into a longer-lived VS near ϕ = 90° results from an intermediate transition into a short-lived VCS that propagates to the edge and is annihilated. This is supported by the gradual evolution seen in the half-loop hysteresis plots shown in Fig. 5(c) and 6(c), where the onset of the extended VS state occurs progressively over several field angles, particularly in the strongly interacting case. Interestingly, such a gradual transition is absent in our micromagnetic simulations, which demonstrate abrupt switching behavior. This discrepancy suggests that local variations across the NR array may drive the experimental transition. We hypothesize that during the angular interval of this transition, only a subset of rings undergoes the ‘enhanced’ VS transition via the intermediate VCS. Collective switching of columns has previously been observed in columns of rectangular nanorings.²⁸ As the field angle increases, a growing fraction of the array follows this pathway until the transition becomes collective, resulting in all rings exhibiting the longer-lived VS configuration. This interpretation highlights the role of spatial heterogeneity and magnetostatic interactions in enabling complex, angle-dependent reversal behaviors that are not captured in simulations assuming ideal uniform conditions.

Conclusions

We have systematically investigated the angular dependence of magnetization reversal in circular and rounded rectangular Ni₈₁Fe₁₉ nanorings under both isolated and strongly interacting conditions. By tracking the entry (H_VS1) and exit (H_VS2) fields of the vortex state across a wide angular range, we show how shape and magnetostatic coupling influence reversal dynamics. In circular rings, coupling increased H_VS1 and decreased H_VS2, with the most significant effects aligned with the applied direction. Rectangular rings exhibited pronounced configurational anisotropy, with H_VS2 varying more strongly than H_VS1. Strong coupling reduced both switching fields, though this effect was non-uniform and angle dependent. A distinct transition near ϕ = 90° was observed in both ring geometries, marked by a drop in H_VS1 and the emergence of three-step switching behavior. This transition was more abrupt in isolated rings but spanned a wider angular range (Δϕ = 13°) in the coupled arrays. We attribute this “enhanced” VS stability regime to an intermediate vortex core state, likely stabilized by curvature along the elliptical hole in rectangular rings. Our findings highlight the potential of utilizing angular and geometric tuning to create nanomagnetic devices with directionally sensitive or multi-state behaviors – features beneficial for applications in neuromorphic computing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5nr02835c.

Acknowledgements

The authors thank Dr Navab Singh for the DUV templates. SEM imaging of the patterned structures was carried out at the GJ Russel Electron Microscope Facility. A. O. A. would like to acknowledge the funding from the Wolfson Foundation and Royal Society.

References

1. S. Parkin and S.-H. Yang, Nat. Nanotechnol., 2015, 10, 195–198.
2. D. Atkinson, D. S. Eastwood and L. K. Bogart, Appl. Phys. Lett., 2008, 92, 022510.
3. R. P. Cowburn, J. Magn. Magn. Mater., 2002, 242–245, 505–511.
4. D. Matatagui, O. V. Kolokoltsev, N. Qureshi, E. V. Mejía-Uriarte, C. L. Ordoñez-Romero, A. Vázquez-Olmos and J. M. Saniger, Sens. Actuators, B, 2017, 240, 497–502.
5. Z. Luo, A. Hrabec, T. P. Dao, G. Sala, S. Finizio, J. Feng, S. Mayr, J. Raabe, P. Gambardella and L. J. Heyderman, Nature, 2020, 579, 214–218.
6. T. Goto, T. Yoshimoto, B. Iwamoto, K. Shimada, C. A. Ross, K. Sekiguchi, A. B. Granovsky, Y. Nakamura, H. Uchida and M. Inoue, Sci. Rep., 2019, 9, 16472.
7. A. V. Chumak, A. A. Serga and B. Hillebrands, J. Phys. D: Appl. Phys., 2017, 50, 244001.
8. A. Barman, G. Gubbiotti, S. Ladak, A. O. Adeyeye, M. Krawczyk, J. Gräfe, C. Adelmann, S. Cotofana, A. Naeemi, V. I. Vasyuchka, B. Hillebrands, S. A. Nikitov, H. Yu, D. Grundler, A. V. Sadovnikov, A. A. Grachev, S. E. Sheshukova, J.-Y. Duquesne, M. Marangolo, G. Csaba, W. Porod, V. E. Demidov, S. Urazhdin, S. O. Demokritov, E. Albisetti, D. Petti, R. Bertacco, H. Schultheiss, V. V. Kruglyak, V. D. Poimanov, S. Sahoo, J. Sinha, H. Yang, M. Münzenberg, T. Moriyama, S. Mizukami, P. Landeros, R. A. Gallardo, G. Carlotti, J.-V. Kim, R. L. Stamps, R. E. Camley, B. Rana, Y. Otani, W. Yu, T. Yu, G. E. W. Bauer, C. Back, G. S. Uhrig, O. V. Dobrovolskiy, B. Budinska, H. Qin, S. van Dijken, A. V. Chumak, A. Khitun, D. E. Nikonov, I. A. Young, B. W. Zingsem and M. Winklhofer, J. Phys.: Condens. Matter, 2021, 33, 413001.
9. I. T. Vidamour, C. Swindells, G. Venkat, L. Manneschi, P. W. Fry, A. Welbourne, R. M. Rowan-Robinson, D. Backes, F. Maccherozzi, S. S. Dhesi, E. Vasilaki, D. A. Allwood and T. J. Hayward, Commun. Phys., 2023, 6, 230.
10. M. Kläui, C. A. F. Vaz, J. A. C. Bland, L. J. Heyderman, C. David, E. H. C. P. Sinnecker and A. P. Guimarães, J. Appl. Phys., 2004, 95, 6639–6641.
11. G. Shimon, A. O. Adeyeye and C. A. Ross, J. Appl. Phys., 2012, 111, 013909.
12. M. Kläui, C. A. F. Vaz, L. Lopez-Diaz and J. A. C. Bland, J. Phys.: Condens. Matter, 2003, 15, R985.
13. Y. Ren, S. Jain, A. O. Adeyeye and C. A. Ross, New J. Phys., 2010, 12, 093003.
14. J. Rothman, M. Kläui, L. Lopez-Diaz, C. A. F. Vaz, A. Bleloch, J. A. C. Bland, Z. Cui and R. Speaks, Phys. Rev. Lett., 2001, 86, 1098–1101.
15. M. Kläui, C. A. F. Vaz, J. A. C. Bland, T. L. Monchesky, J. Unguris, E. Bauer, S. Cherifi, S. Heun, A. Locatelli, L. J. Heyderman and Z. Cui, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 134426.
16. Y. Nakatani, A. Thiaville and J. Miltat, J. Magn. Magn. Mater., 2005, 290–291, 750–753.
17. M.-F. Lai, C.-N. Liao, Z.-H. San, C.-P. Lee, Y.-P. Hsieh and T.-F. Ho, J. Appl. Phys., 2008, 103, 07C517.
18. F. J. Castaño, C. A. Ross, C. Frandsen, A. Eilez, D. Gil, H. I. Smith, M. Redjdal and F. B. Humphrey, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 184425.
19. F. J. Castaño, C. A. Ross, A. Eilez, W. Jung and C. Frandsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144421.
20. W. Zhang and S. Haas, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 064433.
21. E. Saitoh, M. Kawabata, K. Harii, H. Miyajima and T. Yamaoka, J. Appl. Phys., 2004, 95, 1986–1988.
22. M. Kläui, J. Rothman, L. Lopez-Diaz, C. A. F. Vaz, J. A. C. Bland and Z. Cui, Appl. Phys. Lett., 2001, 78, 3268–3270.
23. U. Makartsou, M. Moalic, M. Zelent, M. Mruczkiewicz and M. Krawczyk, Nanoscale, 2023, 15, 13094–13101.
24. F. J. Castaño, C. A. Ross and A. Eilez, J. Phys. D: Appl. Phys., 2003, 36, 2031.
25. P. Vavassori, M. Grimsditch, V. Novosad, V. Metlushko and B. Ilic, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 134429.
26. Y. Ren and A. O. Adeyeye, J. Appl. Phys., 2009, 105, 063901.
27. A. O. Adeyeye, N. Singh and S. Goolaup, J. Appl. Phys., 2005, 98, 094301.
28. A. O. Adeyeye, S. Goolaup, N. Singh, C. C. Wang, X. S. Gao, C. A. Ross, W. Jung and F. J. Castaño, J. Phys. D: Appl. Phys., 2007, 40, 6479.
29. F. S. Ma, V. L. Zhang, Z. K. Wang, H. S. Lim, S. C. Ng, M. H. Kuok, Y. Ren and A. O. Adeyeye, J. Appl. Phys., 2010, 108, 053909.
30. Y. Ren, N. Singh and A. O. Adeyeye, J. Appl. Phys., 2013, 113, 17A335.
31. A. O. Adeyeye and N. Singh, J. Phys. D: Appl. Phys., 2008, 41, 153001.
32. M. R. Scheinfein, LLG Micromagnetics Simulator, 2018, https://web.archive.org/web/20180217080016/, https://llgmicro.home.mindspring.com/.
33. A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, AIP Adv., 2014, 4, 107133.
34. Y. Zheng and J.-G. Zhu, J. Appl. Phys., 1997, 81, 5471–5473.

---