Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ice nucleation by DNA origami†
Sarah A.
Alsalhi
ab,
Jonathan
Bath
c,
Andrew
Turberfield
 *c and
Walther
Schwarzacher
*c and
Walther
Schwarzacher
 *bd
*bd
aDepartment of Physics, College of Science, Princess Nourah bint Abdulrahman University, Riyadh 11671, Saudi Arabia
bH. H. Wills Physics Laboratory, University of Bristol, Bristol BS8 1TL, UK
cClarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, UK. E-mail: andrew.turberfield@physics.ox.ac.uk; Tel: +44 (0)1865 272200
dSyed Babar Ali School of Science and Engineering, LUMS, DHA, Lahore 54792, Pakistan. E-mail: walther@lums.edu.pk; Tel: +92 42 3560 8349
First published on 3rd July 2025
Abstract
Fundamental investigations of ice nucleation, a key process in fields from environmental science to cryobiology, require model systems with chemical and physical structures that are well defined and easily varied. DNA origami is an especially promising model because of the exquisite control that it offers over the physical geometry of the nucleating agent at the nano-scale. Here we compare ice nucleation by solutions of a rectangular DNA origami tile, formed by annealing a 2.6 kbase single-stranded DNA scaffold with ninety shorter ‘staple’ oligonucleotides, to ice nucleation when these components are mixed at the same concentrations but not annealed. Isothermal measurements show that the molecular conformation has a dramatic effect on the ice nucleating efficiency. For an array of droplets containing annealed, well-folded tiles the freezing rate is constant, whereas for unannealed DNA the freezing rate decreases with time. Despite the freezing rate measured at low temperature being higher for the annealed DNA origami samples than for a significant proportion of the unannealed ones, in slow temperature-ramp measurements the latter generally freeze at higher temperatures. We show that this behaviour is consistent with the formation of small numbers of highly efficient nucleating agents in the unannealed samples, likely through molecular aggregation.
Introduction
In the transition from liquid water to ice, heterogeneous ice-nucleating agents (INAs) play a crucial role, facilitating freezing by lowering the free-energy barrier that exists between the liquid and solid phases.1,2 Understanding their function is essential to many fields. For example, incomplete knowledge of the efficiency and distribution of INAs is a significant source of uncertainty in climate models,3,4 because the amount of ice present in clouds influences their radiative properties and therefore their contribution to global warming.5,6 INAs are also extremely important for the survival of life in cold climates7 and in applications ranging from the freeze-drying of foods8 to the cryopreservation of tissue.9Investigating the influence of a specific physical or chemical property of an INA on its ice-nucleating efficiency10,11 is an experimental challenge. It is extremely difficult to find a model system in which just a single parameter can be varied systematically, except for a few simple cases such as self-assembled monolayers of organic molecules.12–14 For example, while it is possible to control the chemical composition and crystal structure of mineral INAs, in practice these exhibit a wide range of ice-nucleating efficiencies because of the existence of active sites that cannot be controlled precisely.15 Biomolecules, in contrast, have the advantage that they can be engineered precisely at the nanoscale, making them very attractive as models. Deoxyribonucleic acid (DNA) is an especially attractive biomolecular model for ice nucleation studies because it possible to design DNA molecules to form two- and three-dimensional structures of pre-determined shape, for example using the DNA origami technique.16,17
Here we study ice nucleation in droplets (immersion nucleation) by a particularly simple DNA origami structure, a rectangular tile of approximate size 40 × 80 × 2 nm. The tiles are assembled by hybridization between a 2.6 kbase, single-stranded, circular scaffold and an excess of 90 short (typically 32 nt), distinct ‘staple’ oligonucleotides when these are annealed by cooling from 96 °C to 25 °C at 1 °C min−1. By comparing ice nucleation by well-formed DNA origami tiles and by a mixture of disordered components before annealing, we provide a direct demonstration of the crucial role that molecular conformation plays in determining ice-nucleating efficiency by biomolecules. Furthermore, comparison between temperature ramp and isothermal measurements for annealed and unannealed origami reveals an interesting behaviour. Isothermal measurements show that, at lower temperatures, droplets containing a fixed concentration of annealed DNA origami freeze more rapidly than droplets containing the same quantity of unannealed origami. However, in temperature ramp experiments the latter tend to freeze at higher temperatures. We show that a simple model based on classical nucleation theory (CNT) can explain such behaviour if the unannealed DNA origami samples contain a small number of highly efficient INAs, such as large aggregates.
Results and discussion
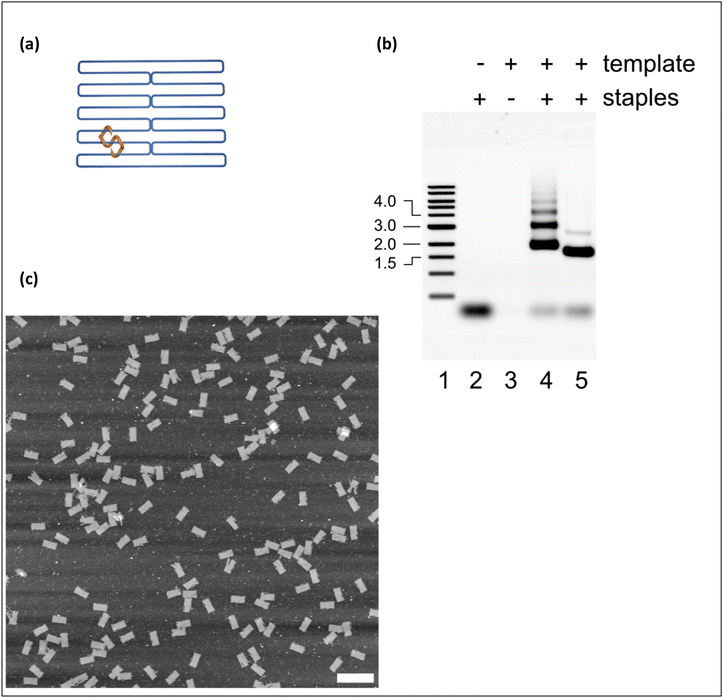
The DNA origami nanostructure used in this study18 is a rectangular tile built from parallel helices linked by reciprocal staple strand crossovers,16 as shown schematically in Fig. 1(a). Further details of preparation and characterization are given in the ESI.†Fig. 1(b) and (c) show that the annealing process yields well-formed tiles. To compare the ice nucleating-efficiency of unannealed DNA origami (unassembled template and staple molecules) and annealed (well-folded) DNA tiles, and thereby probe the influence of molecular conformation, we carried out isothermal freezing measurements (see ESI†). We monitored the times at which droplets of known volume V (typically 1 μL), containing pre-determined DNA concentrations in Tris buffer, froze when held at a fixed target temperature T following rapid cooling (see Fig. S1†).During an isothermal experiment, the probability that a given droplet remains unfrozen after time t, is equal to e−Rit, where Ri is the freezing rate for that droplet at the temperature of measurement, T. Ri is determined by the concentration and efficiency of the INAs present in the droplet and e−Rit is simply the probability of zero freezing events assuming Poisson statistics.19,20 If there is a large number of droplets with the same freezing rate Ri = R, then the probability e−Rt that a droplet remains unfrozen after time t is equal to the experimental unfrozen fraction, defined by  . Here Nliq is the number of unfrozen droplets at time t and Ntot is the number of unfrozen droplets at t = 0. In this case, a log-linear plot of U(t) against t will be a straight line with the gradient proportional to R. If, however, individual droplets have significantly different INA contents then they will no longer have the same freezing rate Ri and a log-linear plot of U(t) against t will no longer be a straight line.21
. Here Nliq is the number of unfrozen droplets at time t and Ntot is the number of unfrozen droplets at t = 0. In this case, a log-linear plot of U(t) against t will be a straight line with the gradient proportional to R. If, however, individual droplets have significantly different INA contents then they will no longer have the same freezing rate Ri and a log-linear plot of U(t) against t will no longer be a straight line.21
Fig. 2 shows isothermal freezing data for 1 μL droplets containing either 100 nM annealed (well-folded) DNA origami tiles or the same mass of unannealed origami at −24.5 °C. The difference between the data for the two samples shows clearly that folding the DNA molecules into tiles has a dramatic influence on their ice-nucleating efficiency. This is likely because folding the DNA into a tile yields a flat surface of sufficient area to support a critical nucleus, i.e. one that is large enough to grow spontaneously. Note that the area required to support a critical nucleus depends on the contact angle between the INA and solid ice (see later), which in turn depends on the surface properties of the INA. The importance of a flat surface area for ice nucleation has previously been demonstrated experimentally using graphene oxide nanosheets.22 Since the plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U(t) is linear for arrays of droplets containing annealed DNA, we can conclude that for these samples R is constant (i.e. the droplets are homogeneous). In contrast, for the droplets containing unannealed DNA the freezing rate is lower and the variation of log
U(t) is linear for arrays of droplets containing annealed DNA, we can conclude that for these samples R is constant (i.e. the droplets are homogeneous). In contrast, for the droplets containing unannealed DNA the freezing rate is lower and the variation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U(t) with time is markedly sublinear, implying a significant variation in Ri from droplet to droplet. The gradient of a log-linear plot of U(t) decreases with increasing t when Ri varies significantly between droplets because as t increases, the unfrozen droplet population becomes dominated by those droplets for which the freezing rate is smaller.23
U(t) with time is markedly sublinear, implying a significant variation in Ri from droplet to droplet. The gradient of a log-linear plot of U(t) decreases with increasing t when Ri varies significantly between droplets because as t increases, the unfrozen droplet population becomes dominated by those droplets for which the freezing rate is smaller.23
 | ||
| Fig. 2 Isothermal freezing data for 1 μL droplets of Tris buffer containing 100 nM annealed (well-folded) DNA origami tiles (red dots) and the same mass of unannealed origami (black dots) at −24.5 °C. The linear fit to the annealed origami data assumes J0 = 275 s−1 and η = 1.0(3) × 106 K3 (see eqn (3)). The fit to the unannealed data assumes J0 = 0.55 s−1, μη = 12.5 and ση = 3.6 (see Table S1†). | ||
If the contribution of a particular INA species j to the freezing rate for a given droplet i is Rij, then Rij is proportional to nij, the number of INAs of species j in the droplet. Assuming randomly distributed INAs, the ratio of the standard deviation of Rij to its mean is proportional to  . Hence, for Ri to vary significantly between droplets, nij must be small. We therefore conclude that nucleation is dominated by rare species. Very similar behaviour is observed at the other temperatures studied (Fig. S2†).
. Hence, for Ri to vary significantly between droplets, nij must be small. We therefore conclude that nucleation is dominated by rare species. Very similar behaviour is observed at the other temperatures studied (Fig. S2†).
The temperature dependence of the freezing rate R(T) for annealed DNA origami obtained from the data presented in Fig. 2 and S2† can be modelled straightforwardly using classical nucleation theory (CNT).1,24 According to CNT, the excess free energy associated with the formation of a spherical nucleus of a new phase within an existing one is given by the sum of a surface term, associated with the interface between the phases, and a bulk term. For the specific case of water freezing, the excess free energy when a sphere of ice of radius r forms is given by
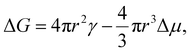 | (1) |
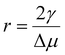 . This value of r is the critical nucleus radius rc. The corresponding value of ΔG is the free energy barrier ΔG* that must be overcome for ice to nucleate from supercooled water in the absence of any INAs and may be found by substituting r = rc into eqn (1):
. This value of r is the critical nucleus radius rc. The corresponding value of ΔG is the free energy barrier ΔG* that must be overcome for ice to nucleate from supercooled water in the absence of any INAs and may be found by substituting r = rc into eqn (1): | (2) |
The rate at which ice is nucleated then becomes the rate at which ΔG* is overcome. Since the effect of introducing a particular INA is to reduce ΔG* by a factor f that depends on the contact angle between the INA and solid ice,25 for that INA the rate at which ΔG* is overcome is proportional to  , where kB is Boltzmann's constant. The greater the ice-nucleating efficiency of the INA, the smaller f will be.
, where kB is Boltzmann's constant. The greater the ice-nucleating efficiency of the INA, the smaller f will be.
Fig. 3 shows that a simple CNT-based model gives an excellent fit to R(T) for the annealed DNA origami samples. To fit the experimental R(T) data, we assume that a single nucleation event leads to rapid (on the timescale of measurement) freezing of the entire droplet and therefore that the freezing rate per droplet R(T) is proportional to the nucleation rate. Hence we use the following CNT-based26,27 expression for the freezing rate:
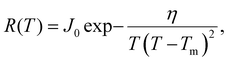 | (3) |
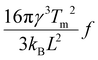 , where L is the latent heat of fusion of ice (per unit volume). Eqn (3) assumes that γ is independent of r, which is the capillarity approximation.25 We also assume that γ and J0 are independent of T to reduce the number of free parameters to two (J0 and η) and because the range of temperatures that we model is small.28 The fitted values of the parameters are J0 = 275 s−1 and η = 1.0 × 106 K3.
, where L is the latent heat of fusion of ice (per unit volume). Eqn (3) assumes that γ is independent of r, which is the capillarity approximation.25 We also assume that γ and J0 are independent of T to reduce the number of free parameters to two (J0 and η) and because the range of temperatures that we model is small.28 The fitted values of the parameters are J0 = 275 s−1 and η = 1.0 × 106 K3.
 | ||
| Fig. 3 Experimental nucleation rate data (solid circles) modelled using classical nucleation theory (CNT) as described in the text (solid line). The fitted values are J0 = 275 s−1 and η = 1.0 × 106 K3 (see eqn (3)). | ||
We can also use CNT to model the isothermal freezing data for the unannealed DNA. We can safely assume that the rare INAs responsible for ice nucleation in these samples will have a wide range of ice nucleating efficiencies, and consequently a wide range of η. Although we do not know how these are distributed, as a first approximation, we assume that the freezing rate for each droplet Ri is dominated by the most efficient INA present in that droplet. We further assume that η for this most efficient INA is log normally distributed with the mean and standard deviation of ln(η/K3) given by μη and ση respectively. Since variations in η have a much greater effect on the freezing rate, we ignore possible variations in J0. Details of our model are given in the ESI.†Fig. 2 and S2† show that this assumption leads to good fits to the data, with values of J0, μη and ση that are mutually consistent across the temperatures studied (see ESI Table S1† for fitted values). Here it is important to point out that the data of Fig. 2 and S2† exclude those droplets that freeze before the required temperature is reached. Since these are likely to be the droplets containing the most efficient INAs, our model will underestimate the maximum ice nucleating efficiency of the unannealed DNA samples.‡ The number of droplets sampled and modelled is nevertheless a significant fraction (40–65%) of the total (see Table S2†).
Note that for heterogeneous nucleation to be effective the contact angle-dependent factor f that appears in the expression for η and determines the ice nucleating efficiency must be less than one. Taking physically reasonable values for L for bulk water (3.1 × 108 J m−3) and a typical value of γ ≈ 25 mJ m−2,28η must therefore be less than approximately 1.5 × 107 K3. Hence the value of η obtained by fitting the experimental values of R(T) for annealed DNA using CNT (η = 1.0 × 106 K3) is physically reasonable. Similarly, for the fits to the freezing data for unannealed DNA, it is interesting to note that the median value of η is typically around η = 3.0 × 105 K3 (see ESI Table S1†). Since a lower value of η corresponds to a higher ice nucleating efficiency, this means that the rare INAs responsible for ice nucleation in the unannealed samples are much more efficient than those in the annealed samples. A reduction from η = 1.0 × 106 K3 to η = 3.0 × 105 K3 corresponds to an increase in the nucleation rate per INA by a factor of approximately 100 at T = −25 °C. INAs in the low-η tail of the efficiency distribution for unannealed DNA will nucleate ice even more rapidly. The rare INAs in the unannealed DNA samples that nucleate ice more efficiently than the DNA tiles are likely to be aggregates of multiple scaffold strands and staples, consistent with earlier work suggesting that aggregation of biomolecules increases their ice nucleating efficiency.29–33
To understand the behaviours of aerosol droplets in the environment, it is often important to know the temperature at which they freeze as the temperature falls. Experimentally, this can be determined by a temperature ramp experiment. Fig. 4 compares temperature ramp data for 1 μL droplets containing 100 nM annealed (well-folded) DNA origami tiles and the same mass of unannealed origami. After pre-cooling to −5 °C at 20 °C min−1, the cooling rate was 1 °C min−1 for both samples. The frozen fraction plotted in Fig. 4 is defined as  , where Nfrozen is the number of unfrozen droplets at temperature T.
, where Nfrozen is the number of unfrozen droplets at temperature T.
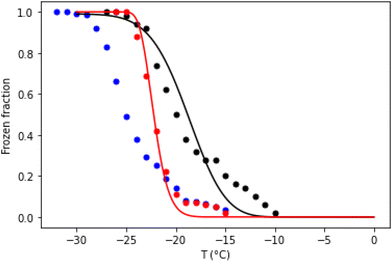 | ||
| Fig. 4 Temperature ramp data for 1 μL droplets of Tris buffer containing 100 nM annealed (well-folded) DNA origami tiles (red dots), the same mass of unannealed origami (black dots), or without DNA (blue dots). Droplet arrays were pre-cooled to −5 °C at 20 °C min−1, after which the frozen fraction was measured as the temperature was reduced further at a rate of 1 °C min−1. The annealed origami data were modelled assuming J0 = 275 s−1 and η = 1.25 × 106 K3 (see eqn (3)). The unannealed origami data were modelled assuming J0 = 0.55 s−1, μη = 12.9 and ση = 0.25 (see text). | ||
Note that in the temperature ramp experiments the unannealed DNA origami samples freeze, on average, before the annealed ones.§ This is despite the fact that our isothermal data show that over the temperature range −24.0 °C to −26.5 °C, a significant fraction of the unannealed DNA origami samples nucleate ice less rapidly than annealed origami. Although remarkable, this behaviour is completely consistent with CNT. It occurs because the unannealed DNA origami samples contain a lower concentration of more effective INAs, which results in both J0 and η being lower for the unannealed DNA origami samples. This means there is a crossover temperature, above which the predicted freezing rate is greater for the unannealed samples (see ESI†), even though the freezing rate is greater at low temperatures for the annealed origami. Hence, in a temperature ramp experiment, the former will generally freeze first, providing the cooling rate is sufficiently slow. For the model of Fig. 4, the crossover temperature is approximately −23.5 °C.
For heterogeneous samples where different droplets have different freezing rates, like the unannealed DNA, numerical simulations are helpful. The solid lines in Fig. 4 are calculated using the same CNT model that was used for Fig. 2 and 3. The numbers of droplets freezing before the start of our isothermal measurements are also qualitatively consistent with this model – see the ESI.†
To calculate the frozen fraction from the freezing rate given by eqn (3) we use
 | (4) |
 is the temperature ramp rate, and (1 − F(T)) is the unfrozen fraction. As before, for the annealed DNA origami samples we assume a homogeneous population of nuclei. For the unannealed samples we again assume that the freezing rate for each droplet is dominated by the most efficient INA and that η for this INA is log normally distributed (see ESI† for the relevant equations). The same values of J0 that were obtained from the fits of Fig. 2 were used to model the data in Fig. 4 but the values of η, and μη were increased while that of ση was decreased to improve the fit to the data.¶ Nevertheless, despite these changes, the freezing rates calculated using our CNT model remain lower for the unannealed DNA than for the annealed DNA at lower temperatures (see Fig. S3 and S4†). This calculation demonstrates the important point that lower freezing rates for certain samples compared to others at low temperatures can be consistent with their freezing faster in a temperature ramp experiment.
is the temperature ramp rate, and (1 − F(T)) is the unfrozen fraction. As before, for the annealed DNA origami samples we assume a homogeneous population of nuclei. For the unannealed samples we again assume that the freezing rate for each droplet is dominated by the most efficient INA and that η for this INA is log normally distributed (see ESI† for the relevant equations). The same values of J0 that were obtained from the fits of Fig. 2 were used to model the data in Fig. 4 but the values of η, and μη were increased while that of ση was decreased to improve the fit to the data.¶ Nevertheless, despite these changes, the freezing rates calculated using our CNT model remain lower for the unannealed DNA than for the annealed DNA at lower temperatures (see Fig. S3 and S4†). This calculation demonstrates the important point that lower freezing rates for certain samples compared to others at low temperatures can be consistent with their freezing faster in a temperature ramp experiment.
Conclusion
The ice nucleating efficiencies of fixed concentrations of unannealed DNA scaffold and staples are very different from those of the same molecules folded into origami tiles. This is a direct demonstration of the importance of molecular conformation for ice-nucleating biomolecules. Isothermal measurements show time-dependent (decreasing) freezing rates for the unannealed DNA sample and constant freezing rates for annealed DNA origami, indicating that the INAs that dominate ice nucleation in the former are at much lower concentration than those in the latter. Although at low temperatures the freezing rate for annealed DNA origami is higher than for unannealed samples, in temperature ramp measurements, on average, the latter freeze first, if the cooling rate is sufficiently slow (see the ESI†). Classical nucleation theory (CNT) explains this phenomenon and provides approximate fits to the data.Our results show the potential of DNA origami as a model ice nucleating agent. DNA origami offers the possibility of studying more complex INA geometries and is amenable to tailored surface functionalization: we believe that it will prove a very valuable tool for future ice nucleation studies.
Author contributions
SAA carried out the ice nucleation experiments. SAA and WS analyzed the ice nucleation data. JB and AT designed and prepared the DNA origami. AT and WS conceived the experiments and wrote the paper. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The datasets generated and the Python codes used during the current study are available in the University of Bristol Research Data Repository, data.bris (https://data.bris.ac.uk/data/), at https://doi.org/10.5523/bris.39wtcv1qdq5xq2misej9ngulvm.Acknowledgements
SAA acknowledges a PhD studentship funded by the Saudi Government.References
- M. Volmer and A. Weber, Z. Phys. Chem., 1926, 119U, 277–301 CrossRef.
- M. Toner, E. G. Cravalho and M. Karel, J. Appl. Phys., 1990, 67, 1582–1593 CrossRef.
- P. J. DeMott, A. J. Prenni, X. Liu, S. M. Kreidenweis, M. D. Petters, C. H. Twohy, M. S. Richardson, T. Eidhammer and D. C. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11217–11222 CrossRef CAS PubMed.
- B. J. Murray, K. S. Carslaw and P. R. Field, Atmos. Chem. Phys., 2021, 21, 665–679 Search PubMed.
- J. F. B. Mitchell, C. A. Senior and W. J. Ingram, Nature, 1989, 341, 132–134 Search PubMed.
- T. Storelvmo, I. Tan and A. V. Korolev, Curr. Clim. Change Rep., 2015, 1, 288–296 CrossRef.
- K. E. Zachariassen and E. Kristiansen, Cryobiology, 2000, 41, 257–279 CrossRef CAS PubMed.
- J. Jin, E. J. Yurkow, D. Adler and T. C. Lee, Food Res. Int., 2018, 106, 90–97 CrossRef CAS PubMed.
- I. Massie, C. Selden, H. Hodgson and B. Fuller, Tissue Eng., Part C, 2011, 17, 765–774 CrossRef CAS PubMed.
- L. Lupi and V. Molinero, J. Phys. Chem. A, 2014, 118, 7330–7337 CrossRef CAS PubMed.
- G. C. Sosso, G. A. Tribello, A. Zen, P. Pedevilla and A. Michaelides, J. Chem. Phys., 2016, 145, 211927 CrossRef PubMed.
- M. Gavish, R. Popovitzbiro, M. Lahav and L. Leiserowitz, Science, 1990, 250, 973–975 CrossRef CAS.
- L. Pharoah, A. K. Bertram and G. N. Patey, J. Phys. Chem. A, 2024, 128, 7214–7225 CrossRef CAS PubMed.
- J. Forbes, A. Bissoyi, L. Eickhoff, N. Reicher, T. Hansen, C. G. Bon, V. K. Walker, T. Koop, Y. Rudich, I. Braslavsky and P. L. Davies, Nat. Commun., 2022, 13, 5019 CrossRef CAS PubMed.
- M. A. Holden, T. F. Whale, M. D. Tarn, D. O'Sullivan, R. D. Walshaw, B. J. Murray, F. C. Meldrum and H. K. Christenson, Sci. Adv., 2019, 5, eaav4316 CrossRef PubMed.
- P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- S. M. Douglas, H. Dietz, T. Liedl, B. Högberg, F. Graf and W. M. Shih, Nature, 2009, 459, 414–418 CrossRef CAS PubMed.
- K. E. Dunn, F. Dannenberg, T. E. Ouldridge, M. Kwiatkowska, A. J. Turberfield and J. Bath, Nature, 2015, 525, 82–86 CrossRef CAS PubMed.
- J. D. Atkinson, B. J. Murray and D. O'Sullivan, J. Phys. Chem. A, 2016, 120, 6513–6520 CrossRef CAS PubMed.
- T. Koop, B. Luo, U. M. Biermann, P. J. Crutzen and T. Peter, J. Phys. Chem. A, 1997, 101, 1117–1133 CrossRef CAS.
- D. A. Knopf, P. A. Alpert, A. Zipori, N. Reicher and Y. Rudich, npj Clim. Atmos. Sci., 2020, 3, 2 CrossRef PubMed.
- G. Bai, D. Gao, Z. Liu, X. Zhou and J. Wang, Nature, 2019, 576, 437–441 CrossRef CAS PubMed.
- R. P. Sear, CrystEngComm, 2014, 16, 6506–6522 RSC.
- I. V. Markov, Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth, and Epitaxy, World Scientific, 2nd edn, 2003 Search PubMed.
- G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Chem. Rev., 2016, 116, 7078–7116 CrossRef CAS PubMed.
- D. Turnbull, J. Chem. Phys., 1950, 18, 768–769 CrossRef CAS.
- D. B. Gardner and H. Wang, Int. J. Refrig., 2024, 163, 32–44 CrossRef.
- T. Koop and B. J. Murray, J. Chem. Phys., 2016, 145, 211915 CrossRef PubMed.
- R. Schwidetzky, I. de Almeida Ribeiro, N. Bothen, A. T. Backes, A. L. DeVries, M. Bonn, J. Fröhlich-Nowoisky, V. Molinero and K. Meister, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2303243120 CrossRef CAS PubMed.
- D. Schmid, D. Pridmore, G. Capitani, R. Battistutta, J.-R. Neeser and A. Jann, FEBS Lett., 1997, 414, 590–594 CrossRef CAS PubMed.
- M. Cascajo-Castresana, R. O. David, M. A. Iriarte-Alonso, A. M. Bittner and C. Marcolli, Atmos. Chem. Phys., 2020, 20, 3291–3315 CrossRef CAS.
- Y. Qiu, A. Hudait and V. Molinero, J. Am. Chem. Soc., 2019, 141, 7439–7452 Search PubMed.
- T. Hansen, J. Lee, N. Reicher, G. Ovadia, S. Guo, W. Guo, J. Liu, I. Braslavsky, Y. Rudich and P. L. Davies, eLife, 2023, 12, RP91976 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental data, simulations, methods and discussion. See DOI: https://doi.org/10.1039/d5nr02731d |
‡ A similar fraction of droplets containing annealed DNA origami tiles also freezes before the required temperature T is reached (see Table S3†), but if all the droplets have the same R(T), this doesn't affect the gradient of a plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U(t), so the measured freezing rate is unaffected. U(t), so the measured freezing rate is unaffected. |
| § The small increase in frozen fraction for the annealed DNA origami samples above ∼−20 °C is also observed in the buffer sample, so is likely associated with an unknown contaminant rather than the DNA tiles. |
| ¶ The adjustment to η is needed because the temperature ramp data cover higher temperatures than the isothermal data and eqn (3) ignores the possible temperature dependence of η. The adjustment to ση partly compensates for deficiencies in the log normal model, which incorporates variation in η but not in J0. |
| This journal is © The Royal Society of Chemistry 2025 |