Size-dependent antiferromagnetism and direct observation of Néel axes in NiO nanoparticles

Abstract

A comprehensive understanding of antiferromagnetism in nanostructures confined in three dimensions remains elusive. This work addresses this fundamental issue by studying samples of highly crystalline single-phase NiO nanoparticles of 6, 20, and 34 nm average size, prepared by an optimized two-step synthesis. All the samples exhibit prominent antiferromagnetic behaviour with an overlapping superparamagnetic contribution due to uncompensated spins at the particle surface and at the crystallite boundaries within the particles, which becomes nearly undetectable for 34 nm particles. Using synchrotron X-ray photoemission electron microscopy combined with magnetic linear dichroism, a determination of the antiferromagnetic Néel axis was obtained for a subset of individual 34 nm particles. No thermal fluctuations of the Néel axes are observed at room temperature; instead, they are stochastically aligned along easy directions compatible with the particle crystal facets resting on the substrate. Consequently, single domain states of two sublattices appear to prevail in this size range, in contrast with a seminal model predicting multi-sublattice arrangements. These findings provide significant insights into antiferromagnetism in nanostructures and open up new possibilities for data storage based on specific states of Néel axes.

---

Introduction

Antiferromagnetic (AF) nanomaterials have attracted significant scientific interest due to their remarkable magnetic properties that diverge significantly from their bulk counterparts. These unique characteristics arise from finite-size effects, which disrupt the crystal lattice symmetry, alter the electronic environment, and modulate magnetic interactions.^1–3 Among these AF nanosystems, nickel oxide (NiO) nanoparticles (NP) stand out for their exceptional properties and diverse applications. Some of the material's most notable characteristics include its p-type semiconductor behaviour with a large band gap of 3.6–4 eV, making it a robust candidate for electronic devices such as solar cells and capacitors operating at high temperatures or requiring high efficiency.^4,5 Additionally, these systems demonstrate outstanding catalytic activity, positioning them as promising agents for degrading harmful gases.^6,7

Beyond their practical applications, NiO NP are of fundamental interest in magnetism due to their unconventional behaviour at the nanoscale. While bulk NiO is a prototypical AF with no net magnetic moment, nanosized NiO systems often exhibit weak ferromagnetism, finite coercivity, and superparamagnetic-like responses. These deviations are commonly attributed to finite-size and surface effects, such as spin disorder, reduced atomic coordination, and the formation of Ni vacancies, all of which can destabilize the AF order.⁸ NiO NP are commonly produced in synthesis processes operating below 700 °C, a temperature range that fosters increased oxygen variability and the formation of vacancies in the crystal lattice.^9,10 The presence of Ni vacancies can shift AF ordering temperature (T_N) and provoke charge-transfer effects.¹¹ Pioneering investigations by Néel suggested that small NiO NP could exhibit a weak ferromagnetic signal that yields SPM properties above a blocking temperature.¹² This AF-to-SPM transition as the particle size decreases was often attributed to an incomplete compensation between the two AF sublattices. However, in the 1990s, Kodama et al.¹³ suggested that the anomalous magnetic properties found in these systems, such as significant values of the remnant magnetization and coercive field, could be attributed to the occurrence of multi-sublattice spin arrangements caused by finite-size and surface effects associated with the reduced size of the particles and changes in coordination of surface spins. While this hypothesis is compelling, definitive experimental evidence supporting the breakdown of the bulk two-sublattice model in NiO NP remains elusive.

The challenge in elucidating the magnetism of NiO nanostructures stems from three primary limitations. Firstly, while there is abundant literature on the synthesis of pure NiO NP,¹⁴ the resulting samples often contain additional Ni phases, most notably metallic Ni, a soft ferromagnet (FM) whose presence can significantly mask any subtle contribution from uncompensated spins in NiO NP. The second challenge is the very limited number of experimental techniques that allow detecting AF order in nanomaterials. The third complication arises from the limitations of ensemble measurements, which average the properties of NiO NP with varying morphologies and crystalline features, potentially masking individual particle characteristics.

In addition to optimizing the synthesis to ensure the purity of the products, chemically specific, magnetically-sensitive, single-particle measurements have become feasible in recent decades due to advancements in electron microscopies and synchrotron radiation facilities.^15–17 In particular, synchrotron-based X-ray Photoemission Electron Microscopy (XPEEM) has enabled magnetic and chemical characterization at the level of individual nanoparticles.^18–20 Further, combining XPEEM with soft X-ray Magnetic Linear Dichroism (XMLD) has proven to be an effective method for characterizing the magnetic domain structures of 3d transition metal oxides.^21,22 While previous studies have successfully employed XMLD to determine the Néel axis in various bulk and thin film AF systems, including NiO,^23–26 LaFeO₃,²⁷ CuMnAs,²⁸ and other AF materials,^29,30 the determination of the AF Néel axis in individual nanostructures confined along the three dimensions has thus far remained unclear.

In this work, we report on the influence of the crystal structure on three samples of NiO NP with sizes ranging from 6 to 34 nm synthesized using two-step chemical approaches. By combining standard and advanced characterization techniques, we investigate the morphology, size distribution, chemical composition, and magnetic properties of these systems. Notably, we present unprecedented, quantitative determination of the AF Néel axis in single NP showing the prevalence of single domain states. Moreover, the study delves into the role of surface and finite-size effects in determining magnetic ordering at the nanoscale. This comprehensive analysis, elucidating the unique AF arrangement at the single-particle level, offers deeper insights into nanoparticle magnetism, contributing significantly to the field of magnetic nanomaterials and their potential applications.

Experimental

Materials

Nickel nitrate (Ni(NO₃)₂·6H₂O, ≥98.5% purity, ref. 72252-50G), nickel acetylacetonate (Ni(acac)₂ 95% purity, ref. 283657-5G). Additional reagents include citric acid (HOC(CO₂H)(CH₂CO₂H)₂, ≥99.5% purity, ref. 251275-500G), oleic acid (C₈H₁₇CH=CH(CH₂)₇COOH, 90% purity, ref. 364525-1L) and octadecene (CH₃(CH₂)₁₅CH=CH₂, 90% purity, ref. O806-1L). All reagents were purchased from Sigma Aldrich. The water was purified using a Millipore Milli-Q lab water system. No further refinement of the reactants was performed.

Synthesis of NiO NP

NiO NP samples reported in this study were synthesized by two-step synthesis approaches, as illustrated in Fig. S1 in ESI.† First, sample NiO6 was prepared by thermal decomposition of 0.27 g (1 mmol) Ni(acac)₂ in 5 mL of 1-octadecene using 1.26 g (4 mmol) of oleic acid as a surfactant agent.³¹ This sample was then subjected to thermal oxidation in air at 350 °C for 48 hours, with a heating rate of 1 °C min⁻¹. Second, sample NiO20 was synthesized via a sol–gel approach using the procedure described by Y. Wu et al.³² Briefly, 0.7894g (2.7 mmol) of nickel(III) nitrate and 0.5223 g (2.7 mmol) of citric acid were separately dissolved in 5 mL of Milli-Q water. The citric acid solution was added dropwise to the nickel nitrate solution in a three-neck flask, and the reaction mixture was stirred continuously on a heating plate at 70 °C overnight. The resulting green gelatinous semi-solid was dried in an oven at 100 °C for 24 hours, and the obtained xerogel was pulverized into a fine powder using a ceramic mortar. To achieve complete oxidation, the sample was annealed in a muffle furnace under air at 425 °C for 4 hours, with a heating rate of 1 °C min⁻¹. After cooling to room temperature, the newly formed black powder was ground again to ensure uniformity. Third, sample NiO30 was prepared following the same sol–gel procedure as NiO20 but with an increased annealing temperature of 475 °C to promote particle growth.

Structural and macroscopic magnetic characterization

Samples for Transmission Electron Microscopy (TEM) were prepared by placing 20 μL of a diluted suspension of NiO NP in hexane, onto a carbon-coated Cu grid and drying for 10 min at 100 °C. The low-resolution TEM measurements were carried out using a Tecnai T20 microscope operating at 80 kV, which also allowed for SAED measurements. In the case of HRTEM measurements, a JEOL JEM 2010F with a working voltage of 200 kV was used.

Histograms of the size distribution of the NiO NP were determined by measuring at least 300 particles with ImageJ software,³³ and fitting the results to a log–normal probability distribution of the form:

where D is the particle diameter, D₀ stands for the most probable value of D, and S is the standard deviation of the distribution of the logarithm of the reduced diameter D/D₀. D₀ and S were determined by fitting experimental histograms obtained from TEM data to eqn (1).³³ The mean particle size D_TEM and the standard deviation σ of the diameter distribution were computed from eqn (2) and (3), respectively, as follows:

D_TEM = D₀e^S2/2, (2)

Finally, the polydispersity index σ_RSD of the samples was estimated by dividing the standard deviation by the mean particle size as σ_RSD = σ/D_TEM.

The structural characterization of the samples was performed by combining the analysis of High Resolution (HR)-TEM and Selected Area Electron Diffraction (SAED) patterns. The interplanar distances (d_hkl) were calculated using Gatan Microscopy Suite® software for HRTEM images,³⁴ while ImageJ graphical analysis was performed for SAED patterns. The interplanar SAED distances were determined by measuring the separation between the central spot and the diffraction spots, followed by converting the reciprocal space distances into real space values. These results were then compared to the X'Pert High Score Plus pattern for bulk NiO (Inorganic Crystal Structure Database, ICSD: 01-071-1179).³⁵

High-Angle Annular Dark-Field Scanning Transmission Electron Microscopy (HAADF-STEM), Energy-Dispersive X-ray spectroscopy (EDX), and Electron Energy Loss Spectroscopy (EELS) were performed using a Titan low-base at the Laboratorio de Microscopías Avanzadas located in the Instituto de Nanociencia y Materiales de Aragón (Spain). Both EDX and EELS spectroscopies were conducted with a spatial resolution of about 1 nm.

Further characterization of the crystal structure was performed by X-ray Diffraction (XRD) using a PANalytical X'Pert PRO MPD diffractometer with Cu Kα radiation (λ = 1.5418 Å), scanning 2θ from 4 to 120° with a step size of 0.026°, and measuring time of 200 s. Each sample was scanned three times for a total duration of three hours. The peak positions were compared with the NiO reference pattern and fitted to determine the crystallite size D_XRD by Rietveld analysis using the FullProf Suite software.³⁶

The presence of remaining organic compounds in the samples was evaluated by Thermogravimetric (TG) analysis, although only results for NiO30 sample are shown in this work. Samples were heated from 30 to 700 °C with a heating rate of 10 °C min⁻¹ in a nitrogen atmosphere using a TGA-SDTA 851e/SF/1100 thermobalance.

X-ray Photoelectron Spectroscopy (XPS) measurements were conducted using a PHI ESCA-5500 spectrometer with monochromatic Al K_α irradiation. The acquired spectra were iteratively fitted using a Gaussian–Lorentzian model with MultiPak software. Surface etching studies were performed with a monatomic Ar ion gun operating at 0.5 keV for 120 min, with XPS measurements taken every 10 min.

The temperature dependence of the magnetization was measured under zero-field-cooled (M_ZFC) and field-cooled (M_FC) conditions. For M_ZFC, the sample was cooled from 300 K to 5 K in zero field; a static field of 50 Oe was then applied, and magnetization was recorded during warming to 300 K. For M_FC, the sample was cooled again to 5 K under 50 Oe, and the magnetization was recorded during the subsequent warming. Hysteresis loops M(H) at 5 K and 300 K were measured within ±70 kOe. Magnetization measurements were normalized based on the NiO amount computed from the TG results. From these curves, we obtained the M_max, the coercive field H_c, and the remnant magnetization M_r. H_c and M_r were computed as H_c = ([H_c⁺] + [H_c⁻])/2 and M_r = ([M_r⁺] + [M_r⁻])/2, respectively, where H_c⁺ and H_c⁻ are the intersections of the hysteresis loop with the positive and negative sides of the H-axis, and M_r⁺ and M_r⁻ are the analogous intersections with the M-axis.

In the blocked state, the high field region of the hysteresis loops was analysed to investigate the amount of magnetization M_u caused by unpaired spins within the AF structure. This was performed by linear extrapolation of the high field region of M(H) to zero field following the expression:

M(H) = M_u + χ_effH, (4)

where χ_eff stands for the effective magnetic susceptibility of the antiferromagnet.¹⁴

The average magnetic diameter D_mag of sample NiO6 was computed from the M(H) curve at 300 K, which corresponds to the SPM regime where interparticle interactions can be neglected. In this regime, M(H) can be fitted to a log–normal distribution P(m) of Langevin functions L(x) associated with the SPM behaviour of the particles plus a linear-field term caused by the effective susceptibility of the AF sublattices and/or the existence of some residual paramagnetic species.^37–39

Here, m is the magnetization of the crystallites that form the particles, due to the unpaired spins, M_s is the saturation magnetization associated with the unpaired spins, k_B is the Boltzmann constant, and χ_p is an effective paramagnetic susceptibility.⁴⁰ The distribution of the activation magnetic volumes V_m of the crystallites was computed from the fitted P(m) considering that m = M_sV_m. Finally, D_mag was estimated from the average value of V_m assuming spherical shapes for the activation magnetic volumes.

The existence of unpaired spins coupled with the AF sublattices was further investigated by studying the shift along the field axis of the hysteresis loops recorded after field cooling the samples under 10 kOe from room temperature down to 5 K. The shift in the field was defined as H_s = (H_c⁺ + H_c⁻)/2.³¹

X-ray magnetic linear dichroism measurements of single NiO NP

To gain insight into the spin orientation of the AF easy axis in single NiO NP, synchrotron-based XPEEM combined with XMLD at the Ni L₂ edges was used.^21,41–44 XMLD provides one of the scarce tools to measure the AF order as the X-ray absorption cross section, dominated by electric dipole terms, includes a resonant magnetic contribution in AF materials proportional to the expectation value of the square of the atomic magnetic moment m² (see e.g. ref. 22 and 45). The XMLD contrast depends strongly on the direction of the X-ray polarization vector with respect to the local AF axes, and in combination with XPEEM, it enables spatially resolved maps of the local AF axis orientation down to the nm scale.^22–27

The XMLD measurements were performed at the Surface/Interface:Microscopy beamline of the Swiss Light Source.^46,47 XMLD images and spectra were measured with the 100% linearly polarized X-rays impinging at a grazing angle of 16° to the sample surface. The polarization axis of the E-vector could be rotated continuously from ω = 0° (linear horizontal polarized light, LH) to ω = 90° (linear vertical polarized light, LV), i.e., between in-plane and completely out-of-plane configurations. More details about the experimental geometry are provided in the following section.

Prior to magnetic imaging, local XAS spectra of the individual NP were obtained by collecting sequences of XPEEM images around the Ni L_2,3 edges using both LH and LV polarized light and analysing the isotropic (nonmagnetic) intensity (sum of LH and LV spectra) as a function of the photon energy. The purpose of these measurements was twofold. First, to verify that the oxidation state of the analysed individual particles agrees with a single NiO phase, and second, to find out the relevant energies providing the largest magnetic XMLD contrast for subsequent imaging.

XPEEM elemental contrast maps of the NiO NP were obtained by a pixel-wise average of two XPEEM images successively recorded with LH and LV polarized light at the A and B positions of the L₂-edge (so-called L_2A, L_2B images, respectively). Typical image acquisition times were about 200 s per photon helicity, corresponding to 1 s per exposure, averaging 10 exposures per image, and acquiring a total of 20 images.

XMLD images were obtained from the pixel-wise division of two such elemental contrast images (L_2A/L_2B) recorded at a given polarization of the E-vector, ω. This procedure ensures that all contrast mechanisms other than those of magnetic origin cancel out because they do not depend on the photon helicity.

For the processing and analysis of the images of both the local isotropic Absorption Spectroscopy (XAS) and XMLD images, rectangular boxes of various sizes were used to ensure the largest and cleanest signal possible for each single NP. It was found that smaller boxes yielded a larger signal-to-noise-ratio (SNR), with the optimal SNR achieved for square boxes of 2 × 2 pixels. Note that, since the lateral spatial resolution of XPEEM is limited to about 30 nm,^42,46 the box size may not reflect the actual size of the NP, but rather its apparent size, as the XAS only indicates the regions where the secondary electrons are photoemitted. Further details about these data analysis considerations and other methodological challenges can be found in related works.^41,48,49

To determine the local AF Néel axis from individual particles out of the XMLD images, it is necessary to understand the angular dependence of the XMLD contrast on both ω and azimuthal angle γ about the sample surface (rotation around z-axis in Fig. 6(a)). The intensity I of the XMLD signal is given by:

I = I₀ + I₁cos² α, (6)

where I₀ is a constant background, I₁ is a constant scale factor, α is the angle between the E-vector and the AF axis (see sketch in Fig. 6(a)), andwhere θ and φ represent the spherical coordinates of the AF axis. Eqn (6) and (7) were used to fit the experimental data. The fitting was performed using a custom code developed in Mathematica.⁵⁰

The XMLD signal is probed first by changing ω at γ = 0°, and subsequently, repeating the XMLD vs. ω scans for additional selected γ values. This approach allows both the in-plane and out-of-plane components of the AF axis to be probed and differentiated. In our case, the selected angles were γ = 0° and 47° while ω was varied in steps of ω = 10° from in-plane to out-of-plane (ω = 0° to ω = 90°) with respect to the sample substrate. Note that the latter polarization is not exactly perpendicular to the sample due to the incident grazing angle of 16° (Fig. 6(a)).

The XMLD-XPEEM study described above was carried out on sample NiO30. The sample was prepared by drop-casting a diluted suspension of NP onto a silicon wafer. Subsequently, a thin carbon film was deposited onto the substrate to prevent charging effects and enhance the SNR of the NP in the XPEEM measurements. All experiments were performed at room temperature, in the absence of any prior field cooling protocol, and at zero applied magnetic field.

Results and discussion

Structural insights of NiO NP across various size ranges

The first part of this work was devoted to analysing the structural properties of the three samples of NiO NP synthesized by the two-step chemical approaches, as discussed in the Methods section. The NiO6 sample was synthesized through the thermal decomposition of Ni(acac)₂ in the presence of oleic acid, followed by a subsequent calcination process (see Fig. S1 in the ESI†). Samples NiO20 and NiO30 were synthesized using a sol–gel approach and calcined.^31,32 Low-resolution TEM characterization presented in Fig. 1(a and b) (images for NiO20 not shown) reveals shared structural features across all three NiO samples, regardless of particle size. For example, all samples exhibit a similar faceted platelet-like shape, attributed to the high temperatures used during calcination, which promote the formation of faceted crystalline structures. Additionally, the NP tend to agglomerate on the TEM grid, likely due to the minimal organic coating adhering to their surfaces, as confirmed by TG analysis of the sample NiO30 (see Fig. S2 in the ESI†).

Fig. 1 Representative low-resolution TEM images of samples (a) NiO6 and (b) NiO30. Panels (c) and (d) correspond to HRTEM images of samples NiO6 and NiO30, respectively. (e) Log–normal functions represent the particle size distributions computed by fitting histograms from low-resolution TEM images for the three samples: NiO6 (black), NiO20 (red), and NiO30 (blue).

The mean particle size and standard deviation computed from the particle size distributions (see eqn (1)–(3)) in Fig. 1(e) are 6 ± 1 nm (NiO6), 20 ± 4 nm (NiO20), and 34 ± 8 nm (NiO30). These results confirm that the three samples are monodisperse with polydispersity index σ_RSD values of around 20%.

Particles shown in HRTEM images in Fig. 1(c, d) and S3 in the ESI† exhibit good crystallinity, either being single crystals for NiO6 and NiO20 or containing the coexistence of crystal domains in NiO30 (Fig. 1(d)). Interestingly, HRTEM images for the NiO NP studied showed either (111) or (200) atomic planes, suggesting preferential growth along these directions. These families of planes are the most stable and densely packed in the fcc crystal structure.⁵¹ Consequently, they are the most energetically favourable for rapid and controlled atomic growth of NiO NP. Furthermore, the particles showed a platelet-like shape with large external facets perpendicular to the growth planes, which are likely the surfaces on which the particles rest on the TEM substrate. Since only (111) and (200) planes are found in HRTEM images, and considering the most densely packed and typical facets for a cubic crystal, we inferred that the facets lying on the substrate preferentially belong to the {220} and/or {200} families. This is because {220} facets contain elements perpendicular to both (111) and (200) atomic planes, while some {200} facets are perpendicular to the (200) planes. However, considering the high stability of the (111) planes, we cannot rule out the possibility that {111} facets may also be present at the substrate interface. This will be relevant in the single-particle magnetic characterization section, where the Néel axis of individual particles is determined from the analysis of combined XMLD and XPEEM data.

The preferential occurrence of these atomic planes was further corroborated through the study of SAED patterns for all three samples. These patterns exhibited similar features, consisting of three rings attributed to the (111), (200), and (220) families of atomic planes (Fig. S4 in the ESI†). The slight expansion observed in the lattice parameters may be attributed to the presence of Ni vacancies in the structure, potentially indicating partial Ni²⁺/Ni³⁺substitution.^9,10

HAADF-STEM images also support a faceted platelet-like shape of the particles. Besides, images reveal a uniform contrast across the particles, suggesting a homogeneous composition and/or a consistent crystalline structure throughout (see inset to Fig. 2(c) and Fig. S5 in the ESI†). This observation was further corroborated by EDX analyses of several NP, which showed similar Ni and O contents within the particles (see Fig. 2(a and b)). It is important to note that all three samples exhibited a deficit in Ni content of approximately 15%. This deficit could be attributed to partial Ni²⁺/Ni³⁺ substitution, potentially influenced by an overrepresentation of oxygen caused by the sample's exposure to air.^9,10

Fig. 2 Compositional EDX and EELS analyses of NiO30 NP. (a) Elemental EDX mapping for nickel (Ni K_α1), revealing homogeneous nickel distribution throughout the entire NP. (b) Elemental EDX mapping for oxygen (O K_α1) showing a consistent oxygen distribution. (c) EELS spectra corresponding to the particle interior (red) and surface (blue). The inset shows a HAADF image displaying the region where the EELS spectra were recorded.

To complement the compositional analysis, EELS measurements were performed on individual NiO30 NP. The quantification of the spectra revealed that, while the particle interior exhibited stoichiometric Ni-to-O ratio, the particle surface showed a slight nickel deficiency, resulting in a core–shell-like compositional structure.

The Ni-to-O ratio was approximately 0.8 : 1 near the surface and about 1 : 1 in the interior (see Fig. 2(c) and S6 in the ESI†). These findings suggest that the slight Ni stoichiometric deficit primarily originates from surface effects, potentially due to defects or air-induced oxidation.

XRD spectra (see Fig. 3) for the three NiO samples showed only the Bragg reflections associated with the fcc structure of bulk NiO, discarding the presence of any parasitic phase, such as Ni or Ni₂O₃. Besides, the peak widths decreased with increasing values of D_TEM, as expected for single crystal NP.⁵² Rietveld fittings were used to gain insight into some crystallographic features such as crystalline size and unit cell parameter, together with the ion occupancies in the two sublattices (see Table 1 and Fig. S7 in the ESI†). The unit cell parameter was within 4.1785(1) and 4.1789(1) Å. Note that these values are slightly larger than the bulk one for stoichiometric NiO (4.175 Å),³⁵ in agreement with typical values in nanostructured NiO, due to finite-size effects and the presence of Ni vacancies.¹⁴ In addition, D_XRD obtained for NiO20 and NiO30 samples were very similar to D_TEM. The latter suggests that NP exhibit consistent crystal quality throughout their entire structure, from the core to the outermost surface, in good agreement with the TEM analysis. Interestingly, the NiO6 sample showed a D_XRD value of 9 ± 1 nm, which was larger than D_TEM and could be due to the contribution of the largest particles present in the sample. The Ni occupancy (0.94–0.95) was slightly lower than the stoichiometric value, what is commonly found in NiO NP synthesized at temperatures below 700 °C.^9,10 Table 1 summarizes the overall structural features, indicating that the three samples are composed of particles of high crystallinity and homogeneous composition.

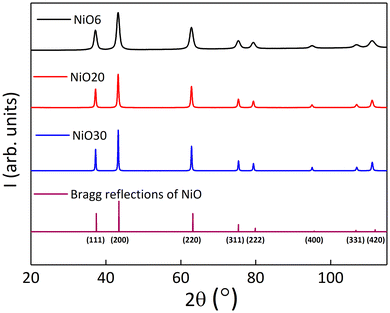Fig. 3 XRD spectra for samples NiO6 (black), NiO20 (red), and NiO30 (blue), along with the expected diffraction pattern of bulk NiO (purple) according to ICSD 01-071-1179.

Table 1 Structural features of samples NiO6, NiO20, and NiO30, comparing crystalline size by TEM, D_TEM, and XRD, D_XRD, unit cell parameter, and Ni occupancy (normalized to that of O). The values in parentheses indicate the estimated uncertainty in the least significant digit

Sample	DTEM (nm)	σRSD (%)	DXRD (nm)	Unit cell parameter (Å)	Ni occupancy
NiO6	6(1)	17	9 (1)	4.1785(1)	0.94(1)
NiO20	20(4)	20	21 (3)	4.1786(1)	0.95(1)
NiO30	34(8)	24	32 (5)	4.1789(1)	0.94(1)

---

To gain further insight into the structural and chemical properties of NiO30, XPS measurements were conducted in the Ni 2p and O 1s core levels. In Fig. 4(a), the main Ni 2p_3/2 peak, located at 853.7 eV, confirms the presence of Ni²⁺ in the NiO lattice.⁵³ This peak is accompanied by a secondary Ni 2p_3/2 component at 855.6 eV, which can be attributed to interactions of Ni²⁺ with non-local oxygen atoms, surface effects, and/or the presence of Ni³⁺ species, such as NiOOH or Ni₂O₃.^54,55 Accordingly, the same two contributions are observed for the Ni 2p_1/2 core level: (a) the main Ni 2p_1/2 peak, found at 871.3 eV, arising from the spin–orbit splitting of Ni 2p electrons, and (b) a secondary component at 873.0 eV. Finally, two satellite peaks, appearing at 860.9 eV for Ni 2p_3/2 and at 879.5 eV for Ni 2p_1/2, respectively, indicate interactions between the photoelectron and unpaired valence electrons, reflecting the correlated electronic nature of the material.⁵⁶

Fig. 4 High-resolution XPS spectra of the Ni 2p (a) and O 1s (b) core levels in NiO30 NP. The peak in the O 1s core level at 531.2 eV can be attributed to surface contamination.

The O 1s core level, shown in Fig. 4(b), reveals a main peak centred at 529.4 eV, associated with oxygen ions in the NiO lattice (Ni–O–Ni bonds). A secondary peak at 531.2 eV suggests variations in the environment, likely caused by oxygen vacancies and/or surface interactions with adsorbed atmospheric species, i.e., surface contamination. To investigate the origin of this secondary peak, etching studies were performed. As shown in Fig. S8 in the ESI,† the secondary peak nearly disappears after etching, confirming its origin from surface contamination. Consequently, from XPS spectra, NiO30 NP are mostly stoichiometric NiO at the bulk of the NP, while some residual oxidation takes place at the surface.

Quantitative analysis of the XPS data revealed a composition of 48.1% oxygen, 45.9% nickel, and 6.0% carbon. The presence of carbon is attributed to minor surface contamination or substrate contributions. This composition indicates a slight nickel deficiency (Ni : O = 0.954), further corroborating the structural characterization results.

Macroscopic magnetic characterization of NiO NP ensembles

The dependence of the magnetic properties on crystal size was studied on the three NiO samples. Table 2 summarizes the overall magnetic features of the samples, while Fig. S9 in the ESI†shows the temperature dependence of M_ZFC−M_FC curves measured from 5 to 300 K under H = 50 Oe. Two types of curves can be distinguished depending on particle size. The curve for NiO6 NP exhibits typical SPM features, with the M_ZFC curve rising gradually until reaching a peak at T_p = 170 K and then decreasing monotonously towards room temperature. Additionally, the temperature corresponding to the onset of irreversibility between the M_ZFC–M_FC curves, T_irr, is slightly higher than T_p, likely due to interparticle interactions. In contrast, NiO20 and NiO30 samples show M_ZFC–M_FC curves characteristic of blocked particles, with T_irr equal to the temperature at which the cooling process was initiated and without any trace of T_p. These findings are consistent with previous works on NiO NP, where small 8–9 nm NiO NP displayed T_p well below 200 K, while 20 nm NiO NP remained blocked at room temperature.⁵⁷ Notably, the rapid increase in magnetization at low temperatures observed in the NiO30 sample may be attributed to a minor paramagnetic contribution from residual Ni-containing species. The ZFC–FC signal in this sample is approximately three times smaller than that of NiO20 and an order of magnitude smaller than that of NiO6, suggesting that similar impurities may be present in all three samples but are only detectable in NiO30.

Table 2 Summary of the magnetic properties of the NiO samples measured at 5 K and 300 K. Values in parentheses indicate the estimated uncertainty in the least significant digit

Sample	Mmax (5 K) (emu g^−1)	Mr (5 K) (emu g^−1)	Hc (5 K) (kOe)	Mmax (300 K) (emu g^−1)	Mr (300 K) (emu g^−1)	Hc (300 K) (kOe)	Hs (300 K) (kOe)
NiO6	1.40(1)	0.13(1)	6.0(1)	1.30(1)	0.00(1)	0.0(1)	9.0(1)
NiO20	1.00(1)	0.10(1)	5.0(1)	0.9(1)	0.00(1)	0.4(1)	7.0(1)
NiO30	0.70(1)	0.00(1)	0.6(1)	0.50(1)	0.00(1)	0.3(1)	0.0(1)

---

Hysteresis loops recorded at 5 K and depicted in Fig. 5 exhibit some common features related to AF order for the three NiO samples,¹⁴ such as irreversibility, small values of remnant magnetization M_r, and the maximum magnetization, M_max less than 1.50 emu g⁻¹. Additionally, samples show a progressive breakdown of the AF order as the particle size decreases, from nearly compensated AF in sample NiO30 with a coercive field H_c ∼0.6 kOe at 5 K to a slight FM for sample NiO6 that exhibits the largest values of both M_max and H_c. This suggests that the particle size plays a crucial role in the magnetic behaviour of NiO samples. Larger particles tend to possess higher crystallinity, yielding a nearly complete AF ordering, while NiO6 NP render a higher proportion of surface atoms (42%), being more susceptible to structural defects and lattice distortions that may give rise to unpaired spins breaking the AF order.

Fig. 5 Hysteresis loops at 5 K for samples NiO6 (black), NiO20 (red), and NiO30 (blue) with a maximum field of H = 70 kOe. The inset shows the corresponding hysteresis loops of the three samples at 300 K, illustrating the effect of increased thermal activation on hysteresis.

Hysteresis loops measured at room temperature, and depicted in the inset of Fig. 5, show small coercivities for the NiO20 and NiO30 samples and negligible coercivity for the NiO6 (see Table 2). This suggests a minimal energy barrier for the reorientation of uncompensated magnetic moments in the three samples, consistent with the thermally induced reduction in magnetic anisotropy characteristic of AF materials at elevated temperatures.¹⁴ The AF ordering of the samples was further analysed by fitting the high-field region of the hysteresis loops to eqn (4) and obtaining the value of the extrapolated magnetization at zero field, M_u. Note that M_u can be used to determine the presence of uncompensated spins and thus provide a quantitative measure of the deviation from an ideal AF ordering. For the NiO6 sample we obtained M_u = 0.22 ± 0.05 emu g⁻¹, indicating a significant contribution to the magnetization from a FM component, likely attributable to uncompensated spins at the particle surface or at structural defects and grain boundaries, which are more prevalent in the smallest particles. In contrast, as the particle size increases, M_u gradually decreases, from 0.10 ± 0.03 emu g⁻¹ for NiO20 to almost zero within the experimental error 0.02 ± 0.05 emu g⁻¹ for NiO30. This reduction indicates a decreasing fraction of uncompensated spins and a strengthening of the AF ordering with increasing particle size. Fig. S10 in the ESI† depicts a fitting of the magnetization as a function of the magnetic field at 300 K for the NiO6 sample to a distribution of Langevin functions as described in the Methods section, demonstrating the SPM behaviour of the uncompensated magnetization (FM component) of the NP. The magnetic diameter, determined by this procedure as 8.5 ± 1.4 nm, is in close agreement with the crystal size in Table 1.

To close this section, Fig. S11 in the ESI† shows the hysteresis loops at 5 K recorded after FC the samples under 10 kOe from room temperature. The shift in these loops, H_s, is found to decrease progressively with particle size (see Table 2). The most pronounced shift is observed for the NiO6 sample, likely due to the coexistence of AF and uncompensated regions within the NP. In contrast, NiO20 and NiO30 samples show minimal loop shifts and coercivity, in agreement with the smaller M_u values. It is important to note that non-zero values of H_s may not necessarily indicate a true exchange bias phenomenon. Instead, they could result from the occurrence of minor loops within the hysteresis loops, which is a common feature when a magnetic system is not fully saturated, even under the maximum applied magnetic field (see the large irreversibility in the hysteresis loops for NiO6 and NiO20 samples shown in Fig. S11 in ESI†).

This section, in a nutshell, show that the magnetic features of the NiO samples exhibit a clear dependence on the particle size. Smaller NiO6 NP display SPM behaviour of the weak FM component superimposed to the dominant AF behaviour, while larger NiO20 and NiO30 NP exhibit blocking of that particle magnetization even at room temperature. Additionally, H_c, M_max, and M_u decrease with increasing particle size, as they are directly related to the progressive reduction of uncompensated spins within the NP, such that NiO30 stands as an almost perfect AF.

Single-particle magnetic characterization: identification of AF Néel axes in NiO30 NP

The identification of the AF Néel axis for sample NiO30 was performed by combining single-particle XAS, XPEEM and XMLD. A schematic diagram of experimental geometry, including the definition of all relevant angles used in this study, is shown in Fig. 6(a). A representative example of an elemental-contrast XPEEM image, collected as described in Methods section, is shown in Fig. 6(b). The bright spots correspond to individual NiO particles (some of which are highlighted with circles and numbers) and occasional dimers or clusters of close-lying particles (excluded from our analysis, except in the case of P1). Illustrative examples of isotropic, local Ni L_3,2-edge XAS spectra of single NP for sample NiO30 are shown in Fig. 6(c) and Fig. S12 in ESI.† The local spectra show a double peak structure at both L₃ and L₂ edges, characteristic for Ni²⁺ in an octahedral crystal field.^22,58 Nevertheless, an individual confirmation of the single-phase NiO nature of each NP was conducted by comparing the measured local isotropic XAS spectra with fits to a weighted linear combination of the reference bulk spectra of both Ni and NiO taken from ref. 24 and 45 (Fig. 6(c) and S12 in the ESI†). The assignment of the oxide phase is chosen to achieve the best compromise between the most relevant criteria, namely the L₂ splitting, the distances between the main peaks, and the ratio between them, as discussed in the literature.^41,48,49 It should be emphasized that all the particles analysed hereafter are compatible with a single NiO phase within an error bar of up to 7%, as determined from the local isotropic absorption spectra. Representative examples of XMLD images, collected as described in the Methods section, are shown in Fig. 7. All NP exhibit stable magnetic XMLD contrast at room temperature under zero applied magnetic field. This observation precludes fluctuations of the AF axis in individual NP within the time frame of our experiments (up to about 36 hours, including all data scans and geometries), although complete spin reversals cannot be excluded as they are not detectable by XMLD. Furthermore, no variation of the XMLD contrast was observed within each single particle when comparing signals extracted from neighbouring boxes of comparable size (2 × 2 pixels), indicating that, within our experimental accuracy (lateral resolution of about 30 nm),^42,46 each NP could correspond to an AF monodomain state. Considering that the NP are single crystalline, as shown in section 3.1, the fact that the size of the nanocrystals matches that of the XMLD contrast is compatible with the usual two-sublattice AF order shown by bulk NiO,⁵⁹ thereby excluding the emergence of a more complex sublattice configuration inside the NP, as discussed in some seminal works.^12,13

Fig. 6 (a) Schematic diagram illustrating the geometry of the XMLD-XPEEM experiments, indicating the rotation angles ω and γ. represents the E-vector of the linearly polarized X-rays (depicted also centered in the particle for clarity). represents a unitary vector along the AF Néel axis of the particle (see Fig. S14† for the possible orientations of in NiO), whose spatial orientation is determined by the spherical coordinates (θ,φ). (b) Elemental-contrast XPEEM image with particles analyzed in this study encircled and labeled, P1 to P7. Scale bar corresponds to 10 μm. (c) Isotropic, local Ni L_3,2-edge XAS spectra (blue symbols) recorded for particle P4 in the XPEEM image shown in panel (b), compared with a fit (black solid line) obtained from a weighted linear combination of the reference bulk spectra of both Ni (0–10%) and NiO (90–100%), taken from ref. 24 and 45. The fit indicates compatibility with a single NiO phase within an error bar of up to 7%.

Fig. 7 Representative XMLD images obtained from the pixel-wise division of two elemental contrast (L_2A/L_2B) images recorded with E-vector angle ω = 0° (LH), 50°, and 90° (LV); left, middle, and right columns, respectively. The in-plane azimuthal angles γ = 0° and 47° correspond to rows (a) and (b), respectively. For ease of comparison, the images in row (b) have been rotated 47°. Particles studied in this work are encircled and labeled. Note that bright/dark contrast corresponds to large/small values of the projection of the E-vector on the AF axis. Scale bar corresponds to 10 μm.

As explained in the Experimental section, for a given experimental geometry with fixed values of ω and γ, the contrast in XMLD images (dissimilar gray levels in Fig. 7) corresponds to different Néel axis orientations in each individual NP. In our case any observed linear dichroic contrast is truly of magnetic origin, as the material has cubic symmetry and thus, no linear dichroism associated with crystal fields is expected, as discussed in different studies.⁶⁰ In addition, considering that the particles are drop-cast onto solid substrates for the XPEEM experiments, no distortion related to strain is expected. Therefore, the cubic crystal lattice parameters shown both in Table 1 and Fig. S4(c) in the ESI† should prevail.

An initial qualitative indication of differing AF axis orientations among individual NiO particles is shown in Fig. 7, which illustrates the change in the XMLD images for γ = 0° and 47° (top and bottom row, respectively) and ω = 0°, 50°, and 90° (left, middle, and right columns, respectively). Note that a few particles, highlighted with circles, show a large particle-to-particle XMLD signal variation between images at ω = 0° and ω = 90°, for γ = 0°. For example, P4 and P7 show a strong contrast reversal from dark gray to white, while P2 from black to light gray, thereby suggesting a strong out-of-plane component of the AF axis, as opposed to P3 where almost no change in contrast is observed. Similarly, regarding the in-plane component of the AF axis, strong XMLD signal variations are also observed at a fixed ω when comparing images for different γ values. For example, at ω = 90°, when comparing images at γ = 0° and γ = 47°, P4 and P5 show a strong contrast reversal from white to gray, while P7 from white to black, indicating that the AF axis has a nonzero in-plane component with dissimilar orientation among different particles.

For a quantitative analysis, the XMLD contrast was computed as a function of ω, in steps of Δω = 10°, for γ = 0° and 47° on a total of 8 individual particles, highlighted with circles in Fig. 6(b) and 7. It should be noted that P1 was treated as two closely spaced particles, P1a and P1b, as discussed further below.

According to eqn (6), the XMLD contrast varies as cos²α, thereby covering all its possible values in the interval 0° ≤ α ≤ 90°. Then, by rotating the E-vector, the out-of-plane component of the AF axis within the rotation plane of the polarization is probed according to eqn (7). Consequently, extrema at specific ω values are expected for each Néel axis orientation with a non-zero component within the rotation plane,²⁷ assuming a single domain state. For instance, at γ = 0°, particles with the in-plane component of their AF axis aligned along the x-axis (φ = 0°) (as illustrated in Fig. 6(a)) will consistently exhibit extrema in the XMLD contrast corresponding to a minimum at ω = 0° and a maximum at ω = 90°, regardless of the degree of canting of the AF axis with respect to the z-axis (angle θ), since cos² α goes as sin² ω for φ = 0° according to eqn (7). In contrast, AF axes with φ ≠ 0° will display extrema in XMLD contrast at shifted values of ω, which depend in a more complex manner on θ. Interestingly, a γ-rotation of the sample is equivalent to an effective change of φ of the AF axis. Therefore, this fact can be exploited to unambiguously determine the orientation of the AF axis by recording the XMLD signal as a function of ω at two sufficiently different values of γ (0° and 47° in our case) and then using eqn (6) to reproduce both sets of experimental data with a unique set of spherical coordinates (θ,φ).

To simultaneously fit the two sets of experimental data corresponding to each particle, interactive plots were generated by varying θ and φ in eqn (7) aiming to best match the location of the extrema in the two experimental curves. The overall curvature and background of the fitted functions were finely tuned by adjusting appropriate values of I₀ and I₁ constants in eqn (6) for each curve. The criterion for assessing the goodness of the final fit involves achieving the best agreement for both the location of the extrema, while simultaneously preserving the overall quality and consistency of the shape of the two sets of data for each particle. It is worth noting that the smaller the value of θ (i.e., the more out-of-plane the AF axis is), the greater the uncertainty in the value of φ required to obtain acceptable fits to the XMLD data. Conversely, as θ approaches the in-plane configuration, the uncertainty in the determination of φ decreases due to the greater sensitivity to the in-plane components.

Fig. 8 shows the experimental XMLD data (symbols) along with their corresponding fits to eqn (6) and (7) (solid lines) for five of the particles shown in Fig. 7 (labelled as P4, P5, P6, and P1, with P1 treated as two closely spaced particles tagged as P1a and P1b). The analysis of the remaining three particles (P2, P3, P7) is shown in Fig. S13 in the ESI.† The fitted values of θ and φ, together with their estimated uncertainties, are listed in Table 3. A schematic illustration of the experimental Néel axes for the studied NP is indicated by red arrows in Fig. 9.

Fig. 8 Experimental XMLD data (symbols) along with their corresponding fits to eqn (6) and (7) (blue solid lines) for five of the particles shown in Fig. 7 (P4, P5, P6 (panels (a–f)), and P1, with P1 treated as two closely spaced particles labelled as P1a and P1b in panels (g–j)).

Fig. 9 Schematic illustration of the experimental Néel axis orientations, indicated by red arrows, for the studied NP, as listed in Table 3. To facilitate a 3D perspective, white arrows show the projection of the Néel axes onto the xy-plane, while black dashed lines are parallel to the x and z axes.

Table 3 Experimental Néel axis orientations of a few selected individual NP from Fig. 7–9, in terms of their spherical coordinates (θ, φ), and expected θ_{hkl} values (multiplicity of the directions indicated in parentheses) for the easy directions of the NiO AF structure. The crystal facets {hkl} on which the NP are likely to be positioned on the surface substrate are {hkl} = {200} and {220}, as per the TEM-based observations. The case corresponding to the {111} was also included, just for completeness

	θ (°)	φ (°)	θ{200} 35.3°(4), 65.9°(8)	θ{220} 30°(4),54.7°(2), 73.2°(4),90°(2)	θ{111} 35.3°(4), 65.9°(8)
P1a	85.2 (6)	356.5 (4)		√	√
P1b	78.6 (6)	346 (3)		√
P2	45.0 (8)	308.5 (10)
P3	29.8 (8)	240.5 (18)	√	√
P4	35.8 (8)	0 (5)	√	√
P5	11.8 (5)	331 (20)
P6	53.8 (5)	303 (4)		√
P7	28 (7)	300 (20)	√	√

---

An example highlighting the importance of measuring the angular dependence in both ω and γ to unambiguously determine the orientation of the AF axis can be extracted from Fig. 8, where two particles, P4 and P1a, which are very similar at γ = 0° (Fig. 8(a) and (g), respectively), exhibit significantly different behaviour at γ = 47° (Fig. 8(b) and (h)), which is due to distinct values of the in-plane component. In contrast, P5 displays similar behaviour regardless of γ (Fig. 8(c) and (d)), indicating the predominance of an out-of-plane component.

For each particle, the evolution of the XMLD signal was studied for a set of regions of interest (typically 2 to 4 boxes per particle, depending on the number of pixels per particle), each box consisting of 2 × 2 pixels. This analysis had two objectives. First, to reduce experimental error in the fits, as some regions may exhibit higher SNR. Second, to assess whether different boxes may yield distinct fitting results. The latter case could arise, for example, from the presence of two closely spaced particles or from a single particle that, despite being monocrystalline, might exhibit the coexistence of different AF axes due e.g., to finite-size effects, leading to an eventual breakdown of the bulk two-sublattice AF model. In our case, the analysis of the XMLD images in such small boxes, combined with the fitting procedure, enabled the detection of slight differences in the AF axis orientation for closely spaced particles such as P1a and P1b, as shown in Fig. 8(g–j). Notably, our analysis reveals that experimental XMLD data from different boxes within each individual particle are in all cases in agreement with single fitting curves, thereby confirming the presence of a unique AF axis per particle.

As is known, NiO is a collinear antiferromagnet that, in bulk single crystals and below T_N, has its spins confined into four equivalent ferromagnetic {111} planes, coupled antiferromagnetically to each other. Within each of these planes, the spins can orient along one of the three 〈112〉 directions, leading to a total of 12 possible spin orientations (see Fig. S14 in the ESI†).^61–63 Drop-casting deposition should yield a stochastic spatial distribution of particles exhibiting random crystallographic orientations such as those apparently show in Fig. 9. However, comparative analysis of experimentally determined interplanar spacings from HRTEM images (Fig. 1 and Figs. S3 in the ESI†) enabled the identification of the facets preferentially resting on the substrate surface, namely {200} and {220}. Consequently, expected values of θ can be calculated by projecting the 12 easy directions of the AF structure along the perpendicular of each of the two families of lying facets on the sample substrate. The results of this calculation are compiled in Table 3, indicating the multiplicity of each angular value in parentheses. Note that a third hypothetical case corresponding to particles lying on {111} facets was also included in Table 3 for completeness. As shown in Table 3, it was found that, within the experimental error bars, 75% of the particles have their AF axes pointing in directions compatible with the two preferential facets found from HRTEM images, with a predominance for AF easy spin directions corresponding to particles lying on the {220} facets. Only two particles (P2 and P5) show θ values not compatible with any of the three facets and only one (P1a) is also compatible with the {111} facets, within the estimated experimental uncertainties. While our limited dataset hinders drawing definitive conclusions, it can nevertheless be inferred that the random orientation of the AF spin axes prevails. Thus, no discernible preferential direction of the AF Néel axes, associated with a source of additional anisotropy energy barrier arising from finite-size effects, is observed.

Furthermore, the good agreement between the experimentally observed AF spin axes of the NP and some of the expected spin directions compatible with their preferential supporting facets, together with the aforementioned fact that XMLD contrast remains constant across neighbouring pixels in the individual particles, is an indication that NP of 34 nm in average diameter are single AF domains with the usual bulk two-sublattice ordering. This finding appears to be in contradiction with the seminal work of Kodama et al.,¹³ which proposes the emergence of more complex AF configurations in NiO NP up to 80 nm in size, featuring 4-, 6-, or 8-sublattice spin ordering, based on energy minimization atomistic simulations. It is important to note, however, that the anticipated multiple-sublattice AF phases in NP typically stem from reduced coordination of their surface spins.¹³ Our NP exhibit high crystallinity extending to their outermost layer and lack of the weak FM commonly associated with uncompensated spins at the particle surface. Consequently, our current study cannot conclusively address this issue.

Conclusions

This work shows the interplay between crystal structure and magnetic features in three platelet-like shaped NiO NP with sizes ranging from 6 to 34 nm that were synthesized following two distinct wet chemistry synthesis approaches. The three samples show consistent crystal structures and growth directions along either (111) or (200) atomic planes. Additionally, compositional studies in single NiO NP discarded the presence of any minority Ni species, although highlight a slight Ni deficiency linked to the low temperature during the annealing step of the syntheses. X-ray diffraction analysis corroborates these findings, further confirming the single-crystal nature and the consistent Ni deficiency. The magnetic behaviour of the samples, as observed through ensemble measurements, exhibits intriguing size-dependent behaviour. While the smallest NiO6 NP display weak SPM, larger particles tend to show AF properties much closer to its bulk counterpart. This size-dependent magnetic behaviour can be attributed to finite-size and surface effects, together with grain boundaries and structural defects, degrading the AF ordering and increasing the relative contribution of unpaired spins to the particle magnetization. All the foregoing becomes less prevalent with a lower surface-to-volume ratio of the NP.

A single, particle-by-particle analysis of the AF axis orientations for a subset of single-phased, highly crystalline NiO NP of 34 nm in diameter was performed by synchrotron-based XPEEM combined with XMLD. Such study on fully three-dimensional nanoscale AF objects extends previous investigations of the orientations of AF domains in bulk and thin films of NiO and other AF systems. The detailed evaluation of the angular dependencies of the magnetic contrast intensity, as a function of both the rotation of the electric vector of the polarized light and the sample azimuthal angle, enabled a quantitative, unambiguous determination of the Néel axes in a set of individual NP of similar structural, chemical, and morphological characteristics, randomly dispersed onto a non-magnetic solid substrate. The observed AF axes are robust against thermal fluctuations at room temperature and seem to be stochastically distributed along some of the 12 possible easy directions compatible with both the multiplicity of the AF structure of NiO and the fact that particles are likely lying on the substrate on one of the most plausible crystal facets, {200} and {220} as from HRTEM images. Contrary to seminal theoretical predictions for NiO NP within this size range, our observations reveal singe domain states without any evidence of a breakdown in the two-sublattice model. This conclusion, supported by the homogeneity of the XMLD signal across adjacent pixels within each NP and the consistency of the fits of the XMLD data as a function of the E-vector for the two azimuthal angles, is attributed to the high crystal quality of the particles up to the outermost layer and to the lack of surface imperfections resulting in uncompensated disordered spins, in agreement with the absence of a weak ferromagnetic contribution in the macroscopic magnetic measurements and the single AF domain state of the particles.

Overall, these findings enrich the comprehension of antiferromagnetism in nanostructures confined along the three dimensions and may pave the way for applications requiring an efficient reading and writing of information using definite states of the AF Néel axis. Further work would be necessary to test the robustness of the observed AF Néel axis orientations against thermal switching across the Néel temperature.

Author contributions

CM, XB, and AFR conceived the research. CM and JA performed the synthesis and the lab-based structural, compositional and magnetic characterization, together with XB. AIF, MGdM, and AFR conducted the synchrotron experiments with support from AK. MGdM, MXA, ÒI, AFR, and AL did the image processing and analysis of the synchrotron data. CM, AL and AFR led the manuscript writing with contributions from all the authors. All authors reviewed the manuscript.

Conflicts of interest

There are not conflicts to declare.

Data availability

All data supporting the findings of this study are available within the article and its ESI.† Additional raw data related to the structural, magnetic, and spectroscopic characterization, including raw TEM, XRD, XPS, and XMLD-XPEEM files, are available from the corresponding authors upon reasonable request.

Acknowledgements

The authors gratefully acknowledge financial support from the Spanish MICIIN (grant numbers PGC2018-097789-B-I00, PID2021-127397NB-I00), Catalan AGAUR (Groups of Excellence 2021SGR00328), and the European Union FEDER funds. Most of the characterization of the samples was performed at the scientific facilities of the University of Barcelona (CCiTUB), with special thanks to the Surface Analysis Laboratory and the X-ray Diffraction personnel. Synchrotron experiments were performed at the SIM Beamline of the Swiss Light Source, Paul Scherrer Institut, Switzerland. Support from project 2023-226 through ELECMI facilities is also acknowledged. HRTEM and EELS measurements were conducted at the Institute of Nanoscience and Materials of Aragón (INA), University of Zaragoza, Spain. The authors express their gratitude to Dr Rodrigo Pacheco for his contributions to the measurements and for the insightful discussions regarding the HRTEM results. CM acknowledges funding from the University of Barcelona and the Spanish Ministry of Universities under the Maria Zambrano Program, funded by the European Union Next Generation EU/PRTR, as well as the Beatriu de Pinós fellowship program (2022 BP 00243). AIF and CM are Serra Húnter fellows.

References

1. S. I. Popkov, A. A. Krasikov, D. A. Velikanov, V. L. Kirillov, O. N. Martyanov and D. A. Balaev, J. Magn. Magn. Mater., 2019, 483, 21–26.
2. Y. Anahory, L. Embon, C. J. Li, S. Banerjee, A. Meltzer, H. R. Naren, A. Yakovenko, J. Cuppens, Y. Myasoedov, M. L. Rappaport, M. E. Huber, K. Michaeli, T. Venkatesan Ariando and E. Zeldov, Nat. Commun., 2016, 7, 12566.
3. X. H. Liu and K. Wang, Antiferromagnetic Materials and Their Manipulations, ed. X. H. Liu and K. W. Wang, Wiley, 2022, ch. 11, pp. 271–293,  DOI:10.1002/9781119698968.ch11.
4. D. Sani, G. Yakubu and S. Sahabi, Int. J. Eng. Technol. Res., 2019, 8, 461–467.
5. M. Carbone, M. Missori, L. Micheli, P. Tagliatesta and E. M. Bauer, Materials, 2020, 13, 1417.
6. D. Delgado, R. Sanchís, J. A. Cecilia, E. Rodríguez-Castellón, A. Caballero, B. Solsona and J. M. L. Nieto, Catal. Today, 2019, 333, 10–16.
7. J. Zhu, Z. Gui, Y. Ding, Z. Wang, Y. Hu and M. Zou, J. Phys. Chem. C, 2007, 111, 5622–5627.
8. P. A. Sheena, H. Hitha and A. Sundareshan, J. Mater. Sci.: Mater. Electron., 2020, 31, 412–420.
9. Y. Lida, K. Shimada and S. Ozaki, Bull. Chem. Soc. Jpn., 1960, 33, 1372–1375.
10. P. Dubey, N. Kaurav, R. S. Devan, G. S. Okram and Y. K. Kuo, RSC Adv., 2018, 8, 5882–5890.
11. J. Milano and M. Grimsditch, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 094415.
12. L. Néel, Ann. Geophys., 1949, 5, 99–136.
13. R. H. Kodama, S. A. Makhlouf and A. E. Berkowitz, Phys. Rev. Lett., 1997, 79, 1393–1396.
14. C. Moya, J. Ara, A. Labarta and X. Batlle, Magnetism, 2024, 4, 252–280.
15. F. L. Deepak, Á. Mayoral and R. Arenal, Advanced Transmission Electron Microscopy: Applications to Nanomaterials, Springer, 2015,  DOI:10.1007/978-3-319-15177-9.
16. N. Shibata, S. Findlay, Y. Kohno, H. Sawada, Y. Kondo and Y. Ikuhara, Nat. Phys., 2012, 8, 611–615.
17. F. Barrows, A. K. Petford-Long and C. Phatak, Commun. Phys., 2022, 5, 324.
18. A. Fraile Rodríguez, A. Kleibert, J. Bansmann, A. Voitkans, L. J. Heyderman and F. Nolting, Phys. Rev. Lett., 2010, 104, 127201.
19. A. Balan, P. M. Derlet, A. Fraile Rodríguez, J. Bansmann, R. Yanes, U. Nowak, A. Kleibert and F. Nolting, Phys. Rev. Lett., 2014, 112, 107201.
20. S. Reimers, Y. Lytvynenko, Y. R. Niu, E. Golias, B. Sarpi, L. S. I. Veiga, T. Denneulin, A. Kovács, R. E. Dunin-Borkowski, J. Bläßer, M. Kläui and M. Jourdan, Nat. Commun., 2023, 14, 174.
21. J. Stöhr, H. A. Padmore, S. Anders, T. Stammler and M. R. Scheinfein, Surf. Rev. Lett., 1998, 5, 1297–1308.
22. G. Van der Laan, N. D. Telling, A. Potenza, S. S. Dhesi and E. Arenholz, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 064409.
23. K. Arai, T. Okuda, A. Tanaka, M. Kotsugi, K. Fukumoto, T. Ohkochi, T. Nakamura, T. Matsushita, T. Muro, M. Oura, Y. Senba, H. Ohashi, A. Kakizaki, C. Mitsumata and T. Kinoshita, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 104418.
24. T. J. Regan, Ph.D. Thesis, Stanford University, 2001.
25. C. Schmitt, L. Baldrati, L. Sanchez-Tejerina, F. Schreiber, A. Ross, M. Filianina, S. Ding, F. Fuhrmann, R. Ramos, F. Maccherozzi, D. Backes, M. Mawass, F. Kronast, S. Valencia, E. Saitoh, G. Finocchio and M. Kläui, Phys. Rev. Appl., 2021, 15, 034047.
26. A. Mandziak, G. D. Soria, J. E. Prieto, M. Foerster, J. de la Figuera and L. Aballe, Nanoscale, 2020, 12, 21225–21233.
27. S. Czekaj, F. Nolting, L. J. Heyderman, P. R. Willmott and G. van der Laan, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 020401.
28. P. Wadley, K. W. Edmonds and M. R. Shahedkhah, et al., Sci. Rep., 2017, 7, 11147.
29. S. Reimers, Y. Lytvynenko and Y. R. Niu, et al., Nat. Commun., 2023, 14, 1861.
30. Y. Lee, C. Kim, S. Son, J. Cui, G. Park, K.-X. Zhang, S. Oh, H. Cheong, A. Kleibert and J.-G. Park, Nano Lett., 2024, 24, 6043–6050.
31. M. Escoda-Torroella, C. Moya, A. F. Rodríguez, X. Batlle and A. Labarta, Langmuir, 2021, 37, 35–45.
32. Y. Wu, Y. He, T. Wu, T. Chen, W. Weng and H. Wan, Mater. Lett., 2007, 61, 3174–3178.
33. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.
34. Gatan Microscopy Suite® (GMS) 3.5, Gatan, Inc., Pleasanton, CA, USA.
35. Inorganic Crystal Structure Database (ICSD), X'pert high score plus pattern for bulk NiO, entry: ICSD 01-071-1179, FIZ Karlsruhe, 2021.
36. J. Rodriguez-Carvajal and T. Roisnel, Int. Union Crystallogr., 1998, 20, 35–36.
37. C. P. Bean and J. D. Livingston, J. Appl. Phys., 1959, 30, S120–S129.
38. X. Batlle, C. Moya, M. Escoda-Torrella, Ò. Iglesias, A. F. Rodríguez and A. Labarta, J. Magn. Magn. Mater., 2022, 543, 168594.
39. B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, John Wiley & Sons, 2009.
40. X. Batlle, M. García del Muro, J. Tejada, H. Pfeiffer, P. Görnert and E. Sinn, J. Appl. Phys., 1993, 74, 3333–3340.
41. A. I. Figueroa, C. Moya, M. X. Aribó, J. Ara, M. G. Del Muro, A. Kleibert, S. Valencia, A. Labarta, X. Batlle and A. F. Rodríguez, Low Temp. Phys., 2024, 50, 852–861.
42. D. Raftrey and P. Fischer, J. Magn. Magn. Mater., 2021, 545, 168734.
43. J. Stöhr, A. Scholl, T. J. Regan, S. Anders, J. Lüning, M. R. Scheinfein, H. A. Padmore and R. L. White, Phys. Rev. Lett., 1999, 83, 1862.
44. J. Stöhr and H. C. Stiegmann, Magnetism, From Fundamentals to Nanoscale Dynamics, Springer eBooks, 2006,  DOI:10.1007/978-3-540-30283-4.
45. T. J. Regan, H. Ohldag, C. Stamm, F. Nolting, J. Lüning, J. Stöhr and R. L. White, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 64, 214422.
46. L. L. Guyader, A. Kleibert, A. F. Rodríguez, S. E. Moussaoui, A. Balan, M. Buzzi, J. Raabe and F. Nolting, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 371–380.
47. U. Flechsig, F. Nolting, A. F. Rodríguez, J. Krempasky, C. Quitmann, T. Schmidt, S. Spielmann, D. Zimoch, R. Garrett, I. Gentle, K. Nugent and S. Wilkins, AIP Conf. Proc., 2010, 1234, 319–322.
48. A. F. Rodríguez, A. Kleibert, J. Bansmann and F. Nolting, J. Phys. D: Appl. Phys., 2010, 43, 474006.
49. A. F. Rodríguez, C. Moya, M. Escoda-Torroella, A. Romero, A. Labarta and X. Batlle, J. Mater. Chem. C, 2018, 6, 875–882.
50. Wolfram Research, Inc., Mathematica, Version 12.2, Wolfram Research, Inc., Champaign, IL, 2024.
51. M. Benedet, C. Maccato, G. Pagot, C. Invernizzi, C. Sada, V. Di Noto, G. A. Rizzi, E. Fois, G. Tabacchi and D. Barreca, J. Mater. Chem. C, 2023, 127, 22304–22314.
52. U. Holzwarth and N. Gibson, Nat. Nanotechnol., 2011, 6, 534–534.
53. A. P. Grosvenor, M. C. Biesinger, R. S. Smart and N. S. McIntyre, Surf. Sci., 2006, 600, 1771–1779.
54. M. A. Peck and M. A. Langell, Chem. Mater., 2012, 24, 4483–4490.
55. J. F. Moulder, Handbook of X-ray Photoelectron Spectroscopy: A Reference Book of Standard Spectra for Identification and Interpretation of XPS Data, Perkin-Elmer, Physical Electronics Division, 1992.
56. M. C. Biesinger, B. P. Payne, L. W. M. Lau, A. R. Gerson and R. St. C. Smart, Surf. Interface Anal., 2009, 41, 324–332.
57. H. Shim, P. Dutta, M. S. Seehra and J. Bonevich, Solid State Commun., 2008, 145, 192–196.
58. D. Alders, L. H. Tjeng, F. C. Voogt, T. Hibma, G. A. Sawatzky, C. T. Chen, J. Vogel, M. Sacchi and S. Iacobucci, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 57, 11623–11631.
59. T. Li, M. Ho, T. Hsu, H. Chiu, K. Wu, J. Peng, C. Wu, T. S. Chan, B. V. Kumar, P. M. Reddy, S. Ke, C. Cheng, A. C. Gandhi and S. Y. Wu, Appl. Surf. Sci., 2021, 578, 152081.
60. M. W. Haverkort, S. I. Csiszar, Z. Hu, S. Altieri, A. Tanaka, H. H. Hsieh, H. Lin, C. T. Chen, T. Hibma and L. H. Tjeng, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 020408(R).
61. W. L. Roth and G. A. Slack, J. Appl. Phys., 1960, 31, S352–S353.
62. W. L. Roth, J. Appl. Phys., 1960, 31, 2000–2011.
63. G. A. Slack, J. Appl. Phys., 1960, 31, 1571–1582.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr01625h

---