Single atom coordination in a manganese–cobalt bi-metallic framework on graphene: geometric and electronic structures

Abstract

Manganese tetra-pyridyl-porphyrins are found to self-organize in an ordered monolayer on graphene. Moreover, post deposition of cobalt ad-atoms steers the geometric reordering of the layer, yielding the formation of a self-assembled bimetallic network, where both Mn and Co are tetra-coordinated with nitrogen. While manganese shifts from Mn(II) towards the +2/+3 oxidation state range, depending on the local Co concentration and not reaching a full Mn(III) configuration, pyridinic cobalt is stabilized in the rarer +1 oxidation state. The actual geometric and electronic structures of the framework are defined by lateral interactions, dominating over the weaker network-graphene bonding.

---

Introduction

The development of energy conversion technologies based on renewable sources is a central issue in research, fostering the transition from fossil fuels to clean energy production.^1–3 Due to the intermittent nature of renewable sources like wind and sun, further improvement of energy storage devices is required.^4,5 Metal–air rechargeable batteries are based on earth-abundant materials like e.g. Zn, and can represent a lower-cost, more environmental friendly and safer alternative to Li-based technologies.^2,4,6 However, developing an efficient air electrode, where both oxygen evolution (OER) and oxygen reduction (ORR) reactions take place during the charge and discharge processes, respectively,³ is an open challenge. The ideal electrode should be bifunctional,⁷ electrocatalytically stable, and with high activity towards both opposite OER and ORR, generally associated with high activation barriers.^2,4 The reactions mechanisms and kinetics are complex and strongly dependent on the adopted electrolyte and material environment, making predictions difficult.^4,8 Therefore, the design of ORR/OER bifunctional catalysts working at room or at least application-compatible temperature is a very hot topic in research.^1–4,7,9

To this purpose, a suitable choice of organic units allows the creation of bi-metallic organic frameworks hosting two inequivalent metal centers and thus creating an ideal base to achieve bifunctionality. Tetra-pyridyl porphyrins (TPyPs) are perfect candidates for this role, as they can self-assemble in bi-metallic M₁TPyP-M₂ coordination networks (where M₁ and M₂ can be chosen among different metals). Furthermore, their specific activity towards OER/ORR has been theoretically predicted,¹⁰ and experimentally observed in recent years.^11–13 Self-assembled FeTPyP and CoTPyP layers on Au(111) are efficient and stable electrocatalysts towards ORR, however easily deteriorating under OER conditions.¹² Interestingly, their bi-metallic combinations M₁TPyP-M₂, where M_1,2 = Fe, Co showed a non-linear increase of the catalytic activity by about two orders of magnitude compared to the M₁TPyP molecular layers, associated with emergent properties of the framework with respect to its constituents.¹¹ Indeed, the observed non-linear effects were associated with a cooperative interplay between the metal centers, due to a global electronic and magnetic structure modification of the metal–organic frameworks (MOFs).¹¹Ab initio simulations of free-standing M₁TPyP-M₂ monolayers with M_1,2 = Fe, Co provided further insight, showing that the single metal atom sites can be magnetically coupled through the polarization of the organic matrix.¹⁰ Furthermore, coordination of the second metal enhances the structural stability of the layers, leading to the formation of Bloch states delocalized throughout the MOF.¹⁰ Recently, the investigation of CO adsorption as a probe ligand on a CoTPyP–Co/Gr/Ir(111) framework at near-ambient pressure provided the experimental confirmation of cooperativity between the peripheral Co units, mediated by the organic backbone.¹⁴ Finally, the spectroscopic investigation of M₁TPyP-M₂ where M_1,2 = Fe, Co ^15,16 and M_1,2 = Cu,⁹ proved the possibility to tune the oxidation state of M₁ by coordination of M₂,^15,16 obtaining a network with inequivalent metal centers even in the case of M₁ = M₂, with Co(II)TPyP yielding Co(III)TPyP–Co(I)¹⁵ and 2HTPyP and Cu co-deposited on Au(111) leading to Cu(II)TPyP–Cu(0).⁹

The choice of a proper supporting substrate for the layer growth is determined by its chemical reactivity and by the trans effect,¹⁷ which can be exploited in principle to selectively tune the electronic configuration of the reactive centers. We focus here on graphene (Gr) to this purpose, being poorly reactive and offering a low degree of coupling with the framework, so to closely resemble a free-standing situation. We describe the growth and characterization in ultra-high vacuum (UHV) conditions of MnTPyP and MnTPyP–Co monolayers on Gr/Ir(111). Gr on Ir(111), which is a good approximation of an almost-free-standing Gr sheet,^18–20 fulfills indeed multiple requirements: it successfully decouples the metal surface and the organic layer,²¹ it introduces the steric constraints of a surface, and at the same time it is chemically inert,²² also passivating the underlying Ir(111) termination, thus representing an optimal playground for near-ambient pressure investigations. We report a combined experimental and ab initio approach, where Scanning Tunneling Microscopy (STM) is exploited to image the self-assembly geometry of the manganese framework, and together with X-ray Photoelectron Spectroscopy (XPS) confirms the expected tetra-coordination of Co at the pyridinic sites. The combination of XPS, UPS, ARPES, NEXAFS, XMCD and IR-Vis SFG allows for a detailed description of the electronic and vibrational structures, witnessing a dramatic reorganization of the electronic and geometric structures and tuning of the metal's oxidation state upon Co addition. The theoretical calculations yield an accurate description of the electronic configuration of the layer, together with charge transfer, confirming the stability of the bonding geometry and correctly reproducing the STM appearance.

Methods

Experimental section

Sample preparation. The Ir(111) surface was cleaned by repeated cycles of Ar+ sputtering at 2 keV and annealing at 1275–1375 K, alternated with exposure to 5 × 10⁻⁸ mbar O₂ at 300–1070 K to get rid of residual carbon contaminants. A single Gr sheet was grown by ethylene chemical vapor deposition (CVD) following established recipes adapted to the characteristics of each used setup: in a simplified version, the clean sample was heated at a temperature higher than 1275 K and exposed to 5 × 10⁻⁸ mbar C₂H₄ for 2 minutes, the pressure was then increased to 3 × 10⁻⁷ mbar for the same amount of time, and finally the temperature was lowered while recovering UHV conditions. Depending on the specific experimental setup, the quality of the Gr sheet was checked with LEED, XPS, or IR-Vis SFG (Fig. S1†). The Mn(III) meso-tetra (4-pyridyl) porphin chloride molecules were purchased from Frontier Scientific. The molecules were outgassed for several hours at 470–525 K to remove gas contaminants and organic residues. The Cl atom ligated to the central metal stabilizes the complex as Mn(III), and is thermally detached from the porphyrins when they are heated.^23–27 Absence of Cl in the deposited layer was verified by XPS, resulting in a reduction of the metal center to Mn(II). The sublimation temperature was varied in the 650–680 K range according to the setup and the crucible-sample distance, achieving deposition rates of approximately 0.06 ML min⁻¹, in order to grow a full monolayer (ML) in about 15–20 minutes. The sample was kept at 473 K during the growth, to promote ordering without affecting stability. The molecular coverage was usually kept below 1 ML to avoid kinetic hindrance in the reordering process and the presence of a second layer. The bi-metallic heterostructure was obtained upon post-evaporation of atomic Co by resistively heating a Co filament of 0.25 mm diameter at the SFG Laboratory and HIPPIE beamline, and from electron bombardment of a Co rod at the AG Cinchetti Laboratory and BOREAS beamline. Co coverage will be expressed referring to a porphyrin monolayer throughout the manuscript, so that 1 ML Co corresponds to 1 Co ad-atom for each molecule in 1 ML MnTPyP. In general, Co was dosed to achieve a Co : MnTPyP ratio slightly lower than unity, to avoid formation of Co clusters due to excess Co.¹⁵ The evaporation rate was calibrated either by Auger Electron Spectroscopy (AES) or XPS, depending on the available method.

Scanning tunneling microscopy. The STM measurements were performed at the Microscopy labs of MAX IV Laboratory with a commercial VT UHV XA STM from Scienta-Omicron, GmbH, with electrochemically etched W tips purchased from Scienta-Omicron, GmbH. Imaging was performed at LN₂. The sign of the bias refers to the bias of the sample with respect to the tip. At variance with the spectroscopy measurements, for the STM characterization we chose to deposit a sub-monolayer coverage of MnTPyP and to post-deposit a less than stoichiometric amount of cobalt, so to yield co-existing phases with different local Co coverage that could be locally observed by STM in a single shot.

Photoelectron spectroscopy. XPS experiments were performed at the HIPPIE beamline of the MAX IV synchrotron radiation facility in Lund (S), allowing also for in situ and operando measurements in gaseous atmosphere.²⁸ Mn and Co 2p_3/2 core level spectra were acquired upon excitation with 1000 eV photons, N 1s with 514 eV, C 1s and Ir 4f_7/2 with 400 eV photons, respectively, in order to optimize photoionization cross section, surface sensitivity, and, thus, the signal-to-noise ratio. A slow raster-scan of ∼0.5 μm s⁻¹ was set up to prevent degradation of the MOF during the measurements. The binding energy scale was calibrated with respect to the Ir 4f_7/2 core level (60.87 eV) as a reference.²⁹ The XPS spectra were best fitted by least squares fitting methods according to the Doniach–Šunjić or Voigt lineshapes,³⁰ depending on the core level, after subtraction of a linear background. The XPS results were indeed preliminary for the following reactivity characterization of the layers at ambient pressure conditions, which are however beyond the purpose of the present work.

Valence band, work function, and momentum-resolved spectroscopy. ARPES and UPS data were acquired at room temperature using a KREIOS PEEM (Specs GmbH) operating in momentum mode,³¹ allowing to record 2D momentum maps with an approximate momentum field-of-view of [k_x, k_y] = [±2.0, ±2.0] Å⁻¹ at a constant kinetic energy.³¹ The measurements were performed using a monochromatized UV helium lamp with the characteristic emission line at 21.2 eV. Beam damage effects were observed only after prolonged exposure, of the order of an hour, thus the sample was moved stepwise to measure on a fresh spot. The spectra were aligned by correcting the binding energy (BE) with the Fermi level, normalized and then the bare Gr valence band (VB) spectrum was subtracted to remove the substrate contribution and have a clearer view of the molecular-related VB features. By measuring the secondary electron onset kinetic energy E_onset it is possible to extract the work function value according to ϕ = hν − (E_Fermi − E_onset), where E_Fermi is the Fermi edge position (the same used to calibrate the energy scale) and hν = 21.2 eV. The bias applied between sample and analyzer ensures collection of the whole photoelectron kinetic energy region of interest, and it is accounted for in the E_Fermi term, together with the analyzer work function.

Sum-frequency generation spectroscopy. Infrared–Visible Sum–Frequency Generation (IR–Vis SFG)^32,33 vibronic spectroscopy measurements were performed in a dedicated setup at the Department of Physics of the University of Trieste.³⁴ A UHV system with a base pressure of 5 × 10⁻¹¹ mbar hosting standard surface science preparation and characterization techniques is directly coupled with a high-pressure cell for in situ IR–Vis SFG spectroscopy (base pressure better than 5 × 10⁻⁹ mbar) described elsewhere.³⁴ The inlet and outlet of the laser beams are provided by UHV-compatible BaF₂ windows. The excitation source (Ekspla, 1064 nm, 30 ps, 50 Hz) delivers a 532 nm (2.33 eV) visible beam, and IR radiation tunable in the 1000–4500 cm⁻¹ range, obtained thanks to second harmonic and parametric generation. The raw spectra were normalized to the impinging infrared and visible excitation intensities, and to a reference SFG signal from clean Au to account for the energy-dependent IR intensity and the time–dependent intensity fluctuations of the sources. The normalized SFG spectra were then analyzed by least-squares fitting to the widely adopted parametric, effective expression of the nonlinear second-order susceptibility.³² The model well reproduces the observed lineshapes, accounting for the resonant IR–Vis vibronic transitions and for the non-resonant background, describing all the interference terms associated with the relative phases, and considering the Lorentzian broadening typical of a stimulated spectroscopic transition and related to the dephasing rate, which in turn stems from the excited-state lifetime and the elastic dephasing of the vibronic state.³⁵ In the figures, we plot the normalized IR–Vis SFG signal intensity (dots), together with the best fit (lines) and the deconvolution of each k^th resonance with its interference with the non-resonant background (color-filled profiles). The latter are calculated with the parameters obtained from the fitting procedure following the literature,³⁴ and by keeping in mind that multiplet solutions are possible due to the non-unicity of the parameter sets.³⁶ Further details and examples can be found in our previous works.^13,34,37 In the present study, spectra were collected in ppp polarization configuration (in decreasing energy order).

Absorption and magnetic dichroism. Both NEXAFS and XMCD measurements were performed at the BOREAS beamline³⁸ in total electron yield mode (i.e. by measuring the drain current of the sample with a Keithley K428 current amplifier). Each spectrum was normalized with the beam intensity by measuring the drain current of a freshly evaporated gold grid in front of the sample. While NEXAFS spectra were acquired with linear-horizontal and linear-vertical polarized radiation, the XMCD measurements were performed by changing the helicity of the incident light (using 100% circular polarized radiation). For both NEXAFS and XMCD, the synchrotron radiation was generated with an Apple II EPU undulator. The photon flux of about 10¹² photons per s was attenuated and the beam was defocused to prevent radiation-induced damage. The spectra collected from the MnTPyP/Gr sample were measured with an incidence angle of 70° from the surface normal, while the Co-MnTPyP/Gr ones were measured with a 60° incidence angle. The NEXAFS spectra were acquired at 200 K, whereas the XMCD spectra were collected at LHe temperature (4–4.5 K), applying a 6 T magnetic field, oriented parallel to the incidence of light. To reduce the noise level in the NEXAFS measurements, a small magnetic field (50 mT) was applied. The photon energy calibration for the nitrogen K-edge was done by setting the first peak to the reference value of the macrocycle at 398.5 eV.¹⁶ The background removal was performed by dividing each spectrum by a cubic spline background function. For the Mn and Co L-edges the same grating was used, and the photon energy calibration was performed using a reference sample. We acquired an absorption spectrum of a CoO sample: the main resonance was set to the reference value of 776.08 eV.³⁹ The background was removed for each polarization separately by subtracting a spline background function.

Theoretical section

Density functional theory (DFT). DFT calculations were performed using the plane-wave pseudopotential method as implemented in the Quantum ESPRESSO distribution.^40–42 All slab-based calculations were described using periodic boundary conditions with simulation cells 20 Å in height, ensuring a sufficient distance of at least 15 Å between the molecules and the periodic image of Gr. The underlying Ir(111) termination was neglected, on the basis of previous experience with similar systems.^15,43 Different in-plane unit cells were adapted to model different systems, namely the MnTPyP molecule, the MnTPyP monolayer, and the metal–organic coordinated bimetallic MnTPyP–Co network. For the single MnTPyP molecule over Gr, the unit cell had an in-plane rectangular periodicity with lattice parameters a = 17.22 Å and b = 17.04 Å, containing a Gr domain with 112 C atoms. For the mono- and bi-metallic layers, oblique lattices were adopted, with the in-plane lattice parameters a₁ = 30.97 Å, b₁ = 14.84 Å and α₁ = 116.2° for monometallic MnTPyP with Gr, a₂ = 28.36 Å, b₂ = 20.23 Å and α₂ = 135.1° for bimetallic MnTPyP–Co over Gr. The unit cells contain two MnTPyP molecules or two MnTPyP–Co units, with 78 and 70 hexagonal units of Gr (containing 2 carbon atoms each). To model the heterostructures of mono- and bi-metallic systems with Gr, the molecules were kept at a starting distance of 3 Å from the substrate. Due to the small mismatch between the molecular and the Gr lattices, the latter was only slightly strained, resulting in a larger Gr lattice parameter of 2.47 Å (wrt 2.46 Å) for the mono-metallic case and in an asymmetric configuration with parameters of 2.48 Å, 2.53 Å, and an angle γ = 118.7° for the bi-metallic case.

Spin-polarized calculations employed the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional within the generalized gradient approximation (GGA) method.⁴⁴ A Hubbard-U correction was introduced to improve the description of the Mn and Co 3d states.⁴⁵ The U parameters were calculated using the self-consistent method proposed by Cococcioni et al.⁴⁶ Using this approach, U = 3.2 eV and U = 6.12 eV have been obtained for Mn and Co, respectively. van der Waals interactions were included using the Grimme-D3 approach.⁴⁷ Vanderbilt ultrasoft pseudopotentials⁴⁸ (of the Garrity–Bennett–Rabe–Vanderbilt type for Mn)⁴⁹ were employed. Plane-wave cutoffs of 60 Ry for the wave functions and 240 Ry for the charge density were applied. The Methfessel–Paxton smearing scheme with a parameter of 0.01 Ry was used for electronic state occupations.^47,50 Geometric optimizations utilized the Broyden–Fletcher–Goldfarb–Shanno algorithm with energy and force convergence thresholds of 1 × 10⁻⁶ Ry and 1 × 10⁻³ a.u., respectively. Reciprocal space sampling used uniform grids of 8 × 8 × 1 k-points for self-consistent field (SCF) and 10 × 10 × 1 k-points for non-self-consistent field (NSCF) calculations in the MnTPyP molecule system. In case of mono- and bi-metallic layers, 4 × 8 × 1 k points were sampled over the first Brillouin zone for electronic structure calculations.

We add here a specific comment on the adopted terminology. Throughout the paper we will refer to HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) also in the case of the 2D, periodic molecular crystal. This is indeed the widely accepted terminology in the case of organic molecular semiconductors, with narrow energy bands, representing the corresponding counterpart of the valence and conduction bands, respectively, which, however, specifically pertain to solid state semiconductors and metals.

STM simulations were conducted using the Tersoff–Hamann approach,⁵¹ assuming a constant density of states for the tip, with an STM image integration range corresponding to the applied bias. All the charge transfer amounts were quantified using the Bader charge analysis method as proposed by the Henkelman group.^52,53 Electron density rearrangement plots due to molecule (M) adsorption on Gr were calculated as the difference between the total system (M/Gr) and the individual, separated components.

Results and discussion

Preliminary characterization of the pristine MnTPyP molecular layer

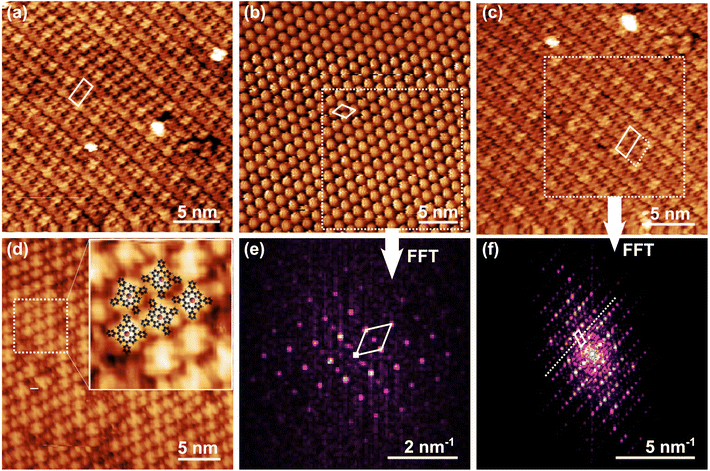
Upon deposition on Gr at, or slightly above (<400 K), room temperature, MnTPyPs self-organize into long-range ordered islands, thanks to the lateral attraction prevailing over the weak interaction with the substrate. Fig. 1 plots in panels (a–d) a set of STM images. The large molecular islands do not show preferential orientational domains, nor preferential alignment driven by the weak Gr moiré corrugation, whereas domain boundaries are often determined by the terrace edges. MnTPyPs arrange into rows made by alternating orientations of the molecules, described by a (1.2 × 2.6) nm² quasi-rectangular monoclinic unit cell, depicted in panels (a, c, solid white lines), containing two non-equivalent molecules. The molecular alignment in alternate rows is evident from the models superimposed in the inset of Fig. 1(d). The pristine 4-fold symmetry of each molecule is broken due to the distortion of the peripheral pyridinic groups, resulting in a 2-fold appearance. In the inset, the lowest energy geometrical arrangement of MnTPyP/Gr, as obtained from ab initio DFT calculations, is superimposed to the STM topographic image, confirming the above statement. Also CoTPyPs are known to adopt a similar layout on the same substrate, yielding a close-to rectangular monoclinic network.⁴³ When the molecular orientation cannot be distinguished due to the specific sample–tip bias or due to the tip properties, as we obtain in Fig. 1(b) for the MnTPyP lattice, the STM image reveals the positions of the Mn atoms, yielding an apparent hexagonal appearance of the unit cell with a size of 1.3 nm. Here, for the MnTPyP layer, to better visualize the unit cell, the 2D Fast Fourier Transforms (FFT) of the images in panels (b, c) were calculated using the 2D FFT built-in function of Gwyddion,⁵⁴ limiting the data set to the regions evidenced by the dashed squares in the corresponding real space images to reduce as much as possible the contribution of drifts, noise and random defects. The results are shown in panels (e, f) of the figure. The quasi-hexagonal reciprocal space unit cell found in panel (e) confirms the (1.3 × 1.3) nm² periodicity already visible in the direct space images. The (2 × 1) cell in panels (a, c) measures (1.2 × 2.5) nm² if calculated from the transformed image in panel (f), again in good agreement with the real-space measurement. In panel (f) we observe the appearance of a fainter row of spots (dotted line) between the brighter rows in the reciprocal-space image. This suggests the presence of a larger real-space periodicity, which is less obvious from the real direct space images and too large for an ab initio simulation. We could speculate that it may be related to the lattice matching with respect to the underlying graphene moiré supercell and its shallow corrugation. The latter is hardly visible “by eye” being superimposed on the strong molecular corrugation and the corresponding image contrast. Thus, the most proper unit cell in direct space would account for a (2 × 2) periodicity, as evidenced by merging the continuous and dashed cells in panel (c).

Fig. 1 (a–d) STM images of the MnTPyP/Gr/Ir(111) layer, collected at LN₂ temperature. The white continuous perimeters in (a) and (c) depict the quasi-rectangular monoclinic unit cell, accounting for the different orientation of the molecules in alternating rows, while in (b) the hexagonal appearance associated with the Mn metal centers of the MnTPyP layer is evident only when the STM image contrast reveals no intramolecular resolution. (d) Image with an enlarged inset and corresponding best molecular geometry as obtained from the DFT calculations. (e and f) 2D FFT (and corresponding reciprocal space unit cells) of the dashed square regions in (b) and (c). [(a) V = −1.80 V, I = 150 pA; (b) V = 1.70 V, I = 150 pA; (c) V = −2.00 V, I = 150 pA; (d) V = 1.80 V, I = 190 pA].

A direct spectroscopic tool to investigate the chemical state and coordination environment of the various atomic species constituting the heterostructures is provided by XPS. A complete set of the relevant core levels of the as-prepared monolayers in UHV is shown in Fig. 2(a–c), together with the best fit and the single spectral components. Concerning the electronic structure, once deposited on the sample, the MnTPyP molecules are expected to exhibit a Mn(II) oxidation state of the central metal atom, analogously to their CoTPyP and FeTPyP counterparts,16 and to transition-metal porphyrins or phthalocyanines in general.9,31,55–58 The best fit of the Mn 2p3/2 spectrum reported in Fig. 2(b) (bottom) has been obtained with three Voigt envelopes centered at 640.5, 641.9, 643.4 eV and a satellite at 646.9 eV. All peaks are forced to share a best-fitted common Lorentzian width of Γ = 0.25 eV to avoid overfitting (the shake-up has Γ = 0.20 eV), while the Gaussian broadening is left free to vary for each feature to include the unresolved multiplet components. As anticipated, by comparison with the literature, the oxidation state of the central metal atom can be assigned to Mn(II), as in the case of MnPc monolayers on HOPG and Ag(111),59,60 multilayers on Co,58 and MnTPP/Ag(111).23 A direct comparison with previous studies is reported in Table S1.† Specifically, Biesinger et al. exploited MnO to access the multiplet splitting structure of Mn(II), and MnO2, Mn2O3 and MnOOH for Mn(III).61–65 Data on MnO and Mn(III) composites are found in the works of Nesbitt and Banerjee,61 Ilton,66 together with Cl-MnTPP/Ag(111).23 Focusing now on a single MnTPyP, it contains 8 nitrogen atoms, grouped into two nonequivalent species: the iminic nitrogen in the macrocycle, bound to Mn, and the external pyridinic species that, according to the literature on similar systems, can be separated into two components in the best fit of the N 1s spectra (Fig. 2(c), bottom). The BE of a tetrapyrrole iminic component can vary by up to 2 eV, depending on the metal embedded in the macrocycle and on the supporting substrate, and is usually found in the 397–399 eV range.57,67–71 Pyridinic nitrogen in M-TPyP (M indicates that it is a metalated porphyrin) and 2HTPyP usually shows a 0.3–1 eV higher BE with respect to the iminic component.9,16 The N 1s spectrum from MnTPyP/Gr can be reproduced by three peaks, best fitted with Voigt functions. Imposing a common lineshape for the elastic features gives a Lorentian width Γ = 0.13 eV and Gaussian broadening of 0.57 eV, while the shake-up widths were left independent and are significantly broader. The two main peaks have similar intensity, as expected, according to the molecular stoichiometry, and the binding energies are 397.8 and 398.3 eV (shake-up at 399.3 eV, details in Table S2†). The former component is close to the iminic peak of other tetra pyridyl porphyrins, and is located in between 2HTPyP (397.4 eV)9 and FeTPyP, CoTPyP (398.5, 398.8 eV).16 The latter peak has 0.5 eV higher BE, analogously to FeTPyP and CoTPyP pyridinic features. We thus reasonably conclude with the assignment of iminic nitrogen at 397.8 eV, pyridinic at 398.3 eV and a shake-up at 399.3 eV. C 1s core levels measured on bare Gr, after the growth of the MnTPyP monolayer and the addition of peripheral Co are all reported in Fig. S2† for completeness. The BE and shape of the Gr peak are barely affected by the growth of the weakly interacting molecular layer, as in the case of FePc on the same substrate,21 while the peak intensity drops due to the screening of the molecular adlayer. New carbon peaks associated with the macrocycle and substituent groups grow at higher binding energies, extending up to ∼285.6 eV, and a small shoulder emerges at ∼283.6 eV, similarly to CoTPyP/Gr/Ir(111).13 NEXAFS data are reported in Fig. 2(e and f) and in Fig. S3† for a direct comparison with the XPS data, respectively. In the N K-edge spectra (Fig. 2f) taken in p-pol, we can identify four sharp resonances at 398.5 (A1), 400.4 (B), 401.5 (C), 402.5 eV (D) and a broader one at higher photon energy, namely at 406.3 eV (E). In s-pol instead, there are only two sharp peaks at 398.5 and 402.5 eV, while only a very residual intensity is present at the energy position where peak B and C develop in p-pol. We can propose a peak assignment by comparing our spectra to data collected for similar systems (i.e. metal-containing porphyrins, phthalocyanines and pyridine). B and C resonances originate from the π* orbitals of the iminic N of the macrocycle.72,73 Based on their dichroism (that is, the intensity difference between the spectra taken in p- and s-pol), we can infer the bonding direction since maximum signal intensity is expected when the impinging electric field polarization is aligned with the specific orbital involved in the excited electronic transition. We can then conclude that the macrocycle is almost flat-lying on the surface and no strong saddling is present. Resonance D is attributed to pyridinic N,74 and appears in both polarizations indicating that the pyridyl moieties are tilted with respect to the surface. A broad resonance (E) is assigned to the iminic N 1s → σ* transition.73 The origin and dichroism of peak A1 are instead less straightforward because two distinct orbitals from the macrocycle with well-defined symmetry contribute with intensity at the same energy position: one lays in the surface plane and the other out of plane.73,75,76 Similarly, in the CoTPP case this feature is partly assigned to a transition into an unoccupied orbital, which is an antibonding combination of a σ-type orbital mainly located on the four N atoms of the porphyrin core and a dx2–y2 orbital on Co.73 In addition, a peak originating from the pyridyl groups is also expected at the same energy.16,74 Therefore, the dichroism of this resonance cannot be used for structural determination (i.e. to infer the saddling angle). The Mn L-edge (Fig. 2e, bottom) exhibits a strong dichroism, originating from the metal coordination within the macrocycle. In the spectra measured with p-polarized light, three peaks of decreasing intensity are observed at 638.1, 638.8, and 639.7 eV, labelled with A-C. In contrast, the s-polarized spectra display two main resonances at 638.1 (A) and 639.9 eV (C1), with the latter being the most intense. This pronounced multiplet structure originates from the effects of the covalent metal–ligand interaction on the unoccupied d-orbitals.77,78 Similar spectra have been observed for Mn porphyrins and phthalocyanines adsorbed at surfaces.77,79,80 According to our calculations, Mn is in a + 2 oxidation state, and its ground state, in 4Eg symmetry, consists of dxy1, dx2–y21, dyz1, dxz1 and dz21 orbitals with a total spin S = 5/2 (Table S4†), consistent with previous observations for MnTPP.81 Therefore, we anticipate an equal contribution from both the in- (dxy1, dx2–y21, dyz1, dxz1) and out-of-plane (dyz1, dxz1, dz21) unoccupied orbitals to the transitions from the 2p-states. Our data support this scenario.

Fig. 2 Core level (a–c) and absorption (d–f) spectra of pristine MnTPyP (magenta) and MnTPyP–Co (blue) monolayers in UHV. Cobalt coordination results in strong modifications both in the XPS and NEXAFS profiles. XPS photon energies: (a and b) 1000 eV, (c) 514 eV. Filled and empty markers in the absorption spectra correspond to s and p polarizations, respectively. The non-equivalent N species are highlighted in the molecular scheme in (d) with colors corresponding to the N 1s deconvolution profiles in (c).

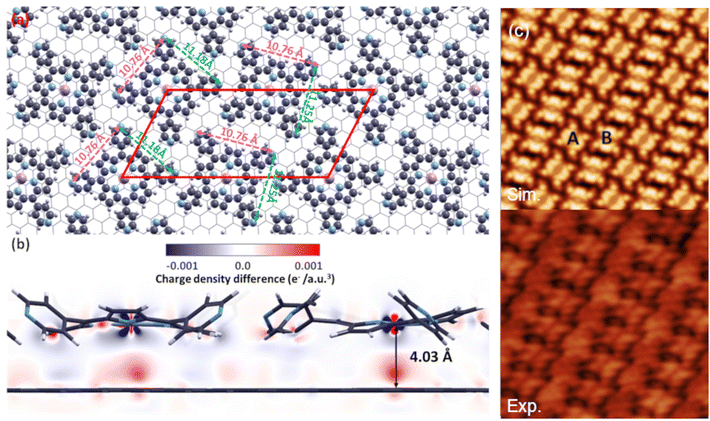
A molecular structure model of a single MnTPyP is displayed in Fig. 3(a–c). The free molecule (panel a) presents multiple degrees of freedom, making the preliminary computational characterization of the MnTPyP with the lowest energy conformers a crucial step for further exploration and understanding of the molecule-support interaction. To describe such typical conformations observed in the porphyrin macrocycle we use two different angles, namely, θ and ψ, representing pyridinic and pyrrole distortions, respectively, with reference to the molecular plane as depicted in Fig. 3(a and b). The optimized free-standing MnTPyP macrocycle adopts the common saddle shape geometry, with two opposite pyrrole rings bending upwards and the N atom pointing up, while the other two pyrrole rings bow downwards, with N pointing down. Similar stable geometries were also found in the case of other metalloporphyrins functionalized with pyridyl and phenol groups.^43,82–84 In the present case, two distorted opposite pyrrole rings deviate from the planar configuration by ψ = 12°/11° (upward/downward). The steric interaction between hydrogen atoms of the pyrrole and pyridyl moieties forces the latter to be rotated alternatively clock- and anticlock-wise by an average dihedral angle θ = 59°, similarly to the recently observed case of the FeTPyP molecule.⁸⁴ To quantify the effects of molecule-substrate and intermolecular interactions on both energy and geometrical conformation in the self-assembled networks (MnTPyP and MnTPyP–Co) on Gr, we first examined the case of a single MnTPyP molecule on the free Gr sheet as reported in Fig. 3(c and e). We compared the adsorption of a single molecule of MnTPyP with Mn sitting at the top, bridge, and hollow sites of the Gr sheet at a best height of 3 Å. We find that, within the computational error bar, the adsorption energy of the MnTPyP macrocycle remains similar for all sampled sites (1.843, 1.844, and 1.825 eV, respectively), suggesting a prevailing contribution from van der Waals with respect to covalent forces. Upon MnTPyP adsorption on Gr, the pyridyl residues accommodate on the substrate, with θ decreasing from 59° to 50°, in agreement with similar systems.^85,86 In general, a stronger interaction between the molecule and the substrate (e.g. for a metallic surface) results in a nearly flattened molecular conformation with a reduced inclination of the pyridyl ring (less than 30°) as observed in the case of Au(111) and Cu(111).^85,86 This distortion of the pyridyl ring yields steric repulsion, which further forces the pyrrole ring of the macrocycle to move upward/downward with ψ = 18/19°. The weak physisorption of MnTPyP on Gr is instead accompanied by a large molecule-substrate distance and by a weak charge density redistribution as depicted in Fig. 3(e). Bader charge analysis suggests an almost negligible charge transfer of 0.195e⁻ from each MnTPyP molecule to Gr, which is clear from the preserved Dirac point position in the projected density of states of Gr of the combined system in Fig. 3(d). A distance of 2.5–2.6 Å, close to twice the van der Waals radius of a hydrogen atom (2.4 Å), is observed between the lowest hydrogen atom of the pyridyl group and the Gr's C atoms, further supporting the prevailing van der Waals interaction type.

Fig. 3 (a and b) Structural skeleton of the free MnTPyP molecule including Mn (pink), N (sky blue), C (dark gray) and H (light gray) atoms, describing the conformation flexibility of the macrocycle from (a) top and (b) side views. The gray plane in (b) represents the plane passing through the central Mn atom; (c) optimized structural model of the MnTPyP molecule adsorbed on Gr; (d) DFT computed projected density of states of C 2p of Gr of MnTPyP/Gr; (e) optimized DFT model (ball-and-stick rendering for the top view and sticks only for the two side views), taken in two different directions showcasing the saddle shape of the molecule, with the calculated electron density rearrangement due to the interaction of the molecule with Gr plotted on the reflection symmetry planes passing through the Mn atom and perpendicular to Gr (color code: pink, blue, light gray, and dark gray spheres represent Mn, N H, and C atoms, respectively).

Upon geometry optimization of the full MnTPyP layer on Gr (Fig. 4), the Gr surface is perfectly flattened with no significant charge redistribution between molecules and Gr as shown in Fig. 4(b). However, as a result of the competition between intermolecular and molecule-substrate interactions, a geometrical reorganization takes place, inducing a re-orientation as shown in Fig. 4(a), yielding an oblique lattice pattern. The flexible nature of the molecule makes it easy to adapt to the environment by changing θ and ψ values. In this case, we can see that the four-fold symmetry of the MnTPyP macrocycle is broken, in favor of a two-fold symmetry with different lateral elongations along the two now inequivalent directions (10.76 and 11.18/11.25 Å, pink and green dashed arrows in Fig. 4(a)), in agreement with the experimental findings. This reflects in the formation of A (B) molecular rows with the long (short) side of the tectons⁸⁷ parallel to each other, respectively rotated by about 60°. STM images simulated using DFT within the Tersoff–Hamann approach are in excellent agreement with the experimental evidence (panel (c) of Fig. 4). In the latter case, the intramolecular resolution is selectively different for the two orientations, compatibly with a similar observation reported for MnTPyP/Cu(111).⁸⁵ The calculated adsorption energy of a MnTPyP molecule embedded in a full monolayer on Gr is 1.63 eV, about 200 meV smaller than for the isolated MnTPyP/Gr molecule, associated with an increased molecule-Gr distance (4.03 Å) and a slightly lower charge transfer (0.113e⁻) from each molecule to the substrate.

Fig. 4 (a) Top view of the optimized structure of the monometallic MnTPyP layer; (b) side view of and charge density difference distribution calculated at 0.001e- isovalue along the plane passing through the Mn atoms and perpendicular to Gr; (c) experimental (bottom) and DFT (top) simulated STM images, the latter being calculated at constant height 2.2 Å above the Mn atom of the MnTPyP layer (color code: pink, blue, light gray, and dark gray spheres represent Mn, N H, and C atoms, respectively) (gray spheres represent Mn, N H, and C atoms, respectively).

Cobalt coordination

Upon addition of the Co ad-atoms, evidence for peripheral coordination is straightforward from the STM imaging. The layer undergoes a geometric re-arrangement to an almost-square superstructure, where each Co ad-atom coordinates four adjacent MnTPyPs through the nitrogen termination of the pyridinic moieties. Fig. 5 reports a Co : MnTPyP < 1 average cobalt concentration case. This was chosen to yield co-existing phases with different local Co coverage that could be locally observed by STM, at variance with the spectroscopy investigations, showing that Co coordination starts with the formation of a local (2 × 2) square reconstruction (panel c, white cell, local Co : MnTPyP = 0.25). The unit cell contains thus a single Co atom, situated at the center of the bright four-leaf clovers visible in the image, and four equivalent porphyrins, each of them having a single pyridyl residue coordinated to Co. Some regions (best evident in panel c) display a locally higher Co coverage (Co : MnTPyP = 0.50), where rows of adjacent squares begin to form, saturating the available coordination sites between adjacent molecules, having now two of their pyridyl residues linked to Co. When each porphyrin is surrounded by four Co atoms, reaching a local Co : MnTPyP = 1 coverage ratio, the structure converges towards a (1 × 1) unit cell (green square in panel c and corresponding model in the inset, showing the optimized best geometry obtained by the calculations). Our observations are well consistent with the arrangement reported for the similar CoTPyP–Co layer,⁴³ as well as more generally expected (also theoretically) for free-standing M₁TPyP-M₂ networks with M_1,2 = Fe, Co, Cu, Zn.^{9,11,15,16,43,84,88}

Fig. 5 (a–c) STM images of the MnTPyP–Co/Gr/Ir(111) layer collected at LN₂ temperature, evidencing the coordination structures corresponding to different local Co coverage values. The quasi-square unit cells formed upon Co coordination are depicted in (c), connecting four Co atoms in a (2 × 2) coordination symmetry (Co/MnTPyP ratio 0.25, white), and a single MnTPyP coordinated to four Co atoms in a (1 × 1) coordination symmetry (Co/MnTPyP ratio 0.25, green), as depicted in the best model (inset) obtained from the DFT calculations. [(a) V = 2.20 V, I = 120 pA; (b) V = 1.85 V, I = 200 pA; (c) V = 2.20 V, I = 90 pA].

The experimental characterization of the electronic structure of the MnTPyP–Co layer can be challenging, especially the study of the Mn and Co core levels, due to the very low absolute surface concentration of the species, of the order of 1% of ML when normalized to the Ir surface and to the Gr sheet unit cells. It is due to the synchrotron brightness and the efficiency of the electron energy analyzer that such a small amount of Co can be reliably detected at levels allowing adequate analysis of the spectral components and peak fitting. In addition, when the Co : MnTPyP ratio is below the 1 : 1 stoichiometry, the electronic signal originates from different coexisting coordination phases that are associated with the effective local Co density, complicating all the XPS, UPS, ARPES, and NEXAFS interpretation due to the presence of inequivalent species and several geometrical arrangements. On the other hand, excess cobalt deposition would lead to the nucleation of Co clusters at the residual bare Gr islands.¹⁵ This is associated to the kinetic hindrance emerging from both Co diffusion into the MnTPyP islands and from the induced geometric rearrangement of the layer. Thus, to this purpose, we chose to keep the Co coverage close to, but lower than, the 1 : 1 stoichiometry. As already anticipated in the case of the pristine MnTPyP layer, the complex multi-peak structure of the Mn and Co 2p_3/2 core level spectra in Fig. 2 is due to multiplet splitting,^61,89,90 and shake-up contributions. Multiplet splitting arises from the interaction of a core hole with unpaired valence band electrons.⁸⁹ This effect is especially remarkable for Mn(II), Mn(III), Mn(IV) and non-metallic Co, giving rise to complex spectra with many overlapping components that are usually extremely challenging, if not impossible, to resolve experimentally.^62,66Fig. 2(a) shows the Co 2p_3/2 spectrum, where four components associated with multiplet splitting and a shake-up contribution can be distinguished, as in the respective Mn spectrum in panel (b). The interaction of the Co single ad-atoms with the pyridyl moieties results in a change of the oxidation state of Co (Table S3†), which neither remains elemental Co(0), nor becomes Co(II) as in metalated porphyrin centers, despite the similar tetra-coordination site. In general, cobalt-based MOFs, depending on the interaction with the substrate, on the specific molecular cage, and on the specific coordination environment, can tune the Co atoms to multiple oxidation states as Co(I),^15,17,91 Co(II),^{15–17,91–93} and Co(III).^15,94 Remarkably, nature can do better, where cobalamin (vitamin B12), exploiting the ligands scission and coordination at both the cis- and trans-sites, is able to tune Co throughout the +1 to the +3 oxidation states range.^15,95 In our case, the best fit of the Co 2p_3/2 core level was obtained with four Voigt peaks sharing a common Lorentzian width (0.15 eV) for the adiabatic components, and progressively broader Gaussian width values for increasing binding energy, as already observed in the case Mn 2p_3/2. The main peaks positions are 778.5, 780.0 and 781.6 eV, with the satellite at 784.7 eV. The most common case in Co-porphyrins is Co(II), but it can be reduced to Co(I) when the metal substrate is strongly interacting like Ag(111)¹⁷ or Cu(100),⁹¹ and can be stabilized as Co(III) in corroles.⁹⁴ Experimentally, the correct attribution of an oxidation state from the XPS data is not trivial due to the simultaneous influence of charge transfer mechanisms that can reduce the metal center, and due to final state effects including multiplet splitting and the possible presence of a Gunnarson–Schönhammer component.^96,97 The latter feature arises from the transfer of a screening charge from valence states of the substrate to an unoccupied molecular orbital that has been attracted below the Fermi level by the core hole.⁹³ Such contribution has been already observed in the literature.^15,16,92,93 Moreover, it is not always straightforward to discriminate the contribution of the actual metal reduction just from the Gunnarsson–Schönhammer (GS) contribution, as pointed out by Lukasczyk et al.⁹³ Nevertheless, a comparison with the cited examples reveals that the Co(I) oxidation state is the most compatible with our XPS data. The observed line positions and relative intensities are indeed comparable with the spectral features of a monolayer CoTPP/Ag(111), with a maximum at 778.2 eV, where the transfer of negative charge from the substrate partially reduces the central metal atom, at variance with the multilayer case where the Co(II) state is preserved due to the suppression of this process associated with the role of the surface.¹⁷ In addition, a very detailed study on the similar CoTPyP–Co MOF revealed that the additional Co, bound to the pyridinic nitrogen, is Co(I) also in that case.¹⁵ The main Co(I) contribution to the Co 2p_3/2 spectrum in the CoTPyP–Co system is centered at 778.6 eV, similarly to our case, with a lineshape that is coverage-dependent due to the coexisting nonequivalent coordination geometries.¹⁵ Finally, the NEXAFS spectra at the Co L₃-edge further support our assignment, in agreement with the CoTPP/Cu(100) case.⁹¹

The pyridinic nitrogen peak in the N 1s spectrum is expected to shift upon Co coordination. Surprisingly, the spectrum of Fig. 2(c) shows dramatic shifts to higher binding energies: the pyridinic and iminic peaks exhibit shifts of +1.7 eV and +0.9 eV, respectively, while the shake-up is shifted by as much as +2.0 eV. This spectroscopic evolution is accompanied by a general Gaussian broadening, accounting for the different possible coordination structures observed in STM, depending on the effective local Co coverage. The N 1s chemical shifts are significantly larger compared to the ones observed after atomic iron coordination in FeTPyP–Fe and CoTPyP–Fe frameworks.¹⁶ The close-to 1 eV change of the iminic component is particularly unprecedented. Such variation in the core level structure indicates that not only the local structure surrounding the Co site is affected by its coordination, but also the overall electronic structure of the MOF is modified, including the molecular macrocycle, analogously to the FeTPyP–Fe case.¹⁶ Further evidence of the electronic reorganization is given by the influence of Co coordination on the Mn 2p_3/2 core level (Fig. 2(b)), reflecting the cooperativity between the metal centers mediated by the organic backbone. The chemical shift of the iminic nitrogen core level can be attributed to the progressive, slight manganese oxidation upon coordination of the molecules and formation of the network, corresponding to an almost rigid shift of the whole Mn spectrum by about +500 meV. The best fit is again obtained with four components, with unaffected lineshape, at 641.0, 642.3, 643.8 and 647.3 eV that are now moving in the direction of the spectral features of a Mn(III) species,^61,62,66 as reported in Table S1.† A full +3 oxidation state is rather unusual in the metal core of a porphyrin, with a few recent examples for Co(III)TPyP–Co,¹⁵ and for corroles,^94,98 while it is instead commonly achieved in metal-porphyrins by ligation of a chlorine adduct to stabilize the molecules.^{16,23–26,99} NEXAFS (Fig. 2(e and f)) supports the picture of a hybrid +2/+3 state, with the Mn L₃-edge undergoing mild evolution with Co coordination (Fig. 2e, top), and with a small XMCD signal (Fig. S3†). More specifically, the relative intensity for the peak A decreases for the s-polarized light, while the relative intensity for the peak B increases in the spectrum measured with p-polarized light. This change in the intensity ratios is attributed to a redistribution of the holes within the related orbitals,⁷⁸ which aligns with our DFT results (Table S4†). We observe no significant shift in the energy position of the absorption resonances upon coordination of Co. This, together with the almost unchanged multiplet structure,⁷⁸ confirms that the oxidation state of the Mn is not switched upon Co coordination. The dichroism at the Mn L₃-edge is also preserved, proving Mn remains within the macrocycle and no trans-metalation occurs.¹⁰⁰ In comparison to the self-assembled MnTPyP monolayer, some changes in the spectral lineshape can be observed also in the N K-edge NEXAFS spectra (Fig. 2f). The first resonance is now split (A₁ and A₂, at 398.6 and 399.2, respectively) and the overall dichroism slightly changes. In s-pol, peak C now exhibits a marginal intensity, while B, if present, would entirely disappear in the declining of peak A₂ in s-pol. This suggests that, upon Co coordination, the macrocycle maintains its almost flat-laying geometry and the MOF formation induces only a minor saddling. The new resonance A₂ can be assigned to the Co-coordinated pyridyl-moieties.¹⁶ Since this resonance is present in both polarizations, it is reasonable to deduce that the pyridyl-rings are still rotated with respect to the molecular plane, even though, resonance D, which is assigned to the pyridinic N as well,⁷⁴ does no longer appear in p-pol. Also in this case, the dichroism of resonance A₁ is difficult to interpret, due to the multiple contributions. A significant dichroic signal can be observed also at the Co L₃-edge (Fig. 2d), due to different orientations of the related d-orbitals. The multiplet structure originates from the crystal field splitting after Co is coordinated in the square planar geometry within the pyridinic nitrogen terminations. In p-polarized light two peaks appear at 776.7 (A) and 778 eV (B), with nearly the same intensity, though the second peak is considerably broader. In contrast, the s-polarized spectrum shows only one broad peak at 778.2 eV (B1) with a shoulder at 779.8 eV. The absence of intensity at peak A in the s-polarized spectrum suggests an origin from the transition into the d_z²-orbital, in agreement with our calculations (half-filled). Since due to our measurement geometry the p-polarized light contains also a significant s-polarization component, the broad peak around 778 eV is visible in both polarisations and is attributed to a predominantly in-plane orbital. Overall, the spectra look similar to the one reported earlier for CoTPP/Cu(100),^101,102 and can be assigned to the Co +1 oxidation state. The XMCD signal measured at the Co L-edge (Fig. S3†) also corroborates the picture of two half-filled orbitals and a high spin S = 1 spin configuration, since the low spin configuration S = 0 with a single unoccupied orbital would not contribute.

Finally, the C 1s core level spectrum (Fig. S2†) exhibits a chemical shift of the porphyrin-related shoulder by about +0.5 eV, together with a broadening: a further proof of the strong influence of Co coordination on the whole organic backbone, associated with both the geometric and electronic structure reorganization processes. At variance with what observed above for the formation of the molecular MnTPyP layer, a shift of ∼180 meV (depending on the Co coverage) of the Gr peak suggests that also the supporting sheet is affected by the coordination of the peripheral Co adatoms, participating in the charge transfer process.

We now focus on the electronic structure close to the Fermi edge (Fig. 6). The VB spectra of the MnTPyP layer on Gr, before and after the addition of Co, are reported in Fig. 6(b). Upon growth of the molecular film, two peaks appear at 1.3 eV and 0.6 eV below the Fermi level. These values are close to the energy of the HOMO and HOMO−1 (0.63 and 1.22–1.23 eV, respectively) of a multilayer MnPC/Co,⁵⁸ and of MnPc/HOPG.⁵⁹ Measured with He(I), the MnPc HOMO was much less intense than the HOMO−1, analogously to our case, while the situation was reversed for hν > 100 eV. Further support in this sense can be found in the literature,^58,59 with other cases of successful decoupling of organic MOFs from an Ir(111) substrate by a Gr sheet.^15,21 It is thus plausible to assign the two peaks observed in the MnTPyP spectrum to the HOMO and HOMO −1. The non-dispersive nature of the HOMO−1 of the MnTPyP layer can be observed in the energy–momentum photoemission intensity map reported in Fig. 6(d), where it is marked with a magenta brace. This map was obtained by a vertical cut at the frontier of the Gr Brillouin zone, crossing the K point as depicted in the schematic of panel (c). The linear dispersion of the Dirac cone of the supporting Gr sheet is well visible (see the map of the pristine Gr sheet in panel (c)). The momentum axis scale through panels (c–e) is centered at the K point. Thus, we are able to see the HOMO−1 feature around k_|| = 1.7 Å⁻¹,^103,104 in agreement with the orbital momentum distribution of ordered porphyrin layers, like CoTPyP,¹⁵ FePc,¹⁰⁴ and NiTPP.¹⁰⁵ This orbital extends between 1 and 1.7 eV, corresponding to the most intense peak in Fig. 6(a). The intense, diffuse photoemission intensity above 2 eV is instead associated to other non-resolved HOMOs (HOMO+n). Both MnTPyP features observed in Fig. 6(a and d) broaden and shift to higher binding energies by about 0.7 eV upon Co coordination Fig. 6(a and e), analogously to Co deposition on a CoTPyP monolayer.¹⁵ In that case, the CoTPyP UPS spectrum between the Fermi level and 15 eV shifts to higher binding energies upon Co addition, by ∼0.8 eV, with the appearance of a new HOMO at 1 eV, originating from a doping-induced shift across the Fermi level of an empty state.¹⁵ This is not the case for the MnTPyP–Co system, instead. The work function (WF) decreases by about ∼0.1 eV upon deposition on Gr of the molecular layer (Fig. 6(b), black and red profiles), which is a relatively small value compared to the reported case of FePc/Gr/Ir/(111) that led to a 0.25 eV WF increase,²¹ or a 0.8 eV WF decrease induced by NiTPP/Cu(100),¹⁰⁵ or for other similar cases due to a variation of the interfacial dipole.¹⁰⁶ A remarkable WF reduction by 0.8 eV (the difference is lower in the case of smaller Co loading) is achieved instead upon Co coordination (blue curve), a surprisingly high value when considering the small amount of added Co (∼1% ML compared to the Ir(111) substrate).

Fig. 6 (a) Valence band spectra of 1 ML MnTPyP and MnTPyP–Co after subtraction of the graphene background. Both spectra show two peaks associated to the molecules, shifting by about +0.7 eV upon Co addition; (b) work function profiles and values for clean Ir(111), Gr/Ir(111), 1 ML MnTPyP/Gr/Ir(111) and MnTPyP–Co/Gr/Ir(111) obtained from the secondary electron onset: deposition of 1 ML MnTPyP reduces the work function by only ∼50 meV, while after Co addition (∼1% ML referring to the substrate) it is reduced by as much as 0.8 eV; (c–e) energy–momentum maps corresponding to the cut centered at the graphene K point schematized in the picture inset: from left to right, Dirac cone section of the bare graphene sheet (c) before, (d) after the growth of the MnTPyP monolayer and (e) upon deposition of the Co ad-atoms, where the non-dispersive HOMO−1 is indicated by the brackets.

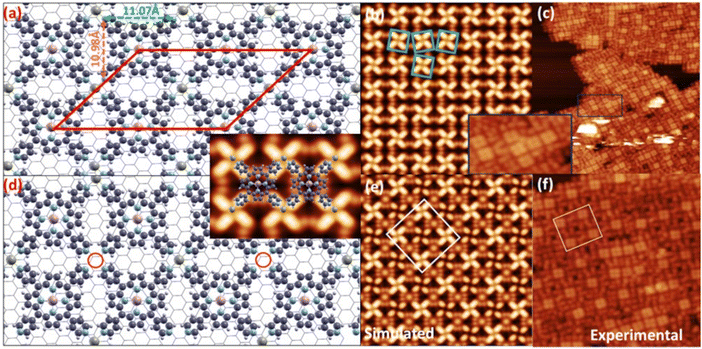
Our DFT simulations confirm that coordination of the peripheral Co ad-atoms drives a major rearrangement of the MnTPyP layer towards a close-to-square symmetry lattice (Fig. 7(a and d), displaying Co : MnTPyP coverage ratios of 1 and 0.5, respectively), with an average Co–N bond length equal to 2.26 Å, larger than 2.2 and 1.9 Å, which correspond to +2 and +3 oxidation states, respectively, thus confirming a + 1 oxidation state for Co in the present case (d⁸s⁰ configuration). The oxidation state of transition metal atoms was estimated using the technique reported in the literature.¹⁰⁷ The orbital occupation values are reported in Table S4.† The situation is less clear-cut for Mn. For a single MnTPyP molecule on Gr, Mn is definitely in a Mn(II) state (d⁵s⁰). In the MnTPyP/Gr layer, one of the two inequivalent Mn atoms appears to be closer to a Mn(III) state (d⁴s⁰), while the other one remains in a Mn(II) state. With 50% saturation of Co, both Mn atoms have the same configuration, somewhat intermediate between Mn(II) and Mn(III). Finally, at full Co saturation, the Mn atoms revert to Mn(II). The DFT results are thus consistent with a shift of the Mn oxidation state, especially at low Co concentration, confirming that a pure Mn(III) state is not achieved, again in agreement with spectroscopy. Concerning the geometrical configuration, upon addition of Co, the self-assembly of the MnTPyP–Co layer is accompanied by the recovery of the pristine molecular symmetry, as the N_py–N_py (pyridyl nitrogen belonging to the same MnTPyP) distance decreases (increases) to 11.07 Å (10.98 Å) from 11.20 Å (10.76 Å). To accommodate the Co atom at the peripheral N sites, the pyridyl moieties are forced to deviate clock-/anticlock-wise, with a subtle change of the dihedral angle (from 50° to 52°). Such conformational changes reflect a small, further increase of the MnTPyP–Co distance from the Gr sheet (from ≃4.03 to ≃4.15 Å). Despite the marginal increase in molecule-substrate distance of ∼3%, the increase in the interaction strength is more pronounced when compared to the monometallic case. The adsorption energy per molecular layer unit upon Co saturation (one MnTPyP and one peripheral Co) raises to 1.997 eV, associated with a net charge transfer of 0.9e⁻ from the molecule to Gr (Fig. 8). In the experimental and simulated STM images shown Fig. 5 and 7(b, c, e and f), the progressive evolution of the MnTPyP–Co layer as a function of the local Co coverage is evident, with the best structural models corresponding to the two situations (Co : MnTPyP ratio 0.5 and 1) depicted in panels (a) and (d) of Fig. 7, respectively. Each bright region in the experimental images is associated to the four bright lobes of the adjacent pyridyl residues coordinated by a single Co ad-atom. The dark spots (panel f) with spiral-like surrounding features correspond instead to a single Co vacancy (red circle in panel d). The central (Mn) and the peripheral (Co) single metal atoms appear different. In order to rule out the possibility that CoTPyP–Mn is formed via a trans-metalation process occurring upon Co deposition, DFT simulations of the CoTPyP–Mn system have also been performed. The total energy of a MnTPyP–Co layer is found to be lower than that of a CoTPyP–Mn layer, by as much as 0.857 eV per molecule, effectively ruling out the formation of a trans-metalated CoTPyP–Mn layer.

Fig. 7 Optimized structure of the bimetallic MnTPyP–Co layer at full (a) and half (d) Co coverage (top views); the red cell in (a) depicts the oblique simulation unit cell; the inset shows a visual representation of the bright and dark regions in the simulated STM images, corresponding to the MnTPyP–Co structure; (b and c) and (e and f) panels plot the (simulated, experimental) STM images corresponding to models in (a) and (d), respectively; the inset shows here the zoom of the region highlighted by the rectangle in (c) (color codes: olive green, pink, blue, light gray, and dark gray spheres represent Co, Mn, N, H, and C atoms, respectively).

Fig. 8 (a) DFT calculated projected density of states C 2p of Gr in mono- and bi-metallic systems; (b) side view of the charge density difference distribution (0.001e- isovalue) along the plane passing through the Co atoms and perpendicular to the plane of the Gr sheet, taken along the shorter unit cell lattice.

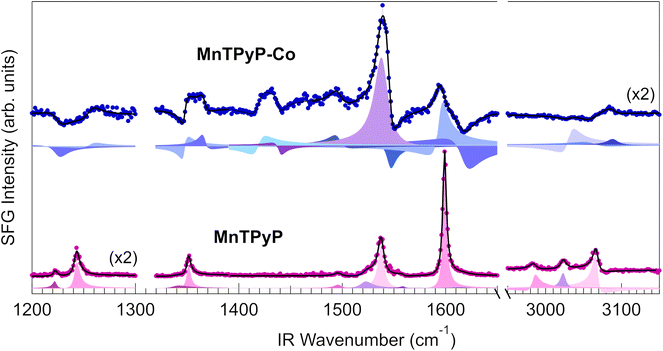
The vibrational fingerprints of the MnTPyP and MnTPyP–Co layers were investigated by means of IR-Vis SFG spectroscopy. Here we show the vibrational profile of the as-prepared mono- and bi-metallic organic frameworks and associate the observed resonances to specific modes. It is found that the dramatic structural and electronic evolution of the MOF upon peripheral cobalt coordination described so far largely affects also the vibronic resonances of the layer. The spectra of the pure molecular layer and of the MOF acquired in the 1200–1650 cm⁻¹ and 2950–3150 cm⁻¹ ranges in ppp polarization are shown in Fig. 9, with the best fit and the deconvolution profiles associated to each resonance, obtained according to the procedure detailed in the Methods section. The resonant line positions are listed in Table S5,† with the assignments based on the study of similar molecules like FeTPyP,^108–110 CoTPyP,^15,111 ZnTPyP,¹¹² 2HTPyP,¹¹³ and MnTPPCl.²⁴ The modes are labelled according to standard literature notation.^108,109,113 Starting from the pristine MnTPyP layer, two distinct resonances are visible at 1222 and 1243 cm⁻¹, associated to pyridinic modes related with the deformation of the external rings and to the stretch of the ring-macrocycle bonds.^{108,109,111–113} While the lowest energy peak attribution is unambiguous, the other resonance could in principle also derive from other macrocycle modes that overlap in this same energy window.^24,109,111 The multiple features in the 1300–1570 cm⁻¹ range are macrocycle bending and stretching signatures, with the exception of the peak at 1522 cm⁻¹ that could be also related to a deformation of the substituent groups, as observed by Blom et al. for FeTPyP and CoTPyP.¹⁰⁹ The sharp, intense peak at 1599 cm⁻¹ is characteristic of M-TPyPs and is recognized as a bending or stretching movement of the external rings.^{108,109,111,112} The Gr phonon mode (Fig. S2†) can still be observed as a faint shoulder on the right of the pyridinic resonance, slightly blue shifted at 1618 cm⁻¹, but its contribution is almost negligible after the molecules deposition, making the precise determination of its position quite challenging. Finally, three intense C–H stretching modes are visible in the 2950–3150 cm⁻¹ spectral range, due to the deformation and rotation of the pyridinic moieties that allow a significant out-of-plane dipolar component. The presence of multiple C–H resonances is associated with the breaking of the degeneracy of formerly equivalent CH bonds due to the steric interaction with both adjacent molecules and the supporting Gr sheet. It is interesting to notice that the non-resonant background amplitude is nearly zero in the MnTPyP spectrum, explaining why all the peaks appear as positive and only slightly asymmetric Lorentzian resonances, with negligible dispersive lineshape contributions due to phase interference effects. The evident increase in non-resonant contribution upon cobalt evaporation, with a non-resonant amplitude about 6 times larger, is connected to the electronic structure changes discussed above. The same effect was observed in the case of a CoTPyP–Co framework, where the increased non-resonant intensity was associated to a reduction of the HOMO–LUMO gap after Co coordination revealed by STS and DFT,¹⁵ introducing new electronic excitation channels and thus enhancing the SFG signal, closer to doubly-resonant SFG transitions.^114,115 The interference between non-resonant and resonant signals results in complex spectral profiles, showing maxima, minima and dispersive lineshapes. Thus, the observed resonances are affected by these striking changes. A general broadening of the resonant peaks is also observed, and is associated with the presence of nonequivalent bonding configurations, as discussed above. The low-energy resonances are blue-shifted by 4–16 cm⁻¹ and two additional peaks associated to macrocycle modes grow in the 1410–1440 cm⁻¹ range. The intense peak at 1539 cm⁻¹ and the double resonance at 1595–1617 cm⁻¹ are related to the pyridinic groups and can be exploited in principle as indirect fingerprints of Co coordination and of ligation at those sites, especially during chemical reactivity experiments. Finally, three resonances can be resolved in the C–H stretching range (2950–3150 cm⁻¹), at about ∼30–50 cm⁻¹ higher wavenumbers than the MnTPyP case.

Fig. 9 SFG spectra, best fit and deconvolution of 0.7 ML MnTPyP (bottom) and MnTPyP–Co on Gr/Ir(111) at about half Co saturation (top). The low-energy resonances are associated to pyridinic modes, the range 1320–1550 cm⁻¹ exhibits prevalently macrocycle modes and the most intense pyridinic modes are observed at 1500–1650 cm⁻¹. The peaks at higher wavenumbers (2900–3200 cm⁻¹) originate from the C–H stretching modes. Addition of the peripheral Co ad-atoms strongly affects the spectra, showing an increase of the non-resonant signal, energy shifts and phase rotations.

Conclusions

In this paper, we demonstrate that a surface-confined metal–organic network self-assembled on a weakly-interacting graphene sheet can display metal centers with tunable electronic structure, analyzed with a combined computational and experimental multi-technique approach. The coordination of Co metal ad-atoms at the peripheral residues of tetra-pyridyl-porphyrins induces the reorganization of both geometric and electronic structures, accompanied by a finer tuning of the tetrapyrrolic Mn metal sites. We found the Co coordinated by the pyridinic end-groups in a + 1 oxidation state, while the Mn changed from a pure +2 oxidation state to a mixed +2/+3 oxidation state upon coordination. Furthermore, in both the pure molecular and the network layers, the unit cells host two molecules. In the case of the network layer, the large unit cell corresponds to the alternating rotation of the end-groups, lowering the four-fold symmetry to two-fold. This is also the case for the pure molecular layer but a further rotation of two neighboring molecules around an angle of 60° to each other is visible. Within this picture, as for the CoTPyP–Co system,^15,43 we show that also in the MnTPyP–Co case the lateral interactions initially predicted by the theoretical work by Mandal et al.¹⁰ play a dominant role in determining the actual electronic and magnetic configuration of the single metal atom sites of the network. In addition, the role of the support (graphene) is not negligible since it affects geometry, by steering the realignment of the pyridyl moieties, and mediates the interaction among the sites. Despite the formally weak interaction between the metalorganic layer and graphene, indeed, the system has to be considered as a whole.

Author contributions

E. V. conceived and designed the project. S. B., M. D. C., D. B., G. Z., O. R., A. N., V. M. and N. V. conducted the experiments. M. C. and G. Z. supervised the k-resolved measurements. Pi. G., V. M. and M. S. provided fundamental assistance at the beamline. A. Y., B. R. and Pa. G performed the theoretical calculations. S. B. and E. V. discussed all results and edited the manuscript. All authors have reviewed and contributed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data for this article, including raw microscopy metadata, are available at the OSF Home repository at https://osf.io/jb2xt/?view_only=212808d5164546849474a96b28d54dcd.

Acknowledgements

This work was funded by Unione Europea – Next Generation EU through projects PRIN2022 XXJNRS 2DOrNotToBe CUP J53D23001510006 and Next Generation EU, Missione 4 Componente 1 CUP J53D23016180001 PRIN PNRR P2022B3WCB 2Dgo3D. We acknowledge MAX IV Laboratory for time on Beamline HIPPIE under proposals 20220031, 20220898 and 20221030, as well as access to the STM laboratory. Research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496. PG acknowledges ISCRA for access to the LEONARDO supercomputer, owned by the EuroHPC Joint Undertaking, hosted by CINECA (Italy). V. M., G. Z. and M. C. acknowledge funding from the DFG (Major Research Instrumentation Individual Proposal INST 212/409-1), and by “the Ministerium für Kultur und Wissenschaft des Landes Nordrhein-Westfalen (NRW)”. V. M. and M. C. acknowledge the support from the EC H2020 programme under grant agreement no. 965046, FET-Open project INTERFAST (Gated interfaces for fast information processing). G. Z. and M. C. acknowledge the support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project ID 513136560. For the NEXAFS and XMCD measurements we acknowledge access to the ALBA synchrotron (BOREAS BL29) under proposal 2024028422.

References

1. F. Cheng and J. Chen, Chem. Soc. Rev., 2012, 41, 2172–2192.
2. X. Chen, Z. Zhou, H. E. Karahan, Q. Shao, L. Wei and Y. Chen, Small, 2018, 14, 1801929.
3. B. Zhu, Z. Liang, D. Xia and R. Zou, Energy Storage Mater., 2019, 23, 757–771.
4. J. Fu, Z. P. Cano, M. G. Park, A. Yu, M. Fowler and Z. Chen, Adv. Mater., 2016, 29(7), 1604685.
5. D. Zhao, Z. Zhuang, X. Cao, C. Zhang, Q. Peng, C. Chen and Y. Li, Chem. Soc. Rev., 2020, 49, 2215–2264.
6. J.-S. Lee, S. Tai Kim, R. Cao, N.-S. Choi, M. Liu, K. T. Lee and J. Cho, Adv. Energy Mater., 2011, 1, 34–50.
7. E. Marini, L. Jörissen and S. Brimaud, J. Power Sources, 2021, 482, 228900.
8. I. Katsounaros, S. Cherevko, A. R. Zeradjanin and K. J. J. Mayrhofer, Angew. Chem., Int. Ed., 2014, 53, 102–121.
9. Y. Li, J. Xiao, T. E. Shubina, M. Chen, Z. Shi, M. Schmid, H. P. Steinrück, J. M. Gottfried and N. Lin, J. Am. Chem. Soc., 2012, 134, 6401–6408.
10. B. Mandal, J. S. Chung and S. G. Kang, J. Phys. Chem. C, 2018, 122, 9899–9908.
11. B. Wurster, D. Grumelli, D. Hötger, R. Gutzler and K. Kern, J. Am. Chem. Soc., 2016, 138, 3623–3626.
12. D. Hötger, M. Etzkorn, C. Morchutt, B. Wurster, J. Dreiser, S. Stepanow, D. Grumelli, R. Gutzler and K. Kern, Phys. Chem. Chem. Phys., 2019, 21, 2587–2594.
13. F. Armillotta, D. Bidoggia, S. Baronio, P. Biasin, A. Annese, M. Scardamaglia, S. Zhu, B. Bozzini, S. Modesti, M. Peressi and E. Vesselli, ACS Catal., 2022, 7950–7959.
14. F. Armillotta, A. Sala and E. Vesselli, J. Phys. Chem. C, 2024, 128(37), 15613–15623.
15. F. Armillotta, D. Bidoggia, S. Baronio, A. Sala, R. Costantini, M. dell'Angela, I. Cojocariu, V. Feyer, A. Morgante, M. Peressi and E. Vesselli, Adv. Funct. Mater., 2024, 34, 2408200.
16. F. Armillotta, D. Bidoggia, P. Biasin, A. Annese, A. Cossaro, A. Verdini, L. Floreano, M. Peressi and E. Vesselli, Cell Rep. Phys. Sci., 2023, 4, 101378.
17. W. Hieringer, K. Flechtner, A. Kretschmann, K. Seufert, W. Auwärter, J. V. Barth, A. Görling, H. P. Steinrück and J. M. Gottfried, J. Am. Chem. Soc., 2011, 133, 6206–6222.
18. I. Pletikosić, M. Kralj, P. Pervan, R. Brako, J. Coraux, A. T. N'Diaye, C. Busse and T. Michely, Phys. Rev. Lett., 2009, 102, 056808.
19. A. A. Taleb, G. Anemone, D. Farías and R. Miranda, Carbon, 2018, 133, 31–38.
20. M. Endlich, H. P. C. Miranda, A. Molina-Sánchez, L. Wirtz and J. Kröger, Ann. Phys., 2014, 526, 372–380.
21. M. Scardamaglia, S. Lisi, S. Lizzit, A. Baraldi, R. Larciprete, C. Mariani and M. G. Betti, J. Phys. Chem. C, 2013, 117, 3019–3027.
22. L. Liao, H. Peng and Z. Liu, J. Am. Chem. Soc., 2014, 136, 12194–12200.
23. J. P. Beggan, S. A. Krasnikov, N. N. Sergeeva, M. O. Senge and A. A. Cafolla, Nanotechnology, 2012, 23, 235606.
24. S. R. Alharbi, A. A. A. Darwish, S. E. A. Garni, H. I. ElSaeedy and K. F. A. El-Rahman, Infrared Phys. Technol., 2016, 78, 77–83.
25. A. A. Attia, A. M. A. El-Barry, E. A. A. El-Shazly and L. M. D. El-Deen, J. Lumin., 2018, 199, 391–399.
26. B. E. Murphy, S. A. Krasnikov, N. N. Sergeeva, A. A. Cafolla, A. B. Preobrajenski, A. N. Chaika, O. Lübben and I. V. Shvets, ACS Nano, 2014, 8, 5190–5198.
27. G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1212.
28. S. Zhu, M. Scardamaglia, J. Kundsen, R. Sankari, H. Tarawneh, R. Temperton, L. Pickworth, F. Cavalca, C. Wang, H. Tissot, J. Weissenrieder, B. Hagman, J. Gustafson, S. Kaya, F. Lindgren, I. Källquist, J. Maibach, M. Hahlin, V. Boix, T. Gallo, F. Rehman, G. D'Acunto, J. Schnadt and A. Shavorskiy, J. Synchrotron Radiat., 2021, 28, 624–636.
29. M. Bianchi, D. Cassese, A. Cavallin, R. Comin, F. Orlando, L. Postregna, E. Golfetto, S. Lizzit and A. Baraldi, New J. Phys., 2009, 11, 063002.
30. S. Doniach and M. Šunjić, J. Phys. C: Solid State Phys., 1970, 3, 285–291.
31. D. M. Janas, A. Windischbacher, M. S. Arndt, M. Gutnikov, L. Sternemann, D. Gutnikov, T. Willershausen, J. E. Nitschke, K. Schiller, D. Baranowski, V. Feyer, I. Cojocariu, K. Dave, P. Puschnig, M. Stupar, S. Ponzoni, M. Cinchetti and G. Zamborlini, Inorg. Chim. Acta, 2023, 557, 121705.
32. C. S. Tian and Y. R. Shen, Surf. Sci. Rep., 2014, 69, 105–131.
33. Y. R. Shen, Nature, 1989, 337, 519–525.
34. M. Corva, Z. Feng, C. Dri, F. Salvador, P. Bertoch, G. Comelli and E. Vesselli, Phys. Chem. Chem. Phys., 2016, 18, 6763–6772.
35. M. Bonn, C. Hess, W. G. Roeterdink, H. Ueba and M. Wolf, Chem. Phys. Lett., 2004, 388, 269–273.
36. B. Busson and A. Tadjeddine, J. Phys. Chem. C, 2009, 113, 21895–21902.
37. M. Corva, F. Mohamed, E. Tomsic, M. Rinaldi, C. Cepek, N. Seriani, M. Peressi and E. Vesselli, J. Phys. Chem. C, 2019, 123, 3916–3922.
38. A. Barla, J. Nicolás, D. Cocco, S. M. Valvidares, J. Herrero-Martín, P. Gargiani, J. Moldes, C. Ruget, E. Pellegrin and S. Ferrer, J. Synchrotron Radiat., 2016, 23, 1507–1517.
39. T. J. Regan, H. Ohldag, C. Stamm, F. Nolting, J. Lüning, J. Stöhr and R. L. White, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 214422.
40. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
41. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
42. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105.
43. D. Bidoggia, F. Armillotta, A. Sala, E. Vesselli and M. Peressi, J. Phys. Chem. C, 2024, 128(4), 1737–1745.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
46. I. Timrov, N. Marzari and M. Cococcioni, Comput. Phys. Commun., 2022, 279, 108455.
47. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
48. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
49. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452.
50. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
51. J. Tersoff and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 805–813.
52. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15.
53. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
54. D. Nečas and P. Klapetek, Open Phys., 2012, 10, 181–188.
55. E. V. Basiuk, L. Huerta and V. A. Basiuk, Appl. Surf. Sci., 2019, 470, 622–630.
56. Y. Bai, F. Buchner, M. T. Wendahl, I. Kellner, A. Bayer, H. P. Steinrück, H. Marbach and J. M. Gottfried, J. Phys. Chem. C, 2008, 112, 6087–6092.
57. C. M. Doyle, J. P. Cunniffe, S. A. Krasnikov, A. B. Preobrajenski, Z. Li, N. N. Sergeeva, M. O. Senge and A. A. Cafolla, Chem. Commun., 2014, 50, 3447–3449.
58. F. Haidu, O. D. Gordan, D. R. T. Zahn, L. Smykalla, M. Hietschold, B. V. Senkovskiy, B. Mahns and M. Knupfer, arXiv,  DOI:10.48550/arXiv.1702.03575.
59. J. L. Zhang, Z. Wang, J. Q. Zhong, K. D. Yuan, Q. Shen, L. L. Xu, T. C. Niu, C. D. Gu, C. A. Wright, A. Tadich, D. Qi, H. X. Li, K. Wu, G. Q. Xu, Z. Li and W. Chen, Nano Lett., 2015, 15, 3181–3188.
60. F. Petraki, H. Peisert, F. Latteyer, U. Aygül, A. Vollmer and T. Chassé, J. Phys. Chem. C, 2011, 115, 21334–21340.
61. H. W. Nesbitt and D. Banerjee, Am. Mineral., 1998, 83, 305–315.
62. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730.
63. D. Banerjee and H. W. Nesbitt, Geochim. Cosmochim. Acta, 1999, 63, 3025–3038.
64. D. Banerjee and H. W. Nesbitt, Geochim. Cosmochim. Acta, 1999, 63, 1671–1687.
65. D. Banerjee and H. W. Nesbitt, Geochim. Cosmochim. Acta, 2001, 65, 1703–1714.
66. E. S. Ilton, J. E. Post, P. J. Heaney, F. T. Ling and S. N. Kerisit, Appl. Surf. Sci., 2016, 366, 475–485.
67. K. Diller, F. Klappenberger, M. Marschall, K. Hermann, A. Nefedov, C. Wöll and J. V. Barth, J. Chem. Phys., 2012, 136, 014705.
68. L. Schio, G. Bavdek, C. Grazioli, C. G. Bolaños, A. Goldoni, A. Vittadini, M. Tormen and L. Floreano, Appl. Surf. Sci., 2023, 616, 156548.
69. E. Annese, J. Fujii, I. Vobornik and G. Rossi, J. Phys. Chem. C, 2011, 115, 17409–17416.
70. F. Buchner, K. Flechtner, Y. Bai, E. Zillner, I. Kellner, H. P. Steinrück, H. Marbach and J. M. Gottfried, J. Phys. Chem. C, 2008, 112, 15458–15465.
71. J. Xiao, S. Ditze, M. Chen, F. Buchner, M. Stark, M. Drost, H. P. Steinrück, J. M. Gottfried and H. Marbach, J. Phys. Chem. C, 2012, 116, 12275–12282.
72. M. P. De Jong, R. Friedlein, S. L. Sorensen, G. Ãhrwall, W. Osikowicz, C. Tengsted, S. K. M. Jönsson, M. Fahlman and W. R. Salaneck, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 1–8.
73. N. Schmidt, R. Fink and W. Hieringer, J. Chem. Phys., 2010, 133(5), 054703.
74. C. Kolczewski, R. Püttner, O. Plashkevych, H. Ågren, V. Staemmler, M. Martins, G. Snell, A. S. Schlachter, M. Sant'Anna, G. Kaindl and L. G. M. Pettersson, J. Chem. Phys., 2001, 115, 6426–6437.
75. I. Cojocariu, H. M. Sturmeit, G. Zamborlini, A. Cossaro, A. Verdini, L. Floreano, E. D'Incecco, M. Stredansky, E. Vesselli, M. Jugovac, M. Cinchetti, V. Feyer and C. M. Schneider, Appl. Surf. Sci., 2020, 504, 144343.
76. J. Uihlein, H. Peisert, H. Adler, M. Glaser, M. Polek, R. Ovsyannikov, M. Bauer and T. Chassé, J. Phys. Chem. C, 2014, 118(49), 28671–28678.
77. P. Gargiani, S. Lisi, G. Avvisati, P. Mondelli, S. Fatale and M. G. Betti, J. Chem. Phys., 2017, 147, 134702.
78. F. Petraki, H. Peisert, P. Hoffmann, J. Uihlein, M. Knupfer and T. Chassé, J. Phys. Chem. C, 2012, 116, 5121–5127.
79. P. L. Cook, X. Liu, W. Yang and F. J. Himpsel, J. Chem. Phys., 2009, 131, 194701.
80. B. E. Murphy, S. A. Krasnikov, N. N. Sergeeva, A. A. Cafolla, A. B. Preobrajenski, A. N. Chaika, O. Lübben and I. V. Shvets, ACS Nano, 2014, 8, 5190–5198.
81. M.-S. Liao, J. D. Watts and M.-J. Huang, Inorg. Chem., 2005, 44, 1941–1949.
82. S. Müllegger, W. Schöfberger, M. Rashidi, L. M. Reith and R. Koch, J. Am. Chem. Soc., 2009, 131, 17740–17741.
83. Q. Zhang, G. Kuang, R. Pang, X. Shi and N. Lin, ACS Nano, 2015, 9, 12521–12528.
84. J. M. Lombardi, D. Grumelli, R. Gutzler, H. F. Busnengo and P. Abufager, J. Phys. Chem. C, 2023, 127, 6569–6577.
85. X. Chen, S. Lei, C. Lotze, C. Czekelius, B. Paulus and K. J. Franke, J. Chem. Phys., 2017, 146, 092316.
86. W. Auwärter, A. Weber-Bargioni, A. Riemann, A. Schiffrin, O. Gröning, R. Fasel and J. V. Barth, J. Chem. Phys., 2006, 124, 194708.
87. D. Su, X. Wang, M. Simard and J. D. Wuest, Supramol. Chem., 1995, 6, 171–178.
88. B. D. B. Cortés, N. Schmidt, M. Enache and M. Stöhr, J. Phys. Chem. C, 2021, 125, 24557–24567.
89. C. S. Fadley and D. A. Shirley, Phys. Rev. A, 1970, 2, 1109–1120.
90. K. Okada, A. Kotani and B. T. Thole, J. Electron Spectrosc. Relat. Phenom., 1992, 58, 325–343.
91. I. Cojocariu, S. Carlotto, G. Zamborlini, M. Jugovac, L. Schio, L. Floreano, M. Casarin, V. Feyer and C. M. Schneider, J. Mater. Chem. C, 2021, 9, 12559–12565.
92. G. Mette, D. Sutter, Y. Gurdal, S. Schnidrig, B. Probst, M. Iannuzzi, J. Hutter, R. Alberto and J. Osterwalder, Nanoscale, 2016, 8, 7958–7968.
93. T. Lukasczyk, K. Flechtner, L. R. Merte, N. Jux, F. Maier, J. M. Gottfried and H.-P. Steinrück, J. Phys. Chem. C, 2007, 111, 3090–3098.
94. J. Herritsch, M. Zugermeier, M. Schmid, M. Chen, J.-N. Luy, P. Schweyen, M. Bröring, R. Tonner-Zech and J. M. Gottfried, J. Porphyrins Phthalocyanines, 2023, 27, 670–681.
95. L. Randaccio, S. Geremia, N. Demitri and J. Wuerges, Molecules, 2010, 15, 3228–3259.
96. O. Gunnarsson and K. Schönhammer, Phys. Rev. Lett., 1978, 41, 1608–1612.
97. K. Schönhammer and O. Gunnarsson, Z. Phys. B, 1978, 30, 297–303.
98. P. S. Deimel, P. C. Aguilar, M. Paszkiewicz, D. A. Duncan, J. V. Barth, F. Klappenberger, W. Schöfberger and F. Allegretti, Chem. Commun., 2020, 56, 11219–11222.
99. A. S. Rury, L. E. Goodrich, M. G. I. Galinato, N. Lehnert and R. J. Sension, J. Phys. Chem. A, 2012, 116, 8321–8333.
100. D. Hötger, P. Abufager, C. Morchutt, P. Alexa, D. Grumelli, J. Dreiser, S. Stepanow, P. Gambardella, H. Fabio Busnengo, M. Etzkorn, R. Gutzler and K. Kern, Nanoscale, 2018, 10, 21116–21122.
101. I. Cojocariu, S. Carlotto, G. Zamborlini, M. Jugovac, L. Schio, L. Floreano, M. Casarin, V. Feyer and C. M. Schneider, J. Mater. Chem. C, 2021, 9, 12559–12565.
102. I. Cojocariu, S. Carlotto, D. Baranowski, M. Jugovac, L. Schio, L. Floreano, M. Casarin, V. Feyer and C. M. Schneider, Inorg. Chim. Acta, 2023, 556, 121657.
103. M. Heber, N. Wind, D. Kutnyakhov, F. Pressacco, T. Arion, F. Roth, W. Eberhardt and K. Rossnagel, Rev. Sci. Instrum., 2020, 15(1), 18–21.
104. M. Scardamaglia, G. Forte, S. Lizzit, A. Baraldi, P. Lacovig, R. Larciprete, C. Mariani and M. G. Betti, J. Nanopart. Res., 2011, 13, 6013–6020.
105. G. Zamborlini, D. Lüftner, Z. Feng, B. Kollmann, P. Puschnig, C. Dri, M. Panighel, G. D. Santo, A. Goldoni, G. Comelli, M. Jugovac, V. Feyer and C. M. Schneider, Nat. Commun., 2017, 8(1), 335.
106. B. de Boer, A. Hadipour, M. M. Mandoc, T. van Woudenbergh and P. W. M. Blom, Adv. Mater., 2005, 17, 621–625.
107. P. H.-L. Sit, R. Car, M. H. Cohen and A. Selloni, Inorg. Chem., 2011, 50, 10259–10267.
108. S. Popovici, W. Leyffer and R. Holze, J. Porphyrins Phthalocyanines, 1998, 02, 249–260.
109. N. Blom, J. Odo, K. Nakamoto and D. P. Strommen, J. Phys. Chem., 1986, 90, 2847–2852.
110. F. Armillotta, PhD Thesis, University of Trieste, 2022.
111. F. Armillotta, A. Pividori, M. Stredansky, N. Seriani and E. Vesselli, Top. Catal., 2020, 63, 1585–1595.
112. K. Araki, P. S. Santos, L. F. C. de Oliveira and H. E. Toma, Spectrosc. Lett., 1995, 28, 119–126.
113. J. R. T. dos Reis, F. F. Leite, K. Sharma, G. A. S. Ribeiro, W. H. N. Silva, A. A. Batista, A. R. Paschoal, W. Paraguassu, M. Mazzoni, N. M. B. Neto and P. T. Araujo, Molecules, 2024, 29, 2362.
114. L. Dalstein, A. Revel, C. Humbert and B. Busson, J. Chem. Phys., 2018, 148(13), 134701.
115. Y. Caudano, C. Silien, C. Humbert, L. Dreesen, A. A. Mani, A. Peremans and P. A. Thiry, J. Electron Spectrosc. Relat. Phenom., 2003, 129, 139–147.

---

Footnote

† Electronic supplementary information (ESI) available: Pristine graphene characterization (LEED, IR-Vis SFG and XPS); Ir 4f and C 1s core levels of the MnTPyP and MnTPyP-Co layers; NEXAFS and XMCD spectra; tables of the best fitting parameters and literature spectroscopy data; spin-resolved orbital occupancy. See DOI: https://doi.org/10.1039/d5nr01383f

---