Magnetically driven lipid vesicles for directed motion and light-triggered cargo release

Abstract

Targeted drug delivery and precision medicine offer great promise for enhancing therapeutic efficacy while minimizing systemic toxicity. Among various platforms, lipid-based delivery systems have attracted significant interest due to their intrinsic biocompatibility and their ability to transport hydrophilic, hydrophobic, and amphiphilic compounds. With recent advances in bottom-up synthetic biology and microfluidics, giant unilamellar vesicles (GUVs) have emerged as a versatile candidate for drug delivery. However, achieving controlled and directed motion of GUVs remains a critical challenge. In this study, we conduct a systematic experimental investigation of GUVs encapsulating magnetic particles (magGUVs) subjected to inhomogeneous magnetic fields. We develop a lattice Boltzmann simulation framework to model the propulsion of GUVs driven by an internally encapsulated particle under a constant force, and compare the simulated speeds with experimental measurements. Furthermore, we demonstrate a proof-of-concept integrating directed motion of magGUVs with controlled, localized release of encapsulated contents via light-induced asymmetric oxidation. This work provides a foundation for the design of lipid-based drug delivery vehicles that combine navigational control with on-demand release capabilities, advancing targeted therapeutic strategies in precision medicine.

---

Jie Feng

Jie Feng is an Assistant Professor in the Department of Mechanical Science & Engineering at the University of Illinois Urbana-Champaign. He received his B.S. from Tsinghua University and his Ph.D. in Mechanical & Aerospace Engineering from Princeton University. He completed his postdoctoral research in Chemical & Biological Engineering at Princeton University before joining the University of Illinois. His research focuses on understanding microscale transport phenomena in complex fluids, and leveraging these insights to address some of challenging problems in energy, the environment, and healthcare. He was recognized as an Emerging Investigator by Soft Matter, RSC Advances and Nanoscale.

---

Introduction

Targeted drug delivery and precision medicine systems offer a promising approach to enhance drug efficacy while reducing systemic drug toxicity by achieving temporally controlled and localized release of a drug at a predetermined target site.^1,2 In the past decade, researchers have focused on developing novel targeting strategies and optimal designs of drug carriers to revolutionize personalized medicine.³ In this quest, lipid-based vesicles are one of the widely used drug delivery systems.⁴ Lipid-based vesicles provide an exciting opportunity as delivery vehicles due to ease in their formulation and versatility to efficiently deliver a variety of hydrophilic and hydrophobic therapeutic compounds, as well as nucleic acids.^3,5 Moreover, lipid-based delivery vehicles could be disrupted via numerous stimuli providing outstanding flexibility in controlled release of phramcoactive compounds, an important aspect of drug delivery systems.⁶ Recent studies indicate that giant unilamellar vesicles (GUVs) have acquired prominence as drug delivery vehicles due to their unique ability to interact with cellular membranes and intracellular organelles.^7,8 Additionally, their efficient internalization by cells further enhances their potential as effective carriers for intracellular therapeutic delivery.⁸ To fully exploit GUVs as delivery vehicles and enhance their efficacy in transporting drug cargo, it is essential to equip GUVs with propulsion and navigational capabilities in biological environments and hard-to-reach tissues.⁹ Several techniques have been used to confer motility to GUVs. For instance, prior efforts included vesicles powered by membrane-bound enzymes catalysis of a substrate,^10,11 vesicles driven by flagellated bacteria that are attached externally to the membranes¹² or internally encapsulated by the vesicles.¹³ However, the potential production of toxic byproducts during enzyme-induced catalysis and the lack of directed motion with bacteria limit the broader use of these techniques.

In recent years, magnetically driven micro/nano motors have gained significant interest,^14,15 as magnetic actuation offers deep tissue penetration and good controllability of the magnetic motors, making it suitable for biomedical applications.¹⁶ Biohybrid systems, such as GUVs driven by encapsulated magnetic particles (magGUVs), combine the versatility of vesicles for encapsulation and release of therapeutic loads, and the directed motion enabled by magnetic actuation. Previous studies show that it is possible to propel a magGUV by rotating an encapsulated magnetic microparticle or nanowire via a rotating magnetic field.^17,18 This approach, however, constrains the broad utility of magGUVs as a delivery vehicle, as it depends on a nearby substrate for rotation-translation coupling. Alternatively, directing magGUVs motion by applying force to encapsulated magnetic particles using an inhomogeneous magnetic field presents a more flexible and controllable strategy. Yet, to the best of our knowledge, no prior studies have systematically investigated the motion of magGUVs under such conditions.

In addition to providing magGUVs the capability of guided motion, it is crucial to rupture the magGUVs membrane to release the therapeutic payloads encapsulated in its lumen. The use of light as an external trigger to destabilize lipid vesicles, is a promising strategy for controlled release of therapeutic payloads. When photosensitizers are present within or near the lipid membrane, light irradiation can induce membrane destabilization through lipid oxidation, leading to rupture of the vesicles and subsequent release of their encapsulated contents.^19,20 In our previous study,²¹ we showed that the asymmetric distribution of the photosensitizer across the vesicles membrane results in asymmetric oxidation of the inner and outer leaflets. Asymmetric oxidation induces packing stresses in the lipid bilayer causing destabilization of the vesicles and the release of their inner contents. However, it remains to be demonstrated whether this mechanism effectively destabilizes magGUVs under dynamic conditions, i.e., while they are in motion.

Here, we characterize directed motion of magGUVs driven by an external force on the encapsulated magnetic particle. We employ the inverted emulsion method to fabricate the magGUVs, and we develop an experimental platform to create the magnetic field gradient to drive the magGUVs. In the platform, the magGUVs are driven by the encapsulated superparamagnetic particle moving along the magnetic gradient as it experiences a magnetic force due to magnetic field gradient. We investigate the speeds and morphologies of the magGUVs in a wide range of sizes. We also demonstrate the use of light-induced asymmetric oxidation to rupture the vesicles and release their inner contents at a targeted location, providing a proof-of-concept for their potential application in targeted therapeutic delivery.

Materials and methods

Materials

1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC) for GUVs fabrication and 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt) (Rh-DPPE) to label the GUVs membrane were purchased from Avanti Polar Lipids. Paraffin oil used in GUVs fabrication was purchased from Sigma-Aldrich (US). Permanent neodymium cylinder magnets (DX0X0, 1′′ in diameter × 1′′ in length) were purchased from K&J Magnetics. The surface magnetic field strength and remanent flux density are 5903 G and 13 200 G, respectively. We purchased the COMPEL™, COOH-modified magnetic particles with a density of 1.1 g cm⁻³ from Bangs Laboratories. To prepare the lipids-in-oil solution (LOS), we dissolved 64 μl (25 mg mL⁻¹) of DOPC and 26 μL (1 mg mL⁻¹) of Rh-DPPE with chloroform in a clean glass vial to form a thin film of dried lipids by evaporating under a gentle air flow. To completely remove chloroform, we kept the vial under vacuum in a desiccator for about 3 hours. Then a 5 mL of paraffin oil was added to the glass vial for a final concentration of ≈400 μM DOPC and 4 μM Rh-DPPE. Afterwards, the lipid-in-oil solution was sonicated in a bath sonicator for 30 min and then incubated for 24 h for fully dissolving lipids in the solution.

Encapsulation of magnetic particles in GUVs

We used the inverted emulsion method to fabricate the GUVs encapsulating magnetic particles.²² We firstly, carefully layered a 200 μL of LOS over a 250 μL of glucose solution in a 2 mL centrifuge tube. Then we incubated the layered solutions for 30 min to form an interfacial lipid monolayer. Subsequently, in a separate centrifuge tube, we added 6 μL of sucrose solution containing magnetic microparticles to a 450 μL of LOS. Afterwards, this tube was mechanically agitated by dragging on a pipette tip rack for about 30 s to yield a water-in-oil emulsion. Next, a 200 μL of this emulsion was gently layered on the top of the glucose-LOS interface and centrifuged at 100g for 5 min. During centrifugation, the emulsion droplets covered with a lipid monolayer were transported across the glucose-LOS interface, acquiring a second lipid monolayer and thus forming GUVs. The droplet transport was facilitated by the density difference between the inner (sucrose solution containing magnetic microparticles) and outer (isomolar glucose solution) phases of the GUVs. Finally, we extracted a 200 μL of GUVs suspension from the bottom of the centrifuge tube. During GUVs fabrication, we note that we used a 1000 mM sucrose solution as the inner phase of GUVs because the density of 1000 mM sucrose solution is 1.1 g cm⁻³, matching the density of magnetic microparticles. Accordingly, to maintain the isomolar conditions of inner and outer phases of GUVs, we used glucose solution with the same mass concentration as an outer solution. All aqueous solutions were made using DI water.

Visualization of GUV motion in a magnetic field gradient

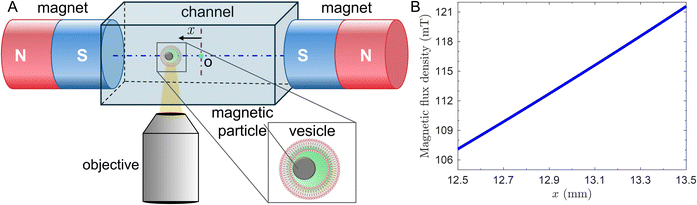
As shown in Fig. 1A, we used two cylindrical permanent magnets placed 55 mm apart with south Poles facing each other, mounted on the 3D-printed platform customized in our laboratory. The platform was designed in such a way that the GUVs could be imaged within a distance of ≈0.5 mm from the axis of the magnets. The whole set-up was mounted on a Nikon TE2000 inverted microscope with phase contrast objective lenses, and the middle of the channel was aligned with the axis of the magnets. In the visualization experiment, an aliquot of fabricated magGUVs was dispersed in a visualization chamber filled with 1000 mM sucrose solution. Therefore, the inner and outer phases of the magGUVs have similar densities to avoid buoyant force. To minimize magGUVs and surface interaction, we coated the bottom surface of the chamber with 10% (w/w) bovine serum albumin.¹³ We sealed the chamber to prevent the generation of osmotic imbalance across the lipid bilayer due to evaporation.¹³ As we place the magGUVs in an inhomogeneous external magnetic field, magnetic microparticles experience a magnetic force in direction of magnetic field gradient and start translating inside the magGUVs. As shown in Fig. 1A, the microparticle ultimately pushes the membrane from inside and thus driving the magGUV along the magnetic field gradient. We recorded the images using a Orca flash 4.0 Hamamatsu sCMOS camera for a trajectory length of ≥150 μm at 5 frames per second. The further analysis of the images was performed using customized Matlab codes and Fiji.²³

Fig. 1 Schematic of experimental set-up to investigate the motion of a vesicle driven by an internally encapsulated magnetic microparticle. (A) To establish the magnetic field gradient, two cylindrical permanent magnets were placed with opposing polarities so that their south Poles faced each other. The microparticle experiences a magnetic force due to magnetic field gradient and pushes the vesicle with it. The magnetic flux density is zero at the middle point O, where x = 0. We captured the motion of the vesicles along the axis of the two magnets on an inverted microscope at x ≈ 13–13.2 mm away from the origin O. (B) Variation of magnetic flux density along the axis of the two magnets obtained from COMSOL Multiphysics simulation of magnetic field between two permanent magnets placed with opposing polarities.

Results and discussion

Characterization of magnetic field and microparticles motion

We employed COMSOL Multiphysics to simulate the magnetic field generated by the permanent magnets (see ESI† for more details). We defined the remanent flux density of 13 200 G for each magnet in opposite directions as provided by the vendor. We used the free triangular mesh to discretize all of the domains and solve for the magnetic field using MUMPS solver. We modeled the experimental setup in a 2D axis-symmetric geometry. Fig. 1B shows the variation in the magnetic flux density along the axis of the two magnets from the simulation. The magnetic flux density varies nearly linearly (<2% change in the gradient of the magnetic flux density) in the field of view where we observe the motion of magGUVs.

We further analyze the motion of bare magnetic microparticles to experimentally validate the external magnetic field gradient as established in our experimental setup. The magnetic microparticles when placed in an external magnetic field experience a magnetic force given by²⁴ F_m = ∇(m·B), where m = MV_p is a magnetic moment of the microparticles, M and V_p are the magnetization strength and volume of the microparticles, respectively. B represents the magnetic flux density. Given the small size of the microparticles, the magnetization is considered uniformly distributed over the microparticles. Moreover, since the microparticles are free to rotate, we assume that the magnetization always aligns itself parallel to the applied magnetic flux density B. Considering these simplifications, the magnetic force on microparticles can be written as F_m = MV_p∇|B|, where M = |M|. For the typical speed and size of magnetic microparticles in current experiments, the Reynolds number (representing the ratio between the inertial and viscous effects) ≪1 and the microparticles move in the Stokes flow regime. Thus, the magnetic force F_m acting on the microparticles is balanced by the Stokes drag F_d = 3πμd_pv_p for a solid sphere in a quiescent fluid.²⁵ Here, v_p is the speed of microparticles driven by an external magnetic field and therefore can be obtained as v_p = MV_p∇|B|/(3πμd_p), where μ is the viscosity of the surrounding fluid and d_p is the diameter of the microparticles.

To theoretically predict the particle velocity, we characterize microparticles diameter d_p and their magnetic response to obtain magnetization M. Fig. 2A shows the size distribution obtained by analyzing the microscope images of the microparticles. The inset of Fig. 2A shows a typical image of microparticles dispersed in an aqueous solution. We obtain a distribution for particle diameter d_p with a mean value of 6.25 μm and a standard deviation of 0.25 μm. Fig. 2B shows the magnetic response of the microparticles provided by the vendor. We fit the magnetic response curve of microparticles to a Langevin function M = M_s(coth H/ζ − ζ/H), where M_s is saturation magnetization of the microparticles, H is applied magnetic field strength and ζ = 14.6 kA m⁻¹ is a fitting parameter. In magnetic field strength H > 200 kA m⁻¹, the magnetization of the microparticles saturates to M_s = 3.1 kA m⁻¹.

Fig. 2 Characterization of size of magnetic microparticles and their motion in a magnetic field gradient. (A) Size histogram of the magnetic microparticles with an average diameter 6.25 ± 0.25 μm. Inset shows microparticles dispersed in a solution for size measurement. The scale bar represents 10 μm. (B) Magnetic response of magnetic microparticles. (C) Representative x-trajectories of magnetic microparticles moving in the applied magnetic field gradient. (D) Speed of the microparticles in fluids with different viscosities shows a inverse variation with the viscosity of the fluids as expected from Stokes’ law. The red curve is the theoretical prediction of microparticle velocity computed from the force experienced by magnetic microparticles in an external magnetic field gradient in the Stokes flow regime. Here, the magnetic flux density ∇|B| is 14.2 T m⁻¹ in x-direction along the magnets axis and the magnetic field strength H is 88.6 kA m⁻¹ for the field of view obtained from COMSOL Multiphysics simulation. Error bars are calculated as the standard deviations of at least 15 measurements.

In the field of view for microparticle motion, ∇|B| remains approximately constant (see Fig. 1B). As expected, the microparticles maintained a constant speed under a nearly uniform magnetic field gradient, leading to a linear relationship between their position and time. In Fig. 2C, we confirm such a linear relationship in different viscous fluids. We further compare the experimental observation of the microparticle speed with theoretical prediction in the Stokes flow regime. Fig. 2D, which shows a reasonably good agreement. Therefore, the above results validate our experimental setup and simulation results for the magnetic field characterization. In the following discussion for magGUV motion, we consider the gradient of the magnetic flux density ∇|B| = 14.6 T m⁻¹ in x-direction along the magnets axis and the magnetic field strength H as 92.0 kA m⁻¹ obtained from the simulation.

Motion of GUVs driven by encapsulated magnetic microparticles

As magGUVs are placed in an inhomogeneous magnetic field, the encapsulated magnetic particle experiences a magnetic force. The microparticle first translates inside the vesicle along the magnetic field gradient until it comes into contact with the GUV membrane. Subsequently, the particle pushes the membrane from within, causing both the particle and the GUV to co-translates at the same speed. Fig. 3 shows the speed of magGUVs (v_v) for a wide range of vesicle diameters (d_v). The speed (v_v) and diameter (d_v) of magGUVs were obtained from the images analyzed in Fiji and Matlab. As shown in Fig. 3A, under the same external magnetic force applied to the encapsulated particle, we observed a general trend of decreasing magGUV speed with increasing size. This reduction in speed is attributed to the greater drag experienced by larger vesicles. Fig. 3B–D show typical shapes of representative vesicles, which remain largely spherical across different sizes when the inner and outer solutions are c_in = c_out = 1000 mM sucrose.

Fig. 3 Experimental measurement and numerical simulation for speed of magGUVs pushed by magnetic microparticles. (A) Experimentally measured speed of magGUVs at different outer sucrose solutions with c_out = 1050 mM, 1000 mM, or 950 mM, while the inner sucrose solution of c_in = 1000 mM was kept the same for all cases (circles, triangles, and squares, respectively). Simulated speeds of magGUVs using lattice Boltzmann methods (diamonds). (B–D) The typical shapes of vesicles of increasing sizes for cases marked in (A). The scale bar represents 10 μm.

To evaluate the impact of osmotic imbalance across magGUVs membrane, we further investigated the motion of magGUVs in outer solutions consisting of c_out = 1050 mM sucrose (hypertonic) and c_out = 950 mM sucrose (hypotonic) while keeping the inner solution as c_in = 1000 mM sucrose. In cases of outer solution c_out = 1050 mM sucrose, water flows out of magGUVs as to achieve the osmotic balance across the membrane, making magGUVs more deformable. Conversely, in cases of outer solution c_out = 950 mM sucrose, water entered the magGUVs, making them more turgid and resistant to deformation. However, as shown in Fig. 3A, we did not observe any significant effect on the motion of magGUVs. Since the magGUVs largely retained their spherical morphology in both conditions, similar to the c_out = 1000 mM sucrose case, we infer that the impact of osmotic imbalance on magGUVs speed is minimal under the conditions of our experiments. In the current experiments, we observed that these particles maintained full encapsulation, with no instances of membrane breaching during GUV motion. We believe this is due to the presence of a lubrication thin film between the magnetic particle and the GUV membrane, which had not fully drained out while the GUV was within the field of view. This observation is consistent with our preliminary results indicating that the film drainage timescale is significantly longer than the duration the GUV remains in view.

We also compared our experimental results with simulations based on the lattice Boltzmann method, as shown in Fig. 3A. To replicate the largely spherical vesicle shapes observed experimentally (Fig. 3B–D), we employed a membrane model with high bending and shear moduli, minimizing deformations (see ESI† for details on the numerical method and parameter values). The simulations tracked the motion of both the enclosing membrane and the encapsulated magnetic particle, driven by a constant external magnetic force, allowing us to compute their co-translational speed for comparison with experimental measurements. While the simulations capture the qualitative trend and order of magnitude of the propulsion speed, further investigation is needed to identify the factors contributing to the higher speeds observed in experiments.

Directed motion and controlled release of inner contents

In this section, we showcase a proof-of-concept demonstration of integrating the magnetic field gradient-induced directed motion of magGUVs and light-triggered local release of inner contents by disrupting magGUVs membrane. In our previous study, we showed that in the presence of asymmetric distribution of photosensitizer across the GUV membrane, light-induced oxidation can be harnessed as a non-contact method causing vesicles to rupture and release their inner contents.^21,26,27 We fabricated magGUVs containing 1000 mM sucrose and 20 mM of a photosensitizer HPTS (8-hydroxypyrene-1,3,6-trisulfonic acid trisodium salt). To avoid osmotic imbalance across the magGUV membrane, we kept an isomolar 1020 mM sucrose as the outer aqueous solution. As shown in Fig. 4A, the magGUV was initially deformed as it was pushed by the magnetic microparticle. However, after magGUV was exposed to intense illumination the deformation disappears, a characteristic feature of vesicles observed in oxidative environments.¹⁹ Since, HPTS was present only inside of magGUV, it leads to faster oxidation of inner leaflet than the outer leaflet of magGUV. Generation of packing stress and spontaneous curvature following light-triggered asymmetric oxidation, resulted in magGUV explosion at t = 53.5 s. A bright cloud at t = 54 s around the magnetic microparticle demonstrates a localized release of magGUV inner contents as well as the encapsulated magnetic microparticle. At t = 56 s, only the magnetic particle was visible indicating the catastrophic disintegration of magGUV (see ESI movie S1†).

Fig. 4 Directed motion and localized release of inner content of a magGUV. (A) MagGUV containing 1 M sucrose and 20 mM HPTS (8-hydroxypyrene-1,3,6-trisulfonic acid trisodium salt) is pushed by the magnetic microparticle along the gradient of magnetic flux density. Snapshots of the vesicle at different times shows the locomotion of the vesicle. At t = 53.5 s, the vesicle is disrupted via light-induced asymmetric membrane oxidation caused by photosensitizing action of HPTS. At t = 54 s, the vesicle is fully disintegrated, releasing the inner content locally. At t = 56 s, the magnetic particle escaped after the vesicle collapsed (see ESI movie S1†). The scale bar represents 20 μm. (B) At t = 54 s, a sudden jump in the slope of microparticle trajectory indicates the escape of the microparticle from the vesicle.

To confirm the escape of the encapsulated magnetic microparticle, we plot the trajectory of the encapsulated microparticle before and after the magGUV explosion in Fig. 4B. We observed a sudden change in the slope of microparticle trajectory about t = 54 s, at the same moment as the magGUV ruptured. The sudden jump in slope indicates an instantaneous increase in the speed of the microparticle. Before explosion, the microparticle was moving slower because of larger drag experienced by the magGUV compared to a bare magnetic microparticle. However, after explosion the microparticle was uncaged and we saw a jump in microparticle speed due to reduction in drag experienced by the microparticle after destruction of magGUV. Therefore, we clearly demonstrate the potential of magGUVs achieving directed motion with an external magnetic field, and localized release using light as a remote stimulus. Both of these features are essential for a successful drug delivery vehicle. Moreover, the use of light as a stimulus to destabilize magGUVs offers excellent temporal, spectral, and spatial control,²⁸ enhancing controlled and localized release of therapeutic compounds and thereby further reducing systemic toxicity. While light offers distinct advantages as a trigger for GUV rupture, its effectiveness in deep tissue applications requires further optimization of illumination parameters and may benefit from complementary strategies such as fiber-optic delivery.²⁹

Conclusion

To summarize, we develop an experimental platform to systematically investigate the motion of magGUVs driven by encapsulated superparamagnetic particles under the influence of nonhomogeneous magnetic field. We used two permanent cylindrical magnets placed in opposite polarity, which creates a nonhomogenous magnetic field in the space between the magnets. We utilized COMSOL Multiphysics to obtain the magnetic flux density generated by the magnets. We validated our experimental setup by characterizing the motion of bare magnetic particles. We found a good match between the theoretical prediction and the experimentally obtained speed of magnetic particles in the Stokes regime. We further investigated the motion of magGUVs and found a general trend of decreasing magGUVs speed with increasing size. The magGUVs mainly maintained a spherical shape during their motions. Moreover, we compared the experimental results with numerical simulations using the lattice Boltzmann method. The numerical simulations captured the order of magnitude of magGUVs speed. Some previous studies have shown GUVs can be significantly deformed by encapsulating active particles.^13,30,31 In their systems, the small size of the enclosed self-propelled particles relative to the vesicle produced significant localized deformations. While in our systems, the relatively large size of the particles and resulting small co-translating speeds lead to typically small capillary numbers so that vesicle remain largely spherical in shape. Investigations are currently underway to examine the effect of membrane deformability on the dynamics of this system. The effect of the non-Newtonian rheology of biological fluids on the vesicle motion and deformation will also be a potential direction to explore. Finally, we demonstrated the use of light-triggered stimulus in the presence of asymmetric distribution of photosensitizer across the membrane to remotely rupture the magGUVs, locally releasing their inner contents. Our work holds promise for advancing the design of vesicle-based drug delivery systems by facilitating the development of vesicle-based delivery vehicles endowed with navigational capabilities and the ability of remotely triggered release of therapeutic payloads.

Author contributions

Conceptualization: V. K. M, O. S. P, J. F. discussions: V. K. M., L. C.-T., O. S. P., Y.-N. Y., J. F. methodology: V. K. M., L. C.-T., C. X., A. D.-M.-I., O. S. P, Y.-N. Y., J. F. investigation: V. K. M., L. C.-T., C. X. data curation: V. K. M., L. C.-T., C. X. software: L. C.-T., A. D.-M.-I., O. S. P, Y.-N. Y. validation: V. K. M., L. C.-T., O. S. P., J. F. visualization: V. K. M., L. C.-T., C. X., O. S. P, J. F. writing – original draft: V. K. M., L. C.-T., O. S. P, J. F. writing – review & editing: V. K. M., L. C.-T., C. X., A. D.-M.-I., O. S. P, Y.-N. Y., J. F. funding acquisition: O. S. P., Y.-N. Y., J. F. supervision: O. S. P., J. F.

Data availability

The graphical and imaging data presented in the manuscript will be available on reasonable request. All details are mentioned in the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge useful discussions with B. Quaife. V. K. M. and J. F. acknowledge partial support by the National Science Foundation (NSF) under grant no. CBET 2323045 and CBET 2426809. O. S. P. acknowledges partial support by NSF under grant no. CBET 2323046 and CBET 2419945. Y. N. Y. acknowledges partial support by NSF under grant no. DMS 1951600, and support from Flatiron Institute, part of Simons Foundation.

References

1. A. P. Singh, A. Biswas, A. Shukla and P. Maiti, Signal Transduction Targeted Ther., 2019, 4, 33.
2. Z. Zhao, A. Ukidve, J. Kim and S. Mitragotri, Cell, 2020, 181, 151–167.
3. M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas and R. Langer, Nat. Rev. Drug Discovery, 2021, 20, 101–124.
4. S. H. Kiaie, S. Mojarad-Jabali, F. Khaleseh, S. Allahyari, E. Taheri, P. Zakeri-Milani and H. Valizadeh, Int. J. Pharm., 2020, 581, 119269.
5. L. Xu, X. Wang, Y. Liu, G. Yang, R. J. Falconer and C.-X. Zhao, Adv. NanoBiomed Res., 2022, 2, 2100109.
6. U. Kauscher, M. N. Holme, M. Björnmalm and M. M. Stevens, Adv. Drug Delivery Rev., 2019, 138, 259–275.
7. O. Staufer, S. Antona, D. Zhang, J. Csatári, M. Schröter, J.-W. Janiesch, S. Fabritz, I. Berger, I. Platzman and J. P. Spatz, Biomaterials, 2021, 264, 120203.
8. F. Lussier, O. Staufer, I. Platzman and J. P. Spatz, Trends Biotechnol., 2021, 39, 445–459.
9. J. Li, B. Esteban-Fernández de Ávila, W. Gao, L. Zhang and J. Wang, Sci. Robot, 2017, 2, eaam6431.
10. S. Ghosh, F. Mohajerani, S. Son, D. Velegol, P. J. Butler and A. Sen, Nano Lett., 2019, 19, 6019–6026.
11. H. Jin, J. Cui and W. Zhan, Langmuir, 2023, 39, 4198–4206.
12. N. Dogra, H. Izadi and T. K. Vanderlick, Sci. Rep., 2016, 6, 29369.
13. L. Le Nagard, A. T. Brown, A. Dawson, V. A. Martinez, W. C. Poon and M. Staykova, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2206096119.
14. X.-Z. Chen, M. Hoop, F. Mushtaq, E. Siringil, C. Hu, B. J. Nelson and S. Pané, Appl. Mater. Today, 2017, 9, 37–48.
15. H. Zhou, C. C. Mayorga-Martinez, S. Pané, L. Zhang and M. Pumera, Chem. Rev., 2021, 121, 4999–5041.
16. Z. Yang and L. Zhang, Adv. Intell. Syst., 2020, 2, 2000082.
17. A. Mateos-Maroto, A. Guerrero-Martínez, R. Rubio, F. Ortega and F. Martínez-Pedrero, ACS Appl. Mater. Interfaces, 2018, 10, 29367–29377.
18. A. Mateos-Maroto, F. Ortega, R. G. Rubio, J.-F. Berret and F. Martínez-Pedrero, Part. Part. Syst. Charact., 2019, 36, 1900239.
19. S. Sankhagowit, S.-H. Wu, R. Biswas, C. T. Riche, M. L. Povinelli and N. Malmstadt, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2615–2624.
20. I. O. Bacellar, M. C. Oliveira, L. S. Dantas, E. B. Costa, H. C. Junqueira, W. K. Martins, A. M. Durantini, G. Cosa, P. Di Mascio and M. Wainwright, et al., J. Am. Chem. Soc., 2018, 140, 9606–9615.
21. V. K. Malik, O. S. Pak and J. Feng, Adv. Sci., 2024, 11, 2400504.
22. A. Moga, N. Yandrapalli, R. Dimova and T. Robinson, ChemBioChem, 2019, 20, 2674–2682.
23. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld and B. Schmid, et al., Nat. Methods, 2012, 9, 676–682.
24. O. Baun and P. Blümler, J. Magn. Magn. Mater., 2017, 439, 294–304.
25. L. G. Leal, Advanced transport phenomena: fluid mechanics and convective transport processes, Cambridge university press, 2007, vol. 7.
26. V. K. Malik, S. Shin and J. Feng, Soft Matter, 2020, 16, 8904–8911.
27. V. K. Malik, O. S. Pak and J. Feng, Phys. Rev. Appl., 2022, 17, 024032.
28. A. Peyret, E. Ibarboure, A. Tron, L. Beauté, R. Rust, O. Sandre, N. D. McClenaghan and S. Lecommandoux, Angew. Chem., Int. Ed., 2017, 56, 1566–1570.
29. M. J. Brun, E. J. Gomez and J. Suh, J. Controlled Release, 2017, 267, 80–89.
30. S. C. Takatori and A. Sahu, Phys. Rev. Lett., 2020, 124, 158102.
31. H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00942a

---