 Open Access Article
Open Access ArticleDynamics of ultrafine silver implanted DNA nanowire formation†
Qifei
Ma
 a,
Mauro
Chinappi
a,
Mauro
Chinappi
 b,
Ali
Douaki
c,
Yanqiu
Zou
d,
Huaizhou
Jin
*e,
Emiliano
Descrovi
b,
Ali
Douaki
c,
Yanqiu
Zou
d,
Huaizhou
Jin
*e,
Emiliano
Descrovi
 f,
Roman
Krahne
f,
Roman
Krahne
 c,
Remo
Proietti Zaccaria
c,
Remo
Proietti Zaccaria
 c,
Roberto
Marotta
c,
Weihong
Wang
ac,
Dan
Cojoc
g,
Karol
kołątaj
h,
Guillermo
Acuna
c,
Roberto
Marotta
c,
Weihong
Wang
ac,
Dan
Cojoc
g,
Karol
kołątaj
h,
Guillermo
Acuna
 h,
Shangzhong
Jin
*a and
Denis
Garoli
h,
Shangzhong
Jin
*a and
Denis
Garoli
 *aci
*aci
aCollege of Optical and Electronic Technology, China Jiliang University, Hangzhou 310018, China. E-mail: jinsz@cjlu.edu.cn
bDepartment of Industrial Engineering, University of Rome Tor Vergata, Italy
cIstituto Italiano di Tecnologia, Via Morego 30, 16163 Genova, Italy
dCollege of Optical Science and Engineering, Zhejiang University, Hangzhou 310027, China
eKey Laboratory of Quantum Precision Measurement, College of Physics, Zhejiang University of Technology, Hangzhou, China. E-mail: 18367198456@163.com
fDipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129 Torino, Italy
gCNR-Istituto Officina dei Materiali (CNR-IOM), SS 14 km 163.5, Area Science Park Basovizza, 34149, Trieste, Italy
hDepartment of Physics, University of Fribourg, Fribourg, CH 1700, Switzerland
iDipartimento di Scienze e metodi dell'ingegneria, Università degli Studi di Modena e Reggio Emilia, 42122 Reggio Emilia, Italy. E-mail: denis.garoli@unimore.it
First published on 9th June 2025
Abstract
Recent research on silver nanowires prepared on DNA templates has focused on two fundamental applications: nano-scale circuits and sensors. Despite their broad potential, the formation kinetics of silver implanted DNA nanowires remains unclear. Here, we present an experimental demonstration of the formation of silver nanowires with a diameter of 2.2 ± 0.4 nm at the single-molecule level through chemical reduction. We conducted equilibrium and perturbation kinetic experiments to measure force during the formation of Ag+–DNA complexes and Ag–DNA complexes, using optical tweezers combined with microfluidics. The addition of AgNO3 resulted in an increase in force of 5.5–7.5 pN within 2 minutes, indicating that Ag+ compacts the DNA structure. In contrast, the addition of hydroquinone caused the force to decrease by 4–5 pN. Morphological characterization confirmed the presence of a dense structure formed by silver atoms bridging the DNA strands and revealed conformational differences before and after metallization. We compare our experimental data with Brownian dynamics simulations using a coarse-grained double-stranded DNA (dsDNA) model that provides insights into the dependency of the force on the persistence length.
Introduction
Silver nanowires have attracted attention due to their high electrical conductivity1,2 and interesting optical properties3–7 that promise great potential in nanoscale circuits8–11 and sensors.12–20 Braun et al.21 first proposed a conducting silver nanowire templated by DNA, which overcomes poor electrical conductivity of DNA molecules and might allow the application of DNA for constructing functional circuits. The morphological, electrical and optical characteristics and stability of silver nanowires are significantly influenced by the effectiveness of their protection groups (i.e. surface functionalization) that shield them from external environmental factors. For instance, the luminescence of silver can either increase or decrease due to external conditions, highlighting the potential for utilizing silver nanowires as sensitive optical detectors for biothiols,13,22 gas,14,17 DNA23–25 and other substances. Additionally, luminescent silver nanowires are efficient emitters with high quantum yields, high molecular extinction coefficients, nanosecond lifetimes and excellent photostability, which can be exploited for the visualization of genomic DNA sequences.12 All of these applications rely on the interactions between DNA, silver ions (Ag+) and silver atoms (Ag), and therefore, insights into the mechanisms of DNA metallization and control of the formation of the silver coating and the morphology of the resulting nanowires are of important interest.To date, relatively few experimental studies26–32 have focused on the interaction between Ag+ and DNA. Current understanding is that Ag+ ions favor coordination with DNA bases over electrostatic binding to DNA phosphates,26 and this coordination with DNA bases can be classified based on the Ag/DNA nucleotide ratio in three types of binding modes.27 Below an Ag/nucleotide ratio of 0.2, the type I complex is predominantly formed, with the guanine N7 atom as the key binding site. At ratios between 0.2 and 0.5, type II complexes are produced, primarily binding to A–T or G–C base pairs. At ratios greater than 0.5, type III complexes develop once the main binding sites in type I and type II complexes are fully saturated. Petty et al.3 explored small (<10 atoms) Ag nanoclusters templated by DNA for time-dependent and size specific formation of nanoclusters using optical and mass spectrometries. They revealed that silver nanoclusters induce different structural changes in DNA as compared to silver ions. These DNA-templated silver nanoclusters exhibit very strong absorption and emission, making them nearly ideal fluorophores for single molecule spectroscopy, suggesting potential utility as biological labels.
Zinchenko et al.33 and Yang et al.34 focused on the conformational changes caused by the formation of silver nanoparticles based on DNA as a template and discussed the conformational behavior of a long single-chain double-stranded DNA in solutions of free silver ions and silver nanoparticles. With this method, ultrathin nanowires could be obtained, and such silver nanowires with a few nanometers in diameter are interesting for nano-scale circuits that go beyond the resolution limit of standard top-down fabrication processes.
Alongside experimental work, theoretical and numerical models have greatly contributed to understanding how ions influence DNA mechanics. Coarse-grained models such as the Peyrard–Bishop–Dauxois (PBD) framework have been widely used to study denaturation and unzipping under force, emphasizing the role of hydrogen bonding and base stacking in modulating pairing stability.35,36 Molecular dynamics platforms, such as OxDNA, further enable detailed simulations of DNA nanostructures in varying ionic environments.37 However, these base-level approaches become computationally demanding for long chains under mechanical loads. In such contexts, alternative coarse-grained models (where each bead represents a DNA segment instead of individual bases) are often preferred. These include worm-like chain (WLC) models, in which structural parameters like persistence length are set as inputs of the model rather than prediction.38
In this work, we used a two-step chemical reduction method21 to prepare the silver implanted DNA nanowires. First, Ag+ was added to the DNA to form Ag+–DNA complexes. Then, hydroquinone was added to reduce Ag+ to Ag atoms, resulting in the formation of the nanowires. By adjusting the concentration of DNA, Ag+ and hydroquinone, we demonstrate the formation of a 2.2 nm diameter silver nanowire at the single-molecule level and investigate the growth dynamics using real-time force spectroscopy measurements. Our study reveals that Ag+ ions have a sensitive impact on DNA conformation, while Ag nanoclusters showed minimal interaction with DNA. By performing atomic force microscopy (AFM) imaging, we track the changes of the DNA conformation and the coverage of metal ions and metal atoms on DNA during the formation of the silver nanowires. We support our experimental findings by analyzing the dependency of the force on the persistence length with Brownian simulations of a coarse-grained dsDNA model.
Results and discussion
Stretching single DNA molecules and AFM characterization
To study the effect of silver ions and silver atoms on the force change of an individual DNA molecule, a single λ-DNA molecule was suspended in PBS buffer using optical tweezers (OTs) at room temperature.The distance between the two beads and the stretching force are related. First, the distance (d) between the two beads is adjusted so that the initial force is about 2 pN (Fig. 1) (the importance of the initial force is discussed in ESI note 1†). During metallization, the distance between the two beads is held constant, and the change in force is measured throughout the process. The experimental procedure involved the sequential addition of reagents. Initially, the introduction of 0.05 mM AgNO3 solution induced the formation of a DNA–Ag+ complex, resulting in an increase in force of 5.5–7.5 pN (Fig. 1b). This indicates that the addition of Ag+ ions causes DNA compaction (d > d1, Fig. 1a), and to maintain a constant distance between the two beads, a larger force is required to stretch the DNA. Subsequently, the addition of 0.002 mM hydroquinone solution facilitated the formation of the DNA–Ag complex, leading to a decrease in force of 4–5 pN (Fig. 1c–e). The growth of silver atoms weakens the compaction of the DNA (d > d2 > d1, Fig. 1a), thereby reducing the pulling force compared to the force observed after the addition of Ag+ ions. Fig. 1b shows force stability after the addition of Ag+ for 60 minutes. Within the first 2 minutes, Ag+ ions fully bind to DNA, and over a period of up to 60 minutes, the structure of the Ag+–DNA complex remains stable, demonstrating that the binding is strong and durable.
In order to have a direct demonstration of the DNA metallization and to verify the growth rate of Ag ions, we performed AFM characterization using similar conditions to the ones used in the tweezer experiments (Fig. 2). The AFM time-series analysis reveals a clear evolution from dispersed Ag+–DNA complexes to continuous nanowires, demonstrating DNA's role as an effective template for guided metal assembly. During AFM sample preparation, unbound Ag+ ions or Ag atoms are removed by DI water washing, confirming that the observed AFM features (Fig. 2b–g) exclusively represent Ag+ or Ag species stably bound to DNA.
After 10 minutes of incubation of Ag+, significant DNA conformational changes are observed. The DNA backbone exhibits pronounced curling or contraction, likely due to Ag+ induced charge neutralization and localized bending. Small aggregates form along the DNA strands, indicating Ag+ ions binding to specific sites (e.g., phosphate groups or nucleobases).
Extended incubation (20–30 min) of Ag+ with DNA templates results in the formation of discrete, linearly aligned nanoparticles along the DNA backbone. This configuration clearly demonstrates DNA's effectiveness as a structural template for nanoparticle organization. However, in the absence of a reducing agent, the deposition process exhibits significant spatial heterogeneity.
Fig. 2(e–g) show silver coated DNA nanowires as prepared in (b–d) with an additional incubation of the Ag+–DNA complex in 0.002 mM hydroquinone for 10 minutes.
When the incubation time of Ag+ is 10 min, discrete nucleation sites form at specific locations, and Ag atoms do not completely cover the DNA strand. Uncoated DNA segments remain clearly visible between metallized regions. So Ag+ ions require finite time to diffuse and properly coordinate with DNA binding sites (phosphate groups and nucleobases). Short incubation (10 min) is insufficient for complete equilibrium binding distribution.
Even as excess Ag+ ions compete for limited high-affinity sites, initial nucleation events create localized charge neutralization, temporarily inhibiting nearby binding. This leads to spatially separated nucleation centers rather than uniform coating. So after extending the incubation time, the sufficient time allows complete surface diffusion of Ag+ to all potential binding sites (additional AFM analyses are discussed in ESI note 2†). As an additional monitor of the silver nanocluster growth, high-resolution transmission electron microscopy (TEM) was performed on DNA incubated for 5 and 20 minutes, respectively, with the Ag+ ions. ESI note 2 and Fig. S5† show the results of these analyses, confirming the time dependence of the Ag wire formation.
It is notable that in the OT experiment the reaction time is shorter than in the microscopy experiments because the microfluidic volume and the ratio of Ag+ ions to DNA are much higher in the OT setup. As demonstrated in Fig. 1c–e, the force−time curves of λ-DNA in the presence of Ag+ (black) and hydroquinone (red) show that within the first 2 minutes, Ag+ ions were reduced to Ag, forming an Ag nanowire, which was further evidenced by AFM imaging of the morphology (Fig. 2). The AFM analysis also enabled demonstrating the good control regarding the final height of metallized DNA, which for this structure was 2.2 ± 0.4 nm (Fig. 2i and ESI Fig. S3†).
The distinct coordination chemistries of Ag+ ions and Ag atoms with DNA structural elements are at the origin of the opposite conformational effects that we observe. Previous studies have demonstrated that Ag+ interacts strongly with nitrogen atoms in DNA bases, especially in GC base pairs.39–44 This specific binding is considered to induce base pair rearrangements, which could be the main reason for the significant reduction in the persistence length of DNA. In contrast to Ag+, the relatively weak interactions44 between Ag atoms and oxygen atoms in DNA permit the DNA to regain its native conformation. This observation is consistent with the circular dichroism spectroscopic studies conducted by Petty et al.,3 which demonstrated that silver nanoclusters induce different structural changes in DNA compared to Ag+. During the reduction process of Ag+, the mechanical force did not fully return to its initial value, suggesting that the formation of small Ag clusters within the DNA structure partially hindered the complete reduction of Ag+. Fig. 2a shows the AFM image obtained by scanning a single λ-DNA. Because of the long chain of the λ-DNA (full length of about 16 μm), only part of the chain is shown with a measured height of about 1.5 nm, in agreement with previous reports.45,46 Extended incubation of Ag+ with DNA resulted in the localized formation of large metallic aggregates, which we attribute to the persistent coiled state of DNA maintained by Ag+ incorporation. This leads to an increased local charge density in specific DNA regions, thereby facilitating the accumulation and progressive growth of larger Ag+ clusters through enhanced electrostatic interactions, consistent with reports by Zinchenko et al.33 However, subsequent addition of hydroquinone destabilized the coiled conformation of the Ag+–DNA complex, facilitating the uniform distribution of Ag atoms along the entire DNA strand. Since in the OT experiments the DNA molecule maintained a linear conformation, it prevented the formation of localized large-scale metallic aggregates.
Yang et al.34 investigated the reductant dependent DNA-templated silver nanoparticle formation using magnetic tweezers. Their findings revealed that Ag+ ions induce a partially condensed coiled state in DNA strands, which is consistent with our OT results. However, their study also demonstrated that the formation of fully compact silver nanoparticles can be controlled by varying the types of reducers and the Ag+/reducer ratio. In our work we focused on a complementary process, which allows fabrication of silver nanowires from Ag+ functionalized DNA by the addition of Ag+ and hydroquinone.
As an additional investigation of the metallization process, we performed a set of Raman spectroscopy measurements on the prepared DNA + Ag using the same preparation conditions as in the AFM experiments. The results are reported in ESI note 3.† As expected, the addition of Ag ions and the growth of small metallic particles/clusters on the DNA produce localized electromagnetic fields and enhance the Raman signal.
DNA model
To interpret the observed increase in the force due to the Ag+ ions, we rely on established knowledge of polymer physics.Several coarse-grained models have been developed to describe DNA mechanics, ranging from base-resolved frameworks37 to segment-based elastic models.47 While some are more accurate in fitting detailed force-extension data,48 for our purposes the simple ideal chain or freely jointed chain model is sufficient to capture the key trends observed in our data without introducing additional parameters. In this model, the polymer consists of N rigid elements of fixed length b, the Kuhn length, so that the total length of the polymer (contour length) is L = Nb. Defining the end-to-end vector R as the vector pointing from the first to the last monomer, the free energy of an ideal chain is given by:
 | (1) |
 | (2) |
In our set-up, the DNA is bound to two beads at a distance L0 whose positions are controlled by OTs (see Fig. 3). Thus, the end-to-end distance is L0, and for the entropic spring model, the DNA exerts a force on the two beads proportional to their distance L0. The interaction between dsDNA and Ag+ is expected to compact the DNA,33,50 a behavior that can be interpreted as a reduction of the persistence length b. Consequently, the equivalent spring constant ke, eqn (2), increases, and so does the force. In summary, this model supports the following interpretation of the increase in force observed in the experiments. In the initial stage, the Ag+ ions make the dsDNA less flexible (smaller persistence length), and consequently, more force is required to keep it stretched by OTs.
As further confirmation of the dependence of the force on the persistence length, we performed Brownian simulations of a coarse-grained dsDNA model represented as a worm-like chain (WLC). Simulations on a reduced system with N = 500 beads, where the two terminal beads are constrained by a harmonic potential to mimic the two OTs, whose distance is 95% of the polymer contour length (i.e., a condition similar to the experimental case), show that the force decreases for more flexible polymers, as shown in Fig. 3b.
Conclusions
We studied the formation dynamics of silver implanted DNA nanowires. Using OT experiments, we found that the addition of 0.05 mM Ag+ resulted in a 5.5–7.5 pN increase in force within 2 minutes, indicating that Ag+ compresses the DNA structure. In contrast, the addition of hydroquinone caused the force to decrease by 4–5 pN within 2 minutes, thus allowing a stretching of the previously compressed DNA–Ag+ structure. The morphologies of the DNA–Ag+ complex and the DNA–Ag complex were examined using AFM, revealing the coverage of metal ions and metal atoms on the DNA during the formation of silver nanowires and metal atoms on DNA and conformational changes of DNA during the formation of silver nanowires. Furthermore, the dependency of the force on the persistence length was analyzed through Brownian simulations of a coarse-grained dsDNA model. In the future, optical tweezers could serve as a powerful tool for studying the mechanical properties and binding mechanics of other DNA-templated nanowires. This includes nanowires based on different metals, binding methods with metals, or special DNA structures, such as DNA origami. Our results suggest that controlling the formation of nanowires may be feasible, opening up a wide range of potential applications in fields ranging from biology to nanoscience.Materials and methods
For the nanomechanical measurements, we used λ-DNA biotinylated at its 5′–3′ ends (Lumicks, Amsterdam, the Netherlands). For AFM imaging, we used λ-DNA from New England Biolabs (NEB). In all experiments, DNA was diluted to a final concentration of 0.04 μg ml−1. Streptavidin-coated polystyrene microbeads with a diameter of 4.34 μm (Spherotech, Chicago, USA) were diluted to a final concentration of 0.05% W/V. Fig. S6(b)† illustrates a tether formation principle between two polystyrene beads. Sodium phosphate buffer (PBS, pH = 7.2), ammonium hydroxide (NH3OH), (3-aminopropyl) triethoxysilane (APTES), AgNO3, and hydroquinone were purchased from Sigma and used without further purification. Purified water was obtained from a Milli-Q system (Miaozhiyi, Nanjing, China). PBS buffer was used as an experimental buffer solution for DNA and microbeads. NH3OH (pH = 10.5) was used as the buffer solution for AgNO3 and hydroquinone.Optical tweezer experiment
Experiments were performed using a dual-trap OT instrument coupled with a five-laminar flow channel microfluidic system (Lumicks, M-Trap, Amsterdam, the Netherlands). The assembly protocol starts with two streptavidin-coated polystyrene beads that are captured in the “beads channel” with the optical traps, and a biotinylated λ-DNA is then attached between two microbeads in the “tether channel”; once the assembly is formed, it is important to ensure that only a single DNA was present between two beads because multiple DNAs influence force changes which will mislead measurements. Fig. S6(c and d)† demonstrate force–extension curves for multiple tethers and a single tether without any metallization, respectively. During DNA metallization, we focused on the dynamics of metallization for a single molecule, so the existence of a single tether is confirmed by comparing with the worm-like chain (WLC) model. To obtain the force–time curve of kinetics of a single DNA metallization, the applied force (the distance between the beads was adjusted and kept constant) was adjusted before proceeding to metallize DNA. Subsequently, the molecule was brought to the “AgNO3 channel”. When the change in force is stable, the whole assembly is finally moved to the “hydroquinone channel” until the change in force is stable again (a schematic diagram of the OT experiment is shown in Fig. S6(a)†). To alleviate hydrodynamic perturbations on DNA, flow was halted during the force measurement.Atomic force microscopy imaging
Morphologies of the DNA–Ag+ and the DNA-AgNPs were collected using an atomic force microscope (AFM, Horiba, Japan), operated in tapping mode. Typical scan speeds were around 0.5 μm s−1. Scanning resolution was 256 pixels per line for all images.To enhance the adsorption of DNA, silicon substrates were cleaned and treated using APTES solution before depositing DNA. The silicon substrates were first treated using a plasma cleaner (100 W, 5 min, O2) to make the silicon extremely hydrophilic. Those silicon substrates were then modified in 100 μL of 0.001% (v/v, ethanol) APTES solution for 10 min, washed several times with 20 mL of ethanol to remove all APTES residues and to get a uniform distribution of reactive amino groups, which enhances the interaction with DNA. Afterwards, they were dried with nitrogen gas and were placed in a drying oven for 45 minutes at 120 °C. Fig. S5† shows the procedure of the AFM sample preparation.
Before sample deposition, the λ-DNA was loaded with silver ions using 0.05 mM AgNO3 basic aqueous solution for 10 and 20 minutes. The Ag+–DNA complex was reduced with 0.002 mM hydroquinone solution for 10 min to form small metallic silver aggregates that were bound to the DNA skeleton. The environment should be dark during sample preparation. For each sample deposition, approximately 6 μl of the final solution was then dropped onto the silicon surface for 3 min. The surface was then cleaned 3 times with 20 μL of distilled water, followed by the removal of any excess solution using filter paper and dried under a gentle nitrogen gas flow before being subjected to AFM.
TEM and negative staining
Samples were adsorbed on plasma-cleaned pure carbon 300 mesh copper grids and stained with a solution of uranyl acetate (1% in distilled water) for 60 s. The grids were then analysed in bright field using a JEOL JEM-1011 (JEOL, Japan) transmission electron microscope equipped with a thermionic source (W filament) operating at an acceleration voltage of 100 kV and with an EMSIS Tolara charge-coupled device (CCD) camera (6 megapixel).Coarse-grained simulations
DNA is modelled as an almost inextensible polymer chain of N beads of mass m and position ri. We used a worm-like chain (WLC) model and the potential energy describing the system is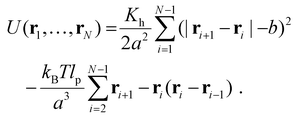 | (3) |
 , where ni+1 is the unit vector from bead i and i + 1.51 However, since our polymer is almost inextensible, we use eqn (3) that is computationally less expensive. The model is solved with an in house code already employed in ref. 52.
, where ni+1 is the unit vector from bead i and i + 1.51 However, since our polymer is almost inextensible, we use eqn (3) that is computationally less expensive. The model is solved with an in house code already employed in ref. 52.
Data availability
Data for this article, including AFM maps, force spectroscopy data, and Raman spectroscopy data are available at Zenodo at https://doi.org/10.5281/zenodo.14955427.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for continued financial support from the National Key Research and Development Project of China (No. 2023YFF0613603), the National Natural Science Foundation of China (No. 22202167), the Provincial Science and Technology Plan Project: Micro and Nano Preparation and Photoelectronic Detection (No. 03014/226063). G. A. and D. G. thank the European Union Program HORIZON-Pathfinder-Open: 3D-BRICKS, Grant Agreement 101099125. D. G. and R. K. acknowledge funding from the European Union under the Horizon 2020 Program, FETOpen: DNA-FAIRYLIGHTS, Grant Agreement 964995.References
- K. C. Kao, W. Hwang and S. Choi, Phys. Today, 1983, 36, 90 CrossRef.
- N. Fardian-Melamed, L. Katrivas, G. Eidelshtein, D. Rotem, A. Kotlyar and D. Porath, Nano Lett., 2020, 20, 4505–4511 CrossRef CAS PubMed.
- J. T. Petty, J. Zheng, N. V. Hud and R. M. Dickson, J. Am. Chem. Soc., 2004, 126, 5207–5212 CrossRef CAS PubMed.
- Z. V. Reveguk, E. V. Khoroshilov, A. V. Sharkov, V. A. Pomogaev, A. A. Buglak and A. I. Kononov, J. Phys. Chem. B, 2024, 128, 4377–4384 CrossRef CAS PubMed.
- Z. Reveguk, R. Lysenko, R. Ramazanov and A. Kononov, Phys. Chem. Chem. Phys., 2018, 20, 28205–28210 RSC.
- A. Gonzàlez-Rosell, C. Cerretani, P. Mastracco, T. Vosch and S. M. Copp, Nanoscale Adv., 2021, 3, 1230–1260 RSC.
- R. R. Ramazanov, T. S. Sych, Z. V. Reveguk, D. A. Maksimov, A. A. Vdovichev and A. I. Kononov, J. Phys. Chem. Lett., 2016, 7, 3560–3566 CrossRef CAS PubMed.
- J. Lee, P. Lee, H. Lee, D. Lee, S. S. Lee and S. H. Ko, Nanoscale, 2012, 4, 6408–6414 RSC.
- P. Peng, W. Guo, Y. Zhu, L. Liu, G. Zou and Y. N. Zhou, Nano-Micro Lett., 2017, 9, 26 CrossRef PubMed.
- P. Zhang, Q. Sui, Z. Liu, C. Hu, C. Li, X. Guo, J. Wang and G. Cai, Chem. Eng. J., 2024, 498, 155277 CrossRef CAS.
- M. Kang, H. Lee, S. Hong and J. Choi, Extreme Mech. Lett., 2023, 63, 102059 CrossRef.
- X. Jin, S. Kannappan, N. D. Hapsari, Y. Jin, K. K. Kim, J. H. Lee and K. Jo, Small Struct., 2023, 4, 2200361 CrossRef CAS.
- Z. Chen, Y. Lin, C. Zhao, J. Ren and X. Qu, Chem. Commun., 2012, 48, 11428–11430 RSC.
- K. Zhao, Q. Chang, X. Chen, B. Zhang and J. Liu, Mater. Sci. Eng., C, 2009, 29, 1191–1195 CrossRef CAS.
- H.-C. Hsu, M.-C. Ho, K.-H. Wang, Y.-F. Hsu and C.-W. Chang, New J. Chem., 2015, 39, 2140–2145 RSC.
- L. Wu, J. Wang, J. Ren and X. Qu, Adv. Funct. Mater., 2014, 24, 2727–2733 CrossRef CAS.
- J. Lu, L. Yang, A. Xie and Y. Shen, Biophys. Chem., 2009, 145, 91–97 CrossRef CAS PubMed.
- Q. Zhang, D. Jiang, C. Xu, Y. Ge, X. Liu, Q. Wei, L. Huang, X. Ren, C. Wang and Y. Wang, Sens. Actuators, B, 2020, 320, 128325 CrossRef CAS.
- R. Mahato, Sk. Masiul Islam and S. Singh, Mater. Today Commun., 2024, 40, 110056 CrossRef CAS.
- Q. Che, Q. Zhao, M. Hu, R. Qin, G. Shan and J. Yang, ACS Appl. Nano Mater., 2021, 4, 12726–12736 CrossRef CAS.
- E. Braun, Y. Eichen, U. Sivan and G. Ben-Yoseph, Nature, 1998, 391, 775–778 CrossRef CAS PubMed.
- Z. Chen, L. Zhou, A. Zhao, Z. Zhang, Z. Wang, Y. Lin, J. Ren and X. Qu, Biosens. Bioelectron., 2014, 58, 214–218 CrossRef CAS PubMed.
- S. Rao, S. Raj, S. Balint, C. B. Fons, S. Campoy, M. Llagostera and D. Petrov, Appl. Phys. Lett., 2010, 96, 213701 CrossRef.
- A. Woo, K. Lim, B. H. Cho, H. S. Jung and M.-Y. Lee, Anal. Sci. Adv., 2021, 2, 397–407 CrossRef CAS PubMed.
- M. Dadmehr, M. Hosseini, S. Hosseinkhani, M. Reza Ganjali and R. Sheikhnejad, Biosens. Bioelectron., 2015, 73, 108–113 CrossRef CAS PubMed.
- D. E. DiRico, P. B. Keller and K. A. Hartman, Nucleic Acids Res., 1985, 13, 251–260 CrossRef CAS PubMed.
- R. M. Izatt, J. J. Christensen and J. H. Rytting, Chem. Rev., 1971, 71, 439–481 CrossRef CAS PubMed.
- J. Kondo, Y. Tada, T. Dairaku, H. Saneyoshi, I. Okamoto, Y. Tanaka and A. Ono, Angew. Chem., Int. Ed., 2015, 54, 13323–13326 CrossRef CAS PubMed.
- T. Dairaku, K. Furuita, H. Sato, J. Šebera, K. Nakashima, J. Kondo, D. Yamanaka, Y. Kondo, I. Okamoto, A. Ono, V. Sychrovský, C. Kojima and Y. Tanaka, Chem. – Eur. J., 2016, 22, 13028–13031 CrossRef CAS PubMed.
- X. Xing, Y. Feng, Z. Yu, K. Hidaka, F. Liu, A. Ono, H. Sugiyama and M. Endo, Chem. – Eur. J., 2019, 25, 1446–1450 CrossRef CAS PubMed.
- J. Kondo, Y. Tada, T. Dairaku, Y. Hattori, H. Saneyoshi, A. Ono and Y. Tanaka, Nat. Chem., 2017, 9, 956–960 CrossRef CAS PubMed.
- U. Javornik, A. Pérez-Romero, C. López-Chamorro, R. M. Smith, J. A. Dobado, O. Palacios, M. K. Bera, M. Nyman, J. Plavec and M. A. Galindo, Nat. Commun., 2024, 15, 7763 CrossRef CAS PubMed.
- A. A. Zinchenko, D. Baigl, N. Chen, O. Pyshkina, K. Endo, V. G. Sergeyev and K. Yoshikawa, Biomacromolecules, 2008, 9, 1981–1987 CrossRef CAS PubMed.
- Z.-Y. Yang, W.-Y. Jiang and S.-Y. Ran, Phys. Chem. Chem. Phys., 2023, 25, 23197–23206 RSC.
- A. Singh and N. Singh, Phys. A, 2013, 392, 2052–2059 CrossRef CAS.
- A. Singh, T. Modi and N. Singh, Phys. Rev. E, 2016, 94, 032410 CrossRef PubMed.
- E. Poppleton, R. Romero, A. Mallya, L. Rovigatti and P. Šulc, Nucleic Acids Res., 2021, 49, W491–W498 CrossRef CAS PubMed.
- G. E. Arnold and R. L. Ornstein, Biophys. J., 1997, 73, 1147–1159 CrossRef CAS PubMed.
- D. A. Maksimov, V. A. Pomogaev and A. I. Kononov, Chem. Phys. Lett., 2017, 673, 11–18 CrossRef CAS.
- M. Fortino, T. Marino, N. Russo and E. Sicilia, Phys. Chem. Chem. Phys., 2016, 18, 8428–8436 RSC.
- A. Ono, S. Cao, H. Togashi, M. Tashiro, T. Fujimoto, T. Machinami, S. Oda, Y. Miyake, I. Okamoto and Y. Tanaka, Chem. Commun., 2008, 4825–4827 RSC.
- H. Mei, I. Röhl and F. Seela, J. Org. Chem., 2013, 78, 9457–9463 CrossRef CAS PubMed.
- N. Lefringhausen, C. Erbacher, M. Elinkmann, U. Karst and J. Müller, Bioconjugate Chem., 2024, 35, 99–106 CrossRef CAS PubMed.
- I. L. Volkov, A. Smirnova, A. A. Makarova, Z. V. Reveguk, R. R. Ramazanov, D. Y. Usachov, V. K. Adamchuk and A. I. Kononov, J. Phys. Chem. B, 2017, 121, 2400–2406 CrossRef CAS PubMed.
- J. Zhang, Y. Ma, S. Stachura and H. He, Langmuir, 2005, 21, 4180–4184 CrossRef CAS PubMed.
- S. H. Park, M. W. Prior, T. H. LaBean and G. Finkelstein, Appl. Phys. Lett., 2006, 89, 033901 CrossRef.
- A. Raudsepp, M. A. K. Williams and G. B. Jameson, Biophys. Rep., 2022, 2, 100045 CAS.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Biophys. J., 1997, 72, 1335–1346 CrossRef CAS PubMed.
- M. Doi and H. See, in Introduction to Polymer Physics, ed. M. Doi and H. See, Oxford University Press, 1995 Search PubMed.
- W.-Y. Jiang and S.-Y. Ran, J. Chem. Phys., 2018, 148, 205102 CrossRef PubMed.
- P. S. Doyle and P. T. Underhill, in Handbook of Materials Modeling: Methods, ed. S. Yip, Springer Netherlands, Dordrecht, 2005, pp. 2619–2630 Search PubMed.
- S. Zeng, M. Chinappi, F. Cecconi, T. Odijk and Z. Zhang, Nanoscale, 2022, 14, 12038–12047 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00934k |
| This journal is © The Royal Society of Chemistry 2025 |



